1 Introduction and background

Metamaterials open the door to materials with unprecedented and flexible refractive indices that can be applied to pathbreaking optical elements for the discovery and observation of novel physical phenomena. Recent advances in terahertz science [1] have rapidly increased the demand for optical elements with highly expanded functions [2–7] and extremely high performance [8, 9] for the manipulation of terahertz waves. However, naturally occurring materials have extremely limited usability in the terahertz waveband, and it is not straightforward to freely design a material with an arbitrary refractive index by conventional design guidelines. Metamaterials can provide an artificial material with an unprecedented refractive index by subwavelength structures which are arrayed in a manner similar to that of atoms or molecules. The design guidelines of metamaterials can shed light on optical elements that dramatically exceed conventional limitations and provide extraordinary high-performance metadevices with on-demand electromagnetic properties [10].

High refractive indices [11, 12] and negative indices [13–16] have recently been reported as metamaterials performing beyond conventional limitations in the terahertz waveband. A large negative permittivity in a cut-through metal slit below a cutoff frequency can be applied to an extreme-sensitivity terahertz polarizer for a high extinction ratio and high transmission power [8, 9]. Zero-index metamaterials [17–21] can be a source of novel physical phenomena such as infinite phase velocities and infinite wavelengths. A zero-index metamaterial has been reported in the optical region, and it can offer a way forward for outstanding applications that explore the fundamentals of quantum science [17]. In addition, sophisticated terahertz elements would contribute considerably to the detection of single photons in the terahertz region [22] and make quantum information and communication possible at low frequencies [23]. Terahertz zero-index materials commonly need three-dimensional complicated designs with meta-atoms [24, 25] since metals behave as nearly perfect conductors in the terahertz waveband but as dielectrics in the optical region. Numerous measurements of ENZ structures and ENZ applications in the terahertz waveband have been reported by different research groups [26–32]. Terahertz ENZ structures, analogous to zero-index metamaterials, can be achieved by a fast wave effect in a cut-through metal slit at higher frequencies than a cutoff frequency. The work in [26] achieved measuring a two-dimensional terahertz concave lens by utilizing terahertz time-domain spectroscopy in 2010; five decades after that, the work in [33] measured an ENZ antenna in the low microwave band with a centimeter wavelength for the first time. The works in [30, 31] reported measurements of a three-dimensional concave lens at 144 GHz of the submillimeter wave band in 2014 and 2015, respectively. However, the potential of the ENZ concept has not been fully demonstrated, and design guidelines based on a physical analysis are essential to be able to continue to provide more attractive terahertz applications, such as for waveform re-shaping [34], directive emission [35], narrow-channel tunneling [36–41], and high emission enhancement [42]. Optical nanocircuits consisting of metamaterials with a range of refractive indices have been reported as metamaterial-inspired nanoelectronics (metactronics) in the optical region [43]. ENZ structures are in demand for the design of the circuits and for applying the ENZ concept to terahertz circuits which would open the door to pioneering research areas in the terahertz waveband.

Here, inspired by the ENZ concept, we demonstrate the design guideline of a terahertz ENZ cut-through metal-slit array antenna to signify the potential of the ENZ structure for three-dimensional applications. A three-dimensional terahertz ENZ antenna at 0.5 THz is fabricated by hollowing a metal-slit array into a concave lens shape. The focusing effect of a terahertz wave was observed by a terahertz imager and reported in 2014 [44]. A mode-matching method [8, 9, 45, 46] can quickly and with high precision analyze the transmission characteristics of a transverse electric (TE) mode in an ENZ structure composed of a cut-through metal-slit array. The mode-matching method has recently shown the propagation characteristics of a transverse magnetic (TM) mode for the design of an extreme-sensitivity terahertz polarizer [8, 9]. Simulation by conventional electromagnetic field simulators is cumbersome for the iterative design owing to the time-consuming analysis. Further, the ENZ antenna can be carefully designed to avoid influence from the Wood’s anomaly [47].

2 Antenna structure

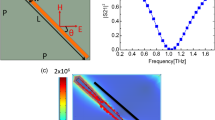
Figure 1 shows a terahertz ENZ cut-through metal-slit array antenna composed of three-dimensional concave metal plates. The structure is hollow and does not suffer from dielectric loss. The fast wave effect of a TE mode in the metal slits produces the ENZ performance. A TE mode is excited in the metal slit for an incident electromagnetic wave with an electric field vector horizontal to the metal slit. The phase velocity ν of an excited TE1 mode in the metal slit is expressed as

$$ v = {c \mathord{\left/ {\vphantom {c {\sqrt {1 - \left( {{c \mathord{\left/ {\vphantom {c {2fs}}} \right. \kern-0pt} {2fs}}} \right)^{2} } }}} \right. \kern-0pt} {\sqrt {1 - \left( {{c \mathord{\left/ {\vphantom {c {2fs}}} \right. \kern-0pt} {2fs}}} \right)^{2} } }} ,$$
(1)

where c is the velocity of light in vacuum, f is the design frequency, and s is the spacing of the metal slits. The effective relative permittivity ε r in the metal slits is expressed as the square of the ratio of c to ν, as follows:

$$\varepsilon_{r} = 1 - \left( {c/2fs} \right)^{2} .$$
(2)
Fig. 1
figure 1

a View of the three-dimensional cut-through metal-slit array antenna with an epsilon near zero. b side view of a cut-through metal slit with a hyperboloid configuration

Full size image

The effective relative permittivity ε r approaches 0 with a narrower slit spacing s, and the ε r approaches 1 for a wider spacing. For a constant slit spacing s, the ε r approaches 0 as the design frequency approaches a cutoff frequency, and the ε r approaches 1 as the design frequency increases above a cutoff frequency. The metal plates are hollow with a hyperboloid configuration to suppress aberration at a focal point. A fast wave effect in the metal-slit array with the hyperboloid configuration produces a phase difference in the electromagnetic waves and a focusing effect.

3 Analysis by the mode-matching method

Figure 2 shows a unit design model for the mode-matching method. This method can analyze a cut-through metal-slit array that is not hollowed into a concave shape to be able to derive transmission characteristics for the design of the antenna. The transmission characteristics of a TE mode can quickly and with high precision be analyzed by the mode-matching method. This analysis enables an iterative design procedure, which is not straightforward for conventional electromagnetic field simulators. The cut-through metal slit is sufficiently large for the wavelength, and the structure is assumed to be infinitely periodic along the x-axis and infinite along the y-axis. Only one period structure of a two-dimensional cut-through metal slit is extracted from a cut-through metal-slit array using periodic boundary walls. The mode-matching method analyzes a step structure #1 with periodic boundary walls and perfect electric conductor walls and a step structure #2 with perfect electric conductor walls and periodic boundary walls. The characteristics of transmission and reflection in the cut-through metal slit can be calculated from the scattering matrix K of the full structure. An incident TE mode wave propagates from the side of the perfect electric conductor walls to that of the periodic boundary walls with a horizontal electrical field to the metal slit. The incident wave E i , the reflected wave E r , and the transmitted wave E t are expressed as

$${\mathbf{E}}_{i} = \hat{y}\sin \left\{ {\left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)\left( {x - {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0pt} 2}} \right)} \right\}\exp ( - j\sqrt {k_{0}^{2} - ({\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s})^{2} } z) ,$$
(3)
$${\mathbf{E}}_{r} = \hat{y}\sum\limits_{m = 1}^{\infty } {A_{m} I_{m} \exp ( + j\sqrt {k_{0}^{2} - \left( {{{m\pi } \mathord{\left/ {\vphantom {{m\pi } s}} \right. \kern-0pt} s}} \right)^{2} } z)} ,$$
(4)
$$\begin{aligned} {\mathbf{E}}_{t} = \hat{y}\sum\limits_{n = 1}^{\infty } {B_{n} I_{n} \exp \left\{ { - j\sqrt {k_{0}^{2} - \left( {{{2n\pi } \mathord{\left/ {\vphantom {{2n\pi } p}} \right. \kern-0pt} p}} \right)^{2} } z} \right\}} \\ +\,\hat{y}\sum\limits_{l = 0}^{\infty } {C_{l} I_{l} \exp \left\{ { - j\sqrt {k_{0}^{2} - \left( {{{2l\pi } \mathord{\left/ {\vphantom {{2l\pi } p}} \right. \kern-0pt} p}} \right)^{2} } z} \right\}} \\ \end{aligned} ,$$
(5)

where I m , I n , and I l are the excitation coefficients, and I m  = sin{mπ/s(x−t/2)}, I n  = sin(2nπx/p), and I l  = cos(2 lπx/p) are the basis functions. The boundary conditions of an electric field E and a magnetic field H are weighted by the basis function and integrated along the boundary surface to obtain the following determinant (6):

$$\left[ {\begin{array}{*{20}c} {Y_{pm} } & {Y_{pn} } & {Y_{pl} } \\ {Y_{qm} } & {Y_{qn} } & {Y_{ql} } \\ {Y_{rm} } & {Y_{rn} } & {Y_{rl} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {A_{m} } \hfill \\ {B_{n} } \hfill \\ {C_{l} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {Z_{p} } \hfill \\ {Z_{q} } \hfill \\ {Z_{r} } \hfill \\ \end{array} } \right] .$$
(6)
Fig. 2
figure 2

Design model for a cut-through metal slit with an epsilon-near-zero structure by the mode-matching method

Full size image

The excitation coefficients A m , B n , and C l can be obtained by solving Eq. (6). Next, the excitation coefficients D s , E t , and F u for the incident wave of a TEM mode from the side of the periodic boundary walls to that of perfect electric conductor walls can be obtained in the same manner using the mode-matching method. The entire electromagnetic field in the step structure can be determined by each excitation coefficient. The scattering matrix S [48] of step structures #1 and #2 can be obtained from the following equation:

$$ \left[ {\begin{array}{*{20}c} {S_{11} } {S_{12}} \\ {S_{21} } {S_{22}} \\ \end{array} } \right] = \left[ {\begin{array}{cc} {A_{m = 1} } & {\sqrt {{s \mathord{\left/ {\vphantom {s {2p}}} \right. \kern-0pt} {2p}}} \sqrt {\sqrt {k_{0}^{2} - \left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)^{2} } /k_{0} } \,F_{\mu = 1} \,} \hfill \\ {\sqrt {{{2p} \mathord{\left/ {\vphantom {{2p} s}} \right. \kern-0pt} s}} \sqrt {k_{0} /\sqrt {k_{0}^{2} - \left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)^{2} } } C_{l = 1} } & {E_{t = 1} } \hfill \\ \end{array} } \right] . $$
(7)

The scattering matrix K of the full structure can be obtained by connecting each scattering matrix S of step structures #1 and #2 with a distance l; the scattering coefficients K 11, K 12, K 21, and K 22 are given as follows:

$$K_{11} = E_{t = 1} + \frac{{A_{m = 1} C_{l = 1} F_{\mu = 1} e^{ - jkl} }}{{e^{ + jkl} - A_{m = 1}^{2} e^{ - jkl} }} ,$$
(8)
$$\begin{aligned} K_{12} = \left( {C_{l = 1} F_{u = 1} - A_{m = 1} E_{t = 1} } \right)e^{ - jkl} \\ + \frac{{\left( {A_{{_{m = 1} }}^{2} C_{l = 1} F_{u = 1} - A_{{_{m = 1} }}^{3} E_{t = 1} } \right)e^{ - j2kl} +\,A_{m = 1} E_{t = 1} }}{{e^{ + jkl} - A_{{_{m = 1} }}^{2} e^{ - jkl} }} \\ \end{aligned},$$
(9)
$$K_{21} = {{C_{l = 1} F_{\mu = 1} } \mathord{\left/ {\vphantom {{C_{l = 1} F_{\mu = 1} } {(e^{ + jkl} - A_{m = 1}^{2} e^{ - jkl} )}}} \right. \kern-0pt} {(e^{ + jkl} - A_{m = 1}^{2} e^{ - jkl} )}},$$
(10)
$$K_{22} = \frac{{A_{m = 1} \left( {C_{l = 1} F_{u = 1} - A_{m = 1} E_{t = 1} } \right)e^{ - jkl} + E_{t = 1} e^{ + jkl} }}{{e^{ + jkl} - A_{{_{m = 1} }}^{2} e^{ - jkl} }},$$
(11)

where \(k = \sqrt {k_{0}^{2} - \left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)^{2} }\). The TE mode transmission power is obtained as follows:

$$T_{TE} = \left| {K_{21} } \right|^{2} \cdot \exp \left( { - 2\alpha_{c} \cdot l} \right).$$
(12)

The loss factor α c of an electric field in a metal [49] can be expressed as

$$\alpha_{c} \, = \,\frac{{2\left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)^{2} \sqrt {{{\omega_{0} \mu } \mathord{\left/ {\vphantom {{\omega_{0} \mu } {2\sigma }}} \right. \kern-0pt} {2\sigma }}} }}{{k_{0} \eta_{0} s\sqrt {k_{0}^{2} - \left( {{\pi \mathord{\left/ {\vphantom {\pi s}} \right. \kern-0pt} s}} \right)^{2} } }},$$
(13)

where ω 0 is the angular frequency, μ is the permeability of the metal, σ is the conductivity of the metal, and η 0 is the wave impedance in free space.

4 Antenna design

The mode-matching method analyzes transmission power in a cut-through metal slit and designs a terahertz ENZ structure. Figure 3 shows the counter map of the TE mode transmission power derived from the mode-matching method. The design frequency is 0.5 THz, and the conductivity σ of gold is 4.1 × 107 S/m. Spacing s of the metal slits and periodicity p = s + t are varied, and the length l in the propagation direction is fixed at 4.0 mm. The counter map demonstrates that s should be wider than approximately 350 µm to obtain good transmission characteristics. The effective permittivity ε r in Eq. (2) shows that s should be as small as possible to achieve an ENZ structure. The spacing s is chosen to be 350 μm from considerations of both transmission characteristics and ENZ structure. A cutoff frequency is 0.43 THz in the parameters; higher-order modes are excited above 0.86 THz, and only the dominant mode propagates at a design frequency of 0.5 THz. The Wood’s anomaly occurs at a frequency f = c/p for the cut-through metal slit with a periodicity p = s + t. The thickness t of the metal should be the smallest possible to distance a design frequency from the frequency of the Wood’s anomaly and achieve stable performance of the ENZ. Based on this, a metal thickness t of 20 µm is chosen to accommodate both the Wood’s anomaly and strength maintenance, and the frequency of the Wood’s anomaly is 0.81 THz.

Fig. 3
figure 3

Transmission power distribution of a TE mode at 0.5 THz for the varied spacing of a metal slit s and periodicity p

Full size image

5 Measurements

Table 1 lists the design parameters of a terahertz ENZ cut-through metal-slit array antenna composed from three-dimensional concave metal plates. The design frequency is 0.5 THz, the spacing s is 350 µm, and the thickness t is 20 µm based on the analysis of the cut-through metal-slit array. The length l is tolerant for an average transmission power and is 4.0 mm here. The effective relative permittivity εr of the concave antenna is 0.27 from Eq. (2) at 0.5 THz. The transmission power of 95.6% through the cut-through metal slit is predicted from the counter map shown in Fig. 3. The metal plates composing the concave antenna with a hyperboloid configuration are expressed as follows [33]:

$$(1 - \varepsilon_{\text{r}} )z^{2} - 2fz(1 - \sqrt {\varepsilon_{\text{r}} } ) + x^{2} + y^{2} = 0 ,$$
(14)

where f is the focal length. Figure 4 shows the power distribution at 4.0 mm at 0.5 THz for the varied spacing of a metal slit s and periodicity p by ANSYS HFSS ver. 14.0.1. The designed focal length is 4.0 mm from the interface to a focusing point for all lenses. The other parameters are set at Table 1. A three-dimensional terahertz ENZ cut-through metal-slit array antenna needs both low relative permittivity due to a narrow spacing s and high transmission characteristics. The analysis of a cut-through metal-slit array in Fig. 3 supports the efficient derivation of initial lens parameters. Figure 5 shows the fabricated three-dimensional terahertz ENZ cut-through metal-slit array antenna. The metal plate is fabricated by etching, and the surface of the metal is coated with gold to reduce conductor losses. The thickness of the gold plating is 0.5 µm considering the skin effect of the metal. The structure is hollow to avoid dielectric losses. Figure 6 shows the measurements and simulations of the two-dimensional electric field distributions for 0.5 THz at 2.0, 3.0, 4.0, 5.0, and 6.0 mm from the top of the antenna. Figure 7 shows the two-dimensional electric field distribution at the focal point. The measurements and simulations demonstrate the focusing effect at 4.0 mm from the top of the antenna. The measured electric field distribution is imaged by a CCD camera utilizing the Pockels effect in a ZnTe electro-optic crystal. Variations of the focused image in the measurements occur due to the residual birefringence of the electro-optic crystal. The anisotropy of the effective relative permittivity between x and y directions causes the asymmetry of the simulated electric field distribution. The simulation of the electric field distribution is obtained by the finite element method simulator ANSYS HFSS ver. 14.0.1. A one-quarter model of the full design is analyzed by image theory to reduce the analytical volume [50]. The effective relative permittivity ε r of the terahertz ENZ antenna is derived from the focal length as 0.26 from the measurements and as 0.27 from the simulations. Both ε r values agree well with the calculated value of 0.27 derived from the effective wavelength expressed in Eq. (2), as shown in Fig. 8. The measurements visualize the beam profile of a terahertz wave and demonstrate the operation of the terahertz ENZ cut-through metal-slit array antenna based on the design guideline.

Table 1 Parameters of the cut-through metal-slit array antenna
Full size table
Fig. 4
figure 4

Power distribution at 4.0 mm at 0.5 THz for the varied spacing of a metal slit s and periodicity p

Full size image
Fig. 5
figure 5

a Photograph of the fabricated three-dimensional terahertz ENZ cut-through metal-slit array antenna with a relative permittivity ε r of 0.26. b Photograph of a fabricated cut-through metal slit with a hyperboloid configuration

Full size image
Fig. 6
figure 6

a Measured two-dimensional electric field distributions at 0.5 THz. b HFSS simulations of the two-dimensional electric distributions at 0.5 THz

Full size image
Fig. 7
figure 7

a Measured two-dimensional electric field distribution at 0.5 THz. b HFSS simulation of two-dimensional electric distribution at 0.5 THz at the focal point 4.0 mm from the top of the antenna

Full size image
Fig. 8
figure 8

Frequency characteristics of the effective relative permittivity from measurements, simulations, and calculations from the effective wavelength

Full size image

6 Conclusions

We demonstrate a terahertz ENZ cut-through metal-slit array antenna by visualization of a focusing effect. The mode-matching method derives the parameters of the array antenna with good transmission characteristics at 0.5 THz. A terahertz ENZ antenna with a concave lens shape is designed utilizing the parameters, fabricated, and measured by a terahertz imager. The antenna structure is hollow to avoid dielectric losses, and the concave shape is hyperboloid to suppress aberration. The permittivity obtained from the measurements (0.26) and that obtained from the simulations (0.27) agree well with the theoretical value of 0.27 obtained from the effective wavelength. The terahertz ENZ structure would offer numerous applications such as high-directivity antennas, beam dividers, beam-steering elements, phase-control devices, and novel filters. Further, the synergy of a terahertz ENZ structure and a structure controlling relative permeability would also offer a way ahead for very attractive applications, such as a transparent metamaterial with a refractive index of exactly zero [51].