Robustness for uncertain multi-objective optimization: a survey and analysis of different concepts

Abstract

In this paper, we discuss various concepts of robustness for uncertain multi-objective optimization problems. We extend the concepts of flimsily, highly, and lightly robust efficiency and we collect different versions of minmax robust efficiency and concepts based on set order relations from the literature. Altogether, we compare and analyze ten different concepts and point out their relations to each other. Furthermore, we present reduction results for the class of objective-wise uncertain multi-objective optimization problems.

1 Introduction

There are (at least) two issues that restrict the applicability of optimization methods in practice. First, in nearly all practical applications of mathematical optimization problems, one has to deal with input data which are not known exactly. This may be due to measurement errors, imprecise data, future developments, fluctuations, or disturbances. Second, most real-world optimization problems do not have one clearly specified objective function but depend on different goals due to many decision makers, each of them having different optimization criteria. Both these issues have been extensively researched in the literature: the fields of stochastic and robust optimization deal with uncertain data while the different optimization criteria are analyzed in the field of multi-objective decision making and optimization.

However, developing a robust optimization theory for multi-objective optimization problems has been started only within the last 2 years, although also most multi-objective optimization problems suffer from uncertain data. A prominent example is portfolio optimization in which different criteria have to be met while the development of the portfolio is uncertain. In portfolio optimization, the uncertainty is often taken into account using objective functions such as the expected revenue, the variance, or the risk, i.e., one deals again with a deterministic multi-objective problem. Our point of view differs from this approach: as usually done in single-objective robust optimization, we consider objective functions which depend on the unknown parameters, i.e., uncertain objective functions. In discrete optimization, the extensively researched field of multi-objective shortest paths leads to several important applications and will be used as leading example in our text. In multi-objective shortest paths, usually not all data are known. While the physical length of a path is deterministic and hence known exactly, the travel time is often not known beforehand. Also, the costs may change according to uncertain fuel consumption, uncertain fuel prices, or uncertain tolls. When transporting dangerous goods, the number of exposed population should be minimized but also is not known beforehand. Another example concerns planning of flight routes, where weather conditions and hence the risk and amount of turbulence are uncertain (see Kuhn et al. 2013 for the latter two examples). Other applications can be found in the optimization of public transport, e.g., when looking for a line concept or a timetable, the usual criteria are to minimize the costs and the travel time of the passengers. However, the number of passengers is not known at the time of planning and has to be estimated, while the travel time can only be computed for the case that everything runs smoothly and is uncertain with respect to disruptions or disturbances.

The goal of our paper is to bridge the gap between theory and practice by providing an overview on concepts for multi-objective robust optimization. We present some new concepts and compare them with recent concepts from the literature. We hence made a first step towards the future goal that practitioners can choose from these concepts the one fitting to the respective robust multi-objective application at hand.

Before going into details we provide an overview about existing related work: the field of multi-objective optimization is well studied, we refer to Ehrgott et al. (2010) for an overview about some recent developments in the area. Also in the field of uncertain optimization, various approaches have been presented throughout the literature such as stochastic optimization or robust optimization. Stochastic optimization (see, e.g., Birge and Louveaux 2011) assumes some probabilistic information about the uncertainties. It includes many concepts, e.g., the expected value, chance constraints or risk measures such as the conditional value-at-risk which has also been applied in the multi-objective setting. In contrast, robust optimization does not assume any probabilistic information but only that the uncertain parameters stem from some uncertainty set (we call the realizations of these uncertain parameters scenarios).

Single-objective robust optimization. For single-objective optimization problems, many concepts of robustness, i.e., what is seen as a desired solution to an uncertain optimization problem have been provided. One of the most known ones is the concept of minmax (or strict) robustness, originally introduced by Soyster (1973) and extensively studied by Ben-Tal and Nemirovski (1998, 1999, 2000) and Ben-Tal et al. (2009). Here, a solution is called robust, if it is feasible for the uncertain optimization problem in every scenario and if it minimizes the objective function in the worst case of all scenarios (note that the worst-case scenario is dependent on the chosen solution). Instead of minimizing the absolute value, also other objective functions can be used, e.g. the absolute or relative regret (see, e.g., Kouvelis and Yu 1997). Since a robust solution is required to be feasible for every scenario, these concepts are known as overconservative. Recently, various alternatives have been introduced.

The concept of light robustness, introduced by Fischetti and Monaci (2009) and generalized in Schöbel (2014), is such an alternative for the case that minmax or regret robustness are too restrictive. In this concept only such solutions are considered which are good enough for the most likely (or ‘normal’) scenario. Among these solutions the most reliable one is chosen. Other alternatives include adjustable robustness (see Ben-Tal et al. 2003), soft robustness (see Ben-Tal et al. 2010), or recovery robustness, see, e.g., Liebchen et al. (2009), Erera et al. (2009) and Goerigk and Schöbel (2014). A recent overview on (single-objective) robustness concepts is given in Goerigk and Schöbel (2015).

Robustness for multi-objective optimization. The concepts for single-objective optimization cannot be extended directly to multi-objective optimization problems since for multi-objective functions the definition of a worst-case scenario is not clear as there is no total order on . Therefore, new concepts of robustness are needed for the multi-objective case. A first approach to extending these concepts was provided by Kuroiwa and Lee (2012). Here, the authors replace the objective functions by their respective worst cases over all scenarios and hence obtain a deterministic multi-objective optimization problem whose efficient solutions are called robust. This approach is closely connected to the concept of minmax robustness for single-objective problems. Throughout this paper we will call it point-based minmax robust efficiency. The concept of set-based minmax robust efficiency introduced by Ehrgott et al. (2014) is an extension of the concept of point-based minmax robust efficiency. Here, for a given feasible solution x, the worst case of the objective vector is interpreted as a set, namely the set of efficient solutions to the multi-objective problem of maximizing the objective function over the uncertainty set. This approach was also followed by Avigad and Branke (2008). From the approach in Ehrgott et al. (2014), Bokrantz and Fredriksson (2013) derived another concept of robustness by replacing the set of objective vectors of a feasible solution under all possible scenarios by its convex hull.

Note that also other papers came up with the same concept as presented in Kuroiwa and Lee (2012): Fliege and Werner (2013) used the concept for an application in Portfolio Optimization, Yu and Liu (2013) applied this concept to multi-objective game theory, and Chen et al. (2012) used it in radiation therapy. Doolittle et al. (2012) also extend the concept of minmax robustness to multi-objective optimization problems and end up with the same concept as Kuroiwa and Lee (2012).

Note that dealing with uncertainties in multi-objective optimization problems has also been done earlier, using approaches from other directions. The first idea to deal with uncertainties in multi-objective optimization we are aware of was provided by Deb and Gupta (2006). The authors extend an idea of Branke (1998) to multi-objective optimization and replace the objective functions by their respective means over a given neighborhood. For the resulting deterministic version they look for efficient solutions. In a second approach, the authors add constraints to the problem formulation such that a solution is feasible if the difference between the respective objective functions and their means does not exceed a pre-defined threshold. Extensions of this approach are given by Gunawan and Azarm (2005) and Barrico and Antunes (2006). However, these approaches do not follow the classical concepts of single-objective robust optimization.

Multi-objective interpretation of uncertain single-objective problems. The topic of our paper, namely to treat multi-objective problems with uncertain objective functions, should not be confused with another line of research: one can interpret uncertain single-objective problems as multi-objective problems by assigning one objective function to each scenario transforming a single-objective uncertain problem to a multi-objective deterministic problem. This is also an ongoing line of research, see, e.g. Sayin and Kouvelis (2005), Hites et al. (2006), Perny et al. (2006), Iancu and Trichakis (2014) and Klamroth et al. (2013) and references therein.

Contribution of this paper. The contribution of this paper is twofold: firstly, we give an overview on recently published concepts on robustness for multi-objective optimization problems, analyzing the relation of the various concepts to each other. Secondly, we extend the concepts of flimsily and highly robust efficiency and propose a multi-objective version of light robustness, again pointing out their relations to already existing concepts. For a special class of multi-objective optimization problems we furthermore provide reduction results for all of the concepts.

The remainder of the paper is structured as follows. After fixing the notation in Sect. 2, we introduce and discuss the concepts of flimsily and highly robust efficiency in Sect. 3. Furthermore, we collect different versions of minmax robust efficiency, concepts of efficiency based on set order relations, and finally extend the concept of light robustness to the multi-objective setting.

In Sect. 4 we analyze and compare the various concepts: Sect. 4.1 draws conclusions for the general case while in Sect. 4.2, we consider a special class of uncertain optimization problems. For this class of problems of objective-wise uncertainty, we present reduction results to finite uncertainty sets in Sect. 5. In Sect. 6, we conclude the paper pointing out open questions and interesting areas for future research.

2 Preliminaries

Multi-objective optimization deals with the problem of minimizing a vector-valued objective function over some feasible set:

Definition 1

Given a feasible set ${\mathcal X}\subseteq {\mathbb {R}^n}$ and an objective function , a multi-objective optimization problem is given by

$$\begin{aligned} \begin{array}{lll} MP&{}\quad \mathrm{min} &{}f(x)\\ &{}\quad \mathrm{s.t.}&{}x \in {\mathcal X}\end{array} \end{aligned}$$

To minimize a vector-valued function we need an order relation on . There are different order relations common in multi-objective optimization. Here we use the following.

Notation 2

(Ehrgott 2005) Let . Then we define

$$\begin{aligned} z \leqq w~&:\Leftrightarrow ~w_i\in [z_i,\infty )\quad \text{ for } \text{ all } i=1,\ldots ,k\\ z \preceq w~&:\Leftrightarrow ~w_i\in [z_i,\infty )\quad \text{ for } \text{ all } i=1,\ldots ,k\quad ~\text{ and }\quad ~z\ne w\\ z < w~&:\Leftrightarrow ~w_i\in (z_i,\infty )\quad \text{ for } \text{ all } i=1,\ldots ,k \end{aligned}$$

A feasible solution $x \in {\mathcal X}$ is called efficient, if there does not exist a solution $x'\in {\mathcal X}$ such that $f(x)\preceq f(x')$.

Analogously, a solution is called strictly or weakly efficient, if there does not exist a solution $x'\in {\mathcal X}{\setminus }\{x\}$ such that $f(x)\leqq f(x')$ or $f(x)< f(x')$, respectively.

Denoting the set by , $x \in {\mathcal X}$ is efficient, if and only if there does not exist $x' \in {\mathcal X}$ such that

(1)

For obtaining strictly and weakly efficiency, we have to replace ${\mathbb {R}^k_\succeq }$ by ${\mathbb {R}^k_\geqq }$, or ${\mathbb {R}^k_>}$, respectively (Fig. 1).

In multi-objective optimization one is mainly interested in finding all feasible solutions ${\overline{x}}\in {\mathcal X}$ which are efficient.

To define an uncertain multi-objective optimization problem, we assume that uncertainties in the problem formulation are given as scenarios from a known uncertainty set ${\mathcal U}\subseteq {\mathbb {R}^m}$. Analogous to (single-objective) robust optimization, we hence assume $f:{\mathcal X}\times {\mathcal U}\mapsto {\mathbb {R}^k}$, i.e., the scenarios in ${\mathcal U}$ influence the values of f. Furthermore, we assume that the feasible set ${\mathcal X}$ is not due to uncertainties and remains unchanged in the different scenarios. If this is not the case we simply replace ${\mathcal X}$ by the set of solutions feasible for every scenario as it is also done in single-objective robust optimization. Now, an uncertain multi-objective optimization problem

$$\begin{aligned} {{\mathcal P}({\mathcal U})}=({{\mathcal P}(\xi )},\xi \in {\mathcal U}) \end{aligned}$$

is defined as the family of parametrized problems

$$\begin{aligned} \begin{array}{lll} {{{\mathcal P}(\xi )}}&{} \mathrm{min}&{}f(x,\xi )\\ &{}\mathrm{s.t.}&{}x \in {\mathcal X}, \end{array} \end{aligned}$$

where $f:{\mathcal X}\times {\mathcal U}\mapsto {\mathbb {R}^k}$ and ${\mathcal X}\subseteq {\mathbb {R}^n}$.

As in single-objective robust optimization, it is not at all clear what a “desired” solution to such a family of problems is. In the following section, we introduce several concepts of robustness transforming the uncertain multi-objective optimization problem to a deterministic problem, called its robust counterpart.

Fig. 1

Illustration of the problem in Example 3

3 Robustness concepts for uncertain multi-objective optimization

Let ${{\mathcal P}({\mathcal U})}=({{\mathcal P}(\xi )},\xi \in {\mathcal U})$ be an uncertain multi-objective optimization problem. In this section we present various concepts of robustness for ${{\mathcal P}({\mathcal U})}$. We illustrate these concepts using the following (simple) example for finding a shortest path.

Example 3

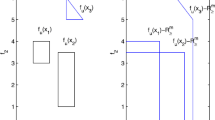
Suppose we want to travel between two specified points A and B. There are three possible paths $x_1$, $x_2$, and $x_3$. We are interested in a short travel time and in low costs. Unfortunately, both, cost and travel time, are not known beforehand. They both depend on the decision, if some festival event takes place or not. We have the following information, see Fig. 1.

• If there is no festival (scenario 1), the traveling time (objective $f_1$) of path $x_1$ which goes straight through the center is the shortest, $x_2$ takes longer, and $x_3$ is the path with longest traveling time. If the festival takes place (scenario 2), all travel times increase. The longest travel time will then be obtained for path $x_1$ (since the center is most crowded), path $x_3$ is slightly better, and path $x_2$ is the fastest option.

• Concerning the costs (objective $f_2$), if there is no festival (scenario 1), the costs of all three paths are similar, path $x_1$ being a bit more expensive than $x_2$ due to the toll restrictions in the center, and $x_3$ the longest and hence most expensive one. These toll restrictions are lifted in case of the festival (scenario 2) to attract many guests, hence the costs are reduced by an amount of 2 for paths $x_1$ and $x_2$, and reduced for path $x_3$ (since it is farthest away from the center) by only 1.5.

This means, the two-dimensional function $f(x,\xi )$ can be summarized in the following table:

Looking only at $\xi _1$ (no festival) we see that path $x_3$ is dominated both by $x_1$ and $x_2$ where the latter are Pareto solutions in this case. If $\xi _2$ takes place, only path $x_2$ is a Pareto solution. We will often illustrate our concepts in objective space as done in Fig. 2 for our example.

Fig. 2

Plot of function f in Example 3

We start with two straightforward ideas which look at each scenario separately.

3.1 Flimsily and highly robust efficiency

Since for any fixed $\xi \in {\mathcal U}$, we obtain a deterministic multi-objective optimization problem ${{\mathcal P}(\xi )}$, a first concept of robustness is to define a feasible solution as robust efficient if it is efficient for at least one scenario.

Definition 4

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a solution ${\overline{x}}\in {\mathcal X}$ is called flimsily robust efficient for ${{\mathcal P}({\mathcal U})}$ if it is efficient for ${{\mathcal P}(\xi )}$ for at least one $\xi \in {\mathcal U}$.

From the definition of flimsily robust efficiency we come directly to the concept of highly robust efficiency, where we call a feasible solution robust efficient, if it is efficient in every scenario.

Definition 5

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a solution ${\overline{x}}\in {\mathcal X}$ is called highly robust efficient for ${{\mathcal P}({\mathcal U})}$ if it is efficient for ${{\mathcal P}(\xi )}$ for all $\xi \in {\mathcal U}$.

Let ${\mathcal X}_{\mathcal E}(\xi )$ be the set of efficient solutions to ${{\mathcal P}(\xi )}$, $\xi \in {\mathcal U}$. Then

$$\begin{aligned} x\text { is highly robust efficient for }{{\mathcal P}({\mathcal U})}\Longleftrightarrow x \in \bigcap _{\xi \in {\mathcal U}} {\mathcal X}_{\mathcal E}(\xi ) \end{aligned}$$

and

$$\begin{aligned} x\text { is flimsily robust efficient for }{{\mathcal P}({\mathcal U})}\Longleftrightarrow x \in \bigcup _{\xi \in {\mathcal U}} {\mathcal X}_{\mathcal E}(\xi ). \end{aligned}$$

As a direct consequence we obtain:

Lemma 6

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem and let x be highly robust efficient for ${{\mathcal P}({\mathcal U})}$. Then x is flimsily robust efficient for ${{\mathcal P}({\mathcal U})}$.

Example 7

Consider the path problem from Example 3. As we already noted, $x_2$ is efficient in both scenarios, $x_1$ is efficient in $\xi _1$ and $x_3$ never is efficient. This means that $x_2$ is highly robust efficient, $x_1$ and $x_2$ are both flimsily robust efficient, and $x_3$ is none of both. This supports our intuition that we should never choose path $x_3$. Flimsily robust efficiency leaves us the choice between both paths $x_1$ and $x_2$ while highly robust efficiency decides for path $x_2$.

We now analyze two special cases, namely the deterministic case ($|{\mathcal U}|=1$) and the single-objective case ($k=1$).

Remark 8

(Special cases of highly robust efficiency)

• 1. For $|{\mathcal U}|=1$, highly robust efficiency, flimsily robust efficiency and (deterministic) efficiency are all equivalent. The highly (flimsily) robust counterpart of ${{\mathcal P}({\mathcal U})}$ hence is just the given deterministic multi-objective optimization problem itself.

• 2. In the case of only $k=1$ objective function, a solution is highly robust efficient if and only if it is optimal for every scenario $\xi \in {\mathcal U}$.

The second statement of the remark shows that being highly robust efficient is a very strict requirement and much more as is requested in single-objective optimization. We also see that it is not very likely that highly robust efficient solutions to ${{\mathcal P}({\mathcal U})}$ exist. However, there is a class of problems where the existence of such a solution is guaranteed, namely if one of the objectives does not contain any uncertain parameters, and if the minimization of this objective has a unique optimal solution.

Lemma 9

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem. Let $i \in \{1,\ldots ,k\}$ be the index of an objective function which is not uncertain, i.e., for which $f_i(x,\xi )\equiv f_i(x)$ for all $\xi \in {\mathcal U}$ and for all $x\in {\mathcal X}$. Furthermore, assume that $\mathrm{min}\{f_i(x): x \in {\mathcal X}\}$ has a unique optimal solution $x^*$. Then $x^*$ is highly robust efficient for ${{\mathcal P}({\mathcal U})}$.

Proof

As $f_i(x^*,\xi )=f_i(x^*) < f_i(x)=f_i(x,\xi )$ for all $x \in {\mathcal X}$ and all $\xi \in {\mathcal U}$ we have that no $y \in {\mathcal X}$ dominates $x^*$ in any scenario $\xi \in {\mathcal U}$. Hence, $x^* \in {\mathcal X}_{\mathcal E}(\xi )$ for all $\xi \in {\mathcal U}$ and consequently $x^*$ is highly robust efficient.

Note that the existence of an objective function which does not contain any uncertainty is not unrealistic in practice. For example, if a traveler wants to minimize the length (in kilometers) and the travel time (in minutes) of his trip, the length is exactly known while the travel time may depend, e.g., on traffic and weather conditions. Similar examples may be found if the cost objective is known but the income may depend on the uncertain demand. A detailed analysis of this situation for bi-objective uncertain problems and more applications can be found in Kuhn et al. (2013).

In the special case of Lemma 9, at least one highly robust efficient solution exists. However, having many highly robust efficient solutions to choose from is not very likely in practice. On the other hand, we may expect a large number of flimsily robust efficient solutions. The next question hence is if highly and flimsily robust efficient solutions are what we would like to have in practical applications, in particular,

• if a planner considers every highly robust efficient solution as desirable,

• and if all solutions, a planner would like to have, are at least flimsily robust efficient?

Both questions are in general not true as the following two examples show:

Example 10

We now consider only two paths, x and y, and again two scenarios. Path x through the city center is drastically shorter than path y in the general scenario. In case of scenario 2, both paths get approximately the same length with x being a bit longer than y. In the normal scenario, both paths cost approximately the same, path y being slightly cheaper than path x. In case of the event, some toll guidance system is in action which makes path x a bit cheaper, but path y extremely unattractive. The objective values

are depicted on the left-hand side of Fig. 3. Intuitively, one would prefer solution x over y, but both solutions are highly robust efficient.

On the right-hand side, we consider three paths x, y, and z, again for two different scenarios with the following objective values:

We see that in scenario 1, y is a bit better than x in both objective functions and x, in turn, clearly dominates z, hence we have a total order of the three paths in scenario 1. In scenario 2, the situation changes: now z is clearly the best solution, followed closely by y while x is the worst. From a practical point of view x might be considered as best choice since it is rather good for both scenarios, while y and z can both be really bad . However, x is not flimsily robust efficient while y and z are.

Fig. 3

Left not every highly robust efficient solution is desirable. Right a solution which may be considered best which is not even flimsily robust efficient

3.2 Minmax robust efficiency

One of the first and most important concepts of robustness for uncertain single-objective optimization is the concept of minmax robust optimality, originally introduced by Soyster (1973) and extensively studied in Ben-Tal and Nemirovski (1998).

Definition 11

(Minmax robust optimality for single-objective problems, Ben-Tal et al. 2009) Given an uncertain single-objective optimization problem ${{\mathcal P}({\mathcal U})}$ (i.e., with $k=1$ objective function), a solution $x\in {\mathcal X}$ is called a minmax robust optimal solution to ${{\mathcal P}({\mathcal U})}$ if it is an optimal solution to

$$\begin{aligned} \begin{array}{lll} \mathrm{min}&{}\underset{\xi \in {\mathcal U}}{\sup }&{}f(x,\xi )\\ \mathrm{s.t.}&{}x\in {\mathcal X}.&{} \end{array} \end{aligned}$$

This means, the worst case of the objective function under all possible scenarios is minimized.

For a vector-valued function f, the definition of the worst case is not as clear as in single-objective optimization, thus an extension of minmax robustness to multi-objective optimization problems is not uniquely defined.

There are three extensions of this concept for single-objective robust optimization to multi-objective robust optimization we are aware of. In the most general one, Ehrgott et al. (2014) generalize the definition of efficiency given in (1) by replacing the single points $f(x) \in {\mathbb {R}^k}$ in (1) by the sets

$$\begin{aligned} {f_{\mathcal U}}(x)=\{f(x,\xi ):\xi \in {\mathcal U}\} \end{aligned}$$

of all possible objective values under all scenarios:

Definition 12

(Set-based minmax robust efficiency, Ehrgott et al. 2014) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution ${\overline{x}}\in {\mathcal X}$ is called set-based minmax robust efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x')\subseteq {f_{\mathcal U}}({\overline{x}})-{\mathbb {R}^k_\succeq }. \end{aligned}$$

Note that Ehrgott et al. (2014) not only introduces set-based minmax robust efficiency but also set-based minmax robust strict efficiency, and set-based minmax robust weak efficiency by replacing ${\mathbb {R}^k_\succeq }$ by ${\mathbb {R}^k_\geqq }$, or ${\mathbb {R}^k_>}$, respectively. However, in this paper we concentrate on the concept of set-based minmax robust efficiency. Nevertheless, a short summary on results for the analogous concepts of robust strict and weak efficiency will be given in Sect. 4.3.

Example 13

Let ${\mathcal X}$, ${\mathcal U}$ and f be given as in Example 3. To understand the concept of set-based minmax robust efficiency, we depict the borders of the respective sets ${f_{\mathcal U}}(x_1)-\mathbb {R}^2_\succeq$ (dashed), ${f_{\mathcal U}}(x_2)-\mathbb {R}^2_\succeq$ (dotted), and ${f_{\mathcal U}}(x_3)-\mathbb {R}^2_\succeq$ (solid) in Fig. 4.

As we can see, ${f_{\mathcal U}}(x_1)-\mathbb {R}^2_\succeq$ does not contain ${f_{\mathcal U}}(x_2)$ nor ${f_{\mathcal U}}(x_3)$. Therefore, $x_1$ is set-based minmax robust efficient. ${f_{\mathcal U}}(x_2)-\mathbb {R}^2_\succeq$ does not contain ${f_{\mathcal U}}(x_1)$ nor ${f_{\mathcal U}}(x_3)$ and is also set-based minmax robust efficient. ${f_{\mathcal U}}(x_3)-\mathbb {R}^2_\succeq$, on the other hand, contains ${f_{\mathcal U}}(x_2)$ and, therefore, is not set-based minmax robust efficient. In this example, set-based minmax robust efficiency hence coincides with flimsily robust efficiency, and it leaves us the choice between the two paths $x_1$ and $x_2$.

Fig. 4

${f_{\mathcal U}}(x_1)-\mathbb {R}^2_\succeq$ (dashed), ${f_{\mathcal U}}(x_2)-\mathbb {R}^2_\succeq$ (dotted), and ${f_{\mathcal U}}(x_3)-\mathbb {R}^2_\succeq$ (solid) for Example 13

In the following example, we show that set-based minmax robust efficiency performs better in the example where we observed that flimsily and highly robust efficiency do not meet our expectations.

Example 14

We continue Example 10 and note that for the case on the left-hand side of Fig. 3, x is the only solution which is set-based minmax efficient, and for the case on the right-hand side, again, x is the only set-based minmax efficient solution. This points to the interpretation that set-based minmax efficiency reflects what a planner might intuitively consider as robust efficient.

For further insight into properties of set-based minmax robust efficiency and approaches for calculating set-based minmax robust efficient solutions, we refer to Ehrgott et al. (2014). Among others, the special cases of set-based minmax efficiency are analyzed there:

Remark 15

(Special cases of set-based minmax robust efficiency, Ehrgott et al. 2014)

• 1. For $|{\mathcal U}|=1$, set-based minmax robust efficiency is equivalent to (deterministic) efficiency. The set-based minmax robust counterpart of ${{\mathcal P}({\mathcal U})}$ hence is the given deterministic multi-objective optimization problem itself.

• 2. In the case of only $k=1$ objective function, a solution is set-based minmax robust efficient if and only if it is minmax robust optimal for the corresponding uncertain (single-objective) problem.

Another extension of minmax robust efficiency to the multi-objective setting has very recently been proposed in Bokrantz and Fredriksson (2013). Based on the concept of set-based minmax robust efficiency the concept of hull-based minmax robust efficiency is defined as follows.

Definition 16

(Hull-based minmax robust efficiency, Bokrantz and Fredriksson 2013) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution ${\overline{x}}\in {\mathcal X}$ is called hull-based minmax robust efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x')\subseteq {{\mathrm{conv\,}}}({f_{\mathcal U}}({\overline{x}}))-{\mathbb {R}^k_\succeq }. \end{aligned}$$

In Bokrantz and Fredriksson (2013), the authors state that any hull-based minmax robust efficient solution is also set-based minmax robust efficient, see Bokrantz and Fredriksson (2013), Proposition 4.2.

Example 17

For our Example 3 we now depict the borders of the sets ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_1))-\mathbb {R}^2_\succeq$ (dashed), ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_2))-\mathbb {R}^2_\succeq$ (dotted), and ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_3))-\mathbb {R}^2_\succeq$ (solid) in Fig. 5.

It turns out that $x_2$ is the only hull-based minmax robust efficient solution since both ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_1))-\mathbb {R}^2_\succeq$ and ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_3))-\mathbb {R}^2_\succeq$ contain ${f_{\mathcal U}}(x_2)$. In contrast to set-based minmax robust efficiency, where dominance between two solutions is defined rather carefully, dominance is more likely in hull-based robust efficiency and hence we obtain less robust efficient solutions to choose from.

Fig. 5

${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_1))-\mathbb {R}^2_\succeq$ (dashed), ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_2))-\mathbb {R}^2_\succeq$ (dotted), and ${{\mathrm{conv\,}}}({f_{\mathcal U}}(x_3))-\mathbb {R}^2_\succeq$ (solid) for Example 17

To conclude this section, we turn our attention to the related concept of point-based minmax robust efficiency by Kuroiwa and Lee (2012). In this concept, the supremum for every objective function is taken separately, yielding a deterministic vector-valued objective function

$$\begin{aligned} {f^{\max }_{\mathcal U}}:= \begin{pmatrix} \underset{\xi \in {\mathcal U}}{\sup }f_1(x,\xi )\\ \underset{\xi \in {\mathcal U}}{\sup }f_2(x,\xi )\\ \vdots \\ \underset{\xi \in {\mathcal U}}{\sup }f_k(x,\xi ) \end{pmatrix}. \end{aligned}$$

The formal definition is as follows.

Definition 18

(Point-based minmax robust efficiency, Kuroiwa and Lee 2012) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution $x\in {\mathcal X}$ is called point-based minmax robust efficient if it is efficient for

$$\begin{aligned} \begin{array}{ll} \mathrm{min}&{}{f^{\max }_{\mathcal U}}\\ \mathrm{s.t.}&{}x\in {\mathcal X}. \end{array} \end{aligned}$$

Note that

$$\begin{aligned} \begin{array}{ll} \mathrm{min}&{}{f^{\max }_{\mathcal U}}\\ \mathrm{s.t.}&{}x\in {\mathcal X}\end{array} \end{aligned}$$

is a deterministic multi-objective optimization problem which can be solved by standard solution techniques for multi-objective problems. For solution techniques to this particular problem structure we refer to Kuroiwa and Lee (2012).

In Ehrgott et al. (2014), Theorem 4.11, the authors point out that every point-based minmax robust strictly efficient solution is also set-based minmax robust strictly efficient. However, this does not hold for the concepts of point-based and set-based minmax robust efficiency (i.e., without strictly). Also, as we can see from solution $x_1$ in Example 13, the reverse conclusion does in general not hold.

Example 19

We use Example 3 and plot ${f^{\max }_{\mathcal U}}$ in Fig. 6

${f^{\max }_{\mathcal U}}(x_2)$ dominates ${f^{\max }_{\mathcal U}}(x_1)$ and ${f^{\max }_{\mathcal U}}(x_3)$; therefore, $x_2$ is point-based minmax robust efficient while $x_3$ and $x_1$ are not. This was to be expected since point-based minmax robust efficiency cannot produce more robust efficient solutions as hull-based robust minmax efficiency.

Fig. 6

Additional plot of ${f^{\max }_{\mathcal U}}$ for Example 3

3.3 Other set-based concepts for uncertain multi-objective optimization

In set-based minmax robust efficiency, the sets

$$\begin{aligned} {f_{\mathcal U}}(x)=\{f(x,\xi ):\xi \in {\mathcal U}\} \end{aligned}$$

for all $x \in {\mathcal X}$ are compared with each other using a certain order relation. More precisely, ${f_{\mathcal U}}(x)$ dominates ${f_{\mathcal U}}(x')$ if

$$\begin{aligned} {f_{\mathcal U}}(x)\subseteq {f_{\mathcal U}}(x')-{\mathbb {R}^k_\succeq }. \end{aligned}$$

In the literature on set-valued optimization, many other order relations for comparing sets can be found. In Ide et al. (2014), Ide and Köbis (2014) these set order relations are used to derive new concepts for uncertain multi-objective optimization problems.

The set order relation used in the concept of set-based minmax robust efficiency is known under the name upper set less order relation, see, e.g., Khan et al. (2014). The counterpart to this order relation is the lower set less order relation, compare again Khan et al. (2014). From this order relation the concept of lower set less ordered efficiency is derived:

Definition 20

(Lower set less ordered efficiency, Ide et al. 2014; Ide and Köbis 2014) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution ${\overline{x}}\in {\mathcal X}$ is called lower set less ordered efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x')+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}). \end{aligned}$$

Example 21

For Example 3, we now depict the borders of the sets ${f_{\mathcal U}}(x_1)+\mathbb {R}^2_\succeq$ (dashed), ${f_{\mathcal U}}(x_2)+\mathbb {R}^2_\succeq$ (dotted), and ${f_{\mathcal U}}(x_3)+\mathbb {R}^2_\succeq$ (solid) in Fig. 7.

$x_1$ and $x_2$ are lower set less ordered efficient while $x_3$ is not since ${f_{\mathcal U}}(x_2)+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}(x_3)$. This is due to the fact that paths $x_1$ and $x_2$ can obtain really good objective values (lowest possible traveling time in case of $x_1$ and lowest possible costs in case of $x_2$). As we can see, lower set less ordered efficiency is a concept that concentrates on optimizing the best cases instead of the worst cases and is, therefore, suitable for a risk affine decision maker who wants to maximize the best possible outcome.

Fig. 7

${f_{\mathcal U}}(x_1)+\mathbb {R}^2_\succeq$ (dashed), ${f_{\mathcal U}}(x_2)+\mathbb {R}^2_\succeq$ (dotted), and ${f_{\mathcal U}}(x_3)+\mathbb {R}^2_\succeq$ (solid) for Example 21

From the concept of lower set less ordered efficiency, two more concepts of robust efficiency can be derived, both based on the respective set order relations, see, e.g., Khan et al. (2014).

Definition 22

(Set less ordered and alternative set less ordered efficiency, Ide et al. 2014; Ide and Köbis 2014) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution ${\overline{x}}\in {\mathcal X}$ is called set less ordered efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x')\subseteq {f_{\mathcal U}}({\overline{x}})-{\mathbb {R}^k_\succeq }\quad \text {~and~}\quad {f_{\mathcal U}}(x')+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}). \end{aligned}$$

A feasible solution ${\overline{x}}\in {\mathcal X}$ is called alternative set less ordered efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x')\subseteq {f_{\mathcal U}}({\overline{x}})-{\mathbb {R}^k_\succeq }\quad \text {~or~}{f_{\mathcal U}}(x')+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}). \end{aligned}$$

While alternative set less ordered efficiency is exactly the intersection of set-based minmax robust efficiency and lower set less ordered efficiency (see Ide and Köbis 2014) and, therefore, optimizes the best and worst cases of a given solution, set less ordered efficiency represents a pre-selection of solutions if it is clear that the extreme cases should be optimized but the decision maker has not decided yet whether to follow a risk averse or risk affine approach.

The last concept of robustness derived from set order relations is the concept of certainly less ordered efficiency, introduced in Ide and Köbis (2014).

Definition 23

(Certainly less ordered efficiency, Ide and Köbis 2014) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$, a feasible solution ${\overline{x}}\in {\mathcal X}$ is called certainly less ordered efficient if there is no $x'\in {\mathcal X}\setminus \left\{ {\overline{x}}\right\}$ such that

$$\begin{aligned} {f^{\max }_{\mathcal U}}(x')\in f_{{\mathcal U}}^{\mathrm{min}} -{\mathbb {R}^k_\succeq }, \end{aligned}$$

where

$$\begin{aligned} f_{{\mathcal U}}^{\max }(x'):= \begin{pmatrix} \underset{\xi \in {\mathcal U}}{\sup }f_1(x',\xi )\\ \vdots \\ \underset{\xi \in {\mathcal U}}{\sup }f_k(x',\xi ) \end{pmatrix}\quad ~~~\text {and}~~~\quad f_{{\mathcal U}}^{\mathrm{min}}(x'):= \begin{pmatrix} \underset{\xi \in {\mathcal U}}{\inf }f_1(x',\xi )\\ \vdots \\ \underset{\xi \in {\mathcal U}}{\inf }f_k(x',\xi ) \end{pmatrix}. \end{aligned}$$

In Ide and Köbis (2014), different relations between these concepts are investigated. Namely, alternative set less ordered efficiency implies both set-based minmax robust and lower set less ordered efficiency and the two latter imply set less ordered efficiency. Set less ordered efficiency on the other hand implies certainly less ordered efficiency (compare Ide and Köbis 2014, Lemmata 21, 28, and 37).

3.4 Lightly robust efficiency

The concept of light robustness for uncertain single-objective optimization problems has been introduced by Fischetti and Monaci (2009) for special classes of uncertain optimization problems and generalized in Schöbel (2014). For the concept of light robustness, a nominal scenario is needed. The nominal scenario is defined as a reference scenario and is frequently used in single-objective robust optimization, e.g., in Ben-Tal and Nemirovski (2000), Bertsimas and Sim (2004) and Ben-Tal et al. (2009), and many other papers. It may be the most likely one, or the most important one, or the undisturbed scenario. Even though the assumption of a nominal scenario may sound contradictory to the idea that robust optimization does not assume any kind of probability distribution of the uncertain parameters, this setting is not unusual. As an example, consider weather conditions. Normally, the weather is neither extremely cold nor extremely hot, but these settings can appear. The nominal scenario here could be the average temperature of the year. Another example is timetabling. In this case the nominal scenario is usually chosen as the scenario in which everything runs smoothly and without any delays. Note that modeling of the nominal scenario is part of modeling of the uncertainty set and can be fixed to whatever seems an important or “normal” scenario.

As already said, a drawback of minmax robustness is its overconservatism. Hedging against all scenarios from the uncertainty set usually comes with a high price, namely the quality in the nominal scenario often drastically decreases. For example, if one wants to hedge against all delays in timetabling, one would need so much buffer that the timetable becomes unattractive to the passengers. These high costs motivate the definition of light robustness, in which a certain nominal quality of the solution is required. For timetabling, this would mean that the timetable should be feasible and not too bad for the nominal scenario (being the one without any delays). In general, a solution is only considered as feasible if its quality is good enough for the nominal scenario. Among all the solutions which satisfy this quality the most reliable one is chosen. Light robustness is usually considered for uncertain optimization problems with deterministic objective and uncertainty in the constraints. Transferring the concept to our case in which we have an uncertain objective and deterministic constraints, we obtain the following definition.

Definition 24

(Light robust optimality for single-objective optimization problems, Schöbel 2014) Given an uncertain single-objective optimization problem ${{\mathcal P}({\mathcal U})}$ (i.e., with $k=1$ objective function), and assume that ${\widehat{x}}$ is an optimal solution to the optimization problem $P(\hat{\xi })$ of the nominal scenario $\hat{\xi }$. Then a solution $x\in {\mathcal X}$ is called a lightly robust optimal solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. a given $\epsilon \ge 0$, if it is an optimal solution to

$$\begin{aligned} \begin{array}{lll} \mathrm{min} &{} \underset{\xi \in {\mathcal U}}{\sup } f(x,\xi )\\ \mathrm{s.t.}&{}f(x,{\widehat{\xi }})\le {\mathop {\min }\limits _{{{\widehat{x}}\in {\mathcal X}}}}~f({\widehat{x}},{\widehat{\xi }})+\epsilon \\ &{} x \in {\mathcal X}\end{array} \end{aligned}$$

The concept of lightly robust efficiency has been already generalized to bi-objective optimization problems with one deterministic objective function in Kuhn et al. (2013). We now extend this concept to general uncertain multi-objective optimization problems.

Given a nominal scenario ${\widehat{\xi }}\in {\mathcal U}$, let ${\mathcal X}_{\mathcal E}({\widehat{\xi }})$ be the set of efficient solutions to ${\mathcal P}({\widehat{\xi }})$.

For each efficient solution ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$ to ${\mathcal P}({\widehat{\xi }})$ and some given $0\preceq \epsilon \in {\mathbb {R}^k}$ we define the uncertain multi-objective optimization problem ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U}):=({{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,\xi ), \xi \in {\mathcal U})$ as the family of parametrized, deterministic multi-objective optimization problems

$$\begin{aligned} \begin{array}{lll} {{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,\xi )&{}\mathrm{min} &{} f(x,\xi )\\ &{}\mathrm{s.t.}&{}f_i({\widehat{x}},{\widehat{\xi }})+\epsilon _i~\forall i\in \{1,\ldots ,k\}\\ &{}&{} x \in {\mathcal X}\end{array} \end{aligned}$$

Definition 25

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$ with nominal scenario ${\widehat{\xi }}\in {\mathcal U}$ and some $\epsilon \in {\mathbb {R}^k_\succeq }$. Then a solution ${\overline{x}}\in {\mathcal X}$ is called lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$ if it is set-based minmax robust efficient for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ for some ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$.

The intuition behind this concept is analogous to the idea of light robustness for uncertain single-objective problems: the objective value should not differ too much from a non-dominated point in the nominal scenario. Therefore, an additional constraint is added to the problem, making sure that the solution chosen is good enough for the nominal case and then one would like to minimize the worst case as done before.

Example 26

To explain the meaning of the concept of lightly robust efficiency we need to increase our example and look at three scenarios ${\mathcal U}:=\{\xi _1,\xi _2,\xi _3\}$, where $\xi _1$ is the nominal scenario, and at four possible paths ${\mathcal X}:=\{x_1,x_2,x_3,x_4\}$. We define $f:{\mathcal X}\times {\mathcal U}\mapsto \mathbb {R}^2$ via the plot in Fig. 8.

In the nominal scenario, $\xi _1$, only $x_1$ is efficient, therefore, for a given $\epsilon \succeq 0$, every lightly robust efficient solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$ is a set-based minmax robust efficient solution to ${{\mathcal L}{\mathcal R}}(x_1,\epsilon ,{\mathcal U})$. We indicate the sets $f_{\mathcal U}(x_1)-\mathbb {R}^2_\succeq$ (solid), $f_{\mathcal U}(x_2)-\mathbb {R}^2_\succeq$ (dotted), $f_{\mathcal U}(x_3)-\mathbb {R}^2_\succeq$ (dashed), and $f_{\mathcal U}(x_4)-\mathbb {R}^2_\succeq$ (dash-dotted) in Fig. 9.

Now, for different choices of $\epsilon$, we obtain different lightly robust efficient solutions: For $\epsilon ^0:=(0,0)$, the only feasible solution to ${{\mathcal L}{\mathcal R}}(x_1,\epsilon ^0,{\mathcal U})$ is $x_1$ itself, therefore, it is the only lightly robust efficient solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. (0, 0).

Fig. 8

Plot of f for Example 26

Fig. 9

$f_{\mathcal U}(x_1)-\mathbb {R}^2_\succeq$ (solid), $f_{\mathcal U}(x_2)-\mathbb {R}^2_\succeq$ (dotted), $f_{\mathcal U}(x_3)-\mathbb {R}^2_\succeq$ (dashed), and $f_{\mathcal U}(x_4)-\mathbb {R}^2_\succeq$ (dash-dotted) for Example 26

Furthermore, for

$$\begin{aligned} \epsilon ^1:=\left( f_i(x_2,\xi _1)-f_i(x_1,\xi _1)\right) _{i=\{1,2\}}, \end{aligned}$$

$x_1$, $x_2$, and $x_4$ are feasible solutions to ${{\mathcal L}{\mathcal R}}(x_1,\epsilon ^1,{\mathcal U})$, while $x_3$ is not. $f_{\mathcal U}(x_1)-\mathbb {R}^2_\succeq$ (respectively, $f_{\mathcal U}(x_2)-\mathbb {R}^2_\succeq$) does not contain $f_{\mathcal U}(x_2)$ nor $f_{\mathcal U}(x_4)$ (respectively, neither $f_{\mathcal U}(x_1)$ nor $f_{\mathcal U}(x_4)$). Therefore, both $x_1$ and $x_2$ are lightly robust efficient to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon ^1$.

As we see, $x_3$ is the only set-based minmax robust efficient solution. Therefore, as soon as $\epsilon$ is chosen in a way that $f(x_3,\xi _1)\preceq f(x_1,\xi _1)+\epsilon$, e.g.

$$\begin{aligned} \epsilon ^2:=\left( f_i(x_3,\xi _1)-f_i(x_1,\xi _1)\right) _{i=\{1,2\}}, \end{aligned}$$

i.e., as soon as $x_3$ is feasible to ${{\mathcal L}{\mathcal R}}(x_1,\epsilon ,{\mathcal U})$, it is the only set-based minmax robust efficient solution to ${{\mathcal L}{\mathcal R}}(x_1,\epsilon ,{\mathcal U})$ and, therefore, the only lightly robust efficient solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$. I.e., $x_3$ is the only lightly robust efficient solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$ for all $\epsilon \succeq \epsilon ^2$.

We note the following observation.

Remark 27

(Special cases of lightly robust efficiency)

• (a) For $|{\mathcal U}|=1$, lightly robust efficiency is equivalent to deterministic efficiency.

• (b) In the case of only $k=1$ objective function, a solution is lightly robust efficient if and only if it is lightly robust optimal for the corresponding single-objective uncertain optimization problem.

• (c) For the case of bi-objective problems with only one uncertain objective function, lightly robust efficiency is equivalent to the definition of lightly robust efficiency in Kuhn et al. (2013).

We conclude that our generalization of lightly robust efficiency is consistent with the literature.

Proof

• (a) Let $|{\mathcal U}|=1$. Every efficient solution ${\overline{x}}$ is lightly robust efficient for ${{\mathcal L}{\mathcal R}}({\overline{x}},\epsilon ,{\mathcal U})$ for $\epsilon =0$. For the other direction, let ${\overline{x}}\in {\mathcal X}$ be lightly robust efficient for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ for some ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$ and some $\epsilon \ge 0$. Assume that ${\overline{x}}$ is not efficient for ${{\mathcal P}({\mathcal U})}$. Then there is some $x'$ such that $f(x')\preceq f({\overline{x}})$. Then $x'$ is feasible for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ since ${\overline{x}}$ is. But according to Remark 15, this is a contradiction since ${\overline{x}}$ is not efficient for $P({\widehat{\xi }})$.

• (b) For $k=1$, the efficient set ${\mathcal X}_{\mathcal E}({\widehat{\xi }})$ is equivalent to the set of optimal solutions to ${\mathcal P}({\widehat{\xi }})$ and, therefore, the constraints

  $$\begin{aligned} f_i(x,{\widehat{\xi }})\le f_i({\widehat{x}},{\widehat{\xi }})+\epsilon _i\quad ~\forall i\in \{1,\ldots ,k\} \end{aligned}$$

  are equivalent to the constraint

  $$\begin{aligned} f(x,{\widehat{\xi }})\le \underset{{\widehat{x}}\in {\mathcal X}}{\mathrm{min}}~f({\widehat{x}},{\widehat{\xi }})+\epsilon . \end{aligned}$$

  This means that the definition of lightly robust efficiency reduces to the definition of light robustness for $k=1$.

• (c) Note that set-based minmax robust efficiency for the special case of bi-objective optimization with only one uncertain objective function reduces to finding the single-objective worst-case for the (unique) uncertain objective, hence the definition for light robustness in Kuhn et al. (2013) is equivalent to our definition for this special case.

4 Analysis and comparison of the concepts

In Example 3, we observed the following relations between the robustness concepts (the ones that have not been computed explicitly follow directly from the relations depicted in Fig. 10).

	$x_1$	$x_2$	$x_3$
Highly re	No	Yes	No
Flimsily re	Yes	Yes	No
Set-based minmax re	Yes	Yes	No
Hull-based minmax re	Yes	Yes	No
Point-based minmax re	No	Yes	No
Lightly re $\forall \epsilon$	Yes	Yes	No
Lower set less ordered e	Yes	Yes	No
Set less ordered e	Yes	Yes	No
Alternative set less ordered e	Yes	Yes	No
Certainly less ordered e	Yes	Yes	No

In this section, we summarize and complete the different relations between the concepts presented in Sect. 3. After summarizing the results for the general setting, we have a look at a special class of optimization problems, namely problems of objective-wise uncertainty. For this class, several implications hold which do not hold in the general case.

4.1 The general case

In Fig. 10, we depict the relations between the ten concepts introduced in Sect. 3. All other implications or non-implications follow by transitivity, such that the figure contains the relation between every pair of concepts. Note that it depends on the choice of $\epsilon$ if a solution x is lightly robust efficient or not. In our analysis we hence distinguish whether a solution is lightly robust efficient for all $\epsilon \ge 0$ or whether there exists an $\epsilon \ge 0$ such that the solution is lightly robust efficient with respect to this particular choice.

Fig. 10

Relationships between the various concepts of robust efficiency for the general setting

Fig. 11

Illustration of Example 28

As indicated in Fig. 10, some of the relations have been shown in other papers (namely in Bokrantz and Fredriksson 2013; Ide and Köbis 2014), and the relation between highly and flimsily robust efficient is already noted in Lemma 6. The remaining implications will be shown in Lemmata 30, 31, 32, 34, and 35.

However, we start with providing the counterexamples showing the implications which do not hold in general.

Example 28

Let ${\mathcal U}:=\{1,2,3,4\}$, with 1 being the nominal scenario, and ${\mathcal X}:=\{\diamond ,+,\text {o },\star ,\square ,\triangle \}$. Let $f:{\mathcal X}\times {\mathcal U}\mapsto \mathbb {R}^2$ be given by the graph in Fig. 11 (we indicate the objective vectors of solution $x\in {\mathcal X}$ in scenario $\xi \in {\mathcal U}$ by $x^\xi$). Note that, due to clearness, we now depict the different solutions by symbols, not the different scenarios, as done before.

As we can see, solution $\star$ is lightly robust efficient w.r.t. every $\epsilon \succeq 0$ since it is efficient for the nominal scenario and there is no $x\in {\mathcal X}$ such that $f_{\mathcal U}(x)\subseteq f_{\mathcal U}(\star )-{\mathbb {R}^k_\succeq }$. However, it is not lower set less ordered efficient (dominated by o), highly robust efficient (dominated by $\diamond$ in Scenario 3), nor point-based minmax robust efficient (dominated by o and $\triangle$).

Solution $\triangle$ is lower set less ordered efficient but not lightly robust efficient for any $\epsilon \succeq 0$ since it is always dominated by solution o (which is feasible for any ${{\mathcal L}{\mathcal R}}(x,\epsilon ,{\mathcal U})$ if $\triangle$ is feasible).

Solution $\square$ is alternative set less ordered robust efficient but neither point-based minmax robust efficient (dominated by o), hull-based minmax robust efficient (dominated by o), nor flimsily robust efficient (dominated by $\star$ in Scenario 1, by o in Scenario 2, by $\triangle$ in Scenario 3, and by o in Scenario 4).

Solution $\diamond$ is highly robust efficient but neither point-based minmax robust efficient nor set less ordered efficient since, for both concepts, it is dominated by Solution $\square$.

Solution $+$ is hull-based minmax robust efficient but neither flimsily robust efficient (dominated by $\star$ in Scenario 1, by $\diamond$ in Scenario 2, by $\triangle$ in Scenario 3, and by o in Scenario 4), lower set less ordered efficient (dominated by o), nor point-based minmax robust efficient (dominated by $\square$).

We summarize the results in this example in the following table.

	$\star$	$\triangle$	$\square$	$\diamond$	$+$	o
Highly re	No	No	No	Yes	No	No
Flimsily re	Yes	Yes	No	Yes	No	Yes
Set-based minmax re	Yes	No	Yes	No	Yes	Yes
Hull-based minmax re	Yes	No	Yes	No	Yes	Yes
Point-based minmax re	No	No	No	No	No	Yes
Lightly re $\forall \epsilon$	Yes	No	No	No	No	Yes
Lower set less ordered e	No	Yes	Yes	No	No	Yes
Set less ordered e	Yes	Yes	Yes	Yes	Yes	Yes
Alternative set less ordered e	No	No	Yes	No	No	Yes
Certainly less ordered e	Yes	Yes	Yes	Yes	Yes	Yes

Another implication that does not hold in general is that point-based minmax robust efficient solutions are always flimsily robust efficient, lightly robust efficient with respect to some $\epsilon \succeq 0$, or set less ordered efficient as the following example shows.

Example 29

Let ${\mathcal U}:=\{\xi _1,\xi _2,\xi _3\}$ with the nominal scenario being $\xi _1$ and the feasible set ${\mathcal X}:=\{x_1,x_2\}$. We define $f:{\mathcal X}\times {\mathcal U}\mapsto \mathbb {R}^2$ via the plot in Fig. 12.

As we can see, $x_1$ is neither flimsily robust efficient, lightly robust efficient for any $\epsilon \succeq 0$, nor set less ordered efficient since it is always dominated by $x_2$. However, both solutions are point-based minmax robust efficient since they do not dominate each other in this concept.

Fig. 12

Illustration of Example 29

Regarding the implications that do hold, in addition to the results from Sect. 3, we first analyze the connection between point-based minmax efficiency and certainly less ordered efficiency.

Lemma 30

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem and let x be point-based minmax robust efficient for ${{\mathcal P}({\mathcal U})}$. Then x is certainly less ordered efficient for ${{\mathcal P}({\mathcal U})}$.

Proof

This is clear from the definitions since $f_{{\mathcal U}}^{\mathrm{min}}(x')-{\mathbb {R}^k_\succeq }\subseteq {f^{\max }_{\mathcal U}}(x')-{\mathbb {R}^k_\succeq }$ for all $x,x'\in {\mathcal X}$. $\square$

We now analyze the connections to lightly robust efficiency. The next lemma shows that a set-based minmax robust efficient solution is always lightly robust efficient to ${{\mathcal P}({\mathcal U})}$ w.r.t. some $\epsilon \succeq 0$:

Lemma 31

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem and let x be set-based minmax robust efficient for ${{\mathcal P}({\mathcal U})}$. Then there exists an $\epsilon \succeq 0$, such that x is a lightly robust efficient solution to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$.

Proof

First, we notice that a set-based minmax robust efficient solution x to ${{\mathcal P}({\mathcal U})}$ is lightly robust efficient to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon$ if and only if it is a feasible solution to ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ for some efficient solution ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$ to the nominal problem ${\mathcal P}({\widehat{\xi }})$. This holds since the feasible set of ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ is a subset of ${\mathcal X}$ for all $\epsilon \succeq 0$ and, therefore, x is set-based minmax robust efficient for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ since it is already set-based minmax robust efficient for ${{\mathcal P}({\mathcal U})}$.

Now, for any ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$, x is a feasible solution to ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ^*,{\mathcal U})$ w.r.t $\epsilon$ for all

$$\begin{aligned} \epsilon \succeq \epsilon ^*:=\left( \max \left\{ 0,~f_i(x,{\widehat{\xi }})-f_i({\widehat{x}},{\widehat{\xi }})\right\} \right) _{i=1,\ldots ,k}. \end{aligned}$$

Therefore, x is lightly robust efficient to ${{\mathcal P}({\mathcal U})}$ w.r.t. $\epsilon ^*$. $\square$

Example 28 shows that the reverse direction does not hold in general (solution $+$ is set-based minmax robust efficient but not lightly robust efficient w.r.t. $\epsilon =(1,1)$). However, with some additional assumptions we can show the reverse direction:

Lemma 32

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$ with a nominal scenario ${\widehat{\xi }}$. Let x be a lightly robust efficient solution for ${{\mathcal P}({\mathcal U})}$ w.r.t. every $\epsilon \succeq 0$. Then x is set-based minmax robust efficient. Furthermore, x is an efficient solution to ${\mathcal P}({\widehat{\xi }})$.

Proof

Let x be a lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ w.r.t. every $\epsilon \succeq 0$. For the first part of the proof we have a look at the feasible sets of ${{\mathcal P}({\mathcal U})}$ and ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ for some ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$. The feasible set of ${{\mathcal P}({\mathcal U})}$ is ${\mathcal X}$, the feasible set of ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$ is

$$\begin{aligned} {\mathcal X}^{{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ):=\left\{ {\overline{x}}\in {\mathcal X}:f_i({\overline{x}},{\widehat{\xi }})\le f_i({\widehat{x}},{\widehat{\xi }})+\epsilon _i\right\} . \end{aligned}$$

Obviously, ${\mathcal X}^{{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ) \subseteq {\mathcal X}$, therefore, x is feasible for ${{\mathcal P}({\mathcal U})}$. Suppose, that x is not set-based minmax robust efficient for ${{\mathcal P}({\mathcal U})}$. Then there exists a solution $x'\in {\mathcal X}$ such that ${f_{\mathcal U}}(x')\subseteq {f_{\mathcal U}}(x)-{\mathbb {R}^k_\succeq }$. With

$$\begin{aligned} \epsilon ':=\left( \max \left\{ 0,~f_i(x',{\widehat{\xi }})-f_i({\widehat{x}},{\widehat{\xi }})\right\} \right) _{i=1,\ldots ,k}, \end{aligned}$$

it holds that $f_i(x',{\widehat{\xi }})\le f_i({\widehat{x}},{\widehat{\xi }})+\epsilon '_i$ and, therefore, $x'$ is feasible for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$. But this contradicts the assumption that x is set-based minmax robust efficient for ${{\mathcal L}{\mathcal R}}({\widehat{x}},\epsilon ,{\mathcal U})$.

For the second part of the proof note that there exists some ${\widehat{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$ such that x is a set-based minmax robust efficient solution to ${{\mathcal L}{\mathcal R}}({\widehat{x}},0,{\mathcal U})$. Therefore, x is in particular feasible for ${{\mathcal L}{\mathcal R}}({\widehat{x}},0,{\mathcal U})$, thus also an efficient solution to ${\mathcal P}({\widehat{\xi }})$. $\square$

Remark 33

Note, that a set-based minmax robust efficient solution $x\in {\mathcal X}$ to ${{\mathcal P}({\mathcal U})}$ which is efficient for ${\mathcal P}({\widehat{\xi }})$ is also lightly robust efficient to ${{\mathcal P}({\mathcal U})}$ w.r.t. every $\epsilon \succeq 0$, since it is then feasible for ${{\mathcal L}{\mathcal R}}(x,\epsilon ,{\mathcal U})$ for every $\epsilon \succeq 0$.

Furthermore, we need to clarify the connection between highly robust efficiency and lightly robust efficiency w.r.t. some $\epsilon \succeq 0$.

Lemma 34

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$ with a nominal scenario ${\widehat{\xi }}$. Let x be highly robust efficient for ${{\mathcal P}({\mathcal U})}$. Then x is lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ w.r.t. some $\epsilon \succeq 0$.

Proof

Choose $\epsilon _0=0\in {\mathbb {R}^k}$. Since x is highly robust efficient, it is efficient for the nominal scenario, i.e, there is no ${\overline{x}}\in {\mathcal X}{\setminus }\{x\}$ such that $f_i({\overline{x}},{\widehat{\xi }})\le f_i(x,{\widehat{\xi }})$ for all i. Therefore, x is the only feasible solution to ${{\mathcal L}{\mathcal R}}(x,\epsilon _0,{\mathcal U})$, thus minmax robust efficient for ${{\mathcal L}{\mathcal R}}(x,\epsilon _0,{\mathcal U})$ and lightly robust efficient w.r.t. $\epsilon _0$ for ${{\mathcal P}({\mathcal U})}$.

With the following lemma, we can complete the analysis of the general case.

Lemma 35

Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$ with a nominal scenario ${\widehat{\xi }}$. Let x be flimsily robust efficient for ${{\mathcal P}({\mathcal U})}$ or lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ with respect to some $\epsilon \succeq 0$. Then x is certainly less ordered efficient for ${{\mathcal P}({\mathcal U})}$.

Proof

Assume that x is not certainly less ordered efficient. Then, by definition, there exists $x'\in {\mathcal X}{\setminus }\{x\}$ such that:

$$\begin{aligned} \forall ~\xi \in {\mathcal U}\quad \forall ~\eta \in {\mathcal U},\quad \mathrm{s.t.},\quad f(x',\xi )\preceq f(x,\eta ). \end{aligned}$$

(2)

From this follows directly that x is not flimsily robust efficient. Furthermore,

$$\begin{aligned} f(x',{\widehat{\xi }})\preceq f(x,{\widehat{\xi }}). \end{aligned}$$

Therefore, if x is feasible for some ${{\mathcal L}{\mathcal R}}({\overline{x}},\epsilon ,\xi )$ with ${\overline{x}}\in {\mathcal X}_{\mathcal E}({\widehat{\xi }})$, $\epsilon \succeq 0$, and $\xi \in {\mathcal U}$, so is $x'$. But since (2) implies that

$$\begin{aligned} \forall ~\xi \in {\mathcal U}~\exists ~\eta \in {\mathcal U},\quad \mathrm{s.t.}\quad f(x',\xi )\preceq f(x,\eta ) \end{aligned}$$

i.e., $f(x,{\mathcal U})\subseteq f(x',{\mathcal U})-{\mathbb {R}^k_\succeq },$ x is not lightly robust efficient with respect to any $\epsilon \succeq 0$ since it is always dominated by $x'$. $\square$

4.2 The case of objective-wise uncertainty

In this section we have a close look at uncertain multi-objective optimization problems where the uncertainties in the different objective functions are independent of each other, i.e., each component of $\xi$ influences at most one of the objective functions. This case has also been investigated in Ehrgott et al. (2014) where the following definition has been introduced.

Definition 36

(Objective-wise uncertainty, Ehrgott et al. 2014) A problem ${\mathcal P}({\mathcal U})$ with ${\mathcal U}\subset {\mathbb {R}^m}$ is of objective-wise uncertainty, if the uncertainties of the objective functions $f_1,\ldots ,f_k$ are independent of each other, namely if ${\mathcal U}={\mathcal U}_1\times \cdots \times {\mathcal U}_k$, where ${\mathcal U}_i\subseteq \mathbb {R}^{m_i}$ with $\sum _{i=1}^km_i=m$ such that

$$\begin{aligned} f(x,\xi ) = \begin{pmatrix} f_1(x,\xi _1)\\ f_2(x,\xi _2)\\ \vdots \\ f_k(x,\xi _k)\\ \end{pmatrix} \end{aligned}$$

where $\xi _i\in {\mathcal U}_i$.

There are several classes which fit this setting. Trivially, all uncertain single-objective optimization problems are of objective-wise uncertainty. Also, the setting of multi-objective optimization with only one uncertain objective function as considered in Kuhn et al. (2013) is an example for objective-wise uncertainty. Furthermore, if the coefficients $\xi _i,~i\in \{1,\ldots ,k\}$ of an optimization problem are uncertain and independent from each other the problem is of objective-wise uncertainty as well. This includes, e.g., the interval-based uncertainty for linear programming, which is probably the most considered case in uncertain single-objective optimization problems, see, e.g., Bertsimas and Sim (2004), Ben-Tal and Nemirovski (2000) for theoretical contributions and many more papers using interval-based uncertainty to model applications.

In Ehrgott et al. (2014), the authors show that for this class of optimization problems under certain circumstances a single worst-case scenario exists:

Lemma 37

(Ehrgott et al. 2014, Lemma 5.2 and Corollary 5.3) Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem of objective-wise uncertainty, where $\underset{\xi \in {\mathcal U}}{\max }~f_i(x,\xi )$ exists for all $x\in {\mathcal X}$ and all $i\in \{1,\ldots ,k\}$. Then for all $x\in {\mathcal X}$

$$\begin{aligned} {\xi ^{\max }}(x):= \begin{pmatrix} \underset{\xi ^1\in {\mathcal U}_1}{{{\mathrm{argmax\,}}}}~f_1(x,\xi ^1)\\ \underset{\xi ^2\in {\mathcal U}_2}{{{\mathrm{argmax\,}}}}~f_2(x,\xi ^2)\\ \vdots \\ \underset{\xi ^k\in {\mathcal U}_k}{{{\mathrm{argmax\,}}}}~f_k(x,\xi ^k)\\ \end{pmatrix}\in {\mathcal U}. \end{aligned}$$

Note that a consequence of Lemma 37 is that ${f^{\max }_{\mathcal U}}(x)= f(x,{\xi ^{\max }}(x)).$

The analogous of a best-case scenario can be shown in the same way and leads to:

Lemma 38

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem of objective-wise uncertainty, where $\underset{\xi \in {\mathcal U}}{\mathrm{min}}~f_i(x,\xi )$ exists for all $x\in {\mathcal X}$ and all $i\in \{1,\ldots ,k\}$. Then for all $x\in {\mathcal X}$

$$\begin{aligned} {\xi ^{\min }}(x):= \begin{pmatrix} \underset{\xi ^1\in {\mathcal U}_1}{{{\mathrm{argmin\,}}}}~f_1(x,\xi ^1)\\ \underset{\xi ^2\in {\mathcal U}_2}{{{\mathrm{argmin\,}}}}~f_2(x,\xi ^2)\\ \vdots \\ \underset{\xi ^k\in {\mathcal U}_k}{{{\mathrm{argmin\,}}}}~f_k(x,\xi ^k)\\ \end{pmatrix}\in {\mathcal U}. \end{aligned}$$

Proof

Analogously to Ehrgott et al. (2014), Lemma 5.2 and Corollary 5.3. $\square$

We can use Lemma 37 to show the following connection between point-based, hull-based, and set-based minmax robust efficiency.

Lemma 39

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem of objective-wise uncertainty where $\underset{\xi \in {\mathcal U}}{\max }~f_i(x,\xi )$ exists for all $x\in {\mathcal X}$ and all $i\in \{1,\ldots ,k\}$. Then point-based minmax robust efficiency, hull-based minmax robust efficient, and set-based minmax robust efficiency are all equivalent for ${{\mathcal P}({\mathcal U})}$.

Proof

For all $x\in {\mathcal X},~\xi \in {\mathcal U},~\xi \ne {\xi ^{\max }}(x)$,

$$\begin{aligned} f(x,\xi )\preceq f(x,{\xi ^{\max }}(x)). \end{aligned}$$

Due to Lemma 37, ${\xi ^{\max }}(x)\in {\mathcal U}$, therefore,

$$\begin{aligned} {f_{\mathcal U}}(x)-{\mathbb {R}^k_\succeq }=\{f(x,{\xi ^{\max }}(x))\}-{\mathbb {R}^k_\succeq }. \end{aligned}$$

Since $\{f(x,{\xi ^{\max }}(x))\}-{\mathbb {R}^k_\succeq }$ is convex, we obtain

$$\begin{aligned} {{\mathrm{conv\,}}}\left( {f_{\mathcal U}}(x)\right) -{\mathbb {R}^k_\succeq }=\{f(x,{\xi ^{\max }}(x))\}-{\mathbb {R}^k_\succeq }, \end{aligned}$$

hence

$$\begin{aligned} {f_{\mathcal U}}(x)-{\mathbb {R}^k_\succeq }=\{f(x,{\xi ^{\max }}(x))\}-{\mathbb {R}^k_\succeq }={{\mathrm{conv\,}}}\left( {f_{\mathcal U}}(x)\right) -{\mathbb {R}^k_\succeq }, \end{aligned}$$

i.e., all three concepts use the same dominance relation and hence obtain exactly the same robust minmax efficient solutions. $\square$

As a consequence, in this section, we only talk about minmax robust efficient solutions and use this term for point-based, hull-based, and set-based minmax robust efficient solutions equivalently.

We remark that Ehrgott et al. (2014) already showed that in the case that ${{\mathcal P}({\mathcal U})}$ is of objective-wise uncertainty, the concepts of set-based and point-based minmax robust efficiency are equivalent (compare Ehrgott et al. 2014, Theorem 5.4).

From Lemma 38, we can deduce that for problems of objective-wise uncertainty every lower set less ordered efficient solution is at least flimsily robust efficient.

Lemma 40

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem of objective-wise uncertainty where $\underset{\xi \in {\mathcal U}}{\mathrm{min}}~f_i(x,\xi )$ exists for all $x\in {\mathcal X}$ and $i\in \{1,\ldots ,k\}$ and let ${\overline{x}}$ be lower set less ordered efficient for ${{\mathcal P}({\mathcal U})}$. Then ${\overline{x}}$ is flimsily robust efficient.

Proof

Assume that ${\overline{x}}$ is not flimsily robust efficient. Then, due to Lemma 38, there exists $x\in {\mathcal X}{\setminus }\{{\overline{x}}\}$ such that

$$\begin{aligned} f(x,{\xi ^{\min }}({\overline{x}}))\preceq f({\overline{x}},{\xi ^{\min }}({\overline{x}})). \end{aligned}$$

With the same argument as in the proof of Lemma 39,

$$\begin{aligned} \{f({\overline{x}},{\xi ^{\min }}({\overline{x}}))\}+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}). \end{aligned}$$

Therefore,

$$\begin{aligned} {f_{\mathcal U}}(x)+{\mathbb {R}^k_\succeq }\supseteq \{f(x,{\xi ^{\min }}({\overline{x}}))\}+{\mathbb {R}^k_\succeq }\supseteq \{f({\overline{x}},{\xi ^{\min }}({\overline{x}}))\}+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}), \end{aligned}$$

in contradiction to the lower set less ordered efficiency of ${\overline{x}}$. $\square$

Lemmata 37 and 38 can also be used to show that for objective-wise uncertain multi-objective optimization problems, there exists the following connection between highly and alternative set less ordered/lightly robust efficiency:

Lemma 41

Let ${{\mathcal P}({\mathcal U})}$ be an uncertain multi-objective optimization problem of objective-wise uncertainty where $\underset{\xi \in {\mathcal U}}{\max }~f_i(x,\xi )$ and $\underset{\xi \in {\mathcal U}}{\mathrm{min}}~f_i(x,\xi )$ exist for all $x\in {\mathcal X}$ and $i\in \{1,\ldots ,k\}$. Let ${\overline{x}}\in {\mathcal X}$ be highly robust efficient. Then ${\overline{x}}$ is alternative set less ordered efficient and lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ w.r.t. every $\epsilon \succeq 0$.

Proof

First note that if ${\overline{x}}\in {\mathcal X}$ is highly robust efficient, it is in particular efficient for ${\mathcal P}({\widehat{\xi }})$. Therefore, it is feasible for ${{\mathcal L}{\mathcal R}}({\overline{x}},\epsilon ,{\mathcal U})$ for every $\epsilon \succeq 0$. We now show that ${\overline{x}}$ is minmax robust efficient for ${{\mathcal P}({\mathcal U})}$, then, due to Remark 33, it is also lightly robust efficient for ${{\mathcal P}({\mathcal U})}$ for all $\epsilon \succeq 0$.

Assume ${\overline{x}}$ is not minmax robust efficient for ${{\mathcal P}({\mathcal U})}$. Then there exists $x\in {\mathcal X}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x)\subseteq {f_{\mathcal U}}({\overline{x}})-{\mathbb {R}^k_\succeq }\end{aligned}$$

Since ${{\mathcal P}({\mathcal U})}$ is of objective-wise uncertainty, ${f_{\mathcal U}}({\overline{x}})\subseteq f\left( {\overline{x}},{\xi ^{\max }}({\overline{x}})\right) -{\mathbb {R}^k_\succeq }$ due to Lemma 37. Therefore,

$$\begin{aligned} {f_{\mathcal U}}(x)\subseteq f\left( {\overline{x}},{\xi ^{\max }}({\overline{x}})\right) -{\mathbb {R}^k_\succeq }\end{aligned}$$

which implies

$$\begin{aligned} f\left( x,{\xi ^{\max }}({\overline{x}})\right) \preceq f\left( {\overline{x}},{\xi ^{\max }}({\overline{x}})\right) \end{aligned}$$

in contradiction to the highly robust efficiency of ${\overline{x}}$.

Due to Ide and Köbis (2014), Lemma 28, which states that a solution is alternative set less ordered efficient if and only if it is both minmax robust and lower set less ordered efficient, we only have to show that ${\overline{x}}$ is lower set less ordered efficient to complete the proof.

Assume ${\overline{x}}$ is not lower set less ordered efficient for ${{\mathcal P}({\mathcal U})}$. Then there exists $x\in {\mathcal X}$ such that

$$\begin{aligned} {f_{\mathcal U}}(x)+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}) \end{aligned}$$

Due to Lemma 38, with the same argument as in the proof of Lemma 39,

$$\begin{aligned} {f_{\mathcal U}}(x)+{\mathbb {R}^k_\succeq }=f(x,{\xi ^{\min }}(x))+{\mathbb {R}^k_\succeq }. \end{aligned}$$

Therefore,

$$\begin{aligned} f(x,{\xi ^{\min }}(x))+{\mathbb {R}^k_\succeq }\supseteq {f_{\mathcal U}}({\overline{x}}), \end{aligned}$$

which implies

$$\begin{aligned} f\left( x,{\xi ^{\min }}(x)\right) \preceq f\left( {\overline{x}},{\xi ^{\min }}(x)\right) , \end{aligned}$$

in contradiction to the highly robust efficiency of ${\overline{x}}$. $\square$

To complete the analysis of the relationships between the various concepts, we finally present a counterexample to the remaining implications.

Example 42

Let ${\mathcal U}:=\{0,1\}^2$, with (1, 1) being the nominal scenario, and ${\mathcal X}:=\{x_1,\ldots ,x_7\}$. Let $f:{\mathcal X}\times {\mathcal U}\mapsto \mathbb {R}^2$ be given in the following way.

Obviously, ${{\mathcal P}({\mathcal U})}$ is of objective-wise uncertainty. We plot f in Fig. 13. We indicate the objective vectors in Scenario (0, 0) by the symbol $x$, in Scenario (0, 1) by the symbol $\square$, in Scenario (1, 0) by the symbol $\triangle$, and in Scenario (1, 1) by the symbol o. Furthermore, we connect objective vectors for the same solution by dashes.

We can see that $x_1$ is lower set less ordered efficient but not lightly robust efficient for any $\epsilon \succeq 0$ since it is always dominated by $x_2$.

$x_2$ on the other hand is lightly robust efficient for every $\epsilon \succeq 0$ since it is efficient in the nominal scenario and minmax robust efficient.

$x_4$ is lightly robust efficient for every $\epsilon \preceq (0.5,0.5)$ but not set less ordered efficient since it is dominated $x_3$.

$x_6$ is minmax robust efficient but not flimsily robust efficient since it is dominated by $x_5$ in Scenarios (0, 0) and (0, 1) and by $x_7$ in Scenarios (1, 1) and (1, 0).

Fig. 13

Counterexample to some implications for problems of objective-wise uncertainty

Summarizing the results from this section, we can adapt Fig. 10 for the setting of objective-wise uncertainty, see Fig. 14.

Fig. 14

Relationships between the various concepts of robust efficiency for the problems of objective-wise uncertainty

As we see in Fig. 14, a lot of implications hold for problems of objective-wise uncertainty which do not hold in the general setting.

4.3 Connections between the concepts of strictly and weakly efficiency

Note that a lot of the general implications in Sect. 4.1 do not hold due to Example 29. However, if we replace ${\mathbb {R}^k_\succeq }$ by ${\mathbb {R}^k_\geqq }$ or ${\mathbb {R}^k_>}$ in the definitions of the respective concepts of robustness, as indicated after Definition 12, we obtain the analogous concepts of robust strictly efficiency and robust weakly efficiency.

For these concepts, the same inclusions hold as before. Moreover, Example 29 does not work for these concepts, therefore, we obtain more inclusions as in the general case. Namely, point-based minmax robust efficiency includes both hull-based and set-based minmax robust efficiency. All the other counterexamples stay valid as we can see in Example 28.

For problems of objective-wise uncertainty, nothing changes.

5 Reduction results for problems of objective-wise uncertainty

Besides the implications between the robustness concepts discussed in the previous section, problems of objective-wise uncertainty also have some other interesting properties. In robust optimization it is often helpful to reduce the size of ${\mathcal U}$. For instance, Ben-Tal and Nemirovski (1999) show that a solution to an uncertain single-objective optimization problem ${{\mathcal P}({\mathcal U})}$ with convex objective function for any fixed $x\in {\mathcal X}$ and discrete uncertainty set ${\mathcal U}$ is minmax robust optimal if and only if it is a minmax robust optimal solution to ${{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}$. Schöbel (2014) shows that this property can be extended to the concept of light robustness. Many more such results are known in single-objective robust optimization, see Goerigk and Schöbel (2015) for an overview. The main advantage of these reduction results applies to polyhedral uncertainty in which the uncertainty set ${\mathcal U}$ is given as the convex hull of a finite set of points, i.e., ${\mathcal U}=conv(\{\xi ^1,\ldots ,\xi ^m\})$. In this case we obtain that ${{\mathcal P}({\mathcal U})}$ is equivalent to $\mathcal{P}(\{\xi ^1,\ldots ,\xi ^m\})$. The latter problem with the finite uncertainty set is often easier to solve. For example, in single-objective robust optimization it can often be directly solved by explicitly adding a set of constraints for every scenario $\xi ^i, i=1,\ldots ,m$, or, as in our case of multi-objective robust optimization, by inspecting each of the scenarios separately.

For uncertain multi-objective optimization problems (Ehrgott et al. 2014) are able to transfer this property to problems of objective-wise uncertainty when considering the concept of minmax robust efficiency (recall that for problems of objective-wise uncertainty, set-based, hull-based, and point-based minmax robust efficiency are equivalent as mentioned after Lemma 39):

Theorem 43

(Ehrgott et al. 2014, Theorem 5.9) Given a discrete uncertainty set ${\mathcal U}=\{\xi ^1,\ldots ,\xi ^m\}$ and an uncertain multi-objective optimization problem ${\mathcal P}({{\mathrm{conv\,}}}({\mathcal U}))$ of objective-wise uncertainty where

$$\begin{aligned} f_1(x,\xi ),\ldots ,f_k(x,\xi ):\,{\mathbb {R}^n}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}\, \end{aligned}$$

are quasiconvex in $\xi$. Then

Furthermore, also for the concepts of lower set less efficiency, alternative set less efficiency, and set less ordered efficiency ${{\mathrm{conv\,}}}({\mathcal U})$ can be equivalently replaced by ${\mathcal U}$. The proof is analogous to the proof of Theorem 5.9 in Ehrgott et al. (2014) and can be found in Ide (2014).

Theorem 44

(Ide 2014, Theorem 3.4 and Remark 3.5) Given an uncertain multi-objective optimization problem ${{\mathcal P}({\mathcal U})}$ of objective-wise uncertainty, where ${\mathcal U}=\{\xi ^1,\ldots ,\xi ^m\}$ and

$$\begin{aligned} f_1(x,\xi ),\ldots ,f_k(x,\xi ):\,{\mathbb {R}^n}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}\, \end{aligned}$$

are quasiconcave in $\xi$. Then

The same holds for the concept of certainly less set ordered efficiency and by assuming additional quasiconvexity of f in $\xi$ also for the concepts of alternative set less and set less ordered efficiency.

We now investigate if such a result also holds for the other robustness concepts for problems of objective-wise uncertainty. Since in Theorem 43 there are no assumptions on the feasible set ${\mathcal X}$, it also holds, if the feasible set is defined as in the lightly robust counterpart with respect to some $\epsilon$. Therefore, we can directly deduce the following corollary:

Corollary 45

Given a discrete uncertainty set ${\mathcal U}=\{\xi ^1,\ldots ,\xi ^m\}$ and an uncertain multi-objective optimization problem ${\mathcal P}({{\mathrm{conv\,}}}({\mathcal U}))$ of objective-wise uncertainty where

$$\begin{aligned} f_1(x,\xi ),\ldots ,f_k(x,\xi ):\,{\mathbb {R}^n}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}\, \end{aligned}$$

are quasiconvex in $\xi$. Then

$$\begin{aligned}&{\overline{x}} \text{ is } \text{ lightly } \text{ robust } \text{ efficient } \text{ for } {{\mathcal P}({\mathcal U})}\\&\qquad \qquad \qquad \qquad \qquad \Leftrightarrow \\&{\overline{x}} \text{ is } \text{ lightly } \text{ robust } \text{ efficient } \text{ for } {{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}\end{aligned}$$

We can also extend this property to the concept of highly robust efficiency:

Theorem 46

Let ${\mathcal U}=\{\xi ^1,\ldots ,\xi ^m\}$ and ${\mathcal P}({{\mathrm{conv\,}}}({\mathcal U}))$ a problem of objective-wise uncertainty where

$$\begin{aligned} f_1(x,\xi ),\ldots ,f_k(x,\xi ):\,{\mathbb {R}^n}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}\, \end{aligned}$$

are affine in $\xi$. Then

$$\begin{aligned}&{\overline{x}}\text { is highly robust efficient for }{{\mathcal P}({\mathcal U})}\\&\qquad \qquad \qquad \qquad \qquad \Leftrightarrow \\&{\overline{x}}\text { is highly robust efficient for }{{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}\end{aligned}$$

Proof

“$\Leftarrow$” is trivial and holds for every uncertain multi-objective optimization problem since ${\mathcal U}\subseteq {{\mathrm{conv\,}}}({\mathcal U})$.

“$\Rightarrow$” Let ${\overline{x}}\in {\mathcal X}$ be highly robust efficient for ${{\mathcal P}({\mathcal U})}$, so for every $\xi ^i\in {\mathcal U}$ there is no $x'\in {\mathcal X}$ such that

$$\begin{aligned} f(x',\xi ^i)\preceq f({\overline{x}},\xi ^i) \end{aligned}$$

Suppose ${\overline{x}}$ is not highly robust efficient for ${{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}$, that is, there exists a ${\widehat{\xi }}\in {{\mathrm{conv\,}}}({\mathcal U})$ (so ${\widehat{\xi }}=\sum ^m_{i=1}\lambda _i\xi ^i$ for some $\xi ^i\in {\mathcal U},~\lambda _i\in {\mathbb {R}_+},~\sum _{i=1}^m\lambda _i=1$) and a ${\widehat{x}}\in {\mathcal X}$ such that

$$\begin{aligned} f({\overline{x}},{\widehat{\xi }})\succeq f({\widehat{x}},{\widehat{\xi }}). \end{aligned}$$

Then for all $i\in \{1,\ldots ,k\}$

$$\begin{aligned} \sum ^m_{j=1}\lambda _jf_i\left( {\overline{x}},\xi ^j\right) =f_i({\overline{x}},{\widehat{\xi }})\ge f_i({\widehat{x}},{\widehat{\xi }})=\sum ^m_{j=1}\lambda _jf_i\left( {\widehat{x}},\xi ^j\right) \end{aligned}$$

Since $\lambda _j\ge 0$ for all j, for every $i\in \{1,\ldots ,k\}$ a $j_i\in \{1,\ldots ,m\}$ exists such that

This inequality is strict for at least one i. Define

Then ${\overline{\xi }}\in {\mathcal U}$ since ${\mathcal P}({\mathcal U})$ is of objective-wise uncertainty due to Ehrgott et al. (2014), Lemma 5.8, which states that ${{\mathcal P}({\mathcal U})}$ is of objective-wise uncertainty if and only if ${\mathcal P}({{\mathrm{conv\,}}}({\mathcal U}))$ is of objective-wise uncertainty. On the other hand,

$$\begin{aligned} f({\overline{x}},{\overline{\xi }})\succeq f({\widehat{x}},{\overline{\xi }}). \end{aligned}$$

This contradicts the highly robust efficiency of ${\overline{x}}$ for ${{\mathcal P}({\mathcal U})}$. $\square$

As we can see, compared to Theorem 43 for the case of minmax robust efficiency we had to alter the assumptions slightly and required $f_i, i \in \{1,\ldots ,k\}$ to be affine and not only quasiconvex. The following example shows that this assumption is in fact necessary, i.e., unlike for minmax robust efficiency) quasiconvexity does not suffice to guarantee the statement of Theorem 43 for the case of for highly robust efficiency.

Example 47

Let ${\mathcal U}=\{-\sqrt{2},\sqrt{2}\}^2$. Then

$$\begin{aligned} {{\mathrm{conv\,}}}({\mathcal U})=[-\sqrt{2},\sqrt{2}]^2. \end{aligned}$$

Now let $f:\,{\mathbb {R}_+}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}^2\,$ given by

$$\begin{aligned} f(x,\xi )= \begin{pmatrix} (\xi _1^2-1)\cdot x\\ (\xi _2^2-1)\cdot x\\ \end{pmatrix}. \end{aligned}$$

Then the problem

$$\begin{aligned} \begin{array}{ll} {\mathcal P}(\xi )&{}{\mathrm{min}~f(x,\xi )}\\ &{}\mathrm{s.t.} x\in {\mathbb {R}_+}\end{array} \end{aligned}$$

is of objective-wise uncertainty and f is convex (thus quasiconvex) but not affine in $\xi$. Furthermore,

$$\begin{aligned} f(x,\xi )=\begin{pmatrix} x\\ x \end{pmatrix}~\forall ~\xi \in {\mathcal U}, \end{aligned}$$

thus $x=0$ is highly robust efficient for ${{\mathcal P}({\mathcal U})}$. But since $\xi =(0,0)\in {{\mathrm{conv\,}}}({\mathcal U})$ and

$$\begin{aligned} f(x,(0,0))=\begin{pmatrix} -x\\ -x \end{pmatrix}, \end{aligned}$$

$x=0$ is not highly robust efficient for ${{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}$ because it is dominated by every other solution $x\in {\mathbb {R}_+}$.

We remark that the assumption of objective-wise uncertainty is crucial in all three previous results, i.e., for minmax robust efficiency, for lightly robust efficiency, and for highly robust efficiency. A counterexample for this, i.e., that the statement of Theorem 43 does not hold if the assumption of objective-wise uncertainty is removed, is provided in Ehrgott et al. (2014). This counterexample can also be used to show that the same holds for Corollary 45. For the concept of highly robust efficiency we finally provide the following counterexample:

Example 48

Let ${\mathcal U}=\{\xi ^1,\xi ^2\}=\{0,2.5\}$, so ${{\mathrm{conv\,}}}({\mathcal U})=[0,2.5]$. Now let

$$\begin{aligned} f:\,{\mathbb {R}_+}\times {{\mathrm{conv\,}}}({\mathcal U})\rightarrow \mathbb {R}^2\, \end{aligned}$$

given by

$$\begin{aligned} f(x,\xi )=\begin{pmatrix} (1-2\xi )\cdot x\\ (-2+\xi )\cdot x\\ \end{pmatrix}. \end{aligned}$$

Then f is affine in $\xi$ but ${{\mathcal P}({\mathcal U})}$ is not of objective-wise uncertainty. Furthermore,

$$\begin{aligned} f(x,\xi ^1)=\begin{pmatrix} x\\ -2x \end{pmatrix} \quad \text{ and } \quad f(x,\xi ^2)= \begin{pmatrix} -4x\\ \frac{1}{2}x \end{pmatrix} \end{aligned}$$

so $x=0$ is highly robust efficient for ${{\mathcal P}({\mathcal U})}$. But since ${\widehat{\xi }}=1\in {{\mathrm{conv\,}}}({\mathcal U})$ and

$$\begin{aligned} f(x,1)= \begin{pmatrix} -x\\ -x \end{pmatrix}, \end{aligned}$$

$x=0$ is not highly robust efficient for ${{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}$ because it is dominated by every other solution $x\in {\mathbb {R}_+}$.

Remark 49

The analogon to Theorem 46 does not hold for the concept of flimsily robust efficiency. Even though a flimsily robust efficient solution to ${{\mathcal P}({\mathcal U})}$ is trivially flimsily robust efficient for ${{\mathcal P}({{{\mathrm{conv\,}}}({\mathcal U})})}$ since ${\mathcal U}\subseteq {{{\mathrm{conv\,}}}({\mathcal U})}$, the other direction does not hold. A shortest path counterexample of objective-wise uncertainty with affine objective functions can be found in Kuhn et al. (2013).

6 Conclusion and further research

In this paper, we presented and compared ten different concepts of robustness for uncertain multi-objective optimization. In particular, we extended the concept of light robustness for uncertain single-objective optimization to the concept of lightly robust efficiency for uncertain multi-objective optimization problems. We pointed out the connections between these various concepts and investigated implications and differences. The class of objective-wise uncertain multi-objective optimization problems was presented and properties of the various concepts of robustness for this special class of optimization problems were investigated. For this class, many more implications between the concepts hold than in the general setting.

The class of problems of objective-wise uncertainty turns out to be much easier treatable since infinite uncertainty sets can be reduced to finite ones in the case of polyhedral uncertainty. Given an uncertain multi-objective optimization problem with polyhedral uncertainty, one can hence artificially separate the uncertainty in the objective functions (by treating the uncertain parameters of different objectives as independent of each other) and use the results for objective-wise uncertainty. This can be seen as approximation to the original uncertain problem. As Sect. 4.2 shows, one may then loose set-based minmax, hull-based minmax, or lower set less ordered efficient solutions. The consequences of such an approximation are a study of further research.

Another future step is to develop efficient algorithms for identifying the set of robust efficient solutions, in particular for the different cases of minmax robustness. To do so, we will consider classes of optimization problems separately; e.g., analyze how far we can go with classical algorithms (such as labeling approaches) for shortest path problems in the robust multi-objective case.

A broader question in this context is the computational tractability of the respective robust counterparts to the multi-objective uncertain optimization problems, i.e., finding the robust efficient solutions to the various concepts. Some work on this has already been done, e.g., in Ehrgott et al. (2014), the authors address this issue concerning set-based minmax robust efficient solutions. For the special case of linear problems, the resulting robust counterparts presented in this paper again are linear programs with an increased number of objectives and/or variables. However, an extensive analysis of the different algorithms and their computational tractability is yet to be done. This is a topic of high practical interest and should also be addressed for the various other concepts mentioned in this survey and the algorithms presented in the respective publications.

Further research also includes discussing suitable models in real-world applications. An application of set-based minmax robust efficiency to a real-world problem in the wood-cutting industry can be found in Ide et al. (2015). Several concepts of robust efficiency are applied to an aircraft route guidance problem in Kuhn et al. (2013) and to location problems in Nakiboglu (2014). Resource efficiency is a topic which is currently under investigation in the robust multi-objective context.