Response of an oscillatory differential delay equation to a single stimulus

Abstract

Here we analytically examine the response of a limit cycle solution to a simple differential delay equation to a single pulse perturbation of the piecewise linear nonlinearity. We construct the unperturbed limit cycle analytically, and are able to completely characterize the perturbed response to a pulse of positive amplitude and duration with onset at different points in the limit cycle. We determine the perturbed minima and maxima and period of the limit cycle and show how the pulse modifies these from the unperturbed case.

1 Introduction

Mammalian hematopoietic systems have complex and complicated regulatory processes that control the production of red blood cells, white blood cells and platelets. However, boiled down to their essence, each is a negative feedback system with a time delay that is controlling the production of primitive cells entering from the hematopoietic stem cell compartment.

Often the numbers of circulating blood cells will display oscillations that are more or less regular. This may occur (Foley and Mackey 2009) because of the existence of a spontaneously occurring disorder like cyclical neutropenia (Dale and Hammond 1988; Haurie et al. 1998; Colijn et al. 2006; Dale and Mackey 2015), periodic thrombocytopenia (Apostu and Mackey 2008; Swinburne and Mackey 2000), periodic leukemia (Colijn and Mackey 2005; Fortin and Mackey 1999), or periodic autoimmune hemolytic anemia (Mackey 1979; Milton and Mackey 1989). Or, it may occur because of the intrusive administration of chemotherapy in a periodic fashion (Krinner et al. 2013) which has the unfortunate side effect of killing both malignant and normal cells.

In either case (spontaneously occurring oscillations due to disease or induced oscillations due to the side effects of chemotherapy) a clinical intervention often consists of trying to administer a recombinant cytokine of the appropriate type to alleviate the more serious symptoms of the oscillation. In the case of cyclical neutropenia this is granulocyte colony stimulating factor (G-CSF) (Dale and Hammond 1988; Dale et al. 1993, 2003), and the same is true during chemotherapy induced neutropenia (Bennett et al. 1999; Clark et al. 2005). G-CSF has among its effects the ability to interfere with apoptosis (pre-programmed death) of cells (Colijn et al. 2007), be this cell death naturally present or induced by an external agent like chemotherapy. Unfortunately the issue of when to administer this (or other) cytokines is hotly debated and this is, without a doubt, because the cytokines in question have an effect on the dynamics of the affected system many days before the desired (or undesired) effect is manifested in the peripheral blood.

It has been noted that the timing of the administration of G-CSF can have profound consequences on the neutropenia. Given at some points in the cycle it can dramatically reduce the neutropenia (increasing the nadir of the cycle) while at other times it can actually make the neutropenia worse by deepening the nadir (Aapro et al. 2011; Barni et al. 2014; Munoz Langa et al. 2012; Palumbo et al. 2012). Thus, from a mathematical perspective the problem is simply “How and when do we deliver a perturbation to a delayed dynamical system in order to achieve some desired objective?”

The problem outlined above can, from a mathematical point of view, be viewed within the context of ‘phase resetting of an oscillator’ and as such has received widespread attention especially within the biological community. This field has a large and varied literature (see Glass and Mackey 1988 for an elementary introduction and Winfree 1980 for an exhaustive treatment of the subject from a historical perspective) which is almost exclusively devoted to the interaction of oscillatory systems in a finite dimensional space (i.e. limit cycles in ordinary differential equations) with a single perturbation or periodic perturbation. Surprisingly, however, there is little that has been done on such interactions when the limit cycle is in an infinite dimensional phase space (e.g a differential delay equation). There are, however, a few authors who have considered such situations. For example, Bodnar et al. (2013a, (2013c), Piotrowska and Bodnar (2014) and Foryś et al. (2014) studied simple models of tumour growth where the delayed model equation has an additional term describing an external influence and reflecting a treatment. There have been a number of both experimental and theoretical papers (Israelsson and Johnsson 1967; Johnsson and Israelsson 1968; Johnsson 1971; Andersen and Johnsson 1972a, b) devoted to the autonomous growth of the tip of Helianthus annuus which describes a variety of patterns as a function of time and which is thought to involve a delay between the sensing of a gravitational stimulus and the bending of the plant (c.f Israelsson and Johnsson 1967 for a very nice historical review of this problem). Another class of problems involving delayed dynamics is related to pulse coupled oscillators which have been treated recently by Canavier and Achuthan (2010), Klinshov and Nekorkin (2011) and Klinshov et al. (2015). Kotani et al. (2012) and Novicenko and Pyragas (2012) have developed phase reduction methods appropriate for delayed dynamics. Finally we should note the recent numerical work on several gene regulatory circuits by Lewis (2003) and Horikawa et al. (2006) for the segmentation clock in zebrafish as well as the work of Doi et al. (2011) on circadian regulation of G-protein signaling. However, none of these papers have addressed the problem that we study here from an analytic point of view. This paper offers a partial study of the problem.

The regulation of the production of blood cells, denoted by x(t) (and typically measured in units of cells/$\mu$L of blood or alternately in units of cells/kG body weight), reduced to the barest of descriptions, can be described most simply by a differential delay equation of the form

$$\begin{aligned} \dfrac{dx}{dt}(t) = -\gamma x(t) + f(x(t-\tau )) \quad \text{ with } \text{ constant } \,\, \gamma > 0, \end{aligned}$$

(1.1)

in which $f:\mathbb {R}\rightarrow \mathbb {R}$ is monotone decreasing such that $\xi _1 \le \xi _2$ implies that $f(\xi _1) \ge f(\xi _2)$. In Eq. (1.1) we must also specify an initial function $\varphi : [-\tau ,0]\rightarrow \mathbb {R}$, in order to obtain a solution. Here we replace the nonlinearity f with a piecewise constant function. This permits us to compute solutions explicitly, so we may analytically study their behaviour, and the response of the solutions to perturbation meant to represent the effect of cytokine administration.

This generic model captures the essence, if not the subtleties, of peripheral blood production. The monotone nature of f is mediated via the effects of the important regulatory cytokines, e.g. G-CSF for the white blood cells, erythropoietin for the red blood cells, and thrombopoietin for the platelets. The administration of exogenous cytokines in an attempt to control the dynamics of (1.1) will typically have an effect that be interpreted as increasing f over some portion of time, and the goal of this paper is to study the effect of such a perturbation on the solution of (1.1).

This paper is organized as follows. Section 2 describes the model and formulates it in a mathematically convenient form. Section 3 provides basic facts about continuous, piecewise differentiable solutions. On a state space of simple initial functions these solutions yield a continuous semiflow. There is a periodic solution whose orbit in state space is stable with strong attraction properties. Section 4 introduces the pulse-like perturbations (a perturbation of constant amplitude a lasting for a finite period of time $\sigma$) of the model which correspond to the effect of medication in the sense that during a finite time interval the production of blood cells is increased. It is shown that the response of the system to such perturbations is continuous provided the latter are not too large. This includes a continuity result for the cycle length map, which assigns to each onset time of increased production a time of return to the periodic orbit, after the end of increased production. The bulk of our results are presented in Sect. 5 where we examine the effect of cytokine perturbation when the perturbation away from the stable periodic orbit begins at different points in the cycle. In particular we look at phase resetting properties of the system—in terms of the cycle length map—and at the minima and maxima compared to the amplitudes of the periodic solution. Section 6 examines the various forms assumed by the cycle length map for different values of the parameters. Section 7 shows how the results of the previous sections may be potentially used to tailor therapy to achieve certain results. The paper concludes with a brief discussion in Sect. 8. There we consider a simple extension in which a pulse-like perturbation may decrease the nadir of the limit cycle as is noted clinically. The proofs of many of the results are given in the two appendices.

2 The model

2.1 Scalar delay differential equations

Consider the delay differential equation (1.1). If f is continuous and monotone decreasing then there is a unique constant solution $t\mapsto x_*$ given by $f(x_*) = \gamma x_*$. If in addition f is, say, continuously differentiable then this constant solution may be stable or not, depending on $\gamma$ and $f'(x_*)$. In case $t\mapsto x_*$ is linearly unstable, that is, the linearized equation

$$\begin{aligned} y'(t)=-\gamma y(t)+f'(x_*)y(t-\tau ) \end{aligned}$$

is unstable then also $t\mapsto x_*$ is unstable as a solution of (1.1). In case f also satisfies a one-sided boundedness condition there exists a periodic solution which is slowly oscillating in the sense that the intersections with the equilibrium level $\xi =x_*$ are spaced at distances larger than the delay $\tau$, and the minimal period is given by three consecutive such intersections. In general slowly oscillating periodic solutions are not unique in the sense that they are not all translates of each other. Depending on $\gamma$ and $f'(x_*)$ there may also exist rapidly oscillating periodic solutions about $\xi =x_*$. These have all consecutive zeros spaced at distances strictly less than the delay $\tau$. In case $f'(\xi )<0$ for all $\xi \in \mathbb {R}$ every rapidly oscillating periodic solution is unstable. For details and for more about (1.1), see e.g. the recent survey by Walther (2014) and the references given there.

2.2 A piecewise constant approximation of the nonlinearity

To obtain solutions which can be computed in terms of elementary functions consider the situation in which the function f is piecewise constant and given by

$$\begin{aligned} f(x) = \left\{ \begin{array}{ll} b_L &{} \qquad \text{ for } \quad x< \theta \\ b_U &{} \qquad \text{ for } \quad x \ge \theta , \end{array} \right. \quad 0<\theta ,\quad 0< b_U < b_L. \end{aligned}$$

(2.1)

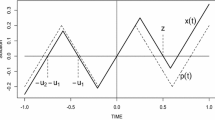
We exclude the special cases $b_L=\gamma \theta$ and $b_U=\gamma \theta$, in order to facilitate the construction of the solution semi-flow in Sect. 3 below, see the skewed dashed lines in Fig. 1 and Remark 3.1.

Fig. 1

The graph of the function f as given in (2.1). The skewed solid line is the graph of $\gamma x$ in general, while the skewed dashed lines are the graphs of $\gamma x$ in the special excluded cases that $b_L=\gamma \theta$ and $b_U = \gamma \theta$

Then we obtain the delay differential equation

$$\begin{aligned} \dfrac{dx}{dt}(t) = - \gamma x(t) + \left\{ \begin{array}{ll} b_L &{} \qquad \text{ for } \quad x(t-\tau ) < \theta \\ b_U &{} \qquad \text{ for } \quad x(t-\tau ) \ge \theta , \end{array} \right. \end{aligned}$$

(2.2)

with $\gamma>0,\theta>0,b_L>b_U>0,\gamma \theta \ne b_U,b_L$, whose solutions satisfy linear, inhomogeneous ordinary differential equations in intervals on which their delayed values remain either below or above the level $\xi =\theta$, resulting in increasing and decreasing exponentials on such intervals. In the situation illustrated in Fig. 1 when the graph of $x\mapsto \gamma x$ passes through the gap of the nonlinearity in Eq. (2.2), so that $b_U<\gamma \theta <b_L$, there is no steady state of Eq. (2.2). Otherwise, if either $\gamma \theta <b_U$ or $b_L<\gamma \theta$ then $x(t)=b_U/\gamma$ or $x(t)=b_L/\gamma$ is the steady state of Eq. (2.2).

Note that in (2.2) there are five parameters $(\gamma , b_U, b_L, \theta , \tau )$ and we can reduce these to three by a change of variables, since with

$$\begin{aligned} \left\{ \begin{array}{lll} \hat{x}(t) = x(t/\gamma )-\theta \\ \hat{\tau }=\gamma \tau \\ \beta _L = -\theta +b_L/\gamma \\ \beta _U = \theta -b_U /\gamma \end{array}\right. \end{aligned}$$

(2.3)

we can rewrite (2.2) in the form

$$\begin{aligned} \dfrac{d\hat{x}}{dt}(t) = \left\{ \begin{array}{ll}- \hat{x}(t) + \beta _L &{} \quad \text{ for } \quad \hat{x}(t-\hat{\tau }) < 0 \\ - \hat{x}(t) -\beta _U &{} \quad \text{ for } \quad \hat{x}(t-\hat{\tau }) \ge 0, \end{array} \right. \end{aligned}$$

(2.4)

where $\beta _L+\beta _U>0$.

Now we have only a three parameter $(\beta _U, \beta _L, \tau )$ system to consider, having reduced (2.2) to

$$\begin{aligned} \dfrac{dx}{dt}(t) = - x(t) + f(x(t-\tau )) \end{aligned}$$

(2.5)

where the function f is of the form

$$\begin{aligned} f(\xi ) = \left\{ \begin{array}{ll} \beta _L &{} \qquad \text{ for } \quad \xi< 0 \\ -\beta _U &{} \qquad \text{ for } \quad \xi \ge 0, \end{array} \right. \quad -\beta _U<\beta _L, \quad \beta _L,\beta _U\ne 0. \end{aligned}$$

(2.6)

The discontinuity of f requires a moment of reflection about what a solution of Eq. (2.5) should be—certainly not a continuous function $x:[-\tau ,\infty )\rightarrow \mathbb {R}$ which is differentiable and satisfies Eq. (2.5) for all $t>0$, as it is familiar from delay differential equations with a functional on the right hand side which is at least continuous. We shall come back to this in Sect. 3.

3 The semiflow of the unperturbed system

For continuity properties, e.g., continuity of the reset map which is to be introduced in Sect. 4, we need to develop a framework.

Consider the initial value problem of Eq. (2.5) for $t>0$, with initial condition $x(t)=\phi (t)$ for $-\tau \le t\le 0$, and where the function $\phi :[-\tau ,0]\rightarrow \mathbb {R}$ is continuous and has at most a finite number of zeros. Let $C=C([-\tau ,0],\mathbb {R})$ denote the Banach space of continuous functions $[-\tau ,0]\rightarrow \mathbb {R}$ equipped with the maximum-norm, $|\phi |_C=\max _{-\tau \le t\le 0}|\phi (t)|$, and set

$$\begin{aligned} Z=\{\phi \in C:\phi ^{-1}(0)\quad \text {finite or empty}\}. \end{aligned}$$

For initial data $\phi \in Z$ we construct continuous solutions of Eq. (2.5) by means of the variation-of-constants formula as follows. Suppose $z_1<z_2<\cdots <z_J$ are the zeros of $\phi$ in $(-\tau ,0)$. On $(0,z_1+\tau ]$ we define

$$\begin{aligned} x(t)=e^{-t}\phi (0)+\int _0^te^{-(t-s)}f(x(t-s))ds \end{aligned}$$

or,

$$\begin{aligned} x(t)=e^{-t}x(0)-\beta _U(1-e^{-t})=-\beta _U+(x(0)+\beta _U)e^{-t} \end{aligned}$$

(3.1)

in case $0<\phi (v)$ in $(-\tau ,z_1)$,

$$\begin{aligned} x(t)= e^{-t}x(0)+\beta _L(1-e^{-t})=\beta _L+(x(0)-\beta _L)e^{-t} \end{aligned}$$

(3.2)

in case $\phi (v)<0$ in $(-\tau ,z_1)$. Notice that on the interval $[0,z_1+\tau ]$ the solution x is either constant with value $-\beta _U\ne 0$ or $\beta _L\ne 0$, or strictly monotone. We conclude that x has at most one zero in $(0,z_1+\tau )$, and if there is a zero then x changes sign at the zero. Let us call such zeros transversal. In case $\phi$ has no zero in $(-\tau ,0)$ we define x(t) analogously, for $0<t\le \tau$. The procedure just described can be iterated and yields a continuous function $x:[-\tau , \infty )\rightarrow \mathbb {R}$ which we define to be the solution of the initial value problem above.

Notice that all segments, or histories, $x_t$ given by

$$\begin{aligned} x_t(s)=x(t+s)\quad \text {for}\,\,t\ge 0\quad \text {and}\quad -\tau \le s\le 0, \end{aligned}$$

belong to the set Z. We assume that $\beta _L,\beta _U\ne 0$ and we write $x^{\phi }$ instead of x when convenient, and define the semiflow $S:[0,\infty )\times Z\rightarrow Z$ of Eq. (2.5) by

$$\begin{aligned} S(t,\phi )=x^{\phi }_t. \end{aligned}$$

The proof of the following result is given in the appendix.

Proposition 3.1

The semiflow S is continuous.

Remark 3.1

Incidentally, let us see what goes wrong in the excluded cases $\beta _U=0$ and $\beta _L=0$. If $\beta _U=0$ then for each $\phi \in Z$ with $\phi (t)>0$ on $[-\tau ,0)$ and $\phi (0)=0$ the formula (3.1)—or, the equation $x'=-x$—yields $x(t)=0$ for all $t\ge 0$, and Z is not positively invariant. On a set $\tilde{Z}\subset C$ of initial data which contains $0\in C$ and negative data $\psi$ with arbitrarily small norm continuous dependence on initial data would be violated for $\beta _U=0$ because (3.2) yields

$$\begin{aligned} |x(\tau )-0|&= |x(\tau )|=|\beta _L+(x(0)-\beta _L)e^{-\tau }|\\&\ge \beta _L(1-e^{-\tau })-\psi (0)e^{-\tau }\ge \dfrac{1}{2}\beta _L(1-e^{-\tau }) \end{aligned}$$

for the solution starting from negative and sufficiently small $\psi \in \tilde{Z}$.

If $\beta _L=0$ then for each $\phi \in Z$ with $\phi (t)<0$ on $[-\tau ,0)$ and $\phi (0)=0$ we have $x(t)=0$ for $t\in [0,\tau ]$, which implies that Z is not positively invariant in this case as well.

For later use we show next that transversal zeros depend continuously on the initial data $\phi \in Z$.

Proposition 3.2

For $\phi \in Z$ and $z>0$ with $x^{\phi }(z)=0\ne x^{\phi }(z-\tau )$ and $\epsilon >0$, there exists $\delta >0$ such that for each $\psi \in Z$ with $|\psi -\phi |_C<\delta$ there is $z'\in (z-\epsilon ,z+\epsilon )$ with $x^{\psi }(z')=0$. Moreover, $x^{\psi }(z'-\tau )\ne 0$.

Proof

By continuity there exists $\eta \in (0,\epsilon )$ so that $x^{\phi }(s)\ne 0$ on $[z-\tau -\eta ,z-\tau +\eta ]\cap [-\tau ,\infty )$. Using (3.1) and (3.2) we infer that on $[z-\eta ,z+\eta ]$ the solution $x^{\phi }$ either equals a nonzero constant or is strictly monotone. As $x^{\phi }(z)=0$ the solution $x^{\phi }$ must be strictly monotone on $[z-\eta ,z+\eta ]$, with $\mathrm {sign}(x^\phi (z-\eta ))\ne \mathrm {sign}(x^{\phi }(z+\eta ))\ne 0$. By continuous dependence on initial data, there exists $\delta >0$ such that for each $\psi \in Z$ with $|\psi -\phi |_C<\delta$ we have

$$\begin{aligned} x^{\psi }(t)\ne 0\quad \text {on}\,\,[z-\tau -\eta ,z-\tau +\eta ]\cap [-\tau ,\infty ) \end{aligned}$$

and

$$\begin{aligned} \mathrm {sign} (x^{\psi }(z-\eta ))=\mathrm {sign} (x^{\phi }(z-\eta )),\quad \mathrm {sign} (x^{\psi }(z+\eta ))=\mathrm {sign} (x^{\phi }(z+\eta )). \end{aligned}$$

Hence $x^{\psi }$ changes sign in $[z-\eta ,z+\eta ]$, so it has a zero $z'$ in this interval. $\square$

The condition $\beta _L<0$ ($\beta _U<0$) in the next result means that in the original model given by Eq. (2.2) the positive constant solution given by $\gamma x^{*}=f(x^{*})$ has its value $x^{*}$ beyond (above) the discontinuity $\theta$ of f. In this case one may interpret $x^{*}=\theta$ as an equilibrium position for (2.2).

Theorem 3.1

If $\beta _U<0$ or $\beta _L<0$ the equilibrium state of the semi-flow S, which is respectively given by $x^\phi (t)=-\beta _U$ or $x^\phi (t)=\beta _L$ with $\phi \in Z$, is globally asymptotically stable.

Proof

In case $\beta _U < 0$ the constant function $\mathbb {R}\ni t\mapsto -\beta _U\in \mathbb {R}$ is a positive solution. Notice that due to (3.1) every solution $x^{\phi }$ with $0<\phi (t)$ on $[-\tau ,0]$ has its values $x^{\phi }(t)$, $t\ge 0$, between $\phi (0)$ and $-\beta _U$ and converges to $-\beta _U$ as $t\rightarrow \infty$. This implies local asymptotic stability of the positive steady state. Moreover, using (3.1) and (3.2) one can show that every solution $x=x^{\phi }$, $\phi \in Z$, becomes positive on some interval $[\tilde{T}-\tau ,\tilde{T}]$, $\tilde{T}\ge 0$, and is given by

$$\begin{aligned} x(t)=-\beta _U+(x(\tilde{T})+\beta _U)e^{-(t-\tilde{T})} \end{aligned}$$

for $t\ge \tilde{T}$, so it tends to $-\beta _U$ as $t\rightarrow \infty$. The proof in case $\beta _L<0$ is analogous. $\square$

The situation becomes more interesting when $\beta _L,\beta _U >0$ which gives $b_U<\gamma \theta <b_L$ for the original parameters, so that the model Eq. (2.2) does not have a steady state, being a constant function. We will show in the next two theorems that in this case there exists a periodic solution and that it is stable, when the semiflow is restricted to the smaller set $Z_0\subset Z$ of all $\phi \in Z$ which have at most one zero and change sign at this zero z in case $-\tau<z<0$.

We first show that $Z_0$ is positively invariant for the semiflow S, i.e., $S(t,\phi )\in Z_0$ for all $t\ge 0$ and $\phi \in Z_0$. Suppose that $\beta _L>0$ and $\beta _U>0$. For $\phi \in Z_0$ and $x=x^{\phi }$ we make the following observations. If $\phi (z)=0$ and $-\tau<z<0$, and $\phi (t)<0$ for $-\tau \le t<z$ and $0<\phi (t)$ for $z<t\le 0$ then by (3.2), $0<x(t)$ on $(z,z+\tau ]=(z,0]\cup (0,z+\tau ]$. In particular, $x_{z+\tau }\in Z_0$; moreover, $x_t\in Z_0$ for all $t\in [0,z+\tau ]$. Using (3.1) there is a smallest $z'$ in $(0,\infty )$ with $x(z')=0$, $x(t)\ne 0$ on $[z'-\tau ,z')$, and x changes sign at $t=z'$, and we can iterate. Thus we obtain $S(t,\phi )\in Z_0$ for all $t\ge 0$. The same holds for arbitrary $\phi \in Z_0$.

Note that the zeros of $x^{\phi }$, $\phi \in Z_0$ arbitrary, in $(0,\infty )$ are all transversal and form a strictly increasing sequence of times $z_j=z_j(\phi )$, $j\in \mathbb {N}$, with

$$\begin{aligned} z_j+\tau <z_{j+1}\quad \text {and}\quad x(z_j-\tau )\ne 0\quad \text {for all}\quad j\in \mathbb {N}. \end{aligned}$$

From Proposition 3.2 we conclude the following concerning solutions $x:[-\tau ,\infty )\rightarrow \mathbb {R}$ starting from initial data $x_0=\phi \in Z_0$.

Corollary 3.1

Let $\beta _L,\beta _U>0$. Then each map

$$\begin{aligned} Z_0\ni \phi \mapsto z_j(\phi )\in (0,\infty ),\quad j\in \mathbb {N}, \end{aligned}$$

is continuous at every point $\phi \in Z_0$ with $\phi (0)\ne 0$.

We now show the existence of a periodic solution.

Theorem 3.2

Let $\beta _L,\beta _U >0$. Then there is a periodic solution $\tilde{x}:\mathbb {R}\rightarrow \mathbb {R}$ of Eq. (2.5) with

$$\begin{aligned} \tilde{x}(t)=-\beta _U+\beta _Ue^{-(t+\tau )}\quad \text {for}\,\,-\tau \le t\le 0. \end{aligned}$$

We have $\tilde{x}(-\tau )=0$, and with $\tilde{z}_j=z_j(\tilde{x}_0)$ for all $j\in \mathbb {N}$,

$$\begin{aligned} \tilde{x}(t)&= \beta _L+(\tilde{x}(0)-\beta _L)e^{-t}\qquad \text {for}\quad 0\le t\le \tilde{z}_1+\tau ,\\ \tilde{x}(t)&= -\beta _U+(\tilde{x}(\tilde{z}_1+\tau )+\beta _U)e^{-(t-(\tilde{z}_1+\tau ))}\qquad \text {for}\quad \tilde{z}_1+\tau \le t\le \tilde{z}_2+\tau . \end{aligned}$$

The minimal period of $\tilde{x}$ is

$$\begin{aligned} \tilde{T}=\tilde{z}_2+\tau . \end{aligned}$$

Proof

Compute the solution (see Fig. 2) starting from $\phi \in Z_0$ given by

$$\begin{aligned} \phi (t)=-\beta _U+\beta _Ue^{-(t+\tau )}. \end{aligned}$$

$\square$

It is convenient to set $\tilde{z}_0=-\tau$.

Corollary 3.2

Let $\beta _L,\beta _U>0$. The minimum of $\tilde{x}$ is given by

$$\begin{aligned} \underline{x}=\tilde{x}(0)= -\beta _U(1- e^{-\tau })<0, \end{aligned}$$

the maximum of $\tilde{x}$ is given by

$$\begin{aligned} \overline{x}=\tilde{x}(\tilde{z}_1+\tau )=\beta _L (1- e^{- \tau })>0, \end{aligned}$$

and

$$\begin{aligned} \tilde{z}_1= & {} \ln \dfrac{\beta _L - \underline{x} }{\beta _L }, \qquad \tilde{z}_2=\tilde{z}_1+\tau +\ln \dfrac{\overline{x} + \beta _U}{ \beta _U},\\ \tilde{T}= & {} \tilde{z}_2+\tau =2\tau +\ln \left( \dfrac{\beta _L - \underline{x} }{\beta _L } \cdot \dfrac{\overline{x} + \beta _U}{ \beta _U}\right) . \end{aligned}$$

Fig. 2

A graph of the periodic solution on the interval $[-\tau ,\tilde{T}]$

Occasionally we shall abbreviate

$$\begin{aligned} t_{\max }=\tilde{z}_1+\tau \end{aligned}$$

for the first non-negative time where $\tilde{x}$ achieves its maximum. Accordingly,

$$\begin{aligned} t_{\min }=0. \end{aligned}$$

Remark 3.2

For $\beta _U >0$ there are infinitely many other periodic orbits in Z, given by periodic solutions of higher oscillation frequencies, compare (Diekmann et al. 1995, Chapter XVI) which deals with the simpler equation

$$\begin{aligned} x'(t)=-\mathrm {sign}(x(t-1)). \end{aligned}$$

Therefore the periodic orbit

$$\begin{aligned} \tilde{O}=\{\tilde{x}_t\in Z:t\in \mathbb {R}\}\subset Z_0 \end{aligned}$$

is not globally attracting on Z.

Theorem 3.3

Let $\beta _L,\beta _U>0$. Then for every $\phi \in Z_0$ we have either

$$\begin{aligned} x^{\phi }(t+z_1(\phi )+\tau )=\tilde{x}(t)\qquad \text {for all}\quad t\ge -\tau \end{aligned}$$

or

$$\begin{aligned} x^{\phi }(t+z_1(\phi )+\tau )=\tilde{x}(t+\tilde{z}_1+\tau )\qquad \text {for all}\quad t\ge -\tau , \end{aligned}$$

and the periodic orbit $\tilde{O}\subset Z_0$ is stable.

Proof

• 1. For $\phi \in Z_0$, $x=x^{\phi }$, and $z_1=z_1(\phi )$ we infer from (3.1) and (3.2) that either x is strictly decreasing on $[z_1,z_1+\tau ]$, or that x is strictly increasing on $[z_1,z_1+\tau ]$. In the first case we obtain

  $$\begin{aligned} x(t+z_1+\tau )=\tilde{x}(t)\qquad \text {for all}\quad t\ge -\tau \end{aligned}$$

  while in the second case,

  $$\begin{aligned} x(t+z_1+\tau )=\tilde{x}(t+\tilde{z}_1+\tau )\qquad \text {for all}\quad t\ge -\tau . \end{aligned}$$

  In both cases, $x^{\phi }_t$ is on the periodic orbit $\tilde{O}$ for $t\ge z_1(\phi )+\tau$.

• 2. There exist $r>0$ and $\rho \in (0,\tilde{z}_1)$ with $\tilde{x}(t)\le -r$ for $\tilde{z}_1-\rho -\tau \le t\le \tilde{z}_1-\rho$ and $\tilde{x}(\tilde{z}_1+\rho )\ge r$. It follows that for each $\psi \in \tilde{O}$ the shifted copy $x^{\psi }$ of $\tilde{x}$ has the property that there exists $u=u(\psi )\in [0,\tilde{T}]$ with $x^{\psi }(t)\le -r$ for $u\le t\le u+\tau$ and $x^{\psi }(u+\tau +2\rho )\ge r$. Observe that for every $\phi \in Z$ with $x^{\phi }(t)<0$ for $u\le t\le u+\tau$ and $x^{\phi }(u+\tau +2\rho )>0$ the solution $x^{\phi }$ has a first zero z in $(u+\tau ,u+\tau +2\rho )$, and $x^{\phi }_{z+\tau }\in \tilde{O}$, which implies that all segments $x^{\phi }_t$ with $t\ge \tilde{T}+2\tau +2\rho$ belong to the orbit $\tilde{O}$.

• 3. Let $\epsilon >0$. Continuous dependence on initial data yields that the map

  $$\begin{aligned} Z\ni \phi \mapsto x^{\phi }|_{[-\tau ,\tilde{T}+2\tau +2\rho ]}\in C([-\tau ,\tilde{T}+2\tau +2\rho ],\mathbb {R}), \end{aligned}$$

  where $x^{\phi }|_{I}$ denotes the restriction of the function $x^{\phi }$ to the interval I, is continuous (with respect to the maximum-norm on the target space). Using uniform continuity on the compact orbit $\tilde{O}\subset Z$ we find $\delta >0$ so that for all $\phi \in Z$ and all $\psi \in \tilde{O}$ with $|\phi -\psi |_C<\delta$ we have

  $$\begin{aligned} |x^{\phi }(t)-x^{\psi }(t)|<\min \left\{ \epsilon ,\dfrac{r}{2}\right\} \qquad \text {for all}\quad t\in [-\tau ,\tilde{T}+2\tau +2\rho ]. \end{aligned}$$

  Let $\phi \in Z$ with $\text {dist}(\phi ,\tilde{O})=\inf _{\psi \in \tilde{O}}|\phi -\psi |_C<\delta$ be given. Then for some $\psi \in \tilde{O}$, $|\phi -\psi |_C<\delta$. Choose $u=u(\psi )\in [0,\tilde{T}]$ according to Part 2. The previous estimate of $|x^{\phi }(t)-x^{\psi }(t)|$ yields $x^{\phi }(t)<0$ for $u\le t\le u+\tau$ and $x^{\phi }(u+\tau +2\rho )>0$. Using part 2 we infer $x^{\phi }_t\in \tilde{O}$ for $t\ge \tilde{T}+2\tau +2\rho$. Altogether,

  $$\begin{aligned} \text {dist}(x^{\phi }_t,\tilde{O})<\epsilon \qquad \text {for}\quad 0\le t\le \tilde{T}+2\tau +2\rho \end{aligned}$$

  and $\text {dist}(x^{\phi }_t,\tilde{O})=0$ for $t\ge \tilde{T}+2\tau +2\rho$.

$\square$

Remark 3.3

One can show that the other periodic orbits are all unstable, and that the domain of attraction of the periodic orbit $\tilde{O}$ is open and dense in Z, compare (Diekmann et al. 1995, Chapter XVI), and the main result of Mallet-Paret and Walther (1994) about Eq. (1.1) with a smooth and strictly monotone function f.

4 Pulse-like perturbations

In the following we assume

$$\begin{aligned} -\beta _U<0<\beta _L \end{aligned}$$

and study a particular, simple deviation from the periodic solution $\tilde{x}$ and the subsequent return to the stable and attracting periodic orbit $\tilde{O}$: We consider a function $x^{(\Delta )}:\mathbb {R}\rightarrow \mathbb {R}$ which up to $t=\Delta \in [0,\tilde{T})$ equals the periodic solution $\tilde{x}$ of Eq. (2.5). Then for $\Delta \le t\le \Delta +\sigma$ the function $x^{(\Delta )}$ is defined by the equation

$$\begin{aligned} x'(t)=-x(t)+f(x(t-\tau ))+a \end{aligned}$$

with a constant $a>0$. This results in a deviation from the periodic solution $\tilde{x}$ which begins at time $t=\Delta$ and lasts until the time $t=\Delta +\sigma$. Informally we speak of a pulse of amplitude a, with $\Delta$ the onset time of the pulse and $\sigma$ the duration of the pulse. For $t\ge \Delta +\sigma$, the function $x^{(\Delta )}$ is given again by Eq. (2.5). For perturbations $a>0$ not too large it will merge into the periodic solution in finite time, compare Theorem 3.3.

An interpretation of this is as follows. Eq. (2.5) is a mathematically convenient form of a (very simple) model for the production and decay of blood cells of a certain type, e.g. neutrophils. The periodic solution $\tilde{x}$ stands for the density of neutrophils in a patient as a function of time, perhaps induced by chemotherapy or as a consequence of cyclical neutropenia but in the absence of any further medical intervention. The function $x^{(\Delta )}$ describes the evolution of the neutrophil density for the case that at time $\Delta -\tau$ some medication has been administered which increases the production of cells in the bone marrow during the time interval $[\Delta -\tau ,\Delta -\tau +\sigma ]$. The constant $a>0$ stands for the increase in production occasioned, for example, by the administration of G-CSF. After the time $\tau >0$ needed for production (and differentiation) of cells, that is, during the time interval $[\Delta , \Delta +\sigma ]$ the neutrophils are released into the blood stream. Later on production and decay of neutrophils is again governed by the patient’s feedback system alone.

For simplicity we assume

$$\begin{aligned} 0<\sigma \le \tau , \end{aligned}$$

from here on, that is, the effect of intervention lasts for a time interval $\sigma$ less than the (production) delay $\tau$. The quantities we are interested in are the local extrema of $x^{(\Delta )}$ and the time required to return to the periodic orbit. The latter is captured by the cycle length map

$$\begin{aligned} T:[0,\tilde{T})\ni \Delta \mapsto T(\Delta )\in \mathbb {R}\cup \{\infty \} \end{aligned}$$

which is defined formally as follows: The zeros of $x^{(\Delta )}$ and of $\tilde{x}$ in $(-\infty ,\Delta ]$ coincide. Suppose $\tilde{z}_J$, $J=j(\Delta )\in \{0,1,2\}$, is the largest one of these zeros, and there exists a smallest zero $z>\tilde{z}_J$ of $x^{(\Delta )}$ with $x^{(\Delta )}(z+t)=\tilde{x}(\tilde{z}_J+t)$ for all $t\ge 0$. Then

$$\begin{aligned} T(\Delta )=z-\tilde{z}_J,\quad \text {and}\quad T(\Delta )=\infty \quad \text {otherwise}. \end{aligned}$$

In case $T(\Delta )<\infty$ let

$$\begin{aligned} \underline{x}_{\Delta }=\min _{\tilde{z}_J\le t\le z}x^{(\Delta )}(t) \end{aligned}$$

and

$$\begin{aligned} \overline{x}_{\Delta }=\max _{\tilde{z}_J\le t\le z}x^{(\Delta )}(t). \end{aligned}$$

Remark 4.1

Observe that in our model situation treatment is considered successful if the minimal value $\underline{x}_{\Delta }$ is above the minimal value

of $\tilde{x}$ while in the opposite case medication actually increases the risk for the patient in the sense that the nadir of the oscillation is lower and would thus lead to more severe cytopenia which is one of the major clinical problems.

The local minima and maxima of the function $x^{(\Delta )}$ and the cycle length $T(\Delta )$ depend on the parameters

$$\begin{aligned} \tau>0,\quad \beta _L>0>-\beta _U,\quad a>0,\quad \sigma \in (0,\tau ],\quad \text {and}\quad \Delta \ge 0. \end{aligned}$$

We assume that

$$\begin{aligned} -\beta _U+a<0, \end{aligned}$$

which will be instrumental in showing that after perturbation solutions do return to the periodic solution $\tilde{x}$, with the consequence that cycle lengths are finite. (For larger parameter a solutions after perturbation may settle down on other, unstable periodic solutions of Eq. (2.5), with higher oscillation frequencies. For more on this, see Remark 5.4.) In the remainder of this section we keep the parameters $\tau , \beta _L, \beta _U, a, \sigma$ fixed. In addition to finiteness of cycle lengths we shall see that the cycle length map and the maps

$$\begin{aligned}{}[0,\tilde{T})\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}\quad \text {and}\quad [0,\tilde{T})\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

are continuous.

For $a>0$ with $-\beta _U+a<0$ the solutions $x=x^{a,\phi }$ of the initial value problem

$$\begin{aligned} x'(t)=-x(t)+f(x(t-\tau ))+a\quad \text {for}\,\,t>0,\,\,x_0=\phi \end{aligned}$$

define a continuous semiflow $S_a:[0,\infty )\times Z\rightarrow Z$ by $S_a(t,\phi )=x^{a,\phi }_t$, see Sect. 3. The set $Z_0$ is positively invariant under $S_a$, and for each $\phi \in Z_0$ the zeros of $x^{a,\phi }$ are all transversal and spaced at distances larger than the delay $\tau$.

The solution $x=x^{(\Delta )}$ during a pulse (which begins at $\Delta \in [0,\tilde{T})$) can now be described as follows: For $\Delta$ given, define $\phi =\tilde{x}_{\Delta }$ and then $\chi =S_a(\sigma ,\phi )=x^{a,\phi }_{\sigma }$. We obtain

$$\begin{aligned} x(t)&= \tilde{x}(t)\quad \text {for}\,\,t\le \Delta ,\\ x(t)&= x^{a,\phi }(t-\Delta )\quad \text {for}\,\,\Delta \le t\le \Delta +\sigma ,\\ x(t)&= x^{\chi }(t-(\Delta +\sigma ))\quad \text {for}\,\,t\ge \Delta +\sigma , \end{aligned}$$

or equivalently,

$$\begin{aligned} x_t&= \tilde{x}_t\quad \text {for}\,\,t\le \Delta ,\\ x_t&= S_a(t-\Delta ,x_{\Delta })\quad \text {for}\,\,\Delta \le t\le \Delta +\sigma ,\\ x_t&= S(t-(\Delta +\sigma ),x_{\Delta +\sigma })\quad \text {for}\,\,t\ge \Delta +\sigma . \end{aligned}$$

Notice that for $x=x^{(\Delta )}$, all zeros are transversal and spaced at distances larger than the delay $\tau$. They form a strictly increasing sequence of points

$$\begin{aligned} z_{\Delta ,j},\quad j\in \mathbb {Z},\quad \text {with}\quad z_{\Delta ,j}=\tilde{z}_j\quad \text {for all integers}\quad j\le j_{\Delta } \end{aligned}$$

where $J=j_{\Delta }\in \{0,1,2\}$ is given by

$$\begin{aligned} \tilde{z}_J\le \Delta <\tilde{z}_{J+1}. \end{aligned}$$

Using $\tilde{x}_t=S(t,\tilde{x}_0)$ for all $t\ge 0$ and the continuity of both semiflows we easily obtain from the previous representation of $x_t=x^{(\Delta )}_t$ that the map

$$\begin{aligned}{}[0,\tilde{T})\times [0,\infty )\ni (\Delta ,t)\mapsto x^{(\Delta )}_t\in C \end{aligned}$$

is continuous, which in turn yields the continuity of the map

$$\begin{aligned}{}[0,\tilde{T})\times [0,\infty )\ni (\Delta ,t)\mapsto x^{(\Delta )}(t)\in \mathbb {R} \end{aligned}$$

since $x^{(\Delta )}(t)=ev(x^{(\Delta )}_t)$ and the evaluation $ev:C\ni \phi \mapsto \phi (0)\in \mathbb {R}$ is continuous. Arguing as in the proof of Proposition 3.2 and using transversality of zeros we obtain the following results.

Proposition 4.1

For $\Delta _0\in [0,\tilde{T})$ and $z>0$ with $x^{(\Delta )}(z)=0$ and $\epsilon >0$ there exists $\delta >0$ such that for each $\Delta \in [0,\tilde{T})$ with $|\Delta -\Delta _0|<\delta$ there is $z'\in (z-\epsilon ,z+\epsilon )$ with $x^{\Delta }(z')=0$.

Corollary 4.1

Each map

$$\begin{aligned}{}[0,\tilde{T})\ni \Delta \mapsto z_{\Delta ,j}\in (0,\infty ),\quad j\in \mathbb {N}, \end{aligned}$$

is continuous.

The proofs of the following results are provided in the appendix.

Proposition 4.2

For every $\Delta \in [0,\tilde{T})$ we have $T(\Delta )=z_{\Delta ,J+2}-z_{\Delta ,J}$ with $J=j_{\Delta }$.

Corollary 4.2

The cycle length map is continuous.

Proposition 4.3

The maps $[0,\tilde{T})\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}$ and $[0,\tilde{T})\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ are continuous.

5 Computation of the response

In the Sects. 5.1–5.4 below we keep the parameters $\tau>0,\beta _L>0>-\beta _U, a>0,\sigma \in (0,\tau ]$ fixed and require $-\beta _U+a<0$ as in the preceding section, and study the behaviour of $x^{(\Delta )}$ depending on the onset of the pulse (at $t=\Delta$) and on its termination (at $t=\Delta +\sigma$) relative to the zeros and extrema

$$\begin{aligned} 0<\tilde{z}_1<\tilde{z}_1+\tau =t_{\max }<\tilde{z}_2<\tilde{z}_2+\tau =\tilde{T}<\tilde{z}_3, \end{aligned}$$

of the periodic solution $\tilde{x}$, on the sign of $x^{(\Delta )}(\Delta +\sigma )$, and on the position of $x^{(\Delta )}(\Delta +\sigma )$ relative to the level $\beta _L$.

The computations that follow in this section can become quite difficult to keep track of, and we therefore use what we hope is a simple and transparent nomenclature to aid the reader in following our progression. The reader may wish to consult Tables 1, 2 and 3 as a way of keeping track of the result.

Table 1 Summary of the effects of a positive pulse $(a > 0, \Delta , \sigma )$ at different times during the limit cycle on the limit cycle minimum ($\underline{x}$), maximum ($\overline{x}$), and period ($\tilde{T}$)

Table 2 Summary of the effects of a positive pulse when $t_{\max }\le \delta _2$

Table 3 Summary of the effects of a positive pulse in the remaining cases where $\delta _1$ is as in (5.6)

If the pulse starts at $\Delta \in [0,t_{\max })$, where the periodic solution is increasing, then we say that we are in the rising phase and we use the letter R. If it starts at $\Delta \in [t_{\max },\tilde{T})$, where the periodic solution is decreasing, then we say that we are in the falling phase and we use the letter F. If $x^{(\Delta )}(t)$ is negative at the beginning of the pulse, i.e., $x^{(\Delta )}(\Delta )<0$, then we use the letter N (negative value at $\Delta$) and otherwise we write P (non-negative value at $\Delta$). We can thus say that we are in the subcase RN when we are at rising phase with a negative value at $\Delta$. Therefore the beginning of the pulse can be coded with two letters which gives four subcases: RN, RP, FN, FP. In the same way we can code the end of the pulse, namely if $\Delta +\sigma \in [t_{\max },\tilde{T})$, where the periodic solution is decreasing, then we are in the falling phase and we use the letter F, otherwise we write R. If $x^{(\Delta )}(\Delta +\sigma )<0$, then we use the letter N and if $x^{(\Delta )}(\Delta +\sigma )\ge 0$ the letter P. Here similarly, we can have four subcases and we combine them together to code each case with four letters. For example the case RNRN corresponds to the rising phase at $\Delta$ and at $\Delta +\sigma$ with negative values of $x^{(\Delta )}$ at $\Delta$ and at $\Delta +\sigma$.

There are three different periods of time that are important: before the pulse occurs, during the pulse, and after the pulse. We can easily write down the values $x^{(\Delta )}(t)$ before the pulse in each phase. If $\Delta \in [0,t_{\max })$ then we have

$$\begin{aligned} x^{(\Delta )}(t) = \beta _L + (\underline{x} - \beta _L) e^{-t } =\tilde{x}(t) \quad \text {for}\quad t \in [ 0, \Delta ] \end{aligned}$$

and the value of $x^{(\Delta )}$ when the pulse turns on is

$$\begin{aligned} x^{(\Delta )}(\Delta ) = \beta _L + (\underline{x} - \beta _L ) e^{-\Delta } =\tilde{x}(\Delta ). \end{aligned}$$

From the definition of $\underline{x}$ it follows that $\beta _L -\underline{x}=\beta _Le^{\tilde{z}_1}$, which gives the following formula

$$\begin{aligned} x^{(\Delta )}(\Delta )=\beta _L - \beta _L e^{\tilde{z}_1-\Delta }\quad \text {for}\quad \Delta \in [0,t_{\max }). \end{aligned}$$

(5.1)

If $\Delta \in [t_{\max },\tilde{T})$ then

$$\begin{aligned} x^{(\Delta )}(t) = -\beta _U + (\overline{x} + \beta _U) e^{-(t- t_{\max })}=\tilde{x}(t) \quad \text {for}\quad t \in [t_{\max },\Delta ] \end{aligned}$$

and

$$\begin{aligned} x^{(\Delta )}(\Delta )= -\beta _U + (\overline{x} + \beta _U) e^{-(\Delta - t_{\max })}. \end{aligned}$$

Since $\overline{x} +\beta _U=\beta _Ue^{\tilde{z}_2-t_{\max }}$, we obtain

$$\begin{aligned} x^{(\Delta )}(\Delta ) = -\beta _U + \beta _U e^{\tilde{z}_2-\Delta }\quad \text {for}\quad \Delta \in [t_{\max },\tilde{T}). \end{aligned}$$

(5.2)

5.1 A pulse during the rising phase

We assume $0\le \Delta <\Delta +\sigma \le t_{\max }$. Then $x^{(\Delta )}(\Delta )$ is given by (5.1). During the pulse,

$$\begin{aligned} x^{(\Delta )}(t) = (\beta _L + a) + \bigl (x^{(\Delta )}(\Delta ) - (\beta _L + a)\bigr ) e^{-(t- \Delta )} \quad \text{ for } \quad t \in [ \Delta , \Delta + \sigma ], \end{aligned}$$

(5.3)

and after the pulse,

$$\begin{aligned} x^{(\Delta )}(t)&= \beta _L + (x^{(\Delta )}(\Delta + \sigma ) - \beta _L) e^{-\left( t-( \Delta + \sigma )\right) }\nonumber \\&\!\!\qquad \text{ for } \quad t>\Delta + \sigma \quad \text{ as } \text{ long } \text{ as }\quad x^{(\Delta )}(t-\tau )<0, \end{aligned}$$

(5.4)

with

$$\begin{aligned} x^{(\Delta )}( \Delta + \sigma ) = \beta _L + a + \bigl (x^{(\Delta )}(\Delta ) - (\beta _L + a)\bigr ) e^{-\sigma }. \end{aligned}$$

Using (5.1) we have

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )=\beta _L - \beta _L e^{\tilde{z}_1-\Delta -\sigma }+a(1-e^{-\sigma }). \end{aligned}$$

(5.5)

• Case $\mathbf {RNR}$ The pulse starts before $\tilde{z}_1=t_{\max }-\tau$, $0\le \Delta <\tilde{z}_1$.

Observe first that $\Delta \in [0,\tilde{z}_1)$ is such that $x^{(\Delta )}(\Delta +\sigma )<0$ if and only if

$$\begin{aligned} \beta _L+a(1-e^{-\sigma })< \beta _L e^{\tilde{z}_1-\Delta -\sigma } \end{aligned}$$

which in view of $\beta _L+a(1-e^{-\sigma })>0$ is equivalent to

$$\begin{aligned} e^{\Delta }< \dfrac{\beta _L e^{\tilde{z}_1-\sigma }}{\beta _L+a(1-e^{-\sigma })}. \end{aligned}$$

Let us define

$$\begin{aligned} \delta _1=\ln \dfrac{\beta _L e^{\tilde{z}_1-\sigma }}{\beta _L+a(1-e^{-\sigma })}=\ln \dfrac{\beta _L+\beta _U(1-e^{-\tau })}{\beta _Le^{\sigma }+a(e^{\sigma }-1)}. \end{aligned}$$

(5.6)

We have

$$\begin{aligned} \delta _1=\tilde{z}_1-\sigma -\ln \dfrac{\beta _L+a(1-e^{-\sigma })}{\beta _L}<\tilde{z}_1. \end{aligned}$$

If $\delta _1>0$ we obtain $x^{(\Delta )}(\Delta +\sigma )<0$ for $0\le \Delta <\delta _1$ and $x^{(\Delta )}(\Delta +\sigma )\ge 0$ for $\Delta \in [\delta _1,\tilde{z}_1)$ while if $\delta _1\le 0$ we have $x^{(\Delta )}(\Delta +\sigma )\ge 0$ for all $\Delta \in [0,\tilde{z}_1)$. We consider three subcases.

• Case $\mathbf {RNRN}$ The pulse parameters $(a,\Delta ,\sigma )$ are such that $x^{(\Delta )}(t)$ remains negative during the pulse, $x^{(\Delta )}(\Delta +\sigma )<0$. Equivalently, $\delta _1>0$ and $\Delta \in [0,\delta _1)= I_{RNRN}$.

Proposition 5.1

If $\Delta \in I_{RNRN}=[0,\delta _1)$ then $\underline{x}_{\Delta }=\underline{x}$, $\overline{x}_{\Delta }=\overline{x}$, and

$$\begin{aligned} T(\Delta )= \tilde{T}+\ln \left( 1-\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1}\right) <\tilde{T}. \end{aligned}$$

(5.7)

In particular, the restriction of the map T to $I_{RNRN}$ is strictly decreasing.

We now consider the case RNRP when $x^{(\Delta )}(\Delta +\sigma )\ge 0$. From Fig. 3 we expect that the first local maximum of $x^{(\Delta )}$ after $t=\Delta$ is achieved before $t=t_{\max }$ and is not smaller than $\overline{x}$. In the following we prove this. Also we shall obtain a result about the cycle length $T(\Delta )$ of $x^{(\Delta )}$. However this time we can not conclude that either $T(\Delta ) > \tilde{T}$ or $T(\Delta ) < \tilde{T}$, see Figs. 3 and 4, respectively.

Fig. 3

A schematic representation of the solution of the DDE when $0\le x^{(\Delta )}(\Delta +\sigma )\le \beta _L$. The unperturbed periodic solution $\tilde{x}$ is the solid line and the solution $x^{(\Delta )}$ is the dashed line

Fig. 4

A schematic representation of the solution of the DDE when $x^{(\Delta )}(\Delta +\sigma )>\beta _L$. As usual, the unperturbed periodic solution $\tilde{x}$ is the solid line and the solution $x^{(\Delta )}$ is the dashed line

From (5.3) in combination with $x^{(\Delta )}(\Delta )<0<\beta _L+a$ we see that $x^{(\Delta )}$ is strictly increasing on $[\Delta ,\Delta +\sigma ]$. So by $0\le x^{(\Delta )}(\Delta +\sigma )$ we obtain a first positive zero $z_{\Delta ,1}$ of $x^{(\Delta )}$, and

$$\begin{aligned} \Delta <z_{\Delta ,1}\le \Delta +\sigma . \end{aligned}$$

Proposition 5.2

If $\Delta \in [\max \{0,\delta _1\},\tilde{z}_1)$ then $T(\Delta )<\infty$, $\underline{x}_{\Delta }=\underline{x}$, $\overline{x}_{\Delta }\ge \overline{x}$, and

$$\begin{aligned} T(\Delta )=\tilde{T}+\ln \left( 1+\dfrac{a(e^{\sigma }-1)}{\beta _U} e^{\Delta -\tilde{z}_2}+\dfrac{a(\beta _L+\beta _U)e^{\tau +\tilde{z}_1-\tilde{z}_2}}{\beta _U(\beta _L+a)}(e^{\Delta -\tilde{z}_1}-1)\right) . \end{aligned}$$

(5.8)

Moreover, the maximal value $\overline{x}_{\Delta }$ is given by $\max \{x^{(\Delta )}(z_{\Delta ,1}+\tau ),x^{(\Delta )}(\Delta +\sigma )\}$ and is strictly increasing with respect to $\Delta \in [\max \{0,\delta _1\},\tilde{z}_1)$.

• Case $\mathbf {RPRP}$ The pulse occurs completely in the interval $[\tilde{z}_1, t_{\max }]$. This is equivalent to $\Delta \in [\tilde{z}_1,t_{\max }-\sigma ]= I_{RPRP}$.

Proposition 5.3

If $\Delta \in [\tilde{z}_{1},t_{\max }-\sigma ]$ then $T(\Delta )<\infty$, $\underline{x}_{\Delta }=\underline{x}$, $\overline{x}_{\Delta }> \overline{x}$, and

$$\begin{aligned} T(\Delta )=\tilde{T}+\ln \left( 1+\dfrac{a(e^{\sigma }-1)}{\beta _U}e^{ \Delta -\tilde{z}_2}\right) >\tilde{T}. \end{aligned}$$

(5.9)

Moreover, the map $\overline{x}_{\Delta }$ is strictly increasing on $I_{RPRP}=[\tilde{z}_{1},t_{\max }-\sigma ]$.

Remark 5.1

For $\delta _1>0$ and $\Delta$ close to $\delta _1$ we have $T(\Delta )<\tilde{T}$.

5.2 A pulse from the rising phase into the falling phase

Here we assume $\Delta \le t_{\max }<\Delta +\sigma$. Then $x^{(\Delta )}(\Delta )$ is still given by (5.1). Since $\sigma \le \tau$, we must have $\Delta > \tilde{z}_1$, thus $x^{(\Delta )}(\Delta )>0$. The largest zero of $\tilde{x}$ in $(-\infty ,\Delta ]$ is $\tilde{z}_1$. Also, with $t_{\max }=\tilde{z}_1+\tau$,

$$\begin{aligned} x^{(\Delta )}(t_{\max })&=\beta _L+a+\bigl (x^{(\Delta )}(\Delta )-(\beta _L+a)\bigr )e^{-( t_{\max }-\Delta )}\\&= \beta _L-\beta _Le^{-\tau }+a\bigl (1-e^{-( t_{\max }-\Delta )}\bigr )\\&= \overline{x} + a(1-e^{\Delta - t_{\max }})\ge \overline{x}, \end{aligned}$$

and we can write

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+a+\bigl (x^{(\Delta )}(t_{\max })+\beta _U-a\bigr )e^{-( t-t_{\max })}\quad \text {for}\quad t\in [t_{\max },\Delta +\sigma ]. \end{aligned}$$

Observe that the function $[t_{\max },\Delta +\sigma )\ni t\mapsto x^{(\Delta )}(t)\in \mathbb {R}$ is decreasing since $x^{(\Delta )}(t_{\max })+\beta _U-a\ge 0$.

We have

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )&= -\beta _U+a+\bigl (x^{(\Delta )}(t_{\max })+\beta _U-a\bigr )e^{-( \Delta +\sigma -t_{\max })}\\&= -\beta _U+a+\bigl (\beta _U e^{\tilde{z}_2-t_{\max }}-ae^{\Delta - t_{\max }}\bigr )e^{-( \Delta +\sigma -t_{\max })}, \end{aligned}$$

which gives

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )=-\beta _U+\beta _Ue^{\tilde{z}_2-( \Delta +\sigma )} +a(1-e^{-\sigma }). \end{aligned}$$

(5.10)

Using

$$\begin{aligned} \tilde{z}_1+\tau<\Delta +\sigma \le \tilde{z}_1+\tau +\sigma <\tilde{z}_2+\tau \end{aligned}$$

we have

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{-\left( t-(\Delta +\sigma )\right) }\quad \text {for}\quad \Delta + \sigma \le t\le \tilde{z}_2+\tau \end{aligned}$$

and in particular

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )=\tilde{x}(\Delta +\sigma )+a(1-e^{-\sigma }), \end{aligned}$$

which yields $x^{(\Delta )}(\Delta +\sigma )>\tilde{x}(\Delta +\sigma )$.

We say that we are in

• Case $\mathbf {RPF}$ We distinguish between the subcases

  P :

  $x^{(\Delta )}(\Delta +\sigma )\ge 0$, see Fig. 5,

  N :

  $x^{(\Delta )}(\Delta +\sigma )<0$, see Fig. 6.

Fig. 5

A schematic representation of the solution of the DDE for the case $\mathbf {RPFP}$. The unperturbed limit cycle is the solid line while the solution with the pulse is the dashed line

Fig. 6

A schematic representation of the solution of the DDE for the case $\mathbf {RPFN}$. The unperturbed limit cycle is the solid line while the solution with the pulse is the dashed line

Note that $\Delta \in (t_{\max }-\sigma ,t_{\max }]$ is such that $x^{(\Delta )}(\Delta +\sigma )\ge 0$ if and only if

$$\begin{aligned} \beta _Ue^{\tilde{z}_2-( \Delta +\sigma )}\ge \beta _U-a(1-e^{-\sigma }). \end{aligned}$$

Since $\beta _U>a\ge a(1-e^{-\sigma })$, we have $\beta _U-a(1-e^{-\sigma })>0,$ which implies that $x^{(\Delta )}(\Delta +\sigma )\ge 0$ if and only if

$$\begin{aligned} e^{\Delta }\le \dfrac{\beta _Ue^{\tilde{z}_2}}{\beta _Ue^{\sigma }-a(e^{\sigma }-1)}. \end{aligned}$$

Let us define $\delta _2$ by

$$\begin{aligned} \delta _2=\ln \dfrac{\beta _Ue^{\tilde{z}_2-\sigma }}{\beta _U-a(1-e^{-\sigma })}. \end{aligned}$$

(5.11)

We conclude that the $\Delta$-intervals in the two subcases are of the form

$$\begin{aligned} I_{ RPFP}&= (t_{\max }-\sigma ,t_{\max }]\cap (-\infty ,\delta _2]\quad \text {and}\\ I_{ RPFN}&= (t_{\max }-\sigma ,t_{\max }]\cap (\delta _2,\infty ). \end{aligned}$$

We have

$$\begin{aligned} \delta _2=\tilde{z}_2-\sigma +\ln \dfrac{\beta _U}{\beta _U-a(1-e^{-\sigma })}. \end{aligned}$$

Notice that $\delta _2>\tilde{z}_2-\sigma ,$ which implies that $\delta _2>t_{\max }-\sigma$. Consequently, if

$$\begin{aligned} \beta _Ue^{\sigma }-a(e^{\sigma }-1)\le \beta _U+\beta _L(1-e^{-\tau }), \end{aligned}$$

which is equivalent to $\delta _2\ge t_{\max }$, then $x^{(\Delta )}(\Delta +\sigma )\ge 0$ for all $\Delta \in (t_{\max }-\sigma ,t_{\max }]$. If the reverse inequality

$$\begin{aligned} \beta _U+\beta _L(1-e^{-\tau })<\beta _Ue^{\sigma }-a(e^{\sigma }-1) \end{aligned}$$

(5.12)

holds then $\delta _2<t_{\max }$ and $\delta _2$ is the maximal value of $\Delta \in (t_{\max }-\sigma ,t_{\max }]$ such that $x^{(\Delta )}(t)$ changes the sign at $\Delta +\sigma$, from a positive value to a negative value, $x^{(\Delta )}(\Delta +\sigma )\ge 0$ for all $\Delta \in (t_{\max }-\sigma ,\delta _2]$ and $x^{(\Delta )}(\Delta +\sigma )< 0$ for all $\Delta \in (\delta _2,t_{\max }]$. Inequality (5.12) can be rewritten as

$$\begin{aligned} \beta _L(1-e^{-\tau })<(\beta _U-a)(e^{\sigma }-1). \end{aligned}$$

Proposition 5.4

If $\Delta \in I_{RPFP}$ then $T(\Delta )<\infty$, $\underline{x}_{\Delta }=\underline{x}$, $\overline{x}_{\Delta }>\overline{x}$, and $T(\Delta )$ is given by formula (5.9) as in Proposition 5.3. The map $I_{RPFP} \ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}$ is strictly decreasing and $I_{RPFP} \ni \Delta \mapsto T(\Delta )\in \mathbb {R}$ is strictly increasing.

Proposition 5.5

If $\Delta \in I_{RPFN}$ then $T(\Delta )<\infty$, $\underline{x}_{\Delta }>\underline{x}$,

$$\begin{aligned} \overline{x}_{\Delta }=\overline{x}+a\bigl (1-e^{\Delta -t_{\max }}\bigr )\ge \overline{x}, \end{aligned}$$

and

$$\begin{aligned} T(\Delta )=\tilde{T}+\ln \left( 1-\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1-\tilde{T}}-\dfrac{a(\beta _L+\beta _U)e^{-\tilde{z}_1}}{\beta _L(\beta _U-a)}(e^{\Delta -\tilde{z}_2}-1)\right) . \end{aligned}$$

(5.13)

Moreover, the map $I_{RPFN} \ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ is strictly increasing and the map $I_{RPFN} \ni \Delta \mapsto T(\Delta )\in \mathbb {R}$ is strictly decreasing.

Remark 5.2

For $\Delta$ close to $\delta _2$ we have $T(\Delta )>\tilde{T}$.

5.3 A pulse during the falling phase

Suppose now that $x^{(\Delta )}(\Delta )$ is given by (5.2) for $\Delta \in [t_{\max },\tilde{T})$. We have

$$\begin{aligned} x^{(\Delta )}(t) = -\beta _U + a + \bigl (x^{(\Delta )}(\Delta ) + \beta _U-a\bigr ) e^{-(t-\Delta )} \end{aligned}$$

for $\Delta \le t\le \Delta +\sigma$ as long as $x^{(\Delta )}(t-\tau )>0$.

We assume that $t_{\max }\le \Delta <\Delta +\sigma \le \tilde{z}_2+\tau =\tilde{T}$. Then the value of $x^{(\Delta )}$ at the end of the pulse is

$$\begin{aligned} x^{(\Delta )}(\Delta + \sigma ) = -\beta _U + a + \bigl (x^{(\Delta )}(\Delta ) +\beta _U - a\bigr ) e^{- \sigma } \end{aligned}$$

and, by (5.2), it is the same as in (5.10). We proceed in steps as before.

• Case $\mathbf {FPF}$ The pulse starts in the interval $[t_{\max },\tilde{z}_2]$. We distinguish between two subcases.

• $\mathbf {P}$ The pulse parameters $(a,\Delta , \sigma )$ are such that $x^{(\Delta )}(t)$ remains non-negative during the pulse, and changes the sign after the pulse, $x^{(\Delta )}(\Delta +\sigma )\ge 0$.

• $\mathbf {N}$ The pulse parameters $(a,\Delta ,\sigma )$ are such that $x^{(\Delta )}$ changes the sign from positive to negative during the pulse (see Fig. 7), $t_{\max }\le \Delta \le \tilde{z}_2$ and $x^{(\Delta )}(\Delta +\sigma )<0$.

Since $\Delta \in [t_{\max },\tilde{z}_2]$ it follows from (5.10) that $x^{(\Delta )}(\Delta +\sigma )\ge 0$ if and only if

$$\begin{aligned} -\beta _U + \beta _U e^{\tilde{z}_2-\Delta -\sigma }+a (1- e^{- \sigma })\ge 0, \end{aligned}$$

or equivalently,

$$\begin{aligned} \beta _U e^{\tilde{z}_2-\Delta }\ge \beta _U e^{\sigma } -a ( e^{ \sigma }-1). \end{aligned}$$

The corresponding $\Delta$-intervals are of the form

$$\begin{aligned} I_{FPFP}=[t_{\max },\tilde{z}_2]\cap (-\infty ,\delta _2] \end{aligned}$$

and

$$\begin{aligned} I_{FPFN}=[t_{\max },\tilde{z}_2]\cap (\delta _2,\infty ). \end{aligned}$$

Proposition 5.6

If $\Delta \in I_{FPFP}$ then $T(\Delta )<\infty$, $\overline{x}_{\Delta }=\overline{x}$, $\underline{x}_{\Delta }=\underline{x}$, and $T(\Delta )$ is given by formula (5.9) in Proposition 5.3.

We turn to case FPFN. From Fig. 7 we expect $\tilde{z}_2\le z_{\Delta ,2}$ and $\underline{x}_{\Delta }=x^{(\Delta )}(z_{\Delta ,2}+\tau )>\tilde{x}(\tilde{z}_2+\tau )=\underline{x}$, that is, the minimum value of $x^{(\Delta )}$ is above the minimum value of $\tilde{x}$.

Fig. 7

A schematic representation of the solution of the DDE for case FPFN. The unperturbed periodic solution $\tilde{x}$ is the solid line while the solution $x^{(\Delta )}$ with the pulse is the dashed line

Proposition 5.7

If $\Delta \in I_{FPFN}$ then $T(\Delta )<\infty$, $\overline{x}_{\Delta }=\overline{x}$, $\underline{x}_{\Delta }>\underline{x}$, and both $\underline{x}_{\Delta }$ and $T(\Delta )$ are as in Proposition 5.5.

Assume now that $\Delta \in (\tilde{z}_2,\tilde{z}_2+\tau -\sigma )$. From $x^{(\Delta )}(\Delta )=-\beta _U+(0+\beta _U)e^{-(\Delta -\tilde{z}_2)}$ and

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )=-\beta _U+a+\bigl (x^{(\Delta )}(\Delta )+\beta _U-a\bigr )e^{-\sigma } \end{aligned}$$

we have $x^{(\Delta )}(\Delta )<0$ and $x^{(\Delta )}(\Delta +\sigma )<0$. Thus we consider the case

• Case $\mathbf {FNFN}$ The pulse parameters $(a,\Delta ,\sigma )$ are such that the pulse begins after $x^{(\Delta )}$ changes the sign from positive to negative and ends before the time $\tilde{T}=\tilde{z}_2+\tau$, $\tilde{z}_2<\Delta$ and $\Delta +\sigma < \tilde{z}_2+\tau$, see Fig. 8.

Fig. 8

A schematic representation of the solution for case $\mathbf {FNFN}$. The unperturbed periodic solution $\tilde{x}$ is the solid line while the solution $x^{(\Delta )}$ with the pulse is the dashed line

From Fig. 8 we expect that the minimum value of $x^{(\Delta )}$ in $[\tilde{z}_2,\tilde{z}_2+\tau ]$ is above the minimum value $\underline{x}$ of $\tilde{x}$, and the cycle length $T(\Delta )$ is below the minimal period $\tilde{T}$ of $\tilde{x}$. Observe that the function $[\Delta ,\Delta +\sigma ]\ni t\mapsto x^{(\Delta )}(t)\in \mathbb {R}$ is increasing (see Fig. 9) if and only if

$$\begin{aligned} x^{(\Delta )}(\Delta )+\beta _U-a<0, \end{aligned}$$

which is equivalent to $\beta _Ue^{\tilde{z}_2}<ae^{\Delta }$. Now, if $t\in [\Delta +\sigma ,\tilde{T}]$ then $\tilde{z}_1\le t-\tau \le \tilde{z}_2$. Thus

$$\begin{aligned} x^{(\Delta )}(t) = -\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr ) e^{-(t-(\Delta +\sigma ))} \end{aligned}$$

and we have

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )+\beta _U=\beta _Ue^{\tilde{z}_2-( \Delta +\sigma )} +a(1-e^{-\sigma }), \end{aligned}$$

which is always positive. Hence, the function $t\mapsto x^{(\Delta )}(t)$ is strictly decreasing on the interval $[\Delta +\sigma ,\tilde{T}]$ and we have

$$\begin{aligned} x^{(\Delta )}(\tilde{T}) = -\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr ) e^{-\left( \tilde{T}-(\Delta +\sigma )\right) } \end{aligned}$$

which becomes

$$\begin{aligned} x^{(\Delta )}(\tilde{T})&=-\beta _U+\bigl (\beta _Ue^{\tilde{z}_2-( \Delta +\sigma )} +a(1-e^{-\sigma })\bigr ) e^{-\left( \tilde{T}-(\Delta +\sigma )\right) }\\&=-\beta _U+\beta _Ue^{-\tau }+a(e^{\sigma }-1) e^{\Delta -\tilde{T}}. \end{aligned}$$

Fig. 9

Graphs of two solutions for case $\mathbf {FNFN}$, where the parameters are $\tau =1$, $\sigma =0.2$, $\beta _U=0.8$, $\beta _L=1$, $a=0.6$, and $\Delta \in \{2.2,2.7\}$, showing that the function $I_{FNFN}\ni \Delta \mapsto \underline{x}_{\Delta }$ is not given by one formula

Define $\overline{\delta }\in \mathbb {R}$ by

$$\begin{aligned} e^{\tilde{T}-\overline{\delta }}=\dfrac{\beta _U+\sqrt{\beta _U ^2+4a\beta _U(e^{\sigma }-1)e^{\tau }}}{2\beta _U}. \end{aligned}$$

Proposition 5.8

If $\Delta \in I_{FNFN}$ then $T(\Delta )<\infty$, $\overline{x}_{\Delta }=\overline{x}$,

$$\begin{aligned} \underline{x}_{\Delta }=\min \{\tilde{x}(\Delta ),x^{(\Delta )}(\tilde{T})\}>\underline{x}, \end{aligned}$$

and

$$\begin{aligned} T(\Delta )=\tilde{T}+\ln \left( 1-\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1-\tilde{T}}\right) <\tilde{T}. \end{aligned}$$

(5.14)

In case $I_{FNFN}\cap (-\infty ,\overline{\delta })\ne \emptyset$ the map

$$\begin{aligned} I_{ FNFN}\cap (-\infty ,\overline{\delta })\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

is strictly increasing while in case $I_{ FNFN}\cap (\overline{\delta },\infty )\ne \emptyset$ the map

$$\begin{aligned} I_{ FNFN}\cap (\overline{\delta },\infty )\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

is strictly decreasing.

Remark 5.3

If $\beta _U e^{\sigma - \tau } < a$ then $\overline{\delta }\in I_{FNFN}=(\tilde{z}_2,\tilde{T}-\sigma )$. If $\beta _U e^{\sigma - \tau } \ge a$ then $\overline{\delta }\ge \tilde{T}-\sigma$.

Remark 5.4

The following relations are equivalent:

$$\begin{aligned} a< \beta _U,\\ a(e^{\sigma }-1)< \beta _U(e^{\sigma }-1),\\ \beta _U< \bigl (\beta _U-a(1-e^{-\sigma })\bigr )e^{\sigma },\\ \ln \dfrac{\beta _U}{\beta _U-a(1-e^{-\sigma })}< \sigma ,\\ \delta _2&< \tilde{z}_2. \end{aligned}$$

Observe that we have $\tilde{z}_2\le \delta _2< \tilde{T}-\sigma$ if and only if

$$\begin{aligned} \beta _U\le a\quad \text {and}\quad a(1-e^{-\sigma })<\beta _U(1-e^{-\tau }), \end{aligned}$$

(5.15)

which is excluded by our standing hypothesis $a<\beta _U$.

Let us briefly address what might happen if (5.15) holds. In that case if $\Delta \in (\tilde{z}_2,\tilde{T}-\sigma )$ then $x^{(\Delta )}(\Delta +\sigma )\ge 0$ if and only if $\Delta \le \delta _2$. We have $I_{FNFN}=(\delta _2,\tilde{T}-\sigma )$ and Proposition 5.8 remains true. The case FNFP is possible with $I_{FNFP}=(\tilde{z}_2,\delta _2]$. Figure 10 and in particular Fig. 11 indicate that in the interval $I_{FNFP}$ the cycle length may not be finite everywhere, due to a higher oscillation frequency of the solution on $[\Delta +\sigma ,\infty )$.

Fig. 10

Graphs of two solutions for case $\mathbf {FNFP}$, where the parameters are $\tau =1$, $\sigma =0.4$, $\beta _U=0.6$, $\beta _L=0.3$, $a=0.95$, and $\Delta \in \{2.15,2.3\}$, showing that $T(\Delta )$ might not exists

Fig. 11

A graph of one solution for case $\mathbf {FNFP}$, where the parameters are $\tau =1$, $\sigma =0.35$, $\beta _U=0.3$, $\beta _L=0.4$, $a=0.7$, and $\Delta =2.22$, suggesting that for certain values of the parameters the solution $x^{(\Delta )}$ might settle down on a rapidly oscillating periodic solution, in which case we would have $T(\Delta )=\infty$

5.4 A pulse from the falling phase into the rising phase

Here we suppose that $\tilde{z}_2<\Delta <\tilde{T}\le \Delta +\sigma$ and that $x^{(\Delta )}(\Delta )$ is given by (5.2) for $\Delta \in [\tilde{T}-\sigma ,\tilde{T})$. We have

$$\begin{aligned} x^{(\Delta )}(t) = -\beta _U + a + \bigl (\tilde{x}(\Delta ) + \beta _U-a\bigr ) e^{-(t-\Delta )} \quad \text{ for } \quad t \in ( \Delta , \tilde{T}] \end{aligned}$$

and the function $[\Delta , \tilde{T}]\ni t\mapsto x^{(\Delta )}(t)\in \mathbb {R}$ is either strictly increasing, or decreasing. We have

$$\begin{aligned} x^{(\Delta )}(\tilde{T})&=-\beta _U+a+\bigl (x^{(\Delta )}(\Delta )+\beta _U-a\bigr )e^{-( \tilde{T}-\Delta )}\\&= -\beta _U+a+(-\beta _U+\beta _U e^{-(\Delta -\tilde{z}_2)}+\beta _U-a)e^{-( \tilde{T}-\Delta )}\\&= - \beta _U+\beta _U e^{-\tau }+a\bigl (1-e^{-(\tilde{T}-\Delta )}\bigr )\\&=\underline{x}+a\bigl (1-e^{\Delta -\tilde{T}}\bigr )>\underline{x}, \end{aligned}$$

which shows that the map

$$\begin{aligned}{}[\tilde{T}-\sigma ,\tilde{T})\ni \Delta \mapsto x^{(\Delta )}(\tilde{T})\in \mathbb {R} \end{aligned}$$

is strictly decreasing.

For $t\in [\tilde{T},\Delta +\sigma ]$ we have

$$\begin{aligned} x^{(\Delta )}(t) = \beta _L+a+\bigl (x^{(\Delta )}(\tilde{T})-(\beta _L+a)\bigr )e^{-( t-\tilde{T})}. \end{aligned}$$

Since

$$\begin{aligned} x^{(\Delta )}(\tilde{T})-(\beta _L+a)=-(\beta _L-\underline{x})- ae^{\Delta -\tilde{T}}<0, \end{aligned}$$

the function $[\tilde{T},\Delta +\sigma ]\ni t\mapsto x^{(\Delta )}(t)\in \mathbb {R}$ is strictly increasing. Also

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )&= \beta _L+a+\bigl (x^{(\Delta )}(\tilde{T})-(\beta _L+a)\bigr )e^{-( \Delta +\sigma -\tilde{T})}\\&= \beta _L+a+\bigl (\underline{x}-a\,e^{\Delta -\tilde{T} }-\beta _L\bigr )e^{-( \Delta +\sigma -\tilde{T})}\\&= \beta _L+(\underline{x}-\beta _L)e^{-( \Delta +\sigma -\tilde{T})} +a(1-e^{-\sigma })\quad (>\tilde{x}(\Delta +\sigma ))\\&= \beta _L-\beta _Le^{\tilde{z}_1-( \Delta +\sigma -\tilde{T})}+a(1-e^{-\sigma }). \end{aligned}$$

• Case $\mathbf {FNR}$ We must distinguish between the two subcases

  N :

  $x^{(\Delta )}(\Delta +\sigma )< 0$, see Fig. 12,

  P :

  $x^{(\Delta )}(\Delta +\sigma )\ge 0$, see Fig. 13.

Fig. 12

A schematic representation of the solution of the DDE for the case $\mathbf {FNRN}$. The unperturbed limit cycle is the solid line while the solution with the pulse is the dashed line

Fig. 13

A schematic representation of the solution of the DDE for the case $\mathbf {FNRP}$

We have $\tilde{T}-\sigma \le \Delta <\tilde{T}$, and the condition for subcase FNRN, namely,

$$\begin{aligned} 0> x^{(\Delta )}(\Delta +\sigma )=\beta _L-\beta _Le^{\tilde{z}_1-( \Delta +\sigma -\tilde{T})}+a(1-e^{-\sigma }), \end{aligned}$$

is equivalent to

$$\begin{aligned} \beta _L+a(1-e^{-\sigma })< \beta _Le^{\tilde{z}_1-( \Delta +\sigma -\tilde{T})}, \end{aligned}$$

or

$$\begin{aligned} e^{\Delta }< e^{\tilde{T}}\dfrac{\beta _L e^{\tilde{z}_1}}{\beta _L e^{\sigma }+a(e^{\sigma }-1)}=e^{\tilde{T}+\delta _1}. \end{aligned}$$

Thus we are in case FNRN if and only if

$$\begin{aligned} \Delta \in [\tilde{T}-\sigma ,\tilde{T})\cap (-\infty ,\tilde{T}+\delta _1)= I_{FNRN}. \end{aligned}$$

and we are in case FNRP if and only if

$$\begin{aligned} \Delta \in [\tilde{T}-\sigma ,\tilde{T})\cap [\tilde{T}+\delta _1,\infty ). \end{aligned}$$

Proposition 5.9

If $\Delta \in I_{FNRN}$ then $T(\Delta )<\infty$, $\overline{x}_{\Delta }=\overline{x}$, $\underline{x}_{\Delta } >\underline{x}$, and $T(\Delta )$ is as in (5.14) of Proposition 5.8. The map $I_{FNRN}\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ is strictly decreasing.

The interval $I_{FNRN}$ in Proposition 5.9 is nonempty if and only if $\delta _1>-\sigma$, which is always the case. To see this observe that

$$\begin{aligned} e^{\delta _1}=e^{-\sigma }\dfrac{\beta _L -\underline{x}}{\beta _L+a(1-e^{-\sigma })}>e^{-\sigma } \end{aligned}$$

since

$$\begin{aligned} -\underline{x}=\beta _U(1-e^{-\tau })>a(1-e^{-\sigma }). \end{aligned}$$

We next proceed to the subcase $\mathbf {FNRP}$. Note that the interval $I_{FNRP}$ is empty if and only if $\delta _1\ge 0$.

Proposition 5.10

If $\Delta \in I_{FNRP}$ then $T(\Delta )<\infty$, $\overline{x}_{\Delta }>\overline{x}$, $\underline{x}_{\Delta }>\underline{x}$, and

$$\begin{aligned} T(\Delta )=\tilde{T}+\ln \left( 1+\dfrac{a(e^\sigma -1)}{\beta _U}e^{\Delta -\tilde{z}_2-\tilde{T}}+ \dfrac{a(\beta _L+\beta _U)e^{\tau +\tilde{z}_1-\tilde{z}_2}}{\beta _U(\beta _L+a)}\left( e^{\Delta -\tilde{z}_1-\tilde{T}}-1\right) \right) . \end{aligned}$$

(5.16)

The map $I_{FNRP}\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ is strictly decreasing as is the map $I_{FNRP}\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}$.

6 The cycle length map

The behaviour of the cycle length map $[0,\tilde{T})\ni \Delta \mapsto T(\Delta )\in \mathbb {R}$, illustrated in Figs. 14 and 15, is different in each of the (sub-) cases discussed in Sects. 5.1–5.4. Each of these cases corresponds to $\Delta$ varying in one of the subintervals $I_{RNRN},\ldots ,I_{FNRP}$ of $[0,\tilde{T})$. If $\Delta$ increases from 0 to $\tilde{T}$ then it travels through those subintervals which are not empty for the given parameter vector $(\tau ,\beta _L,\beta _U,a,\sigma )$ (with $0<\tau ,-\beta _U<0<\beta _L,0<a<\beta _U,0<\sigma \le \tau )$. In other words, for each parameter vector we have a finite sequence of non-empty subintervals, ordered by, say, their left endpoints, whose union is $[0,\tilde{T})$. Below we describe the possible scenarios, in terms of sequences of cases and subcases. Recall also the Tables 1, 2, 3 in Sect. 5.

Fig. 14

A graph of the function $[0,\tilde{T}]\ni \Delta \mapsto T(\Delta )$. The straight line represents the graph of $[0,\tilde{T}]\ni \Delta \mapsto \tilde{T}$. We indicated with dots the values of the boundaries of all cases, and with lines the boundaries of subcases. Here the parameters are $\tau =1$, $\beta _U=0.8$, $\beta _L=0.4$, and $\sigma =0.4$, $a=0.2$, so that $\delta _1>0$ and $\delta _2<t_{\max }$. The figure corresponds to the following sequence of subcases: $\mathbf {RNRN}$, $\mathbf {RNRP}$, $\mathbf {RPRP}$, $\mathbf {RPFP}$, $\mathbf {RPFN}$, $\mathbf {FPFN}$, $\mathbf {FNFN}$, $\mathbf {FNRN}$

Fig. 15

As in Fig. 14, but with $\beta _L=1.4$, which gives $\delta _1\in (-\sigma ,0)$, $\delta _2\in (t_{\max },\tilde{z}_2)$, and the following sequence of subcases: $\mathbf {RNRP}$, $\mathbf {RPRP}$, $\mathbf {RPFP}$, $\mathbf {FPFP}$, $\mathbf {FPFN}$, $\mathbf {FNFN}$, $\mathbf {FNRN}$, $\mathbf {FNRP}$

Before doing so it may be convenient to collect a few facts about the quantities $\delta _1,\delta _2$ which, together with $\tilde{z}_1,\tilde{z}_2,t_{\max },\sigma ,\tilde{T}$, determine the intervals $I_{RNRN},\ldots ,I_{FNRP}$. Recall that $\delta _1$ was defined by (5.6) and that $\delta _2$ was defined by (5.11). From $\beta _U>a$ and $\tau \ge \sigma$ we have $\delta _1>-\sigma$ and $\delta _2<\tilde{z}_2$. The condition $\delta _1>0$ is equivalent to

$$\begin{aligned} (\beta _L+a)(e^{\sigma }-1)<\beta _U(1-e^{-\tau }), \end{aligned}$$

and the case when $\delta _1\in (-\sigma ,0]$ is described by

$$\begin{aligned} a(1-e^{-\sigma })< \beta _U(1-e^{-\tau })\le (\beta _L+a)(e^{\sigma }-1). \end{aligned}$$

Next, the condition $\delta _2< t_{\max }$ is equivalent to

$$\begin{aligned} \beta _L(1-e^{-\tau })< (\beta _U-a)(e^{\sigma }-1) \end{aligned}$$

while the condition $t_{\max }\le \delta _2<\tilde{z}_2$ is equivalent to

$$\begin{aligned} 0< (\beta _U-a)(e^{\sigma }-1)\le \beta _L(1-e^{-\tau }). \end{aligned}$$

Since $\delta _1<\tilde{z}_1$ and $\delta _2>t_{\max }-\sigma$, we conclude that the intervals

$$\begin{aligned} I_{RNRP}=[\min \{0,\delta _1\},\tilde{z}_1),\quad I_{RPFP}=(t_{\max }-\sigma ,\min \{t_{\max },\delta _2\}] \end{aligned}$$

are always nonempty. We have $I_{RPRP}=[\tilde{z}_1,t_{\max }-\sigma ]$, $t_{\max }=\tilde{z}_1+\tau$, and $\tau \ge \sigma$, thus each sequence of cases contains

$$\begin{aligned} \mathbf {RNRP}, \quad \mathbf {RPRP},\quad \text {and}\quad \mathbf {RPFP}. \end{aligned}$$

For $\delta _1>0$ each sequence starts with the case $\mathbf {RNRN}$ and ends with the case $\mathbf {FNRN}$.

For $\delta _1=0$ each sequence starts with the case $\mathbf {RNRP}$ and ends with the case $\mathbf {FNRN}$.

For $\delta _1<0$ each sequence starts with the case $\mathbf {RNRP}$ and ends with the case $\mathbf {FNRP}$.

If $\delta _1>0$ and $0\le \Delta <\delta _1$ then we are in case $\mathbf {RNRN}$. If $\Delta$ grows from $\max \{0,\delta _1\}$ to $\min \{t_{\max },\delta _2\}$ then we have the sequence of cases:

$$\begin{aligned} \mathbf {RNRP}, \quad \mathbf {RPRP},\quad \text {and}\quad \mathbf {RPFP}. \end{aligned}$$

If $\Delta$ grows from $\min \{t_{\max },\delta _2\}$ to $\min \{0,\delta _1\}+\tilde{T}$ and if $\delta _2<t_{\max }$ then we obtain the subsequent cases

$$\begin{aligned} \mathbf {RPFN},\quad \mathbf {FPFN},\quad \mathbf {FNFN},\quad \mathbf {FNRN}. \end{aligned}$$

In case $\delta _2=t_{\max }$ we obtain

$$\begin{aligned} \mathbf {FPFP},\quad \mathbf {FPFN},\quad \mathbf {FNFN},\quad \mathbf {FNRN}. \end{aligned}$$

The same sequence results in case $t_{\max }<\delta _2$. So we have two scenarios for $\Delta$ beyond the interval $I_{RPFP}$ and below $\min \{0,\delta _1\}+\tilde{T}$, which is the endpoint $\tilde{T}$ of the domain of the cycle length map if $\delta _1\ge 0$, while for $\delta _1<0$ the sequence of cases is completed by

$$\begin{aligned} \mathbf {FNRP}. \end{aligned}$$

7 A therapy plan

We first describe the concept of the therapy plan, in case the evolution of the number of cells in the bloodstream (of a patient, without medical treatment) is governed by Eq. (2.2), with the production function f given by (2.1), and $b_U<\gamma \theta <b_L$. For convenience we shall work not with the original variables but with the transformed quantities from Sect. 2, namely, Eq. (2.5) with f satisfying Eq. (2.6) for $-\beta _U<0<\beta _L$. Then the variable x(t) still represents the number of blood cells (of a certain type) in a patient, at time t.

The reader will find it helpful to consult Fig. 16 when following the argument below.

Fig. 16

A schematic representation of the ideas behind the arguments leading to a therapy plan. The unperturbed limit cycle is the solid line while the desired limit cycle due to a perturbation is the dashed line

Suppose there is a critical level $x_d$, larger than the minimum $\underline{x}$ of the periodic oscillation in the patient without treatment. We want to find a therapy plan which consists of medication at certain times $t=t_M$ (which are to be determined) in such a way that the cell density in the patient never falls below the critical level.

Medication at a time $t=t_M$ results in the begin of the production of more (precursors of) cells in the bone marrow, and this increased production lasts for a time interval of duration $\sigma >0$, from the time $t_M$ until the time $t_M+\sigma$. As in Sect. 4 the effect of medication at $t=t_M$ can be expressed by a ’temporal change’ of the production function f, for example, by replacing f by a sum $f_a=f+a$ with $a>0$ as long as $t_M\le t-\tau \le t_M+\sigma$. (Alternatively, one might replace f by a multiple $f_a=af$ with $a>1$.) a depends on the dose of the medication. Because of the delay $\tau$ due to the production process the number of cells in the bloodstream will begin to deviate from their number without treatment not earlier than $t\ge t_M+\tau$, where $t_M+\tau$ equals $\Delta$ in the cases studied in Sect. 5.

We begin with a simple situation and assume that for the time interval $[-\tau ,0]$ in the past the cell density in a patient is known, for example, by measurement, and

$$\begin{aligned} 0<x(t)\quad \text {for}\; -\tau <t\le 0. \end{aligned}$$

$t=0$ stands for the present time. Then we use Eq. (2.5) in order to predict how the cell density would evolve in the patient without treatment: We compute the solution y(t), $t\ge 0$, of Eq. (2.5) with initial data $y(t)=x(t)$, $-\tau \le t\le 0$. The solution y(t) will be a translate of the unique slowly oscillating periodic solution $\tilde{x}$ of Eq. (2.5). There is a first zero $z_1=z_1(y(0))>0$ of y, and there exists a unique time $t_d$ between $z_1$ and $z_1+\tau$, at which y reaches the critical level $x_d$, $y(t_d)=x_d$, from above. (At $z_1+\tau$ y attains its minimum value $\underline{x}<x_d$.)

Having predicted the time $t_d$ we define $t_M=t_d-\tau -\sigma$ as the time of medication. If $t_M$ is positive (is in the future), then it is not too late for medication. After medication at $t=t_M$ the cell density in the patient represented by x(t) will equal y(t) for $-\tau \le t\le t_M+\tau =t_d-\sigma$, because of the delay in Eq. (2.5). For $t_d-\sigma \le t\le t_d$ the release of cells into the circulation will be increased according to

$$\begin{aligned} x'(t)=f(x(t-\tau ))+a-x(t)=-\beta _U+a-x(t) \end{aligned}$$

while for $t\ge t_d$, Eq. (2.5) holds once again.

The question is whether for a range of parameters $a>0$ this can be done in such a way that for $t_d-\sigma \le t< z_1+\tau$ the solution x(t) satisfies $x_d\le x(t)<0$.

If yes then x(t) would increase after time $z_1+\tau$ until there is a zero $z_2$, due to Eq. (2.5), and would coincide on $[z_2,z_2+\tau ]$ with the piece of the unique slowly oscillating periodic solution $\tilde{x}$ of Eq. (2.5) before its maxima.

Upon that the whole process can be repeated. It would result in a periodic therapy plan and a periodic solution x(t) which never falls below the critical value $x_d$ and has a period shorter than the period of $\tilde{x}$. (This latter property comes from $x(z_1+\tau )\ge x_d>\underline{x}$.)

Below we show that there exist parameters $\beta _L,\beta _U,\tau ,\sigma$ and $x_d\in (\underline{x},0)$ and $a>0$ for which the program just described can be carried out. As initial data we consider continuous functions $\phi :[-\tau ,0]\rightarrow \mathbb {R}$ with $0<\phi (t)$ for $-\tau <t\le 0$. Then for some q, $0<q<1$, $q\overline{x}<\phi (0)$. The solution y of the initial value problem

$$\begin{aligned} y'(t)=f(y(t-\tau ))-y(t)\quad \text {for}\,\,t>0,\,\,y_0=\phi \end{aligned}$$

has a first zero at

$$\begin{aligned} z_1=z_1(\phi (0))=\ln \dfrac{\phi (0)+\beta _U}{\beta _U} \end{aligned}$$

and strictly decreases on $[z_1,z_1+\tau ]$ to the value $\underline{x}$. For $\underline{x}<x_d<0$ we find a unique time $t=t_d=t_d(\phi )$ in $(z_1,z_1+\tau )$ with $y(t_d)=x_d$, namely,

$$\begin{aligned} t_d=z_1+\ln \dfrac{\beta _U}{x_d+\beta _U}. \end{aligned}$$

Next we show that for parameters $-\beta _U<0<\beta _L,\tau >0,q\in (0,1)$ and $\sigma >0$ sufficiently small, and $x_d\in (\underline{x},0)$ sufficiently close to $\underline{x}$ we have

$$\begin{aligned} t_d-\tau -\sigma >0. \end{aligned}$$

(7.1)

The inequality (7.1) is equivalent to

$$\begin{aligned} \tau +\sigma <\ln \dfrac{\phi (0)+\beta _U}{\beta _U}+\ln \dfrac{\beta _U}{x_d+\beta _U}= \ln \dfrac{\phi (0)+\beta _U}{x_d+\beta _U}, \end{aligned}$$

which follows from

$$\begin{aligned} \tau +\sigma <\ln \dfrac{q\,\overline{x}+\beta _U}{x_d+\beta _U}. \end{aligned}$$

The preceding inequality can be achieved for $\sigma >0$ sufficiently small and $x_d>\underline{x}$ sufficiently close to $\underline{x}$ provided we have

$$\begin{aligned} \tau <\ln \dfrac{q\,\overline{x}+\beta _U}{\underline{x}+\beta _U}. \end{aligned}$$

(7.2)

We verify this: Using the equations for $\overline{x}$ and $\underline{x}$ from Corollary 3.2 we see that (7.2) is equivalent to

$$\begin{aligned} \tau&< \ln \dfrac{q\,\beta _L(1-e^{-\tau })+\beta _U}{\beta _U-\beta _U(1-e^{-\tau })}\\&= \tau +\ln \dfrac{q\,\beta _L(1-e^{-\tau })+\beta _U}{\beta _U} \end{aligned}$$

or,

$$\begin{aligned} \beta _U<q\,\beta _L(1-e^{-\tau })+\beta _U, \end{aligned}$$

which is equivalent to

$$\begin{aligned} 0<q\,\beta _L(1-e^{-\tau }). \end{aligned}$$

(7.3)

From now on assume that the parameters $-\beta _U<0<\beta _L,\tau>0,\sigma >0$, and $q\in (0,1),x_d\in (\underline{x},0)$ satisfy (7.1). Assume in addition for simplicity that $\sigma$ is so small that we have

$$\begin{aligned} z_1<t_d-\sigma . \end{aligned}$$

(7.4)

Notice that $t_d-z_1=\ln \dfrac{\beta _U}{x_d+\beta _U}$ does not depend on $\phi$. We now define

$$\begin{aligned} t_M=t_M(\phi )=t_d(\phi )-\tau -\sigma \,\,(>0) \end{aligned}$$

as the time of medication. For parameters $a>0$ we consider the continuous function $x:[-\tau ,z_1+\tau ]\rightarrow \mathbb {R}$ which coincides with y(t) for $-\tau \le t\le t_d-\sigma$ and satisfies

$$\begin{aligned} x'(t) = \left\{ \begin{array}{ll} f(x(t-\tau ))+a-x(t)=-\beta _U+a-x(t)&{}\quad \text {for}\,\,t_d-\sigma<t<t_d,\\ f(x(t-\tau ))-x(t)=-\beta _U-x(t) &{}\quad \text {for}\,\,t_d<t<z_1+\tau . \end{array} \right. \end{aligned}$$

It follows that

$$\begin{aligned} x(t_d-\sigma )=y(t_d-\sigma )=-\beta _U+\beta _Ue^{-(t_d-\sigma -z_1)}=-\beta _U\left( 1-e^{-\sigma }\dfrac{x_d+\beta _U}{\beta _U}\right) . \end{aligned}$$

Similarly we get for $t\in [t_d-\sigma ,t_d]$ that

$$\begin{aligned} x(t)&= -\beta _U+a+\bigl (x(t_d-\sigma )-(-\beta _U+a))e^{-(t-(t_d-\sigma )\bigr )}\\&= -\beta _U+a+(y(t_d-\sigma )-(-\beta _U+a))e^{-(t-(t_d-\sigma ))}\\&= y(t)+a(1-e^{-(t-(t_d-\sigma ))})\ge y(t)\ge x_d \end{aligned}$$

which shows that x is monotone and above $x_d$ on this interval. Using

$$\begin{aligned} x(t_d-\sigma )=y(t_d-\sigma )<0 \end{aligned}$$

and monotonicity we conclude that we have $x(t)<0$ on $[t_d-\sigma ,t_d]$ if and only if $x(t_d)<0$. Also,

$$\begin{aligned} x(t_d)=y(t_d)+a\bigl (1-e^{-(t_d-(t_d-\sigma ))}\bigr )=x_d+a(1-e^{-\sigma }) \end{aligned}$$

which gives $x(t_d)<0$ if and only if

$$\begin{aligned} x_d+a(1-e^{-\sigma })<0. \end{aligned}$$

(7.5)

We shall come back to this later, and turn to

$$\begin{aligned} x(z_1+\tau )&= -\beta _U+\bigl (x(t_d)+\beta _U\bigr )e^{-(z_1+\tau -t_d)}\\&= -\beta _U+\bigl (y(t_d)+a(1-e^{-\sigma })+\beta _U\bigr )e^{-(z_1+\tau -t_d)}\\&= y(z_1+\tau )+a(1-e^{-\sigma })e^{-(z_1+\tau -t_d)}\\&= \underline{x}+a(1-e^{-\sigma })e^{-(z_1+\tau -t_d)}>\underline{x}. \end{aligned}$$

It follows that there is a unique $a=a_d>0$ so that

$$\begin{aligned} x(z_1+\tau )=x_d>\underline{x}, \end{aligned}$$

namely,

$$\begin{aligned} a_d = \dfrac{x_d-\underline{x}}{(1-e^{-\sigma })e^{-(z_1+\tau -t_d)}} = \dfrac{(x_d-\underline{x})e^{\tau }(x_d+\beta _U)}{\beta _U(1-e^{-\sigma })}. \end{aligned}$$

(7.6)

We would like to have $x(t)<0$ on $(z_1,z_1+\tau ]$. This follows from $x(z_1+\tau )=x_d<0$ in combination with monotonicity provided we have $x(t_d)<0$, which was characterized by (7.5). So we ask under which conditions $a=a_d$ satisfies (7.5), or equivalently,

$$\begin{aligned} \dfrac{(x_d-\underline{x})e^{\tau }(x_d+\beta _U)}{\beta _U}=a_d(1-e^{-\sigma })<-x_d, \end{aligned}$$

which means

$$\begin{aligned} (x_d-\underline{x})e^{\tau }(x_d+\beta _U)<-\beta _Ux_d. \end{aligned}$$

(7.7)

Recall that $\underline{x}$ depends on $\tau$ and on $\beta _U$; given $\tau$ and $\beta _U$ the preceding inequality holds provided we consider $x_d\in (\underline{x},0)$ close enough to $\underline{x}$.

Assume from now on that $x_d$ is chosen so that (7.7) holds. If we follow the solution x which started from $\phi$ further then we see from Eq. (2.5) and because of $x(t)<0$ on $(z_1,z_1+\tau ]$ that x begins to increase after $t=z_1+\tau$, has a first zero $z_2=z_2(\phi )>z_1+\tau$, and coincides on $[z_2,z_2+\tau ]$ with a translate of the periodic solution $\tilde{x}$ of Eq. (2.5) which has a zero $t=z_2$ and then increases to the value $\overline{x}$ at $t=z_2+\tau$. Notice that if we take this segment of $\tilde{x}$ as the initial value $\phi$ for the function x then $x_{z_2+\tau }=\phi =x_0$, and iteration of the whole procedure yields a periodic solution x. The inequalities $x(t)<0$ for $z_1<t\le z_1+\tau$ and $y(z_1+\tau )=\underline{x}<x_d=x(z_1+\tau )$ in combination with Eq. (2.5) for $z_1+\tau \le t$ imply that after the time $t=z_1+\tau$ the function x reaches the zero level from below before y does so, hence the period $z_2(\phi )+\tau$ of x is shorter than the minimal period $\tilde{T}$ of $\tilde{x}$.

Remark 7.1

1.  Crucial in the concept of the therapy plan is that the time $t_d$ at which the number y(t) of blood cells in case of no medication would fall to the critical level $x_d$ is large enough for medication in the future (at some $t_M>0$) to become effective (during the time interval $[t_M+\tau ,t_M+\tau +\sigma ]$) before the time $t=t_d$. Necessary for this is

$$\begin{aligned} 0<t_d-\tau , \quad \text {or}\,\,\tau <t_d\,\,; \end{aligned}$$

the stronger condition (7.1) which we used in the exposition above can be relaxed.

2.  A practically useful version of the therapy plan would require an extension to more realistic model equations, probably with continuous production functions, in order to get reliable predictions of $t_d=t_d(\phi )$ for a large set of initial conditions, as they may arise from monitoring the number of blood cells in a patient.

8 Discussion

The computation of the response of the periodic solution of (2.5) to a perturbation of the form defined in Sect. 4 is complicated as we have seen in Sect. 5, and the response of the perturbed cycle length can be quite varied as shown in Sect. 6. However, our calculations have shown that in a variety of situations that are dependent on the timing of the pulse, the pulse has had no effect on subsequent minima of the model solution. This is in sharp contrast to what is noted in clinical situations where G-CSF is employed and in which both an amelioration as well as a worsening of neutropenia is clearly documented in response to the G-CSF, and the nature of the response is dependent on when G-CSF is given as well as the dosage. Although it seems to be a curious anomaly that a cytokine like G-CSF, which inhibits apoptosis, should actually make neutropenia worse, in this section we will show that in case the nonlinearity (production function) $f=f_{*}$ in Eq. (1.1) is piecewise constant with three values (see Fig. 17), say,

$$\begin{aligned} f_{*}(\xi )=\beta _L>0\quad \text {for}\,\,\xi<0,\,\,f_{*}(\xi )=-\beta _U<0\quad \text {for}\,\,0\le \xi <\xi _{*} \end{aligned}$$

and

$$\begin{aligned} f_{*}(\xi )=-\beta _{*}<-\beta _U\quad \text {for}\,\,\xi _{*}\le \xi , \end{aligned}$$

then a pulse as in case $\mathbf {RPRP}$ can result in a subsequent minimum of the solution which is lower than the minimum of a periodic solution of the equation without a pulse. This will happen if the pulse pushes the state variable to high values where the negative feedback is so strong that after the delay time it drives the state down to very low values.

Fig. 17

The graph of the function $f_{*}$

In order to see that this actually happens for a suitable range of parameters, assume (in part for simplicity) that $\xi _{*}=\overline{x}$, and define solutions of the equation

$$\begin{aligned} x'(t)=-x(t)+f_{*}(x(t-\tau )), \end{aligned}$$

(8.1)

i.e., of Eq. (1.1) with $f=f_{*}$, as in Sect. 3. Then our former periodic solution $\tilde{x}$ of Eq. (2.5) will also be a solution of Eq. (8.1). Consider a pulse which begins at $\tilde{z}_1$ and ends at $\tilde{z}_1+\tau$, that is, consider the function $x_{*}:\mathbb {R}\rightarrow \mathbb {R}$ which coincides with $\tilde{x}$ on $(-\infty ,\tilde{z}_1]$, is given by

$$\begin{aligned} x'(t)=-x(t)+\beta _L+a\quad \text {for}\,\,\tilde{z}_1\le t\le \tilde{z}_1+\tau , \end{aligned}$$

and by Eq. (8.1) for $t\ge \tilde{z}_1+\tau$. We have

$$\begin{aligned} x_{*}(\tilde{z}_1+\tau )=(\beta _L+a)(1-e^{-\tau })>\beta _L(1-e^{-\tau })=\tilde{x}(\tilde{z}_1+\tau )=\overline{x}=\xi _{*}. \end{aligned}$$

Incidentally, notice that $x_{*}(\tilde{z}_1+\tau )\rightarrow \beta _L+a$ as $\tau \rightarrow \infty$.

The first time $t_{*}>\tilde{z}_1$ at which $x_{*}$ crosses the level $\xi _{*}$ from below is given by

$$\begin{aligned} \xi _{*}=(\beta _L+a)(1-e^{-(t_{*}-\tilde{z}_1)}), \end{aligned}$$

or equivalently,

$$\begin{aligned} \beta _L(1-e^{-\tau })=(\beta _L+a)(1-e^{-(t_{*}-\tilde{z}_1)}), \end{aligned}$$

hence

$$\begin{aligned} e^{\tilde{z}_1-t_{*}}=\dfrac{a+\beta _Le^{-\tau }}{a+\beta _L}. \end{aligned}$$

Notice here that

$$\begin{aligned} e^{\tilde{z}_1-t_{*}}\rightarrow \dfrac{a}{a+\beta _L}\quad \text {as}\,\,\tau \rightarrow \infty . \end{aligned}$$

Next,

$$\begin{aligned} x_{*}(t_{*}+\tau )&= -\beta _U+\bigl (x_{*}(\tilde{z}_1+\tau )+\beta _U\bigr )e^{-(t_{*}+\tau -(\tilde{z}_1+\tau ))}\\&= -\beta _U+\bigl (x_{*}(\tilde{z}_1+\tau )+\beta _U\bigr )e^{\tilde{z}_1-t_{*}}. \end{aligned}$$

We observe that $x_{*}(t_{*}+\tau )$ has a limit as $\tau \rightarrow \infty$. It follows that

$$\begin{aligned} x_{*}(\tilde{z}_1+\tau +\tau )&= -\beta _{*}+\bigl (x_{*}(t_{*}+\tau )+\beta _{*}\bigr )e^{-(\tilde{z}_1+2\tau -(t_{*}+\tau ))}\\&= -\beta _{*}+\bigl (x_{*}(t_{*}+\tau )+\beta _{*}\bigr )e^{t_{*}-\tilde{z}_1}e^{-\tau } \end{aligned}$$

converges to $-\beta _{*}<-\beta _U<\underline{x}=\min \,\tilde{x}(\mathbb {R})$ as $\tau \rightarrow \infty$. So, given $\xi _{*}>0$ and $\beta _L>0>-\beta _U>-\beta _{*}$ and $a>0$ there exists $\tau _0>0$ so that for all $\tau \ge \tau _0$ the solution $x_{*}$ assumes values strictly less than $\underline{x}=\min \,\tilde{x}(\mathbb {R})$.

Our investigations in this paper have been confined to an examination of the response of the limit cycle solution of (2.5) to a single perturbation. However, in many situations of interest biologically (and certainly for the clinical questions that motivated this study) one is interested in the limiting behaviour of the limit cycle in response to periodic perturbations, c.f Winfree (1980), Guevara and Glass (1982), Glass and Winfree (1984), Krogh-Madsen et al. (2004) and Bodnar et al. (2013b) for representative examples. However, considerations of the response to the system we have studied to periodic perturbation is quite beyond the scope of this study as it would entail the development of completely different techniques than the ones that have proved so successful in the study of the response to single perturbations. We are of the opinion that deriving the phase response curve in the face of periodically delivered pulses will only be possible, in general, for certain limiting cases of the pulse parameters, namely $\sigma \simeq 0$ and, possibly, small values of the amplitude a. It is possible that techniques such as those employed in Kotani et al. (2012) may be useful in this regard.

Appendices

Appendix: Proofs of the results from Sects. 3 and 4

Proof of Proposition 3.1

• 1. We begin with continuity of the time- $\tau$-map

  $$\begin{aligned} S(\tau ,\cdot ):Z\ni \phi \mapsto x^{\phi }_{\tau }\in Z. \end{aligned}$$

  Observe that for $0\le t\le \tau$,

  $$\begin{aligned} x^{\phi }(t)=e^{-t}\phi (0)+\int _0^te^{-(t-s)}f(\phi (s-\tau ))ds. \end{aligned}$$

  For $\psi$ and $\phi$ in Z and $0\le t\le \tau$ we have

  $$\begin{aligned} |x^{\psi }(t)-x^{\phi }(t)|\le |\phi (0)-\psi (0)|+\int _{-\tau }^0|f(\psi (s))-f(\phi (s))|ds \end{aligned}$$

  where the integrand is nonzero only on the set

  $$\begin{aligned} N(\psi ,\phi )=\{t\in [-\tau , 0]{:} \ \mathrm { sign}(\psi (t))\ne \mathrm {sign}(\phi (t))\}. \end{aligned}$$

  It follows that

  $$\begin{aligned} |x^{\psi }_{\tau }-x^{\phi }_{\tau }|_C\le |\psi (0)-\phi (0)|+\beta \lambda (N(\psi ,\phi )), \end{aligned}$$

  with the Lebesgue measure $\lambda$ and a positive constant $\beta$. It is easy to see that

  $$\begin{aligned} \lim _{Z\ni \psi \rightarrow \phi \in Z}\lambda (N(\psi ,\phi ))=0. \end{aligned}$$

  (Proof of this in case $\phi \in Z$ has zeros $z_1<z_2<\cdots <z_J$. Let $\epsilon >0$ be given. The complement of the set

  $$\begin{aligned} \bigcup _{j=1}^J\left( z_j-\dfrac{\epsilon }{2J},z_j+\dfrac{\epsilon }{2J}\right) \end{aligned}$$

  in $[-\tau ,0]$ is the finite union of compact intervals on each of which $\phi$ is either strictly positive, or strictly negative. There exists $\delta >0$ so that for every $\psi \in Z$ with $|\psi -\phi |<\delta$ the signs of $\psi (t)$ and $\phi (t)$ coincide on each of the compact intervals. This yields

  $$\begin{aligned} \lambda (N(\psi ,\phi ))\le \sum _{j=1}^J2\dfrac{\epsilon }{2J}=\epsilon .) \end{aligned}$$

  Then it follows easily that

  $$\begin{aligned} \lim _{Z\ni \psi \rightarrow \phi \in Z}(S(\tau ,\psi )-S(\tau ,\phi ))=\lim _{Z\ni \psi \rightarrow \phi \in Z}(x^{\psi }_{\tau }-x^{\phi }_{\tau })=0. \end{aligned}$$

• 2. Iterating we find that for every integer $n>0$ the time-$n\tau$-map $S(n\tau ,\cdot )$ is continuous. Having this we obtain continuous dependence on initial data in the sense that for every $t\ge 0$ and $\phi \in Z$,

  $$\begin{aligned} \lim _{Z\ni \psi \rightarrow \phi \in Z}\max _{-\tau \le s\le t}|x^{\psi }(s)-x^{\phi }(s)|=0. \end{aligned}$$

  Finally, the continuity of S at $(t,\phi )\in [0,\infty )\times Z$ follows by means of the estimate

  $$\begin{aligned} |S(s,\psi )-S(t,\phi )|&\le |S(s,\psi )-S(s,\phi )|+|S(s,\phi )-S(t,\phi )|\\&\le \max _{-\tau \le v\le t+1}|x^{\psi }(v)-x^{\phi }(v)|\\&\quad +\max _{-\tau \le w\le 0}|x^{\phi }(s+w)-x^{\phi }(t+w)| \end{aligned}$$

  for $0\le s\le t+1$ and $\psi \in Z$ from continuous dependence on initial data as before in combination with the uniform continuity of $x^{\phi }$ on $[-\tau ,t+1]$. $\square$

Proof of Proposition 4.2

By definition the value of the cycle length map at $\Delta$ is $T(\Delta )=z-\tilde{z}_J=z-z_{\Delta ,J}$ where z is the smallest zero of $x^{(\Delta )}$ in $(\tilde{z}_J,\infty )$ such that $x^{(\Delta )}(z+t)=\tilde{x}(\tilde{z}_J+t)$ for all $t\ge 0$. We have

$$\begin{aligned} \text {sign}(\tilde{x}(\tilde{z}_J+t))=\text {sign}(x^{(\Delta )}(z_{\Delta ,J}+t))=-\text {sign}(x^{(\Delta )}(z_{\Delta ,J+1}+t)) \end{aligned}$$

for $0<t\le \tau$ since $x^{(\Delta )}$ changes sign at each zero. We infer that $z>z_{\Delta ,J+1}$. Notice that the definition of $J=j_{\Delta }$ implies $\Delta <z_{\Delta ,J+1}$. Hence the next zero $z_{\Delta ,J+2}$ satisfies $z_{\Delta ,J+2}>z_{\Delta ,J+1}+\tau >\Delta +\tau \ge \Delta +\sigma$. Therefore on $(z_{\Delta ,J+2},\infty )$ the function $x^{(\Delta )}$ is given by Eq. (2.5), and satisfies

$$\begin{aligned} \text {sign}(x^{(\Delta )}(z_{\Delta ,J+2}+t))=-\text {sign}(x^{(\Delta )}(z_{\Delta ,J+1}+t))=\text {sign}(\tilde{x}(\tilde{z}_J+t)) \end{aligned}$$

for $0<t\le \tau$. This yields $x^{(\Delta )}(z_{\Delta ,J+2}+t)=\tilde{x}(\tilde{z}_J+t)$ for all $t\ge 0$.

Proposition 9.1

For $\Delta =\tilde{z}_J$, $J=1$ or $J=2$, we have $T(\Delta )=z_{\Delta ,J+1}-z_{\Delta ,J-1}$.

Proof

From $\Delta =\tilde{z}_J$ we obtain $\Delta +\sigma \le \Delta +\tau <z_{\Delta ,J+1}$. This implies that for $t\ge z_{\Delta ,J+1}$ the function $x^{(\Delta )}$ satisfies Eq. (2.5). Using this and the fact that $x^{(\Delta )}$ and $\tilde{x}$ change sign at $\tilde{z}_{J-1}=z_{\Delta ,J-1}$ and at $\tilde{z}_J=z_{\Delta ,J}$ respectively we infer that for all $t\ge z_{\Delta ,J+1}$ we have $x^{(\Delta )}(z_{\Delta ,J+1}+t)=\tilde{x}(\tilde{z}_{J-1}+t)$. It follows that

$$\begin{aligned} z_{\Delta ,J+2}=z_{\Delta ,J+1}+(\tilde{z}_J-\tilde{z}_{J-1}). \end{aligned}$$

Combining this with Proposition 4.2 we find

$$\begin{aligned} T(\Delta )=z_{\Delta ,J+2}-\tilde{z}_J=z_{\Delta ,J+1}-\tilde{z}_{J-1}=z_{\Delta ,J+1}-z_{\Delta ,J-1}. \end{aligned}$$

$\square$

Proof of Corollary 4.2

Let $\Delta _0\in [0,\tilde{T})$ be given and set $J=j(\Delta _0)$. Then $\Delta _0<z_{\Delta _0,J+1}$. Corollary 4.1 yields a neighbourhood N of $\Delta _0$ in $[0,\tilde{T})$ such that for all $\Delta \in N$ we have $\Delta <z_{\Delta ,J+1}$.

• 1. The case $\tilde{z}_J<\Delta _0$. Then by Corollary 4.1, $\tilde{z}_J<\Delta <z_{\Delta ,J+1}$ for all $\Delta$ in a neighbourhood $V\subset N$ of $\Delta _0$ in $[0,\tilde{T})$. For $\Delta \in V$ we get $j(\Delta )=J$, hence $T(\Delta )=z_{\Delta ,J+2}-\tilde{z}_J$, and Corollary 4.1 yields continuity at $\Delta _0$.

• 2. The case $\tilde{z}_J=\Delta _0$. There is a neighbourhood $U\subset N$ of $\Delta _0$ in $[0,\tilde{T})$ with $\tilde{z}_{J-1}<\Delta$ for all $\Delta \in U$. For all $\Delta \in U$ with $\Delta <\tilde{z}_J$ this yields $j(\Delta )=J-1$ and $T(\Delta )=z_{\Delta ,J-1+2}-\tilde{z}_{J-1}$. At $\Delta =\Delta _0$ we have

  $$\begin{aligned} T(\Delta )(\Delta _0)&= z_{\Delta _0,J+2}-\tilde{z}_J\\&= z_{\Delta _0,J+1}-z_{\Delta _0,J-1}\quad \text {(see Proposition 9.1)}\\&= z_{\Delta _0,J+1}-\tilde{z}_{J-1}. \end{aligned}$$

  The continuity of the map $\Delta \mapsto z_{\Delta ,J+1}$ due to Corollary 4.1 now shows that the restriction of the cycle length map to the set $[0,\tilde{z}_J]\cap U$ is continuous. For $\tilde{z}_J\le \Delta \in U\subset N$ we have $\tilde{z}_J\le \Delta <z_{\Delta ,J+1}$, hence $j(\Delta )=J$, and thereby $T(\Delta )=z_{\Delta ,J+2}-\tilde{z}_J$. The continuity of the map $\Delta \mapsto z_{\Delta ,J+2}$ due to Corollary 4.1 shows that the restriction of the cycle length map to the set $U\cap [\tilde{z}_J,\tilde{T})$ is continuous. As both restrictions coincide at $\tilde{z}_J=\Delta _0$ we obtain continuity of the cycle length map at $\Delta _0$. $\square$

Proof of Proposition 4.3

• 1. Let $\Delta _0\in [0,\tilde{T})$ be given. Set $J=j(\Delta )$. Then $\tilde{z}_J\le \Delta _0<z_{\Delta _0,J+1}$. Using Corollary 4.1 we find a neighbourhood N of $\Delta _0$ in $[0,\tilde{T})$ such that for every $\Delta \in N$ we have

  $$\begin{aligned} \tilde{z}_{J-1}<\Delta <z_{\Delta ,J+1}. \end{aligned}$$

  In the following we show continuity of the map $[0,\tilde{T})\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}$. The proof for the other map is analogous.

• 2. For $\Delta \in N\cap [\tilde{z}_J,\infty )$ we have $J=j(\Delta )$, hence

  $$\begin{aligned} \overline{x}_{\Delta }=\max _{\tilde{z}_J\le t\le z_{\Delta ,J+2}}x^{(\Delta )}(t). \end{aligned}$$

  Using this, the uniform continuity of the map

  $$\begin{aligned}{}[0,\tilde{T})\times [0,\infty )\ni (\Delta ,t)\mapsto x^{(\Delta )}(t)\in \mathbb {R} \end{aligned}$$

  on compact sets, and the continuity of the map $\Delta \mapsto z_{\Delta ,J+2}$ (see Corollary 4.1) one can easily show that the map

  $$\begin{aligned} N\cap [\tilde{z}_J,\infty )\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

  is continuous. Similarly we have for $\Delta \in N\cap (-\infty ,\tilde{z}_J)$ that $J-1=j(\Delta )$, hence

  $$\begin{aligned} \overline{x}_{\Delta }=\max _{\tilde{z}_{J-1}\le t\le z_{\Delta ,J+1}}x^{(\Delta )}(t). \end{aligned}$$

  As before one can then easily show that the map

  $$\begin{aligned} N\cap (-\infty ,\tilde{z}_J)\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

  is continuous.

• 3. It remains to prove that in case $\Delta _0=\tilde{z}_J$ (where $N\cap (-\infty ,\tilde{z}_J)\ne \emptyset$) we have $\overline{x}_{\Delta }\rightarrow \overline{x}_{\Delta _0}$ as $\Delta \nearrow \Delta _0$.

  • (a) The case $\Delta _0=\tilde{z}_J$ and $\tilde{x}'(\tilde{z}_J)<0$. Using the fact that $x^{(\Delta _0)}$ changes sign at each zero we obtain $x^{(\Delta _0)}(t)\le 0$ on $[\tilde{z}_j,z_{\Delta _0,J+1}]=[\Delta _0,z_{\Delta _0,J+1}]$, and

    $$\begin{aligned} \overline{x}_{\Delta _0}&= \max _{\tilde{z}_J\le t\le z_{\Delta _0,J+2}}x^{(\Delta _0)}(t)\\&= \max _{z_{\Delta _0,J+1}\le t\le z_{\Delta _0,J+2}}x^{(\Delta _0)}(t)\\&= \overline{x} \end{aligned}$$

    where the last equation holds because $\Delta _0=\tilde{z}_J$ implies $\Delta _0+\sigma<\Delta _0+\tau <z_{\Delta _0,J+1}$ and thereby $x^{(\Delta _0)}(z_{\Delta _0,J+1}+t)=\tilde{x}(\tilde{z}_{J-1}+t)$ for all $t\ge 0$. Using continuity as in Part 2 above we find a neighbourhood $U\subset N$ of $\Delta _0$ in $[0,\tilde{T})$ such that for each $\Delta \in U$ we have

    $$\begin{aligned} x^{(\Delta )}(t)<\dfrac{1}{2}\overline{x}\quad \text {on}\quad [\Delta ,z_{\Delta ,J+1}] \end{aligned}$$

    and $\tilde{z}_{J-1}+\tau <\Delta$. For $\Delta \in U$ with $\Delta <\tilde{z}_J$, we have $J-1=j(\Delta )$, and the preceding inequality yields

    $$\begin{aligned} x^{(\Delta )}(\tilde{z}_{J-1}+\tau )=\tilde{x}(\tilde{z}_{J-1}+\tau )=\overline{x}\quad \left( >\dfrac{1}{2}\overline{x}\right) . \end{aligned}$$

    It follows that

    $$\begin{aligned} \overline{x}_{\Delta }&= \max _{\tilde{z}_{J-1}\le t\le z_{\Delta ,J+1}}x^{(\Delta )}(t)\\&= \max _{\tilde{z}_{J-1}\le t\le \Delta }x^{(\Delta )}(t)\\&= \overline{x}, \end{aligned}$$

    so the map $U\cap (-\infty ,\tilde{z}_J)\ni \Delta \rightarrow \overline{x}_{\Delta }\in \mathbb {R}$ is constant with value $\overline{x}=\overline{x}_{\Delta _0}$.

  • (b) The case $\Delta _0=\tilde{z}_J$ and $\tilde{x}'(\tilde{z}_J)>0$. Then $x^{(\Delta _0)}$ is negative on $(\tilde{z}_{J-1},\tilde{z}_J)$, positive on $(\tilde{z}_J,z_{\Delta _0,J+1})$ and negative on $(z_{\Delta _0,J+1},z_{\Delta _0,J+2})$, and

    $$\begin{aligned} \overline{x}_{\Delta _0}=\max _{\tilde{z}_J\le t\le z_{\Delta _0,J+2}}x^{(\Delta )}(t)=\max _{\tilde{z}_J\le t\le z_{\Delta _0,J+1}}x^{(\Delta )}(t)>0. \end{aligned}$$

    Choose $t_0\in (\tilde{z}_J,z_{\Delta _0,J+1})$ with

    $$\begin{aligned} x^{(\Delta )}(t_0)=\overline{x}_{\Delta _0}>0. \end{aligned}$$

    By continuity there exists a neighbourhood $V\subset N$ of $\Delta _0$ in $[0,\tilde{T})$ such that for every $\Delta \in V$ we have

    $$\begin{aligned} x^{(\Delta )}(t)< \dfrac{1}{2}\overline{x}_{\Delta _0}\quad \text {on}\quad [\tilde{z}_{J-1},z_{\Delta ,J}],\\ z_{\Delta ,J}< t_0<z_{\Delta ,J+1},\\ \dfrac{1}{2}\overline{x}_{\Delta _0}&< x^{(\Delta )}(t_0). \end{aligned}$$

    For $\Delta \in V$ with $\Delta <\tilde{z}_J$ we have $j(\Delta )=J-1$, and we conclude that

    $$\begin{aligned} \overline{x}_{\Delta }&= \max _{\tilde{z}_{J-1}\le t\le z_{\Delta ,J+1}}x^{(\Delta )}(t)\\&= \max _{z_{\Delta ,J}\le t\le z_{\Delta ,J+1}}x^{(\Delta )}(t) \end{aligned}$$

    where by continuity the last term converges to

    $$\begin{aligned} \max _{z_{\Delta _0,J}\le t\le z_{\Delta _0,J+1}}x^{(\Delta _0)}(t)=\overline{x}_{\Delta _0} \end{aligned}$$

    as $V\ni \Delta \nearrow \Delta _0$.

$\square$

Proofs of the results from Sect. 5

Proof of Proposition 5.1

First we show that $x^{(\Delta )}$ has a first positive zero $z_{\Delta ,1}<\tilde{z}_1$. We have $x^{(\Delta )}(t)<0$ for $t \in (-\tau ,\Delta +\sigma )$. For $t \in [\Delta +\sigma ,\infty )$, $x^{(\Delta )}(t)$ is given by (5.4) as long as $x^{(\Delta )}(t-\tau )<0$. Compute

$$\begin{aligned} z_{\Delta ,1} = \Delta +\sigma +\ln \dfrac{\beta _L-x^{(\Delta )}(\Delta +\sigma )}{\beta _L} \ge \Delta +\sigma \end{aligned}$$

from the condition $x^{(\Delta )}(z_{\Delta ,1})=0$. Similarly since $\tilde{x}(\tilde{z}_1) = 0$ we obtain

$$\begin{aligned} \tilde{z}_1=\Delta +\sigma +\ln \dfrac{\beta _L-\tilde{x}(\Delta +\sigma )}{\beta _L}. \end{aligned}$$

Since $\tilde{x}(\Delta +\sigma )<x^{(\Delta )}(\Delta +\sigma )$ we have $z_{\Delta ,1}<\tilde{z}_1$.

The largest zero of $\tilde{x}$ on $(-\infty ,\Delta ]$ is $\tilde{z}_0=-\tau$. Hence the minimal value of $x^{(\Delta )}$ on $[-\tau ,z_{\Delta ,1}]$ is equal to $\underline{x}$. On the interval $[z_{\Delta ,1},z_{\Delta ,1}+\tau ]$, $x^{(\Delta )}(t)$ is given by (5.4). This yields $x^{(\Delta )}(t+z_{\Delta ,1})=\tilde{x}(t+\tilde{z}_1)$ for all $t\ge 0$. It follows that $\overline{x}_{\Delta }=\overline{x}$ and $\underline{x}_{\Delta }=\underline{x}$ and

$$\begin{aligned} T(\Delta )&= \bigl (z_{\Delta ,1}+(\tilde{z}_2-\tilde{z}_1)\bigr )-\tilde{z}_{0}=z_{\Delta ,1}-\tilde{z}_1+\tilde{T}\\&= \tilde{T}+\ln \dfrac{\beta _L-x^{(\Delta )}(\Delta +\sigma )}{\beta _L}-\ln \dfrac{\beta _L-\tilde{x}(\Delta +\sigma )}{\beta _L}\\&= \tilde{T}+\ln \dfrac{\beta _L-x^{(\Delta )}(\Delta +\sigma )}{\beta _L-\tilde{x}(\Delta +\sigma )}. \end{aligned}$$

The formula (5.5) yields

$$\begin{aligned} x^{(\Delta )}(\Delta + \sigma )-\beta _L= -\beta _L e^{\tilde{z}_1-\Delta -\sigma }+a(1-e^{-\sigma }) \end{aligned}$$

and with

$$\begin{aligned} \tilde{x}(\Delta +\sigma )-\beta _L=(\underline{x}-\beta _L)e^{-(\Delta +\sigma )}=-\beta _Le^{\tilde{z}_1-(\Delta +\sigma )} \end{aligned}$$

we find

$$\begin{aligned} T(\Delta )&= \tilde{T}+\ln \dfrac{ \beta _L e^{\tilde{z}_1-\Delta -\sigma }-a(1-e^{-\sigma })}{\beta _Le^{\tilde{z}_1-(\Delta +\sigma )}}\\&= \tilde{T}+\ln \left( 1-\dfrac{a(1-e^{-\sigma })}{\beta _L}e^{\Delta +\sigma -\tilde{z}_1}\right) . \end{aligned}$$

Thus, $T(\Delta ) < \tilde{T}$, and the restriction of $T(\Delta )$ to $I_{RNRN}$ is strictly decreasing. $\square$

From (5.4) it follows that $x^{(\Delta )}$ is strictly decreasing right after $t=\Delta +\sigma$ if and only if $x^{(\Delta )}(\Delta +\sigma )-\beta _L>0$. We have, by (5.5),

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )-\beta _L=-\beta _Le^{\tilde{z}_1-\Delta -\sigma }+a(1-e^{-\sigma }). \end{aligned}$$

Hence, $x^{(\Delta )}(\Delta +\sigma )-\beta _L>0$ if and only if

$$\begin{aligned} e^{\Delta }>\dfrac{\beta _Le^{\tilde{z}_1-\sigma }}{a(1-e^{-\sigma })}. \end{aligned}$$

Let us define

$$\begin{aligned} \hat{\delta }_1=\ln \dfrac{\beta _Le^{\tilde{z}_1-\sigma }}{a(1-e^{-\sigma })}. \end{aligned}$$

(9.1)

We have

$$\begin{aligned} \hat{\delta }_1=\tilde{z}_1-\sigma +\ln \dfrac{\beta _L}{a(1-e^{-\sigma })}>\delta _1. \end{aligned}$$

Thus we divide the case RNRP when $x^{(\Delta )}(\Delta +\sigma )\ge 0$ into the two subcases $0\le x^{(\Delta )}(\Delta +\sigma )\le \beta _L$ and $x^{(\Delta )}(\Delta +\sigma )>\beta _L$ and we consider these two subcases separately as $\mathbf {RNRP1}$ and $\mathbf {RNRP2}$, see Figs. 3 and 4, respectively. The $\Delta$-intervals are of the form

$$\begin{aligned} I_{RNRP1}=[\max \{0,\delta _1\},\tilde{z}_1)\cap [\delta _1,\hat{\delta }_1]\quad \text {and}\quad I_{RNRP2}=[\max \{0,\delta _1\},\tilde{z}_1)\cap (\hat{\delta }_1,\infty ). \end{aligned}$$

• Case $\mathbf {RNRP1}$ The pulse parameters $(a,\Delta ,\sigma )$ are such that $\Delta <\tilde{z}_1$ and $x^{(\Delta )}(\Delta +\sigma )\in [0,\beta _L]$. Then $x^{(\Delta )}$ is increasing right after the pulse.

• Case $\mathbf {RNRP2}$ The pulse parameters $(a,\Delta ,\sigma )$ are such that $\Delta <\tilde{z}_1$ and $x^{(\Delta )}(\Delta +\sigma )>\beta _L$. Then $x^{(\Delta )}$ is strictly decreasing right after the pulse.

Proof of Proposition 5.2

The equation

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,1})=\beta _L+a+\bigl (x^{(\Delta )}(\Delta )-(\beta _L+a)\bigr )e^{-(z_{\Delta ,1}-\Delta )} \end{aligned}$$

together with (5.1) yields

$$\begin{aligned} \nonumber (\beta _L+a)e^{z_{\Delta ,1}}&=\bigl (\beta _L+a-x^{(\Delta )}(\Delta )\bigr )e^{\Delta }\\&=\beta _Le^{\tilde{z}_1}+ae^{\Delta }. \end{aligned}$$

(9.2)

Use $\Delta <z_{\Delta ,1}$ and $a>0,\beta _L>0$ to obtain

$$\begin{aligned} e^{z_{\Delta ,1}}-e^{\tilde{z}_1}=\dfrac{a}{\beta _L}(e^{\Delta }-e^{z_{\Delta ,1}})<0 \end{aligned}$$

and to conclude that $z_{\Delta ,1}<\tilde{z}_1$.

We have

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,1}+\tau )=\beta _L+(x^{(\Delta )}(\Delta +\sigma )-\beta _L)e^{-\left( z_{\Delta ,1}+\tau - (\Delta +\sigma )\right) }, \end{aligned}$$

which by (5.5) can be rewritten as

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,1}+\tau )&=\beta _L+\bigl (-\beta _Le^{\tilde{z}_1-\Delta -\sigma }+a(1-e^{-\sigma })\bigr ) e^{-\left( z_{\Delta ,1}+\tau - (\Delta +\sigma )\right) }\\&=\beta _L-(\beta _Le^{\tilde{z}_1}+ae^{\Delta })e^{-(z_{\Delta ,1}+\tau )}+ae^{-\left( z_{\Delta ,1}+\tau - (\Delta +\sigma )\right) }. \end{aligned}$$

From (9.2) it follows that

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,1}+\tau )=\beta _L-(\beta _L+a)e^{-\tau }+ae^{-\tau }e^{\sigma +\Delta -z_{\Delta ,1}} \end{aligned}$$

(9.3)

and that the function $[\max \{0,\delta _1\},\tilde{z}_1)\ni \Delta \mapsto e^{z_{\Delta ,1}-\Delta }\in \mathbb {R}$ is strictly decreasing, which shows that $x^{(\Delta )}(z_{\Delta ,1}+\tau )$ is strictly increasing with respect to $\Delta \in [\max \{0,\delta _1\},\tilde{z}_1)$. Since $\Delta +\sigma \ge z_{\Delta ,1}$ and $ae^{-\tau }>0$, we get

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,1}+\tau )\ge \beta _L-\beta _Le^{-\tau }=\overline{x}. \end{aligned}$$

Also the function $[\max \{0,\delta _1\},\tilde{z}_1)\ni \Delta \mapsto x^{(\Delta )}(\Delta +\sigma )\in \mathbb {R}$ is increasing.

In subcase $\mathbf {RNRP1}$ the function $x^{(\Delta )}$ is increasing on $[\Delta +\sigma ,z_{\Delta ,1}+\tau ]$ while in subcase $\mathbf {RNRP2}$ it is decreasing on that interval. It follows that in subcase $\mathbf {RNRP1}$,

$$\begin{aligned} \max _{z_{\Delta ,1}\le t\le z_{\Delta ,1}+\tau }x^{(\Delta )}(t)=x^{(\Delta )}( z_{\Delta ,1}+\tau )\ge \overline{x} \end{aligned}$$

while in subcase $\mathbf {RNRP2}$,

$$\begin{aligned} \max _{z_{\Delta ,1}\le t\le z_{\Delta ,1}+\tau }x^{(\Delta )}(t)=x^{(\Delta )}( \Delta +\sigma )\ge x^{(\Delta )}(z_{\Delta ,1}+\tau )\ge \overline{x}. \end{aligned}$$

In both subcases $\max _{z_{\Delta ,1}\le t\le z_{\Delta ,1}+\tau }x^{(\Delta )}(t)$ is increasing with respect to $\Delta$.

Also in both subcases we have $0<x^{(\Delta )}(t)$ for $z_{\Delta ,1}<t\le z_{\Delta ,1}+\tau$. It follows that after $t=z_{\Delta ,1}+\tau \ge \Delta +\sigma$ the function $x^{(\Delta )}$ is given by

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+\bigl (x^{(\Delta )}(z_{\Delta ,1}+\tau )+\beta _U\bigr )e^{-\left( t-(z_{\Delta ,1}+\tau )\right) } \end{aligned}$$

as long as $x^{(\Delta )}(t-\tau )>0$. We obtain a first zero $z_{\Delta ,2}$ of $x^{(\Delta )}$ in $(z_{\Delta ,1}+\tau ,\infty )$, and for all $t\ge 0$, $x^{(\Delta )}(z_{\Delta ,2}+t)=\tilde{x}(\tilde{z}_0+t)$ (recall $\tilde{z}_0=-\tau$). Then

$$\begin{aligned} T(\Delta )=z_{\Delta ,2}-\tilde{z}_0=z_{\Delta ,2}+\tau . \end{aligned}$$

Moreover,

$$\begin{aligned} \overline{x}_{\Delta }&= \max _{-\tau \le t\le z_{\Delta ,2}}x^{(\Delta )}(t)=\max _{z_{\Delta ,1}\le t\le z_{\Delta ,1}+\tau }x^{(\Delta )}(t)\\&= \max \{x^{(\Delta )}(\Delta +\sigma ),x^{(\Delta )}(z_{\Delta ,1}+\tau )\}\\&\ge \overline{x} \end{aligned}$$

is increasing with respect to $\Delta$ in both subcases.

Now the equation

$$\begin{aligned} 0= x^{(\Delta )}(z_{\Delta ,2}) = -\beta _U+\bigl (x^{(\Delta )}(z_{\Delta ,1}+\tau )+\beta _U\bigr )e^{z_{\Delta ,1}+\tau -z_{\Delta ,2}} \end{aligned}$$

yields

$$\begin{aligned} \beta _U e^{z_{\Delta ,2}}=\bigl (x^{(\Delta )}(z_{\Delta ,1}+\tau )+\beta _U\bigr )e^{z_{\Delta ,1}+\tau }. \end{aligned}$$

Also, from (9.2) and (9.3) we obtain

$$\begin{aligned} \beta _U e^{z_{\Delta ,2}}=(\beta _L+\beta _U)e^{z_{\Delta ,1}+\tau }-\beta _L e^{\tilde{z}_1}+a(1-e^{-\sigma }) e^{\Delta +\sigma }. \end{aligned}$$

Since

$$\begin{aligned} \beta _U+\beta _L-\beta _{L}e^{-\tau }=\beta _U+\overline{x}=\beta _Ue^{\tilde{z}_2-t_{\max }} \end{aligned}$$

and $\tilde{z}_2-t_{\max }+\tau =\tilde{z}_2-\tilde{z}_1$, we arrive at

$$\begin{aligned} \beta _L e^{\tilde{z}_1}+\beta _U e^{\tilde{z}_2}=(\beta _L+\beta _U)e^{\tau +\tilde{z}_1}. \end{aligned}$$

(9.4)

Thus

$$\begin{aligned} \begin{aligned} \beta _U e^{z_{\Delta ,2}}&=\beta _Ue^{\tilde{z}_2}+(\beta _L+\beta _U)e^{\tau }(e^{z_{\Delta ,1}}-e^{\tilde{z}_1})+a(e^{\sigma }-1) e^{\Delta } \\&=\beta _Ue^{\tilde{z}_2}+\dfrac{a(\beta _L+\beta _U)e^{\tau }}{\beta _L+a}(e^{\Delta }-e^{\tilde{z}_1})+a(e^{\sigma }-1) e^{\Delta }\quad \text {(with (9.2))}, \end{aligned} \end{aligned}$$

which implies the formula for $T(\Delta )=z_{\Delta ,2}+\tau$, since $\tilde{z}_2+\tau =\tilde{T}$. $\square$

In the case $\mathbf {RPRP}$ we always have $x^{(\Delta )}(\Delta +\sigma )>0$, but in the following proof we need to distinguish between two cases

• Case $\mathbf {RPRP1}$ $0< x^{(\Delta )}(\Delta +\sigma )\le \beta _L$, and

• Case $\mathbf {RPRP2}$ $x^{(\Delta )}(\Delta +\sigma )> \beta _L$.

Proof of Proposition 5.3

Using (5.4) for $\Delta +\sigma \le t\le z_{\Delta ,1}+\tau =\tilde{z}_1+\tau =t_{\max }$ and (5.5) we obtain

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,1}+\tau )&= \beta _L+\bigl (x^{(\Delta )}(\Delta +\sigma )-\beta _L\bigr )e^{-\left( \tilde{z}_1+\tau -(\Delta +\sigma )\right) }\\&= \beta _L-\beta _Le^{-\tau } +a(1-e^{-\sigma })e^{-\left( \tilde{z}_1+\tau -(\Delta +\sigma )\right) }\\&= \overline{x} +a(e^{\sigma }-1)e^{-(\tilde{z}_1+\tau )+\Delta }>\overline{x}, \end{aligned}$$

and $x^{(\Delta )}(z_{\Delta ,1}+\tau )$ is increasing as a function of $\Delta \in I_{RPRP}$. Also $x^{(\Delta )}(\Delta +\sigma )$ is increasing as a function of $\Delta \in I_{RPRP}$. In case $\mathbf {RPRP1}$ the function $x^{(\Delta )}$ is increasing on $[\tilde{z}_1,\tilde{z}_1+\tau ]$ with $x^{(\Delta )}(t)\le \beta _L$ on this interval, hence $\max _{\tilde{z}_1\le t\le \tilde{z}_1+\tau }x^{(\Delta )}(t)=x^{(\Delta )}(\tilde{z}_1+\tau )\le \beta _L$. In case $\mathbf {RPRP2}$ the function $x^{(\Delta )}$ is increasing on $[\tilde{z}_1,\Delta +\sigma ]$ and decreasing on $[\Delta +\sigma ,\tilde{z}_1+\tau ]$, with $x^{(\Delta )}(t)>\beta _L$ on this interval, hence $\max _{\tilde{z}_1\le t\le \tilde{z}_1+\tau }x^{(\Delta )}(t)=x^{(\Delta )}(\Delta +\sigma )>\beta _L$. In both subcases,

$$\begin{aligned} \max _{\tilde{z}_1\le t\le \tilde{z}_1+\tau }x^{(\Delta )}(t)=\max \{x^{(\Delta )}(\Delta +\sigma ),x^{(\Delta )}(\tilde{z}_1+\tau )\}\ge x^{(\Delta )}(\tilde{z}_1+\tau )>\overline{x}, \end{aligned}$$

and $\max _{\tilde{z}_1\le t\le \tilde{z}_1+\tau }x^{(\Delta )}(t)$ is increasing as a function of $\Delta \in I_{RPRP}$.

As $x^{(\Delta )}(t)>0$ on $(\tilde{z}_1,\tilde{z}_1+\tau ]$ we have

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+\bigl (x^{(\Delta )}(\tilde{z}_1+\tau )+\beta _U\bigr )e^{-\left( t-(\tilde{z}_1+\tau )\right) } \end{aligned}$$

for $t\ge \tilde{z}_1+\tau$ as long as $x^{(\Delta )}(t-\tau )>0$. It follows that there is a smallest zero $z_{\Delta ,2}$ of $x^{(\Delta )}$ in $(\tilde{z}_1+\tau ,\infty )$, and

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,2}+t)=\tilde{x}(\tilde{z}_0+t)\quad \text {for all}\quad t\ge 0. \end{aligned}$$

This yields

$$\begin{aligned} T(\Delta )=\bigl (z_{\Delta ,2}+(\tilde{z}_1-\tilde{z}_0)\bigr )-\tilde{z}_1=z_{\Delta ,2}+\tau . \end{aligned}$$

Moreover,

$$\begin{aligned} \overline{x}_{\Delta }&= \max _{\tilde{z}_1\le t\le z_{\Delta ,2}+(\tilde{z}_1-\tilde{z}_0)}x^{(\Delta )}(t)\\&= \max _{\tilde{z}_1\le t\le \tilde{z}_1+\tau }x^{(\Delta )}(t)\\&= \max \{x^{(\Delta )}(\Delta +\sigma ),x^{(\Delta )}(\tilde{z}_1+\tau )\}\ge \overline{x} \end{aligned}$$

is increasing as a function of $\Delta \in I_{RPRP}$, and $\underline{x}_{\Delta }=\underline{x}$.

Recall $t_{\max }=\tilde{z}_1+\tau$. From

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,2})=-\beta _U+\bigl (x^{(\Delta )}(t_{\max })+\beta _U\bigr )e^{-(z_{\Delta ,2}-t_{\max })} \end{aligned}$$

we get

$$\begin{aligned} \beta _U e^{z_{\Delta ,2}}=\bigl (x^{(\Delta )}(t_{\max })+\beta _U\bigr )e^{t_{\max }}=(\overline{x}+\beta _U)e^{t_{\max }}+a(e^{\sigma }-1)e^{\Delta }. \end{aligned}$$

Since $(\overline{x}+\beta _U)e^{t_{\max }}=\beta _{U}e^{\tilde{z}_2}$, we conclude that

$$\begin{aligned} \beta _U e^{z_{\Delta ,2}}=\beta _U e^{\tilde{z}_2} +a(e^{\sigma }-1)e^{\Delta }. \end{aligned}$$

For the cycle length we obtain $T(\Delta )=z_{\Delta ,2}+\tau >\tilde{z}_2+\tau =\tilde{T}$ and the formula for $T(\Delta )$ follows. $\square$

Proof of Remark 5.1

• 1. Let $\delta _1>0$. We first show that the expressions defining $T(\Delta )$ in Proposition 5.1 and in Proposition 5.2 yield the same value for $\Delta =\delta _1$. Consider the argument of $\ln$ in (5.8). We have

  $$\begin{aligned}&\dfrac{a(e^{\sigma }-1)}{\beta _U} e^{\Delta -\tilde{z}_2}+\dfrac{a(\beta _L+\beta _U)e^{\tau +\tilde{z}_1-\tilde{z}_2}}{\beta _U(\beta _L+a)} (e^{\Delta -\tilde{z}_1}-1)\\&\quad =\dfrac{ae^{-\tilde{z}_2}}{\beta _U(\beta _L+a)} \Bigl (\bigl ((\beta _L+a)(e^{\sigma }-1)+(\beta _L+\beta _U)e^{\tau }\bigr )e^{\Delta } -(\beta _L+\beta _U)e^{\tau +\tilde{z}_1}\Bigr ). \end{aligned}$$

  From (5.6) for $\delta _1$ it follows that

  $$\begin{aligned} \beta _Le^\sigma +a(e^\sigma -1)=\beta _Le^{\tilde{z}_1-\delta _1}, \end{aligned}$$

  which gives

  $$\begin{aligned} (\beta _L+a)(e^{\sigma }-1)=\beta _Le^{\tilde{z}_1-\delta _1}-\beta _L. \end{aligned}$$

  Since

  $$\begin{aligned} -\beta _L+(\beta _L+\beta _U)e^{\tau }=e^{\tau }(\beta _U+\overline{x})=\beta _Ue^{\tilde{z}_2-\tilde{z}_1}, \end{aligned}$$

  we obtain

  $$\begin{aligned}&\dfrac{a(e^{\sigma }-1)}{\beta _U} e^{\Delta -\tilde{z}_2}+\dfrac{a(\beta _L+\beta _U)e^{\tau +\tilde{z}_1-\tilde{z}_2}}{\beta _U(\beta _L+a)} (e^{\Delta -\tilde{z}_1}-1)\\&\quad =\dfrac{ae^{-\tilde{z}_2}}{\beta _U(\beta _L+a)} \left( (\beta _Le^{\tilde{z}_1-\delta _1}+\beta _Ue^{\tilde{z}_2-\tilde{z}_1})e^{\Delta } -(\beta _Le^{\tilde{z}_1}+\beta _Ue^{\tilde{z}_2})\right) , \end{aligned}$$

  which for $\Delta =\delta _1$ becomes

  $$\begin{aligned} \dfrac{ae^{-\tilde{z}_2}}{\beta _U(\beta _L+a)} \left( (\beta _Le^{\tilde{z}_1-\delta _1}+\beta _Ue^{\tilde{z}_2-\tilde{z}_1})e^{\Delta } -(\beta _Le^{\tilde{z}_1}+\beta _Ue^{\tilde{z}_2})\right) =\dfrac{a(e^{\delta _1-\tilde{z}_1}-1)}{\beta _L+a}. \end{aligned}$$

  We have

  $$\begin{aligned} \begin{aligned} e^{\delta _1-\tilde{z}_1}-1&=\dfrac{\beta _L}{\beta _Le^{\sigma }+a(e^{\sigma }-1)}-1 =-\dfrac{(\beta _L+a)(e^{\sigma }-1)}{\beta _Le^{\sigma }+a(e^{\sigma }-1)}, \end{aligned} \end{aligned}$$

  which leads to

  $$\begin{aligned} \begin{aligned} \dfrac{a(e^{\delta _1-\tilde{z}_1}-1)}{\beta _L+a}&=-\dfrac{a(e^{\sigma }-1)}{\beta _Le^{\sigma }+a(e^{\sigma }-1)} =-\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\delta _1-\tilde{z}_1} \end{aligned} \end{aligned}$$

  and shows that the formulae for $T(\Delta )$ from Propositions 5.1 and 5.2 yield the same value for $\Delta =\delta _1>0$. From (5.7) of Proposition 5.1, this value is strictly less than $\tilde{T}$.

• 2. By continuity, we infer $T(\Delta )<\tilde{T}$ for $\Delta$ close to $\delta _1>0$.

$\square$

Proof of Proposition 5.4

Since $x^{(\Delta )}(t)>0$ for $\tilde{z}_1<t<\Delta +\sigma$ and $\tilde{z}_1+\tau <\Delta +\sigma$ we obtain that on $[\Delta +\sigma ,\infty )$,

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{-\left( t-(\Delta +\sigma )\right) }\quad \text {as long as}\quad 0<x^{(\Delta )}(t-\tau ). \end{aligned}$$

As $-\beta _U<0$ there is a smallest zero $z_{\Delta ,2}$ of $x^{(\Delta )}$ in $[\Delta +\sigma ,\infty )$, and

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,2}+t)=\tilde{x}(\tilde{z}_2+t)\quad \text {for all}\quad t\ge 0. \end{aligned}$$

It follows that

$$\begin{aligned} T(\Delta )=z_{\Delta ,2}+(\tilde{z}_3-\tilde{z}_2)-\tilde{z}_1=z_{\Delta ,2}+\tilde{T}-\tilde{z}_2=z_{\Delta ,2}-\tilde{z}_0=z_{\Delta ,2}+\tau . \end{aligned}$$

Moreover, $\overline{x}_{\Delta }=x^{(\Delta )}(t_{\max })$ if $\Delta \le \hat{\delta }_2$ (in which case $x^{(\Delta )}$ is decreasing on $[t_{\max },\Delta +\sigma ]$), while for $\Delta >\hat{\delta }_2$ the function $x^{(\Delta )}$ is increasing on $[t_{\max },\Delta +\sigma ]$ and $\overline{x}_{\Delta }=x^{(\Delta )}(\Delta +\sigma )>x^{(\Delta )}(t_{\max })\ge \overline{x}$. Hence $\overline{x}_{\Delta }\ge \overline{x}$. Obviously, $\underline{x}_{\Delta }=\underline{x}$. Also, $\overline{x}_{\Delta }$ is strictly decreasing as a function of $\Delta \in I_{RPFP}$, see (5.10).

From

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,2})=-\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr ) e^{-(z_{\Delta ,2}-(\Delta +\sigma ))} \end{aligned}$$

it follows that

$$\begin{aligned} \beta _U e^{z_{\Delta ,2}}&= \bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{ \Delta +\sigma }\\&= \bigl (\beta _Ue^{\tilde{z}_2-( \Delta +\sigma )} +a(1-e^{-\sigma })\bigr )e^{ \Delta +\sigma }\quad \text {(see (5.10))}\\&= \beta _Ue^{\tilde{z}_2}+a(e^{\sigma }-1)e^{\Delta }. \end{aligned}$$

Hence $z_{\Delta ,2}>\tilde{z}_2$, and thereby

$$\begin{aligned} T(\Delta )=z_{\Delta ,2}+\tau >\tilde{z}_2+\tau =\tilde{T} \end{aligned}$$

Furthermore,

$$\begin{aligned} T(\Delta )&= z_{\Delta ,2}+\tau =\tilde{T}+z_{\Delta ,2}-\tilde{z}_2\\&= \tilde{T}+\ln \left( 1+\dfrac{a(e^{\sigma }-1)e^{\Delta -\tilde{z}_2}}{\beta _U}\right) , \end{aligned}$$

and the map

$$\begin{aligned} I_{RPFP}\ni \Delta \mapsto T(\Delta )\in \mathbb {R} \end{aligned}$$

is strictly increasing. $\square$

Proof of Proposition 5.5

From $x^{(\Delta )}(\Delta +\sigma )<0<x^{(\Delta )}(t_{\max })$ we know that $x^{(\Delta )}$ is strictly decreasing on $[t_{\max },\Delta +\sigma ]$. It follows that there is a single zero in this interval, which is given by

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,2})=-\beta _U+a+\bigl (x^{(\Delta )}(t_{\max })+\beta _U-a\bigr )e^{-(z_{\Delta ,2}-t_{\max })}, \end{aligned}$$

or equivalently,

$$\begin{aligned} (\beta _U-a)e^{z_{\Delta ,2}} = \bigl (x^{(\Delta )}(t_{\max })+\beta _U-a\bigr )e^{t_{\max }}. \end{aligned}$$

Also,

$$\begin{aligned} (\beta _U-a)e^{z_{\Delta ,2}}&= \bigl (\overline{x}+a(1-e^{\Delta -t_{\max }})+\beta _U-a\bigr )e^{t_{\max }}\\&= (\overline{x}+\beta _U)e^{t_{\max }}-ae^{\Delta }, \end{aligned}$$

and we arrive at

$$\begin{aligned} (\beta _U-a)e^{z_{\Delta ,2}}= \beta _U e^{\tilde{z}_2}-ae^{\Delta }. \end{aligned}$$

(9.5)

Since $\beta _U>a$ we infer that the map $I_{RPFN}\ni \Delta \mapsto e^{z_{\Delta ,2}-\Delta }\in \mathbb {R}$ is strictly decreasing.

We have $z_{\Delta ,2}<\Delta +\sigma \le z_{\Delta ,2}+\tau$, and on $[\Delta +\sigma ,z_{\Delta ,2}+\tau ]$,

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{-(t-(\Delta +\tau ))} \end{aligned}$$

is strictly decreasing and negative because we have $x^{(\Delta )}(\Delta +\sigma )+\beta _U>0$ from (5.10). It follows that $x^{(\Delta )}$ is strictly increasing on $[z_{\Delta ,2}+\tau ,\infty )$ as long as $x^{(\Delta )}(t-\tau )<0$. There is a smallest zero $z_{\Delta ,3}$ of $x^{(\Delta )}$ in this interval, and

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,3}+t)&= \tilde{x}(\tilde{z}_1+t)\quad \text {for all}\quad t\ge 0,\\ T(\Delta )&= z_{\Delta ,3}-\tilde{z}_1,\\ \overline{x}_{\Delta }&= x^{(\Delta )}(t_{\max })\ge \overline{x},\\ \underline{x}_{\Delta }&= x^{(\Delta )}(z_{\Delta ,2}+\tau ). \end{aligned}$$

We compute

$$\begin{aligned} \underline{x}_{\Delta }=x^{(\Delta )}(z_{\Delta ,2}+\tau ) = -\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr ) e^{-\left( z_{\Delta ,2}+\tau -(\Delta +\sigma )\right) } \end{aligned}$$

and use

$$\begin{aligned} x^{(\Delta )}(\Delta +\sigma )+\beta _U=\beta _U e^{\tilde{z}_2-(\Delta +\sigma )}+a(1-e^{-\sigma })>0 \end{aligned}$$

from (5.10). This gives

$$\begin{aligned} \underline{x}_{\Delta }=-\beta _U+\bigl (\beta _U e^{\tilde{z}_2} -a e^{\Delta }\bigr )e^{-(z_{\Delta ,2}+\tau )} +ae^{-\left( z_{\Delta ,2}+\tau -(\Delta +\sigma )\right) }. \end{aligned}$$

With (9.5) we obtain

$$\begin{aligned} \underline{x}_{\Delta }&= -\beta _U+(\beta _U-a)e^{-\tau } +ae^{-\left( z_{\Delta ,2}+\tau -(\Delta +\sigma )\right) }\\&= -\beta _U+\beta _U e^{-\tau }+ae^{-\tau }(e^{-z_{\Delta ,2}+\Delta +\sigma }-1). \end{aligned}$$

Since $\Delta +\sigma >z_{\Delta ,2}$ we conclude that

$$\begin{aligned} \underline{x}_{\Delta }>-\beta _U+\beta _U e^{-\tau }=\underline{x}. \end{aligned}$$

We turn to the cycle length $T(\Delta )=z_{\Delta ,3}-\tilde{z}_1$. The equation for $z_{\Delta ,3}$, namely,

$$\begin{aligned} 0&= x^{(\Delta )}(z_{\Delta ,3})=\beta _L+\bigl (x^{(\Delta )}(z_{\Delta ,2}+\tau )-\beta _L\bigr )e^{-\left( z_{\Delta ,3}-(z_{\Delta ,2}+\tau )\right) }\\&= \beta _L+(\underline{x}_{\Delta }-\beta _L)e^{-\left( z_{\Delta ,3}-(z_{\Delta ,2}+\tau )\right) } \end{aligned}$$

yields

$$\begin{aligned} \beta _Le^{z_{\Delta ,3}}&= (\beta _L-\underline{x}_{\Delta })e^{z_{\Delta ,2}+\tau }\\&= (\beta _L+\beta _U)e^{z_{\Delta ,2}+\tau }-(\beta _U e^{\tilde{z}_2} -a e^{\Delta })- ae^{\Delta +\sigma }\\&\qquad \text {(with the formula for}\quad \underline{x}_{\Delta }\quad \text {and (9.5))}\\&= (\beta _L+\beta _U)e^{z_{\Delta ,2}+\tau }-\beta _Ue^{\tilde{z}_2}-a(e^{\sigma }-1)e^{\Delta }. \end{aligned}$$

Since $\tilde{z}_3=\tilde{z}_2+\tau +\tilde{z}_1$, we have

$$\begin{aligned} \begin{aligned} \beta _Le^{\tilde{z}_3}+\beta _Ue^{\tilde{z}_2}&=(\beta _L e^{\tilde{z}_1}+\beta _U e^{-\tau })e^{\tilde{z}_2+\tau }\\&=(\beta _L+\beta _U)e^{\tilde{z}_2+\tau }, \end{aligned} \end{aligned}$$

which gives

$$\begin{aligned} \begin{aligned} \beta _Le^{z_{\Delta ,3}}&= \beta _Le^{\tilde{z}_3}+(\beta _L+\beta _U)e^{\tau }(e^{z_{\Delta ,2}}-e^{\tilde{z}_2})-a(e^{\sigma }-1)e^{\Delta }. \end{aligned} \end{aligned}$$

Now use (9.5) again to obtain

$$\begin{aligned} \begin{aligned} \beta _Le^{z_{\Delta ,3}}&= \beta _Le^{\tilde{z}_3}-\dfrac{a(\beta _L+\beta _U)e^{\tau }}{\beta _U-a} (e^{\Delta }-e^{\tilde{z}_2})-a(e^{\sigma }-1)e^{\Delta }, \end{aligned} \end{aligned}$$

which implies the formula for $T(\Delta )$. We have

$$\begin{aligned} \dfrac{(\beta _L+\beta _U)}{\beta _U-a}e^{\tau }+e^{\sigma }-1 =\dfrac{\beta _Le^{\tilde{z}_1+\tau }+(\beta _U-a)e^{\sigma }+a}{\beta _U-a}. \end{aligned}$$

Thus, the map $I_{RPFN} \ni \Delta \mapsto T(\Delta )\in \mathbb {R}$ is strictly decreasing, since $\beta _U>a$. $\square$

Proof of Remark 5.2

• 1. We first show that the expressions defining $T(\Delta )$ in Proposition 5.3 and in Proposition 5.5 (Eqs. 5.9 and 5.13 respectively) yield the same value for $\Delta =\delta _2$. Consider the argument of $\ln$ in (5.13) of Proposition 5.5. We have

  $$\begin{aligned}&\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1-\tilde{T}}+\dfrac{a(\beta _L+\beta _U)e^{-\tilde{z}_1}}{\beta _L(\beta _U-a)}e^{\Delta -\tilde{z}_2}\\&\quad = \dfrac{ae^{\Delta -\tilde{z}_1-\tilde{T}}}{\beta _L(\beta _U-a)}\Bigl ((\beta _U-a)(e^{\sigma }-1)+(\beta _L+\beta _U)e^{\tau }\Bigr ) \end{aligned}$$

  Note that from the definition of $\delta _2$ it follows that

  $$\begin{aligned} \beta _Ue^{\sigma }-a(e^{\sigma }-1)=\beta _Ue^{\tilde{z}_2-\delta _2}, \end{aligned}$$

  which gives

  $$\begin{aligned} \begin{aligned} (\beta _U-a)(e^{\sigma }-1)+(\beta _L+\beta _U)e^{\tau }&=\beta _Ue^{\sigma }-a(e^{\sigma }-1)+(\beta _L-\underline{x})e^{\tau }\\&=\beta _Ue^{\tilde{z}_2-\delta _2}+\beta _L e^{t_{\max }} \end{aligned} \end{aligned}$$

  and leads to

  $$\begin{aligned}&\dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1-\tilde{T}}+\dfrac{a(\beta _L+\beta _U)e^{-\tilde{z}_1}}{\beta _L(\beta _U-a)}(e^{\Delta -\tilde{z}_2}-1)\\&\quad = \dfrac{ae^{-\tilde{z}_1}}{\beta _L(\beta _U-a)}\Bigl ((\beta _Ue^{-\tau -\delta _2}+\beta _L e^{\tilde{z}_1-\tilde{z}_2})e^{\Delta }-(\beta _L+\beta _U)\Bigr ). \end{aligned}$$

  Observe that for $\Delta =\delta _2$ we have

  $$\begin{aligned} (\beta _Ue^{-\tau -\delta _2}+\beta _L e^{\tilde{z}_1-\tilde{z}_2})e^{\Delta }= \beta _U e^{-\tau }+\beta _Le^{\tilde{z}_1+\delta _2-\tilde{z}_2}. \end{aligned}$$

  Using this we obtain that for $\Delta =\delta _2$,

  $$\begin{aligned} \dfrac{a(e^{\sigma }-1)}{\beta _L}e^{\Delta -\tilde{z}_1-\tilde{T}}+\dfrac{a(\beta _L+\beta _U)e^{-\tilde{z}_1}}{\beta _L(\beta _U-a)}(e^{\Delta -\tilde{z}_2}-1)= \dfrac{a}{(\beta _U-a)}(e^{\delta _2-\tilde{z}_2}-1). \end{aligned}$$

  We have

  $$\begin{aligned} \dfrac{a}{(\beta _U-a)}(e^{\delta _2-\tilde{z}_2}-1)&=\dfrac{a}{(\beta _U-a)}\left( \dfrac{\beta _U}{\beta _Ue^{\sigma }-a(e^{\sigma }-1)}-1\right) \\&=-\dfrac{a(e^{\sigma }-1)}{\beta _Ue^{\sigma }-a(e^{\sigma }-1)}\\&=-\dfrac{a(e^{\sigma }-1)}{\beta _U}e^{\delta _2-\tilde{z}_2}. \end{aligned}$$

  Thus, the formulae (5.9) and (5.13) from Propositions 5.3 and 5.5 are the same for $\Delta =\delta _2$. Since

  $$\begin{aligned} -\dfrac{a(e^{\sigma }-1)}{\beta _U}e^{\delta _2-\tilde{z}_2}<0 \end{aligned}$$

  we also deduce that the value given by both equations for $\Delta =\delta _2$ is strictly larger than $\tilde{T}$.

• 2. By continuity, we infer $T(\Delta )>\tilde{T}$ for $\Delta$ close to $\delta _2$. $\square$

Proof of Proposition 5.6

From $0\le x^{(\Delta )}(t)$ on $[t_{\max },\Delta +\sigma ]$ we infer that $x^{(\Delta )}$ decreases on $[\Delta +\sigma ,\infty )$ as long as $x^{(\Delta )}(t-\tau )>0$. This yields the existence of a smallest zero $z_{\Delta ,2}$ in $[\Delta +\sigma ,\infty )$, and $x^{(\Delta )}(t+z_{\Delta ,2})=\tilde{x}(t+\tilde{z}_2)$ for all $t\ge 0$.

Hence

$$\begin{aligned} T(\Delta )=z_{\Delta ,2}+\tilde{z}_3-\tilde{z}_2-\tilde{z}_1=z_{\Delta ,2}+\tilde{T}-\tilde{z}_2=z_{\Delta ,2}+\tau . \end{aligned}$$

We have

$$\begin{aligned} -\beta _U+\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{-(z_{\Delta ,2}-(\Delta +\sigma ))}=0 \end{aligned}$$

and conclude that

$$\begin{aligned} \begin{aligned} \beta _U e^{z_{\Delta ,2}}&=\bigl (x^{(\Delta )}(\Delta +\sigma )+\beta _U\bigr )e^{\Delta +\sigma }\\&=\bigl (\beta _Ue^{\tilde{z}_2-\sigma -\Delta }+a(1-e^{- \sigma })\bigr )e^{\Delta +\sigma }\\&=\beta _Ue^{\tilde{z}_2}+a(e^{\sigma }-1)e^{\Delta }, \end{aligned} \end{aligned}$$

which implies (5.9), the desired formula for $T(\Delta )$. $\square$

Proof of Proposition 5.7

Since $[\Delta ,\Delta +\sigma ]\subset (t_{\max },\tilde{T})$ we have

$$\begin{aligned} x^{(\Delta )}(t)=-\beta _U+a+\bigl (x^{(\Delta )}(\Delta )+\beta _U-a\bigr )e^{-(t-\Delta )}\quad \text {on}\quad [\Delta ,\Delta +\sigma ]. \end{aligned}$$

Using $x^{(\Delta )}(\Delta )+\beta _U-a>0$ we see that $x^{(\Delta )}$ is strictly decreasing on $[\Delta ,\Delta +\sigma ]$, and has a unique zero $z_{\Delta ,2}$ in $[\Delta ,\Delta +\sigma )$, which is given implicitly by

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,2})=-\beta _U+a+\bigl (x^{(\Delta )}(\Delta )+\beta _U-a\bigr ) e^{-(z_{\Delta ,2}-\Delta )}. \end{aligned}$$

Combining this with (5.2) gives

$$\begin{aligned} (\beta _U-a)e^{z_{\Delta ,2}}=\beta _Ue^{\tilde{z}_2}-ae^{\Delta }, \end{aligned}$$

which is the same as (9.5). As $z_{\Delta ,2}\ge \Delta$ we infer

$$\begin{aligned} \beta _U(e^{z_{\Delta ,2}}-e^{\tilde{z}_2})=a(e^{z_{\Delta ,2}}-e^{\Delta })\ge 0. \end{aligned}$$

Hence $z_{\Delta ,2}\ge \tilde{z}_2$. Since $x^{(\Delta )}(\Delta )\ge 0$ and $\beta _U>a$, the map $[\Delta ,\Delta +\sigma ] \ni t\mapsto x^{(\Delta )}(t)$ is strictly decreasing. The rest of the proof is the same as the proof of Proposition 5.5 starting after (9.5). $\square$

Proof of Proposition 5.8

• 1. We have $x^{(\Delta )}(\tilde{z}_2)=0$, and the function $x^{(\Delta )}$ is strictly decreasing on $[\tilde{z}_2,\Delta ]$, monotone on $[\Delta ,\Delta +\sigma ]$ with $x^{(\Delta )}(t)<0$ for $\Delta \le t<\Delta +\sigma$, and strictly decreasing on $[\Delta +\sigma ,\tilde{T}]$. It follows that $x^{(\Delta )}$ is strictly increasing on $[\tilde{T},\infty )$ as long as $x^{(\Delta )}(t-\tau )<0$. This yields a first zero $z_{\Delta ,3}$ of $x^{(\Delta )}$ in $[\tilde{T},\infty )$ and $x^{(\Delta )}(z_{\Delta ,3}+t)=\tilde{x}(\tilde{z}_1+t)$ for all $t\ge 0$, and thus

  $$\begin{aligned} T(\Delta )= & {} z_{\Delta ,3}+(\tilde{z}_2-\tilde{z}_1)-\tilde{z}_2=z_{\Delta ,3}-\tilde{z}_1,\\ \underline{x}_{\Delta }= & {} \min \{x^{(\Delta )}(\Delta ),x^{(\Delta )}(\tilde{T})\}, \end{aligned}$$

  and

  $$\begin{aligned} \overline{x}_{\Delta }=\overline{x}. \end{aligned}$$

  Observe that

  $$\begin{aligned} {\begin{matrix} x^{(\Delta )}(\tilde{T})&{}=-\beta _U+\beta _U e^{-\tau }+a ( e^{ \sigma }-1)e^{\Delta -\tilde{T}}\\ &{}=\underline{x}+a ( e^{ \sigma }-1)e^{\Delta -\tilde{T}}>\underline{x}. \end{matrix}} \end{aligned}$$

  Using this and $x^{(\Delta )}(\Delta )=\tilde{x}(\Delta )>\underline{x}$ we have $\underline{x}_{\Delta }>\underline{x}$. The equation

  $$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,3})=\beta _L+\bigl (x^{(\Delta )}(\tilde{T})-\beta _L\bigr )e^{-(z_{\Delta ,3}-\tilde{T})} \end{aligned}$$

  is equivalent to

  $$\begin{aligned} \beta _L e^{z_{\Delta ,3}}=\bigl (\beta _L-x^{(\Delta )}(\tilde{T})\bigr )e^{\tilde{T}}, \end{aligned}$$

  which gives

  $$\begin{aligned} {\begin{matrix} \beta _L e^{z_{\Delta ,3}}&{}=(\beta _L+\beta _U)e^{\tilde{T}}-\bigl (\beta _U e^{-\tau }+a ( e^{ \sigma }-1)e^{\Delta -\tilde{T}}\bigr )e^{\tilde{T}}\\ &{}=(\beta _L+\beta _U-\beta _Ue^{-\tau }) e^{\tilde{T}}-a ( e^{ \sigma }-1)e^{\Delta }. \end{matrix}} \end{aligned}$$

  We have $\beta _L+\beta _U-\beta _Ue^{-\tau }=\beta _L e^{\tilde{z}_1}$ and we conclude that

  $$\begin{aligned} \beta _L e^{z_{\Delta ,3}}=\beta _Le^{\tilde{z}_1+\tau +\tilde{z}_2}-a(e^{\sigma }-1)e^{\Delta }, \end{aligned}$$

  from which we obtain (5.14) for $T(\Delta )=z_{\Delta ,3}-\tilde{z}_1$.

• 2. Observe that for every $\Delta \in I_{FNFN}$ we have

  $$\begin{aligned} x^{(\Delta )}(\tilde{T})-\tilde{x}(\Delta )=g(\Delta ) \end{aligned}$$

  with the strictly increasing function

  $$\begin{aligned} g:\mathbb {R}\ni \Delta \mapsto a(e^{\sigma }-1)e^{\Delta -\tilde{T}}+\beta _Ue^{-\tau }-\beta _Ue^{\tilde{z}_2-\Delta }\in \mathbb {R} \end{aligned}$$

  which has a single zero at $\Delta =\overline{\delta }$ since $g(\Delta )\rightarrow -\infty$ as $\Delta \rightarrow -\infty$, $g(\Delta )\rightarrow \infty$ as $\Delta \rightarrow \infty$, and $g(\Delta )=0$ if and only if

  $$\begin{aligned} \beta _U(e^{\tilde{T}-\Delta })^2-\beta _Ue^{\tilde{T}-\Delta }-a(e^{\sigma }-1)e^{\tau }=0, \end{aligned}$$

  or equivalently,

  $$\begin{aligned} e^{\tilde{T}-\Delta }&= \dfrac{1}{2}+\sqrt{\dfrac{1}{4}+\dfrac{a(e^{\sigma }-1)e^{\tau }}{\beta _U}}\\&= \dfrac{\beta _U+\sqrt{\beta _U ^2 +4a\beta _U(e^{\sigma }-1)e^{\tau }}}{2\beta _U}. \end{aligned}$$

  For $\Delta <\overline{\delta }$ in $I_{FNFN}$ we have $g(\Delta )<0$, hence

  $$\begin{aligned} \underline{x}_{\Delta }=\min \{\tilde{x}(\Delta ),x^{(\Delta )}(\tilde{T})\}=x^{(\Delta )}(\tilde{T}), \end{aligned}$$

  and the formula (5.10) for $x^{(\Delta )}(\tilde{T})$ in Part 1 above shows that in case $I_{FNFN}\cap (-\infty ,\overline{\delta })\ne \emptyset$ the map

  $$\begin{aligned} I_{ FNFN}\cap (-\infty ,\overline{\delta })\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

  is strictly increasing. For $\Delta >\overline{\delta }$ in $I_{ FNFN}$ we get $0<g(\Delta )$, hence

  $$\begin{aligned} \underline{x}_{\Delta }=\min \{\tilde{x}(\Delta ),x^{(\Delta )}(\tilde{T})\}=\tilde{x}(\Delta ), \end{aligned}$$

  and we see that in case $I_{ FNFN}\cap (\overline{\delta },\infty )\ne \emptyset$ the map

  $$\begin{aligned} I_{ FNFN}\cap (\overline{\delta },\infty )\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R} \end{aligned}$$

  is strictly decreasing. $\square$

Proof of Remark 5.3

The strictly increasing function g from the previous proof satisfies

and

$$\begin{aligned} g(\tilde{T}-\sigma )=a(e^{\sigma }-1)e^{-\sigma }+\beta _Ue^{-\tau }-\beta _Ue^{\tilde{z}_2-\tilde{T}+\sigma }>0 \end{aligned}$$

if and only if $\beta _U e^{\sigma - \tau } < a$. By the intermediate value theorem the only zero $\overline{\delta }$ of g belongs to the interval $(\tilde{z}_2,\tilde{T}-\sigma )$ in case $\beta _U e^{\sigma - \tau } < a$. Otherwise $\overline{\delta }\ge \tilde{T}-\sigma$. $\square$

Proof of Proposition 5.9

From $0>x^{(\Delta )}(\Delta +\sigma )>x^{(\Delta )}(\tilde{T})$ we obtain $x^{(\Delta )}(t)<0$ on $(\tilde{z}_2,\Delta +\sigma ]$. It follows that on $[\Delta +\sigma ,\infty )$ the function $x^{(\Delta )}$ is strictly increasing as long as $x^{(\Delta )}(t-\tau )<0$, and there is a smallest zero $z_{\Delta ,3}$ of $x^{(\Delta )}$ in $[\Delta +\sigma ,\infty )$. Moreover, $x^{(\Delta )}(z_{\Delta ,3}+t)=\tilde{x}(\tilde{z}_1+t)$ for all $t\ge 0$, hence

$$\begin{aligned} T(\Delta )=z_{\Delta ,3}+(\tilde{z}_2-\tilde{z}_1)-\tilde{z}_2=z_{\Delta ,3}-\tilde{z}_1, \end{aligned}$$

and

$$\begin{aligned} \underline{x}_{\Delta }=x^{(\Delta )}(\tilde{T})>\underline{x}, \end{aligned}$$

and $\overline{x}_{\Delta }=\overline{x}$. As the map $[\tilde{T}-\sigma ,\tilde{T})\ni \Delta \mapsto x^{(\Delta )}(\tilde{T})\in \mathbb {R}$ is strictly decreasing we infer that also the map $I_{FNRN}\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ is strictly decreasing.

From

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,3})=\beta _L+\bigl (x^{(\Delta )}(\Delta +\sigma )-\beta _L\bigr ) e^{-(z_{\Delta ,3}-(\Delta +\sigma ))} \end{aligned}$$

we obtain

$$\begin{aligned} \beta _L e^{z_{\Delta ,3}}&= \bigl (\beta _L- x^{(\Delta )}(\Delta +\sigma )\bigr )e^{ \Delta +\sigma }\\&= \bigl (\beta _L-\beta _L+\beta _Le^{\tilde{z}_1-( \Delta +\sigma -\tilde{T})}-a(1-e^{-\sigma })\bigr )e^{ \Delta +\sigma }\\&= \beta _Le^{\tilde{z}_1+\tilde{T}}- a(e^{\sigma }-1)e^{ \Delta }, \end{aligned}$$

and the formula for $T(\Delta )=z_{\Delta ,3}-\tilde{z}_1$ follows. $\square$

Proof of Proposition 5.10

We have $x^{(\Delta )}(t)<0$ on $(\tilde{z}_2,\tilde{T}]$, and there is a first zero of $x^{(\Delta )}$ in $(\tilde{T},\Delta +\sigma ]$, which is given by

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,3})=\beta _L+a+\bigl (x^{(\Delta )}(\tilde{T})-(\beta _L+a)\bigr )e^{-(z_{\Delta ,3}-\tilde{T})}, \end{aligned}$$

or equivalently,

$$\begin{aligned} (\beta _L+a)e^{z_{\Delta ,3}}&= \bigl (\beta _L+a-x^{(\Delta )}(\tilde{T})\bigr )e^{\tilde{T}}\\&= \bigl (\beta _L+a-(\underline{x}+a-ae^{\Delta -\tilde{T} })\bigr )e^{\tilde{T}}\\&= (\beta _L-\underline{x})e^{\tilde{T}}+ae^{\Delta }\\&=\beta _L e^{\tilde{z}_1+\tilde{T}}+ae^{\Delta }. \end{aligned}$$

Incidentally, this shows that the map $I_{FNRP}\ni \Delta \mapsto z_{\Delta ,3}-\Delta \in \mathbb {R}$ is strictly decreasing.

On $[z_{\Delta ,3},\Delta +\sigma ]$ the function $x^{(\Delta )}$ is strictly increasing. Since $x^{(\Delta )}(t-\tau )<0$ on $(\tilde{z}_2,z_{\Delta ,3})$, we infer that $x^{(\Delta )}$ is strictly increasing on $[z_{\Delta ,3},z_{\Delta ,3}+\tau ]$. Hence $0<x^{(\Delta )}(t)$ on $(z_{\Delta ,3},z_{\Delta ,3}+\tau ]$. This implies that $x^{(\Delta )}$ is strictly decreasing on $[z_{\Delta ,3}+\tau ,\infty )$ as long as $x^{(\Delta )}(t-\tau )>0$, and that there is a first zero $z_{\Delta ,4}$ in $(z_{\Delta ,3}+\tau ,\infty )$. We obtain $x^{(\Delta )}(z_{\Delta ,4}+t)=\tilde{x}(\tilde{z}_2+t)$ for all $t\ge 0$, which yields

$$\begin{aligned} T(\Delta )=z_{\Delta ,4}-\tilde{z}_2, \end{aligned}$$

$\underline{x}_{\Delta }=\min \{\tilde{x}(\Delta ),x^{(\Delta )}(\tilde{T})\}>\underline{x}$, and

$$\begin{aligned} \overline{x}_{\Delta }=x^{(\Delta )}(z_{\Delta ,3}+\tau ). \end{aligned}$$

As in the proof of Proposition 5.9 we infer that the map $I_{FNRP}\ni \Delta \mapsto \underline{x}_{\Delta }\in \mathbb {R}$ is strictly decreasing.

From the formula for $x^{(\Delta )}(\Delta +\sigma )$ we obtain

$$\begin{aligned} x^{(\Delta )}(z_{\Delta ,3}+\tau )&= \beta _L+\bigl (x^{(\Delta )}(\Delta +\sigma )-\beta _L\bigr )e^{-(z_{\Delta ,3}+\tau -(\Delta +\sigma ))}\\&= \beta _L-\beta _Le^{\tilde{z}_1+\tilde{T}-(z_{\Delta ,3}+\tau )} + a(e^{\sigma }-1)e^{\Delta }e^{-(z_{\Delta ,3}+\tau )}, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \overline{x}_{\Delta }=\beta _L-\bigl (\beta _Le^{\tilde{z}_1+\tilde{T}}+ae^{\Delta }\bigr )e^{-(z_{\Delta ,3}+\tau )} + ae^{\sigma +\Delta }e^{-(z_{\Delta ,3}+\tau )}. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \overline{x}_{\Delta }&=\beta _L-(\beta _L+a)e^{-\tau }+ae^{\sigma +\Delta }e^{-(z_{\Delta ,3}+\tau )}\\&=\overline{x} +ae^{-\tau }(e^{\sigma +\Delta -z_{\Delta ,3}}-1)\\&>\overline{x}. \end{aligned} \end{aligned}$$

We also know that the map $I_{FNRP}\ni \Delta \mapsto \overline{x}_{\Delta }\in \mathbb {R}$ is strictly increasing.

From

$$\begin{aligned} 0=x^{(\Delta )}(z_{\Delta ,4})=-\beta _U+\bigl (x^{(\Delta )}(z_{\Delta ,3}+\tau )+\beta _U\bigr )e^{-(z_{\Delta ,4}-(z_{\Delta ,3}+\tau ))} \end{aligned}$$

we have

$$\begin{aligned} \beta _Ue^{z_{\Delta ,4}}= (\beta _L+\beta _U)e^{z_{\Delta ,3}+\tau }-\beta _Le^{\tilde{z}_1+\tilde{T}}+a(e^\sigma -1)e^{\Delta }. \end{aligned}$$

Use (9.4) to obtain

$$\begin{aligned} \beta _Le^{\tilde{z}_1+\tilde{T}}+\beta _U e^{\tilde{z}_2+\tilde{T}}=(\beta _L+\beta _U)e^{\tau +\tilde{z}_1+\tilde{T}} \end{aligned}$$

which, combined with the previous equation, gives

$$\begin{aligned} \beta _Ue^{z_{\Delta ,4}}=\beta _U e^{\tilde{z}_2+\tilde{T}}+ (\beta _L+\beta _U)e^{\tau }\bigl (e^{z_{\Delta ,3}}-e^{\tilde{z}_1+\tilde{T}}\bigr )+a(e^\sigma -1)e^{\Delta }. \end{aligned}$$

Now the formula for $z_{\Delta ,3}$ leads to

$$\begin{aligned} \beta _Ue^{z_{\Delta ,4}}=\beta _U e^{\tilde{z}_2+\tilde{T}}+\dfrac{a(\beta _L+\beta _U)e^{\tau }}{\beta _L+a} \bigl (e^{\Delta }-e^{\tilde{z}_1+\tilde{T}}\bigr )+a(e^\sigma -1)e^{\Delta } \end{aligned}$$

which yields the formula for $T(\Delta )=z_{\Delta ,4}-\tilde{z}_2$. $\square$