Introduction

There are two kinds of soil salinity: dry-land salinity (occurring on land not subject to irrigation) and irrigated-land salinity. Both describe areas where soils contain high levels of salt. Usually, plants and soil organisms are killed or their productivity is severely limited on affected land. Some salt in the soil profile may date back even further, to when the parent rocks themselves were formed. The parent rocks release salts, as they get wet. Other possible sources of salt are ancient drainage basins or inland seas that evaporated during arid periods, leaving behind salt deposits that still remain today.

Under arid or semi-arid conditions and in regions of poor natural drainage, there is increased potential for hazardous accumulation of salts in soils. The processes by which soluble salts enter the soil solution and cause salinity and sodicity include: (1) the application of water containing salts; (2) weathering of primary and secondary minerals in soils; (3) organic matter decay. The importance of each source depends on the type of soil, the climate conditions, and the agricultural management. Accumulation of dispersive cations such as Na in the soil solution and the exchange phase affect the physical properties of the soil including structural stability, hydraulic conductivity, infiltration rate and soil erosion. One of the problems in making use of this wealth of information is, however, a history of confusing and sometimes contradictory terminology that has been used in literature to describe the different types of salt-affected soils. Therefore, we begin with a brief overview of some basic terms of soil classification. Historically, the physical behavior of salt-affected soils has been described in terms of the combined effects of soil salinity, as measured by the electrical conductivity of a saturation extract (ECe), and the exchangeable sodium percent (ESP) on flocculation and soil dispersion. The U.S. Salinity Laboratory Sta. (1954) described the physical properties of a saline soil (ECe>4 dS/m; ESP<15) as follows:

A saline-alkali soil (ECe>4 dS/m; ESP>15) was described as similar to a saline soil as long as excess salts were present. However,

By 1979, the term "alkali" was listed as obsolete by the Soil Science Society of America (though it is still used by farm advisors and others), and the word "sodic" was used in its place and defined as a soil having an ESP>15. Outside the United States, the word "alkali" is generally used in a narrower context referring only to soils (1) with both high sodicity and high pH (ESP>15, pH>8.3) and (2) containing soluble bicarbonate and carbonate (Na/[Cl+SO4]>1) (Gupta and Abrol 1990).

In this context the term "alkali" has meaning because, firstly, swelling and dispersion increase as both ESP and pH increase (Gupta and others 1984; Suarez and others 1984), and, secondly, soil solutions where sodium and bicarbonate plus carbonate are the predominant ions tend to have low salinities and high pH values. On the other hand, the pH of a sodic soil can be either greater or less than seven (Kelley 1951) and such soils can be either saline or nonsaline. Use of the term "alkali" thus allows practical distinctions between saline, sodic and alkali soils in terms of soil management (Bhumbla and Abrol 1979; Gupta and Abrol 1990). In this paper, "saline" and "sodic" are used as defined by the Soil Science Society of America, while "alkali" is used as defined in this paragraph. Despite the usefulness of such simple numerical criteria, it is important to recognize their limitations. For example, scientific research conducted since 1954 has documented many instances in which the tendency for swelling, aggregate failure and dispersion increase as salinity decreases even if the ESP is less than three, that is, nonsaline soil can behave like a sodic soil (Shainberg and Letey 1984; Sumner 1993).

These tendencies increase as ESP does, requiring increasingly higher salinities to stabilize the soil. The boundary between stable and unstable conditions varies from one soil to the next. In addition, the stability boundary for water entry into a soil (infiltration) is different than that for water movement through the soil (unsaturated and saturated hydraulic conductivity); soil surfaces are more sensitive to low salinity, magnesium and exchangeable sodium than is the soil underneath. In short, the numerical criteria used to differentiate between saline, saline-alkali and nonsaline-alkali soils (U.S. Salinity Laboratory Sta. 1954) gives only one point on what is actually a salinity-sodicity continuum. It is important to understand this continuum and its impact on management guidelines for reclamation and subsequent water and soil management.

Scientists have shown that there are a number of factors that determine the vulnerability of sites to salinization (Oster and others 1996). These include: (1) the position of a site within a landscape. Generally the lower it is, the more likely it is that water will reach the surface and cause salinization; (2) soil type and rainfall. The combination of information on these and other factors could allow the prediction of the vulnerability of a site to salinity (Navarro and others 2001). This is where a Geographic Information System (GIS) could play a role. GIS is a computer application that involves the storage, analysis, retrieval and display of data that are described in terms of their geographic location. The most familiar type of spatial data is a map, and GIS is really a way of storing map information electronically. A GIS has a number of advantages over old-style maps. Firstly, because the data are stored electronically they can be analyzed rapidly by computer. In the case of salinity, scientists can use data on rainfall, topography, soil type, and any spatial information that is available electronically to first determine the combinations most susceptible to salinization, and then to predict similar regions that may be at risk. A lot of information is already in a form that can be used in a GIS, and more is being added continually—including that produced by Landsat (Navarro and others 2001). As the databases and prediction techniques improve, farmers and land management agencies will be better placed to wage an assault on salt.

Spatial interpolation is an essential feature of many GIS. It is a procedure for estimating values of a variable at locations that have not been sampled. Maps with isolines or color-smoothed images are usually the visual output of such a process and the maps play a crucial role in decision-making. However, an understanding of the initial assumptions and methods used is key to the spatial interpolation process. And geostatistics gives the formal mathematical support for such a task. In this paper, we focus on the spatial modeling of pH, extractable sodium and electrical conductivity. These variables are clearly associated with soil salinity and their spatial estimation and prediction are of primary scientific interestfor input to further agricultural or environmental activities. The geostatistical framework for our work is outlined below, followed by the real data analysis presented as a case study.

The need of geostatistical methods

A feature common to the Earth sciences is the nature of their data. Most of the properties of interest vary continuously in space and time and cannot be measured or recorded everywhere. Thus, to represent their variation the values of individual variables or class types at unsampled locations must be estimated from information recorded at sampled sites. The need to define spatial variation precisely is clear and geostatistics is largely the application of this theory. It embraces a set of stochastic techniques that take into account both the random and structured nature of spatial variables, the spatial distribution of sampling sites and the uniqueness of any spatial observation (Journel and Huijbregts 1978; Goovaerts 1997).

Spatial statistics is one of the major methodologies of environmental statistics; its applications include producing spatially smoothed or interpolated representations of air pollution fields, calculating regional average means or regional average trends based on data at a finite number of monitoring stations, and performing regression analyses with spatially correlated errors to assess the agreement between observed data and the predictions of some numerical model. This paper considers the analysis of soil data, which can be considered as a partial realization of a random function (stochastic process) over a region, i.e. a spatially continuous process, as characterized by Cressie (1993). Typically, samples are taken at a finite set of points in the region and used to estimate quantities of interest such as the values of the property of interest at other locations. Data of this kind are often called geostatistical data. Geostatistical methods find wide applications, for example in soil science, meteorology, hydrology and ecology. The objectives of a geostatistical analysis are broadly of two kinds: estimation and prediction. Estimation refers to inference about the parameters of a stochastic model for the data. These may include parameters of direct scientific interest, for example those defining a regression relationship between a response and an exploratory variable, and parameters of indirect interest. Prediction refers to inference about the realization of the unobserved signal S(u). In applications, specific prediction objectives might include prediction of the realized value of S(u) at an arbitrary location u within a region of interest A, or prediction of some property of the complete realization of S(u) for all u in A.

Experimental section

Origin of the data: soil analysis

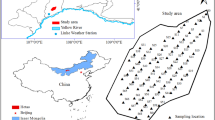
Alicante is a Mediterranean Province (Fig. 1) with a high variety of soil types. It is a transition area from arid and semi-arid to template-humid environments (Guerrero and others 2001). These characteristics have a great influence on the variety of cultivated plants (horticulture, deciduous trees, citrus, cereals). Although most of the province is under the influence of the Mediterranean Sea, the topography and lithology produce an unusual variety of environments (also different kinds of soils) (Antolin 1998).

Fig. 1
figure 1

Map of Province of Alicante in Spain

Full size image

Salinity is a very important problem in arid and semi-arid regions. The Province of Alicante is a region where the climate changes from south (semi-arid) to north (template climate). That is why parameters such as rainfall vary from 250 to 600 mm/year (Perez 1994; Andreu 1997). Moreover, as indicated by Harrach and Nemeth (1982), the variability of soil salinity increases in regions with great microclimatic variety.

Over 400 soil samples (arable layer) from different agricultural sites were collected during a period of two years. Samples were dried at room temperature and the saline characteristics of soils were determined: pH, electrical conductivity (1:5 w/v water extraction) and extractable sodium (ammonium acetate 1 M extraction).

The determination of total elements was performed after mineralization of the humid sample by HNO3 and H2O2 with the use of microwaves. For the estimation of the change elements, an extraction with ammonic acetate was used 1 N to pH 7 (Knudsen and others 1982).

Geostatistical methodology

Data structure

Consider a finite set of spatial sample locations u 1 , u 2 ,..., u n , within a region D and denote u=(u 1 , u 2 ,..., u n ). Geostatistical data consist of measurements taken at the sample locations u. The data vector is denoted by z(u)=(z(u 1 ),..., z(u n )), and the data are regarded as being a realization of a spatial stochastic process {Z(u); u¸ ε D}.

An arbitrary location is denoted by u and the region D is a fixed subset of \( {\Re }^{d} \)with positive d-dimensional volume. We assume that u varies continuously throughout the region D.

Now, assume observations from the additive model

$$ z{\left( {u_{i} } \right)} = f_{x} {\left( {u_{i} } \right)} + \varepsilon {\left( {u_{i} } \right)},i = 1,...,n $$
(1)

where f is the function of interest and possibly depends on spatial covariates given by the matrix X. The random components ε(ui) can be associated with measurement errors and assumed to be Gaussian spatial processes. This model is known as the full interactive model.

Gaussian spatial linear mixed models (GSLMM)

In this section we further develop the full interactive model giving an explicit expression for function f by means of GSLMM models.

The model assumed here considers that the variable Z is a noisy version of a latent spatial process, the signal S(u). The noises are assumed to be Gaussian and conditionally independent given S(u). The model is specified by:

  1. 1.

    Covariates: The mean part of the model is described by the term X(u i )β. X(u i )' denotes a vector of spatially referenced nonrandom variables at location ui and β is the mean parameter.

  2. 2.

    The underlying spatial process \( {\left\{ {S{\left( {\mathbf{u}} \right)}:{\mathbf{u}} \in {\Re }^{d} } \right\}} \) is a stationary Gaussian process with zero mean, variance σ2 and correlation function ρ(h; ϕ), where ϕ is the correlation function parameter and h is the vector distance between two locations.

  3. 3.

    Conditional independence: the variables Z(ui) are assumed to be Gaussian and conditionally independent given the signal:

$$ Z{\left( {u_{i} } \right)}|S \sim N{\left( {X{\left( {u_{i} } \right)}'\beta + S{\left( {u_{i} } \right)},\tau ^{2} } \right)}. $$
(2)

In some applications we may want to consider a decomposition of the signal S(u) into a sum of latent processes Tk(u) scaled by \( \sigma ^{2}_{k} \) Then, the model can be rewritten, in a hierarchical way, as:

Level 1:

$$ Z{\left( {\mathbf{u}} \right)} = X{\left( {\mathbf{u}} \right)}\beta + S{\left( {\mathbf{u}} \right)} + \varepsilon {\left( {\mathbf{u}} \right)} = X{\left( {\mathbf{u}} \right)}\beta + {\sum\limits_{k = 1}^K {\sigma _{k} T_{k} {\left( {\mathbf{u}} \right)} + \varepsilon {\left( {\mathbf{u}} \right)}} } $$
(3)

Level 2: Tk(u)∼ N(0,Rk(ϕ k )), T1,...,TK mutually independent and ε(u)∼N(0, τ 2 I).

Level 3: (β, σ 2, ϕ, τ 2)∼pr(·), where pr(·) defines a prior probability distribution.

The model components are described by:

Z(u):

is a random vector with components Z(u 1 ),..., Z(u n ), related to the measurements at sample locations.

X(u)β=µ(u):

is the expectation of Z(u). X(u) is a matrix of fixed covariates measured at sample locations u. β is a vector parameter. If there are no covariates, X=1 and the mean reduces to a single constant value at all locations.

T k (u):

is a random vector at sample locations, of a standardized latent stationary spatial process Tk. It has zero mean, variance one and correlation matrix Rk(ϕk). The elements of Rk(ϕk) are given by a correlation function ñk(h; ϕk) with parameter ϕk. If the process is isotropic this parameter and the distance h are scalar parameters. The processes T 1 ,..., T k are mutually independent. The signal S is defined by the sum of scaled latent processes \( S{\left( {\mathbf{u}} \right)} = {\sum\nolimits_1^K {\sigma ^{2}_{k} } } \).

σk :

is a scale parameter.

ε(u):

denotes the error (noise) vector at the sample locations u, i.e. a spatially independent process (spatial white noise) with zero mean and variance τ 2. This model-based specification can be related to conventional geostatistics terminology as follows:

1.:

The term trend refers to the mean part of the model, Xβ;

2.:

A latent process corresponds to a structure in the variogram;

3.:

A value of \( \sigma ^{2}_{k} \) corresponds to a partial sill. The sill is the value of \( {\sum\nolimits_1^K {\sigma ^{2}_{k} } } \);

4.:

The nugget effect is quantified by τ 2. In the geostatistics literature this term refers to variation at small distances plus a measurements error.

5.:

The total sill is given by the sum of the sill and the nugget effects.

Spatial prediction: kriging

In geostatistical problems, often the main interest is not parameter estimation but prediction of the variable at a set of locations. Denote by Z(u 0 ) (Z 0 ) the variable to be predicted at the location u 0 .

The optimal point predictor, defined as the one which minimizes the prediction mean square error (MSE), is given by

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} _{0} = E{\left[ {Z_{0} |Z} \right]} $$
(4)

This predictor is called the least squares predictor and its prediction variance is given by V ar [Z 0 |Z].

The values of the conditional expectation (4) can be calculated only if the model distributions are fully specified and the parameters are known. In practice the model parameters are unknown and an approximation to the conditional expectation may be then used. Finding the conditional expectation (4) or an approximation to it, is a central problem in geostatistics, and several methods have been proposed.

Lineal predictor assuming known parameters

The linear predictor, which minimizes the MSE, is called the simple kriging (SK) predictor. The SK predictor requires knowledge of the mean and covariance parameters, i.e. the parameters of the trend, signal and noise should be provided. The SK predictor is of the form

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} _{{SK}} {\left( {u_{0} } \right)} = \lambda _{0} + {\sum\limits_i {\lambda _{1} Z{\left( {u_{i} } \right)}} } $$
(5)

The weights λ i are such that the prediction MSE is minimum. Under the Gaussian model and if all the parameters are known, the SK predictor coincides with the conditional expectation (4), and therefore is optimal.

Lineal predictor filtering the mean and assuming known parameters

A usual estimator can be obtained from the narrower class of unbiased linear predictors, the ordinary kriging (OK) predictor. This predictor filters a constant mean requiring only the knowledge of the covariance parameters. The OK predictor is of the form

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} _{{OK}} {\left( {u_{0} } \right)} = {\sum\limits_i {\lambda _{1} Z{\left( {u_{i} } \right)}} } $$
(6)

The weights λ i are such that the prediction MSE is minimum under the constraint \( {\sum {\lambda _{i} = 1} } \). This constraint ensures the unbiasedness of the estimator. The results provided by OK coincide with those obtained by simple kriging (SK) with the scalar mean parameter β given by its generalized least squares estimator. The OK predictor is widely used in geostatistical applications and is sometimes referred to as the kriging predictor. Other kriging methods like universal and kriging with external trend are extensions of OK allowing for covariates in the mean structure.

A model-based approach

If complete parametric specification for the model components is assumed the conditional expectation (4) can be assessed (Diggle and others 1998; Diggle and Ribeiro 2001). Consider, for example, the Gaussian model specified in (3) extended to include both Z and Z 0 . The joint distribution is given by

$$ {\left( {Z,Z_{0} |\beta ,\sigma ^{2} ,\phi ,\tau ^{2} } \right)} \sim N{\left( {{\left[ {\begin{array}{*{20}c} {X} \\ {{X_{0} }} \\ \end{array} } \right]}\beta ;\tau ^{2} I + {\left[ {\begin{array}{*{20}c} {{V_{z} {\left( {\sigma ^{2} ,\phi } \right)}}} & {{v{\left( {\sigma ^{2} ,\phi } \right)}}} \\ {{v'{\left( {\sigma ^{2} ,\phi } \right)}}} & {{V_{0} {\left( {\sigma ^{2} ,\phi } \right)}}} \\ \end{array} } \right]}} \right)} $$
(7)

Under this model the conditional expectation (4) can be directly obtained if all the parameters are known. Then it coincides with the simple kriging (SK) predictor. For the more realistic scenario of unknown parameters, both classical likelihood-based and Bayesian paradigms can be adopted. Under the model-based perspective, assuming the model in (3) with known parameters, the prediction problem is straightforward. If the subsymbol * denotes parameter known, and \( V{\left( {\sigma ^{2}_{*} ,\phi _{*} } \right)} \) and \( v{\left( {\sigma ^{2}_{*} ,\phi _{*} } \right)} \) from (7) are denoted by V and v, the predictive distribution is given by

$$ {\left( {Z_{0} |Z,\beta _{*} ,\sigma ^{2}_{*} ,\phi _{*} ,\tau ^{2}_{*} } \right)} \sim N{\left( {X_{0} \beta _{*} + v'{\left( {\tau ^{2}_{*} I + V_{z} } \right)}^{{ - 1}} {\left( {z - X\beta _{*} } \right)};\tau ^{2}_{*} I + V_{0} - v'{\left( {\tau ^{2}_{*} I + V_{z} } \right)}^{{ - 1}} v} \right)} $$
(8)

Therefore point predictors and associated uncertainty can be easily obtained. The mean of (8) coincides with the minimum MSE predictor, the conditional expectation.

Under the Bayesian perspective these geostatistical methods can be interpreted as prediction procedures that only take into account the uncertainty in the mean parameters. Then, (1) if X≡1 and X 0 ≡1 (constant mean), we get the usual ordinary kriging (OK) predictor; (2) if X and X 0 are trend matrices with rows given by data coordinates or a function of them, we get the universal or trend kriging (UK or KT) predictor; (3) if X and X 0 are trend matrices with covariates measured at data and prediction locations, we get the kriging with external trend (KTE) predictor.

Case study: spatial analysis of soil salinity in the Province of Alicante (Spain)

The spatial locations taken into account in our study within the region of interest are shown in Fig. 2. We worked with logarithms, as two of the variables needed a Box-Cox transformation to reach Gaussianity.

Fig. 2
figure 2

Map of the Province of Alicante with sampled sites numbered

Full size image

Before interpolation and prediction, we need to know the structure of the spatial variation. This was done in terms of the variogram analysis. The spherical model was chosen as the parametric family that best fitted the empirical variograms of both the logarithm of sodium (Na) and the logarithm of electrical conductivity. However, the Gaussian model was chosen for pH. In any case, the parameters were obtained using the weighted least squares procedure. The results for the logarithm of sodium (with a predominant influence direction of 22.5 °) were: nugget=0.032, sill=0.696, range=37600 meters. The results for the logarithm of electrical conductivity (with a predominant influence direction of 120 ° degrees) were: nugget=0.060, sill=0.425, range=26228 meters. The results for pH (with a predominant influence direction of 120 °) were: nugget=0.0112, sill=0.0476, range=18600 meters. Note that the spatial dependence is defined up to 37 km for the sodium, 26 km for the electrical conductivity and 18.6 km for pH. Also the fact that the nugget values were relatively small, confirm that the measurement error was kept small. For prediction purposes we applied GSLMM methodology, firstly with matrix X=1 to obtain ordinary kriging (OK) predictions for each variable individually (Figs. 3, 4, and 5) and, secondly with X considered a trend matrix to obtain cokriging and external trend kriging for the spatial relationship between sodium and electrical conductivity (Figs. 6 and 7), and for the relationship between sodium and pH (Fig. 8). If we further fit a generalized additive model (GAM) for the relationship between these variables, we obtain an interestingly high value of 0.89 for the correlation coefficient between sodium and electrical conductivity, and a value of 0.85 for the correlation coefficient between sodium and pH, which means that we could use one variable to spatially predict the other.

Fig. 3
figure 3

OK predictions and associated standard error for the logarithm of sodium

Full size image
Fig. 4
figure 4

OK predictions and associated standard error for the logarithm of electrical conductivity

Full size image
Fig. 5
figure 5

OK predictions and associated standard error for pH

Full size image
Fig. 6
figure 6

Cokriging predictions and associated standard error for the logarithm of sodium taking into account its relation to the logarithm of electrical conductivity

Full size image
Fig. 7
figure 7

Spatial predictions and associated standard error of the logarithm of sodium using as an external drift the logarithm of electrical conductivity

Full size image
Fig. 8
figure 8

Spatial predictions and associated standard error of the logarithm of sodium using as an external drift pH

Full size image

Using the Bayesian framework, we analyzed the form of the predictive distribution for sodium, and consequently studied the goodness-of-fit of our methodology comparing the variable predictions to the real data. In Fig. 9 we show the Gaussian predictive distribution for the logarithm of sodium for 9 different sites within the Province of Alicante. This method represents a good method for analyzing the quality of our predictions.

Fig. 9
figure 9

Predictive Gaussian distribution at nine selected locations for the logarithm of sodium

Full size image

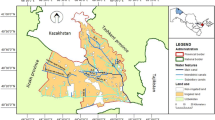
The results show the high dependence of these parameters on climate. Salinity (expressed by electrical conductivity) is higher in the Southerly, semi-arid zone, than in the North. Rainfall may be associated with these results, as in the North the water can leach soils and salts are not presented in the upper horizons in high concentrations. However, in the Northwest an exception is shown. This area of the province has saline soils due to another important factor of soil formation: original lithology (presence of Keuper, Tertiary clays) and the presence of saline lagoons that affected soil characteristics (Navarro-Pedreño and others 1997). Water movement into soils is the key factor in management of salt-affected soils. Infiltration rates (IR) and hydraulic conductivity (K) decrease with decreasing soil salinity and with increasing exchangeable sodium. Infiltration rates are more strongly affected by low salinity and exchangeable sodium levels than are hydraulic conductivities because of the mechanical impact and stirring action of the applied water and the freedom for soil particle movement at the soil surface (Oster and others 1996).

It is known that the variability of soil salinity could be very high in regions with significant microclimatic variability, such as that seen in the study region. The results obtained by geostatistical methods show the important relationship between the electrical conductivity, pH and extractable sodium (Figs. 6, 7, and 8). The results also show the high dependence of these parameters on climate. Salinity is higher in the Southerly, semi-arid zone, than in the North of the province. Rainfall may be associated with these results as in the North the water can leach soils and salts are not presented in high concentrations in the upper horizons. However, the area in the NW of the province has saline soils due to another important factor of soil formation, the underlying, original, lithology. In this case the presence of Tertiary-age marls and clays with a high content of calcium sulfates (gypsum/anhydrite), halite and the presence of saline lagoons which affected soil characteristics. Soil clay contents are important in influencing the stability of soil structure and hydraulic properties because of the large surface area of clay particles, their thin platy shape, and their negative lattice change, which is balanced by exchangeable cations. The type of clay is also important. A dominant clay mineral in semi-arid and arid regions is montmorillonite. Kaolinite is common in more humid regions, while illite is common to both regions. The latter minerals, in their pure state, swell and disperse much less than montmorillonite. However, kaolinitic and illitic soils that contain low percentages of montmorillonite tend to be dispersive (Schofield and Samson 1954; Frenkel and others 1978, 1989).

Conclusions

Although kriging involves an intrinsic smoothing operation and the areas and soil may change abruptly due to local characteristics, this statistical method, which could be improved upon with more soil data, seems to be adequate for predicting soil characteristics. The predictions obtained have special importance before agricultural transformation of the land (from an economical point of view) or environmental restoration (selection of the most appropriate species adapted to soil salinity).

Reclamation of salt-affected soils through tillage, water, crop and amendment practices is an increasingly important tool for improving crop productivity in many areas of the world. Traditionally, reclamation has been driven by the need to turn marginally arable lands to agricultural use by reducing the levels of salinity, exchangeable sodium, and boron in the soil, thereby increasing both crop yields and the number of crop species that can be grown in a specific area. Adverse levels of these substances can, however, be caused by other factors, including limited irrigation (not providing enough water for leaching), inadequate drainage, and the use of moderately saline-sodic waters for irrigation. Use of such poor-quality waters is increasing due to growing municipal demands for the available supplies of good-quality water and the need to dispose of municipal wastewaters and agricultural drainage waters. As a result, a solid understanding of soil reclamation will become an increasingly important component of water and soil management to ensure the long-term sustainability of irrigated agriculture.