Introduction

Several computational cardiac action potential (AP) models have been developed to better understand and examine the biophysical basis of mammalian cardiac myocyte functionality (Winslow et al. 2010). The Hodgkin and Huxley equations established the basis for cardiac models (Hodgkin and Huxley 1952), and later more detailed models including many voltage-gated ionic currents and transporters were developed to explore the cardiac AP morphology (Noble 1960, 2007). These models reconstruct well the characteristics of the cardiac action potential, intracellular ion concentration changes, Ca2+-induced Ca2+-release, and ATP metabolism. Examples of other mammalian cardiac models are: human (Ten Tusscher et al. 2004; Grandi et al. 2009), canine (Ramirez et al. 2000; Hashambhoy et al. 2009), rabbit (Shannon et al. 2004; Mahajan et al. 2008), guinea pig (Luo and Rudy 1994; Pasek et al. 2008), mouse, and rat (Pandit et al. 2001; Korhonen et al. 2009). All these models proved that for different conditions each one has its distinct advantages in investigating different conditions and diseases such as atrial fibrillation (Winslow et al.1999), sick sinus syndrome (Li et al. 2014), and heart failure (Umehara et al. 2019).

In this work, we define a new mathematical model for rat ventricular cardiomyocytes. The Hodgkin–Huxley formalism is used in our model including most of the recently discovered ion channels in rat cardiac myocytes. This model includes but extends the Pandit model (Pandit et al. 2001) by adding four missing channels, namely the rapidly activated outward rectifier (IKr), the slowly activated outward rectifier (IKs), the T-type Ca2+ current (ICaT,), and the background \({Cl}^{-}\) current (IBCl) that are important for pathological cases. Second, we show the importance of these new channels for understanding the effects of ISO application. And last, all model kinetics are modeled independently to make it easy to modify the parameters, conditions, and equations for each. Twelve ionic currents; fast Na+ current, L- and T-type Ca2+ channel, transient K+ current, inward rectifier K+ current, rapid and slowly activated outward rectifier K+ currents, hyperpolarizing-activated current, and four background currents for Na+, K+, Ca2+, and Cl− are included in this way. Moreover, three ion transporters including pump currents and Na+-Ca2+ exchanger together with the Ca2+ mechanism of the sarcoplasmic reticulum and intracellular ion concentrations with ion fluxes are included from the literature (Keizer and Levine 1996; Jafri et al. 1998).

All parameters, conditions, and dynamic equations for this new model are consistent with laboratory data to better represent the properties of rat ventricular cells. In order to verify our model, membrane kinetics are defined based on recent whole-cell current recordings, steady-state activation/inactivation data, and the time constants data. Moreover, maximal ionic conductances are optimized separately according to our rat AP recordings. Our model is robust, computationally efficient, and internally consistent. This new mathematical model simulates the important physiological features of the rat ventricular myocytes. The shape and features of the APs of our model fit well to our own AP recordings and data from previous studies that are reported in the results section.

This work also investigates the effects of isoproterenol (ISO) on ventricular myocytes from rat heart experimentally and computationally. Isoproterenol is a sympathomimetic \(\beta \)-adrenergic agonist that has been used for many years in producing experimental cardiac pathologies and has well-known effects on cardiomyocytes, like increasing the heart rate and the cardiac output. As a result, \(\beta \)-adrenergic stimulation enhances arrhythmias (Lang et al. 2015), accelerates the sinus node (Li et al. 2014), and can progress to heart failure (Wallis et al. 2001). However, \(\beta \)-adrenergic stimulation also alters contractility and modifies action potential duration in normal conditions, and is considered an important functional regulator. Javidgonbadi et al. (2019) reported that electrophysiological abnormalities due to hypertrophic cardiomyopathy can be reduced with β-blocker therapy. Thus, in the mammalian heart, it can be one of the most important adaptive mechanisms. However, little is known about the electrophysiological mechanisms of ISO stimulation-related changes in rat cardiomyocytes. To understand the ISO-induced changes within our model, several simulations were done. Different models can be created depending on the use of this molecule in different doses and for different periods, i.e. hypertrophic cardiomyopathy and myocardial infarction. The literature has divided the application protocol of isoproterenol, which is used to create a cardiac hypertrophy model, into three subclasses. The protocol that we used in this study is the moderate form and belongs to the category of acute treatment (Nichtova et al. 2012). Therefore, in the present study, \(\beta \)-adrenoceptor stimulation was applied to Wistar rats by application of 40 mg/kg ISO per day, which can induce almost maximal effects in cardiomyocytes. The voltage and current clamp measurements were conducted using enzymatically isolated endocardial left ventricular cardiomyocytes of the rats to better understand the changes in the AP due to the presence of ISO. Currents known to be the most sensitive to the presence of ISO were studied to better understand the changes in their dynamics. Our results from the experiments and simulations revealed that (1) the effect of ISO on the parameters of the action potential critically change the AP morphology, (2) the most dramatic change was the increase in action potential duration, (3) the amplitude of action potential did not differ much due to ISO application, (4) the maximum upstroke velocity decreased in the ISO-treated group, and ‘(5) among the newly included four channels (IBCl, ICaT, IKs,

and IKr), three voltage dependent conductance channels ICaT, IKs, s IKr were found to be important ISO- modulated ion channels in rat ventricular myocytes.

Methods

Animals

In this study, 3-month-old male Wistar rats weighing 250–350 g were used. All animals were cared for and handled in accordance with the Akdeniz University ethical review committee. Two experimental groups were designed as Control and ISO (isoproterenol-treated). 40 mg/kg of isoproterenol per day for 7 days was used to generate the ISO group by intraperitoneal injection. Seven days lasting ISO treatment induces hypertrophy of the left ventricle and increases both the left and the right ventricular weight. 0.9% saline solution was applied to Control group.

Endocardial cell isolations

Rats were anesthetized with pentobarbital sodium (20 mg/kg) before rapid excision. The aorta was cannulated on a Langendorff system. Hearts were perfused with Ca2+-free solution [in mM: 145 NaCl, 5 KCl, 1.2 MgSO4, 1.4 Na2HPO4, 0.4 NaH2PO4, 5 HEPES, and 10 glucose (pH adjusted to 7.4 with NaOH, at 37 °C)] for 3–4 min to abduct remaining blood in coronary arteries. Afterward, they were perfused with the same solution containing 0.7–1 mg/ml collagenase (collagenase A, Roche) and 0.04–0.08 mg/ml protease (protease IV) for 20–25 min. In the following steps, the left ventricle was separated from the whole heart, minced into small pieces, triturated by Pasteur pipette, massaged through a nylon mesh, and dissociated cardiomyocytes were washed with the Ca2+−free solution. Later, the calcium concentration of the cardiomyocyte suspension was gradually increased. Calcium-tolerant endocardial cells were kept at room temperature and used for experiments on the same day.

Electrophysiological parameters

In this study, patch-clamp experimental recordings were obtained to record action potential and current–voltage (I–V) relation of voltage-dependent Na+ (INa), transient outward K+ (Ito), steady- state K+ (Iss), and L-type Ca2+ currents (ICaL) using a patch-clamp amplifier (Axon Axopatch 200B, Molecular Devices) in whole-cell configuration. During patch-clamp experiments, cells were studied within the Tyrode solution [in mM: 137 NaCl, 5.4 KCl, 0.5 MgCl2, 1.5 CaCl2, 11.8 HEPES, and 10 glucose (pH adjusted to 7.4 with NaOH, 37 °C)] and pipette resistance was kept between 1.5 and 2.5 MΩ (P700 Puller, Sutter Instrument). The pipette solution contained (in mM) 140 KCl, 5 NaCl, 4 Na2ATP, 4.5 MgCl2, 10 HEPES, 0.25 CdCl2 and pH was kept at 7.2 using NaOH. Action potential was evoked by 4 ms square pulses at 1 Hz. AP amplitude, time to peak, action potential duration (APD) at 20%, 50% and 90% of repolarization, and resting membrane potential were calculated.

During the INa experiment, cells were kept in Tyrode solution and super-perfused with an external solution [in mM: 120 NaCl, 10 TEA, 5 CsCl, 1 MgCl2, 10 glucose, 10 HEPES, 1.5 CaCl2, and 0.5 CdCl2 (pH = 7.4, adjusted with CsOH)]. The patch pipette was filled with internal solution containing (in mM) 120 CsCl, 5 Na-ATP, 5 MgCl2, 10 TEA, 10 HEPES, 1 CaCl2, and 0.3 LiCl (pH = 7.2, adjusted with CsOH). The cells holding potential was − 120 mV and INa was obtained by voltage steps ranging from − 100 mV to + 40 mV with 5 mV increments. For steady-state inactivation, endocardial cells were held for 1 s at potentials from −140 mV to 20 mV with 5 mV additions before a step to − 40 mV to elicit INa. To study recovery from inactivation, endocardial cells were held at − 120 mV and two 20 ms pulses to − 30 mV were applied with 5 ms increment in the interval between pulses of consecutive episodes.

For the measurement of ICaL, cells in the Tyrode solution were super-perfused with the external solution (in mM: 137 NaCl, 5.4 CsCl, 1 MgCl2, 1.8 CaCl2, 5 HEPES). Patch pipettes were filled with a solution containing (in mM) 140 CsCl, 5 NaCl, 4 Na2ATP, 4.5 MgCl2, 10 EGTA, and 10 HEPES; this was kept at pH 7.2 using CsOH. The voltage-clamp protocol consisted of a 100-ms pre-pulse from − 70 mV to − 45 mV to inactivate the sodium channels. Following this step, 300 ms depolarizing voltage steps were performed between − 50 mV and + 50 mV. ICaL was measured as the difference between peak current and steady-state current at the end of the pulse.

In order to record IK, K+ was replaced by Cs in both external and pipette solutions. During K+ current recording, the use of 250 μM cadmium chloride (CdCl2) inhibits calcium current. For the measurement of Ito and Iss, cells were held at − 70 mV and a pre-pulse from − 70 mV to − 45 mV was used to inactivate voltage-dependent Na+ channels. Next, 1000 ms depolarizing voltage steps between − 120 mV and + 70 mV were performed. Ito was measured as the difference between peak current and the last part of the current which was defined as sustained current.

Mathematical model

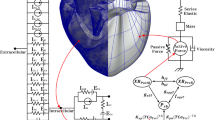
Hodgkin and Huxley examined the behavior of a squid axon under the effects of an applied electric current across the cell membrane. This imposed electric current was modeled in terms of capacitive and ionic currents mathematically for the first time to show spike generation (Hodgkin and Huxley 1952). Here we define a detailed Hodgkin–Huxley type multi-compartment model for ventricular action potential by including most of the ion channels and transporters recorded experimentally from rat cardiomyocytes. This model consists of 12 ion channels and 3 ion transporters based on the electrical circuit depicted in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the rat ventricular cell model. Cell includes 12 ion channels, 3 ion transporters and intracellular compartments (JSR, NSR and myosplasm)

Full size image

The potential difference across the plasma membrane varies according to the following equation:

$${C}_{m}\frac{dV}{dt}\, = \, {-I}_{Na}-{I}_{CaL}-{I}_{CaT}-{I}_{t0}-{I}_{K1}-{I}_{Kr}-{I}_{Ks}-{I}_{f}-{I}_{BCa}-{I}_{BNa}-{I}_{BK}-{I}_{BCl}-{I}_{NaK}-{I}_{NaCa}-{I}_{CaP}+{I}_{app,}$$
(1)

where Cm is the cell capacitance. Here, INa is the Na+ current, ICaL is the L-type Ca2+ current, ICaT is the T-type Ca2+ current, Ito is the transient K+ current, IK1 is the inwardly rectifier K+ current, IKr is the rapidly activating delayed rectifier K+ current, IKs is the slowly activating delayed rectifier K+ current, If is the hyperpolarization-activated current. The model includes Ca2+, Na+, K+ and Cl− background currents as well. There are three ion transporters, namely INaK the Na+-K+ pump current, ICaP the Ca2+ pump current and INaCa the Na+-Ca2+ exchanger.

We describe all the currents using the standard Hodgkin–Huxley formalism with slight modifications. All the currents included in the model obey the following equation:

$${I}_{Y} = \stackrel{-}{{g}_{Y}}{a}^{M}{b}^{N}{c}^{L}\left(V-{E}_{ion}\right), Y=Na,CaL,CaT,{t}_{0},{K}_{1},{K}_{r},{K}_{s},f,{K}_{b},{Ca}_{b},{Na}_{b},C{l}_{b},$$
(2)

where \(\stackrel{-}{{g}_{Y}}\) represents the maximal conductances of the channels, a,b,c denote the activation, fast inactivation and slow inactivation, respectively. M, N and L show the corresponding powers.

The voltage-dependent gating variables like a,b,c above are described in our model as follows:

$$\frac{dx}{dt}=\frac{({x}_{\infty }\left(V\right)-x)}{{\tau }_{x}(V)}, x=n,{n}_{f},{n}_{s},l,{l}_{f},{l}_{s},{Ca}_{i},{c}_{t},{c}_{ti},{k}_{t},{k}_{tf},{k}_{ts},r,{r}_{i},s,y.$$
(3)

All the equilibrium gating variables for both activation and inactivation functions are described with only two parameters as follows:

$$ x (V)=1/(1+e(a_1 V+a_2 ) ), x = n,n_f,n_s,l,l_f,l_s,Ca_i,c_t,c_ti,k_t,k_tf,k_ts,r,r_i,s,y .$$
(4)

All the time constants of the gating variables are modeled according to the following equation:

$${\tau }_{x}\left(V\right)=\frac{1}{\sum_{i=1}^{n}{{a}_{3i}e}^{{a}_{3i+1}V+{a}_{3i+2}}}, i=\mathrm{1,2},\dots ,n.$$
(5)

Reversal potentials of the channels are calculated as the difference between the extracellular and intracellular cell concentrations across the cell membrane according to the Nernst equation (Hille 1992) as following:

$${E}_{ion}=\frac{RT}{zF}ln \frac{{\left[ion\right]}_{out}}{{\left[ion\right]}_{in}}, ion=N{a}^{+}, {C{a}^{2+},K}^{+},C{l}^{-}.$$
(6)

Details of the ion channels along with the transporters and Ca2+ handling mechanism are discussed in the “Results” section.

The model is simple and easy to implement as all the gating variables and time constants follow a specific format as in Eqs. (4) and  (5). All the model plots are supported either with our own recordings or data from the literature. In the additional information section, physical units are considered as in Table 1, unless otherwise specified and the parameters of all the channel dynamics \({a}_{1},\cdots ,{a}_{n}\) are given in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15.

Table 1 AP characteristics for Control (n = 16) and ISO (n = 15) group
Full size table
Table 2 Changes on the channel dynamics after the ISO stimulation (n = 15) and changes applied to model to imitate AP curve
Full size table
Table 3 Physical units used in the text
Full size table
Table 4 Fast Na+ current parameters for Eqs. (4) and (5)
Full size table
Table 5 L-type Ca2+ current parameters for Eqs. (4) and (5)
Full size table
Table 6 T-type Ca2+ current parameters for Eq. (4) and (5)
Full size table
Table 7 Transient K+current parameters for Eq. (4) and (5)
Full size table
Table 8 Inward rectifier K + current parameters for Eq. (4) and (5)
Full size table
Table 9 Rapidly activated outward rectifier K + current parameters for Eq. (4) and (5)
Full size table
Table 10 Slowly activated outward rectifier K + current parameters for Eq. (4) and (5)
Full size table
Table 11 Hyperpolarizing activated current parameters for Eqs. (4) and (5)
Full size table
Table 12 Membrane current and Ca2+ handling mechanism related parameters for Eq. (6) and (18)–(36)
Full size table
Table 13 Conductances of ion channels
Full size table
Table 14 Initial conditions for state variables
Full size table
Table 15 Extracellular ion concentrations
Full size table

Simulation

The results of AP recordings are provided for Control and ISO group as the standard error of the mean (SEM) for all animals and the statistical significance is indicated by p < 0.05. The steady-state variables, time constants, I–V curves and last, AP recordings are fitted to data to find the best set of parameters that minimizes the difference between the model and data. For each membrane current, finding the optimized model parameters is performed in three steps. First, a cost function is defined as the squared error between simulated and experimental responses. Then, the cost function is minimized globally over the steady-state variables, time constants and I-V curves using NLopt (Non-Linear Optimization) library (v2.4.2) integrated into C +  + . Second, with the parameters from the simulated algorithm all channel maximal conductances (\(\stackrel{-}{{g}_{X}}\)) are optimized according to AP recordings by using Bobyqa, Newuoa and Cobyla algorithms. And lastly, our 32nd order Nonlinear Differential Equation System (NDE) is solved with all the optimized parameters by Gear’s Method in the MATLAB environment.

Results

INa, the fast Na+current The Na+ current is known to be mainly responsible for the period of rapid depolarization from a resting potential of − \(\approx \)72 mV to a peak potential of \(\approx \) +42 mV in rat ventricular cardiomyocytes. We include the fast Na+ current, INa as follows:

$${I}_{Na}=\stackrel{-}{{\mathrm{g}}_{Na}}{n}^{3}{n}_{f}{n}_{s}\left(V-{E}_{Na}\right),$$
(7)

where \(\stackrel{-}{{\mathrm{g}}_{Na}}\) is the maximum Na+ conductance. The model has three gates: \(n,{n}_{f }{\mathrm{a}\mathrm{n}\mathrm{d} n}_{s}\). While the \(n\) gate is responsible for activation, inactivation is controlled by \({n}_{f}{ \mathrm{a}\mathrm{n}\mathrm{d} n}_{s}.\) The separation between the inactivation gates is based on the fact that slow inactivation \({n}_{s}\) is much slower than the fast inactivation \({n}_{f}\). We define the steady-state activation \(({n}_{\infty })\) and inactivation (\({{n}_{f}}_{\infty },{{n}_{s}}_{\infty }\)) curves and the time constants (\({\tau }_{n},{\tau }_{{n}_{f}},{\tau }_{{n}_{s}}\)) with Eqs. 4 and 5. The model simulations are in close agreement with typical INa experimental results. The simulated steady-state functions are comparable with the experimental data of Lee et al. (1999) in the bounds of experimental variability (Fig. 2a). The activation gate is almost exponential and the Na+ channel inactivates mostly in the open state. The simulated time constants against the membrane potential are also plotted in Fig. 2B with experimental work from Conforti et al. (1993). The fast activation and the time separation between the fast and slow inactivation gates successfully mimic the physiological cases. We also compare the normalized I–V curves obtained from our model and the recordings of Lee et al. (1999) from rat cardiomyocytes. Results are consistent to validate our model parameters for INa as shown in Fig. 2c.

Fig. 2
figure 2

INa model parameters. a Simulated curves of steady-state activation (n) (—-) and inactivation (nf, ns) ( –- –-) with corresponding experimental data (o, o). b Simulated activation (—-) and inactivation time constants (—-,—-). Experimental data (o) is for \(\tau_{nf}\). c Normalized simulated curve (—-) and experimental data (o) for current-–voltage (I–V) relationship. 100 ms square pulse between − 60 − 25 mV with 5 mV intervals is applied from a holding potential of − 120 mV

Full size image

Ca2 + channels

The opening of voltage-gated calcium channels changes the intracellular Ca2+ concentration that induces contractility, excitability, exocytosis, proliferation, and many more cellular processes (Hansen 2015). It is usually the L-type Ca2+ channels that are associated with these cellular processes; however, T-type Ca2+ channels are also expressed in the cardiovascular system, where they play a functional role (Fares et al., 1996). We include both types of Ca2+ channels in our model.

L-type Ca2+ current, ICaL

The L-type Ca2+ channels start during the upstroke of the AP and it has a vital role by mostly affecting the plateau phase of the AP. In accordance with the studies we define the Ca2+ current formulation as follows:

$${I}_{CaL}=\stackrel{-}{{\mathrm{g}}_{CaL}}l\left[{l}_{{Ca}_{i}}{l}_{f}+\left(1-{l}_{{Ca}_{i}}\right){l}_{s}\right] \left(V-{E}_{Ca}\right),$$
(8)

where \(\stackrel{-}{{\mathrm{g}}_{CaL}}\) is the maximum conductance of the Ca2+ channel and \({E}_{Ca}\) is the reversal potential of Ca2+ obtained from Eq. (6). Here we formulate the activation gate \(l\) as in Eqs. (3)–(5). Based on our experimental data, Ca2+ current activation occurs in about 3.5 ms, half activation is near − 25 mV and the peak value occurs at 0 mV. In the heart, not only voltage-dependent inactivation but also Ca2+-dependent inactivation is directly related to the length of the Ca2+-mediated plateau phase. So we include 3 inactivation gates in our model, namely a voltage-dependent fast inactivation gate \({l}_{f}\) and slow inactivation gate \({l}_{s}\) defined as in Eqs. (3)–(5). And the Ca2+ dependent inactivation is included with \({l}_{{Ca}_{i}}\). We define the steady-state Ca2+ dependent inactivation in terms of the steady-state Ca2+ concentration as follows:

$${{l}_{{Ca}_{i}}}_{\infty }=\frac{1}{1+{a}_{Cai}[Ca{]}_{ss}},$$
(9)

where aCai = 1 is the multiplicative factor of \([Ca{]}_{ss}\) resulted from the optimization. Figure 3a shows the activation–inactivation curves resulting from model simulations and data. The used data points are taken from the work of Katsube et al. (1998). Time constants of steady-state functions of ICaL are shown in Fig. 3b with the related data (Katsube et al. 1998; Sun et al. 2000) and all the curves are in a close agreement with the published experimental findings including the I–V curve in Fig. 3c (Richard et al 1993).

Fig. 3
figure 3

ICaL model parameters. a Simulated curves of steady-state activation (l) (—-) and inactivation (lf, ls) (—-) with corresponding experimental data (o,o). b Simulated curves of activation (—-), fast inactivation (—-) and slow inactivation (—-) time constants and corresponding data points (o,o,o) c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I–V) relationship. 200 ms square pulse between − 80 and  50 mV is applied in 10-mV increment from − 80 mV holding potential

Full size image

T-type Ca2+ current, ICaT

T-type Ca2+ channels are low-voltage-activated transient channels that activate after a rather limited depolarization, with tiny transient currents. We model the T-type Ca2+ channel with activation \({c}_{t}\) and inactivation gate \({c}_{ti}\) as shown below:

$${I}_{CaT}=\stackrel{-}{{\mathrm{g}}_{CaT}} {c}_{t}{c}_{ti}\left(V-{E}_{Ca}\right),$$
(10)

where \(\stackrel{-}{{\mathrm{g}}_{CaT}}\) is the maximum conductance of the T-type calcium channel and \({E}_{Ca}\) is the reversal potential of Ca2+ obtained from Eq. (6). Voltage dependency of steady-state activation and inactivation functions were reported before for ventricular myocytes of the rat (Korhonen et al. 2009). Here again, we reformulate the activation/inactivation gate as in Eqs. (3)–(5) and the parameter estimation technique is used to fit the experimental findings of channel kinetics. Simulated steady-state functions together with the reported data are shown in Fig. 4A. Our results are in close agreement with Zorn-Pauly et al. (2004). We plot the simulated time constants for activation and inactivation dynamics in Fig. 4b. Activation of the channel occurs fast, around 3.5 ms, but the inactivation process is happening slower, taking around 300 ms. To our knowledge, there have been no published reports documenting the data of ICaT time constants in adult rat ventricular myocytes. But we believe that our results are physiologically meaningful as a result of discussions with our biophysics team. I–V curve data as a result of the voltage-clamp technique are taken from Avila et al. (2007). Optimization is done for the channel parameters; data and model are consistent as shown in Fig. 4c.

Fig. 4
figure 4

ICaT model parameters. a Simulated curves of steady-state activation (ct) (—-) and inactivation (cti) (—-) and corresponding data points (o,o). b Simulated curves of activation (—-) and inactivation (—-) time constants. c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I–V) relationship. 200 ms square pulse is applied in the range of − 80 − 60 mV with 10-mV interval

Full size image

K+ channels:

After the depolarization is driven by the Na+ current and the plateau phase is shaped by the Ca2+ currents, the remaining repolarization phase where the membrane returns to the resting potential is dominated by the outward current through voltage-gated K+ channels. We include four types of K+ currents in our model other than background currents that were reported in rat ventricular myocytes. Details of the K+ currents are given below.

Transient K+ current, Ito

The transient outward current (Ito) is a K+ current that activates rapidly on depolarization and is found in almost all cardiac ventricular myocytes. It is one of the main actors in the modulation of cardiac excitability and conduction. We model the transient K+ current with an activation gate \({k}_{t}\), fast inactivation gate \({k}_{tf}\). In addition to the inactivation gate, slower inactivation dynamics are observed during the reactivation phase. Instead of modeling the slow-inactivating transient current separately, we include it with slow inactivation gate \({k}_{ts}\) in our model and we model Ito as follows:

$${I}_{t0}=\stackrel{-}{{g}_{t0}}{k}_{t}{(ak}_{tf}+{bk}_{ts}) \left(V-{E}_{K}\right),$$
(11)

where \(\stackrel{-}{{g}_{t0}}\) is the maximum conductance of the transient K+ channel and \({E}_{K}\) is the K+ channel reversal potential. We model all the channel dynamics again with Eqs. (4)–(6) and all the results of the parameter estimation technique are given in Table 5.

Figure 5a displays simulated and experimental steady-state activation and inactivation traces (Stengl et al. 1998) for Ito and Fig. 5b displays the related traces of gating variable time constants for activation (Agus et al. 1991) and inactivation (Wettwer et al. 1993) as functions of voltage. Peak Ito -V characteristic for simulated and experimental data by Kamiya et al., (1999) is also given in Fig. 5c. All simulations are consistent with the experimental data.

Fig. 5
figure 5

Ito model parameters. a Simulated curves of steady-state activation (kt) (—-) and inactivation (ktf, kts) (—-) with corresponding experimental data (o,o). b Simulated curves of activation (—-), fast inactivation (—-) and slow inactivation (—-) time constants and corresponding data points (o,o,o) c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I-V) relationship. 400 ms square pulse between − 80 and 50 mV is applied in 10-mV increment from a holding potential of -80 mV

Full size image

Inward rectifier K+current, \({I}_{\mathrm{K}1}\)

Inward rectifier K+ current, \({\mathrm{I}}_{\mathrm{K}1},\) is a voltage-dependent current that contributes mostly to the resting membrane potential and to the repolarization phase of the AP. IK1, produces a characteristic region known as ‘negative slope’ conductance and it depends on rectification of extracellular K+ concentration \({\left[K\right]}_{o}\). To model IK1\(, \)we use the equation defined by Luo-Rudy (1994):

$${I}_{K1}={g}_{K1}{k}_{1\infty }\left(V-{E}_{K}\right),$$
(12)

where the conductance \({g}_{K1}=\stackrel{-}{{g}_{K1}}\sqrt{{\left[K\right]}_{o}/5.4}\) depends on the extracellular K+ concentration and the equilibrium activation \({k}_{1\infty }\) is defined as in Eq. (4). Figure 6a shows simulated steady-state activation data for IK1 as a function of voltage. To our knowledge, there have been no published data for steady-state activation of IK1. To verify our steady-state activation formulation, we optimized our parameters according to the voltage clamp experimental results. Model voltage-clamp I-V characteristic profile is plotted with scaled data from Wahler (1992) and displays a close resemblance as shown in Fig. 6b.

Fig. 6
figure 6

IK1 model parameters. a Simulated curve of steady-state activation (k1∞) (—-). b Normalized simulated curve (—-) and different experimental data (o,o,△) for current–voltage (I–V) relationship. 400 ms square pulse between − 120 and  50 mV is applied in 10-mV increment from a holding potential of − 80 mV

Full size image

IKr Rapidly activated outward rectifier \({{\varvec{K}}}^{+} \)current

The voltage-gated rapid delayed rectifier outward K+ current (IKr) is critical to phase 3 of the repolarization. It shows a relatively rapid activation with depolarization. Although it is called a delayed rectifier current, it also shows an inward rectification property at positive potentials. Although IKr has been reported in rat ventricular myocytes, current densities were found to be very low, particularly when compared with the densities of other voltage-gated K+ currents in cardiac cells. Although the density of IKr is low, we include it to make a more complete theoretical model. We model IKr as follows:

$${I}_{Kr}={g}_{Kr}r{r}_{i}\left(V-{E}_{K}\right),$$
(13)

which is consistent with our Eq. (2). First, to our knowledge, there has been no published model formulating IKr as in Eq. (2) in rat ventricular myocytes. Pandit et al. (2001) did not include IKr and the slowly activated outward rectifier K+ current, \({I}_{Ks}\) in their model. Instead, they combine them as the steady-state K+ current Iss. Mostly the Markov models are defined for IKr for species other than rat (Korhonen et al. 2009; Matsuoka et al. 2003).

Figure 7a shows the gating functions and Fig. 7b shows the time constants simulated from the model. The inactivation rate is modeled faster than its activation rate as reported in the literature (Pond et al. 2000), but the corresponding data were not available to compare them. Even though we could not find any data for gating functions and time constants, we succeeded in fitting the channel parameters according to the current–voltage curve reported by Danielsson et al. (2012). I–V characteristics of the model and data are in close agreement as shown in Fig. 7c.

Fig. 7
figure 7

IKr model parameters. a Simulated curves of steady-state activation (r) (—-) and inactivation (ri) (—-). b Simulated curves of activation (—-) and inactivation (—-) time constants. c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I–V) relationship. 400 ms square pulse between − 60  and  40 mV is applied in 10 mV increment from a holding potential of -70 mV

Full size image

Slowly activated outward rectifier \({{\varvec{K}}}^{+} \)current, IKs

Another current affecting the cardiac repolarization is the slowly activating delayed rectifier current IKs. IKs slowly activates at potentials positive to − 30 mV and as it shows very slight inactivation we ignore it in our model. We model IKs with the square of the activation gate s as follows:

$${I}_{Ks}=\stackrel{-}{{g}_{Ks}}{s}^{2}\left(V-{E}_{K}\right),$$
(14)

with maximal conductance \(\stackrel{-}{{g}_{Ks}}\) and reversal potential EK. Channel activation s is obtained as a solution of Eq. (3) with the appropriate rate constants. To verify that our model correctly mimics the behavior of IKs, we make an optimization with the voltage clamp results from the literature to find the correct rate constants. Figure 8a and b shows the simulated results of steady-state activation together with the steady-state time constant. After a thorough investigation of the literature, no reported data for these dynamics were found. However, the simulated current–voltage curve (Fig. 8c) is consistent with more recent rat ventricular voltage clamp data from Danielsson et al. (2012).

Fig. 8
figure 8

IKs model parameters. a Simulated curves of steady-state activation (s). b Simulated curves of activation (—-) time constant. c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I–V) relationship. 400 ms square pulse between − 60 and 40 mV is applied in 10 mV increment from a holding potential of − 70 mV

Full size image

Hyperpolarization-activated current, If

Hyperpolarization-activated current, If is a time-dependent inward current activated by hyperpolarization. The If channel allows the flow of both Na+ and K+ ions. We include the If current equation with the gating variable y, as follows:

$${I}_{f}= \stackrel{-}{{g}_{f}} y\left[{f}_{Na}\left(V- {E}_{Na}\right)+{f}_{K}\left(V- {E}_{K}\right)\right],$$
(15)

where \(\stackrel{-}{{g}_{f}}\) is the current conductance, \({E}_{Na}\) is the Na+ reversal potential, and \({E}_{K}\) is the K+ reversal potential. The equation for the activation gate, y, is consistent with Eq. (3). To validate our If model, we calculate the steady-state activation as a function of voltage and compare this model-generated curve with the experimental data reported by Shi et al. (1999). We observe that both data and simulation are in close agreement (Fig. 9a). Time constant data for If were not found in the literature for rat cardiomyocytes but the result is physiologically meaningful as the activation of the channel is around 2.5 ms. Simulated and experimental voltage clamp data for If are also plotted in Fig. 9c for the voltages from − 160 to − 50 mV. Experimental work of Fares et al. (1998) and model simulation results give similar I–V characteristics.

Fig. 9
figure 9

If model parameters a Simulated curves of steady-state activation (y) and the corresponding data (o). b Simulated curves of activation (—-) time constant. c Normalized simulated curve (—-) and experimental data (o) for current–voltage (I-V) relationship. 400 ms square pulse between − 170, 60 mV is applied in 10 mV increment from a holding potential of − 40 mV

Full size image

Background currents

We include four linear background currents in our model: Na+ current (IBNa), Ca2+ current (IBCa), K+ current (IBK) and Cl− current (IBCl)

$${I}_{Xb}={g}_{xb}\left(V-{E}_{X}\right), X={Na}^{+},{Ca}^{2+},{K}^{+},{Cl}^{-}$$
(16)

These currents represent the leak of related ions across the sarcolemma. The well-known role of background currents is to regulate the resting membrane potential and cardiac excitability. We model them with constant conductance and the densities of the background currents are optimized to attain stability of the intracellular ionic concentrations together with action potential behavior. A previous modeling study (Pandit et al. 2001) did not include the Cl− background current but this passive background current has an important effect on leading membrane potential as stated by Cha et al. (2009).

Pump currents and exchangers

Like many other cells, cardiomyocytes exhibit a large electrochemical gradient that allows Ca2+ entry into the cell from the extracellular fluid. The sarcolemmal Ca2+-pump current, IpCa and Na+-Ca2+ exchanger (NCX) current, INaCa are two sarcolemmal currents helping to drive Ca2+ from the cytoplasm. We include both Ca2+ transporters in our model together with the Na+-K+ pump current that is also responsible for active ion transport across the rat cardiac cell membrane.

Sarcolemmal Ca2+ pump current, ICaP

The sarcolemmal Ca2+ pump is highly dependent on [Ca2+]i, but its transport rate is slow. That is why its contribution to Ca2+ fluxes during the cardiac cycle is small, but it might be more important in the long-term extrusion of Ca2+ by the cell. Since our aim is simplicity in our model we use the simplest biophysical expression of calcium uptake and loss from the sarcoplasmic reticulum with a Michaelis–Menten kinetics:

$${I}_{CaP}={g}_{CaP}\frac{[\mathrm{C}{\mathrm{a}}^{2+}{]}_{i}}{0.0005+[\mathrm{C}{\mathrm{a}}^{2+}{]}_{i}},$$
(17)

where \({g}_{CaP}\) is the maximum rate of ion transport and \([\mathrm{C}{\mathrm{a}}^{2+}{]}_{i}\) is the intracellular Ca2+ concentration. In the model, reaction rate kmpca = 0.0005 mM was used as a value for half activation constant based on experimental results by Caroni and Carafoli (1980).

Na+-Ca2+ exchanger (NCX) current, INaCa

The Na+-Ca2+ exchanger transports 3 Na+ ions per Ca2+ ion and INaCa depends on Na+ and Ca2+ ion gradients as well as the membrane potential. Formulation of the INaCa is first defined by Mullins (1979), simplified by DiFrancesco and Noble (1985), and completed by Luo and Rudy (1994). We use LR formulation for the INaCa current as follows:

$${I}_{NaCa}={g}_{NaCa}\frac{1}{{K}_{m,Na}^{3}+[\mathrm{N}{\mathrm{a}}^{+}{]}_{o}^{3}}\frac{1}{{K}_{m,Ca}+[\mathrm{C}{\mathrm{a}}^{2+}{]}_{o}}\frac{1}{{k}_{sat}{e}^{\left(\eta -1\right)VF/RT}}\{{e}^{\frac{\eta VF}{RT}}[\mathrm{N}{\mathrm{a}}^{+}{]}_{i}^{3}[\mathrm{C}{\mathrm{a}}^{2+}{]}_{o}-{e}^{\frac{\left(\eta -1\right)VF}{RT}}[\mathrm{N}{\mathrm{a}}^{+}{]}_{o}^{3}\left[\mathrm{C}{\mathrm{a}}^{2+}{]}_{i}\right\},$$
(18)

where \({g}_{NaCa}\) is the maximum conductance of Na+-Ca2+ pump current and \(\eta \) is the position of the energy barrier mostly considered as 0.35 and controls the voltage dependence of the current. Here, ksat is the saturation factor that enables saturation at very negative potentials.

Na+-K+ Pump current, INaK

The sodium–potassium pump is responsible for active ion transport across the cell membrane. INaK is crucial for cardiac cell electrophysiology in the formation and continuation of the trans-sarcolemmal sodium and potassium gradients and it is one of the modulators of the cardiac action potential dynamics (Bueno-Orovio et al. 2013). The Na+-K+ pump generates an outward current since more Na+ goes out of the cell than K+ goes in by this pump. Luo and Rudy (1994) formulated the current equation first (the LR model) and after that most of the ventricular models used the same formulation including Pandit et al. (2001) and Korhonen et al. (2009). We use the INaK equation also like LR model:

$${I}_{NaK}=\stackrel{-}{{I}_{NaK}}\frac{1}{1+0.1245{e}^{-0.1VF/RT}+0.0365(\frac{1}{7}\left({e}^{\frac{{\left[{Na}^{+}\right]}_{o}}{67.3}}-1\right)){e}^{-VF/RT}}\frac{1}{1+{\left(\frac{{K}_{m,{Na}_{i}}}{{\left[{Na}^{+}\right]}_{i}}\right)}^{1.5}}\frac{{\left[{K}^{+}\right]}_{o}}{{\left[{K}^{+}\right]}_{o}+{K}_{m,{K}_{o}}},$$
(19)

where the amplitude of INaK is a function of [Na+]i, [K+]o [Na+]o, and the membrane potential, V. We decided the maximum Na+-K+ pump current parameter (\(\stackrel{-}{{I}_{NaK}}\)) as a result of AP optimization with parameter estimation.

Intracellular Ca2+ diffusion and buffering

The work of Keizer and Levine (1996) is modified to model calcium-induced calcium release from SR via ryanodine-sensitive calcium release (RyR) channels. Intracellular Ca2+ fluxes and concentrations are modified from the work of Jafri et al. (1998). All dynamic equations and initial conditions for this new model are optimized according to our recorded rat cardiac cell data and reported in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1314 and 15. This Ca2+ process is included in Fig. 1. Important features of each process are mentioned briefly before the full equations in this section.

Ryanodine receptor RyR channel The studies on the ryanodine receptor (RyR) from cardiac cells show that RyR undergoes a Ca2+-dependent process. Keizer and Levine developed a differential equation model for the regulation of these receptors. Here, O1 and O2 represent the open states and C1 and C2 represent the closed states of the channel. Transitions from C1 to O1 and from O1 to O2 are assumed to be Ca2+-dependent and have been written as depending on the binding of n and m Ca2+ ions, respectively. By using the mass action law with the rate constants \(k_{i}^{ + / - }\) and three kinetic steps as i = a,b,c, the following system of four differential equations are defined:

$$ \frac{{dP_{{O_{1} }} }}{dt} = k_{a}^{ + } \left[ {Ca_{i}^{2 + } ]_{i}^{n} P_{{C_{1} }} - k_{a}^{ - } P_{{O_{1} }} - k_{b}^{ + } } \right[Ca_{i}^{2 + } ]_{i}^{m} P_{{O_{1} }} + k_{b}^{ - } P_{{O_{2} }} - k_{c}^{ + } P_{{O_{1} }} + k_{c}^{ - } P_{{C_{2} }} , $$
(20)
$$ \frac{{dP_{{O_{2} }} }}{dt} = k_{b}^{ + } [Ca_{i}^{2 + } ]_{i}^{m} P_{{O_{1} }} - k_{b}^{ - } P_{{O_{2} }} , $$
(21)
$$ \frac{{dP_{{C_{1} }} }}{dt} = - k_{a}^{ + } [Ca_{i}^{2 + } ]_{i}^{n} P_{{C_{1} }} + k_{a}^{ - } P_{{O_{1} }} , $$
(22)
$$ \frac{{dP_{{C_{2} }} }}{dt} = k_{c}^{ + } P_{{O_{1} }} - k_{c}^{ - } P_{{C_{2} }} , $$
(23)

Intracellular ion fluxes and concentrations SR involves two sub-compartments, a network SR (NSR) and a junctional SR (JSR). Ca2+ enters the NSR and transfers to the JSR. The release of Ca2+ occurs at JSR from clusters of RyRs into a subspace, between the SR and T-tubule membranes.

Ca2+ release flux, Jrelease, from each RyR cluster is calculated as follows:

$$ J_{{{\text{release}}}} = v_{{{\text{rel}}}} \left( {P_{o1} + P_{o2} } \right)\left( {\left[ {Ca^{2 + } } \right]_{{{\text{JSR}}}} - \left[ {Ca^{2 + } } \right]_{{{\text{ss}}}} } \right), $$
(24)

where vrel is the maximum RyR channel Ca2+ flux. Here \(\left[ {Ca^{2 + } } \right]_{{{\text{JSR}}}}\) is the JSR Ca2+ concentration and \(\left[ {Ca^{2 + } } \right]_{ss}\) is the subspace Ca2+ concentration.

Then, Ca2+ is transferred to the cytoplasmic region from the subspace, where it diffuses, binds to buffers, and is taken into the NSR by SERCA pumps.

\(J_{{{\text{xfer}}}}\) is the transfer flux from the subspace to the myoplasm:

$$ J_{xfer} = \frac{{\left[ {Ca^{2 + } } \right]_{ss} - \left[ {Ca^{2 + } } \right]_{i} }}{{\tau_{xfer} }} , $$
(25)

where \(\tau_{{{\text{xfer}}}}\) is the time constant for transfer from the subspace to the myoplasm.

Later, Ca2+ transfers from NSR to JSR as a result of [Ca2+] decrease in the JSR.

The flux due to Ca2+ transfer from NSR to JSR\(, J_{{{\text{TR}}}} ,\) is defined as follows:

$$ J_{TR} = \frac{{\left[ {Ca^{2 + } } \right]_{NSR} - \left[ {Ca^{2 + } } \right]_{JSR} }}{{\tau_{tr} }} , $$
(26)

where \(\left[ {Ca^{2 + } } \right]_{{{\text{NSR}}}}\) is the NSR Ca2+ concentration.

In order to avoid Ca2+ accumulation in the cytosol and for relaxation to occur, SERCA pumps Ca2+ ions back into the NSR to be released upon the next excitation.

The pump flux \(J_{{{\text{uptake}}}}\) is described by the formulation of Shannon et al.(1998):

$$ J_{{{\text{uptake}}}} = \frac{{v_{{{\text{maxf}}}} (\left[ {Ca^{2 + } } \right]_{i} /K_{{{\text{fb}}}} )^{{N_{{{\text{fb}}}} }} - v_{{{\text{maxr}}}} (\left[ {Ca^{2 + } } \right]_{{{\text{NSR}}}} /K_{{{\text{rb}}}} )^{{N_{{{\text{rb}}}} }} }}{{1 + (\left[ {Ca^{2 + } } \right]_{i} /K_{{{\text{fb}}}} )^{{{\text{N}}_{{{\text{fb}}}} }} + (\left[ {Ca^{2 + } } \right]_{{{\text{NSR}}}} /K_{rb} )^{{N_{{{\text{rb}}}} }} }} , $$
(27)

where \(v_{{{\text{maxf}}}}\) and \(v_{{{\text{maxr}}}}\) are the maximum rate of forward and reverse uptake, Kfb and Krb are forward and reverse dissociation constants, and Nfb and Nrb are the forward and reverse Hill exponents.

Ca2+ leak from the SR through RyRs is also calculated as follows:

$$ J_{{{\text{leak}}}} = v_{{{\text{leak}}}} \left( {\left[ {Ca^{2 + } } \right]_{{{\text{NSR}}}} - \left[ {Ca^{2 + } } \right]_{i} } \right), $$
(28)

where \(v_{{{\text{leak}}}}\) is the maximum leak channel Ca2+ flux.

The related ion concentrations are defined as follows:

$$ \frac{{d\left[ {Ca^{2 + } } \right]_{{{\text{JSR}}}} }}{dt} = \beta_{{{\text{JSR}}}} \left\{ {J_{{{\text{TR}}}} - J_{{{\text{release}}}} } \right\} $$
(29)
$$ \frac{{d\left[ {Ca^{2 + } } \right]_{{{\text{NSR}}}} }}{dt} = \left( {J_{{{\text{up}}}} - J_{{{\text{leak}}}} } \right)\frac{{V_{{{\text{myo}}}} }}{{V_{{{\text{NSR}}}} }} - J_{{{\text{tr}}}} \frac{{V_{{{\text{JSR}}}} }}{{V_{{{\text{NSR}}}} }} $$
(30)
$$ \frac{{d\left[ {Ca^{2 + } } \right]_{{{\text{ss}}}} }}{dt} = \beta_{{{\text{ss}}}} \left\{ {J_{{{\text{rel}}}} \frac{{V_{{{\text{JSR}}}} }}{{V_{{{\text{ss}}}} }} - J_{{{\text{xfer}}}} \frac{{V_{{{\text{myo}}}} }}{{V_{{{\text{ss}}}} }} - I_{{{\text{CaL}}}} \frac{{A_{{{\text{cap}}}} C_{{\text{m}}} }}{{2V_{{{\text{ss}}}} F}}} \right\} $$
(31)
$$ \frac{{d\left[ {Ca^{2 + } } \right]_{i} }}{dt} = \beta_{i} \{ J_{{{\text{leak}}}} + J_{{{\text{xfer}}}} - J_{{{\text{up}}}} - J_{{{\text{trpn}}}} - (I_{{{\text{BCa}}}} - 2I_{{{\text{NaCa}}}} + I_{{{\text{Cap}}}} )\frac{{A_{{{\text{cap}}}} C_{{\text{m}}} }}{{2V_{{{\text{myo}}}} F}}\} , $$
(32)

where \(\beta_{{\text{i}}} ,\beta_{{{\text{ss}}}}\) and \(\beta_{{{\text{JSR}}}}\) are buffering factors of intracellular Ca2+ concentration, subspace Ca2+ concentration and junctional sarcoplasmic reticulum concentration, respectively.

Ca2+ in the cytoplasm can bind to two kinds of buffers: a mobile buffer, calmodulin, and a stationary buffer, troponin. where the calmodulin is included as the Ca2+-binding protein in the \(\left[ {Ca^{2 + } } \right]_{i}\) and \(\left[ {Ca^{2 + } } \right]_{ss} , \) calsequestrin is included as the Ca2+-binding protein in the \(\left[ {Ca^{2 + } } \right]_{{{\text{JSR}}}}\). The formulations of buffering factors are defined as follows:

$$ \beta_{i} = \left\{ {1 + \frac{{\left[ {CMDN} \right]_{tot} K_{{\text{m}}}^{{{\text{CMDN}}}} }}{{\left( {K_{{\text{m}}}^{{{\text{CMDN}}}} + \left[ {Ca^{2 + } } \right]_{i} } \right)^{2} }}} \right\}^{ - 1} $$
(33)
$$ \beta_{ss} = \left\{ {1 + \frac{{\left[ {CMDN} \right]_{{{\text{tot}}}} K_{{\text{m}}}^{{{\text{CMDN}}}} }}{{\left( {K_{{\text{m}}}^{{{\text{CMDN}}}} + \left[ {Ca^{2 + } } \right]_{{{\text{ss}}}} } \right)^{2} }}} \right\}^{ - 1} $$
(34)
$$ \beta_{JSR} = \left\{ {1 + \frac{{\left[ {CSQN} \right]_{{{\text{tot}}}} K_{{\text{m}}}^{{{\text{CSQN}}}} }}{{\left( {K_{{\text{m}}}^{{{\text{CSQN}}}} + \left[ {Ca^{2 + } } \right]_{{{\text{JSR}}}} } \right)^{2} }}} \right\}^{ - 1} $$
(35)

Buffering by troponin is described as follows:

$$ J_{{{\text{trpn}}}} = k_{{{\text{htrpn}}}}^{ + } \left[ {Ca^{2 + } } \right]_{i} \left( {\left[ {{\text{HTRPN}}} \right]_{{{\text{tot}}}} - \left[ {{\text{HTRPNCa}}} \right]} \right) - k_{{{\text{htrpn}}}}^{ - } \left[ {{\text{HTRPNCa}}} \right] + + k_{{{\text{ltrpn}}}}^{ + } \left[ {Ca^{2 + } } \right]_{i} \left( {\left[ {{\text{LTRPN}}} \right]_{{{\text{tot}}}} - \left[ {{\text{LTRPNCa}}} \right]} \right) - k_{{{\text{ltrpn}}}}^{ - } \left[ {{\text{LTRPNCa}}} \right] , $$
(36)

where [LTRPN]tot and [HTRPN]tot are total myoplasmic troponin low-affinity site concentration and high-affinity site concentration, respectively. While \(k_{X}^{ + }\) are the related Ca2+ on-rate constants, \(k_{X}^{ - }\) are the related Ca2+ off-rate constants. While all intracellular concentrations are dynamically changing with time in our model, extracellular ion concentrations are assumed to be fixed.

All physical parameters for the model are given in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. Cell compartment volumes are identical to those used by Pandit et al. (2001).

Rat AP Characteristics

After the reformulation of all ionic currents, all maximal conductances are adjusted to microelectrode AP recordings from rat ventricular myocytes to validate model AP characteristics. In Fig. 10a, we display a model AP generated during stimulation at 200 ms in response to 5 ms square pulse of 528 pA amplitude. Figure 10b displays corresponding experimental recording as the average of 16 cells for the Control case. Resting membrane potential, AP duration (APD) at 20, 50 and 90% repolarization (APD20, APD50, APD90), AP overshoot (PO) and time to peak are reported in Table 8 for both model AP and recorded AP. The AP generated with the Control parameters exhibits a spike similar to our experimental recordings.

Fig. 10
figure 10

a Simulated AP for Control case generated at 1 Hz respectively and b experimentally recorded AP as an average of 16 endocardial rat ventricular cells. c Simulated AP after ISO application at 1 Hz, respectively, and d experimentally recorded AP as an average of 15 endocardial rat ventricular cells

Full size image

Isoproterenol induced changes in AP characteristics

In our work we also observe that isoproterenol (ISO) induces changes in rat AP features. The voltage and current clamp measurements were conducted as explained in the Methods section and the resulting ISO-induced AP as the average of 16 cells is plotted in Fig. 10d. Our model can also recapitulate the key features of the recorded AP after the ISO-induced changes as shown in Fig. 10c. We also compare simulated values for Vrest, Time to peak, PO and APD at 20, 50 and 90% repolarization with the Control case. All these results are compared with simulation from the quiescent state and for a single spike as in Table 8. We can see the close consistency between the experimental results and simulations for the Control case.

Once we compare the Control AP with ISO-induced AP, it is clear that isoproterenol caused significant changes in the action potential configuration (Table 8). Major changes are observed in the action potential durations (APD20, APD50 and APD90) by increasing almost three times more compared to that of the Control. While the AP amplitude (PO) did not change with ISO stimulation, resting membrane potential displaced in a positive direction and the maximum upstroke velocity is decreased significantly. All results are qualitatively similar to our experimental measurements made in rat ventricular myocytes.

Table 10 summarizes the main changes in ISO-induced APs and the changes applied to the model to simulate the ISO effect. After the ISO application, we observe an increase in the size of the cells and we increase the capacitance by the same ratio. We calculate the membrane capacitance during the patch experiment first, and later to validate our recordings we evaluate the heart weight / tibia length (HW/TL) ratio, that is not affected by changes in body weight during the experimental period. Thus the HW/TL ratio of the ISO group is increased (~ 32%) from 34.31 g/m \(\pm 0.65 \)(Control) to 45.23 g/m \(\pm 1.08\) (ISO) supporting the increase in Cm by 35% during the patch experiment. Later, we change ionic current parameters in the model that corresponds to currents affecting the dynamics of ISO stimulation observed during the experiments (Table 10). Thus in our model, we simulate the application of ISO through changes to six ionic currents: INa, ICaL, ICaT, Ito, IKr and IKs. The simulated time courses of membrane currents that are responsible for the distinct properties of Control and ISO group during the AP are also shown in Fig. 11.

Fig. 11
figure 11

Simulated results for major ionic currents change by ISO application. a Na+ current for Control case (−) and for ISO case (−). b L-type Ca2+ current (green) for Control (−) and for ISO (−) group. Transient K+ current (red) for for Control (−) and for ISO (–) group. Slow outward rectifier K+ current (blue) for Control (−) and ISO (–) case. c Rapid outward rectifier K+ current (red) under Control (−) and ISO (–) case. T-type Ca2+ current (blue) for Control (−) and for ISO (–) group

Full size image

The Na+ current in ventricular cardiomyocytes is the basic current for the depolarization phase and we observe a decreased behavior of Na+ voltage kinetics for ISO group. Thus, we increase the Na+ conductance and we shift the Na+ half-activation and half-inactivation in a positive direction in the model just as observed in the experiments (Table 10). As a result, our modeling approach shows that even though ISO induced an increase of Na+ density, since the capacitance, the half-activation and -inactivation increased, the magnitude of INa decreases as shown in Fig. 11a. This can explain the decrease in maximum upstroke velocity as reported in Table 10.

Ca2+ current is known as responsible for the plateau phase and our findings on the ICaL demonstrate the underlying mechanism behind the extended APD after the ISO application. Isoproterenol reduced the density of ICaL by 28% during the experiments and we applied this result by decreasing the conductances of ICaL and ICaT by 23% and 18%, respectively, to accurately mimic the ISO-induced changes in AP. As shown in Fig. 11b and c, the decrease in Ca2+ density decreases the magnitude of both Ca2+ currents. Also, the ISO-induced prolongation of AP increases the duration of the Ca2+ currents as well.

Another current affected by ISO stimulation is the K+ current that is mainly responsible for the repolarization phase of the AP. The results of the voltage clamp experiment with I–V characteristics show that although the Ito was not extensively changed, the Ito density substantially declined within -30 to 30 mV compared to that in the Control. Thus, Ito does not support the prolongation of action potential due to ISO in the experiments. Notably, our mathematical modeling of the ionic currents reveals improved kinetics for Ito. We decrease the time constants of the gating functions that make the channel slow in activation by 50% and inactivation by 81%. As a result, Ito density significantly decreases to capture the prolongation effect of the ISO in our model as shown in Fig. 11b.

The steady-state outward K+ currents (Iss) represent another K+ current group that modulates the action potential plateau in ventricular myocytes. These currents contain several components such as IK1, IKrIKs and the background Na+-K+ current. In our experiments, the whole-cell current evoked by the voltage ramps in the ISO-induced ventricular cells reveal that Iss significantly increases relative to that in the Control. In the model, the Iss effect is simulated by the fast and slow delayed rectifier currents IKr and IKs. We increased the densities of IKr and IKs by increasing their conductances to mimic the experimental results (Fig. 11b, c). For the inward rectifier K+ current, IK1, we did not observe any significant change during the experiments and simulations as well.

The current densities are also calculated to eliminate the impact of the capacitance difference between the experimental groups. After all these changes, the simulated results of the action potentials under the absence of ISO (Control) and in the presence of ISO are in close agreement as shown in Fig. 10 and reported in Table 10.

Discussion

Several ventricular myocyte AP models have been developed and published for different species. These models are based on the work of Hodgkin and Huxley (1952) with squid axons. Starting from the work of Noble (1960) and later Beeler and Reuter (1977), DiFrancesco and Noble (1985) and Luo and Rudy (1991) applied the HH definition to cardiac AP and gave the first successful results for different cardiac cell types. Later, these models were developed in more detail for different AP characteristics and pathological cases (Iyer et al. 2004; Ten Tusscher et al. 2004). Winslow et al. (2011) reviewed all these models for different species and different cell types. With rat ventricular myocytes, Pandit et al. (2001) defined the first mathematical model of the rat ventricular AP and later Crampin and Smith (2006) and Korhonen et al. (2009) defined it by analyzing different physiological conditions and modeling the channels with Markov formulations. An essential dissimilarity exists between the model we present in this paper and other rat ventricular myocyte models. It should be emphasized that in our model, all major current equations are completely reformulated (i.e. fast INa, Ito, ICaL, ICaT, IKr, IKs and IK1). Pandit et al. (2001) did not include the currents ICaT, IKr, IKs and IBCl. We show that these channels are important modulators for \(\beta\)-adrenergic stimulation. Moreover, our model reproduces all the currents in an extensive rat dataset. We also simulate the ISO-induced changes in rat cardiac AP with our new model. We believe that the rat ventricular model simulations here are crucial and substantially increase rat-specific model accuracy.

One of the most important features of the model is that action potential duration at 20%, 50%, and 90% of repolarization measurements of APD90,50 and 20 are consistent with our experimental recordings from rat ventricular myocytes. The most affected AP feature from ISO application turned out to be APD. Particularly, stable excitation during the APD is required for healthy contraction. Our model captures the APD properties of the Control group and the prolonged APD feature after ISO application very well. For example, the repolarization rate is essential for simulating any phenomenon related to arrhythmia (Osadchii, 2017); thus this model can be used as a tool to understand such pathological conditions.

We used the Hodgkin–Huxley formalism strictly in reformulating current equations to keep our model computationally efficient and to achieve well-constrained parameters. Models defined before which used the symbolic regression technique controlled the parameter size and kept the same format for the fitted equations. Instead, we fixed the channel dynamics with particular functions and the parameter size was minimized to optimize the real data. The simplicity of this design principle allows us to play with the model with a simple interface in future work. Also, this model gives freedom to users to replace any current with more detailed functions like Markov formulations and analyze different drug effects just as we analyze ISO here. We, however, preferred not to define Markov models in this study and they increase complexity and decrease stability and computational efficiency. Gear’s method was used as a rapid integration technique, as described in the Simulations part of the paper, and the model arrives at a true and accurate steady-state in under 2 s of run time. Our equations are all smoothly varying functions and free of singularities. We used Matlab together with C +  + as a numerical integrator but the model can be easily implemented in any other program, such as XPPAuto (https://www.math.pitt.edu/~bard/xpp/xpp.html), R (https://www.r-project.org), CellML (https://www.cellml.org/), CHASTE, or CARP (CardioSolv LLC.).

Although we have tried to develop a complete model that is supported by experimental recordings from rat ventricular myocytes, we faced some limitations and shortcomings in our work. First, direct measurements of some currents and dynamics in the rat ventricular myocyte are lacking. For example, recordings for gating functions and time constants of IK1, IKr and IKs for rat ventricular cells do not exist to the best of our knowledge. Instead, we were able to define them with current–voltage recordings and physiologically meaningful parameters. Here, we should also point out that the If current is modeled in more positive potentials to reproduce the ISO effect on current modification by using data from neonatal cells, but not normal adult rat cells. In both neonatal and adult rat ventricles, only HCN2 and HCN4 transcripts are present and the difference is that HCN2 dominates more in adult rat cells (5:1 in neonates, 13:1 in adults) (Shi et al., 1999).

Even though the large-conductance Ca2+ activated K+ current (IBK) and small-conductance Ca2+ activated K+ current (ISK) channels are observed in rat cardiac myocytes with low density, there were no data available and we could not integrate them into our model (Gu 2018; Zhang 2018). Another limitation is that between the published data we observed some variability. For the K1 current–voltage relationship (Fig. 6a), we used the average of the available data to optimize our model parameters. Thus, direct experimental measurement of all ionic channels’ dynamics with the same experimental conditions in rat ventricular myocytes would provide additional insights.

Similarly, intracellular Ca2+ handling can be modified or various signaling pathways can be added. We implemented this process from the work of Keizer and Levine (1996) and Jafri et al. (1998) since these formulations are simple and capture the dynamics very well. Most sophisticated models of Ca2+ mechanism can be integrated into this work with more details like the regulation of calcium-calmodulin-dependent enzyme cascade (Hashambhoy et al. 2009) or cytoplasmic ATP-consuming processes (Cortassa et al. 2006), but since our focus was on keeping the model simple we preferred not to include these details.

Using this new model, we were able to both simulate and analyze the mechanism underlying the effects of chronic ISO application in rat ventricular cells in terms of conductances. It is to be noted that the focus of our work was limited to modeling and verifying the changes exhibited by the conductances after chronic ISO application. However, similar chronic ISO effects could also perhaps be modeled in terms of gating kinetics. Voltage dependent channel kinetics can be analyzed mathematically as discussed in the next paragraph and in future work channel kinetics could be tested experimentally also for different pathological cases including ISO-induced hypertrophy.

Recently, Şengül et al. (2014) and Noma et al. (2011) developed measures for defining the contributions of ion channels during AP. Sobie (2009) also developed a method for sensitivity analysis that gives relationships between parameters and target outputs in AP models. Application of these analyses to model development is beyond the scope of this paper; however, for future work, we will analyze the contribution of each ion channel and transporter to the rat ventricular AP mathematically by modifying the work of Şengül et al. (2019). We believe that these results provide worthwhile insights into the clarification of the complex relations between the different ion channel dynamics.