Introduction

The emergence of life on the early Earth is believed to have been preceded by the accumulation of an increasingly diverse and complex set of organic molecules (Orgel 2010). The reaction networks developed by these molecules laid the groundwork of functions critical for life, like energy and information processing. Understanding how the systems-level molecular interactions required for life-like behavior could emerge from simple precursors remains one of the key questions of prebiotic chemistry, but since this question is primarily about collective behaviors, complexity presents an ongoing challenge (Schwartz 2007; Johnson and Hung 2019). While studying a single type of molecule or a single reaction to establish its properties can be useful, it limits what conclusions can be drawn about potential broader community behavior. Experiments involving a greater variety of molecules and reactions can probe more interesting interactions, but have a large search space of variables, and the complexity of the systems make them inherently more difficult to analyze.

Models are useful for understanding complex systems because they can reveal the systematic dependence of various properties on each other and allow us to describe and make predictions about the system behavior. Computational models have been used to explore hypothetical prebiotic chemical networks for many years and have produced many interesting insights (Coveney et al. 2012). However, our current interest is in models that are based on experimental data. Prior experimental works mainly used basic kinetic and thermodynamic governing equations to describe individual reactions or small networks involving fewer than five reactions. For example, Arrhenius expressions have been used to determine the free energies of activation for reactions in a small network (Sakata et al. 2010; Yu et al. 2016; Lee et al. 1996). More abstractly, parameters have been fit to empirical rate equations to describe specific elements of system behavior or distinguish between candidate models (von Kiedrowski 1986; Rout et al. 2022). These methods work well for small systems, but may not apply to larger systems with multiple reactions occurring simultaneously and potentially more intricate network interactions. Serov et al. (2020) approximated the parameters for multiple reactions simultaneously in a peptide reaction network, but the parameter fitting was performed manually, and the network was small. Manual approaches are less rigorous than using a computational strategy and can be difficult to implement for even moderately sized networks. On the other hand, results from more complex experiments have been analyzed using statistical methods, but these do not capture the system dynamics (Surman et al. 2019; Jain et al. 2022). There is a need for approaches to study the dynamical behavior of more complex experimental networks (Ruiz-Mirazo et al. 2014).

Complex network models are broadly applicable and have already been developed extensively for other fields (Newman 2003). One notable example is in systems biology, which has significant parallels to the origins of life. Both involve large interaction networks with potentially limited available data and may include community interactions that are critical to understanding system behavior. Bioinformatics models can be used to analyze experimental data and help understand the molecular interaction networks within living cells (Gauthier et al. 2019). Similar approaches could be useful for furthering experimental chemical origins of life research, but aside from a few reviews and computational investigations, they have generally been overlooked (Johnson and Hung 2019; Ludlow and Otto 2008; Goldman et al. 2013).

Our goal in this study was to investigate how dynamical models, described by ordinary differential equations (ODEs), might be useful for studying origins of life chemistry. These models are theoretically generalizable, but as with all modeling approaches, there are limitations that make them more difficult to apply in some situations. Presenting the benefits and limitations of a model approach in a way that is accessible to experimentalists, which we aim to do, is an important step for linking theory and experiment. Differential equation models are not always suitable for large systems, since constructing them can become difficult, but in well-defined systems they can be used to study detailed mechanistic behavior (Maria 2004). Computational methods can be used to estimate all the parameters efficiently and simultaneously in a moderately complex dynamical network, but validating the physical meaning of the results can be more challenging since these problems may not have a unique and stable solution (Transtrum et al. 2015). However, parameter fitting has still been used to describe nonlinear networks in a variety of fields, including in systems biology for biochemical pathways (Raue et al. 2013; Rodriguez-Fernandez et al. 2006).

We focus specifically on fitting parameters to a set of nonlinear ODEs describing the kinetics of short peptide formation. Peptides are interesting candidates for emergent behavior because they can engage in a variety of intermolecular interactions and their development was likely an important step during the origin of life (Frenkel-Pinter et al. 2020). We studied a simplified network describing peptide formation in a system starting with only two amino acid species, glycine and alanine. By limiting ourselves to two amino acids, we were able to obtain quantitative data on the concentrations of most peptide species as they formed through a possible prebiotic reaction mechanism involving an inorganic phosphate activating agent, trimetaphosphate (TP) (Sibilska et al. 2018).

We found that our model exhibited “sloppiness,” a term originally used by the Sethna lab to describe models based on a set of highly imprecise parameters that still return reasonably accurate predictions (Gutenkunst et al. 2007a). Such models are significantly more sensitive to changes in certain parameter values while remaining largely unaffected by changes in others (Waterfall et al. 2006). We suspect sloppiness may be a common feature in networks relevant to the chemical origin of life. It is known to be extremely common in systems biology, and many of the features that contribute to it, like reversibility of reactions and limited experimental observations, are also common features of prebiotic chemistry networks (White et al. 2016).

Sloppiness occurs when parts of the parameter fitting problem are poorly constrained, resulting in highly imprecise parameter estimates. Our computational study reveals that the peptide network model is sloppy. Due to their high uncertainty, parameters fitted to a sloppy model cannot be treated as true kinetic reaction rates, limiting the hypotheses a sloppy model can be used to evaluate (Gutenkunst et al. 2007a). However, the collective behavior predicted by fitting a sloppy model can be accurate even when fit to relatively sparse experimental data. This makes them useful for tasks such as exploring theoretical long-term behavior and model falsification (Brown et al. 2004; Gutenkunst et al. 2007b; Hettling and van Beek 2011). For these reasons, we concluded that this system was worth investigating and disseminating despite the high variability observed in the parameter estimates.

We attempted to reduce sloppiness using model reduction and statistical design of experiments, but without improvements. As such, it is important to recognize the inherent limitations of the model structure and of the experimental setup. We conclude that fitting accurate kinetic parameters using the approach we present might be difficult. However, ODE models can still be useful tools for characterizing the behavior and stability of prebiotic chemical reaction networks.

Methods

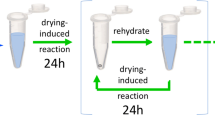
We studied the formation of peptides from amino acids using trimetaphosphate (TP) as an activating agent. For simplicity, our experiments only included two amino acids: glycine and alanine. To maximize peptide bond formation within 24 h, samples at alkaline pH were allowed to dry completely (Sibilska et al. 2018). Various combinations of initial concentrations of glycine and alanine were used to increase the amount of relevant data for parameter fitting and cover a larger range of potential conditions in the network, since concentrations of each species should not affect the values of the kinetic constants. The concentrations of each peptide product were determined using HPLC (see section “Experimental Materials & Methods” for details). Each experimental data point is the average of three experimental replicates.

Parameters were fit to an ODE model describing peptide formation and decomposition in a mass-action style network, depicted in Fig. 1. The complete time-dependent ODEs for the model are provided in Supplementary Information 1. To keep the network a manageable size, we omitted many mechanistic details of peptide formation and only includes canonical peptides, not intermediates or possible side products. For example, no phosphate salts or intermediate products of TP activation were quantifiable in our analysis, so TP was not explicitly included anywhere in the network. To minimize any effect the concentration of TP might have on the kinetics studied, we used a constant ratio of TP to amino acids across all experiments. Isomers such as GGA, GAG, and AGG were grouped together to further reduce the number of parameters and avoid the need to resolve isomers, which tend to co-elute during HPLC analysis. A complete list of fitted parameters, organized by figure, are available on Github at https://github.com/haboigenzahn/OoL-KineticParameterEstimation.

Fig. 1
figure 1

Peptide network. Double-headed arrows represent a reversible reaction connecting two species. Note that many edges share the same reaction parameter, such as the G → GGG and GG → GGG edges representing the reaction G + GG → GGG

Full size image

We expected that the network would provide a good baseline for understanding which reactions were occurring at higher rates. To improve the precision of the parameter estimates, we applied model reduction and statistical experimental design. Details about these approaches can be found in the “Computational Methods” section. Here we will describe the results of these tests and assess the feasibility of obtaining a predictive model and accurate parameter estimates from experimental data.

Results and Discussion

Parameter Estimation

Parameter fitting is performed by tuning the model parameters to minimize a cost function (\(\mathcal{L}\)) that calculates the difference between the model predictions and experimental data; \(\mathcal{L}\) is also called a loss function or a residual. We minimized \(\mathcal{L}\) using the L-BFGS-B algorithm from Scipy’s minimize function (Virtanen et al. 2020). We were also able to approximate the parameter uncertainties, which represent how well the parameters are constrained by experimental data using an asymptotic Gaussian approximation (Vanlier et al. 2013). Parameters determined using sparse or noisy experimental data are less precise than parameters fit with abundant, high precision data, but the structure of the model itself can also significantly contribute to the parameter uncertainty. Validating that the model can theoretically be solved can save time and experimental effort.

We first estimated the parameters for simulated data in the absence of noise, and we were able to accurately recover the parameters used to generate the data (Fig. 2a). When we applied the model to experimental data, it was able to capture general trends. However, the parameter uncertainties were undesirably high (Fig. 2b). For some species, the 95% confidence envelope for the model prediction was larger than the peptide concentrations themselves. Since the optimization can find a local minimum, we repeated the parameter estimation for several different initial guesses. Although the number of initial guesses was limited by the fact that the parameter estimation method can take a full day to finish when all of the experimental data is included, we observed that none of the different initial guesses significantly improved the precision of the parameter estimates and that there did not appear to be any positive correlation between the MSE and the number of highly uncertain parameters (Supplementary Information 2). Trying many initial guesses to find the lowest possible value for the cost function may slightly improve the model predictions, but it does not seem to cause an improvement in the precision of the parameter estimates. Despite the extremely high parameter uncertainties, the accuracy of the model predictions initially seemed promising, so we began to explore the parameter fitting process in more detail to determine how to decrease the parameter uncertainty, starting with the identifiability of the network.

Fig. 2
figure 2

Comparison of fitting data and model predictions. Results are shown for a simulated data and b experimental data, using initial conditions of 75 mM glycine and 25 mM alanine. Both the simulated and experimental data sets included 65 data points and the simulated data had no artificially added noise

Full size image

Identifiability & Sloppiness

Identifiability analysis determines the possibility of a unique and precise estimate of the unknown parameters in a network (Cobelli and DiStefano 1980; Wieland et al. 2021). If a unique solution cannot be obtained, then the model is said to be structurally unidentifiable. A model is practically unidentifiable if its parameters cannot be estimated at an acceptable level of precision. The exact definition of what is considered an acceptable level of precision varies from case to case. Practical unidentifiability indicates that regions of the objective function are relatively flat, making it difficult to find a minimum and it typically results from overfitting (White et al. 2016). Finally, some models exhibit a property known as sloppiness, which occurs when their behavior is highly sensitive to changes in certain combinations of parameters and almost completely insensitive to changes in others (Gutenkunst et al. 2007a). Generally, sloppiness is a consequence of the model structure and its input range (White et al. 2016). Although sloppiness and practical unidentifiability are not synonymous, in practice they often coincide (Chis et al. 2014).

Sloppiness can be recognized by examining the spectrum eigenvalues of the Hessian matrix, sometimes called the sensitivity eigenvalues (see “Computational Methods” section for further detail) (Gutenkunst et al. 2007a). The sensitivity eigenvalues are an indirect estimate of the sensitivity of the cost function to changes in the parameter values and represents the confidence in the estimate of the parameter combination in the direction of the corresponding eigenvector. Small eigenvalues represent high uncertainties and large confidence intervals. Sloppy models have sensitivity eigenvalues that are roughly evenly spaced across three or more orders of magnitude. When the eigenvalue spectrum is this large, the smallest sensitivity eigenvalues tend to correspond to parameter combinations that have minimal effect on the model behavior—these combinations are ‘sloppy’ eigenvectors. The eigenvectors of the largest eigenvalues are referred to as ‘stiff’ and control most of the model behavior. In some models, there is a clear division between the large and small eigenvalues, usually corresponding to a clear separation in length or time scales that renders some of the physical details of the system irrelevant—for example, the kinetic models of many chemical reactions can be simplified when there is a known rate-limiting step (White et al. 2016). In sloppy models, no clear division exists, and the small eigenvalues are rarely united by a single physical phenomenon.

Since rigorously checking for structural identifiability in nonlinear models can be challenging, we tested the identifiability of our model by determining if it could recover the parameters used to generate a set of noiseless, simulated data. We found that all parameters could be recovered with acceptably high accuracy, suggesting that the model was identifiable. Here, we define acceptable accuracy to be when a parameter’s standard deviation is at least one order of magnitude smaller than value of the associated parameter. However, when we examined the effect of noise on model performance, we observed that the parameter standard deviations rise rapidly when even a small amount of noise is introduced (Fig. 3a). The error of the model predictions, on the other hand, rose relatively slowly as noise increased. This suggests that despite the high parameter uncertainties, the general behavior predicted by the model can be accurate even when it is fit using noisy data (Fig. 3b).

Fig. 3
figure 3

Comparison of parameter accuracy and mean squared error (MSE) for two different network structures at various noise levels. For the full reaction network, as the noise in the input data is increased, a the number of parameters with standard deviations within one order of magnitude of the parameter value rises rapidly compared to b the error of the model predictions. When the hydrolysis reactions are removed from the full network, the parameter estimates remain relatively precise as noise is introduced. The MSE of the model predictions are normalized to the MSE of the full network with no artificial noise (2.85e−11). All data sets used simulated experiments created from 25 different initial conditions and 125 data points. The added noise was normally distributed with a constant signal-to-noise ratio, and all negative values were set to zero to prevent negative concentrations

Full size image

Given that this behavior is typical in sloppy models, we checked the sensitivity eigenvalues for both our simulated data and experimental data (Fig. 4a, b). We found that the peptide reaction network is unambiguously sloppy, because the sensitivity eigenvalues of the simulated and experimental data span nearly nine and seven orders of magnitude respectively. To compare the behavior of the peptide reaction network with a similar model that was not sloppy, we modified the network to exclude all hydrolysis reactions (Supplementary Information 3a). Removing reversible pathways from the network eliminates many combinations of parameters that can compensate for one another, which significantly reduced sloppiness (Fig. 4c). To demonstrate that it was the modifications to the structure of the model, rather than its smaller size, that were responsible for the reduction in sloppiness, we also compared it to an even smaller network describing reversible homopolymer reactions (Supplementary Information 3b); this model was determined to have a much larger eigenvalue span (Fig. 4d). To investigate whether the grouping of some species in the peptide network was responsible for the sloppiness of the model, we also checked the sensitivity eigenvalues for a network with the trimer species separated using simulated data (Supplementary Information 3c), and found it made the eigenvalue spread larger (Fig. 4e).

Fig. 4
figure 4

Sensitivity eigenvalues for different models: (a) simulated data for the full network (22 parameters, 35 data points), (b) experimental data generated from a mixture of glycine and alanine (22 parameters, 65 data points), (c) simulated data for a variation of the main network that excludes all hydrolysis reactions (11 parameters, 35 data points), (d) simulated data for network including only one amino acid forming peptides up to tetramer length with hydrolysis reactions included (8 parameters, 35 data points), and (e) simulated data for a network with separated trimers (40 parameters, 80 data points). Each system is normalized to its largest eigenvalue (λ1). All simulated data has no additional noise included

Full size image

The parameter standard deviations were far more sensitive to noise in the full, sloppy network than in the network with no hydrolysis reactions (Fig. 3a). Despite the difference in the confidence of the parameter fits, the prediction accuracy was not significantly different between the two models until significant noise was added to the data (Fig. 3b). This demonstrates a previously mentioned key consequence of sloppy models—although they can make reasonably accurate predictions of system behavior, they should not be used to calculate the values of individual parameters, since the precision required for accurate parameter estimations cannot be experimentally realized.

Sloppiness is a common property in systems biology models, and some of the characteristics that result in sloppiness are likely shared by prebiotic chemistry systems. Reversible reactions and cyclic behaviors can increase the likelihood of sloppiness because they create situations where a particular combination of parameters (for example, the ratio between forward and reverse rates defining an equilibrium constant) is more important for describing the system behavior than the individual parameters themselves. The parameters may become ‘sloppy’ because their individual values can essentially vary freely without affecting the overall model behavior, as long changes in other parameters can compensate to produce a similar overall prediction. Reaction networks that are mostly or entirely reversible, like the peptide reaction network, can therefore become significantly more difficult to fit with high precision than models with comparable sizes, but fewer reversible reactions (Maity et al. 2020). The emergence of cycles and reversible reactions are expected to be important features in the emergence of life-like chemistry (Varfolomeev and Lushchekina 2014; Mamajanov et al. 2014). Therefore, we anticipate that sloppiness may be a common and potentially unavoidable feature of ODE models found in prebiotic chemistry, and its implications should be examined.

Consequences of Collective Fitting

Sloppy models can provide surprisingly accurate predictions despite having low confidence parameter estimates. The collective fit of all the parameters tends to be more accurate and require less data than the individual parameter uncertainties might suggest, since only the stiff parameter combinations must be constrained to achieve accurate predictions. One of the consequences of collective fitting is that the numerical values of parameters estimated for sloppy models cannot be treated as independent kinetic parameters whose quantitative values have physical meaning. Situations where a reaction occurs faster in the presence of one molecule than another are of interest to the chemical origins of life because of their semblance to catalysis. Unfortunately, in sloppy models, the numerical values of the parameters fit in each case are often not comparable. For example, even if the rate constant of one reaction in the peptide network was significantly higher than another, that is not necessarily good evidence that one reaction proceeds faster than the other. The parameters are only meaningful when the entire system is used to describe the specific environment to which they were fit. Fixing individual parameter values to reflect direct measurements or literature values can potentially break the collective fit and significantly increase the error of the prediction, often to the point that it is no longer useful. The lack of physical meaning of the individual parameter values is a significant drawback of sloppy models. However, such models can still be useful for certain tasks. For example, a sloppy model can still be used if the goal is to generate predictions about the behavior of a similar system with slightly different initial conditions, or to predict responses at longer time spans. Moreover, we highlight that sloppiness might simply be a fundamental property of the actual reaction network, that arises from inherent redundancies in the system.

To estimate the minimal data required to get relatively accurate predictions, we created at least three different subsets of the data, trained the model individually with each subset and compared their MSEs (Fig. 5). The simulated data was sampled at time intervals analogous to the experimental results, since those were the points that were physically relevant. When training the model using simulated data, increasing the amount of data used improved the model predictions up to about 40 data points, but with even 25 data points, the error was negligible compared to the experimental results. Similarly, when we repeated the process with experimental data, the average error did not decrease as more data was added beyond 25 data points.

Fig. 5
figure 5

MSE of model predictions depend on quantity of experimental and simulated data. Except for the final points, which include all applicable data, parameters were estimated for three arbitrarily selected data subsets of varying sizes, then the average MSE of those models was determined. Noise was neglected. Error bars show the standard deviation of the three subsets but are too small to be visible for the simulated data

Full size image

We also investigated the effect of using more frequent measurements, as opposed to using a greater number of simulated experiments with different initial conditions. We compared the results of simulated data with a similar number of total data points but double the usual sampling frequency to the simulated results in Fig. 5. Increasing the sampling frequency was comparable or slightly worse than including data from additional simulated initial conditions, except possibly when there is little data available overall (Supplementary Information 4). It did not improve the model’s sensitivity to noise.

Different subsets of the data with the same number of data points could have different MSEs, suggesting that some combinations of experiments may be better for parameter fitting than others. This subject will be discussed further in the section on the design of experiments (DoE). Overall, these results suggest that as few as 25–30 data points are required to fit the system as accurately as the model constraints allow; therefore, reasonably accurate predictive fits can be achieved with a realistically obtainable amount of data. The ability to extrapolate accurate model predictions from short-term experiments has some uses for studying prebiotic chemical reactions, since long time spans are potentially relevant. Models like the one we present here could be used to predict the expected equilibrium outcome of slow reactions based on data from a shorter time span and compare candidate model structures. They may also be a useful way to predict the outcomes of sequential or cyclic processes, provided that the parameters are fit in compatible experimental conditions. Sensitivity analysis can be used to validate the predictions from sloppy models independently from the parameter uncertainties (Gutenkunst et al. 2007a). Model selection, which involves comparing two or more different model structures to determine which one reflects the experimental data most accurately, can also still be performed with sloppy models (Brown and Sethna 2003). However, if finding physically meaningful terms for the parameter values is an important goal, then the aim should be to reduce the sloppiness of the model.

Model Reduction

To address high parameter uncertainty, one may seek to simplify the structure of the model, ideally without compromising the accuracy of the model predictions. This task is referred to as model reduction or network reduction, and it can be an effective way to improve overparameterized models (Apri et al. 2012; Transtrum et al. 2015). However, model reduction methods are generally based on statistical principles and not physical knowledge, and the results should be interpreted within an experimental context. The user must ensure that parameters that might be statistically problematic but are known to be physically significant are not removed from the model.

Since one of the main features of sloppy models is that they contain parameter combinations that are insensitive to changes, model reduction may initially appear to be a straightforward task for sloppy models. However, the fact that the sensitivity eigenvalues are evenly distributed over multiple orders of magnitude poses a challenge for accurate model reduction, as there is no clear cut-off between the parameter combinations that are important and those that are not. Additionally, in practice some parameters are so poorly constrained that they are randomly distributed throughout the sensitivity eigenvectors, so the components of the sensitivity eigenvectors are not entirely reliable indicators of what parameters are influencing them (Gutenkunst et al. 2007a).

We attempted model reduction with the peptide reaction network to determine if it was over-parameterized and if it might be possible to reduce the reactions considered. For example, we expected that some of the hydrolysis reactions could be ignored. Since we wanted to use a model reduction technique that is accessible and easily interpretable for experimentalists, we used sparse principal component analysis (SPCA). SPCA is an extension of principal component analysis (PCA), a popular dimensionality reduction method for linear models (Zou et al. 2006). Using SPCA, we can identify the inputs that capture most of the information in the data. It has been used successfully in control theory and gene network analysis, and there are existing implementations of it in MATLAB and Python (Ma and Dai 2011).

When SPCA was applied to the peptide reaction network, the results were highly variable and unable to adequately represent the data. SPCA frequently suggested removing reactions known to be physically significant, such as the formation of dimers from monomers (Supplementary Information 5). Not only does this not make physical sense, but because these are the initial reactions that occur in the system, removing them severely limits the pathways for longer species to form. Other methods of network reduction may be more effective for sloppy models but are less commonly used and may be more difficult to implement (Transtrum and Qiu 2012; Maiwald et al. 2016). If we choose to pursue additional model reduction efforts, one logical next step may be to inspect the inverse of the covariance matrix to identify which parameters are the most correlated and least constrained by the data (Wasserman2004). This information may be useful for determining which parameters are best to remove or to combine into a single term.

Design of Experiments

If the model structure cannot be altered, another method for reducing sloppiness is to determine if experimental data can be gathered strategically to explore the variable space more thoroughly (Apgar et al. 2010). However, to reduce parameter uncertainty, the selected experiments must provide new information not already captured in the model. Design of experiments (DoE), or experimental design, seeks to identify the experiments that would provide the most useful information for improving prediction accuracies. DoE methods such as factorial design (Fisher 1937), response surface methodology (Box and Wilson 1951), and screening (Shevlin 2017), have been widely adopted across various fields. However, there are several notable caveats in relation to sloppy models (Jagadeesan et al. 2022). First, the precision of parameter fitting for sloppy models is limited by the least accurately determined eigenvectors, so more data measured with the same uncertainty may not help. Second, there is some debate over whether DoE can be used with approximate models without risking the collective fit, as it can inadvertently place too much importance on details not included in the model (White et al. 2016).

In this work, we use a Bayesian experimental design (BED) method that selects experimental designs based on the expected reduction in parameter uncertainty as quantified by the determinant of the Fisher information matrix (FIM) (Transtrum et al. 2015; Thompson et al. 2022). To determine if there was any significant benefit obtained using DoE, we compared the reduction in parameter uncertainty from performing experiments suggested by the BED method to the reduction achieved from performing arbitrarily chosen experiments (Fig. 6). We evaluated the results using two metrics: (i) the percentage of parameters with standard deviations that were large (within an order of magnitude of the relevant parameter) to indicate the overall precision of the parameter estimates, and (ii) the MSE to indicate the accuracy of the model’s predictions.

Fig. 6
figure 6

DoE slightly improved the precision of the parameter estimates and the model prediction accuracy. a Using simulated data with 15% noise, the percentage of large parameter uncertainties (standard deviation within one order of magnitude of the parameter value) remained consistent and b the MSE did not change significantly compared to the initial tests. c Using experimental data, the percentage of large parameter uncertainties decreased slightly and d the model predictions improved relative to the initial tests but did not continue to improve as more data was added. Each round added three additional experiments, consisting of five time points measured for each experiment. For the DoE rounds, three experiments chosen from the top 20 experiments suggested by the DoE algorithm were added. For the control rounds, data from three initial conditions not included in the DoE suggestions were added (50 mM Gly, 25 mM Gly and 25 mM Ala, and 50 mM Ala)

Full size image

In our preliminary tests using simulated data with artificial noise, adding results from experiments suggested by the DoE method did not reduce the number of parameters with large standard deviations or improve the accuracy of the model predictions. This suggests that the poor precision of the parameter estimates may not be caused by poor data coverage, and is instead a consequence of the model structure. When applied to our experimental data, the addition of results suggested by the algorithm did decrease the number of parameters with large standard deviations and improved the model predictions relative to the initial tests, however, there was significantly less improvement from the second round of additional experiments than there was in the first. The simulated results suggest a limit to how much additional data can improve the parameter estimates and highlight that the model structure is responsible for sloppiness. Even after nearly doubling the amount of data included in our original tests, neither the experimental nor the simulated system ever had fewer than 60% of parameters with large standard deviations and the model predictions were essentially unchanged. Overall, it seems unlikely that continued cycles would significantly improve the parameter estimates to the extent that it would allow us to attach any physical significance to their numerical values.

Data suggested by the DoE algorithm typically had similar or better performance than the data that was added arbitrarily. However, we cannot conclude there is a significant improvement from using the DoE algorithm, because during the second round of experiments using arbitrary data produced very similar results in all cases. Concerning the experimental results, conclusively determining whether the selections of the DoE algorithm are an improvement over randomly selected conditions would require performing many additional experiments. Within the existing results, we noted that model prediction errors occasionally increased when more data was added, which can be a consequence of overfitting, however, there was no consistent trend of samples outside of the training data set having significantly higher prediction errors, suggesting overfitting is not likely (Supplementary Information 6). Because the increases in prediction error are small, they are probably an incidental consequence of the noise in the data and the limited sample size.

There are several possible reasons why DoE did not consistently improve the precision of the parameter estimates this model. The precision of a sloppy model is limited by the most variable parts, so experimental noise may be preventing key features from being determined more precisely (Gutenkunst et al. 2007a). The prescribed range of initial conditions may have also been too restrictive. We only included initial conditions with various concentrations of monomers because amino acids and peptides can participate in different reaction mechanisms with TP. Since these mechanisms were not being explicitly separated in the model, initial conditions with large concentrations of peptides could have inadvertently led to measuring the parameters for a different reaction mechanism. Rather than risk measuring the kinetics of a different mechanism, which would undermine the assumption that each experiment had the same kinetic parameter value, we chose to use a more limited system definition. However, this also may have limited our ability to constrain some parts of the network. Finally, as DoE methods are statistically based approaches that rely on existing results, they can be sensitive to noise in the data. As a result, it may be difficult to predict how parameter uncertainties will change as additional data is added. Therefore, because sloppy networks tend to be better at producing accurate predictions than accurate parameter estimates, approaches that aim to improve predictions rather than parameter uncertainties may be more useful.

Model Limitations

The mass-action style model used here is a significant simplification of the reactions occurring in the actual experimental system. TP-activated peptide bond formation involves not only multiple intermediates but likely multiple reaction mechanisms, which were not fully described in this model (Boigenzahn and Yin 2022). Certain products, like the cyclic dimers 2,5-diketopiperazine were not detectable or quantifiable in our analysis. Merging the isomeric peptide species also may have increased the experimental error slightly, since not all isomers have the same absorbance. However, on average, the species balances of glycine and alanine were about 90% accurate, suggesting that any products missed by our analysis were probably not dominant products in the system. While we acknowledge the simplifications and sources of noise in our experiments, it is important to note that the model generated high parameter standard deviations when extremely small amounts of noise were added to simulated data. It may not be possible to fit the current version of the peptide network with high precision from experimental data.

It might be possible to alleviate sloppiness by replacing the generic reversible reactions in this model with more detailed descriptions and measurements of intermediates. However, this would significantly increase the resources needed for experimental and statistical analysis. Additionally, this model does not account for increasing concentration of all species as the sample dries. The volume could be included as a dynamic term in the network model, but it complicates parameter estimation because of the infinite limits that occur as the volume approaches zero. There are also potential reactions that occur almost exclusively in the solid phase (Napier and Yin 2006). We chose to neglect any concentration effects or details of the TP reaction mechanism and instead explored the feasibility of creating a model that predicted overall peptide production.

Conclusion

Although we were able to fit kinetic parameters to the peptide reaction network in our simulated tests, in practice the parameter estimations were poorly constrained due to sloppiness. Neither network reduction nor statistical design of experiments were particularly successful for reducing sloppiness or improving the precision of the parameter estimates for this example. Sloppiness precludes us from drawing any physical conclusions based on the individual values of the parameters estimated in these models, but this approach is still an effective way to make model predictions based on relatively few time points. The predictive capacity of the model may be useful for forming hypotheses about the behavior of systems that pass through multiple conditions sequentially, or simply estimating equilibrium conditions based on short-term experiments.

Our goal was not only to explore the kinetics of these specific reactions, but to evaluate the potential challenges and opportunities of applying mathematical tools, which were originally developed for biological networks to prebiotic chemical systems. Sloppiness is a challenge when studying the kinetics of complex nonlinear system models but may be an interesting property in the broader context of the chemical origins of life; sloppiness has been suggested as a possible non-adaptive explanation for the robustness of many multiparameter biological systems (Daniels et al. 2008). This idea suggests that many complex networks, ranging from those found in biology to those that are randomly generated, have similar behavior across large areas of the parameter space. This implies that robustness, in this case a reaction network’s ability to achieve similar outcomes despite variation in its parameter values, can emerge from complexity even when it is not specifically selected for. The feature of intrinsic robustness in sufficiently large multiparameter networks observed in deep neural networks, which can be dramatically complex but highly accurate, and is an open area of investigation in the machine learning community (Belkin et al. 2019). As a result, there is a significant incentive to work toward studying more complex experimental origins of life systems.

Adapting systems biology tools to study complex origins of life experiments lends itself to an interdisciplinary approach, since many methods can be difficult to implement or even approach without expert assistance. Demonstrative studies like this one can improve experimentalists’ understanding of what data analysis approaches are available, what their limitations are, and what results they can provide. We hope that using computational networks to analyze experiments will become more commonplace and enable the study of more complex origins of life reaction networks.

Computational Methods

The usefulness of a parametric model is limited by our ability to accurately determine the values of the corresponding parameters. A large body of work has detailed various parameter fitting or regression techniques that can be used to build these models (Bard 1974). The most popular parameter estimation method is maximum likelihood estimation (MLE). In MLE, the noise from experimental measurements \(\left(\epsilon \right)\) is treated as a random variable that captures the error between the model predictions and the observed output values:

$$\begin{array}{c}y=m\left(X;{\varvec{\theta}}\right)+\epsilon \end{array}$$
(1)

where \(\epsilon \in {\mathbb{R}}^{S}\), \(S\) is the number of observations (measurements) available, \(m\) is the model and \({\varvec{\theta}}\in {\mathbb{R}}^{n}\) are its \(n\) parameters. The set of output observations is stored in the vector \(y\in {\mathbb{R}}^{S}\), and \(X\in {\mathbb{R}}^{S\times K}\), known as the design or feature matrix, is structured so that the sth row corresponds to the sth observation, \({\mathbf{x}}_{s}\), and the kth column corresponds to the kth input variable \({x}_{k}\). Combining MLE’s assumption that \({\varvec{\theta}}\) and \(X\) are deterministic variables with the most common noise model, the Gaussian or normal distribution (\(\left(\epsilon \sim \mathcal{N}\left(0,\Sigma \right)\right)\), where \(\Sigma\) is the covariance of the noise) allows us to exploit the fact that the sum of normal distributions is also a normal distribution. We can use this to calculate the distribution for the observations vector, \(y\sim \mathcal{N}\left(m\left(X,{\varvec{\theta}}\right),\Sigma \right)\). The goal of MLE is then to find the values of \({\varvec{\theta}}\) that best account for the experimental observations, or the values for \({\varvec{\theta}}\) that best parameterize this output distribution. This is done by determining the values that maximize the log-likelihood function, \(L({\varvec{\theta}})\):

$$\begin{array}{c}{{\varvec{\theta}}}^{*}=\underset{{\varvec{\theta}}}{\mathrm{argmax }}\,L(\theta )=\underset{{\varvec{\theta}}}{\mathrm{argmax}}\,\mathrm{log}f\left({\varvec{y}}|X,{\varvec{\theta}},\Sigma \right)\end{array}$$
(2)

where \(f\left( {\left. {\mathbf{y}} \right|X, {\varvec{\theta}},{\Sigma }} \right)\) is the likelihood (or conditional probability) that the outputs in \(\mathbf{y}\) would be observed given values for \(X\), \({\varvec{\theta}}\), and \(\Sigma\). For the given distribution of \(\mathbf{y}\):

$$\begin{array}{c}f\left(\mathbf{y}|X,{\varvec{\theta}},\Sigma \right)=\left({\left(2\pi \right)}^{-\frac{S}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}}\right)\mathrm{exp}\left(-\frac{1}{2}{\left({\varvec{y}}-m\left(X;{\varvec{\theta}}\right)\right)}^{T}{\Sigma }^{-1}\left({\varvec{y}}-m\left(X;{\varvec{\theta}}\right)\right)\right)\end{array}$$
(3)

The well-known ordinary least squares regression problem is a special case of MLE where the model is linear and \(\Sigma\) is a diagonal matrix composed of identical values \(({\sigma }^{2})\).

A common issue with MLE is that \((2)\) can have multiple solutions (\(L({\varvec{\theta}})\) is nonconvex), as is often the case with nonlinear models. However, some of these solutions may contain parameter values that are not physically sensible, making the solution invalid. One way to overcome this limitation is to shift the goal of \((2)\) from maximizing the probability of measuring the observed outputs given a set of parameters to maximizing the probability of a set of parameters being correct given a set of observations. Mathematically, this is done using Bayes’ theorem, \(f\left( {\left. {\varvec{\theta}} \right|{\mathbf{y}}} \right) \propto f\left( {\left. {\mathbf{y}} \right|{\varvec{\theta}}} \right)f\left( {\varvec{\theta}} \right)\), and changes the likelihood function to:

$$\begin{array}{c}{{\varvec{\theta}}}^{\boldsymbol{*}}=\underset{{\varvec{\theta}}}{\mathrm{argmax}}\,\mathrm{log}f\left(\mathbf{y}|X,{\varvec{\theta}},\Sigma \right)+\mathrm{log}f\left({\varvec{\theta}}\right)\end{array}$$
(4)

where now we no longer assume that \({\varvec{\theta}}\) is deterministic but instead has some distribution (e.g., \({\varvec{\theta}}\sim \mathcal{N}(\overline{{\varvec{\theta}} }, {\Sigma }_{{\varvec{\theta}}})\)) that is captured by the prior \(f({\varvec{\theta}})\). This term can be used to input any prior knowledge or expectation one might have over the values of the model parameters (e.g., must have a certain sign, lay within a specified range) and thereby constrain the search to values of \({\varvec{\theta}}\) that satisfy the desired criteria. If \(\mathbf{y}\) and \({\varvec{\theta}}\) are normally distributed, then \((4)\) can be expressed as:

$${\varvec{\theta}}^{\varvec{*}} = \mathop {{\text{argmin}}}\limits_{{\varvec{\theta}}} \frac{1}{2}\left( {{\mathbf{y}} - m\left( {X;\,{\varvec{\theta}}} \right)} \right)^{T} {\Sigma }^{ - 1} \left( {{\mathbf{y}} - m\left( {X;\,{\varvec{\theta}}} \right)} \right) + \frac{1}{2}\left( {{\varvec{\theta}} - \overline{\varvec{\theta }}} \right)^{T} {\Sigma }_{\theta }^{ - 1} \left( {{\varvec{\theta}} - \overline{\varvec{\theta }}} \right)$$
(5)

Note that the first term will be minimized when the model predictions exactly match the output observations, while the second term will be minimized when θ = \(\overline{{\varvec{\theta}} }\). To perform the optimization of model parameters, we use the L-BFGS-B algorithm from SciPy’s minimize function with a tolerance for termination of 1e−3. As a result, Bayes’ estimation seeks to balance the fit of the model with the prior knowledge over the parameters that is available. We use an Expectation–Maximization (EM) algorithm to determine the covariance matrix of the measurement noise and the parameter prior that maximizes the model evidence (Thompson et al. 2022).

Due to the randomness in \(\mathbf{y}\), the selected parameters \({{\varvec{\theta}}}^{\boldsymbol{*}}\) will exhibit an inherent uncertainty that is determined by how well the estimates are constrained by experimental data. The parameter uncertainty is largely controlled by the model structure as well as the quality and quantity of the available data. If a model is selected where certain inputs are not strong predictors of the outputs or are dependent on other inputs, or if the dataset is too small or contains redundant samples, then \({{\varvec{\theta}}}^{\boldsymbol{*}}\) will be imprecise. This is a major issue as it can lead to overfitting, where \(m\) is not able to make accurate predictions at values of \(x\) that are outside of the dataset.

An estimate of the parameter uncertainty can be obtained from the eigenvalues of the Hessian matrix, \(\mathcal{H}(\mathbf{y};{\varvec{\theta}})\), also known as the Fisher information matrix (FIM) in the context of parameter estimation, which is defined as:

$$\begin{array}{c}{\mathcal{H}}_{i, j}=\frac{{\partial }^{2}L}{\partial {\theta }_{i}\partial {\theta }_{j}}\end{array}$$
(6)

The eigenvalues of the Hessian serve as an estimate of data sufficiency. From calculus we know that the second derivative of a function, f″, determines if a critical point \(\left(f{\prime}=0\right)\) is a maximum \(\left(f{\prime}{\prime}<0\right)\), a minimum \(\left(f{\prime}{\prime}>0\right)\), or an inflection point \(\left(f{\prime}{\prime}=0\right)\), which could be either a minimum, a maximum, or neither. Additionally, we can also estimate how sharp or defined an extremum is from the value of f″. As a result, we can use \(\mathcal{H}\left(\mathbf{y};{\varvec{\theta}}\right)\) to gauge the quality of the obtained solution. For example, if all the eigenvalues of \(\mathcal{H}\left(\mathbf{y};{\varvec{\theta}}\right)\) are large and positive \(\left(\gg 0\right)\), this implies that \({{\varvec{\theta}}}^{*}\) sits in a well-defined minimum and provides a precise estimate of the parameters. If all the eigenvalues are positive and one or more are small \(\left(\ll 1\right)\), then the minimum is not sharp, and the parameter estimates will be ill-defined and exhibit high variability. Finally, if \(\mathcal{H}\left(\mathbf{y};{\varvec{\theta}}\right)\) has any eigenvalues equal to zero, then \({{\varvec{\theta}}}^{*}\) lays on a flat surface and cannot be uniquely estimated from the data; in other words, \({{\varvec{\theta}}}^{*}\) has infinite variability.

If the precision of \({{\varvec{\theta}}}^{*}\) is deemed to be too low, there are two methods that can be used to improve the quality of the estimates. The first, known as system identification, involves the structure of the model and the selection of the input variables. We can determine the relative importance of the input variables using a feature importance technique such as automatic relevance determination (ARD), or model class reliance (MCR), or as used in this paper, sparse principal component analysis (SPCA) (Zou et al. 2006). This information can then be used to restructure m to eliminate any redundant inputs.

If system identification is not able to reduce the uncertainty of the parameter estimates to a desired level, a second approach is to collect additional data. However, the data must provide additional information beyond what is already contained in the current dataset to have any chance of improving the parameter estimates. One way to achieve this is by using a design of experiments (DoE) algorithm to select experiments that have a maximal value. Depending on the goal of the experiments (optimization, discovery, or both), their value can be measured by the information content they provide or by their predicted proximity to a desired set of properties. There is a rich variety of DoE algorithms to select from such as response surface methodology (RSM), screening, factorial design (Fisher 1937; Box and Wilson 1951; Shevlin 2017). A common metric to evaluate the optimality of candidate experimental designs is the determinant of the FIM. For any candidate experimental design, \(X\), the FIM is computed as

$$\begin{array}{c}{\mathcal{H}}_{i,j} =\frac{{\partial }^{2}L}{\partial {\theta }_{i}\partial {\theta }_{j}}={\Sigma }_{{\theta }_{i,j}}^{-1}+\frac{\partial m\left(X,{\varvec{\theta}}\right)}{\partial {\theta }_{i}}{\Sigma }^{-1}\frac{\partial m\left(X,{\varvec{\theta}}\right)}{\partial {\theta }_{j}}\end{array}$$
(7)

where evaluations of the gradient with respect to model parameters is computed using the forward sensitivity equations (Ma et al. 2021).

While DoE can be very useful for improving parameter uncertainties, there are several challenges. Calculating the expected information gain (EIG) can be time consuming due to the number of operations that need to be performed for larger systems. As a result, obtaining a new batch of experiments can easily take on the order of hours depending on the size of the dataset and the number of parameters involved. Even for moderately sized models, the quantity or precision of an experimental system may not be sufficient for accurate predictions of the information generated by each experiment to be made in the first place, or the experiments that would provide the information may not be feasible in reality. Both cases seriously hinder the effectiveness of DoE methods.

Selection of experiments for the DoE method was performed as in Thompson et al. (2022). Experimental data was normalized using linear scaling to ensure that the concentration values for each species spanned \(\left[\mathrm{0,1}\right]\). Scaling the data ensures that low abundance species still affect the parameter fits, which was necessary since the experimental results span several orders of magnitude. Parameters values were limited to \(\left[\mathrm{0,10}\right]\) for simplicity, though we found that raising the upper bound had no effect if the initial guesses were single digit. Negative values had no physical meaning since both directions of the reversible reactions were already included. All computational methods were performed using Python 3.2.2. We used automatic differentiation in PyTorch to calculate the gradients of the loss function and SciPy to solve the initial value problems. Relevant code is available at https://github.com/haboigenzahn/OoL-KineticParameterEstimation.

Simulated data for testing was generated in Python 3.2.2 using SciPy 1.7.1 solve_ivp. The parameters for the simulated data were loosely based on the parameter fits of the experimental data but were rounded to integers (Supplementary Information 7). Network figures were generated using Cytoscape 3.7.2 (Shannon et al. 1971).

Experimental Materials & Methods

All chemicals were of analytical grade purity and used without further purification. Materials were obtained from suppliers as follows: trisodium trimetaphosphate (TP) and trifloroacetic acid (TFA) from Sigma-Aldrich, sodium hydroxide from Fisher Scientific, acetone from Alfa Aesar, 9-fluorenylmethoxycarbonyl chloride (FMOC) from Creosalus, acetonitrile from VWR Chemicals, and sodium tetraborate anhydrous from Acros Organics. Reactions were carried out in 1.5 mL low-retention Eppendorf tubes. Peptide standards came from various sources: glycine, diglycine, triglycine, pentaglycine, dialanine and Ala-Gly from Sigma-Aldrich, tetraglycine from Bachem, Gly-Gly-Ala from Chem-Impex International, Ala-Gly-Gly from ChemCruz, Ala-Ala-Gly from Pepmic, and Gly-Ala-Gly, Gly-Ala-Ala, Ala-Gly-Ala and trialanine from Biomatik.

Samples were prepared with 0.15 M NaOH, various concentrations of glycine and alanine, and TP in equimolar concentration to the total amount of amino acid. Details of the initial conditions chosen are included in the supplemental information (Supplementary Information 8). Samples were placed on a heat block preheated to 90 °C with the caps open and allowed to dry for 24 h. At the end of each day of drying, samples were rehydrated with 1000 μL milliQ water preheated to about 65 °C, capped and vortexed (Pulsing Vortex Mixer, Fisher Scientific) 3000 rpm until everything was dissolved, which took 1–3 min per sample.

To analyze the samples with UV-HPLC, they were first derivatized using FMOC, which increases the retention time and signal strength of peptide analytes. For the FMOC derivatization, 25 μL of sample was diluted with 75 μL milliQ water to put the large monomer peaks in a quantifiable range. Each sample was then mixed with 100 μL 0.1 M sodium tetraborate buffer for pH control. Finally, 800 μL 3.125 mM FMOC dissolved in acetone was added to each sample. For a sample of 0.1 M amino acid, this results in an equal concentration of FMOC and amino acid, and a slight excess of FMOC in any samples where peptide bond formation had occurred. Linear calibration curves were determined for all species using this approach (Supplementary Information 9), which were used to estimate peptide concentration based on the integrated absorbance values of the HPLC peaks of the samples.

Samples were analyzed with a Shimadzu Nexera HPLC with a C-18 column (Phenomenex Aeris XB-C18, 150 mm × 4.6 mm, 3.6 μL). Products were measured at 254 nm. UV-HPLC analysis was performed using Solvent A: milliQ water with 0.01% v/v trifluoroacetic acid (TFA) and Solvent B: acetonitrile with 0.01% v/v TFA. The following gradient was used: 0–4 min, 30% B, 4–12 min, 30–100% B, 14–15 min, 100–30% B, 15–17 min, 30% B. The solvent flow rate was 1 mL/min. Peak integration was performed using LabSolutions with the ‘Drift’ parameter set to 10,000.