Computational Models of Polymer Synthesis Driven by Dehydration/Rehydration Cycles: Repurination in Simulated Hydrothermal Fields

Abstract

Cycles of biologically relevant reactions are an alternative to an origin of life emerging from a steady state away from equilibrium. The cycles involve a rate at which polymers are synthesized and accumulate in microscopic compartments called protocells, and two rates in which monomers and polymers are chemically degraded by hydrolytic reactions. Recent experiments have demonstrated that polymers are synthesized from mononucleotides and accumulate during cycles of hydration and dehydration, which means that the rate of polymer synthesis during the dehydrated phase of the cycle is balanced (but not dominated) by the rate of polymer hydrolysis during the hydrated phase of the cycle. Furthermore, depurination must be balanced by the reverse process of repurination. Here we describe a computational model that was inspired by experimental results, can be generalized to accommodate other reaction parameters, and has qualitative predictive power.

Introduction

The process by which life can begin on a habitable planet such as the early Earth remains a fundamental question of biology. A basic function of life is nucleic acid synthesis and replication of genetic information. Therefore, understanding the origin of life must also include a mechanism by which the first nucleic acids were synthesized. Because ribozymes can serve both as catalysts and to store and use genetic information, there is a consensus that the most primitive forms of life used RNA, while DNA and proteins became incorporated at a later stage of evolution.

Previous studies have demonstrated that RNA-like polymers can be synthesized non-enzymatically from mononucleotides such as adenosine monophosphate and uridine monophosphate (UMP). The conditions used are simulations of wet–dry cycles that commonly occur in fresh water pools and hot springs associated with volcanic land masses (Rajamani et al. 2008; Damer and Deamer 2015). The products range from 10 to $>100$ nucleotides in length with linking phosphoester bonds. The chemical potential driving polymerization is provided by the concentration of reactants and reduction of water activity during dehydration (Ross and Deamer 2016). Agents such as monovalent salts promote the polymerization (Da Silva et al. 2015) and if lipids are present the polymers become encapsulated in cell-sized vesicles called protocells (DeGuzman et al. 2014). The polymers are not synthesized in a single step, but instead accumulate up to a steady state during multiple cycles, which means that polymer synthesis during dehydration must be balanced by hydrolysis during hydration.

However, the same conditions that drive synthesis of polymers can also cause decomposition reactions. For instance, hydrolytic depurination is well known to damage DNA (Lindahl 1993). Lorig-Roach and Deamer (2018) reported depurination rates of adenosine monophosphate (AMP) undergoing polymerization in simulated prebiotic conditions. Pearce et al. (2017) performed a computational analysis of the fate of adenine in hydrothermal pools on prebiotic land masses. Adenine is a component of ribonucleic acid, and their approach assumed a synthetic reaction by which adenine could be incorporated into RNA, a process that would require synthesis of the N glycoside bonds between the purine base and ribose phosphate. Although this bond has been previously considered to be difficult to produce, Nam et al. (2018) recently reported a facile reaction occurring in microdroplets that synthesized nucleosides from four different nucleobases including adenine.

Here we analyze a proposed synthesis by wet–dry cycling that takes into account condensation reactions by which phosphoester bonds link nucleotides into RNA, hydrolysis rates that break the bonds, depurination rates in which adenine is lost from the monomers or polymers, and a hypothetical repurination rate that restores the adenine. Given certain assumed rates, we show that RNA synthesis is feasible but that repurination is essential to avoid collapse of the system.

In proposing our own computational models of prebiotic polymer synthesis, it is important to take stock and review previous efforts in this field while highlighting the ways in which our model differs. Ma et al. (2007a) produced a Monte Carlo simulation of the evolution of prebiotic RNA molecules which assumed the existence of primordial RNA replicases. Ma et al. (2007b, 2011) simulated the development of RNA replicases and the self-replication of RNA. By contrast, our model takes a linear algebraic approach as opposed to a Monte Carlo approach and does not assume the existence of primordial enzymes. Our simulation models the origins of terrestrial RNA rather than the subsequent evolution, self-replication, and propagation of functional polymers. Furthermore, these alternative models do not consider cyclic reactions, which is perhaps the most striking difference between our model and theirs. Walker et al. (2012) concern themselves with precisely the sort of cyclic reactions manifest in our model. They, however, also use a Monte Carlo approach and are largely focused on the development of functional polymers. Perhaps the most similar model to ours can be found in Higgs (2016) in which theoretical features of cyclic reactions are analyzed. This model also uses Monte Carlo methods to simulate the dynamics of polymer accumulation. Compared to these alternative models, ours may appear quite simple. That being said, the simplicity of our model allows the exploration of such phenomena as the repurination of nucleotides.

Methods

The reactions we will model can be described as a steady state between rates of condensation and hydrolysis reactions:

$${\text{Monomers}} \leftrightarrow {\text{polymers}} + {\text{H}}_{2} {\text{O}}.$$

More specifically, we are modeling the polymerization and hydrolysis of mononucleotides and ribonucleic acid:

$${\text{n}}\left( {{\text{Mononucleotides}}} \right)\left( {{\text{AMP UMP GMP CMP}}} \right) \leftrightarrow {\text{ribonucleic acid}} + {\text{nH}}_{2} {\text{O}},$$

where AMP, UMP, GMP, and CMP are standard abbreviations for AMP, UMP, guanosine monophosphate, and cytidine monophosphate, respectively. In biological RNA, the mononucleotides are linked by 3′–5′ phosphodiester bonds between the ribose groups on neighboring mononucleotides. It is important to note that when such links are formed by non-enzymatic reactions, 2′–5′ phosphodiester bonds can also form, so the polymers in the computational model are best described as RNA-like molecules.

The second reaction that is to be modeled is depurination of the purine nucleotides AMP and GMP, which is also a hydrolysis reaction. For example,

$${\text{AMP }}({\text{adenosine monophosphate}}) + {\text{H}}_{2} {\text{O}} \leftrightarrow {\text{adenine}} + {\text{ribose phosphate}}.$$

Depurination is a spontaneous process that occurs in the RNA and DNA of living cells, but is continuously repaired by specialized enzymes. In the prebiotic chemistry leading to the origin of cellular life, repair enzymes were absent, so depurination has the potential to affect nucleotides as well as nucleic acids that might be synthesized by polymerization of nucleotides.

In order to investigate polymer synthesis caused by wet–dry cycles in hydrothermal fields, we constructed a computational model of the process informed by laboratory results. The model incorporates rates of synthesis during each cycle, and rates of two decomposition reactions: breakage of phosphoester linkages by hydrolysis and depurination of monomers as well as polymers. The model was conceived analytically and was implemented computationally in MATLAB. The MATLAB scripts were developed using data from laboratory simulations of RNA synthesis in hydrothermal fields; the underlying algorithm is sufficiently general to model the synthesis and approach to a steady state of any mixture of monomers and polymers by furnishing the code with appropriate constants.

Preliminary attempts to model systems of monomers and polymers undergoing synthesis and decomposition reactions incorporated nested summations and binomial expansions, which made them difficult to code. For this reason, the mathematical structures reported here have been simplified into matrix formats. Specifically, we have used Kirchhoff loops to provide novel insights into the interplay between condensation reactions and decomposition reactions. By creating two variables, $M_0$ for the initial mass of monomers, and $P_0$ for the initial mass of polymers in a reacting system, the initial state of the reactants of the system can be stored in a column vector $s_0$ defined as follows:

$$s_{0} \equiv \left[ {\begin{array}{*{20}c} {P_{0} } \\ {M_{0} } \\ \end{array} } \right].$$

(1)

This vector acts as a “box” which stores all the pertinent information about the initial system.

A transformation matrix C then describes the transformation of the system caused by the chemical processes that occur in one cycle of hydration and dehydration.

$$ C \equiv \left[ {\begin{array}{*{20}c} {1 - h - d_{{\text{p}}} } & m \\ h & {1 - m - d_{{\text{m}}} } \\ \end{array} } \right]. $$

(2)

In this matrix, h is the percentage of polymer mass converted back into monomer mass via hydrolysis per cycle, m is the percentage of monomer mass converted into polymer mass via dehydration synthesis per cycle, $d_{\text{m}}$ is the percentage of monomer mass depurinated per cycle, and $d_{\text{p}}$ is the percentage of polymer mass depurinated per cycle. An important note is that h does not keep track of all hydrolysis reactions that take place on a given polymer, but instead keeps track of just the hydrolysis reactions that cut a polymer of length n into a polymer of length $n - k$ along with k monomers. Similarly, m does not keep track of all forms of polymerization but instead only those polymerization reactions that result in k monomers binding to a polymer of length n to form a polymer of length $n+k$. These are the specific classes of hydrolysis and polymerization reactions that cause a variance in the mass of polymer and monomer present in the system.

Operating on the state vector $s_0$ with the transformation matrix C gives the state vector $s_1$ which contains the mass values of polymers and monomers present in the system after the system has undergone one cycle of hydration and dehydration ($P_1$ and $M_1,$ respectively).

$$\begin{aligned} Cs_0 = \begin{bmatrix} 1 - h - d_p&m \\ h&1 - m - d_m \\ \end{bmatrix} \begin{bmatrix} P_0 \\ M_0 \\ \end{bmatrix} = \begin{bmatrix} P_1 \\ M_1 \\ \end{bmatrix} = s_1 \end{aligned}.$$

(3)

By iteratively multiplying $s_0$ by C, new state vectors are generated that contain the mass values of polymers and monomers at any given “cycle count” n ($P_n$ and $M_n,$ respectively). That is, by applying the transformation C an n number of times, we can find the amount of polymer and monomer mass in the system after an n number of cycles.

$$C^{n} s_{0} = \left[ {\begin{array}{*{20}c} {1 - h - d_{{\text{p}}} } & m \\ h & {1 - m - d_{{\text{m}}} } \\ \end{array} } \right]^{n} \left[ {\begin{array}{*{20}c} {P_{0} } \\ {M_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {P_{n} } \\ {M_{n} } \\ \end{array} } \right] = s_{n}.$$

(4)

Note that without the presence of $d_{\text{m}}$ and $d_{\text{p}}$, the column elements in each column of the matrix C sum to unity. This is a property of systems in which some quantity (in this case mass M) is conserved. A common application of this principle is the conservation of current in circuit loops where it is total charge that is conserved instead of mass. The $d_{\text{m}}$ and $d_{\text{p}}$ terms were added to account for depurination, which are chemical reactions that cause the system to fail to conserve mass. It is this failure of the system to conserve mass that will lead to a sharp decline in the mass of polymer in the system when depurination is accounted for.

In the interest of clarity and transparency, we have stated our underlying assumptions below:

• A reaction synthesizes AMP from adenine supplied by interplanetary dust particles or meteorites (Pearce et al. 2017).

• AMP can be polymerized by a condensation reaction driven by the free energy of wet/dry cycling.

• Depurination of AMP or its polymers is a hydrolysis reaction that reaches a steady state with repurination.

Results

We will now develop the matrix C step-by-step in order to account for all the chemical processes described above in such a way that the qualitative predictions made by our model are consistent with experimental observations. The computationally generated results that accompany the development of C reveal kinetic insights related to the chemical reaction.

Dehydration Synthesis of Polymers

First, consider the rate of phosphodiester bond synthesis by condensation. Such a consideration requires the introduction of the factor m in the matrix, where m is the fraction of monomer mass converted into polymer mass per cycle. This yields the proto-matrix $C_{\text{p}}$ which accounts only for polymer accumulation via polymerization.

$$C_{\text{p}} = \left[ {\begin{array}{*{20}c} 1 & m \\ 0 & {1 - m} \\ \end{array} } \right].$$

(5)

Figure 1a shows $s_0$ iteratively multiplied by $C_{\text{p}}$ and plotted for several thousand cycles, which far exceeds what is possible in laboratory simulations but may be pertinent to geological time scales on the early Earth.

Fig. 1

a Shows the accumulation of polymer mass using the initial conditions $m = 0.001$, $M_0 = 100$, and $P_0 = 0$. b Shows the result when both synthesis and hydrolysis rates are included in the matrix, the mass value of polymers and monomers asymptotically approach a steady state with new values. Initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$, and $h = 0.00012$. Once hydrolysis is taken into account, polymer yield is decreased from $100\%$ to some lower value determined by the value of h, the proportion of polymer converted to monomer per cycle

It is obvious that if only polymer synthesis is taken into consideration, all of the mass in the system must eventually appear as polymers, so that the mass of polymers asymptotically approaches 100 (the initial quantity of monomer $M_0$) while the mass of monomers asymptotically approaches 0.

Hydrolysis

We now incorporate the hydrolysis of polymers back into monomers. To model hydrolysis, we place the factor h into the matrix, where h is the fraction of polymer mass converted back into monomer mass per cycle via hydrolysis. This yields the proto-matrix $C_h$ where $C_h$ accounts for both polymerization and hydrolysis.

$$C_{h} = \left[ {\begin{array}{*{20}c} {1 - h} & m \\ h & {1 - m} \\ \end{array} } \right].$$

(6)

Figure 1b shows that the system approaches a steady state in which the rates of synthesis applied over the course of the dehydrated phase of the cycle and the rate of hydrolysis applied over the hydrated phase of the cycle are equal.

Depurination

The monomers of nucleic acids are not indefinitely stable, and two of the most significant decomposition reactions are depurination and deamination, both of which have the effect of removing monomers as potential reactants. Here we model depurination as an example, but other degradative reactions could also be incorporated in the model. Depurination was incorporated as shown in the equation below, and its effect on monomer and polymer mass is illustrated in Fig. 2a, b.

$$C = \left[ {\begin{array}{*{20}c} {1 - h - d_{{\text{p}}} } & m \\ h & {1 - m - d_{{\text{m}}} } \\ \end{array} } \right],$$

(7)

where C accounts for polymer build-up and break-down as well as monomer depurination and polymer depurination.

Fig. 2

a Shows that depurination dramatically reduced polymer yield. Initial conditions: $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, $d_{\text{p}} = 0$ , and $d_{\text{m}} = 0.12$. b Shows that at a certain depurination rate, a small amount of polymer is still synthesized in the initial cycles. However, monomer mass is rapidly reduced to near zero a short time later, after which point polymer mass is slowly lost to hydrolysis. Initial conditions: $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, $d_{\text{p}} = 0$, and $d_{\text{m}} = 0.12$. Note that this figure does not take into account depurination of polymers

For a small number of cycles (Fig. 2a), the system asymptotically approached a minimum polymer mass with a yield < 2%. Figure 2b shows the same reaction coordinates when the number of cycles was increased to 5000, and it is obvious that depurination ultimately leads to collapse of the system as hydrolysis of the accumulated polymers forms monomers. Depurination then degrades the monomers into products that cannot undergo polymerization.

Splitting the Matrix

In the initial modeling exercise, one matrix was sufficient to express the outcome in both wet and dry phases of the cycle. However, hydrolysis and depurination only occur when the system is in the wet phase, and dehydration synthesis only happens when the system is in the dry phase. For this reason, the matrix was split into two matrices: a wet matrix which models chemical reactions during the hydrated phase of the cycle (referred to as W) and a dry matrix which models chemical reactions during the dehydrated phase of the cycle (referred to as D):

$$D = \left[ {\begin{array}{*{20}c} 1 & m \\ 0 & {1 - m} \\ \end{array} } \right]$$

(8)

$$W = \left[ {\begin{array}{*{20}c} {1 - h - d_{{\text{p}}} } & 0 \\ h & {1 - d_{{\text{m}}} } \\ \end{array} } \right]$$

(9)

$$DWs_{n} = s_{{n + 1}}.$$

(10)

The model now multiplies the state vector $s_n$ by the W matrix, uses the transformed values of $s_n$ as coordinates for a data point placed on the output graph, multiplies the once-transformed $s_n$ vector by the D matrix, and then uses the now twice-transformed values of $s_n$ (denoted as $s_{n+1}$) as coordinates for a new data point on the same graph. Using this notation, the vector $s_n$ denotes the value of $s_0$ after n such cycles of wet and dry matrices have been applied to $s_0$. The program was also modified to incorporate the time intervals used in experimental systems, estimated to be 2 min in the wet phase and 30 min in the dry phase (Da Silva et al. 2015; DeGuzman et al. 2014).¹ The values of the s vector are now plotted against time instead of cycle count. Figure 3a, b shows how splitting the matrix affects the previous iterations of the matrix shown in Fig. 1a, b.

From a distance, the graphs produced by the split matrices W and D are qualitatively the same as those produced by the single unsplit matrix C. Closer inspection, however, reveals oscillations in the polymer and monomer mass of the system caused by the cycles of polymer accumulation in the dry phase and polymer hydrolysis in the wet phase.

Figure 3c shows a closer view of the data given in Fig. 3b. The discrete values of the model now undergo micro-oscillations depending on the state of each cycle. The amount of polymer goes up slightly in the dry phase and decreases in the wet phase, then up even more in subsequent dry phase. As a corollary, the monomer mass decreases in the dry phase, increases in the wet phase, and decreases further in the subsequent dry phase. Depurination in the context of the split system has the same effect as depurination in the context of the non-split system, leading to a total collapse of polymer mass (Fig. 3d).

Fig. 3

a Reaction time in a $1.5 \times 10^{4}$ cycle simulation of polymer synthesis absent hydrolysis. Initial conditions $m = 0.001$, $M_0 = 100$ , and $P_0 = 0$. b Steady state mass in a $1.5 \times 10^4$ cycle simulation that includes both polymer synthesis and hydrolysis. Initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$ , and $h = 0.00012$. c A magnified scale of the split matrix hydrolysis graph showing the discrete changes introduced by the distinct wet and dry phases. d Steady state mass in a 100-cycle simulation that includes depurination along with polymer synthesis and hydrolysis. Initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, and $d_{\text{m}} = 0.12$

Repurination

No matter how slowly depurination occurs, the system will ultimately collapse due to loss of monomer. For this reason, we will assume that there was a process of repurination. Modeling repurination requires the doubling of the dimension of the wet and dry matrices W and D as well as the state vector $s_n$ in order to keep track of the amount of degraded monomer $\mu _n$ as well as the amount of degraded polymer $\pi _n$ present in the system after an n number of cycles.

$$s_{n} = \left[ {\begin{array}{*{20}c} {\pi _{n} } \\ {P_{n} } \\ {M_{n} } \\ {\mu _{n} } \\ \end{array} } \right]$$

(11)

For D we introduce a new variable $r_{\text{m}}$ to represent the monomer repurination rate, that is, the percentage of degraded monomer $\mu$ that gets converted back into monomer M during every dry phase. We also define the variable $r_{\text{p}}$ to represent the polymer repurination rate, that is, the percentage of degraded polymer $\pi$ that gets converted back into polymer P during every dry phase.

Transforming the polymer vector from $s_n$ to $s_{n+1}$ now requires the following operation:

$$DWs_{n} = s_{{n + 1}}$$

(12)

where

$$D = \left[ {\begin{array}{*{20}c} {1 - r_{p} } & 0 & 0 & 0 \\ {r_{p} } & 1 & m & 0 \\ 0 & 0 & {1 - m} & {r_{m} } \\ 0 & 0 & 0 & {1 - r_{m} } \\ \end{array} } \right]$$

(13)

and

$$W = \left[ {\begin{array}{*{20}c} 1 & {d_{p} } & 0 & 0 \\ 0 & {1 - h - d_{p} } & 0 & 0 \\ 0 & h & {1 - d_{m} } & 0 \\ 0 & 0 & {d_{m} } & 1 \\ \end{array} } \right].$$

(14)

These operations, when iterated, produce the graphs shown in Fig. 4.

Fig. 4

a 4000 cycle simulation using the initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, $d_{\text{m}} = 0.12$, $r_{\text{m}} = 0.04$, and $\mu _0 = 0$. b Same as (a) but with $10^7$ cycles using the initial conditions $m =0.001$, $M_0 =100$, $P_0 =0$, $h=0.00012$, $d=0.12$, $r_{\text{m}}=0.04$, and $\mu _0 =0$. c Expanded scale of a 40,000 cycle simulation using the initial conditions of (a). d 2000 cycle simulation showing the effect of repurination using the initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, $d_{\text{m}} = 0.12$, $r_{\text{m}} = 0.04$, and $\mu _0 = 0$. Note that for all these figures we took $r_{\text{p}}=0$, $d_{\text{p}}=0$, and $\pi _0=0$

This result makes it clear that repurination can reverse the effects of depurination so that the system does not undergo collapse; by modeling repurination as a back reaction that works against depurination, a steady state is reached between the masses of intact and degraded monomers in the system. A steady state is reached at a polymer mass of around 65 (that is 65% yield), noticeably lower than the system without depurination and repurination present. The apparent “thickness” of the line describing monomers is an artifact of the repurination that prevents the polymer collapse. The monomer quantity oscillates between cycles because monomer is depurinated in the wet phase and repurinated in the dry phase. Note that the steady state between intact and degraded monomer results from the fact that the mass of intact monomer depurinated per cycle equals the mass of degraded monomer that is repurinated per cycle. A closer view of the “thick” segment of the line illustrates this feature (Fig. 4c).

When accounting for repurination of polymers, a similar equilibrium between depurinated and repurinated polymer is reached as shown in Fig. 5.

Fig. 5

40000 cycle simulation using the initial conditions $m = 0.001$, $M_0 = 100$, $P_0 = 0$, $h = 0.00012$, $d_{\text{m}} = 0.12$, $r_{\text{m}} = 0.04$, $d_{\text{p}} = 0.012$, $r_{\text{p}} = 0.004$, $\mu _0 = 0$, and $\pi _0 = 0$

Discussion

The computational approach described here leads to significant insights as well as several predictions that can be tested in future experimentation. We will begin by summarizing the conclusions derived from the single matrix and split matrix.

Single Matrix

Our single matrix model reveals the following information: firstly, dehydration synthesis causes the polymer mass of the system to asymptotically approach the maximum value of 100 corresponding to 100% polymer yield. Secondly, hydrolysis has the effect of lowering the maximum accumulation of polymer mass. Finally, depurination allows for a spike in polymer mass which then quickly collapses to zero corresponding to 0% polymer yield.

Split Matrix

Splitting the matrix into wet and dry phases of the hydration/dehydration cycle produced similar qualitative effects except that the split matrix shows oscillations caused by build-up of polymers in the dry phase and the break-down of polymers in the wet phase.

Repurination eliminates the collapse of the polymer mass value caused by depurination, but the monomer–polymer steady state is reached more slowly. This steady state is also reduced from where it would be if depurination and repurination were not considered.

Comparison with Laboratory Simulations of Polymer Synthesis and Hydrolysis

It is useful to compare the computational model with actual experimental results. Figure 6 shows non-enzymatic polymer synthesis in which a 1:1 mixture of 10 mM AMP and UMP was exposed to wet–dry cycles (Da Silva et al. 2015). The mass of polymer synthesized is presented as yields expressed as percent of initial content of monomers. The results can be compared to the graph shown in Fig. 1b, with a reasonable match to the changing ratio of monomers to polymers in 25 cycles.

Fig. 6

(Reproduced with permission from Da Silva et al. (2015))

Polymer synthesis. A mixture of AMP and UMP (10 mM) was put through 25 wet–dry cycles of 30 min each in the presence of ammonium chloride to promote polymerization. Polymer products were isolated by ethanol precipitation and amounts determined by nanodrop analysis of UV absorbance.

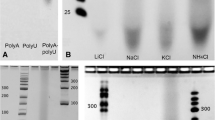
Experimental results for hydrolysis of polymers and depurination of monomers are presented in Fig. 7a, b. Hydrolysis of a known polymer composed of polyadenylic acid (polyA) and polyuridylic acid (polyU) is illustrated both as a gel and a quantitative graph. The hydrolysis and depurination rates were used as parameters in the equations.

Fig. 7

(a Reproduced with permission from DeGuzman et al. (2014))

a Shows a gel in which duplicate samples of 20 μg of a polyA–polyU mixture exposed to four sequential 30-min hydration/dehydration (HD) cycles at 85 °C, pH 3, then precipitated in ethanol. The graph below shows the percent of polymer remaining after each cycle. b Depurination of AMP during wet–dry cycling.

Predictions for Future Experiments

The experimental results clearly demonstrate that polymers accumulate when AMP and UMP are used as monomers. Although the computational model took experimental results into account, further testing is essential to determine its validity. For instance, it would be fruitful to perform experiments in which multiple wet–dry cycles are run with known initial amounts of monomers. During the course of the experiment, samples are taken to determine the polymer mass that has accumulated, the concomitant decrease in monomer mass and the amount of depurination. If the polymer accumulates, then repurination may be occurring as a back reaction. This would be highly significant because there is no known mechanism by which repurination can occur. On the other hand, if depurination were the only factor controlling monomer availability for polymerization, then our model predicts that synthesis of RNA-like polymers cannot reach a steady state, which implies that RNA would be unable to accumulate and give rise to an RNA World.

Sharing the Algorithm

An editable version of the software code is available here at (https://github.com/Spencerkt/Polymer-Synthesis-via-Dehydration-Rehydration). The website includes a README that describes the process by which parameters of simulations can be matched to parameters of experiments.

Conclusion

The computational models presented in this paper qualitatively describe the evolution of monomers and polymers undergoing wet and dry cycling in hydrothermal pools. Dehydration synthesis of RNA polymers from ribonucleotides in combination with the hydrolysis of RNA polymers back into ribonucleotides yield a steady state yield of RNA polymers. Furthermore, depurination of mononucleotides and RNA polymers must be accompanied by repurination reactions to achieve a steady state of synthesis balanced by hydrolysis. The computational models presented in this paper require the steady state to incorporate a repurination component to prevent its collapse. This is an important prediction of the hydrothermal field scenario, and future research should be directed toward testing it.