Introduction

When genetic recombination is present, the historical relationships among individuals over the length of a chromosome do not form an ordinary phylogenetic tree, but instead a tangled graph called the ancestral recombination graph (ARG) (Griffiths and Marjoram 1997). Reconstructing or inferring an ARG is substantially more difficult than reconstructing a phylogenetic tree. The limited historical information in a short genomic segment is often insufficient to determine the history of that segment, and increasing sequence length does not help as it increases the number of segments rather than the information available for each segment.

Given the high uncertainty in any inference of the ARG, it seems more satisfactory to infer a collection or “cloud” of ARGs corresponding to a dataset, rather than attempting to infer the single best ARG. Several programs (LAMARC, Kuhner 2006; InferRho, Wang and Rannala 2008, 2009) generate such a cloud, but generally as a step in making inferences of parameters such as scaled population size or recombination rate. Little has been done with the inferred ARGs themselves.

The cloud contains information which would be of interest to biologists, such as the numbers and approximate locations of well-supported recombination events, and the tree topologies of sequence regions of interest. However, a collection of thousands or millions of ARGs is merely data and not information until it can be processed to make it humanly comprehensible.

Clouds of ordinary (non-recombinant) phylogeny estimates are routinely summarized by construction of a consensus tree, which contains features that are common to the trees in the cloud. Several consensus methods exist with greater or lesser requirements on the degree of agreement required in the cloud of trees before a feature will be incorporated into the consensus tree. Phylogenetic consensus trees are used to summarize the clouds of trees produced by Bayesian phylogenetic analyses (Huelsenbeck and Ronquist 2001), bootstraps (Felsenstein 1985), and the trees produced by the use of different genetic loci or types of data (Swofford 1991).

As authors of an ARG-inference program, we have always wondered about qualities of the inferred ARGs. Standard phylogeny consensus methods cannot be applied to ARGs, and as far as we know, no ARG consensus methods exist. In this study, we develop an ARG consensus algorithm and illustrate its performance via simulation. Having a consensus algorithm for ARGs should increase the usefulness of clouds of inferred ARGs by showing the aspects of the ARG on which they agree. The consensus ARG could also be considered an inference of the true underlying ARG.

Methods

Approaches to the ARG Consensus

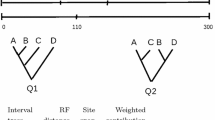
ARG Nomenclature The most complete representation of an ARG is as a directed acyclic graph explicitly showing recombinations and common-ancestry events. However, it is often more convenient to represent the ARG in terms of a series of non-recombinant regions (“intervals”) along the sequence, along with the phylogenetic tree (“interval tree”) of each region. For example, the ms program (Hudson 2002), which simulates ARGs according to the coalescent with recombination model, outputs interval boundaries and interval trees. The interval-tree representation does not contain all of the information in the underlying ARG: it lacks the number of recombinations occuring at each site, the times at which recombinations occurred, and the specific sequences involved as recombination partners. However, molecular data can be simulated on an ARG using only the interval-tree representation with no loss of accuracy (Hudson 2002), because for each site, only the branching tree of that site is relevant. No information about the specific time or nature of recombinations is needed in order to evolve the individual sites. The interval-tree ARG representation can therefore be considered to contain as much of the information in the original ARG as could ever be inferred from molecular data. An example of two interval-tree ARGs is shown in Fig. 1. Note that the interval boundaries are determined by the locations of recombinations in each ARG and thus differ between the ARGs.

Fig. 1
figure 1

Two ARGs (P and Q) expressed as interval trees. Branch lengths are not to scale. Figure reprinted from Kuhner and Yamato (2015a) with permission

Full size image

What Constitutes a Good Consensus? We developed two criteria to judge performance of an ARG consensus algorithm: similarity of the number of recombination breakpoints to the original material, and topological similarity to the original material. Each of these criteria can be judged with respect to the cloud of ARGs from which the consensus was made. If the cloud of ARGs represents estimates of an underlying “true” ARG, the consensus ARG can also be compared to this true ARG.

We chose to focus purely on topological similarity, ignoring branch lengths, because most existing tree consensus methods consider only topology.

Our criteria are therefore:

  1. (1)

    A good consensus should have about as many recombinations as the average ARG in the cloud. If the cloud ARGs are informative about the underlying true ARG, it should also have about as many recombinations as the true ARG.

  2. (2)

    A good consensus should be as close or closer to the average ARG in the cloud, in terms of topological distance, as the cloud ARGs are to one another. Conceptually, this means that the consensus should be near the center of the cloud of ARGs if they could be arranged in space according to topological similarity. If the cloud ARGs are informative about the underlying true ARG, the consensus should also be as close or closer to the true ARG as the average cloud ARG is. (We cannot predict the size of this advantage by geometrical arguments, as we do not believe the space of ARGs related by topological distance is Euclidian.)

As an alternative, Lapointe and Cucumel (2003) proposed that the performance of a consensus method could be judged by a method they called “pertinence.” This method creates clouds of random trees, determines the consensus of each, and asks whether the consensus of the actual cloud is closer to its cloud than a consensus of random trees is to its random trees. This appears to us to be mainly a test of whether the cloud contains phylogenetic information, and only secondarily of whether the consensus method can extract it. We feel no doubt that the clouds of ARGs from a LAMARC run, which are topologically quite similar to one another (as shown by the RF scores in Table 1), contain phylogenetic information, so we have not assessed pertinence.

We will begin construction of an ARG consensus method by considering a very simple algorithm, the naive ARG consensus, and then sequentially improving it until performance is satisfactory.

Naive Consensus Given a cloud of ARGs recorded in interval-tree format, we can define global intervals as those contiguous runs of sites which are never interrupted by a recombination in any ARG in the cloud. For example, the global intervals of the two ARGs in Fig. 1, assuming that breakpoints are labeled with the number of the site to their right, are 0–99, 100–109, 110–149, and 150–300. A naive approach to the ARG consensus is to construct the consensus of the trees in each global interval, using an existing algorithm such as majority-rule consensus (Margush and McMorris 1981), and assign the resulting consensus tree to that global interval. If a consensus method which produces fully resolved trees (for example, by breaking ties arbitrarily) is used, the resulting structure will be an interval-tree ARG.

The weakness of this approach is that as the size of the cloud increases, the number of unique recombination breakpoints in it will also increase, and thus the number of inferred recombination breakpoints in the ARG consensus will tend to increase. In Fig. 1, ARG P has two recombinations and ARG Q has one, but their naive consensus would have three. At the limit of an extremely large cloud, each global interval may be only one site in length. It seems actively misleading to present an ARG with thousands of recombinations as the consensus of ARGs which average only a few recombinations each, and such an ARG would also be cumbersome and difficult to understand or display graphically.

Despite this problem, the naive consensus is attractive due to its simplicity. Alternative approaches which attempt to harmonize the topological structures of multiple ARGs are enormously more complex. We therefore looked for ways to improve performance of the naive consensus.

Topology-Only Consensus Most existing consensus-tree algorithms, including majority-rule consensus, do not attempt a consensus of the branch lengths, as it is not apparent what length should be assumed for a branch that is not present in a given tree. Since we are using majority-rule consensus, our first refinement will be to consolidate adjacent intervals whose interval trees have the same topology, even if they differ in branch lengths. This removal of topologically irrelevant recombinations is applied to the cloud ARGs before constructing the consensus, and additionally to the ARG consensus after it is constructed. For fairness, whenever we compare the consensus with a true or cloud ARG, we also remove topologically irrelevant recombinations from those. The advantage of this step is that it reduces the number of breakpoints under consideration without losing any topological information.

Biglink Consensus Our next refinement is to ground the cloud of ARGs in the molecular data from which they were inferred. We will describe these data as DNA sequences, but any form of molecular data which is arranged linearly and contains both variable and non-variable positions can be handled in the same way.

Along a DNA sequence, there will be sites that vary among the given taxa and sites that do not. Imagine that we are considering possible locations for a given recombination somewhere within a run of invariant sites. As there are no variable sites in this region, the only difference in the likelihood of the data on different ARGs will come from the differing number of invariant sites assigned to the left or right intervals, and thus to different interval trees. In practice this likelihood difference tends to be extremely small. (In a parsimony context, to which these consensus methods are also potentially relevant, the difference is actually zero as invariant sites do not affect the parsimony score.) It is therefore reasonable to treat all breakpoint locations within a run of invariant sites as interchangeable, and thus to collapse the run of sites into a single candidate location. We will call the single location defined by a run of invariant sites a “biglink.”

If we treat all recombinations within a biglink as being at the same location, the number of possible recombination locations drops considerably. The magnitude of this decrease depends on the variability of the data. As an example, the two haplotypes of an average human have approximately one variable site per kilobase, so reducing ARGs drawn for these two haplotypes to biglinks will reduce the number of possible recombination locations approximately a thousandfold.

Further refinements of the biglink idea are possible. A position may be variable and yet uninformative about a particular recombination: for example, a site with a private polymorphism in taxon A provides no information about a putative recombination affecting the descent of taxa B, C and D. However, using such a refinement to define biglinks is difficult as the boundaries of the biglink would then vary among taxa. In the given example, the variable site would define a biglink boundary for recombinations involving A, but not for recombinations involving B–D. It is not clear how to construct consensus trees from partially overlapping global intervals. We have therefore not pursued this idea further.

Threshold Consensus Testing on simulated data (see “Results”) shows that the biglink consensus still yields excess recombinations in the consensus tree in some cases. This excess could arise either because the cloud ARGs reflect a genuine recombination in the underlying data but cannot agree on its exact biglink location, or because the cloud contains many randomly-placed inferred recombinations. Graphing the distribution of cloud recombinations across the sequence in a test case (Fig. 2) suggests that the latter effect is substantial. The graph of recombination locations in the cloud shows peaks corresponding to correctly detected recombinations, but also a noisy background corresponding to randomly placed recombinations. We therefore considered requiring the number of recombinations at a given biglink to reach a given threshold before that biglink would be treated as a breakpoint in the consensus.

Fig. 2
figure 2

Breakpoint locations in the cloud of ARGs (gray bars) and the true ARG (small arrows) for case 18 from the simulation with 8 tips, \(\Theta =0.01\), \(r=0.02\). (This case was chosen for illustrative value.) Topologically irrelevant recombinations have been removed from both the true and cloud ARGs. Note that there are many cloud recombinations which may be misplaced inferences of the actual recombinations, but also substantial numbers far from any true recombination

Full size image

In the naive consensus, a global interval necessarily corresponds to just one interval tree per cloud ARG. This is also true of the biglink consensus, if we think of moving the inferred recombinations in the cloud ARGs to a fixed location within each biglink (say, the center). However, in threshold consensus a global interval may contain internal recombinations, as long as the number of ARGs containing such recombinations does not reach the threshold. The question then arises of which interval tree or trees these ARGs contribute to the consensus for this global interval. For example, in Fig. 1 we might find that the first breakpoint in ARG P does not reach the threshold and should be disregarded. This leaves us with a choice between interval trees P1 and P2 to represent this region.

We chose to contribute all interval trees spanning the consolidated global interval, weighted by the number of biglinks within the interval spanned by each interval tree. Thus, in Fig. 1 we would use interval trees P1 and P2 as ARG P’s contribution to the consensus for the interval between positions 0 and 110, weighting them according to the number of variable sites within the region spanned by each. Weighting by sites would also be possible, but we expect that the information provided by each interval tree is more closely proportional to the number of variable sites it spans than to the total number of sites.

This defines a family of threshold methods, depending on the cutoff chosen for how many cloud ARGs must show a recombination at a given biglink in order for it to be treated as a breakpoint. We defined the threshold t as a percentage of the total ARGs in the cloud. The alternative of requiring an absolute number of ARGs to show the recombination seems likely to lead to too few recombinations in consensus ARGs from small clouds, and too many in consensus ARGs from large clouds.

It is not clear a priori what the threshold value should be. The lowest meaningful value is 1/(number of ARGs sampled), yielding the basic biglink consensus in which any biglink with at least one recombination is considered. The highest threshold value of 1.0 yields a method which incorporates recombinations into the consensus only if there is perfect agreement on them, which is almost surely too stringent. We used computer simulation to test threshold values for data of different levels of polymorphism and recombination.

Implementation

Consensus Algorithms We implemented threshold consensus using a three-step algorithm. In the first step, global intervals were defined using the chosen biglink and threshold rules. In the second step, a majority-rule consensus was made for the interval trees for each global interval (weighted as described under “threshold consensus”) using the CONSENSE program from PHYLIP 3.6 (Felsenstein 2005). We used the “extended majority-rule” option, which calculates a majority-rule consensus and then resolves the tree, if necessary, by adding additional clades compatible with those already present. In the third step, the consensus trees returned from individual CONSENSE runs were combined into an interval-tree ARG. C++ programs for steps 1 and 3, and a shell script for running all three steps, are available on Dryad (doi:10.5061/dryad.9rt50).

Simulations We used the values 0.002, 0.01, and 0.1 for the polymorphism parameter \(\Theta =4N_e\mu\). The lowest value produces data with approximately the variability of human autosomal DNA, and the highest produces data with approximately the variability of HIV-1 sequences. We used the values 0.0 (no recombination), 0.02, and 1.0 for the recombination rate parameter \(r=C/\mu\). The parameter combination with \(\Theta =0.1\) and \(r=1.0\) proved to exceed internal limits of our simulation program due to extreme numbers of recombinations, so we replaced it with \(\Theta =0.1\) and \(r=0.2\). We chose this wide range of parameters to assess performance of the consensus method on clouds of greater or lesser internal agreement.

We simulated “true” ARGs of 8, 12, and 20 taxa using the ms program (Hudson 2002), which generates ARGs according to the coalescent with recombination distribution. Thus, we are modeling the types of ARGs expected to arise within a single population. We simulated 10 kb of DNA data per taxon along the true ARG using the SeqGen program (Rambaut and Grassly 1997) with an F84 mutational model with equal nucleotide frequencies and a transition/transversion ratio of 2.0. To generate a cloud of ARGs from the DNA data, we used LAMARC 2.1.10 (Kuhner 2006). This program performs a Bayesian search among possible ARGs using the coalescent with recombination as its prior. Analyses were done with the same mutational model used in data generation. Bayesian priors on the \(\Theta\) parameter were uniform from 50 to 150% of the true \(\Theta\). Bayesian priors on the r parameter were uniform from 0 to 0.01 for \(r=0\) and uniform from 75 to 125% of the true r otherwise. We discarded the first 250,000 ARGs as burn-in and then sampled every tenth ARG for a total of 10,000 sampled ARGs. We used two chains with temperatures 1.0 and 1.2 and chain-swapping attempts every 20 steps. Search effort was allocated 70% to ARG rearrangement and 30% to parameter improvement.

A major goal of these simulations was to determine whether there is a single optimal threshold across varying degrees of polymorphism and recombination. Based on trial runs, we examined threshold values including the minimum (1/number of ARGS in the cloud, in this case 0.0001) and values from 0.05 to 0.6 in increments of 0.05, as well as 0.8 and 1.0.

Our main simulation parameters allow fairly accurate inference of the ARG. To assess performance of the consensus method when ARG inference was flawed, we also did two additional runs with \(\Theta =0.002\) and \(r=0.1\) in which we deliberately mis-specified the prior on r such that it excluded the truth. In the “low” condition we specified priors from 0 to 0.01, and in the “high” condition we specified priors from 0.15 to 0.25. We expected that these runs would produce clouds which were poorly centered on the ARG used to generate the data.

Assessment To assess the quality of our consensus ARGs, we compared them to the true ARG and the cloud of ARGs in two ways: similarity of recombination counts, and similarity of interval-tree topologies. Before comparison, topologically irrelevant breakpoints were removed from all ARGs.

  1. (1)

    We counted interval breakpoints in the true, consensus, and cloud ARGs. This is a proxy for counting recombinations, although it scores only one recombination even if two or more occurred at the same position. (Since the consensus ARG does not distinguish single from multiple recombinations at the same position, we could not perform a count of actual recombinations.) This metric will tend to see more breakpoints in the original true and cloud ARGs than in the consensus ARG, as breakpoints in the original ARGs are allowed to fall at any point in the sequence and therefore two or more can fall between a pair of adjacent variable sites, which cannot happen in the consensus ARG.

  2. (2)

    We compared the topologies of the true, consensus, and cloud ARGs using the ARG comparison measure ARG-RF (Kuhner and Yamato 2015a), which is an extension of the topology-only Robinson-Foulds metric (Robinson and Foulds 1981) to ARGs. Python code implementing this measure is available on Dryad (Kuhner and Yamato 2015b). A successful consensus should be closer to the true ARG than the average cloud ARG is, and should also be closer to the average cloud ARG than they are to each other. For ARG-RF comparisons involving cloud ARGs, we used 100 randomly chosen cloud ARGs rather than the entire 10,000 ARGs in order to save computational effort. The same randomly chosen ARGs were used for all threshold values within a given experiment.

An RF distance of two units between two ARGs indicates that on average there is one topological difference between their interval trees across the sequence. The maximum RF distance is \(2n-2\) where n is the number of tips. The RF distance between two randomized phylogenetic trees is generally close to the maximum distance (Penny et al. 1982), and we expect that this will also be true for ARGs. In all figures, we present RF/2, which has a simple interpretation where one unit indicates an average of one error per inferred tree.

Results

Fig. 3
figure 3

Breakpoints in the consensus. Mean number of breakpoints in the consensus ARG. Left-hand panels breakpoints in the consensus ARG as a proportion of those in the true ARG. Right-hand panels breakpoints in the consensus ARG as a proportion of the average number in the cloud ARGs. Upper panels cases with \(\Theta r<=4\times 10^{-5}\). Middle panels cases with \(\Theta r>4\times 10^{-5}\). The legend gives values of \(\Theta\), r, and (in parentheses) the number of tips sampled. Bottom panels the case with \(\Theta =0.002\) and \(r=0.1\) with high, low, and correct priors (lines for the correct prior are repeated from panels a and b for comparison)

Full size image
Fig. 4
figure 4

Topological accuracy of the consensus. Topological accuracy of the consensus ARG. Left-hand panels RF/2 score between truth and cloud minus RF/2 score between truth and consensus. This represents the improvement in agreement with the truth obtained using the consensus rather than an average member of the cloud. Right-hand panels RF/2 score between cloud and cloud minus RF/2 score between consensus and cloud. This represents the increased agreement between a random cloud ARG and the consensus versus two random cloud ARGs. Upper panels cases with \(\Theta r<=4\times 10^{-5}\). Middle panels cases with \(\Theta r>4\times 10^{-5}\). The legend gives values of \(\Theta\), r, and (in parentheses) the number of tips sampled. Bottom panels the case with \(\Theta =0.002\) and \(r=0.1\) with high, low, and correct priors (lines for the correct prior are repeated from panels a and b for comparison)

Full size image

To limit the number of cases shown per graph, we divided the cases into those where \(\Theta r\) was greater than \(4\times 10^{-5}\) and those where it was less than or equal to that value, as there appeared to be a clear difference in results between those two groups. Fig. 3 shows numbers of breakpoints, and Fig. 4 shows topological comparisons.

Breakpoint Results When the number of breakpoints in the consensus was compared with the number in the true ARG (Fig. 3, left panels), the consensus tended to have more breakpoints for very low values of the threshold, and fewer breakpoints for higher values, with the crossover point varying somewhat with case. Figure 3 panel e shows results when the prior on r was incorrect, forcing more or fewer recombinations into the cloud ARGs. The too-high prior had little effect on the results, but in the case of the too-lower prior the consensus had far fewer breakpoints than the true ARG for all values of the threshold. In general, a low threshold (0.05–0.15) was best for obtaining roughly the same number of breakpoints in the consensus as in the true ARG.

We also compared the breakpoints in the consensus with those in the cloud from which it was made (Fig. 3, right panels). For the cases with higher values of \(\Theta r\), there were fewer breakpoints in the consensus than in the cloud even at the lowest threshold. We were initially surprised by this finding, since at the lowest threshold the consensus should potentially incorporate all breakpoints found in any member of the cloud. However, when a consensus is made of the interval trees on either side of a poorly supported breakpoint, the resulting consensus trees are very often identical; the breakpoint between them will then separate two identical topologies and will be removed from the final consensus.

When the prior on r was incorrect (Fig. 3, panel f), the too-high prior behaved much like the correct prior, but the consensus for the too-low prior had roughly as many breakpoints as the average cloud ARG. This suggests preferential retention of the few breakpoints present in the average cloud ARG, presumably because they were broadly supported.

In general, matching of consensus breakpoints to cloud breakpoints was best obtained with a low threshold (0.05–0.1). Thresholds greater than 0.5 had markedly too few breakpoints in all cases.

Topological Accuracy Results The cases fell into three distinct categories with regard to topological accuracy as a function of threshold (Fig. 4). When the recombination rate r was zero, threshold had no effect on topological accuracy (dashed lines in Fig. 4 upper panels). When the product \(\Theta r\) was non-zero but no greater than \(4\times 10^{-5}\), topological accuracy declined slightly for high thresholds, with the decline apparent between thresholds of 0.35-0.6 for different cases (solid lines in Fig. 4 upper panels). For larger values of \(\Theta r\), accuracy declined with threshold, with sharp decreases in accuracy past a threshold of around 0.5 (Fig. 4 lower panels).

The left-hand panels in Fig. 4 compare accuracy of the consensus with that of the cloud. For zero or low values of \(\Theta r\), the consensus was closer to the truth than was the mean cloud ARG for all threshold values. For high values of \(\Theta r\) , this was true up to around threshold 0.5, beyond which accuracy declined, often to the point that a random cloud ARG would be a better representation of the truth than the consensus was.

The right-hand panels in Fig. 4 compare the consensus–cloud distance to the average cloud–cloud distance. If the consensus is closer to cloud members than they are to one another, this places the consensus in the center of the cloud. This was true for cases with zero or low \(\Theta r\) for all thresholds. For high \(\Theta r\) accuracy declined for high thresholds, and in some cases the consensus was not centered in the cloud for thresholds above 0.5.

When the prior on r was incorrect (Fig. 4 bottom panels) the too-high prior was almost indistinguishable from the correct prior, but the too-low prior, which reduced the recombinations in the cloud ARGs, led to a lessened advantage for the consensus over the cloud, although the consensus was still superior to the cloud in all cases.

Overall, for topological accuracy low thresholds were preferable to high ones. The threshold of 0.0 showed slight declines in accuracy compared to 0.05 in some cases; the best threshold may therefore be 0.05, with 0.1–0.2 showing very similar performance.

While Fig. 4 shows improvement in the consensus over the cloud, it is also of interest to see how well each case did in terms of actual RF scores. Table 1 presents RF/2 for all four possible comparisons, using consenuses built under the well-performing threshold of 0.05. The cases show a wide range in topological accuracy, with the RF/2 distance from the true ARG to an average cloud ARG varying from 0.32 to 5.85. Across this entire range, however, the topological accuracy of the consensus was always superior to that of an average cloud member.

Table 1 Topological accuracy at threshold 0.05
Full size table

Discussion

Our results show that the threshold consensus, for a low value of the threshold, is topologically closer to the true ARG than the average cloud ARG is. Topological features of the cloud ARGs which made it into the consensus ARG were preferentially those found in the true ARG. This is exactly what one would hope for from a consensus method, and supports the usefulness of threshold consensus.

For low thresholds the threshold consensus is also well centered in the cloud, being topologically closer to the cloud ARGs than they are to each other. While the threshold consensus was somewhat less successful when the cloud was generated under a mis-specified prior, especially a too-low prior, it was still centered among the cloud ARGs.

Cases with more tips in the ARG are, not surprisingly, less topologically accurate, but otherwise follow the same patterns. This shows that the choice to express the threshold as a percentage is robust across modest variation (8–20 tips) in number of tips and thus difficulty of ARG reconstruction.

We therefore recommend use of a threshold between 0.05 and 0.2 for optimal recovery of the breakpoint count and topology, both with respect to the true ARG and cloud ARGs.

In the cases presented, agreement between consensus and cloud was a reasonable proxy for agreement between consensus and truth. In a typical data study, agreement between consensus and truth cannot, of course, be directly assessed; however, an investigator might calculate the agreement between consensus and cloud as a check on success of the threshold consensus method.

Limitations of this Study The number and size of simulations conducted were modest. In Supplementary Materials, we present four replicate simulations of one case, showing high agreement between the replicates. This indicates that the size of each simulation was large enough to give consistent results. However, it is possible that cases dramatically different from those we have simulated (for example, cases with recombinational or mutational saturation, or with much larger numbers of tips) would prefer a different threshold, or otherwise differ from the results shown here. In particular, we suspect that saturated data might yield a consensus with far fewer recombinations than the true ARG.

Support Statistics on the Consensus ARG When a consensus is made of a cloud of trees originating from a bootstrap or Bayesian analysis, it is common to annote each branch in the consensus tree with the proportion of cloud trees supporting it. This can also be done with the interval trees of the consensus ARG, annotating each branch in each interval tree with the proportion of ARGs whose interval tree (or trees) governing this interval contain that branch. This presents no conceptual difficulty, although usefully displaying the resulting confidence values to the user (like displaying the ARG itself) is challenging if the number of intervals is large.

The proportion of cloud ARGs supporting a breakpoint at a given biglink location could similarly be noted as a measure of support for that breakpoint.

It should be remembered that whether or not the resulting support values actually represent statistical certainty in the ARG depends critically on how the cloud was generated. If the cloud arose from a Bayesian sampler, the support values can be considered to approximate posterior probabilities; they are not identical to posterior probabilities because information from several intervals of the cloud ARGs is consolidated into a single interval in the consensus ARG. If the cloud instead arose from bootstrapping followed by ARG inference, the support values are likely to behave like bootstrap support values; that is, they will overstate the probability that a poorly supported branch is in the true ARG, and understate the probability that a strongly supported branch is in the true ARG (Hillis and Bull 1993). Such support values are often practically useful despite their statistical bias. However, if the cloud arose by some other means, such as use of multiple different algorithms to infer the ARG, it will be difficult to assign a statistical meaning to the support values. For example, inadvertant use of several algorithms which are basically the same will overstate support for ARG features preferred by those algorithms. We would not recommend reporting support values when the cloud of ARGs cannot be considered a random or representative sample, as they are likely to mislead.

Future Directions We have ignored branch length estimates throughout, which also implies ignoring recombinations which do not yield a change in tree topology between adjacent intervals, even if they do yield a change in branch lengths. More information might be extracted using the Buneman consensus (Buneman 1971) or the median branch length consensus (Felsenstein 2004), both of which are able to make use of branch length information. In such a study, an appropiate metric for comparing the consensus to the truth would be the ARG-RFL metric (Kuhner and Yamato 2014).

It will be desirable to test performance of the support values described above, particularly the breakpoint support values.

We recommend that programs which infer a cloud of ARGs should make a threshold consensus, ideally with support values for both branches and breakpoints, available to the user. We hope that doing so will spur interest in the ARG as a useful inference of population history in itself, rather than merely a nuisance parameter.