Introduction

In the absence of gene duplication, sections of the genome containing protein coding genes are thought to evolve conservatively because of strong negative selective pressure. Gene duplications (single gene, chromosomal segment or whole genome duplication) produce a redundant gene copy and thus release one or both copies from the negative selective pressure. There are several different models for the retention of a duplicate pair and these make different predictions as to how the duplicate pair evolves. The null model is the neutral model. Under this model, both copies are released from negative selective pressure and evolve neutrally (ratio of number of replacement substitutions per replacement site to number of silent substitutions per silent site equal to 1). Both sequences are then effectively randomly exploring sequence space with the inevitable outcome that one of the duplicates eventually fixes a null mutation. This model would therefore appear to have little relevance to the modeling of the mode of retention of gene duplicates as it is unable to capture the observation that a small but significant number of duplicates are retained in the genome (Lynch and Conery 2000). The classical model (Ohno 1970) postulates that, as long as one of the copies retains the ancestral function, the other copy is free to accumulate mutations that lead to either loss or gain/change in function (neofunctionalisation). Loss of function will remove a gene from selective pressure and it will eventually pseudogenise. Because the vast majority of potential mutations are classically thought to be of this kind, this is thought to be the most common fate of a duplicate under this model. Gain or change in function will ensure that the mutation gets fixed in the population by natural selection and that the duplicate copy is retained in the genome. The duplication–degeneration–complementation (DDC) model (Force et al. 1999) takes into account the modularity of the regulatory regions of genes and demonstrates how degenerative mutations in complementary regions can lead to retention of both duplicate copies through the evolutionary requirement to retain all the regulatory regions of the original gene. As this model does not require beneficial mutations to explain the retention of both duplicates in a pair, it has been characterised as near-neutral.

There are several other non-neutral models of gene duplicate retention which postulate different functions for the retained duplicate: “increased robustness” by maintaining a highly conserved backup copy (Kuepfer et al. 2005), “increased dosage” by increasing expression from a gene that is already highly expressed with little mutational capacity to further increase expression, and “dosage compensation” by maintaining expression levels for stoichiometric reasons (Aury et al. 2006). However, the dosage compensation model presupposes that whole sets of interacting genes with strong stoichiometric constraints have been duplicated and, as such, is more relevant as a retention model for duplicates resulting from a whole genome duplication (WGD) than for duplicates resulting from small-scale duplication (SSD). “Increased dosage” and “increased robustness” both imply strong negative selective pressure on the coding regions of gene duplicates and, as we shall show, this is not the case for SSD duplicates. Thus, we retain the neutral model as our null model, and neo- and subfunctionalisation as our main hypotheses for the mode of retention of SSD gene duplicates.

Concrete examples of both neofunctionalisation and subfunctionalisation have been identified (Force et al. 1999; Roth et al. 2005; Duarte et al. 2006) but direct positive identification of these fates on a genomic scale is difficult. In the case of neofunctionalisation, multiple homologous sequences are required in a phylogenetic context to obtain enough power to reject the null hypothesis of neutral evolution and identify sites under positive selection (Nielsen and Yang 1998; Yang 1998). In the case of subfunctionalisation, positive identification requires the ability to accurately identify regulatory modules computationally, so that one can ascertain to what extent duplicate pairs retained in the genome have complementary regulatory modules. However, accurate regulatory module prediction by computational means is notoriously difficult due to the degenerate nature of regulatory sequences and to their limited length.

The DDC model predicts high rates of retention of duplicates if the number of regulatory modules is high and/or the null mutation rate of each regulatory module is of a similar order of magnitude as the null mutation rate in coding regions. The classical model on the other hand is incapable of producing high levels of retention without large numbers of beneficial mutations, which are thought to be rare relative to degenerative or neutral mutations (Force et al. 1999). Exactly how rare is still an open issue as recent population genetic studies indicate that beneficial mutations may be much more common than previously thought (Eyre-Walker 2006). The fact that, following whole genome duplications, a large percentage of duplicates are retained after many tens of millions of years has been used as support for the DDC model, e.g. X. laevis (Hughes and Hughes 1993), teleosts (van de Peer et al. 2003) and maize (Ahn and Tanksley 1993). However, the view that subfunctionalisation may be the dominant fate of duplicates that are preserved following a WGD does not imply that subfunctionalisation is the dominant fate of duplicates that are preserved following smaller-scale duplication (tandem or segmental duplication). Moreover, recent results suggest that different modes of gene duplicate retention are quite likely for paralogs that arose through different duplication mechanisms (Guan et al. 2007). A WGD produces a context for the duplicated gene that is radically different from the context that results from a SSD. In particular, following a WGD all genes are duplicated, so all interacting genes and all regulatory regions of a given duplicate are also duplicated. Thus, there are good reasons to believe that the fate of retained duplicates may be different for duplicates that result from SSD. Moreover, there are only three hypothesised WGDs in the deep branches of the vertebrate phylogenetic tree, one or two shared by all vertebrates and one in the teleost lineage (Blomme et al. 2006), whereas the rate at which duplicates are produced from SSDs has been estimated to be of the order of 0.01 per gene per million years (Lynch and Conery 2000). Thus, the probability of a chordate gene duplicating as a result of a SSD is not negligible relative to the probability of a gene duplicating in a WGD and establishing the characteristics of duplicates resulting from SSDs is important (Gu et al. 2002).

The goal of this paper is to produce an accurate characterisation of the pseudogenisation rate and the rate of accumulation of replacement substitutions for duplicates that are the result of a SSD. It is then possible to establish whether these characteristics are more consistent with neutral, neo- or subfunctionalisation models of duplicate evolution. Neo- and subfunctionalisation are not mutually exclusive modes of evolution for gene duplicates and it has been suggested that the subfunctionalisation of a duplicate pair may increase the probability of the fixation of a fitness-enhancing mutation in the coding region of a gene (Lynch and Force 2000). First, a subfunctionalisation event will stabilise a duplicate pair in the genome, thereby increasing the chance that a beneficial neofunctionalising mutation will arise. Second, the partitioning of gene expression patterns may reduce the pleiotropic constraints on a gene locus, thereby allowing natural selection to tune each duplicate member of a pair to its specific subfunction. Given that genes that have been preserved in a genome through subfunctionalisation can subsequently neofunctionalise, it is important to realise that there is a distinction between characterising the nature of subsequent evolution after gene duplication and determining the driving force for retention after duplication. In the tests that we use, we cannot distinguish between neofunctionalisation and subfunctionalisation followed rapidly by neofunctionalisation. We use the term neofunctionalisation to refer to a gene that is likely to have evolved a novel function based upon its substitution patterns regardless of the mode of retention. The term subfunctionalisation is reserved for a duplicate pair that shows the retention profile expected when complementary loss of expression is occurring or has occurred without any new or fine-tuning of function.

Materials and Methods

Gene Duplicate Pair Dataset

Our dataset consists of all gene duplication events that could be identified from the putative amino acid sequences of each of the following chordate species: Ciona intestinalis (sea squirt), Canis familiaris (dog), Homo sapiens (human), Pan troglodytes (chimp), Mus musculus (mouse), Rattus norvegicus (rat), Gallus gallus (chicken) and Xenopus tropicalis (frog). The protein sequences were obtained from release 31 of Ensembl (Birney et al. 2006). Annotated genome sequence was also available for Danio rerio (zebrafish) and Takifugu rubripes (puffer fish), but these genomes have been subject to WGDs in the time interval we are interested in modeling (van de Peer et al. 2003), so we did not include them in our dataset as we wish to focus on SSDs.

For each species, the amino acid sequences were first masked for low complexity regions using CAST (Promponas et al. 2000) before an all-against-all BLAST (Altschul et al. 1997) was performed for the proteins of each species (substitution matrix = BLOSUM62, gap opening cost = 11, gap extension cost = 1). The Blast sequence pairs (query and target sequences) were then filtered to identify the pairs that are most likely to represent duplication events. First, all hits with an e-value greater than 10−10 are removed to ensure a high probability of homology between the query and the target sequences. This low e-value may result in a failure to detect older duplication events, but for the use we wish to make of the data, it is more important to ensure a high probability of homology than to capture ancient duplication events. Second, using the genome annotation data from Ensembl, we eliminate pairs where query and target are from the same gene to remove pairs representing a hit between alternative splices of the same gene. Third, for all pairs with the same query, we eliminate all hits except the one with the lowest e-value to ensure that one query only has one hit. Fourth, we eliminate one pair from all sets of reciprocal pairs (pairs in which the query sequence of one pair is the target sequence of the other and vice versa). Thus, at this stage, each query amino acid sequence has a unique target sequence with good evidence of homology, the target is not a transcript from the same gene as the query, and there are no redundant reciprocal hits. Finally, for all pairs where the query protein is the product of the same gene, we retain only the pair that has the best alignment between query and target (the alignment that has the highest percentage of columns not containing gaps). This final filtering step ensures that we have at most one pair for each query gene.

We align each pair of amino acid sequences using Muscle (Edgar 2004) with the standard settings and then convert from amino acid to nucleotide alignments. We rely on the alignment algorithm to place gaps in the alignment at positions where there is low evidence of homology between amino acids and then remove from the alignment all sections containing gaps. One could take a more conservative approach to homology and also remove columns of the alignment that do not contain gaps but have weak evidence of being homologous sites, but this risks biasing the measurement of replacement substitutions downwards.

For each alignment, we use the CodeML program from the PAML package (Yang 1997) in pairwise mode to estimate the cumulative number of silent substitutions per silent site (S) and the cumulative number of replacement substitutions per replacement site (R). We use the term cumulative because R and S are the number of substitutions that have accumulated between the two sequences since the duplication event and because we will be referring to dR/dS, the instantaneous rate of accumulation of replacement substitutions. This explains our somewhat alternative notation: it is more common to refer to S as dS (where S stands for synonymous) and to R as dN (where N stands for nonsynonymous), but this notation would result in confusing notation for the instantaneous rate of accumulation of replacement substitutions (dR/dS). We estimate two models: one with a replacement/silent rate ratio fixed at 1 (ω = 1) and one where we estimate the replacement/silent rate ratio (both models also estimate the transition/transversion rate ratio and the codon frequencies from the nucleotide frequencies). We can then use the value of the log-likelihood functions of the two models to perform a likelihood ratio test of neutral evolution for each pair of duplicates (H 0: ω = 1, H 1: ω ≠ 1). By using this approach to estimating S and R, we are ignoring the fact that these ratios vary along the sequence, so our estimates of S and R are averages across sites. Since we are estimating R and S in pairwise mode, i.e. not using a tree, we are calculating the average R and S between the two extant sequences, so we are unable to measure whether there is any asymmetry in the accumulation rate of R between the genes in a duplicate pair. However, this information is not necessary in this study. Finally, it is important to note that S is the expected number of substitutions per silent site which may range from zero to infinity (it is not the proportion of differences which ranges from 0 to 1). Because of this, values of S up to 3 can be considered useful as estimates of the number of substitutions per silent site.

Alignment Quality Control

Key to this study is the accurate estimation of R and S for a duplicate pair and this depends on good quality alignments between the sequences in each duplicate pair. In order to assess the quality of the alignments, we group all duplicate pairs into groups of size 0.1 S and, for each group, calculate the mean and the median fraction of alignment columns that are gap free. For duplicate pairs with a low S value indicating a recent duplication event, we would expect a fraction of gap free columns close to 1 (close to no columns containing gaps). For duplicate pairs with a higher S value (longer time since duplication), one would expect to observe a lower fraction of gap free columns, but the absolute level should still be high. We fit a simple linear equation to each set of data (see Fig. 1 in the supplementary material). For all species, the median lies above the mean indicating the skewness of the distribution of the percentage of gap free columns. The datasets for C. familiaris, H. sapiens, M. musculus and R. norvegicus clearly contain good quality alignments: the alignment quality measure is close to 1.0 for pairs with low S, all median curves are above 0.9 and are flat or slightly downward sloping indicating, as we would expect, that the quality of the alignment decreases with time since duplication. These results also validate the methods we use for building our dataset. For the four other species (C. intestinalis, G. gallus, P. troglodytes and X. tropicalis), the quality of the alignments is clearly lower and, in particular, the quality of the alignments for pairs with low S is much lower than 1.0. Further analysis suggests that the lower quality of these datasets is due to the underlying genome annotations. In particular, in many sequence pairs, one of the sequences is often lacking one or more sections of the paired sequence. Therefore, we exclude the four species with low alignment quality from our analysis, which results in the species analysed being exclusively mammalian.

Key Methodological Assumption

This study makes the key assumption that silent substitutions have no effect on fitness and, therefore, that silent substitutions per silent site accumulate at a rate proportional to time. This rate may be different in different lineages, but it is reasonable to assume that it is constant within a lineage over evolutionarily short periods of time, i.e. a few tens of millions of years. Eventually, silent sites get saturated with substitutions, leading to inaccurate estimation of S, but this should not be the case before S > 3.

Gene Duplicate Survival Analysis

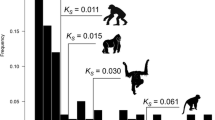
To obtain estimates of the rates of gene duplication (birth) and pseudogenisation (death), we model the survival of duplicate pairs by assuming that gene “birth” and “death” are steady-state processes. We model on the interval 0 < S < 0.3 to ensure a high likelihood that the assumptions of S rate constancy and of non-saturation are valid. To approximate the age distribution of duplicate pairs, we compute counts of duplicate pairs in intervals of size S = 0.01 which represents on average 1.1 million years. Since the distribution of S is right skewed within each group, we give each group the median S value for the group (see Fig. 1).

Fig. 1
figure 1

Age distribution of duplicate pairs. Total column height: counts of duplicate pairs within each interval of size 0.01 S. Crosses: median S value for each interval. Shaded area: duplicate pairs with R/S significantly different from 1. Nonshaded area: duplicate pairs with R/S not significantly different from 1. Solid line: fitted Weibull function. Dotted line: fitted exponential function

Full size image

Because the numbers of duplicate pairs of a specific age are counts, they can be assumed to be independent Poisson variables. The parameter of the Poisson distribution is its mean and the mean number of duplicate pairs observed in an age group (surviving duplicate pairs) is a function of the group’s age (time since duplication). Two common survival functions are the Weibull function \( Q(t) = e^ {{\rho_1} ^{{\rm t}^{\rho_2}}} \) where T is the time of death and its special case, the exponential function where ρ 2 = 1. We use these survival functions and S as a proxy for time to model the mean of the Poisson distribution:

$$ {E(N_{{S_{i}}})\, = \,N_{0} e^{{\rho _{1} }}{^{{S^{{\rho _{2} }}_{i}}}}} $$
(1)

where \( {N_{{S_{i} }} } \) is the number of duplicate pairs observed at age S i , and N 0, ρ 1 and ρ 2 are fitted parameters.

We fit the model to the data by quasi-maximum likelihood, first estimating all three parameters and then by fixing ρ 2 = 1 (see Table 1 for results and the supplementary materials for code). A plot of the standardised residuals against the fitted values of the dependent variable show that the model is correctly specified and, in particular, that there is no overdispersion in the data (see the supplementary material). Since the models are nested, we can use a likelihood ratio to test whether we can reject the exponential model (H 0: ρ 2 = 1, H 1: ρ 2 ≠ 1). For all species, we reject the null hypothesis at the 1% level.

Table 1 Weibull function (unrestricted) and exponential function (restricted) modeling of duplicate pair survival on the interval 0 < S < 0.3
Full size table

The hazard function λ(t) is defined as the event (death/failure/pseudogenisation) rate at time t conditional on survival to time t or later:

$$ {\lambda (t)\, = {\mathop {\lim }\limits_{\Delta t \to 0} }\,{{Pr(t\,<\,T\,<\,t\,+\,\Delta t | T>\,t)} \over {\Delta t}}\, = \, - Q'(t)/Q(t)} $$
(2)

Using S as a proxy for time: \( {\lambda (S)\, = \, - \rho {}_{1}\rho {}_{2}S^{{\rho _{2} - 1}} } \) for the Weibull survival function. λ(S) = –ρ 1 for the exponential survival function.

For all species, the fitted parameters satisfy ρ 1 < 0 and 0 < ρ 2 < 1. Together with the better fit of the Weibull function, this implies that the rate of pseudogenisation of a duplicate decreases with time. The estimated values of the parameters indicate very rapid decline of the pseudogenisation rate, with the rate falling by a factor of at least five within a few tens of millions of years (see Fig. 2).

Fig. 2
figure 2

Duplicate pair hazard functions. Solid line: hazard function for the Weibull survival function. Dotted line: hazard function for the exponential survival function

Full size image

Since we have built our dataset from the fully sequenced genomes, we can use the youngest duplicate pairs to estimate the rate of gene duplication. As mentioned earlier, we have been careful to exclude duplicate pairs that consist of alternative splices of the same gene and the nature of our raw data excludes the possibility that duplicate pairs consist of allelic variants. Therefore, we are confident that our data can be used to estimate the rate of gene duplication. We count the number of genes in the first age group S < 0.01 which we convert to an estimate of the number of duplications per gene per S (see Table 1 in the supplementary material). These results confirm the previous result that the rate of duplication per gene is of the same order of magnitude as the rate of mutation per nucleotide site (Lynch and Conery 2000).

Accumulation of Replacement Substitutions Modeling

In order to investigate the accumulation of replacement substitutions, we plot all duplicate pairs with S < 3 in Fig. 3 and we model R as a function of S on this interval. Figure 3 shows that duplicate pairs accumulate replacement substitutions per replacement site at a rate that declines with increasing S until approximately S = 2, beyond which the rate of accumulation appears to be approximately constant. The equation:

$$ {{{\rm{d}}R} \over {{\rm{d}}S}}\, = \,\theta _{1} \, + \,\theta _{2} \exp \,( - \theta _{3} S) $$
(3)
Fig. 3
figure 3

Substitutions per replacement site (R) as a function of substitutions per silent site (S). First column: close-up of origin, second column: all data. Solid lines: middle line is Eq. (4) fitted to the data, lowest and highest lines are the 5% and 95% quantiles of the distribution of R for a given value of S derived using Eqs. (4) and (5). Dashed line: equation R = S (neutral model). Dot and dash line: equation satisfying dR/dS = 1 at values of S corresponding to less than 4 MY and dR/dS = θ 1 at higher values of S (subfunctionalisation model)

Full size image

for which, dR/dS = θ 1+θ 2 at S = 0 and dR/dS → θ 1 as S → ∞ (for θ 3 > 0), can be used to model this relationship between R and S. This equation models the biologically grounded expectation that following duplication negative selective pressure is relaxed on one or both copies but subsequently returns for those duplicates that escape pseudogenisation.

However, the data presents a number of challenges. First, the relationship between S and R is nonlinear. Second, the data are heteroscedastic with the variance of R increasing rapidly at low S before stabilising at high values of S. Finally, the distribution of R for a given value of S is skewed, thus ruling out the possibility of assuming that the errors are normally distributed. We address these issues using the nls2 package (Bouvier and Huet 1994) together with the statistical software R (R Development Core Team 2005). The nls2 package makes it possible to explicitly model the variance of the error term as well as the nonlinear relationship between S and R. Moreover, by estimating the model parameters using the quasi-likelihood method, we do not need to assume that the errors are normally distributed (Bouvier and Huet 1994). Thus, the complete nonlinear regression model is:

$$ {R_{i} \, = \,\theta _{1} S_{i} \, + \,(\theta _{2} /\theta _{3} )(1 - \exp ( - \theta _{3} S_{i} ))\, + \,\varepsilon _{i} } $$
(4)
$$ Var(\varepsilon _{i} )\, = \,\sigma ^{2} (\tau _{1} S_{i} \, + \,\exp (\tau _{2} (1 - \exp ( - \tau _{3} S_{i} )))),\,E(\varepsilon _{i} )\, = \,0 $$
(5)

where the ε i are assumed to be independent random variables for i varying from 1 to n. The error term of Eq. (4) captures both the randomness of R and the fact that different duplicate pairs are subject to different modes of evolution (neo- or subfunctionalisation). Equation (4) is obtained by integrating Eq. (3) and adding a random error term. No intercept term is needed as a new duplicate will satisfy R = 0 and S = 0. Equation (5) was chosen as it can accommodate the change of the variance as a function of S: Var(ε i ) = σ 2 at S i = 0, it can be an increasing function on S i > 0 and dVar(ε i )/dS i tends to the constant σ 2 τ 1 as S i → ∞.

The results of fitting the model consisting of Eqs. (4) and (5) to the data using quasi-likelihood are in Table 2 (R code available in the supplementary materials). The residuals for H. sapiens are plotted in Fig. 4, which clearly shows the heteroscedasticity of the error term with a rapid increase at low values of S followed by a slower increase at high S (other species have a very similar pattern). It is also possible to see the non-normality of the distribution of the error term. Figure 4 also includes a plot of the standardised residuals, which shows that we have adequately dealt with the heteroscedasticity of the error since the variance of the standardised residuals is relatively constant at different levels of S. From the standardised residual data, we determine the 5% and 95% quantiles and use these together with the fitted Eqs. (4) and (5) to determine the band capturing 90% of duplicate pairs (Fig. 3). Finally, we plot Eq. (3) with the parameter estimates for a visualisation of the change in the slope of Eq. (4) in Fig. 5.

Table 2 Modeling of the cumulative number of substitutions per replacement site as a function of the cumulative number of substitutions per silent site
Full size table
Fig. 4
figure 4

Residuals and standardised residuals. Residuals resulting from the fitting of Eq. (4) to the duplicate pair data using quasi-likelihood and an error model as defined in Eq. (5). Solid line: E(ε i ) = 0. Dashed line: 5% and 95% quantiles of the distribution of standardised residuals

Full size image
Fig. 5
figure 5

Rate of accumulation of R as a function of S post-duplication. Solid line: Eq. (3) with the fitted parameters of Eq. (4). Dashed line: dR/dS = θ 1, the asymptotic rate of accumulation of R as a function of S

Full size image

Results and Discussion

Gene Death Rates

Overview

The better fit of the unrestricted survival model demonstrated by the likelihood-ratio test and the Weibull function’s downward sloping hazard function (see Table 1 and Fig. 2) imply that duplicate genes pseudogenise at a rate that declines rapidly with time since duplication. The fitted survival functions show that the duplicate gene half-life is on average very short (approximately 0.03 S), but as a consequence of the downward sloping hazard function, 95% loss takes at least 10 times as long for all species (see Table 1) which means that a non-negligible fraction of gene duplicates benefit from a window of opportunity of several tens of millions of years in which they can potentially evolve new function or regulation. This pattern of decline of the duplicate gene death rate is not unique to our data. It is also clearly visible in other datasets built for several different species (H. sapiens, C. elegans, S. cerevisae and D. melanogaster) and using different methods (Lynch and Conery 2000; Lynch and Conery 2003), although we believe that it has not been previously noted that it is a downward sloping convex hazard function that provides the best fit to the data. This result is interesting, first because it shows that duplicates pseudogenise at a rate that decreases with time since duplication but also, and more importantly, because the models of gene duplicate evolution make different predictions for the shape of the hazard function.

Neutral Model

In order to establish which mode of evolution our duplicate pair data is most consistent with, we determine the qualitative properties of the death rate implied by the three main modes of evolution. For the neutral and the subfunctionalisation model, we assume that one functional allele is sufficient for the function to be retained (the double recessive model) and that beneficial mutations are rare relative to degenerate mutations. Provided the product of population size and genic mutation rate is less than 0.01 (Li 1980), the frequency of double null homozygotes will be sufficiently low such that all allele frequencies will evolve in an effectively neutral manner. The rate of fixation of a mutation in the population will then be approximately equal to the rate of mutation. It is reasonable to assume that the rate of null mutation at the level of the gene is constant across time, thus, in the neutral model, we would expect to observe a constant pseudogenisation rate across time.

Subfunctionalisation Model

To derive the prediction for the subfunctionalisation model, we consider the situation described in the DDC model (Force et al. 1999). Both members of a recent duplicate pair have z independently mutable regulatory subfunctions, all of which are essential at least in single copy and all of which mutate at identical rates (u r ) to alleles lacking the relevant subfunction through the fixation of a null mutation (see Fig. 6). The coding region of the gene is subject to null mutation at rate u c . If one of the duplicate copies experiences the fixation of a null mutation and assuming that there is more than one regulatory module, then the probability of pseudogenisation on this first null mutation event conditional on not having pseudogenised for a gene with z regulatory regions (\( P^{z}_{1} \)) is the total coding region null mutation rate divided by the total mutation rate for the two copies:

$$ P^{z}_{1} \, = \,{{u_{c} } \over {u_{c} \, + \,zu_{r} }} $$
Fig. 6
figure 6

Potential fates of a duplicate gene pair with multiple regulatory regions, adapted from (Force et al. 1999). Small boxes: regulatory regions, big boxes: coding regions, black box: functional, white box: fixed null mutation. Arrows represent potential null mutations to regulatory or coding regions. The base of the arrow identifies the mutated region (if the base encompasses multiple regions, then this symbolises a mutation to one of these regions) and the tips of the arrows point to a representation of the outcome if such a mutation is fixed in the population: pseudo.: pseudogenisation, subfunc.: subfunctionalisation, neg. select.: negatively selected against, i.e. unlikely to reach fixation in the population. The dotted arrow represents several intermediary states between the second and last state. These states are not drawn as the potential mutations from these states are identical to those in the second state. The model focuses on mutations fixed in the population, so the diagram shows the state of a single gamete. Note that the diagram represents the case where a null mutation to a regulatory region of sequence A is fixed first, the case where a null mutation to a regulatory region of sequence B is the first to be fixed is symmetrical

Full size image

We define \( t^{z}_{i} \) as the mean time to the i th null mutation conditional on previous null mutation events not having caused pseudogenisation and \( \Delta t^{z}_{i} \, = \,t^{z}_{i} \, - \,t^{z}_{{i - 1}} \). If the times to mutational events are exponentially distributed then the mean time to this first event is the inverse of the total mutation rate for the two copies:

$$ \Delta t^{z}_{1} \, = \,t^{z}_{1} \, = \,{1 \over {2(u_{c} \, + \,zu_{r} )}} $$

If the duplicate pair survives the first mutational event, then the first null mutation must have occurred in one of the regulatory modules of one of the copies. Subsequent null mutations are not possible on the equivalent regulatory module of the unaffected gene as this subfunction needs to be retained. Subsequent null mutations in the coding region of the unaffected gene are excluded for the same reason (see Fig. 6). Thus, the probability of pseudogenisation conditional on pseudogenisation having not already occurred is:

$$ P^{z}_{i} \, = \,{{u_{c} } \over {u_{c} \, + \,2(z - i + 1)u_{r} }}\,{\rm\,\,{and}}\,\Delta t^{z}_{i} \, = \,{1 \over {u_{c} \, + \,2(z - i + 1)u_{r} }}\,{\rm\,\,{for}}\,\,1\, < \,i\, < \,z $$

If both copies have failed to pseudogenise after z–1 null mutation events, then pseudogenisation can occur either by a null mutation to the last intact regulatory module or by a null mutation to the coding region of the gene copy that has been accumulating null mutations to its regulatory modules. Thus:

$$ P^{z}_{z} \, = \,{{u_{c} \, + \,u_{r} } \over {u_{c} \, + \,2u_{r} }}\,{\rm\,\,{and}}\,\,\Delta t^{z}_{z} \,{1 \over {u_{c} \, + \,2u_{r} }} $$

Finally, \( {P^{z}_{i} } \) = 0 for i > z as any duplicate pair has either already pseudogenised or subfunctionalised once z null mutational events have been fixed and, thus, has a very low probability of pseudogenising (for the sake of simplicity we set this to 0). The mean time to the i th mutational event is:

$$ t^{z}_{i} \, = \,{\sum\limits_{j = 1}^i {\Delta t^{z}_{j} \, = \,t^{z}_{1} \, + \,{\sum\limits_{j = 2}^i {\Delta t^{z}_{j} \, = \,{1 \over {2(u_{c} \, + \,zu_{r} )}}\, + \,{\sum\limits_{j = 2}^i {{1 \over {u_{c} \, + \,2(z\, - \,j\, + \,1)u_{r} \,}}} }} }} } $$

The continuous hazard function is defined in Eq. (2). We define \( \lambda ^{z}_{t} \) as the hazard rate of a duplicate pair with z regulatory modules at time t. An approximation of \( \lambda ^{z}_{t} \) at \( t^{z}_{{i - 1}} \) is:

$$ \lambda ^{z}_{{\,t^{z}_{{i - 1}} }} \, = \,\,{{P^{z}_{i} } \over {t^{z}_{i} \, - \,t^{z}_{{i - 1}} }}\, = \,{{P^{z}_{i} } \over {\Delta t^{z}_{i} }} $$

Further, we assume this to be the approximation of \( \lambda ^{z}_{t} \) for \( t^{z}_{{i - 1}} \, \le \,t\, < \,t^{z}_{i} . \) Thus:

$$ \lambda ^{z}_{t} \, = \,\left\{ \eqalign{ & {2u_{c}} ,\,\,\,0\,\, \le \,t\,\, < \,t^{z}_{1} \cr & u_{c} ,\,\,\, \,t^{z}_{1} \,\, \le \,\,t\, < \,t^{z}_{{z - 1}} \cr & u_{c} \, + \,u_{r} ,\,\,\, \,t^{z}_{{z - 1}} \,\, \le \,\,t\, < \,t^{z}_{z} \cr & 0,\,\,\,\,\,\,t^{z}_{z} \le \,\,t} \right. $$

Therefore, for an individual duplicate pair or for a group of duplicates pairs with the same number of regulatory regions, the pseudogenisation rate is constant for \( t^{z}_{1} \, \le \,\,t\,\, < \,t^{z}_{{z - 1}} \) which for reasonable values of u c , u r and z is the majority of the interval [0, \( t^{z}_{z} \)]. The intuition for this result is simple. Null mutations to the regulatory regions do not cause pseudogenisation (except if all regulatory regions have suffered a null mutation). Thus, the rate of pseudogenisation of a duplicate is equal to the rate at which null mutations occur in the coding region of one gene of the pair (except prior to the first null mutation to a regulatory region being fixed) and this rate is assumed to be constant. The way in which the regulatory modules are modelled here might be considered an oversimplification. Indeed, back mutation to regain function at a regulatory site is expected to have a significant probability, given the plasticity of transcription factor binding to DNA (Berg et al. 2004). Moreover, regulatory modules for different subfunctions are unlikely to be independent blocks on the DNA molecule; instead they are likely to be partially overlapping, embedded or even shared (Force et al. 1999). However, incorporating such features into the model does not alter the way in which pseudogenisation occurs, namely through a mutation to coding region of one of the genes in the pair. Thus, it is a relatively robust result that the pseudogenisation rate is constant for all states of the duplicate pair between the fixing of the first null mutation to a regulatory region and the penultimate degenerate mutation to the regulatory region.

The dataset for which we have modelled duplicate survival consists of gene duplicate pairs with different numbers of regulatory regions. We consider a set of duplicate genes with a minimum of two regulatory regions (as subfunctionalisation is only possible in this model if the gene has two regulatory regions) and a maximum of Z regulatory regions. We denote by x k the number of genes with k regulatory regions and by Λ t the mean pseudogenisation rate at time t:

$$ \Lambda _{t} \, = \,{{{\sum\nolimits_{k\, = \,2}^Z {x_{k} \lambda ^{k}_{t} } }} \over {{\sum\nolimits_{k\, = \,2}^Z {x_{k} } }}} $$

We compute the value of this function for all \( t^{k}_{i} \) where k may vary from 2 to Z and i may vary from 1 to k (see Fig. 7). In the computations, we use the following values: u c = 10−7/yr which corresponds to u c = 13/unit of S for the average silent substitution rate (see Table 2 of the supplementary materials), γ = u r /u c = 0.1 or 0.5, Z = 12 and two possible distributions for x k : normal and uniform. These values are chosen because they are realistic and because they fall within the ranges for which the subfunctionalisation model has been shown to produce high probabilities of gene duplicate retention (Force et al. 1999). All four Bezier curve approximations have similar qualitative features: (1) an initial short period of higher hazard (caused by the possibility of the first null mutation occurring in one of the two coding regions), (2) a period of relatively constant hazard (shorter for the uniform distribution than for the normal distribution) and (3) a period of declining hazard which is for the most part concave (it is convex shortly before reaching zero in the case of the normal distribution). The short initial phase of heightened hazard would be difficult to detect in our dataset because the length of this initial phase may be shorter than the size of duplicate age groups (0.01 S), as can be seen in the second column of Fig. 7. Thus, what we would expect to observe at the very least in our data, if the DDC model is correct, is an initially constant and then broadly decreasing concave mean hazard function.

Fig. 7
figure 7

Mean hazard function under the subfunctionalisation model. Columns: values of γ = u r /u c = 0.1 (first column) or 0.5 (second column). Rows: distribution of z that is either uniform (first row) or normal (second row). Dotted line: mean hazard function. Solid line: Bezier curve approximation of degree n (the number of time points at which a value of the mean hazard function is computed) that connects the endpoints of the mean hazard function

Full size image

Neofunctionalisation Model

We now turn to the derivation of the prediction of the classical model where both null and beneficial mutations are considered possible. We assume that such mutations occur at constant rates. In this model, for those duplicates that have not previously fixed a null mutation, the probability of having fixed a neofunctionalising mutation in the time since duplication (t) increases at a decreasing rate with t (all probabilities in this section are conditional on a null mutation not having been fixed). In the absence of beneficial mutations, the probability of fixing a null mutation within Δt is constant. When allowing for fitness-enhancing mutations, it is reasonable to assume that the probability of fixing a null mutation within Δt becomes a decreasing function of the probability of having fixed a beneficial mutation. Moreover, since the probability of fixing a null mutation is never equal to 0, the probability of fixing a null mutation within Δt must decrease at a decreasing rate as a function of the probability of having fixed a beneficial mutation. Thus, under the neofunctionalisation model, the pseudogenisation rate (or hazard function), which is a function of the probability of fixing a null mutation within Δt conditional on not having fixed a null mutation as defined in Eq. (2), must decrease at a decreasing rate as a function of time since duplication (convex function).

Summary

Our duplicate pair dataset probably contains pairs that are following different modes of evolution (neutral, neo- and subfunctionalisation) but in different proportions. Figure 2 suggests that duplicate pairs following the neofunctionalisation model are the dominant type of duplicate as this matches the prediction of the classical model namely a downward sloping convex hazard function. Subfunctionalisation or neutral modes are probably rarer modes of evolution as a constant or downward sloping concave hazard function are difficult to reconcile with the convex Weibull hazard function that we have shown to be a near perfect fit to the data (Fig. 1 and Table 1).

Other, more circumstantial, evidence against the pure subfunctionalisation model is provided by the level of the hazard rate which, for all four species, is in the range [5.0, 10.0] for S = 0.3. If pure subfunctionalisation was the dominant mode of evolution, one would expect the hazard rate to rapidly approach a very low value as explained above.

Accumulation of Replacement Substitutions

Overview

The average value of dR/dS at S = 0 is 0.64 with a range from 0.59 to 0.73 (see Table 2). These estimates are higher than early estimates for M. musculus (38%) and H. sapiens (44%) (Lynch and Conery 2000) and lower than a more recent estimate for H. sapiens (89%) (Lynch and Conery 2003). The estimates for the asymptotic dR/dS range from 0.03 to 0.07 and average 0.05, which concords with other estimates. The estimates of θ 3 imply that the rate of decline towards this asymptotic value is such that the average dR/dS at S = 0.2 is still 0.42 (see Fig. 5).

There are several possible causes for the discrepancy with previous estimates of dR/dS at S = 0. First, we build a dataset using different methods and, in particular, we ensure that a duplicate pair does not consist of alternative splices of the same gene. Second, we rely on the alignment algorithm to determine whether amino acids in a duplicate pair are homologous or not. Third, we fit our model to the estimates of R rather than the natural logarithm of R. Fourth, because the errors are not normally distributed, we use quasi-likelihood to fit the model to the data. We believe these differences in methodology are well founded and therefore should produce better estimates.

We conclude that, at least for mammalian species, the rate of accumulation of replacement substitutions is high following duplication for a majority of duplicates and that this rate declines towards its asymptotic value at a rate that lets duplicates accumulate large numbers of replacement substitutions for several tens of millions of years before they either pseudogenise or come under strong negative selective pressure. Although even the slope of the 95% quantile only exceeds 1 at low S, more sophisticated measurements of R/S that do not simply average over all sites and over the two branches since the duplication event, would probably reveal that at least some sites are under positive selection. For example, the application of a tertiary windowing method (Berglund et al. 2005), which searches for positive selection in a defined window of a protein structure, did detect many lineages in gene families with positive selection, when the average R/S ratio indicated negative selection.

Evaluation of the different models

The different modes of evolution make different predictions regarding the accumulation of replacement substitutions. The neutral model predicts that the duplicate pair coding sequence evolves neutrally, i.e. dR/dS = 1. The subfunctionalisation model predicts that the coding region of a duplicate initially evolves neutrally (dR/dS = 1) followed by strong negative selective pressure when and if the duplicate subfunctionalises. The neofunctionalisation model predicts released negative selective pressure on all sites and some sites experiencing positive selective pressure, thus it is not necessarily the case that dR/dS > 1 on the full protein length.

Our data shows that few duplicate pairs are evolving neutrally and, for those that are, the period of neutral evolution is short. Figure 3 shows the vast majority of duplicate pairs located beneath the R = S curve even for S close to zero and a Wald test of H 0: θ 1 + θ 2 = 1 rejects this null hypothesis at the 1% level (see Table 2). This shows that the average duplicate pair is not evolving neutrally, but this does not exclude the possibility that a minority of duplicates are. However, if such a minority exists, it must be small: despite the fact that the likelihood ratio test of neutrality for a duplicate pair (H 0: ω = 1, H 1: ω ≠ 1) has almost no power to reject the null hypothesis of neutrality at very low levels of divergence (low S), by S ≃ 0.15 a majority of pairs reject the null hypothesis in all species (Fig. 1). Further evidence is provided by the band capturing 90% of observations in Fig. 3 (first column), where the 95% quantile curve falls below the R = S curve at some point in the interval 0.1 < S < 0.25, thus confirming that the initial period of neutrality is short for the duplicates that are evolving neutrally.

In Fig. 3, we plot a curve that is the mean predicted path of a subfunctionalising duplicate pair. This path consists of an initial period of neutral evolution prior to subfunctionalisation followed by a period of negative selective pressure after subfunctionalisation. An estimate of the mean time to subfunctionalisation is 4 million years (Force et al. 1999), which we convert to S using the estimated rate of substitution per silent site (Yang and Nielsen 1998; Dimcheff et al. 2002; Springer et al. 2003; Axelsson et al. 2005) (see supplementary materials Table 2) and we use θ 1 as the estimate of the rate of accumulation of replacement substitutions when the sequence is under negative selective pressure. Both figures show how this path lies outside (or inside but very close to) the 5% quantile curve. This suggests that very few duplicates are subfunctionalising. This data also shows that the “increased dosage” and “increased robustness” modes of evolution, which require high levels of negative selection on the coding sequence of duplicate genes, are not common fates for gene duplicates.

Although the nature of our data prevents us from producing positive evidence of neofunctionalisation, the data does not contradict the prediction of the neofunctionalisation model and shows that only a very small minority of the duplicate pairs appear to be evolving under a neutral or subfunctionalisation model.

The asymptotic rate of accumulation of replacement substitutions

One may argue that the picture of long term gene evolution generated in the previous section is more simplistic and more conservative than the way in which orthologs and older duplicates actually evolve.

It is potentially simplistic in the sense that we model the background rate of accumulation of replacement substitutions as a constant when studies using gene families show that a degree of punctuated equilibrium is observed in the evolution of orthologues (Messier and Stewart 1997; Roth and Liberles 2006), with major differences in selective pressure after duplication and after speciation for genes with different functions and proteins with different folds (Seoighe et al. 2003; Rastogi et al. 2006).

It is conservative in the sense that the estimated background rate of dR/dS is probably too low. Indeed, pairwise comparisons of rat and mouse orthologues give a value of 0.13 (Wolfe and Sharp 1993), indicating a higher background rate of selection than that detected here. This means that our characterisation of the expectation for the DDC model probably produces an overly strict test of subfunctionalisation.

The weaknesses in our estimation of the background rate of accumulation of replacement substitutions are in fact twofold. First, because we are estimating θ 1 from this pairwise data, the variance of our estimates is higher than if we had used shorter branches. This was shown in reference to ancestral sequence reconstruction, where fewer sequences and longer branches led to greater error in estimation, with a pairwise comparison being at the extreme of this (Koshi and Goldstein 1996). Second, and more importantly, there are several potential sources of downward bias. One possible source of bias is that the bulk of the data comes from young duplicates and θ 1 is largely estimated from the rate of evolution of the slowest evolving duplicates, where those evolving more quickly are initially contributing to estimating θ 2 more than θ 1. However, we were able to discard this as a possible source of bias by performing a linear regression on duplicates for which S > 1.5 and showing that the slope of the equation was the same as the asymptotic value of dR/dS from the fitted Eq. (3). Another possible source of bias is that when a gene duplicates it is quite likely that a proportion of sites are not fully released from negative selective pressure and, thus, are not free to accumulate replacement substitutions. This would lead to a situation where one class of sites becomes saturated while the other class experiences little change, thus explaining a downward-biased estimate of R even though R < 1. In this case, once saturation hits a class of sites, the asymptotic measurement of dR/dS would be expected to be related to class shifting, or to the rate shift parameter in the heterotachy model (Galtier 2001; Lopez et al. 2002). Finally, in building our dataset we only retained blast hits with an e-value less than 10−10 which may have resulted in more divergent gene duplicates being excluded and thus a downward-biased estimate of R.

If we consider the estimate of 0.13 as the estimate of the background rate of dR/dS instead of our estimated rate, then the subfunctionalisation path lies above the 5% quantile and the evidence against subfunctionalisation is weakened. However, we still find it unlikely that a majority of duplicates are following a subfunctionalisation model of evolution as the estimate of dR/dS is significantly higher than 0.13 for S < 0.5 (Fig. 5), implying that the mean duplicate sequence is not accumulating R at the background rate and thus cannot have subfunctionalised in the strict sense of the term (partitioning of expression patterns).

The above result combined with the result that, if duplicates evolve neutrally, they only do so for a short period following duplication, is consistent with a view presented during a modeling study, where the process of subfunctionalisation and neofunctionalisation were directly linked to molecular function (peptide binding according to physical constraint where the gene also needed to properly fold to maintain the binding pocket) (Rastogi and Liberles 2005). In this case, where there was an explicit rather than a random mapping between substitution and function, subfunctionalisation (modelled as a modular process of binding specificity rather than regulation) was indeed observed to be important, but occurred quickly and those subfunctionalising always represented a small fraction of the total population. Quickly, this was coupled to neofunctionalization and a combination of many sites under negative selection with an important subset under positive selection to give an average value indicative of slightly negative selection.

Conclusion

In this paper, we have shown that the Weibull survival function provides the best fit to the age distribution data which, given the estimated values of the parameters, implies a decreasing convex hazard function which is most consistent with duplicate pairs following a neofunctionalisation model of evolution. We have also demonstrated that there is a strong release from negative selective pressure following duplication with 0 << dR/dS < 1 at low values of S: sufficiently lower than 1 for the hypothesis of neutral evolution to be rejected and sufficiently higher than the negative selection rate of dR/dS for pure subfunctionalisation to be considered a minor fate for genes that are not the result of whole-genome duplication events. These findings suggest that, for the smaller-scale duplicates that evade pseudogenisation, neofunctionalisation is a common fate (either alone or in combination with subfunctionalisation). While current thinking suggests that subfunctionalisation is a major fate of retained duplicates following whole genome duplication, further work is needed to determine whether this is the case or whether alternative fates such as dosage compensation or neofunctionalisation are more common. If subfunctionalisation is shown to be an important fate following WGD, it will be interesting to establish whether this is pure subfunctionalisation or whether it is coupled with neofunctionalisation.