Introduction

The degree to which an amino acid site is free to vary is strongly dependent on its structural and functional importance. An amino acid that plays an essential role, such as one within the active site of the protein, is unlikely to change over evolutionary time. Hence, the evolutionary rate at an amino acid site is indicative of how conserved this site is and, in turn, allows evaluating the importance of this site in maintaining the structure/function of the protein (Lichtarge and Sowa 2002). In silico detection of conserved regions can thus focus mutagenesis experiments on functionally important residues (e.g., Donaudy et al. 2003).

Conservation levels are typically inferred from a multiple sequence alignment of homologous proteins. Numerous methods for detecting site-specific conservation have been previously proposed. Nineteen such scores, developed in the last 30 years, have recently been reviewed by Valdar (2002). Though evolution is the driving force which determines site conservation, hardly any of these methods takes the evolutionary relationships among the sequences (phylogeny) into account (but see Lichtarge et al. 1996; Armon et al. 2001).

Conservation levels and evolutionary rates are, in fact, synonymous. A conserved site is slow evolving while a variable site evolves rapidly. It is this observation that places the problem of conservation-score estimation in the realm of probabilistic evolutionary models. Although probabilistic models are extensively used in phylogenetic and in molecular evolutionary studies, they have only recently been applied for evaluating site-specific evolutionary rates in proteins (Dean and Golding 2000; Pupko et al. 2002). Such methods have been shown to be superior to those reviewed by Valdar (2002) since they take into account the branch lengths of the phylogenetic tree and make use of explicit probabilistic-based evolutionary models (Pupko et al. 2002). We note that evolutionary rates are commonly measured as the number of replacements per amino acid site per year. Here we define a site-specific rate as the evolutionary rate of the site relative to the average evolutionary rate across all sites. Site-specific rates are hence unitless.

All algorithms of rate inference presented to date are composed of two basic steps: (1) construct the phylogenetic tree and (2) infer site-specific rates. Various inference methods differ in the manner in which step 2 is performed, while all rely on the assumption that the phylogeny is absolutely correct. Such an approach may lead to erroneous results if the inferred phylogeny does not reflect the true underlying evolutionary relationships among the sequences. As demonstrated in Fig. 1, inferred rates might be substantially different under two different topologies. An alternative approach would consider the phylogeny as an additional parameter of the model and would compute site-specific rates taking into account alternative tree topologies. More accurate predictions of evolutionary rates are thus expected since the inherent uncertainty in the phylogeny is integrated in the computation. Such a comprehensive evolutionary approach calls for the use of Bayesian phylogenetics.

Figure 1
figure 1

The rate of a position depends on the assumed phylogenetic tree. The inferred evolutionary rate is different for the two topologies. a The inferred rate would be relatively low since only one replacement is sufficient to explain the data. b The inferred rate would be higher since at least two replacements are necessary. Branches that differ between the two trees are dashed. Capital letters in parentheses are one-letter abbreviations for amino acids.

Full size image

Bayesian estimation of phylogeny is based upon the posterior probability distribution of trees. The posterior probability distribution for an unrooted phylogenetic tree involves a huge number of tree topologies [(2n−5)!/2n−3(n−3)! unrooted trees for n sequences (Felsenstein 2004)]. For each such tree, there are infinite possibilities of branch length combinations. This parameter space is too complex to solve analytically. Markov chain Monte Carlo (MCMC) (Metropolis et al. 1953; Hastings 1970) is a numerical method that can be used for Bayesian inference from this complex parameter space. MCMC is firmly grounded in probability theory (see, e.g., Gelman et al. 1995) and has recently been applied in phylogenetic studies (Yang and Rannala 1997; Larget and Simon 1999; Mau et al. 1999; Li et al. 2000; Huelsenbeck and Ronquist 2001; McGuire et al. 2001; Jow et al. 2002). In this paper we describe a novel Bayesian method for site-specific rate estimation. Using MCMC, we integrate over the space of all possible tree topologies, branch lengths, and evolutionary model parameters to obtain site-specific rate estimates that account for the stochastic nature of the underlying evolutionary process. We show that by doing so a significant improvement in site-specific rate estimation is achieved.

Methods

The Evolutionary Model

In this study, the JTT model of amino acid replacements (Jones et al. 1992) with among-site rate variation, as specified by a gamma distribution, is used. The only additional parameter required by this model is the shape parameter of the gamma distribution, α. Thus, the free parameters in our model are τ, t, and α, which are the tree topology, the branch lengths, and the among-site rate variation parameter, respectively.

Site-Specific Rate Estimation Given a FixedPhylogenetic Tree

A phylogenetic tree T= (τ, t) is defined by its tree topology τ and associated branch lengths t. The branch lengths of the phylogenetic tree represent the average evolutionary rate across all sites. A relative site-specific rate r indicates how fast this site evolves relative to the average rate across all sites. For example, a rate of 2.0 indicates a site that evolves two times faster than the average. Thus, site-specific rates inferred here are not absolute evolutionary rates that require knowledge of divergence times but, rather, represent a comparative quantity.

Within the Bayesian framework, the posterior probability of any given rate r is obtained from the likelihood function and the prior probability. The most commonly chosen prior distribution for modeling rate variation across sites is the gamma distribution. The gamma distribution has a single parameter, α, which determines its shape (Swofford et al. 1996; Yang 1996). Given a tree T and a parameter α, the posterior probability for any given rate r is obtained using Bayes’ (1763) theorem

$$ P(r|data,T,\alpha )={{P(data|r,T)P(r|\alpha )} \over {\int\limits_{r'=0}^\infty {P(data|r',T)P(r'|\alpha )dr'} }} $$
(1)

where the likelihood P(data|r,T) can be calculated using Felsenstein’s (1981) postorder tree traversal algorithm, and P(r|α) is the prior distribution on the rates. A detailed description of the calculation is given by Mayrose et al. (2004). We denote by P both probabilities and densities, depending on the context. The gamma distribution is approximated by a discrete rate distribution with k = 16 categories (Yang 1994). For the task of site-specific rate inference this number of categories sufficiently approximates the continuous gamma distribution (Mayrose et al. 2004). After the discrete approximation Eq. (1) becomes

$$ P(r=r_i |data,T,\alpha ) \cong {{P(data|r_i ,T)} \over {\sum\limits_{j=1}^k {P(data|r_j ,T)} }} $$
(2)

The prior probabilities in Eq. (1) are canceled out since all rate categories have equal prior probabilities (l/k).

The goal is to estimate the site-specific rates for all positions. Our site-specific rate estimate is defined as the expectation of r over its posterior rate distribution:

$$ E(r|data,T,\alpha ) \cong \sum\limits_{j=1}^k {r_j P(r_j |data,T,\alpha )} $$
(3)

This estimate was shown to be more accurate than the maximum likelihood (ML) estimate that assumes no prior rate distribution (Mayrose et al. 2004).

Evolutionary-Rate Inference over the Entire Tree Space

Equation (3) can be read as “the expectation of r given that the tree topology is τ, the set of associated branch lengths is t, and the shape of the gamma distribution is α.” In the case where the combined state ω = {τ, t, α} is unknown, we can use the law of total probability to obtain a site-specific rate estimate over the whole tree space and over all α values:

$$ E(r|data)=\sum\limits_{i=1}^{C_s } {\int\limits_{t_i } {\int\limits_a {E(r|data,\tau _i ,t_i,\alpha )P(\tau _i ,t_i,\alpha |data)dt_i d\alpha {\rm{ }}} } } $$
(4)

The symbol τi labels the ith tree topology, t i is the set of branch lengths associated with this topology, and C s is the number of possible topologies for a data set containing S sequences. According to Bayes’ law, the second term on the right-hand side of Eq. (4) can be expressed as

$$ P(\tau _i ,t_i ,\alpha |data)={{P(data|\tau _i ,t_i ,\alpha )P(\tau _i ,t_i ,\alpha )} \over {\sum\limits_{j=1}^{C_s } {\int\limits_{t_j } {\int\limits_{\alpha '} {P(data|\tau _i ,t_j ,\alpha ')P(\tau _j ,t_j ,\alpha ')dt_j d\alpha '} } } }} $$
(5)

Each one of the expressions within Eq. (5) can be readily computed. However, the enumeration over all possible tree topologies and, for each topology, the integration over all possible combinations of branch lengths and α values is intractable for realistic-sized problems. MCMC is therefore used to generate a large sample from the posterior probability distribution of states without the explicit computations of these sums and integrals.

MCMC

The basic Metropolis–Hastings MCMC algorithm (Metropolis et al. 1953; Hastings 1970; Gelman et al. 1995) follows a two-step process. First, a new state, ω*, is proposed according to some stochastic proposal mechanism. Second, the new state is either accepted or rejected according to a transition probability. If the proposed state, ω*, is accepted, it becomes the next state of the chain, ωn+1. Otherwise the chain remains in its current state and so ωn+1 = ωn. The transition probability is defined as

$$ \eqalign{P(\omega ^* |\omega^{\prime\prime}) &\equiv \min \left[ 1, \underbrace {{P(\omega ^* |data)} \over {P(\omega ^n |data)}}_{\rm Posterior\ ratio} \times \underbrace{{f(\omega ^n |\omega ^*)} \over {f(\omega ^* |\omega ^n )}}_{{\rm Hasting\ ratio}} \right] \cr &= {\min \left[ {1,\underbrace {{{P(data|\omega ^* )} \over {P(data|\omega ^n )}}}_{{\rm{Likelihood\ ratio}}} \times \underbrace {{{P(\omega ^* )} \over {P(\omega ^n )}}}_{{\rm{Prior\ ratio}}} \times \underbrace {{{f(\omega ^n |\omega ^* )} \over {f(\omega ^* |\omega ^n )}}}_{{\rm{Hasting\ ratio}}}} \right]}} $$
(6)

f(ω*|ωn) is the probability of proposing the new state given the old one and f(ωn|ω*) is the probability of the reverse move, which is not actually made. These two terms are calculated based on the specific proposal mechanism implemented, which defines how a new state will be proposed given the current state of the chain. The advantage of the formulation in Eq. (6) is that the complex denominator in Eq. (5) is canceled out. The above formula reduces to three ratios, each of which can be readily calculated. Note that if the right-hand term in Eq. (6) is bigger than 1.0, the move is always accepted. This reflects a general tendency of the chain to go “uphill” when possible and to go “downhill” only occasionally. The starting state of the chain, ω0, is chosen randomly from the entire parameter space. The points sampled during an initial portion of the chain (called burn-in) are discarded since they are still characteristic of the starting point and do not reflect properly the posterior distribution. The proportion of the time any single state is visited after the burn-in stage is a valid approximation of its posterior probability.

For each state ω in the sample, a site-specific rate estimation is calculated (Eq. [3]). The result of the algorithm is a rate estimate (\(\hat {r} \)) over all states sampled. This estimate can be expressed as

$$ \hat r={1 \over N}\sum\limits_{i=1}^N {E(r|\omega ^i ,data)} $$
(7)

where N is the number of sampled states. Note that this expression is different from the estimate presented in Eq. (4). In Eq. (4) a rate distribution over the entire tree space is first obtained, and only then is the expectation derived. However, the MCMC algorithm ensures that as N becomes large enough, \( \hat {r} \) converges to the expectation in Eq. (4).

MCMC Implementation

In each step of the Markov chain a new state is proposed according to a predefined proposal mechanism. We have implemented four different types of moves (described below). At each step we choose one of these moves randomly according to a predefined distribution. All move types are symmetrical, i.e., the probability of moving from state X to state Y is the same as the probability of the reverse move from Y to X. The Hastings ratio in Eq. (6) thus equals 1.0.

The nearest-neighbor interchange (NNI) proposal randomly selects an internal branch of the tree. It then randomly interchanges two of four “neighboring” subtrees, one from each end of the internal branch. The lengths of all branches are kept unchanged. The NNI proposal, or equivalent variations of it, is currently employed in all four MCMC computer programs available for phylogeny (Larget and Simon 1999; Huelsenbeck and Ronquist 2001; McGuire et al. 2001; Jow et al. 2002).

A second proposal mechanism changes the length of a randomly chosen branch according to a sliding window mechanism: a window of some fixed width, δ, is placed around the current length of the branch, x. δ is a tuning parameter. The proposed length, x*, is then chosen uniformly from the interval (x − δ, x + δ). If x* becomes negative an NNI move is employed, and the length of the proposed branch is set to |x*|. If the branch is an external branch, then the topology of the tree remains the same. This proposal mechanism mainly results in branch length changes but can also induce a local topology change via an NNI move (see also Jow et al. 2002).

The third proposal mechanism modifies all branch lengths of the tree simultaneously. For each branch a number u is randomly drawn from the interval (1, 1 + ε), where ε is a tuning parameter. For a branch of length d, a new length, d*, proposed with equal probability to be either (d × u) or (d / u). The fourth proposal mechanism modifies the gamma distribution parameter α to be either (α × u) or (α / u), where u is randomly drawn from the interval (1, 1 + ζ).

The values of the tuning parameters (δ, ε, and ζ) need to be carefully chosen for an efficient MCMC algorithm to traverse the entire parameter space. As a rule of thumb, the acceptance rate should be between 20 and 60% to provide a good mixing of the data (Huelsenbeck 2000). In the present implementation, the starting value for each tuning parameter is 0.1. During the burn-in period, each tuning parameter is increased or decreased depending on the acceptance rate of the move it controls, so that the acceptance rate will be between 20 and 60%.

A practical problem associated with MCMC is to determine how many steps are necessary in order to obtain a good approximation of the posterior distribution. The most useful diagnosis is to run multiple independent chains each with a different starting point (Huelsenbeck et al. 2002). If these chains converge to the same estimated rates, it is a strong indication that the chains have appropriately sampled the parameter space. Here convergence is defined when all pairwise correlation coefficients between the inferred rates from all chains are higher than 0.99. The rates inferred by the independent chains are then averaged to produce final rate estimates. A second diagnostic was performed to ensure that, at all sites, estimated rates have reached their limiting values. We therefore test if all rate estimates are restricted to a small interval of size ε for more than M steps. In all runs conducted, ε and M were set to 0.01 and 800, respectively. These values appear to balance between computation time limitations (which calls for a large ε and a small M) and precision (which calls for a small s and a large M). According to this diagnostic tool the run is halted when all sites have converged to their limiting values. Combining the two tests described above, the run is halted when both diagnostic criteria are satisfied.

Prior Probabilities

In order to calculate the transition probability between states (Eq. [6]) a prior distribution for ω must be specified. Since there is no a priori biological justification for supporting any particular prior, a simple factorized prior P(ω) = P(τ i )P(t i )P(α) was chosen (as in Jow et al. 2002). A discrete uniform prior was set over topologies such that P(τ i ) = 1/C s . Continuous uniform priors were given for branch lengths and α. The interval of possible branch lengths was set to (0, 5) while the interval for α was set to (0, 10). This choice ensures that all reasonable values of the parameters are reachable.

The Computer Program

The MCMC rate-inference algorithm described here is implemented in the program McRate, written in C++. The program is available at http://www.tau.ac.il/∼talp/MCMC/McRate.html. The sole obligatory input to McRate is a multiple sequence alignment file. The program allows users to specify a number of optional parameters such as the burn-in period and number of chains.

Simulations

Simulations were used in order to compare the accuracy of the rates inferred by McRate and those inferred by an empirical Bayesian approach, in which inference is based on a single phylogenetic tree (i.e., rates are inferred using Eq. [3]). We refer to this single tree method as ST. Our simulation runs were conducted using two different schemes. The first simulation set tested the effect of different rate distributions, while the second set tested different model trees.

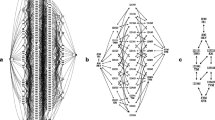
For the first set, we chose a model tree with 17 operational taxonomic units (OTUs) (Fig. 2a). This tree was chosen because it was shown to be a difficult case for phylogeny inference (Alfaro et al. 2003). The rate at each position was drawn from a specified rate distribution. Three different sets of rate distributions were examined: (1) a gamma distribution with α = 0.3 that represents a severe among-site rate variation, (2) a gamma distribution with α = 1.0 that represents a case of little among-site rate variation, and (3) an empirical distribution inferred by ST from a multiple sequence alignment of 57 potassium channel proteins (see Biological Results, below). This distribution can be considered a realistic one because it is based on a large number of homologs and because of the good quality of the alignment. In all runs, the simulated rates were scaled so that the average equals 1.0.

Figure 2
figure 2

Model trees used for simulations. The scale in the upper left corner is indicative of branch length. The number of OTUs is (a) 17, (b) 7, and (c) 27.

Full size image

In the second set of simulations, we used model trees with different number of OTUs. In addition to the 17-OTU model tree used in the first simulation set, we generated two trees with 7 and 27 OTUs (Figs. 2b and c). For this set of simulations, the rates were drawn from a gamma distribution with α = 0.3. In all runs, the simulated rates were scaled so that the average equals 1.0.

Site-specific rates were drawn from the given rate distribution and were assigned to each site. Protein sequences were then generated by simulating evolutionary changes along the branches of the given model tree. The simulation used the JTT model of amino acid replacement (Jones et al. 1992), in which each site evolves independently. For each run, 100 sites were generated in this manner. The generated sequences were given as input to both McRate and ST. ST requires for its computations an assumed phylogenetic tree and a given α parameter. Two different tree reconstruction algorithms were examined: (1) ST-ML, in which an ML tree was constructed using the Semphy program (Friedman et al. 2002) and (2) ST-NJ, in which the tree was constructed according to the neighbor-joining (NJ) algorithm (Saitou and Nei 1987) with pairwise distances estimated by ML. Branch lengths in the resulting tree were then optimized using ML. In both cases the α parameter was inferred from the data by maximizing P(data| α,T) using a 16-category discrete gamma distribution (Yang 1994). For each simulation condition studied (e.g., a 7-OTU tree with α = 0.3) a total of 30 identical and independent simulation runs were conducted.

In each simulation run, three vectors of rates were inferred: one vector by McRate and two by ST (ST-NJ and ST-ML). The accuracy of inference was analyzed by the sum-of-squares (SOS) distance between the simulated rates and the rates inferred by each method. The SOS distances obtained from McRate and ST are dependent because, for each run, inferences were performed based on the same simulated data. For each simulation condition tested, 30 SOS measures were obtained for each inference method. A two-sided Wilcoxon nonparametric test between two dependent samples (Sokal and Rohlf 1981) was then performed in order to check whether the inference techniques attain comparable accuracy. A nonparametric test was used to eliminate the assumption that the SOS measures are normally distributed. The null hypothesis is that the two methods produce equal results. Rejection of the null hypothesis indicates that the rates inferred with one of the methods are significantly more accurate than those inferred by the other.

Results

Simulation Results

A comparison between the inference accuracy of McRate and the two ST methods for different number of OTUs is shown in Table 1. In all cases McRate is found to be the most accurate method, while ST-NJ seems the least accurate one. This difference is significant in all but one case (Table 1). The simulation shows that the accuracy of all three methods increases as the number of OTUs increases. This finding is expected since more data are available at each position for rate inference.

Table 1 Simulation results: Model trees with different numbers of OTUsa
Full size table

The simulation results obtained with different rate distributions showed a similar trend (Table 2). Mc-Rate is superior to both ST methods under all distributions, although this superiority is not always statistically significant. As Table 2 shows, the shape of the rate distribution influences the accuracy of rate inference. Mayrose et al. (2004) have recently shown that the accuracy of prediction decreases when the amount of among-site rate variation increases (small α values in the gamma distribution). Our results here show that McRate superiority over ST is more noticeable in these cases (Table 2). The difference between McRate and ST-ML is 0.23 and 0.04 when simulating with α = 0.3 and α = 1.0, respectively. Thus, when inference accuracy is less reliable, McRate superiority is more pronounced. In order to obtain a conclusive conclusion regarding McRate’s advantage, we pooled the data from all simulation scenarios (Tables 1 and 2). McRate was found to be significantly superior over both ST methods (p < 0.00001) for this comprehensive data set.

Table 2 Simulation results: Different rate distributionsa
Full size table

McRate integrates both over trees and α values. Another set of simulations was constructed in order to identify which of these factors contributes most to the accuracy. Three MCMC schemes were compared. (1) In McRate, the integration is over all parameters. (2) In McRate_Tree, the integration is over trees only, keeping the α parameter constant. The α used is the mean value estimated using the MCMC integration over all parameters, i.e., the resulting α estimate of McRate above. (3) In McRate_Alpha, the integration is over α values only. The tree was inferred by ML and was kept constant. Table 3 shows that the SOS scores of the McRate and McRate_Tree are almost identical. It seems that in most cases averaging over topologies is the main effect responsible for the greater reliability of the rate estimates.

Table 3 Simulation results obtained using different MCMC schemes
Full size table

Biological Results: The Potassium Channel

Potassium channels are tetrameric integral membrane proteins that form transmembrane aqueous pores through which K+ ions can flow. Potassium channels take part in many different cellular processes including cell volume regulation, hormone secretion, and electrical impulse formation in electrically excitable cells (MacKinnon 2003). The most fundamental role carried out by all K+ channels is to allow the rapid permeation of K+ ions while rejecting, with extreme efficiency, the smaller Na+ ions (or other potential competitors). The solved three-dimensional (3D) structures of a bacterial K+ channel (Doyle et al. 1998; Jiang et al. 2002) have clarified the mechanism of selective ion transfer across the membrane.

We used McRate to study the conservation pattern of the potassium channel protein family. Fifty-seven homologous sequences of the Streptomyces lividans potassium channel, for which the 3D structure is known (PDB ID: 1bl8 [Doyle et al. 1998]), were used in the analysis. The homologous sequences were obtained by a BLAST search (Altschul et al. 1997) against the SwissProt database (http://us.expasy.org/sprot/). A multiple sequence alignment of these homologs was built using CLUSTALW (Thompson et al. 1994). The alignment was given as input to the McRate program. Three independent chains with burn-in period of 10,000 steps were run until convergence was reached (see Methods). The conservation scores were then projected onto the 3D structure. For this projection the continuous rates estimated are mapped into nine different colors (bins), as in the ConSurf server (Glaser et al. 2003). The range of each bin varies so that each one contains one-ninth of the sites. We define highly conserved sites as those that fall in bin 8 or 9. A total of 98 sites were visualized, which corresponds to the length of the sequence in the PDB entry.

The conservation pattern obtained by McRate correlates well with the known functional features that contribute to the channel’s high potassium selectivity and throughput. A well-conserved surface patch of residues (all in the most conserved bin) is found at the extracellular entryway (Fig. 3a). This patch functions as the selectivity filter of the channel. The backbone of this signature sequence forms a rigid opening into which K+ ions fit precisely, but in which the smaller Na+ ions would fit only loosely (Miller 2000). Not surprisingly, mutating these amino acids disrupts the channel’s ability to discriminate between K+ and Na+ ions (Heginbotham et al. 1994). A second conserved region is formed by residues of medium to high conservation levels (Fig. 3b). This region forms the inner vestibule, which is lined mostly by hydrophobic residues. This hydrophobic lining provides the diffusing K+ ion with a direct inert path through the membrane (Doyle et al. 1998). The medium conservation levels can be explained since the residues are bound only by a hydrophobic constraint. McRate also detected some highly conserved sites other than those forming the two patches above. Noteworthy, these conserved residues are known to be important in maintaining the function and structure of the channel (e.g., sites involved in interhelical contacts or in the allosteric mechanism of pore closing and opening).

Figure 3
figure 3

The conservation pattern of the potassium channel as inferred by McRate. a The four subunits are viewed from the extracellular side. b Conservation scores are shown on one subunit only, oriented with the extracellular surface on top. Conservation scores are color-coded onto the van der Waals surface of the protein. The K+ ions are yellow.

Full size image

In order to evaluate McRate’s potential advantage over existing methods, the conservation pattern of the potassium channel was studied with two additional methods. First, we used ST-ML—the second-best performing method in our simulations. Second, we estimated the rate at each site with the maximum parsimony (MP) score calculated on the ML tree. The MP method represents a very fast yet naïve approach for rate estimation. The conservation analysis obtained using ST-ML identified approximately the same conserved patches as McRate. The similarity between these two methods is also reflected in the high correlation between the estimated rates (r2 = 0.934). We note, however, that 35 of 98 sites were assigned to a different conservation bin with differences spanning up to three bins. Some of these differences were located in functionally important domains.

Results obtained from the MP method were substantially different from those calculated by either McRate or ST-ML. The main conserved patch was only partially detected. Moreover, the patch comprising the hydrophobic lining could not be identified due to its average conservation. Additionally, only 16 sites fell into the same conservation bins as in the analysis performed by McRate. The calculation time required by the three methods varied substantially. McRate’s analysis took about a day, and only a few minutes for ST-ML and MP (using Pentium 4, 2.40 GHz, with 512 MB of RAM).

Discussion

The MCMC approach presented here has a number of advantages. It allows us to effectively integrate over all possible trees and model parameters. MCMC samples from the entire phylogeny space, rather than relying on a single best tree. Moreover, prior distributions are assumed for all parameters of the evolutionary model (e.g., the gamma shape parameter, α). The inference of evolutionary rates is then based on all possible values of the parameters in addition to all possible trees.

The simulation results indicated that the MCMC approach, as implemented with the computer program McRate, is superior to methods that rely on a single tree. McRate and the ST method utilize the same probabilistic approach for computing site-specific rates, i.e., the expectation over the posterior rate distribution. Therefore, McRate’s improved accuracy clearly arises from considering different evolutionary scenarios rather than the particular rate computation method implemented. McRate advantage was verified for different model trees and different distributions of simulated rates. Our simulations revealed that the performance of ST is, at best, similar to McRate under some scenarios. Our simulations further showed that when ST is based on the ML tree, rather than on the NJ tree, better results are obtained. This difference evidently arises from using a better tree-inference technique.

When presenting the first Bayesian rate-inference technique for DNA sequences, Yang and Wang (1995) found a very high correlation between the rates inferred from an ML tree and those obtained by using a star-like tree. They have subsequently argued that the prediction of evolutionary rates is tolerant to errors in phylogenetic tree reconstruction. This means that inferred rates would be highly similar, no matter which tree is assumed. If this hypothesis proves factual then averaging over many possible trees will have little effect on the predicted rates. However, their conclusion was based on 4-OTU trees only. Yang and Wang’s (1995) conclusion is compatible with our results obtained when 4-OTU trees were simulated (results not shown). In these cases the correlations between rates inferred by McRate and ST were extremely high (r > 0.99), which means that the differences between the two methods are trivial. However, upon inclusion of additional taxa, our simulations showed that the topology has a substantial effect on the estimated rates.

McRate’s capabilities for predicting functionally important protein regions were demonstrated using the thoroughly studied potassium channel protein family. Both McRate and ST-ML successfully recovered the known functional regions. The difference is limited to specific sites that are assigned to different conservation bins. However, in light of McRate’s superiority in most simulation schemes it is likely that its predication regarding the potassium channel is more accurate. The MP analysis demonstrated that such a naïve method is too simplistic for real biological examples. Our results indicate that even the most conserved area was only partly recovered. Indeed, poor performance was also observed when using the MP score in all simulations schemes (results not shown).

Bayesian methods in phylogeny were recently criticized in the context of overestimating the Baye-sian support for internal nodes as compared with the traditional bootstrap and jackknife techniques (Simmons et al. 2004; Suzuki et al. 2002). In this study, however, the Bayesian technique is used only to obtain a large set of plausible trees and not to produce a measure of support to one single best tree.

We expect that in cases where the phylogenetic tree is hard to recover (short sequences, many gapped positions, etc.), the differences between MCMC and the single-tree approach will intensify. Practically, McRate is time-consuming and should be the tool of choice when there are indications that the inferred phylogenetic tree is unreliable.