1 Introduction

Future space systems are looking toward higher thrust, longer operating duration, more reliable and reusable systems. In the development process of these systems, the thermal protection is critical to ensure that materials are within acceptable temperature limits. Transpiration cooling has been proven as an effective mechanism of heat dissipation by numerous investigations.

The early investigation of transpiration cooling can be traced to Hartnett and Eckert [1] in 1950s. This investigation has been extended into many fields for both military and aerospace applications, such as the combustion chambers of scram-jet engines, the leading edges of hypersonic vehicles [2, 3], the first stages of gas turbine blades [4, 5], and rocket nozzles [6, 7]. In recent years, the problems of the ablation materials in missile launching systems, reentry vehicles, and rocket motor nozzles have come to investigators’ attention [8, 9]. The ablation of wall mass can release the latent heat of phase change and resist the high heat flux. This process is called ablation cooling. However, Choi et al. [2] indicated, “the ablative heat dissipation mechanism appears inapplicable for continuous operation of hypersonic vehicles because of significant ablation loss of combustor wall materials”. Therefore, it would be an interesting subject to control the ablation loss.

In the most studies mentioned above, the transpiration cooling was only seen as a single process and the influence of material ablation on the cooling effect was not considered, even though in some situations both can appear simultaneously. Therefore, it is necessary to predict the integrative performance of transpiration and ablation cooling. This paper develops a model to investigate the process of ablation and transpiration cooling numerically. The objective is to control the ablative process and avoid the ablation by transpiration cooling.

2 Physical model and mathematical formulation

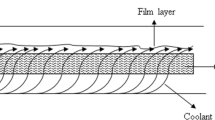
The physical model considered in this work is sketched in Fig. 1. It is a porous plate, its upper surface is exposed to a severe heat flux \(\dot{q},\) which could result in an ablation of the plate and the thickness decreases from initial value s 0 to s with a speed of \(\dot{s}(t)\) in the opposite direction to y. To control this ablation, coolant is injected into the plate from below through the coolant channel with a mass flow rate of \(\dot{m}_{\rm c}.\) Assuming that the ablative phenomenon can be controlled, the thickness loss is small enough, and the variation of the porosity and permeability due to the ablation can be neglected. There are only two phases, solid matrix and coolant fluid, in the porous plate. For one-dimensional problems, according to Amiri and Vafai [10, 11], energy equations for the two phases are:

$$(1 - \varepsilon )(\rho c)_{\rm s} \frac{{\partial T_{\rm s}}}{{\partial t}} = \frac{\partial}{{\partial y}} \left(k_{{\rm seff}} \frac{{\partial T_{\rm s}}} {{\partial y}}\right) - h_{{\rm sf}} a_{{\rm sf}} (T_{\rm s} - T_{\rm f})$$
(1)
$$(\rho c)_{\rm f} \left(\varepsilon \frac{{\partial T_{\rm f}}}{{\partial t}} + v_{\rm f} \frac{{\partial T_{\rm f}}}{{\partial y}}\right) = \frac{\partial}{{\partial y}}\left(k_{{\rm feff}} \frac{{\partial T_{\rm f}}}{{\partial y}}\right) + h_{{\rm sf}} a_{{\rm sf}} (T_{\rm s} - T_{\rm f}),$$
(2)

where the fluid effective thermal conductivity consists of the stagnant and dispersion conductivity and is constructed based on the experimental finding of Wakao and Kaguei [12] as follow:

$$k_{{\rm feff}} = k_{\rm f} {\left[ {\varepsilon + 0.5\left(\frac{{\rho _{\rm f} vd_{\rm p}}}{{\mu _{\rm f}}}\right)\Pr} \right]}.$$

The solid effective thermal conductivity is dependent on the stagnant conductivity and the porosity:

$$k_{{\rm seff}} = k_{\rm s} (1 - \varepsilon ).$$

Assuming that the solid matrix and the coolant fluid have the same temperature T s=T f, introducing an overall thermal conductivity,

$$k_{{\rm eff}} = (1 - \varepsilon )k_{{\rm seff}} + \varepsilon k_{{\rm feff}} $$

and an overall heat capacity,

$$(\rho c)_{{\rm eff}} = (1 - \varepsilon )(\rho c)_{\rm s} + \varepsilon (\rho c)_{\rm f} $$

by adding Eqs. 1 and 2 together with constant coolant mass flow rate \(\dot{m}_{\rm f} = \rho _{\rm f} v_{\rm f},\) we can obtain a local thermal equilibrium equation:

$$(\rho c)_{{\rm eff}} \frac{{\partial T}}{{\partial t}} + \dot{m}_{\rm f} c_{\rm f} \frac{{\partial T}}{{\partial y}} = \frac{\partial}{{\partial y}}\left(k_{{\rm eff}} \frac{{\partial T}}{{\partial y}}\right).$$
(3)

This equation is conditionally valid. Kim and Jang [13] predicated that when the interstitial heat transfer coefficient is proportional to the Reynolds number with a power greater than 1, the assumption of local thermal equilibrium is valid. For sintered metals, Kar and Dybbs [14] suggested the Nusselt number based on the interstitial heat transfer coefficient as:

$${\rm Nu} = \frac{{h_{{\rm sf}} d_{\rm p}}}{{k_{\rm f}}}\sim C \operatorname{Re}^{n}_{{d_{\rm p}}}\;\hbox{if}\;0 < \operatorname{Re} _{{d_{\rm p}}} < 10^{2}, $$

where C is a coefficient and the power n is about 1.35. In this paper, the porous plate is made of sintered metal and the considered Reynolds number less than 100. Thus, the assumption of local thermal equilibrium is suitable.

Fig. 1
figure 1

One-dimension model of ablation and transpiration cooling

Full size image

2.1 Initial and boundary conditions

At the beginning of transpiration cooling, the porous plate is at a uniform temperature:

$$t = 0\quad T(y) = T_{0},\quad \hbox{for all}\;y.$$
(4)

At the interface of the porous plate and coolant channel, the convective boundary condition presented by Glass and Dilley [15] as well as Landis and Bowman [16] is used in this paper.

$$t > 0\quad h(T - T_{\rm c}) = k_{{\rm eff}} \frac{{\partial T}}{{\partial y}}\quad\hbox{at}\;y = 0.$$
(5)

The interface of the plate and heat flux is a moving boundary due to ablation. This is a typical Stefan boundary problem [17] and was described by [18]

$$t > 0\quad k_{{\rm eff}} \left. {\frac{{\partial T}}{{\partial y}}} \right|_{{y = s(t)}} - (1 - \varepsilon )\rho _{\rm s} L\left. {\frac{{{\rm d}s(t)}}{{{\rm d}t}}} \right|_{{y = s(t)}} = \dot{q}\quad\hbox{at}\; y = s(t).$$
(6a)

Here, L is the latent heat of solid material. Zhang and Faghri [19] used the coefficient (1 − ɛ) to deal with the porosity of the plate. When the temperature at the interface reaches the melting point of the material, the boundary moves with a speed of

$$\left. {\dot{s}(t) = \frac{{{\rm d}s(t)}}{{{\rm d}t}}} \right|_{{y = s(t)}}\quad \hbox{if}\; T = T_{m}.$$
(6b)

When the temperature is lower than the melting point, the thickness of the porous plate maintains s 0 and the moving speed \(\dot{s}(t)\) is zero.

2.2 Non-dimensionalization

To solve the problem of the moving boundary, the front-fixing method is used by Landau transformation [16]:

$$Y = \frac{y}{{s(t)}}.$$
(7)

Introducing the following dimensionless parameters:

$$\theta = \frac{{T - T_{\rm c}}}{{T_{m} - T_{\rm c}}},\quad \tau = \frac{t}{{{s^{2}_{0} (\rho c)_{{\rm effc}}} \mathord{\left/ {\vphantom {{s^{2}_{0} (\rho c)_{{\rm effc}}} {k_{{\rm effc}}}}} \right. \kern-\nulldelimiterspace} {k_{{\rm effc}}}}},\quad S = \frac{{s(t)}}{{s_{0}}},$$
(8)

where T c and T m are the coolant temperature at the entry of the coolant channel and the melting temperature of the solid material, respectively, the thermal properties k effc and (ρc)effc are taken at the reference temperature T c, using these parameters, Eq. 3 can be written as:

$$\frac{{\partial \theta}}{{\partial \tau}} + \frac{1}{S}{\left[ {\frac{{(\rho c)_{{\rm effc}}}}{{(\rho c)_{{\rm eff}}}}\frac{{c_{\rm f}}}{{c_{{\rm fc}}}}M - Y\frac{{{\rm d}S}}{{{\rm d}\tau}}} \right]}\frac{{\partial \theta}}{{\partial Y}} = \frac{1}{{S^{2}}}\frac{{(\rho c)_{{\rm effc}}}}{{(\rho c)_{{\rm eff}}}}\frac{\partial}{{\partial Y}}\left(\frac{{k_{{\rm eff}}}}{{k_{{\rm effc}}}}\frac{{\partial \theta}}{{\partial Y}}\right).$$
(9)

Here, \(M = \frac{{\dot{m}_{\rm f} c_{{\rm fc}} s_{0}}}{{k_{{\rm effc}}}}\) is defined as dimensionless coolant mass flow rate and can be written as: \(M = \operatorname{Re} _{{d_{\rm p}}} \frac{{s_{0}}}{{d_{\rm p}}}\frac{{c_{{\rm fc}} \mu _{{\rm fc}}}}{{k_{{\rm effc}}}}.\) To ensure the validity of the assumed local thermal equilibrium, the Reynolds number should be less than 100. Based on the thermal properties of coolant and sintered metal used in this paper, the variation of (s 0/d p)(c fc μ fc)(k effc) is estimated in the range of approximately 1 ∼ 10. From this expression, it can be concluded that when the coolant mass flow rate M is less than 1,000, the assumed local thermal equilibrium is suitable.

The corresponding dimensionless initial and boundary conditions are:

$$\tau = 0,\quad \theta (Y) = \theta _{0},\quad\hbox{for all}\;Y$$
(10)
$$\tau > 0,\quad \frac{{k_{{\rm eff}}}}{{k_{{\rm effc}}}}\frac{1}{S}\frac{{\partial \theta}}{{\partial Y}} = Bi \cdot \theta\quad \hbox{at}\;Y = 0$$
(11)
$$\tau > 0,\quad \left. {\frac{1}{Q}\frac{{k_{{\rm eff}} }}{{k_{{\rm effc}} }}\frac{1}{S}\frac{{\partial \theta }}{{\partial Y}}} \right|_{{Y = 1}} \left. { - \frac{1}{{\rm Ste}}\frac{{\rho _{\rm s} }}{{\rho _{{\rm sc}} }}\frac{{{\rm d}S}}{{{\rm d}\tau }}} \right|_{{Y = 1}} = 1\quad \theta = 1\;{\text{at}}\;Y = 1\quad {\text{with}}\;{\text{ablation}}$$
(12a)
$$\tau > 0, \quad \left. {\frac{1}{Q}\frac{{k_{{\rm eff}}}}{{k_{{\rm effc}}}}\frac{1}{S}\frac{{\partial \theta}}{{\partial Y}}} \right|_{{Y = 1}} = 1,\quad \hbox{at}\; Y = 1 \quad \hbox{without ablation}.$$
(12b)

In Eqs. 12a and 12b, the Stefan number, dimensionless heat flux and the Biot number are defined as:

$${\rm Ste} = \frac{{\dot{q}(\rho c)_{{\rm ec}} s_{0}}}{{(1 - \varepsilon )\rho _{\rm s} k_{{\rm ec}} L}}, Q = \frac{{\dot{q}s_{0}}}{{k_{{\rm effc}} (T_{m} - T_{\rm c})}}\;\hbox{and}\; Bi = \frac{{hs_{0}}}{{k_{{\rm effc}}}}.$$

3 Description of numerical algorithm

In order to reduce the inaccuracy caused by the first-order upwind scheme at the moving boundary, the two-order upwind scheme suggested by Christoper [20] is used to discretize convective term:

$$\left. {\frac{{\partial \theta}}{{\partial Y}}} \right|_{i} = \frac{{3\theta ^{{n + 1}}_{i} - 4\theta ^{{n + 1}}_{{i - 1}} + \theta ^{{n + 1}}_{{i - 2}}}}{{2\Delta Y}}.$$

To avoid handling the penta-diagonal matrix generated in the above process, the deferred correction method presented by Khosla and Rubin [21] is used.

$$\left. {\frac{{\partial \theta}}{{\partial Y}}} \right|_{i} = \frac{{\theta ^{{n + 1}}_{i} - \theta ^{{n + 1}}_{{i - 1}}}}{{\Delta Y}} + \frac{{\theta ^{n}_{i} - 2\theta ^{n}_{{i - 1}} + \theta ^{n}_{{i - 2}}}}{{2\Delta Y}}.$$

The variable thermal properties with temperature and the moving boundary make this problem nonlinear. It can be solved only through an iterative method. The main steps of the iteration are:

  1. 1.

    The initial temperature field is given at first;

  2. 2.

    Using the boundary condition Eq. 12b, the temperature field is calculated at current time step (t), until convergence;

  3. 3.

    Comparing the temperature field with the melting point:

    1. 1.

      When the melting point temperature is reached,

      1. (a)

        Using the temperature field obtained and the boundary condition Eq. 12a, the moving speed of the boundary is computed,

      2. (b)

        The thermal equilibrium equation is solved by utilizing the moving speed;

      3. (c)

        Repeat step (a) and (b), until convergence, go to step 4;

    2. 2.

      If the temperature is lower than the melting point, the result obtained by step 2 can be seen to be acceptable.

  4. 4.

    Return to step 2 for the computation of the next time step, until steady state. The convergent criterion used in the paper is:

    $${\left| {\frac{{\theta ^{{n + 1}}_{{i,{\rm new}}} - \theta ^{{n + 1}}_{{i,{\rm old}}}}}{{\theta ^{{n + 1}}_{{i,{\rm new}}}}}} \right|} < 10^{{- 6}}\;\hbox{at all grid points}.$$

In this paper, 70 uniform grid elements and time step 5.0 × 10− 4 are used in the computations. In addition, the grid and time independent solutions are verified by using time step 2.0 × 10− 4 for grid number 100 and time step 1.0 × 10− 4 for grid number150.

To verify the computer program, we have compared the analytical solution of a melting problem presented by Christoper [20] with the numerical results, which are obtained under the conditions of constant thermal properties, porosity, and zero coolant flow rate (ɛ=0, M=0). As shown in Fig. 2, the relative differences between the analytical and numerical results are small enough, indicating that this program could be seen to be reasonable.

Fig. 2
figure 2

Comparison of analytical and numerical results

Full size image

4 Results and discussions

The porous flat plate used in this paper is made of chromium-nickel alloy (1Cr18Ni9Ti), which has a porosity of 15%, and a melting temperature of 1,250 K. The simulations are carried out under different conditions.

Figure 3 compares the numerical results obtained when the thermal dispersion is considered and neglected at initial temperature 0.3 and 0.6, respectively, and the variation of thermal properties are considered. The comparisons indicate that at different initial temperatures, whether the ablation occurs (θ = 1) or not (θ < 1), the effect of the thermal dispersion is substantially small (10−4) and, therefore, can be neglected. The reason is that in the local thermal equilibrium model, the overall thermal conductivity is mainly dominated by the solid effective thermal conductivity.

Fig. 3
figure 3

Influence of thermal dispersion on the transient temperature at the hot side

Full size image

Figure 4 illustrates the influence of the thermal properties on numerical results at different initial temperatures. The steady temperatures are not influenced by the initial temperatures under the conditions of constant or variable thermal properties. Yet, the hot surface temperatures calculated by constant thermal properties are higher than that by variable thermal properties. The ablative phenomenon (θ=1) in the case of constant thermal properties occurs and persists for a short time, while the temperature of the porous matrix is still lower than the melting point (θ < 1) in the case of variable thermal properties. From this phenomenon, we believe that the variation of thermal properties in the investigation of the ablation should be considered, because it plays a crucial role in estimating the actual ablation problems. In this paper, the method suggested by Gonzo [22] is cited to estimate the variable thermal properties.

Fig. 4
figure 4

Influence of thermal property on the transient temperature at the hot side

Full size image

Figure 5 shows the temperature profile with time at the surface exposed in the heat flux at the different initial temperatures. From this figure, we can find that through a long enough period of cooling, the surface temperatures will reach the same steady value, while the transient cooling effects are distinctly different. When cooling begins at lower initial temperatures, the peak values of the temperature are less than 1, thus the ablation does not occur. The peak values of the temperature increases as the initial temperature increases, up to the maximum value of θ = 1. In this situation, the transpiration cooling cannot avoid the ablation, the ablation and transpiration cooling appear simultaneously. This result indicates that the transient effect is very important for the ablation problems.

Fig. 5
figure 5

Influence of initial temperature on transient transpiration cooling effect

Full size image

Figure 6 illustrates the influence of the initial temperature on the ablative depth of the porous matrix. It is clear that a higher initial temperature will result in a longer ablative time and a larger thickness loss.

Fig. 6
figure 6

Influence of initial temperature on ablation thickness

Full size image

Figure 7 illustrates the influence of the coolant flow rate on transpiration cooling effect at the same initial temperature. A high coolant flow rate can reduce the peak values to an extend that avoids the ablation. The final steady temperature will also be reduced with the increase in the coolant flow rate. From Figs. 5, 6 and 7, it can be extrapolated to decrease the ablative depth or to avoid the ablation using transpiration cooling, the initial temperature and the coolant flow rate are important control parameters.

Fig. 7
figure 7

Influence of coolant flow rate on transpiration cooling effect

Full size image

Figure 8 shows that at the same coolant injection rate and initial temperature, the variation of heat flux will also result in different cooling effects. With an increase in the heat flux, the effect of transpiration cooling falls, the hot surface temperature rises, and duration of the ablative process increases.

Fig. 8
figure 8

Influence of heat flux on transpiration cooling effect

Full size image

Figure 9 shows that a large change in the Stefan number from 0.5 up to 20 has a substantially small effect on the hot surface temperature and the ablative duration.

Fig. 9
figure 9

Hot side temperature is the Stefan number independent

Full size image

Figure 10 illustrates the variation of the ablative thickness with the Stefan number. A larger Stefan number will result in a higher speed of ablation and a larger thickness loss because a larger Stefan number corresponds to a lower latent heat. Figures 9 and 10 represent an interesting phenomenon that the hot surface temperature and the duration of the ablation process are almost independent of the Stefan number, while the ablative speed and the thickness loss are sensitive to the Stefan number. Therefore, the Stefan number is an important parameter in controlling the ablative depth.

Fig. 10
figure 10

Ablation thickness is sensitive to the Stefan number

Full size image

Figure 11 shows the influence of the Biot number on the cooling process at different initial temperatures. The final steady results are not observably influenced by the variation in the Biot numbers or initial temperatures, and the ablation process cannot be avoided by a larger Biot number. However, the transient cooling effects are significantly dependent on the Biot number: a larger Biot number can rapidly reduce the hot surface temperatures to the steady value because the larger Biot number enhances the convective heat exchange between the coolant and the boundary of the porous plate. This phenomenon also indicates that the transient effect of cooling should be considered.

Fig. 11
figure 11

Influence of the Biot number on transpiration cooling process

Full size image

Figure 12 demonstrates the variation of the ablative thickness with the Biot number. From this figure we can find that the ablative speeds at different Biot numbers are almost the same, because all of the profiles have the same slope. However, the duration of the ablation process is significantly reduced with an increase in the Biot number, hence the ablative thickness can also be reduced. Both Figs. 11 and 12 represent another interesting phenomenon: the peak value of the hot surface temperature and the ablative speed are independent of the Biot number, but the ablative duration and the thickness loss are sensitive to the Biot number. Although a larger Biot number cannot prevent the ablation, it enhances the transient cooling effect and reduces the ablative duration. Therefore, the Biot number is another important parameter in controlling the process of the ablation and transpiration cooling.

Fig. 12
figure 12

Influence of the Biot number on ablation thickness

Full size image

5 Conclusions

  • In the investigation of ablative problem, the variation of the thermal properties of the materials should be considered, because it greatly influences the accuracy to estimate the actual ablation process.

  • The coolant flow rate, the intensity of the heat flux, and the initial temperature at which transpiration cooling begins are important parameters in controlling ablative process.

  • Although the Stefan number cannot influence the hot surface temperature and the ablative duration, it influences the ablative depth of the porous matrix through the reduction of ablative speed.

  • The ablative speed is not sensitive to the Biot number, but an increase in the Biot number can shorten ablative duration and reduce ablative thickness.

  • The final results of the hot side temperature are independent of the Stefan number, Biot number, and initial cooling temperatures; however, these parameters play a crucial role in the transient cooling. Therefore, in the investigation of ablation problems, the transient effects should be considered.