1 Introduction

Owing to their numerous applications in industrial manufacturing process, the problem of heat transfer in the boundary layers of a continuously stretching surface with a given temperature or heat flux moving in an otherwise quiescent fluid medium has attracted the attention of researchers for the past 3 decades. Some of the application areas are hot rolling, paper production, metal spinning, drawing plastic films, glass blowing, continuous casting of metals and spinning of fibers. In particular the extradite from the die is drawn and simultaneously stretched into a sheet, which is then solidified through quenching or gradual cooling by direct contact with water. Annealing and thinning of copper wires is another example. In all these cases, the quality of the final product depends on the rate of heat transfer at the stretching surface. By drawing the strips in an electrically conducting fluid subjected to a magnetic field the rate of cooling can be controlled and the final products of desired characteristic might be achieved.

Flow in the boundary layer on a moving continuous solid surface was investigated first by Sakiadias [1–2]. It was observed that the boundary layer growth is in the direction of motion of the continuous solid surface and is different from that of the Blasius flow past a flat plate. Still the boundary layer theory and the basic differential equations are applicable. Koldenhof [3] investigated the heat transfer in the case of movement of fine threads through a liquid. A combined analytical and experimental study of the flow and temperature fields in the boundary layer on a continuous moving surface has been carried out by Tsou et al. [4]. Measurement of the laminar velocity field were in excellent agreement with the analytical predictions. Crane [5] gave similarity solution in closed analytical form for steady 2D incompressible boundary layer flow caused by the stretching sheet with linear velocity. Several researchers have discussed the problem to obtain the thermal and kinematic behavior by considering different power law and exponential variations of stretching velocity and temperature distributions [6–14]. Most of them have applied similarity solution method.

Elbashbeshy [8] has discussed heat transfer over a stretching surface with variable surface heat flux. The effect of temperature dependent viscosity on heat transfer over a continuously moving surface has been analyzed by Elbashbeshy and Bazid [11]. Vajravelu and Hadjinicolaou [12] studied the heat transfer characteristics in the laminar boundary layer of a viscous fluid over a linearly stretching surface with variable wall temperature subject to suction or blowing. They considered the effects of viscous dissipation and internal heat generation. Recently, Magyari et al. [14] reported analytical and computational solutions when the surface moves with rapidly decreasing velocity using self similarity method. In many of the works referred above, the buoyancy force is not taken into consideration. But the following papers reveal the significance of buoyancy force. By considering the effect of buoyancy, Ali and Al-Yousef [15] analyzed mixed convection heat transfer from an uniformly stretching vertical surface with power function form for wall temperature. With general power function form for stretching velocity of the wall, the same problem has been analyzed with surface suction/injection by Ali and Al-Yousef [16]. Lin et al. [17] considered the buoyancy force when the horizontal plate is moving parallel or reversibly to a free stream. The effect of buoyancy on moving plate in rolling and extrusion processing, casting processing is discussed by Karwe and Jaluria [18–19]. It was found that the effect of thermal buoyancy is more significant when the plate is moving vertically upward than when it is moving horizontally.

The effect of viscous dissipation in natural convection process has been studied by Gebhart [20], Gebhart and Mollendorf [21]. It is observed that the effect of viscous dissipation is more predominant in vigorous natural convection and mixed convection processes. They also have shown the existence of similarity solution for the external flow over an infinite flat vertical surface having an exponential variation of surface temperature. The steady free convection flow and heat transfer from an exponentially stretching vertical surface with an exponential temperature distribution has been analyzed by Magyari and Keller [13] both analytically and numerically. They neglected the effect of viscous dissipation in the medium and also the body force which is more significant in the vertical wall configuration.

In this article, we aim at presenting a similarity solution for mixed convection flow and heat transfer from an exponentially stretching surface by considering viscous dissipation effect in the medium. Both the wall temperature and free stream flow are given specific forms of profiles which permit similarity solution. The analysis showed that the buoyancy and viscous dissipation have significant influence on the non-dimensional skin friction and heat transfer coefficients.

2 Governing equations

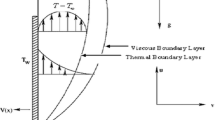
Consider the laminar flow and thermal boundary layers on an impermeable plane vertical wall stretching with velocity uw=u0ex/L and with temperature distribution Tw=T∞+T0e2x/L moving through a quiescent incompressible fluid of constant temperature T∞ as shown in the Fig. 1. The x-axis is directed along the continuous stretching surface and points in the direction of motion. The y-axis is perpendicular to plate and to the direction of slot (z-axis) whence the continuous stretching plane surface issues. u, v are the velocity components in the x- and y-directions. Now, the governing equations under the boundary layer and Boussinesq approximations may be written as:

$$ \frac{{\partial u}} {{\partial x}} + \frac{{\partial v}} {{\partial y}} = 0 $$
(1)
$$ u\frac{{\partial u}} {{\partial x}} + v\frac{{\partial u}} {{\partial y}} = \nu \frac{{\partial ^2 u}} {{\partial y^2 }} + g\beta (T - T_\infty ) $$
(2)
$$ u\frac{{\partial T}} {{\partial x}} + v\frac{{\partial T}} {{\partial y}} = \alpha \frac{{\partial ^2 T}} {{\partial y^2 }} + \frac{1} {{\rho c_p }}\left( {\frac{{\partial u}} {{\partial y}}} \right)^2 $$
(3)

along with the boundary conditions

$$ y = 0,\quad u_{\text{w}} = u_0 {\text{e}}^{x/L} ,\quad v = 0,\quad T_{\text{w}} = T_\infty + T_0 {\text{e}}^{2x/L} $$
(4a)
$$ y \to \infty ,\quad u \to 0,\quad T \to T_\infty . $$
(4b)
Fig. 1
figure 1

Schematic of mixed convection heat transfer from an exponentially stretching surface.

Full size image

Here, α is the thermal diffusivity constant, cp is the specific heat and ν is the kinematic viscosity of the ambient fluid. The above set of partial differential equations are converted into ordinary differential equations using the following similarity transformation

$$ \eta = \left( {\frac{{\text{Re} }} {2}} \right)^{1/2} \frac{y} {L}{\text{e}}^{x/2L} $$
(5)
$$ \psi (x,y) = \sqrt 2 \nu \text{Re} ^{1/2} {\text{e}}^{x/{\text{2}}L} f(\eta ) $$
(6)
$$ T(x,y) = T_\infty + T_0 {\text{e}}^{2x/L} \theta (\eta ) $$
(7)

where η is the similarity variable. The Reynolds’ number is defined as Re = uw L/ν. Let ψ be the stream function defined such that u=∂ψ/∂y and v=− ∂ψ/∂x so that it automatically satisfies the continuity Eq. 1. With the above similarity transformation the governing partial differential equations reduce to a set of ordinary differential equations as

$$ f''' + ff'' - 2(f')^2 = \pm \frac{{{\text{Gr}}}} {{{\text{Re}}^2 }}\theta $$
(8)
$$ \theta '' = \Pr (4f'\theta - f\theta ') - {\text{Gb}}(f'')^2 $$
(9)

and the boundary conditions are transformed to

$$ \eta = 0,\quad f(0) = 0,\quad f'(0) = 1,\quad \theta (0) = 1 $$
(10a)
$$ \eta \to \infty ,\quad f'(\infty ) = 0,\quad \theta (\infty ) = 0. $$
(10b)

The non-dimensional numbers are defined as the Grashof number given by Gr=gβ T0e2x/L L3/ν2, the viscous dissipation parameter known as the Gebhart number, given by Gb=u 20 /cp T0 and the Prandtl number given by Pr = ν/α.

Here u0 is the velocity parameter and T0 is the temperature parameter of the stretching surface. In Eq. 8, the positive sign indicates the aiding flow and the negative sign indicates the opposing flow [16].

3 Results and disscustions

The set of ordinary differential Eqs. 8 and 9 along with the boundary conditions Eq. 10 are solved by giving approximate initial guess values for the missing initial conditions of f′′(0), θ′ (0) and these values are matched with the corresponding boundary conditions at f′(∞) and θ(∞). NAG software routine is used for integrating the corresponding first order system of equations and shooting and matching the initial and boundary conditions. The results are observed upto the accuracy 5×10−5. Extensive calculations have been performed to obtain the flow and temperature fields for a wide range of parameters 0<Pr<5, 0≤Gb≤ 1, and −3<Gr/Re2 ≤ 20. When Gr/Re2 = 0, the flow becomes a forced convection flow and when Gr/Re2 is large, the flow becomes free convection flow.

Typical velocity and temperature profiles in the boundary layer are plotted for selected values of the governing parameters. The non-dimensional velocity across the boundary layer is plotted for varying values of Gr/Re2 and varying Gb in Figs. 2 and 3 respectively, while fixing the other parameter values to depict the flow field. The magnitude of the velocity increased as the value of the flow governing parameter increases. Also, the fluid velocity is observed to be increased in the medium because of the internal heat generated due to viscous dissipation in the medium.

Fig. 2
figure 2

Effect of mixed convection parameter Gr/Re2 on non-dimensional velocity f′.

Full size image
Fig. 3
figure 3

Effect of viscous dissipation parameter Gb on non-dimensional velocity f′.

Full size image

The non-dimensional temperature distribution inside the boundary layer is presented in Figs. 4 and 5. The thermal boundary layer thickness is decreased with increasing Gr/Re2, where as it is increased with the increasing Gb. This is clearly seen from the Figs. 4 and 5. The temperature of the fluid in the medium will be at higher level when viscous dissipation is considered than when it is neglected. So it is natural that the value of θ′(0) is reduced when Gb is increased. That leads to reduction in the heat transfer rate. These results presented here are in conformity with the previous studies, for example as in Ali and Al-youself [15, 16].

Fig. 4
figure 4

Effect of viscous dissipation parameter Gb on non-dimensional temperature θ.

Full size image
Fig. 5
figure 5

Effect of mixed convection parameter Gr/Re2 on non-dimensional temperature θ.

Full size image

The skin friction acting on the surface in contact with the ambient fluid of constant density is

$$ \tau _{\text{w}} = \rho \nu \left. {\frac{{\partial u}} {{\partial y}}} \right|_{y = 0} = \left( {\frac{{\rho \nu u_0 }} {L}} \right)\left( {\frac{{\operatorname{Re} }} {2}} \right)^{1/2} {\text{e}}^{3x/2L} f''(0) $$
(11)

and the non-dimensional skin friction coefficient can be written as

$$ \frac{{C_{\text{f}} }} {{(\text{Re} _x /2)^{ - 1/2} }} = f''(0) $$
(12)

The local surface heat flux through the wall with k as thermal conductivity of the fluid is given by

$$ q_{\text{w}} = - k\left. {\frac{{\partial T}} {{\partial y}}} \right|_{y = 0} = - \frac{{k(T_{\text{w}} - T_\infty )}} {L}\left( {\frac{{\operatorname{Re} }} {2}} \right)^{1/2} {\text{e}}^{x/2L} \theta '(0) $$
(13)

The local Nusslet number is given by

$$ {\text{Nu}}_x = \frac{{xq_{\text{w}} }} {{k(T_{\text{w}} - T_\infty )}} $$
(14)

and the non-dimensional heat transfer coefficient is written as

$$ \frac{{{\text{Nu}}_x }} {{\sqrt {x/2L} \sqrt {\text{Re} _x } }} = - \theta '(0). $$
(15)

In Eqs. 12 and 15, the local Reynold’s number is used and is given by

$$ \text{Re} _x = \frac{{xu_{\text{w}} }} {\nu }. $$
(16)

The non-dimensional skin friction and heat transfer coefficients are plotted against various parameters in Figs. 6, 7, 8, 9 and 10. The heat transfer coefficient is increased with the Prandtl number and also as the value of the flow governing parameter is increased. The effect of viscous dissipation parameter is to reduce the heat transfer coefficient significantly. This is true for all values of the flow governing parameter considered in the study and is clearly depicted in Fig. 7.

Fig. 6
figure 6

Variation of non-dimensional heat transfer coefficient with Pr for fixed values of Gr/Re2 and Gb.

Full size image
Fig. 7
figure 7

Variation of non-dimensional heat transfer coefficient with Gb for fixed values of Gr/Re2 and Pr.

Full size image

The non-dimensional skin friction coefficient is plotted in Figs. 8, 9, and 10. From the first set of curves in Fig. 8, it is clear that the skin friction coefficient increased as the mixed convection flow governing parameter is increased. But with increasing value of Prandtl number, the skin friction coefficient is decreased. Marginal changes are seen in the skin friction coefficient with the viscous dissipation parameter. This is clear from the second set of curves in Fig. 8 and also from the Fig. 9. Figure 10 summarises the effect of Gr/Re2 on the skin friction coefficient for fixed Pr (first set of curves) and for fixed Gb (second set of curves).

Fig. 8
figure 8

Variation of non-dimensional skin friction coefficient with Pr for fixed values of Gr/Re2 and Gb.

Full size image
Fig. 9
figure 9

Variation of non-dimensional skin friction coefficient with Gb for fixed values of Gr/Re2 and Pr.

Full size image
Fig. 10
figure 10

Variation of non-dimensional skin friction coefficient with Gr/Re2 for fixed values of Pr and Gb.

Full size image

The effect of governing parameters on heat transfer coefficient and skin friction coefficient in the opposing flow has been presented in Tables 1 and 2. For a particular value of Pr and Gb, as the intensity of the opposing flow is increased the heat transfer coefficient is reduced, where as the magnitude of the skin friction coefficient is increased. It is very clear from these tables that for a particular value of Pr and Gr/Re2 as Gb takes higher values heat transfer coefficient is decreased, where as the magnitude of skin friction coefficient is increased. For the parameter values considered in the present study, it is noticed that even in the opposing flow, the non-dimensional heat transfer coefficient is reduced where as the non-dimensional skin friction coefficient is increased due to the presence of viscous dissipation in the medium.

Table 1 Non-dimensional heat transfer coefficient vs. mixed convection parameter
Full size table
Table 2 Non-dimensional skin friction coefficient vs. mixed convection parameter
Full size table

4 Conclusions

Convection heat transfer in the laminar flow region from an exponentially stretching surface has been studied taking into consideration, the effect of buoyancy and the viscous dissipation in the medium. It is assumed that the impermeable surface is stretching with an exponential velocity uw=u0ex/L in a quiescent fluid and the surface is maintained at a temperature Tw=T∞+T0 e2x/L. With this combination of functions for velocity and wall temperature, the similarity solution is possible when the effect of viscous dissipation is considered in the medium. The flow governing mixed convection parameter Gr/Re2, the viscous dissipation parameter Gb and the Prandtl number Pr are the non-dimensional parameters arising from the governing equations. The role of each parameter on heat transfer and skin friction coefficient is studied.

The observations are as follows: The velocity boundary layer thickness is increased with the increase of both mixed convection and viscous dissipation parameters. A rapid growth in the non-dimensional skin friction coefficient is noticed with the mixed convection parameter. This signifies the influence of buoyancy on the skin friction coefficient. As the value of mixed convection parameter is increased, the thermal boundary layer thickness is reduced where as due to viscous dissipation the same is increased thereby reducing the non-dimensional heat transfer coefficient. Where as, the non-dimensional skin friction coefficient is increased due to viscous dissipation in the medium.