Résumé
Nous étudions les propriétés locales des espaces de Berkovich sur Z. À l’aide de théorèmes de Weierstraß, nous montrons que les anneaux locaux de ces espaces sont noethériens, réguliers dans le cas des espaces affines et excellents. Nous prouvons également que le faisceau structural est cohérent. Nos méthodes s’adaptent à d’autres anneaux de base (corps valués, anneaux de valuation discrète, anneaux d’entiers de corps de nombres, etc.) et traitent de façon unifiée espaces complexes et p-adiques.
Avoid common mistakes on your manuscript.
1 Introduction
Les fondations de la géométrie analytique complexe étaient établies depuis longtemps lorsque John Tate a proposé, en 1961, la définition d’une géométrie analytique p-adique possédant des propriétés analogues (cf. [19]). Ce sujet a, par la suite, suscité un vif intérêt et plusieurs géométries p-adiques (ou sur d’autres corps valués complets) ont vu le jour, chacune possédant ses spécificités. Mentionnons la théorie de Michel Raynaud, où les espaces sont vus comme des fibres génériques de schémas formels (cf. [18]), et celle de Roland Huber, qui permet de retrouver les points du topos (cf. [12] et [13]).
Dans ce texte, nous nous intéresserons à une autre de ces géométries : celle développée par Vladimir G. Berkovich (cf. [1] et [2]). Outre ses nombreux succès dans des domaines variés (programme de Langlands, intégration motivique, dynamique, théorie de Hodge p-adique, etc.), elle possède la particularité intéressante de permettre de définir des espaces analytiques sur tout anneau de Banach. En particulier, les espaces de Berkovich sur le corps des nombres complexes C (muni de la valeur absolue usuelle |.|∞) existent et ne sont autres que les espaces analytiques complexes usuels. Mieux encore, on peut définir des espaces de Berkovich sur l’anneau des entiers Z (également muni de la valeur absolue usuelle |.|∞) et l’on obtient alors des espaces naturellement fibrés en espaces analytiques complexes et p-adiques. Pourtant, en dehors du cas des espaces définis sur un corps valué complet, bien peu de résultats sont connus. Signalons tout de même l’ouvrage [16] où le cas de la droite de Berkovich sur Z est traité de façon approfondie.
Dans cet article, nous nous proposons de contribuer à l’étude locale des espaces de Berkovich de dimension supérieure sur Z (ou, plus généralement, sur un anneau d’entiers de corps de nombres), espaces que nous imaginons comme des fibrations en espaces affines au-dessus du spectre analytique \(\mathcal {M} ( \mathbf {Z} )\). En géométrie analytique complexe, cette étude repose de façon cruciale sur le théorème de division de Weierstraß, un théorème qui permet de diviser une fonction analytique par une autre, au voisinage d’un point, de façon à obtenir un reste polynomial. Si, dans ce dernier cadre, tous les points sont définis sur le corps de base C, il en va tout autrement dans notre situation, où le corps résiduel  d’un point x peut être une extension non triviale du corps
d’un point x peut être une extension non triviale du corps  sur lequel sa fibre est définie. Dans ce texte, nous démontrons un théorème de division de Weierstraß pour les points dits rigides des fibres (ceux en lesquels l’extension
sur lequel sa fibre est définie. Dans ce texte, nous démontrons un théorème de division de Weierstraß pour les points dits rigides des fibres (ceux en lesquels l’extension  est algébrique).
est algébrique).
Le théorème de division de Weierstraß est l’ingrédient essentiel permettant d’accéder à la structure des anneaux locaux. Nous poursuivons notre travail en démontrant que ceux de l’espace \(\mathbf {A}^{n,\mathrm {an}}_{ \mathbf {Z} } \) sont noethériens et réguliers, puis que le faisceau structural est cohérent, généralisant ainsi en toute dimension les résultats de [16]. Nous les complétons encore en démontrant que les anneaux locaux sont excellents. Pour des espaces analytiques généraux sur Z, ou un anneau d’entiers de corps de nombres, ces résultats entraînent immédiatement que les anneaux locaux sont excellents et que le faisceau structural est cohérent. Ces anneaux locaux étant également henséliens (cf. [16]), ils vérifient l’approximation d’Artin. Nous donnons un exemple concret d’application de ce résultat.
Signalons pour finir que, bien que notre intérêt résidât principalement dans l’étude des espaces analytiques sur un anneau d’entiers de corps de nombres, nous nous sommes efforcés, lorsque cela ne compliquait pas outre mesure les preuves, d’énoncer les résultats dans une généralité maximale en tâchant en particulier de limiter les conditions imposées à l’anneau de Banach  sur lequel les espaces sont définis. Ainsi le théorème de division de Weierstraß vaut-il sur un anneau de Banach quelconque (avec cependant une condition technique lorsque la fibre contenant le point x est définie sur un corps
sur lequel les espaces sont définis. Ainsi le théorème de division de Weierstraß vaut-il sur un anneau de Banach quelconque (avec cependant une condition technique lorsque la fibre contenant le point x est définie sur un corps  imparfait et trivialement valué). Quant aux résultats de noethérianité, régularité et cohérence pour l’espace affine analytique
imparfait et trivialement valué). Quant aux résultats de noethérianité, régularité et cohérence pour l’espace affine analytique  , nous les démontrons lorsque l’anneau de Banach
, nous les démontrons lorsque l’anneau de Banach  appartient à une classe qui contient non seulement les anneaux d’entiers de corps de nombres mais aussi les corps valués et les anneaux de valuation discrète.
appartient à une classe qui contient non seulement les anneaux d’entiers de corps de nombres mais aussi les corps valués et les anneaux de valuation discrète.
Précisons qu’à l’exception de celles utilisées pour démontrer l’excellence, nos méthodes, inspirées de celles de la géométrie analytique complexe, ne nécessitent aucune connaissance a priori de la géométrie des espaces de Berkovich sur un corps dépassant celle des résultats classiques en dimension 1. En particulier, nous obtenons de nouvelles preuves des résultats de noethérianité et régularité pour les anneaux locaux des espaces \(\mathbf {A}^{n,\mathrm {an}}_{k} \), où k est un corps valué complet, ainsi que de la cohérence du faisceau structural, par des méthodes qui traitent de façon unifiée corps archimédiens et corps ultramétriques.
Ajoutons quelques mots concernant la structure du texte. Dans la première section, nous rappelons quelques notations et définitions, ainsi que des résultats élémentaires, ayant trait aux espaces de Berkovich sur un anneau de Banach, tirés de [1] et [16]. Ainsi que nous l’avons expliqué plus haut, nous souhaitons étudier les points rigides des fibres. Pour ce faire, un moyen naturel consiste à les envoyer, par un morphisme fini, sur des points rationnels. C’est pourquoi nous consacrons les sections 3 et 4 à établir quelques propriétés d’algèbres et de morphismes finis, moyennant deux conditions techniques (D) et (N), par des arguments adaptés de [16]. Dans les deux sections suivantes, nous étudions les conditions introduites : nous montrons que la condition (D) est toujours vérifiée et donnons des critères pratiques pour que la condition (N) le soit. Nous établissons en passant le fait que les corps résiduels κ(x) des points des espaces de Berkovich sont des corps henséliens. À la section 7, nous regroupons les résultats obtenus pour relier l’anneau local en un point rigide à l’anneau local en un point rationnel, puis, à la section 8, démontrons le théorème de division de Weierstraß annoncé. Enfin, dans les trois dernières sections, nous utilisons ce résultat pour étudier de façon précise le faisceau structural de l’espace affine sur certains anneaux de Banach (corps valués, anneaux de valuation discrète, anneaux d’entiers de corps de nombres, notamment). Nous démontrons que les germes de ce faisceau sont des anneaux locaux noethériens et réguliers, excellents si l’anneau de base est de caractéristique nulle, puis que le faisceau lui-même est cohérent et noethérien au sens de M. Kashiwara.
2 Rappels
Fixons un anneau de Banach  et un entier n∈N. Au chapitre 1 de [1], V. Berkovich explique comment définir un espace localement annelé
et un entier n∈N. Au chapitre 1 de [1], V. Berkovich explique comment définir un espace localement annelé  (noté également
(noté également  si n=0), qu’il appelle espace affine analytique de dimension n sur
si n=0), qu’il appelle espace affine analytique de dimension n sur  . Ensemblistement, ses points sont les semi-normes multiplicatives sur l’anneau de polynômes
. Ensemblistement, ses points sont les semi-normes multiplicatives sur l’anneau de polynômes  dont la restriction à
dont la restriction à  est bornée par la norme donnée ∥.∥. Pour tout point x de cet espace, associé à une semi-norme multiplicative |.|
x
, on définit un corps résiduel
est bornée par la norme donnée ∥.∥. Pour tout point x de cet espace, associé à une semi-norme multiplicative |.|
x
, on définit un corps résiduel  de la façon suivante. L’ensemble
de la façon suivante. L’ensemble  est un idéal premier de
est un idéal premier de  et |.|
x
induit une valeur absolue sur le corps
et |.|
x
induit une valeur absolue sur le corps  . Son complété
. Son complété  sera le corps résiduel voulu. Remarquons que nous disposons d’une « application d’évaluation » naturelle
sera le corps résiduel voulu. Remarquons que nous disposons d’une « application d’évaluation » naturelle  .
.
V. Berkovich munit alors l’ensemble  ainsi construit de la topologie la plus faible qui rende continues les applications
ainsi construit de la topologie la plus faible qui rende continues les applications  , pour
, pour  . Le fait que les corps résiduels
. Le fait que les corps résiduels  soient munis d’une valeur absolue permet de définir une notion de convergence uniforme, puis de fonction analytique. Précisément, les fonctions analytiques sur un ouvert U de
soient munis d’une valeur absolue permet de définir une notion de convergence uniforme, puis de fonction analytique. Précisément, les fonctions analytiques sur un ouvert U de  sont les applications
sont les applications

telles que, pour tout x∈U, on ait  et qui sont localement limites uniformes de fractions rationnelles (c’est-à-dire d’éléments de l’anneau total des fractions de
et qui sont localement limites uniformes de fractions rationnelles (c’est-à-dire d’éléments de l’anneau total des fractions de  ) sans pôles. Ces constructions définissent un faisceau, noté
) sans pôles. Ces constructions définissent un faisceau, noté  .Footnote 1
.Footnote 1
Signalons que nous nous permettrons encore d’écrire  lorsque V n’est pas ouvert. En général, il faudrait le définir comme l’anneau des sections continues de l’espace étalé correspondant au-dessus de V. Si V est une partie compacte de
lorsque V n’est pas ouvert. En général, il faudrait le définir comme l’anneau des sections continues de l’espace étalé correspondant au-dessus de V. Si V est une partie compacte de  , cela revient à poser
, cela revient à poser

où U décrit l’ensemble des voisinages ouverts de V.
Soit x un point de  . Nous dirons qu’un élément f de
. Nous dirons qu’un élément f de  est défini sur une partie U de
est défini sur une partie U de  contenant x s’il possède un antécédent par le morphisme
contenant x s’il possède un antécédent par le morphisme  .
.
Signalons qu’à la fin du premier chapitre de [1], V. Berkovich propose une définition générale d’espace analytique sur  .Footnote 2 Un espace localement annelé
.Footnote 2 Un espace localement annelé  est appelé modèle local d’un espace analytique sur
est appelé modèle local d’un espace analytique sur  s’il existe un entier n, un ouvert U de
s’il existe un entier n, un ouvert U de  et un faisceau
et un faisceau  d’idéaux de type fini de
d’idéaux de type fini de  tels que
tels que  soit isomorphe au support du faisceau
soit isomorphe au support du faisceau  , muni du faisceau
, muni du faisceau  . Un espace analytique sur
. Un espace analytique sur  est un espace localement annelé qui possède un recouvrement par des ouverts isomorphes à un modèle local.
est un espace localement annelé qui possède un recouvrement par des ouverts isomorphes à un modèle local.
Nous allons maintenant rappeler divers notions et résultats tirés de [16]. Nous y renvoyons le lecteur intéressé par des précisions supplémentaires.
Soit n∈N. Soit V une partie compacte de  . On note
. On note  l’anneau des fractions rationnelles sans pôles sur V et
l’anneau des fractions rationnelles sans pôles sur V et  son complété pour la norme uniforme ∥.∥
V
sur V. Posons
son complété pour la norme uniforme ∥.∥
V
sur V. Posons  , où W décrit l’ensemble des voisinages compacts de V dans
, où W décrit l’ensemble des voisinages compacts de V dans  . Remarquons que, pour tout point x de
. Remarquons que, pour tout point x de  , nous avons
, nous avons

Soit x un point de  . Nous dirons qu’un élément f de
. Nous dirons qu’un élément f de  est
est  -défini (resp.
-défini (resp.  -défini) sur un voisinage compact V de x s’il possède un antécédent par le morphisme
-défini) sur un voisinage compact V de x s’il possède un antécédent par le morphisme  (resp.
(resp.  ).
).
Rappelons quelques définitions tirées de [16], §1.2. On dit qu’une partie compacte V de  est rationnelle s’il existe un entier p, des polynômes P
1,…,P
p
,Q de
est rationnelle s’il existe un entier p, des polynômes P
1,…,P
p
,Q de  ne s’annulant pas simultanément sur
ne s’annulant pas simultanément sur  et des nombres réels r
1,…,r
p
>0 tels que
et des nombres réels r
1,…,r
p
>0 tels que

Remarque 2.1
Lorsque  est un corps ultramétrique complet k, toute partie compacte rationnelle de \(\mathbf {A}^{1,\mathrm {an}}_{k} \) au sens précédent est un domaine rationnel d’un disque fermé de rayon strictement positif.
est un corps ultramétrique complet k, toute partie compacte rationnelle de \(\mathbf {A}^{1,\mathrm {an}}_{k} \) au sens précédent est un domaine rationnel d’un disque fermé de rayon strictement positif.
Réciproquement, soit V un domaine rationnel d’un disque fermé D de rayon R>0. Nous pouvons supposer que ce disque est centré en 0. Il existe des fonctions f 1,…,f p ,g définies sur D, sans zéros communs, et des nombres réels r 1,…,r p >0 tels que
La fonction g ne s’annule pas sur V et elle y est donc minorée en valeur absolue par un nombre réel m>0. Par conséquent, une modification suffisamment petite des fonctions f 1,…,f p ,g ne changera pas l’espace V et nous pouvons donc supposer que ces fonctions sont des polynômes. On vérifie que la partie V peut s’écrire
C’est donc une partie compacte rationnelle de \(\mathbf {A}^{1,\mathrm {an}}_{k} \) au sens précédent.
On dit qu’une partie compacte V de  est spectralement convexe si le morphisme naturel
est spectralement convexe si le morphisme naturel

induit un homéomorphisme entre  et V et si le morphisme induit
et V et si le morphisme induit
est un isomorphisme d’espace annelés.
Proposition 2.2
Soit V
un compact rationnel de
 . Alors V
est spectralement convexe et, pour toute partie compacte U
de V, le morphisme naturel
. Alors V
est spectralement convexe et, pour toute partie compacte U
de V, le morphisme naturel

est un isomorphisme.
Exposons maintenant quelques résultats du paragraphe § 2.1 de [16] (en nous contentant de la dimension 1). Soit t>0. Définissons l’algèbre  comme l’algèbre constituée des séries de la forme ∑
n∈N
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de
comme l’algèbre constituée des séries de la forme ∑
n∈N
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de  telle que la série ∑
n∈N
∥a
n
∥t
n converge. Cette algèbre est complète pour la norme définie par
telle que la série ∑
n∈N
∥a
n
∥t
n converge. Cette algèbre est complète pour la norme définie par
Soient s,t∈R vérifiant 0<s≤t. Définissons l’algèbre  comme l’algèbre constituée des séries de la forme ∑
n∈Z
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de
comme l’algèbre constituée des séries de la forme ∑
n∈Z
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de  telle que la famille (∥a
n
∥max(s
n,t
n))
n∈Z
est sommable. Cette algèbre est complète pour la norme définie par
telle que la famille (∥a
n
∥max(s
n,t
n))
n∈Z
est sommable. Cette algèbre est complète pour la norme définie par
Nous prolongeons cette définition en posant  et ∥.∥0,t
=∥.∥
t
.
et ∥.∥0,t
=∥.∥
t
.
Posons  (avec variable T),
(avec variable T),  et notons π:X→B le morphisme de projection. Pour toute partie V de B et tous s,t∈R, définissons
et notons π:X→B le morphisme de projection. Pour toute partie V de B et tous s,t∈R, définissons

Lorsque V=B, nous supprimerons l’indice dans la notation. Si V est un singleton {b}, nous omettrons les accolades.
Comme on s’y attend, les spectres des algèbres  , pour t>0, et
, pour t>0, et  , pour t≥s>0 ou t>s=0, sont canoniquement isomorphes à \(\overline{D}(t)\) et \(\overline{C}(s,t)\) respectivement.
, pour t≥s>0 ou t>s=0, sont canoniquement isomorphes à \(\overline{D}(t)\) et \(\overline{C}(s,t)\) respectivement.
Indiquons maintenant une relation entre norme en tant que série et norme uniforme. Pour éviter de distinguer les cas entre disques et couronnes, introduisons la relation suivante sur R + : nous posons s≺t si s<t ou s=0.
Rappelons également que l’anneau de Banach  est dit uniforme si sa norme est « power-multiplicative », c’est-à-dire qu’elle commute à l’opération d’élévation à une puissance entière ou, de manière équivalente, qu’elle coïncide avec la norme uniforme sur
est dit uniforme si sa norme est « power-multiplicative », c’est-à-dire qu’elle commute à l’opération d’élévation à une puissance entière ou, de manière équivalente, qu’elle coïncide avec la norme uniforme sur  . Il est souvent commode de supposer que l’anneau de Banach
. Il est souvent commode de supposer que l’anneau de Banach  est uniforme et c’est une hypothèse sous laquelle nous nous sommes constamment placés dans [16]. Remarquons qu’elle impose à l’anneau
est uniforme et c’est une hypothèse sous laquelle nous nous sommes constamment placés dans [16]. Remarquons qu’elle impose à l’anneau  d’être réduit et permet d’identifier canoniquement
d’être réduit et permet d’identifier canoniquement  à un sous-anneau de
à un sous-anneau de  (cf. [16], lemme 1.1.25). Cette hypothèse montre son utilité lorsque l’on cherche à décrire explicitement des anneaux de fonctions.
(cf. [16], lemme 1.1.25). Cette hypothèse montre son utilité lorsque l’on cherche à décrire explicitement des anneaux de fonctions.
Proposition 2.3
Supposons que l’anneau de Banach
 est uniforme. Soient
s,u∈R
+
et
\(t,v \in \mathbf {R} _{+}^{*}\)
tels que
s≺u≤v<t. Pour tout élément f
de
est uniforme. Soient
s,u∈R
+
et
\(t,v \in \mathbf {R} _{+}^{*}\)
tels que
s≺u≤v<t. Pour tout élément f
de
 , nous avons
, nous avons
avec la convention que s/(u−s)=0 si s=0.
Démonstration
Il s’agit de majorer la norme en tant que série par la norme uniforme, autrement dit, de majorer les coefficients d’une série en fonction de sa norme uniforme sur un disque ou une couronne. On se ramène au cas où  est un corps valué en considérant une fibre sur laquelle le maximum de la fonction est atteint. On utilise ensuite soit la description explicite de la norme sur les disques ou les couronnes, si le corps est ultramétrique, soit la formule de Cauchy, s’il est archimédien. Nous renvoyons à la proposition 2.1.3 de [16] pour les détails (et la généralisation en dimension supérieure). □
est un corps valué en considérant une fibre sur laquelle le maximum de la fonction est atteint. On utilise ensuite soit la description explicite de la norme sur les disques ou les couronnes, si le corps est ultramétrique, soit la formule de Cauchy, s’il est archimédien. Nous renvoyons à la proposition 2.1.3 de [16] pour les détails (et la généralisation en dimension supérieure). □
Nous pouvons déduire de ce résultat une description de l’anneau  d’une couronne compacte.
d’une couronne compacte.
Proposition 2.4
Supposons que l’anneau de Banach
 est uniforme. Soient
s,t∈R
tels que 0≤s≤t. Alors le morphisme naturel
est uniforme. Soient
s,t∈R
tels que 0≤s≤t. Alors le morphisme naturel

est un isomorphisme.
Démonstration
Il suffit de montrer que ce morphisme est surjectif. Soit f un élément de  . Il existe s′,t′∈R vérifiant s′≺s≤t<t′ tels que
. Il existe s′,t′∈R vérifiant s′≺s≤t<t′ tels que  . Par définition, nous pouvons écrire la fonction f comme limite uniforme de fractions P
n
/Q
n
, avec
. Par définition, nous pouvons écrire la fonction f comme limite uniforme de fractions P
n
/Q
n
, avec  , les polynômes Q
n
ne s’annulant pas sur \(\overline{C}(s',t')\).
, les polynômes Q
n
ne s’annulant pas sur \(\overline{C}(s',t')\).
Comme indiqué précédemment, cette couronne n’est autre que le spectre de l’algèbre  . D’après le corollaire 1.2.4 de [1], les polynômes Q
n
sont inversibles dans cette algèbre. Par conséquent, (P
n
/Q
n
)
n≥0 est une suite d’éléments de
. D’après le corollaire 1.2.4 de [1], les polynômes Q
n
sont inversibles dans cette algèbre. Par conséquent, (P
n
/Q
n
)
n≥0 est une suite d’éléments de  qui converge vers f pour la norme uniforme sur \(\overline{C}(s',t')\). La proposition précédente assure qu’elle converge dans
qui converge vers f pour la norme uniforme sur \(\overline{C}(s',t')\). La proposition précédente assure qu’elle converge dans  pour la norme ∥.∥
s″,t″, quels que soient s″,t″∈R vérifiant s′≺s″≺s et t<t″<t′. On en déduit le résultat voulu. □
pour la norme ∥.∥
s″,t″, quels que soient s″,t″∈R vérifiant s′≺s″≺s et t<t″<t′. On en déduit le résultat voulu. □
Si W est une partie compacte et spectralement convexe de  , nous avons muni l’anneau
, nous avons muni l’anneau  de la norme uniforme sur
de la norme uniforme sur  . Par conséquent, dans ce cas, l’anneau de Banach
. Par conséquent, dans ce cas, l’anneau de Banach  est toujours uniforme.
est toujours uniforme.
Corollaire 2.5
Soit V une partie compacte de B qui possède un système fondamental de voisinages spectralement convexes. Soient s,t∈R tels que 0≤s≤t. Alors le morphisme naturel

où W décrit l’ensemble des voisinages compacts de V dans B, est un isomorphisme.
Remarquons que le résultat vaut, en particulier, lorsque la partie V est un compact rationnel ou un point.
Corollaire 2.6
Soit b un point de B. Notons 0 b le point 0 de la fibre X b . Alors le morphisme naturel

où V décrit l’ensemble des voisinages compacts de b dans B, est un isomorphisme.
Corollaire 2.7
Soit b un point de B. Soit r≥0. Alors le morphisme naturel

où V décrit l’ensemble des voisinages compacts de b dans B, est un isomorphisme.
Démonstration
Seule la surjectivité pose problème. Soit  . Il existe un voisinage V de b et un nombre réel t>r tel que
. Il existe un voisinage V de b et un nombre réel t>r tel que  . Soit t
1∈]r,t[.
. Soit t
1∈]r,t[.
Utilisons le corollaire précédent pour trouver un élément g=∑
n≥0
a
n
T
n de  , avec W⊂V et t
0>0, dont le germe en 0
b
est f. En utilisant la description explicite des sections sur \(\overline{D}_{c}(t)\), pour tout c∈W, on montre que
, avec W⊂V et t
0>0, dont le germe en 0
b
est f. En utilisant la description explicite des sections sur \(\overline{D}_{c}(t)\), pour tout c∈W, on montre que  . D’après la proposition 2.3, nous avons
. D’après la proposition 2.3, nous avons
On en déduit que, pour tout t
2∈]r,t
1[, la série \(\sum_{n\ge0} \|a_{n}\|_{W} t_{2}^{n}\), où ∥a
n
∥
W
désigne la norme uniforme de a
n
sur W, converge et donc que g appartient à l’algèbre  . □
. □
En appliquant ce corollaire fibre à fibre et en identifiant les coefficients des développements, nous obtenons le résultat suivant. Pour toute partie compacte W de B et tout nombre réel t>0, nous noterons  l’algèbre constituée des séries de la forme ∑
n∈N
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de
l’algèbre constituée des séries de la forme ∑
n∈N
a
n
T
n, où (a
n
)
n≥0 est une suite d’éléments de  telle que la série ∑
n∈N
∥a
n
∥
W
t
n converge.
telle que la série ∑
n∈N
∥a
n
∥
W
t
n converge.
Corollaire 2.8
Soit V une partie de B. Soit r≥0. Alors le morphisme naturel

où W décrit l’ensemble des voisinages compacts de V dans B, est un isomorphisme.
Dans l’étude qui suit, il est superflu d’exiger que l’anneau de Banach  soit uniforme. En cas de besoin, nous pourrions de toute façon nous y ramener par le lemme suivant, dont la démonstration ne présente aucune difficulté.
soit uniforme. En cas de besoin, nous pourrions de toute façon nous y ramener par le lemme suivant, dont la démonstration ne présente aucune difficulté.
Lemme 2.9
Notons
 le séparé complété de l’anneau
le séparé complété de l’anneau
 pour la semi-norme spectrale ∥.∥∞
sur
pour la semi-norme spectrale ∥.∥∞
sur
 . Alors le morphisme naturel
. Alors le morphisme naturel

est un isomorphisme d’espaces annelés.
Pour toute la suite du texte, nous fixons un anneau de Banach  . Nous notons
. Nous notons  ,
,  et π:X→B le morphisme de projection. Pour tout n∈N, nous notons
et π:X→B le morphisme de projection. Pour tout n∈N, nous notons  .
.
3 Théorème de Weierstraß global
Dans cette section, nous reprenons, en les précisant, les résultats de [16], §5.2. Les preuves ne demandant que des modifications mineures, nous ne nous y attarderons pas. Insistons sur le fait que nous ne requérons aucune hypothèse d’uniformité sur l’anneau de Banach  .
.
Soient d∈N et  un polynôme unitaire de degré d.
un polynôme unitaire de degré d.
Théorème 3.1
(Théorème de division de Weierstraß global)
Il existe un nombre réel v>0 vérifiant la propriété suivante : pour toute
 -algèbre de Banach
-algèbre de Banach
 telle que le morphisme structural
telle que le morphisme structural
 diminue les normes, pour tout nombre réel w≥v
et tout élément F
de
diminue les normes, pour tout nombre réel w≥v
et tout élément F
de
 , il existe un unique couple
, il existe un unique couple
 tel que
tel que
-
(i)
F=QG+R ;
-
(ii)
R soit un polynôme de degré strictement inférieur à d.
En outre, il existe une constante C>0 indépendante de w,  et F, telle que l’on ait les inégalités
et F, telle que l’on ait les inégalités
Pour la suite de cette section, fixons une  -algèbre de Banach
-algèbre de Banach  telle que le morphisme structural
telle que le morphisme structural  diminue les normes. Nous munissons l’algèbre quotient
diminue les normes. Nous munissons l’algèbre quotient  de la semi-norme résiduelle
de la semi-norme résiduelle  induite par la norme
induite par la norme  sur
sur  . Par définition, quel que soit F dans
. Par définition, quel que soit F dans  , nous avons
, nous avons

Si  est une
est une  -algèbre de la forme
-algèbre de la forme  , où U est une partie compacte de
, où U est une partie compacte de  , munie de la norme spectrale ∥.∥
U
, nous noterons ∥.∥
U,w,rés la norme
, munie de la norme spectrale ∥.∥
U
, nous noterons ∥.∥
U,w,rés la norme  .
.
Corollaire 3.2
Pour tout nombre réel w≥v, les propriétés suivantes sont satisfaites :
-
(i)
la semi-norme
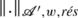 définie sur le quotient
définie sur le quotient
 est une norme ;
est une norme ; -
(ii)
l’anneau
 est complet pour la norme
est complet pour la norme
 .
.
Puisque le polynôme G est unitaire et de degré d, l’application

est bijective. Nous noterons  la norme définie sur
la norme définie sur  en prenant le maximum des normes des coordonnées. Nous pouvons alors définir une norme
en prenant le maximum des normes des coordonnées. Nous pouvons alors définir une norme  sur
sur  par la formule
par la formule

Si  est une
est une  -algèbre de la forme
-algèbre de la forme  , où U est une partie compacte de
, où U est une partie compacte de  , munie de la norme spectrale ∥.∥
U
, nous noterons ∥.∥
U,div la norme
, munie de la norme spectrale ∥.∥
U
, nous noterons ∥.∥
U,div la norme  .
.
Corollaire 3.3
Pour tout nombre réel w≥v
les normes
 et
et
 définies sur
définies sur
 sont équivalentes. Plus précisément, pour tout élément F
de
sont équivalentes. Plus précisément, pour tout élément F
de
 , nous avons
, nous avons

4 Morphismes finis
Soit  un polynôme unitaire non constant. Considérons le morphisme d’anneaux de Banach
un polynôme unitaire non constant. Considérons le morphisme d’anneaux de Banach  et le morphisme d’espaces annelés φ:Z
G
→B, où Z
G
désigne le fermé de Zariski de X défini par G=0, qu’il induit. C’est un morphisme fini dont nous allons établir quelques propriétés. Nous suivons ici [16], § 5.3.
et le morphisme d’espaces annelés φ:Z
G
→B, où Z
G
désigne le fermé de Zariski de X défini par G=0, qu’il induit. C’est un morphisme fini dont nous allons établir quelques propriétés. Nous suivons ici [16], § 5.3.
Dans [16], définition 5.2.5, nous avons introduit une condition appelée (R G ). Nous la remplaçons ici par la condition suivante.
Définition 4.1
Soit U une partie compacte de B. On dit que U satisfait la condition (N
G
) si elle est spectralement convexe et s’il existe un nombre réel v>0 tel que, pour tout w≥v, la semi-norme ∥.∥
U,w,rés soit équivalente à la norme spectrale sur  .
.
Dans [16], § 5.3, nous ne nous sommes en réalité servi de (R G ) que pour démontrer (N G ) (cf. proposition 5.2.7) et cette dernière condition suffit dans tous les raisonnements.
Remarque 4.2
La condition (N
G
) énonce une équivalence entre deux normes sur un module de type fini sur l’anneau de Banach  . On peut y penser comme une généralisation du résultat classique d’équivalence des normes pour les espaces vectoriels de dimension finie sur un corps valué complet K (que l’on ne peut appliquer que si la norme spectrale est bien une norme sur K[T]/(G(T)), autrement dit, lorsque le polynôme G est sans facteurs multiples).
. On peut y penser comme une généralisation du résultat classique d’équivalence des normes pour les espaces vectoriels de dimension finie sur un corps valué complet K (que l’on ne peut appliquer que si la norme spectrale est bien une norme sur K[T]/(G(T)), autrement dit, lorsque le polynôme G est sans facteurs multiples).
L’on peut également considérer le cas où l’algèbre  est une algèbre affinoïde. Une algèbre finie sur une algèbre affinoïde étant elle-même affinoïde, on retrouve alors un résultat connu, dans le cas des algèbres réduites (cf. [1], proposition 2.1.4(ii) et [4], théorème 6.2.4/1).
est une algèbre affinoïde. Une algèbre finie sur une algèbre affinoïde étant elle-même affinoïde, on retrouve alors un résultat connu, dans le cas des algèbres réduites (cf. [1], proposition 2.1.4(ii) et [4], théorème 6.2.4/1).
Remarque 4.3
Remarquons, dès à présent, que la condition (N
G
) est satisfaite si le polynôme G est de degré 1, puisque l’on dispose alors d’un isomorphisme admissible  . Nous donnerons à la section 6 des critères plus généraux.
. Nous donnerons à la section 6 des critères plus généraux.
Nous reprenons ici la proposition 5.3.3 de [16].
Proposition 4.4
Soit U
une partie compacte de B
qui satisfait la condition (N
G
). Les normes ∥.∥
U,div, ∥.∥
U,w,rés, pour
w≥v, et la norme spectrale sur
 sont alors équivalentes. De plus, nous avons un isomorphisme admissible naturel
sont alors équivalentes. De plus, nous avons un isomorphisme admissible naturel

où
 est calculé en considérant φ
−1(U) comme partie de X.
est calculé en considérant φ
−1(U) comme partie de X.
Remarque 4.5
Dans la preuve de la proposition 5.3.3 de [16], on considère en réalité φ
−1(U) comme partie de  . Cela ne change rien à la preuve.
. Cela ne change rien à la preuve.
Dans [16], définition 5.3.5, nous avons introduit une condition appelée (I G ). Nous la modifions ici de la façon suivante.
Définition 4.6
Notons \(G(b)(T) = \prod_{i=1}^{r} h_{i}(T)^{n_{i}}\) la décomposition en produit de polynômes irréductibles et unitaires de G(b)(T) dans  . On dit que le point b de B satisfait la condition (D
G
) s’il existe des polynômes unitaires H
1,…,H
r
à coefficients dans
. On dit que le point b de B satisfait la condition (D
G
) s’il existe des polynômes unitaires H
1,…,H
r
à coefficients dans  tels que
tels que
-
(i)
\(G = \prod_{i=1}^{r} H_{i}\) dans
 ;
; -
(ii)
quel que soit i∈[[1,r]], \(H_{i}(b) = h_{i}^{n_{i}}\).
Comme précédemment, signalons que nous n’avons utilisé la condition (I G ) dans [16], § 5.3 que pour démontrer (D G ) (cf. la discussion qui suit la définition 5.3.5) et que cette dernière condition suffit dans tous les raisonnements.
Remarque 4.7
Géométriquement, la condition (D G ) signifie que tous les points du fermé de Zariski Z G défini par G=0 au-dessus de b sont définis au voisinage de b. Nous montrerons à la section 5 que la condition (D G ) est toujours vérifiée.
Énonçons maintenant l’analogue du théorème 5.3.8 de [16]. La démonstration étant en tout point identique, nous ne la reprendrons pas.
Théorème 4.8
Soit b un point de B. Supposons que le point b vérifie la condition (D G ) et possède un système fondamental de voisinages compacts qui satisfont la condition (N G ). Alors le morphisme

est un isomorphisme de
 -modules.
-modules.
5 Hensélianité et condition (D)
Nous nous intéressons ici à des propriétés d’hensélianité dans les espaces analytiques sur  . Commençons par rappeler un résultat (cf. [16], corollaire 2.5.2 ; l’hypothèse d’uniformité sur l’anneau de Banach
. Commençons par rappeler un résultat (cf. [16], corollaire 2.5.2 ; l’hypothèse d’uniformité sur l’anneau de Banach  qui y figure est superflue, ce dont on se convainc à l’aide du lemme 2.9).
qui y figure est superflue, ce dont on se convainc à l’aide du lemme 2.9).
Théorème 5.1
Soient
 un espace analytique sur
un espace analytique sur
 et z
un point de Z. L’anneau local
et z
un point de Z. L’anneau local
 est hensélien.
est hensélien.
Une lègère modification de la preuve conduit au résultat suivant.
Théorème 5.2
Soit b
un point de
 . Le corps résiduel κ(b) est un corps hensélien.
. Le corps résiduel κ(b) est un corps hensélien.
Démonstration
Si le point b est archimédien, le corps κ(b) est égal à R ou C ; il est donc hensélien.
Supposons maintenant que le point b est ultramétrique. Il suffit de montrer que l’anneau de valuation κ(b)o est hensélien. Soient P un polynôme unitaire à coefficients dans κ(b)o et f un élément de κ(b)o tel que |P(f)(b)|<1 et |P′(f)(b)|=1.
Considérons un voisinage compact V de b dans B sur lequel le polynôme P se relève en un polynôme à coefficients dans  unitaire et l’élément f se relève en un élément de
unitaire et l’élément f se relève en un élément de  . Nous choisissons de tels relevés et les notons identiquement.
. Nous choisissons de tels relevés et les notons identiquement.
Notons M=∥f∥ V et N=∥P(f)∥ V . Quitte à restreindre V, nous pouvons supposer que N<1 et que P′(f) est inversible sur V. Notons m=∥P′(f)−1∥ V .
Il existe un polynôme Q[T
1,T
2] à coefficients dans  tel que, pour tous u et v dans
tel que, pour tous u et v dans  , on ait
, on ait
Notons C le maximum des normes des coefficients du polynôme Q.
Il existe un élément λ de l’intervalle [0,1] tel que ∥2∥ V ≤2λ. D’après le théorème d’Ostrowski, pour tout entier n, nous avons alors ∥n∥ V ≤n λ. Le lemme 1.3.2 de [16] permet d’en déduire que

Notons r le nombre de coefficients du polynôme Q et d son degré total. L’inégalité précédente entraîne

Pour tout ε>0, quitte à rétrécir le voisinage V, nous pouvons rendre les quantités M, m, C et 2λ inférieures à 1+ε. Au cours de cette opération, le nombre réel N ne peut que diminuer. Fixons un nombre réel K dans l’intervalle ]N,1[. Nous pouvons choisir le voisinage V de façon que l’on ait Nm<1 et Nm 22λr Cmax(1,M d)≤K.
Soit g un élément de  . Nous avons
. Nous avons
Posons
Si ∥g∥ V ≤m, nous avons, pour tout point c de V
et, en particulier,
En utilisant cette dernière inégalité et le fait que  est complet, on montre que la série ∑
n≥0
R
∘n(−P′(f)−1) (où R
∘n désigne la puissance n
ème pour la composition) converge vers un élément s de
est complet, on montre que la série ∑
n≥0
R
∘n(−P′(f)−1) (où R
∘n désigne la puissance n
ème pour la composition) converge vers un élément s de  . Cet élément satisfait l’égalité s−R(s)=−P′(f)−1 et donc P(f+P(f)s)=0.
. Cet élément satisfait l’égalité s−R(s)=−P′(f)−1 et donc P(f+P(f)s)=0.
Calculons maintenant au point b qui, rappelons-le, est supposé ultramétrique. D’après les inégalités qui précèdent, nous avons |s(b)|=|P′(f)−1(b)|=1, d’où |P(f)s(b)|<1 et |(f+P(f)s)(b)|≤1. L’élément h=f+P(f)s de  défini donc un élément de κ(b)o qui coïncide avec f modulo κ(b)oo et annule le polynôme P. □
défini donc un élément de κ(b)o qui coïncide avec f modulo κ(b)oo et annule le polynôme P. □
Corollaire 5.3
Soient
 un espace analytique sur
un espace analytique sur
 et z
un point de Z. Le corps résiduel κ(z) est un corps hensélien.
et z
un point de Z. Le corps résiduel κ(z) est un corps hensélien.
Corollaire 5.4
Soient b
un point de
 et G(T) un polynôme unitaire non constant à coefficients dans
et G(T) un polynôme unitaire non constant à coefficients dans
 . Alors le point b
satisfait la condition (D
G
).
. Alors le point b
satisfait la condition (D
G
).
Démonstration
Notons e l’exposant caractéristique du corps κ(b). Écrivons la décomposition de G(T) en produit de facteurs irréductibles dans κ(b)[T] sous la forme
où les G i sont des polynômes unitaires et irréductibles deux à deux distincts et les n i des entiers.
Puisque l’anneau  est hensélien, il existe des polynômes H
1,…,H
r
unitaires à coefficients dans
est hensélien, il existe des polynômes H
1,…,H
r
unitaires à coefficients dans  tels que
tels que
-
(i)
\(G(T) = \prod_{i=1}^{r} H_{i}(T)\) dans
 ;
; -
(ii)
pour tout i, \(H_{i}(T) = G_{i}(T)^{n_{i}}\) dans κ(b)[T].
Soit i∈[[1,r]]. Il existe un polynôme irréductible et séparable g
i
à coefficients dans κ(b) et un entier a
i
tel que \(G_{i}(T) = g_{i}(T^{e^{a_{i}}})\). Puisque le corps κ(b) est hensélien, le polynôme g
i
(T) est encore irréductible dans  (cf. [5], VI, § 8, exercices 14a et 12b ou [2], proposition 2.4.1). Par conséquent, il existe un polynôme irréductible h
i
à coefficients dans
(cf. [5], VI, § 8, exercices 14a et 12b ou [2], proposition 2.4.1). Par conséquent, il existe un polynôme irréductible h
i
à coefficients dans  et un entier m
i
≥1 tels que \(g_{i}(T^{e^{a_{i}}}) = h_{i}(T)^{m_{i}}\) dans
et un entier m
i
≥1 tels que \(g_{i}(T^{e^{a_{i}}}) = h_{i}(T)^{m_{i}}\) dans  .
.
Finalement, l’écriture
est la décomposition en produit de facteurs irréductibles du polynôme G(T) dans  . On en déduit le résultat voulu. □
. On en déduit le résultat voulu. □
6 Condition (N)
Soient d∈N
∗ et  un polynôme unitaire de degré d. Nous noterons
un polynôme unitaire de degré d. Nous noterons
Dans cette section, nous présentons différents résultats permettant d’assurer que la condition (N G ) est satisfaite.
6.1 Condition de finitude du bord analytique
Nous commençons par énoncer un critère particulièrement adapté aux espaces ultramétriques. On y retrouve l’hypothèse sur le polynôme G mentionnée à la remarque 4.2.
Définition 6.1
Soit n∈N. Soit V une partie compacte et spectralement convexe de  . On dit qu’une partie fermée Γ de V est un bord analytique de V si elle vérifie la condition suivante :
. On dit qu’une partie fermée Γ de V est un bord analytique de V si elle vérifie la condition suivante :

On appelle bord de Shilov de V le plus petit bord analytique, pour la relation d’inclusion, de V, s’il existe.
Proposition 6.2
Soit U une partie compacte et spectralement convexe de B. Supposons qu’il existe des parties V 1,…,V r de U telles que
-
(i)
pour tout i∈[[1,r]], V i est compacte et satisfait la condition (N G ) ;
-
(ii)
la réunion Γ U =⋃1≤i≤r V i est un bord analytique de U.
Alors U satisfait également la condition (N G ).
Notons
 le morphisme de projection. Alors la partie
Γ
U,G
=φ
−1(Γ
U
) est un bord analytique de
le morphisme de projection. Alors la partie
Γ
U,G
=φ
−1(Γ
U
) est un bord analytique de
 .
.
Démonstration
Le corollaire 3.2 assure qu’il existe un nombre réel v tel que, pour tout w≥v, la semi-norme ∥.∥
U,w,rés soit une norme sur l’algèbre  et qu’elle soit équivalente à la norme ∥.∥
U,div. Notons ∥.∥
U,∞ la norme spectrale associée. C’est la norme uniforme sur
et qu’elle soit équivalente à la norme ∥.∥
U,div. Notons ∥.∥
U,∞ la norme spectrale associée. C’est la norme uniforme sur

Pour prouver que les deux normes sont équivalentes, et donc que la condition (N
G
) est satisfaite, il suffit de montrer qu’il existe une constante D telle que, pour tout élément F de  , nous ayons
, nous ayons
Soit i∈[[1,r]]. Les normes ∥.∥
i,div et ∥.∥
i,∞ sur  sont équivalentes : il existe un nombre réel D
i
>0 tel que, pour tout élément f de
sont équivalentes : il existe un nombre réel D
i
>0 tel que, pour tout élément f de  , on ait
, on ait
Soit F un élément de  . Puisque le polynôme G est unitaire et de degré p, l’élément F possède un unique représentant dans
. Puisque le polynôme G est unitaire et de degré p, l’élément F possède un unique représentant dans  de la forme
de la forme
avec  . Par définition, nous avons
. Par définition, nous avons
où ∥.∥
U
désigne la norme spectrale sur  .
.
Il existe j∈[[0,p−1]] et i∈[[1,r]] tels que \(\|F\| _{U,\mathrm{div}} = \|a_{j}\|_{V_{i}}\), où \(\|.\|_{V_{i}}\) désigne la norme spectrale sur  . Nous avons alors
. Nous avons alors
Ceci démontre la première partie du résultat.
Remarquons maintenant que
d’où l’on tire
En écrivant la même inégalité pour F n, avec n∈N ∗, puis en prenant la racine n ème et en faisant tendre n vers l’infini, on montre que
Par conséquent, la partie Γ
U,G
est un bord analytique de  . □
. □
Corollaire 6.3
Soit U une partie compacte et spectralement convexe de B. Supposons qu’elle possède un bord analytique Γ U fini tel que, pour tout point γ de Γ U , le polynôme G(γ)(T) soit sans facteurs multiples. Alors elle satisfait la condition (N G ).
En outre, avec les notations de la proposition 6.2, la partie Γ
U,G
est un bord analytique fini de
 .
.
Introduisons maintenant des notations. Nous noterons B
um la partie ultramétrique de B, c’est-à-dire l’ensemble des points b de B en lesquels la valeur absolue canonique sur le corps  est ultramétrique. Soit V une partie compacte de B
um. Pour tout nombre réel r>0, définissons l’algèbre
est ultramétrique. Soit V une partie compacte de B
um. Pour tout nombre réel r>0, définissons l’algèbre  comme l’algèbre constituée des séries à coefficients dans
comme l’algèbre constituée des séries à coefficients dans  de la forme
de la forme
telles que la série ∑ n∈N ∥a n ∥r n converge. Cette algèbre est complète pour la norme définie par
Pour tous r,s∈R vérifiant 0<r≤s, définissons  comme l’algèbre constituée des séries à coefficients dans
comme l’algèbre constituée des séries à coefficients dans  de la forme
de la forme
telles que la famille (∥a n ∥ V max(r n,s n)) n∈Z soit sommable. Cette algèbre est complète pour la norme définie par
Prolongeons cette définition en posant  et ∥.∥
V,0,s,um=∥.∥
V,s,um.
et ∥.∥
V,0,s,um=∥.∥
V,s,um.
Lemme 6.4
Soit V une partie compacte et spectralement convexe de B um. Soient r,s∈R vérifiant 0=r<s ou 0<r≤s. Le morphisme

induit un isomorphisme d’algèbres normées

Démonstration
On reprend le raisonnement de la preuve du lemme 5.6.3 de [16]. □
Dans la section 8, nous utiliserons la condition (N
G
) au-dessus d’une partie de  et pour un polynôme G de la forme P(S)−T, où T désigne la variable sur
et pour un polynôme G de la forme P(S)−T, où T désigne la variable sur  . Nous allons donc maintenant concentrer nos efforts sur cette situation.
. Nous allons donc maintenant concentrer nos efforts sur cette situation.
Introduisons quelques notations pour les lemniscates. Pour toute partie W de B, tout polynôme  et tous nombres réels r et s, définissons
et tous nombres réels r et s, définissons
et
Proposition 6.5
Soit U
une partie compacte et spectralement convexe de B
um. Supposons qu’elle possède un bord analytique fini Γ
U
. Soit P(S) un polynôme unitaire non constant à coefficients dans
 . Soient
r,s∈R
vérifiant 0=r<s
ou 0<r≤s. Alors la couronne
\(\overline{C}_{U}(r,s)\)
satisfait la condition (N
P(S)−T
).
. Soient
r,s∈R
vérifiant 0=r<s
ou 0<r≤s. Alors la couronne
\(\overline{C}_{U}(r,s)\)
satisfait la condition (N
P(S)−T
).
En outre, la couronne \(\overline{C}_{U}(r,s)\) possède un bord analytique fini, ainsi que la lemniscate \(\overline{C}_{U}(P;r,s)\)
Démonstration
Soit γ∈Γ U . L’algèbre

n’est autre que l’algèbre affinoïde de la lemniscate \(\overline {C}_{\gamma}(P,r,s)\). C’est donc une algèbre  -affinoïde réduite. D’après la proposition 2.1.4(ii) de [1], sa norme résiduelle est équivalente à sa norme spectrale, autrement dit la couronne \(\overline{C}_{\gamma}(t,s)\) satisfait la condition (N
P(S)−T
).
-affinoïde réduite. D’après la proposition 2.1.4(ii) de [1], sa norme résiduelle est équivalente à sa norme spectrale, autrement dit la couronne \(\overline{C}_{\gamma}(t,s)\) satisfait la condition (N
P(S)−T
).
D’après le lemme 6.4, la partie \(\bigcup_{\gamma\in \varGamma_{U}} \overline{C}_{\gamma}(r,s)\) est un bord analytique de \(\overline{C}_{U}(r,s)\) et l’on conclut par la proposition 6.2.
Pour γ∈Γ U , notons Γ γ le bord de Shilov de la couronne \(\overline{C}_{\gamma}(t,s)\). L’ensemble fini \(\bigcup_{\gamma\in\varGamma_{U}} \varGamma_{\gamma}\) est alors un bord analytique de Γ U . L’assertion finale découle de la proposition 6.2. □
Corollaire 6.6
Soit U
une partie compacte et spectralement convexe de B
um. Supposons qu’elle possède un bord analytique fini Γ
U
. Soient P(S) et Q(T) des polynômes unitaires et non constants à coefficients dans
 . Soient
r,s∈R
vérifiant 0=r<s
ou 0<r≤s. Alors la lemniscate
\(\overline {C}_{U}(Q;r,s)\)
satisfait la condition (N
P(S)−T
).
. Soient
r,s∈R
vérifiant 0=r<s
ou 0<r≤s. Alors la lemniscate
\(\overline {C}_{U}(Q;r,s)\)
satisfait la condition (N
P(S)−T
).
Démonstration
D’après la preuve de la proposition précédente, la partie \(\bigcup_{\gamma\in\varGamma_{U}} \overline{C}_{\gamma}(Q;r,s)\) est un bord analytique de \(\overline{C}_{U}(Q;r,s)\). Nous pouvons donc appliquer le même raisonnement que dans cette preuve afin de conclure. □
Afin d’aller plus loin, démontrons un résultat sur la topologie de X.
Proposition 6.7
Soient x
un point de X
et U
un voisinage de x. Alors, il existe un voisinage V
de b=π(x) dans B, un polynôme
 à coefficient dominant inversible et deux nombres réels
r,s≥0 vérifiant
r≺|P(T)(x)|<s
tels que
à coefficient dominant inversible et deux nombres réels
r,s≥0 vérifiant
r≺|P(T)(x)|<s
tels que
et
Démonstration
Nous pouvons supposer que U est ouvert. Il existe alors un polynôme  et deux nombres réels r,s≥0 tels que r≺|P(T)(x)|<s et
et deux nombres réels r,s≥0 tels que r≺|P(T)(x)|<s et
Les coefficients de P(T) sont limites de quotients d’éléments de  dont les dénominateurs ne s’annulent pas en b. Nous pouvons donc supposer que P(T) est à coefficients dans l’anneau total des fractions de
dont les dénominateurs ne s’annulent pas en b. Nous pouvons donc supposer que P(T) est à coefficients dans l’anneau total des fractions de  . Nous pouvons également supposer que son coefficient dominant ne s’annule pas en b. Soit
. Nous pouvons également supposer que son coefficient dominant ne s’annule pas en b. Soit  un dénominateur commun à tous les coefficients de P(T). Puisqu’il ne s’annule pas en b, nous avons
un dénominateur commun à tous les coefficients de P(T). Puisqu’il ne s’annule pas en b, nous avons
Par conséquent, nous pouvons supposer que P(T) est à coefficients dans  .
.
D’après [16], corollaire 1.1.12, la partie
est un voisinage compact du point x dans X. Par conséquent, K∖U est une partie compacte de X. Sa projection est une partie compacte de B qui évite le point b. On obtient le résultat annoncé en prenant pour V un voisinage de b dans B∖π(K∖U). □
Corollaire 6.8
Pour tout n∈N, le morphisme de projection

est ouvert.
Définition 6.9
Un point b de B est dit ultramétrique typique s’il appartient à l’intérieur de B um et s’il possède un système fondamental de voisinages compacts, spectralement convexes et admettant un bord analytique fini.
Proposition 6.10
Soit b
un point ultramétrique typique de B. Soit n∈N. Tout point de
 est ultramétrique typique.
est ultramétrique typique.
Démonstration
Soit x∈(X
n
)
b
. D’après la proposition 6.7, il possède un système fondamental de voisinages de la forme \(\overline{C}_{U}(P;r,s)\), où U est un voisinage compact et spectralement convexe de b dans B
um qui possède un bord analytique fini, P un polynôme unitaire à coefficients dans  et r,s∈R. On conclut alors par la proposition 6.5. □
et r,s∈R. On conclut alors par la proposition 6.5. □
Proposition 6.11
Soit b
un point ultramétrique typique de B. Soit P
un polynôme unitaire non constant à coefficients dans
 . Tout point de (X
n
)
b
possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition (N
P(S)−T
).
. Tout point de (X
n
)
b
possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition (N
P(S)−T
).
Démonstration
On utilise la proposition 6.7 et le corollaire 6.6. □
6.2 Condition de séparabilité
Intéressons-nous maintenant à une autre condition impliquant (N G ) : il s’agit de la condition (R G ) que nous avons introduite à la définition 5.2.5 de [16].
Définition 6.12
Soit U une partie compacte de B. On dit que U satisfait la condition (R G ) si elle est spectralement convexe et possède un bord analytique Γ U sur lequel la fonction |Rés(G,G′)| est bornée inférieurement par un nombre réel m U >0.
Énonçons à présent un lemme classique.
Lemme 6.13
Notons
\(G(T) = T^{d} + \sum_{k=0}^{d-1} g_{k} T^{k}\). Pour tout point b
de B
et toute racine α
de G(b)(T) dans une clôture algébrique de
 , nous avons
, nous avons
Proposition 6.14
Toute partie compacte et spectralement convexe de B qui vérifie la condition (R G ) vérifie aussi la condition (N G ).
Démonstration
Soit U une partie compacte et spectralement convexe de B qui vérifie la condition (R
G
). Considérons le nombre réel v dont il est question dans le théorème 3.1 appliqué à  . Posons \(v' = \max(v,1,\allowbreak \sum_{k=0}^{d-1} \|g_{k}\|)\), avec les notations du lemme précédent. Nous pouvons alors reprendre la preuve de la proposition 5.2.7 de [16]. (On y considérait v′=max(v,max0≤k≤d−1(∥g
k
∥1/(d−k))), ce qui n’est en fait correct que lorsque la partie U est contenue dans la partie ultramétrique de B.)
. Posons \(v' = \max(v,1,\allowbreak \sum_{k=0}^{d-1} \|g_{k}\|)\), avec les notations du lemme précédent. Nous pouvons alors reprendre la preuve de la proposition 5.2.7 de [16]. (On y considérait v′=max(v,max0≤k≤d−1(∥g
k
∥1/(d−k))), ce qui n’est en fait correct que lorsque la partie U est contenue dans la partie ultramétrique de B.)
En deux mots, il faut montrer que la norme d’un polynôme F calculée en prenant le maximum des normes des coefficients de son reste R dans la division euclidienne par G est majorée, à une constante multiplicative près, par sa norme sur le fermé de Zariski Z G défini par l’équation G=0. Il est possible d’exprimer le reste R en fonction de ses valeurs aux points de Z G , et d’en déduire la majoration souhaitée, pour peu que l’on connaisse ses valeurs en suffisamment de points. C’est ce qu’assure la condition (R G ), en demandant que les points de Z G correspondent à des racines simples de G. □
Comme précédemment, nous allons maintenant nous restreindre au cas où G est de la forme P(S)−T.
Si Q est un polynôme à coefficients dans un anneau de Banach, nous noterons ∥Q∥∞ le maximum des normes de ses coefficients.
Lemme 6.15
Soient b
un point de B. Soit Q
0
un polynôme séparable et unitaire de degré d≥1 à coefficients dans
 . Il existe
r,η>0 vérifiant la propriété suivante : pour tout nombre réel
t∈]0,r], pour tout polynôme Q
à coefficients dans
. Il existe
r,η>0 vérifiant la propriété suivante : pour tout nombre réel
t∈]0,r], pour tout polynôme Q
à coefficients dans
 et de degré d
tel que ∥Q−Q
0∥∞≤η, le disque
\(\overline{D}_{b}(t)\)
satisfait la condition (N
Q(S)−T
).
et de degré d
tel que ∥Q−Q
0∥∞≤η, le disque
\(\overline{D}_{b}(t)\)
satisfait la condition (N
Q(S)−T
).
Démonstration
Par hypothèse, le polynôme \(R(T) = \textrm{R\'{e}s}_{S}(Q_{0}(S)-T,Q_{0}'(S))\) de  ne s’annule pas en 0. Il existe donc un nombre réel r>0 tel que R(T) soit minoré par |R(0)|/2 en tout point du disque \(\overline{D}_{b}(r)\). Par conséquent, il existe un nombre réel η>0 tel que, pour tout polynôme Q à coefficients dans
ne s’annule pas en 0. Il existe donc un nombre réel r>0 tel que R(T) soit minoré par |R(0)|/2 en tout point du disque \(\overline{D}_{b}(r)\). Par conséquent, il existe un nombre réel η>0 tel que, pour tout polynôme Q à coefficients dans  et de degré d tel que ∥Q−Q
0∥∞≤η, le polynôme Rés
S
(Q(S)−T,Q′(S)) soit minoré par |R(0)|/4 sur \(\overline {D}_{b}(r)\). Le disque \(\overline{D}_{b}(r)\) satisfait alors la condition (R
Q(S)−T
), et donc la condition (N
Q(S)−T
). □
et de degré d tel que ∥Q−Q
0∥∞≤η, le polynôme Rés
S
(Q(S)−T,Q′(S)) soit minoré par |R(0)|/4 sur \(\overline {D}_{b}(r)\). Le disque \(\overline{D}_{b}(r)\) satisfait alors la condition (R
Q(S)−T
), et donc la condition (N
Q(S)−T
). □
Lemme 6.16
Soit b
un point de B. Soit
P(S) un polynôme unitaire de degré d≥1 à coefficients dans
 dont l’image dans
dont l’image dans
 est séparable. Soit Q(T) un polynôme unitaire à coefficients dans
est séparable. Soit Q(T) un polynôme unitaire à coefficients dans
 .
.
Soient s,s′∈R tels que 0<s′<s. Il existe s 1,s 2∈R vérifiant s′<s 1<s 2<s et un voisinage V de b dans B sur lequel les coefficients de Q sont définis tels que, pour tout v∈[s 1,s 2] et tout voisinage compact et spectralement convexe U de b dans V, la lemniscate \(\overline {D}_{U}(Q;v)\) satisfasse la condition (R P(S)−T ) et donc (N P(S)−T ).
Soient r,r′,s,s′∈R tels que 0<r<r′<s′<s. Il existe r 1,r 2,s 1,s 2∈R vérifiant r<r 2<r 1<r′ et s′<s 1<s 2<s et un voisinage V de b dans B sur lequel les coefficients de Q sont définis tels que, pour tout u∈[r 2,r 1], tout v∈[s 1,s 2] et tout voisinage compact et spectralement convexe U de b dans V, la lemniscate \(\overline{C}_{U}(Q;u,v)\) satisfasse la condition (R P(S)−T ) et donc (N P(S)−T ).
Démonstration
Nous ne traiterons que le premier cas, le second se démontrant par les mêmes méthodes. Quitte à remplacer  par
par  où W désigne un voisinage compact et rationnel de b, nous pouvons supposer que Q est à coefficients dans
où W désigne un voisinage compact et rationnel de b, nous pouvons supposer que Q est à coefficients dans  .
.
Considérons le polynôme  . Par hypothèse, le polynôme R(b)(T) n’est pas nul. Il existe donc s
1,s
2∈R qui vérifient les inégalités de l’énoncé et tels que R(b)(T) ne s’annule pas sur le compact \(\overline{C}_{b}(Q;s_{1},s_{2})\). On en déduit qu’il existe un voisinage V de b tel que R(T) ne s’annule pas sur \(\overline {C}_{V}(Q;s_{1},s_{2})\).
. Par hypothèse, le polynôme R(b)(T) n’est pas nul. Il existe donc s
1,s
2∈R qui vérifient les inégalités de l’énoncé et tels que R(b)(T) ne s’annule pas sur le compact \(\overline{C}_{b}(Q;s_{1},s_{2})\). On en déduit qu’il existe un voisinage V de b tel que R(T) ne s’annule pas sur \(\overline {C}_{V}(Q;s_{1},s_{2})\).
Soit U un voisinage compact et spectralement convexe de b dans V. Pour tout v∈[s 1,s 2], la lemniscate \(\overline {D}_{U}(Q;v)\) possède un bord analytique contenu dans \(\overline {C}_{U}(Q;s_{1},s_{2})\). Par conséquent, la lemniscate \(\overline {D}_{U}(Q;v)\) satisfait la condition (R P(S)−T ). □
Proposition 6.17
Soit b
un point de B. Soit
P(S) un polynôme unitaire non constant à coefficients dans
 dont l’image dans
dont l’image dans
 est séparable. Alors, tout point de X
b
possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition (R
P(S)−T
) et donc (N
P(S)−T
).
est séparable. Alors, tout point de X
b
possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition (R
P(S)−T
) et donc (N
P(S)−T
).
Démonstration
Soient x un point de X
b
et U un voisinage ouvert de x dans X. D’après la proposition 6.7, il existe un voisinage compact V de b dans B, un polynôme unitaire Q(T) à coefficients dans  et deux nombres réels r et s vérifiant 0≤r<s tels que r≺|Q(x)|<s et \(\overline {C}_{V}(Q;r,s) \subset U\). Le résultat découle alors du lemme 6.16. □
et deux nombres réels r et s vérifiant 0≤r<s tels que r≺|Q(x)|<s et \(\overline {C}_{V}(Q;r,s) \subset U\). Le résultat découle alors du lemme 6.16. □
7 Endomorphismes de la droite
Soient d∈N
∗ et P un polynôme de degré d à coefficients dans  dont le coefficient dominant est inversible. Le morphisme naturel
dont le coefficient dominant est inversible. Le morphisme naturel

qui envoie T sur P(S), induit un morphisme continu φ de la droite X dans elle-même.
Nous pouvons appliquer dans ce contexte certains des résultats de la partie précédente. Expliquons comment obtenir un analogue de la proposition 4.4.
Proposition 7.1
Soit U
une partie compacte de X (avec variable T) qui satisfait la condition (N
P(S)−T
). Les normes ∥.∥
U,div
et ∥.∥
U,w,rés, pour
w≥v, sont alors équivalentes à la norme spectrale sur
 . De plus, nous avons un isomorphisme admissible naturel
. De plus, nous avons un isomorphisme admissible naturel

En particulier, pour tous r,s≥0 et toute partie compacte et spectralement convexe W de X tels que \(\overline{C}_{W}(r,s)\) satisfait la condition (N P(S)−T ), nous avons un isomorphisme admissible naturel

Démonstration
Considérons le plan  avec variables S et T et notons π
T
:X
2→X sa projection sur la variable T. Notons Z le fermé de Zariski de \(\pi_{T}^{-1}(U)\) défini par P(S)=T. D’après la proposition 4.4, nous avons un isomorphisme admissible
avec variables S et T et notons π
T
:X
2→X sa projection sur la variable T. Notons Z le fermé de Zariski de \(\pi_{T}^{-1}(U)\) défini par P(S)=T. D’après la proposition 4.4, nous avons un isomorphisme admissible  .
.
Notons  la projection sur la variable S. Nous avons un isomorphisme admissible
la projection sur la variable S. Nous avons un isomorphisme admissible  (ce que l’on démontre soit directement, soit en invoquant de nouveau la proposition 4.4 et la remarque 4.3). On conclut en remarquant que l’on a également un isomorphisme admissible
(ce que l’on démontre soit directement, soit en invoquant de nouveau la proposition 4.4 et la remarque 4.3). On conclut en remarquant que l’on a également un isomorphisme admissible  et que π
S
(Z) n’est autre que φ
−1(U). □
et que π
S
(Z) n’est autre que φ
−1(U). □
Corollaire 7.2
Pour tout
s≥0 et toute partie compacte et spectralement convexe W
de B
tels que
\(\overline{D}_{W}(s)\)
satisfait la condition (N
P(S)−T
), l’anneau
 est dense dans
est dense dans
 pour la norme uniforme.
pour la norme uniforme.
Pour tous
r,s∈R
vérifiant 0<r≤s
et toute partie compacte et spectralement convexe W
de B
tels que
\(\overline{C}_{W}(r,s)\)
satisfait la condition (N
P(S)−T
), l’anneau
 est dense dans
est dense dans
 pour la norme uniforme.
pour la norme uniforme.
Nous pouvons maintenant reprendre les résultats de la fin de la section 4 mutatis mutandis, en utilisant les résultats du corollaire 5.4 et des propositions 6.11 et 6.17.
Théorème 7.3
Soit V une partie de B telle qu’en tout point b qui n’est pas ultramétrique typique, le polynôme P(b)(T) soit séparable. Alors, le morphisme

est un isomorphisme de
 -modules.
-modules.
En particulier, pour toute partie U de V, le morphisme naturel

est un isomorphisme.
Démonstration
D’après le corollaire 5.4 et la proposition 6.17, tout point de X V satisfait la condition (D P(S)−T ) et possède un système fondamental de voisinages compacts qui satisfont la condition (N P(S)−T ). □
Énonçons un cas particulier dont nous nous servirons par la suite.
Corollaire 7.4
Soit V une partie de B telle qu’en tout point b qui n’est pas ultramétrique typique, le polynôme P(b)(T) soit séparable. Soient r,s≥0. Le morphisme naturel

est un isomorphisme.
8 Théorème de Weierstraß local
Ainsi que nous l’avons expliqué dans l’introduction, l’objectif principal de ce texte est de démontrer un théorème de division Weierstraß donnant accès à la structure des anneaux locaux des espaces de Berkovich affines. En géométrie analytique complexe, où ce théorème est connu depuis longtemps et joue un rôle majeur, tous les points sont définis sur C et l’on se ramène par translation, à traiter le cas du point 0. Dans [16], nous nous sommes déjà intéressé à l’analogue de cette situation et avons démontré un théorème de division de Weierstraß au voisinage du point 0 d’une fibre X b , avec b∈B (cf. théorème 2.2.3). Cependant les fibres X b contiennent en général bien d’autres types de points pour lesquels il serait utile de disposer d’un tel théorème.
Définition 8.1
Soit b un point de B. Soit n∈N. Un point x de  (avec variables T
1,…,T
n
) au-dessus de b est dit rigide si
(avec variables T
1,…,T
n
) au-dessus de b est dit rigide si  est une extension finie de
est une extension finie de  , autrement dit, si T
1(x),…,T
n
(x) sont algébriques sur
, autrement dit, si T
1(x),…,T
n
(x) sont algébriques sur  .
.
Un point x de  au-dessus de b est dit rigide épais si κ(x) est une extension finie de κ(b), autrement dit, si T
1(x),…,T
n
(x) sont algébriques sur κ(b). Un point rigide qui n’est pas épais est appelé point rigide maigre.
au-dessus de b est dit rigide épais si κ(x) est une extension finie de κ(b), autrement dit, si T
1(x),…,T
n
(x) sont algébriques sur κ(b). Un point rigide qui n’est pas épais est appelé point rigide maigre.
Définition 8.2
Soient b un point de B et x un point rigide de X
b
. Il existe un unique polynôme irréductible et unitaire  qui s’annule au point x. Nous l’appellerons polynôme minimal du point x.
qui s’annule au point x. Nous l’appellerons polynôme minimal du point x.
Remarquons que x est un point rigide épais si, et seulement si, P(T) appartient à κ(b)[T].
Le théorème qui suit est un théorème de division de Weierstraß au voisinage d’un point rigide x quelconque d’une fibre X
b
, avec b∈B. Lorsque le point x est épais, les coefficients de son polynôme minimal P sont définis au voisinage de b et l’on peut utiliser les résultats des sections précédentes pour étudier le morphisme d’un voisinage de X
b
dans lui-même défini par P. Lorsque le point x est maigre, en revanche, son polynôme minimal P n’est défini que sur  et il nous faudra utiliser des polynômes auxiliaires proches de P mais qui s’étendent au voisinage de b.
et il nous faudra utiliser des polynômes auxiliaires proches de P mais qui s’étendent au voisinage de b.
Théorème 8.3
(de division de Weierstraß)
Soit b
un point de B. Soit
 un polynôme irréductible et unitaire de degré d. Si le polynôme P
est inséparable et si le corps résiduel
un polynôme irréductible et unitaire de degré d. Si le polynôme P
est inséparable et si le corps résiduel
 est trivialement valué, supposons que le point b
est ultramétrique typique.
est trivialement valué, supposons que le point b
est ultramétrique typique.
Notons x
le point rigide de la fibre X
b
défini par l’équation P=0. Soit G
un élément de l’anneau local
 . Supposons que son image dans
. Supposons que son image dans
 n’est pas nulle et notons n
sa valuation
P-adique.
n’est pas nulle et notons n
sa valuation
P-adique.
Alors, pour tout
 , il existe un unique couple
, il existe un unique couple
 tel que
tel que
-
(i)
F=QG+R ;
-
(ii)
 est un polynôme de degré strictement inférieur à nd.
est un polynôme de degré strictement inférieur à nd.
Démonstration
Si le degré d du polynôme P est nul, le résultat est évident. Nous supposerons donc que d≥1. Il existe  tels que
tels que
Soit  .
.
Il existe un nombre réel r>0 et un voisinage U de X
b
∩{|P|≤r} dans X sur lequel F et G soient définis. Il existe un élément inversible H de  tel que G=P
n
H. Quitte à diminuer r, nous pouvons supposer que H et H
−1 sont définis sur X
b
∩{|P|≤r} dans X
b
. Fixons un nombre réel s∈]0,r[. Soit ε>0. Nous imposerons plus tard d’autres conditions (qui ne dépendront que de s et de P) sur cet élément.
tel que G=P
n
H. Quitte à diminuer r, nous pouvons supposer que H et H
−1 sont définis sur X
b
∩{|P|≤r} dans X
b
. Fixons un nombre réel s∈]0,r[. Soit ε>0. Nous imposerons plus tard d’autres conditions (qui ne dépendront que de s et de P) sur cet élément.
• Supposons que le polynôme P est séparable. D’après le lemme 6.15, quitte à diminuer r, nous pouvons trouver un polynôme P
ε
(S) unitaire de degré d à coefficients dans  vérifiant ∥P
ε
(b)−P∥∞≤ε et tel que le disque \(\overline{D}_{b}(r)\) satisfasse la condition \((N_{P_{ \varepsilon }(S)-T})\).
vérifiant ∥P
ε
(b)−P∥∞≤ε et tel que le disque \(\overline{D}_{b}(r)\) satisfasse la condition \((N_{P_{ \varepsilon }(S)-T})\).
Nous pouvons en outre supposer que le polynôme P ε (b)(S) est séparable. Dans ce cas, d’après la proposition 6.17, tout point de \(\overline{D}_{b}(r)\) possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition \((N_{P_{ \varepsilon }(S)-T})\).
• Supposons que la valeur absolue associée au point b est ultramétrique, mais pas triviale. Nous pouvons trouver un polynôme P
ε
(S) unitaire de degré d à coefficients dans  tel que ∥P
ε
(b)−P∥∞≤ε. Nous pouvons supposer que le polynôme P
ε
(b)(S) est séparable. Dans ce cas, d’après la proposition 6.17, tout point de \(\overline {D}_{b}(r)\) possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition \((N_{P_{ \varepsilon }(S)-T})\).
tel que ∥P
ε
(b)−P∥∞≤ε. Nous pouvons supposer que le polynôme P
ε
(b)(S) est séparable. Dans ce cas, d’après la proposition 6.17, tout point de \(\overline {D}_{b}(r)\) possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition \((N_{P_{ \varepsilon }(S)-T})\).
Notons η
r
l’unique point du bord de Shilov du disque \(\overline {D}_{b}(r)\). Puisque T(η
r
) est transcendant sur  et que le polynôme P
ε
(b)(S) est séparable, le polynôme
et que le polynôme P
ε
(b)(S) est séparable, le polynôme  l’est aussi. Le disque \(\overline{D}_{b}(r)\) satisfait donc la condition \((N_{P_{ \varepsilon }(S)-T})\), en vertu du corollaire 6.3.
l’est aussi. Le disque \(\overline{D}_{b}(r)\) satisfait donc la condition \((N_{P_{ \varepsilon }(S)-T})\), en vertu du corollaire 6.3.
• Supposons finalement que le polynôme P est inséparable et le corps  trivialement valué. Nous pouvons alors relever P en un polynôme à coefficients dans
trivialement valué. Nous pouvons alors relever P en un polynôme à coefficients dans  que nous noterons P
ε
. Par hypothèse, le point b est ultramétrique typique. D’après la proposition 6.5, le disque \(\overline{D}_{b}(r)\) satisfait la condition \((N_{P_{ \varepsilon }(S)-T})\). D’après la proposition 6.11, tout point de \(\overline{D}_{b}(r)\) possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition \((N_{P_{ \varepsilon }(S)-T})\).
que nous noterons P
ε
. Par hypothèse, le point b est ultramétrique typique. D’après la proposition 6.5, le disque \(\overline{D}_{b}(r)\) satisfait la condition \((N_{P_{ \varepsilon }(S)-T})\). D’après la proposition 6.11, tout point de \(\overline{D}_{b}(r)\) possède un système fondamental de voisinages compacts et spectralement convexes qui satisfont la condition \((N_{P_{ \varepsilon }(S)-T})\).
Quitte à diminuer ε, nous pouvons supposer que X
b
∩{|P
ε
|≤r} est un voisinage du point x dans X
b
∩U et que H et H
−1 sont définis sur X
b
∩{|P
ε
|≤r} dans X
b
. Un argument de compacité montre qu’il existe un voisinage compact V de b dans B tel que X
V
∩{|P
ε
|≤r} soit contenu dans U. Quitte à restreindre V, nous pouvons supposer que  .
.
Considérons l’anneau de Banach  . D’après le théorème 3.1 et le corollaire 3.2, il existe un nombre réel v>0 tel que, pour tout w≥v et toute A-algèbre de Banach A′ telle que le morphisme structural A→A′ diminue les normes, la semi-norme ∥.∥
w,rés définie sur le quotient A′[S]/(P
ε
(S)−T) soit une norme. En outre, d’après le corollaire 3.3, il existe une constante C>0 tel que pour toute telle algèbre A′ et tout élément F de A′[S]/(P
ε
(S)−T), nous ayons
. D’après le théorème 3.1 et le corollaire 3.2, il existe un nombre réel v>0 tel que, pour tout w≥v et toute A-algèbre de Banach A′ telle que le morphisme structural A→A′ diminue les normes, la semi-norme ∥.∥
w,rés définie sur le quotient A′[S]/(P
ε
(S)−T) soit une norme. En outre, d’après le corollaire 3.3, il existe une constante C>0 tel que pour toute telle algèbre A′ et tout élément F de A′[S]/(P
ε
(S)−T), nous ayons
Lorsque l’algèbre A′ sera de la forme  , nous noterons ∥.∥
W,t,w,rés et ∥.∥
W,t,div les normes ∥.∥
A′,w,rés et ∥.∥
A′,div respectivement.
, nous noterons ∥.∥
W,t,w,rés et ∥.∥
W,t,div les normes ∥.∥
A′,w,rés et ∥.∥
A′,div respectivement.
Par choix de P
ε
, le disque \(\overline{D}_{b}(r)\) satisfait la condition \((N_{P_{ \varepsilon }(S)-T})\). Il existe donc un nombre réel v′>0 et une constante D>0 tel que, pour tout w′≥v′ et tout élement f de  , on ait
, on ait
où ∥.∥
w′,rés désigne la norme résiduelle sur  induite par la norme ∥.∥
w′ sur
induite par la norme ∥.∥
w′ sur  , l’algèbre
, l’algèbre  étant munie de la norme spectrale.
étant munie de la norme spectrale.
Soit w 0≥max(v,v′). Dorénavant toutes les normes résiduelles seront calculées avec ce rayon w 0.
En utilisant la proposition 2.3 pour comparer les normes sur  et
et  , on montre que, pour tout f dans
, on montre que, pour tout f dans  , nous avons
, nous avons
Le corollaire 7.4 assure que la fonction H
−1 possède un représentant dans  . Par conséquent, elle est approchable uniformément sur X
b
∩{|P
ε
|≤r} par des éléments de
. Par conséquent, elle est approchable uniformément sur X
b
∩{|P
ε
|≤r} par des éléments de  . Quitte à restreindre V, nous pouvons donc supposer qu’il existe
. Quitte à restreindre V, nous pouvons donc supposer qu’il existe  tel que
tel que
D’après les corollaires 7.4 et 2.7, quitte à restreindre V de nouveau, nous pouvons supposer que les germes des fonctions F et G au voisinage de x possèdent également des représentants dans  .
.
Soit W un voisinage compact de b dans V. Tout élément φ appartenant à  peut s’écrire de façon unique sous la forme
peut s’écrire de façon unique sous la forme
où les α
i
(φ) sont des éléments de  et les β
i
(φ) des éléments de
et les β
i
(φ) des éléments de  de degré strictement inférieur à n. Posons
de degré strictement inférieur à n. Posons
Remarquons que β(φ) est un polynôme en S de degré inférieur à nd−1. Nous avons
Remarquons que
d’où l’on tire
Considérons, à présent, l’endomorphisme

Quel que soit  , nous avons
, nous avons
Or
et
Quitte à diminuer ε, nous pouvons donc supposer que
puis, quitte à restreindre le voisinage V de b, que
L’endomorphisme A W =Id+(A W −Id) est alors inversible et les éléments \(Q=\alpha (A_{V}^{-1}(F))K\) et \(R=\beta(A_{V}^{-1}(F))\) vérifient QG+R=F. Ceci prouve l’existence d’un couple (Q,R) vérifiant les propriétés de l’énoncé.
Démontrons à présent l’unicité. Soit un couple  vérifiant les propriétés de l’énoncé. Nous pouvons choisir le voisinage U de x au début de la preuve de façon que Q′ et R′ soient définis sur U. D’après les corollaires 7.4 et 2.7, les germes des fonctions Q′ et R′ au voisinage de x possèdent des représentants dans
vérifiant les propriétés de l’énoncé. Nous pouvons choisir le voisinage U de x au début de la preuve de façon que Q′ et R′ soient définis sur U. D’après les corollaires 7.4 et 2.7, les germes des fonctions Q′ et R′ au voisinage de x possèdent des représentants dans  , pour un certain voisinage compact W de b dans V. L’injectivité du morphisme A
W
permet alors de conclure. □
, pour un certain voisinage compact W de b dans V. L’injectivité du morphisme A
W
permet alors de conclure. □
Remarque 8.4
Nous avons déjà énoncé, dans [16], un résultat de division de Weierstraß partiel au voisinage des points rigides épais, sous certaines conditions (cf. théorème 5.4.4). La démonstration en est malheureusement incorrecte (dû à une réduction liminaire inconsidérée). Le théorème proposé ici est, de toute façon, plus général.
Énonçons maintenant un corollaire très utile.
Corollaire 8.5
Soit b
un point de B. Si son corps résiduel
 est imparfait et trivialement valué, supposons que le point b
est ultramétrique typique. Soit x
un point de X
b
qui ne soit pas un point rigide épais. Soit f
un élément de
est imparfait et trivialement valué, supposons que le point b
est ultramétrique typique. Soit x
un point de X
b
qui ne soit pas un point rigide épais. Soit f
un élément de
 tel que f(x)=0. Alors f
est nul dans
tel que f(x)=0. Alors f
est nul dans
 .
.
Démonstration
Supposons que x soit un point de type 2, 3, 4 ou de type 1 non rigide. Dans ce cas, l’anneau local  est un corps et le résultat est immédiat.
est un corps et le résultat est immédiat.
Il nous reste à traiter le cas où x est un point rigide maigre. Considérons son polynôme minimal unitaire  . Notons d son degré. Supposons, par l’absurde, que f n’est pas nul dans
. Notons d son degré. Supposons, par l’absurde, que f n’est pas nul dans  . Notons n sa valuation P-adique dans
. Notons n sa valuation P-adique dans  . Appliquons le théorème 8.3 avec F=S
nd et G=f. Il assure qu’il existe un polynôme R à coefficients dans
. Appliquons le théorème 8.3 avec F=S
nd et G=f. Il assure qu’il existe un polynôme R à coefficients dans  et de degré strictement inférieur à nd tel que F=Qf+R. En particulier, le polynôme non nul F−R s’annule en x. On en déduit que le point x est épais, ce qui contredit l’hypothèse. □
et de degré strictement inférieur à nd tel que F=Qf+R. En particulier, le polynôme non nul F−R s’annule en x. On en déduit que le point x est épais, ce qui contredit l’hypothèse. □
Une fois le théorème de division de Weierstraß démontré, nous pouvons en déduire, par un raisonnement classique, le théorème de préparation de Weierstraß. Remarquons qu’il ne vaut que pour les points rigides épais.
Théorème 8.6
(de préparation de Weierstraß)
Soit b
un point de B. Soit
P(S)∈κ(b)[S] un polynôme unitaire de degré d
dont l’image dans
 est irréductible. Si le polynôme P
est inséparable et si le corps résiduel
est irréductible. Si le polynôme P
est inséparable et si le corps résiduel
 est trivialement valué, supposons que le point b
est ultramétrique typique.
est trivialement valué, supposons que le point b
est ultramétrique typique.
Notons x
le point rigide de la fibre X
b
défini par l’équation P=0. Soit G
un élément de l’anneau local
 . Supposons que son image dans
. Supposons que son image dans
 n’est pas nulle et notons n
sa valuation
P-adique.
n’est pas nulle et notons n
sa valuation
P-adique.
Alors il existe un unique couple
 tel que :
tel que :
-
(i)
 est un polynôme unitaire de degré nd
vérifiant
Ω(b)(S)=P(S)n
dans
est un polynôme unitaire de degré nd
vérifiant
Ω(b)(S)=P(S)n
dans
 ;
; -
(ii)
E est inversible dans
 ;
; -
(iii)
G=ΩE.
Démonstration
Supposons qu’un tel couple  existe et écrivons Ω=P
n+R, où
existe et écrivons Ω=P
n+R, où  est un polynôme de degré strictement inférieur à nd. Nous avons alors P
n=E
−1
G−R dans
est un polynôme de degré strictement inférieur à nd. Nous avons alors P
n=E
−1
G−R dans  et le théorème de division de Weierstraß assure l’unicité des éléments E et R, et donc Ω.
et le théorème de division de Weierstraß assure l’unicité des éléments E et R, et donc Ω.
Pour démontrer l’existence, appliquons le théorème de division de Weierstraß à P
n et G. On en déduit qu’il existe des éléments Q de  et R de
et R de  , R étant de degré strictement inférieur à nd, tels que P
n=QG+R. On vérifie que Q est inversible dans
, R étant de degré strictement inférieur à nd, tels que P
n=QG+R. On vérifie que Q est inversible dans  et que les éléments E=Q
−1 et Ω=P
n−R conviennent. □
et que les éléments E=Q
−1 et Ω=P
n−R conviennent. □
Une autre conséquence classique du théorème de division de Weierstraß a trait aux morphismes finis. Nous pouvons, en effet, maintenant, généraliser le théorème 7.3 en relâchant l’hypothèse sur le polynôme P. Cette partie est classique, du moins en ce qui concerne les espaces analytiques complexes, et se trouve rédigée dans [10], I, § 2, par exemple. Nous renvoyons le lecteur désireux de lire les détails dans le cadre plus général où nous nous sommes placés à [16], § 5.5. Nous nous contenterons ici d’indiquer les énoncés des résultats.
Reprenons le cadre décrit à la section 7. Soient d∈N
∗ et P un polynôme de degré d à coefficients dans  dont le coefficient dominant est inversible. Considérons le morphisme φ de la droite affine X dans elle-même induit par le polynôme P.
dont le coefficient dominant est inversible. Considérons le morphisme φ de la droite affine X dans elle-même induit par le polynôme P.
Il peut être décrit de la façon suivante. Notons  , avec variables S et T. Considérons le fermé de Zariski Z de X
2 défini par le polynôme G(S,T)=P(S)−T et identifions-le à la droite affine X (avec variable S). Le morphisme φ est alors la composée du plongement de X dans X
2 et de la projection sur la deuxième coordonnée T.
, avec variables S et T. Considérons le fermé de Zariski Z de X
2 défini par le polynôme G(S,T)=P(S)−T et identifions-le à la droite affine X (avec variable S). Le morphisme φ est alors la composée du plongement de X dans X
2 et de la projection sur la deuxième coordonnée T.
Théorème 8.7
Soient b
un point de B
et x
un point de X
b
(avec variable T). Si son corps résiduel
 est imparfait et trivialement valué, supposons que le point x
est ultramétrique typique. Notons
φ
−1(x)={y
1,…,y
t
}⊂Z. Soit
est imparfait et trivialement valué, supposons que le point x
est ultramétrique typique. Notons
φ
−1(x)={y
1,…,y
t
}⊂Z. Soit
 . Alors, il existe un unique élément (r,q
1,…,q
t
) de
. Alors, il existe un unique élément (r,q
1,…,q
t
) de
 vérifiant les propriétés suivantes :
vérifiant les propriétés suivantes :
-
(i)
pour tout i∈[[1,t]], nous avons f i =q i G+r dans
 ;
; -
(ii)
le polynôme r est de degré strictement inférieur à d.
Théorème 8.8
Supposons que tout point b
de B
dont le corps résiduel
 est de caractéristique non nulle et trivialement valué est ultramétrique typique. Alors, le morphisme
est de caractéristique non nulle et trivialement valué est ultramétrique typique. Alors, le morphisme

est un isomorphisme de
 -modules.
-modules.
En particulier, pour toute partie U de X, le morphisme naturel

est un isomorphisme.
Corollaire 8.9
Supposons que tout point b
de B
dont le corps résiduel
 est de caractéristique non nulle et trivialement valué est ultramétrique typique. Supposons que le faisceau
est de caractéristique non nulle et trivialement valué est ultramétrique typique. Supposons que le faisceau
 est cohérent. Alors, pour toute partie U
de X
et tout faisceau cohérent
est cohérent. Alors, pour toute partie U
de X
et tout faisceau cohérent
 sur φ
−1(U), le faisceau
sur φ
−1(U), le faisceau
 est cohérent.
est cohérent.
Remarquons que le résultat du théorème 8.8 s’étend en dimension supérieure.
Corollaire 8.10
Supposons que tout point b
de B
dont le corps résiduel
 est de caractéristique non nulle et trivialement valué est ultramétrique typique. Soit n∈N
∗. Pour tout m∈[[1,n]], soit
est de caractéristique non nulle et trivialement valué est ultramétrique typique. Soit n∈N
∗. Pour tout m∈[[1,n]], soit
 un polynôme qui, vu comme polynôme en la variable T
m
n’est pas constant et possède un coefficient dominant inversible. Considérons l’endomorphisme de
un polynôme qui, vu comme polynôme en la variable T
m
n’est pas constant et possède un coefficient dominant inversible. Considérons l’endomorphisme de
 qui, pour tout
m∈[[1,n]], envoie T
m
sur P
m
. Notons
qui, pour tout
m∈[[1,n]], envoie T
m
sur P
m
. Notons
 le morphisme entre espaces analytiques associé.
le morphisme entre espaces analytiques associé.
Alors, pour toute partie U
de
 , le morphisme naturel
, le morphisme naturel

est un isomorphisme.
Remarque 8.11
En nous plaçant au voisinage d’un point de  , nous pourrions relâcher les conditions sur les polynômes P
m
.
, nous pourrions relâcher les conditions sur les polynômes P
m
.
9 Premières propriétés des anneaux locaux
Dans cette partie, nous revenons à notre objectif initial : l’étude des anneaux locaux des espaces affines analytiques sur Z et les anneaux d’entiers de corps de nombres. Nous démontrons ici qu’ils sont noethériens et réguliers. Les preuves que nous proposons valent en fait pour les anneaux locaux des espaces  , où
, où  appartient à une classe d’anneaux de Banach plus générale, qui contient notamment les corps valués complets (archimédiens ou non) et les anneaux de valuation discrète.
appartient à une classe d’anneaux de Banach plus générale, qui contient notamment les corps valués complets (archimédiens ou non) et les anneaux de valuation discrète.
Bien entendu, ces résultats sont déjà connus pour les espaces de Berkovich sur un corps valué ultramétrique complet (cf. [2], théorèmes 2.1.4 et 2.2.1). Le cas d’un point rationnel se démontre par des méthodes classiques de géométrie rigide (cf. [4], proposition 7.3.2/7), qui reposent in fine sur un théorème de division de Weierstraß global : il vaut pour les algèbres de Tate, qui sont des algèbres de fonctions sur des disques de rayon strictement positif, et se démontre par des arguments de réduction (cf. [4], théorème 5.2.1/2). Pour traiter le cas d’un point x quelconque, V. Berkovich effectue le changement de base  , opération qui rend le point x rationnel. Un résultat de L. Gruson (cf. [11]) montre que ce changement de base est fidèlement plat et permet de conclure. Il semble difficile d’adapter ces arguments pour les espaces de Berkovich globaux (en particulier le dernier, puisque le changement de base
, opération qui rend le point x rationnel. Un résultat de L. Gruson (cf. [11]) montre que ce changement de base est fidèlement plat et permet de conclure. Il semble difficile d’adapter ces arguments pour les espaces de Berkovich globaux (en particulier le dernier, puisque le changement de base  n’est pas plat en général). C’est pourquoi nous avons choisi de mettre en œuvre une méthode purement locale, basée sur les théorèmes de Weierstraß démontrés à la section précédente. Notre méthode présente, de surcroît, l’avantage d’unifier les approches complexe et p-adique.
n’est pas plat en général). C’est pourquoi nous avons choisi de mettre en œuvre une méthode purement locale, basée sur les théorèmes de Weierstraß démontrés à la section précédente. Notre méthode présente, de surcroît, l’avantage d’unifier les approches complexe et p-adique.
Nous démontrerons les résultats de noethérianité et régularité annoncés en supposant que les anneaux locaux de l’espace de base B sont assez simples. Précisons.
Définition 9.1
Soit C une partie compacte de B. Soit  un système fondamental de voisinages compacts et spectralement convexes de C. On dit qu’un idéal I de
un système fondamental de voisinages compacts et spectralement convexes de C. On dit qu’un idéal I de  est
est  -fortement de type fini relativement à
-fortement de type fini relativement à  s’il existe des éléments f
1,…,f
p
de I qui sont
s’il existe des éléments f
1,…,f
p
de I qui sont  -définis sur tous les éléments de
-définis sur tous les éléments de  et vérifient la propriété suivante : pour tout voisinage compact V de C, il existe une famille de nombres réels strictement positifs
et vérifient la propriété suivante : pour tout voisinage compact V de C, il existe une famille de nombres réels strictement positifs  telle que, pour tout élément f de I
telle que, pour tout élément f de I
 -défini sur V et tout élément U de
-défini sur V et tout élément U de  contenu dans \(\overset{\circ}{V}\), il existe des éléments a
1,…,a
p
de
contenu dans \(\overset{\circ}{V}\), il existe des éléments a
1,…,a
p
de  satisfaisant
satisfaisant

Une famille (f
1,…,f
p
) vérifiant les propriétés précédentes est appelée  -système
de générateurs fort de l’idéal I relativement à
-système
de générateurs fort de l’idéal I relativement à  . On dit également qu’elle engendre
. On dit également qu’elle engendre
 -fortement l’idéal I relativement à
-fortement l’idéal I relativement à  .
.
Définition 9.2
Soit C une partie de B. Nous dirons qu’un système fondamental de voisinages  de C est fin s’il contient un système fondamental de voisinages de tous ses éléments.
de C est fin s’il contient un système fondamental de voisinages de tous ses éléments.
Définition 9.3
Soit b un point de B. Nous dirons qu’un anneau local noethérien  de dimension n est fortement régulier s’il existe des éléments f
1,…,f
n
de \(\mathfrak {m} _{b}\) et un système fondamental fin
de dimension n est fortement régulier s’il existe des éléments f
1,…,f
n
de \(\mathfrak {m} _{b}\) et un système fondamental fin  de voisinages compacts et spectralement convexes de b dans B tels que la famille (f
1,…,f
n
) engendre
de voisinages compacts et spectralement convexes de b dans B tels que la famille (f
1,…,f
n
) engendre  -fortement l’idéal maximal \(\mathfrak {m} _{b}\) relativement à
-fortement l’idéal maximal \(\mathfrak {m} _{b}\) relativement à  .
.
Dans ces conditions, nous dirons que l’anneau local  est un corps fort (resp. un anneau fortement de valuation discrète) si n=0 (resp. n=1).
est un corps fort (resp. un anneau fortement de valuation discrète) si n=0 (resp. n=1).
Remarque 9.4
Un corps fort est un corps et la condition supplémentaire que nous imposons s’apparente au principe du prolongement analytique. Remarquons que, si B est localement connexe et si le principe du prolongement analytique y vaut, alors tout anneau local  qui est un corps est un corps fort.
qui est un corps est un corps fort.
Un anneau fortement de valuation discrète est un anneau de valuation discrète et la condition supplémentaire est l’analogue de la condition (U) introduite dans [16], définition 2.2.9. Remarquons que si la condition est vérifiée pour une uniformisante, alors elle l’est pour toutes. Cette condition nous semble naturelle à imposer dans un cadre analytique : elle permet, par exemple, de montrer qu’une série dont tous les coefficients sont multiples d’une uniformisante π est elle-même multiple de π.
Définition 9.5
Un anneau de Banach  est dit de base si, pour tout point b de son spectre
est dit de base si, pour tout point b de son spectre  , il existe un système fondamental fin de voisinages compacts et spectralement convexes
, il existe un système fondamental fin de voisinages compacts et spectralement convexes  vérifiant les propriétés suivantes :
vérifiant les propriétés suivantes :
-
(i)
l’anneau local
 est un anneau local noethérien, fortement régulier relativement à
est un anneau local noethérien, fortement régulier relativement à  et de dimension inférieure à 1, c’est-à-dire un corps fort ou un anneau fortement de valuation discrète ;
et de dimension inférieure à 1, c’est-à-dire un corps fort ou un anneau fortement de valuation discrète ; -
(ii)
si
 est de caractéristique non nulle et trivialement valué, tout élément de
est de caractéristique non nulle et trivialement valué, tout élément de  est contenu dans B
um et possède un bord analytique fini (ce qui entraîne que le point b est ultramétrique typique).
est contenu dans B
um et possède un bord analytique fini (ce qui entraîne que le point b est ultramétrique typique).
Remarque 9.6
Dans la suite, nous allons nous intéresser aux points de  sur un anneau de Banach de base au sens de la définition qui précède. Indiquons quelques exemples importants d’anneaux de Banach
sur un anneau de Banach de base au sens de la définition qui précède. Indiquons quelques exemples importants d’anneaux de Banach  qui vérifient cette propriété et où nos résultats valent donc inconditionnellement :
qui vérifient cette propriété et où nos résultats valent donc inconditionnellement :
-
(i)
un corps k muni d’une valeur absolue (archimédienne ou non) pour laquelle il est complet ;
-
(ii)
un corps k muni de la norme max(|.|0,|.|), où |.| est une valeur absolue sur k (cf. [3]) ;
-
(iii)
un anneau de valuation discrète muni d’une norme associée à la valuation ;
-
(iv)
l’anneau Z muni de la valeur absolue usuelle |.|∞ ou, plus généralement, un anneau d’entiers de corps de nombres A muni de la norme max σ (|σ(.)|∞), où σ décrit l’ensemble des plongements complexes de K=Frac(A) (cf. [16], § 3.1).
Dans un premier temps, nous allons étudier la propriété de génération forte et montrer qu’elle passe des anneaux locaux de  à ceux de
à ceux de  . Nous commencerons par quelques résultats sur les fonctions définies au voisinage de couronnes.
. Nous commencerons par quelques résultats sur les fonctions définies au voisinage de couronnes.
Proposition 9.7
Soient b
un point de B
et
 un système fondamental fin de voisinages compacts et spectralement convexes de b. Supposons que l’idéal
\(\mathfrak {m} _{b}\)
de
un système fondamental fin de voisinages compacts et spectralement convexes de b. Supposons que l’idéal
\(\mathfrak {m} _{b}\)
de
 possède un
possède un
 -système de générateurs forts (f
1,…,f
p
) relativement à
-système de générateurs forts (f
1,…,f
p
) relativement à
 .
.
Soient r
et s
deux nombres réels vérifiant 0≤r≤s
et
s>0. Notons
 l’ensemble des couronnes compactes de la forme
\(\overline{C}_{U}(u,v)\), avec
l’ensemble des couronnes compactes de la forme
\(\overline{C}_{U}(u,v)\), avec
 et 0≤u≺r≤s<v. C’est un système fondamental fin de voisinages compacts et spectralement convexes de
\(\overline{C}_{b}(r,s)\)
et la famille (f
1,…,f
p
) engendre
et 0≤u≺r≤s<v. C’est un système fondamental fin de voisinages compacts et spectralement convexes de
\(\overline{C}_{b}(r,s)\)
et la famille (f
1,…,f
p
) engendre
 -fortement relativement à
-fortement relativement à
 l’idéal I
de
l’idéal I
de
 formé des éléments qui s’annulent sur
\(\overline{C}_{b}(r,s)\). En outre, si
n=1 et si
\(\bigcap_{m\ge0} \mathfrak {m} _{b}^{m} = (0)\), alors ⋂
m≥0
I
m=(0).
formé des éléments qui s’annulent sur
\(\overline{C}_{b}(r,s)\). En outre, si
n=1 et si
\(\bigcap_{m\ge0} \mathfrak {m} _{b}^{m} = (0)\), alors ⋂
m≥0
I
m=(0).
Démonstration
Soient V un voisinage compact de \(\overline{C}_{b}(r,s)\), f un élément de I qui est  -défini sur V et \(\overline {C}_{U}(u,v)\) un élément de
-défini sur V et \(\overline {C}_{U}(u,v)\) un élément de  contenu dans \(\overset{\circ }{V}\). L’intérieur de V contient une partie de la forme \(\overline{C}_{U_{0}}(u_{0},v_{0})\), où U
0 est un voisinage compact et spectralement convexe de U dans B et 0≤u
0≺u≤v<v
0. D’après la proposition 2.4, nous pouvons écrire f sous la forme ∑
k∈Z
a
k
T
k, où (a
k
)
k∈Z
est une famille d’éléments de
contenu dans \(\overset{\circ }{V}\). L’intérieur de V contient une partie de la forme \(\overline{C}_{U_{0}}(u_{0},v_{0})\), où U
0 est un voisinage compact et spectralement convexe de U dans B et 0≤u
0≺u≤v<v
0. D’après la proposition 2.4, nous pouvons écrire f sous la forme ∑
k∈Z
a
k
T
k, où (a
k
)
k∈Z
est une famille d’éléments de  telle que la famille \((\|a_{k}\|_{U_{0}} \max(u_{0}^{k},v_{0}^{k}) )_{k\in \mathbf {Z} }\) est sommable.
telle que la famille \((\|a_{k}\|_{U_{0}} \max(u_{0}^{k},v_{0}^{k}) )_{k\in \mathbf {Z} }\) est sommable.
Puisque  est fin, nous pouvons choisir un élément U
1 de
est fin, nous pouvons choisir un élément U
1 de  tel que \(\overset{\circ}{U_{0}} \supset U_{1} \supset \overset{\circ}{U_{1}} \supset U\). Puisque f est un élément de I, pour tout k∈Z, a
k
s’annule en b. Par conséquent, il existe des éléments α
1,k
,…,α
p,k
de
tel que \(\overset{\circ}{U_{0}} \supset U_{1} \supset \overset{\circ}{U_{1}} \supset U\). Puisque f est un élément de I, pour tout k∈Z, a
k
s’annule en b. Par conséquent, il existe des éléments α
1,k
,…,α
p,k
de  tels que
tels que

Par conséquent, pour tout i∈[[1,p]], la famille \((\|\alpha _{i,k}\|_{U_{1}} \max(u_{0}^{k},v_{0}^{k}))_{k\in \mathbf {Z} }\) est sommable et la série A
i
=∑
k∈Z
α
i,k
T
k définit donc un élément de  . De plus, nous avons
. De plus, nous avons

et, pour tout i∈[[1,p]],
d’après la proposition 2.3.
Supposons maintenant que p=1 et \(\bigcap_{m\ge0} \mathfrak {m} _{b}^{m} = (0)\). Si f∈⋂ m≥0 I m, alors, pour tout k∈Z, \(a_{k} \in \bigcap_{m\ge0} (f_{1}^{m})\), d’où nous déduisons que f=0. □
Corollaire 9.8
Soient b
un point de B
et U
0
un voisinage compact de b. Soient
P
un polynôme unitaire à coefficients dans
 et r
et s
deux nombres réels vérifiant 0≤r≤s
et
s>0. Soit
et r
et s
deux nombres réels vérifiant 0≤r≤s
et
s>0. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes de b
dans U
0
et
u, v
deux nombres réels tels que 0≤u≺r≤s<v. Supposons que, pour tout élément U
de
un système fondamental fin de voisinages compacts et spectralement convexes de b
dans U
0
et
u, v
deux nombres réels tels que 0≤u≺r≤s<v. Supposons que, pour tout élément U
de
 et pour tous
u′, v′ vérifiant
u≺u′≺r
et
s<v′<v, la couronne
\(\overline{C}_{U}(u',v')\)
satisfait la condition (N
P(S)−T
). Notons
et pour tous
u′, v′ vérifiant
u≺u′≺r
et
s<v′<v, la couronne
\(\overline{C}_{U}(u',v')\)
satisfait la condition (N
P(S)−T
). Notons
 l’ensemble des couronnes compactes de la forme
\(\overline{C}_{U}(P;u',v')\), avec
l’ensemble des couronnes compactes de la forme
\(\overline{C}_{U}(P;u',v')\), avec
 , u≺u′≺r
et
s<v′<v.
, u≺u′≺r
et
s<v′<v.
Supposons que l’idéal
\(\mathfrak {m} _{b}\)
possède un
 -système de générateurs forts (f
1,…,f
p
) relativement à
-système de générateurs forts (f
1,…,f
p
) relativement à
 . Alors la famille (f
1,…,f
p
) est un
. Alors la famille (f
1,…,f
p
) est un
 -système de générateurs fort relativement à
-système de générateurs fort relativement à
 pour l’idéal I
de
pour l’idéal I
de
 formé des éléments qui s’annulent sur
\(\overline{C}_{b}(P;r,s)\). En outre, si
p=1 et si
\(\bigcap _{m\ge 0} \mathfrak {m} _{b}^{m} = (0)\), alors ⋂
m≥0
I
m=(0).
formé des éléments qui s’annulent sur
\(\overline{C}_{b}(P;r,s)\). En outre, si
p=1 et si
\(\bigcap _{m\ge 0} \mathfrak {m} _{b}^{m} = (0)\), alors ⋂
m≥0
I
m=(0).
Démonstration
On utilise le corollaire précédent et l’isomorphisme admissible démontré à la proposition 7.1. □
Introduisons encore un peu de vocabulaire.
Définition 9.9
Soit b un point de B. Soit x un point de X
b
. Nous dirons que le point x est transcendant si l’extension  est transcendante. Nous dirons que le point x est localement transcendant si l’extension κ(x)/κ(b) est transcendante.
est transcendante. Nous dirons que le point x est localement transcendant si l’extension κ(x)/κ(b) est transcendante.
Soit x un point de X
n
, avec n∈N, au-dessus de b. Nous dirons que le point x est purement localement transcendant si les éléments 1,T
1(x),…,T
n
(x) de  sont algébriquement indépendants sur κ(b).
sont algébriquement indépendants sur κ(b).
Remarque 9.10
Lorsque n=1, un point x est localement transcendant si, et seulement si, il n’est pas rigide épais, c’est-à-dire si et seulement s’il est de type 2, 3, 4, de type 1 transcendant ou rigide maigre.
Revenons à un entier n∈N quelconque. Pour m∈[[0,n]], notons x m ∈X m , la projection de x sur ses m premières coordonnées. Dans ce cas, le point x est purement localement transcendant si, pour tout m∈[[1,n]], le point x m est localement transcendant sur x m−1. Cela ne dépend pas des coordonnées choisies.
Corollaire 9.11
Soient b
un point de B
et x
un point de X
n
, avec
n∈N
∗, au-dessus de b. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’idéal
\(\mathfrak {m} _{b}\)
possède un
 -système de générateurs forts (f
1,…,f
p
) relativement à
-système de générateurs forts (f
1,…,f
p
) relativement à
 et que le point x
est purement localement transcendant. Alors il existe un système fondamental fin de voisinages compacts et spectralement convexes
et que le point x
est purement localement transcendant. Alors il existe un système fondamental fin de voisinages compacts et spectralement convexes
 du point x
tel que (f
1,…,f
p
) soit également un
du point x
tel que (f
1,…,f
p
) soit également un
 -système de générateurs fort pour
\(\mathfrak {m} _{x}\)
relativement à
-système de générateurs fort pour
\(\mathfrak {m} _{x}\)
relativement à
 . En outre, si
p=1 et si
\(\bigcap_{m\ge 0} \mathfrak {m} _{b}^{m} = (0)\), alors
\(\bigcap_{m\ge0} \mathfrak {m} _{x}^{m} = (0)\).
. En outre, si
p=1 et si
\(\bigcap_{m\ge 0} \mathfrak {m} _{b}^{m} = (0)\), alors
\(\bigcap_{m\ge0} \mathfrak {m} _{x}^{m} = (0)\).
En particulier, si
 est un corps fort, alors
est un corps fort, alors
 est un corps fort et si
est un corps fort et si
 est un anneau fortement de valuation discrète d’uniformisante π, alors
est un anneau fortement de valuation discrète d’uniformisante π, alors
 est également un anneau fortement de valuation discrète d’uniformisante π.
est également un anneau fortement de valuation discrète d’uniformisante π.
Si
 est de caractéristique non nulle et trivialement valué, nous pouvons choisir
est de caractéristique non nulle et trivialement valué, nous pouvons choisir
 de sorte que tout élément de
de sorte que tout élément de
 soit contenu dans (X
n
)um
et possède un bord analytique fini.
soit contenu dans (X
n
)um
et possède un bord analytique fini.
Démonstration
Une récurrence permet de se ramener au cas où n=1. Nous allons traiter le cas où le point x est un point de type 2 ou 3 ou 4. Le cas où c’est un point de type 1 se traite de façon similaire, en remplaçant, dans le raisonnement qui suit, les couronnes par des disques.
Soit  un système fondamental fin de voisinages compacts et spectralement convexes du point b par rapport auquel la famille (f
1,…,f
p
) engendre fortement \(\mathfrak {m} _{b}\). Soit W un voisinage ouvert du point x dans X. Il existe un polynôme unitaire
un système fondamental fin de voisinages compacts et spectralement convexes du point b par rapport auquel la famille (f
1,…,f
p
) engendre fortement \(\mathfrak {m} _{b}\). Soit W un voisinage ouvert du point x dans X. Il existe un polynôme unitaire  tel que 0<r<|P
0(S)(x)|<s et \(\overline{C}_{b}(P_{0};r,s)\) soit une partie connexe de W. Nous allons distinguer trois cas, selon les propriétés du corps résiduel
tel que 0<r<|P
0(S)(x)|<s et \(\overline{C}_{b}(P_{0};r,s)\) soit une partie connexe de W. Nous allons distinguer trois cas, selon les propriétés du corps résiduel  .
.
• Supposons que la valuation de  n’est pas triviale. Nous pouvons approcher les coefficients de P
0 par des éléments de
n’est pas triviale. Nous pouvons approcher les coefficients de P
0 par des éléments de  de façon à obtenir un polynôme unitaire
de façon à obtenir un polynôme unitaire  satisfaisant encore les propriétés énoncées. Nous pouvons, en outre, supposer que
satisfaisant encore les propriétés énoncées. Nous pouvons, en outre, supposer que  est séparable. D’après le corollaire 6.8, le morphisme de projection π est ouvert. On en déduit qu’il existe un voisinage ouvert U
0 de b dans B sur lequel les coefficients de P sont définis et tel que \(\overline{C}_{U_{0}}(P;r,s) \subset W\).
est séparable. D’après le corollaire 6.8, le morphisme de projection π est ouvert. On en déduit qu’il existe un voisinage ouvert U
0 de b dans B sur lequel les coefficients de P sont définis et tel que \(\overline{C}_{U_{0}}(P;r,s) \subset W\).
D’après le lemme 6.16, il existe un voisinage ouvert U 1 de b dans U 0 et r 1,r 2,s 1,s 2∈R vérifiant 0<r≤r 2<r 1<|P(S)(x)|<s 1<s 2≤s tels que, pour tout voisinage compact et spectralement convexe U de b dans U 1, tout u∈[r 2,r 1] et tout v∈[s 1,s 2], le disque \(\overline{C}_{U}(u,v)\) satisfasse la condition (N P(S)−T ). Remarquons que, puisque \(\overline{C}_{b}(P;r,s)\) est connexe, pour tous u,v vérifiant u<|P(S)(x)|<v, la lemniscate \(\overline {C}_{b}(P;u,v)\) est encore connexe.
Notons  l’ensemble des parties de la forme \(\overline {C}_{U}(P;r,s)\) avec
l’ensemble des parties de la forme \(\overline {C}_{U}(P;r,s)\) avec  , U⊂U
1, u∈]r
1,r
2[ et v∈]s
1,s
2[. On vérifie qu’il est fin. Notons
, U⊂U
1, u∈]r
1,r
2[ et v∈]s
1,s
2[. On vérifie qu’il est fin. Notons  la réunion des ensembles
la réunion des ensembles  , pour W décrivant l’ensemble des voisinages ouvert de x dans X. C’est un système fondamental fin de voisinages compacts et spectralement convexes de x dans X.
, pour W décrivant l’ensemble des voisinages ouvert de x dans X. C’est un système fondamental fin de voisinages compacts et spectralement convexes de x dans X.
Soient V un voisinage compact de x dans X et \(\overline {C}_{U}(P;u,v)\) un élément de  contenu dans \(\overset{\circ }{V}\). Soit f un élément de
contenu dans \(\overset{\circ }{V}\). Soit f un élément de  tel que f(x)=0. D’après le corollaire 8.5, l’image de f dans
tel que f(x)=0. D’après le corollaire 8.5, l’image de f dans  est nulle. Par le principe du prolongement analytique, la fonction f est nulle sur \(\overline{C}_{b}(P;u,v)\), car \(\overline {C}_{b}(P;u,v)\) est connexe. On conclut alors à l’aide du corollaire 9.8.
est nulle. Par le principe du prolongement analytique, la fonction f est nulle sur \(\overline{C}_{b}(P;u,v)\), car \(\overline {C}_{b}(P;u,v)\) est connexe. On conclut alors à l’aide du corollaire 9.8.
• Supposons que le corps  est de caractéristique nulle. Nous pouvons alors supposer que le polynôme
est de caractéristique nulle. Nous pouvons alors supposer que le polynôme  est séparable. Il est alors possible de trouver un polynôme
est séparable. Il est alors possible de trouver un polynôme  satisfaisant les mêmes propriétés que précédemment et, en particulier, le fait que
satisfaisant les mêmes propriétés que précédemment et, en particulier, le fait que  soit séparable. Le raisonnement se poursuit identiquement.
soit séparable. Le raisonnement se poursuit identiquement.
• Supposons que le corps  est de caractéristique non nulle et trivialement valué. Nous pouvons alors relever le polynôme
est de caractéristique non nulle et trivialement valué. Nous pouvons alors relever le polynôme  en un polynôme
en un polynôme  . Par hypothèse, tout élément de
. Par hypothèse, tout élément de  est contenu dans B
um et possède un bord analytique fini. La proposition 6.5 permet alors d’adapter le raisonnement précédent. □
est contenu dans B
um et possède un bord analytique fini. La proposition 6.5 permet alors d’adapter le raisonnement précédent. □
Intéressons-nous maintenant aux points rigides épais. Le raisonnement est similaire, mais un peu plus simple.
Proposition 9.12
Soient b
un point de B
et
 un système fondamental fin de voisinages compacts et spectralement convexes de b. Supposons que l’idéal
\(\mathfrak {m} _{b}\)
de
un système fondamental fin de voisinages compacts et spectralement convexes de b. Supposons que l’idéal
\(\mathfrak {m} _{b}\)
de
 possède un
possède un
 -système de générateurs forts (f
1,…,f
p
) relativement à
-système de générateurs forts (f
1,…,f
p
) relativement à
 . Notons x
le point 0 de la fibre X
b
.
. Notons x
le point 0 de la fibre X
b
.
Notons
 l’ensemble des disques compacts de la forme
\(\overline {D}_{U}(v)\), avec
l’ensemble des disques compacts de la forme
\(\overline {D}_{U}(v)\), avec
 et
v>0. C’est un système fondamental fin de voisinages compacts et spectralement convexes du point x
et la famille (f
1,…,f
p
,T) engendre
et
v>0. C’est un système fondamental fin de voisinages compacts et spectralement convexes du point x
et la famille (f
1,…,f
p
,T) engendre
 -fortement relativement à
-fortement relativement à
 l’idéal maximal
\(\mathfrak {m} _{x}\)
de
l’idéal maximal
\(\mathfrak {m} _{x}\)
de
 .
.
Si tout élément de
 est contenu dans B
um
et possède un bord analytique fini, alors tout élément de
est contenu dans B
um
et possède un bord analytique fini, alors tout élément de
 est contenu dans X
um
et possède un bord analytique fini.
est contenu dans X
um
et possède un bord analytique fini.
Démonstration
Soient V un voisinage compact de x, f un élément de \(\mathfrak {m} _{x}\)
 -défini sur V et \(\overline{D}_{U}(v)\) un élément de
-défini sur V et \(\overline{D}_{U}(v)\) un élément de  contenu dans \(\overset{\circ}{V}\). L’intérieur du voisinage V contient une partie de la forme \(\overline{D}_{U}(v_{0})\) avec v
0>v. D’après la proposition 2.4, nous pouvons écrire f sous la forme ∑
k≥0
a
k
T
k, où (a
k
)
k∈Z
est une famille d’éléments de
contenu dans \(\overset{\circ}{V}\). L’intérieur du voisinage V contient une partie de la forme \(\overline{D}_{U}(v_{0})\) avec v
0>v. D’après la proposition 2.4, nous pouvons écrire f sous la forme ∑
k≥0
a
k
T
k, où (a
k
)
k∈Z
est une famille d’éléments de  telle que la série \(\sum_{k\ge0} \|a_{k}\|_{U} v_{0}^{k}\) converge.
telle que la série \(\sum_{k\ge0} \|a_{k}\|_{U} v_{0}^{k}\) converge.
Puisque f est un élément de \(\mathfrak {m} _{x}\), a
0 s’annule en b. Par conséquent, il existe des éléments α
1,…,α
p
de  tels que
tels que

Or, d’après la proposition 2.3, nous avons
Ce raisonnement nous permet de remplacer f par f−a 0, et donc de supposer que a 0=0.
La série ∑
k≥0∥a
k+1∥
U
v
k converge et la série ∑
k≥0
a
k+1
T
k définit donc un élément g de  . De plus, nous avons f=Tg dans
. De plus, nous avons f=Tg dans  et
et
car le maximum de la fonction g sur toute fibre est atteint sur le cercle {|T|=v}. On en déduit le résultat voulu.
L’assertion finale de l’énoncé découle du lemme 6.4. □
En reprenant, à présent, le raisonnement des corollaires 9.8 et 9.11, nous obtenons le résultat suivant.
Corollaire 9.13
Soit b
un point de B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’idéal
\(\mathfrak {m} _{b}\)
possède un
 -système de générateurs forts (f
1,…,f
p
) relativement à
-système de générateurs forts (f
1,…,f
p
) relativement à
 . Soit x
un point rigide épais de X
b
. Alors il existe un système fondamental fin de voisinages compacts et spectralement convexes
. Soit x
un point rigide épais de X
b
. Alors il existe un système fondamental fin de voisinages compacts et spectralement convexes
 du point x
tel que la famille (f
1,…,f
p
,P(T)), où
du point x
tel que la famille (f
1,…,f
p
,P(T)), où
 est un polynôme unitaire relevant le polynôme minimal du point x, soit un
est un polynôme unitaire relevant le polynôme minimal du point x, soit un
 -système de générateurs fort pour
\(\mathfrak {m} _{x}\)
relativement à
-système de générateurs fort pour
\(\mathfrak {m} _{x}\)
relativement à
 . Dans le cas où
. Dans le cas où
 est de caractéristique non nulle et trivialement valué, nous pouvons choisir
est de caractéristique non nulle et trivialement valué, nous pouvons choisir
 de sorte que tout élément de
de sorte que tout élément de
 soit contenu dans X
um
et possède un bord analytique fini.
soit contenu dans X
um
et possède un bord analytique fini.
Soit n∈N. Soit x
un point rigide épais de X
n
au-dessus de b. Alors il existe un système fondamental fin de voisinages compacts et spectralement convexes
 du point x
et des éléments
g
1,…,g
n
de
\(\mathfrak {m} _{x}\)
tels que la famille (f
1,…,f
p
,g
1,…,g
n
) engendre
du point x
et des éléments
g
1,…,g
n
de
\(\mathfrak {m} _{x}\)
tels que la famille (f
1,…,f
p
,g
1,…,g
n
) engendre
 -fortement l’idéal
\(\mathfrak {m} _{x}\)
relativement à
-fortement l’idéal
\(\mathfrak {m} _{x}\)
relativement à
 . Dans le cas où
. Dans le cas où
 est de caractéristique non nulle et trivialement valué, nous pouvons choisir
est de caractéristique non nulle et trivialement valué, nous pouvons choisir
 de sorte que tout élément de
de sorte que tout élément de
 soit contenu dans (X
n
)um
et possède un bord analytique fini.
soit contenu dans (X
n
)um
et possède un bord analytique fini.
Approfondissons maintenant notre étude des points rigides épais.
Lemme 9.14
Soient b
un point de
 . Soient n∈N
et x
un point rigide épais de
. Soient n∈N
et x
un point rigide épais de
 au-dessus de b. Supposons que l’anneau local
au-dessus de b. Supposons que l’anneau local
 est un anneau fortement de valuation discrète d’uniformisante π.
est un anneau fortement de valuation discrète d’uniformisante π.
Alors, pour tout élément non nul f
de
 , il existe un unique couple (v,g) dans
, il existe un unique couple (v,g) dans
 vérifiant les propriétés suivantes :
vérifiant les propriétés suivantes :
-
(i)
f=π v g dans
 ;
; -
(ii)
g≠0 dans
 .
.
Démonstration
Le résultat se démontre par récurrence sur la dimension n. Pour n=0, c’est évident.
Supposons maintenant que n≥1 et que le résultat est vérifié en dimension n−1. Notons y∈X
n−1 la projection de x sur ses n−1 premières coordonnées. Notons x′ le point 0 de la fibre de X
n
au-dessus de y. Soit P(S)∈κ(y)[S] le polynôme minimal du point rigide épais x au-dessus de y. Relevons-le en un polynôme unitaire à coefficients dans  que nous noterons identiquement. D’après le théorème 8.8, nous disposons d’un isomorphisme naturel
que nous noterons identiquement. D’après le théorème 8.8, nous disposons d’un isomorphisme naturel  . Il suffit donc de démontrer le résultat pour le point x′. Or tout élément de
. Il suffit donc de démontrer le résultat pour le point x′. Or tout élément de  possède un développement en série convergente à coefficients dans
possède un développement en série convergente à coefficients dans  (cf. corollaire 2.6), ce qui permet de conclure par récurrence. (Le fait que l’anneau soit fortement de valuation discrète est utilisé pour montrer qu’en divisant par la puissance de π choisie, on obtient encore une série convergente.) □
(cf. corollaire 2.6), ce qui permet de conclure par récurrence. (Le fait que l’anneau soit fortement de valuation discrète est utilisé pour montrer qu’en divisant par la puissance de π choisie, on obtient encore une série convergente.) □
Lemme 9.15
Soient b
un point de
 . Soient n∈N
et x
un point rigide de
. Soient n∈N
et x
un point rigide de
 (avec variables
T
1,…,T
n
) au-dessus de b. Soit f
un élément de
(avec variables
T
1,…,T
n
) au-dessus de b. Soit f
un élément de
 dont l’image dans
dont l’image dans
 n’est pas nulle.
n’est pas nulle.
Alors il existe un changement de variables de la forme
avec
u
1,…,u
n−1∈N
tel que, après ce changement de variables, si l’on note
y∈X
n−1
le projeté de x
sur ses
n−1 premières coordonnées, l’image de f
dans
 ne soit pas nulle.
ne soit pas nulle.
Démonstration
Remarquons que le résultat concerne la restriction de la fonction f à X
b
. Nous pouvons donc supposer que  est un corps K. Remarquons encore qu’il suffit de démontrer le résultat après extension des scalaires. Nous pouvons donc supposer que K est algébriquement clos. Le point x est alors un point (α
1,…,α
n
) de K
n et, d’après le corollaire 2.6, la fonction f s’écrit comme une série
est un corps K. Remarquons encore qu’il suffit de démontrer le résultat après extension des scalaires. Nous pouvons donc supposer que K est algébriquement clos. Le point x est alors un point (α
1,…,α
n
) de K
n et, d’après le corollaire 2.6, la fonction f s’écrit comme une série
dont le rayon de convergence est strictement positif. Par hypothèse, l’un des coefficients \(a_{k_{1},\ldots,k_{n}}\) n’est pas nul. Soient u 1,…,u n−1∈N. Montrer que le changement de base de l’énoncé convient revient à montrer que la série
n’est pas nulle. En s’armant de courage, on démontre le résultat recherché. □
Remarque 9.16
Les fastidieux calculs finaux de la preuve précédente peuvent être évités si l’on s’autorise à utiliser les résultats connus sur les espaces analytiques au-dessus d’un corps.
Théorème 9.17
Soit b
un point de
 . Soit
. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’anneau local
 est un anneau local noethérien, fortement régulier relativement à
est un anneau local noethérien, fortement régulier relativement à
 et de dimension inférieure à 1. Soient
n∈N
et x
un point rigide épais de
et de dimension inférieure à 1. Soient
n∈N
et x
un point rigide épais de
 au-dessus de b.
au-dessus de b.
Alors l’anneau local
 est noethérien et fortement régulier et nous avons
est noethérien et fortement régulier et nous avons

Si
 est de caractéristique non nulle et trivialement valué, il existe un système fondamental fin
est de caractéristique non nulle et trivialement valué, il existe un système fondamental fin
 de voisinages compacts et spectralement convexes de x
tel que tout élément de
de voisinages compacts et spectralement convexes de x
tel que tout élément de
 soit contenu dans
soit contenu dans
 et possède un bord analytique fini et tel que l’anneau local
et possède un bord analytique fini et tel que l’anneau local
 soit fortement régulier relativement à
soit fortement régulier relativement à
 .
.
Démonstration
Nous allons nous contenter de démontrer ce résultat lorsque  est un anneau fortement de valuation discrète, le cas où c’est un corps fort se traitant de façon similaire mais plus simple. Soit π une uniformisante forte de
est un anneau fortement de valuation discrète, le cas où c’est un corps fort se traitant de façon similaire mais plus simple. Soit π une uniformisante forte de  .
.
Nous ne traiterons pas le cas où  est de caractéristique non nulle et trivialement valué, ni l’assertion finale, où il faut s’assurer que la propriété d’être ultramétrique typique reste vérifiée à chaque étape du raisonnement. Cela n’entraîne aucune difficulté supplémentaire.
est de caractéristique non nulle et trivialement valué, ni l’assertion finale, où il faut s’assurer que la propriété d’être ultramétrique typique reste vérifiée à chaque étape du raisonnement. Cela n’entraîne aucune difficulté supplémentaire.
Commençons par montrer que  est noethérien. Nous allons procéder par récurrence sur n. Si n=0, cela découle des hypothèses.
est noethérien. Nous allons procéder par récurrence sur n. Si n=0, cela découle des hypothèses.
Supposons maintenant que n≥1 et que le résultat est vrai en dimension n−1. Soit I un idéal de  . Nous pouvons supposer qu’il n’est pas nul. En appliquant le lemme 9.14, on montre qu’il existe un entier v et un idéal J de
. Nous pouvons supposer qu’il n’est pas nul. En appliquant le lemme 9.14, on montre qu’il existe un entier v et un idéal J de  tels que I=π
v
J et J contient un élément f dont l’image dans
tels que I=π
v
J et J contient un élément f dont l’image dans  n’est pas nulle.
n’est pas nulle.
Il suffit de démontrer que l’idéal J est de type fini. Notons y la projection de x sur ses n−1 premières coordonnées. D’après le lemme 9.15, quitte à effectuer un changement de variables, nous pouvons supposer que l’image de f dans  n’est pas nulle. Nous pouvons alors utiliser le théorème de division de Weierstraß 8.3 (en choisissant pour B une algèbre de la forme
n’est pas nulle. Nous pouvons alors utiliser le théorème de division de Weierstraß 8.3 (en choisissant pour B une algèbre de la forme  où W est un voisinage rationnel de y dans X
n−1 assez petit et pour b le point y) et diviser tout élément de
où W est un voisinage rationnel de y dans X
n−1 assez petit et pour b le point y) et diviser tout élément de  par f avec un reste polynomial. On se ramène donc à montrer qu’un idéal d’un anneau de polynômes sur
par f avec un reste polynomial. On se ramène donc à montrer qu’un idéal d’un anneau de polynômes sur  est de type fini. Par récurrence, l’anneau
est de type fini. Par récurrence, l’anneau  est noethérien et le résultat s’ensuit.
est noethérien et le résultat s’ensuit.
Intéressons-nous à présent à la régularité et la dimension de l’anneau  . Si n=0, les résultats annoncés sont vrais.
. Si n=0, les résultats annoncés sont vrais.
Supposons que n≥1 et qu’ils sont vérifiés en dimension n−1. Notons x′ le point 0 de la fibre de X
n
au-dessus de y. Soit P(S)∈κ(y)[S] le polynôme minimal du point rigide épais x au-dessus de y. Relevons-le en un polynôme unitaire à coefficients dans  que nous noterons identiquement. D’après le théorème 8.8, il existe un isomorphisme naturel
que nous noterons identiquement. D’après le théorème 8.8, il existe un isomorphisme naturel  . Sur l’expression explicite de
. Sur l’expression explicite de  comme anneau de séries convergentes, on remarque qu’il est de dimension supérieure à
comme anneau de séries convergentes, on remarque qu’il est de dimension supérieure à  , par hypothèse de récurrence. Le même résultat vaut pour
, par hypothèse de récurrence. Le même résultat vaut pour  .
.
D’après le corollaire 9.13, l’idéal maximal \(\mathfrak {m} _{x}\) est engendré  -fortement par n+1 éléments. On en déduit que l’anneau local est de dimension n+1, régulier et même fortement régulier. □
-fortement par n+1 éléments. On en déduit que l’anneau local est de dimension n+1, régulier et même fortement régulier. □
Nous arrivons finalement au théorème annoncé. Les hypothèses en sont notamment vérifiées lorsque l’on choisit pour anneau de Banach  l’un de ceux qui figurent à la remarque 9.6. Le résultat vaut donc en particulier sur Z et les anneaux d’entiers de corps de nombres.
l’un de ceux qui figurent à la remarque 9.6. Le résultat vaut donc en particulier sur Z et les anneaux d’entiers de corps de nombres.
Théorème 9.18
Soit b
un point de
 . Soit
. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’anneau local
 est noethérien, fortement régulier relativement à
est noethérien, fortement régulier relativement à
 et de dimension inférieure à 1. Soient
n∈N
et x
un point de
et de dimension inférieure à 1. Soient
n∈N
et x
un point de
 au-dessus de b. Alors l’anneau local
au-dessus de b. Alors l’anneau local
 est noethérien et fortement régulier.
est noethérien et fortement régulier.
Si
 est de caractéristique non nulle et trivialement valué, il existe un système fondamental fin
est de caractéristique non nulle et trivialement valué, il existe un système fondamental fin
 de voisinages compacts et spectralement convexes de x
tel que tout élément de
de voisinages compacts et spectralement convexes de x
tel que tout élément de
 soit contenu dans
soit contenu dans
 et possède un bord analytique fini et tel que l’anneau local
et possède un bord analytique fini et tel que l’anneau local
 soit fortement régulier relativement à
soit fortement régulier relativement à
 .
.
Démonstration
Comme précédemment, nous ne traiterons pas le cas où  est imparfait et trivialement valué, qui n’ajoute pas de difficulté réelle.
est imparfait et trivialement valué, qui n’ajoute pas de difficulté réelle.
Pour tout m∈[[0,n]], notons  la projection du point x sur ses m premières coordonnées. Quitte à changer l’ordre des coordonnées, nous pouvons supposer qu’il existe un entier k∈[[0,n]] vérifiant les propriétés suivantes :
la projection du point x sur ses m premières coordonnées. Quitte à changer l’ordre des coordonnées, nous pouvons supposer qu’il existe un entier k∈[[0,n]] vérifiant les propriétés suivantes :
-
(i)
le point x k est purement localement transcendant au-dessus de b ;
-
(ii)
le point x est rigide épais au-dessus de x k .
D’après le corollaire 9.11, si l’anneau local  est noethérien et fortement régulier de dimension inférieure à 1, alors il en est de même pour l’anneau local
est noethérien et fortement régulier de dimension inférieure à 1, alors il en est de même pour l’anneau local  . On conclut alors par le théorème 9.17. □
. On conclut alors par le théorème 9.17. □
Corollaire 9.19
Soit
 un anneau de Banach de base au sens de la définition 9.5. Soit
un anneau de Banach de base au sens de la définition 9.5. Soit
 un espace analytique sur
un espace analytique sur
 . Alors, en tout point z
de Z, l’anneau local
. Alors, en tout point z
de Z, l’anneau local
 est noethérien et universellement caténaire.
est noethérien et universellement caténaire.
10 Excellence des anneaux locaux
Dans cette partie, nous allons nous intéresser à l’excellence des anneaux locaux des espaces analytiques sur Z et les anneaux d’entiers de corps de nombres. Pour les définitions et propriétés de base des anneaux excellents, nous renvoyons à [15], § 34. En géométrie analytique complexe, ce résultat est bien connu et se démontre généralement à l’aide de critères jacobiens (cf. [15], théorème 102 et remarque suivante). Sur un corps valué complet, c’est un résultat difficile, en particulier en caractéristique non nulle, dû en toute généralité à A. Ducros (cf. [7], théorème 2.13).
Comme dans la partie précédente, nos résultats valent en réalité pour les anneaux locaux des espaces  , où
, où  appartient à une classe d’anneaux de Banach plus générale. Celle-ci contient tous les exemples indiqués à la remarque 9.6, avec l’hypothèse supplémentaire que les anneaux considérés soient de caractéristique nulle.
appartient à une classe d’anneaux de Banach plus générale. Celle-ci contient tous les exemples indiqués à la remarque 9.6, avec l’hypothèse supplémentaire que les anneaux considérés soient de caractéristique nulle.
Signalons que, cette fois-ci, nous ne redémontrons pas les résultats d’excellence pour les anneaux locaux des espaces sur les corps valués, mais les utilisons dans notre preuve (pour les corps de caractéristique non nulle uniquement).
Théorème 10.1
Soit b
un point de
B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’anneau local
 est un corps fort relativement à
est un corps fort relativement à
 de caractéristique nulle. Soient
n∈N
et x
un point de
de caractéristique nulle. Soient
n∈N
et x
un point de
 au-dessus de b. Alors l’anneau local
au-dessus de b. Alors l’anneau local
 est excellent.
est excellent.
Démonstration
Nous allons démontrer ce résultat par récurrence sur n. Si n=0, il est vérifié. Supposons maintenant que n≥1 et que le résultat est vrai en dimension n−1.
En procédant comme dans la preuve du théorème 9.18, on se ramène au cas où x est un point rigide épais au-dessus de b. D’après le corollaire 8.10 et la remarque qui le suit, l’anneau local  est fini sur l’anneau local
est fini sur l’anneau local  au point 0 de la fibre (X
n
)
b
. Puisque l’excellence est stable par passage à une algèbre de type fini, nous pouvons supposer que x=0. L’anneau local
au point 0 de la fibre (X
n
)
b
. Puisque l’excellence est stable par passage à une algèbre de type fini, nous pouvons supposer que x=0. L’anneau local  possède alors une description explicite comme algèbre de séries convergentes à coefficients dans le corps
possède alors une description explicite comme algèbre de séries convergentes à coefficients dans le corps  (cf. corollaire 2.6).
(cf. corollaire 2.6).
Nous savons déjà que  est noethérien et universellement caténaire (car régulier). Il nous reste à montrer que ses fibres formelles sont géométriquement régulières. Soit \(\mathfrak {p} \) un idéal premier de
est noethérien et universellement caténaire (car régulier). Il nous reste à montrer que ses fibres formelles sont géométriquement régulières. Soit \(\mathfrak {p} \) un idéal premier de  . Nous voulons montrer que l’algèbre
. Nous voulons montrer que l’algèbre  est géométriquement régulière sur \(\kappa( \mathfrak {p} )\).
est géométriquement régulière sur \(\kappa( \mathfrak {p} )\).
Supposons tout d’abord que \(\mathfrak {p} \) n’est pas nul. Il contient alors une série f non constante. Notons y∈X n−1 la projection de x sur ses n−1 premières coordonnées. D’après le lemme 9.15, quitte à changer l’ordre des variables, nous pouvons supposer que la restriction de f à (X n ) y n’est pas nulle. Le théorème de préparation de Weierstraß 8.6 permet alors de supposer que f est un polynôme en T n . D’après le théorème de division de Weierstraß, nous avons un isomorphisme

Pour montrer que  est géométriquement régulière sur \(\kappa( \mathfrak {p} )\), nous pouvons remplacer
est géométriquement régulière sur \(\kappa( \mathfrak {p} )\), nous pouvons remplacer  par
par  . Par récurrence, ce dernier anneau est excellent, donc le résultat est vérifié.
. Par récurrence, ce dernier anneau est excellent, donc le résultat est vérifié.
Supposons maintenant que \(\mathfrak {p} =(0)\). Notons K le corps des fractions de  . Il nous reste à montrer que l’algèbre
. Il nous reste à montrer que l’algèbre  est géométriquement régulière sur K. Remarquons déjà qu’elle est régulière, puisque c’est un localisé de
est géométriquement régulière sur K. Remarquons déjà qu’elle est régulière, puisque c’est un localisé de  . Puisque nous nous sommes placés en caractéristique nulle, cela suffit pour conclure. □
. Puisque nous nous sommes placés en caractéristique nulle, cela suffit pour conclure. □
Théorème 10.2
Soit b
un point de
B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini.
est contenu dans B
um
et possède un bord analytique fini.
Supposons que l’anneau local
 est noethérien, fortement régulier relativement à
est noethérien, fortement régulier relativement à
 , de dimension inférieure à 1 et de caractéristique nulle. Soient
n∈N
et x
un point de
, de dimension inférieure à 1 et de caractéristique nulle. Soient
n∈N
et x
un point de
 au-dessus de b. Alors l’anneau local
au-dessus de b. Alors l’anneau local
 est excellent.
est excellent.
Démonstration
Le théorème qui précède traitant le cas des corps forts, nous pouvons supposer que  est un anneau fortement de valuation discrète. Choisissons-en une uniformisante π. Nous allons démontrer le résultat par récurrence sur n. Si n=0, il est vérifié. Supposons maintenant que n≥1 et que le résultat est vrai en dimension n−1.
est un anneau fortement de valuation discrète. Choisissons-en une uniformisante π. Nous allons démontrer le résultat par récurrence sur n. Si n=0, il est vérifié. Supposons maintenant que n≥1 et que le résultat est vrai en dimension n−1.
En procédant comme précédemment, on se ramène au cas du point x=0 de la fibre (X
n
)
b
et à montrer à montrer que les fibres formelles de  sont géométriquement régulières. Soit \(\mathfrak {p} \) un idéal premier de
sont géométriquement régulières. Soit \(\mathfrak {p} \) un idéal premier de  . Nous voulons montrer que l’algèbre
. Nous voulons montrer que l’algèbre  est géométriquement régulière sur \(\kappa( \mathfrak {p} )\).
est géométriquement régulière sur \(\kappa( \mathfrak {p} )\).
Si \(\mathfrak {p} \) contient \(\mathfrak {m} _{b}\), alors nous pouvons remplacer l’anneau local  par
par  . Le résultat découle alors du théorème 2.13 de [7].
. Le résultat découle alors du théorème 2.13 de [7].
Supposons, à présent, que \(\mathfrak {p} \) ne contient pas \(\mathfrak {m} _{b}\), autrement dit, ne contient pas π. Si \(\mathfrak {p} \) n’est pas nul, il contient une série qui n’est pas divisible par π. Nous pouvons alors appliquer le raisonnement du théorème précédent, basé sur les théorèmes de Weierstraß, pour faire décroître la dimension et conclure par récurrence.
Finalement, le cas où \(\mathfrak {p} =(0)\) se traite comme précédemment en utilisant la régularité de  et le fait que le corps des fractions de
et le fait que le corps des fractions de  est de caractéristique nulle. □
est de caractéristique nulle. □
Corollaire 10.3
Soit
 un anneau de Banach de base au sens de la définition 9.5 et supposons que, pour tout point b
de
un anneau de Banach de base au sens de la définition 9.5 et supposons que, pour tout point b
de
 , l’anneau local
, l’anneau local
 est de caractéristique nulle. Soit
est de caractéristique nulle. Soit
 un espace analytique sur
un espace analytique sur
 . Alors, en tout point z
de Z, l’anneau local
. Alors, en tout point z
de Z, l’anneau local
 est excellent.
est excellent.
On peut imaginer diverses applications de ces résultats. Les anneaux des espaces analytiques sur Z étant henséliens et excellents, ils vérifient l’approximation d’Artin, d’après [17]. Nous pouvons par exemple appliquer ce résultat à l’anneau local  au point 0 de la fibre de \(\mathbf {A}^{n,\mathrm {an}}_{ \mathbf {Z} } \) au-dessus de la valeur absolue triviale. Cet anneau possède une description explicite : il est constitué des séries de la forme
au point 0 de la fibre de \(\mathbf {A}^{n,\mathrm {an}}_{ \mathbf {Z} } \) au-dessus de la valeur absolue triviale. Cet anneau possède une description explicite : il est constitué des séries de la forme

l’entier N dépendant de la série, qui possèdent un rayon de convergence strictement positif en toutes les places (cf. [16], proposition 3.2.7 pour une description valant pour tous les anneaux d’entiers de corps de nombres et une preuve). On en déduit que tout système d’équations polynomiales à coefficients dans  (par exemple un système à coefficients dans Q[T]) qui possède une solution dans
(par exemple un système à coefficients dans Q[T]) qui possède une solution dans  en possède une dans
en possède une dans  , et même que l’on peut trouver une solution dans
, et même que l’on peut trouver une solution dans  arbitrairement proche (pour la topologie T-adique) d’une solution formelle donnée. C’est une vaste généralisation d’un théorème d’Eisenstein concernant le cas d’une équation en une variable.
arbitrairement proche (pour la topologie T-adique) d’une solution formelle donnée. C’est une vaste généralisation d’un théorème d’Eisenstein concernant le cas d’une équation en une variable.
11 Cohérence du faisceau structural
Pour finir, nous nous intéressons à la cohérence du faisceau structural des espaces analytiques sur Z et les anneaux d’entiers de corps de nombres. C’est l’analogue du théorème fondateur de K. Oka en géométrie anaytique complexe. De nouveau, la preuve que nous proposons vaut dans un cadre plus général, par exemple pour les espaces analytiques sur les corps valués complets (archimédiens ou non) et les anneaux de valuation discrète.
La cohérence du faisceau structural est déjà connue pour les espaces de Berkovich sur un corps valué ultramétrique complet. On la déduit aisément de la noethérianité des algèbres affinoïdes, elle-même découlant du théorème de division de Weierstraß global pour les algèbres de Tate (cf. [7], lemme 0.1 pour une preuve détaillée). Cette méthode ne nous semble pas pouvoir être adaptée pour des espaces sur un anneau de Banach quelconque. En effet, sur C déjà, la noethérianité de l’anneau des fonctions analytiques au voisinage d’un disque de dimension supérieure à 2 est un résultat difficile (cf. [8], théorème (I, 9)), dont la preuve utilise d’ailleurs la cohérence du faisceau structural. C’est pourquoi nous avons choisi d’utiliser plutôt des méthodes locales adaptées de la géométrie analytique complexe.
Commençons par quelques résultats de prolongement analytique.
Définition 11.1
Soit  un espace localement annelé. Soit s un point de S. Nous dirons que le principe du prolongement analytique vaut au voisinage de s si, pour tout élément non nul f de
un espace localement annelé. Soit s un point de S. Nous dirons que le principe du prolongement analytique vaut au voisinage de s si, pour tout élément non nul f de  , il existe un voisinage ouvert U de s vérifiant les propriétés suivantes :
, il existe un voisinage ouvert U de s vérifiant les propriétés suivantes :
-
(i)
f est définie sur U ;
-
(ii)
pour tout point t de U, l’image de f dans
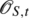 n’est pas nulle.
n’est pas nulle.
Nous dirons que le principe du prolongement analytique vaut sur S s’il vaut au voisinage de tous ses points.
Remarque 11.2
Soit  un espace localement annelé sur lequel vaut le principe du prolongement analytique. La version classique du principe du prolongement analytique est alors vérifiée. Soient U une partie ouverte et connexe de S et f un élément de
un espace localement annelé sur lequel vaut le principe du prolongement analytique. La version classique du principe du prolongement analytique est alors vérifiée. Soient U une partie ouverte et connexe de S et f un élément de  . S’il existe un point s de U tel que f soit nulle dans
. S’il existe un point s de U tel que f soit nulle dans  , alors f est nulle dans
, alors f est nulle dans  .
.
Remarquons également que le principe du prolongement analytique vaut au voisinage de tout point s en lequel l’anneau local  est un corps.
est un corps.
Lemme 11.3
Soit b
un point de B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini. Supposons que
est contenu dans B
um
et possède un bord analytique fini. Supposons que
 est un anneau fortement de valuation discrète relativement à
est un anneau fortement de valuation discrète relativement à
 et que le principe du prolongement analytique vaut au voisinage de b.
et que le principe du prolongement analytique vaut au voisinage de b.
Soit x
un point de X
n
, avec
n∈N. Si le point x
est purement localement transcendant, alors l’anneau local
 est un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage de x.
est un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage de x.
Démonstration
Soit π une uniformisante de  . D’après le corollaire 9.11, l’anneau local
. D’après le corollaire 9.11, l’anneau local  est un anneau fortement de valuation discrète d’uniformisante π. Pour montrer que le principe du prolongement analytique vaut au voisinage de x, il suffit de montrer qu’il existe un voisinage ouvert U de x sur lequel son uniformisante π est définie et tel que, pour tout point y de U, l’image de π dans
est un anneau fortement de valuation discrète d’uniformisante π. Pour montrer que le principe du prolongement analytique vaut au voisinage de x, il suffit de montrer qu’il existe un voisinage ouvert U de x sur lequel son uniformisante π est définie et tel que, pour tout point y de U, l’image de π dans  n’est pas nulle. Choisissons pour U l’image réciproque d’un voisinage ouvert de b sur lequel la même propriété est vérifiée. On montre que l’ouvert U convient en utilisant le fait que le morphisme de projection est ouvert (cf. corollaire 6.8). □
n’est pas nulle. Choisissons pour U l’image réciproque d’un voisinage ouvert de b sur lequel la même propriété est vérifiée. On montre que l’ouvert U convient en utilisant le fait que le morphisme de projection est ouvert (cf. corollaire 6.8). □
Proposition 11.4
Soient b
un point de B
et x
un point rigide épais de X
b
. Soit f
un élément de
 dont l’image dans
dont l’image dans
 n’est pas nulle. Alors il existe un voisinage U
de x
tel que, pour tout point y
de U, l’image de f
dans
n’est pas nulle. Alors il existe un voisinage U
de x
tel que, pour tout point y
de U, l’image de f
dans
 ne soit pas nulle.
ne soit pas nulle.
Démonstration
Dans un premier temps, supposons qu’il existe  tel que x=α dans X
b
. On démontre alors le résultat en utilisant la description explicite de l’anneau local (cf. corollaire 2.6) et la description des voisinages comme des disques. Plus précisément, nous pouvons montrer l’existence d’un voisinage ouvert U de x tel que, pour tout c∈π(U), l’ensemble des points y de X
c
∩U où f(y) n’est pas nulle est dense dans X
c
∩U.
tel que x=α dans X
b
. On démontre alors le résultat en utilisant la description explicite de l’anneau local (cf. corollaire 2.6) et la description des voisinages comme des disques. Plus précisément, nous pouvons montrer l’existence d’un voisinage ouvert U de x tel que, pour tout c∈π(U), l’ensemble des points y de X
c
∩U où f(y) n’est pas nulle est dense dans X
c
∩U.
Passons maintenant au cas où le point x est un point rigide épais. Il est annulé par un polynôme  . Nous pouvons supposer que
. Nous pouvons supposer que  . Considérons l’algèbre de décomposition universelle
. Considérons l’algèbre de décomposition universelle  du polynôme P sur
du polynôme P sur  . C’est une algèbre finie sur
. C’est une algèbre finie sur  , que l’on peut munir d’une norme de Banach de façon que le morphisme
, que l’on peut munir d’une norme de Banach de façon que le morphisme  soit borné. Considérons le morphisme
soit borné. Considérons le morphisme  associé. C’est un morphisme fini au sens topologique (i.e. continu, fermé et à fibres finies) et surjectif. Posons \(\varphi^{-1}(x) = \{ x'_{1},\ldots ,x'_{r}\}\). Soit i∈[[1,r]]. Il existe
associé. C’est un morphisme fini au sens topologique (i.e. continu, fermé et à fibres finies) et surjectif. Posons \(\varphi^{-1}(x) = \{ x'_{1},\ldots ,x'_{r}\}\). Soit i∈[[1,r]]. Il existe  tel que le point \(x'_{i}\) soit égal à \(\alpha'_{i}\) dans sa fibre au-dessus de
tel que le point \(x'_{i}\) soit égal à \(\alpha'_{i}\) dans sa fibre au-dessus de  . D’après le raisonnement effectué au début de la preuve, il possède donc un voisinage ouvert \(U'_{i}\) tel que l’ensemble des points ou f n’est pas nulle soit dense dans chaque fibre. Puisque le morphisme φ est fini, l’image réciproque de la réunion des \(U'_{i}\) est un voisinage de x dans X. Il satisfait la propriété requise. □
. D’après le raisonnement effectué au début de la preuve, il possède donc un voisinage ouvert \(U'_{i}\) tel que l’ensemble des points ou f n’est pas nulle soit dense dans chaque fibre. Puisque le morphisme φ est fini, l’image réciproque de la réunion des \(U'_{i}\) est un voisinage de x dans X. Il satisfait la propriété requise. □
Corollaire 11.5
Soit b
un point de B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini. Supposons que l’anneau local
est contenu dans B
um
et possède un bord analytique fini. Supposons que l’anneau local
 est noethérien, fortement régulier relativement à
est noethérien, fortement régulier relativement à
 et de dimension inférieure à 1.
et de dimension inférieure à 1.
Soit x un point de X n , avec n∈N, au-dessus de b. Supposons que le principe du prolongement analytique vaut au voisinage de b. Alors il vaut au voisinage du point x.
Démonstration
Nous supposerons que l’anneau local  est un anneau fortement de valuation discrète, le cas où c’est un corps fort se traitant de façon similaire, mais plus simple.
est un anneau fortement de valuation discrète, le cas où c’est un corps fort se traitant de façon similaire, mais plus simple.
Quitte à changer l’ordre des variables, nous pouvons supposer qu’il existe un entier m∈[[0,n]] tel que, en notant y la projection de x sur ses m premières coordonnées, nous ayons les propriétés suivantes : x est un point rigide épais au-dessus de y et y est purement localement transcendant au-dessus de b. D’après le lemme 11.3, l’anneau local  est un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage du point y. Quitte à remplacer b par y et B par un voisinage compact rationnel de y, nous pouvons supposer que le point x est rigide épais au-dessus de b.
est un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage du point y. Quitte à remplacer b par y et B par un voisinage compact rationnel de y, nous pouvons supposer que le point x est rigide épais au-dessus de b.
Si n=0, le résultat est immédiat. Supposons donc que n≥1. Soit f un élément de  . Soit π une uniformisante de
. Soit π une uniformisante de  . D’après le lemme 9.14, il existe v∈N et
. D’après le lemme 9.14, il existe v∈N et  tels que f=π
v
g dans
tels que f=π
v
g dans  et g≠0 dans
et g≠0 dans  . Nous voulons montrer qu’il existe un voisinage ouvert U de x sur lequel f est défini et tel que f soit non nulle dans
. Nous voulons montrer qu’il existe un voisinage ouvert U de x sur lequel f est défini et tel que f soit non nulle dans  , pour tout z∈U. Il suffit de démontrer ce résultat pour g. D’après le lemme 9.15, quitte à effectuer un changement de variables, nous pouvons supposer que l’image de g dans
, pour tout z∈U. Il suffit de démontrer ce résultat pour g. D’après le lemme 9.15, quitte à effectuer un changement de variables, nous pouvons supposer que l’image de g dans  , où x′ est la projection de x sur ses n−1 premières coordonnées n’est pas nulle. La proposition qui précède permet alors de conclure. □
, où x′ est la projection de x sur ses n−1 premières coordonnées n’est pas nulle. La proposition qui précède permet alors de conclure. □
Nous allons, à présent, nous atteler à la preuve du résultat de cohérence annoncé. Pour ce faire, il nous faudra imposer des conditions sur l’espace  . Comme dans la preuve de la noethérianité et de la régularité des anneaux locaux, nous supposerons qu’en tout point b de B, l’anneau local
. Comme dans la preuve de la noethérianité et de la régularité des anneaux locaux, nous supposerons qu’en tout point b de B, l’anneau local  est un corps fort ou un anneau fortement de valuation discrète. Nous supposerons en outre que le principe du prolongement analytique vaut sur B. Ces conditions sont vérifiées dans le cas des espaces dont nous avons dressé la liste à la remarque 9.6.
est un corps fort ou un anneau fortement de valuation discrète. Nous supposerons en outre que le principe du prolongement analytique vaut sur B. Ces conditions sont vérifiées dans le cas des espaces dont nous avons dressé la liste à la remarque 9.6.
Commençons par un lemme, de démonstration immédiate, qui nous permettra, entre autres, de traiter le cas des points où l’anneau local est un corps.
Lemme 11.6
Soient n∈N
et x
un point de X
n
. Soient U
un voisinage ouvert de x
dans X
n
et
f
1,…,f
p
, avec
p∈N
∗, des éléments de
 . Notons (e
1,…,e
p
) la base canonique de
. Notons (e
1,…,e
p
) la base canonique de
 . Notons
. Notons
 le noyau du morphisme
le noyau du morphisme

Supposons qu’il existe un indice i
tel que l’image de f
i
dans
 soit inversible. Alors il existe un voisinage ouvert V
de x
dans U
tel que, pour tout
y∈V, la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
de
soit inversible. Alors il existe un voisinage ouvert V
de x
dans U
tel que, pour tout
y∈V, la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
de
 engendre le germe
engendre le germe
 .
.
Le lemme suivant nous permettra de traiter le cas des points où l’anneau local est de valuation discrète.
Lemme 11.7
Soit b
un point de B. Soit
 un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
un système fondamental fin de voisinages compacts et spectralement convexes du point b. Si
 est de caractéristique non nulle et trivialement valué, supposons que tout élément de
est de caractéristique non nulle et trivialement valué, supposons que tout élément de
 est contenu dans B
um
et possède un bord analytique fini. Supposons que
est contenu dans B
um
et possède un bord analytique fini. Supposons que
 est un anneau fortement de valuation discrète relativement à
est un anneau fortement de valuation discrète relativement à
 et que le principe du prolongement analytique vaut au voisinage de b.
et que le principe du prolongement analytique vaut au voisinage de b.
Soient n∈N
et x
un point de (X
n
)
b
purement localement transcendant. Soient U
un voisinage ouvert de x
dans X
n
et
f
1,…,f
p
, avec
p∈N
∗, des éléments de
 . Notons (e
1,…,e
p
) la base canonique de
. Notons (e
1,…,e
p
) la base canonique de
 . Notons
. Notons
 le noyau du morphisme
le noyau du morphisme

Supposons qu’il existe un indice i
tel que l’image de f
i
dans
 ne soit pas nulle. Alors il existe un voisinage ouvert V
de x
dans U
tel que, pour tout
y∈V, la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
de
ne soit pas nulle. Alors il existe un voisinage ouvert V
de x
dans U
tel que, pour tout
y∈V, la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
de
 engendre le germe
engendre le germe
 .
.
Démonstration
D’après le lemme 11.3, l’anneau local  est un anneau de valuation discrète et le principe du prolongement analytique vaut au voisinage de x. Choisissons une uniformisante π de
est un anneau de valuation discrète et le principe du prolongement analytique vaut au voisinage de x. Choisissons une uniformisante π de  . Quitte à restreindre U, nous pouvons supposer que l’image de π n’est nulle dans aucun des anneaux locaux
. Quitte à restreindre U, nous pouvons supposer que l’image de π n’est nulle dans aucun des anneaux locaux  , avec z∈U. Il existe un entier positif v et des éléments g
1,…,g
p
de
, avec z∈U. Il existe un entier positif v et des éléments g
1,…,g
p
de  , tel que l’on ait f
i
=π
v
g
i
, pour tout i, et que l’un des g
i
soit inversible dans
, tel que l’on ait f
i
=π
v
g
i
, pour tout i, et que l’un des g
i
soit inversible dans  . Quitte à restreindre U, nous pouvons supposer que la factorisation y vaut. Remarquons que, puisque les anneaux locaux de X
n
sont intègres (car réguliers), le noyau du morphisme de l’énoncé ne change pas lorsque l’on remplace les f
i
par les g
i
. Le lemme précédent permet alors de conclure. □
. Quitte à restreindre U, nous pouvons supposer que la factorisation y vaut. Remarquons que, puisque les anneaux locaux de X
n
sont intègres (car réguliers), le noyau du morphisme de l’énoncé ne change pas lorsque l’on remplace les f
i
par les g
i
. Le lemme précédent permet alors de conclure. □
Nous pouvons maintenant adapter la preuve de la cohérence du faisceau structural sur les espaces affines complexes. Nous nous sommes inspiré de celle proposée dans l’ouvrage [9].
Théorème 11.8
(Lemme d’Oka)
Soit n∈N
∗. Soient y
un point de X
n−1
et x
un point rigide épais de (X
n
)
y
. Soient
p,q∈N
∗. Soit λ
une matrice de taille
p×q
à coefficients dans
 , l’ensemble des polynômes de degré inférieur à ℓ, avec
ℓ∈N. Soit μ
une matrice de taille
q×1 à coefficients dans
, l’ensemble des polynômes de degré inférieur à ℓ, avec
ℓ∈N. Soit μ
une matrice de taille
q×1 à coefficients dans
 , avec
m∈N. Soit
d≥max(ℓ,m). Supposons que la suite
, avec
m∈N. Soit
d≥max(ℓ,m). Supposons que la suite

est exacte. Supposons encore que l’un des coefficients de μ
n’est pas nul dans
 . Alors la suite
. Alors la suite

est exacte.
Démonstration
On reprend la preuve, qui repose exclusivement sur le théorème de division de Weierstraß, du théorème II.C.3 de [9]. □
Nous arrivons finalement au théorème annoncé. Les hypothèses en sont vérifiées lorsque l’on choisit pour anneau de Banach  l’un de ceux qui figurent à la remarque 9.6. Le résultat vaut donc en particulier sur Z et les anneaux d’entiers de corps de nombres.
l’un de ceux qui figurent à la remarque 9.6. Le résultat vaut donc en particulier sur Z et les anneaux d’entiers de corps de nombres.
Théorème 11.9
Soit
 un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
 . Alors, pour tout n∈N, le faisceau structural sur
. Alors, pour tout n∈N, le faisceau structural sur
 est cohérent.
est cohérent.
Démonstration
Nous reprenons ici la stratégie de la preuve du théorème IV.C.1 de [9]Footnote 3 en lui apportant les modifications nécessaires.
On procède par récurrence. Si n=0, le résultat découle des hypothèses faites sur B ainsi que du lemme 11.7.
Supposons que n≥1 et que le faisceau structural sur X
n−1 est cohérent. Soient b un point de B, x un point de X
n
au-dessus de b et U un voisinage ouvert de x dans X
n
. Soient  , avec p∈N
∗. Considérons le morphisme
, avec p∈N
∗. Considérons le morphisme  associé. Nous voulons montrer qu’il existe un voisinage ouvert V de x dans U sur lequel le noyau de ce morphisme est de type fini. Si tous les f
i
sont nuls dans
associé. Nous voulons montrer qu’il existe un voisinage ouvert V de x dans U sur lequel le noyau de ce morphisme est de type fini. Si tous les f
i
sont nuls dans  , c’est évident. Nous supposerons donc que tel n’est pas le cas. Si le point x est purement localement transcendant, cela découle du lemme 11.7.
, c’est évident. Nous supposerons donc que tel n’est pas le cas. Si le point x est purement localement transcendant, cela découle du lemme 11.7.
Supposons maintenant que le point x n’est pas purement localement transcendant. Pour k∈[[0,n]], notons x
k
∈X
k
la projection du point x sur ses k premières coordonnées. Quitte à changer l’ordre des variables, nous pouvons supposer qu’il existe m∈[[0,n−1]] tel que le point x
m
soit purement localement transcendant au-dessus de b et que le point x soit rigide épais au-dessus de x
m
. Dans ce cas, l’anneau local  est un corps fort ou un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage de x
m
.
est un corps fort ou un anneau fortement de valuation discrète et le principe du prolongement analytique vaut au voisinage de x
m
.
Supposons que  est un anneau fortement de valuation discrète. Choisissons-en une uniformisante π. Quitte à restreindre U, nous pouvons supposer qu’elle est définie sur U et nulle dans aucun anneau local
est un anneau fortement de valuation discrète. Choisissons-en une uniformisante π. Quitte à restreindre U, nous pouvons supposer qu’elle est définie sur U et nulle dans aucun anneau local  , avec z∈U. D’après le lemme 9.14, il existe un entier positif v et des éléments g
1,…,g
p
de
, avec z∈U. D’après le lemme 9.14, il existe un entier positif v et des éléments g
1,…,g
p
de  , tel que l’on ait f
i
=π
v
g
i
, pour tout i, et que l’un des g
i
ne soit pas nul dans
, tel que l’on ait f
i
=π
v
g
i
, pour tout i, et que l’un des g
i
ne soit pas nul dans  . En raisonnant comme dans la preuve du lemme 11.7, on montre que l’on peut remplacer les f
i
par les g
i
et donc supposer que l’un des f
i
n’est pas nul dans
. En raisonnant comme dans la preuve du lemme 11.7, on montre que l’on peut remplacer les f
i
par les g
i
et donc supposer que l’un des f
i
n’est pas nul dans  . Remarquons que cette condition est automatiquement vérifiée dans le cas où
. Remarquons que cette condition est automatiquement vérifiée dans le cas où  est un corps. Nous supposerons désormais que f
1 n’est pas nul dans
est un corps. Nous supposerons désormais que f
1 n’est pas nul dans  .
.
D’après le lemme 9.15, nous pouvons supposer que f
1 possède une image non nulle dans  . Le théorème de division de Weierstraß permet alors, par une manipulation algébrique simple, de supposer que f
2,…,f
p
sont des polynômes à coefficients dans
. Le théorème de division de Weierstraß permet alors, par une manipulation algébrique simple, de supposer que f
2,…,f
p
sont des polynômes à coefficients dans  . Le théorème de préparation de Weierstraß permet de supposer que f
1 lui-même est un tel polynôme. Soit m∈N un majorant du degré de tous ces polynômes. Le morphisme μ induit alors, sur un voisinage ouvert V de x
n−1 un morphisme
. Le théorème de préparation de Weierstraß permet de supposer que f
1 lui-même est un tel polynôme. Soit m∈N un majorant du degré de tous ces polynômes. Le morphisme μ induit alors, sur un voisinage ouvert V de x
n−1 un morphisme

D’après l’hypothèse de récurrence, les faisceaux qui apparaissent ci-dessus sont cohérents et le noyau du morphisme est donc de type fini. On peut donc compléter le morphisme en une suite exacte

Quitte à restreindre U, nous pouvons supposer que sa projection sur X
n−1 est contenue dans V. D’après la proposition 11.4, nous pouvons également supposer que, pour tout point y de U, l’image de f
1 dans  n’est pas nulle, où y
n−1 désigne la projection de y sur ses n−1 premières coordonnées.
n’est pas nulle, où y
n−1 désigne la projection de y sur ses n−1 premières coordonnées.
Soit y un point de U. S’il est rigide épais sur y n−1, le théorème 11.8 assure que la suite précédente induit une suite exacte

Si le point y n’est pas rigide épais sur y
n−1, d’après le corollaire 8.5, nous avons f
1(y)≠0. Le lemme 11.6 assure alors que le noyau du morphisme  est engendré par la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
, où (e
1,…,e
p
) désigne la base canonique de
est engendré par la famille (f
j
e
i
−f
i
e
j
)1≤i<j≤p
, où (e
1,…,e
p
) désigne la base canonique de  . En regroupant ces résultats, nous montrons que le noyau du morphisme μ est de type fini sur U, ce qui conclut la preuve. □
. En regroupant ces résultats, nous montrons que le noyau du morphisme μ est de type fini sur U, ce qui conclut la preuve. □
Corollaire 11.10
Soit
 un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
 . Soit
. Soit
 un espace analytique sur
un espace analytique sur
 . Alors le faisceau structural
. Alors le faisceau structural
 est cohérent.
est cohérent.
Suivant une suggestion de P. Schapira, nous démontrons maintenant que le faisceau structural d’un espace analytique sur Z, ou un anneau d’entiers de corps de nombres, est noethérien au sens de M. Kashiwara. Rappelons tout d’abord la définition de cette notion (cf. [14], définition A.7).
Définition 11.11
Soit  un espace localement annelé. Un faisceau
un espace localement annelé. Un faisceau  de
de  -modules est dit noethérien s’il vérifie satisfait les propriétés suivantes :
-modules est dit noethérien s’il vérifie satisfait les propriétés suivantes :
-
(i)
 est un faisceau de
est un faisceau de  -modules cohérent ;
-modules cohérent ; -
(ii)
pour tout point s de S, le
 -module
-module  est noethérien ;
est noethérien ; -
(iii)
pour tout ouvert U de S et toute famille
 de faisceaux de sous-
de faisceaux de sous- -modules cohérents de
-modules cohérents de  , le faisceau de
, le faisceau de  -modules
-modules  est cohérent.
est cohérent.
Le faisceau structural  est dit noethérien s’il est noethérien sur lui-même.
est dit noethérien s’il est noethérien sur lui-même.
Nous avons déjà démontré les deux premières propriétés. La dernière se déduit aisément du résultat suivant (cf. [6], II (3.22)).
Proposition 11.12
Soit
 un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
 .
.
Soit
 un espace analytique sur
un espace analytique sur
 . Soit U
un ouvert de Z,
. Soit U
un ouvert de Z,  un faisceau de
un faisceau de
 -modules cohérent et
-modules cohérent et
 une suite croissante de sous-faisceaux cohérents de
une suite croissante de sous-faisceaux cohérents de
 . Alors, tout point x
de U
possède un voisinage V
sur lequel la suite stationne.
. Alors, tout point x
de U
possède un voisinage V
sur lequel la suite stationne.
Démonstration
Le faisceau  est localement quotient d’un
est localement quotient d’un  -module libre
-module libre  . En tirant en arrière, on se ramène à traiter le cas où
. En tirant en arrière, on se ramène à traiter le cas où  , puis
, puis  . En utilisant le fait que
. En utilisant le fait que  est lui-même localement quotient du faisceau structural sur un espace affine
est lui-même localement quotient du faisceau structural sur un espace affine  , on se ramène finalement à ce dernier cas.
, on se ramène finalement à ce dernier cas.
Nous allons procéder par récurrence sur l’entier n. Si n=0, le résultat découle facilement des hypothèses.
Supposons maintenant que n≥1 et que le résultat est vérifié pour X
n−1. Soit x un point de U. Si pour tout k≥0, nous avons  , alors la suite est constamment nulle au voisinage de x. Supposons donc qu’il existe k
0≥0 tel que
, alors la suite est constamment nulle au voisinage de x. Supposons donc qu’il existe k
0≥0 tel que  . Soit f un élément non nul de
. Soit f un élément non nul de  . Si le point x est localement transcendant sur b, alors
. Si le point x est localement transcendant sur b, alors  est un corps et f est inversible sur un voisinage V de x dans U. Dans ce cas, la suite stationne à
est un corps et f est inversible sur un voisinage V de x dans U. Dans ce cas, la suite stationne à  sur V.
sur V.
Il nous reste à traiter le cas où x n’est pas localement transcendant. Quitte à effectuer un changement de variables, nous pouvons supposer que le point x est rigide épais sur sa projection x
n−1 sur les n−1 premières coordonnées et que l’image de f dans  n’est pas nulle. En utilisant le théorème de préparation de Weiestraß, nous pouvons nous ramener au cas où f est un polynôme, dont nous noterons d le degré. D’après la proposition 11.4, il existe un voisinage V de x dans U tel que, pour tout point y de U, l’image de f dans
n’est pas nulle. En utilisant le théorème de préparation de Weiestraß, nous pouvons nous ramener au cas où f est un polynôme, dont nous noterons d le degré. D’après la proposition 11.4, il existe un voisinage V de x dans U tel que, pour tout point y de U, l’image de f dans  n’est pas nulle, où y
n−1 désigne la projection de y sur ses n−1 premières coordonnées.
n’est pas nulle, où y
n−1 désigne la projection de y sur ses n−1 premières coordonnées.
Notons  le
le  -module cohérent formé des polynômes en T
n
de degré strictement inférieur à d. Le théorème de division de Weierstraß assure que, pour tout point y de V et tout entier k≥k
0, la fibre
-module cohérent formé des polynômes en T
n
de degré strictement inférieur à d. Le théorème de division de Weierstraß assure que, pour tout point y de V et tout entier k≥k
0, la fibre  est engendrée par f et
est engendrée par f et  . On conclut en appliquant l’hypothèse de récurrence à la suite de
. On conclut en appliquant l’hypothèse de récurrence à la suite de  -modules cohérents
-modules cohérents  . □
. □
Corollaire 11.13
Soit
 un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
un anneau de Banach de base au sens de la définition 9.5 et supposons que le principe du prolongement analytique vaut sur
 . Soit
. Soit
 un espace analytique sur
un espace analytique sur
 . Alors le faisceau structural
. Alors le faisceau structural
 est noethérien.
est noethérien.
Notes
Dès le chapitre 2 de [1], V. Berkovich se restreint au cas où l’anneau de Banach
 appartient à une certaine classe : celle des algèbres affinoïdes sur un corps valué k. Les définitions de l’ensemble
appartient à une certaine classe : celle des algèbres affinoïdes sur un corps valué k. Les définitions de l’ensemble  et de sa topologie sont inchangées. En revanche, le faisceau structural ne coïncide avec celui que nous venons de décrire que lorsque l’algèbre affinoïde est réduite.
et de sa topologie sont inchangées. En revanche, le faisceau structural ne coïncide avec celui que nous venons de décrire que lorsque l’algèbre affinoïde est réduite.Dans le cas où
 , cette définition redonne les espaces analytiques complexes usuels. Dans le cas où k est un corps ultramétrique complet, en revanche, elle est plus restrictive que celle que V. Berkovich propose par la suite. Toutefois, elle permet de retrouver les analytifiées de variétés algébriques et, plus généralement, les bons espaces sans bord.
, cette définition redonne les espaces analytiques complexes usuels. Dans le cas où k est un corps ultramétrique complet, en revanche, elle est plus restrictive que celle que V. Berkovich propose par la suite. Toutefois, elle permet de retrouver les analytifiées de variétés algébriques et, plus généralement, les bons espaces sans bord.Le lecteur prendra garde au fait que ce que nous appelons, selon la terminologie classique, faisceau cohérent est appelé dans cet ouvrage « faisceau d’Oka ».
Bibliographie
Berkovich, V.G.: Spectral Theory and Analytic Geometry over Non-Archimedean Fields. Mathematical Surveys and Monographs, vol. 33. Am. Math. Soc., Providence (1990)
Berkovich, V.G.: Étale cohomology for non-Archimedean analytic spaces. Publ. Math. Inst. Hautes Études Sci. 1993(78), 5–161 (1994)
Berkovich, V.G.: A non-Archimedean interpretation of the weight zero subspaces of limit mixed Hodge structures. In: Algebra, Arithmetic, and Geometry: in Honor of Yu.I. Manin, Vol. I. Progr. Math., vol. 269, pp. 49–67. Birkhäuser Boston, Boston (2009)
Bosch, S., Güntzer, U., Remmert, R.: Non-Archimedean Analysis. Grundlehren der Mathematischen Wissenschaften, vol. 261. Springer, Berlin (1984). A systematic approach to rigid analytic geometry
Bourbaki, N.: Éléments de mathématique. Fasc. XXX. Algèbre commutative. Chapitre 5: Entiers. Chapitre 6: Valuations. Actualités Scientifiques et Industrielles, vol. 1308. Hermann, Paris (1964)
Demailly, J.-P.: Complex Analytic and Differential Geometry, http://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook.pdf
Ducros, A.: Les espaces de Berkovich sont excellents. Ann. Inst. Fourier (Grenoble) 59(4), 1443–1552 (2009)
Frisch, J.: Points de platitude d’un morphisme d’espaces analytiques complexes. Invent. Math. 4, 118–138 (1967)
Gunning, R.C., Rossi, H.: Analytic Functions of Several Complex Variables. Prentice-Hall, Englewood Cliffs (1965)
Grauert, H., Remmert, R.: Theory of Stein Spaces. Classics in Mathematics. Springer, Berlin (2004). Translated from the German by Alan Huckleberry, reprint of the 1979 translation
Gruson, L.: Théorie de Fredholm p-adique. Bull. Soc. Math. Fr. 94, 67–95 (1966) (French)
Huber, R.: Continuous valuations. Math. Z. 212(3), 455–477 (1993)
Huber, R.: A generalization of formal schemes and rigid analytic varieties. Math. Z. 217(4), 513–551 (1994)
Kashiwara, M.: D-Modules and Microlocal Calculus. Am. Math. Soc., Providence (2003). (English; translated from the Japanese by Mutsumi Saito)
Matsumura, H.: Commutative Algebra, 2nd edn. Mathematics Lecture Note Series, vol. 56. Benjamin/Cummings, Reading (1980)
Poineau, J.: La droite de Berkovich sur Z. Astérisque 334, (2010), xii+284 pp.
Popescu, D.: General Néron desingularization and approximation. Nagoya Math. J. 104, 85–115 (1986) (English)
Raynaud, M.: Géométrie analytique rigide d’après Tate, Kiehl, … . In: Table Ronde d’Analyse non archimédienne, Paris, 1972, pp. 319–327. Soc. Math. France, Paris (1974). Bull. Soc. Math. France, Mém. No. 39–40
Tate, J.: Rigid analytic spaces. Invent. Math. 12, 257–289 (1971)
Remerciements
Nous remercions Antoine Chambert-Loir et Antoine Ducros pour leurs remarques et conseils.
Author information
Authors and Affiliations
Corresponding author
Additional information
L’auteur est membre du projet jeunes chercheurs « Berko » de l’Agence Nationale de la Recherche.
Rights and permissions
About this article
Cite this article
Poineau, J. Espaces de Berkovich sur Z : étude locale. Invent. math. 194, 535–590 (2013). https://doi.org/10.1007/s00222-013-0451-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-013-0451-6


 définie sur le quotient
définie sur le quotient
 est une norme ;
est une norme ; est complet pour la norme
est complet pour la norme
 .
. ;
; ;
; est un polynôme de degré strictement inférieur à nd.
est un polynôme de degré strictement inférieur à nd. est un polynôme unitaire de degré nd
vérifiant
Ω(b)(S)=P(S)n
dans
est un polynôme unitaire de degré nd
vérifiant
Ω(b)(S)=P(S)n
dans
 ;
; ;
; ;
; est un anneau local noethérien, fortement régulier relativement à
est un anneau local noethérien, fortement régulier relativement à  et de dimension inférieure à 1, c’est-à-dire un corps fort ou un anneau fortement de valuation discrète ;
et de dimension inférieure à 1, c’est-à-dire un corps fort ou un anneau fortement de valuation discrète ; est de caractéristique non nulle et trivialement valué, tout élément de
est de caractéristique non nulle et trivialement valué, tout élément de  est contenu dans B
um et possède un bord analytique fini (ce qui entraîne que le point b est ultramétrique typique).
est contenu dans B
um et possède un bord analytique fini (ce qui entraîne que le point b est ultramétrique typique). ;
; .
.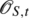 n’est pas nulle.
n’est pas nulle. est un faisceau de
est un faisceau de  -modules cohérent ;
-modules cohérent ; -module
-module  est noethérien ;
est noethérien ; de faisceaux de sous-
de faisceaux de sous- -modules cohérents de
-modules cohérents de  , le faisceau de
, le faisceau de  -modules
-modules  est cohérent.
est cohérent. appartient à une certaine classe : celle des algèbres affinoïdes sur un corps valué k. Les définitions de l’ensemble
appartient à une certaine classe : celle des algèbres affinoïdes sur un corps valué k. Les définitions de l’ensemble  et de sa topologie sont inchangées. En revanche, le faisceau structural ne coïncide avec celui que nous venons de décrire que lorsque l’algèbre affinoïde est réduite.
et de sa topologie sont inchangées. En revanche, le faisceau structural ne coïncide avec celui que nous venons de décrire que lorsque l’algèbre affinoïde est réduite. , cette définition redonne les espaces analytiques complexes usuels. Dans le cas où k est un corps ultramétrique complet, en revanche, elle est plus restrictive que celle que V. Berkovich propose par la suite. Toutefois, elle permet de retrouver les analytifiées de variétés algébriques et, plus généralement, les bons espaces sans bord.
, cette définition redonne les espaces analytiques complexes usuels. Dans le cas où k est un corps ultramétrique complet, en revanche, elle est plus restrictive que celle que V. Berkovich propose par la suite. Toutefois, elle permet de retrouver les analytifiées de variétés algébriques et, plus généralement, les bons espaces sans bord.