Phase Transitions, Logarithmic Sobolev Inequalities, and Uniform-in-Time Propagation of Chaos for Weakly Interacting Diffusions

Abstract

In this article, we study the mean field limit of weakly interacting diffusions for confining and interaction potentials that are not necessarily convex. We explore the relationship between the large N limit of the constant in the logarithmic Sobolev inequality (LSI) for the N-particle system and the presence or absence of phase transitions for the mean field limit. We show that the non-degeneracy of the LSI constant implies uniform-in-time propagation of chaos and Gaussianity of the fluctuations at equilibrium. As byproducts of our analysis, we provide concise and, to our knowledge, new proofs of a generalised form of Talagrand’s inequality and of quantitative propagation of chaos by employing techniques from the theory of gradient flows, specifically the Riemannian calculus on the space of probability measures.

1 Introduction

Systems of interacting particles, driven by stochastic forces, have attracted a lot of interest in recent years. For systems of identical (or exchangeable) particles in which the pair-wise interactions scale like the inverse of the number of particles, several probabilistic and variational techniques have been developed that enable us to pass to the mean field limit as the number of particles tends to infinity. More specifically, in this article we deal with systems of the form

$$\begin{aligned} \textrm{d}X_t^i=-\nabla V(X_t^i)\textrm{d}{t}- \frac{1}{N}\sum _{j=1}^N\nabla _1 W(X_t^i,X_t^j) \textrm{d}{t}+\sqrt{2\beta ^{-1}}\textrm{d}B_t^i, \end{aligned}$$

(1.1)

with chaotic initial data and appropriate assumptions on the confining and interaction potentials. In this case, the empirical measure of the process defined in (1.1) converges to the solution of the McKean–Vlasov PDE, a nonlinear nonlocal PDE that governs the evolution of the one-particle density.

A natural problem that one would like to address is how to obtain sharp quantitative estimates on the rate at which the empirical measure of the particle system converges to the mean field limit, as the number of particles N goes to infinity. When considering arbitrarily long time scales, this problem is intimately connected to the rate of convergence to equilibrium as time t goes to infinity. For the study of such quantitative results, a crucial role is played by the Poincaré (PI) and logarithmic Sobolev (LSI) inequalities. Our focus in this paper is on elucidating the connection between the validity of the LSI for the N-particle Gibbs measure, uniformly in the number of particles N, and on the properties of the mean field limit.

More specifically, the results of this manuscript (see Theorems 2.6 and 2.8) provide evidence for the following statement

$$\begin{aligned} \lim _{N\rightarrow \infty } \lambda _{{{\,\textrm{LSI}\,}}}^N =\lambda _{{{\,\textrm{LSI}\,}}}^\infty \,, \end{aligned}$$

where $\lambda _{{{\,\textrm{LSI}\,}}}^N$ and $\lambda _{{{\,\textrm{LSI}\,}}}^\infty$ are the optimal LSI constant for the N-particle system and the optimal constant in the Energy-Dissipation inequality for the mean field limit, respectively. For more details, see Conjecture 1.

On the one hand, we show that the non-degeneracy of the N-particle LSI constant implies that the particle system is well-approximated by its mean field limit. More specifically, if $\liminf _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$, then we prove uniform-in-time propagation of chaos for the N-particle system and characterise the limit of the fluctuations at equilibrium as Gaussian (see Theorems 2.12 and 2.16). On the other hand, it is straightforward to check that when the mean field equation admits several steady states, which coincide with invariant measures of the associated nonlinear McKean SDE, propagation of chaos is not uniform in time. In this case, we show that the N-particle LSI constant degenerates at rate 1/N, i.e $\lambda ^N_{ {{\,\textrm{LSI}\,}}}\le C/N$ (see Theorem 2.6). Putting these results together provides strong support for the validity of the following statement:

The positivity of the mean field LSI constant, the absence of phase transitions, the Gaussianity of the limiting equilibrium fluctuations around the mean field limit, and the validity of uniform-in-time propagation of chaos are all formally equivalent.

In completely general terms, a phase transition refers to an abrupt change in system behavior when a control parameter (e.g. temperature, pressure, etc) changes. In the equilibrium statistical mechanics of lattice systems, the non-uniqueness of the infinite-volume grand canonical Gibbs measure is referred to as a phase transition [31]. The presence of such a phase transition can then be detected with the help of some order parameter, for example the thermodynamic pressure for the nearest-neighbour Ising model, or the average magnetisation of the ensemble for the mean-field Curie–Weiss model. Based on the behaviour of these quantities (or rather on the behaviour of the infinite-volume partition function), one can then characterise the phase transitions as either continuous (second-order) or discontinuous (first-order).

The situation in our setting is more complicated but closely mirrors the one for lattice systems. Indeed, the system we consider can be thought of as a spin system with mean field interaction and the “spins” taking values in some uncountable state space $\Omega$. The difference between the system we consider and the Ising and Curie–Weiss model lies in the fact that, except in a small number of specific examples, it is extremely hard to specify an order-parameter or understand the exact behaviour of the infinite-volume partition function. An additional important difference is that for our work we will be more interested in the non-uniqueness of critical points of the free energy, which correspond to an important change in the long time behavior of the system, as opposed to non-uniqueness of its minimisers. In either case, the similarity with spin systems is instructive enough that it will serve the reader well to remember this analogy as we discuss the notion of phase transition we work with.

A detailed characterisation of phase transitions for McKean-Vlasov PDEs on the torus without a confining potential was given in [11]. In particular, the presence of phase transitions for this setting as it relates to non-uniqueness of minimisers of the free energy functional was discussed in detail. However, as mentioned earlier, in this paper we are more interested in characterising these phase transitions as they relate to non-uniqueness of critical points of the free energy.

For convex confining and interaction potentials (when the state space is Euclidean), the system does not undergo phase transitions. In fact, uniform-in-time propagation of chaos and uniqueness of the steady state for the mean field PDE have been established, see for example in [47] or the more recent [42]. Moreover, in [13] under a uniform convexity assumption of the potentials, the authors show exponentially fast relaxation to the unique steady state of the mean field system. Our focus in this paper is on dealing with non-convex potentials which may exhibit phase transitions and thus could not be expected to always (for all temperatures) exhibit uniform-in-time propagation of chaos.

The relation between the non-degeneracy of the constant in the PI or the LSI, the absence of phase transitions, and the exponentially fast decay of correlations has been studied extensively for unbounded spin systems [70]. Conversely, in these works the equivalence between the slow decay of correlations and the fact that the constant in the LSI becomes degenerate at the phase transition has been established. Uniform estimates on the constant in the LSI beyond the convex case have been established recently [34], under the Lipschitzian spectral gap condition for the single particle. We remark that this assumption is reminiscent of the assumptions on the conditional measures for the two-scale LSI [32, 45, 52]. We utilize the latter approach to show the non-degeneracy of the LSI for our N-particle Gibbs measure in the high temperature/weak interaction regime, see Theorem 2.20.

In the probability literature, the study of the LSI in the context of linear Fokker–Planck equations goes back to the classical $\Gamma _2$ functional introduced by Bakry and Emery [3]. More recently, contractivity for interacting particle systems has been studied in the context of entropic interpolation and Schrödinger bridges [2, 29, 30, 56]. These techniques yield proofs of both the Talagrand [16] and Sobolev [22] inequalities, under lower curvature conditions on the underlying manifold. We also mention the novel coupling techniques introduced by Eberle in [24] that produce contractivity estimates in a tailored transportation cost distance. This approach was then later used to prove uniform-in-time propagation of chaos estimates under a relative smallness assumption on the interaction potential [23, 33].

Our approach in this paper exploits the fact that both the N-particle system (or rather its Fokker–Planck equation) and its mean field limit are gradient flows of a particular energy functional with respect to the 2-Wasserstein distance. We can use this structural feature of the system to study the limit of all the relevant quantities as $N\rightarrow \infty$. This approach was pioneered by Hauray and Mischler in [37], and later used by the authors in [10, 20] to study both propagation of chaos and periodic homogenization for the interacting particle system. The advantage of this approach is that we can often make minimal assumptions on the regularity of the confining and interaction potentials: we will essentially assume that they are both only semi-convex, which is natural for 2-Wasserstein gradient flows (see [1]). We refer to [9, 40, 57, 61] for the reader interested in propagation of chaos results with more singular potentials.

1.1 Organization of the paper

Section 2 contains the precise description of the problem that we study and of our main assumptions and the statements of all our main results. Section 3 presents background material and preliminary results that are used later on. Section 4 connects our results to the phenomenon of phase transitions and discusses possible properties that could capture the radical change of behavior in our system. Section 5 contains some technical results on the convergence of the relevant quantities and functionals as $N\rightarrow \infty$ which play an important role in the proofs of our main theorems. Sections 6 to 12 contain the proofs of Theorems 2.6, 2.8, 2.10, 2.12, 2.16, 2.19 and 2.20, respectively.

2 Main Results

We consider $\{X_t^i\}_{i=1,\dots ,N}\subset {\mathbb {R}}^d$, the positions of N indistinguishable interacting particles at time $t \ge 0$, satisfying the following system of SDEs:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \textrm{d}X_t^i=-\nabla V(X_t^i)\textrm{d}{t}- \frac{1}{N}\sum _{j=1}^N\nabla _1 W(X_t^i,X_t^j) \textrm{d}{t}+\sqrt{2\beta ^{-1}}\textrm{d}B_t^i\\ \displaystyle \textrm{Law}(X_0^1,\dots ,X_0^N)=\rho _{\mathrm {\textrm{in}}}^{\otimes N}\in {\mathcal {P}}_{2,\mathrm {\textrm{sym}}}(({\mathbb {R}}^d)^N), \end{array}\right. } \end{aligned}$$

(2.1)

where $V:{\mathbb {R}}^d\rightarrow {\mathbb {R}}$, $W:{\mathbb {R}}^d\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}$, $\beta >0$ is the inverse temperature, $B_t^i,i=1,\dots ,N$ are independent d-dimensional Brownian motions, and the initial position of the particles is i.i.d with law $\rho _{\mathrm {\textrm{in}}}$. The chaoticity assumption on the initial data is not necessary but it greatly simplifies the exposition. Similarly, the state space ${\mathbb {R}}^d$ can be replaced by the periodic domain ${\mathbb {T}}^d$ or any convex set $\Omega \subset {\mathbb {R}}^d$ with normal reflecting boundary conditions, see, for example, [63]. We denote the space of symmetric Borel probability measures on $\Omega ^N$ with finite second moment by ${\mathcal {P}}_{2,\mathrm {\textrm{sym}}}(\Omega ^N)$, i.e. probability measures which are invariant under the relabeling of variables (or probability measures that arise as laws of exchangeable random variables). Throughout the paper, we will always work with probability measures that have finite second moment; to avoid burdensome notation, we forego the subscript 2 from now on and simply write ${\mathcal {P}}_{\mathrm {\textrm{sym}}}(\Omega ^N)$.

To ensure well-posedness of the evolution problem and coercivity, we make the following assumptions.

Assumption 2.1

The confining potential V is lower semicontinuous, bounded below, $K_V$-convex for some $K_V\in {\mathbb {R}}$ and there exists $R_0>0$, and $\delta >0$, such that $V(x)\ge |x|^\delta$ for $|x|>R_0$.

Assumption 2.2

The interaction potential W is lower semicontinuous, $K_W$-convex for some $K_W\in {\mathbb {R}}$, bounded below, symmetric $W(x,y)=W(y,x)$, vanishes along the diagonal $W(x,x)=0$, and there exists $C\in [0,\infty )$, such that

$$\begin{aligned} |\nabla _1 W(x,y)|\le C(1+|W(x,y)|+V(x)+V(y)). \end{aligned}$$

(2.2)

Remark 2.3

The K-Convexity assumptions on the potentials are short hand for global lower bounds on their Hessians

$$\begin{aligned} D^2 V\ge K_V I^{d\times d}\qquad \text{ and }\qquad D^2 W\ge K_W I^{2d\times 2d} \end{aligned}$$

with $K_V,$ $K_W\in {\mathbb {R}}$. Unlike a convexity assumption on the potentials, i.e. K-convexity with $K=0$ (see [47] for results in the convex case), these assumptions are weak enough to include models that exhibit phase transitions at sufficiently low temperatures, for example, the double well potential $V(x)=(1-|x|^2)^2$ with quadratic interactions $W(x,y)=|x-y|^2$, also known as the Desai–Zwanzig model [18].

Remark 2.4

The more technical bound (2.2) replaces the more classical doubling condition [1, Section 10.4.42] which is used to characterise the minimal sub-differential of the interaction energy [1, Theorem 10.4.11].

To quantify the convergence as $t\rightarrow \infty$ in (3.9), we can apply the standard relative entropy estimate [67]. More specifically, we consider the Lyapunov functional given by the scaled relative entropy of $\rho ^N (t)$, the law of the N-particle system (2.1), see (3.1) with respect to the equilibrium Gibbs measure $M_N = \frac{1}{Z_N} e^{-\beta H_N}$, see (3.4):

$$\begin{aligned} E^N[\rho ^N(t)]-E^N[M_N]=\overline{{\mathcal {E}}}(\rho ^N(t)|M_N):=\frac{1}{N}\int _{\Omega ^N}\log \left( \frac{\rho ^N(t)}{M_N}\right) \rho ^{N}(t)\;\textrm{d}x, \end{aligned}$$

where we use the notation $\overline{{\mathcal {E}}}:{\mathcal {P}}(\Omega ^N)\times {\mathcal {P}}(\Omega ^N)\rightarrow [0,\infty ]$ to denote the scaled relative entropy. Formally, taking a time derivative and using the PDE (3.1) we obtain the scaled relative Fisher information $\overline{{\mathcal {I}}}:{\mathcal {P}}(\Omega ^N)\times {\mathcal {P}}(\Omega ^N)\rightarrow [0,\infty ]$:

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\overline{{\mathcal {E}}}(\rho ^N(t)|M_N) \!=\!-\beta ^{-1}\frac{1}{N} \int _{\Omega ^N}\left| \nabla \log \left( \frac{\rho ^N(t)}{M_N}\right) \right| ^2\rho ^{N}(t)\;\textrm{d}x \!=:\!-\beta ^{-1} \overline{{\mathcal {I}}}(\rho ^N(t)|M_N). \end{aligned}$$

(2.3)

The convergence (3.9) in relative entropy is exponential whenever we can show that the N-particle log Sobolev constant is bounded away from zero:

$$\begin{aligned} 0<\lambda _{{{\,\textrm{LSI}\,}}}^N:=\inf _{\rho ^N\in {\mathcal {P}}(\Omega ^N)\setminus \{M_N\}}\frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^N|M_N)}{\overline{{\mathcal {E}}}(\rho ^N|M_N)}. \end{aligned}$$

(2.4)

Following the classical work of Bakry–Emery [3, 38, 44], we can find mild conditions for the positivity of the log Sobolev constant whenever the domain $\Omega$ is ${\mathbb {R}}^d$.

Theorem A

Under  Assumptions 2.1 and 2.2, consider

$$\begin{aligned} H_N(x)=\sum _{i=1}^NV(x_i)+\frac{1}{2N}\sum _{j=1}^N\sum _{i=1}^N W(x_i,x_j), \end{aligned}$$

if there exists $R>1$ and $\lambda >0$ such that

$$\begin{aligned} D^2H^N(x)\ge \lambda I^{Nd\times Nd}\qquad \text{ for } \text{ every } |x|>R\text{, } \end{aligned}$$

(2.5)

then we have that $\lambda _{{{\,\textrm{LSI}\,}}}^N>0$.

Remark 2.5

The strict convexity at infinity condition (2.5) can arise from either the convexity of the interaction or the confining potential. We expect that the sharp condition for the Gibbs measure $M_N$ to satisfy $\lambda _{{{\,\textrm{LSI}\,}}}^N>0$ uniformly in N is related to the behavior of the mean field limit dissipation inequality (2.7). We will discuss this in more detail in Conjecture 1.

For the mean field limit, we can perform a similar analysis with the relative mean field energy

$$\begin{aligned} E^{MF}[\rho ]:=\beta ^{-1}\int _{\Omega }\rho \log \rho \;\textrm{d}x+\frac{1}{2}\int _{\Omega ^{2}}W(x,y)\;\textrm{d}\rho (x)\; \textrm{d}\rho (y)+\int _{\Omega }V(x)\; \textrm{d}\rho (x). \end{aligned}$$

More specifically, given $\rho (t)$ the solution to (3.3), we can differentiate to obtain the dissipation

$$\begin{aligned}{} & {} \displaystyle \frac{\textrm{d}}{\textrm{d}t} E^{MF}[\rho (t)]-\inf E^{MF}\nonumber \\ {}{} & {} \quad =-\int _{\Omega } |\beta ^{-1}\nabla \log \rho (t)+\nabla W\star \rho (t)+\nabla V|^2\rho (t)\;\textrm{d}x=:-D(\rho (t)). \end{aligned}$$

(2.6)

Hence, we obtain exponential decay of the mean field energy to its minimum value, as long as the so-called infinite volume log Sobolev constant, given by

$$\begin{aligned} 0<\lambda _{{{\,\textrm{LSI}\,}}}^\infty :=\inf _{\begin{array}{c} \rho \in {\mathcal {P}}(\Omega )\\ \rho \notin {\mathcal {K}} \end{array}} \frac{D(\rho )}{E^{MF}[\rho ]-\inf E^{MF}}, \end{aligned}$$

(2.7)

is positive, where

$$\begin{aligned} {\mathcal {K}}=\{\rho \in {\mathcal {P}}(\Omega ):\; E^{MF}[\rho ]=\inf E^{MF}\}. \end{aligned}$$

(2.8)

Understanding the behavior of the log Sobolev constant is the first step to understanding the long time behavior of the system. Our first result relates the limit of the particle system log Sobolev constant (2.4) with the mean field or infinite volume log Sobolev constant (2.7):

Theorem 2.6

Under Assumptions 2.1 and 2.2, we have

$$\begin{aligned} \limsup _{N\rightarrow \infty } \lambda _{{{\,\textrm{LSI}\,}}}^N\le \lambda _{{{\,\textrm{LSI}\,}}}^\infty . \end{aligned}$$

Moreover, if the mean field energy $E^{MF}$ (3.8) admits a critical point that is not a minimiser, then $\lambda _{{{\,\textrm{LSI}\,}}}^\infty =0$, and there exists $C>0$ such that

$$\begin{aligned} \lambda _{{{\,\textrm{LSI}\,}}}^N\le \frac{C}{N}. \end{aligned}$$

Remark 2.7

The lower semicontinuity of $\lambda _{{{\,\textrm{LSI}\,}}}^N$ follows from showing that

$$\begin{aligned} \liminf _{N \rightarrow \infty }\frac{\overline{{\mathcal {I}}}(\rho ^N|M_N)}{\overline{{\mathcal {E}}}(\rho ^N|M_N)}\ge \frac{ \int _{{\mathcal {P}}(\Omega )}D(\rho )\;dP_\infty (\rho )}{\int _{{\mathcal {P}}(\Omega )}E^{MF}(\rho )-\inf E^{MF} \;dP_\infty (\rho )}, \end{aligned}$$

whenever $\rho ^N\rightharpoonup P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ with $\text {supp }P_\infty \not \subset {\mathcal {K}}$. The convergence of $\rho ^N$ is interpreted in the sense of de Finetti–Hewitt-Savage, see Sect. 5.

Our result complements similar results that have been obtained for unbounded spin systems [70] and the references therein. On the other hand, when $\lambda ^\infty _{{{\,\textrm{LSI}\,}}}>0$, we can show that the regularized log Sobolev constant

$$\begin{aligned} \lambda _{{{\,\textrm{LSI}\,}}}^{N,\varepsilon }:=\inf _{\rho ^N:\;\overline{{\mathcal {E}}}(\rho ^N|M_N)>\varepsilon }\frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^N|M_N)}{\overline{{\mathcal {E}}}(\rho ^N|M_N)} \end{aligned}$$

does not degenerate. More specifically,

$$\begin{aligned} \lim _{N\rightarrow \infty }\lambda _{{{\,\textrm{LSI}\,}}}^{N,\varepsilon }\ge \lambda ^\infty _{{{\,\textrm{LSI}\,}}}>0. \end{aligned}$$

This result implies that relaxation to neighborhoods of the stationary state of the particle dynamics (3.1) happens exponentially fast, uniformly in N.

Theorem 2.8

Under Assumptions 2.1 and 2.2, assume that $\lambda ^\infty _{{{\,\textrm{LSI}\,}}}>0$, and that $\rho _{\mathrm {\textrm{in}}}$ in (2.1) has finite energy and bounded higher order moments, i.e.

$$\begin{aligned} E^{MF}[\rho _{\mathrm {\textrm{in}}}]<\infty \qquad \text{ and }\qquad \int _{\Omega }|x|^{2+\delta }\;\textrm{d}\rho _{\mathrm {\textrm{in}}}<\infty ,\qquad \text{ for } \text{ some }\ \delta >0. \end{aligned}$$

(2.9)

Then, for every $\varepsilon >0$, there exists $N_0 \in {\mathbb {N}}$, such that for every $N>N_0$ we have

$$\begin{aligned} \overline{{\mathcal {E}}}(\rho ^N(t)|M_N)\le \max \left\{ \varepsilon , e^{-\frac{1}{2}\lambda _{{{\,\textrm{LSI}\,}}}^\infty t}\;\overline{{\mathcal {E}}}(\rho ^{\otimes N}_{\textrm{in}}|M_N)\right\} . \end{aligned}$$

Remark 2.9

For chaotic measures, we can take the limit $N\rightarrow \infty$ of the relative entropy to obtain

$$\begin{aligned} \lim _{N \rightarrow \infty }\overline{{\mathcal {E}}}(\rho ^{\otimes N}_{\textrm{in}}|M_N)= E^{MF}[\rho _{\textrm{in}}]-\inf E^{MF} \,. \end{aligned}$$

This is discussed in more detail in Theorem 5.6.

Unfortunately, we are not able to fully characterise the limit of $\lambda ^N_{{{\,\textrm{LSI}\,}}}$ in terms of the mean field limit. Despite this, Theorem 2.6 and Theorem 2.8 provide us with evidence which is convincing enough to make the following conjecture.

Conjecture 1

Under Assumptions 2.1 and 2.2, we have the equality

$$\begin{aligned} \lim _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}=\lambda ^\infty _{{{\,\textrm{LSI}\,}}}. \end{aligned}$$

The results of our paper provide us with a strong indication that: (a) the absence of phase transitions (loosely defined to mean that the mean field limit has a unique non-degenerate stationary state, see Property A), (b) the non-degeneracy of the infinite volume log Sobolev constant, and (c) the validity uniform-in-time propagation of chaos are all equivalent.

2.1 Consequences of the non-degeneracy of the log Sobolev inequality

Bearing Conjecture 1 in mind, we now explore the implications of the non-degeneracy of the LSI constant in the limit $N \rightarrow +\infty$. We begin by noticing that if the log Sobolev constant does not degenerate in N, then the invariant Gibbs measure $M_N$ of the N-particle system is well approximated by the unique minimiser of the mean field energy.

Theorem 2.10

Under Assumptions 2.1 and 2.2, assume that $\limsup _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$. Then, there exists a unique steady state $\rho _\beta$ to (3.3). Moreover, there exists $C>0$, such that

$$\begin{aligned} {\overline{d}}^2_2(\rho _\beta ^{\otimes N},M_N)\le \frac{2}{\lambda _{{{\,\textrm{LSI}\,}}}^N}\overline{{\mathcal {E}}}(\rho _\beta ^{\otimes N}|M_N)\le \frac{2}{(\lambda _{{{\,\textrm{LSI}\,}}}^N)^2}\overline{{\mathcal {I}}}(\rho _\beta ^{\otimes N}|M_N) \le \frac{C}{N}. \end{aligned}$$

Remark 2.11

The previous estimate is sharp, see [43, Section 5] for an explicit example of Gaussian measures.

Interpolating the previous result with more standard propagation of chaos estimates that depend on the convexity constant of the potentials, we obtain the following uniform-in-time propagation of chaos result.

Theorem 2.12

Under Assumptions 2.1 and 2.2, let $\rho ^N$ and $\rho$ denote the unique solutions to the particle (3.1) and mean field (3.3) Fokker–Planck equations given by Theorem D. Assume that $\rho _{\textrm{in}}$ has finite energy $E^{MF}[\rho _{\textrm{in}}]<\infty$, that the gradient of the square of the interaction potential is uniformly integrable, i.e.

$$\begin{aligned} \sup _{t\in [0,\infty ]}\int _\Omega |\nabla _1 W|^2\star \rho (t)\rho (t)\;\textrm{d}{x}<\infty \,, \end{aligned}$$

(2.10)

and that $\liminf _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}=:\lambda ^\infty >0$. Then, we have the estimate

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le \frac{C}{N^\theta }\qquad \text{ for } \text{ all }\ t>0, \end{aligned}$$

with $\theta =1/2$ if $K_V+K_W>0$, and $\theta <\frac{1}{2}\frac{\lambda ^\infty }{\lambda ^\infty -2(K_V+K_W)}$ if $K_V+K_W\le 0$.

Remark 2.13

The integrability assumption (2.10) is trivially true when W is uniformly Lipschitz. Also, this assumption is satisfied when the potentials are attractive enough in the far field, so that we can obtain uniform exponential bounds for the tail behavior of the mean field solution.

Remark 2.14

We note that for strictly convex confining and convex interaction potentials, $K_V >0,$ $K_W\ge 0$ uniform-in-time propagation of chaos with $\theta =1/2$ has already been shown in [47]. The main difference with this work is that our approach utilizes the convexity of the entropy along the 2-Wasserstein distance to obtain a contraction estimate. This approach can be easily extended to manifolds with Ricci curvature bounded from below [46], where we need to consider the sign of

$$\begin{aligned} K_{\textrm{Ric}}+K_V+K_W \end{aligned}$$

with $K_{\textrm{Ric}}$ the lower bound on the Ricci curvature of the underlying Riemannian manifold.

Remark 2.15

We do not expect $\theta$ in the above theorem to be sharp for $K_V+K_W<0$. In fact, at sufficiently high temperatures a comparable result for the 1-Wasserstein distance has been obtained by coupling methods in [25] with $\theta =1/2$.

2.2 Additional results

2.2.1 Fluctuations at equilibrium

We can also use the non-degeneracy of the LSI constant to identify the fluctuations at equilibrium.

Theorem 2.16

Let $\Omega ={\mathbb {T}}^d$ and assume that $\liminf _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$, then the fluctuations process

$$\begin{aligned} \eta ^N(t)=\sqrt{N}\left( \frac{1}{N}\sum _{i=1}^N\delta _{X_t^i}-\rho _\beta \right) \,, \end{aligned}$$

where $(X_t^1,...,X_t^N)$ is the solution to (2.1) with initial law given by the invariant Gibbs measure $M_N$, satisfies

$$\begin{aligned} \sup _{N \in {\mathbb {N}}, t\in [0,T]}{\mathbb {E}} \left[ *\right] {\Vert \eta ^N(t)\Vert _{H^{-s}({\mathbb {T}}^d)}^2}<\infty , \end{aligned}$$

for any $T>0,\,s>d/2+1$.

Moreover, assume that V, W are smooth and that the linearised operator (3.3) around $\rho _\beta$

$$\begin{aligned} {\mathcal {L}}_{\rho _\beta } \eta = \beta ^{-1} \Delta \eta + \nabla \cdot (\rho _\beta \nabla W \star \eta ) + \nabla \cdot (\eta \nabla W \star \rho _\beta ) + \nabla \cdot (\nabla V \eta ) \, , \end{aligned}$$

satisfies, for all $\phi \in \text {C}^\infty ({\mathbb {T}}^d)$, the following coercivity inequality

$$\begin{aligned} \langle - {\mathcal {L}}_{\rho _\beta } \phi ,\phi \rangle _{L^2({\mathbb {T}}^d)} \ge c \Vert \nabla \phi \Vert ^2_{L^2({\mathbb {T}}^d)} \end{aligned}$$

(2.11)

for some $c>0$.

Then, for any $m>d/2+3$, $\eta ^N$ converges in law, as a $C([0,T];H^{-m}({\mathbb {T}}^d))$-valued random variable, to the unique stationary solution $\eta ^\infty$ of the following linear SPDE

$$\begin{aligned} \partial _t\eta ^\infty ={\mathcal {L}}_{\rho _\beta }\eta ^\infty +\nabla \cdot (\sqrt{\rho _\beta }\xi ) \end{aligned}$$

(2.12)

where $\xi$ is space-time white noise, (see Lemma 12.6 and Remark 12.5 for the well-posedness of (2.12)).

Remark 2.17

The unique invariant measure of the SPDE (2.12) ${\mathcal {G}} \in {\mathcal {P}}(H^{-m}({\mathbb {T}}^d))$ is a centred Gaussian measure with a covariance operator that can be computed explicitly, at least in the case $V \equiv 0$ and $W (x,y)=W(x-y)$. See Sect. 12.1.

We mention the result of Fernandez and Meleard [27] (see also [62, 66]) which characterises the fluctuations of the particle dynamics with respect to the mean field limit for finite time horizons, under a stronger closeness assumption for the initial data. To our knowledge, the first available results for fluctuations at equilibrium is due to Dawson [18] for the so-called Desai–Zwanzig model, i.e. for bistable and quadratic confinig and interaction potentials, respectively. In addition, Dawson shows that, at the critical temperature where the continuous phase transition occurs, equilibrium fluctuations are non-Gaussian and persistent. Their temporal structure can be characterized by means of a nonlinear scalar SDE, whereas the spatial structure of the fluctuations is described by the second eigenfunction in the null space of the linearized McKean-Vlasov operator. It is an interesting open problem if this behavior is universal for any system which undergoes a (continuous/second order) phase transition.

Remark 2.18

The extra smoothness assumptions on V and W are used to have a well-defined semigroup associated to the linearised operator ${\mathcal {L}}_{\rho _\beta }$ which regularizes instantaneously arbitrary initial data in $H^{-m}({\mathbb {T}}^d)$. This can be quantified by requiring V and $W\in W^{m+\epsilon ,\infty }({\mathbb {T}}^d)$ for any $\epsilon >0$. For fluctuation results with singular potentials we refer the reader to the recent preprint [69].

2.2.2 Talagrand’s inequality

For both the N-particle and the mean field problems, when the log Sobolev constant is positive we can show that the relative energy behaves quadratically with respect to the 2-Wasserstein distance. This is essentially the content of Talagrand’s inequality [65]. One of our contributions in this paper is a new proof of a generalised version of this inequality using gradient flow techniques.

Theorem 2.19

Under Assumptions 2.1 and 2.2,

$$\begin{aligned} E^N[\rho ^N]-E^{N}[M_N]\ge \frac{\lambda ^N_{{{\,\textrm{LSI}\,}}}}{2}{\overline{d}}^2_2(\rho ^N,M_N)\qquad \text{ and }\qquad E^{MF}[\rho ]-\inf E^{MF}\ge \frac{\lambda ^\infty _{{{\,\textrm{LSI}\,}}}}{2}d^2_2(\rho ,{\mathcal {K}}),\nonumber \\ \end{aligned}$$

(2.13)

where ${\mathcal {K}}$ is the set of minimisers of $E^{MF}$ (2.8), and $d^2_2(\rho ,{\mathcal {K}})=\inf _{\mu \in {\mathcal {K}}}d_2^2(\rho ,\mu ).$

An optimal transport-based proof of inequality (2.13) for only $E^N$ can be found in [68, Theorem 22.17] and [53, Theorem 1]. We also refer to [16] for a proof using entropic interpolation. In Sect. 6, we provide a different more intuitive proof of (2.13) for general energies $E:{\mathcal {P}}(\Omega )\rightarrow {\mathbb {R}}\cup \{+\infty \}$, the main simplification with respect to the proof of [53] is the use of the foundational results of [1] for metric gradient flows, which allow us to extend the result to a more general setting. Our strategy is to use the associated gradient flow structure and what is sometimes referred to as Otto calculus [51], the formal Riemannian calculus on $({\mathcal {P}}(\Omega ),d_2)$. We should note that one of the main differences in Talagrand’s inequality for the N-particle energy and for the mean field energy is that the set of minimisers ${\mathcal {K}}$ does not need to be a single point in the mean field case.

2.2.3 Non-degeneracy of the LSI constant in specific cases

Putting aside for the time the validity of Conjecture 1, we show that the LSI constant $\lambda _{{{\,\textrm{LSI}\,}}}^N$ does not degenerate in the high temperature regime when $\Omega$ is compact, or when the confinement V satisfies an LSI inequality and the interaction strength is small enough.

Theorem 2.20

Assume that there exists a constant $C>0$ such that

$$\begin{aligned} \Vert W\Vert _{{L}^\infty (\Omega ^2)},\, \Vert D^2_{x y} W\Vert _{{L}^\infty (\Omega ^2)} <C \,. \end{aligned}$$

We then have the following two scenarios:

• (a) Compact state space: Assume $\Omega$ is compact and its normalised Lebesgue measure $\textrm{d}{x}$ satisfies a log Sobolev inequality. Then, there exists a $0<\beta _{{{\,\textrm{LSI}\,}}}=\beta _{{{\,\textrm{LSI}\,}}}(C)$ such that for all $\beta <\beta _{{{\,\textrm{LSI}\,}}}$, we have

  $$\begin{aligned} \liminf _{N\rightarrow \infty } \lambda ^N_{{{\,\textrm{LSI}\,}}}>0 \,. \end{aligned}$$

• (b) Unbounded domain: Assume $\Omega ={\mathbb {R}}^d$ and that the one-particle measure $Z_V^{-1}e^{-V} \textrm{d}{x}$ satisfies a log Sobolev inequality with constant $\lambda ^V_{{{\,\textrm{LSI}\,}}}>0$. Then, there exists an $\epsilon _{{{\,\textrm{LSI}\,}}}=\epsilon _{{{\,\textrm{LSI}\,}}}(C, \lambda ^V_{{{\,\textrm{LSI}\,}}},\beta )>0$, such that for any $0\le \epsilon < \epsilon _{{{\,\textrm{LSI}\,}}}$ we have

  $$\begin{aligned} \liminf _{N\rightarrow \infty } \lambda ^{\epsilon , N}_{{{\,\textrm{LSI}\,}}}>0 \,, \end{aligned}$$

  where $\lambda ^{\epsilon , N}_{{{\,\textrm{LSI}\,}}}$ is the log Sobolev constant of the Gibbs measure ${\tilde{M}}_N= Z_N^{-1}e^{-\beta H^\epsilon _N} \textrm{d}{x}$ with

  $$\begin{aligned} H^\epsilon _N(x)=\sum _{i=1}^NV(x_i)+\frac{\epsilon }{2N}\sum _{i=1}^N\sum _{j=1}^N W(x_i,x_j) \,. \end{aligned}$$

The above result relies crucially on the two-scale approach to log Sobolev inequalities introduced in [52], which is based on the analysis of the marginal and conditional measures of $M_N$. For the convenience of the reader, we describe the main result of [52] in Theorem 11.2. In addition to the above high temperature result, it is also possible to obtain a sharper result in certain specific scenarios. Consider, for instance, the O(2) (classical XY, noisy Kuramoto, Brownian mean field) model $\Omega ={\mathbb {T}}$, $W(x,y)=-\cos (2 \pi (x-y))$, and $V \equiv 0$ [8, 14, 50]. It is known that this system exhibits a phase transition (of type A, B, and C, see Definition 4.6). Due to the particularly simple nature of the model, it is possible to show that the N particle log Sobolev constant $\lambda ^N_{{{\,\textrm{LSI}\,}}}$ is asymptotically non-degenerate all the way up to the critical inverse temperature $\beta _c=2$. We state without proof the following result due to Bauerschmidt and Bodineau [5], see also [6].

Theorem B

([5, Theorem 1]) Consider the Gibbs measure $M_N$ of the mean field O(2) model and denote by $\lambda _{{{\,\textrm{LSI}\,}}}^N$ its log Sobolev constant. Then, for all $0< \beta <\beta _c=2$, we have that

$$\begin{aligned} \liminf _{N\rightarrow \infty } \lambda ^N_{{{\,\textrm{LSI}\,}}}>0 \,. \end{aligned}$$

Remark 2.21

An essentially similar argument as in [5, Theorem 1], can be used to show that the system with $\Omega ={\mathbb {T}}$, $W(x,y)=-\cos (2 \pi k(x-y))$, and $V \equiv 0$ for some $k \in {\mathbb {N}}$ has a uniform LSI all the way up to the critical inverse temperature $\beta _c$ which coincides with $\beta _\sharp$, defined in Eqn. (4.4) in Proposition 4.3.

3 Overview of Existing Results

In this section, we put together a few well known results from the theory of propagation of chaos for weakly interacting diffusions that will be useful in the sequel.

The particle system Our starting point, is the a system weakly interacting diffusions. We consider $\{X_t^i\}_{i=1,\dots ,N}\subset {\mathbb {R}}^d$, the positions of N indistinguishable interacting particles at time $t \ge 0$, satisfying the following system of SDEs:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \textrm{d}X_t^i=-\nabla V(X_t^i)\textrm{d}{t}- \frac{1}{N}\sum _{j=1}^N\nabla _1 W(X_t^i,X_t^j) \textrm{d}{t}+\sqrt{2\beta ^{-1}}\textrm{d}B_t^i\\ \displaystyle \textrm{Law}(X_0^1,\dots ,X_0^N)=\rho _{\mathrm {\textrm{in}}}^{\otimes N}\in {\mathcal {P}}_{2,\mathrm {\textrm{sym}}}(\Omega ^N), \end{array}\right. } \end{aligned}$$

where $V:{\mathbb {R}}^d\rightarrow {\mathbb {R}}$, $W:{\mathbb {R}}^d\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}$, $\beta >0$ is the inverse temperature, $B_t^i,i=1,\dots ,N$ are independent d-dimensional Brownian motions, and the initial position of the particles is i.i.d with law $\rho _{\mathrm {\textrm{in}}}$. We assume that the potentials V and W are coercive and semi-convex, see Assumption 2.1 and Assumption 2.2. We take the set to be either $\Omega ={\mathbb {T}}^d$, ${\mathbb {R}}^d$ or a convex set in ${\mathbb {R}}^d$, in the latter case we consider the case normal reflecting boundary conditions, see [63].

The Fokker–Planck equation Applying Ito’s formula, it follows that the curve $\rho ^N:[0,\infty )\rightarrow {\mathcal {P}}_{\textrm{sym}}({\mathbb {R}}^{d N})$ describing the evolution of the law of the process $(X_t^1,...,X_t^N)\in {\mathbb {R}}^{d N}$ satisfies the following linear Fokker–Planck equation (also referred to as Liouville or Forward Kolmogorov equation):

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho ^N =\beta ^{-1}\Delta \rho ^N+\nabla \cdot (\rho ^N\;\nabla H_N)&{}\hbox { in}\ (0,\infty )\times \Omega ^{N},\\ \rho ^N(0)=\rho _{\textrm{in}}^{\otimes N}, \end{array}\right. } \end{aligned}$$

(3.1)

where the Hamiltonian $H_N$ is given by

$$\begin{aligned} H_N(x)=\sum _{i=1}^NV(x_i)+\frac{1}{2N}\sum _{i=1}^N\sum _{j=1}^N W(x_i,x_j), \end{aligned}$$

$\rho _{\textrm{in}}\in {\mathcal {P}}({\mathbb {R}}^{d})$. When we consider particles on the torus, the linear Fokker–Planck equation (3.1) is equipped with periodic boundary conditions. In the case that $\Omega \subset {\mathbb {R}}^d$ is a convex set, we need include the null-flux boundary conditions $(\nabla \rho ^N+\rho ^N\nabla H_N)\cdot \textbf{n}_{\Omega ^N}=0$ on $(0,\infty )\times \partial \Omega ^{N}$, and $\textbf{n}_{\Omega ^N}$ is the unit normal to $\Omega ^{N}$.

de Finetti/Hewitt–Savage To take the limit as $N\rightarrow \infty$, we will crucially use the exchangeability (or symmetry) of the underlying particle system whose law is governed by (3.1). This implies that the joint law $\rho ^N$ is symmetric (or exchangeable) for all times, that is

$$\begin{aligned} \rho ^N(t)\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N) \quad \text { for all } t\ge 0. \end{aligned}$$

The main point is that we can characterise the limit $N\rightarrow \infty$ of ${\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$ as ${\mathcal {P}}({\mathcal {P}}(\Omega ))$, which denotes the Borel probability measures with bounded second moment defined over the metric space $({\mathcal {P}}(\Omega ),d_2)$, where $d_2$ is the 2-Wasserstein distance. Following de Finetti [19] and Hewitt–Savage [39], we know that any tight sequence $(\rho ^N)_{N\in {\mathbb {N}}}$, with $\rho ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^{N})$, i.e. with tight (in ${\mathcal {P}}(\Omega )$) l^th marginals for all $l \in {\mathbb {N}}$, has a limit $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ along a subsequence which we do not relabel such that

$$\begin{aligned} \rho ^N\rightharpoonup P_\infty , \end{aligned}$$

where weak convergence is given by duality with cylindrical test functions, which are dense in $C({\mathcal {P}}(\Omega ))$. That is, for any $l\in {\mathbb {N}}$ and $\varphi \in C_c(\Omega ^l)\subset C({\mathcal {P}}(\Omega ))$, we have

$$\begin{aligned} \lim _{N \rightarrow \infty }\int _{\Omega ^l}\varphi (y)\;\textrm{d}\rho ^N_l(y)=\int _{{\mathcal {P}}(\Omega )}\left( \int _{\Omega ^{l}}\varphi (y)\;\textrm{d}\rho ^{\otimes l}(y)\right) \;\textrm{d}P_\infty (\rho ), \end{aligned}$$

(3.2)

where

$$\begin{aligned} \rho ^N_l\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^l)\qquad \text{ is } \text{ the }\ l\text{-th } \text{ marginal } \text{ of }\ \rho ^N. \end{aligned}$$

In essence, this means that in the limit $N\rightarrow \infty$, symmetric probability measures can be characterised as convex combinations of chaotic measures. For more details, we refer the reader to [10, 37, 58]. In the sequel, we will use the notation $\rho ^N \rightharpoonup P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ to denote this notion of weak convergence for any sequence $(\rho ^N)_{N\in {\mathbb {N}}}$ with $\rho ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^{N})$.

Moreover, a metric version of this result can be obtained by considering the appropriately scaled 2-Wasserstein distance, i.e.

$$\begin{aligned} {\overline{d}}_2:=\frac{1}{\sqrt{N}}d_2, \end{aligned}$$

where $d_2$ is the classical 2-Wasserstein on ${\mathcal {P}}(\Omega ^N)$. We consider the lift mapping $T:\Omega ^N\rightarrow {\mathcal {P}}(\Omega )$ induced by the empirical measures. That is to say

$$\begin{aligned} T(x_1,...,x_N)=\frac{1}{N}\sum _{i=1}^N\delta _{x_i}\in {\mathcal {P}}(\Omega ), \end{aligned}$$

we have that the push forward belongs to the limiting space

$$\begin{aligned} T\#\rho ^N\in {\mathcal {P}}({\mathcal {P}}(\Omega )). \end{aligned}$$

In fact, Hauray–Mischler [37] showed that this embedding ${\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$ into ${\mathcal {P}}({\mathcal {P}}(\Omega ))$ is an isometry, which implies that it does not lose any information. Specifically, if $\mu ^N$ and $\nu ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$, then

$$\begin{aligned} {\overline{d}}_2(\mu ^N,\nu ^N)={\mathfrak {D}}_2(T\#\mu ^N,T\#\nu ^N), \end{aligned}$$

where ${\mathfrak {D}}_2$ is the 2-Wasserstein distance defined on the probabilities with second moment bounded over the metric space $({\mathcal {P}}_2({\mathbb {R}}^d),d_2)$. For more details, see Theorem 5.3. This metric on ${\mathcal {P}}({\mathcal {P}}(\Omega ))$ is closely related to the convergence discussed above as we will explain further in Proposition 5.5.

The mean field limit and nonlinear behaviour Within this formalism, the limit $N\rightarrow \infty$ of the equation (3.1) can be written as

$$\begin{aligned} \rho ^N(t)\rightharpoonup \delta _{\rho (t)}\in {\mathcal {P}}({\mathcal {P}}(\Omega ))\qquad \text{ for } \text{ all }\ t\ge 0, \end{aligned}$$

or in terms of the law of the empirical measure

$$\begin{aligned} {\mathfrak {D}}_2(T\#\rho ^N(t),\delta _{\rho (t)})\rightarrow 0\qquad \text{ for } \text{ all }\ t\ge 0, \end{aligned}$$

where $\delta _{\rho (t)}$ denotes the delta measure concentrated on the measure $\rho (t)\in {\mathcal {P}}(\Omega )$. This is equivalent to the marginals tensorizing in the limit in the following manner

$$\begin{aligned} \rho ^N_l(t)\rightharpoonup \rho (t)^{\otimes l}, \end{aligned}$$

for every $l\in {\mathbb {N}}$. The curve $\rho (t)$ is the unique solution of the nonlinear McKean equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t\rho =\beta ^{-1}\Delta \rho +\nabla \cdot \left( \rho \left( \nabla V+\nabla W\star \rho \right) \right) &{}\hbox { on}\ (0,\infty )\times \Omega \\ (\nabla \rho +\rho (\nabla V+\nabla W\star \rho ))\cdot \textbf{n}_\Omega =0&{}\hbox { on}\ (0,\infty )\times \partial \Omega \\ \rho (0)=\rho _{\textrm{in}}, \end{array}\right. } \end{aligned}$$

(3.3)

with

$$\begin{aligned} W\star \rho (x):=\int _{\Omega } W(x,y)\;\textrm{d}\rho (y) \,. \end{aligned}$$

One of the most salient differences between the particle dynamics (3.1) and the mean field dynamics (3.3) is that, whereas the Fokker–Planck equation governing the evolution of the N-particle system is linear, the mean field PDE (3.3) is nonlinear. As is well known, a consequence of this is that for non-convex confining/interaction potentials the mean field dynamics might have more than one stationary state. In contrast to the particle dynamics (3.1) which has a unique steady state given by the Gibbs measure

$$\begin{aligned} M_N:=\frac{e^{-\beta H_N(x)}}{Z_N} \textrm{d}{x} \qquad \text{ with }\qquad Z_N:=\int _{\Omega ^N} e^{-\beta H_N(y)}\;\textrm{d}y. \end{aligned}$$

(3.4)

As stated before, the mean field limit can admit more than a single steady state, with the full characterisation being the set of solutions to the self-consistency equation

$$\begin{aligned} \beta ^{-1}\log \rho _*+W\star \rho _*+V=C_*\qquad \text{ on }\ \Omega \ \text {for some}\ C_*\in {\mathbb {R}}, \end{aligned}$$

(3.5)

This is discussed in detail in Proposition 4.1. See also [11, 18] and the references therein.

Fig. 1

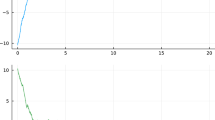
A rough schematic showing two possible kinds of phase transition: The upper diagram shows a typical continuous phase transition. In this setting, the unique critical point (shown in blue) loses its local stability through a local (pitchfork) bifurcation which gives rise to new locally stable critical points. The lower diagram shows a typical discontinuous phase transition. In this setting, the unique critical point retains its local stability but new critical points arise in the free energy landscape through a saddle node bifurcation

Phase transitions The uniqueness/non-uniqueness of steady states of the mean field system (3.3) depends on both the temperature of the system (or, equivalently, the strength of the interaction) and the convexity properties of the confining and interaction potentials V and W. At sufficiently high temperatures, the diffusion is strong enough that the expected escape time of particles from local minima of the potentials is bounded uniformly in the number of particles. Indeed, a perturbation argument shows that, at sufficiently high temperatures, the self-consistency equation (3.5) has a unique solution, see Proposition 4.2. When we cool the system and the potentials are non-convex, particles can get trapped for arbitrarily long time scales in local minima and condense [4]. In statistical physics terms, the system changes from a gaseous state to a liquid or solid state. In the mean field limit, this change of behavior can be characterised by the local or global instability of the minimisers of the mean field energy (see (3.8)), see for instance [11, 15] and Fig. 1 for a loose picture of the change in the mean field energy landscape as the temperature of the system is varied. For more details on the possible definitions of a phase transition, see Sect. 4.

$\Gamma$-convergence Taking advantage of the 2-Wasserstein gradient flow structure of (3.1) and (3.3) (see [1, 10, 59]), the main tool that we will use to obtain a quantitative understanding of the limit $N\rightarrow \infty$ is $\Gamma$-convergence with respect to the topology introduced by de Finetti/Hewitt-Savage-type convergence (3.2). To illustrate this technique, we use it to characterise the limit $N\rightarrow \infty$ of the Gibbs measure $M_N$. Following the pioneering work of Messer and Spohn [50], we notice that $M_N$ is the unique minimiser over probability measures of the energy per unit particle

$$\begin{aligned} E^N[\rho ^N]=\frac{1}{N}\left( \beta ^{-1}\int _{\Omega ^N}\rho ^N\log \rho ^N\;\textrm{d}{x}+\int _{\Omega ^N} H_N \rho ^N\;\textrm{d}{x}\right) . \end{aligned}$$

(3.6)

Taking $N\rightarrow \infty$, we can characterise the thermodynamic limit of the energy $E^N$ as $E^N\rightarrow ^{\Gamma }E^\infty :{\mathcal {P}}({\mathcal {P}}(\Omega ))\rightarrow {\mathbb {R}}\cup \{+\infty \}$, where

$$\begin{aligned} E^\infty [P]:=\int _{{\mathcal {P}}(\Omega )}E^{MF}[\rho ]\textrm{d}P(\rho ), \end{aligned}$$

(3.7)

with the mean field energy $E^{MF}:{\mathcal {P}}(\Omega )\rightarrow {\mathbb {R}}\cup \{+\infty \}$ given by

$$\begin{aligned} E^{MF}[\rho ]:=\beta ^{-1}\int _{\Omega }\rho \log (\rho )\;\textrm{d}x+\frac{1}{2}\int _{\Omega ^{2}}W(x,y)\;\textrm{d}\rho (x)\; \textrm{d}\rho (y)+\int _{\Omega }V(x)\; \textrm{d}\rho (x),\nonumber \\ \end{aligned}$$

(3.8)

see [37] or Theorem 5.6 for a more modern proof. Using the fact that $M_N$ is the minimiser of (3.6), we know that any accumulation point of the sequence $M_N$ (in the sense of de Finetti/Hewitt–Savage) $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ needs to be a minimiser of (3.7), which implies $P_\infty$ is supported in the set of minimizers ${\mathcal {K}}=\{\rho \in {\mathcal {P}}(\Omega )\;:\;\inf E^{MF}=E^{MF}[\rho ]\}$. Moreover, we may conclude that the minimal energy converges

$$\begin{aligned} \lim _{N\rightarrow \infty } \left( -\frac{1}{\beta N}\log Z_N \right) =\lim _{N\rightarrow \infty } E^N[M_N]=E^\infty [P_\infty ]=\inf _{P\in {\mathcal {P}}({\mathcal {P}}(\Omega ))}E^\infty [P] =\inf _{\rho \in {\mathcal {P}}(\Omega )} E^{MF}[\rho ], \end{aligned}$$

where we have used that (3.7) is a potential energy, which also implies that $P_\infty$ needs to be supported on the minimisers of $E^{MF}$. This convergence and related results are discussed in further detail in Sect. 5.

Under our previous hypothesis, we have the following standard result.

Theorem C

Under Assumptions 2.1 and 2.2, $E^{MF}$ is bounded below and has at least one minimiser.

The lower bound follows from Jensen’s inequality, while the existence of a minimiser follows from the direct method of calculus of variations. Under the extra assumption that $E^{MF}$ admits a unique minimiser $\rho _\beta \in {\mathcal {P}}({\mathbb {R}}^d)$, we have

$$\begin{aligned} M_N\rightharpoonup \delta _{\rho _\beta }\in {\mathcal {P}}({\mathcal {P}}(\Omega )) \,. \end{aligned}$$

Qualitative long time behavior Due to the linearity of the N-particle system, we know that (3.1) admits a unique steady state (given by the Gibbs measure $M_N$). Using compactness, La-Salle’s principle for gradient flows [12, Theorem 2.13] implies that the dynamics will always accumulate on the set of steady states of equation (3.1). Using the uniqueness of the steady state, we can see that independently of the initial condition

$$\begin{aligned} \lim _{t \rightarrow \infty }\rho ^N(t)= M_N \,, \end{aligned}$$

(3.9)

in the sense of weak convergence of probability measures. This convergence can be further quantified by utilizing the Log Sobolev inequality, to show exponentially fast convergence to the Gibbs measure [48]. On the other hand, if the McKean–Vlasov equation admits multiple steady states, then the limit $t\rightarrow \infty$ for the mean field dynamics will depend on the choice of initial condition. More specifically, if we take the initial condition $\rho _{in}=\rho _*$ to be a non-minizing critical point of the mean-field dynamics, then we have

$$\begin{aligned} \lim _{N\rightarrow \infty }M_N=\lim _{N\rightarrow \infty }\lim _{t\rightarrow \infty }\rho ^N(t)\ne \lim _{t\rightarrow \infty }\lim _{N\rightarrow \infty }\rho ^N(t)=\delta _{\rho _*}, \end{aligned}$$

where the non-equality follows from the fact that the limit of $M_N$ needs to be concentrated on ${\mathcal {K}}$ the set minimizers of $E^{MF}$, and $\rho _*\notin {\mathcal {K}}$ by assumption.

In this case, the limiting dynamics (3.3) do not approximate the particle dynamics (2.1) for arbitrarily long times. In this paper we provide evidence that phase transitions constitute the natural obstruction to obtaining uniform-in-time propagation of chaos estimates. See Theorem 2.12 for sufficient conditions for the mean field approximation to be valid uniformly in time.

Gradient flows in the 2-Wasserstein distance The perspective of the proofs in this paper is that the evolution of the N-particle law (3.1) and the mean field limit (3.3) are respectively the gradient flows of $E^N$ and $E^{MF}$ with respect to the scaled 2-Wasserstein distance $\bar{d}_2$ and the 2-Wasserstein distance on ${\mathcal {P}}(\Omega )$. In fact, the $\lambda$-convexity assumption on the potentials and the doubling condition (2.2) can be used to obtain uniqueness of the gradient flow solutions. The next fundamental result is essentially a restatement of [1, Theorem 11.2.8], for the compact case see [59].

Theorem D

If Assumptions 2.1 and 2.2 hold, then for any $\rho _{\textrm{in}}\in {\mathcal {P}}(\Omega )$ there exists unique distributional solutions $\rho ^N\in C([0,\infty );{\mathcal {P}}_{\textrm{sym}}(\Omega ^N))$ and $\rho \in C([0,\infty );{\mathcal {P}}(\Omega ))$ to (3.1) and (3.3), respectively, which are the gradient flows of $E^N$ (3.6) and $E^{MF}$ (3.8) with respect to the scaled 2-Wasserstein distance ${{\bar{d}}}_2$ and the 2-Wasserstein distance $d_2$ on ${\mathcal {P}}(\Omega )$, respectively. Moreover, these solutions can be characterized by the energy dissipation inequalities (2.3) and (2.6), respectively.

Remark 3.1

We note that these gradient flow solutions have the property that associated the dissipation functionals are well defined for any $t>0$.

We remark here that in [10] an alternative proof of propagation of chaos is provided which employs the $\Gamma$-convergence result and the convergence of the gradient flow structures.

4 Phase Transitions

We start our discussion by stating and proving the following result which provides us with a particularly useful characterisation of steady states.

Proposition 4.1

Under Assumptions 2.1 and 2.2 the following statements are equivalent:

• 1. $\rho \in {\mathcal {P}}(\Omega )$ is a critical point of the mean field free energy $E^{MF}$, that is to say

  $$\begin{aligned} |\partial E^{MF}|^2(\rho ):=D(\rho )=\int _{\Omega } |\beta ^{-1}\nabla \log \rho (t)+\nabla W\star \rho (t)+\nabla V|^2\rho (t)\;\textrm{d}{x} =0. \end{aligned}$$

• 2. $\rho \in {\mathcal {P}}(\Omega )$ is a steady state of the mean field equation (3.3), i.e. it is distributional weak solution of the PDE

  $$\begin{aligned} \beta ^{-1}\Delta \rho + \nabla \cdot (\rho (\nabla W \star \rho +\nabla V)) =0 \, \quad x \in \Omega \,. \end{aligned}$$

• 3. $\rho$ solves the self-consistency equation:

  $$\begin{aligned} \rho - \frac{1}{Z_\beta }e^{-\beta (W \star \rho +V) } =0 \, ,\qquad Z_\beta = \int _{\Omega } e^{-\beta (W \star \rho +V) } \textrm{d}{x} \, . \end{aligned}$$

  (4.1)

Furthermore, for all $\beta >0$, $E^{MF}$ has at least one global minimiser which is a critical point, and any critical point $\rho \in {\mathcal {P}}(\Omega )$ of $E^{MF}$ is Lipschitz, strictly positive, and has moments of all orders.

Proof

The proof of the equivalence of the three characterisations follows from similar arguments to [11, Proposition 2.4] and so we omit the proof. The fact that $E^{MF}$ has a critical point follows from Theorem C.

Now, using (4.1), we know that any critical point $\rho \in {\mathcal {P}}(\Omega )$ is of the form

$$\begin{aligned} \frac{1}{Z_\beta }e^{-\beta (W \star \rho + V)} \, , \end{aligned}$$

which is Lipschitz and strictly positive. We now use Assumption 2.2 to assert that, since W is bounded below,

$$\begin{aligned} \rho \le Z_\beta ^{-1} e^{\beta C} e^{-\beta V} \, . \end{aligned}$$

Thus, by Assumption 2.1, any critical point $\rho \in {\mathcal {P}}(\Omega )$ of $E^{MF}$ has moments of all orders. $\square$

Furthermore, we have the following result regarding uniqueness of critical points.

Proposition 4.2

Under the assumptions of Theorem 2.20 there exists a unique critical point $\rho _\beta \in {\mathcal {P}}(\Omega )$ of the mean field free energy $E^{MF}$.

Proof

The proof of this result follows by combining the results of Theorems 2.10 and 2.20. We know from Theorem 2.20 that the logarithmic Sobolev inequality holds uniformly for $M_N$. We can then use Theorem 2.10 to argue that for $\beta$ sufficiently small, the mean field free energy $E^{MF}$ must have a unique critical point $\rho _\beta$. $\square$

When we discuss non-uniqueness of critical points, we will often restrict ourselves to the case in which $V=0, W (x,y)=W(x-y)$, and $\Omega ={\mathbb {T}}^d$. This case lends itself particularly well to analysis as the Lebesgue measure $\rho _\infty (\textrm{d}{x})= \textrm{d}{x}$, what we shall hereafter refer to as the “flat state”, is always a critical point of $E^{MF}$ for all $\beta >0$. We shall see later that in this setting it is possible to provide relatively clean examples of the different types of phase transitions that we consider in this paper. For an example of what a typical phase transition looks like, see Fig. 1 for a schematic of the free energy landscape in the vicinity of a phase transition.

We now introduce and motivate a list of properties that may serve as a proxy for the absence of well-defined order parameter. We discuss how these properties relate to each other, specifically in the “flat case”. We start by looking at the linearisation of the mean field dynamics (3.3):

Property A

Fix $\beta >0$. We say that the system (3.3) satisfies Property A if $E^{MF}$ has a unique critical point $\rho _\beta$ and the linearised operator associated to right hand side of (3.3) has a spectral gap under the interaction weighted inner product. More specifically, we have that

$$\begin{aligned} \inf _{\eta \in C^\infty _0(\Omega ),\int _\Omega \eta \textrm{d}{x}=0} \frac{\langle - {\mathcal {L}}_{\rho _\beta } \eta ,\eta \rangle _{W,\rho _\beta }}{\Vert \eta \Vert _{W,\rho _\beta }^2} >0 \, , \end{aligned}$$

(A)

where

$$\begin{aligned} {\mathcal {L}}_{\rho _\beta } \eta = \beta ^{-1} \Delta \eta +\nabla \cdot (\nabla V \eta )+ \nabla \cdot (\rho _\beta \nabla W \star \eta ) + \nabla \cdot (\eta \nabla W \star \rho _\beta ) \, , \end{aligned}$$

and

$$\begin{aligned} \langle \eta ,\nu \rangle _{W,\rho _\beta }= \frac{\beta ^{-1}}{2} \int _{\Omega } \eta \nu \rho _\beta ^{-1} \textrm{d}{x} + \frac{1}{2}\int _{\Omega }(W\star \eta )\nu \textrm{d}{x} \end{aligned}$$

with $\Vert \eta \Vert _{W,\rho _\beta }^2= \langle \eta ,\eta \rangle _{W,\rho _\beta }$.

The above property captures essentially the local stability of the critical point $\rho _\beta$. Loss of the local stability of $\rho _\beta$ is a precursor to a phase transition. In the setting of a continuous phase transition (see the upper half of Fig. 1), one expects this property to fail exactly at the critical temperature $\beta =\beta _c$. The weighted inner product arises naturally through the linearisation of the mean field log Sobolev constant, or more specifically through the linearisation of the mean field energy $E^{MF}$, see (4.2). We note that the bilinear form $\langle \cdot ,\cdot \rangle _{W,\rho _\beta }$ is positive semi-definite when $\rho _\beta$ is the unique critical point. For the classical XY model (see the discussion before Theorem B), it is known that the system exhibits a continuous phase transition [11, Proposition 6.1]. In this case, the non-local inner product above it is related to the inner product that was introduced in [8] to understand the spectral gap ahead of the phase transition. In the absence of the interaction term, it reduces to the standard weighted inner product that symmetrises the Fokker–Planck operator, see [54]. In the periodic translation invariant case $\Omega ={\mathbb {T}}^d$, $W(x,y)=W(x-y)$, and $V \equiv 0$, when $\rho _\infty =\textrm{d}{x}$ is the unique critical point of $E^{MF}$, the weighted inner product $\langle \cdot ,\cdot \rangle _{W,\rho _\infty }$ is equivalent to the standard $L^2$ inner product. Thus, in this situation, checking Property A is satisfied is equivalent to checking that ${\mathcal {L}}_{\rho _\infty }$ has a spectral gap in the standard $L^2$ inner product. This relationship will be made clearer in Proposition 4.3. Before discussing Property A in more detail, we introduce the next property which measures the local degeneracy of the self-consistency equation (4.1).

Property B

Fix $\beta >0$. We denote by $T:{L}^2(\Omega )\rightarrow {L}^2(\Omega )$ the nonlinear map associated to the self-consistency equation (4.1):

$$\begin{aligned} T (\rho ) := \rho - \frac{1}{Z_\beta }e^{-\beta (W \star \rho +V) } =0 \, ,\qquad Z_\beta = \int _{\Omega } e^{-\beta (W \star \rho +V) } \textrm{d}{x} \, . \end{aligned}$$

(B)

We say that the system (3.3) satisfies Property B if $E^{MF}$ has a unique critical point $\rho _\beta$ and the Fréchet derivative $D_{\rho }T$ of T at $\rho _\beta$ is nondegenerate, that is to say it has a trivial kernel consisting only of constant functions.

Under additional conditions, see [11], violation of the above property implies the presence of a local bifurcation around the minimiser $\rho _\beta$. A simple condition that implies the presence of a local bifurcation is when the algebraic multiplicity of the 0 eigenvalue of $D_\rho T$ at $\rho _\beta$ is odd. Local bifurcations also arise, if the map T can be rewritten as a so-called potential operator and its Frechét derivative $D_\rho T$ has a non-zero crossing number, see [41]. The above property exactly captures the second-order degeneracy of the mean field free energy around the unique critical point $\rho _\beta$. Indeed, formally expanding $E^{MF}[\rho ]$ about $\rho _\beta$ we obtain

$$\begin{aligned} E^{MF}[\rho ]=&E^{MF}[\rho _\beta ] + \int _{\Omega } \beta ^{-1}\frac{\eta ^2}{2}\rho _\beta ^{-1}+\frac{1}{2} W \star \eta \eta \textrm{d}{x} + O(\eta ^3)\, \nonumber \\ =&E^{MF}[\rho _\beta ] + \beta ^{-1}\int _{\Omega } \left( D_{\rho }T[\rho _\beta ]\eta \right) \eta \rho _\beta ^{-1}\textrm{d}{x} + O(\eta ^3) \, , \end{aligned}$$

(4.2)

with $\eta =\rho -\rho _\beta$. Thus, if Property B is satisfied the mean field free energy is nondegenerate at second order near the critical point $\rho _\beta$.

The third and final property considers the validity of the Dissipation Inequality.

Property C

Fix $\beta >0$. We say that the system (3.3) satisfies Property C if the infinite-volume log Sobolev constant is positive. More precisely, if we have that

$$\begin{aligned} \lambda ^\infty _{{{\,\textrm{LSI}\,}}}:=\inf _{\rho \in {\mathcal {P}}(\Omega ), \rho \not \in {\mathcal {K}}} \frac{D(\rho )}{E^{MF}[\rho ]- \min _{{\mathcal {P}}(\Omega )}E^{MF}}>0 \, . \end{aligned}$$

(C)

The third and final property captures global aspects of the free energy landscape. Indeed, one would expect it to be violated in both the situations described in Fig. 1. For the case of the discontinuous phase transition, the lower half of Fig. 1, Property C would be violated because of the presence of a non-minimising critical point of $E^{MF}$ which is represented by the red circles. Thus, the numerator of (C) vanishes while the denominator is strictly positive. As an explicit example of a system which exhibits such a phase transition, one can consider $\Omega ={\mathbb {T}}$, with the bi-chromatic interaction potential $W(x,y)=-\cos (2 \pi (x-y))-\cos (4 \pi (x-y))$, and $V \equiv 0$ (cf. [11, Theorem 5.11]). On the other hand, in the case of a continuous phase transition, the upper half of Fig. 1, the fact that Property C should be violated is more subtle. To observe this, we linearise the right hand side of (C) about the unique minimiser $\rho _\beta$ at $\beta =\beta _c$. For the dissipation, we have that

$$\begin{aligned} D(\rho )=&2 \int _{\Omega }|\beta ^{-1} \nabla \frac{\eta }{\rho _\beta } +\nabla W \star \eta |^2 \textrm{d}{\rho _\beta } + O(\eta ^3) \, , \end{aligned}$$

with $\eta =\rho -\rho _\beta$. Combining the above expression with (4.2), we obtain to leading order

$$\begin{aligned} \frac{D(\rho )}{E^{MF}[\rho ]-E^{MF}[\rho _\beta ]} \approx \frac{4 \int _{\Omega }|\beta ^{-1} \nabla \frac{\eta }{\rho _\beta } +\nabla W \star \eta |^2 \textrm{d}{\rho _\beta }}{\int _{\Omega }\beta ^{-1}\eta ^2 + W\star \eta \eta \rho _\beta \textrm{d}{\rho _\beta ^{-1}}} \, . \end{aligned}$$

(4.3)

Moreover, we notice that

$$\begin{aligned} (-{\mathcal {L}}_{\rho _\beta }\eta ,\eta )_{W,\rho _\beta }=&\frac{1}{2}\int _{\Omega }|\beta ^{-1}\nabla \frac{\eta }{\rho _\beta } + \nabla W \star \eta |^2 \textrm{d}{\rho _\beta } \, . \end{aligned}$$

Using (4.3), it follows that to leading order

$$\begin{aligned} \frac{D(\rho )}{E^{MF}[\rho ]-E^{MF}[\rho _\beta ]} \approx 4\frac{\langle -{\mathcal {L}}_{\rho _\beta }\eta ,\eta \rangle ^2_{W,\rho _\beta }}{\Vert \eta \Vert _{W,\rho _\beta }^2} \, . \end{aligned}$$

Hence, in the setting of a continuous phase transition the infinite volume log Sobolev constant captures the spectral gap of ${\mathcal {L}}_{\rho _\beta }$, and thus also captures the loss of local stability of $\rho _\beta$.

We now present the following result which characterises how the various properties we have discussed relate to each other in the periodic spatially homogeneous case.

Proposition 4.3

Assume $\Omega ={\mathbb {T}}^d$, $V\equiv 0,$ $W(x,y)=W(x-y)$, and denote

$$\begin{aligned} \beta _\sharp :=\frac{1}{ \min (0,-\min _{k \in {\mathbb {Z}}^d \setminus \left\{ 0\right\} }{\hat{W}}(k))}\in (0,\infty ]. \end{aligned}$$

(4.4)

Then, for $\beta <\beta _\sharp$ the linearised operator ${\mathcal {L}}_{\textrm{d}{x}}$ satisfies the spectral gap property (10.3), and the kernel of the Fréchet derivative of the self-consistency equation (10.4) is non degenerate at the “flat state”. For $\beta \ge \beta _\sharp$, Properties A and B are violated.

Furthermore, for all $\beta \ne \beta _\sharp$, Property C implies Property A and Property B.

Remark 4.4

We emphasize that Proposition 4.3 does not ensure that Properties A and B are satisfied for $\beta <\beta _\sharp$. In fact, for the bi-chromatic potential case $W(x,y)=-\cos (2 \pi (x-y))-\cos (4 \pi (x-y))$, we know that the “flat state” is not the unique steady state for some $\beta <\beta _\sharp$ violating the uniqueness requirement of Properties A and B, see [11, Theorem 5.11].

Proof

We will first argue that Properties A and B are equivalent. It follows from the fact that $\rho _\infty (\textrm{d}{x}) \equiv \textrm{d}{x}$ is always a critical point of $E^{MF}$ (in the flat case) that if $E^{MF}$ has a unique critical point, it must be $\rho _\infty$. For any mean zero $\eta \in C_0^\infty (\Omega )$, we have from the previous calculation, that

$$\begin{aligned} \frac{\langle -{\mathcal {L}}_{\rho _\infty } \eta ,\eta \rangle _{W,\rho _\beta } }{\Vert \eta \Vert _{W,\rho _\beta }^2}=&\frac{1}{2}\frac{\int _{\Omega }|\beta ^{-1}\nabla \eta + \nabla W * \eta |^2\textrm{d}{x}}{ \int _{\Omega }(\beta ^{-1}\eta + W * \eta )\eta \textrm{d}{x} } \, , \end{aligned}$$

where we have used the fact that $\rho _\beta$ is the Lebesgue measure on ${\mathbb {T}}^d$. It is easy to check that the above expression is strictly positive if and only if $\beta <\frac{1}{ \min (0,-\min _{k \in {\mathbb {Z}}^d {\setminus } \left\{ 0\right\} }{\hat{W}}(k))} =\beta _\sharp$. Similarly, computing the Fréchet derivative of T at $\rho _\infty$, we obtain

$$\begin{aligned} D_\rho T [\rho _\infty ] \eta = \eta + \beta W * \eta \, . \end{aligned}$$

Again, the above linear operator has a trivial kernel if and only if $\beta < \beta _\sharp$. It follows that Properties A and B are equivalent.

We will now show that Property C implies Property B for $\beta \ne \beta _\sharp$. We know that Property B is satisfied if and only if $E^{MF}$ has unique critical point and $\beta <\beta _\sharp$. Assume it is violated. Then, either $E^{MF}$ has more than one critical point or $\beta \ge \beta _\sharp$ (or both).

Consider the case in which $\beta <\beta _\sharp$ but $E^{MF}$ has more than one critical point one of which is $\rho _\infty$. Furthermore, we know from [35, Lemma 5.6] that $\rho _\infty$ is a strict local minimum. If at least one of the other critical points is not a minimiser then clearly Property C is violated since the numerator can be chosen to be zero while the denominator remains positive. We will now argue that this is the case. Assume it is not, that is all other critical points are minimisers. Then, we can apply the mountain pass theorem in ${\mathcal {P}}(\Omega )$ (using the fact that $\rho _\infty$ is a strict local minimum) [35, Theorem 1.1] to construct a new non-minimising critical point thus obtaining a contradiction.

Consider now the case in which $\beta >\beta _\sharp$. In this situation, we note from [11, Proposition 5.3] that $\rho _\infty$ is a non-minimising critical point of $E^{MF}$. Thus, Property C is again violated. $\square$

Remark 4.5

We note here that one would expect the Properties A to C to be equivalent to each other. However, we unable to show that this holds true in general.

Given the above result, we are now finally in a position to present our definition of a phase transition in the “flat case”.

Definition 4.6

(Phase transition) Assume $V\equiv 0, W(x,y)=W(x-y),$ and $\Omega ={\mathbb {T}}^d$. Then, we say that the system (3.3) exhibits a phase transition of type A (resp. type B, type C) if there exists a $0<\beta _c<\infty$ such that for all $0<\beta <\beta _c$ Property A (resp. type B, type C) is satisfied, and for $\beta _c<\beta$ Property A (resp. type B, type C) is violated.

Except for the Brownian mean field model see Theorem B, we can not ensure that the existence of a phase transition in the sense of Definition 4.6. Combining Theorem 2.20 with analysis in [11, 15], we can show the following result.

Theorem 4.7

Assume $V\equiv 0,\; W(x,y)=W(x-y),$ and $\Omega ={\mathbb {T}}^d$. If W is ${\textbf{H}}$-stable, that is to say ${\hat{W}}(k)\ge 0$ for all $k \in {\mathbb {Z}}^d {\setminus } \left\{ 0\right\}$, then the system (3.3) satisfies Properties A and B for all $\beta \in (0,\infty )$.

If there exists $k \in {\mathbb {Z}}^d \setminus \left\{ 0\right\}$ such that ${\hat{W}}(k)<0$, then there exists $\beta _1<\beta _\sharp$ such that Properties A to C are satisfied for all $\beta <\beta _1$, and Properties A to C are violated for all $\beta >\beta _\sharp$.

Proof

If W is ${\textbf{H}}$-stable, it follows from linear convexity $\rho _\infty =\textrm{d}{x}$ is the unique critical point of $E^{MF}$ for all $0<\beta <\infty$, hence Properties A and B cannot be violated, see [11, Proposition 5.8]. On the other hand, if $\beta _\sharp <\infty$, we know from Proposition 4.3 that Properties A to C are violated for all $\beta >\beta _\sharp$.

By Theorem 2.20 and Theorem 2.6, we know that there exists $\beta _{{{\,\textrm{LSI}\,}}}$ such that $0<\beta <\beta _{{{\,\textrm{LSI}\,}}}$ then Property C is satisfied. Finally, by Proposition 4.3 we have that Properties A and B are also satisfied. $\square$

5 The Limit ${\mathcal {P}}_{\textrm{sym}}(\Omega ^N)\rightarrow {\mathcal {P}}({\mathcal {P}}(\Omega ))$

In this section, we recall some useful results that allows us to characterise the various relevant objects in the limit as $N\rightarrow \infty$. We follow the approach taken by Hauray and Mischler in [37]. We start by defining the empirical measure.

Definition 5.1

Given some $\rho ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$, the empirical measure is the ${\mathcal {P}}(\Omega )$-valued random variable which is given by

$$\begin{aligned} \mu ^{(N)}:=\frac{1}{N}\sum _{i=1}^N\delta _{x_i}\qquad \text{ where }\ (x_1,...,x_N)\ \text {is distributed according} \rho ^N. \end{aligned}$$

We denote the law of the empirical measure $\mu ^{(N)}$ on ${\mathcal {P}}(\Omega )$ by

$$\begin{aligned} {\hat{\rho }}^N\in {\mathcal {P}}({\mathcal {P}}(\Omega )) \,. \end{aligned}$$

The topology we consider throughout most of the manuscript is the one induced by the scaled 2-Wasserstein distance.

Definition 5.2

Given $\rho _1^N,\,\rho _2^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$, the scaled 2-Wasserstein distance between them is given by

$$\begin{aligned} {\overline{d}}_2(\rho _1^N,\rho _2^N)=\inf _{\begin{array}{c} X\sim \rho _1^N\\ Y\sim \rho _2^N \end{array}}\left( \frac{1}{N}{\mathbb {E}}[|X-Y|^2]\right) ^{1/2}, \end{aligned}$$

where $X,\, Y$ are $\Omega ^N$-valued random variables.

Similarly, given $P_1,\,P_2\in {\mathcal {P}}({\mathcal {P}}(\Omega ))$, the 2-Wasserstein distance between them is given by

$$\begin{aligned} {\mathfrak {D}}_2(P_1,P_2)=\inf _{\begin{array}{c} {\mathcal {X}}\sim P_1\\ {\mathcal {Y}}\sim P_2 \end{array}}\left( {\mathbb {E}}[d_2^2({\mathcal {X}},{\mathcal {Y}})]\right) ^{1/2} \end{aligned}$$

where ${\mathcal {X}},\, {\mathcal {Y}}$ are ${\mathcal {P}}(\Omega )$-valued random variables.

A fundamental result we need to understand the convergence ${\mathcal {P}}_{\textrm{sym}}(\Omega ^N)\rightarrow {\mathcal {P}}({\mathcal {P}}(\Omega ))$ is the fact that the mapping $\rho ^N\mapsto {\hat{\rho }}^N$ is an isometry for the appropriately scaled 2-Wasserstein distance defined in  Definition 5.2. Indeed, we have the following result.

Theorem 5.3

([37, Proposition 2.14]) For each $\mu ^N,\,\nu ^N\in {\mathcal {P}}_{\mathrm {\textrm{sym}}}(\Omega ^N)$, we have

$$\begin{aligned} {\overline{d}}_2(\mu ^N,\nu ^N)={\mathfrak {D}}_2({\hat{\mu }}^N,{\hat{\nu }}^N) \,. \end{aligned}$$

Proof

We present only a sketch of the proof of this result. The first inequality ${\overline{d}}_2(\mu ^N,\nu ^N)\ge {\mathfrak {D}}_2({\hat{\mu }}^N,{\hat{\nu }}^N)$ follows from the mapping in Definition 5.1$X\mapsto {\mathcal {X}}$, i.e. given $X=(X_1,...,X_N)$ an $\Omega ^N$-valued random variable with law $\mu ^N$, we define

$$\begin{aligned} {\mathcal {X}}:=\frac{1}{N}\sum _{i=1}^N\delta _{X_i} \,, \end{aligned}$$

is a ${\mathcal {P}}(\Omega )$-valued random variable with law ${\hat{\mu }}^N$. The converse inequality follows from taking the inverse mapping and exploiting the symmetry of $\mu ^N$ and $\nu ^N$. $\square$

Using this result, we can provide a metric notion of the de Finetti/Hewitt–Savage convergence.

Definition 5.4

We say that the sequence $(\rho ^N)_{N\in {\mathbb {N}}}$ such that $\rho ^N\in {\mathcal {P}}_{\mathrm {\mathrm {\textrm{sym}}}}(\Omega ^N)$ converges in the 2-Wasserstein distance to $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ if

$$\begin{aligned} \lim _{N\rightarrow \infty } {\mathfrak {D}}_2({\hat{\rho }}^N,P_\infty )=0, \end{aligned}$$

where ${\hat{\rho }}^N$ is the law of the empirical measure (as a ${\mathcal {P}}(\Omega )$-valued random variable) associated to $\rho ^N$.

We now have the following result which connects the above convergence to the one introduced in (3.2).

Proposition 5.5

For any sequence $(\rho ^N)_{N\in {\mathbb {N}}}$ with $\rho ^N \in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$ and

$$\begin{aligned} \sup _{N \in {\mathbb {N}}} \int _{\Omega }|x|^\gamma \;\textrm{d}\rho _1^N(x)<\infty \end{aligned}$$

(5.1)

for some $\gamma >2$, the metric convergence in Definition 5.4 is equivalent to the original marginal convergence of (3.2).

Proof

We first notice that by the results of Diaconis and Freedman [21], for a fixed $l\in {\mathbb {N}}$, the marginal $\rho ^N_l$ coincides in the limit as $N \rightarrow \infty$ with the l^th product of the empirical measure. More specifically, for any $\varphi \in C^\infty _c(\Omega ^l)$ we have that

$$\begin{aligned} \left| \int _{\Omega ^l}\varphi \;\textrm{d}\rho ^N_l-\int _{{\mathcal {P}}(\Omega )}\left( \int _{\Omega ^l}\varphi \;\textrm{d}\mu ^{\otimes l}\right) \;\textrm{d}{\hat{\rho }}^N(\mu )\right| \le l^2\frac{\Vert \varphi \Vert _{L^\infty (\Omega ^l)}}{N} \,. \end{aligned}$$

(5.2)

Furthermore, (5.1) implies that ${\hat{\rho }}^N$ is tight in ${\mathcal {P}}(\Omega )$. Indeed, we have

$$\begin{aligned} \int _{{\mathcal {P}}(\Omega )}d_2^{\gamma }(\rho ,\delta _0)\;\textrm{d}{\hat{\rho }}^N(\rho )\le \int _{\Omega }|x|^\gamma \; \textrm{d}\rho ^N_1 \, . \end{aligned}$$

Now if ${\hat{\rho }}^N$ converges in the sense of Definition 5.4 to $P_\infty$ we know that it must converge when tested against every element of $C_b({\mathcal {P}}(\Omega ))$. Since cylindrical test functions are a subset of $C_b(\Omega )$, it is clear from (5.2) that $\rho ^N$ must also converge to $P_\infty$ in the sense of (3.2).

On the other hand if $\rho ^N$ converges to $P_\infty$ in the sense of (3.2) we know that, under (5.1), the sequence ${\hat{\rho }}^N$ is relatively compact in $({\mathcal {P}}({\mathcal {P}}(\Omega )),{\mathfrak {D}}_2)$. By the Stone–Weierstrass theorem cylindrical functions are dense in $C_b({\mathcal {P}}(\Omega ))$ (see [58, Theorem 2.1 ]), which tells us that the limits in (5.2) and Definition 5.4 coincide. $\square$

Next, we discuss the limit of the associated free energy and dissipation functionals.

Theorem 5.6

Under Assumptions 2.1 and 2.2, consider a sequence $(\rho ^N)_{N\in {\mathbb {N}}}$ with $\rho ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$ such that $\rho ^N\rightarrow P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ in the sense of Definition 5.4. Then,

$$\begin{aligned} \liminf _{N\rightarrow \infty } E^N[\rho ^N]\ge E^\infty [P_\infty ]\qquad \text{ and }\qquad \liminf _{N\rightarrow \infty } \overline{{\mathcal {I}}}(\rho ^N|M_N)\ge \int _{{\mathcal {P}}(\Omega )} D(\rho )\;dP_\infty (\rho ) \end{aligned}$$

where $E^N$, $E^\infty$, $\overline{{\mathcal {I}}}$, and $D(\rho )$ are defined by (3.6), (3.7), (2.3), and (2.6), respectively. Moreover, for any $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ we consider

$$\begin{aligned} \rho ^N_*=\left( \int _{{\mathcal {P}}(\Omega )}\rho ^{\otimes N}\;\textrm{d}P_\infty (\rho )\right) \in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N), \end{aligned}$$

then there exists a sequence of $t_N\rightarrow 0^+$ such that

$$\begin{aligned} \lim _{N\rightarrow \infty } E^N[S_{t_N}^N\rho _*^N]= E^\infty [P_\infty ]\qquad \text{ and }\qquad \lim _{N\rightarrow \infty } \overline{{\mathcal {I}}}(S_{t_N}^N\rho _*^N|M_N)=\int _{{\mathcal {P}}(\Omega )} D(\rho )\;dP_\infty (\rho ),\nonumber \\ \end{aligned}$$

(5.3)

where $S_t^N:{\mathcal {P}}(\Omega ^N)\rightarrow {\mathcal {P}}(\Omega ^N)$ is the solution operator to Fokker–Planck equation (3.1).

Proof

The convergence of the relative entropy functional follows directly from the classical arguments in [50]. A more modern proof can be found in [37]. The convergence of the relative Fisher information with respect to the Lebesgue measure is covered in [37]. Our case is slightly more involved due to the minimal regularity assumptions on the potentials. Formally, expanding the square we obtain after integrating by parts

$$\begin{aligned} \overline{{\mathcal {I}}}(\rho ^N,M_N)=&\frac{1}{N}\int _{\Omega ^N} |\nabla \log \rho ^N-\nabla H^N|^2 \textrm{d}\rho ^N\nonumber \\ =&\int _{\Omega ^N} (|\nabla \log \rho ^N|^2+2\Delta H^N +|\nabla H^N|^2)\textrm{d}\rho ^N \, . \end{aligned}$$

The first term of the above expression is exactly the relative Fisher information with respect to the Lebesgue measure and so is already covered in [37]. Under stronger regularity assumptions on the potentials, the second and third term fall within the type of functionals already considered in [50]. The main obstruction to conclude under Assumptions 2.1 and 2.2 is that $\Delta V$ and $\Delta W$ are merely signed measures bounded below, so we need to adapt the proofs of [37] to a lower regularity setting. We will circumvent the regularity problem by appealing again and again to convexity. More specifically, by Assumptions 2.1 and 2.2, we know that

$$\begin{aligned} \overline{{\mathcal {I}}}^{1/2}(\rho ^N | M_N)=\sup _{\nu ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)} \left( \frac{E^N[\rho ^N]-E^N[\nu ^N]}{{\overline{d}}_2(\rho ^N,\nu ^N)}-\frac{K_V+K_W}{2}{\overline{d}}_2(\rho ^N,\nu ^N)\right) _+ \,, \end{aligned}$$

see [1, Theorem 2.4.9]. We pick $\nu ^N$ to be the recovery sequence for a generic $Q_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$, using the lower semicontinuous convergence of $E^N$, and the isometry Theorem 5.3, to obtain

$$\begin{aligned} \liminf _{N\rightarrow \infty } \overline{{\mathcal {I}}}^{1/2}(\rho ^N | M_N)\ge \sup _{Q_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))}\left( \frac{E^\infty [P_\infty ]-E^\infty [Q_\infty ]}{{\mathfrak {D}}_2(P_\infty ,Q_\infty )}-\frac{K_V+K_W}{2}{\mathfrak {D}}_2(P_\infty ,Q_\infty )\right) _+. \end{aligned}$$

To obtain equality, we consider $S_t:{\mathcal {P}}(\Omega )\rightarrow {\mathcal {P}}(\Omega )$ the solution operator associated to (3.3) which is well-defined by Theorem D and consider the curve $Q_\infty =S_t\#P_\infty$, which coincides with the unique gradient flow of $E^\infty$ with respect to ${\mathfrak {D}}_2$ (see [10, Lemma 19]). Taking $t\rightarrow 0^+$, we obtain

$$\begin{aligned} \lim _{t\rightarrow 0^+}&\left( \frac{E^\infty [P_\infty ]-E^\infty [S_t\#P_\infty ]}{{\mathfrak {D}}_2(P_\infty ,S_t\#P_\infty )} -\frac{K_V+K_W}{2}{\mathfrak {D}}_2(P_\infty ,S_t\#P_\infty )\right) _+\\ =&\left( \int _{{\mathcal {P}}(\Omega )} D(\rho )\;\textrm{d}P_\infty (\rho )\right) ^{1/2} \, , \end{aligned}$$

obtaining the desired lower semicontinuity result

$$\begin{aligned} \liminf _{N\rightarrow \infty }{\mathcal {I}}(\rho ^N|M_N)\ge \int _{{\mathcal {P}}(\Omega )} D(\rho )\;\textrm{d}P_\infty (\rho ). \end{aligned}$$

Now we focus on showing that given $P\in {\mathcal {P}}({\mathcal {P}}(\Omega ))$, we can find a sequence of $t_N\rightarrow 0^+$ such that

$$\begin{aligned} S_{t_N}^N\rho _*^N=S_{t_N}^N\left( \int _{{\mathcal {P}}(\Omega )}\rho ^{\otimes N} \;\textrm{d}P(\rho )\right) \end{aligned}$$

attains the limit (5.3). We use the gradient flow convergence ${\mathcal {P}}_{sym}(\Omega ^N)\rightarrow {\mathcal {P}}({\mathcal {P}}(\Omega ))$ of [10] to characterize

$$\begin{aligned} \lim _{N\rightarrow \infty }\overline{{\mathcal {I}}}(S_t^N\rho _*^N|M_N)=\int _{{\mathcal {P}}(\Omega )}D(S_t\rho )\;dP(\rho ) \qquad \hbox { for a.e.}\ t>0, \end{aligned}$$

where $S_t$ is the solution operator associated to the McKean-Vlasov equation (3.3). Indeed, by the Sandier-Serfaty framework for convergence of gradient flows [60, Theorem 1], we notice that we have convergence of the corresponding dissipation functionals

$$\begin{aligned} \lim _{N\rightarrow \infty }\overline{{\mathcal {I}}}(S_t^N\rho _*^N|M_N)\rightarrow |\partial E^{\infty }[S_t\#P]|^2=\int _{{\mathcal {P}}(\Omega )}D(S_t\rho )\;dP(\rho ) \qquad \text{ for } \text{ a.e. }\ t>0. \end{aligned}$$

Using the convexity Assumptions 2.1 and 2.2 we know that $e^{t(\lambda _V+\lambda _W)}D(S_t\rho )$ is monotone in t, so combining it with lower semicontinuity yields $D(S_t\rho )\rightarrow D(\rho )$ as $t\rightarrow 0^+$. Hence, taking the limit $t\rightarrow 0^+$ and applying monotone convergence theorem we obtain

$$\begin{aligned} \lim _{t\rightarrow 0^+}\lim _{N\rightarrow \infty }\overline{{\mathcal {I}}}(S_t^N\rho _*^N|M_N)=\int _{{\mathcal {P}}(\Omega )}D(\rho )\;dP(\rho ). \end{aligned}$$

Taking a sequence of $t_N$ small enough we have the desired limit (5.3)

$$\begin{aligned} \lim _{N\rightarrow \infty }\overline{{\mathcal {I}}}(S_{t_N}^N\rho _*^N|M_N)=\int _{{\mathcal {P}}(\Omega )}D(\rho )\;dP(\rho ). \end{aligned}$$

$\square$

Standard arguments of $\Gamma$-convergence also yield the convergence of the minimal energy.

Corollary 5.7

Any accumulation point $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ of the sequence $(M_N)_{N\in {\mathbb {N}}}$ satisfies

$$\begin{aligned} \textrm{supp}(P_\infty )\subset \{\rho :\; E^{MF}[\rho ]=\min _{{\mathcal {P}}(\Omega )} E^{MF}\} \end{aligned}$$

and

$$\begin{aligned} E^N[M_N]=-\frac{1}{N}\log (Z_N){\mathop {\rightarrow }\limits ^{N \rightarrow \infty }} \min _{{\mathcal {P}}(\Omega )} E^{MF} \,. \end{aligned}$$

(5.4)

We remark that the convergence (5.4) coincides with the standard definition of the thermodynamic limit from statistical mechanics (see [38, Ch. 3]).

Theorem 5.8

(HWI inequality) Let V and W be K-convex. Given two arbitrary probability measures $\mu ^N,\,\nu ^N\in {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$, it holds

$$\begin{aligned} \overline{{\mathcal {E}}}(\mu ^N|M_N)\le \overline{{\mathcal {E}}}(\nu ^N|M_N)+{\overline{d}}_2(\mu ^N,\nu ^N)\sqrt{\overline{{\mathcal {I}}}(\mu ^N|M_N)}-\frac{K}{2}{\overline{d}}^2_2(\mu ^N,\nu ^N) \,. \end{aligned}$$

(5.5)

Proof

The proof of this result can be found in [68, Theorem 30.22]. We just present the main idea of the proof for the reader’s convenience. We consider $\gamma :[0,1]\rightarrow {\mathcal {P}}_{\textrm{sym}}(\Omega ^N)$ the 2-Wasserstein geodesic between $\mu ^N$ and $\nu ^N$. Under the hypothesis of K convexity of the potentials, we obtain that $t\rightarrow \overline{{\mathcal {E}}}(\gamma (t)|M_N)$ is K-convex, which implies the desired inequality (5.5). $\square$

Corollary 5.9

Assume that Assumptions 2.1 and 2.2 hold true and that the sequence $(\rho ^N)_{N\in {\mathbb {N}}}$ with $\rho ^N \in {\mathcal {P}}_{\mathrm {\textrm{sym}}}(\Omega ^N)$ converges to $P_\infty \in {\mathcal {P}}({\mathcal {P}}(\Omega ))$ in the sense of Definition 5.4 and

$$\begin{aligned} \sup _{N \in {\mathbb {N}}} \overline{{\mathcal {I}}}(\rho ^N|M_N)<\infty \,, \end{aligned}$$

then

$$\begin{aligned} \lim _{N\rightarrow \infty }\overline{{\mathcal {E}}}(\rho ^N|M_N)=E^\infty [P_\infty ]-\min _{{\mathcal {P}}(\Omega )} E^{MF}. \end{aligned}$$

Proof

Given $P_\infty$, we consider the recovery sequence $(\rho ^N_*)_{N \in {\mathbb {N}}}$ from Theorem 5.6. By the HWI inequality (5.5), we have

$$\begin{aligned} \overline{{\mathcal {E}}}(\rho ^N|M_N)\le \overline{{\mathcal {E}}}(\rho _*^N|M_N)+{\overline{d}}_2(\rho ^N,\rho _*^N)\sqrt{\overline{{\mathcal {I}}}(\rho ^N|M_N)}-\frac{K}{2}{\overline{d}}^2_2(\rho ^N,\rho _*^N) \,. \end{aligned}$$

Using that both sequences converge to $P_\infty$ and that $(\rho ^N_*)_{N \in {\mathbb {N}}}$ is a recovery sequence, we obtain

$$\begin{aligned} \limsup _{N\rightarrow \infty } \left( E^N[\rho ^N]-E^N[M_N]\right) =\limsup _{N\rightarrow \infty } \overline{{\mathcal {E}}}(\rho ^N|M_N) \le E^\infty [P_\infty ]-\min _{{\mathcal {P}}(\Omega )} E^{MF}\,. \end{aligned}$$

The reverse inequality follows from Theorem 5.6. $\square$

Remark 5.10

A version of this result without the potentials V and W can be found in [37, Proposition 3.8].

6 Proof of Theorem 2.19

Proof of Theorem 2.19

We prove the result only for $E^{MF}$, as the proof for $E^N$ and even more general energies $E:{\mathcal {P}}(\Omega )\rightarrow [0,\infty ]$ is analogous, see Remark 6.1. We consider $\rho :[0,\infty )\rightarrow {\mathcal {P}}(\Omega )$, the unique 2-Wasserstein gradient flow of $E^{MF}$ with initial condition $\rho _0 \in {\mathcal {P}}(\Omega )$, see Theorem D.

We notice that if $\lambda ^\infty _{{{\,\textrm{LSI}\,}}}=0$, then there is nothing left to prove. Hence, we can assume without loss of generality that $\lambda ^\infty _{{{\,\textrm{LSI}\,}}}>0$, which implies (cf. Property C and 4.1) that $E^{MF}$ does not have any non-minimising steady state. Using the version of LaSalle’s invariance principle for gradient flows proved in [12, Theorem 4.11], we know that $\rho (t)$ accumulates on the set of steady states of $E^{MF}$, as $t\rightarrow \infty$. Using the fact that all steady states are minimisers, we can find a sequence of times $t_n\rightarrow \infty$ such that

$$\begin{aligned} \rho (t_n)\rightharpoonup \rho _\infty \end{aligned}$$

(6.1)

for some $\rho _\infty \in {\mathcal {K}}$. Differentiating $E^{MF}[\rho (t)]$ with respect to time and using that $\lambda ^\infty _{{{\,\textrm{LSI}\,}}}>0$ we obtain

$$\begin{aligned} \frac{\textrm{d}{}}{\textrm{d}{t}}\left( E^{MF}[\rho (t)]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}\right)&=-\int _{\Omega }|\beta ^{-1}\nabla \log \rho (t)+\nabla V+\nabla W\star \rho (t)|^2\;\textrm{d}{\rho (t)}\\&\le -\sqrt{\lambda _{{{\,\textrm{LSI}\,}}}^\infty } \left( E^{MF}[\rho (t)]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}\right) ^{1/2}\\&\quad \times \left( \int _{\Omega }|\beta ^{-1}\nabla \log \rho (t)+\nabla V+\nabla W\star \rho (t)|^2\;\textrm{d}{\rho }(t)\right) ^{1/2}. \end{aligned}$$

Integrating from 0 to $t_n$ for some $n \in {\mathbb {N}}$, we obtain

$$\begin{aligned}&\left( E^{MF}[\rho (t_n)]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}\right) ^{1/2}-\left( E^{MF}[\rho _0]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}\right) ^{1/2}\\&\quad \le -\left( \frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty }{2}\right) ^{1/2}\int _0^{t_n}\left( \frac{1}{2}\int _{\Omega }|\beta ^{-1}\nabla \log \rho (s)+\nabla V+\nabla W\star \rho (s)|^2\;\textrm{d}{\rho }(s)\right) ^{1/2}\;\textrm{d}{s}\\&\quad \le -\left( \frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty }{2}\right) ^{1/2} d_2(\rho _0,\rho (t_n)), \end{aligned}$$

where the last inequality follows from the Benamou–Brenier [7] formulation of the 2-Wasserstein distance. Taking $t_n\rightarrow \infty$, applying (6.1), and rearranging, we end up with

$$\begin{aligned} \left( E^{MF}[\rho _0]-\inf _{{\mathcal {P}}(\Omega )}E^{MF}\right) ^{1/2}\ge \left( \frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty }{2}\right) ^{1/2} d_2(\rho _0,\rho _\infty )\ge \left( \frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty }{2}\right) ^{1/2} d_2(\rho _0,{\mathcal {K}}). \end{aligned}$$

The desired inequality (2.13) follows by squaring both sides. $\square$

Remark 6.1

This proof can easily be adapted to general $E:{\mathcal {P}}(\Omega )\rightarrow (0,\infty ]$, that are regular enough to admit gradient flow solutions from arbitrary initial data, and that sub-level sets are weakly compact to ensure convergence of the gradient flows to steady states [12, Theorem 2.12].

7 Proof of Theorem 2.6

Proof of Theorem 2.6

For the proof of the first part of the theorem, we consider some $\rho \in {\mathcal {P}}(\Omega )$ such that $E^{MF}[\rho ]>\inf _{{\mathcal {P}}(\Omega )} E^{MF}>-\infty$, see Theorem C. By Theorem 5.6 and Corollary 5.9 applied to $P_\infty =\delta _\rho$, the recovery sequence $P^N$ satisfies

$$\begin{aligned} \lim _{N \rightarrow \infty }\overline{{\mathcal {E}}}(P^N|M_N)= E^{MF}[\rho ]-\inf _{{\mathcal {P}}(\Omega )} E^{MF} \qquad \text{ and }\qquad \lim _{N \rightarrow \infty } \overline{{\mathcal {I}}}(P^N|M_N)= D(\rho ). \end{aligned}$$

Using the definition of the log Sobolev constant and passing to the limit as $N \rightarrow \infty$, we observe

$$\begin{aligned} \limsup _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}\le \limsup _{N\rightarrow \infty } \frac{\overline{{\mathcal {I}}}(P^N|M_N)}{\overline{{\mathcal {E}}}(P^N|M_N)}=\frac{D(\rho )}{E^{MF}[\rho ]-\inf E^{MF}}. \end{aligned}$$

Taking the infimum over all $\rho \notin {\mathcal {K}}$, we obtain

$$\begin{aligned} \limsup _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}\le \lambda ^\infty _{{{\,\textrm{LSI}\,}}}=\inf _{\rho \notin {\mathcal {K}}}\frac{D(\rho )}{E^{MF}[\rho ]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}}. \end{aligned}$$

This completes the proof of the first half of the theorem.

Next, we consider the case when there exists a non-minimising steady state $\rho _*\in {\mathcal {P}}(\Omega )$, that is

$$\begin{aligned} D(\rho _*)=0\qquad \text{ and }\qquad E^{MF}[\rho _*]>\inf _{{\mathcal {P}}(\Omega )} E^{MF}. \end{aligned}$$

Consider now the sequence $\rho _*^{\otimes N} \in {\mathcal {P}}_{\mathrm {\textrm{sym}}}(\Omega ^N)$. We have

$$\begin{aligned} \lambda _{N}^{{{\,\textrm{LSI}\,}}} \le&\frac{{\overline{{\mathcal {I}}}}(\rho _*^{\otimes N}| M_N)}{{\overline{{\mathcal {E}}}}(\rho _*^{\otimes N}| M_N)}. \end{aligned}$$

By Theorem 5.6 and Corollary 5.9, we can pass to the limit in the denominator to obtain

$$\begin{aligned} \lim _{N\rightarrow \infty }{\overline{{\mathcal {E}}}}(\rho _*^{\otimes N}| M_N)=E^{MF}[\rho _*]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}>0. \end{aligned}$$

Thus, we have that for N large enough

$$\begin{aligned} \lambda _{N}^{{{\,\textrm{LSI}\,}}} \le \frac{2}{E^{MF}[\rho _*]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}} {\overline{{\mathcal {I}}}}(\rho _*^{\otimes N}| M_N)\,. \end{aligned}$$

The desired bound

$$\begin{aligned} \lambda _{N}^{{{\,\textrm{LSI}\,}}}\le \frac{C}{N} \end{aligned}$$

follows from the decay estimate for the Fisher information proved in Lemma 7.1. $\square$

Lemma 7.1

Under Assumptions 2.1 and 2.2, assume that $\rho _*$ is a critical point of the mean field free energy $E^{MF}$, then we have the following bound

$$\begin{aligned} {\mathcal {I}}(\rho _*^{\otimes N}|M_N)= & {} \left( 1-\frac{1}{N}\right) \int _{\Omega } \left( |\nabla _1 W|^2\star \rho _*(x_1)-|\nabla _1 W\star \rho _*(x_1)|^2\right) \rho _*(x_1)\;\textrm{d}{x_1}\\{} & {} +\frac{1}{N}\int |\nabla _1 W\star \rho _*(x_1)|^2\rho _*(x_1)\textrm{d}{x_1}\\{} & {} \le C\,. \end{aligned}$$

Proof of Lemma 7.1

We start by expanding ${\mathcal {I}}(\rho _*^{\otimes N}|M_N)$ as follows

$$\begin{aligned} {\mathcal {I}}(\rho _*^{\otimes N}|M_N)=&\int _{\Omega ^N} \left| \nabla \left( \log \rho _*^{\otimes N}+\beta \sum _i V(x_i)+\frac{\beta }{2N}\sum _{i,j}W(x_i,x_j) \right) \right| ^2\rho _*^{\otimes N}\;\textrm{d}{x}\\ =&\sum _i \int _{\Omega ^N} \left| \frac{\nabla \rho _*(x_i)}{\rho _*(x_i)}+\beta \nabla V(x_i)+\frac{\beta }{N}\sum _{j}\nabla _1 W(x_i,x_j) \right| ^2\rho _*^{\otimes N}\; \textrm{d}{x}\\ =&N \int _{\Omega ^N} \left| -\beta \nabla _1 W \star \rho _*(x_1)+\frac{\beta }{N}\sum _{j}\nabla _1 W(x_1,x_j) \right| ^2\rho _*^{\otimes N}\;\textrm{d}{x}\\ =&N\beta ^2 \int _{\Omega ^N} \left( |\nabla _1 W \star \rho _*(x_1)|^2-\frac{2}{N} \nabla _1W \star \rho _*(x_1) \cdot \sum _j \nabla _1W(x_1,x_j)\right. \\&\left. \qquad \qquad \qquad \qquad \qquad +\frac{1}{N^2}\sum _{j,k}\nabla _1W(x_1,x_j)\cdot \nabla _1W(x_1,x_k) \rho _*^{\otimes N}\right) \;\textrm{d}{x}, \end{aligned}$$

where we have used the symmetry (exchangeability) of the particle system to write the integrand in terms of the variable $x_1$ and the fact that $\rho _*$ is a critical point of the mean field energy $E^{MF}$ which itself implies that

$$\begin{aligned} \beta ^{-1}\log \rho _* +W\star \rho _*+V=C. \end{aligned}$$

Next, proceeding term by term, we notice the following cancellation (for simplicity, we assume that $W(x,x)=0$, otherwise we can change V by an additive constant such that this holds):

$$\begin{aligned}{} & {} \int _{\Omega ^N} |\nabla _1 W\star \rho _*(x_1)|^2\rho _*^{\otimes N}\;\textrm{d}{x}\\{} & {} \quad = \int _\Omega |\nabla _1 W\star \rho _*(x_1)|^2\rho _*(x_1)\;\textrm{d}{x_1}, \\{} & {} \qquad -\int _{\Omega ^N} \frac{2}{N} \nabla _1 W\star \rho _*(x_1) \cdot \sum _j \nabla _1 W(x_1,x_j)\rho _*^{\otimes N}\;\textrm{d}{x}\\{} & {} \quad =-\left( 2-\frac{2}{N}\right) \int _\Omega |\nabla _1W\star \rho _*(x_1)|^2\rho _*(x_1)\;\textrm{d}{x_1}, \end{aligned}$$

and

$$\begin{aligned}&\int _{\Omega ^N} \frac{1}{N^2}\sum _{j,k}\nabla _1W(x_1,x_j)\cdot \nabla _1W(x_1,x_k) \rho _*^{\otimes N}\;\textrm{d}{x}\\&\quad =\frac{(N-1)(N-2)}{N^2}\int _\Omega |\nabla _1W\star \rho _*(x_1)|^2\rho _*(x_1)\;\textrm{d}{x_1} \\&\qquad +\frac{N-1}{N^2}\int |\nabla _1 W|^2\star \rho _*(x_1)\rho _*(x_1)\textrm{d}{x_1} \, . \end{aligned}$$

Putting the previous identities together, we obtain

$$\begin{aligned} {\mathcal {I}}(\rho _\beta ^{\otimes N}|M_N)=&\left( 1-\frac{1}{N}\right) \int _{\Omega } \left( |\nabla _1 W|^2\star \rho _*(x_1)-|\nabla _1 W\star \rho _*(x_1)|^2\right) \rho _*(x_1)\;\textrm{d}{x_1}\\ {}&+\frac{1}{N}\int |\nabla _1 W\star \rho _*(x_1)|^2\rho _*(x_1)\textrm{d}{x_1} \, . \end{aligned}$$

Finally, the second inequality in the statement follows from applying Jensen’s inequality to obtain

$$\begin{aligned} |\nabla _1 W|^2\star \rho _*(x)\ge |\nabla _1 W\star \rho _*(x)|^2\qquad \text{ for } \text{ every } x \in \Omega \text{. } \end{aligned}$$

The final bound follows from the assumption that W grows at most polynomially (cf. Assumption 2.2) and the fact that all steady states have finite moments of every order by Proposition 4.1. $\square$

8 Proof of Theorem 2.8

Proof of Theorem 2.8

We prove the statement of the theorem by contradiction. To this end, we assume that there exists a sequence $N_i\rightarrow \infty$ and a sequence of times $t_i>0$

$$\begin{aligned} 0<t_{i}<\frac{2}{\lambda ^\infty _{{{\,\textrm{LSI}\,}}}}\log ((E^{N_i}[\rho _{\textrm{in}}^{\otimes N_i}]-E^{N_i}[M_{N_i}])/\varepsilon ) \end{aligned}$$

such that

$$\begin{aligned} \overline{{\mathcal {E}}}(\rho ^{N_i}(t_i)|M_{N_i})>\max (\varepsilon , e^{-\frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty t_i}{2}}(E^{N_i}[\rho _{\textrm{in}}^{\otimes N_i}]-E^{N_i}[M_{N_i}]). \end{aligned}$$

Using the finite energy assumption on the initial condition (2.9), and Assumptions 2.1 and 2.2 which imply that $E^N$ is uniformly bounded below, we have that

$$\begin{aligned} \sup _i t_i\le \sup _{i}\frac{2}{\lambda ^\infty _{LSI}}\log ((E^{N_i}[\rho _{\textrm{in}}^{\otimes N_i}]-E^{N_i}[M_{N_i}])/\varepsilon )=:T(\varepsilon )<\infty . \end{aligned}$$

(8.1)

By the relative entropy dissipation estimate (2.3), we obtain

$$\begin{aligned} \overline{{\mathcal {E}}}(\rho ^{N_i}(t_i)|M_{N_i})>e^{-\frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty t_i}{2}}(E^{N_i}[\rho _{\textrm{in}}^{\otimes N_i}]-E^{N_i}[M_{N_i}]) \end{aligned}$$

which implies that there exists at least one $s_i\in (0,t_i)$ such that

$$\begin{aligned} \frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})}{\overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})}<\frac{\lambda _{{{\,\textrm{LSI}\,}}}^\infty }{2}. \end{aligned}$$

The contradiction will arise if we can show that

$$\begin{aligned} \liminf _{i\rightarrow \infty } \frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})}{\overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})}\ge \lambda ^\infty _{{{\,\textrm{LSI}\,}}}=\inf _{\rho \notin {\mathcal {K}}} \frac{D(\rho )}{E^{MF}[\rho ]-\inf _{{\mathcal {P}}(\Omega )} E^{MF}}. \end{aligned}$$

First, we consider the case when

$$\begin{aligned} \liminf _{i\rightarrow \infty }\overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})=\infty \,. \end{aligned}$$

By using the monotonicity of the relative entropy (2.3) and the finite energy assumption in the statement of the theorem, we obtain

$$\begin{aligned} \overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})\le \overline{{\mathcal {E}}}(\rho _{\textrm{in}}^{\otimes N_i}|M_{N_i})= E^{MF}[\rho _{\textrm{in}}]-E^N[M_N]<\infty . \end{aligned}$$

Hence, we can conclude

$$\begin{aligned} \liminf _{i\rightarrow \infty } \frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})}{\overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})}=\infty >\lambda ^\infty _{{{\,\textrm{LSI}\,}}}. \end{aligned}$$

Therefore, we can assume that up to a subsequence, which we do not relabel,

$$\begin{aligned} \sup _i \overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})<\infty . \end{aligned}$$

By the bounded higher moment hypothesis in (2.9), the uniform boundedness of $s_i$ (8.1), and the propagation of moments along the flow for K-convex potentials [10], we have that $\rho ^{N_i}(s_i)$ has uniformly bounded moments of order $2+\delta$. By Proposition 5.5, we obtain that there exists $P_*\in {\mathcal {P}}({\mathcal {P}}({\mathbb {R}}^d))$, such that up to a (not relabeled) subsequence, $\rho ^{N_i}(s_i)\rightarrow P_*$ in the sense of Definition 5.4. By the HWI inequality Theorem 5.8 and Corollary 5.9, we obtain the strong convergence in the relative entropy term, which yields

$$\begin{aligned} \varepsilon \le \lim _{i\rightarrow \infty } \overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})= \int _{{\mathcal {P}}({\mathbb {R}}^d)} \left( E^{MF}[\rho ]-\inf E^{MF} \right) \;\textrm{d}{P_*}(\rho ). \end{aligned}$$

Combining this limit with the $\liminf$-inequality of Theorem 5.6 for the dissipation we obtain that

$$\begin{aligned} \liminf _{i\rightarrow \infty } \frac{\beta ^{-1}\overline{{\mathcal {I}}}(\rho ^{N_i}(s_i)|M_{N_i})}{\overline{{\mathcal {E}}}(\rho ^{N_i}(s_i)|M_{N_i})}\ge \frac{\int _{{\mathcal {P}}({\mathbb {R}}^d)} D(\rho ) \;\textrm{d}{P_*}(\rho )}{\int _{{\mathcal {P}}({\mathbb {R}}^d)} E^{MF}[\rho ]-\inf E^{MF} \;\textrm{d}{P_*}(\rho )}\ge \lambda ^\infty _{{{\,\textrm{LSI}\,}}}, \end{aligned}$$

where the last inequality follows from the point-wise inequality

$$\begin{aligned} D(\rho )\ge \lambda ^\infty _{{{\,\textrm{LSI}\,}}} (E^{MF}[\rho ]-\inf E^{MF}) \,. \end{aligned}$$

This is the desired contradiction and the result now follows. $\square$

9 Proof of Theorem 2.10

Proof of Theorem 2.10

The fact that there are no non-minimizing critical points follows from the non-degeneracy $\liminf \lambda ^N_{LSI}>0$ and Theorem 2.6. The uniqueness of the minimiser in the limit follows from applying the Talagrand inequality (2.13), which states that the energy grows quadratically around the Gibbs measure $M_N$. We take $\rho _1$ and $\rho _2$, two minimisers of $E^{MF}$, and show that they must coincide. By the triangle and Talangrand inequality, we have

$$\begin{aligned} d^2_2(\rho _1,\rho _2)={\overline{d}}^2_2(\rho _1^{\otimes N},\rho _2^{\otimes N})&\le 2{\overline{d}}^2_2(\rho _1^{\otimes N},M_N)+2{\overline{d}}^2_2(M_N,\rho _2^{\otimes N})\\&\le \frac{4}{\lambda ^N_{{{\,\textrm{LSI}\,}}}}(E^{MF}[\rho _1]+E^{MF}[\rho _2]-2E^N[M_N]). \end{aligned}$$

The fact that $\rho _1$ is equal to $\rho _2$ follows from taking the limit in the previous inequality, using the hypothesis that $\limsup _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$, and Corollary 5.9 to obtain

$$\begin{aligned} \lim _{N\rightarrow \infty }E^N[M_N]=E^{MF}[\rho _1]=E^{MF}[\rho _2]=\inf _{{\mathcal {P}}(\Omega )} E^{MF}. \end{aligned}$$

The quantitative convergence of $M_N$ to $\rho _\beta$, follows from the bound in Lemma 9.1. $\square$

Lemma 9.1

Under Assumptions 2.1 and 2.2, assume that $\liminf _{N\rightarrow \infty }\lambda _{{{\,\textrm{LSI}\,}}}^N=:\lambda ^\infty >0$. Consider $M_N$ the N particle Gibbs measure and $\rho _\beta$ the unique minimiser of the mean field energy. Then, for N large enough,

$$\begin{aligned} {\overline{d}}_2(\rho _\beta ^{\otimes N}, M_N)\le \frac{2}{\lambda ^\infty }\frac{\displaystyle \int _\Omega |\nabla _1 W|^2\star \rho _\beta \rho _\beta \;\textrm{d}{x}}{\sqrt{N}}\le \frac{C}{\sqrt{N}}. \end{aligned}$$

Proof of Lemma 9.1

Using the Talagrand and log Sobolev inequality, we have for N large enough

$$\begin{aligned} {\overline{d}}^2_2(\rho _\beta ^{\otimes N}, M_N)\le \frac{2}{\lambda _{{{\,\textrm{LSI}\,}}}^N} \frac{{\mathcal {E}}(\rho _\beta ^{\otimes N}|M_N)}{N}\le \frac{2}{(\lambda _{{{\,\textrm{LSI}\,}}}^N)^2}\frac{{\mathcal {I}}(\rho _\beta ^{\otimes N}|M_N)}{N}\le \frac{4}{(\lambda ^\infty )^2} \frac{{\mathcal {I}}(\rho _\beta ^{\otimes N}|M_N)}{N}. \end{aligned}$$

The result now follows from bounding the Fisher information using Lemma 7.1. $\square$

10 Proof of Theorem 2.12

We start by revisiting the classical propagation of chaos results [47, 64] by using a convexity approach based on the 2-Wasserstein distance.

Theorem 10.1

Under Assumptions 2.1 and 2.2, if $K_V+K_W(1-1/N)\ne 0$, then

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le \frac{1-e^{-\frac{K_V+K_W(1-1/N)}{2}t}}{K_V+K_W(1-1/N)}\left( \frac{\sup _{s\in [0,t]}\left( \int _\Omega |\nabla _1 W|^2\star \rho (s)\rho (s)\;\textrm{d}{x}\right) ^{1/2}}{N^{1/2}}\right) , \nonumber \\ \end{aligned}$$

(10.1)

else if $K_V+K_W(1-1/N)= 0$, then

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le \frac{t}{2}\left( \frac{\sup _{s\in [0,t]}\left( \int _\Omega |\nabla _1 W|^2\star \rho (s)\rho (s)\;\textrm{d}{x}\right) ^{1/2}}{N^{1/2}}\right) . \end{aligned}$$

(10.2)

Proof of Theorem 10.1

Using [1, Theorem 8.4.7], we differentiate the 2-Wasserstein distance between $\rho ^N$ and $\rho ^{\otimes N}$ along their respective flows (3.1) and (3.3), to obtain

$$\begin{aligned} \frac{\textrm{d}{}}{\textrm{d}{t}}{\overline{d}}_2^2(\rho ^N,\rho ^{\otimes N})&=-\frac{1}{N}\int _{\Omega ^N\times \Omega ^N} (x-y)\cdot \bigg (\nabla _x\left( \beta ^{-1}\log \rho ^N(x)+ H_N(x)\right) \nonumber \\&\qquad -\nabla _y\left( \sum _{i=1}^N\beta ^{-1}\log \rho (y_i)+V(y_i)+ W\star \rho (y_i)\right) \bigg )\;\textrm{d}{\Pi }(x,y), \end{aligned}$$

(10.3)

where $\Pi \in {\mathcal {P}}(\Omega ^N\times \Omega ^N)$ denotes the optimal transport plan between $\rho ^N$ and $\rho ^{\otimes N}$. The convexity along 2-Wasserstein geodesics of the entropy functional as discussed in [49] implies that (cf. [1, Section 10.1.1])

$$\begin{aligned} \int _{\Omega ^N\times \Omega ^N} (x-y)\cdot (\beta ^{-1}\nabla _x\log \rho ^N(x)-\beta ^{-1}\nabla _y\log \rho ^{\otimes N}(y))\;\textrm{d}{\Pi }(x,y)\ge 0, \end{aligned}$$

(10.4)

where we have used that $\nabla \log \rho ^N$ and $\nabla \log \rho ^{\otimes N}$ are in the sub-differential of the entropy at $\rho ^N$ and $\rho ^{\otimes N}$, respectively (cf. [1, Theorem 10.4.6]).

Applying inequality (10.4) to (10.3), we obtain

$$\begin{aligned}&\frac{\textrm{d}{}}{\textrm{d}{t}}{\overline{d}}_2^2(\rho ^N,\rho ^{\otimes N})\le -\frac{1}{N}\int _{\Omega ^N\times \Omega ^N} (x-y)\cdot \bigg (\nabla _xH_N(x)-\nabla _yH_N(y)\nonumber \\&\qquad +\nabla _y\left( \frac{1}{2N} \sum _{i,j=1}^NW(y_i,y_j)-\sum _{i=1}^NW\star \rho (y_i)\right) \bigg )\;\textrm{d}{\Pi }(x,y)\nonumber \\&\quad \le -(K_V+K_W(1-1/N))\underbrace{\frac{1}{N}\int _{\Omega ^N\times \Omega ^N} |x-y|^2\;\textrm{d}{\Pi }(x,y)}_{={\overline{d}}_2^2(\rho ^N,\rho ^{\otimes N})}\nonumber \\&\qquad -\underbrace{\frac{1}{N}\int _{\Omega ^N\times \Omega ^N}(x-y)\cdot \nabla _y \bigg (\frac{1}{2N}\sum _{i=1}^N\sum _{j=1}^N W(y_i,y_j)-\sum _{i=1}^N W\star \rho (y_i)\bigg )\;\textrm{d}{\Pi }(x,y)}_{{\mathcal {R}}}, \end{aligned}$$

(10.5)

where the last inequality follows from the convexity hypothesis on the potentials (cf. Assumptions 2.1 and 2.2). To estimate the second term ${\mathcal {R}}$, we employ Cauchy-Schwarz inequality and use the fact that $\Pi$ is the optimal transference plan to obtain

$$\begin{aligned} {\mathcal {R}} \le {\overline{d}}_2(\rho ^N,\rho ^{\otimes N})\left( \underbrace{\frac{1}{N}\int _{\Omega ^N}\left| \nabla \left( \frac{1}{2N}\sum _{i=1}^N\sum _{j=1}^N W(y_i,y_j)-\sum _{i=1}^N W\star \rho (y_i)\right) \right| ^2\;\textrm{d}{\rho }^{\otimes N}}_{I} \right) ^{1/2} \end{aligned}$$

(10.6)

Expanding the square, using the symmetry of the underlying system and the fact that $W(y,y)=0$, we obtain

$$\begin{aligned} I&=\int _{\Omega ^N}\left| \frac{1}{N}\sum _{j=2}^N\nabla _1 W(y_1,y_j)-\nabla _1 W\star \rho (y_1)\right| ^2\;\textrm{d}{\rho }^{\otimes N}\\&=\int _{\Omega ^N}\underbrace{\frac{1}{N^2}\sum _{j=2}^N\sum _{k=2}^N\nabla _1 W(y_1,y_j)\nabla _1 W(y_1,y_k)}_{A}-\underbrace{\frac{2}{N}\sum _{j=2}^N\nabla _1 W(y_1,y_j)\nabla _1W\star \rho (y_1) }_{B}\\&\qquad \qquad +(\nabla _1 W\star \rho (y_1))^2\;\textrm{d}{\rho }^{\otimes N}. \end{aligned}$$

Going term by term, we have

$$\begin{aligned} A= & {} \frac{(N-1)(N-2)}{N^2}\int _\Omega (\nabla _1 W\star \rho (y_1))^2\;\textrm{d}{\rho }(y_1) +\frac{(N-1)}{N^2}\int _\Omega |\nabla _1 W|^2\star \rho (y_1)\;\textrm{d}{\rho }(y_1), \\ B= & {} -2\frac{N-1}{N}\int _\Omega (\nabla _1 W\star \rho (y_1))^2\;\textrm{d}{\rho }(y_1). \end{aligned}$$

Using these identities, we are left with

$$\begin{aligned} I&=\frac{1}{N}\left( 1-\frac{1}{N}\right) \int _\Omega |\nabla _1 W|^2\star \rho (y_1)-(\nabla _1 W\star \rho (y_1))^2\;\textrm{d}{\rho }(y_1)\\&\quad +\frac{1}{N^2}\int _{\Omega }(\nabla _1 W\star \rho (y_1))^2\;\textrm{d}{\rho }(y_1)\\&\le \frac{1}{N} \int _\Omega |\nabla _1 W|^2\star \rho (y_1)\;\textrm{d}{\rho }(y_1), \end{aligned}$$

where the last inequality follows from Jensen’s inequality. Replacing the previous equation in (10.6), combined with (10.5), we obtain

$$\begin{aligned} \frac{\textrm{d}{}}{\textrm{d}{t}}{\overline{d}}_2^2(\rho ^N,\rho ^{\otimes N})\le&-(K_V+K_W(1-1/N)) {\overline{d}}_2^2(\rho ^N,\rho ^{\otimes N})\\&+{\overline{d}}_2(\rho ^N,\rho ^{\otimes N})\frac{\left( \int _\Omega |\nabla _1 W|^2\star \rho \,\rho \;\textrm{d}{x}\right) ^{1/2}}{N^{1/2}}. \end{aligned}$$

The estimates (10.1) and (10.2) now follow from Grönwall’s inequality. $\square$

We are now ready to prove Theorem 2.12.

Proof of Theorem 2.12

Using the uniform integrability assumption on the gradient of W (2.10), the estimates of Theorem 10.1 simplify to

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le \frac{C}{N^{1/2}} {\left\{ \begin{array}{ll} \frac{1-e^{t(K_V+K_W(1-1/N))/2}}{K_V+K_W(1-1/N)}&{}\hbox { if}\ K_V+K_W(1-1/N)\ge 0\\ \frac{t}{2}&{}\hbox { if}\ K_V+K_W(1-1/N)= 0\\ \frac{e^{t|K_V+K_W(1-1/N)|/2}-1}{|K_V+K_W(1-1/N)|}&{}\text{ if }\ K_V+K_W(1-1/N)\le 0 \end{array}\right. }\nonumber \\ \end{aligned}$$

(10.7)

Next, we derive a competing estimate by employing the triangle inequality and the long time behavior of the flows. More specifically,

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le&\;{\overline{d}}_2(\rho ^N(t),M_N)+{\overline{d}}_2(M_N,\rho _\beta ^{\otimes N})+{\overline{d}}_2(\rho _\beta ^{\otimes N},\rho ^{\otimes N}(t)) \nonumber \\ =&\; {\overline{d}}_2(\rho ^N(t),M_N)+{\overline{d}}_2(M_N,\rho _\beta ^{\otimes N})+d_2(\rho _\beta ,\rho (t)) \, . \end{aligned}$$

(10.8)

For the first term, we use the Talagrand inequality (2.13)

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),M_N)\le \left( \frac{2}{\lambda _{{{\,\textrm{LSI}\,}}}^N}\right) ^{1/2}\overline{{\mathcal {E}}}^{1/2}(\rho ^N(t)|M_N). \end{aligned}$$

By the log Sobolev inequality we obtain exponential contraction of the relative entropy

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),M_N)\le e^{-\frac{\lambda _{{{\,\textrm{LSI}\,}}}^N}{2} t}\left( \frac{2}{\lambda _{{{\,\textrm{LSI}\,}}}^N}\right) ^{1/2}\overline{{\mathcal {E}}}^{1/2}(\rho _{\textrm{in}}^{\otimes N}(t)|M_N) \le Ce^{-\frac{\lambda _\infty }{4} t}, \end{aligned}$$

(10.9)

where in the last equality we have used the hypothesis $\rho _{\textrm{in}}$ has finite energy and that the log Sobolev constant does not degenerate.

For the second term, we use Lemma 9.1 to obtain

$$\begin{aligned} {\overline{d}}_2(\rho _\beta ^{\otimes N}, M_N)\le \frac{C}{\sqrt{N}}. \end{aligned}$$

(10.10)

For the third term, we use the limiting Talgrand inequality and the limiting log Sobolev inequality to obtain the exponential contraction estimate

$$\begin{aligned} d_2(\rho (t),\rho _\beta )&\le \left( \frac{2}{\lambda _\infty }\right) ^{1/2}(E^{MF}[\rho (t)]-E^{MF}[\rho _\beta ])^{1/2}\nonumber \\&\le \left( \frac{2}{\lambda _\infty }\right) ^{1/2}e^{-\frac{\lambda _\infty }{2} t}(E^{MF}[\rho _{\textrm{in}}]-E^{MF}[\rho _\beta ])^{1/2}\nonumber \\&\le Ce^{-\frac{\lambda _\infty }{2} t}. \end{aligned}$$

(10.11)

Combining (10.8) with (10.9), (10.10) and (10.11) we obtain the estimate

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le C\left( e^{-\frac{\lambda _\infty }{4}t}+\frac{1}{\sqrt{N}}\right) . \end{aligned}$$

(10.12)

The result now follows from interpolating the estimates (10.7) and (10.12). In the case, $K_V+K_W(1-1/N)>0$ the desired estimate follows directly from (10.7). For $K_-:=K_V+K_W(1-1/N)<0$, we consider the distinguished time scale $T_N:= \log N^\gamma$, for some $\gamma >0$ to be chosen in terms of $K_-$. Applying (10.12), we obtain

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t)) \le C\left( N^{-\gamma \frac{\lambda _\infty }{4}}+N^{-\frac{1}{2}}\right) \qquad \text{ for }\ t>T_N. \end{aligned}$$

For $t < T_N$, we apply (10.7)1 to obtain

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t)) \le CN^{-\frac{1+\gamma K_-}{2}} \, . \end{aligned}$$

Choosing

$$\begin{aligned} \gamma =\left( \frac{\lambda _\infty }{2}-K_-\right) ^{-1}, \end{aligned}$$

we obtain that for every $t\in (0,\infty )$

$$\begin{aligned} {\overline{d}}_2(\rho ^N(t),\rho ^{\otimes N}(t))\le \frac{C}{N^\theta } \end{aligned}$$

is satisfied with

$$\begin{aligned} \theta =\frac{1}{2}\frac{\lambda _\infty }{\lambda _\infty -2K_-}. \end{aligned}$$

$\square$

11 Proof of Theorem 2.20

As mentioned earlier, our proof of Theorem 2.20 will rely on the two-scale approach to log Sobolev inequalities introduced in [52] and discussed further in [32], see also [45]. Before we introduce the main result of [52], we introduce some preliminary notions.

Definition 11.1

(Conditional measures). Given a probability measure $\mu _N \in {\mathcal {P}}(\Omega ^N)$ we define the conditional measures $\mu _{N,i}, i \in {1,\dots ,N}$ as the family of measures indexed by $x_j,\, j \ne i$ such that for all $\varphi \in C_b(\Omega ^N)$

$$\begin{aligned} \int _{\Omega ^N}\varphi \textrm{d}{\mu _N} = \int _{\Omega ^{N-1}} \int _{\Omega } \varphi \textrm{d}{\mu _{N,i}} \textrm{d}{\mu _{N\setminus \left\{ i\right\} }} \, , \end{aligned}$$

where $\mu _{N\setminus \left\{ i\right\} }$ is the marginal of $\mu _N$ obtained by integrating out $x_i \in \Omega$.

We can now the state the result of interest.

Theorem 11.2

([52, Theorem 1]) Let $\Omega$ be a smooth, connected, and complete Riemannian manifold and consider the Gibbs measure $\mu _N$

$$\begin{aligned} \mu _N(\textrm{d}{x})= Z_{N}^{-1}e^{-\beta H_N} \textrm{d}{x} \, , \end{aligned}$$

where $\textrm{d}{x}$ is the Riemannian volume measure and $H_N: \Omega ^N \rightarrow {\mathbb {R}}$ is a smooth Hamiltonian. Assume there exists some constants $\kappa _{ij}$, such that for all $i \ne j$

$$\begin{aligned} \Vert D^2_{x_i x_j} H_N\Vert \le \kappa _{ij} \qquad \text{ for } \text{ all }\ x \in \Omega ^N , \end{aligned}$$

where $\Vert \cdot \Vert$ is the operator norm of $D^2_{x_ix_j}H_N$. Furthermore, assume that the conditional measures $\mu _{N,i}$ satisfy the log Sobolev inequality with uniform constant $\lambda _{{{\,\textrm{LSI}\,}}}^{N,i}$ for all ${\hat{x}} \in \Omega ^{N-1}$. Consider the matrix $A \in {\mathbb {R}}^{N \times N}$ with entries $A_{ii}=\lambda ^{N,i}_{{{\,\textrm{LSI}\,}}}$ and $A_{ij}=-\beta \kappa _{ij}$; if

$$\begin{aligned} A \ge C I^{N\times N} \, , \end{aligned}$$

then the measure $\mu _N$ satisfies a log Sobolev inequality with constant C.

Relying on Theorem 11.2, we present now the proof of Theorem 2.20.

Proof of Theorem 2.20

We note first that from the Definition 11.1, the conditional measure $M_{N,i}$ of $M_N$ can be expressed as

$$\begin{aligned} M_{N,i}(\textrm{d}{x_i})=&M_N(\textrm{d}{x_i}| x_1, \dots ,x_{i-1} ,x_{i+1},\dots , x_N)=\frac{M_N}{(M_N)_{N\setminus \left\{ i\right\} }} \, , \end{aligned}$$

where $(M_N)_{N\setminus \left\{ i\right\} }$ is the marginal of $M_N$ obtained by integrating out $x_i$. We are thus left with

$$\begin{aligned} M_{N,i}&= \frac{ \exp \left( -\beta (V(x_i) + \frac{1}{N}\sum _{j=1}^N W(x_i,x_j) ) -\beta (\sum _{j\ne i ,j=1}^N V(x_j) +\frac{1}{2N}\sum _{j,k=1,j,k\ne i} W(x_j,x_k))\right) }{\int _{\Omega } \exp \left( -\beta H_N\right) \textrm{d}{x_i}}\\&=Z_{N,i}^{-1} \exp \left( -\beta (V(x_i) + \frac{1}{N}\sum _{j=1}^N W(x_i,x_j) )\right) , \end{aligned}$$

where

$$\begin{aligned} Z_{N,i}=\int _{\Omega } \exp \left( -\beta (V(x_i) + \frac{1}{N}\sum _{j=1}^N W(x_i,x_j) )\right) \textrm{d}{x_i} \, . \end{aligned}$$

We now assert that the conditional measure $M_{N,i}$ satisfies a log Sobolev inequality. We first treat the case in which $\Omega$ is compact, e.g. Theorem 2.20 (a). By the Holley–Stroock perturbation lemma [3, Proposition 5.1.6], we have that

$$\begin{aligned} \lambda ^{N,i}_{{{\,\textrm{LSI}\,}}}\ge e^{- 2 \beta (\Vert W\Vert _{{L}^\infty (\Omega ^2)} + \Vert V\Vert _{{L}^\infty (\Omega ^)})} \lambda _{{{\,\textrm{LSI}\,}}}^\Omega \, , \end{aligned}$$

for all $x_j, j\ne i, j=1,\dots ,N$ and where $\lambda _{{{\,\textrm{LSI}\,}}}^\Omega$ is the optimal log Sobolev constant of the Lebesgue measure on $\Omega$.

We remark that because of the exchangeability of the underlying particle system, we have that $\lambda ^{N,i}_{{{\,\textrm{LSI}\,}}}=\lambda ^{N,j}_{{{\,\textrm{LSI}\,}}}$ for all $i,j = 1,\dots ,N$.

Note now that

$$\begin{aligned} D^2_{x_i x_j}H_N(x_1,\dots ,x_N) = \frac{1}{N}D^2_{x_i x_j} W(x_i,x_j) \, . \end{aligned}$$

Using the hypothesis that $W\in W^{2,\infty }(\Omega ^2)$, we can bound

$$\begin{aligned} \Vert D^2_{x_i x_j}H_N\Vert _{{L}^\infty (\Omega ^N)} \le \frac{1}{N} \Vert D^2_{x y} W\Vert _{{L}^\infty (\Omega ^2)} =: \kappa _{ij} \, , \end{aligned}$$

for all $i,j=1,\dots ,N$. We will show that the matrix $A \in {\mathbb {R}}^{N \times N}$ from Theorem 11.2 is positive definite, by showing that it is diagonally dominant. In fact, for $\beta$ sufficiently small we have that

$$\begin{aligned} A_{ii}-\sum _{j\ne i}|A_{ij}|\ge e^{- 2 \beta (\Vert W\Vert _{{L}^\infty (\Omega ^2)} + \Vert V\Vert _{{L}^\infty (\Omega ^)})} \lambda _{{{\,\textrm{LSI}\,}}}^\Omega -\beta \frac{N-1}{N} \Vert D^2_{x y} W\Vert _{{L}^\infty (\Omega ^2)}>c >0\, , \end{aligned}$$

holds true for all N with the constant c independent of N. Applying Theorem 11.2, Theorem 2.20 (a) now follows.

For the proof of Theorem 2.20 (b) we can apply essentially the same perturbative argument as before but now around the $1-$particle measure $Z_{V}^{-1}e^{-V} \textrm{d}{x}$. For $\epsilon$ sufficiently small, we obtain that the analogous bound

$$\begin{aligned} A_{ii}-\sum _{j\ne i}|A_{ij}|\ge e^{- 2\epsilon \beta \Vert W\Vert _{{L}^\infty (\Omega ^2)} } \lambda _{{{\,\textrm{LSI}\,}}}^V-\epsilon \beta \frac{N-1}{N} \Vert D^2_{x y} W\Vert _{{L}^\infty (\Omega ^2)}>c >0\, \end{aligned}$$

holds true for all N with the constant c independent of N. $\square$

12 Proof of Theorem 2.16

To simplify the computations in this section, we will take the following definition of the negative Sobolev norm $H^{-s}_0({\mathbb {T}}^d)$ of mean-zero distributions is given by

$$\begin{aligned} \Vert h\Vert _{H^{-s}({\mathbb {T}}^d)}^2:=\sum _{j\in {\mathbb {N}}}|\langle h, \phi _j \rangle |^2, \end{aligned}$$

(12.1)

where $(\phi _j)_{j\in {\mathbb {N}}}$ is a given a smooth orthonormal basis for the Sobolev space $H^{s}_0({\mathbb {T}}^d)$ of mean zero functions.

We remark that Theorem 2.16 can also be proved when $\Omega = {\mathbb {R}}^d$, under appropriate assumptions on the confining and interaction potentials so that the Sobolev embedding theorems needed in the proof in the appropriate weighted spaces are satisfied. In particular, we can construct an appropriate orthonormal basis using the eigenfunctions of the linearised McKean-Vlasov operator around the stationary state in the weighted inner-product that symmetrizes this operator. See [55] for an application of this approach to the study of inference for McKean SDEs.

Lemma 12.1

(Law of large numbers). Assume that $\liminf _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$. Let $\mu ^{(N)}$ be the empirical measure associated to the N-particle Gibbs measure $M_N \in {\mathcal {P}}_{\textrm{sym}}(({\mathbb {T}}^d)^N)$. Then, for any $s>\frac{d+2}{2}$, there exists $C>0$ such that

$$\begin{aligned} {\mathbb {E}}_{M_N}\left[ *\right] {\Vert \mu ^{(N)}-\rho _\beta \Vert _{H^{-s}({\mathbb {T}}^d)}^2}\le \frac{C}{N} \,, \end{aligned}$$

where $\rho _\beta \in {\mathcal {P}}({\mathbb {T}}^d)$ is the unique critical point of the mean field energy $E^{MF}$.

Remark 12.2

Solutions to the linear SPDE (12.6) are supported in $H^{-s}$ with $s>d/2$, see Lemma 12.4. Hence, the Law of Large Numbers does not hold for any $H^{-s}$ with $s< d/2$.

Proof

We consider $\rho _\beta ^{(N)}$ the empirical measure associated to $\rho _\beta ^{\otimes N} \in {\mathcal {P}}_{\textrm{sym}}(({\mathbb {T}}^d)^N)$, i.e. $\rho _\beta ^{(N)}$ the probability-measure valued random variable defined as

$$\begin{aligned} \rho _\beta ^{(N)}=\frac{1}{N}\sum _{i=1}^N\delta _{X_i}\qquad \text{ such } \text{ that }\ (X_1,...,X_N)\ \text {are distributed according to} \rho _\beta ^{\otimes N} \,. \end{aligned}$$

By the triangle inequality we have that

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert \mu ^{(N)}-\rho _\beta \Vert ^2_{H^{-s}({\mathbb {T}}^d)}}\le 2\left( {\mathbb {E}}\left[ *\right] {\Vert \mu ^{(N)}-\rho _\beta ^{(N)}\Vert ^2_{H^{-s}({\mathbb {T}}^d)}} + {\mathbb {E}}\left[ *\right] {\Vert \rho _\beta ^{(N)}-\rho _\beta \Vert ^2_{H^{-s}({\mathbb {T}}^d)}}\right) \nonumber \\ \end{aligned}$$

(12.2)

We start by controlling the first term ${\mathbb {E}}\left[ *\right] {\Vert \mu ^{(N)}-\rho _\beta ^{(N)}\Vert ^2_{H^{-s}({\mathbb {T}}^d)}}$. We consider the optimal coupling between $\mu ^{(N)}$ and $\rho _\beta ^{(N)}$ such that

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {d_2^2(\mu ^{(N)},\rho _\beta ^{(N)})}={\mathfrak {D}}_2^2\left( {\hat{\mu }}^N,{\hat{\rho }}_\beta ^N\right) \,, \end{aligned}$$

where ${\hat{\mu }}^N=\textrm{Law}\left( \mu ^{(N)}\right) \in {\mathcal {P}}({\mathcal {P}}({\mathbb {T}}^d))$, ${\hat{\rho }}_\beta ^N=\textrm{Law} \left( \rho _\beta ^{(N)}\right) \in {\mathcal {P}}({\mathcal {P}}({\mathbb {T}}^d))$, and ${\mathfrak {D}}_2$ is the 2-Wassertein distance defined on the space of probability measures of the metric space $({\mathcal {P}}({\mathbb {T}}^d),d_2)$. Then by the isometry from Theorem 5.3, we obtain

$$\begin{aligned} {\mathfrak {D}}_2^2\left( {\hat{\mu }}^N,{\hat{\rho }}_\beta ^N\right) ={\overline{d}}_2^2(M_N,\rho _\beta ^{\otimes N})\le \frac{C}{N}, \end{aligned}$$

where we have used Lemma 9.1 and the fact that $\liminf _{N\rightarrow \infty }\lambda ^N_{{{\,\textrm{LSI}\,}}}>0$ for the last inequality. Next, we use the bound $d_2^2(\mu ^{(N)},\rho _\beta ^{(N)})\ge d_1^2(\mu ^{(N)},\rho _\beta ^{(N)})$, and Kantorovich’s duality [68, Chapter 5] to obtain

$$\begin{aligned} d_2^2(\mu ^{(N)},\rho _\beta ^{(N)})\ge \sup _{\Vert \varphi \Vert _{W_0^{1,\infty }({\mathbb {T}}^d)}\le 1} \int \phi \textrm{d}{\mu ^{(N)}(x)}-\int \phi \textrm{d}{\rho _\beta ^{(N)}(x)}. \end{aligned}$$

Using that $s>d/2+1$, we can use general Sobolev inequalities, see for instance ( [26, Chapter 5]), to get that there exists a dimensional constant c that $\Vert \varphi \Vert _{W_0^{1,\infty }({\mathbb {T}}^d)}\le c \Vert \varphi \Vert _{H^s({\mathbb {T}}^d)}$. This implies the inequality

$$\begin{aligned} d_2^2(\mu ^{(N)},\rho _\beta ^{(N)})\ge \frac{1}{c} \Vert \mu ^{(N)}-\rho _\beta ^{(N)}\Vert ^2_{H^{-s}({\mathbb {T}}^d)} . \end{aligned}$$

Combining the previous three expressions, we obtain the first desired bound

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert \mu ^{(N)}-\rho _\beta ^{(N)}\Vert ^2_{H^{-s}({\mathbb {T}}^d)}}\le \frac{C}{N}. \end{aligned}$$

(12.3)

Next, we bound ${\mathbb {E}}\left[ *\right] {\Vert \rho _\beta ^{(N)}-\rho _\beta \Vert ^2_{H^{-s}({\mathbb {T}}^d)}}$. We take $\{\phi _j\}_{j=0}^\infty$ to be the orthonormal basis of $H^{s}_0({\mathbb {T}}^d)$ from (12.1). Expanding the square, we obtain

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert \rho _\beta ^{(N)}-\rho _\beta \Vert ^2_{H^{-s}({\mathbb {T}}^d)}}&={\mathbb {E}}\left[ *\right] {\sum _{j=1}^\infty |\langle \rho _\beta ^{(N)}-\rho _\beta ,\phi _j\rangle |^2}\\&=\sum _{j=1}^\infty {\mathbb {E}}\left[ *\right] {\left| \frac{1}{N}\sum _{i=1}^N\phi _j(X_i)- \int \phi _j\rho _\beta \;\textrm{d}{x}\right| ^2}\\&=\frac{1}{N}\sum _{j=1}^\infty \int \phi _j^2\rho _\beta \;\textrm{d}{x}-\frac{1}{N}\left( \int \phi _j\rho _\beta \;\textrm{d}{x}\right) ^2\\&\le \frac{\Vert \rho _\beta \Vert _{L^\infty ({\mathbb {T}}^d)}}{N}\sum _{j=1}^\infty \Vert \phi _j\Vert _{{L}^2({\mathbb {T}}^d)}^2. \end{aligned}$$

Noticing that $s>d/2$ implies that the embedding $H^{s}_0({\mathbb {T}}^d)\rightarrow {L}^2({\mathbb {T}}^d)$ is Hilbert–Schmidt, we can use the boundedness of $\rho _\beta$ to obtain

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert \rho _\beta ^{(N)}-\rho _\beta \Vert ^2_{H^{-s}({\mathbb {T}}^d)}}\le \frac{C}{N} \,. \end{aligned}$$

(12.4)

Combining (12.2) with (12.3) and (12.4), we obtain the desired conclusion. $\square$

Remark 12.3

An alternative proof of inequality (12.4) can be found in [37, Theorem 5.1].

We now consider the implications of having uniform control of the log Sobolev constant on the fluctuations of the stationary solutions to (2.1), i.e. solutions of (2.1) started at stationarity. To this end, we consider the empirical measure process $t \mapsto \mu ^{(N)}(t)$ defined by

$$\begin{aligned} \mu ^{(N)}(t):=\frac{1}{N} \sum _{i=1}^{N}\delta _{X_t^i}, \end{aligned}$$

where $X_t=(X_t^{1},\dots ,X_t^{N})$ is the solution to (2.1) started from the unique invariant Gibbs measure $M_N$. Our goal is to analyze the corresponding fluctuation process $t \mapsto \eta ^{N}(t)$ defined by

$$\begin{aligned} \eta ^{N}(t):=\sqrt{N}(\mu ^{(N)}(t)-\rho _{\beta }), \end{aligned}$$

where $\rho _{\beta }$ is, as in Lemma 12.1, the unique minimizer of $E^{MF}$. As a direct consequence of the estimates from Lemma 12.1 and using the fact that $\liminf _{N\rightarrow \infty }\lambda ^{N}_{LS}>0$, we have the uniform bound

$$\begin{aligned} \sup _{N,t}{\mathbb {E}}\left[ *\right] {\Vert \eta ^N(t)\Vert _{H^{-s}({\mathbb {T}}^d)}^2}<\infty \qquad \text{ for } \text{ any }\ s>d/2+1. \end{aligned}$$

(12.5)

In the sequel, we will use the above estimate together with the classical martingale method, c.f. [17, Chapter 8], to establish convergence in law as $N \rightarrow \infty$ of $\eta ^N$ to the stationary solution $\eta$ of the following linear SPDE

$$\begin{aligned} \partial _t\eta ={\mathcal {L}}_{\rho _\beta }\eta +\nabla \cdot (\sqrt{\rho _\beta }\xi ), \end{aligned}$$

(12.6)

where $\xi$ is a mean-zero space-time white noise on ${\mathbb {R}}_{+} \times {\mathbb {T}}^{d}$ and ${\mathcal {L}}_{\rho _\beta }$ is the linearisation of the McKean-Vlasov operator (3.3) around the unique invariant measure $\rho _\beta$ defined by

$$\begin{aligned} {\mathcal {L}}_{\rho _\beta }\psi =\beta ^{-1}\Delta \psi +\nabla \cdot (\nabla W\star \psi \,\rho _\beta )+\nabla \cdot (\nabla W\star \rho _\beta \,\psi )+\nabla \cdot (\nabla V\,\psi ). \end{aligned}$$

The SPDE (12.6) can be solved using classical methods, the three typical notions of solution being the mild, weak, and martingale formulations. As is typical, the martingale formulation is the most convenient for identifying the limiting law of a tight subsequence of $\eta ^N$, while the mild formulation provides a clearer picture of the uniqueness in law and hence the convergence in law of the full sequence.

Let U denote the closed mean-zero subspace of $L^{2}({\mathbb {T}}^{d};{\mathbb {T}}^{d})$ and $H:=H^{-s}({\mathbb {T}}^{d})$ for $s>\frac{d}{2}$. Let $({\mathcal {X}},{\mathcal {F}}, ({\mathcal {F}}_t)_{t \ge 0},{{\mathbb {P}}})$ be a stochastic basis, i.e a complete filtered probability space with a right continuous filtration endowed with an ${\mathcal {F}}_t$-adapted U-valued cylindrical Wiener process ${{\textbf {W}}}$ and let $\eta _{0}$ be an H-valued ${\mathcal {F}}_0$-measurable random variable independent of ${{\textbf {W}}}$. The mild formulation of (12.6) with initial condition $\eta _{0}$ involves stochastic integration in Hilbert spaces, c.f. [17, Chapter 4], which we quickly review for our specific case below. Let ${\textbf{L}}^{2}_{0}(U;H)$ denote the Hilbert–Schmidt operators from U to H equipped with the standard Hilbert–Schmidt norm $\Vert \cdot \Vert _{{\textbf{L}}_2^0(U;H)}$. Given $T>0$ and $\Phi \in L^{2}([0,T];{\textbf{L}}^{2}_{0}(U;H))$, the stochastic integral $[0,T]\ni t\mapsto \int _{0}^{t}\Phi (s)d {{\textbf {W}}}(s)$ is well defined as a continuous ${\mathcal {F}}_t$-martingale with trajectories in C([0, T]; H). We remind the reader that the relevance of ${\textbf{L}}^{2}_{0}(U;H)$ in this context is that the Itô isometry takes the following form

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\left\| \int _{0}^{t}\Phi (s)d {{\textbf {W}}}(s) \right\| _{H}^{2}}=\int _{0}^{t}\Vert \Phi (s)\Vert _{{\textbf{L}}^{2}_{0}(U;H) }^{2}\textrm{d}s. \end{aligned}$$

The mild solution $t \mapsto \eta ^{\infty }(t) \in H$ to (12.6) with initial condition $\eta _{0}$ is then given by the following stochastic convolution:

$$\begin{aligned} \eta ^\infty (t):=e^{t{\mathcal {L}}_{\rho _{\beta }}}\eta _{0}+\int _{0}^{t}e^{(t-s){\mathcal {L}}_{\rho _{\beta }} } \nabla \cdot \big (\sqrt{\rho _{\beta }}d{{\textbf {W}}}(s) \big ). \end{aligned}$$

(12.7)

Lemma 12.4

The mild solution (12.7) is well-defined as a stochastic process with trajectories in C([0, T]; H).

Proof

In light of our remarks in the preceding paragraph, it suffices to show that $s \mapsto \Phi (s)$ defined by $U \ni u \mapsto e^{(t-s){\mathcal {L}}_{\rho _{\beta }} }\nabla \cdot (\sqrt{\rho _{\beta }}u ) \in H$ belongs to $L^{2}( [0,T];{\textbf{L}}^{2}_{0}(U;H) )$. Given an orthornormal basis $\{e_{k}\}_{k=1}^{\infty }$ of U, using the definition of the Hilbert–Schmidt norm and integrating by parts leads to

$$\begin{aligned} \int _{0}^{T}\Vert \Phi (s)\Vert _{{\textbf{L}}^{2}_{0}(U;H) }^{2}\textrm{d}s&=\sum _{k=1}^{\infty }\int _{0}^{T}\Vert e^{(t-s){\mathcal {L}}_{\rho _{\beta }} }\nabla \cdot \big (\sqrt{\rho _{\beta }}e_{k}\big )\Vert _{H}^{2} \textrm{d}{s}\nonumber \\&=\sum _{j,k=1}^{\infty }\int _{0}^{T} \langle e_{k},\sqrt{\rho _{\beta } }\nabla e^{(t-s){\mathcal {L}}_{\rho _{\beta }}^{*} }\phi _{j} \rangle _{U}^{2}\textrm{d}s \nonumber \\&=\sum _{j=1}^{\infty } \int _{0}^{T} \Vert \sqrt{\rho _{\beta } } \nabla e^{(t-s){\mathcal {L}}_{\rho _{\beta }}^{*} }\phi _{j}\Vert _{U}^{2}\textrm{d}s, \end{aligned}$$

(12.8)

where in the first step we have used (12.1) for the definition of the $H^{-s}$ norm with $\{\phi _j\}_{j\in {\mathbb {N}}}$ any orthonormal basis of $H^s_0$, in the second step we have used the adjoint operator, and in the last step we used Parseval’s identity in U. Finally, we note that the coercivity hypothesis for ${\mathcal {L}}_{\rho _{\beta }}$ (see Lemma 12.8) implies that

$$\begin{aligned} \int _{0}^{t} \Vert \nabla e^{(t-s){\mathcal {L}}_{\rho _{\beta }}^{*} }\phi _{j}\Vert _{U}^{2}\textrm{d}{s} \le C \Vert \phi _{j}\Vert _{L^{2}({\mathbb {T}}^d)}^{2}. \end{aligned}$$

Combining this with (12.8) and using the fact that $\rho _{\beta } \in L^{\infty }({\mathbb {T}}^{d})$, yields

$$\begin{aligned} \int _{0}^{T}\Vert \Phi (s)\Vert _{{\textbf{L}}^{2}_{0}(U;H) }^{2} \textrm{d}{s} \le C\Vert \rho _\beta \Vert _{L^\infty ({\mathbb {T}}^d)} \sum _{j=1}^{\infty }\Vert \phi _{j}\Vert _{L^{2}({\mathbb {T}}^d)}^{2}. \end{aligned}$$

(12.9)

Since $s>\frac{d}{2}$, the embedding of $H^{s}_0({\mathbb {T}}^d)$ into $L^{2}({\mathbb {T}}^d)$ is Hilbert–Schmidt. Thus, the above series converges, completing the proof of the lemma. $\square$

Remark 12.5

We note that the representation (12.7) immediately implies that solutions to (12.6) are unique in law, i.e. (12.6) satisfies weak uniqueness. That is to say, given two different stochastic bases $({\mathcal {X}}, {\mathcal {F}}, ({\mathcal {F}}_t)_{t \ge 0}, {{\mathbb {P}}},{{\textbf {W}}})$ and $(\tilde{{\mathcal {X}}}, \tilde{{\mathcal {F}}}, (\tilde{{\mathcal {F}}}_t)_{t \ge 0}, {\tilde{{{\mathbb {P}}}}}, \widetilde{{{\textbf {W}}}} )$ defining solutions $\eta$ and ${\tilde{\eta }}$ to (12.6) on their respective probability spaces through the formula (12.7), the laws of $\eta$ and ${\tilde{\eta }}$ agree on C([0, T]; H) for any $T>0$, as long as $\eta _0$ and ${\tilde{\eta }}_0$ are equal in law on H.

For our purposes, it is easier to work with the martingale formulation of (12.6), which is in turn motivated by the weak formulation of (12.6). Hence, we note in passing that the mild solution (12.7) has the property that for each $t \in [0,T]$ the following equality holds in $H^{-s}({\mathbb {T}}^d)$, for $s>\frac{d+2}{2}$,

$$\begin{aligned} \eta ^\infty (t)=\eta _{0}+\int _{0}^{t}{\mathcal {L}}_{\rho _{\beta }}\eta ^{\infty }(s) \;\textrm{d}{s}+\int _{0}^{t} \nabla \cdot (\sqrt{\rho _{\beta }}d{{\textbf {W}}}_{s}). \end{aligned}$$

(12.10)

Lemma 12.6

Let $({\mathcal {X}}, {\mathcal {F}},({\mathcal {F}}_{t})_{t \ge 0}, {{\mathbb {P}}})$ be a filtered probability space. Assume that $\eta (t)$ is a continuous-time ${\mathcal {F}}_t$-adapted H-valued stochastic process and define $t \mapsto M(t)$ by

$$\begin{aligned} M(t):=\eta (t)-\eta _{0}-\int _{0}^{t}{\mathcal {L}}_{\rho _{\beta }}\eta (s)\;\textrm{d}{s}. \end{aligned}$$

(12.11)

Assume that the following two conditions hold:

• For all $\varphi \in C^{\infty }({\mathbb {T}}^d)$ it holds that

  $$\begin{aligned} t \mapsto \langle M(t),\varphi \rangle \quad \text{ is } \text{ an }\ {\mathcal {F}}_t\text{-martingale. } \end{aligned}$$

  (12.12)

• For all $\varphi ,\psi \in C^{\infty }({\mathbb {T}}^d)$ it holds that

  $$\begin{aligned} t \mapsto \langle M(t),\varphi \rangle \langle M(t),\psi \rangle -t\int _{{\mathbb {T}}^d} \nabla \phi \cdot \nabla \psi \rho _{\beta }\;\textrm{d}{x} \quad \text{ is } \text{ an }\ {\mathcal {F}}_t\ \text{ martingale }. \end{aligned}$$

  (12.13)

Then, $\eta$ is equal in law on C([0, T]; H) to the mild solution (12.7).

Proof

By [17, Theorem 8.2], it follows that on a suitable extension of the probability space, $\eta$ is a weak solution in the sense of (12.10). By [17, Theorem 5.4], the weak and mild solutions coincide on that probability space, so equality in law follows from Remark 12.5. $\square$

Using the above lemma, we are now finally in a position to prove convergence of the fluctuations.

Theorem 12.7

Assume that $\liminf _{N\rightarrow \infty }\lambda ^{N}_{LS}>0$ and that V and W are smooth. Then, for any $m>d/2 + 3$ the fluctuation process $\eta ^{N}$ converges in law on $C([0,T];H^{-m}({\mathbb {T}}^d))$ to the unique stationary mild solution $\eta ^\infty$ of the SPDE (12.6).

Proof

The proof has four steps. In Step 1, we apply Itô’s formula to show that $\eta ^{N}$ satisfies (12.14), an approximate version of the weak formulation (12.10). In Step 2, we combine Step 1 with the uniform bound (12.5) to show that the laws of $(\eta ^{N})_{N \in {\mathbb {N}}}$ on $C([0,T];H^{-m}({\mathbb {T}}^d))$ are uniformly tight for m large enough. In Step 3, we pass to the limit in the martingale problem and verify the assumptions of Lemma 12.6 to identify the limit along any tight subsequence. In Step 4, we conclude the uniqueness of the limit and hence the proof of the theorem.

Step 1. In this step, we show that for all $\varphi \in C^{\infty }({\mathbb {T}}^{d})$ it holds

$$\begin{aligned} \textrm{d}\langle \eta ^{N},\varphi \rangle =\langle \eta ^{N}, {\mathcal {L}}_{\rho _\beta }^{*} \varphi \rangle \textrm{d}t+\langle R_{N}, \varphi \rangle \textrm{d}t +\sqrt{2}(\beta N)^{-\frac{1}{2}}\sum _{i=1}^{N}\nabla \varphi (X_t^i) \cdot \textrm{d}B_t^i,\qquad \end{aligned}$$

(12.14)

where $X_t^i$ is the solution to (2.1) and $R_{N}$ is defined as

$$\begin{aligned} R_{N}:=N^{-\frac{1}{2}}\nabla \cdot (\eta ^N \nabla _{1} W\star \eta ^N) \,. \end{aligned}$$

Indeed, Itô’s formula gives

$$\begin{aligned} \textrm{d}\varphi (X_t^i)=&\left( \beta ^{-1} \Delta - \nabla V \cdot \nabla \right) \varphi (X_t^i) \textrm{d}t -\frac{1}{N}\sum _{j=1}^{N} \nabla _{1} W(X_t^i,X_t^j) \cdot \nabla \varphi (X_t^i)\textrm{d}t\\&+\sqrt{2}\beta ^{-1}\nabla \varphi (X_t^i) \cdot \textrm{d}B_t^i \, . \end{aligned}$$

We now sum over $i=1,\dots ,N$, divide by N, and use the identity

$$\begin{aligned} \frac{1}{N^{2}}\sum _{i,j=1}^{N} \nabla _{1}W(X_{t}^i,X_{t}^j) \cdot \nabla \varphi (X_{t}^i)=&\frac{1}{N}\sum _{i=1}^{N} \nabla _{1} W*\mu ^{(N)}(X_{t}^i) \cdot \nabla \varphi (X_{t}^i)\nonumber \\ =&\langle \mu ^{(N)}, \nabla _{1} W \star \mu ^{(N)} \cdot \nabla \varphi \rangle \, , \end{aligned}$$

to obtain

$$\begin{aligned} \textrm{d}\langle \mu ^{(N)},\varphi \rangle = \langle \mu ^{(N)}, \beta ^{-1} \Delta \varphi - (\nabla V+\nabla _{1}W\star \mu ^{(N)}) \cdot \nabla \varphi \rangle \textrm{d}t+\sqrt{2}\beta ^{-\frac{1}{2}}\frac{1}{N} \sum _{i=1}^{N} \nabla \varphi (X^{i}_t) \cdot d B_{t}^i \end{aligned}$$

Next, we insert the identity $\mu ^{(N)}=\rho _{\beta }+N^{-\frac{1}{2}}\eta ^{N}$ to deduce

$$\begin{aligned} \textrm{d}\langle \eta ^{N},\varphi \rangle&= N^{1/2}\underbrace{\langle \rho _\beta , \beta ^{-1} \Delta \varphi - (\nabla V+\nabla _{1}W\star \rho _\beta ) \cdot \nabla \varphi \rangle }_{=0} \textrm{d}t\nonumber \\&\quad +\underbrace{\langle \eta ^N, \beta ^{-1} \Delta \varphi - (\nabla V+\nabla _{1}W\star \rho _\beta ) \cdot \nabla \varphi \rangle +\langle \rho _\beta , \nabla _{1}W\star \eta ^N \cdot \nabla \varphi \rangle }_{=\langle \eta ^N,{\mathcal {L}}_{\rho _\beta }^*\varphi \rangle } \textrm{d}t\nonumber \\&\quad +\underbrace{N^{-1/2}\langle \eta ^N, \nabla _{1}W\star \eta ^N \cdot \nabla \varphi \rangle }_{\langle R^N,\varphi \rangle }+\frac{\sqrt{2}}{\beta N^{\frac{1}{2}}} \sum _{i=1}^{N} \nabla \varphi (X^{i}_t) \cdot d B_{t}^i \end{aligned}$$

The first identity follows from the fact that $\rho _{\beta }$ is a steady state and the second follows from integration by parts and Fubini’s theorem (using the symmetry of W).

Step 2. In this step, we will show that the laws of $(\eta ^{N})_{N \in {\mathbb {N}}}$ on $C([0,T];H^{-m}({\mathbb {T}}^d))$ for $m>m_{0}:=d/2 + 3$ are uniformly tight. To this end, we define a decomposition of $t \mapsto \eta ^{N}(t)$ via the equality $\eta ^{N}(t)=Y_{N}(t)+M_{N}(t)$, where

$$\begin{aligned} Y_{N}(t):=\eta ^N(0)+\int _{0}^{t} \big ( {\mathcal {L}}_{\rho _{\beta }}\eta ^{N}(r)+R^{N}(r) \big )\; \textrm{d}{r}. \end{aligned}$$

We claim that for $m>m_{0}$ and all $p \ge 1$ there exist constants $C,C_p>0$ such that

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert Y^{N}(t_1)-Y^{N}(t_2)\Vert _{H^{-m}({\mathbb {T}}^d)}^{2}}&\le C|t_1-t_2|^{2}, \end{aligned}$$

(12.15)

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert M^{N}(t_1)-M^{N}(t_2)\Vert _{H^{-m}({\mathbb {T}}^d)}^{p}}&\le C_{p}|t_1-t_2|^{\frac{p}{2}}. \end{aligned}$$

(12.16)

To obtain (12.15), first observe that at each fixed time we have

$$\begin{aligned} \Vert R_{N}\Vert _{H^{-m}({\mathbb {T}}^d)}=&\Vert \nabla \cdot (\eta ^N\nabla _{1}W\star (\mu ^{(N)}-\rho _{\beta }))\Vert _{H^{-m}({\mathbb {T}}^d)}\nonumber \\ \le&\Vert \eta ^N\nabla _{1}W\star (\mu ^{(N)}-\rho _{\beta })\Vert _{H^{1-m}({\mathbb {T}}^d)}\nonumber \\ \le&C_s\Vert \eta ^{N}\Vert _{H^{1-m}({\mathbb {T}}^d)}\Vert \nabla W\star (\mu ^{(N)}-\rho _{\beta })\Vert _{W^{{m-1},\infty }({\mathbb {T}}^d)}\nonumber \\ \le&C_{s}\Vert W\Vert _{W^{m,\infty }({\mathbb {T}}^d)}\Vert \eta ^{N}\Vert _{H^{1-m}({\mathbb {T}}^d)}. \end{aligned}$$

(12.17)

Furthermore, note that the regularity of V, W, and $\rho _{\beta }$ implies the operator ${\mathcal {L}}_{\rho _{\beta }}$ is bounded from $H^{2-m}({\mathbb {T}}^d)$ to $H^{-m}({\mathbb {T}}^d)$. Therefore, integrating in time, taking the second moment, and applying the Cauchy–Schwartz inequality we find

$$\begin{aligned} {\mathbb {E}}\left[ *\right] {\Vert Y^{N}(t_{1})-Y^{N}(t_{2})\Vert _{H^{-m}({\mathbb {T}}^d)}^{2}}\le&{\mathbb {E}}\left( \int _{t_{1}}^{t_{2}}\Vert {\mathcal {L}}_{\rho _{\beta }}\eta ^N(r)\Vert _{H^{-m}({\mathbb {T}}^d)}+{\mathbb {E}}\Vert R_{N}\Vert _{H^{-m}({\mathbb {T}}^d)}\textrm{d}{r}\right) ^2\\ \le&C|t_{2}-t_{1} | \int _{t_{1}}^{t_{2}}{\mathbb {E}}\Vert \eta ^{N}\Vert _{H^{2-s}({\mathbb {T}}^d)}^{2}+{\mathbb {E}}\Vert \eta ^{N}\Vert _{H^{1-m}({\mathbb {T}}^d)}^{2}\;\textrm{d}{r} \\ \le&C|t_{2}-t_{1}|^{2}{\mathbb {E}}\Vert \eta ^{N}(0) \Vert _{H^{2-m}({\mathbb {T}}^d)}^{2} \, , \end{aligned}$$

where we used the stationarity of $\eta ^{N}$ in the last step. The inequality (12.15) now follows immediately from the bound (12.5), since our choice of m implies $m-2>1+\frac{d}{2}$. We now turn our attention to the estimate (12.16). Note that for any smooth $\varphi$ it holds that

$$\begin{aligned} {\mathbb {E}}\left[ *\right] { | \langle M^{N}(t)-M^{N}(s), \varphi \rangle |^{p} }\le&C {\mathbb {E}}\bigg (\frac{1}{N}\sum _{i=1}^{N}\int _{s}^{t}|\nabla \varphi (X_t^{i})|^{2}\textrm{d}t \bigg )^{\frac{p}{2}}\nonumber \\ \le&C |t-s|^{\frac{p}{2}} \Vert \nabla \varphi \Vert _{L^{\infty }({\mathbb {T}}^d)}^{2}. \end{aligned}$$

(12.18)

We take $\varphi$ to be elements of a basis of $H^{m}_0({\mathbb {T}}^d)$, the inequality (12.16) holds as long as

$$\begin{aligned} \sum _{j\in {\mathbb {N}}}\Vert \nabla \varphi _j \Vert _{L^{\infty }({\mathbb {T}}^d)}^{2}<\infty . \end{aligned}$$

The above estimate follows when we take $m>d/2+1$. Finally, we note that by an argument entirely analogous to the one showing (12.15) and (12.16), we can also show

$$\begin{aligned} \sup _{N \in {\mathbb {N}}}{\mathbb {E}}\left[ *\right] {\sup _{t \in [0,T]} \Vert \eta ^N(t)\Vert _{H^{-m}({\mathbb {T}}^d)}^{2}}<\infty , \end{aligned}$$

(12.19)

by using that $M^{N}(0)=0$ and $Y^{N}(0)=\eta ^{N}(0)$ together with (12.5). Combining (12.15), (12.16), and (12.19) we obtain the tightness of the laws of $(\eta ^{N})_{N \in {\mathbb {N}}}$ as a consequence of [28, Theorem 2.2] and Chebyshev’s inequality. Specifically, we use the embedding of $W^{1-\varepsilon ,2}([0,T];H^{-m+\varepsilon }({\mathbb {T}}^d))+W^{\frac{1}{2},p}([0,T]; H^{-m+\epsilon }({\mathbb {T}}^d))$ into $C([0,T];H^{-m}({\mathbb {T}}^d) )$ for $p>2$ and $\varepsilon >0$ sufficiently small.

Step 3. In light of Step 2 and the Skorokhod representation theorem, passing to a subsequence (which we do not relabel) we can find a new probability space $(\tilde{{\mathcal {X}}},\tilde{{\mathcal {F}}},\tilde{{\mathbb {P}}})$, a new sequence $({\tilde{\eta }}^{N})_{N \in {\mathbb {N}}}$, and a limiting random variable $\eta$ such that ${\tilde{\eta }}^{N}$ is equal in law to $\eta ^{N}$ for all $N \in {\mathbb {N}}$ and converges ${\tilde{{{\mathbb {P}}}}}$-a.s to $\eta$ in $C([0,T];H^{-m}({\mathbb {T}}^d))$. In this step, we claim that (12.12) and (12.13) hold true.

To this end, for each $t>0$, we denote by $r_{t}$ the restriction operator from $C([0,T];H^{-m}({\mathbb {T}}^d))$ to $C([0,t];H^{-m}({\mathbb {T}}^d))$ and define a filtration $(\tilde{{\mathcal {F}}}_{t})_{t \ge 0}$ by letting $\tilde{{\mathcal {F}}}_{t}=\sigma (r_{t}\eta )$ for $t>0$, i.e. the sigma algebra generated by $r_t\eta$. Recalling the definition (12.11) of $t \mapsto M(t)$, we will show that that for all times $s<t$, functions $\varphi , \psi \in C^{\infty }({\mathbb {T}}^{d})$, and bounded, continuous functions $\Gamma : C([0,s];H^{-m}({\mathbb {T}}^d)) \mapsto {\mathbb {R}}$ it holds that

$$\begin{aligned}&{\mathbb {E}}\left[ *\right] { \Gamma (r_{s}\eta ) \langle M(t)-M(s),\varphi \rangle }=0. \end{aligned}$$

(12.20)

$$\begin{aligned}&{\mathbb {E}}\big [ \Gamma (r_{s}\eta ) \big ( \langle M(t), \varphi \rangle \langle M(t), \psi \rangle - \langle M(s), \varphi \rangle \langle M(s), \psi \rangle \nonumber \\&\qquad -(t-s)\langle \rho _{\beta } \nabla \varphi , \nabla \psi \rangle \big ) \big ]=0. \end{aligned}$$

(12.21)

By the definition of conditional expectation and Egorov’s theorem, (12.20) and (12.21) imply (12.12) and (12.13) hold true with respect to the filtration $(\tilde{{\mathcal {F}}}_{t})_{t \ge 0}$. To prove (12.20) and (12.21), define $t \mapsto {\tilde{M}}^{N}(t)$ as in Step 2 but with ${\tilde{\eta }}_{N}$ in place of $\eta ^N$.

Since ${\tilde{\eta }}^{N}$ and $\eta ^{N}$ are equal in law, (12.14) implies that

$$\begin{aligned}&{\mathbb {E}}\big [ \Gamma (r_{s}{\tilde{\eta }}_{N}) \langle {\tilde{M}}^{N}(t)-{\tilde{M}}^{N}(s),\varphi \rangle \big ]=0. \end{aligned}$$

(12.22)

$$\begin{aligned}&{\mathbb {E}}\big [\Gamma (r_{s} {\tilde{\eta }}_{N} ) \big ( \langle {\tilde{M}}_{N} (t), \varphi \rangle \langle {\tilde{M}}_{N} (t), \psi \rangle - \langle {\tilde{M}}_{N} (s), \varphi \rangle \langle {\tilde{M}}_{N}(s), \psi \rangle \nonumber \\&\qquad \qquad -(t-s)\langle \rho _{\beta } \nabla \varphi , \nabla \psi \rangle \big ) \big ]=0. \end{aligned}$$

(12.23)

By a calculation similar to (12.17), it follows that for each $t \le T$

$$\begin{aligned} \bigg \Vert \int _{0}^{t}{\tilde{R}}_{N}(s)ds \bigg \Vert _{H^{-(m+1)}({\mathbb {T}}^d)} \le C N^{-1/2}\Vert {\tilde{\eta }}_{N}\Vert _{C([0,T];H^{-m}({\mathbb {T}}^d) )}^{2}, \end{aligned}$$

which converges to zero ${\tilde{P}}$-a.s. As a consequence, we obtain $\langle {\tilde{M}}^{N}(t), \varphi \rangle$ converges ${\tilde{P}}$-a.s. to $\langle M(t), \varphi \rangle$ as a consequence of the a.s. convergence of ${\tilde{\eta }}^{N}$ to $\eta ^{\infty }$. In addition, for all $t>0$, the sequence $\langle {\tilde{M}}^{N}(t), \varphi \rangle$ is uniformly bounded in $L^{p}(\tilde{{\mathcal {X}}})$ for all $p \ge 1$ as a consequence of the equality in law of ${\tilde{\eta }}^{N}$ and $\eta ^{N}$ and the estimate (12.18). Using the Vitali convergence theorem, we may pass to the limit in (12.22) and (12.23) to obtain (12.20) and (12.21) as desired.

Step 4. In light of Step 3 and Lemma 12.6, every subsequence of $\eta ^N$ has a further subsequence which converges to a stationary mild solution to (12.6) on some probability space. Note that $\eta$ inherits stationarity from ${\tilde{\eta }}^{N}$ in the $N \rightarrow \infty$ limit. Hence, it suffices to show that all limit points induce the same law on $C([0,T];H^{-m}({\mathbb {T}}^d))$. In light of Remark 12.5, the problem further reduces to showing that the initial distributions are the same. However, if $\eta$ satisfies (12.7) and is stationary, we can explicitly check that its law is a Gaussian on $H^{-m}({\mathbb {T}}^d)$ for all $t \ge 0$. This follows from [36, Theorem 5.22 and Proposition 5.23], (12.9), and the fact that for all $f \in H^{-m}({\mathbb {T}}^d)$, we have

$$\begin{aligned} \lim _{t \rightarrow \infty }\Vert e^{t {\mathcal {L}}_{\rho _\beta }} f\Vert _{H^{-m}} =0 \,. \end{aligned}$$

The fact that this holds true follows from the coercivity assumption and the fact that the semigroup $e^{t{\mathcal {L}}_{\rho _\beta }}$ is smoothing, i.e. it maps $H^{-m}({\mathbb {T}}^d)$ to $L^2({\mathbb {T}}^d)$ for all $t>0$. $\square$

We finish this section with the implication of the coercivity property, that is used in the proof to show the Hilbert–Schmidt property of the appropriate operators.

Lemma 12.8

Assume that ${\mathcal {L}}_{\rho _\beta }$ satisfies

$$\begin{aligned} \langle -{\mathcal {L}}_{\rho _\beta }\phi ,\phi \rangle \ge c\Vert \nabla \phi \Vert _{L^2({\mathbb {T}}^d)}^2 \end{aligned}$$

for some $c>0$, then

$$\begin{aligned} \int _0^\infty \Vert \nabla e^{t{\mathcal {L}}^*_{\rho _\beta }}\phi \Vert _{L^2({\mathbb {T}}^d)}^2\;\textrm{d}{t}\le \frac{\Vert \phi \Vert _{L^2}^2}{2c}. \end{aligned}$$

Proof

We use the short hand notation $\phi _t=e^{t{\mathcal {L}}^*_{\rho _\beta }}\phi$. We then have

$$\begin{aligned} \partial _t \phi _t -{\mathcal {L}}_{\rho _\beta }^*\phi _t=0 \,. \end{aligned}$$

Multiplying by $\phi _t$ and integrating, we obtain the identity

$$\begin{aligned} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}{t}}\Vert \phi _t\Vert ^2_{L^2({\mathbb {T}}^d)}-\langle {\mathcal {L}}_{\rho _\beta }\phi _t,\phi _t\rangle =0. \end{aligned}$$

Applying the coercivity bound, we obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}{t}} \Vert \phi _t\Vert _{L^2({\mathbb {T}}^d)}^2+2c\Vert \nabla \phi _t\Vert _{L^2}^2 \le 0. \end{aligned}$$

Integrating in time we obtain

$$\begin{aligned} 2c \int _0^\infty \Vert \nabla \phi _t\Vert _{L^2({\mathbb {T}}^d)}^2\;\textrm{d}{t}\le \Vert \phi _0\Vert _{L^2}^2=\Vert \phi \Vert _{L^2({\mathbb {T}}^d)}^2 \,, \end{aligned}$$

which is the desired estimate. $\square$

12.1 Properties of the invariant measure of (2.12)

We discuss briefly about the proporties of the invariant measure of the SPDE for the fluctuations, Eqn. (2.12). The unique invariant measure of the SPDE (2.12) ${\mathcal {G}} \in {\mathcal {P}}(H^{-m}({\mathbb {T}}^d))$ is a centred Gaussian measure with covariance operator $Q_{{\mathcal {G}}}$ given by

$$\begin{aligned} Q_{{\mathcal {G}}}(\varphi ,\psi ):=\lim _{t \rightarrow \infty }\int _0^t \int _{{\mathbb {T}}^d} \nabla e^{t{\mathcal {L}}_{\rho _\beta }^*}\varphi \cdot \nabla e^{t{\mathcal {L}}_{\rho _\beta }^*}\psi \, \rho _\beta \,\textrm{d}{x} \textrm{d}{t} \,, \end{aligned}$$

for any mean-zero $\varphi ,\;\psi \in C^\infty ({\mathbb {T}}^d)$ and where ${\mathcal {L}}_{\rho _\beta }^*$ denotes the flat $L^2$-adjoint.

In the specific case that $V \equiv 0$ and $W (x,y)=W(x-y)$, we can obtain a more explicit characterisation of ${\mathcal {G}}$. Indeed, since $\liminf _{N \rightarrow \infty } \lambda _{{{\,\textrm{LSI}\,}}}^N >0$, we know from Proposition 4.2 (and the discussion following it) that $E^{MF}$ has a unique critical point which is given by $\rho _\infty (\textrm{d}{x})=\textrm{d}{x}$. We can then obtain an explicit representation of the action of the semigroup $e^{t {\mathcal {L}}^*_{\textrm{d}{x}}}$ in Fourier space as follows

$$\begin{aligned} {\hat{\varphi }}_t(k) = e^{-4 \pi ^2 |k|^2(\beta ^{-1}+ {\hat{W}}(k)) t} {\hat{\varphi }}(k) \quad k \in {\mathbb {Z}}^d, k \ne 0 \,, \end{aligned}$$

where $\varphi _t = e^{t {\mathcal {L}}^*_{\textrm{d}{x}}} \varphi$ for some mean-zero $\varphi \in C^\infty ({\mathbb {T}}^d)$. This leaves us with the formula

$$\begin{aligned} Q_{{\mathcal {G}}}(\varphi ,\psi ) = \sum _{k \in {\mathbb {Z}}^d, k \ne 0}\frac{{\hat{\varphi }}(k) {\hat{\psi }}(k)}{8 \pi ^2 (\beta ^{-1} + {\hat{W}}(k))} \,, \end{aligned}$$

where we have used the fact that the coercivity inequality (2.11) is equivalent to the fact that $\beta ^{-1} + {\hat{W}}(k) >0$ for all $k \in {\mathbb {Z}}^d, k \ne 0$, which is also equivalent to the condition $\beta <\beta _\sharp$, see Proposition 4.3.

In other words, ${\mathcal {G}}$ is the unique centred Gaussian measure with Cameron–Martin space given by the closure of all smooth mean-zero functions $\varphi$ under the norm

$$\begin{aligned} \Vert \varphi \Vert _{{\mathcal {H}}_{{\mathcal {G}}}}^2 = 8 \pi ^2 \left( \beta ^{-1}\int _{{\mathbb {T}}^d}\varphi ^2 \textrm{d}{x} + \int _{{\mathbb {T}}^d} (W* \varphi )\varphi \textrm{d}{x} \right) \,. \end{aligned}$$

Since, $\beta ^{-1}+ {\hat{W}}(k)>0$ for all $k \in {\mathbb {Z}}^d, k \ne 0$, the above norm is equivalent to the standard $L^2({\mathbb {T}}^d)$ norm. The above norm is also the same, up to a multiplicative constant, as the norm introduced in Property A.

One can further use the structure of the covariance operator $Q_{{\mathcal {G}}}$ to read off that ${\mathcal {G}}$ is supported on $H^{-\frac{d}{2}-}({\mathbb {T}}^d)$ distributions. Thus, the limiting equilibrium fluctuations have the regularity of spatial white noise, which is not surprising considering the fact that their Cameron–Martin space is “basically” $L^2({\mathbb {T}}^d)$.