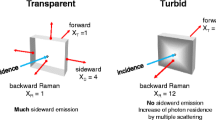
Abstract
Raman intensities from reflection (X R ) and transmission (X T ) setups are compared by calculations based on random walk and analytical approaches with respect to sample thickness, absorption, and scattering. Experiments incorporating strongly scattering organic polymer layers and powder tablets of pharmaceutical ingredients validate the theoretical findings. For nonabsorbing layers, the Raman reflection and transmission intensities rise steadily with the layer thickness, starting for very thin layers with the ratio X T /X R = 1 and approaching for thick layers, a lower limit of X T /X R = 0.5. This result is completely different from the primary irradiation where the ratio of transmittance/reflectance decays hyperbolically with the layer thickness to zero. In absorbing materials, X R saturates at levels that depend strongly on the absorption and scattering coefficients. X T passes through a maximum and decreases then exponentially with increasing layer thickness to zero. From the calculated radial intensity spreads, it follows that quantitative transmission Raman spectroscopy requires diameters of the detected sample areas be about six times larger than the sample thickness. In stratified systems, Raman transmission allows deep probing even of small quantities in buried layers. In double layers, the information is independent from the side of the measurements. In triple layers simulating coated tablets, the information of X T originates mainly from the center of the bulk material whereas X R highlights the irradiated boundary region. However, if the stratified sample is measured in a Raman reflection setup in front of a white diffusely reflecting surface, it is possible to monitor the whole depth of a multiple scattering sample with equal statistical weight. This may be a favorable approach for inline Raman spectroscopy in process analytical technology.

Raman spectroscopy in turbid matter
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There is an increasing demand for analytical techniques based on Raman radiation generated in the volume of a multiple scattering sample [1, 2]. Areas of application are inline process monitoring [3] with fast-quality control in pharmaceutical manufacturing [4–6], in situ characterization of surface reactions on supported catalysts [7], counterfeit detection of pharmaceutical products through the packaging [8], noninvasive characterization of tissues [9], or bone diseases [10] in medicine and security screenings through bottles, e.g., for the detection of solid and liquid explosives and illicit drugs [11]. Several approaches to quantify active pharmaceutical ingredients in pharmaceutical mixtures by transmission Raman spectroscopy in combination with multivariate data analysis have been published [5, 12, 13]. Applications for the measurement of Raman radiation of diffusely reflecting and transmitting materials have been proposed [14].
Raman radiation originates in the volume of the cited materials mainly from multiple scattered primary radiation, and the Raman signal itself is also elastically scattered many times before it leaves the sample. Hence, the external spatial distribution of Raman radiation depends strongly on the sample geometry. The simplest situation is met for laterally extended and thick (“semi-infinite”) layers with planar boundaries. Here, Raman backscattering is the only applicable measuring geometry. The detected Raman radiation is biased to sample depths close to the irradiated surface ranging from some micrometers to several millimeters, where the depth penetration depends on the albedo and thickness of the sample [15]. Spatially offset Raman spectroscopy [16] marks an approach to overcome the sub-sampling restrictions of conventional backscattering Raman spectroscopy and provides an access to deeper volumes of the sample. Similar to radially resolved diffuse reflectance absorption spectroscopy [17], the detection is separated with a lateral offset to the laser excitation. Raman spectra can be extracted in combination with multivariate data analysis from different depths of turbid samples [16].
In thin samples with typical thicknesses of z 0 ≤ 1 cm, the backscattering mode can be expanded by forward scattering (= transmission) Raman spectroscopy. This type of detection was worked out already in 1967 by Schrader and Bergmann [18] and received its revival in 2006 by Matousek and Parker [19]. The transmitted Raman signal averages over the whole sample depth with weight maximum in the center of the sample [20, 21]. The weak signal strength of transmitted Raman radiation can be enhanced by a dielectric mirror system [22].
The theoretical analysis of Raman intensities is based almost exclusively on the model of radiative transfer (RT). This model uses geometrical optics and ignores, e.g., interference, diffraction, or polarization of radiation. The most convenient solutions start from the two-flux model of Kubelka–Munk (KM) adding two additional Raman fluxes in the directions of transmission and reflection, respectively. The system of differential equations was first solved for arbitrary layer thicknesses with the approximation that absorption and scattering are independent of the wavelength of radiation [18]. More general solutions can be adapted from the radiation balance of fluorescence in scattering media [23] which behaves formally equal to Raman scattering. Results with wavelength dependent absorption and scattering coefficients were first published for semi-infinite layers [24, 25] and later also for arbitrary layer thicknesses [26–28]. The KM model works well for uniform diffuse irradiation of large sample areas. Laser Raman spectroscopy uses collimated irradiation of small sample areas. Hence, the model has to be modified for these boundary conditions. The full solution of the equation of transfer requires lengthy numerical procedures. However, we have shown that the depth penetration upon normal incidence can excellently be described with the classical diffusion approximation of RT [15], whereas the radial penetration upon spot irradiation requires higher order expansions into spherical harmonics or Monte Carlo simulations [17]. The latter method has already successfully been applied to describe Raman scattering in turbid media [21].
In this paper, we compare collimated and diffuse irradiation and calculate the transmitted and reflected Raman intensities as function of the layer thickness, absorption coefficient, and scattering coefficient. We emphasize composite layers and describe methods how to enhance the fractions of the desired intensities in forward and backward directions, respectively. The radial spreads of the emitted Raman signals are determined and critically confronted with the limited aperture of the detection system. The calculated results are experimentally tested with organic polymers and basic materials for pharmaceutical tablets. The enhancement of reflected and transmitted Raman intensities by a white diffuse reflectance standard is investigated.
Theory
The termini back- and forward-scattering are well defined for the angular distribution of single scattered radiation. In the multiple scattering regime, there is no principal difference between the angular distributions of radiation from outside sources or inside sources. Both types of radiation become after some scattering processes more or less isotropic and are diffusely reflected or transmitted. In other words, radiation that originally is scattered in forward direction can leave the sample in backward direction, and vice versa. In order to avoid confusion with the single scattering events we use in the following the terminologies “Raman reflection vs. Raman transmission” for the phenomena of emission through the irradiated vs. non-irradiated sample surfaces, and “Raman reflectance vs. Raman transmittance” for the quantitative Raman fluxes leaving the turbid medium. These termini are useful also in cases where one knows nothing about scattering.
Kinetic reaction scheme
A polarizable cylindrical disc of thickness z 0 and radius ρ 0 is irradiated in direction cosθ 0 = μ 0 (with θ 0 = angle of incidence) relative to the principal cylinder axis with monochromatic light (Fig. 1). The primary polarizations P move in the sample by multiple elastic scattering processes and leave the disc finally with probability w R as reflectance R, and with probability w T as transmittance T. A part of P is absorbed with probability w A , and part is transformed with probability w X into Raman excitations X. The latter undergo similar scattering and absorption processes as P.
Kinetic reaction scheme. The primary excitation P moves randomly in the scattering layer of thickness z 0, is diffusely reflected (R), diffusely transmitted (T d ), directly transmitted without being scattered (T c ), absorbed (A p ), or converted into Raman excitation (X). The Raman excitation moves also randomly in the layer, is reflected through the irradiated sample plane (X R ), transmitted through the opposite plane (X T ), or re-absorbed (A X ). Table 1 gives definitions of the rate parameters
All partial reaction rates are assumed to be of first order. Table 1 gives definitions of the rate parameters. It is also assumed that Lambert Beer’s law is valid for particulate multiple scattering materials, resulting in the attenuation approach \( \mathrm{d}I = -I\left( {\sigma +\kappa +\alpha } \right)\mathrm{d}\lambda =-I\varepsilon \mathrm{d}\lambda \) and the product representations of the differential reaction probabilities
The formation of Raman excitation is then dX = αPdλ.
The random walk approach
The path length Δλ j between scattering event j − 1 and j is generated as random number 0 < Rnd j < 1 from the probability transformation of Beer’s law. The scattering cosine is taken as arbitrary, cosθ = 2Rnd − 1, (isotropic scattering)
The total path length from entrance to reflection or transmission, λ R or λ T, respectively, is obtained as a sum of path lengths between all scattering events. The layer is irradiated with a large number N 0 > 106 of very weak light beams (“photons”) that can be scattered only in total. The numbers of reflected (N R ) and transmitted (N T ) beams are counted and the individual radial distances (ρi) from incidence as well as the individual path lengths (λ R,i or λ T,i ) are determined. The reflectance and transmittance of primary light is then
Equations (2) assume attenuation of the beams according to Beer’s law under neglect of the very small generation coefficient of Raman excitation (α < 10−7 cm−1 in dense materials). The corresponding external Raman signals are obtained as solutions of the consecutive first order reaction of scheme 1
The X signals are made dimensionless (as R and T) by division through the magnitude and dimension unit of the incident primary radiation. Equations (3a) and (3b) assume equal random walk statistics of primary and Raman excitations (σ P = σ X = σ). The equations simplify for κ P = κ X = κ to
These relations are reasonable approximations for nonresonant Raman scattering where κ represents some background absorption that does not contribute to the Raman generation coefficient. Finally, the simplest equations are obtained for “quasi-white” multiple scattering materials with negligible absorption, κ→0
Where < λ R > and < λ T > are the mean path lengths of reflected and transmitted photons, respectively, and Td is the scattered transmittance of primary radiation. Equations (5) are acceptable approximations for thick layers. For thin layers, where an important part of the incident radiation is transmitted prior to scattering as \( {T_{\mathrm{c}}}=\exp \left( {-\varepsilon {{\mathrm{z}}_0}/{\mu_0}} \right) \), and R and T d are low, Eqs. (5) must be modified to
The path lengths λ* are here counted not from entrance but from the first scattering event. Table 2 presents limiting values for very thin layers with R≈T d→0, and for very thick nonabsorbing layers with R→1.
The analytical approach
Upon homogeneous irradiation, the flux density Φ P of the primary radiation depends inside the layer only on the depth coordinate z. The Raman flux density is generated according to
where ΦP is normalized to the flux density of the incident irradiation at z = 0. The integral external Raman intensities emitted as reflectance or transmittance are then [25]
Equations (8a and 8b) assumes isotropic angular distribution of Φ P . The other integrands denote reflectances and transmittances at the Raman wavelength of layers with virtual thicknesses of z and z 0–z, respectively. Analytical solutions of Eqs. (8a and 8b) were obtained for σ P = σ X, κ P = κ X and diffuse irradiation [18] using the Kubelka-Munk model as well as for the more general case of arbitrary optical parameters [26–28]. All quantities that are necessary for solving the integrals upon normal incidence can be found in [15]. The simplest solutions of Eqs. (8a and 8b) are obtainable upon diffuse incidence for white pigments with σ P = σ X = σ and κ = 0. The corresponding transmittances and reflectances are inserted from column 5 of Table 2, and the flux density of primary radiation is assumed to decrease linearly with z according to Fick’s law (see also Kubelka [29])
where τ = 3σz/4 and τ0 = 3σz 0/4. Integration over z0 yields for nonabsorbing layers
Limiting values are summarized in Table 2. In the single scattering regime (σz 0 << 1), the transmittances and reflectances of primary and Raman radiation show the same linear increase with the layer thickness z 0. In the multiple scattering regime (σz 0 >> 1), the reflectance of primary radiation approaches unity and the transmittance decreases hyperbolically with z 0 to zero. In contrast, Raman reflectance and Raman transmittance rise steadily with z0 approaching for thick layers a constant ratio X R /X T = 2 independent of the scattering coefficient and the geometry of irradiation. The high Raman transmittance is a consequence of the long mean pathway < λ T > of transmitted radiation that rises with z 0 2 and overcompensates the z 0 −1 decrease of T d , resulting according to Eq. (5) in a linear increase of X T with z 0.
Influence of background absorption
Results for weakly absorbing multiple scattering layers
Completely nonabsorbing materials are fiction. The absorption coefficient can be as low as κ = 10−6 cm−1, corresponding to damping of 0.5 dB km−1, which is typical for optical glass fiber cables in the NIR. In polymeric hydrocarbons the damping at λ = 600–1,000 nm is higher due to the absorption of C–H vibration overtones, and in functional low molecular materials, the absorption increases further due to forbidden electronic singlet-triplet (π,π*) or (n,π*) transitions. In addition, the absorption of fine powders can increase by adsorbed impurities or coordinatively unsaturated surface states. Figure 2 depicts calculated Raman intensities of weak absorbers with diffuse reflectances R ∞ > 0.9. For thin layers, the Raman intensity increases almost linearly with z 0, but then the rise becomes smaller. For thick layers, the reflected intensity X R saturates at levels that depend strongly on the absorption coefficient. The transmitted intensity X T passes through a maximum and decreases then exponentially with z 0 to zero. As shown in curves No. 3 of Fig. 2, the model of calculation is of secondary importance. Equations (4) and (8a and 8b) yield equal results in the region of practical interest. Only for very thin layers, τ0 < 3, the random walk approach produces slightly higher Raman intensities than the diffusion approach. However, these differences cannot be visualized in the scale range of Fig. 2. The strong decrease of X T with absorption is a consequence of the long path length of transmitted radiation. Especially the long branch of the λ T distribution is subjected to attenuation resulting in a strong reduction of the mean value < λ T > as well as of the transmittance T d , and finally to complete damping of Raman transmission in thick layers. Note the different intensity scales for X R and X T .
Calculated Raman intensities in reflection mode (left) and transmission mode (right) of multiple scattering layers upon diffuse irradiation inserting a typical scattering coefficient of microcrystalline powders and small absorption coefficients as parameter. See table for details. The smooth lines are calculated with Eqs. (8a and 8b) for κ p = κ x = κ; the noisy lines are simulated with the random walk model of Eqs. (1) and (4). The two calculation methods yield indistinguishable results. Note the different ordinate scales of the two graphs
From the practical point of view, it is noteworthy that absorption can be ignored in layers not thicker than 3 mm, which are typical for many pharmaceutical tablets, when the maximum diffuse reflectance exceeds R ∞ > 0.97.
Results for thick absorbing multiple scattering layers
The saturation of Raman reflection and the exponential damping of Raman transmission (see curves 3 and 4 in Fig. 2) is calculated from Eqs. (8a and 8b) for the limit of thick absorbing layers and the boundary conditions σ P = σ X = σ, κ P = κ X = κ, σ >> κ
Here, γ is the attenuation coefficient that can be expressed in the isotropic diffusion approximation or in terms of the Kubelka–Munk scattering (S KM) and absorption (K KM) coefficients as
where b = (a 2 − 1)1/2 and a = (S KM + K KM)/S KM. The diffuse reflectance of optically thick layers is R ∞ = a – b.
The reflected Raman signal X ∞ is independent of the layer thickness and proportional to the generation coefficient α, i.e., proportional to the density of the Raman active species. However, the signal is also very sensitive to attenuation by background absorption, as can be seen from Fig. 3. Hence, the analytical application to thick layers makes sense only if the background absorption can be kept as constant. The corresponding transmitted signal X T∞ is very weak and decreases exponentially with the background absorption and the layer thickness. It should be noted that both types of Raman signals decrease much stronger with the absorption coefficient than the diffuse reflectance of primary radiation.
Raman intensities X R and X T, diffuse reflectance R, mean generation depth < z gen > of X R of an optically thick scattering layer with σ = 200 cm−1, z 0 = 0.5 cm as function of the background absorption coefficient κ. The reflectance is presented in absolute values. Other data are normalized to unity at κ = 0, where < z gen > = 0.124 cm
Axial generation depth profiles of Raman signals in multiple scattering, nonabsorbing layers
The differentials of Eqs. (8a and 8b) directly yield the depth profiles of Raman generation emitted as X R and X T , respectively. Alternatively, the profiles are available from the random walk approach [21]. Figure 4 presents the result of the diffusion approximation for a nonabsorbing layer. The reflected Raman signal originates mainly from regions facing the irradiated surface. Upon diffuse incidence, the contributions to X R is proportional to (Φp(z))2 and falls off monotonically with z. The mean value of the generation depth approaches < zXR >≈0.25 z 0, almost independent of the scattering coefficient and its anisotropy. Upon normal incidence, the generation profile of X R passes through a maximum close to the irradiated surface. Then the profile decays in a similar way as for diffuse irradiation. The transmitted Raman signal is generated mainly in the deep interior of the layer. The generation profile follows approximately a symmetric parabola with the apex in the center of the layer. Hence, X T probes mainly the central regions whereas the boundaries contribute only little to the signal.
Depth origins of Raman emission in a scattering layer (z 0 = 0.5 cm, σ = 100 cm−1, and κ = 0). X R emission in the reflection mode, X T emission in the transmission mode. Comparison of diffuse irradiation and collimated irradiation of normal incidence (μ 0 = 1). Note: X T is magnified against X R by a factor of 2
Radial spread of Raman intensities in multiple scattering, nonabsorbing layers
The distance between photon incidence and photon emission is an important parameter, e.g., the design of detection units or for the resolution of spectral images. The general analytical solution of the trinomial system (σ, κ, and z 0) is not yet available. We prefer the numerical random-walk approach and determine the number of reflected, N R (ρ), and transmitted, N T (ρ), photons as function of the distance ρ from the axis of incidence, as well as the associated path lengths λ R (ρ) and λ T (ρ). From these quantities and Eqs. (5) or (6), the radial Raman intensities are accessible. The result for nonabsorbing layers with negligible contribution of collimated transmittance T c is then
where R′ and T d ′ are the distant dependent radial reflectances and transmittances of the primary radiation, respectively, per circle ring of width Δρ. The radial spreads of R′(ρ) and T′(ρ) upon point irradiation are extensively described in [30]. In order to simplify the evaluation of Eq. (14), the scattering coefficient is assumed to be independent of the wavelength. Further assumptions are σ >>> α and σ >> z 0 −1.
Figure 5 summarizes representative radial intensity distributions of reflected and transmitted Raman signals. Neglecting secondary terms, the main features are as follows:
Numerical random-walk approach: calculated radial Raman intensities in reflectance and transmittance directions as function of the radial distance ρ from the axis of incidence (μ 0 = 1). Number of incident photons N0 = 1E7. Left part, z 0 = 0.1 cm, σ = 100 cm−1. Right part, z 0 = 0.2 cm, σ = 50, and 100 cm−1. Radial resolution Δρ = 0.001 cm (left curves) and, in order to reduce noise, Δρ = 0.01 cm (right curves). Note the equal ordinate but different abscissa scales
The radial width of the transmitted signal X T ′ is linearly proportional to the layer thickness z 0 and almost independent of the scattering coefficient σ. The amplitude of X′ T’ is independent of z 0 and σ. The mean radial spread can be approximated by
However, the long distance tail extends much wider than the mean value. Hence, the sample radius should be ρ 0 ≥ 3z 0 in order to obtain quantitative correct transmission intensities. Ignoring the small contribution of the scattering coefficient, the binomial radial distribution of X T ′ can be approximated in the nonabsorbing multi-scattering limit by a Gaussian distribution with a pre-exponential factor that normalizes the (0 ≤ ρ ≤ ∞)—integral of the square bracket to unity.
Despite its approximate character, Eq. (16) reproduces the radial spread of X T over a wide range of layer thicknesses and scattering coefficients. Figure 6 shows the radial spread of Raman transmittance X T ′ from multiple scattering layers for layer thicknesses from 0.1 to 0.5 cm based on the analytical approximation of Eq. (16) and on Monte-Carlo simulations. The analytical approximation matches closely the Monte-Carlo simulations. Figure 6 demonstrates clearly that quantitative intensity conclusions in a transmission setup should only be drawn for layer thicknesses not substantially greater than 0.1 cm if the radius ρ D of the detected surface area is limited to 0.3 cm.
The radial distribution of Raman reflectance behaves more complex than Eq. (16), and we did not yet find a satisfying analytical approximation. The X′ R —range of very small distances ρ < σ −1 depends predominantly on the scattering coefficient. The range σ −1 < ρ < z 0 of medium distances depends both on the scattering coefficient and on the layer thickness. The far-distance range ρ > z 0 becomes equal to X T ′, see Fig. 5. Here, the density Φ P of primary radiation is distributed symmetrically to the central layer plane (z = z 0/2) resulting in equal probabilities for reflectance and transmittance. Despite its complex nature, the mean value of radial spread yields in good approximation
However, this equation does not render the wide spread of the long distance tail that requires sample radii and detector apertures as large as in the transmission mode in order to acquire correct reflectance intensities.
Experimental
The Raman reflection and transmission spectra are measured with the nonconfocal RamanRXN1™ analyzer from Kaiser Optical Systems, Ann Arbor, MI equipped with an Invictus™ 785-nm NIR diode laser specified for a maximum output power of 450 mW. The laser irradiates the sample via an optical fiber and additional optics with an accessible wavelength range of Δν = 0 to 1,800 cm-1 Raman shift.
Figure 7 presents schematically the irradiation and detection geometries of the analyzer. The Raman radiation is collected in both the reflection and transmission setup via an array of 50 optical fibers (PhAT™ probe). In the reflection setup a circular area of the sample is homogeneously irradiated via one optical fiber and f = 25 cm optics. The irradiated area with diameter of 0.6 cm is much smaller than the total sample area. The emitted Raman radiation and reflected primary radiation are collected via the PhAT™ probe, carefully separated with filter elements and then transferred to the volume phase transmission grating and the Peltier cooled CCD matrix detector to generate the Raman spectra. In the transmission setup, the laser is guided into a transmission illuminator that irradiates the bottom side of the sample with a diameter of 0.1 cm. The detection unit is the same as for the reflection setup. The Raman intensities X R and X T in reflection and transmission are calibrated with liquid cyclohexane in a thin optical cuvette.
Raman measurements on a cylindrical sample with variable thickness z 0 and fixed diameter 2ρ 0 = 4 cm in the setups for reflection (left) and transmission (right).The Raman radiation is collected in both cases with the PhAT™ head. A circular area of the sample with 0.6 cm diameter is imaged via a lens with 25-cm focal length onto the Raman probe. In the reflection setup, a laser illuminates the sample via an optical fiber and the focusing lens from top with a circular area of 0.6 cm diameter. In the transmission setup, a laser illuminates the bottom side of the sample with 0.1 mm beam diameter
A Lambda 9™ spectrophotometer from PerkinElmer, Waltham, MA with integrating sphere is used for determining the scattering coefficient of poly-tetrafluorethylene (PTFE, Teflon™) by measuring in diffuse transmission and diffuse reflection spectra followed by calculations with the diffusion model [15].
PTFE as optical diffuse material for thickness dependent investigations is supplied by GigahertzOptik, Türkenfeld, Germany in thicknesses of 0.02 and 0.15 cm. Additional thicknesses up to 0.5 cm were cut from a PTFE cylinder with 4 cm diameter or prepared as stacks from the 0.02 cm layer. Cellulose is purchased as filters type MN 615 from Macherey-Nagel, Düren, Germany with 0.015 cm thickness. Acetylsalicylic acid (ASA), product No. 158185000 from Acros Organics, Geel, Belgium, is used to press a cylindrical disc with 2 cm diameter and 0.425 cm thickness as inner layer of a composite triple layer. The upper and the lower layer consists of a PTFE layer (Fig. 11). A white diffuse reflectance standard is produced with a powder press using BaSO4, product No. 11845 from FlukaChemie, Buchs, Switzerland. Thin layers of PTFE and cellulose are placed on the white standard in reflection setup to demonstrate a Raman enhancement (Fig. 13).
Experimental results and discussion
Raman intensity as function of the layer thickness
The calculated Raman intensities in transmission and reflection modes are experimentally tested with PTFE layers of different thicknesses z 0 = 0.02–0.5 cm. The material is strongly scattering, quasi nonabsorbing in the vis–NIR range, and its Raman spectrum is well known [14, 31–33]. We evaluate especially the emission at v = 733 cm−1 Raman shift (A1 stretching mode νs(CF2)) which marks the most intense band in the PTFE Raman spectrum, and the intense sub-band of the characteristic PTFE-triplet located at v = 1,382 cm−1 Raman shift (a component of two split F2 symmetry lines [34, 35], exact assignment not yet available).
Figure 8 summarizes the experimental results. Up to z 0 ≤ 0.15 cm, the measured intensities increase linearly with the layer thickness. Then X R flattens, and X T passes through a maximum. We determine the scattering coefficient of PTFE from the diffuse reflectance and transmittance of a thin layer to σ 800 = 220 cm−1 and then fit the Raman data with the help of Eqs. (8a and 8b). Both X R and X T can be reproduced with the same apparent absorption coefficient of κ app = 0.029 cm−1 (see the curved lines in Fig. 8), corresponding to an albedo of ω = 0.99986 and a maximum diffuse reflectance of R ∞ = 0.975. This range of data sets is often found in the literature for “white” pigment powders. However, if one looks critically on PTFE as highly pure material with negligible vibrational overtone or electronic absorption, the experimental absorption coefficient seems to be extremely high. Hence, we include the constant detector aperture and the strongly z 0-dependent radial Raman spread in the evaluation process (for illustration, see Fig. 6, where it becomes obvious that not all transmitted radiation is collected for thick layers with our detection system, thus quantitative intensity conclusions require aperture radii greater than three times the layer thicknesses), and obtain linear intensity correlations up to z 0 = 0.5 cm for the reflected as well as for the transmitted Raman radiation. The correction reduces the absorption coefficient to a reasonable value of κ < 10−3 cm−1 and increases the maximum diffuse reflectance to R ∞ > 0.995. It should be noticed that detection losses due to the wide radial spread of transmitted signals is one of the main error sources for quantitative determination of small absorption coefficients in scattering materials.
Reflection and transmission Raman intensities at Δν = 1,382 cm−1 Raman shift (X R , left and X T , right) as function of the thickness of PTFE layers. The open circles represent the raw data from the experiment. The curved lines are calculated for X R and X T with the same absorption coefficient κ = 0.029 cm−1 and σ = 200 cm−1. The solid squares with fitted straight lines show the Raman data corrected for finite detector aperture with the help of radial intensity spread curves as in Figs. 5 and 6
Composite layers
Double layers
Double layers with two axially separated different Raman emitters A and B produce signals that do not depend only on the thickness of the emitting layer but also on the thickness and position of the co-layer. Figure 9 illustrates the situation for given emitter thickness and variable co-layer thickness.
The reflected Raman intensity X R of the front layer increases strongly with the thickness of the back layer because part of the initially transmitted Raman signal is now reflected, but mainly because the density ΦP of the primary radiation becomes higher. The reflected intensity of the back layer behaves in the opposite way. If we assume equal thicknesses, z A = z B = z 0/2, then the reflected signal is determined to about 85 % by the front layer and only to 15 % by the back layer. The experimental result is shown in Fig. 13. The ratio in this example is 80 and 20 %, here it has to be taken into account, that the layers do not possess equal thicknesses.
The experiment in reflection geometry (Fig. 10, graphs X R ) proves this result in acceptable accuracy. The double layer of cellulose and PTFE is irradiated alternatively from one of the two sides. The PTFE signal from the front side is approximately four times as high as from the back side (see, e.g., the Raman band of PTFE at 1,382 cm−1).
Raman reflection and transmission intensities X R and X T of a double layer of 0.020 cm PTFE and 0.015 cm cellulose with P orientation of PTFE to the detector and C orientation of cellulose to the detector. The spectra are fluorescence corrected. The reflection spectra differ clearly from each other; the transmission spectra coincide nearly perfectly and show the independence from the side of irradiation. The reflection spectra are vertically displaced to the transmission spectra
Contrary to X R , transmission Raman spectra are expected to be independent of the side of irradiation, see Fig. 9. In both arrangements, X T first increases with the co-layer thickness and then falls down slowly to zero. The spectra of Fig. 10 prove experimentally the independency of the side of irradiation in transmission geometry with a double layer of PTFE and cellulose.
Triple layers
Triple layers A/B/A simulate coated or encapsulated powders, and are expected according to Fig. 4 to behave as follows: X R highlights the spectrum of A, X T highlights the spectrum of B since the generation probability of the central layer is much higher than of the border layers.
Figure 11 shows experimental data for a triple layer arrangement of PTFE (0.15 cm)/ASA (0.425 cm)/PTFE (0.15 cm). The Raman band at 733 cm−1 shift originates from PTFE, the three other bands from ASA. The Raman reflection setup emphasizes clearly the spectrum of PTFE, the transmission setup the spectrum of ASA.
Raman reflection (X R) and transmission intensities (X T) from a composite triple layer system of PTFE 0.15 cm/ASA 0.425 cm/PTFE 0.15 cm. The band at 733 cm−1 Raman shift results from PTFE and is assigned to ν s (CF2)Sym. A1. The remaining bands are assigned to acetylsalicylic acid. The Raman spectrum of ASA does not comprise a band at Δν = 733 cm−1
Stack of layers
Stack of layers allow to assign the position of a given component in a multi-layer of a second component. We investigate the Raman emission of an ASA layer in a stack of four additional mannitol layers as function of the position of ASA. The central position yields much more intense X T -spectra than the border position. Figure 12 compares the experimental data of Svensson et al. (presented at FACSS 2009 [30]) with model calculations according to Fig. 3. The correlation is not perfect but it shows clearly that the central layer regions contribute more to the transmission Raman signal than the border layers.
Transmitted Raman intensity X T (ASA/Mannitol) of a 0.1-cm ASA layer in a stack of four additional 0.1 cm mannitol layers as function of the position of ASA in the stack. The experimental results are compared with model calculations according to Fig. 3. Intensities are relative to the sum of all five positions. Experimental results were presented by Svensson et al. at FACSS 2009 [30]
Enhancement of reflected or transmitted Raman intensities by a white diffuse reflectance standard
Reflecting optical elements are widely used for luminance or contrast amplification. Matousek [22] described an elegant method of Raman enhancement with the help of dielectric mirrors and band-pass filters. In this chapter, we substitute the mirrors by diffuse reflectance standards which are suitable for on-line applications and easy to use over a wide wavelength range. For reflectance enhancement, the thin Raman active layer with diffuse reflectance R 0 and transmittance T 0 is placed in front of a thick standard like microcrystalline barium sulfate (BaSO4) or elemental sulfur, and irradiated with intensity I 0 = 1. For random walk simulations and analytical solutions with the diffusion approximation we use normal incidence which comes close to the experimental condition of Raman excitation. For demonstration of the principal effects we simplify to diffuse incidence. The transmitted light T 0 is repeatedly reflected between the standard and the layer resulting in back-irradiation of the layer with intensity
where R B is the diffuse reflectance of the standard. We neglect absorption, which is a reasonable approximation in thin “white” layers, resulting in R 0 + T 0 = 1, and assume a perfect reflectance standard with R B = 1. Then Eq. (18) simplifies to
The layer is irradiated in this case from both sides with the same intensity. As consequence, the density of the exciting radiation which decays in the free-standing layer linearly with the sample depth, see Eq. (9), is now doubled with its mirror image Φ p, backward resulting in a constant density over the whole layer thickness
Upon normal incidence μ0 = 1, the transmittance and thus the back-radiation density at τ 0 increases against diffuse incidence by a factor of 5/4 (see Table 2), and the density at τ = 0 starts with a lower value of three
The expected enhancement of Raman reflectance is then a product of two factors
-
1.
The transmitted part X T is backscattered and enhances X R by a factor of 1.5 (thick layers) up to a factor of 2 (very thin layers), see Table 2;
-
2.
The density of primary radiation increases upon diffuse incidence by a factor of 2, and upon normal incidence by a factor of ≤2.5.
Hence, the total enhancement lies somewhere between a factor of 3 and 4.
Figure 13 presents a series of experimental results on a thin PTFE layer (0.02 ± 0.001 cm) in combination with a thin cellulose layer (0.015 ± 0.002 cm) and a thick BaSO4 reflectance standard (0.5 cm). The Raman intensities are normalized to the backscattered band maximum X R at Δν = 733 cm−1 of the single PTFE layer. Addition of the cellulose layer as background strongly increases X R of PTFE (case II of Fig. 13) whereas X T remains almost unaffected. Addition of cellulose as foreground (case III) strongly reduces X R whereas X T remains again almost unaffected. These results are often quoted as argument that X T is superior to X R in composite systems since X R probes only the regions close to the surface whereas X T probes also the deep parts of the sample. The cases V and VI of Fig. 13 give clear evidence how to overcome these restrictions. The bi-layer system is now measured in both orientations on the BaSO4 standard. The backscattered intensity increases in both orientations strongly against the free-standing bi-layer. The increase of case VI with PTFE inside is even somewhat stronger than case V with PTFE directly exposed to the laser. Most of the results agree with the model calculations of Fig. 9 and Eqs. (18)–(20) for diffuse incidence. The increase from case V to case VI can be explained only with normal incidence where, according to Eq. (21), the deep layer produces somewhat higher signals than the layer directly exposed to the surface. Apart from these minor corrections, the general statement is valid for analytical applications: Raman reflection spectroscopy probes the whole depth of a multiple scattering sample with equal statistical weight if the sample is placed in front of a white diffuse reflector.
Experimental Raman intensities (integrated emission band with maximum at Δv = 733 cm−1) of PTFE with layer thickness z 0 = 0.02 cm in different configurations. I, Free-standing layer; II, in front of a cellulose filter paper with thickness z 0 = 0.015 cm; III, behind the paper, IV: PTFE on a thick BaSO4diffuse reflectance standard; V, configuration II on BaSO4; VI, configuration III on BaSO4. The remitted Raman intensity of the single PTFE-layer is normalized to X R = 1. The experimental errors are ΔX≈±0.02X
Figure 14 illustrates case IV of Fig. 13 with three prominent Raman bands of a thin PTFE layer placed on a BaSO4 diffuse reflectance standard. The Raman reflection signals are intensified approximately by a factor of 3.5 relative to the self-supporting PTFE layer of case I.
Detail of Raman reflection spectra of PTFE with layer thickness z 0 = 0.20 cm. Black spectrum, PTFE self-supporting; dark yellow spectrum, PTFE on BaSO4 background (Raman bands with asterisks result from BaSO4). The Raman reflection intensities of the bands at 1,216, 1,301, and 1,382 cm−1 of PTFE on BaSO4 are intensified approximately by a factor of 3.5 relative to the self-supporting PTFE layer (intensities from integrated emission bands)
Enhancement of X T can be achieved with a white diffuse reflector in front of the Ramanactive layer. The front reflector contains a small pinhole of diameter d ≤ 1 mm for collimated laser irradiation. The pinhole reduces the effective diffuse reflectance of the front reflector to R eff < 1, where the reduction depends on the radial spreads of the reflected primary and Raman radiations. The repeated reflection of I 0 between the Raman active layer and the front reflector with R p, eff produces, similar to Eq. (18), an additional irradiance in forward direction
The total irradiance is then
and, instead of Eq. (9), the radiation density inside the layer is
Equation (24) is inserted in Eq. (8b), and the enhanced X T can be calculated after replacing the reflectance R (z) of the virtual layer without front reflector by the modified reflectance R (z), eff’ that considers the influence of the front reflector with the effective reflectance R X, eff for Raman radiation
The achievable enhancement of X T depends strongly on the layer thickness and the pinhole diameter. Thin layers as PTFE of Fig. 13 with z 0 = 0.02 cm require according to random walk simulations very small pinholes of d≈100 μm in order to obtain an enhancement by a factor of five. The same enhancement is obtained for thicker layers of z 0≈0.2 cm already with a large pinhole of d≈1 mm.
It should be noted that the signal of highly enhanced X T is generated mainly close to the irradiated surface and no longer symmetrically to the sample center, as it is the case shown in Fig. 3. Enhanced X T has lost its ability of deep sample probing and has transferred this quality to enhanced X R .
Conclusions
In scattering layers with negligible background absorption and no axial concentration gradients, the reflected and transmitted Raman intensities (X R and X T ) show a linear increase with the layer thickness whereas X T is at least half as intense as X R . Under the initially mentioned conditions both the reflection and transmission setups are equally suitable modes. The radial expansion of the signals increases linearly with the layer thickness, where X T spreads wider than X R . For correct intensity measurements, the diameter of the detected surface area must be in the transmission mode at least six times the layer thickness.
In scattering layers with some background absorption, the Raman intensities are reduced by re-absorption. X R saturates for thick layers at levels that depend strongly on the absorption coefficient. X T passes through a maximum and then reduces to zero. Hence, the R-mode is superior in those cases to the T-mode. The strong decrease of X T with absorption is a consequence of the long path length of transmitted radiation. Both X T and X R decrease much stronger with the absorption coefficient than the diffuse reflectance of primary radiation.
In composite layers with axial concentration gradients we get complementary information from the R- and T-modes. The mean reflected signal originates from the first quarter of the layer depth, whereas the mean transmitted signal originates predominantly from the central regions. Here, for probing the inner volume of a sample the T-mode is superior to the R-mode.
The intensity of Raman signals can be significantly enhanced by reflecting mirrors arranged in the close environment of the sample. We propose especially white diffuse reflectors at the sample backside. This arrangement intensifies X R by a factor of 3 to 4 and produces constant irradiation densities over the whole sample depth. Hence, X R probes in this configuration the whole sample with equal statistical weight. Highly enhanced X T is generated close to the irradiated surface. Enhanced X T has lost its ability of deep sample probing and has transferred this quality to enhanced X R . The authors consider enhanced Raman reflection spectroscopy as promising tool for process analytical technology.
References
Salzer R, Siesler HW (eds) (2009) Infrared and Raman spectroscopic imaging, 1st edn. Wiley, Weinheim
Buckley K, Matousek P (2011) Recent advances in the application of transmission Raman spectroscopy to pharmaceutical analysis. J Pharm Biomed Anal 55:645–652. doi:10.1016/j.jpba.2010.10.029
Wikström H, Lewis IR, Taylor LS (2005) Comparison of sampling techniques for in-line monitoring using Raman spectroscopy. Appl Spectrosc 59(7):934–941
Kalantri PP, Somani RR, Makhija DT (2010) Raman spectroscopy: a potential technique in analysis of pharmaceuticals. Der Chemica Sinica 1:1–12
Johansson J, Sparen A, Svensson O, Folestad S, Claybourn M (2007) Quantitative transmission Raman spectroscopy of pharmaceutical tablets and capsules. Appl Spectrosc 61:1211–1218. doi:10.1366/000370207782597085
Sparén A, Johansson J, Svensson O, Folestad S, Clayborn M (2009) Transmission Raman spectroscopy for quantitative analysis of pharmaceutical solids. Am Pharmaceut Rev 62–71
Gao X, Jehng J-M, Wachs IE (2002) In situ UV–vis–NIR diffuse reflectance and Raman spectroscopic studies of propane oxidation over ZrO2-supported vanadium oxide catalysts. J Catal 209(1):43–50. doi:10.1006/jcat.2002.3635
Eliasson C, Matousek P (2007) Noninvasive authentication of pharmaceutical products through packaging using spatially offset Raman spectroscopy. Anal Chem 79(4):1696–1701. doi:10.1021/ac062223z
Stone N, Baker R, Prieto CH, Matousek P (2008) Novel Raman signal recovery from deeply buried tissue components. In: Mahadevan-Jansen A, Petrich W, Alfano RR, Katz A (eds) Biomedical optical spectroscopy. Proceedings of SPIE. SPIE-OSA, p 68530N. doi:10.1117/12.786442
Srinivasan S, Schulmerich M, Cole JH, Dooley KA, Kreider JM, Pogue BW, Morris MD, Goldstein SA (2008) Image-guided Raman spectroscopic recovery of canine cortical bone contrast in situ. Opt Express 16(16):12190–12200
Matousek P (2006) Inverse spatially offset Raman spectroscopy for deep noninvasive probing of turbid media. Appl Spectrosc 60(11):1341–1347
Eliasson C, Macleod NA, Jayes LC, Clarke FC, Hammond SV, Smith MR, Matousek P (2008) Non-invasive quantitative assessment of the content of pharmaceutical capsules using transmission Raman spectroscopy. J Pharm Biomed Anal 47:221–229. doi:10.1016/j.jpba.2008.01.013
Hargreaves MD, MacLeod NA, Smith MR, Andrews D, Hammond SV, Matousek P (2011) Characterization of transmission Raman spectroscopy for rapid quantitative analysis of intact multi-component pharmaceutical capsules. J Pharm Biomed Anal 54:463–468. doi:10.1016/j.jpba.2010.09.015
Nah S, Kim D, Chung H, Han S-H, Yoon M-Y (2007) A new quantitative Raman measurement scheme using Teflon as a novel intensity correction standard as well as the sample container. J Raman Spectros 38(5):475–482. doi:10.1002/jrs.1667
Oelkrug D, Brun M, Rebner K, Boldrini B, Kessler RW (2012) Penetration of light into multiple scattering media; model calculations and reflectance experiments. Part I: the axial transfer. Appl Spectrosc 66(8):934–943. doi:10.1366/11-06518
Matousek P, Clark IP, Draper ERC, Morris MD, Goodship AE, Everall N, Towrie M, Finney WF, Parker AW (2005) Subsurface probing in diffusely scattering media using spatially offset Raman spectroscopy. Appl Spectrosc 59(4):393–400
Oelkrug D, Brun M, Hubner P, Egelhaaf H-J (1996) Optical parameters of turbid materials and tissues as determined by laterally resolved reflectance measurements. Proc SPIE 2925:106–115. doi:10.1117/12.260831
Schrader B, Bergmann G (1967) Die Intensität des Ramanspektrums polykristalliner Substanzen. Fresenius J Anal Chem 225(2):230–247. doi:10.1007/bf00983673
Matousek P, Parker AW (2006) Bulk Raman analysis of pharmaceutical tablets. Appl Spectrosc 60(12):1353–1357. doi:10.1366/000370206779321463
Everall N, Matousek P, MacLeod N, Ronayne KL, Clark IP (2010) Temporal and spatial resolution in transmission Raman spectroscopy. Appl Spectrosc 64:52–60. doi:10.1366/000370210790571963
Everall N, Priestnall I, Dallin P, Andrews J, Lewis I, Davis K, Owen H, George MW (2010) Measurement of spatial resolution and sensitivity in transmission and backscattering Raman spectroscopy of opaque samples: impact on pharmaceutical quality control and Raman tomography. Appl Spectrosc 64:476–484. doi:10.1366/000370210791211646
Matousek P (2007) Raman signal enhancement in deep spectroscopy of turbid media. Appl Spectrosc 61(8):845–854
Oelkrug D (1994) Fluorescence spectroscopy in turbid media and tissues. In: Lakowicz JR (ed) Topics in fluorescence spectroscopy, vol 4. Plenum Press, New York, pp 223–253. doi:10.1007/0-306-47060-8_8
Allen E (1964) Fluorescent white dyes: calculation of fluorescence from reflectivity values. J Opt Soc Am 54(4):506–514
Oelkrug D, Kortüm G (1968) Zur Berechnung der Lumineszenzreabsorption bei pulverförmigen Substanzen. Zeitschrift für Physikalische Chemie NF 58:181–188. doi:10.1524/zpch.1968.58.1_4.181; see also Kortüm G (1969) Reflectance Spectroscopy, Springer, Berlin
Fukshansky L, Kazarinova N (1980) Extension of the Kubelka–Munk theory of light propagation in intensely scattering materials to fluorescent media. J Opt Soc Am 70(9):1101–1111
Gade R, Kaden U (1990) True luminescence spectra and luminescence quantum yields of molecules adsorbed on light-scattering media. Part 1.—theory. J Chem Soc Chem, Faraday Trans 86(22):3707–3712
Oelkrug D, Brun M, Mammel U (1994) Spatial fluorescence profiles in multiple light scattering systems. J Lumin 60–61:422–425. doi:10.1016/0022-2313(94)90181-3
Kubelka P (1948) New contributions to the optics of intensely light-scattering materials. Part I. J Opt Soc Am 38(5):448–448
Oelkrug D, Brun M, Hubner P, Rebner K, Boldrini B, Kessler RW (2012) Penetration of light into multiple scattering media: model calculations and reflectance experiments. Part II: the radial transfer. Appl Spectrosc 66(8):934–943
Koenig JL, Boerio FJ (1969) Raman scattering and band assignments in polytetrafluoroethylene. J Chem Phys 50(7):2823–2829
Peacock CJ, Hendra PJ, Willis HA, Cudby MEA (1970) Raman spectrum and vibrational assignment for poly(tetrafluoroethylene). J Chem Soc Inorg Phys Theor 2943–2947
Rabolt JF, Fanconi B (1978) Raman scattering from finite polytetrafluoroethylene chains and a highly oriented TFE-HFP copolymer monofilament. Macromolecules 11(4):740–745. doi:10.1021/ma60064a025
Legeay G, Coudreuse A, Legeais J-M, Werner L, Bulou A, Buzaré J-Y, Emery J, Silly G (1998) AF fluoropolymer for optical use: spectroscopic and surface energystudies; comparison with other fluoropolymers. Eur Polym J 34(10):1457–1465. doi:10.1016/s0014-3057(97)00289-9
Bratescu MA, Saito N, Takai O (2006) Treatment of immobilized collagen on poly(tetrafluoroethylene) nanoporous membrane with plasma. Jpn J Appl Phys, Part 1 45:8352–8357. doi:10.1143/jjap.45.8352
Acknowledgment
We thank Kaiser Optical Systems for the allocation of a RamanRXN1™ system.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Oelkrug, D., Ostertag, E. & Kessler, R.W. Quantitative Raman spectroscopy in turbid matter: reflection or transmission mode?. Anal Bioanal Chem 405, 3367–3379 (2013). https://doi.org/10.1007/s00216-013-6719-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00216-013-6719-2