1 Introduction

On October 2016, almost 200 nations adopted the Kigali Amendment to the Montreal Protocol, a deal which is meant to phase-down production and use of hydrofluorocarbons (HFCs) and thought of having a decisive contribution to keep the global temperature rise under 2 \(^{\circ }{\mathrm{C}}\), a target agreed at the Paris climate conference of 2015. HFCs, which are largely used [1] as second-generation replacements to the environmental hazardous CFCs [2,3,4,5,6,7], possess elevated values of global warming potential [8] (GWP), therefore contributing to the global warming problem addressed in the Paris and Kigali meetings. Hydrofluoroethers (HFEs) and hydrofluoropolyethers (HFPEs) are considered and recommended as an alternative [9,10,11,12,13,14,15] to be used as third-generation replacements because of their zero ozone depletion potential (ODP) and low GWP [13, 16,17,18,19,20,21].

Tropospheric oxidant attack by OH radicals is considered to be the main degradation pathway of oxygenated volatile organic compounds (OVOCs) [22,23,24,25]. However, there is not a great deal of research on the atmospheric chemistry aspects of the mechanisms, kinetics and reactivity of HFPEs toward the OH radical [17, 26,27,28,29,30,31,32].

HFPEs represent a family of linear oligomeric fluorinated compounds with the generic formula of [14]

$$\begin{aligned} {\mathrm{R}}{-}(\mathrm{OCF}_2\mathrm{CF}_2)_{ p}(\mathrm{OCF}_2)_q{-}\mathrm{OR} \end{aligned}$$
(1)

where p and q define the number of repeating monomeric units. When R is chosen to be an alkyl substituent, these HFPEs are called \(\alpha ,\omega\)-dialkoxyfluoropolyethers (DA-FPEs) and are considered to be promising in terms of having low atmospheric impact [27, 30,31,32,33,34,35,36]. Previous investigations concerning the calculation of these rate constants for DA-FPEs are extremely limited [27, 31, 32], with experimental work [27] solely focusing on \(\alpha ,\omega\)-dimethoxyfluoropolyethers (DM-FPEs) [37, 38], which are obtained when \(\mathrm{\mathrm R{=}CH}_3\). This class has been developed as potential CFC replacement for foaming and fire extinguishing agents, cleaning agents for sophisticated electronic devices and heat transfer fluids [27, 34, 36, 39, 40]. Regarding its atmospheric degradation, it has been claimed [27, 30, 36, 37] that the extra reactive sites for OH radical attack provided by the \({\mathrm{CH}}_3\) groups in DM-FPEs are advantageous in limiting their atmospheric lifetimes, hence reducing GWP. A very recent investigation [31] has shed new light on this subject, suggesting that the reactivity patterns of DA-FPEs toward OH are mainly related to the barrier heights involving only the \(\alpha\)-hydrogens on the alkyl groups, i.e., to the chemical environment at the \(\alpha\)-carbons. As a consequence, branching ratios for the \(\alpha\)-hydrogens were also shown to be much larger than for \(\beta\) and \(\gamma\)-hydrogens: \(\varGamma _{\alpha }^{\mathrm{R}} \gg \varGamma _{\beta ,\gamma }^{\mathrm{R}}\) for \({\mathrm{R}}={\mathrm{C}}_2{\mathrm{H}}_5,~{\mathrm{C}}_3{\mathrm{H}}_7\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\).

Reactions between OH and HFPEs can be represented by the following generic equation:

$$\begin{aligned} {\mathrm{R}}{-}(\hbox {OCF}_2\hbox {CF}_2)_{ p}(\hbox {OCF}_2)_{ q}{-}\hbox {OR} + \mathrm{OH} \xrightarrow {{k_{pq}^{\mathrm{R}}}}~{\text {products}} \end{aligned}$$
(2)

In order to solidify our understanding of the reactivity patterns of DA-FPEs, we have chosen to extend our studies by considering a longer perfluoropolyether chain (p0q2 instead of p0q1 of ref [31]) and two specific R terminating groups: \({\mathrm{R}}{=}{\hbox {C}}_2\hbox {H}_5\) and \({\mathrm{CH}}(\hbox {CH}_3)_2\), which simplifies the above equation to

$$\begin{aligned} {\mathrm{R}}{-}(\hbox {OCF}_2)_2{-}\hbox {OR} + \mathrm{OH} \xrightarrow {{k_{02}^{\mathrm{R}}}}~{\text {products}} \end{aligned}$$
(3)

with associated rate constants \(k_{02}^{{\mathrm{C}}_2{\mathrm{H}}_5}\) and \(k_{02}^{{\mathrm{CH}}{({\mathrm{CH}}_3)}_2}\).

The calculations were performed employing a cost-effective protocol [31] developed for bimolecular reactions and based on multiconformer transition state theory (MC-TST) [41,42,43,44]. Such methodology has been successfully used very recently in the calculation of complex cases of reaction (2), namely p0q2, p0q3 and p2q0 for \(\hbox {R}{=}\hbox {CH}_3\) [32]. The computational details of such procedure will be given in the next section, and the results and discussion are subsequently presented. The conclusions are gathered in the last section.

2 Computational methods

In order to calculate the rate coefficients associated with reaction (3), some considerations should be made beforehand. We start by stating that the reactions between HFPEs and OH share mechanistic details found in many radical–molecule reactions of atmospheric interest (see Refs. [45, 46] and references therein), namely a reaction path in which there is the formation of pre-reactive complexes (PRC) and product complexes (PC) connected to the hydrogen abstraction transition states (TS). Such reaction path has been presented in detail in previous work [31, 32]. We should also state that HFPEs are known to have a rich conformational variety  [31, 32, 47,48,49]. Including such conformational richness in the transition state theory equations [50] leads to MC-TST [31, 41,42,43,44] or to improvements and extensions to variational TST [Refs. [51, 52] and references therein]. For the bimolecular reactions here studied, the MC-TST equation can be written as [31]

$$\begin{aligned} k_{pq}^{\mathrm{R}} = \kappa (T) \frac{k_\mathrm{B}T}{h Q_\mathrm{OH}} \frac{\sum _i^M \frac{\alpha _i \omega _{{\text {TS}}_i} Q_{{\text {TS}}_i} }{\sigma _{\mathrm{rot},{\text {TS}}_i}} }{\sum _j^N \frac{\alpha _j \omega _{{\text {HFPE}}_j} Q_{{\text {HFPE}}_j} }{\sigma _{\mathrm{rot},{\text {HFPE}}_j}} } \mathrm{e}^{-V^{\ddagger }/k_\mathrm{B}T} \end{aligned}.$$
(4)

Here, the Q’s represent the partition functions for reactants and transition states, which are evaluated for translational, electronic, vibrational and rotational energies with \(Q=q_\mathrm{t}q_\mathrm{e}q_\mathrm{v}q_\mathrm{r}\). The sum in the denominator of Eq. (4) runs through the total number of N available HFPE conformers, while the numerator runs through all possible (M) available transition state conformers [31, 42, 50] which are accounted by considering an OH attack on each hydrogen atom of a particular HFPE conformer [31, 32]. Thus, M is found by multiplying the number of hydrogen atoms of each HFPE conformer by the total number of HFPE conformers, \(M=n_{\mathrm{H}} \times N\). For the two cases presented in this work, we will have \(n_{\mathrm{H}}=10\) and 14 for \({\mathrm{R}}=\hbox {C}_2\hbox {H}_5\) and \({\mathrm{CH}}(\hbox {CH}_3)_2\), respectively. The quantities represented by \(\omega _{{\text {HFPE}}_j}=\mathrm{e}^{-(E_{{\text {HFPE}}_j}-E_{{\text {HFPE}}_0})/k_\mathrm{B}T}=\mathrm{e}^{-\varDelta E_{{\text {HFPE}}_j}/k_\mathrm{B}T}\), \(\omega _{{\text {TS}}_i}=\mathrm{e}^{-(E_{{\text {TS}}_i}-E_{{\text {TS}}_0})/k_\mathrm{B}T}=\mathrm{e}^{-\varDelta E_{{\text {TS}}_i}/k_\mathrm{B}T}\), \(\sigma _{\mathrm{rot},{\text {HFPE}}_j}\), \(\sigma _{\mathrm{rot},{\text {TS}}_i}\), \(\alpha _j\) and \(\alpha _i\) are the thermal weight factors, rotational symmetry numbers [42] and reaction path degeneracy parameters [31] of conformations \({\text {HFPE}}_j\) and \({\text {TS}}_i\), respectively. The zero-point energy (ZPE)-corrected energy of conformations \({\text {HFPE}}_j\) and \({\text {TS}}_i\) is represented by \(E_{{\text {HFPE}}_j}\) and \(E_{{\text {TS}}_i}\). The quantity \(V^{\ddagger }\) is calculated as \(V^{\ddagger }=E_{{\text {TS}}_0}-(E_{{\text {HFPE}}_0}+E_\mathrm{OH})\) and represents the difference between the ZPE-corrected energy of the most stable transition state conformation and the ZPE-corrected energy of the most stable reactants [31, 42, 44, 50]. Finally, \(\kappa (T)\) is the tunneling correction associated with the lowest energy TS, calculated through the Eckart method [53], widely used in atmospheric chemistry studies [44, 50, 54,55,56,57,58,59,60,61,62,63,64,65,66,67,68].

The necessary electronic structure calculations were performed with the GAMESS package [69], with the choice of model chemistry being made according to our own cost-effective philosophy [31, 49]. We have utilized the M08-HX/apcseg-2//M08-HX/pcseg-1 model chemistry, with the optimizations and single-point energies being performed with M08-HX [70] from the Minnesota family of functionals and with Jensen’s [71] new segmented polarization consistent double- and triple-\(\zeta\) basis sets.

Our choice of opting for DFT calculations relies on the fact that they can be accurate while having a low CPU time scaling (typically around \(K^4\), where K is a measure of the size of the molecule), a very important feature concerning calculations on increasingly complex HFPEs. On the other hand, the Minnesota family of functionals is used with good accuracy in many research investigations concerning the reactivity of VOCs [47, 65, 67, 72,73,74,75,76,77,78,79,80,81,82,83]. Although M06-2X [84] is more frequently used than M08-HX [70], we point out that for hydrogen transfer barrier heights, M08-HX has a mean unsigned error (MUE) 0.2 \({\mathrm{kcal~mol}}^{-1}\) lower than M06-2X for the DBH76 data set [85,86,87] and 0.4 \(\mathrm{kcal~mol}^{-1}\) lower than M06-2X for the HTBH38 data set, a component of DBH76 [84, 88]. The more recent M11 [89] functional has a MUE for the HTBH38 data set almost 0.6 \(\mathrm{kcal~mol}^{-1}\) higher than M08-HX. Our previous calculations [49] also reveal that M06-2X and M08-HX yield similar geometries and relative energies for various DA-FPEs.

We performed the M08-HX calculations using the new segmented polarization consistent basis sets of Jensen [71] without (pcseg-n) and with diffuse augmentation (aug-pcseg-n), which have been optimized for DFT methods. These basis sets represent not only an improvement (both in accuracy and in computational efficiency) to the previous polarization consistent (pc-n) basis sets [90,91,92,93,94] but also a low error alternative to several other basis sets [71], regarding DFT calculations. It was also shown [71] that the basis set errors of pcseg-n at a given \(\zeta\) quality level are lower than other existing basis sets while being among the computationally most efficient.

The \(V^{\ddagger }\) barrier height and the \(\kappa (T)\) tunneling factor were also calculated at the more expensive M08-HX/apcseg-2//M08-HX/pcseg-2 level of theory in order to have an error bar associated with the rate constants.

The several steps and details making up our cost-effective protocol have been carefully described in our previous work [31, 32], and the reader is referred to those publications for a more in-depth analysis.

3 Results and discussion

One of the important aspects of the aforementioned protocol [31] is the reduction in the number of necessary electronic structure calculations. This relates directly to the magnitude of the N and M indexes of Eq. (4). In the particular case of the calculations performed in this work, the reduction in the number of DA-FPE conformers originating from the removal of duplicates and enantiomers after conformer generation is minimal: 3 and 5% for \({\mathrm{R}}{=}\hbox {C}_2\hbox {H}_5\) and \({\mathrm{CH}}(\hbox {CH}_3)_2\), respectively. This reduction was achieved by performing a similarity evaluation (SE) step [31], which consists of running a pairwise comparison between all generated DA-FPE conformers using a superimposing algorithm [95] and evaluating geometrical similarity by minimizing the sum over all distances between each corresponding atom in a pair of structures. The SE step is applied only to the reactants [31], since it is assumed that each OH attack on a unique DA-FPE conformer will originate a unique TS structure. The reduction in the number of TS conformers, which will be explained next, is quite considerable and essential in lowering the computational effort: 71 and 79% for \({\mathrm{R}}{=}\hbox {C}_2\hbox {H}_5\) and \({\mathrm{CH}}(\hbox {CH}_3)_2\), respectively. This means that for \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) we have \(N=229\) and \(M=670,\) while for \({\mathrm{CH}}({\mathrm{CH}}_3)_2\) we end up with \(N=218\) and \(M=686\). Note that if we wanted to generate all possible TS conformers, then M would have the values of 2290 and 3052 for \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\), respectively. This reduction was achieved by ordering the DA-FPE conformers by ZPE-corrected energy and generating the TS conformers from the set of DA-FPEs that summed up to 90% of the total fractional population. Such an approach was shown to introduce a low error on the final rate constants [31] while achieving major computational savings by reducing the number of TS optimizations [31, 32], as it is also the case in the present investigation.

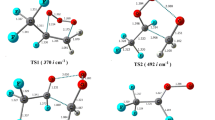
We now present the two IRC paths connecting the TS to PRC and PC for the studied cases, calculated at the M08-HX/pcseg-1 level (Fig. 1) along with the necessary data to calculate both tunneling factors (Table 1). It can be observed that the tunneling factors decrease with the size of the R alkyl substituent. This is essentially related to the values of the imaginary frequency of the transition states and becomes even more evident by comparing these numbers to the ones making up the \(\kappa _{02}^{{\mathrm{CH}}_3}\) case [32]. This progressive decrease in the imaginary frequencies was shown [31] to be related to the reduction in the inductive effects [6, 12, 47, 48, 96] felt by the abstracted hydrogen atom, which can also be used to rationalize the increasing values of the perpendicular looseness [97] (sum of the making and forming bond distances): 2.54 Å for \(\mathrm R{=}{\mathrm{CH}}_3\) [32], 2.57 and 2.60 Å for \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\), respectively.

Fig. 1
figure 1

Full IRC paths for the \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\) cases, calculated at the M08-HX/pcseg-1 level of theory and plotted with respect to each of the PRC (\(s=0~\mathrm{amu}^{1/2}~\mathrm{a}_{0}\))

Full size image
Table 1 Necessary data to calculate the \(\kappa _{02}^{\mathrm{R}}\) tunneling factors: imaginary frequencies of the transition states (\(\nu ^{\ddagger }\), in \(\mathrm{cm}^{-1}\), calculated at the M08-HX/pcseg-1 level) and forward and reverse barrier heights (\(V_1\) and \(V_2\), in \({\mathrm{kcal~mol}^{-1}}\), calculated at the M08-HX/apcseg-2//M08-HX/pcseg-1 level)
Full size table

The MC-TST rate constants for the two reactions studied in this work are collected in Table 2, along with the value of \(k_{02}^{{\mathrm{CH}}_3}(\mathrm{MC -\mathrm TST})\) [32]. It can be seen that replacing the methyl groups by ethyl groups increases the rate constant by more than twenty times, but a replacement by the isopropyl groups leads to a lower increase of slightly over ten times. A similar behavior is observed for the p0q1 case [31], and this will be explored in more detail in future work when all calculations for \({\mathrm{R}}{=}\hbox {CF}_2\hbox {H}\) are available. We should stress that the error bars of Table 2 are obtained by observing the effect of calculating \(V^{\ddagger }\) and \(\kappa (T)\) at the M08-HX/apcseg-2//M08-HX/pcseg-2 level of theory, which will ultimately affect the rate constants [31, 32]. However, it should be noted that the M08-HX functional has a MUE of 1 \(\mathrm{kcal~mol}^{-1}\) for the DBH76 data set [70]. Using this value as a systematic error in the barrier heights, the errors bars for \(k_{02}^{{\mathrm{C}}_2{\mathrm{H}}_5}\) and \(k_{02}^{{\mathrm{CH}}({\mathrm{CH}}_3)_2}\) become \(2.3 \times 10^{-13}\) and \(1.3 \times 10^{-13}\) \(\mathrm{cm}^3\,\mathrm{molecule}^{-1}\,\mathrm{s}^{-1}\), respectively.

Table 2 MC-TST rate constants for the reaction between the OH radical and \({\mathrm{R}}{-}(\hbox {OCF}_2)_2{-}\hbox {OR}\) calculated at 298.15 K
Full size table

In order to better understand the effect of increasing the chain length from p0q1 to p0q2 for the \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\) cases, we have used our own approach [32] for the \({{\mathrm{R}}}{=}{\mathrm{CH}}_3\) case, where we fix R and calculate the ratio between the “long-chain” rate constant and the “short-chain” one that we consider as reference. Here, we will take \(k_{01}^{\mathrm{R}}\) as the reference and calculate the two ratios as

$$\begin{aligned} \eta _{02}^{\mathrm{R}}(\hbox {MC-TST}) = \frac{k_{02}^{\mathrm{R}} (\hbox {MC-TST}) }{k_{01}^{\mathrm{R}} (\hbox {MC-TST}) } \end{aligned}.$$
(5)

This equation can be written in a way [31, 32] we can distinguish its three different contributions originating from Eq. (4)

$$\begin{aligned} \eta _{02}^{\mathrm{R}}(\hbox {MC-TST}) = \frac{\kappa _{02}^{\mathrm{R}} }{\kappa _{01}^{\mathrm{R}} } \frac{{\mathcal {Q}}_{02}^{\mathrm{R}}(90\%) }{{\mathcal {Q}}_{01}^{\mathrm{R}}(90\%) } \frac{\varDelta _{02}^{\mathrm{R}} }{\varDelta _{01}^{\mathrm{R}} } \end{aligned}$$
(6)

with the first term concerning the ratio between tunneling factors, the second term concerning just the ratio between the sums of Eq. (4) and the third term concerning the ratio between the terms involving the exponential function containing the barrier heights. The results for \(\eta\) and their different contributions are given in Table 3, where we also include the \(\eta _{02}^{{\mathrm{CH}}_3}\) case [32] for clarity. Interestingly, both \(\eta\) values calculated in this work are the same, which means that increasing the chain length from p0q1 to p0q2 reduces the rate constant by a factor of 0.41 for both \({\mathrm{R}}={\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\) cases. However, such an agreement is seen to be fortuitous, as the three contributions for each of the \(\eta\) values are considerably different. Such a fortuitous agreement in the \(\eta\) values is also seen [32] between \(\eta _{02}^{{\mathrm{CH}}_3}\) and \(\eta _{03}^{{\mathrm{CH}}_3}\), which of course leads to the question of what will happen to the \(\eta _{03}^{{\mathrm{C}}_2{\mathrm{H}}_5}\) and \(\eta _{03}^{{\mathrm{CH}}({\mathrm{CH}}_3)_2}\) cases. The close agreement between \(k_{02}^{{\mathrm{CH}}_3}\) and \(k_{03}^{{\mathrm{CH}}_3}\) [32], although seen to be fortuitous by inspection of the three contributions to the \(\eta\) values, seems to suggest that increasing the chain length from p0q2 to p0q3 could also leave the rate constants practically unchanged for \({\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5\) and \({\mathrm{CH}}({\mathrm{CH}}_3)_2\) cases. Testing this hypothesis would require time-consuming calculations that remain outside the scope of our present objectives, at least for the time being.

Table 3 The three contributions for \(\eta _{02}^{\mathrm{R}}\) (see Eq. (6) and text) and its final value
Full size table

In terms of the importance of which carbon sites determine \(V^{\ddagger }\), it is seen that the chemical environment in the \(\alpha\)-carbons defines the barrier height and the higher reactivity of the compounds with \({{\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5}\) and \({{\mathrm{CH}}({\mathrm{CH}}_3)_2}\) [31]. Such a claim is supported not only by the values of the branching ratios (\(\varGamma _{\alpha ,\beta }^{\mathrm{R}}\)) concerning the hydrogen abstractions at the \(\alpha\) and \(\beta\) carbons (\(\varGamma _{\alpha }^{{\mathrm{C}}_2{\mathrm{H}}_5}=97\%\), \(\varGamma _{\beta }^{{\mathrm{C}}_2{\mathrm{H}}_5}=3\%\) and \(\varGamma _{\alpha }^{{\mathrm{CH}}({\mathrm{CH}}_3)_2}=78.8\%\) and \(\varGamma _{\beta }^{{\mathrm{CH}}({\mathrm{CH}}_3)_2}=21.2\%\)), but also with the values of the lowest barrier heights of each type of hydrogen [31, 76] (\(V_{\alpha ,\beta }^{\ddagger ,\mathrm R}\)), calculated at the M08-HX/apcseg-2//M08-HX/pcseg-1 level: \(V_{\alpha }^{\ddagger ,{\mathrm{C}}_2{\mathrm{H}}_5}=0.47\), \(V_{\beta }^{\ddagger ,{\mathrm{C}}_2{\mathrm{H}}_5}=1.40\); \(V_{\alpha }^{\ddagger ,{\mathrm{CH}}({\mathrm{CH}}_3)_2}=-\,1.17\), \(V_{\beta }^{\ddagger ,{\mathrm{CH}}({\mathrm{CH}}_3)_2}=0.63\) \({\mathrm{kcal~mol}^{-1}}\).

3.1 Atmospheric lifetimes

The atmospheric lifetime of DA-FPEs will be determined by their reaction with OH radicals. By using a value of \([{\mathrm{OH}}]=1 \times 10^{6} \, {\text{molecules}}\,{\text{cm}}^{-3}\) for the global average concentration [98], the tropospheric lifetimes can be estimated via \(\tau _{02}^{\mathrm{R}}=1/k_{02}^{\mathrm{R}}[\mathrm{OH}]\). Using the calculated MC-TST rate constants, we obtain the following lifetimes: \(\tau _{02}^{{\mathrm{C}}_2{\mathrm{H}}_5} \approx 41\) days and \(\tau _{02}^{{\mathrm{CH}}({\mathrm{CH}}_3)_2} \approx 72\) days.

4 Conclusions

In this investigation, we have calculated the theoretical rate constants for the reactions between two DA-FPEs and the OH radical. To our knowledge, it is the first time these rate coefficients (\(k_{02}^{{\mathrm{C}}_2{\mathrm{H}}_5}\) and \(k_{02}^{{\mathrm{CH}}({\mathrm{CH}}_3)_2}\)) are being reported. Due to the size and conformational complexity of these species, our calculations were performed within the framework of a cost-effective protocol for MC-TST based on DFT electronic structure calculations, developed to tackle challenging bimolecular hydrogen abstraction reactions such as the ones here presented. If one includes the \(k_{02}^{{\mathrm{CH}}_3}\) rate constant in the discussion, it can be concluded that: (1) OH-initiated oxidation rate constants of the DA-FPEs involving the ethyl and isopropyl groups have the same order of magnitude, which in turn is approximately 10 times larger than the corresponding rate constant for the dimethoxyfluoropolyether, \(k_{02}^{{\mathrm{CH}}_3}\); (2) the branching ratios concerning the \(\alpha\)-hydrogens are much larger than the ones concerning the \(\beta\)-hydrogens; and (3) within the protocol’s uncertainties and approximations, the chain length is seen to have a small effect on the rate constant, which is consistent with experimental work performed on DM-FPEs. We stress that items (1) and (2), which concern the present p0q2 case, are consistent with the equivalent reactions for the p0q1 case [31].

The work here presented represents the toughest challenge so far to this cost-effective protocol, and it shows its practical predictive ability. An extension of this study for the p0q3 (and even p0q4) would of course be welcomed, but we should point out that even considering all simplifications (for example, optimizing less than 30% of the possible TS conformers) and using 16-, 20-, 24-, 28- and 36-core servers, the optimizations and single-point energy calculations for this work alone amounted to a total wall clock time equivalent to 10 and 22 months of uninterrupted calculations for \({{\mathrm{R}}{=}{\mathrm{C}}_2{\mathrm{H}}_5}\) and \({{\mathrm{CH}}({\mathrm{CH}}_3)_2}\), respectively.