Research on viscosity of metal at high pressure

Abstract

A new experimental technique, the flyer-impact method, is proposed in this article to investigate the viscosity coefficient of shocked metals. In this technique, a shock wave with a sinusoidal perturbation on the front is induced by the sinusoidal profile of the impact surface of the sample by use of a two-stage light-gas gun, and the oscillatory damping process of the perturbation amplitude is monitored by electric pins. The damping processes of aluminum at 78 and 101 GPa and iron at 159 and 103 GPa are obtained by this technique, which supplement the existing data by measuring the viscosity coefficient via a dynamic high-pressure method. Applying the formula of Miller and Ahrens to fit the experimental data, the shear viscosity coefficients of aluminum at 78 and 101 GPa are $1350\,\pm \,500$ and $1200\,\pm \,500~\hbox {Pa}\,\hbox {s}$, respectively, and those of iron at 159 and 103 GPa are $1150\,\pm \,1000$ and $4800\,\pm \,1000~\hbox {Pa}\,\hbox {s}$, respectively. The values measured by the flyer-impact method, approximately $10^{3}~\hbox {Pa}\, \hbox {s}$, are consistent with those measured by Sakharov’s method, while still greatly differing from those measured by static high-pressure methods. In dynamic high-pressure experiments, the shear viscosity is related to dislocation motion in the solid material, while that in static high-pressure experiments is related to the diffusion motion of atoms or molecules in liquids. Therefore, there are different physical meanings of shear viscosity in dynamic and static high-pressure experiments, and there is no comparability among these results.

1 Introduction

Under the conditions of high temperature and high pressure, condensed matter is regarded as a fluid and its dynamic processes are depicted by hydrodynamic models [1]. It is necessary to know the constitutive equations and the certain kinetic transport properties of matter, such as diffusivity, viscosity, thermal conductivity, conductivity, etc. In these transport properties, viscosity represents the relation between viscous stress and the strain rate in the fluid, which contains the bulk viscosity and shear viscosity. In fact, viscosity is one of the essential physical parameters which is related to the interaction among particles at short range, even to the structural phase transition [1]. Therefore, research on viscosity has become one of the key aspects in physical mechanics and the condensed matter physics field.

One of the applications of viscosity lies in the research of geodynamics. It is well known that the depth of the outer core of the earth that is composed mainly of iron ranges from 2900 to 5100 km, corresponding to pressure varying over the range 136–329 GPa and temperatures exceeding 4000 K [1]. The geomagnetism that is generated by the flow of liquid iron in the outer core protects the earth from the impact of charged particles from outer space, and it also provides the basis of geomagnetic navigation. Furthermore, it gives rise to the interaction between the earth’s core and mantle, together with convection in the mantle, by which heat generated by the cooling in the inner core arrives at the boundary of the earth’s core and mantle [2]. Therefore, research into the transport properties, especially viscosity, of materials in the outer core on the condition of high temperature and high pressure is an important issue in understanding the dynamic evolution processes of the earth.

In addition, the shear viscosity coefficients of materials in the outer core are the basic parameters to simulate the magnetic generator of the outer core [3, 4], and research on the absorbency of the materials in the outer core to seismic waves is related to the knowledge of their bulk viscosity. Besides, the viscosity coefficients of silicates in the mantle are the fundamental parameters for research in volcanic activity and mantle evolution [5–7].

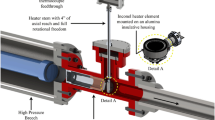
At present, the experimental techniques for measuring shear viscosity coefficients of condensed matter are mainly divided into two approaches: the static high-pressure experimental technique and the dynamic pressure experimental technique. In static high-pressure experiments, the accuracy of directly measured velocities of a sphere (typically made of platinum, tungsten or iridium) falling through molten iron or its compounds has been considerably improved upon by applying the shadow technique of displacement recording [8–15]. This became possible through the use of hard X-rays for observing the specimen. Figure 1 shows the typical experimental method to measure a specimen’s shear viscosity coefficient in static high-pressure experiments, and the changing trend of shear viscosity coefficients of iron (Fe) with varying pressures is shown in Fig. 2.

Fig. 1

Diagrammatic sketch of typical static high-pressure experiment method to measure a specimen’s shear viscosity coefficient

Fig. 2

The shear viscosity coefficients of iron measured in static high-pressure experiments. Filled circle measured by Terasak at al. [11]. Filled square measured by Rutter et al. [10]

The main method to measure shear viscosity coefficients of matter at high pressure and high temperature by dynamic high-pressure experiment is to investigate the damping process of the amplitude of a shock front with small perturbations. The explosion experimental technique and data processing method to measure the shear viscosity coefficient of shocked matter were first proposed by Sakharov and Zaidel [16, 17] and the schematic representation of this experimental technique is shown in Fig. 3. Figure 4 illustrates the optical record for this technique, where $S_{1}, S_{2}, S_{3}, {\ldots }$ are the position records of streak camera records, and $t_{0}, t_{1}, t_{2}$ are the corresponding moments when the shock wave arrives. It is seen that there are changes not only in the amplitudes of perturbation, but also in the phase of the perturbation after the shock wave has propagated different distances through the sample.

Fig. 3

Diagrammatic sketch of Sakharov Explosion Method. An explosive assembly (a) generates a shock that first enters a sinusoidally grooved sample disc (b). The sinusoidal grooves generate perturbations in the shock front that then propagate into the sample wedge (c). The profile of the shock front is detected as a function of time by the light emitted upon shocking a thin gap filled with a noble gas such as argon [flash gap, (d)] by the arrival of the shock at the free surface of the wedge. The emitted light is shuttered by the shock-induced opacity of a plastic sheet (e), and a mask (f)

Fig. 4

The optical record of high-speed photography in Sakharov’s experiment

The experimental curves for aluminum with 31 GPa shock loading with different wavelengths of perturbation measured by the Sakharov Explosion Method were given by Mineev in 1997 [18], as shown in Fig. 5. The wavelength of the sample for data 1 is 20 mm and that of data 2 is 10 mm, and the ratio of initial amplitude and wavelength ($a_0 /\lambda )$ is 0.139. Table 1 lists the shear viscosity coefficients of aluminum (Al) and lead (Pb) for various initial densities and various shock pressures measured by Mineev et al. [18].

Fig. 5

The damping process of perturbation amplitude of aluminum at 31 GPa measured by Mineev et al. [18]

The order of magnitude of shear viscosity coefficients measured by the Sakharov Explosion Method is $\sim$ $10^{3}~\hbox {Pa}\, \hbox {s}$ [16, 18–24] and that measured by static high-pressure experiments is $\sim$ $10^{-3}$–$10^{-2}~\hbox {Pa}\, \hbox {s}$ [8–15]. The great difference between them has perplexed scientists until now: is the significant difference a result of the diversity of the material measured in dynamic and static experiments or the uncertainty in the measured values of the viscosity coefficients? Although there are certain differences existing in the objects that are induced by different experimental techniques for static and dynamic methods and the samples are under conditions of different temperatures and pressures in static and dynamic experiments, it is an uncommon phenomenon in the field of high-pressure research, such as measuring the phase transition zone of iron [25–32], that the discrepancy of shear viscosity coefficients measured by static and dynamic methods is several orders of magnitude.

Table 1 The shear viscosity coefficients of Al and Pb measured by Mineev et al. [18]

Numerous measurements of shear viscosity coefficients have been performed by static methods, and there is great coincidence in the results obtained. So there is high credibility for the data measured by static experiments, and it is also supported by molecular dynamic simulations [33–37]. Meanwhile, the dynamic method to investigate the shear viscosity coefficient of condensed matter is predominately carried out by Mineev et al., by adopting the Sakharov Explosion Method. Therefore, the results measured by Mineev et al. are widely questioned.

There are several shortcomings present in the Sakharov Explosion Method. Firstly, the typical initial amplitude in Mineev’s experiments that have been published [18] seems comparatively large. As a result, distortion in the waveform of the shock front when propagating forward in the sample would be generated, and as a result, the shape of the shock front would no longer be sinusoidal. The appearance of waveform distortion brings about errors in determining the initial moment of perturbation, and the amplitude and propagation distance of the shock front are also difficult to determine. Secondly, there are many uncontrollable factors in explosion experiments, such as a stable, plane shock wave, which is very difficult to generate in the sample (b) (see Fig. 3). Certain uncontrollable factors such as spallation may occur when the shock wave emerges from the grooved sample (b). The data processing method proposed by Zaidel [17] does not take into account the influence of the initial conditions in the actual experiments on the damping processes of the shock front. Finally, the complication of sample preparation and sample assembly would introduce errors which greatly interfere with the results.

Thus, a controllable and reliable experimental technique that can introduce a relatively stable initial field with small perturbation is necessary to improve the accuracy of measuring the shear viscosity coefficient by investigating the damping of the amplitude of a shock front with small perturbations. At the same time, a theoretical model that takes the initial conditions into account is required. In this article, the Flyer-Impact Technique is developed to measure shear viscosity coefficients of shocked metals in order to further analyze the significant discrepancy of shear viscosity coefficients measured by static and dynamic experiments.

2 Flyer-impact experiment

This article proposes a new technique to generate a perturbed shock wave by a flyer impacting the sample and explores the corresponding electric pin technique to measure the damping process of the amplitude of the sinusoidal shock front. This technique is called the Flyer-Impact Technique, which is shown in Fig. 6, and is used specifically in a two-stage light-gas gun. The perturbation of the shock front is introduced by use of a wedge-shaped sample with sinusoidal grooves on its impact surface. Subsequently, two shock waves with sinusoidal fronts are formed, one forward into the sample and the other back into the flyer. The size of the sample is also indicated in Fig. 6. The wavelength of the sample is 6 mm and the depth of the groove is 0.6 mm. Thus, the relative amplitude of this experiment ($a_0 /\lambda =0.05$, where $a_0$ is the initial amplitude and $\lambda$ is the wavelength) is far smaller than that of Mineev’s [18], such that it can effectively avoid the generation of distortion in the waveform.

Fig. 6

Schematic diagram of the flyer-impact method, including the size of sample and the introduction of perturbation on the shock front

The inner diameter of the flyer in our experiment is 24 mm, which restricts the size of the sample that can be used: the lateral release wave would affect the measurement results if it reaches the wedged surface of the sample in advance of the shock wave, and the angle of lateral release wave propagation in our experiment is about $40^{\circ }$. In order to measure the total duration of the damping process, the size of the sample given in Fig. 6a has been optimized. The thickness of a sample that would not be affected by the lateral release wave is 3.53–9.19 mm (a calculation diagram is shown in Fig. 7), and the following experiments have proven that the amplitude damping and the entire reverse-phase oscillation process can be observed in this design.

Fig. 7

Calculation diagram of influence range of lateral release wave in our experiments

In this experiment, the shock wave is generated and propagates forward in the sample when the flyer impacts the crests of the grooves on the sample surface, and when the flyer impacts the troughs of the grooves on the sample, the shock front that was generated in the crests has propagated ahead of the troughs of the grooves because the velocity of the shock wave is faster than that of the flyer, so a shock wave with a sinusoidal front is produced in the sample. The initial time, which is necessary to determine the damping behavior of perturbations in our experiments, is the moment that the flyer just arrives at the troughs of the grooves on the impacted sample surface, that is, the instant that the air gap is completely closed (shown in Fig. 6b). The corresponding perturbation amplitude, called the initial amplitude ($a_0$), is defined as the half of the difference between the propagated distance of the shock front in the sample at the position of the crest of the grooves, while the gap is closed, and the depth of the grooves, i.e., $a_0 =(D-W)\cdot h/2W$, in which h is the depth of the grooves, W and D are the velocity of the flyer and shock wave, respectively.

The arrival times of the shock front at the different positions on the back surface of the wedge-shaped sample are detected by several tens of electric pins without an insulation layer on their heads (shown in Fig. 8). Five groups of electric pins are, respectively, positioned at the location where three crests and two troughs of the shock front will arrive, in order to monitor the geometrical shape of the shock front after it passes through a known distance. To ensure all the pin heads are at a common plane, they are first precisely positioned in a Plexiglas mold, then the part of the pins extending out of the planar surface of the mold is cut, and then the surface of the mold is ground until all pin heads appear on the plane, and finally the planar surface is optically polished to a better flatness. The polished plane of the Plexiglas mold is pushed onto the back wedged surface of the metal sample, where a metal foil of $10~\upmu \hbox {m}$ thickness is sandwiched as a spacer between them at their edge area to protect the pins from electrical discharge. When the shock wave arrives at a pinned point in the sample, the surface layer will be accelerated to a velocity of nearly twice the particle velocity behind the shock front. It will freely fly through the spacer and then impact on the heads of the pins. Once the metal surface touches the pin, the discharge to the ground will occur without time delay, because there is no insulation layer on the head of the pins. A group of electrical resistances connected in series is paralleled with the $50\, \Omega$ input impedance of the oscilloscope. When the shock front comes to the rear surface of the wedged sample, the pins at the minimal thickness (i.e., the bottom one in Fig. 8) are first shortened to the grounded metal sample, and the voltage on the oscilloscopes will suddenly drop down to a lower value. Once the shock front in turn arrives at the position of the next nearest pin, the resistance between the two touched pins will be switched off, and the input voltage to the oscilloscope will abruptly jump down to another lower value. In this way, the instances when a shock wave arrives at the subsequent pins in a common group can be recorded by a single channel of the oscilloscope. In our experiments, five channels are used to record all arrival times at 50 pinned positions in five groups, which are, respectively, arranged in five lines along the crests and troughs of the grooves.

Table 2 The experimental parameters

Fig. 8

Schematic diagram of electric pin technique

Aluminum (Al) and iron (Fe) are the materials of the samples, and the corresponding experimental parameters are listed in Table 2 for our four experiments. The Hugoniot parameters of flyers and samples are listed in Table 3, and the shocked pressures calculated are listed in Table 4. Figure 9 shows typical signals recorded by Tektronix TDS684C oscilloscopes, in which the arrival times are easily read out.

In our experiments, errors in machining of samples, assembly errors in the target, and errors in circuitry and testing system would affect the experimental results. The electric pins are fixed in the Plexiglas mold, and the error of measuring the amplitude of the perturbation because of the error in the position of an electric pin (0.1 mm) is controlled to within 10 ns. A metal foil of $10~\upmu \hbox {m}$ thickness is sandwiched as a spacer between the sample and the Plexiglas mold at their edge area. The error of the gap between the sample and the Plexiglas mold is within $2~\upmu \hbox {m}$, so the error of measuring the amplitude of the perturbation induced by this error is controlled to within 0.5 ns. The error of the depth of the sample’s groove (precision of 0.03 mm) would induce deviations in measuring the amplitude of perturbation and calculating the propagation distance of the shock wave. It can be calculated that the errors are 1–1.5 ns and 3 %, respectively. At the same time, the error induced by the response of the circuitry and oscilloscope is about 0.5 ns. Therefore, in our experiments, the error of measuring the time difference that the crests and the troughs of the shock wave arrive at the back surface of the wedge-shaped sample is less than 14.5–15.5 ns, and the error in propagation distance of the shock wave is controlled to within 9 %. This error is acceptable for an experimental measurement of the shear viscosity coefficient of shocked metal.

Table 3 The Hugoniot parameters and initial density of flyers and samples

Table 4 The shocked pressure of the current experiments

Fig. 9

A typical signal for time of arrival measurement

3 Analysis of experimental results

The typical signals in our experiments are shown in Fig. 9. The shape of the perturbed shock front and its development with propagation distance are approximately mapped out by simply connecting the points of the same thickness with sinusoidal trend curves, as shown in Fig. 10 for the shot with aluminum at 78 GPa. Although the exact shape of the shock front could not be plotted using only the five data points of arrival time, the behavior of damping and oscillation of the perturbation amplitude can be determined because the most important points of maximum and minimum on the sinusoidal shock front can be identified. It can be seen from Fig. 10 that the entire oscillation period of the perturbation on the sinusoidal shock front, which is significant to investigate the viscosity coefficient of metal by dynamic methods, can be observed. The damping curves (perturbation amplitude relative to its initial value versus propagated distance relative to the wavelength of sinusoidal perturbation) of aluminum at 78 and 101 GPa and iron at 159 and 103 GPa are determined by flyer-impact experiments, shown in Figs. 11 and 12.

Fig. 10

Perturbation development with propagation distance of Al at 78 GPa. The distances from the crests of initial sample to the pinned points by the electric pins are given on the right side

Fig. 11

The oscillatory damping curves of perturbed shock wave in aluminum

Fig. 12

The oscillatory damping curves of perturbed shock wave in iron

Equations (86) and (96) from Miller and Ahrens [1], which are too long to write out, are applied to investigate the corresponding shear viscosity coefficients in our experiments. To solve the analytical solution for the case of a non-ideal initial field, two parameters ($\alpha$ and S) are adopted to describe it,

$$\begin{aligned} \alpha\approx & {} \frac{\beta \left| {2-\sigma } \right| }{2k_0 \xi _0 \left[ {1+\beta \left( {\sigma -1} \right) } \right] } \end{aligned}$$

(1)

$$\begin{aligned} S= & {} -\frac{\sigma \left( {1-\delta } \right) }{2\left( {1+\delta } \right) k_0 \xi _0 } \end{aligned}$$

(2)

so $v_x$, $v_y$ and P in the initial field can be described as,

$$\begin{aligned} v_x= & {} \frac{\left( {\sigma -1} \right) \left( {1+\delta } \right) }{\sigma \left( {1-\delta } \right) }k_0 v\xi _0 Se^{-\alpha k_0 x}\cos \left( {k_0 y} \right) \end{aligned}$$

(3)

$$\begin{aligned} v_y= & {} -k_0 v\left( {\sigma -1} \right) \xi _0 e^{-\alpha k_0 x}\sin \left( {k_0 y} \right) \end{aligned}$$

(4)

$$\begin{aligned} P= & {} \frac{-2\left( {\sigma -1} \right) \rho v}{\sigma \left( {1-\delta } \right) }k_0 v\xi _0 Se^{-\alpha k_0 x}\cos \left( {k_0 y} \right) , \end{aligned}$$

(5)

where $v_0$ is the shock velocity; $U_p$ is the particle velocity; c is the bulk sound velocity; $\sigma =v_0 /v$; $\beta =v/c$; $\delta =\frac{\sigma -s\left( {\sigma -1} \right) }{\sigma +s\left( {\sigma -1} \right) }$, where s is the Hugoniot parameter in $u_s =C_0 +su_P$; $\varepsilon \equiv \frac{1-\beta ^{2}}{\beta ^{2}}$; $k_0 =\frac{2\pi }{\lambda }$, where $\lambda$ is the wavelength of sinusoidal perturbation; $\xi _0$ is the initial perturbation amplitude.

In Miller and Ahrens’ formula, $\alpha$ and S represent the lateral perturbation gradient and the longitudinal perturbation gradient of the initial conditions, respectively, which are defined in the Sakharov Explosion Experiment as (1) and (2). The initial field of the Flyer-Impact Experiment is different than that of the Sakharov Explosion Experiment, whose pressure distribution is more uniform, so ${\alpha }^{\prime }$ and ${S}^{\prime }$ in the Flyer-Impact Experiment should be discussed further.

In the Flyer-Impact Experiment, two shock waves are generated propagating inside the sample and the flyer with the shock velocity of $v_0$ and ${v}^{\prime }_0$, respectively, when the flyer impacts the crests of the grooves on the sample. When the flyer touches the troughs of the sample’s grooves, which is the initial moment of perturbation, the time elapsed from when the flyer contacts the crests to when it contacts the troughs is:

$$\begin{aligned} t_0 =h/W, \end{aligned}$$

(6)

where h is the depth of the grooves and W is the speed of the flyer. At this moment, the propagation distances of two shock waves in the sample and the flyer are $v_0 t_0$ and ${v}^{\prime }_0 t_0$. So the lateral perturbation distance in the initial field is:

$$\begin{aligned} L_0 =v_0 t_0 +{v}^{\prime }_0 t_0 =\left( {v_0 +{v}^{\prime }_0 } \right) h/W. \end{aligned}$$

(7)

According to Miller and Ahrens’ hypothesis, $L_0$ equals $1/k_0 {\alpha }^{\prime }$:

$$\begin{aligned} \frac{1}{k_0 {\alpha }^{\prime }}=\left( {v_0 +{v}^{\prime }_0 } \right) h/W \end{aligned}$$

so

$$\begin{aligned} {\alpha }^{\prime }=\frac{W}{\left( {v_0 +{v}^{\prime }_0 } \right) k_0 h}. \end{aligned}$$

(8)

At present, the parameters that can be determined in Miller and Ahrens’ formula are listed in Tables 5 and 6. And the unknown parameters are: the longitudinal perturbation gradient of initial perturbation ${S}^{\prime }$, the bulk viscosity coefficient $\kappa$ and the shear viscosity coefficient $\eta$. The fitting curve of Miller and Ahrens’ formula would be affected by these parameters, so it is necessary to define the influencing weight of these parameters and determine their values.

Table 5 The parameters of aluminum as applied in Miller and Ahrens’ formula

Table 6 The parameters of iron as applied in Miller and Ahrens’ formula

Figure 13 shows the fitting curves of Miller and Ahrens’ formula on the non-ideal initial condition of aluminum at 78 GPa, assuming ${S}^{\prime }=S/8$, including one fitting curve with $\kappa =500~\hbox {Pa}\, \hbox {s}$ and $\eta =500~\hbox {Pa}\, \hbox {s}$ and another fitting curve with $\kappa =1500~\hbox {Pa}\, \hbox {s}$ and $\eta =500~\hbox {Pa}\, \hbox {s}$ and the other fitting curve with $\kappa =500~\hbox {Pa}\, \hbox {s}$ and $\eta =1500~\hbox {Pa}\, \hbox {s}$. It is apparent that the fitting curve is greatly influenced by the shear viscosity coefficient $\eta$, while it is hardly affected by the bulk viscosity coefficient $\kappa$. Therefore, the fitting curve is mainly influenced by the shear viscosity coefficient but not the bulk viscosity coefficient, and the value that can be obtained by fitting the experimental data by use of Miller and Ahrens’ formula is the shear viscosity coefficient under the condition that the longitudinal perturbation gradient ${S}^{\prime }$ is defined.

Fig. 13

The influence of shear viscosity coefficient and bulk viscosity coefficient to fitting curves of Al at 78 GPa

Fig. 14

The fitting curves under ${S}^{\prime }$ take different values

Figure 14 shows the fitting curves with different values of ${S}^{\prime }$ of aluminum at 78 GPa by Miller and Ahrens’ formula. It is seen that the fitting curve is also greatly affected by ${S}^{\prime }$: the attenuation speed of the perturbation amplitude is faster while the value of $\left| {{S}^{\prime }} \right|$ (${S}^{\prime }$ is negative) is greater. However, the different fitting curves with various ${S}^{\prime }$ would intersect at a certain point, which is called the “intersect point” in this article. As shown in Fig. 13 ($\eta =1500~\hbox {Pa}\, \hbox {s}$), the four fitting curves intersect at the point of $x=0.9608$, $y=-0.1367$, and the “intersect point” does still exist while the shear viscosity coefficient $\eta$ varies.

Table 7 lists the coordinates of intersect points while the shear viscosity coefficients take on different values for fitting the results for aluminum at 78 GPa by Miller and Ahrens’ formula. It is seen from Table 7 that the x coordinate of the intersect point remains constant while the y coordinate varies when the shear viscosity coefficients take different values. Taking the intersect points of the fitting curves of aluminum at 78 GPa as the comparison with the data from the Flyer-Impact Experiment, as shown in Fig. 15, the trend line of experimental data passes through the middle between the intersect points corresponding to shear viscosity coefficients of 1000 and $1500~\hbox {Pa}\, \hbox {s}$. Under this condition, the intersect point of the fitting curve passes through the trend line of experimental data when the shear viscosity coefficient is $1350~\hbox {Pa}\, \hbox {s}$. Thus, it can be concluded that the shear viscosity coefficient of aluminum at 78 GPa as determined by the Flyer-Impact Experiment is $1350~\hbox {Pa}\, \hbox {s}$, and the longitudinal perturbation gradient ${S}^{\prime }$ can be derived while $\eta$ has been defined.

Table 7 The coordinates of intersect points obtained while the shear viscosity coefficients take on different values for aluminum at 78 GPa

Fig. 15

The comparison of intersection points with experimental data of Flyer-Impact Experiment with aluminum at 78 GPa

Fig. 16

The fitting curves of aluminum at 78 GPa by use of Miller and Ahrens’ formula

Fig. 17

The fitting curves of aluminum at 101 GPa by use of Miller and Ahrens’ formula

Fig. 18

The fitting curves of iron at 159 GPa by use of Miller and Ahrens’ formula

Figure 16 shows the fitting curves of the oscillating shock front of aluminum at 78 GPa by Miller and Ahrens’ formula, where for ${S}^{\prime }=-0.1162$ the best fitting is obtained. The shear viscosity coefficient of aluminum at 78 GPa is $1350~\hbox {Pa}\, \hbox {s}$, and the error induced from the experimental result is $500~\hbox {Pa}\, \hbox {s}$. Similarly, the shear viscosity coefficient of aluminum at 101 GPa is $1350~\hbox {Pa}\, \hbox {s}$, and the error induced from the experimental result is $500~\hbox {Pa}\, \hbox {s}$ (${S}^{\prime }=-0.1646)$, as shown in Fig. 17. The shear viscosity coefficient of iron at 159 GPa is $1150~\hbox {Pa}\, \hbox {s}$, and the error induced from the experimental result is $1000~\hbox {Pa}\, \hbox {s}$ (${S}^{\prime }=-0.2379)$, as shown in Fig. 18. The shear viscosity coefficient of iron at 103 GPa is $4800~\hbox {Pa}\, \hbox {s}$, and the error induced from the experimental result is $1000~\hbox {Pa}\, \hbox {s}$ (${S}^{\prime }=-0.3811)$, as shown in Fig. 19. In summary, the shear viscosity coefficients from our experiments that are obtained by fitting with Miller and Ahrens’ non-ideal initial field formula are listed in Table 8.

Fig. 19

The fitting curves of iron at 103 GPa by use of Miller and Ahrens’ formula

Table 8 The shear viscosity coefficients as measured in Flyer-Impact Experiment

4 Discussion

Mineev et al. have measured the shear viscosity coefficients of many materials at shocked high pressure by the Sakharov Explosion Method, such as Al, Pb, Fe, U, etc. [18–24]. Figure 20 shows the comparison of the shear viscosity coefficients of aluminum measured in our experiments with those measured by Mineev [23], and the dotted line in the figure is the curve of shear viscosity coefficient as a function of pressure as calculated by Ogorodnikov [38]. Both Mineev and Ogorodnikov consider that the shear viscosity coefficient of aluminum increases with the increase of pressure; however, it decreases with the increase of pressure as the pressure exceeds 65 GPa. There is a small difference between the shear viscosity coefficients measured by the Flyer-Impact Experiment and the two values with lower uncertainties ($\hbox {pressure}~\approx 31~\hbox {GPa}$ and $\approx 204~\hbox {GPa}$) as measured by Mineev. Although the shear viscosity coefficients measured in our experiment differ from the two values with large uncertainties (at pressure $\approx$ $65~\hbox {GPa}$ and $\approx$ $103~\hbox {GPa}$) measured in Mineev’s experiment, the values of shear viscosity coefficients measured in those two experiments are still in the same order of magnitude ($10^{3}~\hbox {Pa}\, \hbox {s}$). Thus, the results measured by the Flyer-Impact Experiment and by the Sakharov Explosion Method approximately agree with each other. The data obtained from our experiments are limited, so it is difficult to determine the trend of shear viscosity varying with the change of pressure.

Fig. 20

Comparison of shear viscosity coefficients for aluminum with the results of Mineev’s experiments

There is not much difference in the shear viscosity coefficients of iron between those measured in our experiments and in Mineev’s [24], which is represented in Fig. 21. Together with the value at 31 GPa given by Mineev, the shear viscosity coefficients of iron exhibit a character that first increases and then decreases with the increase of pressure.

Fig. 21

Comparison of shear viscosity coefficients for iron with the results of Mineev’s experiments

There is still considerable disagreement in measuring shear viscosity coefficients of metal (especially iron) at high pressure until now: the order of magnitude of it measured by static high-pressure experiments and molecular dynamic simulations is $\sim$ $10^{-3}$–$10^{-2}~\hbox {Pa}\, \hbox {s}$ [8–15, 33–37] while that measured by the Sakharov Explosion Method is about $10^{3}~\hbox {Pa}\, \hbox {s}$ [17–24], and the effective shear viscosity coefficient in the inner core of the earth measured by the Maxwell model of rheology reaches up to $10^{12}$–$10^{17}~\hbox {Pa}\, \hbox {s}$ [39]. This article proposes a new experimental method to measure the shear viscosity coefficient of metals for the purpose of proving the reality of this argument. The difference of several hundreds to several 1000 $\hbox {Pa}\, \hbox {s}$ of shear viscosity coefficients measured between the Flyer-Impact Experiment and the Sakharov Explosion Method seems rather small given the current situation. Our experiments have at least proven the credibility of the magnitude of shear viscosity coefficients measured in Mineev’s experiments, and it is an indisputable fact that there exists five to six orders of magnitude difference between static and dynamic high-pressure experiments to measure the shear viscosity coefficient of metal at high pressure.

In the research field of shock waves, the medium is always regarded as fluid and then the influence of material strength on shock phenomenon in shock processes is ignored [40]. However, in certain aspects, there are considerable effects that material strength of the fluid medium can have upon shock processes, which is greatly different from an ideal liquid medium [21]. The measurement of viscosity coefficient of shocked metal, which is the subject of this article, belongs to this aspect.

There is an obvious feature in the shear viscosity coefficients of metals measured by Mineev that the viscosity coefficient decreases along with the increase of pressure after the material melts partially. The shear viscosity coefficient of aluminum measured by Mineev at 65 GPa is about $10{,}000~\hbox {Pa}\, \hbox {s}$, and that at 202 GPa decreases to below $2000~\hbox {Pa}\, \hbox {s}$, and the shear viscosity coefficient of porous aluminum (the initial density relative to the normal density is 1.43) at 202 GPa even decreases to below $200~\hbox {Pa}\, \hbox {s}$ [22]. Thus, the shear viscosity coefficients measured in dynamic high-pressure experiments is lower, while the shock pressure and temperature of the sample is higher (the material is closer to the molten phase).

In the measurement of the shear viscosity coefficient of metals at high pressure, the subject of research in static high-pressure experiments and molecular dynamic simulations is the liquid state, while that in dynamic high-pressure experiments is a solid or a partially melting solid. In the research of static high-pressure experiments and molecular dynamic simulations, shear viscosity originates from diffusion of atoms and molecules, and in this case, the velocity gradient between layers in liquid is slowed down because of diffusion of atoms and molecules among layers. In research into dynamic high-pressure experiments, shear viscosity originates from dislocation motion: the atoms and molecules are fixed in lattices and cannot diffuse, and the dislocation and slippage is generated in shock processes, which slows down the velocity gradient between layers.

In the research of dynamic high-pressure experiments, shear viscosity originates from dislocation motion, and dislocation motion would be affected by material strength. That is to say that the shear viscosity coefficient measured in dynamic high-pressure experiments contains the influence of material strength, so the viscosity in dynamic experiments should be more properly called the “effective viscosity”, which differs greatly from static high-pressure experiments and molecular dynamic simulations because the material studied is liquid without the influence of material strength.

Through the above analysis, the reason why the magnitude of shear viscosity coefficients measured in dynamic high-pressure experiments is 5–6 orders of magnitude greater than that measured in static high-pressure experiments and molecular dynamic simulations could be understood: the materials researched have different physical states (solid and liquid), so the mechanism that generates the observed viscosity is inconsistent (dislocation vs. diffusion of molecules), and when the physical state of the material examined in dynamic high-pressure approaches the liquid state, the measured shear viscosity coefficients are much lower than those in the solid phase.

5 Conclusions

This article proposes the Flyer-Impact Experiment method to measure the shear viscosity coefficients of aluminum and iron under shock compression at pressures of megabar, and the results obtained are summarized here:

• 1. The measurement of the shear viscosity coefficient of metal at shocked high pressure is realized using two-stage light-gas gun loading conditions. The initial flow field obtained by the present Flyer-Impact Experiment is different from that of Sakharov, and it provides a new experimental method to investigate the viscosity of a material by the use of shock wave techniques. The flow field generated in this way is more uniform than that generated in Sakharov’s, and it approaches the condition of a small perturbation. The Flyer-Impact Experiment is more controllable and reliable than the Sakharov Explosion Method.

• 2. A new electric pin technique is specifically designed to measure the time-dependent distance between the peak and trough points of the disturbed shock front, which simplifies the testing technique of dynamic high-pressure experiment under the precondition of ensuring high accuracy.

• 3. The oscillatory damping curves of a shock front in aluminum at 78 and 101 GPa and in iron at 159 and 103 GPa were obtained, with the entire oscillation period being observed by the Flyer-Impact Experiment method and discrete electric pin technique. The damping and reversal process of the sinusoidal shock front can be noticed clearly in these oscillatory curves. These damping curves with whole oscillation period are original experimental data deriving from this research.

• 4. Miller and Ahrens’ formula for non-ideal initial conditions is applied to fit the data of the Flyer-Impact Experiment, and the shear viscosity coefficients of aluminum at 78 and 101 GPa are $1350\pm 500~\hbox {Pa}\, \hbox {s}$ and $1200\pm 500~\hbox {Pa}\, \hbox {s}$, respectively, and the shear viscosity coefficients of iron at 159 GPa and 103 GPa are $1150\pm 1000~\hbox {Pa}\, \hbox {s}$ and $4800\pm 1000~\hbox {Pa}\, \hbox {s}$, respectively. Our results show that the shear viscosity coefficients measured by Mineev are reliable, at least in terms of their magnitude, and the significant discrepancy on shear viscosity coefficients measured by dynamic high-pressure experiments and static high-pressure experiments are induced by the differences in the loading processes.