Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations

Abstract

The Sentinel-3 mission takes routine measurements of sea surface heights and depends crucially on accurate and precise knowledge of the spacecraft. Orbit determination with a targeted uncertainty of less than 2 cm in radial direction is supported through an onboard Global Positioning System (GPS) receiver, a Doppler Orbitography and Radiopositioning Integrated by Satellite instrument, and a complementary laser retroreflector for satellite laser ranging. Within this study, the potential of ambiguity fixing for GPS-only precise orbit determination (POD) of the Sentinel-3 spacecraft is assessed. A refined strategy for carrier phase generation out of low-level measurements is employed to cope with half-cycle ambiguities in the tracking of the Sentinel-3 GPS receiver that have so far inhibited ambiguity-fixed POD solutions. Rather than explicitly fixing double-difference phase ambiguities with respect to a network of terrestrial reference stations, a single-receiver ambiguity resolution concept is employed that builds on dedicated GPS orbit, clock, and wide-lane bias products provided by the CNES/CLS (Centre National d’Études Spatiales/Collecte Localisation Satellites) analysis center of the International GNSS Service. Compared to float ambiguity solutions, a notably improved precision can be inferred from laser ranging residuals. These decrease from roughly 9 mm down to 5 mm standard deviation for high-grade stations on average over low and high elevations. Furthermore, the ambiguity-fixed orbits offer a substantially improved cross-track accuracy and help to identify lateral offsets in the GPS antenna or center-of-mass (CoM) location. With respect to altimetry, the improved orbit precision also benefits the global consistency of sea surface measurements. However, modeling of the absolute height continues to rely on proper dynamical models for the spacecraft motion as well as ground calibrations for the relative position of the altimeter reference point and the CoM.

1 Introduction

Sentinel-3 is the latest satellite mission of the Copernicus (or Global Monitoring for Environment and Security, GMES) program (Aschbacher and Milagro-Pérez 2012; Fletcher 2012). It focuses on ocean monitoring and carries various related instruments including the Sea and Land Surface Temperature Radiometer (SLSTR), the Ocean and Land Colour Instrument (OLCI), the Sentinel-3 Ku/C Radar Altimeter (SRAL), and a Microwave Radiometer (MWR). The altimeter is used for measurements of open sea, coastal and inland waters, as well ice surfaces. It offers a range noise of 1 cm or less in the various operation modes (Le Roy 2007) and takes interleaved measurements at two frequencies (C- and Ku-band) for the correction of ionospheric path delays. A root-mean-square (rms) error of less than 3cm (2cm) in radial direction is officially specified(targeted) for the post-facto orbit reconstruction of Sentinel-3 (Fernández et al. 2016), but a better than 1cm accuracy is in fact desirable to support the long-term monitoring of sea level changes and to achieve continuity with time series of past altimetry missions such as TOPEX/Poseidon (Bertiger et al. 1994) and Jason-1/2 (Luthcke et al. 2003; Cerri et al. 2010).

Fig. 1

Artist’s drawing of the Sentinel-3 spacecraft showing the location of the GPS and DORIS antennas, the SAR altimeter antenna and the laser retroreflector (LRR). Base image courtesy of ESA–Pierre Carril

To support this effort, the Sentinel-3 spacecraft (Fig. 1) hosts a precise orbit determination (POD) package comprising a Global Positioning System (GPS) receiver and a Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS; Auriol and Tourain 2010) instrument, as well as a laser retroreflector (LRR) for satellite laser ranging (SLR). GPS and DORIS both provide a continued coverage with measurements and thus enable two fully independent types of orbit determination solutions or, alternatively, a combined radiometric solution. SLR tracking of Sentinel-3A, in contrast, is so far primarily used as a means for orbit validation in view of sparse and geographically constrained observations.

Within this study, precise orbit solutions of Sentinel-3A (S3A) are exclusively obtained from GPS observations. The employed GPS receiver has been developed by RUAG Space, Austria, and makes use of the second-generation Advanced GPS GLONASS ASIC (AGGA-2; Sinander and Silvestrin 1997). It offers $3\times 8$ channels for tracking of the civil L1 C/A code as well as the military P(Y)-code on the L1 and L2 frequencies. A semi-codeless tracking technique is used to track the encrypted P(Y)-code, which builds on the Z-tracking technique (Woo 2000) but employs an improved approach for estimating the W-bit of the unknown encryption code (Silvestrin and Cooper 2000). The S3A receiver closely matches the receivers previously flown on the Swarm constellation (van den IJssel et al. 2016) as well as the Sentinel-1 and Sentinel-2 satellites, but uses a refined navigation filter that offers an improved (1m 3D RMS) real-time positioning accuracy.

Orbit determination using GPS code and carrier phase observations is nowadays a well-proven technique and serves as the primary source of orbit information in numerous geodetic and remote sensing missions in low Earth orbit (Flohrer et al. 2011; Bock et al. 2014; van den IJssel et al. 2015). It likewise forms the basis for the Copernicus POD service (CPOD) which generates precise orbit products for all current Sentinel satellites on an operational basis. Interagency comparisons with other GPS-based POD solutions generated by the members of the CPOD Quality Working Group demonstrate consistency of these solutions at the 2-cm 3D rms level and SLR residuals of 1.5–2 cm (Fernández et al. 2016). While this performance is well in accord with mission requirements, it is potentially still limited by the fact that all solutions are based on a float-valued adjustment of carrier phase ambiguities. As shown, for example, in Jäggi et al. (2007), Laurichesse et al. (2009) and Bertiger et al. (2010), substantial further improvement in precision and accuracy of POD solutions for satellite in low Earth orbit (LEO) can indeed be expected when exploiting the integer nature of double-difference carrier phase ambiguities.

Within this work, we present the first application of ambiguity fixing to GPS-based POD of the Sentinel-3A satellite and demonstrate a notable improvement in the precision of the resulting orbit. On the other hand, ambiguity fixing is found to have only limited impact on the radial leveling of the satellite orbit, which is mainly determined by the dynamical models.

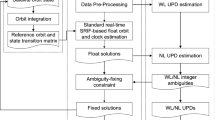
The article first discusses the employed strategy for generation of GPS observations from low-level GPS instrument data, which forms an important prerequisite for POD and ambiguity fixing (Sect. 2). Dynamical and observation models used in the POD processing are presented in Sect. 3, and the employed single-receiver ambiguity fixing approach is discussed in Sect. 4. Uncertainties in the knowledge of the GPS antenna phase center, the LRR, and the center-of-mass (CoM) locations of the Sentinel-3 spacecraft are addressed in Sect. 5, and calibrations using flight data are obtained. The achieved orbit determination performance and its validation using SLR observations are finally presented in Sect. 6.

2 Generation of GPS observations

Other than common geodetic receivers that directly provide their users with pseudorange and carrier phase range observations, the Sentinel GPS receivers provide raw values of the code and phase generators driving the tracking loops for the individual signals. Out of these, the common GPS measurements need to be formed as part of a dedicated ground processing (Fernández Martìn 2017), before the data can be processed with established point positioning or POD software. Despite being inconvenient and a potential risk of errors at first sight, this concept ultimately provides enhanced flexibility for different applications and helps to best exploit the available observations.

As part of the tracking process, a code replica is continuously aligned to achieve a maximum correlation with the incoming signal and the instantaneous code phase at the measurement latching epoch provides the corresponding signal transmit time. A pseudorange p can then be formed in the ground processing by subtracting this transmit time from the receive time at the instant of the measurement and multiplying the result with the speed of light c. Different options exist to create a receiver timescale from the Instrument Measurement Time (IMT) that provides the time since boot based on the 28.333 MHz core clock oscillator. Within this study, a receiver timescale

$$\begin{aligned} t_\text {r}(t)= & {} [ t_\text {GPS,nav}(t_\text {ref}) + (\text {IMT}(t)-\text {IMT}(t_\text {ref})) ] \nonumber \\&+ P(\text {IMT}(t)-\text {IMT}(t_\text {ref})) \end{aligned}$$

(1)

is established. Here, the leading term in square brackets runs at the speed of the core clock (i.e., the IMT) and is aligned with an estimate $t_\text {GPS,nav}(t_\text {ref})$ of GPS time obtained from the receivers’ navigation solution at an initial epoch $t_\text {ref}$ near the start of each day. To compensate the oscillator drift and higher-order variations, a polynomial clock offset correction P (of up to fourth order) is, furthermore, applied that minimizes the difference between $t_\text {r}$ and $t_\text {GPS,nav}$. The resulting receiver timescale is closely aligned to the GPS timescale but also ensures full traceability between the native oscillator frequency and the receiver clock offsets estimates in the POD processing. Furthermore, all measurement epochs in the receiver time are full seconds (within a few tens of nanoseconds), since the receiver actively aligns its measurement epochs to integer seconds of GPS time.

For carrier tracking, the incoming signal is first down-converted to an intermediate frequency and then mixed with the output of a numerically controlled oscillator (NCO). The phase locked loop (PLL) senses the phase offset of the resulting signal and drives it to zero by continuously adjusting the NCO frequency (Misra and Enge 2006). At the instant of a measurement, the instantaneous (fractional cycle) NCO phase $\phi _\text {NCO}$ and the total number of NCO phase roll overs $n_\text {NCO}$ are reported by the receiver. Out of these values, the carrier phase range

$$\begin{aligned} \varphi (t) = \lambda \Big (f_{\text {NCO},\text {nom}}\cdot (t-t_0) - (n_\text {NCO}(t)+\phi _\text {NCO}(t)) \Big ) \end{aligned}$$

(2)

needs to be formed within the ground processing. Here, $\lambda$ denotes the carrier wavelength, $f_{\text {NCO},\text {nom}}$ is the NCO frequency for a nominal (i.e., non-Doppler-shifted) signal, and $t_0$ is a reference epoch at or near the start time of carrier phase tracking for the particular satellite and signal.

The carrier phase range obtained in this way is an ambiguous measurement that exhibits an unknown but constant offset from the corresponding pseudorange. Under certain provisions, between-receiver and between-satellite double differences of the carrier phase range formed in the above manner exhibit a double-difference (DD) ambiguity that is an integer multiple of the wavelength. To ensure this property, $f_{\text {NCO},\text {nom}}\cdot t_0$ should be an integer value for all tracking channels which can be achieved by a proper choice of $t_0$. Furthermore, the tracking process must ensure that double differences of the fractional NCO phases $\phi _\text {NCO}$ are themselves integer-valued.

The binary phase shift keying (BPSK) modulation of the legacy GPS signals involves a $180^\circ$ change in the signal phase at data bit transitions. Following the code and carrier removal, a data bit transition also results in a sign change of the in-phase (I) and quadrature (Q) components of the accumulated correlation values. To enable continuous tracking of the signal phase in the phase locked loop, a two-quadrant phase discriminator is employed that is insensitive to data bit changes (Betz 2016). The resulting “Costas-loop” can track the incoming signal across data bit transitions, but induces a potential half-cycle offset in the reported NCO phase that is constant during uninterrupted carrier phase tracking and depends on the data bit sign at start of track. This offset also translates into a potential half-cycle bias of the carrier phase range derived from the NCO phase measurement. As a result, the DD carrier phase ranges will no longer exhibit integer-cycle ambiguities but half-cycle ambiguities which are more difficult to resolve in the data processing (see, e.g., Allende-Alba and Montenbruck 2016; Jäggi et al. 2016).

In order to recover the true NCO phase (and thus to obtain carrier phase range observations with integer-valued DD ambiguities), the sign of the data bit stream obtained from the down-converted signal after code/carrier removal must be determined. In practice, the receiver checks for the occurrence of the specified preamble (1000101100 for GPS L1 C/A code) or the inverted bit pattern (0111010011) in the received data bit stream to decide whether all data bits need to be inverted. The same information can also be used to decide on the presence of a half-cycle bias in the measured Costas-loop NCO phase and to compute a corrected carrier phase range observation according to

$$\begin{aligned} \varphi= & {} \lambda \Big (f_{\text {NCO},\text {nom}}\cdot (t-t_0) - (n_\text {NCO}(t)+\phi _\text {NCO}^\text {Costas}(t)) \Big ) \nonumber \\&+ \left\{ \begin{array}{c} 0 \\ \lambda /2 \end{array} \right\} \; \text {for} \; \left\{ \begin{array}{l} \text {normal} \\ \text {inverted} \end{array} \right\} \text {preamble} . \end{aligned}$$

(3)

Making use of receiver telemetry data indicating the sign of the preamble for the L1 C/A signal after successful decoding of the data stream, it is thus possible to obtain L1 carrier phases that exhibit integer-valued double-difference ambiguities. However, different considerations apply for the L2 carrier in view of the semi-codeless tracking technique employed for the P(Y)-code modulation.

In the Z-tracking scheme (Woo 2000), the instantaneous value of the W-bit is independently estimated for the L1 and L2 signals. After down-conversion to the respective intermediate frequencies and mixing with the in-phase and quadrature phase of the L1 and L2 NCOs, the signal is first multiplied with a P-code replica and then integrated over the W-bit duration of about 2. More specifically, a W-bit length equal to 22 P-code chips is assumed within the AGGA-2 framework, which is slightly larger than in the original Z-tracking concept. Based on the expected noise distribution, a decision on the sign of W-bit is taken. If successful, the estimated L1 W-bit is then used to strip the remaining W-code on L2. Vice versa the L2 W-bit estimate is applied to fully demodulate the L2 signal. The resulting signals can then be integrated (over typical timescales of a few 100 ms), to obtain IQ-vectors with a proper signal-to-noise ratio. The Z-tracking requires steering of the L2 NCO as well as the P1 and P2 code-shift based on the IQ-vectors of distinct prompt and early/late correlator arms. The L1 NCO, in contrast, is already steered as part of the L1 C/A code tracking that also delivers the L1 phase observation. Since the P(Y)-code signals on L1 and L2 carry, in general, the same navigation data as the L1 C/A code signal, this data modulation can be removed in the P(Y)-code tracking. Accordingly, no Costas-loop is required and the L2 carrier can be tracked with a four-quadrant discriminator. Likewise, the W-bit estimation and stripping involves no sign ambiguity which might induce a half-cycle bias in the L2 tracking. On the other hand, however, the Z-tracking utilizes the NCO phase from the L1 C/A code tracking, which is itself subject to half-cycle biases as discussed above. These half-cycle biases are inherited by the L2 NCO phase and will affect the resulting L2 carrier beat phase observation unless specific action is taken for their removal. However, the resulting half-cycle bias would be identical for L1 and L2. Therefore, the difference of L1 and L2 NCO phases is ensured to be of integer nature, which implies that the L1-L2 DD wide-lane carrier phase ambiguity is likewise of integer nature if both the L1 and L2 phase measurements were left uncorrected. This has empirically been confirmed in previous studies for the AGGA-2-based receivers on Metop as well as the Swarm satellites (Jäggi et al. 2016; Allende-Alba and Montenbruck 2016).

To obtain integer-valued DD ambiguities of the L2 carrier phase, the correction given in (3) is likewise applied to the L2 carrier phase ranges, i.e., a half-cycle is added to both the L1 C/A carrier phase range and the L2 P(Y) carrier phase range from (2), whenever the preamble in the L1 C/A tracking is inverted.

Specifications for GPS measurement generation in the CPOD ground segment do not presently take into account such corrections, and the resulting RINEX (Receiver INdependent EXchange format; IGS RINEX WG and RTCM-SC104 2015) observation files are therefore affected by half-cycle biases that essentially inhibits ambiguity fixing in the POD process. An independent processor for the raw telemetry of the RUAG GPS receivers has therefore been developed for the present study and used to create RINEX files with proper full-cycle double-difference ambiguities.

Prior to the application with actual Sentinel-3 flight data, the desired property of the resulting L1 and L2 carrier phase range observations has been validated using observations collected in a pre-flight test campaign by CNES/ESA/RUAG (F. Mercier, priv. comm), where engineering models of the Sentinel GPS receiver and a commercial geodetic receiver were jointly operated with a common rooftop antenna. Within this zero-baseline configuration, carrier phase observations can simply be differenced to isolate the DD ambiguities and to verify their integer nature.

3 POD concepts, models, and data

Sentinel-3 orbit solutions presented in this study are obtained with DLR’s GNSS High precision Orbit determination Software Tools (GHOST) using a reduced dynamic approach as described in Montenbruck et al. (2005). It makes use of a dynamical orbit model considering gravitational and non-gravitational forces as well as complementary empirical accelerations that are adjusted along with the initial state vector of the LEO satellite and scaling factors for individual force model constituents. Measurement-related estimation parameters include the epochwise receiver clock offsets as well as a float-valued ambiguity of the ionosphere-free carrier phase combination for each continuous tracking pass. A summary of the employed models is given in Table 1.

Table 1 GHOST models and data sets for Sentinel-3A precise orbit determination and SLR validation

Table 2 Sentinel-3A macro-model (Fernández Martìn 2016)

While gravitational forces can well be described by established models, the same is not necessarily true for non-gravitational surface forces such as drag and radiation pressure. Within this study, a macro-model formulation is employed, which approximates the actual spacecraft (as shown in Fig. 1) by a rectangular box and a single solar panel (Table 2). While the orientation of the spacecraft body is rigorously modeled by the measured attitude, the solar panel is assumed to be Sun-facing at all times.

Solar radiation pressure (SRP) for the illuminated surface elements is described through fractions $\alpha$, $\delta$, and $\rho$ of absorbed, diffusely reflected and specularly reflected photons in the visible wavelength regime using the formulation of Milani et al. (1987). Following Cerri et al. (2010) a spontaneous, diffuse re-emission of absorbed photons is assumed for the six body faces, which are mainly covered by multilayer insulation for thermal protection. On the other hand, no net-force due to thermal re-emission is taken into account for the solar panels, which is equivalent to assuming identical temperatures for the front and backside of the solar array. In practice, this deficiency can be compensated by adjusting an overall scaling factor for the solar radiation pressure as part of the orbit determination process. Sun illumination of the satellite is taken into account using a conical shadow model for a spherical Earth.

The modeling of Earth radiation pressure (ERP) follows the approach of Knocke et al. (1988) but employs a slightly different division of the visible surface of the Earth around the satellite’s footprint into 3 rings with a total of 22 segments. The amount of reflected solar radiation as well as thermal radiation is evaluated for each of these segments based on Earth radiation data (albedo and emissivity) provided by the Clouds and Earth’s Radiant Energy System (CERES; Priestley et al. 2011). For computational efficiency, the monthly high-resolution CERES maps are approximated through a second-order Legendre-polynomial expansion in latitude and a periodic function in time-of-year, while neglecting the longitudinal variation (Knocke et al. 1988).

Drag and lift forces for each individual plate of the box-wing macro-model are computed based on Sentman’s method as described in Sutton (2009) and Doornbos (2012) using atmospheric composition and total density data from the US Naval Research Laboratory Mass Spectrometer and Incoherent Scatter Radar 2000 (NRLMISE-00) model (Picone et al. 2002). Observed solar flux and geomagnetic activity data are obtained from the Space Weather Prediction Center (SWPC) of the US National Oceanic and Atmospheric Administration (NOAA).

Given the prevailing uncertainties in spacecraft parameters and environmental data for the description of surface forces, global scaling parameters (with nominal values of 1.0) for the atmospheric forces $C_D$, the solar radiation pressure $C_\mathrm{R}$ and the Earth radiation pressure $C_\mathrm{E}$ can be adjusted as part of the orbit determination. The first two of these parameters are generally well observable and are thus estimated with loose a priori constraints ($\sigma _\text {CD,apr}=\sigma _\text {CR,apr}=2.5$). Earth radiation pressure, in contrast, acts mainly in the radial direction and correlates strongly with potential radial position errors of the GPS antenna relative to the spacecraft center of mass. A tightly constrained value of the $C_\mathrm{E}=1$ is therefore employed, placing full confidence into the ERP model.

In addition to the global scale factors, empirical accelerations are considered in the dynamical model to cope with remaining deficiencies of the a priori model and to achieve a description of the orbital motion compatible with the precision of the GPS measurements. These accelerations are described as piecewise constant values over consecutive intervals of typically 10-min duration with components in radial (R), along-track (T), and cross-track (N) direction. Within each interval, the empirical accelerations are constrained to zero a priori values with standard deviations of ${5} \hbox { nm}/\hbox {s}^{2}$ (R) and $10 \hbox { nm}/\hbox {s}^{2}$ (T, N).

A ten-month data period is covered in this study. It starts with the begin of routine GPS receiver operation in late March 2016 and ends in late January 2017 prior to the reference frame transition of the International GNSS Service (IGS) from IGb08 to IGS14 on 29 Jan. 2017 (Rebischung 2016). Raw GPS receiver data made available at a 1 Hz by the CPOD ground segment were used to generate RINEX observation files as described in Sect. 2. Out of these, 24-h orbit determination solutions were generated on a daily basis using a 30-s measurement interval consistent with the epochs of IGS high-rate GPS clock products. To support single-receiver ambiguity fixing, GPS orbit and clock products of the CNES/CLS (Centre National d’Études Spatiales / Collecte Localisation Satellites) analysis center (see Sect. 4.4) were used throughout the analysis.

4 Single-receiver ambiguity resolution

4.1 Observation model

Pseudorange and carrier phase range observations between a single receiver (subscript $_\text {r}$) and a single satellite (superscript $^\text {s}$) on the first and second frequency (indices $_1$ and $_2$ for GPS L1 and GPS L2) are described by the generic observation model

$$\begin{aligned} \begin{array}{lcl} p_{\text {r};1}^\text {s}&{}=&{} (\rho +\xi _{\text {r};1}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) + I_{\text {r};1}^\text {s}+ c(d_{\text {r};1}-d_{1}^\text {s}) \\ p_{\text {r};2}^\text {s}&{}=&{} (\rho +\xi _{\text {r};2}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) + I_{\text {r};2}^\text {s}+ c(d_{\text {r};2}-d_{2}^\text {s}) \\ \varphi _{1;\text {r}}^\text {s}&{}=&{} (\rho +\zeta _{1;\text {r}}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) - I_{\text {r};1}^\text {s}+ c(\delta _{\text {r};1}-\delta _{1}^\text {s}) \\ &{} &{} + \lambda _1 N_{\text {r};1}^\text {s}+ \lambda _1\omega _\text {r}^\text {s}\\ \varphi _{2;\text {r}}^\text {s}&{}=&{} (\rho +\zeta _{2;\text {r}}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) - I_{\text {r};2}^\text {s}+ c(\delta _{\text {r};2}-\delta _{2}^\text {s}) \\ &{} &{} +\,\lambda _2 N_{\text {r};2}^\text {s}+\,\lambda _2\omega _\text {r}^\text {s}\end{array} \end{aligned}$$

(4)

(Hauschild 2017). Here $\rho$ denotes the geometric range between the antenna reference points of the satellite (at the time of signal transmission) and receiver (at time of signal reception), while corrections related to phase center offsets and variations are expressed by $\xi$ and $\zeta$ for the different observation types. Deviations of the satellite and receiver clock from the reference timescale of the employed GPS clock product are described by the satellite and the receiver clock offsets ($\mathrm{d}t^\text {s}$, $\mathrm{d}t_\text {r}$). Ionospheric propagation effects (I) result in a code delay and phase advance that are of similar magnitude and vary predominantly with the inverse square of the signal frequency f.

Signal-specific range biases related to the transmitter and receiver chain are expressed by $cd_{\text {r};i}$ and $cd_i^\text {s}$ for pseudorange observations, as well as $c\delta _{\text {r};i}$ and $c\delta _i^\text {s}$ for carrier phase ranges. Within the frame of this work, it is assumed that individual bias contributions are purely additive. The overall bias can thus be split into a satellite-related part (that is independent of the receiver) and a receiver-related part (that is fully independent of the satellite). These biases are, furthermore, assumed to be constant (or at least to vary slowly) over the data arc.

Beside the biases, the carrier phase range includes the ambiguities $N_{\text {r};i}^\text {s}$, which relate to the arbitrary initial value of the cycle counter of the phase measurement process.

Finally, the measurement model takes into account the phase windup effect ($\omega _\text {r}^\text {s}$) which results from a time-varying orientation of the effective receiver and transmitter antennas. Similar to the geometric range and the phase center corrections, the phase windup can be described based on knowledge of the satellite and receiver positions and their variation over time (Wu et al. 1993).

As a concluding remark, we note that biases in the observation model (4) cannot be separated uniquely from the clock terms and the integer ambiguity without further conventions or information on either of those values.

4.2 Ionosphere-free combination

Ionospheric path delays can largely be eliminated by forming the “ionosphere-free” (IF) combination

$$\begin{aligned} x_{\text {IF}} := \text {IF}(x_{1},x_{2}) := (\alpha +1) x_{1} - \alpha x_{2} \end{aligned}$$

(5)

of a quantity x based on measurements $x_1$ and $x_2$ on two frequencies $f_1$ and $f_2$ with

$$\begin{aligned} \alpha = \frac{f_2^2}{f_1^2-f_2^2} \end{aligned}$$

(6)

(Misra and Enge 2006). Neglecting higher-order ionospheric contributions, the following model for the IF pseudorange or carrier phase range observations is obtained:

$$\begin{aligned} \begin{array}{lcl} p_{\text {r};\text {IF}}^\text {s}&{}=&{} ( \rho +\xi _{\text {r};\text {IF}}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) + c (d_{\text {r};\text {IF}}-d^\text {s}_\text {IF}) \\ \varphi _{\text {r};\text {IF}}^\text {s}&{}=&{} ( \rho +\zeta _{\text {r};\text {IF}}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) + c(\delta _{\text {r};\text {IF}}-\delta _{\text {IF}}^\text {s}) \\ &{} &{} +\, \text {IF}(\lambda _1 N_{\text {r};1}^\text {s}, \lambda _2 N_{\text {r};2}^\text {s}) +\,\text {IF}(\lambda _1,\lambda _2) \omega _\text {r}^\text {s}. \end{array} \end{aligned}$$

(7)

It may be noted that the ionosphere-free combination of the code biases vanishes, when referring the satellite and receiver clock offsets to a conventional signal combination (e.g., GPS L1/L2 P(Y) tracking) and using the same signals for the observations. While this applies throughout the present work, the generic observation model is retained for better transparency and applications using other types of code observations.

Introducing the “wide-lane” and “narrow-lane” wavelengths

$$\begin{aligned} \lambda _\text {wl}= \frac{c}{f_1-f_2} \quad \text {and} \quad \lambda _\text {nl}= \frac{c}{f_1+f_2} , \end{aligned}$$

(8)

as well as the wide-lane ambiguity

$$\begin{aligned} N_{\text {r};\text {wl}}^\text {s}=N_{\text {r};1}^\text {s}- N_{\text {r};2}^\text {s}\end{aligned}$$

(9)

the model for the carrier phase range may be rewritten as

$$\begin{aligned} \varphi _{\text {r};\text {IF}}^\text {s}= & {} (\rho +\zeta _{\text {r};\text {IF}}^\text {s}) + c(\mathrm{d}t_\text {r}-\mathrm{d}t^\text {s}) + c(\delta _{\text {r};\text {IF}}-\delta _{\text {IF}}^\text {s}) \nonumber \\&+\, \lambda _\text {nl}\left( N_{\text {r};1}^\text {s}+ \frac{\lambda _\text {wl}}{\lambda _2} N_{\text {r};\text {wl}}^\text {s}\right) +\, \lambda _\text {nl}\omega _\text {r}^\text {s}, \end{aligned}$$

(10)

which describes the dependence of the ionosphere-free combination on the phase ambiguities in a manner adapted to the ambiguity resolution approach pursued in Sect. 4.

4.3 Melbourne–Wuebbena combination

The Melbourne–Wuebbena (MW) combination (commonly attributed to Melbourne 1985; Wübbena 1985) is a geometry- and ionosphere-free linear combination formed from dual-frequency code and phase observations that is widely used for cycle slip detection and resolution of the wide-lane ambiguity (Hofmann-Wellenhof et al. 2007; Xu 2010). When working in the range domain (rather than phase cycles), the MW combination is defined as

$$\begin{aligned}&\text {MW}(\varphi _1,\varphi _2,p_1,p_2) \nonumber \\&\quad = \left( \frac{f_1\varphi _1-f_2 \varphi _2}{f_1-f_2} \right) - \left( \frac{f_1p_1+f_2p_2}{f_1+f_2} \right) \nonumber \\&\quad = \left( \frac{c}{f_1-f_2}\right) \cdot \left[ \left( \frac{\varphi _1}{\lambda _1} - \frac{\varphi _2}{\lambda _2} \right) - \frac{f_1-f_2}{f_1+f_2} \left( \frac{p_1}{\lambda _1} + \frac{p_2}{\lambda _2} \right) \right] .\nonumber \\ \end{aligned}$$

(11)

Inserting (4) into (11), the following observation model for the MW combination is obtained:

$$\begin{aligned}&\text {MW}(\varphi _{\text {r};1}^\text {s},\varphi _{\text {r};2}^\text {s},p_{\text {r};1}^\text {s},p_{\text {r};2}^\text {s}) \nonumber \\&\quad =\lambda _\text {wl}N_{\text {r};\text {wl}}^\text {s}+ \text {MW}(\zeta _{\text {r};1}^\text {s},\zeta _{\text {r};2}^\text {s},\xi _{\text {r};1}^\text {s},\xi _{\text {r};2}^\text {s}) \nonumber \\&\qquad +\,c\,\text {MW}(\delta _{\text {r};1},\delta _{\text {r};2},d_{\text {r};1},d_{\text {r};2}) - c\,\text {MW}(\delta _{1}^\text {s},\delta _{2}^\text {s},d_{1}^\text {s},d_{2}^\text {s}) . \nonumber \\ \end{aligned}$$

(12)

Besides the geometric range $\rho$ and the clock offsets ($\mathrm{d}t_\text {r}$, $\mathrm{d}t^\text {s}$), both the first-order ionospheric delays $I_{\text {r};i}^\text {s}$ and the phase windup $\omega _{\text {r};i}^\text {s}$ are rigorously eliminated when forming the MW combination. On the other hand, the MW combination is still affected by code and phase variations of the receive and transmit antennas, as well as the code and phase biases.

Practical experience (Laurichesse et al. 2009) suggests that the impact of code and carrier phase variations ($\xi$, $\zeta$) as well as other measurement errors (noise, multipath) is sufficiently small in comparison with the wide-lane wavelength of about 86 cm (for GPS L1 and L2 observations) to neglect them in the resolution of wide-lane ambiguities. The MW observation model can then be expressed as

$$\begin{aligned} \begin{array}{lcl} \text {MW}(\varphi _{\text {r};1}^\text {s},\varphi _{\text {r};2}^\text {s},p_{\text {r};1}^\text {s},p_{\text {r};2}^\text {s})\approx & {} \lambda _\text {wl}N_{\text {r};\text {wl}}^\text {s}+ \lambda _\text {wl}( \mu _{r;\text {wl}} -\mu _\text {wl}^\text {s}) \end{array} \end{aligned}$$

(13)

with

$$\begin{aligned} \begin{array}{lcl} \mu _{r;\text {wl}} &{}=&{} c\,\text {MW}(\delta _{\text {r};1},\delta _{\text {r};2},d_{\text {r};1},d_{\text {r};2}) / \lambda _\text {wl}\\ \mu _\text {wl}^\text {s}&{}=&{} c\,\text {MW}(\delta _{1}^\text {s},\delta _{2}^\text {s},d_{1}^\text {s},d_{2}^\text {s}) / \lambda _\text {wl}\end{array} \end{aligned}$$

(14)

denoting the MW combination of the receiver and satellite biases in units of the wide-lane wavelength. As a consequence of these biases, the single-receiver MW combination itself is not an integer multiple of the wide-lane wavelength. The integer nature is only revealed when forming between-satellite and between-receiver double differences, in which case the respective biases are eliminated.

4.4 CNES-CLS wide-lane satellite bias and clock products

The wide-lane biases (14) aggregate various unknown code and phase biases and cannot be unambiguously determined from observed values of the MW combination. However, their fractional values $\widehat{\mu }_\text {wl}=\mu _\text {wl}-\lfloor \mu _\text {wl}\rfloor$ can be inferred from observations of a global station network, when applying a zero-mean constraint to separate satellite and receiver contributions (Loyer et al. 2012). Fractional satellite wide-lane biases $\widehat{\mu }_\text {wl}^\text {s}$ obtained in this way are provided on a daily basis as part of the CNES-CLS wide-lane satellite bias (WSB) product.

Complementary to these biases, the CNES-CLS clock product provides high-rate (30 s) values of the satellite “phase clock offset”

$$\begin{aligned} c\widehat{dt}^\text {s}= c\mathrm{d}t^\text {s}+ \left[ c\delta _\text {IF}^\text {s}- \lambda _1 k_1^\text {s}- \lambda _\text {nl}\frac{\lambda _\text {wl}}{\lambda _2} \lfloor \mu _\text {wl}^\text {s}\rfloor \right] \end{aligned}$$

(15)

for its users. The phase clock offset aggregates various contributions of code and phase biases that are not independently observable along with the satellite “code clock offset” $c\mathrm{d}t^\text {s}$. It also includes a free integer constant $k_1^\text {s}$ that is adjusted in such a way as to limit difference of the code and phase clock offsets to less than half an L1 wavelength.

Introducing a corresponding receiver phase clock offset

$$\begin{aligned} c\widehat{dt}_\text {r}= c\mathrm{d}t_\text {r}+ \left[ c\delta _{\text {r};\text {IF}} - \lambda _1 k_{\text {r},1} - \lambda _\text {nl}\frac{\lambda _\text {wl}}{\lambda _2} \lfloor \mu _{\text {r};\text {wl}}\rfloor \right] , \end{aligned}$$

(16)

the observation model can finally be expressed in the following form:

$$\begin{aligned} p_{\text {r};\text {IF}}^\text {s}= & {} ( \rho +\xi _{\text {r};\text {IF}}^\text {s}) + c(\widehat{dt}_\text {r}-\widehat{dt}^\text {s}) + c (d_{\text {r};\text {IF}}-d^\text {s}_\text {IF}) +e_{\text {r};\text {IF}}^\text {s}\nonumber \\ \varphi _{\text {r};\text {IF}}^\text {s}= & {} (\rho +\zeta _{\text {r};\text {IF}}^\text {s}+ \lambda _\text {nl}\omega _\text {r}^\text {s}) + c(\widehat{dt}_\text {r}-\widehat{dt}^\text {s}) \nonumber \\&+\, \lambda _\text {nl}\left( \widehat{N}_{\text {r};1}^\text {s}+\,\frac{\lambda _\text {wl}}{\lambda _2} \widehat{N}_{\text {r};\text {wl}}^\text {s}\right) . \end{aligned}$$

(17)

It closely resembles the standard model described by (7) and (10) but differs in two important details. First, the pseudorange model includes a contribution $e_{\text {r};\text {IF}}^\text {s}$ that signifies the difference of code and phase clocks. Since no distinct code clock offsets are provided in the CNES-CLS products, this term has to be neglected in the processing at the expense of a potential increase in the pseudorange residuals. At a magnitude of less than a wavelength, this is generally tolerable in view of other code measurement and modeling errors, such as multipath or the neglect of code-specific antenna phase patterns. Secondly, (17) involves a modified value

$$\begin{aligned} \widehat{N}_{\text {r};\text {wl}}^\text {s}= N_{\text {r};\text {wl}}^\text {s}+ \lfloor \mu _{r;\text {wl}} \rfloor - \lfloor \mu _\text {wl}^\text {s}\rfloor = \text {MW}/\lambda _\text {wl}- \widehat{\mu }_{\text {r};\text {wl}} + \widehat{\mu }_\text {wl}^\text {s} \end{aligned}$$

(18)

of the wide-lane integer ambiguity that can be unambiguously determined from the MW combination for given values of the fractional satellite wide-lane ambiguity $\widehat{\mu }_\text {wl}^\text {s}$.

4.5 Pass-by-pass ambiguity fixing

Within the GHOST reduced dynamic orbit determination process, all observations are assigned to “passes,” where each pass represents a continuous tracking arc for a specific GPS satellite (Montenbruck et al. 2005). Ideally, a pass corresponds to the visibility period of a given satellite within the antenna’s field of view, but cycle-slips may result in a split-up into multiple shorter passes. For LEO satellites typical pass durations amount to 10–40 min and a representative total of $n_p=450$ passes arises for a 30 satellite GPS constellation and 15 orbital revolutions of the LEO satellite per day. Within each pass, the carrier phase ambiguity remains constant and the ambiguity fixing can thus be performed considering entire passes rather than individual, epochwise observations.

As a first step, we compute the average value $(\overline{\text {MW}}_{\text {r}}^\text {s})_I$ of the Melbourne–Wuebbena combination for each pass I and correct the resulting value with the fractional wide-lane satellite bias:

$$\begin{aligned} m_I = ((\overline{\text {MW}}_{\text {r}}^\text {s})_I/\lambda _\text {wl}+ \widehat{\mu }_\text {wl}^\text {s}) . \end{aligned}$$

(19)

Following (18), the vector

$$\begin{aligned} (m_I) = (\widehat{N}_{\text {r};\text {wl}}^\text {s})_I + \widehat{\mu }_{\text {r};\text {wl}} + \varepsilon _{m,I} \end{aligned}$$

(20)

for all passes $I=0,\ldots n_p$ can be split into a sum of pass-specific integer values $(\widehat{N}_{\text {r};\text {wl}}^\text {s})_I$ and a common fractional wide-lane bias $\widehat{\mu }_{\text {r};\text {wl}}$ of the receiver. The additional term $\varepsilon _{m,I}$ indicates residual errors in the pass-averaged wide-lane combination caused by receiver noise and multipath, time variable biases, as well as model simplifications such as neglected differential phase center offsets.

Estimation of $(\widehat{N}_{\text {r};\text {wl}}^\text {s})_I$ and $\widehat{\mu }_{\text {r};\text {wl}}$ from observed values $m_I$ represents a classical mix-integer problem that can, for example, be solved using the least squares ambiguity decorrelation method (LAMBDA; Teunissen 1995). However, a simple integer rounding of between-pass differences $m_I-m_{I_0}$ is sufficient in practice to determine integer estimates of $(\widehat{N}_{\text {r};\text {wl}}^\text {s})_I - (\widehat{N}_{\text {r};\text {wl}}^\text {s})_{I_0}$ for a suitably chosen reference pass $I_0$ in view of the moderate standard deviation $\sigma (\varepsilon _m)$ of less than 0.1 cycles. After determining the integer-valued differences, the sum of $(\widehat{N}_{\text {r};\text {wl}}^\text {s})_{I_0}$ and $\widehat{\mu }_{\text {r};\text {wl}}$ can be adjusted and split into the wide-lane ambiguity of the reference pass and the fractional wide-lane ambiguity of the receiver. As a result, the integer-valued single-receiver wide-lane ambiguities $(\widehat{N}_{\text {r};\text {wl}}^\text {s})_I$ for all passes are obtained. In a subsequent step, these values are used to estimate the single-receiver L1 ambiguity $(\widehat{N}_{\text {r};1}^\text {s})_I$ for each pass.

Fig. 2

Distribution of wide-lane ambiguity residuals for a sample one-day data arc (DOY 2016/100). The solid line indicates a normal distribution with the same standard deviation

For the purpose of illustration, a histogram of wide-lane ambiguity residuals $\varepsilon _m = m - \widehat{N}_{\text {r};\text {wl}}^\text {s}+ \widehat{\mu }_{\text {r};\text {wl}}$ is shown in Fig. 2 for day-of-year (DOY) 100 of 2016. In the given example, 99% of the wide-lane residuals are confined to less than $3\sigma =0.23$ by magnitude, which confirms the applicability of integer rounding for the wide-lane ambiguity resolution. Vice versa, only 4 out of 404 passes exhibit wide-lane ambiguities within $3\sigma$ of $\pm \,0.5$, which furthermore confirms that the receiver provides integer-valued wide-lane ambiguities with high reliability.

Prior to resolution of the L1 ambiguity, float-valued carrier phase range biases $B_I$ for each pass are estimated within the established reduced dynamic orbit determination approach (Montenbruck et al. 2005). These biases reflect essentially the average difference between ionosphere-free pseudorange and carrier phase observations and are based on the observation model

$$\begin{aligned} \begin{array}{lcl} p_{\text {r};\text {IF}}^\text {s}&{}=&{} ( \rho +\xi _{\text {r};\text {IF}}^\text {s}) + c(\widetilde{dt}_\text {r}-\widehat{dt}^\text {s}) + c (d_{\text {r};\text {IF}}-d^\text {s}_\text {IF}) \\ \varphi _{\text {r};\text {IF}}^\text {s}&{}=&{} ( \rho +\zeta _{\text {r};\text {IF}}^\text {s}+ \lambda _\text {nl}\omega _\text {r}^\text {s}) + c(\widetilde{dt}_\text {r}-\widehat{dt}^\text {s}) - B_I. \end{array} \end{aligned}$$

(21)

Here, the symbol $\widetilde{dt}_\text {r}$ is used to denote the receiver clock estimated in the float ambiguity orbit determination, which will, in general, be different from that of the ambiguity-fixed solution due to the impact of slowly varying biases.

Based on comparison with (17), the bias $B_I$ and the individual ambiguities for the respective passes I are related by

$$\begin{aligned} \begin{array}{lcl} -B_I= & {} + \lambda _\text {nl}\left( \widehat{N}_{\text {r};1}^\text {s}+ \frac{\lambda _\text {wl}}{\lambda _2} \widehat{N}_{\text {r};\text {wl}}^\text {s}\right) + c(\widehat{dt}_\text {r}-\widetilde{dt}_\text {r}). \end{array} \end{aligned}$$

(22)

This yields again a mixed-integer problem

$$\begin{aligned} b_I = (\widehat{N}_{\text {r};1}^\text {s})_I + \tau \end{aligned}$$

(23)

for the estimation of the pass-specific $N_1$ ambiguities and the scaled clock difference

$$\begin{aligned} \tau = + c(\widehat{dt}_\text {r}-\widetilde{dt}_\text {r})/ \lambda _\text {nl}\end{aligned}$$

(24)

from known values

$$\begin{aligned} b_I = -B_I/\lambda _\text {nl}- \frac{\lambda _\text {wl}}{\lambda _2} (\widehat{N}_{\text {r};\text {wl}}^\text {s})_I \end{aligned}$$

(25)

of the carrier phase range bias and the previously fixed integer ambiguity of each pass.

Fig. 3

Evolution of the fractional L1 biases for a sample one-day data arc (DOY 2016/100). For each pass, the graph shows the fractional value of the float-valued bias $b_I$ (in units of narrow-lane cycles) versus the center-time of the pass. For improved clarity, cycle rollovers between adjacent passes have been removed to evidence the long-term variation

In practice, estimation of the $N_1$ ambiguity is hampered by the fact that $\tau$ is not a constant, but exhibits slow variations over time that may well exceed a (narrow-lane) cycle. This is illustrated in Fig. 3, which shows the fractional part of estimated $b_I$ values for each pass prior to the ambiguity fixing. Besides a long-term drift of roughly 2 cycles, superimposed quasiperiodic variations may be recognized that partly correlate with the orbital period of 1.7 h. As a result, it is not possible to directly solve (23) for an integer-valued set of passwise ambiguities $(\widehat{N}_{\text {r};1}^\text {s})_I$ and a common float-valued parameter $\tau$.

On the other hand, $\tau$ is found to vary only slightly between adjacent passes I and J, i.e., passes of different GPS satellites with slightly shifted and/or overlapping time intervals. In this case, $\tau$ can be eliminated and the between-passes single difference $\varDelta (\bullet )_{IJ} = (\bullet )_I-(\bullet )_J$ can be obtained with good confidence from

$$\begin{aligned} \varDelta b_{IJ} = \varDelta (\widehat{N}_{\text {r};1}^\text {s})_{IJ} + \varDelta \varepsilon _{b,IJ} , \end{aligned}$$

(26)

where $\varDelta \varepsilon _{b,IJ}$ indicates the residual errors in the differenced biases b. Its standard deviation $\sigma (\varDelta \varepsilon _b)$ amounts to typically 0.11 narrow-lane cycles (corresponding to roughly 12 mm) in the GHOST orbit determination of Sentinel-3A (Fig. 4).

Fig. 4

Distribution of relative $N_1$ ambiguity residuals for a sample one-day data arc (DOY 2016/100). The solid line indicates a normal distribution with the same standard deviation

Table 3 Coordinates for modeling of GNSS and SLR observations

Similar to the wide-lane ambiguity resolution, a simple integer rounding can again be used for determining integer-valued relative $N_1$ ambiguities from (26). In order to avoid a potentially adverse impact of wrongly fixed ambiguities, a conservative threshold of $\varDelta \varepsilon _{b,IJ}< 0.15 cy$ is adopted for acceptance of the rounded $\varDelta (\widehat{N}_{\text {r};1}^\text {s})_{IJ}$ value as the proper relative ambiguity for the two passes. Once accepted, a soft constraint

$$\begin{aligned} \begin{array}{lcl} B_J-B_I= & {} + \lambda _\text {nl}\left( \varDelta ( \widehat{N}_{\text {r};1}^\text {s})_{IJ} + \frac{\lambda _\text {wl}}{\lambda _2} \varDelta (\widehat{N}_{\text {r};\text {wl}}^\text {s})_{IJ} \right) \end{array} \end{aligned}$$

(27)

with standard deviation $\sigma (B_J-B_I)= 0.1$ mm is applied as a priori information for the subsequent iteration of the orbit determination process.

Roughly 85% of the $\varDelta (\widehat{N}_{\text {r};1}^\text {s})$ ambiguity differences can be fixed to integer values in the first ambiguity resolution step in case of Sentinel-3A. The associated constraints on between-pass carrier range biases applied in the subsequent iteration of the reduced dynamic orbit determination notably improve the stiffness of the resulting orbit compared to the previous float solution. Likewise carrier range biases that were not yet constrained benefit from constraints on the other passes and converge to values that enable fixing. Typically, two iterations with ambiguity fixing are sufficient to resolve between-pass ambiguities for about 99% of all passes.

5 Offset calibration

By default, the orbit determination process makes use of known locations of the GPS antenna phase center (PC) and center-of-mass (CoM), and the same applies for the LRR location in the SLR-based orbit validation. The respective coordinates are commonly obtained from design information as well as complementary ground measurements of the spacecraft and equipment suppliers. The CoM location and its temporal variation throughout the mission can, furthermore, be obtained from a mass model of the satellite along with mass variations derived from tank pressure measurements and a book keeping of thruster activity. Values recommended for Sentinel-3A precise orbit determination are collated in Table 3.

While the respective information is typically made available by the spacecraft manufacturer with formal accuracies of millimeters or better, experience in past geodetic and remote sensing missions suggests the potential presence of inconsistencies at a level of 1–3 cm (Luthcke et al. 2003; Montenbruck et al. 2008; Swatschina et al. 2011; Peter et al. 2017). An effort is therefore made in this section, to assess the validity of these values for Sentinel-3A and to derive corrections were needed.

As a starting point, reduced dynamic orbits as well as complementary kinematic position solutions were obtained for a 20-day period using the reference values for the position of the GPS antenna reference point and CoM as well as the nominal phase center offset (PCO) from Table 3. The reduced dynamic solution directly yields a CoM trajectory constrained by the dynamical model; the kinematic GPS processing (Švehla and Rothacher 2003), in contrast, computes the position of the antenna phase center and uses the nominal PCO to infer the CoM trajectory.

Similar to other missions, a systematic discrepancy between both results can be observed for Sentinel-3, which evidences a 30-mm excess height of the modeled antenna phase center relative to the CoM. SLR observations, on the other hand, indicate a proper consistency of LRR and CoM positions, which suggests that the discrepancy is mainly related to the assumed phase center location. Given the fact that the location of the mechanical antenna reference point can be measured directly and with good accuracy, the employed PCO value appears as the most plausible cause of the observed difference between kinematic and reduced dynamic orbits. A 30-mm reduction in the PCO z-component (i.e., the component in the direction of the up-looking antenna boresight) is therefore adopted for further use in this study.

This value is in close accord with corrections derived within the Sentinel-1A mission (29 mm; Peter et al. 2017) and may hint at a systematic error or misinterpretation in the manufacturer-provided PCO for the patch-excited-cup (PEC; Öhgren et al. 2011) GPS antenna of the Sentinel satellites. It may be noted that this empirical correction of the radial antenna offset has only marginal ($\approx$ 2 mm) impact on the resulting radial position in a reduced dynamic orbit determination, since the orbit height is tightly constrained by the dynamical model and the observed orbital period. However, the modified phase center location offers improved modeling of the carrier phase observations, which is evidenced by an overall reduction in the carrier phase residuals (e.g., from 6 to 5 mm on DOY 2016/100) and proper consistency of the kinematic and reduced dynamic orbit determination.

In a second step, a map of phase variations (PV) is determined as a function of the azimuth and elevation in the antenna diagram. These phase variations describe line-of-sight-dependent deviations of the wavefront from a sphere around the adopted phase center. These distortions may be related to static multipath or other near-field effects caused by the spacecraft structure in the vicinity of the GPS antenna. As such, ground calibrations of stand-alone antennas or antennas with simplified satellite mock-ups often fail to represent the actual phase variations observed in orbit. It has therefore become common practice to conduct an in-flight calibration and to derive a dedicated PV map from the actual observations.

Fig. 5

Polar plot of phase variations for the Sentinel-3 main GPS antenna as derived from residuals of the ionosphere-free L1/L2 carrier phase combination. The $+y$-axis (azimuth ${0}^{\circ }$) of the antenna frame coincides with the $+$ x-axis of the spacecraft body that points into the anti-flight direction

For Sentinel-3A, we make use of a residuals stacking approach (Jäggi et al. 2009) with two iterations to obtain the phase map shown in Fig. 5 from averaged phase residuals over a 20-day data set. Peak values amount to 10–15 mm, but typical phase variations are substantially smaller. Application of the PV map in the orbit determination has no discernible impact (< 1 mm) on the radial component of the estimated CoM orbit, but the carrier phase residuals are again clearly reduced (e.g., from 5 to 4 mm on DOY 2016/100).

When fixing ambiguities, a mean shift in cross-track direction of about 9 mm is encountered relative to the float solution with PCO/PV correction, while the radial position remains unchanged (< 1 mm). The cross-track shift is accompanied by mean empirical accelerations of about ${10}\, \hbox {nm}/\hbox {s}^{2}$ which are not, however, present in the float solution. These findings provide strong evidence for an inconsistency $\varDelta r_\text {N}$ of about 10 mm between the true and assumed cross-track (y-) component of the assumed GPS antenna offset from the center-of-mass.

In the float ambiguity solution, this inconsistency can largely be absorbed by carrier phase ambiguities (Jäggi et al. 2009), which enable a consistent dynamical modeling of the CoM trajectory and the carrier phase observations even in the presence of an erroneous cross-track antenna offset. The ambiguity fixing, in contrast, offers a high geometric accuracy and tightly constrains the horizontal (i.e., along-track and cross-track) components of the modeled antenna phase center to the “true” trajectory. In case of an erroneous antenna offset, the motion of the CoM will no longer coincide with the orbital plane described by the dynamical model. This mismatch can, however, be compensated by an additional cross-track acceleration

$$\begin{aligned} \varDelta a_\text {N} = \frac{GM_\oplus }{r^2} \cdot \frac{\varDelta r_\text {N}}{r} , \end{aligned}$$

(28)

where ${GM_\oplus }/{r^2}\approx {7.7} {\hbox {m}/\hbox {s}^2}$ is the gravitational acceleration of the Earth at the orbital radius $r\approx {7200}\hbox { km}$ of Sentinel-3A (Meindl et al. 2013). When adjusting empirical accelerations as part of the reduced dynamic orbit determination, a 9-mm error in the cross-track component of the antenna offset will therefore result in a mean value of the cross-track acceleration of about ${10}\,\hbox {nm}/\hbox {s}^2$. Since the empirical accelerations are always constrained to zero, slightly smaller values may arise in practice, depending on the employed a priori variance.

While the observed cross-track shift between float and fixed solutions as well as the cross-track acceleration bias in the ambiguity-fixed solution provide clear evidence of an error in the GPS antenna offset from the CoM, the GPS data analysis does not allow to uniquely attribute the mismatch to either a GPS antenna location error, a CoM location error or a combination thereof. Further insight may, however, be gained from the analysis of SLR observations that may be used to identify systematic offsets in the modeled LRR trajectory (Hackel et al. 2016). Based on the analysis of SLR residuals for the entire ten-month data arc, the LRR trajectory obtained from the float ambiguity solution (and using nominal LRR–CoM offsets) is indeed found to require a cross-track correction $\varDelta r_\text {N}$ of 10.5 mm. The LRR trajectory obtained from the ambiguity-fixed solution (and using nominal LRR–CoM offsets), in contrast, agrees with the SLR observations within $|\varDelta r_\text {N}|< {1}\,\hbox {mm}$.

Fig. 6

Impact of an erroneous CoM location in the spacecraft body frame on float ambiguity POD (a) and ambiguity-fixed POD (b). The true center-of-mass in the schematic drawing of the Sentinel-3A satellite (as seen from above) is marked by a black cross, while the position reported by the spacecraft operator is indicated by a red dot. The blue and green dots show the location of the main GPS antenna and the laser retroreflector, respectively. Solid lines indicate the true trajectories, while dashed lines describe computed trajectories based on nominal offset values

These results provide strong evidence for a cross-track bias of 1 cm in the reported CoM position, and the best match of SLR and GPS observations can indeed be obtained when reducing the y-coordinate of the CoM by this amount (Table  3). For better illustration, Fig. 6 shows the computed trajectories of the LRR, CoM, and GPS antenna for the float ambiguity solution and the ambiguity-fixed solution. In the first case (Fig. 6a), the computed CoM trajectory agrees with the true CoM orbit; however, both the computed orbits of both the LRR and the GPS antenna are offset by the CoM bias. However, this offset only shows up in the SLR residuals, whereas it is absorbed in the estimated carrier phase ambiguities and cannot be recognized from the GPS residuals. The ambiguity-fixed solution, in contrast, enforces the modeled trajectory of the GPS antenna phase center to coincide with the true orbit. The same applies for the modeled LRR trajectory, which confirms the validity of the assumed relative cross-track position of the LRR and GPS antenna phase center. At the same time, however, a wrong position is reported for the CoM trajectory, and non-physical empirical cross-track accelerations are required to shift the modeled orbit plane with respect to its true location. For completeness, we note that the Sentinel-3A satellite employs a yaw steering attitude, which aligns the principal body axes with the nadir and ground track direction. On average over an orbit the cross-track direction ($+N$) matches the $+y$-body axis, while the along-track direction T coincides with the $-x$-axis of the spacecraft.

In view of the good consistency of the nominal LRR–GPS y-offset with SLR and GPS observations in the ambiguity-fixed POD, a systematic cross-track (y-) bias in the operator supplied CoM coordinates appears as the most plausible explanation of the various features observed in our POD solutions. For the final processing, we therefore adopt a correction of $\varDelta y_\text {CoM}= 10\,\hbox {mm}$ to the nominal CoM location in the spacecraft body frame (Table 3). An independent conformation of this interpretation and the proposed value of the CoM shift might be obtained in future work from the analysis of DORIS measurements, provided that good confidence in the DORIS phase center location can be obtained from independent pre-flight calibrations.

6 Results and validation

Based on the single-receiver ambiguity resolution presented in Sect. 3 and using the empirical corrections to the nominal phase center offset, phase variations and center-of-mass location discussed in Sect. 5, reduced dynamic orbits of Sentinel-3A have been determined for a ten-month period starting in late March 2016 and ending in January 2017. As a baseline, data were processed in daily 24-h arcs based on RINEX observation files for the same day. Complementary to this a one-month interval was processed in 30-h arcs centered at noon of each day to assess the consistency of consecutive solutions in the overlap region near midnight. The precision and accuracy of the ambiguity-fixed orbits in relation to float solutions are assessed through overlap comparisons as well as satellite laser ranging residuals.

Fig. 7

Concept of overlap comparison

Fig. 8

Satellite laser ranging residuals for Sentinel-3A precise orbit determination using float ambiguity estimation (a) and single-receiver ambiguity fixing (b) over a ten-month data arc

The overlap comparison is traditionally used in orbit determination to assess the internal consistency of a specific processing scheme (Tapley 2004; Bertiger et al. 1994). It evaluates the difference of two solutions based on distinct but overlapping data arcs in the interval common to both arcs. To avoid the impact of a decreased accuracy near the begin and end of each orbit determination, the comparison interval can further be decreased to a subset of the overlap region. In the present case, consecutive 30-h solutions offer a 6-h overlap ($21^\text {h}$ of previous day to $03^\text {h}$ of current day), but we confine the comparison to the central interval of $\pm \,{2}$ h around midnight (Fig. 7) to exclude arc boundary degradations. In a purely dynamic orbit determination, the entire set of observations processed in a given arc contributes to the resulting orbit in an equal manner. Accordingly, the orbits in the overlap region are strongly influenced by the different data arcs and the difference in the overlap region is often a good indicator of the overall orbit determination accuracy. For reduced dynamic orbit determination in contrast, the estimated orbit in a given interval is largely driven by the observations in this period, while the estimation of empirical accelerations or other stochastic parameters notably attenuates the influence of observations further apart. As a result, overlap comparisons of reduced dynamic orbit determination solutions can at best be used as an indicator of repeatability (precision) but are still useful to compare different techniques.

As shown in Table 4, the traditional POD scheme with float ambiguity estimation provides a representative overlap consistency of 3 mm in the central 4-h interval, while the ambiguity-fixed solutions typically match to better than 1 mm. This improved consistency can largely be understood by the strong geometric constraints imposed by the ambiguity fixing irrespective of the particular data arc. However, this statement only applies if all ambiguities are fixed to their correct values. This becomes evident from an increased fraction of large (1–2 cm) peak errors encountered in the ambiguity-fixed solutions. Further analysis will be required to examine this cases and the reason for a potentially inconsistent ambiguity fixing in more detail. Overall, however, the overlap analysis confirms the benefit of ambiguity fixing for the precision of POD solutions.

Table 4 Overlap consistency (3D position difference within $\pm \,2\,\hbox {h}$ around midnight) of Sentinel-3A POD solutions for DOY 90–120/2016

For a fully independent assessment of the orbit determination performance, laser ranging measurements are compared with the expected station-to-satellite distance based on POD solutions obtained from the GPS tracking. The modeling of SLR makes use of station coordinates referred to the SLRF2008 frame to ensure best consistency with the IGb08 frame of the GPS orbit products that is inherited to the resulting Sentinel-3A orbit determination solutions. Line-of-sight-dependent range corrections for the Sentinel-3A LRR are based on values previously computed for the design-compatible reflector of Cryosat-1 (Montenbruck and Neubert 2011). Other relevant processing standards are summarized in Table 1.

Using a subset of ten high-performance stations of the global International Laser Ranging Service (ILRS; Pearlman et al. 2002) network, RMS residuals of 13 and 11 mm are obtained for the float ambiguity processing and the ambiguity-fixed solutions, respectively (Fig. 8). Both values include a mean bias of about 2 mm and are based on observations above a ${10}^{\circ }$ station elevation mask and considering an outlier threshold of 0.2 m.

Based on analysis of the SLR residuals for different line-of-sight directions, a radial position error $\varDelta r_\text {R}\approx -\,3\,\hbox {mm}$ of the modeled LRR trajectory can be inferred that is common to both solutions. Potential explanations for this mean offset include a corresponding error in the adopted radial component of the LRR–CoM offset, an error

$$\begin{aligned} \varDelta a_\text {R} = -3\frac{GM_\oplus }{r^2} \cdot \frac{\varDelta r_\text {R}}{r} \approx {10}\, \hbox {nm}/\hbox {s}^2, \end{aligned}$$

(29)

in the radial acceleration of the employed dynamical model, or even a scale inconsistency of the GPS-based IGb08 frame and the SLR-based SLRF08 reference frame. Even though none of these options can be excluded without independent measurements and analyses, a 3-mm error in the radial component of SLR–CoM offset appears as a very plausible explanation in view of the (notably larger) lateral CoM errors discussed in Sect. 5.

While the 15% reduction in the RMS SLR residuals provides clear evidence of an improved overall accuracy of the ambiguity-fixed POD solutions, the assessment is heavily masked by station-specific ranging biases of up to 1.5 cm of the individual stations. For better interpretation, we therefore present the mean and standard deviation ($\sigma$) of the SLR residuals for each contributing station in Table 5.

Table 5 SLR residuals and number of normal points ($N_\text {np}$) for individual ILRS stations employed in the Sentinel-3A orbit validation from end March 2016 to end January 2017

Considering only the standard deviation of SLR residuals for individual stations, an even more dramatic performance improvement enabled by the ambiguity fixing may be recognized. In case of four stations (Graz, Herstmonceux, Matera, and Potsdam), the standard deviation decreases by up to one-third, leaving residuals of down to $\sigma =6$ mm. On average over all stations, the standard deviation amounts to 7.2 mm for the ambiguity-fixed orbits as opposed to 10.4 mm for the float ambiguity processing.

7 Summary and conclusions

Reduced dynamic orbits for the Sentinel-3A spacecraft have been determined based on ambiguity-fixed GPS carrier phase observations over a ten-month period following the launch and initial checkout. The single-receiver ambiguity fixing concept employed here makes use of wide-lane bias products and clock offset products prepared by the CNES/CLS analysis center and publicly made available as part of the International GNSS Service. It employs a passwise resolution of wide-lane and $N_{1}$ ambiguities that greatly facilitates an upgrade of legacy POD software packages based on zero-difference processing. Use of this scheme in DLR’s GHOST software confirms the applicability of the CNES/CLS products for external users using independent in-house processing tools. These aspects and the lean set of required auxiliary data make the CNES/CLS products particularly attractive for an ambiguity-fixed precise orbit determination in a wider range of LEO missions.

Compared to float ambiguity solutions, an improved self-consistency and precision of the resulting orbits has been confirmed through overlap analyses and comparison of the GPS-based orbits with satellite laser ranging observations. For high-grade SLR stations, line-of-sight range errors with a standard deviation down to 5 mm were achieved considering all observations above a ${10}^{\circ }$ elevation limit, which marks a 30% improvement compared to the float solution. Along with the improved precision, the ambiguity fixing helps to reveal systematic biases in the assumed offset of the GPS antenna phase center from the spacecraft center of mass. Considering both GPS and SLR observations, strong indications for a 1-cm lateral error in the reported CoM location are obtained. This offset is essentially absorbed in the adjusted carrier phase ambiguities when using a float ambiguity processing scheme.

The orbital radius of the CoM in the reduced dynamic orbit determination is mostly driven by the employed dynamical model and only weakly sensitive to corresponding antenna offset errors unless empirical accelerations in radial direction are adjusted with loose a priori constraints. As such, ambiguity fixing itself cannot contribute to a better absolute height calibration and remaining systematic errors in the orbit height will ultimately be absorbed in instrumental biases of the SAR altimeter relative to other altimetry missions. Even though the absolute height modeling continues to rely on proper dynamical models for the spacecraft motion as well as ground calibrations for the relative position of the altimeter reference point and the CoM, the improved stability of ambiguity-fixed orbits can be expected to contribute to a better global consistency of sea surface measurements. However, a corresponding analysis as well as comparison with orbit solutions based on DORIS tracking exceeds the scope of the present study and are left for further work.

Ambiguity fixing of Sentinel-3A carrier phase observations has first been enabled in the current study through correction of half-cycle biases in the raw receiver data by taking into account the polarity of the decoded navigation data stream. A corresponding modification of the Level 0 GPS instrument data processing in the operational ground segment is encouraged to enable generation of ambiguity-fixed Sentinel-3A orbit products by a wider range of analysis centers.