The solid angle hidden in polyhedron gravitation formulations

Abstract

Formulas of a homogeneous polyhedron’s gravitational potential typically include two arctangent terms for every edge of every face and a special term to eliminate a possible facial singularity. However, the arctangent and singularity terms are equivalent to the face’s solid angle viewed from the field point. A face’s solid angle can be evaluated with a single arctangent, saving computation.

1 Introduction

Blokh (1997) describes Fedor Sludskii’s pioneering derivation of a homogeneous polyhedron’s gravitation (Sludskii 1863). Other early papers are published by Mehler (1866), Mertens (1868), and Cayley (1874). When digital computers eased calculation a century later, geophysicists devised and reworked polyhedral formulations to study subsurface bodies and strata (Paul 1974; Barnett 1976; Okabe 1979; Waldvogel 1979; Golizdra 1981). Astrodynamicists began using polyhedral formulations in the 1990’s to evaluate gravitation of non-spherical solar-system bodies (Werner and Scheeres 1997; Rossi et al. 1999; Hudson et al. 2000; Scheeres et al. 2002, 2003; Richardson and Melosh 2006; Ikeda et al. 2008; Silva et al. 2011; Binzel et al. 2015).

Many derivations of homogeneous polyhedral gravitation begin with the volume integral for potential $\iiint _{B} \frac{1}{r} \mathrm {d}V$, where $B$ is the polyhedron and $r$ is the distance between the field (observation) point and differential volume element $\mathrm {d}V$ (the gravitational constant and uniform density factors are omitted throughout this paper to reduce clutter). The volume integral is reduced to a sum of surface integrals over polygonal faces $f$ of the polyhedron (Sect. 2 of this paper). Each surface integral resembles $\iint _{f} \frac{1}{r} \mathrm {d}S$, where $r$ is the distance between the field point and differential surface element $\mathrm {d}S$ of the face. This can be reduced to a line integral around the face’s boundary (Sect. 4). The ultimate result can be expressed as an arctangent and a logarithm term at both ends of every edge of every face.

Strakhov et al. (1986b), Pohánka (1988), and Strakhov and Lapina (1990) present the derivations of polyhedron gravitation and recommend alternate formulations to improve performance and accuracy. Holstein and Ketteridge (1996) present an error analysis based on the aspect ratio or angular extent of the polyhedron viewed from the field point. Holstein et al. (1999) show that underlying expressions of various algorithms are mathematically equivalent, and analyze computational effort in terms of floating-point operations (FLOPS) and accuracy.

If the field point is inside the body or on its surface, the integrand $1 / r$ is singular at the field point and the integral is improper. Leathem (1913, Sect. 12) and Kellogg (1929, Ch. VI) show that these singularities can be ignored. For a polyhedron, there remains an “edge singularity” (Appendix C.1) where the field point is embedded in an edge (Plouff 1976; Pohánka 1988; D’Urso 2014).

However, many formulations contain a “prism singularity” (Sect. 3) where the orthogonal projection of the field point onto the polyhedral face plane is within the face, whether or not the field point is inside the body. A singular point can be eliminated by removing a ball or disc centered on the singularity from the integration domain, and shrinking that region to zero radius. Applying this procedure to the prism singularity results in a term called the “prism correction” in this paper (Sect. 3.1). Other papers showing this prism correction include Plouff (1976, p. 729), Göetz and Lahmeyer (1988, Eq. 6), Kwok (1991, Eq. 12), Petrović (1996, Appendix D), Tsoulis and Petrović (2001, Eqs.  23–25), D’Urso (2013, Eq. 19), and Conway (2015, Sect. 2.1). Determining whether each face needs to be corrected, and then the correction value itself, requires additional computation.

Holstein and Ketteridge (1996) eliminate a face’s prism singularity by inserting an extra integrand term (Sect. 5). Their formulation still has two arctangents per edge of every face.

Werner and Scheeres (1997) use a very different formulation which interprets a face’s arctangents as a solid angle and eliminates any prism singularity. The formulation allows a non-convex polyhedron and/or non-convex faces. A surface integrand is interpreted as a differential solid angle (Sect. 7). The face’s solid angle results when this surface integration is performed. A polygon’s solid angle can be evaluated by summing vertex angles of a corresponding spherical polygon (Sect. 8) instead of by integration. A single arctangent for each face replaces the multiple arctangents appearing in most formulations. Showing this equivalence (Sect. 11,12) and reducing computational effort (Sect. 13) are the main goals of this paper.

This paper contains derivations only of a homogeneous polyhedron’s potential, not its acceleration or gravity-gradient tensor. Numerical or computational properties of the solid-angle formulation are not analyzed. A numeric comparison of this paper’s formulation with others appears in Sect. 15.

1.1 Notation and terminology

Scalar symbols, such as $r$ are italic, and vector symbols, such as $\mathbf {r}$ are bold. A vector’s norm is denoted with the corresponding scalar: $\Vert {\mathbf {r}}\Vert = r$; $\Vert {\varvec{\rho }}\Vert = \rho$. A unit-length direction vector wears a hat: $\hat{\mathbf {r}}= \mathbf {r}/ r$.

A coordinate is signed, perhaps, computed by the inner product of a position vector and a unit-length direction vector. A distance or length is non-negative.

An angle $\alpha$ can be convex $(\alpha > 0)$ or reflex $(\alpha < 0)$.

Both two- and four-quadrant arctangent functions appear. Two-quadrant $\mathrm {arctan}$ ranges $[-\pi /2, \pi /2]$, while four-quadrant $\mathrm {atan2}$ ranges $(-\pi , \pi ]$. Only positive factors can be algebraically canceled or moved between numerator and denominator of four-quadrant $\mathrm {atan2}$’s argument (Appendix A.1). The notation

using a double solidus indicates this restriction.

Fig. 1

Points, vectors, and coordinates associated with a single edge $\overline{12}$ of a face

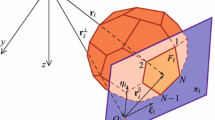
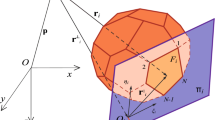
The following definitions are shown in Fig. 1.

For a polyhedron and its polygonal faces, $f$ and $e$ index “face” and “edge”, respectively ($e$ can be used, because the exponential function $\mathrm {e}^x$ does not appear in this paper).

Each face $f$ has a unit-length face-normal vector $\hat{\mathbf {n}}_f$ which is orthogonal to the face and points from the body into unoccupied space.

Face vertices are labeled 1, 2, $\dots$ when circulating anti-clockwise around $\hat{\mathbf {n}}_f$. The beginning and ending vertices of any edge are labeled 1 and 2, respectively.

Each edge $e$ of each face $f$ has a unit-length edge normal vector $\hat{\mathbf {n}}_{ef}$ which lies in the face plane, is orthogonal to the edge, and points from the face into unoccupied space.

Edge-tangent vectors do not explicitly appear in this paper. The cross product $\hat{\mathbf {n}}_f\times \hat{\mathbf {n}}_{ef}$ parallels such an edge-tangent vector and points in the positive direction from vertex 1 to vertex 2.

Informally, a point is above another with respect to a face if it is in the $\hat{\mathbf {n}}_f$ direction, otherwise below. A point in a face plane is right of an edge if it is in the $\hat{\mathbf {n}}_{ef}$ direction, otherwise left. In Fig. 1, $F$ is above $P$ and right of $T$.

The orthogonal projection of the field point P onto a face plane is a point called the foot, denoted $F$. The foot might not lie within the face itself. Even though a foot is associated with a face, to reduce clutter, it is not denoted with its face’s subscript ($F_{f}$).

The orthogonal projection of a face’s foot (or of the field point) onto the infinite line containing an edge of that face is a point called the toe, denoted $T$. Each edge has its own toe. To reduce clutter, it is not denoted with its edge’s subscript ($T_{e}$). The toe might not lie within the edge itself.

Vector $\mathbf {r}$ originates at the field point. Vector $\varvec{\rho }$ originates at the foot and lies in the face plane.

The vertical coordinate of face $f$’s foot relative to the field point is denoted $v_{f}$. It can be computed as the inner product of the face’s normal vector $\hat{\mathbf {n}}_f$ and a vector $\mathbf {r}$ from the field point to any point in the face plane (such as one of the face’s vertices). If the face is above the field point, $v_{f}> 0$, and oppositely.

The horizontal coordinate of edge $e$’s toe relative to face $f$’s foot is denoted $h_{ef}$. Its direction is orthogonal to the edge. It can be computed as the inner product of the edge’s normal vector $\hat{\mathbf {n}}_{ef}$ and a vector $\varvec{\rho }$ from the foot to any point on the infinite line containing the edge (such as either of the edge’s vertices). It is also the inner product of $\hat{\mathbf {n}}_{ef}$ and $\mathbf {r}$, where $\mathbf {r}= \varvec{\rho }+ v_{f}\hat{\mathbf {n}}_f$. If foot $F$ is to the right of toe $T$, $h_{ef}> 0$, and oppositely.

Fig. 2

Tangential coordinates $s$ of edge vertices 1, 2 shared by faces A, B

Both faces sharing an edge have the same toe. Due to face winding, the shared edge’s beginning vertex for face A is the ending vertex for face B and vice versa (Fig. 2). Tangential coordinate $s$ measures from the toe. Its sign depends on whether the toe$\rightarrow$vertex direction matches ($+$) or opposes (−) face winding. $s_{1ef}$ and $s_{2ef}$ are tangential coordinates of vertices 1 and 2 of edge $e$ of face $f$. $s_{1ef}< s_{2ef}$ for any edge of any face. Positive edge-length $\ell _{e}\mathop {=}\limits ^{\text {def}}s_{2eA} - s_{1eA} = s_{2eB} - s_{1eB}$ is independent of face.

The product $s_{1ef}s_{2ef}$ is a diagnostic for the foot lying on an edge itself $(s_{1ef}s_{2ef}\le 0)$ or off its ends $(s_{1ef}s_{2ef}> 0)$.

Elementary relationships exist among these coordinates and distances for a point R lying on an edge: $\rho ^2 = s^2 + h_{ef}^2$ and $r^2 = \rho ^2 + v_{f}^2 = s^2 + h_{ef}^2 + v_{f}^2$.

2 Polyhedron potential reduced to surface integrals

The integral

$$\begin{aligned} U&= U(P) \mathop {=}\limits ^{\text {def}}\iiint _{B} \frac{1}{r} \mathrm {d}V\end{aligned}$$

(1)

appears in potential theory, where $U$ is the potential of a homogeneous body $B$ and $r$ is the distance between field point $P$ and differential volume element $\mathrm {d}V$ (The gravitational constant and uniform density factors are omitted to reduce clutter.). At this early stage, $B$ is not necessarily a polyhedron.

2.1 Body singularity

Distance $r$ vanishes where the field point is in the 3D body or on its boundary. In such geometries, the integrand in Eq. 1 is singular and $U$ is improper. Leathem (1913, Sect. 12), Kellogg (1929, Ch. VI, Lemma III(a)), and D’Urso (2013, Eqs. 6–9) show that this “body singularity” can be ignored.

2.2 Gauss divergence theorem reduces $\iiint _{B} \mathrm {d}V/ r$ to a surface integral

The integrand $1/r$ in Eq. 1 can be expressed as the divergence of a vector field in spherical-polar coordinates:

Then, the Gauss divergence theorem is used to convert Eq. 1 to a surface integral over the boundary $\partial B$ of $B$:

where $\hat{\mathbf {n}}_{\partial V}$ is the surface-normal vector and $\mathrm {d}\partial V$ is the differential surface element.

For the remainder of this paper, the homogeneous 3D body $B$ is assumed to be a polyhedron. The surface integral is written as a summation of surface integrals over its planar faces. Each face $f$ is a polygon with n straight edges and a like number of vertices. The number of vertices can vary from face to face. Each face has a constant, outward-pointing surface-normal vector $\hat{\mathbf {n}}_f$ which is substituted for $\hat{\mathbf {n}}_{\partial V}$. For notational convenience, differential surface element $\mathrm {d}S$ is substituted for $\mathrm {d}\partial V$.

During the surface integration over a face, all vectors $\mathbf {r}$ terminate in the face plane. The inner product of such $\mathbf {r}$ with $\hat{\mathbf {n}}_f$ results in the constant vertical coordinate $v_{f}$ of face $f$ relative to the field point (Fig. 1). Being constant, $v_{f}$ can be brought outside the integral:

(2)

A substantial portion of this paper is devoted to evaluating the surface integral $U_{f}$ for the potential of a planar face

$$\begin{aligned} U_{f}&= U_{f}(P) \mathop {=}\limits ^{\text {def}}\iint _f\frac{1}{r} \mathrm {d}S\end{aligned}$$

(3)

for each face $f$. The field point $P$ does not necessarily lie in the face plane.

2.3 Face singularity

Let $\rho$ represent distance in the face plane from the foot (Fig. 1). If the field point is above or below the face ($v_{f}\ne 0$), or in the face plane but outside the face ($\rho > 0$ everywhere), the integrand $1 / r= 1 / \sqrt{\rho ^2 + v_{f}^2}$ in Eq. 3 is non-singular and $U_{f}$ proper. However, $r$ vanishes if and where the field point is embedded in the face $(r= v_{f}= \rho = 0)$. In such geometries, the integrand is singular and $U_{f}$ is improper. Leathem (1913, Sect. 12) and Kellogg (1929, Ch. VI, Lemma III(b)) show that this “face singularity” can be ignored.

2.4 $1/r$ equivalent to a divergence in cylindrical coordinates

The integrand $1/r$ in Eq. 3 can be expressed as the divergence of a vector field in cylindrical coordinates:

where integration constant $C$ will be chosen to advantage in Sect. 5. This is plugged into Eq. 3:

(4)

3 Prism singularity

We are poised to use Green’s theorem in the plane to convert Eq. 4 to a line integral around the face boundary. However, $\rho$ in the denominator vanishes at the foot if it is in the face, that is, wherever the field point is within an infinite right prism having the face as its cross-section. In such geometries, the vector field does not exist at the foot and a precondition of Green’s theorem in the plane is violated. Unlike the body and face singularities, this “prism singularity” cannot be ignored.

Fig. 3

Prism singularity manifesting itself

$1/r$ in surface integral Eq. 3 does not have the prism singularity. It appears in Eq. 4 when $1/r$ is expressed as the divergence of a vector field having $\rho$ in the denominator.

The prism singularity manifests itself by artificially increasing $U_{f}$ where the foot is within the face (Fig. 3). In that figure, potential values due to a rectangular face extending $(\pm 1, \pm 0.6)$ units in x and y are sampled within a larger square extending $\pm 2$ units in x and y and $v_{f}= 0.2$ units beneath the face. Figure 3a shows the correct potential surface determined by numerical integration of $\iint _{f} \mathrm {d}S/ r$. Figure 3b shows the singularity displacing the potential surface vertically by $2 \pi |v_{f}|$ where the foot is within the face and $U_{f}$ evaluated from Eq. 4 with $C=0$. The vertical scale is the same in both diagrams.

3.1 Prism correction for prism singularity

The integration constant $C$ in Eq. 4 is inert in the following development and can be treated as zero. However, an important simplification using $C$ appears in Sect. 5.

One approach to eliminate the prism singularity is to puncture the face plane—determine the singularity’s effect $U_{F}$ at $F$, and subtract it from a straightforward integration of the entire face $f$:

In this paper, $U_{F}$ is called the “prism correction”.

$U_{F}$ is evaluated by integrating over a sector $\sigma (F, \rho , \Delta \phi _{F})$ in the face plane centered on the foot $F$ and of finite radius $\rho$. The sector can be thought of as the intersection of the face with a disc centered on the foot. Later, $\rho$ will be shrunk to zero. $\Delta \phi _{F}$ is the angular extent of the face surrounding the foot:

$$\begin{aligned} \Delta \phi _{F}= {\left\{ \begin{array}{ll} 2 \pi , &{} \text {foot wholly inside face} \\ \pi , &{} \text {foot on edge} \\ \text {interior } \measuredangle P_j, &{} \text {foot at planar vertex} P_j \\ 0. &{} \text {foot outside face}. \end{array}\right. } \end{aligned}$$

The intermediate sector result is denoted $U_{\sigma }$.

The sector boundary $\partial \sigma$ is parameterized as a circular arc in polar coordinates $(\phi ,\rho$) and straight segments connecting the foot to the ends of the arc. On the straight sides of the sector, boundary-normal vector $\hat{\mathbf {n}}_{\partial F}$ is orthogonal to radial-basis vector $\hat{\mathbf {e}}_{\rho }$ and that segment of the boundary contributes nothing. On the circular arc, $\mathrm {d}s= \rho \mathrm {d}\phi$, boundary-normal vector $\hat{\mathbf {n}}_{\partial F}$ equals radial-basis vector $\hat{\mathbf {e}}_{\rho }$, their inner product is 1, and both $\rho$ and $r$ are constant:

The prism correction $U_{F}$ for the face is the limit of $U_{\sigma }$ as sector radius $\rho$ is shrunk to zero:

$$\begin{aligned} U_{F}&\mathop {=}\limits ^{\text {def}}\lim _{\rho \rightarrow 0^+} U_{\sigma }= \lim _{\rho \rightarrow 0^+} \Delta \phi _{F}(r+ C) = \Delta \phi _{F}(|{v_{f}}| + C) \end{aligned}$$

(5)

since $\lim _{\rho \rightarrow 0^+} r= |{v_{f}}|$. Thus, the prism singularity increases potential $U_{f}$ by $\Delta \phi _{F}(|{v_{f}}| + C)$ as demonstrated in Fig. 3.

This leaves a new problem: determining whether the foot lies within a polygonal face or on its boundary. If the face is convex, a half-space algorithm is simple enough: if a point is left of a face’s every edge, then the point is inside the face. More complex algorithms determine whether a point lies inside a non-convex face (D’Urso and Russo 2002). However, algorithms can encounter numeric difficulties determining whether a point is exactly on an edge or vertex instead of being slightly inside or outside (Holstein and Ketteridge 1996, p. 359)

The prism correction $U_{F}$ is for an entire face. Later, developments are more surgical. The prism singularity is eliminated by incorporating new terms for each edge instead of the entire face (Sect. 5). Still later, developments eliminate the prism singularity using a solid angle (Sect. 7 et seq.).

4 Polygon potential reduced to line integrals

We return to the task of integrating Eq. 4, fully aware of the prism singularity, the punctured face ${f- \{F\}}$, and the prism correction $U_{F}$.

Green’s theorem in the plane (Spiegel 1959, p. 110, problem 4) resembles the Gauss divergence theorem but relates a planar surface integral to a line integral around the surface’s boundary $\partial S$:

$\hat{\mathbf {n}}_{\partial S}$ represents the outward-pointing boundary-normal vector. The boundary integration evolves in an anti-clockwise direction according to the right-hand rule wrapping the surface-normal vector.

This theorem is used to convert the surface integral in Eq. 4 to a line integral around the boundary:

(6)

The line integral around the boundary $\partial f$ is a summation of straight line integrals along the edges $e$ of face $f$. The outward-pointing boundary-normal vector $\hat{\mathbf {n}}_{\partial S}$ becomes an outward-pointing edge-normal vector $\hat{\mathbf {n}}_{ef}$, constant for each straight edge (Fig. 1). $\mathrm {d}s$ is substituted for $\mathrm {d}\partial S$, where $s$ is the coordinate measured along each edge.

The inner product of $\hat{\mathbf {n}}_{ef}$ and $\varvec{\rho }$ results in the constant horizontal coordinate $h_{ef}$ of edge $e$ relative to the foot of face $f$ (Fig. 1). Being constant, $h_{ef}$ can be brought outside the integral:

(7)

Now, the straight-line integral

$$\begin{aligned} E_{ef}&\mathop {=}\limits ^{\text {def}}\int _e\frac{r+ C}{\rho ^2} \mathrm {d}s= \int _{s_{1ef}}^{s_{2ef}} \frac{r+ C}{\rho ^2} \mathrm {d}s\end{aligned}$$

(8)

must be evaluated, where $s_{1ef}$ and $s_{2ef}$ are the edge’s vertex coordinates measured from the toe.

4.1 Conventional formulation

Several papers arrive at Eqs. (7 and 8) with integration constant $C$ omitted and the prism singularity present, though perhaps not shown in the formula:

$$\begin{aligned} E_{ef}&= \int _e\frac{r}{\rho ^2} \mathrm {d}s\end{aligned}$$

(9)

or, the polyhedron potential $U$ expression in full:

$$\begin{aligned} U&= \tfrac{1}{2} \sum _{f\in \text {faces}} v_{f}\sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\int _e\frac{r}{\rho ^2} \mathrm {d}s. \end{aligned}$$

With adjustments for notation, this appears as early as Mertens (1868, p. 288). Many papers (such as those cited in the Introduction) address the prism singularity by incorporating the prism correction $U_{F}$:

$$\begin{aligned} U&= \tfrac{1}{2} \sum _{f\in \text {faces}} v_{f}\Biggl [ \Biggl ( \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\int _e\frac{r}{\rho ^2} \mathrm {d}s\Biggr ) - U_{F}\Biggr ] . \end{aligned}$$

Petrović (1996, Eq. 17) presciently separates the integrand into

$$\begin{aligned} \frac{r}{\rho ^2} = \frac{1}{r} + v_{f}^2 \cdot \frac{1}{\rho ^2 r} \end{aligned}$$

(10)

with antiderivatives

$$\begin{aligned} \int \frac{1}{r( s)} \mathrm {d}s&= \ln (r+ s), \\ \int \frac{1}{\rho ^2 (s) \; r( s)} \mathrm {d}s&= \frac{1}{h_{ef}v_{f}} \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r}. \end{aligned}$$

Hence

$$\begin{aligned} U_{{f- \{F\}}}&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\int _e\frac{r}{\rho ^2} \mathrm {d}s- U_{F}\nonumber \\&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\int _{s_{1ef}}^{s_{2ef}} \left( \frac{1}{r} + v_{f}^2 \cdot \frac{1}{\rho ^2 r} \right) \mathrm {d}s- U_{F}\nonumber \\&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\left[ \ln (r+ s)+ \frac{v_{f}^2}{h_{ef}v_{f}} \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \right] _{1ef}^{2ef} - U_{F}\nonumber \\&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ h_{ef}\ln (r+ s)+ v_{f}\mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \right] _{1ef}^{2ef} - U_{F}. \end{aligned}$$

(11)

Both $s$ and $r$ are affected by the lower and upperbounds $\vert _{1ef}^{2ef}$.

5 Eliminating the prism singularity

Although their approach is quite different, Holstein and Ketteridge (1996, Eq. 3) eliminate the prism singularity and the prism correction by setting the integration constant $C= - |{v_{f}}|$ in Eq. 5. This is allowed, since $v_{f}$ is constant during the surface integration (Eq. 4). It is easy to see why this works. The prism correction

$$\begin{aligned} U_{F}= \Delta \phi _{F}(|{v_{f}}| + C) \end{aligned}$$

vanishes if $C= - |{v_{f}}|$.

The corresponding vector field lacks the prism singularity:

$$\begin{aligned} \left. \frac{r+ C}{\rho ^2} \varvec{\rho }\right| _{C= - |{v_{f}}|}&= \frac{r- |{v_{f}}|}{\rho ^2} \cdot \frac{r+ |{v_{f}}|}{r+ |{v_{f}}|} \varvec{\rho }= \frac{r^2 - |{v_{f}}|^2}{\rho ^2 (r+ |{v_{f}}|)} \varvec{\rho }\\&= \frac{\rho ^2}{\rho ^2 (r+ |{v_{f}}|)} \rho \hat{\mathbf {e}}_{\rho } = \frac{\rho }{r+ |{v_{f}}|} \hat{\mathbf {e}}_{\rho }. \end{aligned}$$

Eq. 4 is altered to the following which does not puncture the face or need the prism correction:

The first integrand term $r/ \rho ^2$ has been dealt with previously (Eq. 10 et al.). Another antiderivative takes care of the second:

$$\begin{aligned} \int \frac{1}{\rho ^2(s)} \mathrm {d}s= \frac{1}{h_{ef}} \mathrm {arctan}\frac{s}{h_{ef}} . \end{aligned}$$

Hence

$$\begin{aligned} U_{f}&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\int _{s_{1ef}}^{s_{2ef}} \left( \frac{1}{r} + v_{f}^2 \cdot \frac{1}{\rho ^2 r} - |{v_{f}}| \cdot \frac{1}{\rho ^2} \right) \mathrm {d}s\nonumber \\&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\left[ \ln (r+ s)+ v_{f}^2 \cdot \frac{1}{h_{ef}v_{f}} \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \right. \nonumber \\&\quad \left. - |{v_{f}}| \cdot \frac{1}{h_{ef}} \mathrm {arctan}\frac{s}{h_{ef}} \right] _{1ef}^{2ef} \nonumber \\&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\left[ \ln (r+ s)\right] _{1ef}^{2ef} \nonumber \\&{\phantom {=}} + \underbrace{ \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ v_{f}\mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} - |{v_{f}}| \mathrm {arctan}\frac{s}{h_{ef}} \right] _{1ef}^{2ef} }_{A_{f}} . \end{aligned}$$

(12)

Two kinds of terms have appeared, logarithm and arctangent. The main emphasis of this paper is interpreting and evaluating the arctangent terms $A_{f}$.

The simpler logarithm factor

$$\begin{aligned} L_{ef}&\mathop {=}\limits ^{\text {def}}\ln (r+ s)\bigr \vert _{1ef}^{2ef} = \ln \frac{r_{2e}+ s_{2ef}}{r_{1e}+ s_{1ef}} \end{aligned}$$

and its “edge singularity” are discussed in Appendix C. (Note: distance $r$ between the field point and edge vertex 1 is the same for the two faces touching the edge. Hence, it is notated $r_{1e}$ instead of $r_{1ef}$, and likewise for $r_{2e}$.)

5.1 $G$ and $H$ angles

The first arctangent factor in Eq. 12 (the same as the sole arctangent in Eq. 11) is now defined as

$$\begin{aligned} G_{1ef}&\mathop {=}\limits ^{\text {def}}\mathrm {arctan}\dfrac{v_{f}}{h_{ef}} \dfrac{s_{1ef}}{r_{1e}},&G_{2ef}&\mathop {=}\limits ^{\text {def}}\mathrm {arctan}\dfrac{v_{f}}{h_{ef}} \dfrac{s_{2ef}}{r_{2e}}. \end{aligned}$$

(13)

The second arctangent factor in Eq. 12 is defined as

$$\begin{aligned} H_{1ef}&\mathop {=}\limits ^{\text {def}}\mathrm {arctan}\frac{s_{1ef}}{h_{ef}},&H_{2ef}&\mathop {=}\limits ^{\text {def}}\mathrm {arctan}\frac{s_{2ef}}{h_{ef}}. \end{aligned}$$

(14)

5.2 Combining $G$ and $H$

Substituting $v_{f}\rightarrow |{v_{f}}|$ throughout Eq. 12’s first $\mathrm {arctan}$ term does not alter its value and allows an overall factor of $|{v_{f}}|$ to be collected (Holstein and Ketteridge, 1996, Appendix A):

$$\begin{aligned} A_{f}&= |{v_{f}}| \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ \mathrm {arctan}\frac{|{v_{f}}|}{h_{ef}} \frac{s}{r} - \mathrm {arctan}\frac{s}{h_{ef}} \right] _{1ef}^{2ef} \end{aligned}$$

(15a)

$$\begin{aligned}&= |{v_{f}}| \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \big [ G^*- H\big ]_{1ef}^{2ef} , \end{aligned}$$

(15b)

where $G^*$ indicates that $G$ has been written with $|{v_{f}}|$.

Both $G^*$ and $H$ range $[-\pi /2, \pi /2]$, since they are computed with two-quadrant $\mathrm {arctan}$. Appendix A.2 indicates they can be combined as in Holstein and Ketteridge (1996). Subscripts are removed in the following derivation to reduce clutter:

$$\begin{aligned} \tan G^*= \frac{s|{v}|}{rh} , \quad \tan H= \frac{s}{h} . \end{aligned}$$

Then

where $r_{T}^2 \mathop {=}\limits ^{\text {def}}h^2 + |{v}|^2$ is the square of the distance between the field point and the edge’s toe An edge’s toe is located at the same point for both faces bounded by that edge. The distance between the field point and an edge’s toe does not depend on which of the two faces is involved. It is notated $r_{T}$ instead of $r_{Tef}$. The expression for $A_{f}$ then reads

$$\begin{aligned} A_{f}&= |{v_{f}}| \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left. \mathrm {arctan}\frac{- sh_{ef}}{r_{T}^2 + r|{v_{f}}|} \right| _{1ef}^{2ef} \end{aligned}$$

(16)

Two-quadrant $\mathrm {arctan}$ is used, because the denominator is non-negative, forcing the angle to lie in quadrants I or IV. That is, using a barrier fraction is unnecessary.

6 Gores

A polygonal face can be decomposed into “gores” by connecting a common point in the face plane to each vertex with a straight-line segment. A gore is the triangular region enclosed by the common point and the two vertices of an edge. Even a triangular face can be decomposed into three triangular gores.

A gore is necessarily about a specific edge of a specific face. Hence, a subscript $g$ suffices instead of $ef$, e.g., $s_{1g}$ instead of $s_{1ef}$. However, notation for $h_{ef}$ and $v_{f}$ will not be changed.

Although not yet apparent, Holstein and Ketteridge (1996) and this paper’s Eq. 12 decompose a face into gores using the foot as the common point.

6.1 Geometric interpretation of $H\vert _{1g}^{2g}$

There is a simple geometric interpretation of $H\vert _{1g}^{2g}$ appearing in Eq. 15b. Figure 4 shows that the definite integral—the difference of the two angles—is the plane angle $\measuredangle 1F2$ at vertex $F$ of the gore; the vertex angle $H_{F}\mathop {=}\limits ^{\text {def}}H\vert _{1g}^{2g}$ at the foot $F$.

This interpretation suggests that the two $H$ in Eq. 15b should be combined to compute $H_{F}$. This is in contrast to Sect. 5.2 where they are paired individually with the two $G$.

Here is a derivation of the combination.

(17)

where $\ell _{e}\mathop {=}\limits ^{\text {def}}s_{2g}- s_{1g}$ is the edge length. Due to geometry (two vertices along an edge), the magnitude of angle $H_{F}$ subtended at the foot cannot exceed $\pi$ radians.

Fig. 4

Definite integral $H_{F}\mathop {=}\limits ^{\text {def}}H_{2g}- H_{1g}$ is gore’s vertex angle $\measuredangle 1F2$

Fig. 5

Gores’ signed $H_{F}$ sum to $\Delta \phi _{F}$

6.2 Tie-in with prism correction

The angle $\Delta \phi _{F}$ in prism correction Eq. 5 can be decomposed into the sum of vertex angles $H_{F}$ of a face’s gores as shown in Holstein et al. (1999, p. 1439) and Conway (2015, Sect. 2.2). In the two diagrams of Fig. 5, triangular face 123 is segmented into gores using common point $F$. Signed vertex angles $H_{12}$, $H_{23}$, $H_{31}$ at the foot (i.e., $H_{F}$ for the three gores) evolve clockwise or anti-clockwise according to the direction of corresponding edges. In the left diagram, $F$ is inside the face. Vertex angles all evolve anti-clockwise and sum to $2 \pi$. In the right diagram, $F$ is outside the face; outside edge 12. Corresponding vertex angle $H_{12}$ evolves clockwise and is negative. Vertex angles sum to 0.

7 Polyhedron potential expressed using a solid angle

Two $\mathrm {arctan}$ terms (Eq. 13) in definite integral Eq. 3 are augmented with two more (Eq. 14) to eliminate the prism singularity. For a face having n edges, 4n $\mathrm {arctan}$s are evaluated. Pairs $(G, H)$ are combined, resulting in two $\mathrm {arctan}$s for each edge in definite integral Eq. 16. For a face having n edges, only 2n $\mathrm {arctan}$s are needed and a prism correction is unnecessary.

Now, a different formulation begins. Arctangent terms in Eqs. (12, 15a, 16) will be shown to be spherical polygon vertex angles or their complements. $A_{f}$ (Eq. 12) will be related to the signed solid angle $\Omega _{f}$ subtended by the face when viewed from the field point. Ultimately, the $2n\, \mathrm {arctan}$s for a face will be replaced by a single four-quadrant $\mathrm {atan2}$.

7.1 Potential reformulated to reveal solid angle $\Omega _{f}$

The following formal lemma is used afterwards:

(18)

The apparent prism singularity in the LHS has disappeared in the final RHS. The singularity if $r= 0$ is discussed in Appendix B.1.

Next, Eq. 10 is substituted into Eq. 4 (with $C= 0$) and the integrand separated into a pair of surface integrals:

(19)

Green’s theorem in the plane is used on the first surface integral. In the second, the integrand is evaluated in situ using Eq. 18 and left as a surface integral:

None of the integrands has the prism singularity.

$(v_{f}/ r^3) \mathrm {d}S$ in the remaining surface integral is the signed differential solid angle $\mathrm {d}\Omega$ of the planar differential element $\mathrm {d}S$ viewed from the field point (Werner 1994, Appendix A). Hence, the surface integral

$$\begin{aligned} \iint _f\frac{v_{f}}{r^3} \mathrm {d}S&= \iint _f\mathrm {d}\Omega \mathop {=}\limits ^{\text {def}}\Omega _{f}\end{aligned}$$

(20)

is the face’s signed solid angle $\Omega _{f}$ viewed from the field point.

The signs of $\Omega _{f}$ and $v_{f}$ match, i.e., if the face is above the field point, $\Omega _{f}> 0$, and oppositely. The greatest solid-angle magnitude $|{\Omega _{f}}|$ possibly subtended by a planar face is one hemisphere; $2 \pi$ steradians. However, the limit is never actually achieved (Appendix B.2). Signed $\Omega _{f}$ ranges $(-2\pi , 2\pi )$.

Another formula for the potential $U_{f}$ of a polygonal face results:

$$\begin{aligned} U_{f}&= \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}L_{ef}- v_{f}\, \Omega _{f}. \end{aligned}$$

(21)

Substituting this into Eq. 2 results in the potential $U$ of a homogeneous polyhedron:

$$\begin{aligned} U&= \tfrac{1}{2} \sum _{f\in \text {faces}} v_{f}\Biggl [ \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}L_{ef}- v_{f}\, \Omega _{f}\Biggr ] \nonumber \\&= \tfrac{1}{2} \sum _{f\in \text {faces}} v_{f}\sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}L_{ef}- \tfrac{1}{2} \sum _{f\in \text {faces}} v_{f}^2 \, \Omega _{f}. \end{aligned}$$

(22)

This has been written as a nested summation of logarithm terms over faces and edges, and another summation of solid-angle terms over faces.

7.2 Solid angle $\Omega _{f}$ related to arctangent terms $A_{f}$

Comparing Eqs. (11, 12, 15, 16) with Eq. 21 shows

$$\begin{aligned} A_{f}&= - v_{f}\, \Omega _{f}, \end{aligned}$$

where signed solid angle

$$\begin{aligned} \Omega _{f}&= \displaystyle {\text {sgn}}v_{f}\cdot \Delta \phi _{F}- \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \right] _{1ef}^{2ef} \end{aligned}$$

(23a)

$$\begin{aligned}&= \displaystyle \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ {\text {sgn}}v_{f}\cdot \mathrm {arctan}\frac{s}{h_{ef}} - \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \right] _{1ef}^{2ef} \end{aligned}$$

(23b)

$$\begin{aligned}&= \displaystyle \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ {\text {sgn}}v_{f}\cdot H- G\right] _{1ef}^{2ef} \end{aligned}$$

(23c)

$$\begin{aligned}&= \displaystyle {\text {sgn}}v_{f}\cdot \sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} \left[ \mathrm {arctan}\frac{sh_{ef}}{r_{T}^2 + r|{v_{f}}|} \right] _{1ef}^{2ef} . \end{aligned}$$

(23d)

8 The solid angle of a spherical polygon

So far, it has been shown that a polygonal face’s arctangent and prism-correction terms are equivalent to the signed solid angle $\Omega _{f}$ subtended by the face viewed from the field point. Next is shown a way of evaluating $\Omega _{f}$ (other than Eq. 23) which involves summing spherical vertex angles of the face or its gores projected onto a sphere. Spherical vertex angles can be evaluated via spherical trigonometry instead of by integration.

Fig. 6

Planar and spherical polygons

The image of a planar polygon centrally projected onto a sphere is a spherical polygon whose edges are great-circular arcs (Fig. 6). The measure of spherical vertex angle $\overline{S}_j$ can be evaluated using direction vectors from field point $P$ to planar vertices $P_i, P_j, P_k$. (To reduce clutter, $\overline{S}_j$ is not subscripted with its face.)

Todhunter (1886, Sect. 99, p. 73) and Selby and Girling (1965, Mensuration Formulæ, p. 495) indicate that the planar polygon’s solid angle magnitude $|{\Omega _{f}}|$ can be evaluated using the vertex angles $\overline{S}_j, j \in 1,\dots ,n$ of the n-sided spherical polygon:

$$\begin{aligned} |{\Omega _{f}}|&= \sum _{j=1}^n \overline{S}_j-(n-2)\pi . \end{aligned}$$

(24)

This is called the spherical excess; the sum of a spherical polygon’s vertex angles $\sum \overline{S}_j$ exceeds the sum of a corresponding planar polygon’s interior vertex angles $\sum P_j = (n-2)\pi$.

Such an angle-summation method will be pursued in the following sections to reveal the relation between these spherical vertex angles $\overline{S}_j$ and angles $G$ and $H$ or $\Delta \phi _{F}$ in the conventional formulations. However, a more efficient alternative is spelled out in Sect. 13.2.

Spherical trigonometry assumes spherical vertex angles and edge arcs are positive and in the range $[0 , \pi )$, i.e., are convex. However, in this paper, it is advantageous to associate a negative sign with a reflex spherical vertex in a non-convex polygonal face.

8.1 Measure of spherical vertex angle $\overline{S}_j$

The following formulas for a spherical vertex angle $\overline{S}_j$ are derived in Werner and Scheeres (1997, Sect. 2.5.2). The formulas are for computing the magnitude $|{\Omega _{f}}|$, not the signed $\Omega _{f}$. They accommodate a general non-convex polygon winding anti-clockwise. A reflex vertex angle $(\overline{S}_j < 0)$ is handled automatically.

The formulas are expressed in terms of unit-length vectors $\hat{\mathbf {r}}_i, \hat{\mathbf {r}}_j, \hat{\mathbf {r}}_k$ from the field point toward three consecutive vertices $P_i, P_j, P_k$ taken anti-clockwise around the planar polygon’s face. For brevity, define and likewise for $c_{jk}$ and $c_{ki}$.

The cosine and sine of spherical vertex angle $\overline{S}_j$ are:

$$\begin{aligned} \left. \begin{array}{rl} \cos \overline{S}_j &{} = \dfrac{c_{ki} - c_{ij} c_{jk}}{\sqrt{1 - c_{ij}^2} \sqrt{1 - c_{jk}^2}} , \\ \sin \overline{S}_j &{} = \dfrac{{\text {sgn}}v_{f}\cdot \begin{bmatrix} \hat{\mathbf {r}}_i, \hat{\mathbf {r}}_j, \hat{\mathbf {r}}_k \end{bmatrix}}{\sqrt{1 - c_{ij}^2} \sqrt{1 - c_{jk}^2}} , \end{array} \right\} \end{aligned}$$

(25)

where $\begin{bmatrix} \hat{\mathbf {r}}_i, \hat{\mathbf {r}}_j, \hat{\mathbf {r}}_k \end{bmatrix}$ is the box product (scalar triple product) of the three vectors.

An obvious way to proceed¹ is to compute the spherical vertex angle $\overline{S}_j$ for use in Eq. 24:

(26)

Positive denominators of $\cos \overline{S}_j$ and $\sin \overline{S}_j$ are canceled. These $\overline{S}_j$ range $(-\pi , \pi )$, so four-quadrant $\mathrm {atan2}$ must be used.

9 Sign complications

Eq. 26 accommodates the negative sign associated with a reflex $\overline{S}_j$. However, two further signs must be incorporated into $\Omega _{f}$. One handles the face being above or below the field point $({\text {sgn}}v_{f})$. Another is necessary if the face is a gore, to handle its clockwise or anti-clockwise winding $({\text {sgn}}h_{ef})$. This second sign is unnecessary for a general face which, by convention, always winds anti-clockwise.

9.1 Face below field point

Eq. 20 shows that the signs of $\Omega _{f}$ and $v_{f}$ match. Hence, signed solid angle $\Omega _{f}$ must incorporate the sign of $v_{f}$:

$$\begin{aligned} \Omega _{f}&\mathop {=}\limits ^{\text {def}}{\text {sgn}}v_{f}\cdot |{\Omega _{f}}| = {\text {sgn}}v_{f}\cdot \left( \sum _{j=1}^n \overline{S}_j - (n - 2) \pi \right) \\&= \left( \sum _{j=1}^n {\text {sgn}}v_{f}\cdot \overline{S}_j \right) - {\text {sgn}}v_{f}\cdot (n - 2) \pi . \end{aligned}$$

In the summation, the new factor cancels one already appearing in $\overline{S}_j$ (Eq. 26):

(27)

Then, the signed solid angle $\Omega _{f}$ is

$$\begin{aligned} \Omega _{f}&= \sum _{j=1}^n S_j - {\text {sgn}}v_{f}\cdot (n - 2) \pi . \end{aligned}$$

(28)

${\text {sgn}}v_{f}$ is $+1$ if the face is above the field point. Eqs. (27, 28) handle that case without change.

9.2 A spherical triangle’s signed solid angle

When the face is a triangle, $n=3$. The symbol $\Omega _\triangle$ is adopted for this special case:

$$\begin{aligned} \Omega _\triangle&= S_1 + S_2 + S_3 - {\text {sgn}}v_{f}\cdot \pi . \end{aligned}$$

This triangular face is in general position; not necessarily a gore having one vertex at the foot. Vertices 1, 2, 3 must wind anti-clockwise around the triangle. They are associated cyclically with indices i, j, k.

Of course, it is impossible for a triangle to have a reflex vertex; all must be convex.

Since a triangle has only three vertices, the box products in all three $S_j$ numerators (Eq. 27) are the same.

(29)

Further sign alterations are needed to handle clockwise gore winding.

9.3 Gore winding

The triangular solid angle $\Omega _\triangle$ is relabeled $\Omega _{g}$, indicating that this is for a gore which may or may not wind the same direction as its face.

Eq. 26 for spherical vertex angle $\overline{S}_j$ assumes that vertices i, j, k are encountered in anti-clockwise order. In the left half of Fig. 7, foot $F$ is left of the edge, and the anti-clockwise winding of gore $12F$ matches the face winding (center) as assumed. However, in the right half of Fig. 7, $F$ is right of the edge and gore $12F$ winds clockwise, opposite the face. If Eq. 26 or Eq. 27 is used to compute a gore’s solid angle, then a compensating factor $({\text {sgn}}h_{ef})$ must be incorporated in the signed solid angle.

We might think that the entire RHS of Eq. 29 should be multiplied by $({\text {sgn}}h_{ef})$. However, the situation is more subtle. Next, it is shown that the box product $\begin{bmatrix} \hat{\mathbf {r}}_1, \hat{\mathbf {r}}_2, \hat{\mathbf {r}}_3 \end{bmatrix}$ appearing in the three $\mathrm {atan2}$ numerators of Eq. 29 already changes sign as needed. Only the final $\pi$ term needs the new factor.

9.4 Sign of box product

For notation, $\hat{\mathbf {r}}_3 \rightarrow \hat{\mathbf {r}}_{F}$ is substituted for the unit vector pointing to the gore’s foot $F$. $\hat{\mathbf {r}}_{1g}$ and $\hat{\mathbf {r}}_{2g}$ point to the gore’s other two vertices, encountered in anti-clockwise order around the face from which the gore is taken.

Fig. 7

Gore winding matches (left) or opposes (right) face winding (center)

The numerator $\begin{bmatrix} \hat{\mathbf {r}}_{F}, \hat{\mathbf {r}}_{1g}, \hat{\mathbf {r}}_{2g} \end{bmatrix}$ is evaluated as the determinant of a $3 \times 3$ matrix formed by the three vectors $\mathbf {r}_{F}, \mathbf {r}_{1g}, \mathbf {r}_{2g}$, each normalized to a unit vector. Before normalization, all $v$ coordinates of these three are the same, namely $v_{f}$. Furthermore, the $h$ coordinates of $\mathbf {r}_{1g}$ and $\mathbf {r}_{2g}$ are both $h_{ef}$, and the $s$ and $h$ coordinates of $\mathbf {r}_{F}$ are zero. (Note: it is important for the box product that vector components form a right-handed coordinate system. An acceptable order is $(h,s,v)$. See Fig. 1.)

Unit-length direction vectors to the three vertices are

$$\begin{aligned} \left. \begin{array}{rl} \hat{\mathbf {r}}_{F}&= \begin{pmatrix} 0, 0, v_{f}\end{pmatrix} / |{v_{f}}| = \begin{pmatrix} 0, 0, {\text {sgn}}v_{f}\end{pmatrix},\\ \hat{\mathbf {r}}_{1g}&{} = \begin{pmatrix} h_{ef}, s_{1g}, v_{f}\end{pmatrix} / r_{1g},\\ \hat{\mathbf {r}}_{2g}&{} = \begin{pmatrix} h_{ef}, s_{2g}, v_{f}\end{pmatrix} / r_{2g}, \end{array} \right\} \end{aligned}$$

(30)

with the convention $s_{2g}> s_{1g}$.

The box product becomes

$$\begin{aligned} \begin{bmatrix} \hat{\mathbf {r}}_{F}, \hat{\mathbf {r}}_{1g}, \hat{\mathbf {r}}_{2g} \end{bmatrix}&= \det \begin{bmatrix} 0&0&{\text {sgn}}v_{f}\\ h_{ef}&s_{1g}&v_{f}\\ h_{ef}&s_{2g}&v_{f}\end{bmatrix} \div (r_{1g}r_{2g}) \nonumber \\&= {\text {sgn}}v_{f}\cdot \frac{(s_{2g}- s_{1g}) h_{ef}}{r_{1g}r_{2g}} \nonumber \\&= {\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \frac{ \ell _{e}\, |{h_{ef}}| }{r_{1g}r_{2g}} . \end{aligned}$$

(31)

$({\text {sgn}}v_{f})$ appeared naturally in the algebra, but $({\text {sgn}}h_{ef})$ was forced to appear. The non-negative fraction corresponds to locating the face above the field point ($v_{f}> 0$) and locating the foot left of the edge ($h_{ef}> 0)$. It is known that the $\overline{S}_j$ and the gore’s solid angle $\Omega _{g}$ are positive in that configuration.

Hence, $({\text {sgn}}v_{f}\cdot {\text {sgn}}h_{ef})$ carries all the sign information. It automatically accommodates the foot/field point lying left or right of the edge $({\text {sgn}}h_{ef})$, as well as the face/gore lying above or below the field point $({\text {sgn}}v_{f})$.

The box product already changes sign to accommodate gore winding. Only the final $\pi$ term in $\Omega _{g}$ needs a factor $({\text {sgn}}h_{ef})$. Formulas for a gore’s signed solid angle read:

$$\begin{aligned} \Omega _{g}&= {\text {sgn}}v_{f}\cdot (\overline{S}_{1g} + \overline{S}_{2g} + \overline{S}_{F} - {\text {sgn}}h_{ef}\cdot \pi ) \end{aligned}$$

(32a)

$$\begin{aligned}&= S_{1g}+ S_{2g}+S_{F}- {\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \pi \end{aligned}$$

(32b)

$$\begin{aligned}&= \mathrm {atan2}\Biggl ( \,\begin{array}[c]{@{}c@{}} \begin{bmatrix} \hat{\mathbf {r}}_{F}, \hat{\mathbf {r}}_{1g}, \hat{\mathbf {r}}_{2g} \end{bmatrix} \\ \hline \hline c_{2F} - c_{F1} c_{12} \end{array}\, \Biggr ) + \mathrm {atan2}\Biggl ( \,\begin{array}[c]{@{}c@{}} \begin{bmatrix} \hat{\mathbf {r}}_{F}, \hat{\mathbf {r}}_{1g}, \hat{\mathbf {r}}_{2g} \end{bmatrix} \\ \hline \hline c_{F1} - c_{12} c_{2F} \end{array}\, \Biggr )\nonumber \\&{\phantom {=}} + \mathrm {atan2}\Biggl ( \,\begin{array}[c]{@{}c@{}} \begin{bmatrix} \hat{\mathbf {r}}_{F}, \hat{\mathbf {r}}_{1g}, \hat{\mathbf {r}}_{2g} \end{bmatrix} \\ \hline \hline c_{12} - c_{2F} c_{F1} \end{array}\, \Biggr ) - {\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \pi . \end{aligned}$$

(32c)

10 A gore’s spherical vertex angles

Inner products for factors in $\tan S_j$ denominators (Eq. 32c) are:

(33)

Denominators of the three $\tan S_j$ are:

$$\begin{aligned} c_{2F} - c_{F1} c_{12}&= \frac{|{v_{f}}|}{r_{2g}} - \frac{|{v_{f}}|}{r_{1g}} \frac{h_{ef}^2 + s_{1g}s_{2g}+ v_{f}^2}{r_{1g}r_{2g}} \\&= \frac{r_{1g}^2 - (h_{ef}^2 + s_{1g}s_{2g}+ v_{f}^2)}{r_{1g}^2 r_{2g}} |{v_{f}}| \\&= \frac{(h_{ef}^2 + s_{1g}^2 + v_{f}^2) - (h_{ef}^2 + s_{1g}s_{2g}+ v_{f}^2)}{r_{1g}^2 r_{2g}} |{v_{f}}| \\&= \frac{s_{1g}(s_{1g}- s_{2g})}{r_{1g}^2 r_{2g}} |{v_{f}}| = \frac{-s_{1g}}{r_{1g}} \frac{\ell _{e}|{v_{f}}|}{r_{1g}r_{2g}} , \\ c_{F1} - c_{12} c_{2F}&= \dots = \frac{s_{2g}}{r_{2g}} \frac{\ell _{e}|{v_{f}}|}{r_{1g}r_{2g}} , \\ c_{12} - c_{2F} c_{F1}&= \frac{h_{ef}^2 + s_{1g}s_{2g}+ v_{f}^2}{r_{1g}r_{2g}} - \frac{|{v_{f}}|}{r_{2g}} \frac{|{v_{f}}|}{r_{1g}} \\&= \frac{h_{ef}^2 + s_{1g}s_{2g}}{r_{1g}r_{2g}} . \end{aligned}$$

The tangents of a gore’s spherical vertex angles are:

$$\begin{aligned} \tan S_{1g}&= \,\begin{array}[c]{@{}c@{}} \frac{\ell _{e}}{r_{1g}r_{2g}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline \frac{-s_{1g}}{r_{1g}} \frac{\ell _{e}{| v_{f}|}}{r_{1g}r_{2g}} \end{array}\, \cdot \frac{r_{1g}^2 r_{2g}/ \ell _{e}}{r_{1g}^2 r_{2g}/ \ell _{e}} \nonumber \\&= \frac{r_{1g}}{{| v_{f}|}} \,\begin{array}[c]{@{}c@{}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline -s_{1g} \end{array}\, \cdot \frac{{| v_{f}|}}{{| v_{f}|}} = \frac{r_{1g}}{v_{f}^2} \,\begin{array}[c]{@{}c@{}} h_{ef}v_{f} \\ \hline \hline -s_{1g} \end{array}\, ,\end{aligned}$$

(34a)

$$\begin{aligned} \tan S_{2g}&= \,\begin{array}[c]{@{}c@{}} \frac{\ell _{e}}{r_{1g}r_{2g}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline \frac{s_{2g}}{r_{2g}} \frac{\ell _{e}{| v_{f}|}}{r_{1g}r_{2g}} \end{array}\, \cdot \frac{r_{1g}r_{2g}^2 / \ell _{e}}{r_{1g}r_{2g}^2 / \ell _{e}} \nonumber \\&= \frac{r_{2g}}{{| v_{f}|}} \,\begin{array}[c]{@{}c@{}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline s_{2g} \end{array}\, \cdot \frac{{| v_{f}|}}{{| v_{f}|}} = \frac{r_{2g}}{v_{f}^2} \,\begin{array}[c]{@{}c@{}} h_{ef}v_{f} \\ \hline \hline s_{2g} \end{array}\, ,\end{aligned}$$

(34b)

$$\begin{aligned} \tan S_{F}&= \,\begin{array}[c]{@{}c@{}} \frac{\ell _{e}}{r_{1g}r_{2g}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline \frac{h_{ef}^2 + s_{1g}s_{2g}}{r_{1g}r_{2g}} \end{array}\, \cdot \frac{r_{1g}r_{2g}}{r_{1g}r_{2g}} = \ell _{e}\,\begin{array}[c]{@{}c@{}} h_{ef}{\text {sgn}}v_{f} \\ \hline \hline h_{ef}^2 + s_{1g}s_{2g} \end{array}\, . \end{aligned}$$

(34c)

Barriers separating signed factors indicate that four-quadrant $\mathrm {atan2}$ must be used to recover $S_{1g}$, $S_{2g}$, and $S_{F}$.

11 Geometric interpretations leading to gore’s solid angle

Next, the four $\mathrm {arctan}$s in definite integral Eq. 23b are related geometrically to a spherical gore’s three vertex angles Eq. 34.

Signs on $h_{ef}$ and $v_{f}$ complicate geometric interpretations. Factors $({\text {sgn}}h_{ef})$ and $({\text {sgn}}v_{f})$ will be omitted in this section. Further, to reduce clutter, $h$ and $v$ will be written for $|{h_{ef}}|$ and $|{v_{f}}|$. All will be restored in Sect. 12 which contains an algebraic derivation.

11.1 Geometric interpretation of indefinite integral $G$

(Adapted from Macmillan (1930, Sect. 43)). The subject of this investigation is the indefinite integral term in Eq. 13:

$$\begin{aligned} G= \mathrm {arctan}\frac{s}{r} \frac{v}{h} . \end{aligned}$$

Fig. 8

Angle $G$ is the complement of spherical vertex angle $\overline{S}$

Define angles $\sin \beta \mathop {=}\limits ^{\text {def}}s/ r$ and $\tan \phi \mathop {=}\limits ^{\text {def}}v/ h$, as shown in Fig. 8. Then

$$\begin{aligned} \tan G= \frac{s}{r} \frac{v}{h} = \sin \beta \tan \phi . \end{aligned}$$

(35)

Consider spherical triangle $FBC$ in Fig. 8. Spherical vertex angle $\sphericalangle FBC$ is a right angle, while $\sphericalangle BCF$ is $\overline{S}$. From Napier’s rules for right spherical triangles (Todhunter 1886, Sect. 62, pp. 35–37),

$$\begin{aligned}&\sin \beta = \cot \overline{S}\cdot \tan \left( \tfrac{\pi }{2} - \phi \right) = \tan \left( \tfrac{\pi }{2} - \overline{S}\right) \cdot \cot \phi \nonumber , \\&\therefore \tan \left( \tfrac{\pi }{2} - \overline{S}\right) = \sin \beta \tan \phi . \end{aligned}$$

(36)

In comparing Eqs. (35, 36), angle $G$ is the complement of spherical vertex angle $\overline{S}$:

$$\begin{aligned} G= \tfrac{\pi }{2} - \overline{S}. \end{aligned}$$

The principal value $[-\pi /2, \pi /2]$ of $\mathrm {arctan}$ for $G$ is mapped to the required range $[0 , \pi )$ of unsigned $\overline{S}$:

$$\begin{aligned} \begin{array}{l@{\quad }|@{\quad }c@{\quad }l@{\quad }c} G&{} + \frac{\pi }{2} &{} 0 &{} - \frac{\pi }{2} \\ \hline \overline{S}&{} 0 &{} \frac{\pi }{2} &{} \pi \end{array} \end{aligned}$$

Hence, it is unnecessary to use four-quadrant $\mathrm {atan2}$ when evaluating $G$; two-quadrant $\mathrm {arctan}$ suffices. However, $\mathrm {atan2}$ is necessary when evaluating $\overline{S}$.

11.2 Geometric interpretation of definite integral $H\vert _{1g}^{2g}$

A geometric interpretation of the $H$ terms in Eq. 23c has already been derived in Sect. 6.1. The definite integral $H\vert _{1g}^{2g}$ is the planar angle $H_{F}$ at the gore’s foot. Since $h> 0$ in this geometric section, $H_{F}> 0$.

Fig. 9

Complementary angles $\overline{S}$ and $G$ for a gore

11.3 Assembling the geometric expressions

Figure 9 shows spherical gore $F\,1'\,2'$ as the image of planar gore $F1 2$ projected onto a sphere centered at field point $P$.

Planar and spherical vertex angles at tangent-point $F$ are equal, i.e., $H_{F}= \overline{S}_{F}$.

Spherical vertex angles $\overline{S}_{1g}$ and $\overline{S}_{2g}$ are complements of angles $G_{1g}, G_{2g}$. There is a sign subtlety, because $G_{2g}- G_{1g}$ is a definite integral, while spherical vertex angles $\overline{S}_{1g}$, $\overline{S}_{2g}$ are both positive. The definite integral should be thought of as $G_{2g}+ (-G_{1g})$). The complementary angles are:

$$\begin{aligned} \overline{S}_{1g}+ (- G_{1g})&= \pi /2 \qquad \Leftrightarrow \qquad G_{1g}= \overline{S}_{1g}- \pi /2 \\ \overline{S}_{2g}+ G_{2g}&= \pi /2 \qquad \Leftrightarrow \qquad G_{2g}= \pi /2 - \overline{S}_{2g}\end{aligned}$$

Then, Eq. 23b becomes Eq. 32:

$$\begin{aligned}&{ \biggl [ \mathrm {arctan}\frac{s}{h} - \mathrm {arctan}\frac{v}{h} \frac{s}{r} \biggr ]_{1g}^{2g} = \bigl [H- G\bigr ]_{1g}^{2g} } \\&= (H_{2g}- H_{1g}) - (G_{2g}- G_{1g}) \\&= H_{F}- \left[ \left( \pi /2 - \overline{S}_{2g}\right) - \left( \overline{S}_{1g}- \pi /2 \right) \right] \\&= \overline{S}_{F}+ \overline{S}_{1g}+ \overline{S}_{2g}- \pi = \sum _{j=1}^n \overline{S}_j - (n-2)\pi \Bigr \vert _{n=3} = |{\Omega _{g}}| . \end{aligned}$$

Not only have the four arctangents in Eq. 23b been related to the vertex angles of a spherical gore, but their combination has been shown to equal the solid angle $|{\Omega _{g}}|$ as asserted by Eq. 23.

12 Algebraic derivations leading to gore’s solid angle

Sect. 11 demonstrates geometric relationships between $G$ and $H$ with $\overline{S}$ and solid-angle magnitude $|{\Omega _{g}}|$. In this section, the relationships are derived algebraically. The signs and clutter which were omitted in Sect. 11 are reinstated.

12.1 Fully signed complementary angles

Sect. 11 demonstrated that without signs, $G$ and $\overline{S}$ are complementary spherical vertex angles summing to $\pi / 2$. Fully signed angular pairs $(S_{1g}, -G_{1g})$ and $(S_{2g}, G_{2g})$ are now shown to be signed complements; sum to $({\text {sgn}}v_{f}\cdot {\text {sgn}}h_{ef}\cdot \pi / 2)$. The $({\text {sgn}}v_{f})$ factor compensates for a face being below the field point (Sect. 9.1). The $({\text {sgn}}h_{ef})$ factor compensates for a gore winding clockwise if the foot is right of the edge (Sect. 9.3).

The identity $\mathrm {arctan}\, a = \mathrm {atan2}\, (a // 1)$ allows $G$ to be expressed using $\mathrm {atan2}$ instead of $\mathrm {arctan}$. To show $G$ and $S$ are signed complements, first signs are extracted:

Arguments of the two $\mathrm {atan2}$s are reciprocals; hence, the two angles are complements.

Thus, $G$ and $S$ are signed complementary angles:

$$\begin{aligned} S_{1g}+ (-G_{1g})&= S_{2g}+ G_{2g}= {\text {sgn}}v_{f}\cdot {\text {sgn}}h_{ef}\cdot \pi / 2 ; \\ G_{1g}&= S_{1g}- {\text {sgn}}v_{f}\cdot {\text {sgn}}h_{ef}\cdot \pi / 2, \\ G_{2g}&= {\text {sgn}}v_{f}\cdot {\text {sgn}}h_{ef}\cdot \pi / 2 - S_{2g}. \end{aligned}$$

12.2 Algebraic interpretation of definite integral $H\vert _{1g}^{2g}$

Eq. 23b indicates that $\tan H_{F}$ from Eq. 17 is multiplied by ${\text {sgn}}v_{f}$ when forming $\Omega _{g}$:

Inspection shows that this equals $\tan S_{F}$ (Eq. 34c).

12.3 Assembling the algebraic expressions

Using fully signed quantities tailored for a gore, Eq. 23b becomes Eq. 32:

$$\begin{aligned}&\biggl [ {\text {sgn}}v_{f}\cdot \mathrm {arctan}\frac{s}{h_{ef}} - \mathrm {arctan}\frac{v_{f}}{h_{ef}} \frac{s}{r} \biggr ]_{1g}^{2g}\\&\quad = \bigl [ {\text {sgn}}v_{f}\cdot H- G\bigr ]_{1g}^{2g} \\&\quad = {\text {sgn}}v_{f}\cdot (H_{2g}- H_{1g}) - (G_{2g}- G_{1g}) \\&\quad = {\text {sgn}}v_{f}\cdot H_{F}- \left[ \begin{array}{l} ({\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \pi /2 - S_{2g}) \\ - (S_{1g}- {\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \pi /2) \end{array} \right] \\&\quad = S_{F}+ S_{1g}+ S_{2g}- {\text {sgn}}h_{ef}\cdot {\text {sgn}}v_{f}\cdot \pi \\&\quad = {\text {sgn}}v_{f}\cdot ( \overline{S}_{F}+ \overline{S}_{1g}+ \overline{S}_{2g}- {\text {sgn}}h_{ef}\cdot \pi ) = \Omega _{g}. \end{aligned}$$

Hence, the conventional arctangent expressions have been shown to equal the gore’s signed solid angle.

13 Solid angle from a single arctangent (E pluribus unum)

Another goal of this paper has been accomplished: edge-by-edge arctangent expressions in the conventional polyhedron gravitation formulations have been shown equivalent to a gore’s spherical vertex angles. This was shown geometrically (Sect. 11) and algebraically (Sect. 12).

However, no performance has been gained. Actually, performance has degraded; only two $\mathrm {arctan}$ are evaluated for a gore in Eq. 16, while three $\mathrm {atan2}$ are evaluated in Eq. 32c.

However, we can do better.

13.1 Planar triangle’s solid angle

A simple expression for a planar triangle’s signed solid angle $\Omega _\triangle$ is derived in van Oosterom and Strackee (1983), Eriksson (1990), and Werner and Scheeres (1997, Sect. 2.5.4). The triangle is in general position, and is not necessarily a gore having one vertex at the foot. Let $\mathbf {r}_1$, $\mathbf {r}_2$, and $\mathbf {r}_3$ be vectors from the field point to the three vertices ordered anti-clockwise according to the right-hand rule and the outward-pointing face-normal vector $\hat{\mathbf {n}}_f$. This simple expression for $\Omega _\triangle$ (contrast with Eq. 29) is evaluated using four-quadrant $\mathrm {atan2}$:

(37)

Eq. 37 is coordinate-free; all factors are vectors or distances.

This formula, like Eq. 32, automatically handles the triangular face being above or below the field point. Correction for gore winding (Sect. 9.3) is not needed, because the triangle’s vertices are required to be in anti-clockwise order.

13.2 Solid angle of a general polygonal face

Several ways exist to compute $\Omega _{f}$ for a general non-triangular planar face of n vertices. The face might be separated into gores with a common point (not necessarily the foot) and the triangle formula Eq. 37 used on each, requiring n $\mathrm {atan2}$ evaluations. Alternately, the face might be triangularized with chords, requiring $n-2$ evaluations of Eq. 37.

A more direct approach does not triangulate a general face. As shown in Eq. 26, vector geometry and a single $\mathrm {atan2}$ function can be used to compute each spherical vertex angle $\overline{S}_j, j \in 1,\dots ,n$. Then

$$\begin{aligned} |{\Omega _{f}}|&= \sum _{j=1}^n \overline{S}_j - (n-2) \pi = 2 \pi + \sum _{j=1}^n (\overline{S}_j - \pi ) . \end{aligned}$$

(38)

However, this requires n $\mathrm {atan2}$s to compute all $\overline{S}_j$ for the face. Note: the factor $({\text {sgn}}h_{ef})$ to accommodate a gore’s possible clockwise winding does not appear. For this general face, the winding is required to be anti-clockwise always.

One way to compute $|{\Omega _{f}}|$ without computing each $\overline{S}_j$ is first to compute the cosine and sine of $|{\Omega _{f}}|$ from the collection of cosines and sines of $\overline{S}_{j}$ available from Eq. 25 (Werner and Scheeres (1997, Sect. 2.5.3)). A matrix-vector form of the well-known formulas for the cosine and sine of the sum of two angles

$$\begin{aligned} \begin{bmatrix} \cos (\alpha + \beta ) \\ \sin (\alpha + \beta ) \end{bmatrix} = \begin{bmatrix} \cos \alpha&- \sin \alpha \\ \sin \alpha&\cos \alpha \end{bmatrix} \begin{bmatrix} \cos \beta \\ \sin \beta \end{bmatrix} \end{aligned}$$

is used iteratively. Each $2 \times 2$ matrix expresses a rotation by one of the $\overline{S}_j$. The cosine and sine of the initial angle are expressed as a two-element vector $\begin{bmatrix} \cos 2 \pi&\sin 2 \pi \end{bmatrix} = \begin{bmatrix} 1&0 \end{bmatrix}$.

$$\begin{aligned} \begin{bmatrix} \cos |{\Omega _{f}}| \\ \sin |{\Omega _{f}}| \end{bmatrix}&= \left( \prod _{j=1}^n \begin{bmatrix} \cos (\overline{S}_j - \pi )&-\sin (\overline{S}_j - \pi ) \\ \sin (\overline{S}_j - \pi )&\cos (\overline{S}_j - \pi ) \end{bmatrix} \right) \begin{bmatrix} \cos 2 \pi \\ \sin 2 \pi \end{bmatrix} \nonumber \\&= \begin{bmatrix} -\cos \overline{S}_{n}&+\sin \overline{S}_{n} \\ -\sin \overline{S}_{n}&-\cos \overline{S}_{n} \end{bmatrix} \dots \begin{bmatrix} -\cos \overline{S}_{2}&+\sin \overline{S}_{2} \\ -\sin \overline{S}_{2}&-\cos \overline{S}_{2} \end{bmatrix} \nonumber \\&{\phantom {=}} \times \begin{bmatrix} -\cos \overline{S}_{1}&+\sin \overline{S}_{1} \\ -\sin \overline{S}_{1}&-\cos \overline{S}_{1} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}. \end{aligned}$$

(39)

Then, positive $|{\Omega _{f}}|$ is computed from the half-angle formula $\tan \tfrac{1}{2} A = (1 - \cos A) / \sin A$ (Appendix A.3):

(40)

The numerator is non-negative and the denominator is signed. The result of $\mathrm {atan2}$ lies in quadrants I and II; ranges $[0 , \pi )$. This is doubled to produce $|{\Omega _{f}}|$ ranging $[0 , 2\pi )$ steradians (Appendix B.2 shows solid angle never achieves the upper limit, so the interval is semi-open). Finally, signed $\Omega _{f}$ ranging $(-2\pi , 2\pi )$ steradians is computed by applying a sign:

$$\begin{aligned} \Omega _{f}= {\text {sgn}}v_{f}\cdot |{\Omega _{f}}| . \end{aligned}$$

Thus, no matter how many vertices a face has, computing its signed solid angle $\Omega _{f}$ in Eq. 21 requires evaluating a single arctangent. No prism correction is needed, since the prism singularity has been avoided. This reduction of effort is the main goal of this paper.

Considerations for evaluating $\Omega _{f}$ and $\Omega _\triangle$ appear in Sect. D.1.

13.3 Alternate formulation

Strakhov et al. (1986a, Eqs. 27–29) recognize the solid angle in their formulation and present an economic formula for $|{\Omega _{g}}|$. A hybrid of that and this paper’s notation is used here:

$$\begin{aligned} \Lambda&\mathop {=}\limits ^{\text {def}}\frac{\ell _{e}}{r_{1g}+ r_{2g}},&\Sigma&\mathop {=}\limits ^{\text {def}}\tfrac{1}{2} (r_{1g}+ r_{2g}- \ell _{e}\Lambda ),&\gamma&\mathop {=}\limits ^{\text {def}}\frac{h_{ef}\Lambda }{|{v_{f}}| + \Sigma }. \end{aligned}$$

(41)

($\Lambda$ and $\Sigma$ have interesting geometric interpretations. Consider an ellipse passing through the field point with the gore’s edge vertices as foci. This ellipse’s plane is different from the gore’s. First, $(r_{1g}+ r_{2g}) / 2$ is the semimajor axis $a$. In addition, $\Lambda = \ell _{e}/ (r_{1g}+ r_{2g})$ is the eccentricity $\epsilon$, an expression reappearing in Appendix C. Next

$$\begin{aligned} \Sigma&= \frac{r_{1g}+ r_{2g}}{2} \left( 1 - \frac{\ell _{e}}{r_{1g}+ r_{2g}} \Lambda \right) = a(1 - \epsilon ^2) = p, \end{aligned}$$

the ellipse’s focal parameter or semi-latus rectum. However, an elliptical interpretation of $\gamma = h_{ef}\epsilon / (|{v_{f}}| + p)$ is not apparent, since $h_{ef}$ and $v_{f}$ are not in the ellipse’s plane.)

Hence, both $\Lambda$ and $\Sigma$ ($\epsilon$ and $p$) are positive, as is $\gamma$’s denominator. The numerator of $\gamma$ has the sign of $h_{ef}$.

When expanded, $\gamma$ is found to be $\tan |{\Omega _{g}}|/2$:

a specialization of Eq. 37 to a gore. A barrier fraction is not required. As already stated, the numerator of $\gamma$ is signed and the denominator is positive. Hence, arctangent ranges $[-\pi /2, \pi /2]$ and two-quadrant $\mathrm {arctan}$ suffices.

Eqs. (39, 40) compute a face’s solid angle magnitude by accumulating its cosine and sine from constituent expressions and using them in a half-angle formula. Strakhov et al. (1986a, Eq. 40) and Strakhov and Lapina (1990, Eq. 36) get the same result by accumulating solid angles of a face’s gores. Their expression $\gamma$ (Eq. 41) for a gore’s $\tan \tfrac{1}{2} |{\Omega _{g}}|$ is assigned as the imaginary part of a complex variable $(1 + i\gamma )$. Then, $|{\Omega _{f}}|$ is twice the argument of these complex variables’ product:

$$\begin{aligned} |{\Omega _{f}}| = 2 \arg \prod _{j=1}^n (1 + i\gamma _j) . \end{aligned}$$

14 Summary

Many formulations proceed in ways similar to Eqs. (6, 11) to evaluate the potential of a single polyhedral face. The entire integrand is manipulated using Green’s theorem, resulting in a single boundary integral possibly enclosing a prism singularity. Ultimately, two $\mathrm {arctan}$s for each straight edge of each face (Eq. 3) are evaluated, as well as logarithm terms which possess an edge singularity (Appendix C.1) in certain geometries.

One way of handling the prism singularity is to incorporate a prism correction $U_{F}$ for the entire face (Eq. 5). An auxiliary algorithm determines whether the foot is within the face, on an edge, or at one of its vertices.

Conceptually, a face can be segmented into gores, all having the foot as a common vertex. The factor $\Delta \phi _{F}$ in a face’s prism correction $U_{F}$ is the sum of gore vertex angles $H_{F}$ at the foot (Sect. 6.2).

The prism singularity and prism correction can be eliminated by two additional $\mathrm {arctan}$s for each edge of the face (Eq. 12). These angles can be incorporated into the two already required for each edge (Eq. 16).

The solid-angle approach shown in Eq. 19 also eliminates the prism singularity and prism correction. The integrand is separated into two terms. One results in the same logarithm term and edge singularity as in the conventional formulations. The other integrand equals a differential solid angle $\mathrm {d}\Omega$ of the differential surface element $\mathrm {d}S$ viewed from the field point. A face’s signed solid angle $\Omega _{f}$ can be evaluated using vector geometry and spherical trigonometry, and requires a single $\mathrm {atan2}$ for an entire face no matter how many vertices (Sect. 12). Eq. 37 is a closed-form expression for the solid angle of a triangular face.

Fig. 10

Count of arctangent terms for various formulations

Figure 10 summarizes the number of arctangent functions (dots) required for evaluating the solid angle of a quadrilateral. The first two diagrams are shown as gores. (a) Eq. 12 requires two $\mathrm {arctan}$ at both vertices of each gore’s edge, a total of 16 for a quadrilateral. (b) Eq. 3 with the prism correction, or Eq. 16 without, requires a single $\mathrm {arctan}$ at both vertices of each gore’s edge, a total of eight. (c) Eqs. (24, 26) require one $\mathrm {atan2}$ for every vertex, a total of four. (d) Eq. 40 requires a single $\mathrm {atan2}$ for the entire face, no matter how many vertices.

15 Numeric comparisons

The term “prism” is sometimes understood to mean a right rectangular parallelepiped, a block-shaped body having right-angled corners. Here, this paper’s formulation is used to compute the potential of a prism at three singular points. Numeric results are compared with Tsoulis (2012) and D’Urso (2014).

The subject prism is aligned with the coordinate axes, and has one corner at the origin and the diagonally opposite corner at (20, 10, 10) m. Density 2670 kg m$^{-3}$ and gravitational constant G = 6.67259E-11 m$^{3}$ kg$^{-1}$ s$^{-2}$ are from Tsoulis (2012, p. F2).

Table 1 Numeric potential comparisons at singular points among this paper, Tsoulis (2012), and D’Urso (2014)

Table 1 displays numeric potential values of the three formulations at three singular points, at a vertex with coordinates (0, 0, 0) m, along an edge at coordinates (5, 0, 0) m, and in a face at coordinates (0, 3, 2) m. Underlined leading digits indicate where the other papers’ results match this paper’s. The final column displays the relative difference $|{A-B}|/A$, where A is this paper’s result and B is the other papers’.

The table shows good agreement among the formulations at all three singular points. This paper’s potential values agree with Tsoulis (2012, Table 1) to about seven decimal digits² and with D’Urso (2014, Table 1) to about fourteen.

16 Conclusion

A solid-angle formulation is mathematically equivalent to the conventional formulations of homogeneous-polyhedron gravitational potential. The solid-angle formulation requires only one $\mathrm {atan2}$ evaluation instead of n or 2n $\mathrm {arctan}$ evaluations for a face of n vertices. All formulations require logarithm evaluations as well. Evaluating fewer arctangents should take less time.

In addition, the prism singularity is absent from the solid-angle formulation. There is no need to evaluate a point-in-polygon algorithm for each face to determine whether it needs a prism correction.

This paper contains solid-angle expressions only for gravitational potential. Expressions for acceleration and gravity-gradient tensor appear in Werner and Scheeres (1997, Sect. 2.6).

The numerical or computational properties of this paper’s solid-angle formulas have not been analyzed.

Appendices

Appendix

Arctangents

Two-quadrant $\mathrm {arctan}$ ranges $[-\pi /2, \pi /2]$, while four-quadrant $\mathrm {atan2}$ ranges $(-\pi , \pi ]$. The separately signed numerator and denominator of $\mathrm {atan2}$ are arguments of a computer’s atan2 function.

Derivations are often in terms of an angle’s tangent expressed as a fraction, e.g., $\tan A = N / D$. If the angle A itself is desired, the arctangent of the fraction is taken. Numerator and denominator signs guide the choice between two-quadrant $\mathrm {arctan}$ and four-quadrant $\mathrm {atan2}$.

If the denominator can be negative, four-quadrant $\mathrm {atan2}$ must be used. If the numerator is positive, $\mathrm {atan2}$ ranges through quadrants I and II; if negative, III and IV.

If the denominator is non-negative, two-quadrant $\mathrm {arctan}$ can be used regardless of the numerator, as the angle ranges through quadrants I and IV only.

1.1 Negative factors and barrier fractions

Arctangent arguments are fractions in this paper. Only positive factors can be canceled algebraically between a four-quadrant $\mathrm {atan2}$ argument’s numerator and denominator—canceling a negative factor or inverting it between numerator and denominator reverses the quadrant diametrically. Such a “barrier fraction” is specially notated with a double solidus:

Two-quadrant $\mathrm {arctan}$ lacks this problem:

$$\begin{aligned} \mathrm {arctan}\frac{-y}{-x} = \mathrm {arctan}\frac{y}{x} , \qquad \mathrm {arctan}\frac{-y}{x} = \mathrm {arctan}\frac{y}{-x} . \end{aligned}$$

A negative sign or a ${\text {sgn}}()$ factor can be extracted from $\mathrm {atan2}$’s numerator but not from its denominator:

Negative signs and ${\text {sgn}}()$ factors can be extracted from both numerator and denominator of $\mathrm {arctan}$:

$$\begin{aligned} \mathrm {arctan}\frac{-y}{x} = \mathrm {arctan}\frac{y}{-x} = - \mathrm {arctan}\frac{y}{x}. \end{aligned}$$

The two- and four-quadrant arctangents are related:

$$\begin{aligned} \mathrm {arctan}\, a = \mathrm {atan2}\, ( a // 1 ) . \end{aligned}$$

1.2 Difference of two angles

It is easy to derive

$$\begin{aligned} \tan (A-B)&= \frac{\sin (A-B)}{\cos (A-B)} = \frac{\sin A \cos B - \cos A \sin B}{\cos A \cos B + \sin A \sin B}\\&\quad \ \div \frac{\cos A \cos B}{\cos A \cos B} \\&= \frac{\tan A - \tan B}{1 + \tan A \tan B} . \end{aligned}$$

A and B must both be limited to $(-\pi /2, \pi /2)$ to avoid infinities. Their difference can range $(-\pi , \pi )$. If angular difference $A-B$ is desired instead of its tangent, four-quadrant $\mathrm {atan2}$ must be used instead of two-quadrant $\mathrm {arctan}$:

(D’Urso and Russo (2002) present a similar investigation. The three cases of their $\mathrm {arctan}$ formulation are subsumed using $\mathrm {atan2}$ instead.)

In the derivation of $\tan (A-B)$, both numerator and denominator are divided by a common factor ($\cos A \cos B$). For the difference $A-B$ to lie in the correct quadrant, that common factor must be positive. This happens automatically if A and B lie in quadrants I or IV where cosine is positive.

If A and B were to lie in quadrants II or III, both cosines are negative and their product is positive. Seemingly, this case is allowed by the derivation. However, the difference $A-B$ can range $(-2\pi , 2\pi )$, outside the range of $\mathrm {atan2}$. To eliminate this case, angles A and B must be restricted to quadrants I and IV.

1.3 Half-angle formula

Eq. 40 uses the half-angle formula $\tan \tfrac{1}{2} A = (1 - \cos A) / \sin A$. Its derivation shows a restriction on the range of A.

$$\begin{aligned} \tan \frac{A}{2}&= \frac{\sin \frac{A}{2}}{\cos \frac{A}{2}} \cdot \frac{2 \sin \frac{A}{2}}{2 \sin \frac{A}{2}} = \frac{2 \sin ^2 \frac{A}{2}}{2 \sin \frac{A}{2} \cos \frac{A}{2}}\\&= \frac{1 - (\cos ^2 \frac{A}{2} - \sin ^2 \frac{A}{2})}{2 \sin \frac{A}{2} \cos \frac{A}{2}} \\&= \frac{1 - \cos (\frac{A}{2} + \frac{A}{2})}{\sin (\frac{A}{2} + \frac{A}{2})} = \frac{1 - \cos A}{\sin A} . \end{aligned}$$

Four-quadrant $\mathrm {atan2}$ is used to evaluate the half-angle itself:

(42)

In order that the common factor $(2 \sin \frac{A}{2})$ not affect the quadrant, $(\sin \frac{A}{2})$ must be positive. This occurs automatically when $\frac{A}{2}$ lies in quadrants I and II; $0 \le \frac{A}{2} \le \pi$ or $0 \le A \le 2 \pi$.

This can also be determined by inspection of Eq. 42: the numerator $(1 - \cos A)$ is non-negative and the denominator $(\sin A)$ is signed. $\mathrm {atan2}$ ranges through quadrants I and II as does A / 2.

Solid-angle properties

Solid-angle magnitude $|{\Omega _{f}}|$ can be thought of as the area of the image of face $f$ centrally projected onto a unit-radius sphere centered on the field point $P$ (Fig. 6). Signed solid angle has the same sign as $v_{f}$.

1.1 Removable singularity in face plane

Integrand $v_{f}/ r^3 = v_{f}/ (\rho ^2 + v_{f}^2)^{3/2}$ and solid angle $\Omega _{f}= \iint _{f} (v_{f}/ r^3) \mathrm {d}S$ in Eq. 20 are well defined where the field point $P$ is not in the face plane ($v_{f}\ne 0$), or is in the face plane ($v_{f}= 0$) but not in the face ($\rho > 0$). However, the integrand is improper where $P$ lies in the face or on its boundary ($v_{f}= \rho = r= 0$).

To investigate this singularity, a disc of radius $\rho$ centered on $P$ is eliminated from the integration domain. The integrand behavior as $\rho$ decreases to zero is

$$\begin{aligned} \lim _{\rho \rightarrow 0^{+}} \frac{v_{f}}{r^3} \Bigr \vert _{v_{f}= 0}&= \lim _{\rho \rightarrow 0^{+}} \frac{v_{f}}{(\rho ^2 + v_{f}^2)^{3/2}} \Bigr \vert _{v_{f}= 0}\\&= \lim _{\rho \rightarrow 0^{+}} \frac{0}{\rho ^3} = 0 . \end{aligned}$$

The integrand vanishes on the disc’s boundary independently of $\rho > 0$. It is improper only at $\rho = 0$.

Hence, Eq. 20 contains a removable singularity. Solid angle $\Omega _{f}$ can be defined as 0 wherever the field point is in the face plane.

1.2 Limit as field point approaches face plane

This section analysis is based on a non-convex face of five vertices. It has a reflex vertex at the origin and remaining convex vertices have coordinates $(\pm 1, \pm 1, 0)$. (Note: the $(h,s,v)$ coordinate system used in this paper’s derivations changes with every edge of every face. In this section, coordinates are expressed in a facial coordinate system $(x,y,v)$.)

Let $P$ approach the plane of a face on a straight trajectory normal to the face. Coordinates (x, y) of the field point and foot are constant; only the vertical coordinate $v_{f}$ varies. Solid angle $\Omega _{f}= \Omega _{f}(v_{f})$ evaluated on this trajectory is found to be an odd function of $v_{f}$. ($\Omega _{f}$ is not necessarily strictly an odd function if the trajectory is not parallel to $\hat{\mathbf {n}}_f$.)

Fig. 11

Solid angle $\Omega _{f}$ along trajectories through a face plane

The three diagrams in Fig. 11 show $\Omega _{f}(v_{f})$ for chosen locations of the foot $F$. Open semicircles where the function trace meets the vertical axis indicate that $\Omega _{f}(v_{f})$ never achieves the limit as $v_{f}\rightarrow 0$. The solid dot at (0, 0) is $\Omega _{f}(0)$. Function traces in the three are explained subsequently.

The subject face depicted in the lower-right quadrant of each diagram is scaled and positioned independently of the $\Omega _{f}(v_{f})$ traces. Single letters abbreviate foot locations for the several trajectories: X is exterior to the face at coordinates $(-0.3,0,0)$, I is interior to the face at $(0.5,-0.5,0)$, E is on an edge at (1, 0, 0), C is at a convex vertex at $(1,-1,0)$, and R is at the reflex vertex at (0, 0, 0).

Figure 11a shows a case where $F$ lies exterior to the face at X. Let $P$ approach the face plane from beneath, so that $v_{f}$ and $\Omega _{f}$ are initially positive. From a large distance, the image area and $\Omega _{f}$ are small. $v_{f}$ decreases and $\Omega _{f}$ increases as the field point approaches the face plane. Since $F$ is outside the face, the image projects obliquely onto the field-point-centered sphere. There is some positive value of decreasing $v_{f}$ where the image area and $\Omega _{f}$ begin decreasing, because the face begins to appear edge-on from $P$. Both $v_{f}$ and $\Omega _{f}$ continue decreasing until they vanish where $P$ enters the face plane at $F$. Signs reverse once the field point is above the face plane where both $v_{f}$ and $\Omega _{f}$ are negative. Hence, $\Omega _{f}(v_{f})$ is an odd, continuous function of $v_{f}$ where $F\not \in f$.

Figure 11b shows a case where foot $F$ lies interior to the face at I. As before, $\Omega _{f}$ is small and positive where $P$ begins from a great distance below. As $P$ approaches $F$, $\Omega _{f}$ increase monotonically, because the image is not projected obliquely. Where the field point is infinitesimally beneath the face, the image covers virtually an entire hemisphere. The limit is

$$\begin{aligned} \lim _{v_{f}\rightarrow 0^{+}} \Omega _{f}(v_{f}) = 2 \pi \text { steradians,}\, F\in f. \end{aligned}$$

However, $\Omega _{f}$ vanishes wherever $P$ is exactly in the face plane (Appendix B.1). Hence, $\Omega _{f}(v_{f})$ is discontinuous, changing abruptly from $2 \pi ^{-}$ to 0 as $v_{f}\rightarrow 0^{+}$. The discontinuity is likewise apparent if $P$ approaches the face from above where $v_{f}$, $\Omega _{f}$, and the limit are negative:

$$\begin{aligned} \lim _{v_{f}\rightarrow 0^{-}} \Omega _{f}(v_{f}) = -2 \pi \text { steradians,}\, F\in f. \end{aligned}$$

Therefore, $\Omega _{f}(v_{f})$ is a discontinuous odd function of $v_{f}$ where $F\in f$.

In cases where foot $F$ lies within an edge or coincides with a vertex, the limit of magnitude $|{\Omega _{f}}|$ is the planar face’s interior angle measured there. The interior angle lies in the interval $(\pi ,2 \pi )$ for a reflex vertex.

$$\begin{aligned} \lim _{v_{f}\rightarrow 0} {|\Omega _{f}(v_{f})|}&= {\left\{ \begin{array}{ll} 2 \pi , &{} \text {foot wholly inside face} \\ \pi , &{} \text {foot on edge} \\ \text {interior } \measuredangle P_j, &{} \text {foot at planar vertex } P_j \\ 0. &{} \text {foot outside face} \end{array}\right. } \\ \Omega _{f}&= 0. \quad \text {field point}\, P\, \text {in face plane}. \end{aligned}$$

Figure 11c shows five cases of signed $\Omega _{f}(v_{f})$. Traces are labeled I, R, E, C, and X as explained previously. All but exterior trace X are discontinuous as $v_{f}$ passes through 0.

In summary, the range of solid angle $\Omega _{f}$ for any field-point location $P$ is the open interval $(- 2 \pi , 2 \pi )$. $\Omega _{f}$ vanishes if $P$ is anywhere in the face plane. $\Omega _{f}(v_{f})$ is continuous where foot $F$ is outside the face and discontinuous where $F$ is inside the face or on its boundary.

Logarithm factor

In this appendix, $r_{1e}, r_{2e}, s_{1ef}, \text {and } s_{2ef}$ are abbreviated to $r_{1}, r_{2},s_{1}$, and $s_{2}$.

The integral $\int _e\mathrm {d}s/ r$ appears in Eq. 3 et seq. as part of $U_{f}$. By elementary means, it is found to be

$$\begin{aligned} L_{ef}= \int _e\frac{1}{r} \mathrm {d}s= \int _{s_{1}}^{s_{2}} \frac{1}{r(s)} \mathrm {d}s= \ln \frac{r_{2}+ s_{2}}{r_{1}+ s_{1}}. \end{aligned}$$

(43)

Macmillan (1930, Sects. 43, 98) manipulates the argument into a coordinate-free expression. The following lemma is used:

$$\begin{aligned} r_{2}^2 - r_{1}^2&= (h^2 + s_{2}^2 + v^2) - (h^2 + s_{1}^2 + v^2) = s_{2}^2 - s_{1}^2 . \end{aligned}$$

Recall edge-length $\ell _{e}\mathop {=}\limits ^{\text {def}}s_{2}- s_{1}$. The logarithm argument becomes

$$\begin{aligned} \frac{r_{2}+ s_{2}}{r_{1}+ s_{1}}&= \frac{2 r_{2}+ (s_{2}+ s_{1}) + (s_{2}- s_{1})}{2 r_{1}+ (s_{2}+ s_{1}) - (s_{2}- s_{1})} \cdot \frac{s_{2}- s_{1}}{s_{2}- s_{1}} \\&= \frac{2 r_{2}(s_{2}- s_{1}) + (s_{2}^2 - s_{1}^2) + (s_{2}- s_{1})^2}{2 r_{1}(s_{2}- s_{1}) + (s_{2}^2 - s_{1}^2) - (s_{2}- s_{1})^2} \\&= \frac{2 r_{2}\ell _{e}+ (r_{2}^2 - r_{1}^2) + \ell _{e}^2}{2 r_{1}\ell _{e}+ (r_{2}^2 - r_{1}^2) - \ell _{e}^2} = \frac{(r_{2}+ \ell _{e})^2 - r_{1}^2}{r_{2}^2 - (r_{1}- \ell _{e})^2} \\&= \frac{(r_{2}+ \ell _{e}+ r_{1}) (r_{2}+ \ell _{e}- r_{1})}{(r_{2}+ r_{1}- \ell _{e}) (r_{2}- r_{1}+ \ell _{e})} = \frac{r_{1}+ r_{2}+ \ell _{e}}{r_{1}+ r_{2}- \ell _{e}} , \end{aligned}$$

that is

$$\begin{aligned} L_{ef}= \int _{e} \frac{1}{r} \mathrm {d}s= \ln \frac{r_{1}+ r_{2}+ \ell _{e}}{r_{1}+ r_{2}- \ell _{e}} . \end{aligned}$$

(44)

This formulation is coordinate-free; all quantities are distances.

When numerator and denominator are divided by $r_{1}+ r_{2}$,

$$\begin{aligned} L_{ef}&= \int _{e} \frac{1}{r} \mathrm {d}s= \ln \frac{1 + \ell _{e}/ (r_{1}+ r_{2})}{1 - \ell _{e}/ (r_{1}+ r_{2})} = 2 \mathrm {artanh}\frac{\ell _{e}}{r_{1}+ r_{2}} \end{aligned}$$

(45)

which is advocated by Strakhov et al. (1986a, p. 478). Holstein and Ketteridge (1996, p. 361) likewise indicate that $\mathrm {artanh}(t)$ is more accurate than $\tfrac{1}{2} \ln [(1+t) / (1-t)]$ for small t.

The requirement that $\ell _{e}/ (r_{1}+ r_{2})$ be limited to $\mathrm {artanh}$’s domain $(-1,1)$ is automatically satisfied by the triangle inequality, unless $P$ is embedded in the edge and the fraction is exactly 1. However, that is the edge singularity (Appendix C.1) and must be dealt with separately (Sect. D.1).

Macmillan (1930, §98) observes that the $\mathrm {artanh}$ argument can be interpreted as the eccentricity of an ellipse passing through the field point with foci at the edge vertices (Sect. 13.3).

1.1 Edge singularity

The integrand of antiderivative $\int \mathrm {d}s/ r$ is undefined where $r= 0$. This occurs if and where the field point is on the edge. Consider the logarithm argument $(r_{2}+ s_{2})/(r_{1}+ s_{1})$ of the definite integral. If the field point is on the edge, $h_{ef}= v_{f}= 0$ and $r= |{s}|$. Coordinate $s_{1}\le 0$ and is exactly the same magnitude as distance $r_{1}$. Hence, denominator $r_{1}+ s_{1}$ vanishes and the logarithm argument is undefined, as is the logarithm itself (Plouff (1976, p. 732), Pohánka (1988, p. 743), D’Urso (2014, Sect. 3.2)). This is termed the “edge singularity”.

Such a logarithmic singularity is very weak (Greenberg, 1978, p. 21, prob. 1.20):

$$\begin{aligned} \lim _{x \rightarrow \infty } x^{-\alpha } \ln x = 0 \end{aligned}$$

for real $\alpha > 0$, no matter how small (Abramowitz and Stegun, 1964, Eq. 4.1.30).

The logarithm terms of the entire polyhedron’s potential $U$ (Eq. 22) read

$$\begin{aligned} \frac{1}{2} \sum _{f\in \text {faces}} v_{f}\sum _{\begin{array}{c} e \in f\text {'s}\\ \text {edges} \end{array}} h_{ef}\ln \frac{r_{2}+ s_{2}}{r_{1}+ s_{1}}. \end{aligned}$$

The weak logarithmic singularity is overcome by the product $h_{ef}v_{f}= 0$ which multiplies $L_{ef}$ (Nagy et al. 2000, Eq. 5):

$$\begin{aligned} h_{ef}v_{f}\ln \frac{r_{2}+ s_{2}}{r_{1}+ s_{1}}\bigg \vert _{h_{ef}= v_{f}= 0} = 0. \end{aligned}$$

A factor related to $h_{ef}v_{f}$ appears with $L_{ef}$ for acceleration (first derivative of potential). However, for the gravity-gradient tensor (second derivative), there is no such factor to overcome the logarithmic singularity, and the edge singularity is manifest.

Implementation

1.1 Programming considerations

Appendix B.1 shows that $\Omega _{f}$ vanishes if field point $P$ is in the plane of face $f$ ($v_{f}= 0$). A computer subroutine which computes $\Omega _{f}$ should first check for this condition. If $|{v_{f}}|$ exceeds a small tolerance value $\delta$, the field point is a significant distance from the face plane and the subroutine proceeds evaluating Eqs. (25, 39, 40) for a non-triangular face or the simpler Eq. 37 for a triangle. However, if $|{v_{f}}|$ is less than $\delta$, the field point is in or very close to the face plane and the subroutine immediately returns 0. The following problems occur without this short circuit:

• If $P$ coincides with vertex $P_{j}$, distance $r_{j}$ between $P$ and $P_{j}$ vanishes. Direction vector $\hat{\mathbf {r}}_{j} = \mathbf {r}_{j} / r_{j}$ is undefined.

• If $P$, $P_{i}$, and $P_{j}$ are colinear, then is $\pm 1$. Likewise, $c_{jk}$ is $\pm 1$ if $P$, $P_{j}$, and $P_{k}$ are colinear. In either case, denominator $\sqrt{1 - c_{ij}^2} \sqrt{1 - c_{jk}^2}$ vanishes in Eq. 25 and $\cos \overline{S}_j$ and $\sin \overline{S}_j$ are undefined.

Appendix C.1 shows that $L_{ef}$ is undefined if field point P lies within that edge. A computer subroutine which computes $L_{ef}$ might check whether denominators $r_{1}+ s_{1}$ or $r_1 + r_2 - \ell _{e}$ in Eqs. 43 or 44 are closer to zero than some tolerance, or whether dimensionless $\ell _{e}/ (r_1 + r_2)$ in Eq. 45 is close to 1. If any such condition is true, the entire logarithm term $v_{f}h_{ef}L_{ef}$ for the potential of that edge vanishes. The undefined $L_{ef}$ need not be evaluated.

1.2 Pseudocode to compute $U_{f}$

Pseudocode for computing a single face’s $U_{f}$ (Eq. 21) follows. The code avoids edge singularities (Appendix C.1), and forces $\Omega _{f}= 0$ if the field point is too close to the face plane (Appendix B.2).

Constants, such as edge-length $\ell _{e}$ and face- and edge-normal vectors $\hat{\mathbf {n}}_f$, $\hat{\mathbf {n}}_{ef}$ can be prepared when the polyhedron is initialized. Small positive $\delta$ controls detection of the edge singularity and the solid-angle discontinuity. Field-point-relative vectors $\mathbf {r}_i$ and distances $r_i$ are to be computed before using the code.