Abstract
The existent methods for constructing ambiguity sets in distributionally robust optimization often suffer from over-conservativeness and inefficient utilization of available data. To address these limitations and to practically solve multi-stage distributionally robust optimization (MDRO), we propose a data-driven Bayesian-type approach that constructs the ambiguity set of possible distributions from a Bayesian perspective. We demonstrate that our Bayesian-type MDRO problem can be reformulated as a risk-averse multi-stage stochastic programming problem and subsequently investigate its theoretical properties such as consistency, finite sample guarantee, and statistical robustness. Moreover, the reformulation enables us to employ cutting planes algorithms in dynamic settings to solve the Bayesian-type MDRO problem. To illustrate the practicality and advantages of the proposed model and algorithm, we apply it to a distributionally robust inventory control problem and a distributionally robust hydrothermal scheduling problem, and compare it with usual formulations and solution methods to highlight the superior performance of our approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multi-stage stochastic programming (MSP) has gained a lot of attention in many applications where decision-making processes involve uncertainty and unfold over time. These include a wide range of fields such as multiperiod portfolio selection (Edirisinghe 2005), pension fund management (Klein Haneveld et al. 2010), power system operations (Pan and Guan 2016; Sen et al. 2006), the production and trading of gas (Allevi et al. 2008) and electricity (Hochreiter et al. 2006). MSP is well-suited for these problems as it can naturally capture the stochastic nature of the underlying data process, which are often represented as multivariate stochastic processes. The decisions made at individual stages of a MSP depend on the observed values of the data process, resulting in an optimization problem in functional spaces. The goal is to find optimal decisions that minimize the total expected cost subject to a series of constraints. While classical MSPs focus on the risk-neutral behavior through the expectation operator, they may fail to capture those small-probability events that can have significant real-world impacts. To address this limitation, risk-averse multi-stage stochastic programming (RMSP) has recently been proposed in Krokhmal et al. (2011) and Rockafellar and Uryasev (2000) by including some risk measure in its objective function. The key issue for this kind of models is the proper selection of the risk measure. Several notable works have explored the properties of risk measures in RMSP, including coherent risk measures (Artzner et al. 1999), time-consistent risk measures (Allevi et al. 2008; Ruszczyński and Shapiro 2006), and the regularity of risk measures (Rockafellar and Uryasev 2013).
Despite their usefulness, MSPs and RMSPs face challenges in obtaining exact probability distributions of the random process due to the partial observability of distribution information. To address this issue, multi-stage distributionally robust optimization (MDRO) has been proposed in recent years. It models all possible probability distributions at individual stages within a certain range, called the ambiguity set, based on available information about distributions or historical data. Naturally, constructing the ambiguity sets becomes a critical modeling issue in MDRO.
A few approaches have been introduced to construct stage-wise ambiguity sets of distributions of data processes in MDRO, which include methods like the nested distance (Arora and Gao 2022) and \(\infty \)-Wasserstein distance (Bertsimas et al. 2023). However, these approaches face serious computational difficulties due to the complexity of the ambiguity set. Additionally, without the support of dynamic programming equations, it remains unclear whether these methods satisfy the time consistency, which requires an optimal policy to remain optimal based on observed realizations. Time consistency has nowadays become a basic requirement for rational decision-making under many situations. To address these shortcomings, at present, several alternative and tractable methods turn to constructing the ambiguity sets under the assumption of stage-wise independence. The theoretical support for this assumption is that the inter-stage dependence case can be transformed to the stage-wise independent case by expanding the state variable space as shown in Shapiro (2011). Like that for other stochastic optimization models, the stage-wise independence assumption greatly facilitates the reformulation of MDRO due to the applicability of the dynamic programming principle, which ensures the time consistency, and thus is adopted in almost all the current studies about MDROs. Various methods have been proposed for constructing ambiguity sets under the setting of stage-wise independence, including moment-based approaches (Xin and Goldberg 2021; Yu and Shen 2022; Liu et al. 2018) and statistical-distance-based approaches (e.g., \(\chi ^2\)-divergence in Philpott et al. 2018, Wasserstein distance in Duque and Morton 2020). However, it is important to acknowledge that moment-based methods may not always provide sufficient robustness for distributions with skewness or heavy tails. Meanwhile, computing the \(\chi ^2\)-divergence or Wasserstein distance can be time-consuming, particularly for high-dimensional problems or the cases with large sample sizes. Thus, while the assumption of stage-wise independence has practical advantages in MDRO, it is essential to consider new methods for constructing ambiguity sets ensuring their completeness and the easy solvability of resulting optimization model in various situations.
Furthermore, constructing proper ambiguity sets under continuous distributions can be challenging and may lack implementability. Fortunately, there exists a promising approach to address this issue, as demonstrated in Jiang and Guan (2018). This study revealed that the MDRO model with ambiguity sets constructed using a discrete distribution can perform remarkably well even when the underlying distribution is continuous. By establishing connections with existing statistics literature, a unified treatment is proposed in Bertsimas et al. (2018) and it can encompass both discrete and continuous distributions. On the other hand, the adoption of discrete distributions in MDROs can be advantageous. It effectively reduces excessive conservatism, which is often associated with ambiguity sets constructed under continuous distributions, and maintains the practical validity of the resulting MDRO model while providing tractable solutions. Therefore, to enhance tractability and practicality, the majority of existing researches on MDRO settles for the assumption that stage-wise distributions have finite support, as exemplified in studies like Huang et al. (2017), Philpott et al. (2018) and Van Parys et al. (2021). However, these works may not have sufficient theoretical groundwork. They lack in-depth examinations of the asymptotic performance of the proposed model, as well as the finite sample guarantee, which are essential components in validating data-driven models. Due to this, another focus of this study is to establish a comprehensively theoretical framework under the finite support assumption.
It is worth highlighting that, under certain circumstances, MDRO can be transformed into RMSP with some coherent risk measure. This allows for a more straightforward solution, making RMSP a favorable alternative for practical implementation, for instance, in Huang et al. (2017) and Pichler and Shapiro (2021). Although there exist quite a few algorithms for MDRO problems, a notable portion of research has been focused on addressing sequential decision-making problems with linear objective functions. Particularly, when dealing with stagewise independent uncertainties, a popular choice is to use the nested cutting plane algorithm for linear MDRO problems (Philpott et al. 2018; Shapiro 2011). However, it is crucial to acknowledge that solving convex MDRO problems, in general, can be highly challenging. As the number of decision stages increases, the problem’s dimensionality expands significantly (see, Georghiou et al. 2019), leading to computational bottlenecks. Efficiently handling such high-dimensional problems with limited computational resources remains an open research area in MDRO.
It is important to point out that the existing MDRO literature heavily relies on accurate estimates of potential probability distributions or distributional information such as moments from historical data. However, as observed in Pichler and Xu (2022) and Xu and Zhang (2021), several factors, like data quality and sample size, can lead to the inaccurate estimates of empirical distributions. These inaccuracies may introduce biases in the construction of ambiguity sets, thereby impacting the optimization results. Consequently, it becomes necessary to examine the quantitative stability of the optimization outcomes, especially in scenarios involving data contamination. Despite the potential implications of biased ambiguity sets on the accuracy of the optimization model, the current MDRO literature lacks comprehensive investigations into the effects of bias, particularly in the context of contaminated data.
The parameterization assumption of distributions has become a prevailing practice in coping with many real decision-making problems under uncertainty, for instance, the Poisson distribution to represent demand in inventory problems (Lin et al. 2022), the exponential distribution to model inflow in hydrothermal scheduling (Huang et al. 2017), but the direct construction of uncertainty sets for relevant distributional parameters remains an avenue of research deserving exploration. Recently, in Gupta (2019) and Rebennack (2022), a statistical approach called Bayesian-type ambiguity sets has emerged as an intriguing alternative to overcome the limitations of traditional ambiguity sets. In contrast to the usual approach of directly constructing ambiguity sets for distributions, under parametric assumptions on the distribution, Bayesian-type ambiguity sets are specified by Bayesian confidence regions for the parameters, which incorporate both prior knowledge and data samples (see, Gelman et al. 1995). Intuitively, the Bayesian confidence region encompasses parameters that fall within a “small" neighborhood of the corresponding parameters of the empirical distribution. Recall that from the Bayesian perspective, one can treat probability as a personal belief based on an individual’s experience about the possibility of an event, known as a priori probability. By adjusting the prior probability to reflect one’s understanding of the random phenomenon while continuously updating it through sample data, a Bayesian-type ambiguity set has been recently constructed in Gupta (2019) and Petrik and Russel (2019)) with theoretical guarantees such as finite sample guarantee and asymptotic convergence, as compared to traditional ambiguity sets. However, the ambiguity set for a single-stage Bayesian DRO problem is constructed in Gupta (2019) by using an upper bound of the Bayesian confidence region, rather than the exact Bayesian confidence region. Furthermore, the study in Petrik and Russel (2019) primarily demonstrates the superiority of a Bayesian-type ambiguity set through numerical experiments for a Markov Decision Process (MDP) problem. Recently, Chen et al. (2023) have proposed a novel method to approximate the ambiguity set in a chance constrained problem with exact Bayesian confidence regions and shown its advantages in constructing a proper size ambiguity set through continuously updating the posterior distribution. Therefore, this article focuses on the MDRO problem, employing a data-driven method to construct ambiguity sets directly from exact Bayesian confidence regions derived from historical data samples, called the Bayesian-type MDRO problem.
Based on the above comprehensive assessment of current literature, we will systematically investigate a class of convex MDRO problems by constructing ambiguity sets via a Bayesian perspective. The main contributions of this paper are as follows:
-
We introduce a convex MDRO problem with Bayesian-type ambiguity sets. It is less conservative than existing data-driven models such as Jiang and Guan (2018) and Philpott et al. (2018). And the proposed model extends the current Bayesian-type DRO models, such as those in Gupta (2019) and Petrik and Russel (2019), and has good theoretical foundations such as finite sample guarantee and asymptotic convergence.
-
Considering that real-world data is often subject to perturbations, we establish the statistical robustness of our model to demonstrate its highly appeal for modeling complex decision-making problems in the face of uncertainty.
-
We show that the proposed Bayesian-type MDRO can be reformulated as an RMSP where stage-wise recourse functions are a convex combination of the expectation and the conditional value at risk (CVaR) of random costs. This reformulation avoids the difficulty of directly solving the MDRO problem due to its nested minimax structure.
-
A customized cutting plane algorithm is developed for solving the RMSP problem by deriving cutting plane approximations to the convex cost-to-go functions derived from dynamic programming equations.
-
The proposed models and algorithm are validated by applying them to the distributionally robust inventory control problem and hydrothermal scheduling problem.
The rest of this article is structured as follows. Section 2 introduces the Bayesian-type MDRO model and constructs ambiguity sets that contain real distributions with high probability through a data-driven Bayesian approach. Section 3 demonstrates the equivalence between the proposed Bayesian-type MDRO and a tractable RMSP and investigates its theoretical properties such as finite sample guarantee, asymptotic convergence and quantitative statistical robustness. Section 4 develops a specific cutting plane algorithm for solving our Bayesian-type MDRO. In Sect. 5, we apply our Bayesian-type MDRO model and algorithm to a distributionally robust inventory control problem and a distributionally robust hydrothermal scheduling problem and present experimental results. Finally, Sect. 6 summarizes our findings.
2 Multistage distributionally robust optimization with Bayesian confidence region
MSP has become an important framework for modeling sequential decision-making under uncertainty, where one chooses his optimal decisions at each stage through minimizing the conditional expectation of an objective function, based on the decisions at previous stages and the history of the random data process up to that stage. The nested formulation of a T \((2\le T<\infty )\) stage MSP is as follows:
where stage-wise objective functions \(f_1:{\mathbb {R}}^a\rightarrow {\mathbb {R}}\), \(f_t:{\mathbb {R}}^{a}\times {\mathbb {R}}^{k}\rightarrow {\mathbb {R}}\), \(2\le t\le T\) are continuous and convex in \(x_t\in {\mathbb {R}}^{a}\) and are continuous with respect to (w.r.t.) \(\xi _t\in \Xi _t\subset {\mathbb {R}}^{k}\). Here, \(\xi _t\) represents the random vector at stage t, and \(\Xi _t\) denotes the support set of \(\xi _t\). Moreover, \({\mathbb {P}}_{t}^c\) denotes the underlying distribution of \(\xi _t\). Without loss of generality, we assume the feasible solution regions at different stages are compact and convex sets, which are denoted as \({\mathcal {X}}_1=\{x_1:A_1x_1\le b_1\}\) and \({\mathcal {X}}_t:={\mathcal {X}}_t(x_{t-1},\xi _t)=\{x_t:A_tx_t\le b_t-B_tx_{t-1}\}\), \(B_t:=B_t(\xi _t)\), \(A_t:=A_t(\xi _t)\) and \(b_t:=b_t(\xi _t)\) are dimensionality matched matrices and vectors that depend on \(\xi _t\). For concise expression, we assume the dimensionalities of decision vectors at different stages are the same, so are the dimensionalities of random vectors at different stages. All the presentations and conclusions here-in-after hold for the general situation with stage-dependent dimensionalities.
For many complex multi-period decision-making problems in practice, exact probability distributions of \(\xi _t\) \((2\le t\le T)\) are often unavailable, leading to the proposal of MDRO as a robust extension to usual MSPs under full information assumption. This approach allows for robust decision-making in the presence of ambiguous distributions and provides a more realistic representation of the sequential decision-making problem under uncertainty. Corresponding to (1), the general nested formulation of MDRO can be described as
Here, the ambiguity set \({\mathcal {P}}_{t}\) \((2\le t\le T)\) for the possible probability distributions of \(\xi _t\) at stage t should contain the true distribution \({\mathbb {P}}_{t}^c\) with high probability. For reasons presented in the introduction, we assume the random variables \(\xi _t\) are stage-wise discrete and independent for \(t=2, \cdots , T\), like that in most of relevant studies (e.g., Duque and Morton 2020; Huang et al. 2017, and Philpott et al. 2018). This assumption can accommodate various uncertainty structures (e.g., autoregressive stochastic models in Shapiro (2011)) by appropriate reformulations. Additionally, if \(f_t(x_t, \xi _t) = c_tx_t\) as a linear function with \(c_t:= c_t(\xi _t)\), (2) can be simplified into a linear MDRO problem.
In contrast to existing MDRO researches, we adopt the Bayesian analysis technique, which has been commonly utilized in studies on reinforcement learning and optimization (see, e.g., Delage and Mannor 2010; Gupta 2019 and Xu and Mannor 2009), to construct the ambiguity set \({\mathcal {P}}_{t}\). Specifically, we assume that the true distribution \({\mathbb {P}}_t^c\) of \(\xi _t\) belongs to a parameterized family of distributions \({\mathcal {P}}_{\Theta _{t}}:=\{{\mathbb {P}}_{{\varvec{\theta }}_t},{\varvec{\theta }}_t\in \Theta _{t}\}\), where \(\Theta _{t}\) represents the parameter space. Let \({\varvec{\theta }}_t^c\in \Theta _{t}\) be the unknown true parameter corresponding to \({\mathbb {P}}_{{\varvec{\theta }}_t^c}:={\mathbb {P}}_t^c\). The key aspect of our framework is to quantify our knowledge about \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\) from the available data using a confidence region for the parameter \({\varvec{\theta }}_t^c\) of the true distribution. In a Bayesian framework, it is important to note that \({\varvec{\theta }}_t^c\) represents a specific realization of the belief random variable \({{\varvec{\theta }}}_t\), whose posterior distribution can be computed with available data. Therefore, in a data-driven way, we can construct the uncertainty sets for the distribution parameters to derive the ambiguity sets for the distributions of the MDRO model. This approach, which we refer to as Bayesian-type MDRO, represents a key aspect of our framework. Our concrete construction is as the following.
2.1 Bayesian confidence region for distributions
In reality, even for general continuous distributions, what we really have are often finite realizations or observations of related random vectors. Considering this and for the tractability purpose, we assume that \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\) has a known, finite support, as usually done in previous studies such as Bertsimas et al. (2018), Huang et al. (2017), Philpott et al. (2018) and Van Parys et al. (2021). The support set is denoted as supp\(({\mathbb {P}}_{{\varvec{\theta }}_t^c})=\{\xi _t^1,\cdots ,\xi _t^{n} \}\). We naturally set \({\theta }^c_{t,j}={\mathbb {P}}_{{\varvec{\theta }}_t^c}({{\xi }}_t=\xi _t^j)\) for \(j =1,\cdots ,n\). The probability simplex \(\Theta _t\equiv \{{\varvec{\theta }}_t\in {\mathbb {R}}^n_+:{\varvec{e}}^T{\varvec{\theta }}_t=1\}\) stands for the possible values of the parameter vector \({\varvec{\theta }}_t\), here \({\varvec{e}}\) is the n-dimensional vector of all ones. For the sake of simplicity, we assume a consistent number N of discretization points in the sample set \({{\mathcal {S}}_t} = \{{\hat{\xi }}_t^1,\cdots ,{\hat{\xi }}_t^{N}\}\) across different stages. With a prior probability density function (pdf) of \(p({\varvec{\theta }}_t)\) and the observed sample set \({{\mathcal {S}}_t}\), the pdf of the posterior distribution \({\mathbb {P}}_{{\mathcal {S}}_t}\) is derived from Bayes’ formula as follows:
where \(p({\mathcal {S}}_t|{\varvec{\theta }}_t)=\prod _{i=1}^{N}p({\hat{\xi }}_t^i|{\varvec{\theta }}_t)\) is the likelihood function of the data set \({{\mathcal {S}}_t}\).
To construct the ambiguity set in a data-driven way, we specify the parameter region \(\Theta _t({\mathcal {S}}_t, \alpha )\) as the set that satisfies \({\mathbb {P}}_{{\mathcal {S}}_t}({{\varvec{\theta }}_t^c}\in {\Theta _t}({{\mathcal {S}}_t}, \alpha ))=1-\alpha \), here \(\alpha >0\) is a sufficiently small constant. This region induced by the Bayesian prior and posterior distributions, also known as Bayesian confidence region in Berger (2013) and Gelman et al. (1995), is essential for constructing the ambiguity set. Specifically, the generated confidence region must cover the true values of the parameters with high probability, with respect to the computed posterior distribution \({\mathbb {P}}_{{\mathcal {S}}_t}\). Then we define \({\mathcal {P}}_{\Theta _{t}({{\mathcal {S}}_t}, \alpha )}=\{{\mathbb {P}}_{{\varvec{\theta }}_t}|{\varvec{\theta }}_t\in {\Theta _t}({{\mathcal {S}}_t}, \alpha )\}\) as the ambiguity set of the probability distribution of the random vector \(\xi _t\) at stage \(t=2,\cdots ,T\). Based on the above illustration, we conclude that the constructed \({\mathcal {P}}_{\Theta _{t}({{\mathcal {S}}_t}, \alpha )}\) must cover the true distribution \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\) with high probability w.r.t. \({\mathbb {P}}_{{\mathcal {S}}_t}\), i.e., \({\mathbb {P}}_{{\mathcal {S}}_t}({\mathbb {P}}_{{\varvec{\theta }}_t^c}\in {\mathcal {P}}_{\Theta _{t}({{\mathcal {S}}_t}, \alpha )})=1-\alpha \).
It is worth noting that the updates of the posterior distribution \(p({\varvec{\theta }}_t|{{\mathcal {S}}_t})\) in (3) and the confidence region \(\Theta _t({\mathcal {S}}_t, \alpha )\), as previously explained, are induced from the prior distribution \(p({\varvec{\theta }}_t)\). Thus the choice of a prior distribution plays a crucial role in constructing reliable confidence regions. A poorly chosen prior distribution may result in \(p({\varvec{\theta }}_t|{{\mathcal {S}}_t})\) not having a closed-form, leading to an infinite-dimensional posterior (see, Lin et al. 2022). To avoid this issue, we adopt the approach in Raiffa and Schlaifer (1961) and utilize a family of conjugate distributions. By using a conjugate prior, the posterior distribution must belong to the same family of distributions as the prior, preserving the finite dimensionality of the posterior as well as the parameter space of the conjugate distribution. Since it offers various analytical benefits as described in Agarwal and Daumé (2010) and Gupta (2019), Bayesian conjugate prior is a well-established and widely-used method in many areas.
Recall that Dirichlet distribution is a conjugate prior for multinomial distribution. Without loss of generality, we use the Dirichlet prior for \({{\varvec{\theta }}}_t\) in our construction of ambiguity sets. That is, we assume that within our belief, \({{\varvec{\theta }}}_t\) follows a Dirichlet distribution with parameter \(\tau _t'\), which leads to the pdf \(p({\varvec{\theta }}_t)=B(\tau _t')^{-1}\prod _{j=1}^{n}{\theta }_{t,j}^{\tau _{t,j}'-1}\). Here \(\tau _{t,j}'>0\) for all \(j=1,\cdots ,n\) and \(B(\tau _t')\) is a normalizing constant. Under Bayesian inference, the posterior distribution \({\mathbb {P}}_{{\mathcal {S}}_t}\) is also Dirichlet with updated parameters \(\tau _t\), \(\tau _{t,j}=\tau _{t,j}'+x_j\), where \(x_j:=\sum _{i=1}^{N}{\mathbb {I}}({\hat{\xi }}_t^i=\xi _t^j)\) denotes the number of realizations of \(\xi _t^j\). Then the update of the posterior distribution is as follows
Example 1
It is often the case that people lack a clear understanding of the occurrence of random events, leaving them without any prior information to rely on. In such situations, it becomes necessary to choose a prior distribution without any particular preference. One approach to achieve this is by setting \(\tau _{t}'={\varvec{e}}\), which effectively transforms the Dirichlet prior distribution into a uniform distribution on the simplex. Another important prior distribution, proposed by Jeffreys (1998), holds great significance in non-informative cases and finds applications in various domains (e.g., Berger and Pericchi 1996; Gelman et al. 2008). In our setting, we can easily calculate the Fisher information of the multinomial distribution as
and then the Jeffery prior \(p({\varvec{\theta }}_t):=|J({{\varvec{\theta }}}_t)|=B(\frac{1}{2}{\varvec{e}})^{-1}\prod _{j=1}^{n}{\theta }_{t,j}^{-1/2}\) becomes a Dirichlet prior distribution with the parameter chosen as \(\tau _{t}'=\frac{1}{2}{\varvec{e}}\). Other ways of selecting a priori parameters \(\tau _t'\) in the literature are described in Gelman et al. (1995). In this article, a parameter setting that does not contain specific preferences is referred to as the uninformative case; otherwise, it is referred to as the informative case.
Therefore, choosing Dirichlet distribution as the prior can not only simplify the calculation and lead to a closed-form posterior distribution, but also reflect various generalized prior knowledge through the different selections of parameter \(\tau _t'\). With this selection of prior distribution, we will then consider the construction of confidence region in combination with Bayesian analysis. As discussed in Gelman et al. (1995), we can obtain the following approximation:
where \(I({\varvec{\theta }}_t)\) is the observed information matrix
With the update (4) of the posterior distribution \( p({\varvec{\theta }}_t|{{\mathcal {S}}_t})\) with respect to the corresponding sample set \({{\mathcal {S}}_t}\), the posterior \({\hat{{\varvec{\theta }}}_t}\) and the observed information matrix can be easily calculated as
and
Combining (6) and (7) with (5), we can deduce an approximation posterior pdf for \(\theta _{t,j}\) as
Moreover, by setting \(\alpha '=1-\root n \of {1-\alpha }\) and defining \(z_{1-\frac{\alpha '}{2}}\) as the \({1-\frac{\alpha '}{2}}\) quantile of the standard normal distribution, we can specify the Bayesian confidence region for \({\varvec{\theta }}_t\) as follows:
This configuration results in a \((1 - \alpha )\)-confidence set of \({\mathbb {P}}_{{\varvec{\theta }}^c}\) with respect to the posterior distribution \({\mathbb {P}}_{{\mathcal {S}}_t}\). Specifically, we have
Following this demonstration, we can define a well-founded ambiguity set \({\mathcal {P}}_t\) in a Bayesian framework as follows, which will be utilized in subsequent sections:
We introduce \(r_{t,j}:=\frac{{\hat{\theta }}_{t,j}z_{1-\frac{\alpha '}{2}}}{(\tau _{t,j}-1)^{1/2}}\) and \(r_t:=\otimes _{j=1}^nr_{t,j}\) to ease notation. What’s more, we use \({\mathcal {B}}(\hat{{\varvec{\theta }}}_t,r_t):=\Theta _{t}({{\mathcal {S}}_t},\alpha )\) to show that the uncertainty set is a ball with center \(\hat{{\varvec{\theta }}}_t\), which will be used in Sect. 3.
Remark 1
Since the observed information in (7) is a diagonal matrix w.r.t. \({\mathbb {P}}_{{\mathcal {S}}_t}\), we have \({\mathbb {P}}_{{\mathcal {S}}_t}\left( \theta _{t,j}\text { is accepted at level }\alpha '\text { for all }j =1,\cdots ,n\right) =\prod _{j=1}^n(1-\alpha ')= 1-\alpha \) by independence. Thus the multivariate confidence region \(\Theta _{t}({{\mathcal {S}}_t},\alpha )\) defined in (8), which rejects if \({\theta }_{t,j}\) doesn’t belong to the univariate confidence region at level \(\alpha '\) for all \(j=1,\cdots ,n\), is a valid confidence region. Moreover, the confidence region (8) indicates that we will wrongly reject \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\in \{{\mathbb {P}}_{{\varvec{\theta }}_t}|{\varvec{\theta }}_t\in {\bar{\Theta }}_t({{\mathcal {S}}_t},\alpha )\}\) w.r.t. \({{\mathcal {S}}_t}\) with probability at most \(\alpha \).
2.2 Comparation with typical ambiguity sets
In Sect. 2.1, we introduced a data-driven method to create the confidence region (8), thus \({\mathcal {P}}_{\Theta _{t}({{\mathcal {S}}_t},\alpha )}\) as the ambiguity set of the underlying distribution \({\mathbb {P}}_t^c\) from a Bayesian perspective. This ambiguity set covers the true distribution with probability \(1-\alpha \) under repeated sampling with any fixed true \({\varvec{\theta }}_t^c\). To demonstrate the superiority of the proposed sets, we compare them with the ambiguity sets constructed by different statistical methods, e.g., \(\phi \)-divergence in Philpott et al. (2018) and \(L_\infty \) norm in Jiang and Guan (2018), which are frequently used in MDRO studies.
Firstly, we consider three types of distances in terms of \(\phi \)-divergence, namely variation distance, Hellinger distance, and modified \(\chi ^2\) distance, to construct the ambiguity set as follows,
Here \(\chi ^2_{n,1-\alpha }\) represents the \(100(1 - \alpha )\%\) percentile of the \(\chi ^2_{n}\) distribution with n degrees of freedom. These ambiguity sets, with respect to the fixed true \({\varvec{\theta }}_t^c\), can all cover the true distribution with probability \(1-\alpha \).
As an example, let us consider the case where 100 experiments are performed on the binomial distribution B(0.4, 0.6) with 45 and 55 occurrences of the two scenarios, respectively. When constructing ambiguity sets for this instance using variation distance (blue ones), Hellinger distance (black ones) and modified \(\chi ^2\) distance (green ones), respectively, the nominal distributions \({\hat{\theta }}_{t,j}\) are all empirical distributions estimated using maximum likelihood estimation. In contrast, the nominal distributions \({\hat{\theta }}_{t,j}\) in the Bayesian framework (8) are the modes of the maximum posterior distribution. To ensure a fair comparison, we set the Bayesian prior parameter \(\tau _{t,j}'=1\) for \(j=1,2\), which ensures that the distribution corresponding to the maximum a posteriori estimate is an empirical distribution. The corresponding ambiguity set (red ones) is constructed under the uninformative prior. Furthermore, we consider the Bayesian-type ambiguity set constructed with an informative prior (yellow ones), at which the Bayesian prior parameters are set as \(\tau _{t,1}'=400\) and \(\tau _{t,2}'=600\). The ambiguity sets constructed by different methods at the same confidence level \(\alpha =10\%\) are depicted in Fig. 1. At the same confidence level \(\alpha \), the ambiguity sets induced by different distances and our Bayesian methods have different shapes and sizes. It can be observed from Fig. 1 that the ambiguity sets constructed using Bayesian methods tend to be smaller than most of those constructed using classical statistical methods. In other words, our Bayesian-type MDRO approach would be helpful for alleviating the overly conservative issue in current MDRO approaches. Furthermore, the traditional statistical and uninformative Bayesian methods cannot incorporate prior knowledge of the true distribution into the constructed ambiguity sets, which results in the centers of the ambiguity sets tending to be the empirical distribution, i.e., \(\hat{{\varvec{\theta }}}_t=(0.45,0.55)\). On the other hand, the Bayesian-type ambiguity set that incorporates prior knowledge can be adjusted through the prior parameter \(\tau _{t}'\), resulting in the center \(\hat{{\varvec{\theta }}}_t=(0.405,0.595)\) of the distribution becoming much closer to the true distribution \({\varvec{\theta }}^c_t=(0.4,0.6)\) with the same data. These observations suggest that the Bayesian-type ambiguity set, especially when combined with prior information, can significantly reduce the random perturbation and improve the robustness and performance in the small sample case.
Furthermore, the Bayesian-type ambiguity set (8) can be treated as a generalization of the following ambiguity set corresponding to the \(L_\infty \) norm in Jiang and Guan (2018),
This ambiguity set can also cover the true distribution with probability \(1-\alpha \). Since \(\Theta ^{L_\infty }_{t}({{\mathcal {S}}_t},\alpha )\) has the same shape as \(\Theta _{t}({{\mathcal {S}}_t},\alpha )\), we now construct a more complex example to further demonstrate the superiority of the Bayesian-type ambiguity set.
In this example, we consider 500 experiments on the multinomial distribution M(0.2,0.2,0.1,0.5) with 110, 100, 40 and 250 occurrences of the four cases, respectively. To ensure a fair comparison with the \(L_\infty \) norm ambiguity set (blue ones), we similarly set the Bayesian prior parameters as \(\tau _{t,j}'=1\) for all \(j=1,2,3,4\), which ensures that the distribution corresponding to the maximum a posteriori estimate is an empirical distribution. The corresponding ambiguity set (red ones) is constructed under the uninformative prior. Furthermore, we consider the Bayesian-type ambiguity set constructed with an informative prior (yellow ones), at which the Bayesian prior parameters are set as \(\tau _{t,1}'=200\), \(\tau _{t,2}'=200\), \(\tau _{t,3}'=100\), \(\tau _{t,4}'=500\), respectively. The ambiguity sets constructed by different methods at the same confidence level \(\alpha =10\%\) are shown in Fig. 2. For pictorial purpose, we plot here the results w.r.t. \({\theta }_1\) and \({\theta }_{2}\) (the left figure), \({\theta }_3\) and \({\theta }_{4}\) (the right figure), respectively. All the observations from Fig. 1 are applicable to Fig. 2. What’s more, Fig. 2 further shows that the ambiguity set constructed by the \(L_\infty \) norm needs to ensure that the radius of each dimension is less than an identical value, resulting in over-conservative probability sets for the remaining dimensions except for the dimension at which the maximum arrives. On the contrary, the Bayesian-type ambiguity set can utilize the data to adaptively choose the corresponding radiuses for individual dimensions, overcoming the over-conservation of the \(L_\infty \) norm method.
In conclusion, the proposed Bayesian-type ambiguity sets are more accurate and optimistic than existent ambiguity sets in describing the profile of the ambiguous probability distributions, with or without prior knowledge. Furthermore, when there is prior information, employing appropriate prior parameters can further improve the performance of the derived Bayesian-type ambiguity set.
3 Reformulation and asymptotic analyses
Based on the general framework of the MDRO problem in (2) and the introduced Bayesian-type ambiguity set (8), we can now propose a new kind of models, called the Bayesian-type MDRO problem, as follows:
After deriving a reformulation of (10) in the form of RMSP, we will carry out a series of theoretical investigations in order to lay a solid foundation for our Bayesian-type MDRO model.
3.1 Equivalent reformulation
As the data process \(\{\xi _{t}\}\) is stage-wise independent, we can easily derive the corresponding dynamic programming equation to the nested formulation (10). Let \(Q_T(x_{T-1}, \xi _T)\) denote the optimal value function of the final stage problem:
Then the optimal value function \(Q_{t}(x_{t-1}, \xi _{t})\), called the recourse function as that in MSPs, for stage \(2\le t\le T\) can be recursively defined as:
Moreover, the optimal value of the first stage problem is defined as follows:
Recently, a few studies (e.g., Philpott et al. 2018; Pichler and Shapiro 2021) have revealed the equivalence between the worst-case value function (11) and the minimization of a coherent risk measure under certain regularity conditions. Inspired by these works, we derive an equivalent reformulation of (11) as an RMSP problem.
Our analysis relies on the following basic assumption.
Assumption 1
The Bayesian-type MDRO problem satisfies the relatively complete recourse.
The relatively complete recourse here has the same meaning as that for usual MSPs. This assumption has been widely adopted in the literature about theoretical studies of MSP and its variants, for example in Jiang and Guan (2018). Moreover, it is worth noting that the support set \(\Xi _t\) of \(\xi _t\) is always bounded owning to our construction skill of \({\mathbb {P}}_{{\varvec{\theta }}_t}\), making Assumption 1 a natural assumption. With this, the compactness assumption about stage-wise feasible regions and the continuity assumption about stage-wise objective functions, the boundness of the recourse function holds easily, i.e., \(\sup _{\xi _t\in \Xi _t}|Q_{t+1}(x_{t}, \xi _{t+1})|<\infty \) for all \(x_{t}\in {\mathcal {X}}_t\), \(2\le t\le T\).
In order to derive the reformulation of the Bayesian-type MDRO (10), we first consider the lower and upper bounds of the uncertainty set for stage t, which are respectively denoted as
Moreover, we introduce \({\varvec{\theta }}_t^{u-l}:={\varvec{\theta }}_t^{u}-{\varvec{\theta }}_t^{l}\) to ease notation.
The following theorem resembles Theorem 6 in Jiang and Guan (2018) and generalizes it to the parametric setting. Specifically, it proposes a reformulation which transforms the Bayesian-type MDRO problem (11) into an RMSP with the risk function being a convex combination of an expected cost and a CVaR.
Theorem 1
Let \({\mathbb {P}}_{{\varvec{\theta }}_t^l}\) and \({\mathbb {P}}_{{\varvec{\theta }}_t^{u-l}}\) denote the probability measures induced by \({\varvec{\theta }}^l\) and \({\varvec{\theta }}^{u-l}\) as
Here \(P_{{\varvec{\theta }}_{t}^l}:=\sum _{j=1}^n\theta _{t,j}^l\in (0,1)\) and \(P_{{\varvec{\theta }}_{t}^{u}}:=\sum _{j=1}^n\theta _{t,j}^u>1\). Then for any fixed \(x_{t-1}\), the worst-case expected recourse function at stage t can be reformulated as follows:
Proof
Without loss of generality, we assume that \(Q_t(x_{t-1}, \xi _t^i)\le Q_t(x_{t-1}, \xi _t^j)\) for all \(i\le j\) and \(i,j \in \{1,\cdots ,n\}\). With the discrete distribution assumption of the data process, \(\sup _{{\varvec{\theta }}_t\in \Theta _{t}({\mathcal {S}}_t,\alpha )}{\mathbb {E}}_{{\mathbb {P}}_{{\varvec{\theta }}_t}}\left[ Q_t(x_{t-1}, \xi _t)\right] \) is equal to the optimal value of the following optimization problem:
where \({\varvec{\theta }}_t\in \Theta _{t}({\mathcal {S}}_t,\alpha )\) is reflected by the constraints in (13). The Lagrangian dual function corresponding to problem (13) can be expressed as follows:
where \(z_u\), \(z_l\) and \(z_0\) are the dual variables corresponding to the boundedness constraints and the equality constraint, respectively. Thus we have
where \(j^*:= \sup \{j\in \{1,\cdots ,n\}:Q_t(x_{t-1},\xi _t^j)<z_0 \}\) if \(Q_t(x_{t-1},\xi _t^1)<z_0 \), and \(j^ *:= 0\) if \(Q_t(x_{t-1},\xi _t^1)\ge z_0 \). The proof completes with the definition of CVaR. \(\square \)
Based on Theorem 1, the cost-to-go function \({\mathcal {Q}}_T(x_{T-1})\) defined as the distributionally robust problem \(\sup _{{\varvec{\theta }}_T\in \Theta _{T}({\mathcal {S}}_T,\alpha )}{\mathbb {E}}_{{\varvec{\theta }}_T}Q_T(x_{T-1}, \xi _T)\) can be reformulated to a risk-averse stochastic programming problem as a convex combination of a CVaR and an expectation:
Backward to stage \(T-1\), we can obtain the reformulation of \(Q_{T-1}(x_{T-2}, \xi _{T-1})\) by substituting (14) into (11). Repeating this process for each stage, the dynamic programming equations can be rewritten as:
where \({\mathcal {Q}}_{t+1}(x_{t},z_{t})\) is defined as
for \(t=1,\cdots ,T-1\).
Finally, the Bayesian-type MDRO at the first stage can be reformulated as:
3.2 Consistency analysis
As we know, the original motivation of MDRO is to cope with the ambiguity about stage-wise distributions. With the accumulation of information or data, we hope that the stage-wise ambiguity sets become more and more accurate, typically smaller and smaller in terms of their sizes. Ideally, we want to recover the solution of the original MSP through solving a sequence of MDROs. This is exactly what we discuss in this subsection. We demonstrate the consistency of the Bayesian-type MDRO model (10) as the data size N increases to infinity. Our analysis reveals that, as the data size used to construct the ambiguity set at each stage approaches infinity, the optimal objective values and solution sets of Bayesian-type MDRO problems converge to the corresponding optimal value and solutions of the original MSP under the true but unknown distributions.
Recall that with our Bayesian perspective, the nested formulation of traditional MSPs (1) can be rewritten as:
Similar to that of the Bayesian-type MDRO problem, we can derive the dynamic programming equations for problem (17) by utilizing the inter-stage independence of the data process. We define \(Q_T^c(x_{T-1}, \xi _T)\) as the optimal value of the final stage problem:
The optimal value or recurse function \(Q^c_{t}(x_{t-1}, \xi _{t})\) for stage \(t\ge 2\) is determined as
and the optimal value of the first stage problem is determined as follows:
Let \(r_{t,j}:=r_{t,j}(N)\) represent that \(r_{t,j}\) is a function of the data size N. And “w.p.1" stands for “with probability one" with respect to the probability measure \({\mathbb {P}}_{{\varvec{\theta }}_t^c}^\infty :={\mathbb {P}}_{{\varvec{\theta }}_t^c}\times {\mathbb {P}}_{{\varvec{\theta }}_t^c}\cdots \) throughout our discussion. First of all, we present propositions that will be needed to prove the convergence conclusion. These propositions indicate \(r_{t,j}(N)\rightarrow 0\) as \(N\rightarrow \infty \) for \(t=2,\cdots ,T\), based on the ambiguity set construction described in Sect. 2.2.
Proposition 2
For any \(\alpha \in (0,1)\), \(r_{t,j}(N)\) converges to zero and \(\hat{{\varvec{\theta }}}_{t}\) converges to the true parameter \({\varvec{\theta }}_{t}^c\) in probability \({\mathbb {P}}_{{\mathcal {S}}_t}\) for \(t=2,\cdots ,T\) w.p.1.
Proof
Based on the construction of Bayesian confidence region (8), the convergence of \(r_{t,j}(N)\rightarrow 0\) is obvious as the sample size \(N\rightarrow \infty \). Moreover, it is easy to see that \(\Theta _{t}\) is a convex and compact set with nonempty interior and \(\ln p({\varvec{\theta }}_{t})\) is bounded on \(\Theta _{t}\) due to its continuity w.r.t. \({\varvec{\theta }}_{t}\). Then, we can deduce from Theorem 2.5 in Chen et al. (2023) that the distance from \({\varvec{\theta }}_{t}\) to the true parameter \({\varvec{\theta }}_{t}^c\) converges in probability \({\mathbb {P}}_{{\mathcal {S}}_t}\) to zero for \(t=2,\cdots ,T\) w.p.1. \(\square \)
Proposition 3
Under Assumption 1, the expectation function \({\mathbb {E}}_{{{\mathbb {P}}_{{\varvec{\theta }}_{t+1}}}}\big [Q_{t+1}(x_{t}, \xi _{t+1})-z_{t}\big ]^+\) is continuous w.r.t. \((x_{t},z_t)\in {\mathcal {X}}_t\times {\mathbb {R}}\), for \(t=1,\cdots ,T-1\) and fixed \({\varvec{\theta }}_{t+1}\).
Proof
The proof is by mathematical induction on t.
For any given point \(({\bar{x}}_{T-1},{\bar{z}}_{T-1})\in {\mathcal {X}}_{T-1}\times {\mathbb {R}}\), consider the sequence \(\{(x_{T-1}^i),z_{T-1}^i\}_{i\in {\mathbb {N}}}\) that converges to \(({\bar{x}}_{T-1},{\bar{z}}_{T-1})\). Since \(Q_T(x_{T-1}, \xi _T)\) is convex and continuous in \(x_{T-1}\) on \({\mathcal {X}}_{T-1}\) as shown in Shapiro et al. (2014), it is obvious that \((Q_{T}(x_{T-1}, \xi _{T})-z_{T-1})^+\) is convex and continuous on \({\mathcal {X}}_{T-1}\times {\mathbb {R}}\) for fixed \(\xi _{T}\in \Xi _T\). Therefore,
Based on Assumption 1, there exists an \(M\in {\mathbb {R}}^+\) such that \((Q_{T}(x_{T-1}^i, \xi _{T})-z^i_{T-1}(\xi _{T-1}))^+\le M\) for each \(i\in {\mathbb {N}}\) and each \(\xi _{T}\in \Xi _T\). We can now interchange the limitation and expectation and obtain
which is induced by the dominated convergence theorem. Therefore we have proved the proposition for stage T.
Assuming that the conclusion holds for stage \(t + 1,\cdots ,T - 1\), we now show that it also holds for t. Consider the cost-to-go function \({\mathcal {Q}}_{t+1}(x_{t},z_{t})\) defined as
We deduce that \({\mathcal {Q}}_{t+1}(x_{t},z_{t})\) is convex and continuous in \(x_{t}\) on \({\mathcal {X}}_{t}\) and so is \(Q_{t}(x_{t-1}, \xi _{t})\). Then we have \((Q_{t}(x_{t-1}, \xi _{t})-z_{t-1}(\xi _{t-1}))^+\) is convex and continuous in \({\mathcal {X}}_{t-1}\times {\mathbb {R}}\) as well. The rest of the proof is parallel to that for stage T.
Thus, by the principle of mathematical induction, we have completed the proof. \(\square \)
To demonstrate the convergence property, we will use the notations \(u_t(r_{[t+1]})\) and \(U_t(r_{[t+1]})\) to denote the optimal objective value and the optimal solution set for the induced stage t problem of the Bayesian-type MDRO with respect to the ambiguity set \(\Theta _{t}({\mathcal {S}}_t,\alpha )\), where \(r_{[t+1]}=\max _{i=t+1}^T\max _{j=1}^nr_{i,j}\). Concretely, they can be determined as:
Similarly, we use \(u_t(0)\) and \(U_t(0)\) to denote the optimal objective value and the optimal solution set of the induced stage t problem of the MSP with respect to the true underlying distribution \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\). Specifically,
To describe the convergence of optimal solution sets, we need the following definitions.
Definition 1
(Xu and Zhang 2021) For two sets \(S_1, S_2 \subset X\), we define the deviation of \(S_1\) from \(S_2\) under the metric d, denoted by \({\mathbb {D}}\left( S_1, S_2 \right) \), as
where \(d\left( x, S_2\right) :=\inf _{y\in S_2}||x-y||\) and \(||\cdot ||\) denotes an arbitrary norm. Moreover, the Hausdorff distance between \(S_1\) and \(S_2\) is defined as \({\mathbb {H}}\left( S_1, S_2 \right) :=\max \left\{ {\mathbb {D}}\left( S_1, S_2 \right) , {\mathbb {D}}\left( S_2, S_1\right) \right\} \).
With the above definition, we can now state the main results as follows.
Theorem 4
For all \(1\le t\le T-1\) and under Assumption 1, as the data size N tends to \(\infty \), we have \(r_{[t+1]}\rightarrow 0\), and \(u_t(r_{[t+1]})\rightarrow u_t(0)\) in probability \({\mathbb {P}}_{{\mathcal {S}}_t}\) w.p.1. Furthermore, \(U_t(r_{[t+1]})\) converges to \(U_t(0)\) in probability \({\mathbb {P}}_{{\mathcal {S}}_t}\) w.p.1, in the sense that \(\lim _{N\rightarrow \infty }{\mathbb {D}}(U_t(r_{[t+1]}),U_t(0))=0\).
Proof
The conclusion \(r_{t+1,j}\rightarrow 0\) as \(N\rightarrow \infty \) can be easily established using Proposition 2. Therefore, we can interchange \(N\rightarrow \infty \) and \(\max _j r_{t+1,j}\rightarrow 0\) for all \(t\ge 1\) in our proof.
Firstly, we prove the convergence for stage T. By Lemma 5 in Jiang and Guan (2018), we can specifically denote the objective function of the Bayesian-type MDRO problem at stage \(T-1\) with \(r_{[T]}\) and MSP w.r.t. \({\mathbb {P}}_{{\varvec{\theta }}_{T}^c}\) by \({\hat{g}}_{T-1}(x_{T-1},z_{T-1},r_{[T]})\) and \(g_{T-1}^c(x_{T-1},z_{T-1})\), respectively. Concretely,
With the continuity of \({\mathbb {E}}_{{\mathbb {P}}_{{\varvec{\theta }}_{T}}}\left[ Q_{T}(x_{T-1}, \xi _{T})-z_{T-1}\right] ^+\) in \((x_{T-1},z_{T-1})\) on \({\mathcal {X}}_{T-1} \times {\mathbb {R}}\), which has been proved in Proposition 3, the objective function \(g_{T-1}^c(x_{T-1},z_{T-1})\) of MSP is also continuous in \((x_{T-1},z_{T-1})\) on \({\mathcal {X}}_{T-1} \times {\mathbb {R}}\). Thus for any \(\epsilon >0\), we can find an open neighborhood \(B_1({\bar{x}}_{T-1},{\bar{z}}_{T-1})\) such that
Similarly, as \({\hat{g}}_{T-1}(x_{T-1},z_{T-1},r_{[T]})\) is continuous in \((x_{T-1},z_{T-1})\) on \({\mathcal {X}}_{T-1} \times {\mathbb {R}}\), we can find an open neighborhood \(B_2({\bar{x}}_{T-1},{\bar{z}}_{T-1})\) such that
Defining
for all \(({\bar{x}}_{T-1},{\bar{z}}_{T-1})\in {\mathcal {X}}_{T-1} \times {\mathbb {R}}\) gives us that
and
Moreover, since the sequence \(\{{\hat{\theta }}_{T,j}\}\) converges to \(\theta ^c_{T,j}\) and \(\{r_{T,j}\}\) converges to 0 for \(j=1,\cdots ,n\), we have
which tends to 0 as N increases to infinity for each \({\bar{\xi }}_{T}\). Thus the cumulative density function (cdf) \(F_{{\varvec{\theta }}_{T}^l}({\bar{\xi }}_{T})\) converges to the true cdf \(F_{{\varvec{\theta }}_{T}^c}({\bar{\xi }}_{T})\). And we can get
It is easy to see that \(P_{{\varvec{\theta }}_{T}^l}\rightarrow 1\) and \(P_{{\varvec{\theta }}_{T}^u}-P_{{\varvec{\theta }}_{T}^l}\rightarrow 0\) as \(N\rightarrow \infty \) by definition. Then with Lemma 5 in Jiang and Guan (2018), we have
for all \(({\bar{x}}_{T-1},{\bar{z}}_{T-1})\in {\mathcal {X}}_{T-1} \times {\mathbb {R}}\). Therefore, there exists a \({\bar{r}}_{[T]}({\bar{x}}_{T-1},{\bar{z}}_{T-1})>0\) such that
Remind that \({\mathcal {X}}_{T-1}\) is compact, we can define \({\underline{M}}_t:=\min _{x_t\in {\mathcal {X}}_t,\xi _{t+1}\in \Xi _{t+1}}Q_{t+1}(x_{t}, \xi _{t+1})>-\infty \) and \({\overline{M}}_t:=\sup _{x_t\in {\mathcal {X}}_t,\xi _{t+1}\in \Xi _{t+1}}Q_{t+1}(x_{t}, \xi _{t+1})<+\infty \) due to Assumption 1. It can then be deduced that \(z_{T-1}\in [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) for both MSP and Bayesian-type MDRO problems. Due to the compactness of \({\mathcal {X}}_{T-1}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\), we can find a finite set of points \(({\bar{x}}_{T-1}^m,{\bar{z}}_{T-1}^m) \) such that
This means that for any \((x_{T-1},z_{T-1})\in {\mathcal {X}}_{T-1}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\), one can find an \(m'\in \{1,\cdots ,M\}\) such that \((x_{T-1},z_{T-1})\in B({\bar{x}}_{T-1}^{m'},{\bar{z}}_{T-1}^{m'})\).
By the finite coverage shown in (18), there exists a finite positive lower bound \({\bar{r}}_{[T]}=\min _{m=1,\cdots ,M}{\bar{r}}_{[T]}({\bar{x}}^m_{T-1},{\bar{z}}^m_{T-1})\). Consequently, we have
for all \((x_{T-1},z_{T-1})\in {\mathcal {X}}_{T-1}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) and \(r_{[T]}\in [0,{\bar{r}}_{[T]}]\). Therefore we have proved that \({\hat{g}}_{T-1}(x_{T-1},z_{T-1},r_{[T]})\) uniformly converges to \(g_{T-1}^c(x_{T-1},z_{T-1})\) in probability \({\mathbb {P}}_{{\mathcal {S}}_{T-1}}\) on \({\mathcal {X}}_{T-1}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) as N tends to infinty.
Denote \((x_{T-1}^*(r_{[T]}),z_{T-1}^*(r_{[T]}))\) as an optimal solution to the stage T problem of Bayesian-type MDRO, and \((x_{T-1}^*(0),z_{T-1}^*(0))\) as an optimal solution to that of MSP, respectively. We have
and
for all \(r_{[T]}\in [0,{\bar{r}}_{[T]}]\). Thus we have proven that \(u_{T-1}(r_{[T]})\) converges to \(u_{T-1}(0)\).
Assume that the convergence property of the optimal value function is true for \(t + 1,\cdots ,T - 1\). We now show that it also holds for t.
Let \({\hat{g}}_{t-1}(x_{t-1},z_{t-1},r_{[t]})\) represent the objective function of the Bayesian-type MDRO problem at stage \(t-1\) w.r.t. \(r_{[t]}\), i.e.,
and we denote the objective function of MSP at stage \(t-1\) w.r.t. \({\mathbb {P}}_{{\varvec{\theta }}_{t}^c}\) as \(g_{t-1}^c(x_{t-1},z_{t-1})\), i.e.,
Similarly, since \(\{\hat{{\theta }}_{t,j}\}\) converges to \(\theta ^c_{t,j}\) and \(\{r_{[t]}\}\) converges to 0 as \(N\rightarrow \infty \) for \(j=1,\cdots ,n\), we can deduce that for any \(\delta >0\), there exists an N large enough such that
and hence we have
Similarly, it is easy to see that \(P_{{\varvec{\theta }}_{t}^l}\rightarrow 1\) and \(P_{{\varvec{\theta }}_{t}^u}-P_{{\varvec{\theta }}_{t}^l}\rightarrow 0\) as N tends to infinity. Then we have
for all \(({\bar{x}}_{t-1},{\bar{z}}_{t-1})\in {\mathcal {X}}_{t-1} \times {\mathbb {R}}\). Therefore, there exists a \({\bar{r}}_{t}({\bar{x}}_{t-1},{\bar{z}}_{t-1})>0\) such that
Moreover, due to the continuity of \({\hat{g}}_{t-1}({x}_{t-1},{z}_{t-1},r_{[t]})\) and \(g_{t-1}^c({x}_{t-1},{z}_{t-1})\) in \((x_{t-1},z_{t-1})\) on \({\mathcal {X}}_{t-1} \times {\mathbb {R}}\), we can similarly prove that \({\hat{g}}_{t-1}(x_{t-1},z_{t-1},r_{[t]})\) uniformly converges to \(g_{t-1}^c(x_{t-1},z_{t-1})\) in probability \({\mathbb {P}}_{{\mathcal {S}}_{t-1}}\) on \({\mathcal {X}}_{t-1}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) as N tends to infinity. Consequently, we complete the proof about the convergence property of the optimal value function at each stage by the principle of mathematical induction.
With the consistency of the optimal value function at each stage, we then establish the consistency of the optimal solution set, that is, \( \lim _{N\rightarrow \infty }{\mathbb {D}}\left( U_t(r_{[t+1]}),U_t(0)\right) =0\).
Suppose that for some stage t, the convergence property for the optimal solution set does not hold. We can then find an \(\epsilon _0>0\), a positive sequence \(\{r_{[t+1]}^m \}_{m\in {\mathbb {N}}}\) which converges to 0, and a sequence \(\{(x_{t}^m,z_{t}^m)\}\) in \({\mathcal {X}}_{t}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) with \((x_{t}^m,z_{t}^m)\in U_t(r_{[t+1]}^m)\), such that \(d((x_{t}^m,z_{t}^m),U_t(0))>\epsilon _0\) for all \(m\in {\mathbb {N}}\). Therefore, there exist a vector \(({\bar{x}}_{t},{\bar{z}}_{t})\in {\mathcal {X}}_{t}\times [{\underline{M}}_{T-1},{\overline{M}}_{T-1}]\) and a set \({\mathbb {N}}_1\subseteq {\mathbb {N}}\) such that \(\{(x_{t}^{m_1},z_{t}^{m_1})\}_{m_1\in {\mathbb {N}}_1}\) converges to \(({\bar{x}}_{t},{\bar{z}}_{t})\) using the Bolzano-Weierstrass theorem. Based on continuity of \({\hat{g}}_{t}\) and (19), we have
It is obvious that \(\lim _{m_1\rightarrow \infty }{\hat{g}}_{t}({\bar{x}}_{t}^{m_1},{\bar{z}}_{t}^{m_1},r_{[t+1]}^{m_1})=u_t(0)\) since \(\lim _{r_{[t+1]}\rightarrow 0} u_t(r_{[t+1]}) = u_t(0)\) and \(\{(x_{t}^m,z_{t}^m)\}\in U_t(r_{[t+1]}^n)\). Then we obtain
which means that \(({\bar{x}}_{t},{\bar{z}}_{t})\in U_t(0)\). Therefore, we have \(d(({\bar{x}}_{t},{\bar{z}}_{t}), U_t(0))=0\). This contradicts the assumption \(d(({\bar{x}}_{t},{\bar{z}}_{t}), U_t(0))\ge \epsilon _0>0\), which completes the proof for any \(t=2,\cdots ,T\). \(\square \)
Theorem 4 demonstrates the convergence of the proposed Bayesian-type MDRO model in terms of the uncertainty set \(\Theta _{t}({\mathcal {S}}_t,\alpha )\) we construct. An important implication of this theorem is that the optimal value and optimal solution got with the Bayesian-type MDRO model will overcome the over-conservativeness of current MDRO models and converge to the optimal value and optimal solution of the original MSP when the amount of available data tends to infinity. Although this result is critical for understanding the asymptotic behavior of the Bayesian-type MDRO model, it does not provide our method’s performance in finite sample settings. Therefore, in the next subsection, we focus on the finite sample properties of the proposed Bayesian-type MDRO model.
3.3 Finite-sample performance guarantee
In many practical problems (e.g., machine learning in Chernozhukov et al. (2023)), one often needs to deal with datasets of finite size. Finite sample guarantee provides statistical assurance that the optimization problem will yield a solution that is close to the true solution with high probability. Existing studies have mainly focused on finite sample guarantee for single-stage DROs (see, e.g., Bertsimas et al. 2018; Gao 2022; Esfahani and Kuhn 2018). It is crucial to extend these guarantees to MDRO problems, especially the Bayesian-type MDRO problem in order to ensure optimal performance when we deal with complex dynamic decision-making problems under distribution ambiguity.
In this subsection, we examine how Bayesian confidence regions affect the finite sample performance of Bayesian-type MDROs. We define the true cost of the Bayesian-type MDRO solution for stage t as:
Here \({\bar{x}}_i\) denotes the Bayesian-type MDRO solution at stage i based on the given sample set \({\mathcal {S}}_{i+1}\), that is,
Theorem 5
With respect to the finite sample sets \({{\mathcal {S}}_{2}},\cdots ,{{\mathcal {S}}_{T}}\), we have
where \({\mathbb {P}}_{\otimes _{t=2}^T{\mathcal {S}}_{t}}\) is the joint distribution of posterior distributions \({\mathbb {P}}_{{\mathcal {S}}_{2}},\cdots ,{\mathbb {P}}_{{\mathcal {S}}_{T}}\).
Proof
Suppose \({\varvec{\theta }}^c_{T}\in \Theta _{T}({\mathcal {S}}_{T},\alpha )\), we can deduce that
for all \(x_{T-1}\). Therefore, we have \(u_{T-1}(r_{T}) \ge {\bar{u}}_{T-1}(0)\). In terms of probabilities, this implies
As the inequality
holds for each stage t, the proof can be deduced by recursion. \(\square \)
Remark 2
Theorem 5 tells us that, for any fixed level \(\epsilon \), by setting the degree of credibility to \(\alpha =1-\root T-1 \of {1-\epsilon }\), the Bayesian-type MDRO optimal value \(u_1(r_{[2]})\) and the true cost of the Bayesian-type solution \({\bar{u}}_1(0)\) will satisfy \(u_1(r_{[2]})\ge {\bar{u}}_1(0)\) with probability at least \(1-\epsilon \) with respect to the data sampling process \({{\mathcal {S}}_{2}},\cdots ,{{\mathcal {S}}_{T}}\). This conclusion holds for any optimal policy \(({\bar{x}}_1,\cdots ,{\bar{x}}_T)\) to the Bayesian-type MDRO problem (10).
The statistical property in Theorem 5 explicitly establishes a connection between the objective performance of the corresponding MDRO decision and that of the original MSP problem under full information.
3.4 Quantitative statistical robustness.
The previous studies rely on an assumption that the Bayesian-type ambiguity set is constructed with samples at individual stages without any noise. Based on this assumption, it has been demonstrated that as the number N of samples approaches infinity, the optimal value and solution of the Bayesian-type MDRO problem converge to those of the original MSP under the true probability distribution \({\mathbb {P}}_{{\varvec{\theta }}_t^c}\). However, as pointed out in quite a few studies like Pichler and Xu (2022) and Xu and Zhang (2021), sample data may potentially be contaminated or corrupted. Thus, in this part, our focus shifts towards investigating the potential impact of data contamination on the construction of the ambiguity sets at individual stages. The central issue we address is whether we can still rely on the optimal values and solutions obtained through solving Bayesian-type MDRO problems when the data is contaminated.
To be more specific, we no longer assume that the independently and identically distributed (iid) samples \(\xi ^1_t, \cdots , \xi ^N_t\) are generated by the true distribution \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\). In practice, it is possible to obtain \(\vec {\xi }_{t}:=(\xi ^1_t, \cdots , \xi ^N_t)\) from another distribution that may be potentially contaminated by noise. This distribution, denoted as \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\), generates perceived data \({\tilde{\xi }}^1_t, \cdots , {\tilde{\xi }}^N_t\) that contain noise. We treat \({\tilde{\xi }}^1_t, \cdots , {\tilde{\xi }}^N_t\) as samples perturbed from \(\xi ^1_t, \cdots , \xi ^N_t\), and view \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\) as a perturbation of \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\). For ease of discussion, we assume that \({\tilde{\xi }}^1, \cdots , {\tilde{\xi }}^N\) are also iid samples as that in Pichler and Xu (2022) and Xu and Zhang (2021). The empirical distributions with respect to \(\vec {\xi }_{t}\) and \(\vec {{\tilde{\xi }}}_t:=({\tilde{\xi }}^1_t, \cdots , {\tilde{\xi }}^N_t)\) are denoted as \({\mathbb {P}}_{t,N}:=\hat{{\varvec{\theta }}_t}(\vec {\xi }_{t})\) and \( {\mathbb {Q}}_{t,N}:=\hat{{\varvec{\theta }}_t}(\vec {{\tilde{\xi }}}_t)\), respectively.
To address the aforementioned issue, we introduce the concept of statistical robustness. We use \(\Xi _t^{\otimes N}\) to represent the Cartesian product of N multiples of \(\Xi _t\), and define the Borel sigma algebra \({\mathcal {B}}\left( \Xi _t^{\otimes N}\right) \) on this product space. The corresponding distribution \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}\) is derived on the space \(\left( \Xi _t^{\otimes N}, {\mathcal {B}}\left( \Xi _t^{\otimes N}\right) \right) \), where each \(\left( \Xi _t, {\mathcal {B}}\left( \Xi _t\right) \right) \) has a marginal distribution \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\), and \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}\) has a marginal distribution \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\). For a given sample size N, we denote the mapping \(T_N:\otimes _{t=2}^T\left( \Xi _t^{\otimes N}\right) \rightarrow {\mathbb {R}}\) as a statistical function. Here, \(T_N\left( \vec {\xi }_{2}, \cdots ,\vec {\xi }_{T}\right) \) indicates that the statistical estimator is determined by the samples \(\vec {\xi }_{2}, \cdots ,\vec {\xi }_{T}\). Our objective is to assess whether \(T_N\left( \vec {{\tilde{\xi }}}_2,\cdots \vec {{\tilde{\xi }}}_T\right) \) is sufficiently close to \(T_N\left( \vec {\xi }_{2}, \cdots ,\vec {\xi }_{T}\right) \) under the data contamination. In other words, when \(T_N\left( \vec {{\tilde{\xi }}}_2,\cdots \vec {{\tilde{\xi }}}_T\right) \) is close to \(T_N\left( \vec {\xi }_{2}, \cdots ,\vec {\xi }_{T}\right) \), it is justifiable to utilize \(T_N\left( \vec {{\tilde{\xi }}}_2,\cdots \vec {{\tilde{\xi }}}_T\right) \) since obtaining pollution-free data \(\{\vec {\xi }_{2}, \cdots ,\vec {\xi }_{T}\}\) practically is never feasible.
Our demonstrations rely on the following definition.
Definition 2
(Römisch (2003)) A metric with \(\zeta \)-structure is defined as follows:
where \({\mathcal {G}}\) represents a family of real-valued measurable functions.
Formulation (20) encompasses a broad spectrum of metrics in probability theory, such as those described by Zolotarev (1983). Specifically, when
the metric \(d_{{\mathcal {G}}}({\mathbb {P}}, {\mathbb {Q}})\) simplifies to the Kantorovich metric, denoted as \(d_{K, k}({\mathbb {P}}, {\mathbb {Q}})\). Here, the subscripts K, k are used to indicate the Kantorovich metric in the set of all probability measures defined over \({\mathbb {R}}^k\).
Let \({\phi _t}: {\mathbb {R}}^{k} \rightarrow [0, \infty )\) be a continuous function and define \({\mathcal {M}}_{k,t}^{\phi _t}\) as the subset of probability measures that satisfy the generalized moment condition of \({\phi _t}\) (one can refer to Xu and Zhang (2021) for details), given by:
The following lemma establishes a relationship between the distances \(d_{\mathcal {G}}\left( {\mathbb {P}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}, {\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}\right) \) and \(d_{K, k}({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}, {\mathbb {Q}}_{{{\varvec{\theta }}}_t^c})\) when \({\mathcal {G}}\) is the set defined in (21).
Lemma 1
Let \(\vec {\xi }:=\left( \vec {\xi }_{2},\cdots , \vec {\xi }_{T}\right) \in \otimes _{t=2}^T\left( \Xi _t^{\otimes N}\right) \) and let \(\psi :\otimes _{t=2}^T\left( \Xi _t^{\otimes N}\right) \rightarrow {\mathbb {R}}\) be a Lipschitz continuous function with a modulus bounded by L/N for a fixed constant \(L>0\). Define \(\Psi \) as the set of such functions:
Then, we have \(d_\Psi \left( \otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}, \otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}\right) \le L d_{K, k}(\otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}, \otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c})\).
Proof
We define \(\left( \vec {\xi }_{2}, \cdots , \vec {\xi }_{T}\right) =(\vec {\xi }^{1},\cdots ,\vec {\xi }^N)^T\) where \(\vec {\xi }^{i}:=(\vec {\xi }_{2,i}, \cdots , \vec {\xi }_{T,i})\) for \(i=1,\cdots ,N\). Since \(\xi _{t}\)s are independent for all stages, the joint distribution of \(\vec {\xi }^{i}\) is \(\otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\) and the same is true when \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\) is replaced by \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\). Therefore, the proof is completed by applying Lemma 2.1 in Xu and Zhang (2021). \(\square \)
With this result, we can establish an upper bound for \(d_\Psi \left( \otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}, \otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}^{\otimes N}\right) \) in terms of \(d_{K, k}(\otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}, \otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c})\).
Theorem 6
(Quantitative statistical robustness) Assume that for any N, we have
Let \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c},\ {\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\in {\mathcal {M}}_{k,t}^{\phi _t},\ 2\le t\le T\), where \({\phi _t}(y):=\Vert y\Vert , y \in \Xi _t\). Then
for any sample size N.
Proof
With the definition (20), we have that
Here \({\mathcal {G}}_L\) is defined in (21). Moreover, it follows from (22) that
for all \(g \in {\mathcal {G}}_L\). This implies that \(g\left( T_N(\cdot )\right) \) is Lipschitz continuous over \(\otimes _{t=2}^T\left( \Xi _t^{\otimes N}\right) \) with a Lipschitz modulus bounded by L/N. By utilizing Lemma 1 with \(\psi =g \circ T_N\), it follows that that the right-hand side of (23) is bounded by \(L d_{K, k}(\otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}, \otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c})\).
To complete the proof, we need to demonstrate the well-definedness of the metric \(d_{K, 1}\). In other words, both expressions below are well-defined for any \(g\left( T_N\right) \):
and
For given \(\vec {\xi }_0:=\left( \vec {\xi }_{2,0} \cdots , \vec {\xi }_{T,0}\right) \), we have by (24) that,
Since (24) implies the Lipschitz continuity of \(g\left( T_N(\cdot )\right) \), the measurability is evidently achieved. Recall that \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c} \in {\mathcal {M}}_{k,t}^{\phi _t}\), we can then deduce that:
Here the first inequality holds by empolying (25) and the last inequality holds because \(\int _{\Xi _t}\left\| \xi _{t}^i-\xi _{t,0}^i\right\| {\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\left( d \xi ^i_t\right) <\infty \) for \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c} \in {\mathcal {M}}_{k,t}^{\phi _t}\). With the boundedness and measurability of \(g\left( T_N(\cdot )\right) \), we obtain the well-definedness of \(\int _{\Xi _2^{\otimes N}}\cdots \int _{\Xi _T^{\otimes N}}g \left( T_N\left( \vec {\xi }_{2}^N,\cdots ,\vec {\xi }_{T}^N\right) \right) {\mathbb {P}}_{{{\varvec{\theta }}}_T^c}^{\otimes N}\left( d \vec {\xi }_{T}^N\right) \cdots {\mathbb {P}}_{{{\varvec{\theta }}}_2^c}^{\otimes N}\left( d \vec {\xi }_{2}^N\right) \). The same conclusion holds when \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\) is replaced by \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\). \(\square \)
Theorem 6 indicates that the statistical estimator based on the perceived data \(\vec {{\bar{\xi }}}_{2}, \cdots , \vec {{\bar{\xi }}}_{T}\) is close to the one based on the real data \(\vec {{\hat{\xi }}}_{2}, \cdots , \vec {{\hat{\xi }}}_{T}\) uniformly for all N, given that \(\otimes _{t=2}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\) is close to \(\otimes _{t=2}^T{\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\).
In the following, we consider a Bayesian-type MDRO model centered at \({\mathbb {Q}}_{t,N}\) with fixed radius \(r_t\) for each stage t. Then similar to what we did in Sect. 3.1, we have
and the optimal value \({\hat{Q}}_{t}(x_{t-1}, \xi _{t})\) for stage \(t\ge 2\) can be recursively determined as
Moreover, the optimal value of the first stage problem is determined as follows:
Let \(u_t\left( \vec {{\tilde{\xi }}}_{t+1},\cdots ,\vec {{\tilde{\xi }}}_T\right) \) be the optimal value of problem (26) with \(\vec {{\tilde{\xi }}}_i\) generated by \({\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\) and \(u_t\left( \vec {{\xi }}_{t+1},\cdots ,\vec {{\xi }}_T\right) \) the one with \(\vec {{\xi }}_i\) generated by \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}\), for \(t+1\le i\le T\). Remind that \(u_t\left( \vec {{\xi }}_{t+1},\cdots ,\vec {{\xi }}_T\right) \) is the same as \(u_t\left( r_{[t+1]}\right) \) defined before. Then \(u_t\left( \vec {{\tilde{\xi }}}_{t+1},\cdots ,\vec {{\tilde{\xi }}}_T\right) \) and \(u_t\left( \vec {{\xi }}_{t+1},\cdots ,\vec {{\xi }}_T\right) \) are two statistical estimators of the optimal value of the Bayesian-type MDRO and we are interested in the difference between the two estimators, that is, the difference between \(\otimes _{i=t+1}^T{\mathbb {Q}}_{{{\varvec{\theta }}}_i^c}\circ u_t\left( \vec {{\tilde{\xi }}}_{t+1},\cdots ,\vec {{\tilde{\xi }}}_T\right) ^{-1}\) and \(\otimes _{i=t+1}^T{\mathbb {P}}_{{{\varvec{\theta }}}_i^c}\circ u_t\left( \vec {{\xi }}_{t+1},\cdots ,\vec {{\xi }}_T\right) ^{-1}\).
Theorem 7
(Quantitative statistical robustness of model (26)) Suppose that for each stage t, the recourse functions \(Q_t(x_{t-1}, \xi _t)\) and \({\hat{Q}}_t(x_{t-1}, \xi _t)\) are globally Lipschitz continuous in \(\xi _{t}\) uniformly for \(x_{t-1} \in {\mathcal {X}}_{t-1}\), i.e., there exists a positive constant \(L_1\) such that
Let \({\mathbb {P}}_{{{\varvec{\theta }}}_t^c}, {\mathbb {Q}}_{{{\varvec{\theta }}}_t^c}\in {\mathcal {M}}_{k,t}^{\phi _t},\ \forall 2\le t\le T\), where \({\phi _t}(y):=\Vert y\Vert , y \in \Xi _t\). Then
for any sample size N.
Proof
We first verify the Lipschitz continuity of \({u}_{T-1}\left( {\tilde{\xi }}_T^1, \cdots , {\tilde{\xi }}_T^N\right) \) w.r.t. \(\left( {\tilde{\xi }}_T^1, \cdots , {\tilde{\xi }}_T^N\right) \). Since \({\hat{Q}}_T(x_{T-1}, \xi _T)=Q_T(x_{T-1}, \xi _T)\) is uniformly Lipschitz continuous w.r.t. \(\xi _T\), it follows that \(\frac{{\mathcal {H}}_1}{L_1} \subset {\mathcal {G}}_L\), which implies
Here, we define \({\mathcal {H}}_1:=\big \{f_{T-1}(x_{T-1},\xi _{T-1})+{Q}_{T}(x_{T-1}, \cdot ):x_{T-1}\in {\mathcal {X}}_{T-1},\ \xi _{T-1}\in \Xi _{T-1}\big \}\). Then we have that
where the third inequality from the last is based on Theorem 1 in Pichler and Xu (2022). By changing the order of \( u_{T-1}(\vec {{\xi }}_T)\) and \(u_{T-1}(\vec {{\hat{\xi }}}_T)\), we can draw the conclusion that
which implies that for fixed \(x_{T-2}\) and \(\xi _{T-1}\),
As for stage \(T-1\), we have that

We can thus deduce by recursion that
and the rest follows from Theorem 6 by setting \(T_N\left( \vec {\xi }_{2} \cdots , \vec {\xi }_{T}\right) = g( u_1\left( \vec {\xi }_{2} \cdots , \vec {\xi }_{T}\right) )\). \(\square \)
Remark 3
The proof process is interesting due to the use of the triangular inequality, which allows us to divide the difference between the two optimal values \(u_{T-2}(\vec {{\xi }}_{T-1},\vec {{\xi }}_T)\) and \(u_{T-2}(\vec {{\hat{\xi }}}_{T-1},\vec {{\hat{\xi }}}_T)\) into two distinct parts denoted as \(\dagger \) and \(\dagger \dagger \). In the first part \(\dagger \), the objective function remains the same, but the ambiguity sets for the distribution are different. This implies that only the samples from stage \(T-1\) are perturbed, while those from stage T remained unperturbed. Consequently, the upper bound for this part is determined solely by the samples at stage \(T-1\). On the other hand, in the second part \(\dagger \dagger \), the objective functions differ, but the ambiguity set of the distribution remains the same. This can be interpreted as only the samples in stage T being perturbed, while those in stage \(T-1\) remain unaffected. As a result, the upper bound for this segment is controlled solely by the samples in stage T.
It can be seen that the globally Lipschitz continuity of recourse functions \(Q_t(x_{t-1}, \xi _t)\) and \({\hat{Q}}_t(x_{t-1}, \xi _t)\) w.r.t. \(\xi _t\) plays an indispensable role in establishing the quantitative statistical robustness of our proposed Bayesian-type MDRO model. Considering this, we now provide a sufficient condition for ensuring such continuity. To this end, we extend the pseudo-Lipschitzian definition introduced in Pichler and Xu (2022) to the following “global" one.
Definition 3
For a given pair \(\left( x_{t-1}^{\prime }, \xi _{t}^{\prime }\right) \in {{\mathcal {X}}_{t-1}} \times {\Xi _{t}}\) and \(x_t^{\prime } \in {\mathcal {X}}_t\left( x_{t-1}^{\prime }, \xi _{t}^{\prime }\right) \), a set-valued mapping \({\mathcal {X}}_t: {{\mathcal {X}}_{t-1}} \times {\Xi _{t}} \rightrightarrows {\mathbb {R}}^a\) is referred to as globally pseudo-Lipschitzian at \(\left( x_{t-1}^{\prime }, \xi _{t}^{\prime }\right) \) if there exist a neighbourhood \(B(x_t^{\prime })\) of \(x_t^{\prime }\) and a positive constant \(L_{{\mathcal {X}}_t}\) such that the following conditions hold for any \((x_{t-1}, \xi _{t})\) in \({{\mathcal {X}}_{t-1}} \times {\Xi _{t}}\):
and
Here \({\mathcal {B}}\) represents the unit ball in \({\mathbb {R}}^a\).
Proposition 8
(Globally Lipschitz continuity of recourse functions) Suppose that for \(t=2,\cdots ,T\), \({{\mathcal {X}}_t}(x_{t-1}, \xi _{t})\) is globally pseudo-Lipschitzian at every \(\left( x_{t-1}^{\prime }, \xi _{t}^{\prime }\right) \in {{\mathcal {X}}_{t-1}} \times {\Xi _{t}}\). Furthermore, there exists a positive constant \(L_{f_t}\) such that
holds for any \( \xi _{t}, \xi _{t}^\prime \in {\Xi _{t}}\) and \(x_t\in B(x_t^{\prime })\) as defined in Definition 3. Then there exists a positive constant \(L_t\) such that
and
for all \((x_{t-1}, \xi _{t}) \in {{\mathcal {X}}_{t-1}} \times {\Xi _{t}}\) and \(2\le t\le T\).
Proof
To establish this result, we begin by noting that the Lipschitz continuity condition expressed in (29) at stage T is equivalent to the Lipschitz continuity of the objective function of the Bayesian-type MDRO problem at that stage. Consequently, under the given assumptions, the conclusion for stage T follows directly from Proposition 4 in Pichler and Xu (2022), i.e.,
Combining (29) with (30), we have that for stage \(T-1\),
This demonstrates that the objective function of the Bayesian-type MDRO problem at stage \(T-1\) also exhibits the globally Lipschitz continuity. Similarly, by utilizing (27)–(28) and Proposition 4 in Pichler and Xu (2022), we can establish the globally Lipschitz continuity of \(Q_{T-1}(x_{T-2}, \xi _{T-1})\). Consequently, we complete the proof for \(t=2,\cdots ,T\) by the principle of mathematical induction.
The same conclusion holds when Q is replaced by \({\hat{Q}}\). \(\square \)
With Theorem 7 and Proposition 8, we can deduce that, under some moderate conditions, the optimal value and solution derived from the Bayesian-type MDRO model remain reliable and can be effectively utilized as long as the contamination does not lead to substantial deviations of distributions.
The above findings underscore the robustness of our approach when confronted with data contamination, thereby reinforcing its practical applicability and overall reliability. It emphasizes the importance of moderate levels of contamination that do not introduce substantial disruptions to the performance of the model. As a result, our Bayesian-type MDRO framework proves itself to be a resilient solution in such scenarios.
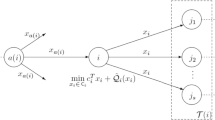
4 Cutting plane algorithm
The cutting plane method was initially proposed by Kelley (1960), which has been extended from different perspectives and successfully applied to solve convex programs (see, Kiwiel 1983; Lan and Shapiro 2023). Especially, several studies demonstrate the practicality of customized cutting plane algorithms for solving nonsmooth convex programs. Considering this and Theorem 1 which reformulates the Bayesian-type MDRO model into an RMSP problem, we will develop a risk-averse variant of the cutting plane algorithm to solve our problem.
To apply the cutting plane type algorithm to solve problem (10), we first collect historical data and generate two reference distributions \({\mathbb {P}}_{{\varvec{\theta }}_t^l}\) and \({\mathbb {P}}_{{\varvec{\theta }}_t^{u-l}}\) for each stage \(t = 2, \cdots , T\). \(\Xi _t:=\{\xi _{t}^{i},i=1,\cdots ,n_t\}\) is used to represent the possible realizations of \(\xi _{t}\), and the corresponding reference probabilities are denoted as \(p_{t,i}^l\) and \(p_{t,i}^{u-l}\). Then, (15) can be approximated as
for \(i=1,\cdots ,n_t\), where \({\bar{x}}_{t-1}\) is the decision variable obtained from stage \(t-1\). Here we define
as the corresponding approximation to the cost-to-go function. To simplify notation, we use \(x_t\), \(z_t\) here instead of \(x_t(\xi _{t}^{i})\), \(z_t(\xi _{t}^{i})\).
At the first stage, we solve the following approximated optimization problem:
Recall that the subdifferential of \([{\hat{Q}}_{t+1,j}(x_t)-z_t]^+\) at point \(({\bar{x}}_t,{\bar{z}}_t)\) is
Thus, if \({\textbf{g}}_{t+1,i}\in \partial {\hat{Q}}_{t+1,i}\left( {\bar{x}}_t\right) \) for \(i=1,\cdots ,n_{t+1}\), it is not difficult to obtain the subgradient of \(\hat{{\mathcal {Q}}}_{t+1}\left( x_t, z_t\right) \) at \(\left( {\bar{x}}_t, {\bar{z}}_t\right) \) by the chain rule of subdifferentials as follows:
where \({\mathcal {J}}_{t+1}:=\{j:{\hat{Q}}_{t+1,i}\left( {\bar{x}}_t\right) >{\bar{z}}_t,\ j=1,\cdots ,n_{t+1}\}\).
Suppose \({\mathfrak {Q}}_{t+1}(x_t(\xi _{t}^{i}))\) is the current approximation to the cost-to-go function at stage \(t + 1\) for \(t = 1,\cdots , T - 1\). With the cutting hyperplane of \(\hat{{\mathcal {Q}}}_{t+1}\left( x_t, z_t\right) \) at \(\left( {\bar{x}}_t, {\bar{z}}_t\right) \) defined as
we can update the lower approximation to \(\hat{{\mathcal {Q}}}_{t+1}\left( x_t, z_t\right) \) by adding the new cutting hyperplane (32), i.e., \({\mathfrak {Q}}_{t+1}\left( x_t, z_t\right) :=\max \left\{ {\mathfrak {Q}}_{t+1}\left( x_t, z_t\right) , h_{t+1}\left( x_t, z_t\right) \right\} \).
During the backward steps, the optimization problem (31) is approximated using the cutting hyperplane \({\mathfrak {Q}}_{t+1}\left( x_t, z_t\right) \). Specifically, we approximate the expected cost-to-go function by solving the following optimization problem:
for each possible realization \(\xi _{t}^{i}\).
At the first stage, we solve the optimization problem
and find the optimal objective value, which serves as a lower bound to the optimal value of the Bayesian-type MDRO problem. This backward process enables us to refine the approximation to the cost-to-go functions and generate cutting planes to improve the lower bounds on the optimal value function.
A Monte Carlo simulation is carried out during the forward steps. For each stage, we draw M samples \(\{\xi _{t,i},i=1\cdots ,M\}\) from the set \(\Xi _t\) and solve the optimization problem (33) under each realization, while storing the optimal solution \({\hat{x}}_{t,i}\) for each combination (t, i). These corresponding optimal values enable us to calculate a new upper bound
where
for \(t=2, \cdots , T\) and
for each combination (t, i).
With the above preparation, we can develop the corresponding risk-averse variant of the cutting plane algorithm designed to solve the Bayesian-type MDRO problem (10). Detailed description of this algorithm is provided in Algorithm 1.
Moreover, it is not difficult to deduce from Proposition 3.1 in Shapiro (2011) that the almost sure convergence holds for Algorithm 1 under mild regularity conditions.
Proposition 9
Suppose in the backward steps the optimal solutions are employed and Assumption 1 is satisfied. Then there exists a sufficiently large iteration number K in Algorithm 1 such that the optimal policy generated from the forward step procedure of Algorithm 1 is the optimal solution to the Bayesian-type MDRO problem (10) with probability 1.
Proof
Given the boundedness of the recourse function under Assumption 1, it can be inferred that (15) and (16) have finite optimal values for all realizations \(\Xi _t\). Additionally, the independent sampling in the Monte Carlo simulation ensures the subsampling procedure (i.e., \(\{\xi _{t,i},i=1\cdots ,M\}\) is a subset of \(\Xi _t\)) in the forward steps. Therefore, the proposition is established through a direct application of Proposition 3.1 in Shapiro (2011). \(\square \)
Remark 4
In the Monte Carlo simulation, the uncertainty about the estimate of \({\bar{v}}\) in (35) can be quantified using the standard deviation of the estimator
Consequently, \(\left[ {\bar{v}}-z_{\varepsilon /2}\delta _{v},{\bar{v}}+z_{\varepsilon /2}\delta _{v}\right] \) represents the \(1-\varepsilon \) confidence interval for the true value of \({\bar{v}}\). We employ the uncertainty surrounding the upper bound estimate as the convergence criterion, which means that the algorithm is stopped once \({\underline{v}}\in \left[ {\bar{v}}-z_{\varepsilon /2}\delta _{v},{\bar{v}}+z_{\varepsilon /2}\delta _{v}\right] \). This stopping criterion establishes a connection between the acceptable accuracy of the simulation (determined by the sample size M) and the performance of the optimal policy generated by the proposed cutting plane algorithm. In other words, to ensure the overall performance of Algorithm 1, the sample size M for the Monte Carlo simulation should be properly selected according to the characteristics of the concrete Bayesian-type MDRO problem (10) to be solved.
Cutting planes Algorithm for Bayesian-type MDRO (10)
5 Numerical experiments
As a demonstration of our theoretical results and Algorithm 1, we consider in this section a distributionally robust inventory control problem and a distributionally robust hydrothermal scheduling problem, respectively. These kinds of real problems have been widely studied in many papers like Xu et al. (2018), Shapiro and Cheng (2021), Huang et al. (2017) and Philpott et al. (2018). We start by introducing the two problems and formulating their mathematical models under our Bayesian-type MDRO framework. Numerical experiments are then carried out to validate the developed theory and assess the practicality of the proposed Bayesian-type MDRO model, as well as Algorithm 1.
To construct the uncertainty set \(\Theta _t\) \((2\le t\le T)\), we randomly generate and collect N independent historical data as detailed in (8), with \(\alpha =5\%\). We can then solve the derived Bayesian-type MDRO problem using Algorithm 1 and obtain the optimal value V.
To compare our approach against existing methods, we also solve the derived risk-neutral MSP problem by the SAA method and the corresponding MDRO problem with the \(L_\infty \) ambiguity set. Specifically, we use the following approaches for comparison.
-
(1)
Bayesian-type MDRO: For each scenario, we randomly generate and collect N independent historical data as detailed in (8) to construct the uncertainty set \(\Theta _t\) \((2\le t\le T)\). We then employ the generated ambiguity set and solve the corresponding Bayesian-type MDRO model outlined in (10) using Algorithm 1.
-
(2)
\(L_\infty \) MDRO in Huang et al. (2017): In this approach, the solution is obtained by solving the MDRO problem defined with the \(\Theta _t^{L_\infty }\) ambiguity set, as described in (9).
-
(3)
risk-neutral MSP: This method involves deriving a maximum likelihood estimation (MLE) estimator, \(\varvec{{\hat{\theta }}}\), from the data set. The estimated parameters are then used to solve the corresponding problems based on the estimated distribution \({\mathbb {P}}_{\varvec{{\hat{\theta }}}}\).
To evaluate the obtained optimal solutions, we measure their performance by calculating the relative gap, defined as Gap\(=\frac{V-V_{true}}{V_{true}}\) between the Bayesian-type MDRO optimal value V, and the risk-neutral MSP optimal value \(V_{true}\) with respect to the true distribution, got from the problem like (17). To further evaluate the deviations between the optimal values obtained by different methods and the true optimal value \(V_{true}\), we run 100 repetitive experiments independently and examine the variance of Gap. As we can see, the larger the variance is, the larger the error of the estimated optimal value would be.
All the experiments have been performed on a 64-bit PC with 12 GB of RAM and a 3.20 GHz processor, solved under Julia environment by HiGHS solver.
5.1 Problem description
This subsection details the model description, parameter setting and problem solution for the inventory control problem and the hydrothermal scheduling problem.
5.1.1 Inventory control problem
We consider a T \((2\le T<\infty )\) stage inventory control problem. As usually done in the literature, we denote the unit ordering cost at stage t as \(o_t\), the unit holding cost at stage t as \(h_t\) and the unit shortage penalty as \(p_t\). The demand at stage t is random, represented as \(\xi _t\), \(1\le t\le T\), which forms an i.i.d. process. The current inventory level at stage t is denoted by \(y_t\), with the initial inventory given as \(y_0=0\). The order quantity at stage t is represented as \(x_t\). Quite a few studies about inventory control problem assume that \(\xi _t\) follows a Poisson distribution (e.g., Shapiro and Cheng 2021; Shapiro et al. 2014). In light of our Bayesian-type MDRO framework and empirical observations in these researches, we also assume \(\xi _t\), \(1\le t\le T\), follows a Poisson distribution, and can collect historical demands, denoted as the set \({\mathcal {S}}_{t}\), and then construct the ambiguity set as \({\mathcal {P}}_{\Theta _{t}({\mathcal {S}}_{t},\alpha )}=\{{\mathbb {P}}_{{\varvec{\theta }}_t},{\varvec{\theta }}_t\in \Theta _{t}({\mathcal {S}}_{t},\alpha )\}\). Here \(\Theta _{t}({\mathcal {S}}_{t},\alpha )\) is the Bayesian confidence region based on available distribution information, as defined in (8).
With the above preparation, the Bayesian-type MDRO formulation of the inventory control problem proposed in Shapiro and Cheng (2021) can be described as:
where \(c_t(x_t(\xi _t),y_{t-1},\xi _t)=p_{t} [\xi _{t}-(y_{t-1}+x_{t}(\xi _{t}))]^++h_{t}[y_{t-1}+x_{t}(\xi _{t})-\xi _{t}]^+\). Here, \(\xi _1\) is a pre-specified constant and the constraints for \(t = 2,\cdots , T\) should hold almost surely w.r.t. \(\xi _t\).
We consider an inventory problem over 6 stages. The above stage-wise parameters are set as \(o_t = 2\), \(h_t = 4\), and \(p_t = 6\), \(1\le t\le 6\). The distribution of demand follows a Poisson distribution with the arrival rate \(\lambda =10\). Under the above parameter setting, the risk-neutral MSP optimal value, \(V_{true}\), of the above 6-stage inventory control problem can be determined easily by a classical cutting plane algorithm as \(V_{true}=171.3951\).
With respect to the sample size, Fig. 3 plots the optimal values obtained from the Bayesian-type MDRO approach, the \(L_\infty \) MDRO and the risk-neutral MSP with the SAA approach, respectively, and Fig. 4 depicts the corresponding variance of Gap, with \(V_{true}\) as the benchmark, for the considered inventory control problem.
Considering the space limitation and the similarity of numerical observations, we will consolidate the analysis and comparison of empirical results in the following Sect. 5.2.
5.1.2 Hydrothermal scheduling problem
To formulate a T \((2\le T<\infty )\) stage hydrothermal scheduling problem mathematically, we define the sets of power plants and storage facilities as \({\mathcal {G}}\) and \({\mathcal {S}}\), respectively. For each stage \(t=1,\cdots , T\), \(c_t^g\) represents the unit generation cost of power plant \(g\in {\mathcal {G}}\), \(I_t^s\) denotes the inflow to storage facility \(s\in {\mathcal {S}}\), \({\bar{G}}^g\), \({\underline{G}}^g\), \({\bar{S}}^s\), and \({\underline{S}}^s\) denote the maximum and minimum generation limits for each power plant \(g\in {\mathcal {G}}\) and the maximum and minimum storage capacities for each storage facility \(s\in {\mathcal {S}}\), respectively. To ensure that the combined hydroelectric and thermal generation meets the total power demand \(D_t\) at stage t, we introduce a penalty cost of \(c_t^u\) for each unit of unsatisfied demand.
We define \(x_t^g\) as the energy produced by power plant \(g\in {\mathcal {G}}\) at stage t, and \(x_t^u\) as the amount of energy unmet at stage t, and define \(x_t^s\) as the energy produced by storage facility \(s\in {\mathcal {S}}\) at stage t, the overflow amount as \(o_t^s\), and the energy storage level as \(v_t^s\) at stage t. Here, \(v_0^s\) is the initial energy storage.
In practice, except for the initial stage 1 where we know the exact values of \(c_1^g\) and \(c_1^u\), and thus can find the deterministic optimal decisions \(x_1^g\) and \(x_1^u\), we do not know the exact distributions of random \(c_t^g\) and \(c_t^u\) at stage t \((2\le t\le T)\), which result in the randomness of decisions \(x_t^g\) and \(x_t^u\). Concretely, we assume these parameters depend on some random vector \(\xi _t\) corresponding to the uncertain environment at stage t. The distributions of relevant random vectors in existing studies about hydrothermal scheduling problem are generally parameterized. For instance, an exponential distribution is advocated in Huang et al. (2017) for the random vector, a log-normal distribution is adopted in De Matos et al. (2017) for the random vector, while others (see for example Philpott et al. (2018)) presume the random vector to be discrete. To better balance the modeling preciseness and tractablility, we adopt a modeling framework different from typical distributionally robust hydrothermal scheduling problems. In light of our Bayesian-type MDRO framework and empirical observations in the above researches, we assume the possible distributions of \(\xi _t\) belong to a parameterized family of distributions \({\mathcal {P}}_{\Theta _{t}({\mathcal {S}}_{t},\alpha )}=\{{\mathbb {P}}_{{\varvec{\theta }}_t},{\varvec{\theta }}_t\in \Theta _{t}({\mathcal {S}}_{t},\alpha )\}\). Here \(\Theta _{t}({\mathcal {S}}_{t},\alpha )\) is the parameter space based on available information about distributions as defined in (8).
Based on the symbols introduced above, the Bayesian-type distributionally robust hydrothermal scheduling problem can be modeled as:
Here, the constraints for \(t=2, \cdots , T\) should hold almost surely w.r.t. \(\xi _t\). Constraints (37) ensure the balance of power demand and generation. Constraints (38) impose on the balance of storage facility. Constraints (39) and (40) represent the limitations of the power plants and the storage facilities, respectively. Lastly, constraints (41) enforce the non-negativity of decision variables.
In the following, we will apply the previously proposed formulations and algorithm to solve problem (36)–(41). Specifically, we consider a problem of scheduling electrical generation over 15 stages, with a demand of \(D_t=150\) MWh in each stage. Similar as the settings in papers like Philpott et al. (2018), we model the inflows using a multinomial distribution of M(1/6,1/3,1/2), corresponding to the inflow of (0, 50, 100). The power plant’s marginal cost is \(c_t^g=10t\) for stage t, while the storage facility has a marginal cost of 0 MWh. The unit penalty cost is set as \(c_t^u=1000\) MWh. We set a maximum capacity for the storage facility s as \({\bar{S}}^s=200\) MWh and assume the storage is full at the first stage with \(v_0^s=200\) MWh. Under the above parameter setting, \(V_{true}\) can be determined easily by a classical cutting plane algorithm as \(V_{true}=73000\).
Figure 5 plots the optimal values of the hydrothermal scheduling problem obtained from the Bayesian-type MDRO approach, the \(L_\infty \) MDRO and the risk-neutral MSP with the SAA approach, respectively, with \(V_{true}\) as the benchmark. Table 1 shows the corresponding gaps with respect to different sample sizes and the CPU times (in seconds) under different methods, complementing Fig. 5. Since we transform the encountered MDRO problem (36)–(41) into an RMSP problem for resolution, the solution time of our cutting plane algorithm does not significantly rely on the number of samples. Therefore, we have selected the average solution time at a sample size of 30 for CPU times to be showcased.
Figure 6 shows the variance of Gap for the hydrothermal scheduling problem under different methods with respect to different sample sizes. Table 2 shows the corresponding gaps with respect to different sample sizes, complementing Fig. 6.
5.2 Comparative analyses
Based on the results presented in Figs. 3-6 and Tables 1-2, we can draw the following observations:
-
With the increase of the sample size, the optimal values obtained with all MDRO approaches are monotonically decreasing and the optimal value under each approach is getting closer to the true optimal value, as expected.
-
The SAA approach can yield an optimal value that is close to \(V_{true}\), since it doesn’t consider the robustness of the sample data. However, the variance of the Gap under the SAA approach is always greater than other approaches except for relatively large sample size N.
-
For a given sample size, our Bayesian-type MDRO approach outperforms the \(L_\infty \) MDRO in the sense of a lower variance of the Gap. This is due to the fact that our framework can overcome the over-conservativeness of existing ambiguity sets. Therefore, our Bayesian-type MDROs can provide a better optimal solution to the real problem.
-
Our informative Bayesian-type MDRO approach outperforms the uninformative one, highlighting the benefit of incorporating prior knowledge into the construction of ambiguity sets. This is particularly helpful in the situation with small sample sizes.
-
Unlike other methods, our Bayesian-type MDRO approach is more robust with respect to the sample size and the solution time, making it attractive for solving complex MDRO problems with limited sample data or high-dimensional random vectors.
-
Since the proposed Bayesian-type MDRO problem is reformulated as an RMSP problem, the solution framework is similar to that of the SAA method for MDRO. Therefore, the CPU times for both the informative Bayesian-type MDRO approach and uninformative Bayesian-type MDRO approach are comparable and near to that of the SAA method, but the CPU time of the \(L_\infty \) MDRO is much larger. The facts underscore the effectiveness of our cutting plane algorithm.
In conclusion, the numerical results demonstrate the effectiveness of our proposed method in solving the MDRO problem with reduced conservatism, while ensuring robustness.
6 Conclusions
This paper focuses on constructing ambiguity sets in MDRO problems from a Bayesian perspective. The proposed approach introduces a novel framework for constructing distribution ambiguity sets that leverages decision maker’s prior knowledge of the true underlying distributions, as well as posterior data, to construct more precise and thus concise ambiguity sets. We demonstrate that the proposed Bayesian-type MDRO problem can be reformulated as an RMSP problem, which can be effectively solved with the cutting plane algorithm. Theoretical analyses of our model provide valuable insights into its asymptotic properties, finite sample guarantee and statistical robustness. Our numerical study shows that our method outperforms typical approaches and can offer practical solutions especially when data acquisition is difficult or when we face with the highly computational cost challenges of MDRO problems.
Our method relies on the assumption of inter-stage independent and discrete distributions. Future research can explore its applicability to more complex MDRO problems with dependent distributions among stages. Moreover, it is also worthwhile combining our methodology with other optimization algorithms and investigating its practicality in real-world applications.
References
Agarwal A, Daumé H (2010) A geometric view of conjugate priors. Mach Learn 81:99–113
Allevi E, Bertocchi M, Innorta M, Vespucci M (2008) A stochastic optimization model for a gas sale company. IMA J Manag Math 19(4):403–416
Arora R, Gao R (2022) Data-driven multistage distributionally robust optimization with nested distance: Time consistency and tractable dynamic reformulations. Preprint. Submitted June 22. https://optimization-online.org/?p=20641
Artzner P, Delbaen F, Eber J-M, Heath D (1999) Coherent measures of risk. Math Financ 9(3):203–228
Berger JO (2013) Statistical decision theory and Bayesian analysis. Springer, New York
Berger JO, Pericchi LR (1996) The intrinsic Bayes factor for model selection and prediction. J Am Stat Assoc 91(433):109–122
Bertsimas D, Gupta V, Kallus N (2018) Robust sample average approximation. Math Program 171:217–282
Bertsimas D, Shtern S, Sturt B (2023) A data-driven approach to multistage stochastic linear optimization. Manage Sci 69(1):51–74
Chen Z, Ma W, Ji B (2023) Data-driven approximation of distributionally robust chance constraints using Bayesian credible intervals. Preprint https://doi.org/10.48550/arXiv.2306.12735
Chernozhukov V, Newey WK, Singh R (2023) A simple and general debiased machine learning theorem with finite-sample guarantees. Biometrika 110(1):257–264
De Matos VL, Morton DP, Finardi EC (2017) Assessing policy quality in a multistage stochastic program for long-term hydrothermal scheduling. Ann Oper Res 253:713–731
Delage E, Mannor S (2010) Percentile optimization for Markov decision processes with parameter uncertainty. Oper Res 58(1):203–213
Duque D, Morton DP (2020) Distributionally robust stochastic dual dynamic programming. SIAM J Optim 30(4):2841–2865
Edirisinghe N (2005) Multiperiod portfolio optimization with terminal liability: bounds for the convex case. Comput Optim Appl 32:29–59
Esfahani PM, Kuhn D (2018) Data-driven distributionally robust optimization using the Wasserstein metric: Performance guarantees and tractable reformulations. Math Program 171(1–2):115–166
Gao R (2022) Finite-sample guarantees for Wasserstein distributionally robust optimization: Breaking the curse of dimensionality. Operations Research. (Forthcoming)
Gelman A, Carlin JB, Stern HS, Rubin DB (1995) Bayesian data analysis. Chapman and Hall/CRC, Boca Raton
Gelman A, Jakulin A, Pittau MG, Su Y-S (2008) A weakly informative default prior distribution for logistic and other regression models. Ann Appl Stat 2(4):1360–1383
Georghiou A, Tsoukalas A, Wiesemann W (2019) Robust dual dynamic programming. Oper Res 67(3):813–830
Gupta V (2019) Near-optimal Bayesian ambiguity sets for distributionally robust optimization. Manage Sci 65(9):4242–4260
Hochreiter R, Pflug GC, Wozabal D (2006) Multi-stage stochastic electricity portfolio optimization in liberalized energy markets. In: System modeling and optimization: proceedings of the 22nd IFIP TC7 conference held from July 18–22, 2005, in Turin, Italy 22. Springer, pp 219–226
Huang J, Zhou K, Guan Y (2017) A study of distributionally robust multistage stochastic optimization. Preprint https://doi.org/10.48550/arXiv.1708.07930
Jeffreys H (1998) The theory of probability. OuP, Oxford
Jiang R, Guan Y (2018) Risk-averse two-stage stochastic program with distributional ambiguity. Oper Res 66(5):1390–1405
Kelley JE Jr (1960) The cutting-plane method for solving convex programs. J Soc Ind Appl Math 8(4):703–712
Kiwiel KC (1983) An aggregate subgradient method for nonsmooth convex minimization. Math Program 27:320–341
Klein Haneveld WK, Streutker MH, Vlerk MH (2010) Indexation of Dutch pension rights in multistage recourse ALM models. IMA J Manag Math 21(2):131–148
Krokhmal P, Zabarankin M, Uryasev S (2011) Modeling and optimization of risk. Surv Oper Res Manag Sci 16(2):49–66
Lan G, Shapiro A (2023) Numerical Methods for Convex Multistage Stochastic Optimization. Preprint https://doi.org/10.48550/arXiv.2303.15672
Lin Y, Ren Y, Zhou E (2022) Bayesian risk Markov decision processes. Adv Neural Inf Process Syst 35:17430–17442
Liu Q, Wu J, Xiao X, Zhang L (2018) A note on distributionally robust optimization under moment uncertainty. J Numer Math 26(3):141–150
Pan K, Guan Y (2016) Strong formulations for multistage stochastic self-scheduling unit commitment. Oper Res 64(6):1482–1498
Petrik M, Russel RH (2019) Beyond confidence regions: tight Bayesian ambiguity sets for robust MDPs. Adv Neural Inf Process Syst 32:7047–7056
Philpott AB, Matos VL, Kapelevich L (2018) Distributionally robust SDDP. CMS 15:431–454
Pichler A, Shapiro A (2021) Mathematical foundations of distributionally robust multistage optimization. SIAM J Optim 31(4):3044–3067
Pichler A, Xu H (2022) Quantitative stability analysis for minimax distributionally robust risk optimization. Math Program 191(1):47–77
Raiffa H, Schlaifer R (1961) Applied statistical decision theory. Wiley, New York
Rebennack S (2022) Data-driven stochastic optimization for distributional ambiguity with integrated confidence region. J Global Optim 84(2):255–293
Rockafellar RT, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2:21–42
Rockafellar RT, Uryasev S (2013) The fundamental risk quadrangle in risk management, optimization and statistical estimation. Surv Oper Re Manag Sci 18(1–2):33–53
Römisch W (2003) Stability of stochastic programming problems. Handb Oper Res Manag Sci 10:483–554
Ruszczyński A, Shapiro A (2006) Conditional risk mappings. Math Oper Res 31(3):544–561
Sen S, Yu L, Genc T (2006) A stochastic programming approach to power portfolio optimization. Oper Res 54(1):55–72
Shapiro A (2011) Analysis of stochastic dual dynamic programming method. Eur J Oper Res 209(1):63–72
Shapiro A, Cheng Y (2021) Central limit theorem and sample complexity of stationary stochastic programs. Oper Res Lett 49(5):676–681
Shapiro A, Dentcheva D, Ruszczyński A (2014) Lectures on stochastic programming: modeling and theory, 2nd ed. Society for Industrial and Applied Mathematics, Philadelphia, PA. https://doi.org/10.1137/1.9781611973433
Van Parys BP, Esfahani PM, Kuhn D (2021) From data to decisions: distributionally robust optimization is optimal. Manage Sci 67(6):3387–3402
Xin L, Goldberg DA (2021) Time (in) consistency of multistage distributionally robust inventory models with moment constraints. Eur J Oper Res 289(3):1127–1141
Xu H, Zhang S (2021) Quantitative statistical robustness in distributionally robust optimization models. Pac J Optim Spec Iss 19:335–361
Xu H, Liu Y, Sun H (2018) Distributionally robust optimization with matrix moment constraints: Lagrange duality and cutting plane methods. Math Program 169:489–529
Xu H, Mannor S (2009) Parametric regret in uncertain Markov decision processes. In: Proceedings of the 48h IEEE conference on decision and control (CDC) held jointly with 2009 28th Chinese control conference. IEEE, pp 3606–3613
Yu X, Shen S (2022) Multistage distributionally robust mixed-integer programming with decision-dependent moment-based ambiguity sets. Math Program 196(1–2):1025–1064
Zolotarev VM (1983) Probability Metrics. Teoriya Veroyatnostei i ee Primeneniya 28(2):264–287
Funding
This research was supported by the National Key R &D Program of China (2022YFA1004000, 2022YFA1004001) and National Natural Science Foundation of China under Grant Number 11991023.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest:
The authors declare that they have no Conflict of interest.
Code availability:
The code that supports the findings of this study is available from the corresponding author upon request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ma, W., Chen, Z. Multi-stage distributionally robust convex stochastic optimization with Bayesian-type ambiguity sets. Math Meth Oper Res (2024). https://doi.org/10.1007/s00186-024-00872-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00186-024-00872-1