1 Introduction

Uncertainty is the main feature of nowadays business environment. The firms conducting the projects investment are facing an increasing number of uncertain market factors like market demand, investment cost, product’s price, operating cost, and so on. With the increasing complexity of the current economy, unexpected events such as financial crises, pandemics (e.g., COVID-19), natural disasters (e.g., hurricanes or earthquakes), the disclosure of new information (e.g., technological innovation or political risk) and other sources(e.g., Martzoukos and Trigeorgis 2002; Wu and Yen 2007) may lead to sudden increases or decreases in these uncertain factors, which in turn can have a significant impact on firms’ investment decisions. How to measure and characterize the uncertain factors scientifically and accurately has become an increasingly important problem which should be solved firstly. Real options models that study investment under uncertainty typically assume that once the investment is undertaken, the firm can possess a project that can generate cash flows immediately(e.g., Dixit and Pindyck 1994; McDonald and Siegel 1986; Mauer and Ott 2000). However, the vast majority of investment projects require a considerable amount of time to complete construction before they can be put into production. The period of time, from completion of investment to product launch, is known as investment lags or time-to-build in the existing literatures. Due to industry attributes, enterprise characteristics or many other factors(e.g., Agliardi and Koussis 2013; Bar-Ilan and Strange 1996; Koeva 2000), the time-to-build is uncertain, furthermore, the time-to-build becomes more important when there is competition between firms because they are directly related to the dynamics of the leader-follower relationship in the duopoly market.

In this paper, we consider a homogeneous good market where there are two sources of uncertainty: the market demand and investment cost, which are subjected to the unexpected events. The stochastic shocks admit a jump-diffusion process. We assume that once conducting the investment, the firm will obtain a production plant that requires an uncertain time-to-build before it can be put into production. Thus, we build a two-factor jump-diffusion model to investigate the duopoly firms’ optimal investment decisions, involving the optimal investment timing and capacity level, in the presence of time-to-build. In particular, we allow the firms’ time-to-build to be asymmetric, which leads to that the firm who invests later may launch new product earlier due to the relative advantage of time-to-build. Further, we study the effects of the uncertainty and asymmetry of time-to-build on the duopoly firms’ investment strategies.

We find that the impact of time-to-build on the firm’s optimal investment timing depends on the nature of unexpected events. More specifically, if the unexpected events are positive, that is, the market demand jumps up and investment cost jumps down, the longer the average time-to-build, the firm will invest in advance, otherwise, the reverse. This is mainly because in a more positive market environment, the marginal revenue from a larger expected net present value is discounted more heavily and the marginal cost of waiting is the option value to continue with a staged project. This is a novel result in that the existing literature on the time-to-build indicates that the impact of time-to-build on firm’s investment strategy is independent of the uncertainty of market factors.

We also show that, the uncertainty of time-to-build has a significant impact on the leader-follower relationship of the duopoly firms. In particular, when the duopoly firms’ time-to-build are significantly asymmetric, the dominated firm with a relative disadvantage in time-to-build will succeed in the preemptive game of the leader-follower relationship and become the market leader. The main reason is that the dominant firm believes that even if the investment timing is later, the relative advantage of time-to-build can allow its products to enter the market one step ahead of the dominated firm. In other words, the relative advantage of time-to-build weakens the dominant firm’s preemptive motivation.

Finally, we find that the time-to-build has distinct impacts on the firm’s optimal capacity level in different types of market structures. In a monopolistic market, the firm’s capacity decision is not affected by time-to-build. In a duopoly market, the longer the dominated firm’s time-to-build, the higher the leader’s capacity level, even if the dominated firm becomes the leader. This also precisely indicates that when the time-to-build of the dominated firm increases, it not only accelerates the investment, but also becomes aggressive in capacity decision-making.

Contributions devoting to exploring the duopoly firms’ optimal investment strategies in the presence of time-to-build are continuously emerging in recent years. By taking the time-to-build into account, Grenadier (1996) developed an equilibrium framework for strategic option exercise games. Grenadier (2000) examined the competitive equilibrium in the presence of time-to-build. By incorporating time-to-build and operating flexibility into a incremental investment model, Aguerrevere (2003) derived the impacts of competitive interactions on investment decisions and on the dynamics of the price of a nonstorable commodity. Pacheco-de-Almeida and Zemsky (2003) added time-to-build to a multi-period strategic investment model and showed that there came into being a novel equilibrium in incremental investment due to the time-to-build. Genc (2017) investigated when investment is subject to time-to-build versus when it is not, how the firms’ equilibrium investment strategies varied in a stochastic and competitive dynamic market. All these models consider the exist of time-to-build in the strategic real option models, we also do this, but in addition, we add the uncertainty and asymmetry of time-to-build to the duopoly firms. Weeds (2002) incorporated the uncertainty of the investment lags into the R &D competition analysis and focused on the investment strategy under the winner-takes-all patent system. Within a continuous time dynamic framework, Jeon (2021) surveyed the influences of uncertain and asymmetric time-to-build on the leader-follower relationship in duopoly market. Our article extends this line of research to a continuous-discrete time dynamic framework in which both the market demand and investment cost are subjected to the shocks of the unexpected events.

The existing real-options literature on capacity-timing games usually employ the Geometric Brownian motion (GBM) to describe the changing paths of uncertain market factors (e.g., Azevedo and Paxson 2014; Huisman and Kort 2004, 2015; Huberts et al. 2019; Lavrutich et al. 2016; Lavrutich 2017; Nielsen 2002; Smets 1993; Siddiqui and Takashima 2012; Weeds 2002). Admittedly, we know that the advantage of GBM is that it yields a more simplified closed-form solution of the firm’s investment decision, which is a very intuitive and can be analyzed efficiently, as referred by Eberlein and Glau (2014). However, in nowadays, the world global market encompasses unexpected events that may lead to sudden increases or decreases in demand for certain products or investment cost. For instance, after the 9/11 terrorist attacks, railway passenger traffic in the United States surged by 60%. Apple’s quarterly data on global iPhone sales from 2007 to 2016 shows that the launch of new products has led to jumps in product demand. In 2015, due to the groundbreaking emissions scandal in the news, Volkswagen’s global sales plummeted, and the stock prices of Volkswagen and Porsche fell by over 8% (e.g., Nunes and Pimentel 2017). At the beginning of 2020, the COVID-19 broke out worldwide, and experts called on people to wear masks, which directly led to the sudden increases in demand for N95 masks. Jumps in stochastic investment cost may arise from the disclosure of new information regarding technological innovation, competition, political risks, regulatory effects and other sources and its impact (e.g., Martzoukos and Trigeorgis 2002; Wu and Yen 2007). These sharp increases or decreases appearing in the original continuous changing paths of market demand and investment cost can’t be captured by GBM any more. The existing literature on real options(e.g., Dixit and Pindyck 1994; Eberlein and Glau 2014; Hagspiel et al. 2015; Johannes 2004; Lee and Mykland 2008; Liang et al. 2013; Merton 1976; Murto 2007; Mason and Wilmot 2014; Nunes and Pimentel 2017; Pan 2002) suggest the use of jump-diffusion process, in which discrete value changes are superimposed on the Brownian motion. These studies, although also analysed the firms’ optimal investment decisions under a jump-diffusion model, overlooking the presence of time-to-build in the investment projects.

The contribution of our paper can be summarized from the following two angles. First, to the best of our knowledge, this is the first paper to investigate the optimal investment problem of duopolistic firms with two sources of uncertainty in the presence of time-to-build. We extend the model of Wu and Hu (2022) by considering the uncertain time-to-build, which follows a jump exponential distribution. Second, this paper considers a more complex economic environment, in which the stochastic demand and investment cost of project are shocked by unexpected events and driven by jump-diffusion processes. We extend the model considered by Jeon (2021) to the two-factor jump-diffusion model. Based on this model, the influences of unexpected events on project investment are discussed.

The remainder of this study is organized as follows. Section 2 describes the dynamics of stochastic processes involved. Section  3 studies the monopolist problem under two-factor jump-diffusion model in the presence of time-to-build, whereas the duopoly framework is studied in Sect. 4. Given these arguments, we present the results of comparative statics regarding time-to-build and compare the main result between two-factor diffusion model and jump-diffusion model in Sect. 5. Section 6 provides a summary of this whole article, and put forward the proposals for future research.

2 Basic setup and assumption

In this section, we will introduce the related mathematical model and assumptions that applied to investigate the optimal investment decision. We extend the problem studied in Jeon (2021) from only one source of uncertainty to two, namely, market demand \(X=\{X_t,t\ge 0\}\) and investment cost per unit of capacity (including unit operating cost) \(Y=\{Y_t,t\ge 0\}\). Furthermore, we suppose that both of them follow jump-diffusion process:

$$\begin{aligned}&\frac{d X_{t}}{X_{t-}}=\mu _{X}d t+\sigma _{X} d W_{t}^{X}+d \sum _{i=1}^{N_{t}^{X}} U_{i}^{X}, X_{0}=x_{0}>0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{d Y_{t}}{Y_{t-}}=\mu _{Y}d t+\sigma _{Y} d W_{t}^{Y}+d \sum _{i=1}^{N_{t}^{Y}} U_{i}^{Y}, Y_{0}=y_{0}>0 \end{aligned}$$
(2)

where \(\mu _j,\sigma _j,(j=X,Y)\) represent the drift and the instantaneous volatility respectively. \(x_0,y_0\) denote the initial values of the processes X and Y respectively. Here we employ the superscript X or Y for each parameter to make a distinction between the two processes. We assume that all processes \(\{W_t^j,t\ge 0\},\{N_t^j,t\ge 0\}\) and random variables \(\{U_i^j\}_{i\in {\mathbb {N}}}\) are independent from each other and defined on a filtered probability space \(\{\Omega ,{\mathcal {F}},\{{\mathcal {F}}_{t}\}_{t\ge 0},P\}\) satisfying the usual conditions, where \(\{W_t^j,t\ge 0\}\) is a Brownian motion process, \(\{N_t^j,t\ge 0\}\) is a time-homogeneous Poisson process with arrival intensity \(\lambda _j\), representing the total numbers of unexpected events that has arrived up to time t, \(\{U_i^j\}_{i\in {\mathbb {N}}}\) are the random percentage of jumps with values in \((-1,+\infty )\), which are independent and identically distributed in a same random variable U with mean \(m_j=E(U_i^j )=E(U)\). \(X_{t-},Y_{t-}\) represent the values of the state variables before a jump. It is noteworthy that if the parameters related to jumps equal to zero (i.e., either \(\lambda _j=0\) or \(U_i^j=0\) with probability one), then the jump-diffusion process can be simplified to the standard GBM. Since this paper is more concerned with the effects of uncertain time-to-build of duopoly firms on the investment strategies, we assume that the two stochastic processes, X, Y, are independent of each other.

As with Wu and Hu (2022), we consider the following two scenarios likewise: (1)jumps in demand, \(U^X\), takes negative values (implying downward jumps) while jumps in investment cost, \(U^I\), takes positive values (implying upward jumps). Briefly speaking, \(m_X<0\) and \(m_Y>0\); (2) Contrary to the first case, \(m_X>0\) and \(m_Y<0\). We also impose that \(r>\mu _j+\lambda _j m_j (j=X,Y)\) where \(r>0\) is the (constant) interest rate to guarantee the optimal investment time is finite (therewith, excluding trivial cases).

Moreover, the firm’s time-to-build, a period from the instant the decision to invest is taken to the instant the investment decision is implemented and generating new revenues, is supposed to be uncertain and independent from the demand and investment cost shocks. Following Jeon (2021), we character it by an exponential distribution with an intensity parameter \(\xi \).

3 Benchmark case: monopoly market

We consider a continuous-discrete time framework in which a profit-maximizing, risk-neutral firm has an opportunity to undertake an irreversible investment when facing uncertain demand and investment cost in the presence of uncertain time-to-build. The investment problem involves deciding on the investment timing and the capacity level of the production plant. The price and total investment cost at time t are given by

$$\begin{aligned} P_{t}&= X_{t}\left( 1-\eta Q_{t}\right) \end{aligned}$$
(3)
$$\begin{aligned} I_{t}&= Q_{t} Y_{t} \end{aligned}$$
(4)

where \(Q_t\) is total market output and \(\eta >0\) is a constant. If \(Q_t<1/\eta \) holds, it indicates that the market is upper bounded, i.e., the number of potential customers in that market is limited. The inverse demand function (3) that being linear in quantity also has been adopted in Aguerrevere (2003), He and Pindyck (1992), Pindyck (1988), Wu and Hu (2022). \(I_{t}\) is the total investment cost (including the operating cost) the firm needs to undertake once investing with capacity level \(Q_t\). As with Huisman and Kort (2015), we assume that the firm always produces up to capacity to avoid complicating the analysis.

In the next section, we first study the investment problem of monopoly firm, and the optimal social welfare decision is derived secondly.

3.1 Investment timing and capacity decisions

The monopoly firm is going to choose the optimal investment timing and capacity level to maximize the expected firm’s value considering the time-to-build. Thus, the firm’s investment problem can be formalized as follows:

$$\begin{aligned} V_{M}(X, Y)=\max _{T_{M}\ge 0,Q_{M}\ge 0}E^{(X,Y)}\left\{ \int _{{\widetilde{T}}_{M}}^{+\infty }e^{-rt}Q_{M}\left[ X_{t}\left( 1-\eta Q_{M}\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(5)

where \({\widetilde{T}}_{M}=T_{M}+\tau \) denotes the manufacturing timing and \(T_M\) is the investment timing, \(\tau \) is the investment lags. \(Q_{M}\) is the capacity level that the firm conducts at \(T_M\). \(E^{(X,Y)}\) denotes the expectation operator conditional on the initial state \((X_0,Y_0 )=(X,Y)\) and the subscript M indicates monopoly. The maximum is taken over all stopping times \(T_M\) with respect to the filtration generated by the joint process \((X_t,Y_t)\).

The investment problem can be solved as an optimal stopping problem in dynamic programming. By applying the strong Markov property and Fubini’s theorem, we can rewrite (5) in a simply way as follows:

$$\begin{aligned} V_{M}(X, Y)=\max _{T_{M} \ge 0, Q_{M} \ge 0} J(X,Y,Q_{M})=J^{T_M^{*}}(X,Y) \end{aligned}$$
(6)

where \(J(\cdot ,\cdot )\) is the performance criterion, \(T_M^{*}\) is called the optimal stopping time, and

$$\begin{aligned} J(X,Y,Q_{M})=E^{(X,Y)}\left[ e^{-rT_{M}}G_{M}(X_{T_{M}},Y_{T_{M}},Q_{M})\right] \end{aligned}$$
(7)

with

$$\begin{aligned} G_{M}\left( X, Y, Q_{M}\right) =\xi Q_{M}\left[ \frac{\left( 1-\eta Q_{M}\right) X}{b_{X}\left( \xi +b_{X}\right) }-\frac{ Y}{b_{Y}\left( \xi +b_{Y}\right) }\right] \end{aligned}$$
(8)

describes the expected discounted revenue flow the firm can receive after the products are listed on the market, where \(b_{i}=r-(\mu _{i}+\lambda _{i} m_{i}),(i=X,Y)\).

Referring to Nunes and Pimentel (2017), we solve the investment problem (5) by utilizing a method of variable transformation that reduces the two-dimensional investment problem to one dimension. Specifically, let \(\theta _t=\frac{X_t}{Y_t}\) be a new state variable representing the demand-to-cost ratio with \(\theta _0=\theta \), then the monopoly firm’s value function (5) can be re-written in view of this new variable as follows:

$$\begin{aligned} V_{M}(X, Y)=Y v_{M}(\theta ) \end{aligned}$$
(9)

where \(v_{M}(\theta )\) is needed to be solved. \(G_{M}\left( X,Y,Q_{M}\right) =Yg_{M}\left( \theta ,Q_{M}\right) \) with

$$\begin{aligned} g_{M}\left( \theta , Q_{M}\right) =\xi Q_{M}\left[ \frac{\left( 1-\eta Q_{M}\right) \theta }{b_{X}\left( \xi +b_{X}\right) }-\frac{1}{b_{Y}\left( \xi +b_{Y}\right) }\right] \end{aligned}$$
(10)

Following the standard arguments in real option literatures, we next successively derive the value of the firm, optimal timing of investment and capacity level in Theorem 1.

Theorem 1

(The monopolist optimal investment policy) Given the current demand-to-cost ratio \(\theta \), the monopolist optimal capacity equals to

$$\begin{aligned} Q_{M}^{*}(\theta )=\frac{1}{2\eta }\left( 1-\frac{\xi +b_{X}}{\xi +b_{Y}}\frac{1}{\theta }\right) \end{aligned}$$
(11)

The value function of the monopolist is

$$\begin{aligned} v_{M}(\theta )=\left\{ \begin{aligned}&\frac{\xi }{(\beta _{1}^{2}-1)\eta b_{Y}(\xi +b_{Y})}\left( \frac{\theta }{\theta _{M}^{*}}\right) ^{\beta _{1}} ,~~~~~~0<\theta <\theta _{M}^{*}\\&\frac{\xi }{4\eta \theta b_X(\xi +b_{X})}\left( \theta -\frac{b_X(\xi +b_{X})}{b_Y(\xi +b_{Y})}\right) ^{2}, ~~~ \theta \ge \theta _{M}^{*} \end{aligned}\right. \end{aligned}$$
(12)

where \(\beta _1\) is the positive root \((>1)\)(e.g., Nunes and Pimentel 2017) of \(Q(\beta )\):

$$\begin{aligned} Q(\beta )&=\frac{1}{2}(\sigma _{X}^{2}+\sigma _{Y}^{2})\beta (\beta -1)+(\mu _{X}-\lambda _{Y})\beta -(r-\mu _{Y}+\lambda _{X}+\lambda _{Y})\nonumber \\&\quad +\lambda _{X}E\left[ (1+U^{X})^{\beta }\right] +\lambda _{Y}E\left[ (1+U^{Y})^{1-\beta }\right] =0 \end{aligned}$$
(13)

The optimal investment threshold \(\theta _{M}^{*}\) and the corresponding capacity level \(Q_M^*\) are

$$\begin{aligned} \theta _{M}^{*}&=\frac{(\beta _{1}+1)b_X(\xi +b_{X})}{(\beta _{1}-1)b_Y(\xi +b_{Y})} \end{aligned}$$
(14)
$$\begin{aligned} Q_{M}^{*}&\equiv Q_{M}^{*}(\theta _{M}^{*})=\frac{1}{(\beta _{1}+1)\eta } \end{aligned}$$
(15)

Proof

See Appendix A.1. \(\square \)

Obviously, time-to-build can affect the firm’s investment timing rather than the capacity choice. The specific impact can be summarized as the following Corollary 1:

Corollary 1

The monotonicity of the investment threshold regarding to time-to-build depends on the relationship between \(b_X\) and \(b_Y\). Furthermore, as time-to-build converges to 0(i.e., \(\xi \rightarrow +\infty \)), the optimal investment threshold converges to that in the absence of time-to-build.

$$\begin{aligned}&\frac{d}{d\xi }\theta _{M}^{*}>0~if~b_{X}<b_{Y};\frac{d}{d\xi }\theta _{M}^{*}\le 0~if~b_{X}\ge b_{Y} \end{aligned}$$
(16)
$$\begin{aligned}&\lim _{\xi \rightarrow +\infty }\theta _{M}^{*}=\frac{\left( \beta _{1}+1\right) b_{X}}{\left( \beta _{1}-1\right) b_{Y}} \end{aligned}$$
(17)

According to Corollary 1, if \(b_X<b_Y\), a larger expected time-to-build \(\frac{1}{\xi }\) leads to a smaller \(\theta _{M}^{*}\), resulting in accelerating the investment. Otherwise, if \(b_X\ge b_Y\), the firm should delay the investment as the expected time-to-build \(\frac{1}{\xi }\) increases. This confirms Bar-Ilan and Strange (1996) while is in contrast to Jeon (2021), who showed that a larger expected time-to-build results in deferring the investment. This is largely because they simply assume only one source of uncertainty and don’t consider the unexpected events. By comparison, we suppose that both market demand and investment cost are uncertain and driven by the jump-diffusion process, resulting in that the change of the investment trigger with respect to expected time-to-build depending on the relationship of the expected growth rate of those two uncertainties.

3.2 Consumer surplus and social welfare

To investigate the effects of investment timing and capacity level on the social welfare, we first calculate the consumer surplus. Given the current market demand and investment cost X, Y, and the firm’s capacity choice Q, the instantaneous consumer surplus equals to:

$$\begin{aligned} \int _{P(Q)}^{X}D(P)dP=\int _{X(1-\eta Q)}^{X}\frac{1}{\eta }\left( 1-\frac{P}{X}\right) dP=\frac{1}{2}\eta XQ^{2} \end{aligned}$$
(18)

where the price P is given by (3). Accordingly, the total expected consumer surplus (CS) is equal to

$$\begin{aligned} CS_{M}(X,Q)=E^{(X,Y)}\left[ \int _{0}^{+\infty }e^{-rt}\frac{\eta }{2}X_{t}Q^{2}dt\right] =\frac{\xi \eta XQ^{2}}{2b_X(\xi +b_{X})} \end{aligned}$$
(19)

The expected producer surplus, exactly corresponding to the monopolist value, is given by

$$\begin{aligned} PS_{M}(X,Y,Q)=\xi Q\left[ \frac{(1-\eta Q)X}{b_X(\xi +b_{X})}-\frac{Y}{b_Y(\xi +b_{Y})}\right] \end{aligned}$$
(20)

Then, as the sum of the consumer surplus and producer surplus, the expected total social welfare equals to

$$\begin{aligned} SW_{M}(X,Y,Q)&=CS_{M}(X,Q)+PS_{M}(X,Y,Q)\nonumber \\&=\xi Q\left[ \frac{(1-\frac{\eta }{2}Q)X}{b_X(\xi +b_{X})}-\frac{Y}{b_Y(\xi +b_{Y})}\right] \end{aligned}$$
(21)

Let \(SW_{M}(X,Y,Q)=Y sw_{M}(\theta ,Q)\), then

$$\begin{aligned} sw_{M}(\theta ,Q)=\xi Q\left[ \frac{\left( 1-\frac{\eta }{2} Q\right) \theta }{b_X(\xi +b_{X})}-\frac{1}{b_Y(\lambda +b_{Y})}\right] \end{aligned}$$
(22)

By taking the optimal investment threshold and capacity level in Theorem 1 into (22), we can derive the expected social welfare at the investment timing as:

$$\begin{aligned} sw_{M}(\theta _{M}^{*},Q_{M}^{*})=\frac{3\xi }{2(\beta _{1}^{2}-1)\eta b_Y(\xi +b_{Y})} \end{aligned}$$
(23)

On the other hand, from the perspective of a social planner, by maximizing the total social welfare, the optimal investment threshold and capacity level are

$$\begin{aligned} \theta _{MW}^{*}&=\frac{(\beta _{1}+1)b_X(\xi +b_{X})}{(\beta _{1}-1)b_Y(\xi +b_{Y})}=\theta _{M}^{*} \end{aligned}$$
(24)
$$\begin{aligned} Q_{MW}^{*}&=\frac{2}{(\beta _{1}+1) \eta }=2Q_{M}^{*} \end{aligned}$$
(25)

Substituting (24) and (25) into (22), the expected social welfare with the goal of welfare maximization at the investment timing is given by

$$\begin{aligned} sw_{M}(\theta _{MW}^{*},Q_{MW}^{*})=\frac{2\xi }{(\beta _{1}^{2}-1)\eta b_Y(\xi +b_{Y})} \end{aligned}$$
(26)

Hence, the welfare loss at the investment timing in the monopoly market is equal to

$$\begin{aligned} wl_{M}=\frac{sw_{M}(\theta _{MW}^{*},Q_{MW}^{*})-sw_{M}(\theta _{M}^{*},Q_{M}^{*})}{sw_{M}(\theta _{M W}^{*},Q_{MW}^{*})}=\frac{1}{4} \end{aligned}$$
(27)

Following the above arguments, we can draw the conclusion that in the presence of time-to-build, the optimal investment threshold of welfare-maximizing is equal to that of firm’s value maximization, while the optimal capacity of the former is twice that of the latter, resulting in a welfare loss of \(\frac{1}{4}\).

4 Duopoly market

In this section, by adding an additional firm, we extend the investment problem from the monopoly market to the duopoly market, in which two risk-neutral firms compete with homogenous goods and make the investment strategy involving investment timing and capacity choice. As with the existing literatures about timing games(e.g., Fudenberg and Tirole 1985), the firm that invests earlier is called the leader and that invests later is called the follower. In the meanwhile, if the order of entering has been already known before investing, in other words, there is no competition for leadership, we claim that the duopoly firms’ roles are exogenous. Otherwise, we claim that the roles are endogenous, indicating that two firms compete to be the first investor.

Next, we first examine the optimal investment strategies for the former case in Sect. 4.1. Afterwards the optimal investment strategies for the latter case in which the firms’ roles are exogenous are investigated in Sect. 4.2. Given these arguments, in Sect. 4.3, we discuss the welfare-maximizing investment policy.

4.1 Exogenous role

In the duopoly market, there are two firms of type A and B, who are asymmetric with time-to-build. Denote type i firm’s time-to-build as \(\tau _{i}\), which follows an exponential distribution with parameter \(\xi _{i}\),\(i=A,B\). Due to the asymmetry of the investment lags, the product of the leader who invests earlier may enter the market later than that of the follower. Specifically, there are three possible scenarios, as shown in Fig. 1. The specific explanation is as follows:

Fig. 1
figure 1

Three possible scenarios regarding timing of investment and time-to-build

Full size image

  • Case 1: \(T_{L}<{\widetilde{T}}_{L}<T_{F}\), indicating that the time that the leader’s product enters the market, \({\tilde{T}}_{L}\), is earlier than the follower’s investment timing, \(T_{F}\), and thus the follower’s product enters the market afterwards.

  • Case 2: \(T_{F}<{\widetilde{T}}_{L}<{\widetilde{T}}_{F}\), indicating that the time the leader’s product enters the market is between the follower’s investment timing and the manufacturing time, and thus the follower’s product enters the market afterwards.

  • Case 3: \(T_{F}<{\widetilde{T}}_{F}<{\widetilde{T}}_{L}\), indicating that the time the leader’s product enters the market is later than the follower’s although its investment timing is earlier.

Now we proceed to investigate the duopoly firms’ optimal investment timing and capacity choice. Assuming that the market roles are exogenous, without lose of generality, here we specify the firm i as the leader and thus firm j as the follower, \(i,j\in \{A,B\}\). Denote the type i leader’s investment timing, manufacturing timing and capacity choice as \(T_L^{i},{\widetilde{T}}_L^{i},Q_L^{i}\). Given the leader had invested, then the possible investment timing of the type j follower can be expressed as \(T_{F0}^{j}=\inf \left\{ t\in (0,{\widetilde{T}}_{L}^{i})\mid \theta _{t}\ge \theta _{F0}^{j}\right\} \), \(T_{F1}^{j}=\inf \left\{ t\in ({\widetilde{T}}_{L}^{i},+\infty )\mid \theta _{t}\ge \theta _{F1}^{j}\right\} \), representing the investment timing of the follower is earlier and later than the manufacturing timing of the leader respectively. The capacity levels of the type j follower corresponding to these two cases are denoted as \(Q_{F0}^{j}\) and \(Q_{F1}^{j}\). Similarly, the type i leader’s investment timing can be described as \(T_{L}^{i}=\inf \left\{ t\in (0,T_{F0}^{j})\mid \theta _{t}\ge \theta _{L}^{i}\right\} \).

With these assumptions, the type i and j firms’ roles playing in the duopoly market and their corresponding investment strategies can be charactered by the following tuple:

$$\begin{aligned} {\mathcal {S}}_{ij}=\left\{ i,j,\theta _{L}^{i},Q_{L}^{i},\theta _{F0}^{j},Q_{F0}^{j},\theta _{F1}^{j},Q_{F1}^{j}\right\} \end{aligned}$$
(28)

Following the standard approach in the Option Games, we explore the investment problem by backward derivation. First, we study the investment decision of the follower in Case 1, in which the leader’s product has entered the market. For a given level of the type i leader’s investment capacity \(Q_L^i\), the type j follower’s investment problem in Case 1 can be formalized as:

$$\begin{aligned}&v_{F1}^{j}(\theta ,Q_{L}^{i})=\frac{1}{Y}V_{F1}^{j}(X,Y,Q_{L}^{i})\nonumber \\&\quad =\frac{1}{Y}{\max _{T_{F1}^{j}\ge 0,Q_{F1}^{j}\ge 0}}E^{(X,Y)}\left\{ \int _{{\widetilde{T}}_{F1}^{j}}^{+\infty }e^{-rt}Q_{F 1}^{j}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F 1}^{j})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(29)

where \({\widetilde{T}}_{F1}^{j}=T_{F1}^{j}+\tau _{j}\) represents the type j follower’s manufacturing timing in Case 1. Given these, the type j follower’s optimal investment strategy can be derived in the following Theorem 2.

Theorem 2

(Follower’s optimal investment strategy after the entry of leader’s product) Given the current demand-to-cost ratio \(\theta \), the product of type i leader have already entered the market with the capacity level \(Q_L^i\), then the type j follower’s optimal capacity level \(Q_{F1}^{j*} (\theta ,Q_L^i )\) is equal to

$$\begin{aligned} Q_{F1}^{j*}(\theta ,Q_{L}^{i})=\frac{1}{2\eta }\left( 1-\eta Q_{L}^{i}-\frac{1}{\theta }\frac{\xi _{j}+b_{X}}{\xi _{j}+b_{Y}}\right) \end{aligned}$$
(30)

The value function of the follower \(v_{F1}^j(\theta ,Q_L^i)\) is

$$\begin{aligned} v_{F1}^j(\theta ,Q_L^i)=\left\{ \begin{array}{lr} g_{F1}^{j}(Q_{L}^{i})\left( \frac{\theta }{\theta _{F1}^{j*}(Q_{L}^{i})}\right) ^{\beta _{1}}, &{}\theta <\theta _{F1}^{j*}(Q_{L}^{i}) \\ g_{F1}^{j}(\theta ,Q_{L}^{i}),&{}\theta \ge \theta _{F1}^{j*}(Q_{L}^{i}) \end{array}\right. \end{aligned}$$
(31)

where \(g_{F1}^{j}(Q_{L}^{i}):=g_{F1}^{j}\left( \theta _{F1}^{j*}(Q_{L}^{i}),Q_{L}^{i},Q_{F1}^{j*}(Q_{L}^{i})\right) \) and \(g_{F1}^{j}(\theta ,Q_{L}^{i}):=g_{F1}^{j}\bigg (\theta ,Q_{L}^{i},Q_{F1}^{j*}(\theta ,Q_{L}^{i})\bigg )\) with

$$\begin{aligned} g_{F1}^{j}(\theta _{F1}^{j},Q_{L}^{i},Q_{F1}^{j})=\frac{\xi _{j}Q_{F1}^{j}\theta _{F1}^{j}\left( 1-\eta (Q_{L}^{i}+Q_{F 1}^{j})\right) }{b_X(\xi _{j}+b_{X})}-\frac{\xi _{j}Q_{F1}^{j}}{b_Y(\xi _{j}+b_{Y})} \end{aligned}$$
(32)

The optimal investment threshold \(\theta _{F 1}^{j*}(Q_{L}^{i})\) and capacity level \(Q_{F1}^{j*}(Q_{L}^{i})\) are

$$\begin{aligned} \theta _{F1}^{j*}(Q_{L}^{i})&=\frac{(\beta _{1}+1)b_X(\xi _{j}+b_{X})}{(\beta _{1}-1)b_Y(\xi _{j}+b_{Y})(1-\eta Q_{L}^{i})} \end{aligned}$$
(33)
$$\begin{aligned} Q_{F1}^{j*}(Q_{L}^{i})&\equiv Q_{F1}^{j*}\left( \theta _{F1}^{j*}(Q_{L}^{i}),Q_{L}^{i}\right) =\frac{1-\eta Q_{L}^{i}}{(\beta _{1}+1)\eta } \end{aligned}$$
(34)

Proof

See Appendix A.2.1. \(\square \)

Note that the follower’s optimal capacity level shown in (34) appears to be independent of \(\xi _i\),\(\xi _j\). But in fact, the capacity choice of the follower depends on the leader’s capacity level \(Q_L^i\), and the leader makes the capacity choice after fully considering the investment lags of duopoly firms. To be brief, \(\xi _i\),\(\xi _j\) affect the output level of the follower indirectly by influencing the output level of the leader, which will be discussed in the next section.

Next, we continue to analyse the type j follower’s optimal investment strategies of Cases 2 and 3, in which the product of the type i leader has not been on the market yet due to the investment lags. In these two cases, not only the leader’s capacity level but also the time-to-build of both two firms should be taken into consideration when the follower makes the investment decision. Thus, the type j follower’s value function can be formalized as:

$$\begin{aligned} v_{F0}^{j}\left( \theta ,Q_{L}^{i}\right) =\frac{1}{Y}V_{F0}^{j}\left( X,Y,Q_{L}^{i}\right) =\frac{1}{Y}{\max _{T_{F0}^{j}\ge 0,Q_{F0}^{j} \ge 0}}E^{(X,Y)}\left[ I_{V_{F0}}+II_{V_{F0}}+III_{V_{F0}}\right] \qquad \end{aligned}$$
(35)

where

$$\begin{aligned} I_{V_{F0}}&=1_{\left\{ {\widetilde{T}}_{L}^{i}<T_{F 0}^{j}\right\} }\left\{ e^{-r{\widetilde{T}}_{L}^{i}}V_{F1}^{j}(X_{{\widetilde{T}}_{L}^{i}},Y_{{\widetilde{T}}_{L}^{i}},Q_{L}^{i})\right\} \end{aligned}$$
(36)
$$\begin{aligned} II_{V_{F0}}&=1_{\left\{ T_{F0}^{j}\le {\widetilde{T}}_{L}^{i}<{\widetilde{T}}_{F0}^{j}\right\} }\left\{ \int _{{\widetilde{T}}_{F0}^{j}}^{+\infty }e^{-rt}Q_{ F0}^{j}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F0}^{j})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(37)
$$\begin{aligned} III_{V_{F0}}&=1_{\left\{ {\widetilde{T}}_{L}^{i} \ge {\widetilde{T}}_{F0}^{j}\right\} }\left\{ \int _{{\widetilde{T}}_{F0}^{j}}^{{\widetilde{T}}_{L}^{i}}e^{-rt} Q_{F0}^{j}\left[ X_{t}(1-\eta Q_{F0}^{j})-Y_{t}\right] dt\right. \nonumber \\&\quad \left. +\int _{{\widetilde{T}}_{L}^{i}}^{+\infty } e^{-rt}Q_{F0}^{j}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F 0}^{j})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(38)

where \({\widetilde{T}}_{F0}^{j}=T_{F0}^{j}+\tau _{j}\) denotes the type j follower’s manufacturing timing and \(T_{F0}^{j}\) is the timing of investment, which is earlier than the entry time of the leader’s product.

The expression (36) corresponds to Case 1, and the optimal investment decision of the follower has been concluded in Theorem 2. The expression (37) corresponds to Case 2, where the entry time of the leader’s product is between the follower’s investment timing and manufacturing timing. (38) corresponds to Case 3, where the entry time of the follower’s product is even earlier than that of the leader. Following the same arguments as before, we can derive the type j follower’s optimal investment decision as follows:

Theorem 3

(Follower’s optimal investment strategy before the entry of leader’s product) Given the current demand-to-cost ratio \(\theta \) and the type i leader’s capacity level \(Q_L^i\), then the type j follower’s optimal capacity level \(Q_{F0}^{j*} (\theta ,Q_L^i )\) is equal to

$$\begin{aligned} Q_{F0}^{j*}(\theta ,Q_{L}^{i})=\frac{1}{2\eta }\left[ \frac{(1-\eta Q_{L}^{i}) \xi _{i}+\left( \xi _{j}+b_{X}\right) \left( 1-\frac{\xi _{i} \eta Q_{L}^{i}}{\xi _{i}+b_{X}}\right) }{\xi _{i}+\xi _{j}+b_{X}}-\frac{b_X\left( \xi _{j}+b_{X}\right) }{\theta b_Y\left( \xi _{j}+b_{Y}\right) }\right] \end{aligned}$$
(39)

The value function of the follower \(v_{F0}^{j}(\theta , Q_{L}^{i})\) is

$$\begin{aligned} v_{F0}^{j}(\theta , Q_{L}^{i})=\left\{ \begin{array}{l} g_{F0}^{j}(Q_{L}^{i})\left( \frac{\theta }{\theta _{F0}^{j *}\left( Q_{L}^{i}\right) }\right) ^{\gamma _{i}}+g_{F1}^{j}(Q_{L}^{i})\left\{ \left( \frac{\theta }{\theta _{F 1}^{j *}\left( Q_{L}^{i}\right) }\right) ^{\beta _{1}}\right. \\ \quad \left. -\left( \frac{\theta }{\theta _{F 0}^{j *}\left( Q_{L}^{i}\right) }\right) ^{\gamma _{i}}\left( \frac{\theta _{F 0}^{j *}\left( Q_{L}^{i}\right) }{\theta _{F 1}^{j *}\left( Q_{L}^{i}\right) }\right) ^{\beta _{1}}\right\} , ~~~0<\theta <\theta _{F 0}^{j *}(Q_{L}^{i}) \\ g_{F0}^{j}(\theta ,Q_{L}^{i}), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\theta \ge \theta _{F0}^{j*}(Q_{L}^{i}) \end{array}\right. \end{aligned}$$
(40)

where \(g_{F0}^{j}(Q_{L}^{i}):=g_{F0}^{j}\left( Q_{L}^{i},\theta _{F0}^{j*}(Q_{L}^{i}),Q_{F0}^{j*}(Q_{L}^{i})\right) \) and \(g_{F0}^{j}(\theta ,Q_{L}^{i}):=g_{F0}^{j}\Big (\theta ,Q_{L}^{i},Q_{F0}^{j*}(\theta ,Q_{L}^{i})\Big )\) with

$$\begin{aligned} g_{F0}^{j}(\theta _{F0}^{j},Q_{F0}^{j},Q_{L}^{i})&=\frac{\xi _{j}Q_{F0}^{j}\theta _{F 0}^{j}}{b_X\left( \xi _{i}+\xi _{j}+b_{X}\right) }\left[ \frac{\xi _{i}\left( 1-\eta (Q_{L}^{i}+Q_{F 0}^{j})\right) }{\xi _{j}+b_{X}}\right. \nonumber \\&\quad \left. +\left( 1-\eta Q_{F0}^{j}\right) -\frac{\xi _{i}\eta Q_{L}^{i}}{\xi _{i}+b_{X}}\right] -\frac{Q_{F0}^{j}\xi _{j}}{b_Y(\xi _{j}+b_{Y})} \end{aligned}$$
(41)

The optimal investment threshold \(\theta _{F0}^{j*}(Q_{L}^{i})\) and the corresponding capacity level \(Q_{F0}^{j*}(Q_{L}^{i})\) are implicitly derived from (39) and

$$\begin{aligned}&\frac{(\gamma _i-\beta _{1})(1-\eta Q_{L}^{i}) \xi _{j}}{(\beta _{1}-1)^{2}b_Y(\xi _{j}+b_{Y})\eta }\left( \frac{\theta _{F0}^{j *}(Q_{L}^{i})}{\theta _{F1}^{j*}(Q_{L}^{i})}\right) ^{\beta _{1}}+\frac{\gamma _{i}Q_{F0}^{j *}(\theta ,Q_{L}^{i})\xi _{j}}{b_Y(\xi _{j}+b_{Y})}\nonumber \\&\quad =\frac{(\gamma _{i}-1)\xi _{j}Q_{F0}^{j*}(\theta ,Q_{L}^{i})\theta _{F0}^{j *}(Q_{L}^{i})}{b_X(\xi _{i}+\xi _{j}+b_{X})}\nonumber \\&\qquad \times \left[ \frac{\xi _{i}\left( 1-\eta (Q_{L}^{i}+Q_{F0}^{j*}(\theta ,Q_{L}^{i}))\right) }{\xi _{j}+b_{X}}+\left( 1-\eta Q_{F0}^{j *}(\theta ,Q_{L}^{i})\right) -\frac{\xi _{i}\eta Q_{L}^{i}}{\xi _{i}+b_{X}}\right] \end{aligned}$$
(42)

Proof

See Appendix A.2.2. \(\square \)

It is worth mentioning that, unlike \(Q_{F1}^{j*}(Q_{L}^{i})\), \(Q_{F0}^{j*}(Q_{L}^{i})\) is directly affected by both firms’ time-to-build according to (39). This is principally because there is no product on the market yet when the follower invests with \(Q_{F0}^{j}\), the asymmetry of both firms’ time-to-build makes it possible for the entry time of the follower’s product earlier than that of the leader.

We now proceed to examine the type i leader’s optimal investment strategy. Taking the follower’s investment timing and capacity choice into account, the value function of the type i leader can be formalized as follows:

$$\begin{aligned} v_{L}^{i}(\theta )=\frac{1}{Y}V_{L}^{i}(X,Y)=\frac{1}{Y}{\max _{T_{L}^{i}\ge 0,Q_{L}^{i}\ge 0}}E^{(X,Y)}\left[ I_{L}+II_{L}+III_{L}\right] \end{aligned}$$
(43)

where

$$\begin{aligned} I_{L}&=1_{\left\{ {\widetilde{T}}_{L}^{i}<T_{F0}^{j*}\right\} }\left\{ \int _{{\widetilde{T}}_{L}^{i}}^{{\widetilde{T}}_{F1}^{j*}}e^{-rt} Q_{L}^{i}\left[ X_{t}\left( 1-\eta Q_{L}^{i}\right) -Y_{t}\right] dt\right. \nonumber \\&\quad \left. +\int _{{\widetilde{T}}_{F1}^{j*}}^{+\infty }e^{-rt} Q_{L}^{i}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F1}^{j*})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(44)
$$\begin{aligned} II_{L}&= 1_{\left\{ T_{F0}^{j*}\le {\widetilde{T}}_{L}^{i}<{\widetilde{T}}_{F0}^{j *}\right\} }\left\{ \int _{{\widetilde{T}}_{L}^{i}}^{{\widetilde{T}}_{F0}^{j*}}e^{-rt}Q_{L}^{i}\left[ X_{t}\left( 1-\eta Q_{L}^{i}\right) -Y_{t}\right] dt\right. \nonumber \\&\quad \left. +\int _{{\widetilde{T}}_{F0}^{j*}}^{+\infty }e^{-rt} Q_{L}^{i}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F0}^{j*})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(45)
$$\begin{aligned} III_{L}&= 1_{\left\{ {\widetilde{T}}_{L}^{i}\ge {\widetilde{T}}_{F0}^{j*}\right\} }\left\{ \int _{{\widetilde{T}}_{L}^{i}}^{+\infty }e^{-rt} Q_{L}^{i}\left[ X_{t}\left( 1-\eta (Q_{L}^{i}+Q_{F0}^{j*})\right) -Y_{t}\right] dt\right\} \end{aligned}$$
(46)

where \({\widetilde{T}}_{F0}^{j*}\) and \({\widetilde{T}}_{F1}^{j*}\) represent the manufacturing timing of the type j follower, given the optimal investment in (29) and (35) respectively.

(44) corresponds the Case 1 above, in which the investment timing of the follower is later than the entry time of the leader’s product. (45) corresponds to Case 2, that is, the entry time of the leader’s product is between the follower’s investment timing and manufacturing timing. (46) corresponds to the Case 3, indicating that although the type i leader’s investment timing is earlier, the entry time of leader’s product is even later than that of the type j follower’s product. Following the similar arguements, the type i leader’s optimal investment strategy can be obtained in the following Theorem 4.

Theorem 4

(Leader’s optimal investment strategy) Given the current demand-to-cost ratio \(\theta \), the value function of the type i leader when invests at \(\theta _{L}^{i}\) with capacity \(Q_{L}^{i}\) is

$$\begin{aligned} v_{P}^{i}(\theta )=\left\{ \begin{array}{lr} g_{L}^{i}(\theta _{L}^{i*},Q_{L}^{i*})\left( \frac{\theta }{\theta _{L}^{i*}}\right) ^{\beta _{1}}, &{}0<\theta <\theta _{L}^{i*} \\ g_{L}^{i}(\theta ,Q_{L}^{i*}), &{}\theta \ge \theta _{L}^{i*} \end{array}\right. \end{aligned}$$
(47)

where \(g_{L}^{i}(\theta _{L}^{i*}, Q_{L}^{i*})=g_{L}^{i}(\theta ,Q_{L}^{i})\mid _{\theta =\theta _{L}^{i*},Q_{L}^{i}=Q_{L}^{i*}}\), \(g_{L}^{i}(\theta ,Q_{L}^{i*})=g_{L}^{i}(\theta ,Q_{L}^{i})\mid _{Q_{L}^{i}=Q_{L}^{i*}}\) and \(g_{L}^{i}(\theta ,Q_{L}^{i})=g_{L}^{i}\left( \theta ,Q_{L}^{i},\theta _{F0}^{j*}(Q_{L}^{i}),Q_{F0}^{j *}(Q_{L}^{i}),\theta _{F1}^{j*}(Q_{L}^{i}),Q_{F1}^{j*}(Q_{L}^{i})\right) \) with

$$\begin{aligned}&g_{L}^{i}\left( \theta ,Q_{L}^{i},\theta _{F0}^{j},Q_{F0}^{j},\theta _{F1}^{j},Q_{F1}^{j}\right) =\frac{\xi _{i}(1-\eta Q_{L}^{i})Q_{L}^{i} \theta }{b_X(\xi _{i}+b_{X})}-\frac{\xi _{i}Q_{L}^{i}}{b_Y(\xi _{i}+b_{Y})}\nonumber \\&\quad -\left( \frac{\theta }{\theta _{F0}^{j}}\right) ^{\gamma _{i}}\frac{\xi _{i}\xi _{j}\eta Q_{L}^{i}Q_{F0}^{j}\theta _{F 0}^{j}}{b_X(\xi _{i}+\xi _{j}+b_{X})}\left( \frac{1}{\xi _{i}+b_{X}}+\frac{1}{\xi _{j}+b_{X}}\right) \nonumber \\&\quad -\left[ \left( \frac{\theta }{\theta _{F1}^{j}}\right) ^{\beta _{1}}-\left( \frac{\theta }{\theta _{F 0}^{j}}\right) ^{\gamma _{i}}\left( \frac{\theta _{F0}^{j}}{\theta _{F1}^{j}}\right) ^{\beta _{1}}\right] \frac{\xi _{j}\eta Q_{L}^{i}Q_{F 1}^{j} \theta _{F1}^{j}}{b_X(\xi _{j}+b_{X})} \end{aligned}$$
(48)

The optimal investment threshold \(\theta _{L}^{i*}\) and capacity \(Q_{L}^{i*}\) are implicitly derived from

$$\begin{aligned} \underset{\theta _{L}^{i}\ge 0,Q_{L}^{i}\ge 0}{\arg \max }g_{L}^{i}(\theta _{L}^{i}, Q_{L}^{i}) \end{aligned}$$
(49)

Proof

See Appendix A.2.3. \(\square \)

According to (48), the type i leader’s capacity level \(Q_{L}^{i*}\) is directly related with both firms’ time-to-build, as with \(Q_{F0}^{j*}(Q_{L}^{i})\). This is mainly because that, due to the asymmetry of both firms’ time-to-build, the type i leader does not know which strategies the type j follower will adopt when undertaking the investment with capacity \(Q_L^i\).

On the basis of the Theorems 2–4, we can directly obtain the Corollary 2 as follows.

Corollary 2

The type i and j firms’ optimal investment strategies acting as the exogenous leader and follower respectively can be summarized as follows:

$$\begin{aligned} {\mathcal {S}}_{ij}^{*}=\left\{ i,j,\theta _{L}^{i*},Q_{L}^{i*},\theta _{F0}^{j*}(Q_{L}^{i*}),Q_{F0}^{j*}(Q_{L}^{i*}),\theta _{F1}^{j *}(Q_{L}^{i*}),Q_{F1}^{j*}(Q_{L}^{i*})\right\} \end{aligned}$$
(50)

For the sake of notation, hereafter, terms in (48) can be abbreviated as follows:

$$\begin{aligned} \psi _{i j}^{0}:=\left( \frac{\theta _{L}^{i}}{\theta _{F 0}^{j}}\right) ^{\gamma _{i}};~\psi _{i j}^{1}:=\left( \frac{\theta _{L}^{i}}{\theta _{F 1}^{j}}\right) ^{\beta _{1}}-\left( \frac{\theta _{L}^{i}}{\theta _{F 0}^{j}}\right) ^{\gamma _{i}}\left( \frac{\theta _{F 0}^{j}}{\theta _{F 1}^{j}}\right) ^{\beta _{1}} \end{aligned}$$
(51)

4.2 Endogenous role

In this section, we relax the assumption that firms’ roles are exogenous and endogenize the roles in a duopoly market. With this setting, the first-mover advantage gives the duopoly firms an incentive to preempt the market and thus determine their market position through competition. By considering the preemption incentives we next investigate the roles of the duopoly firms as well as the corresponding investment strategies.

If the type i firm chooses to invest as a follower after the type j firm’s entry with capacity \(Q_{L}^{j}\), given the current demand-to-cost ratio \(\theta \), then its value is \(v_{F0}^{i}(\theta ,Q_{L}^{j})\), given in (35). Otherwise, if the type i firm intends to preempt the market, then its value as a preemptive leader can be formalized as follows:

$$\begin{aligned} v_{P}^{i}(\theta )=\left\{ \begin{array}{lr} g_{L}^{i}(\theta ,Q_{L}^{i*}(\theta )), &{} 0<\theta \le \theta _{F0}^{j*}(Q_{L}^{i*}(\theta )) \\ g_{S}^{i}(\theta ,Q_{L}^{i*}(\theta )), &{}\theta >\theta _{F0}^{j*}(Q_{L}^{i*}(\theta )) \end{array}\right. \end{aligned}$$
(52)

where

$$\begin{aligned} g_{S}^{i}(\theta ,Q_{L}^{i})&=\frac{\xi _{i} Q_{L}^{i}\theta }{b_X(\xi _{i}+\xi _{j}+b_{X})}\left\{ (1-\eta Q_{L}^{i})-\frac{\xi _{j}\eta Q_{F0}^{j*}(Q_{L}^{i})}{\xi _{j}+b_{X}}\right. \nonumber \\&\quad \left. +\frac{\xi _{j}}{\xi _{i}+b_{X}}\left[ 1-\eta \left( Q_{L}^{i}+Q_{F0}^{j *}(Q_{L}^{i})\right) \right] \right\} -\frac{\xi _{i}Q_{L}^{i}}{b_Y(\xi _{i}+b_{Y})} \end{aligned}$$
(53)

indicates that the profits the type i firm expects to benefit from the simultaneous investment, which happens when the current demand-to-cost ratio \(\theta \) is high enough and even exceeds the type j firm’s investment threshold \(\theta _{F0}^{j*}(Q_{L}^{i *}(\theta ))\).

As for the preemptive motive, if the firm’s value acting as a preemptive leader dominates that of a follower, then it will preempt the market. Otherwise, it prefers to enter as a follower. Thus, we can define the preemptive threshold of the type i firm as \(\theta _{P}^{i}=\inf \{\theta >0,v_{P}^{i}(\theta )\ge v_{F0}^{j}(\theta ,Q_{L}^{j})\}\), at which there is no difference between investing as a preemptive leader and a follower. Following Huisman and Kort (2015); Wu and Hu (2022); Thijssen et al. (2012), since the first to enter the market can enjoy a short-lived monopoly profit, we assume that at least one firm has a preemption motive in the preemption game, that is, \(\theta _{P}^{i}\cup \theta _{P}^{j}\ne \emptyset ,i\ne j,i,j\in \{A,B\}\).

Firstly, assume that only one firm has the preemption motivation and we designate as firm i. Due to the absence of entry competition, the optimal investment strategy of a preemptive leader is consistent with that of a dominate leader. Secondly, we assume that both firms have the preemptive incentives and the type i firm succeeds in preempting, that is, \(\theta _{P}^{i*}<\theta _{P}^{j*}\). Naturally, the type j firm comes to be a follower. Within this scenario, if \(\theta _{P}^{i*}<\theta _{P}^{j*}<\theta _{L}^{i*}\), the type i firm will implement the investment at \(\theta _{P}^{j*}\) for the reason that it can still be the market leader till \(\theta _{P}^{j*}\). Otherwise, if \(\theta _{P}^{i*}<\theta _{L}^{i*}<\theta _{P}^{j*}\), the type i firm invests at \(\theta _{L}^{i*}\) as a dominate leader since the type j firm’s too low preemptive motivation.

In summary, the endogenous roles of the duopoly firms as well as the corresponding optimal investment strategies can be concluded in the the following Theorem 5.

Theorem 5

(Optimal investment strategy with preemptive incentive) Given the current demand-to-cost ratio \(\theta \),the type i firm’s optimal preemptive threshold \(\theta _{P}^{i*}\) can be derived from

$$\begin{aligned} v_{P}^{i}(\theta _{P}^{i*})=v_{F0}^{i}(\theta _{P}^{i*},Q_{P}^{j*}) \end{aligned}$$
(54)

where \(Q_{P}^{j*}=\underset{Q_{L}^{j}\ge 0}{\arg \max }g_{L}^{i}(\theta _{P}^{i*},Q_{L}^{j})\) for \(i,j\in \{A,B\}\) and \(i\ne j\).

A) if \(\theta _{P}^{i*}\ne \emptyset \) for \(i\in \{A,B\}\) and \(\theta _{P}^{i*}<\theta _{P}^{j*}\) for \(i\ne j\), and

    (a) if \(\theta _{P}^{j*}<\theta _{L}^{i*}\), the optimal investment strategy is

$$\begin{aligned} {\mathcal {S}}^{*}=\left\{ i,j,\theta _{P}^{j*},Q_{P}^{i*},\theta _{F0}^{j*}(Q_{P}^{i*}),Q_{F0}^{j*}(Q_{P}^{i*}), \theta _{F1}^{j*}(Q_{P}^{i*}),Q_{F1}^{j*}(Q_{P}^{i*})\right\} \end{aligned}$$
(55)

            where \(Q_{P}^{i*}=Q_{L}^{i*}(\theta _{P}^{j*})\).

    (b) if \(\theta _{P}^{j*}>\theta _{L}^{i*}\), the optimal investment strategy is

$$\begin{aligned} {\mathcal {S}}^{*}={\mathcal {S}}_{ij}^{*}=\left\{ i,j,\theta _{L}^{i*},Q_{L}^{i*},\theta _{F0}^{j*}(Q_{L}^{i*}),Q_{F0}^{j *}(Q_{L}^{i*}),\theta _{F1}^{j*}(Q_{L}^{i*}),Q_{F1}^{j*}(Q_{L}^{i*})\right\} \end{aligned}$$
(56)

            where \(Q_{L}^{i*}=Q_{L}^{i*}(\theta _{L}^{i*})\).

B) if \(\theta _{P}^{i*}\ne \emptyset \) and \(\theta _{P}^{j*}=\emptyset \) for \(i\ne j\), the optimal investment strategy is (56).

Proof

See Appendix A.2.4. \(\square \)

4.3 Social welfare

Given the firms’ roles are exogenous and the corresponding investment strategies are \({\mathcal {S}}_{ij}\) in (28), we analyze the social welfare in the duopoly market in this section. On the basis of the arguments in Sect. 3.2, given the current demand-to-cost ratio \(\theta \), the consumer surplus in the duopoly market can be formalized as:

$$\begin{aligned}&cS_D\left( \theta ,{\mathcal {S}}_{ij}\right) =\frac{1}{Y}CS_D\left( X,Y,{\mathcal {S}}_{ij}\right) \nonumber \\&\quad =\frac{1}{Y}E^{(X,Y)}\left[ 1_{\{{\overline{T}}_L^i<T_{F0}^j\}}\left\{ \int _{{\overline{T}}_L^i}^{{\overline{T}}_{F1}^j}e^{-rt} \frac{\eta }{2}X_t(Q_L^i)^2 dt+\int _{{\overline{T}}_{F1}^j}^{+\infty }e^{-rt}\frac{\eta }{2}X_t\left( Q_L^i+Q_{F1}^j\right) ^2dt\right\} \right. \nonumber \\&\qquad \left. +1_{\left\{ T_{F0}^j\le {\overline{T}}_L^i<{\overline{T}}_{F0}^j\right\} }\left\{ \int _{{\overline{T}}_L^i}^{{\overline{T}}_{F0}^j}e^{-rt} \frac{\eta }{2}X_t\left( Q_L^i\right) ^2d t+\int _{{\overline{T}}_{F0}^j}^{+\infty }e^{-rt}\frac{\eta }{2}X_t\left( Q_L^i+Q_{F0}^j\right) ^2dt\right\} \right. \nonumber \\&\qquad \left. +1_{\left\{ {\overline{T}}_L^i\ge {\overline{T}}_{F0}^j\right\} }\left\{ \int _{{\overline{T}}_{F0}^j}^{{\overline{T}}_L^i}e^{-rt} \frac{\eta }{2}X_t(Q_{F0}^j)^2 dt+\int _{{\overline{T}}_L^i}^{+\infty }e^{-rt}\frac{\eta }{2}X_t\left( Q_L^i+Q_{F0}^j\right) ^2dt\right\} \right] \end{aligned}$$
(57)

Note that (57) is similar to (35) in the form of expression, we can calculate it by a similar method as in Appendix A.2.3. After a series of complicated manipulation, (57) can be re-written as follows:

$$\begin{aligned}&cs_D\left( \theta ,{\mathcal {S}}_{ij}\right) =\frac{\eta }{2b_X}\left( \frac{\theta }{\theta _L^i}\right) ^{\beta _1}\left\{ \frac{\xi _i \theta _L^i(Q_L^i)^2}{\xi _i+b_X}+\psi _{ij}^1\frac{\xi _j\theta _{F1}^j\left( 2Q_L^iQ_{F1}^j+(Q_{F1}^j)^2\right) }{\xi _j+b_X}\right. \nonumber \\&\quad \left. +\psi _{ij}^0\theta _{F0}^j\left[ -\frac{\xi _i(Q_L^i)^2}{\xi _i+b_X}+\frac{\xi _i}{\xi _i+\xi _j+b_X}\left( (Q_L^i)^2 +\frac{\xi _j\left( 2Q_L^iQ_{F0}^j+(Q_{F0}^j)^2\right) }{\xi _j+b_X}\right) \right. \right. \nonumber \\&\quad \left. \left. +\frac{\xi _j}{\xi _i+\xi _j+b_X}\left( (Q_{F 0}^j)^2+\frac{\xi _i\left( 2Q_L^i Q_{F0}^j+(Q_L^i)^2\right) }{\xi _i+b_X}\right) \right] \right\} \end{aligned}$$
(58)

The expected producer surplus exactly corresponds to the sum of the duopoly firms’ values, that is

$$\begin{aligned} ps_{D}(\theta ,{\mathcal {S}}_{ij})=v_{L}^{i}(\theta ,{\mathcal {S}}_{ij})+v_{F}^{j}(\theta ,{\mathcal {S}}_{ij}) \end{aligned}$$
(59)

where

$$\begin{aligned} v_{F}^{j}(\theta ,{\mathcal {S}}_{ij})=\left( \frac{\theta }{\theta _{L}^{i}}\right) ^{\beta _{1}}v_{F0}^{j}(\theta _{L}^{i},{\mathcal {S}}_{ij}) \end{aligned}$$
(60)

denotes the value of the follower before the leader undertakes the investment. Accordingly, the social welfare level in the duopoly market can be derived as follows:

$$\begin{aligned}&sw_D\left( \theta ,{\mathcal {S}}_{ij}\right) =cs_D\left( \theta ,{\mathcal {S}}_{ij}\right) +ps_D\left( \theta ,{\mathcal {S}}_{ij}\right) = \left( \frac{\theta }{\theta _L^i}\right) ^{\beta _1}\left\{ \frac{\xi _i\theta _L^iQ_L^i(2-\eta Q_L^i)}{2b_X(\xi _i+b_X)}-\frac{\xi _i Q_L^i}{\xi _i+b_X}\right. \nonumber \\&\quad \left. +\psi _{ij}^1\left\{ \frac{\xi _j\theta _{F1}^jQ_{F1}^j(2-2\eta Q_L^i-\eta Q_{F1}^j)}{\xi _j+b_X}-\frac{\xi _jQ_{F1}^j}{\xi _j+b_Y}\right\} +\psi _{ij}^0\left\{ \frac{\theta _{F0}^{j}}{2b_{X}}\left[ -\frac{\xi _i Q_L^i(2-\eta Q_L^i)}{\xi _i+b_X}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\frac{\xi _i}{\xi _i+\xi _j+b_X}\left( Q_L^i(2-\eta Q_L^i)+\frac{\xi _jQ_{F0}^j(2-2\eta Q_L^i-\eta Q_{F0}^j)}{\xi _j+b_X}\right) \right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\frac{\xi _j}{\xi _i+\xi _j+b_X}\left( Q_{F0}^j(2-\eta Q_{F0}^j)+\frac{\xi _iQ_L^i(2-\eta Q_L^i-2\eta Q_{F0}^j)}{\xi _i+b_X}\right) \right] -\frac{\xi _jQ_{F0}^j}{\xi _j+b_Y}\right\} \right\} \end{aligned}$$
(61)

Based on these discussions, the optimal investment policy in light of social welfare-maximizing from the perspective of a social planner when the type i firm is exogenous leader and type j firm is follower can be concluded in the following Theorem 6.

Theorem 6

(Welfare-maximizing policy for exogenous roles) Given the type i leader’s product has entered into the market already, the type j follower’s social welfare-maximizing investment strategies are

$$\begin{aligned} \theta _{F1}^{j**}(Q_{L}^{i})&=\frac{(\beta _{1}+1)b_X(\xi _{j}+b_{X})}{(\beta _{1}-1)b_Y(\xi _{j}+b_{Y})(1-\eta Q_{L}^{i})}=\theta _{F1}^{j*}(Q_{L}^{i}) \end{aligned}$$
(62)
$$\begin{aligned} Q_{F1}^{j**}(Q_{L}^{i})&=\frac{2(1-\eta Q_{L}^{i})}{(\beta _{1}+1)\eta }=2Q_{F1}^{j*}(Q_{L}^{i}) \end{aligned}$$
(63)

Given the type i leader’s product hasn’t been on the market yet, the type j follower’s social welfare-maximizing investment strategies, \(\theta _{F0}^{j**}(Q_{L}^{i})\) and \(Q_{F0}^{j**}(Q_{L}^{i})\), can be implicitly derived from

$$\begin{aligned} Q_{F0}^{j**}(Q_{L}^{i})&=\frac{1}{\eta }\left[ 1-\frac{(\xi _{j}+b_{X})\eta Q_{L}^{i} \xi _{i}}{\xi _{i}+\xi _{j}+b_{X}}\left( \frac{1}{\xi _{i}+b_{X}}+\frac{1}{\xi _{j}+b_{X}}\right) \right. \nonumber \\&\quad \left. -\frac{b_X\left( \xi _{j}+b_{X}\right) }{\theta _{F_{0}}^{j* *}(Q_{L}^{i})b_Y(\xi _{j}+b_{Y})}\right] \end{aligned}$$
(64)

and

$$\begin{aligned}&\frac{2(\gamma _{i}-\beta _{1})(1-\eta Q_{L}^{i})\xi _{j}}{(\beta _{1}-1)^{2}b_Y(\xi _{j}+b_{Y}) \eta }\left( \frac{\theta _{F0}^{j**}(Q_{L}^{i})}{\theta _{F1}^{j**}(Q_{L}^{i})}\right) ^{\beta _{1}}+\frac{\gamma _{i}Q_{F0}^{j**}(Q_{L}^{i}) \xi _{j}}{b_Y(\xi _{j}+b_{Y})}=\frac{(\gamma _{i}-1)\theta _{F0}^{j**}(Q_{L}^{i})}{2b_X}\nonumber \\&\quad \times \left\{ \frac{\xi _{i}}{\xi _{i}+\xi _{j}+b_X}\left[ Q_{L}^{i}(2-\eta Q_{L}^{i})+\frac{\xi _{j}Q_{F0}^{j**}(Q_{L}^{i})\left( 2-\eta Q_{F0}^{j**}(Q_{L}^{i})-2\eta Q_{L}^{i}\right) }{\xi _{j}+b_{X}}\right] \right. \nonumber \\&\quad \left. +\frac{\xi _{j}}{\xi _{i}+\xi _{j}+b_{X}}\left[ Q_{F0}^{j**}(Q_{L}^{i})\left( 2-\eta Q_{F0}^{j**}(Q_{L}^{i})\right) \frac{\xi _{i} Q_{L}^{i}\left( 2-\eta Q_{L}^{i}-2\eta Q_{F0}^{j**}(Q_{L}^{i})\right) }{\xi _{i}+b_{X}}\right] \right\} \end{aligned}$$
(65)

The type i leader’s social welfare-maximizing investment strategies, \(\theta _{L}^{i**}\) and \(Q_{L}^{i**}\), can be implicitly derived from

$$\begin{aligned} \underset{\theta _{L}^{i}\ge 0,Q_{L}^{i}\ge 0}{\arg \max }g_{W}^{i}(\theta _{L}^{i},Q_{L}^{i}) \end{aligned}$$
(66)

where \(g_{W}^{i}(\theta _{L}^{i},Q_{L}^{i})=g_{L}^{i}\left( \theta _{L}^{i},Q_{L}^{i},\theta _{F0}^{j**}(Q_{L}^{i}),Q_{F0}^{j**}(Q_{L}^{i}),\theta _{F1}^{j**}(Q_{L}^{i}), Q_{F1}^{j**}(Q_{L}^{i})\right) \) with

$$\begin{aligned}&g_{W}^{i}\left( \theta _{L}^{i},Q_{L}^{i},\theta _{F0}^{j},Q_{F0}^{j},\theta _{F1}^{j},Q_{F1}^{j}\right) \nonumber \\&\quad =\frac{\xi _{i}\theta _{L}^{i}Q_{L}^{i}(2-\eta Q_{L}^{i})}{2b_X(\xi _{i}+b_{X})}+\psi _{ij}^{1}\left\{ \frac{\xi _{j}\theta _{F1}^{j}Q_{F1}^{j}(2-\eta Q_{F1}^{j}-2\eta Q_{L}^{i})\xi _{j}\theta _{F1}^{j}}{2b_X(\xi _{j}+b_{X})}-\frac{\xi _{j}Q_{F1}^{j}}{\xi _{j}+b_{Y}}\right\} \nonumber \\&\qquad +\psi _{ij}^{0}\left\{ \frac{\theta _{F0}^{j}}{2b_X}\left[ -\frac{\xi _{i} Q_{L}^{i}(2-\eta Q_{L}^{i})}{\xi _{i}+b_{X}}\right. \right. \nonumber \\&\qquad +\frac{\xi _{i}}{\xi _{i}+\xi _{j}+b_{X}}\left( Q_{L}^{i}(2-\eta Q_{L}^{i})+\frac{\xi _{j}Q_{F0}^{j}(2-2\eta Q_{L}^{i}-\eta Q_{F 0}^{j})}{\xi _{j}+b_{X}}\right) \nonumber \\&\qquad +\left. \left. \frac{\xi _{j}}{\xi _{i}+\xi _{j}+b_{X}}\left( Q_{F0}^{j}(2-\eta Q_{F 0}^{j})+\frac{\xi _{i} Q_{L}^{i}(2-\eta Q_{L}^{i}-2\eta Q_{F 0}^{j})}{\xi _{i}+b_{X}}\right) \right] -\frac{\xi _{j}Q_{F0}^{j}}{\xi _{j}+b_{Y}}\right\} \nonumber \\&\qquad -\frac{\xi _{i} Q_{L}^{i}}{\xi _{i}+b_{X}} \end{aligned}$$
(67)

Proof

See Appendix A17. \(\square \)

To sum up, the investment strategy for the exogenous roles in view of social welfare-maximizing can be abbreviated as

$$\begin{aligned} {\mathcal {S}}_{ij}^{**}=\left\{ i,j,\theta _{L}^{i**},Q_{L}^{i**},\theta _{F0}^{j**},Q_{F0}^{j**},\theta _{F1}^{j**},Q_{F1}^{j**}\right\} \end{aligned}$$
(68)

Note that in order for distinguishing the optimal investment strategies in view of social welfare-maximizing from those of market-chosen, we here employ the superscript \(**\) to denote them.

Based on these arguments, the welfare-maximizing policy and welfare loss in the duopoly market can be summarized in the following Corollary 3.

Corollary 3

(Welfare-maximizing policy and welfare loss in duopoly market) The welfare-maximizing policy is

$$\begin{aligned} {\mathcal {S}}^{**}=\underset{i,j\in \{A,B\}}{\arg \max }sw_{D}\left( \theta ,{\mathcal {S}}_{ij}^{**}\right) \end{aligned}$$
(69)

for \(i\ne j\), in the meanwhile, the expected welfare loss in duopoly market is

$$\begin{aligned} wl_{D}(\theta )=\frac{sw_{D}^{**}(\theta )-sw_{D}^{*}(\theta )}{sw_{D}^{**}(\theta )} \end{aligned}$$
(70)

where \({sw}_{D}^{**}(\theta )=sw_{D}^{**}\left( \theta ,{\mathcal {S}}^{**}\right) \) and \(sw_{D}^{*}(\theta )=sw_{D}^{*}\left( \theta , {\mathcal {S}}^{*}\right) \)

The Corollary 3 indicates that, by comparing \({\mathcal {S}}_{AB}^{**}\) and \({\mathcal {S}}_{BA}^{**}\), a social planner designates the market leader and follower so that the corresponding investment strategies can maximize the social welfare level.

5 Numerical illustration

In this section, we explore the impacts of time-to-build as well as the uncertainty of both market demand and investment cost on the optimal investment strategies through numerical analysis. Simultaneously, the economic implications are expounded at brief length. The parameters we apply for numerical computation are given by the following Table 1.

Table 1 Parameters for the numerical computation
Full size table

5.1 Monopoly case

We start with the monopoly case to implement the discussions. To better highlight and illustrate the main results obtained in this paper, we examine four different models simultaneously, which are: (1) one-factor diffusion model of Jeon (2021; 2) two-factor diffusion model; (3) two-factor jump-diffusion model with upward jumps in demand and downward jumps in investment cost; (4) two-factor jump-diffusion model with downward jumps in demand and upward jumps in investment cost. Following Westman and Hanson (2000) and Wu and Hu (2022), by applying the principle of Gauss-Statistics quadrature, we substitute the complex and unmeasurable probability density function of \(U^{X}\) and \(U^{Y}\) with statistical moments \(\delta _{i},Sk_{i},i=X,Y\) to solve (A2). The numerical simulation results are shown in Figs. 2 and  3 below.

Fig. 2
figure 2

Optimal investment threshold of monopolist for different expected time-to-build

Full size image

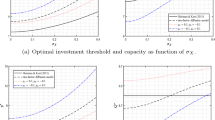
Since the time-to-build doesn’t affect the monopolistic capacity choice, we merely show its impact on the optimal investment threshold. As show in Fig. 2, the above three dashed lines represent the impacts of the average time-to-build on the optimal investment threshold under the two-factor model, and the black solid line at the bottom depicts the impact under one-factor diffusion model, which corresponds to Jeon (2021). Firstly, in terms of the two-factor model, the influence of the average time-to-build on the optimal investment threshold depends on the relationship between the expected growth rate of the market demand and investment cost. More specifically, here we set \(\mu _X>\mu _Y\). If jumps are not considered, the optimal investment threshold under the two-factor diffusion model monotonically decreases with respect to the average time-to-build, that is, when the average time-to-build increases, the firm should invest in advance. Otherwise, if jumps are considered and the market demand jumps up(down) and the investment cost jumps down(up), resulting in the expected growth rate of the market demand \(\mu _X+\lambda _Xm_X\) is greater(less) than that of the investment cost \(\mu _Y+\lambda _Ym_Y\). In such a circumstance, increasing the average time-to-build makes the firm accelerate(delay) the investment. This confirms Bar-Ilan and Strange (1996), but contrast to the conclusion in Jeon (2021), who show that the firm should adopt a waiting strategy when considering the investment lags. This is largely because the investment cost in their model is affirmatory and thus the optimal investment timing simply depends on market demand and time-to-build. However, two sources of uncertainty are be considered in our paper, and consequently, the uncertain market demand, in conjunction with uncertainty of the investment cost, makes early investment more lucrative if the expected growth rate of demand exceeds that of the investment cost. Otherwise, the verse. Secondly, compared with the one-factor diffusion model in Jeon (2021), the optimal investment threshold under the two-factor model is larger, which indicates that adding an uncertain factor will delay the investment of the firm. Furthermore, we find that in the two-factor model, when the market demand jumps up (down) and the investment cost jumps down (up), the firm’s optimal investment threshold is less (greater)than that of the two-factor diffusion model. This is mainly because the upward (downward) market demand and downward (upward) investment cost represent a relatively upbeat (downbeat) economic environment, in which the firm should speed up (down) the investment.

Fig. 3
figure 3

Optimal investment decisions of monopolist for different uncertainties of market demand and investment cost (\(\frac{1}{\xi } =2\))

Full size image

Figure 3 shows the influences of the volatility of market demand and investment cost on the optimal investment threshold and capacity level in four different cases given other parameters are constant. As we can observed, both \(\theta _{M}^{*}\) and \(Q_{M}^{*}\) increase with \(\sigma _X\) and \(\sigma _Y\), implying that it is profitable for the monopoly firm to postpone the investment with a greater capacity in a more volatile market, which confirms Jeon (2021), although only the uncertain market demand is considered and follows GBM in their model. However, compared with only one-factor-model in Jeon (2021), when considering two uncertain factors, the firm will wait for the demand-to-cost ratio to reach a higher level before investing. Furthermore, in comparison to two-factor diffusion model, the upward (downward) jumps in demand and downward (upward) jumps in investment cost in the two-factor jump-diffusion model combine to make the monopoly firm to accelerate (postpone) the investment with larger (smaller) capacity. This is consistence with the conclusion of Wu and Hu (2022) where the time-to-build is not considered.

5.2 Duopoly case

We next proceed to investigate how the degree of asymmetry in the investment lags between the duopoly firms affects their market positions in the preemption game and the corresponding equilibrium investment strategies. In order to better compare the main results obtained in this paper with those between previous scholars, as in the monopoly case, we still present the results of the numerical analysis under four different models. First, type A and type B firms are designated as dominant and dominated firms, respectively, based on the time-to-build, where the expected time-to-build \(\frac{1}{\xi _{A}}\) of the dominant firm is relatively shorter. Based on these assumptions, we fix \(\frac{1}{\xi _{A}}\) and let \(\frac{1}{\xi _{B}}\) vary in the range of [2, 7] to observe the market roles played by the duopoly firms as well as the changing trends in investment thresholds and capacity levels, and further elaborate the impact of the asymmetry in time-to-build on the market roles of the duopoly firms and the corresponding optimal investment strategies. The main results are shown in Table 2 below.

Firstly, we investigated the impact of asymmetry in time-to-build on the leader-follower relationship in the duopoly market. As shown in Table 2, when \(\frac{1}{\xi _{B}}\le 4,\theta _{P}^{A*}<\theta _{P}^{B*}\), but when \(5\le \frac{1}{\xi _{B}}\le 7,\theta _{P}^{A*}>\theta _{P}^{B*}\). Therefore, we can conclude that, when the degree of asymmetry is small, the dominant firm (i.e., type A) wins the preemptive game of the leader-follower relationship and invests first to be the market leader. Naturally, the dominated firm (i.e., type B) invests as the follower later. However, when the firms’ time-to-build are significantly asymmetric, the dominated firm (i.e., type B) wins the game and becomes the market leader. This is mainly because the dominant firm (i.e., type A) believes that even if it invests late, its products will enter the market earlier than the dominated firm (i.e., type B) due to the significant relative advantage of time-to-build. In other words, the relative advantage of time-to-build weakens the dominant firm’s preemptive motivation, thereby changing the leader-follower relationship of duopoly firms.

Secondly, we investigate the impacts of asymmetry in time-to-build on the duopoly firms’ optimal investment strategies. As shown in Table 2, we find that both firms’ preemptive investment thresholds, \(\theta _{P}^{A*},\theta _{P}^{B*}\), and capacity levels, \(Q_{P}^{A*},Q_{P}^{B*}\),\(Q_{P}^{A*},Q_{P}^{B*}\), monotonically increase with respect to time-to-build of the dominated firm (i.e., type B), which indicates that increasing the difference of duopoly firms’ time-to-build will weakens their incentives to preempt and thus delay investment, while the delay in investment timing allows firms to increase capacity levels. In the meanwhile, given the duopoly firms’ leader-follower relationship has been determined, with the increase of the dominated firm’s time-to-build, \(\frac{1}{\xi _{B}}\), the possible optimal investment thresholds for the follower, \(\theta _{F0}^{A*},\theta _{F1}^{A*},\theta _{F0}^{B*},\theta _{F1}^{B*}\), monotonically increase while the corresponding optimal capacity levels, \(Q_{F0}^{A*},Q_{F1}^{A*},Q_{F0}^{B*},Q_{F1}^{B*}\), decrease, implying that the follower should also defer the investment. However, the output level of the followers decreases because the leader who has entered the market first has increased its output and the follower can only scale down due to the limited market capacity.

Further, after comparing the optimal investment thresholds and capacity levels in different models we draw the conclusion that, consistent with the monopoly market, the optimal investment threshold and capacity level in the two-factor model are greater than those in the one-factor diffusion model of Jeon (2021). Moreover, in the two-factor model, if the market demand jumps up (down) and the investment cost jumps down (up), the optimal investment threshold in the two-factor jump-diffusion model is smaller (larger) than that in the two-factor diffusion model, while the capacity level is larger (smaller). This means that when the economic environment is upbeat (downbeat), firms should accelerate(delay) the investment with higher(lower) capacity level.

Table 2 Equilibrium investment strategies in a duopoly with asymmetric time-to-build under two sources of uncertainty
Full size table

6 Conclusion

In this paper, we apply the real option game method to investigate how the uncertain time-to-build affects the investment timing and capacity decision-making of duopoly firms taking the unexpected events into consideration. Based on the theoretical framework of Duopoly Option Game, we introduce Poisson jump process to characterize the effect of unexpected events on the product market and employ exponential distribution to simulate the uncertainty of time-to-build. Owing to the jump-diffusion model, we can study the investment strategies of duopoly firms in the presence of uncertain time-to-build in a more realistic economic environment and consequently obtain more accurate and reliable conclusions compared with Jeon (2021).

We have found that whether in the monopoly market or duopoly market, the impact of time-to-build on the optimal investment threshold of the firm depends on the jumping directions of both market demand and investment cost caused by unexpected events. Specifically, when the market demand jumps up (down) and the investment cost jumps down (up), the longer the average time-to-build, the smaller (larger) the optimal investment threshold of the firm as well as the earlier (later) the investment timing. This conclusion is consistent with Kauppinen et al. (2018), and the main reason for this result is that the marginal revenue from a larger expected net present value is discounted more heavily and the marginal cost of waiting is the option value to continue with a staged project. In the duopoly market, duopoly firms with asymmetric time-to-build have a preemptive game on the order of entering the market, and the dominated firm with relative disadvantage can also become market leader in the game equilibrium. Different from the conclusion that the capacity level in the monopoly market is not affected by the time-to-build, in the duopoly market, when the difference of asymmetry of the time-to-build increases, the leader should increase capacity level while the follower should reduce. Moreover, compared with the two-factor diffusion model without considering the emergencies, the optimal investment threshold in the two-factor jump-diffusion model with market demand upward (downward) and investment cost downward(upward) is smaller (larger) and the capacity level is larger (smaller).

There are still some problems that need to be further studied in the future. Firstly, we limit our model to that the firm can merely invest one time, one can relax this assumption later on and allow the firm to invest in a project in multiple stages (stepwise investment) instead of a single stage (lumpy investment). Secondly, it is worth mentioning that the obtained results are derived in the absence of hidden entry. One can extend the model for a positioned firm and several hidden firms competing a follower position, and consequently examine how the asymmetry of time-to-build affects the investment strategies of the firms. What’s more, further studies can extend the competition from homogeneous goods to differentiated ones when taking time-to-build into account.