1 Introduction

3D curved slot structures are widely used in aero-engine systems, such as blisks and the leading edge protection cap (LPC) [1]. These parts are usually made of titanium alloy, which is a typical difficult-to-cut material that tends to accumulate the cutting heat during milling and aggravate the tool wear. Moreover, the wall width and thickness are small, which can easily lead to machining distortion. At the same time, a large amount of material is removed during the process, so it is also a key issue to improve the machining efficiency. Trochoidal milling [2] is gradually becoming an effective process method for the efficient machining of thin-walled curved slots because of its advantages, such as low and smooth milling force, good heat dissipation of the tool and workpiece, and high machining efficiency [3,4,5,6]. However, with the demand for efficient machining of slot parts, the transition from traditional three-axis trochoidal milling to five-axis has made the tool path planning more complex. The resulting global interference and singularity problems will directly affect the machining efficiency and quality of the workpiece.

In order to improve the machining stability and efficiency of trochoidal milling, many scholars have conducted several researches in terms of tool path planning and parameter optimization. Elber et al. [7] first applied trochoidal path to cavity machining and developed a trochoidal tool path solving algorithm based on the medial axis transformation. Further, Han et al. [8] determined the optimal tool combination and skeleton for trochoidal milling of the pocket, which effectively improved machining efficiency. Rauch et al. [9] proposed a trochoidal tool path generation model for pocket milling. Compared with the circular model, the smoothness of the path and the machining efficiency were improved. Wang et al. [10] proposed an adaptive trochoidal toolpath model for complex pockets, which maintained a stable material removal rate (MRR) by adjusting the step distance and the trochoidal radius. This method reduced the fluctuation of cutting force and improved the machining efficiency. Xu et al. [11] used a polynomial curve as the trochoidal tool path, which enabled the machining of arbitrary curved slots with constant width. As the extension of Ref. [11], Li et al. [12] proposed a trochoidal tool path generation model based on Hermite interpolation polynomials for the arbitrary boundary slots. The length of tool path was effectively reduced compared with the circular model, which improved the machining efficiency. These methods demonstrated that it is effective to improve the machining efficiency by optimizing the shape of the trochoidal tool path. However, these studies can only be used for machining simple shaped slots or cavities with fixed tool orientation during milling, which is a limitation for 3D curved slots that require five-axis machining.

There was less research related to multi-axis trochoidal milling, but in recent years, scholars have gradually started to study the expansion of trochoidal milling to four- or five-axis machining. Sona [13] first proposed the concept of five-axis trochoidal milling, and successfully extended the three-axis trochoidal tool path to five-axis by establishing the correlation between the trochoidal tool path and the bottom surface and sidewalls of the curved slot. The five-axis trochoidal tool path generation method for slots of ruled surface was developed, which enriched the application scope of trochoidal milling. Luo et al. [14] proposed a four-axis trochoidal tool path generation method for blisk machining, including the generation of tool contact curves in the parameter domain and the control of interference-free tool orientations. The correctness of the tool path planning method was verified by milling experiments. Li et al. [15] designed the guide curve of the trochoidal milling through the medial axis transformation, and used the Hermite interpolation polynomial as the trochoidal path to establish a five-axis trochoidal tool path planning method for complex 3D curved slots. Based on Ref. [15], Li et al. [16] further established the principle of deep slots layering and formed a multi-layer five-axis trochoidal milling process for the deep slots of complex surfaces. In addition, Bo et al. [17] proposed a method for trochoidal flank milling of 3D cavities considering both tool shape optimization and trochoidal milling toolpath planning. Finally, the purpose of improving the machining accuracy of trochoidal milling was achieved.

The above studies provided novel and effective ideas for the efficient processing of 3D curved slots. However, they ignored a problem that the kinematics of the machine tool is more complex after the introduction of the rotation axes in multi-axis milling, and it has great influence on processing efficiency and quality. Especially when the tool orientations pass through the singular position of the machine tool workspace, the movement of the rotation axis will not be solved, where rotation axis of the machine tool will move discontinuously and rapidly, and may even reverse 180° [18]. Due to the limitation of the acceleration threshold for the machine tool, the instantaneous large angle rotation may cause the actual feed speed to be less than the set value, thereby reducing the machining efficiency [19]. In addition, sudden changes of the rotation axis cause transient large displacement compensation movements of the translational axes, which can reduce machining accuracy and even damage the surface of the workpiece [20]. Therefore, the singularity in five-axis machining is harmful and urgent to be avoided.

At present, path repositioning is one of the common methods to avoid the singularity [19, 21]. For narrow slots, the feasible space of the tool orientations is small and the global interference is serious, which make this method inapplicable for avoiding singularity. In recent years, some researches have been conducted to avoid singularity by means of workpiece repositioning. In order to reduce the tracking errors in five-axis machining, Yang et al. [22] identified the optimal placement of parts on the five-axis machine tool tables by minimizing the forces transmitted to the rotary drives as torque disturbances. Cripps et al. [23] proposed a method of reorienting the workpiece on the table of machine to achieve singularity avoidance. However, they did not optimize the selection of the workpiece orientation. Gao et al. [24] proposed a workpiece setup optimization method by combining singularity avoidance with machine accessibility. The method improved the kinematic performance and machining efficiency of five-axis machining. In general, the advantage of workpiece repositioning is that the tool path generation method is unchanged, so that new interference will not be introduced. This method has certain applicability to the non-singular machining of 3D curved narrow slots.

In view of the above analysis, the efficient five-axis trochoidal tool path planning method is urgently needed for the rough machining of 3D curved slots. Meanwhile, the singularity problem has not been reported in previous trochoidal milling studies, but its impact on machining efficiency and quality cannot be ignored. Therefore, in this study, an interference-free and singularity-free five-axis trochoidal milling process method for 3D curved slots is proposed in an innovative way. Firstly, the mathematical model of trochoidal CL path is first established in the 2D parameter domain, and mapped back to the 3D physical domain to obtain the CL data. Then, the efficient solution method for the interference-free tool orientations of the narrow slot structure is proposed combined with the theory of the vector rotations and quadratic interpolation. In the aspect of singularity avoidance, the inverse kinematics model of the non-orthogonal five-axis machine tool is established, as well as the clamping orientation expression of the workpiece on the machine table. Based on the above all, the workpiece orientation is adjusted by maximizing the machining efficiency, and finally, the non-singular five-axis trochoidal milling process is verified on the machine.

The organizational structure of this study is as follows. In Section 2, the five-axis trochoidal tool path planning method is introduced, including the generation of CL path in the parameter domain and the solution of interference-free tool orientations. In Section 3, the inverse kinematics model of non-orthogonal machine tool is established and the optimization method of workpiece clamping orientation is introduced. In Section 4, the computer simulation and milling experiment are given to verify the effectiveness of the proposed method. This study concludes in Section 5.

2 Trochoidal tool path planning

In this section, the method of the trochoidal CL path generation is introduced firstly. Then, the calculation of the tool orientations without interference is given, which initially realize the five-axis trochoidal tool path planning for 3D curved slots. It also provides a reliable tool path generation method for the subsequent optimization of non-singular workpiece orientation.

2.1 Cutter location path planning for 5-axis trochoidal milling

The trochoidal tool path for a complete cycle consists of a cutting path and a linking path, as shown in Fig. 1. The removal of channel material is accomplished by milling the workpiece at a small tool-workpiece envelope angle in the cutting paths. The linking paths connect the cutting paths during the adjacent trochoidal cycles to ensure the continuity of the tool path, while helping the cutter to cool down quickly and improve the cutter life. In this section, the bottom surface (BS) and its associated representation are defined first; then, the expression of the trochoidal CL path is established in the parameter domain of the BS. Finally, the parameter path is mapped back to the physical domain to obtain the 3D trochoidal CL path located on the BS.

Fig. 1
figure 1

Schematic diagram of a 3D curved slot

Full size image

A 3D curved slot consists of the left sidewall LS(u, v) and the right sidewall RS(u, v). For trochoidal down milling, the cutter cuts in through the right sidewall and out through the left sidewall. Considering the machining allowance and the tool radius, the CL guide surfaces at both sidewalls can be expressed as,

$$\left\{\begin{array}{c} LGS\left(u,v\right)= LS\left(u,v\right)+{n}_L\left(u,v\right)\cdot \left({Z}_b+{R}_t\right)\\ {} RGS\left(u,v\right)= RS\left(u,v\right)+{n}_R\left(u,v\right)\cdot \left({Z}_b+{R}_t\right)\end{array}\right.u,v\in \left[0,1\right]$$
(1)

In which, LGS(u, v) is the CL guide parameter surface of the left sidewall, RGS(u, v) is the CL guide parameter surface of the right sidewall, nL and nR are the normal vectors of both sidewalls, Zb is the roughing or semi-finishing allowance, and Rt is the tool radius.

When planning the single-layer trochoidal tool path, the ruled surface is constructed by the lower boundary curve of the two guide surfaces, which is used as the bottom surface (BS) of the CL path. The expression of BS is given by,

$$BS\left(\xi, \eta \right)= LGS\left(\xi, 0\right)\cdot \eta + RGS\left(\xi, 0\right)\cdot \left(1-\eta \right)\enspace \xi, \eta \in \left[0,1\right]$$
(2)

In which, ξ and η are two parameters of the BS.

It can be seen from Eq. (2) that the ruled surface BS is a parametric surface, and the relationship between its coordinates in three-dimensional space and parameters can be expressed as,

$$BS\left(\xi, \eta \right)={\left(x\left(\xi, \eta \right),y\left(\xi, \eta \right),z\left(\xi, \eta \right)\right)}^T\enspace \xi, \eta \in \left[0,1\right]$$
(3)

The above relationship is shown in Fig. 2. There is a one-to-one mapping relationship between the square parameter domain consisting of parameters ξ and η and the physical domain of BS in 3D space. Therefore, the trochoidal tool path located on the BS can be obtained by planning the tool path in the parameter domain and mapping it to the physical domain.

Fig. 2
figure 2

Parameter domain (left) and physical domain (right) of the BS

Full size image

As shown in Fig. 3a, the cutting segment path is generated in the parameter domain of BS. To simplify the calculation, the cutting path of the first trochoidal cycle in the parameter domain is defined as cutting in from (0, 0) and cutting out from (0, 1). The parametric expression of the cutting path is given by,

$$\left\{\begin{array}{c}{\xi}_i^c=\left(-{k}_1+{k}_2\right){t}^3+\left({k}_1-2{k}_2\right){t}^2+{k}_2t+\sum_{j=0}^{i-1}\varDelta \xi \\ {}{\eta}_i^c=-2{t}^3+3{t}^2\end{array}\right.\enspace t\in \left[0,1\right]$$
(4)
Fig. 3
figure 3

Trochoidal CL path in the parameter domain: a initial CL path; b CL path after left shift

Full size image

In which, \({\xi}_i^c\) and \({\eta}_i^c\) are the ξ-and η-directional parametric equations for the ith trochoidal cycle, k1 and k2 are the tangent vector dimensions at the two end points of the path, and Δξ is the step parameter of the trochoidal periodic topology.

The linking path is the curve connecting the end point of the previous cycle of the cutting path to the starting point of the current cycle, which can be expressed as,

$$\left\{\begin{array}{c}{\xi}_i^l=\left({k}_2-{k}_1-2\varDelta \xi \right){t}^3+\left(-{k}_2+2{k}_1+3\varDelta \xi \right){t}^2-{k}_1t+\sum_{j=0}^{i-1}\varDelta \xi \\ {}{\eta}_i^l=-2\left(1-t\right){}^3+3\left(1-t\right){}^2\end{array}\right.\enspace t\in \left[0,1\right]$$
(5)

In which, \({\xi}_i^l\)and \({\eta}_i^l\)are the ξ-and η-directional parametric equations for the ith trochoidal cycle.

The values of (k1, k2, Δξ) are artificially given or obtained by optimization, and then, the parameters ξ and η of the trochoidal tool path can be obtained by substituting into Eqs. (4) and (5). However, there is a problem that the tool-workpiece envelope angle in the first trochoidal tool path can be very large, resulting in very high tool loads and possibly even tool breakage and spindle failure. To avoid this problem, a parameter δξ is introduced to shift the trochoidal tool path to the left by a distance, thus ensuring that the tool load is at a low level in the first cycle, as shown in Fig. 3b. The value of δξ is given by,

$$\delta \xi =\max \left({\xi}_1^c\right)-\varDelta \xi$$
(6)

In which, \(\max \left({\xi}_1^c\right)\) is the maximum value of the ξ parameter in the cutting path of the first cycle.

Substituting into Eqs. (4) and (5), the improved mathematical expressions of the trochoidal tool path are given by,

$$\left\{\begin{array}{c}{\xi}_i^c=\left(-{k}_1+{k}_2\right){t}^3+\left({k}_1-2{k}_2\right){t}^2+{k}_2t+\sum_{j=0}^{i-1}\varDelta \xi -\delta \xi \\ {}{\eta}_i^c=-2{t}^3+3{t}^2\end{array}\right.\enspace t\in \left[0,1\right]$$
(7)
$$\left\{\begin{array}{c}{\xi}_i^l=\left({k}_2-{k}_1-2\varDelta \xi \right){t}^3+\left(-{k}_2+2{k}_1+3\varDelta \xi \right){t}^2-{k}_1t+\sum_{j=0}^{i-1}\varDelta \xi -\delta \xi \\ {}{\eta}_i^l=-2\left(1-t\right){}^3+3\left(1-t\right){}^2\end{array}\right.\enspace t\in \left[0,1\right]$$
(8)

Finally, the coordinates of the trochoidal CL path in the 3D bottom surface can be obtained by substituting the parameters ξ and η into Eq. (2). In this way, the mapping of the trochoidal CL path in the parameter domain to the physical domain is implemented, as shown in Fig. 4.

Fig. 4
figure 4

Trochoidal CL path in the parameter domain and physical domain.

Full size image

2.2 Tool orientation planning for 5-axis trochoidal milling

The tool orientations corresponding to the cut-in/cut-out points of a trochoidal cycle are defined as the critical tool orientations, which are first solved initially. As shown in Fig. 5, based on the upper and lower boundary curves of both sidewalls, the critical tool orientations are preliminarily obtained as,

$$\left\{\begin{array}{c}{T}_{wi}^L= LS\left({u}_i,1\right)- LS\left({u}_i,0\right)\\ {}{T}_{wi}^R= RS\left({u}_i,1\right)- RS\left({u}_i,0\right)\end{array}\right.$$
(9)
Fig. 5
figure 5

Initial planning for critical tool orientations

Full size image

In which, \({T}_{wi}^L\) is the left sidewall tool orientation for the ith trochoidal cycle and \({T}_{wi}^R\) is the right sidewall tool orientation for the ith trochoidal cycle.

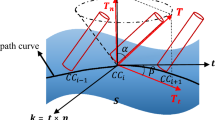
Then, the remaining tool orientations in the trochoidal cycle is solved by the quaternion spherical linear interpolation, which ensures a smooth transition of the tool orientations, as shown in Fig. 6. The relational equation can be expressed as,

$${T}_{wi}(t)=\frac{\sin \left(\left(1-t\right)\alpha \right)}{\sin \alpha }{T}_{wi}^R+\frac{\sin \left( t\alpha \right)}{\sin \alpha }{T}_{wi}^L \enspace t\in \left[0,1\right]$$
(10)
Fig. 6
figure 6

Quadratic spherical linear interpolation

Full size image

In which, Twi is the tool orientation for the ith trochoidal cycle and α is the angle between the tool orientations of the left and right sidewall.

Since the 3D slot exhibits curved characteristics, the initial planning of tool orientations may lead to global interference. Since the interference between the tool at the sidewall boundaries and the workpiece is the most pronounced, and considering the efficiency of interference detection and tool path planning, only the global interference of critical tool orientations is detected in this study. The projection method proposed in Ref. [25] is adopted to complete the interference detection.

For tool orientations with interference, many studies determined interference-free tool orientations based on the tool orientation feasible region. This method requires solving for all feasible directions of the tool orientations, which leads to a large computational effort. For curved slots with double sidewalls constraint, we can plainly think of a way by keeping the tool gradually away from the sidewall until the interference is eliminated. Therefore, instead of solving for all feasible tool orientations, a fast method of solving for the non-interference critical tool orientations is proposed. As shown in Fig. 7, it is assumed that the critical tool orientation with interference is Tj, the corresponding CL point is Mj, the unit tangent vector of the trochoidal path at this point is vi, and the adjusted tool orientation is Tn. In the proposed method, taking the point Mj as the center of rotation, Tj rotates about vi by an Angle γi to form Tn. According to Rodrigues’ rotation formula, the rotation can be expressed as,

$${T}_n=\cos {\gamma}_i{T}_j+\left(1-\cos {\gamma}_i\right)\left({T}_j\cdot {v}_i\right)\cdot {v}_i+\sin {\gamma}_i{v}_i\times {T}_j$$
(11)
Fig. 7
figure 7

Elimination of global interference

Full size image

In which, γi is increased from 0, and the interference detection is applied to the corresponding tool orientation until there is no interference between the tool and the sidewall. The tool orientation Tn is determined to be the critical tool orientation at CL point Mj. All the critical tool orientations in the 3D curved slot are traversed, and the initial tool orientations without interference remain constant, while the tool orientations with global interference are adjusted by using the proposed method. The corrected tool orientations are substituted into Eq. (10), and recalculated to obtain the new tool orientation data.

Finally, combining the data of CL points and the tool orientations, the complete five-axis trochoidal path of a 3D curved slot is formed.

3 Optimization of workpiece orientation without singularity

Quadratic spherical linear interpolation can improve the smoothness among the tool orientations. However, it is not the same as smooth motion of the five-axis machine tool rotation axes, especially when the machine happens to be located near the singularity point. Therefore, in this section, the machine structure and inverse kinematics are first introduced to reveal the relationship between the tool orientations and the machine rotation angle. And then, the expression of the workpiece setup on the machine table is given. Based on these, the non-singular workpiece orientation optimization method is proposed. This method offsets the whole tool orientations without changing the trochoidal tool path generation method in Section 2, so as to avoid the machine tool singular position.

3.1 Inverse kinematics of a non-orthogonal five-axis machine tool

The structure of the non-orthogonal five-axis machine tool with dual rotary tables is shown in Fig. 8a. The rotation axes of the machine are non-orthogonal, and the angle between the B- and C-axis is 45°. The two axes intersect at the vertical distance H from the table plane. When the B-axis rotation angle is 0°, the C-axis coincides with the Z-axis of the machine, as shown in Fig. 8b. The working range of the B-axis is [0,180°], and the working range of the C-axis is (−∞, +∞).

Fig. 8
figure 8

Structure of the non-orthogonal five-axis machine tool: a 3D construction of machine tool; b non-orthogonal rotation axes

Full size image

First, a few important coordinate systems and parameters are explained.

  1. (1)

    Machine coordinate system (MCS). MCS is a fixed coordinate system which takes the machine origin as the origin of the coordinate system.

(2) Table coordinate system (TCS). The three axes in TCS are defined as parallel and in the same direction as MCS. The tool orientation in TCS is defined as T = Txi + Tyj + Tzk.

(3) Workpiece coordinate system (WCS). WCS is defined as a coordinate system determined from the geometry of the workpiece. The tool orientation in WCS is defined as Tw = Twxi′ + Twyj′ + Twzk′.

In this study, the vector method is proposed to solve for the machine B-and C-axis rotation. As the translation of the coordinates does not affect the relationship between the tool orientation and the rotation axes, the origin of the tool orientation T and the B-axis are moved to the origin of MCS for ease of analysis. The relationship between the tool orientation and the rotation of the machine is shown in Fig. 9, where the unit vector of the Z-axis is T0. The rotation of T0 about the B-axis and T about the z-axis intersect at point M. Two rotations are required to bring the tool orientation T back to the unit vector T0 in the Z-axis direction as follows. (1) T rotates around the Z-axis to the point M, and the corresponding angle is the C-axis rotation. It consists of two parts. One is angle C2, which is the rotation angle of the B-axis driving the C-axis when the B-axis returns to zero. The other is the rotation angle C1 of the C-axis after the B-axis has returned to zero. (2) OM rotates around the B-axis (OO2) back to T0, and the corresponding angle is the B-axis rotation. The relationship between the vectors can be derived as,

$$\left\{\begin{array}{c} OM=O{O}_1+{O}_1M={T}_zk+\sqrt{{T_x}^2+{T_y}^2}\left(\cos {C}_2i-\sin {C}_2j\right)\\ {} OM=O{O}_2+{O}_2M=\frac{1}{2}\left(-j+k\right)+\left[\frac{\sqrt{2}}{2}\sin Bi+\frac{1}{2}\cos B\left(j+k\right)\right]\end{array}\right.$$
(12)
$${C}_1=\left\{\begin{array}{c}+\operatorname{arccos}\left(\frac{T_x}{\sqrt{{T_x}^2+{T_y}^2}}\right)\enspace{T}_y\ge 0\\ {}-\operatorname{arccos}\left(\frac{T_x}{\sqrt{{T_x}^2+{T_y}^2}}\right)\enspace{T}_y<0\end{array}\right.$$
(13)
Fig. 9
figure 9

Relationship between tool orientation and machine rotation

Full size image

According to Eqs. (12) and (13), the rotation angle of the C-axis is given as,

$$B=\operatorname{arccos}\left(2{T}_z-1\right)$$
(14)
$$C={C}_1+{C}_2=\left\{\begin{array}{c}\operatorname{arccos}\left(\frac{T_x}{\sqrt{{T_x}^2+{T_y}^2}}\right)+\arcsin \left(\frac{1-{T}_z}{\sqrt{{T_x}^2+{T_y}^2}}\right)\enspace {T}_y\ge 0\\ {}-\operatorname{arccos}\left(\frac{T_x}{\sqrt{{T_x}^2+{T_y}^2}}\right)+\arcsin \left(\frac{1-{T}_z}{\sqrt{{T_x}^2+{T_y}^2}}\right)\enspace{T}_y<0\end{array}\right.$$
(15)

With the above analysis, given the tool orientation T in TCS, the rotation angle values corresponding to the B- and C-axis of the machine tool can be solved.

3.2 Workpiece setup on machine table

Prior to milling, the workpiece is fixed in a specific position and orientation on the table and a transformation relationship exists between WCS and TCS as shown in Fig. 10. The position of the workpiece in TCS is denoted by (a, b, c), and the orientation is denoted by the Euler angle (ψ, θ, ϕ). Through the transformation from WCS to TCS, the coordinates of CL point and the tool orientations considering the workpiece setup are obtained as,

$${\left(L,1\right)}^T= Trans\left(a,b,c\right)\cdot Rot\left(Z,\psi \right)\cdot Rot\left(Y,\theta \right)\cdot Rot\left(X,\phi \right)\cdot {\left({L}_w,1\right)}^T$$
(16)
$${\left(T,0\right)}^T= Rot\left(Z,\psi \right)\cdot Rot\left(Y,\theta \right)\cdot Rot\left(X,\phi \right)\cdot {\left({T}_w,0\right)}^T$$
(17)
Fig. 10
figure 10

Diagram of workpiece setup

Full size image

In which, Lw is the CL point in WCS, L is the CL point in TCS, Trans(a, b, c) is the standard translation matrix, and Rot(Z, ψ), Rot(Y, θ), Rot(X, ϕ) are the standard rotation matrices.

It can be seen that the tool orientations are only affected by the rotation matrices Rot(Z, ψ), Rot(Y, θ), and Rot(X, ϕ), but immune to the translation matrix Trans(a, b, c), which means that the position of the workpiece does not affect the singularity of the machine. Therefore, only the orientation of the workpiece in TCS is discussed in this study.

According to the definition of the Euler angle, the meaning of the angle ψ is the rotation of the tool orientation T about the ZT-axis. Combined with the inverse kinematics of the machine tool in Section 3.1, it is clear that the tool orientation corresponds to a constant B-axis rotation and an increase in the C-axis rotation by ψ. Therefore, the amplitude in machine tool rotation between adjacent tool orientations is constant, which means that the angle ψ has no effect on the singularity of machine tool. By setting the angle of ψ to 0°, Eq. (18) can be simplified as,

$${\left(T,0\right)}^T= Rot\left(Y,\theta \right)\cdot Rot\left(X,\phi \right)\cdot {\left({T}_w,0\right)}^T$$
(18)

Based on the above analysis, the singularity avoidance of the machine can be achieved by adjusting the angle pair (θ, ϕ). The process of optimization is described in detail in the next section.

3.3 Optimization of workpiece orientation

When singularities occur during machining, the large rotation of the C-axis of the machine will affect the machining efficiency and quality, which is very harmful to the workpiece machining and needs to be eliminated. The singularity can be eliminated by workpiece reorientation, which is an effective method without changing the relative direction of the tool orientations and the workpiece.

As shown in Fig. 11, the tool orientations solved using the method in Section 2 can be expressed on the unit ball created in TCS. The singularity of the machine will occur when the tool orientations are located in a cone with the ZT-axis as the rotation axis, which is called the singularity cone [19]. The angle between the base line of the singular cone and the ZT-axis is called the taper angle λ. It can be seen that each tool orientation corresponds to a cone on the unit ball. According to the above analysis, singularity occurs when the cone corresponding to the tool orientation Ti is inside the singular cone. Obviously, singularity is so harmful to the machining process that it needs to be avoided. The specific process is described below.

Fig. 11
figure 11

Singular cone and tool orientation on unit ball

Full size image

For the tool path in a given workpiece orientation, it is first determined whether there are tool orientations that lie within the singular cone. For ease of analysis, the initial workpiece orientation is determined by using the minimum inclusion block, setting each axis of WCS parallel and in the same direction as TCS, so the initial the angle pair is (θ, ϕ) = (0, 0). The angle λi between Ti and the ZT-axis is expressed as,

$${\lambda}_i=\operatorname{arccos}\left({T}_i\cdot k\right)\enspace i=1,2,\dots n$$
(19)

In which, Ti is the unit tool orientation corresponding to the ith CL point in the toolpath, and k is the unit vector corresponding to ZT-axis.

When λi > λ, Ti lies outside the singular cone boundary and the machine does not have singularity. When λi ≤ λ, Ti lies inside the singular cone boundary, in which the machine generates singularity and requires repositioning of the workpiece. In this way, an angle pair (θ, ϕ) should be found, which can eliminate machine singularity while improving the efficiency and smoothness of the milling process. When establishing the optimization function, following considerations are made.

  1. (1)

    When the amplitude of machine rotation angle corresponding to the adjacent tool orientation is too large, the actual feed speed cannot reach the set value due to the acceleration limitation of the machine motion axis, resulting in lower machining efficiency. Also, the frequent changes in feed speed cause the milling process to become unstable. Therefore, a small rotary axis angle amplitude is beneficial for improving machining efficiency and enhancing process smoothness.

  2. (2)

    To avoid singularity, the angle between the tool orientation and the ZT-axis after workpiece orientation optimization should be larger than the taper angle of the singularity cone.

  3. (3)

    Considering the structural constraints of the fixture, and the collision between the spindle and both of the fixture and the table respectively, the angle pair (θ, ϕ) should be limited to a certain angle range according to the actual situation, so that the optimized tool orientations are closer to the original orientations [23].

  4. (4)

    Considering that the rotation range of B-axis of machine tool is [0, 180°], the B-axis rotation angle corresponding to the tool orientations after workpiece orientation optimization cannot exceed this range.

Based on the above analysis, the objective function and constraints are given as,

$${\displaystyle \begin{array}{c}\min \left(\sum \left(\left|{C}_{i+1}-{C}_i\right|\right)\right)\\ {}s.t.{\lambda}_i>\lambda \\ {}\theta, \phi \in \varOmega \\ {}B\in \left[\textrm{0,180}{}^{\circ}\right]\end{array}}$$
(20)

To ensure that all tool orientations lie outside the singular cone after optimization, the corresponding taper angles of all tool orientations are first calculated and the maximum value is recorded. Then, the maximum taper angle is used as the basis to calculate the value range limits of the angle pair. Considering that the values of the angle pair are symmetrical, the value ranges of θ and ϕ are obtained by,

$${\varOmega}_{\textrm{max}}=-{\varOmega}_{\textrm{min}}={\lambda}_{\textrm{max}}+\lambda$$
(21)

In which, the Ωmax and the Ωmin are the maximum and minimum values of θ and ϕ, and λmax is the maximum taper angle corresponding to the tool orientations under the initial workpiece orientation.

The angles θ and ϕ are first discretized equally, and then the sum of the differences of the C-axis angles for each orientation is solved and compared. Finally, the angle pair (θ, ϕ) with the smallest sum value is used as the optimized workpiece orientation, and the optimized tool orientations are shown in Fig. 11.

4 Experimental verification

4.1 Experiment setup

The method proposed in this study is implemented based on the MATLAB software. The comparative milling experiment is conducted on a DMU70V five-axis CNC machining center equipped with HEIDENHAN iTNC640 system. The maximum rotation speed is 18,000 r/min, and the repetitive positioning accuracy is 0.003 mm. The milling tool used is SANDVIK 2F340-06090-050-SC 1745 solid carbide end mill with five effective cutting edge. The diameter is 6 mm, and the corner radius is 0.5 mm. The total length is 57 mm, of which the usable length is 20 mm. The material of experimental workpiece is TC4 titanium alloy, and the machining object is a 3D curved slot with a dimension of 150 mm × 20 mm × 15 mm (as shown in Fig. 12), which is machined by a single-layer milling operation.

Fig. 12
figure 12

The machining object

Full size image

To verify the effectiveness of the proposed method, a set of comparative experiments is designed. The treatment group is the trochoidal tool path planning in the initial workpiece orientation using the method proposed in section 2. On the basis of the treatment group, the experiment group uses the method proposed in Section 3 to optimize the workpiece orientation and generate a non-singular five-axis trochoidal tool path. To ensure the uniformity of variables for the comparison experiments, the process parameters for both groups are set as following. A layer of five-axis trochoidal tool path is generated with the tangent vector dimensions k1 = k2 = 0.1 at both endpoints and step parameter Δu = 0.005. The spindle speed is set to 3000 r/min, the feed speed is set to 500 mm/min, and the down milling is adopted.

For the workpiece shown in Fig. 12, the initial workpiece orientation can be expressed as the angle pair (θ, ϕ) = (0°, 0°), as shown in Fig. 13a. The range of values of the angle pair (θ, ϕ) are obtained from Eq. (21) as θ, ϕ ∈ (−18°, 18°).Then, the workpiece orientation is optimized using Eq. (20), which is solved as angle pair (θ, ϕ) = (10°, 0°), as shown in Fig. 13c. The result of trochoidal tool path in the initial and optimized workpiece orientation is shown in Fig. 13 b and d. It should be pointed out that Fig. 13 only illustrates the distribution of part tool orientations for easy observation. In addition, Fig. 14 shows the distribution of all tool orientations on the unit ball. It can be seen that part of the tool orientations for the initial workpiece orientation lies within the boundary of the singular cone, while the tool orientations after workpiece orientation optimization have completely avoided the singular cone boundary.

Fig. 13
figure 13

Calculation of trochoidal tool path: a initial workpiece orientation, b initial trochoidal tool path, c optimized workpiece orientation, and d optimized trochoidal tool path

Full size image
Fig. 14
figure 14

Distribution of tool orientations: a initial workpiece orientation; b optimized workpiece orientation

Full size image

4.2 Results and analysis

Before the milling process, the simulation was first performed in VERICUT to verify the correctness of the tool path and CNC code. The machining simulation result before and after global interference elimination are shown in Fig. 15. As can be seen in Fig. 15a, there is an obvious overcutting phenomenon in some positions of the sidewall surface, and the maximum overcut amount reaches 0.24 mm. After eliminating the global interference by adjusting the tool orientations, there is no overcut on the sidewall surface, as shown in Fig. 15b, which illustrates the effectiveness of the interference-free trochoidal toolpath planning method proposed in Section 2 of this study. In addition, the orientation of the workpiece on the table before and after optimization is shown in Fig. 16a and b. Since the fixture used in the experiment is a self-centering vise, which cannot adjust the clamping angle of the workpiece, the different clamping orientations of the workpiece are indirectly characterized by preprocessing the surface of the blank. Then, the milling of the slots is carried out, and the result is shown in Fig. 16c.

Fig. 15
figure 15

Simulation results of the 3D curved slot: a before interference elimination; b after interference elimination

Full size image
Fig. 16
figure 16

Workpiece orientation and milling results: a initial workpiece orientation, b optimized workpiece orientation, and c results of milling slots

Full size image

By observing the milling process of the two slots, it can be seen that they are both milled correctly, but the movements of the machine table (rotation axes) are different considerably. In the initial workpiece orientation, when the workpiece is machined at certain positions, the machine table suddenly rotated significantly and the actual feed speed is obviously less than the set value. In the optimized workpiece orientation, the large rotation of the machine table is eliminated, and the feed speed always maintains the set value. According to the inverse kinematics analysis of the machine tool in Section 3.1, the C-axis rotation angle corresponding to the trochoidal tool path in two orientations can be obtained, as shown in Fig. 17. Fig. 17 a shows the C-axis rotation corresponding to several cycles of the trochoidal tool path, and it can be seen that the C-axis rotation angle changes drastically in the initial orientation compared to the optimized orientation. In addition, Fig. 17b shows more visually that there is no abrupt change in C-axis rotation and the amplitude is maintained at a low value in the optimized orientation, which indicates that the optimization of the workpiece orientation can effectively avoid the singularities.

Fig. 17
figure 17

C-axis rotation in initial and optimized workpiece orientation: a rotation of C-axis; b amplitude of C-axis rotation

Full size image

Finally, the total machining time is recorded using the machine monitoring function, and the optimized milling time is 835 s compared to 2930 s before optimization, representing a 71.5% improvement in machining efficiency.

5 Conclusions

This study proposes a non-singular five-axis trochoidal milling process method for 3D curved slots. Some conclusions are as following.

  1. (1)

    The trochoidal CL path model in the parameter domain is established based on the cubic parametric spline curve, and the tool path mapping to the physical domain is completed. Based on the critical tool orientations, combined with the quaternion theory and the efficient interference elimination strategy, the interference-free tool orientations planning is completed. And the simulation results verify the effectiveness of the trochoidal tool path generation method.

  2. (2)

    Aiming at the singular phenomenon in the trochoidal milling process, considering the machining efficiency, the workpiece orientation optimization strategy is proposed. The results of the computer simulation show that under the optimized workpiece orientation, the machine C-axis rotation angle changes smoothly compared with the initial orientation, and achieves a five-axis trochoidal tool path generation without singularities.

  3. (3)

    A singularity-free and efficient five-axis trochoidal milling process method is developed. The milling experimental results verify the effectiveness of the tool path generation method, and the comparison experiment shows that the machining efficiency of the proposed method is improved by 71.5%.

In conclusion, the proposed process method provides a reference for efficient milling of workpieces such as 3D curved slots.