1 Introduction

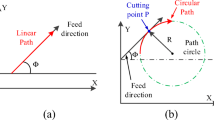
Rough machining process is a key process in high-speed CNC machining to remove large portion of materials. Its purpose is to quickly cut the workpiece to a specified shape. In choosing rough machining strategy, traditional method of the zig-zag or the contour parallel processing method by full immersion tend to cause large cutting forces and tool wear in marching. Trochoidal milling [1] becomes the popular strategy in the rough milling process, owing to its advantages in low cutting force, low tool wear, and high cutting efficiency. In trochoidal milling processing, as shown in Fig. 1, the tool path is composed of a circular and a linear motion which is called the circle based pattern. Each trochoidal cycle has two sections: active section and non-active section. In the active section, the cutter contacts with the workpiece which avoids full immersion to reduce cutting force and increase heat dissipation. The non-active section connects each active section with no cutting force loading in this area. When the non-active section path is too long, it will reduce the cutting efficiency. The important issue in trochoidal milling is to improve the cutting effectiveness while reducing the path in non-active cutting section.

Fig. 1
figure 1

The area of trochoidal tool path

Full size image

In the past, a trochoidal milling path is generated by the circular mathematical model, and each circular path is connected by a straight line to reduce the computation loading. As a result, the path has only the C0continuity in the circular based trochoidal milling. Ibaraki et al. [2] proposed the use of straight lines for connection in the non-active area to improve cutting efficiency, but the path remains with C0continuity. Otkur and Lazoglu [1] analyzed the mathematical model of the cutter workpiece contact area, estimated the engagement angle, and proposed a dual trochoidal tool path to improve the cutting efficiency. Rauch et al. [3] proposed the comparison of two kinds of trochoidal path generation methods and analyzed the force variations and tool parameters during machining. Their research also came up with a solution to deal with the corner and entry point issues of trochoidal machining. Because trochoidal machining path contains cutting and non-cutting portions, Ferreira and Ochoa [4] proposed an optimization algorithm to shorten the non-cutting path and processing time. Li et al. [5] proposed a spline-based new pattern trochoidal tool path in slotting process. They divided trochoidal path into active and non-active area, and using the Hermite curve to connect each active area to achieve C1continuity. Huang et al. [6] proposed the new pattern trochoidal tool path based on an ellipse model and medial axis transformation for pocketing processing. They improved cutting efficiency by keeping the engagement angle in the active area. The above-mentioned two methods tried to increase the engagement angles in the cutting area by using parametric curves to replace traditional circular pattern. However, the tradeoff is the cost to increase computation load for the machine controller to process the many tiny segments interpolated by the spline curves.

For the generation of the guiding curve of the milling process, the medial axis can be used as a topological skeleton which allows the maximum allowable internal sphere rolling along the interior of the object. Some literatures have integrated the trochoidal path and medial axis theory for machining application. Yamaji et al. [7] found that the overloading path and medial axis coincide during traditional machining and they proposed a mixed machining strategy by combining trochoidal and conventional machining methods. Since the trochoidal path is the trajectory of a fixed point on a circle which rolls along its guiding curve, the medial axis can serve conveniently as the guiding curve. Traditional medial axis calculation is very time consuming and inefficient due to its nonlinear nature of solutions. Instead we applied a direct method, which did not need to solve nonlinear equations, to obtain an approximate medial axis based on an offset method in a computational geometry theorem [8] and the polar ball theory based on the characteristics of the graphics [9].

In practical applications, traditional CNC only offers straight line and circle interpolation operations. Hence, the circular type trochoidal path can utilize G1 and G2/G3 codes quite efficiently. However, if we want to increase the engagement angles by modifying the front-end cutting shape, such as the elliptical shape using a Hermite curve [6], the parametric curve needs to be broken down into a large number of short line segments. This could cause several drawbacks: (1) Velocity and acceleration discontinuities will result in variation of the feed rate in the two-segment junction points. (2) Acceleration discontinuity will result in machine vibration and reduce machine and tool life. (3) Massive NC data transfer may cause CNC system overloading. All of the above stifle the performance of high speed machining. To overcome these problems, many literatures in the past solved these issues by using a parametric curve interpolation algorithm known as Non-Uniform Rational B-Splines (NURBS) interpolation. Commercial CNC companies [10],11 also integrated this technology into their controller products. It is interesting to know that with the availability of NURBS interpolation already adopted by modern controllers, there seems to find no research work in the past to use NURBS to represent a trochoidal tool path. Unlike cubic splines or Hermite curves used by [5] and [6], a NURBS curve can represent an exact circle and its shape can be modified by moving the control points. Traditional NURBS curve typically uses 9 control points with degree 2 to represent a full circle. Degree elevation can be used to increase its degree to 3 to maintain the  C2 continuity. By combining two degree-3 NURBS curves (one to represent the medial axis and the other one the circular path), we can generate a doubleNURBS trochoidal path to maintain C2 continuity throughout the tool path, still with the full flexibility to modify the shape of the tool path. With modern controllers capable of processing NURBS, many research works have presented feed rate scheduling and interpolation schemes for NURBS-based tool paths. Shpitalni et al. [12] proposed their new CNC interpolator, which can handle general curves by reducing the order of the path interpolation algorithm. However, in NURBS interpolation, a fixed feed rate may lead to a great chord error in the sharp corners. Yeh et al. [13] proposed an interpolation algorithm that confines the chord error within a specific tolerance range during the process. The change in feed rate is based on the chord error and radius of the curvature. Farouki and Tsai [14] modified the Taylor second-order approximation interpolation and compared the curve accuracy at different orders of approximation. Xu et al. [15] proposed an adaptive feed rate algorithm by referencing the curvature of a path. Tsai and Cheng [16] presented a predictor–corrector interpolator algorithm to control the variation in feed rate and verify the convergences.

This paper proposes a new trochoidal tool path generation method based on double-NURBS curve. Unlike traditional circular trochoidal tool path that combines circular and linear paths to approximate the trochoidal path, the double-NURBS tool path can truly represent a trochoidal path with C2 continuity throughout the entire tool path. In the front-end cutting area, the control points of the NURBS can be modified to increase the cutter-workpiece engagement angles; in the back-end non-active area, the NURBS curve can be modified to shorten the non-cutting distance and the machining time. With the existing feed rate scheduling and interpolation methods that have been developed and integrated with controllers, trochoidal tool path process parameters such as maximun cutting force (related to maximun engagement angle) and feed rate can be fully implemented using our proposed doube NURBS approach.

Compared with traditional trochoidal tool paths, the proposed approach has three distinct features:

  • Use the Voronoi diagram and curve fitting method to generate the medial axis of the pocketing contours and the proposed trochoidal tool path by a degree-3 double-NURBS curve to achiecve C2 continuity.

  • Enlarge and extend the engagement angles in the cutting area by modifying the front-end NURBS curve to improve the cutting productivity.

  • Modify the control points of the NURBS curve in the non-active area to shorten the non-cutting distance and improve the machining efficiency.

The remainder of this paper is organized as follows. The double-NURBS trochoidal tool path generation is developed in Section 2, including the guiding curve and NURBS curve. In Section 3, we analyze the engagement angle and optimize the NURBS curve in the active and non-active areas to improve cutting efficiency. Section 4 demonstrates pocketing machining with the double-NURBS algorithm, including tool path generation and cutting force analysis. Finally, in Section 5, contributions of this work are summarized and future research directions are also given.

2 Double NURBS-based trochoidal toolpath generation

In mathematics, the trochoidal path can be described by a circle rolling from point A to B along a guiding curve, typically a straight line. A point on the circumference will form a continuous path in the space in the rolling process and is called a trochoidal path as shown in Fig. 2.

Fig. 2
figure 2

Trochoidal curve

Full size image

The mathematical equation of a trochoidal path can be defined as [3]:

$$\left\{\begin{array}{c}X={X}_{i}+{v}_{xi}{S}_{tr}\frac{\theta }{2\pi }+{R}_{trocho}\mathit{cos}\theta \\ Y={Y}_{i}+{v}_{yi}{S}_{tr}\frac{\theta }{2\pi }+{R}_{trocho}\mathit{sin}\theta \end{array}\right.$$
(1)

As shown in Fig. 3, the corresponding parameters are: the center of the trochoidal path \({O}_{i}({X}_{i},{Y}_{i})\), direction unit vector of center on the guide curve \({{\varvec{v}}}_{i}\left({v}_{xi},{v}_{yi}\right),\) the radius of the trochoidal path \(({R}_{trocho})\), step length \(({S}_{tr})\) and rotating angle \((\theta )\). Also in the figure, \({R}_{tool}\) is the radius of the cutting tool and \({R}_{dc}\) is the radial depth of cut.

Fig. 3
figure 3

Geometry of the trochoidal machining path [3]

Full size image

The processing path calculated by a trochoidal algorithm has C2 continuity; this will be helpful for the milling machine due to a smoother path. Note that the radial depth of cut \({R}_{dc}\) varies as angle changes and needs to be constrained to avoid the occurrence of full immersion (\({R}_{dc}={R}_{tool}\)) during the roughing process. Using analytic geometry, \({R}_{dc}\) can be calculated once the tool center and the two end engagement points defining the engagement angle are found (see [6, 17]) and thus its maximum value \({R}_{dcmax}\) can be obtained. This, however, requires a numerical solution process which could be tedious to implement [17].

Alternatively, a simpler approximation can be used for \({R}_{dcmax}\) based on a circular trochoidal-like model, which essentially connects two circles with a short linear segment. Rauch et al. [3] developed a closed-form expression of \({R}_{dcmax}\) and established its validity as a conservative estimate for the true trochoidal \({R}_{dcmax}\). Such a circular trochoidal-like path is very easy to implement and hence, it is widely applied to existing CAM software. However, since this circle-based path is not really a trochoidal path, it still suffers a discontinuous acceleration problem in the junction point of the circle and the linear segment. Note that, as suggested in [3], we used this circular model based results (Eqs. (2) and (3) below) only for the purpose of effective parameter selection to aid in the trochoidal path planning.

Equation (2) shows the maximum radial depth of cut, based on the circular model [3], in relation to the tool radius, the trochoidal path radius, and the step length:

$$R_{{dc}_{max}}=\left(1+\frac{R_{tool}}{R_{trocho}}\right)S_{tr}-\frac1{2R_{trocho}}S_{tr}^2$$
(2)

If the maximum depth of cut is specified, then the corresponding maximum step length \({S}_{tr}\) can be obtained:

$${S}_{tr}={R}_{trocho}+{R}_{tool}-\sqrt{{({R}_{trocho}+{R}_{tool})}^{2}-2{R}_{trocho}{R}_{{dc}_{max}}}$$
(3)

For completeness, the detail derivation of Eqs. (2)–(3) is given in Appendix A.

Since the trochoidal tool path moves forward along its guiding curve, Eq. (3) can be readily used to set the maximum step length to generate a processing path, as shown in Fig. 4. Moreover, trochoidal machining paths can be integrated with traditional methods since they can avoid the full immersion condition of a cutter and ensure a secure entry point.

Fig. 4
figure 4

Trochoidal tool path with arbitrary guiding curve

Full size image

In practical CNC implementation, a trochoidal tool path must be split into a large number of short line segments and increase the loading of the controller during data importing. NURBS has the advantages of great flexibility and precision for modeling and has been integrated with many commercial CNC controllers. Since a degree-3 NURBS curve provides exact C2 continuity, in the following, we develop and redefine the trochoidal tool path along with its medial axis guiding curve (see Fig. 5) using a double-NURBS curve. In addition to its advantage of continuity, the NURBS-based trochoidal computation architecture can be integrated directly into a PC-based controller and enhance the value of the controller.

Fig. 5
figure 5

The demo of approximating NURBS-based medial axis path

Full size image

2.1 NURBS-based trochoidal path generation

In this sub-section, the equation of a trochoidal path using a double-NURBS curve will be presented. Since a trochoidal path is the trajectory of a fixed point on a circle which rolls along its guiding curve, we begin with using the NURBS curve [18] to define a circle which is formulated in Eq. (4):

$$C\left(t\right)=\frac{\sum_{j=0}^{n}{N}_{j,p}(t){w}_{j}\stackrel{\rightharpoonup}{{P}_{j}}}{\sum_{j=0}^{n}{N}_{j,p}(t){w}_{j}}$$
(4)

where \({N}_{j,p}(t)\) is the basis function of degree-p shown in Eqs. (5) and (6) \({P}_{j}\) is the control points, \({w}_{j}\) represents the weighting value and t is the parameter. \(U\left\{{t}_{0},\dots ,{t}_{m}\right\}\) is the knot sequence with the relation \(m=n+p+1\).

$${N}_{j,0}\left(t\right)=\left\{\begin{array}{c}1,{ t}_{j}\le t\le {t}_{j+1} \\ 0, otherwise\end{array}\right.$$
(5)
$${N}_{j,p}\left(t\right)=\frac{t-{t}_{j}}{{t}_{j+p}-{t}_{j}}{N}_{j,p-1}\left(t\right)+\frac{{t}_{j+p+1}-t}{{t}_{j+p+1}-{t}_{j+1}}{N}_{j+1,p+1}\left(t\right)$$
(6)

From [18], we see that a circle is a special case for a NURBS curve and can be established by 9 control points and specific weights and a knot vector. The detailed settings of a NURBS-based circle are listed as follows: degree-2, knot sequence \(U=\left\{ 0, 0, 0, 1/4, 1/4, 1/2, 1/2, 3/4, 3/4, 1, 1,1\right\}\), weights \({w}_{j}=\left\{1,\frac{\sqrt{2}}{2},1,\frac{\sqrt{2}}{2},1,\frac{\sqrt{2}}{2},1,\frac{\sqrt{2}}{2},1\right\}\), and radius R. Figure 6 shows the distribution of the 9 control points. Theoretically, the modeling of a circle using NURBS formulation can use either 9 control points or 6 control points (a triangle based control hull). Since our purpose is to create a NURBS parametric curve that represents a trochoidal circular path but also can be modified to extend the engagement angle (see Section 3), more control points will have more flexibility to alter or modify the shape. Therefore, in this work, we chose to use the NURBS circle with 9 control points rather than 6. We use de Boor algorithm to evaluate the NURBS curve which can be processed in parallel using FPGA or GPU (see [19]); hence, the computation load is almost equivalent even with more number of control points.

Fig. 6
figure 6

Control point distribution of NURBS-based circle

Full size image

Figure 7 demonstrates the size variation of a NURBS-based circle when the radius changes along the guiding curve. By combining Eqs. (1) and (4), the NURBS-based trochoidal path can be written as:

Fig. 7
figure 7

NURBS-based circle changes depend on radius

Full size image
$$\begin{array}{c}t=\frac{\theta }{2\pi }-\mathrm{int}\left(\frac{\theta }{2\pi }\right), t\in \left[\mathrm{0,1}\right]\\ T\left(u,t\right)={O}_{i}+{{\varvec{v}}}_{i}{S}_{tr}\mathrm{u}(\theta )+\frac{\sum_{j=0}^{8}{N}_{j,2}(t){w}_{j}\stackrel{\rightharpoonup}{{P}_{j}}}{\sum_{j=0}^{8}{N}_{j,2}(t){w}_{j}}\end{array}$$
(7)

Equation (7) represents the trochoidal path of each step distance \({S}_{tr}\) for any given center position. In other words, using this parametric NURBS equation, the complete set of trochoidal paths can be generated with a change of the circle center, which moves along the guiding curve. However, the connection between the trochoidal NURBS curve and the guiding NURBS curve has yet to be established. In Section 2.2, the equation of a double NURBS-based trochoidal machining path will be developed.

2.2 Double NURBS-based trochoidal path

The proposed double NURBS-based trochoidal path \(T\left(u\right)\) is a combination of two NURBS curves and is shown in Eq. (8):

$$T\left(u\right)=T\left(u,t(u)\right)=G\left(u\right)+C\left(t\right)$$
(8)

The two NURBS curves are guiding curve \(G\left(u\right)\) and rolling path \(C\left(t\right)\). As mentioned in the above section, \(C\left(t\right)\) is a circle modeled by the NURBS curve and \(G\left(u\right)\) is an approximate medial axis path by the curve fitting method [22]:

$$G(u)=\frac{\sum_{i=0}^{n}{N}_{i,3}(u){w}_{i}^{G}\stackrel{\rightharpoonup}{{Q}_{i}}}{\sum_{i=0}^{n}{N}_{i,3}(u){w}_{i}^{G}}$$
(9)
$$C\left(t\right)=\frac{\sum_{j=0}^{n}{N}_{j,p}(t){w}_{j}\stackrel{\rightharpoonup}{{P}_{j}}}{\sum_{j=0}^{n}{N}_{j,p}(t){w}_{j}}$$
(10)

In Eq. (9), \({N}_{i,3}(u)\) is the basis function of the B-spline and \({Q}_{i}\) represents the control points of the NURBS-based medial axis path. \({w}_{i}^{G}\) is the weighting of NURBS \(G\left(u\right)\) and u is the parameter. An approximate NURBS-based medial axis path is shown in Fig. 5.

In constructing the guiding curve from the discrete points of the medial axis, in additional to a NURBS curve, there could be other considerations of using linear G01 line segments, B-Splines, or Pythogorean Hodograph (PH) curve [20, 21] that has the advantage of providing precise interpolation positions based on variant feed rates. Since our goal is to convert the trochoidal circular path into parametric curves for machining, only NURBS can represent an exact circular path efficiently and directly without complex transformation. It would be natural and reasonable to convert the discrete points of the medial axis to a NURBS based guiding curve so that the complete tool path representation is unified (and simplified).

The trochoidal radius \({R}_{tro}\) is a function of u and varies depending on its center location. The step distance, given by Eq. (3), is also a function of u and is modified as follows:

$${S}_{tr}\left(u\right)={R}_{tro}\left(u\right)+{R}_{tool}-\sqrt{{({R}_{tro}\left(u\right)+{R}_{tool})}^{2}-2{R}_{tro}\left(u\right){R}_{{dc}_{max}}}$$
(11)

Next the synchronization of \(G\left(u\right)\) and \(C\left(t\right)\) is addressed; that is, it is necessary to relate u and t so that the full trochoidal path can be generated with a single parameter. The double NURBS-based trochoidal tool path is the combination of a NURBS-based medial axis path \(G\left(u\right)\) and a rolling path \(C\left(t\right)\). For a trochoidal-based path, a complete trochoidal path cycle could be achieved for each step distance moving forward. The exact step distance value on a guiding curve can be evaluated by Eq. (11). Here we assume that there is a normalized trochoidal parameter \({\widehat{u}}_{k}\in \left[\mathrm{0,1}\right]\) on G \(\left(u\right)\). The next parameter \({\widehat{u}}_{k+1}\) can be calculated by second order Taylor approximation interpolation algorithm [14] and shown in Eq. (12):

$${\widehat{u}}_{k+1}={\widehat{u}}_{k}+\frac{{S}_{tr}({\widehat{u}}_{k})}{\Vert {G}^{\mathrm{^{\prime}}}({\widehat{u}}_{k})\Vert }+\frac{A\left({\widehat{u}}_{k}\right)}{\Vert {G}^{\prime}({\widehat{u}}_{k})\Vert }\cdot \frac{{{T}_{s}}^{2}}{2} - \frac{{G}^{\prime}({\widehat{u}}_{k})\cdot {G}^{\prime\prime}({\widehat{u}}_{k})}{{\Vert G\mathrm{^{\prime}}({\widehat{u}}_{k})\Vert }^{4}}\cdot \frac{{{S}_{tr}({\widehat{u}}_{k})}^{2}}{2}$$
(12)

\(A\left({\widehat{u}}_{k}\right)\) is the acceleration and \({G}^{\prime}({\widehat{u}}_{k})\) and \({G}^{\prime\prime}({\widehat{u}}_{k})\) are the first and second derivatives of \(G\left(u\right)\), respectively. Here, \(A\left({\widehat{u}}_{k}\right)\) can be taken to be zero assuming uniform feed rate along the curve and \({S}_{tr}({\widehat{u}}_{k})\) is the step distance, and Eq. (13) then simplifies to:

$${\widehat{u}}_{k+1}={\widehat{u}}_{k}+\frac{{S}_{tr}({\widehat{u}}_{k})}{\Vert {G}^{\mathrm{^{\prime}}}({\widehat{u}}_{k})\Vert }-\frac{{G}^{\mathrm{^{\prime}}}({\widehat{u}}_{k})\cdot {G}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}({\widehat{u}}_{k})}{{\Vert G\mathrm{^{\prime}}({\widehat{u}}_{k})\Vert }^{4}}\cdot \frac{{{S}_{tr}({\widehat{u}}_{k})}^{2}}{2}$$
(13)

We normalize u as \({\widehat{u}}\) to be between [0, 1] and the parameter \({\widehat{u}}_{k+1}\) at the start of the next trochoidal cycle of the NURBS-based guiding curve can be obtained by second order Taylor approximation interpolation. This means the guiding curve step distance will also depend on the varying of the trochoidal radius. Figure 8 shows the relationship between the trochoidal radius \({R}_{tro}({\widehat{u}}_{k})\) change and the step distance\({S}_{tr}({\widehat{u}}_{k})\).

Fig. 8
figure 8

The relation between \({R}_{tro}({\widehat{u}}_{k})\) and \({S}_{tr}({\widehat{u}}_{k})\)

Full size image

After the trochoidal parameter is defined, the connection between u and t can also be established readily as follows:

$$t\left(u\right)=\frac{u-{\widehat{u}}_{k}}{{\widehat{u}}_{k+1}-{\widehat{u}}_{k}}$$
(14)

Combining Eq. (8), (11), (13), (14), the two NURBS-based curves can then be combined and rewritten as:

$$T\left(u\right)=\frac{\sum_{i=0}^{n}{N}_{i,p}(u){w}_{i}^{G}\stackrel{\rightharpoonup}{{Q}_{i}}}{\sum_{i=0}^{n}{N}_{i,p}(u){w}_{i}^{G}}+\frac{\sum_{j=0}^{8}{N}_{j,2}(t\left(u\right)){w}_{j}\stackrel{\rightharpoonup}{{P}_{j}}}{\sum_{j=0}^{8}{N}_{j,2}(t\left(u\right)){w}_{j}}$$
(15)

Figure 8 shows the machining tool path generated by the double NURBS-based trochoidal generation algorithm using Eq. (15).

In constructing the guiding curve using the medial axis, it is worth mentioning the method we used to construct the discrete medial axis. Early works of Held [23] and Lee [24] show that given sufficient sample points from the boundaries of an enclosed shape, the Voronoi vertices approximate the medial axis. Therefore, the method we used to obtain the medial axis is by using the discrete sample points of the boundary curves to obtain the dual Voronoi vertices after we applied the Delaunay triangulation. These Voronoi vertices serve as the approximation of the discrete medial axis. However, not all Voronoi vertices lie on the interior medial axis which is what we need. Amenta, et al. [25] proposed the medial axis transform (MAT) by using the Delaunay triangulation to calculate not only the Voronoi vertices but also separate them into inner and outer poles, both for 3D and 2D. Following Amenta’s work, we showed that by using only the outer poles, we can sculpt out the concave regions of the triangulated surface from the sample points [26]. With further refinement, the method can be extended to reconstruct surface with sharp edges [27]. But in this work, by using the same method to obtain the inner poles (the Voronoi vertices inside the machined region), not only we can use them to approximate the medial axis for the guiding curve, we can also use the polar radius in 2D to obtain the radius of the NURBS circle for the trochoidal circular path.

3 Improve the trochoidal tool path

In Section 2, we develop a new trochoidal tool path generation algorithm, based on a double-NURBS curve, for the C1continuity. The processing efficiency is the same with the circle-based trochoidal tool path. To improve the efficiency, we will deform the original circular NURBS curve to have more engagement angles in the cutting area, and shorten the travel distance in the non-active area. To achieve this goal while still maintaining the C2 continuity, we will elevate the degree of the original NURBS circle from 2 to 3, so that not only more control points can be used to deform the shape but also help reducing unnecessary machine vibration by keeping the C2continuity.

3.1 Degree elevation of the circle

In the last section, we use the degree-2 NURBS to represent the trochoidal circle. The curve has \({C}^{1}\) continuity. In the path planning, it leads to the jerk discontinuity in the jerk and increases the cutting force in the milling process. To improve this issue, we use degree elevation to raise degree to 3 without changing the shape of the circle, as is shown in Fig. 9.

Fig. 9
figure 9

Degree elevation of the circle

Full size image

We show the quadrant of the circle in Fig. 10. The circle arc is a NURBS, whose degree p is 2. Based on Eq. (16), the control points \(\left\{\stackrel{\rightharpoonup}{{p}_{l}^{0}}\right\}=\left\{\stackrel{\rightharpoonup}{{p}_{o}^{0}},\stackrel{\rightharpoonup}{{p}_{1}^{0}},\stackrel{\rightharpoonup}{{p}_{2}^{0}}\right\}\), \(\left\{{w}_{i}^{0}\right\}=\left\{1,1/\sqrt{2},1\right\}\), and the knots \(U=\left\{0, 0, \mathrm{0,1},\mathrm{1,1}\right\}\).

Fig. 10
figure 10

The quadrant of the circle

Full size image
$$C\left(u\right)=\frac{\sum_{i=0}^nN_{i,2}(u){w_i^0\overset\rightharpoonup P_i^0}}{\sum_{i=0}^nN_{i,2}(u)w_i^0},0\leq u\leq1$$
(16)

Using the degree elevation algorithm [18], we reformulate the control points, weights and curve (Eq. (17)-(20)).

$$C\left(u\right)=\frac{\sum_{i=0}^nN_{i,2}(u){w_i^0\overset\rightharpoonup P_i^0}_{}^{}}{\sum_{i=0}^nN_{i,2}(u)w_i^0}=\frac{\sum_{i=0}^nN_{i,3}(u){w_i^1\overset\rightharpoonup P_i^1}_{}^{}}{\sum_{i=0}^nN_{i,3}(u)w_i^1},0\leq u\leq1$$
(17)
$$w_i^1\overset\rightharpoonup P_i^1=\left(1-\alpha_i\right)w_i^0\overset\rightharpoonup P_i^0+\alpha_iw_{i-1}^0\overset\rightharpoonup P_{i-1}^0$$
(18)
$${w}_{i}^{1}=\left(1-{\alpha }_{i}\right){w}_{i}^{0}+{\alpha }_{i}{w}_{i-1}^{0}$$
(19)
$${\alpha }_{i}=\frac{i}{p+1}$$
(20)

First, we insert the knot of the curve:

$$U\mathrm{^{\prime}}=\left\{0, 0, \mathrm{0,0},\mathrm{1,1},\mathrm{1,1}\right\}$$
(21)

The degree of the circle is raised to 3, and the weights of the new curve are:

$${w}_{0}^{1}= {w}_{0}^{0}$$
(22)
$${w}_{1}^{1}=\frac{2}{3}{w}_{1}^{0}+\frac{1}{3}{w}_{0}^{0}$$
(23)
$${w}_{2}^{1}=\frac{1}{3}{w}_{2}^{0}+ \frac{2}{3}{w}_{1}^{0}$$
(24)
$${w}_{3}^{1}= {w}_{2}^{0}$$
(25)

After getting the new weights of the curve, we recalculate the control points of the curves \(\left\{\stackrel{\rightharpoonup}{{P}_{i}^{1}}\right\}=\left\{\stackrel{\rightharpoonup}{{P}_{0}^{1}},\stackrel{\rightharpoonup}{{P}_{1}^{1}},\stackrel{\rightharpoonup}{{P}_{2}^{1}}, \stackrel{\rightharpoonup}{{P}_{3}^{1}}\right\}\):

$$\overset\rightharpoonup P_0^1=\frac{w_0^0\overset\rightharpoonup P_0^0}{w_0^1}$$
(26)
$$\overset\rightharpoonup P_1^1=\frac{\frac23w_1^0\overset\rightharpoonup P_1^0+\frac13w_0^0\overset\rightharpoonup P_0^0}{w_1^1}$$
(27)
$$\overset\rightharpoonup P_2^1=\frac{\frac13{w_2^0\overset\rightharpoonup P_2^0}+\frac23{w_1^0\overset\rightharpoonup P_1^0}}{w_2^1}$$
(28)
$$\overset\rightharpoonup P_3^1=\frac{w_2^0\overset\rightharpoonup P_2^0}{w_3^1}$$
(29)

Figure 11 shows the NURBS circle based on p = 2 and Fig. 12 shows the semicircle NURBS circle based on p = 3. After getting the control points of the degree-3 NURBS, we recalculate the weights of the curve w’. Figure 13 compares the NURBS circle with p = 2 and p = 3 

Fig. 11
figure 11

The full circle of NURBS in p = 2

Full size image
Fig. 12
figure 12

The semicircle of NURBS in p = 3

Full size image
Fig. 13
figure 13

Compare the NURBS circle in p = 2 and p = 3

Full size image

3.2 Calculate the engagement angle in the active area

The engagement angle in the cutting process affects the cutting force and tool life. With the same depth of cut, the cutting force increases and tool life reduces when the engagement angle increases. The engagement angles α, as shown in Fig. 14, is calculated between the current and previous path of the trochoidal tool path.

Fig. 14
figure 14

Engagement angle in trochoidal tool path

Full size image

In Fig. 14, \({{\varvec{O}}}_{tool}\) is the current tool center. Point A is the contact point with tool and previous path. Point C is the contact point with tool and current path. \({{\varvec{O}}}_{current}\) and \({{\varvec{O}}}_{previous}\) are the points on the guiding curve.. Based on the Eqs.(30)-(34), we can obtain positions of the point C and A.[17]:

$$\begin{array}{cc}{{\varvec{O}}}_{tool}= {{\varvec{O}}}_{current}+ {R}_{current}{e}^{i\left(\varphi -{\varphi }_{start}\right)}& {\varphi }_{start}\le \varphi \le {\varphi }_{end}\end{array}$$
(30)
$${\varvec{C}} = {{\varvec{O}}}_{current}+ {(R}_{current }+ {R}_{tool}){e}^{i(\varphi - {\varphi }_{start})}$$
(31)
$$\theta ={\mathrm{cos}}^{-1}(\frac{{R}_{previous}^{2}+{\overline{{{\varvec{O}}}_{tool}{{\varvec{O}}}_{previous}}}^{2}-{R}_{tool}^{2}}{2{R}_{current}\Vert \stackrel{\rightharpoonup}{{{\varvec{O}}}_{tool}{{\varvec{O}}}_{previous}}\Vert })$$
(32)
$$\gamma=\mathit{cos}^{-1}(\frac{\overset\rightharpoonup{O_{previous}O_{current}}^2+\overset\rightharpoonup{O_{tool}O_{previous}}^2-R_{current}^2}{2\Arrowvert\overset\rightharpoonup{O_{previous}O_{current}}\Arrowvert\Arrowvert\overset\rightharpoonup{O_{tool}O_{previous}}\Arrowvert})$$
(33)
$${{A}}={{{O}}}_{previous}+ {R}_{previous}{e}^{i(\gamma +\theta )}$$
(34)

We obtain the engagement angles α by Eq. (35).

$$\alpha=\cos^{-1}\frac{\overset\rightharpoonup{O_{tool}C}\cdot\overset\rightharpoonup{O_{tool}A}}{\Arrowvert\overset\rightharpoonup{O_{tool}C}\Arrowvert\Arrowvert\overset\rightharpoonup{O_{tool}A}\Arrowvert}=\cos^{-1}\left(\frac{\overset\rightharpoonup{O_{tool}C}\cdot\overset\rightharpoonup{O_{tool}A}}{R_{tool}^2}\right)$$
(35)

The engagement angles α profile in the tranditional trochoidal tool path is shown in Fig. 15. The engagement angle starts from zero and increases after the cutter-and-workpiece contact. When the maximun engagement angle has arrived, the profile dropss immediately. The cutting efficiency is not very satisfactory.

Fig. 15
figure 15

Engage angle in circle pattern

Full size image

3.3 Improve the cutting active section

In the previous section, we calculate the maximun engagement angles α in the circular based trochoidal path. To impoved the cutting efficiency, we propose a new method based the bell shape planning to adjust the engagement angles α. Figure 16 show the relationship between the engagament angle and rotation angle of trochoidal path. We divide the engagament angle curve into areas of acceleration, extended maximun angle, and deceleration section.

Fig. 16
figure 16

Bell-shaped engage angle planning

Full size image

The planning in the acceleration section is by Eqs. (36), (37):

$$\alpha (s) ={\propto }_{start}+ {{C}_{1}\varphi }^{2}, \varphi <\frac{{\varphi }_{1}-{\varphi }_{start}}{2}$$
(36)
$$\alpha \left(s\right)={\propto }_{max}- {C}_{1}{\left({\varphi }_{1} - \varphi \right)}^{2}, \frac{{\varphi }_{1}-{\varphi }_{start}}{2} < \varphi < {\varphi }_{1}$$
(37)

The boundary condition in the acceleration section:

$${C}_{1} = \frac{2{(\propto }_{max} - {\propto }_{start })}{{{(\varphi }_{1}-{\varphi }_{start})}^{2}}$$
(38)

The planning in the deceleration section is by Eqs. (39), (40):

$$\alpha \left(s\right)= {\propto }_{max }- {C}_{2}{\left({\varphi }_{end} - \varphi \right)}^{2}, {\varphi }_{2} <\varphi < {\varphi }_{2}+\frac{{(\varphi }_{end}- {\varphi }_{2})}{2}$$
(39)
$$\alpha (s) ={\propto }_{end} - {C}_{2}{\left({\varphi }_{end} - \varphi \right)}^{2}, {\varphi }_{2}+\frac{{(\varphi }_{end}- {\varphi }_{2})}{2}<\varphi < {\varphi }_{end}$$
(40)

The boundary condition in the deceleration section:

$${C}_{2} = \frac{2{(\propto }_{max} - {\propto }_{end})}{{({\varphi }_{end}- {\varphi }_{2})}^{2}}$$
(41)

Finally, based on Eqs. (36)–(41), we organize the engage angle planning model as follows:

$$\alpha \left(s\right)=\left\{\begin{array}{c}{\propto }_{start}+ {{C}_{1}\varphi }^{2}, \varphi <\frac{{\varphi }_{1}-{\varphi }_{start}}{2}\\ {\propto }_{max}- {C}_{1}{\left({\varphi }_{1} - \varphi \right)}^{2}, \frac{{\varphi }_{1}-{\varphi }_{start}}{2} < \varphi < {\varphi }_{1}\\ \begin{array}{c}{\propto }_{max} , {\varphi }_{1} <\varphi < {\varphi }_{2}\\ {\propto }_{max }- {C}_{2}{\left({\varphi }_{end} - \varphi \right)}^{2}, {\varphi }_{2} <\varphi < {\varphi }_{2}+\frac{{(\varphi }_{end}- {\varphi }_{2})}{2}\\ {\propto }_{end} - {C}_{2}{\left({\varphi }_{end} - \varphi \right)}^{2}, {\varphi }_{2}+\frac{{(\varphi }_{end}- {\varphi }_{2})}{2}<\varphi < {\varphi }_{end}\end{array}\end{array}\right.$$
(42)

By changing the engagement angle, we improve the cutting efficiency in the trochoidal tool path. The result of the engagemnet angle is shown in Fig. 17, where the blue curve is generated by the circuler model and the orange curve is generated by the new pattern model. In the boundary condtion of the engagement angle planning, the tool path will be greatly modified when the change of α is larger. It is easy to cause overcutting in the milling process. To overcome this problem, we set the boundary condition by Eq. (43).

Fig. 17
figure 17

Circular and new pattern engagement angle comparison

Full size image
$${\alpha ^{\prime}}_{max}-\alpha <0.2{\alpha }_{max}$$
(43)

3.4 Tool path generation in the active section

In the last secttion, we update the engagement angle by our proposed method. Based on Eq. (44), we obtain the new contact points \({{\varvec{A}}\boldsymbol{^{\prime}}}_{{\varvec{i}}}=\left\{{A{^{\prime}}}_{1}, {A{^{\prime}}}_{2},\dots ,{A{^{\prime}}}_{n}\right\}\) in \({{C}^{\prime}}_{A}\left(u\right)\), where \({\mathbf{R}}_{z,{O}_{tool,i}}({{\alpha }^{\prime}}_{i})\) is the rotation matrix with \({O}_{tool, i}\) as the center and \({{\alpha }^{\prime}}_{i}\) is the updated engagement angle. Point Ci is the contact point in the current path in Fig. 14.

$${{{\varvec{A}}}^{\prime}}_{i}={ \mathbf{R}}_{{\varvec{z}},{O}_{tool,i}}({{\alpha }^{\prime}}_{i}) {{\varvec{C}}}_{{\varvec{i}}}$$
(44)

After getting the new contact points, we use the psudo-inverse solution for the formulation of least-squares problem, of which the steps are shown in Eqs. (45)–(48), to obtain the new control points \(\stackrel{\rightharpoonup}{{P}^{1}}=\left\{{P}_{0}^{1}, {P}_{1}^{1},\dots ,{P}_{6}^{1}\right\}\) of which the knots are\({U}^{\prime}=\{\mathrm{0,0},\mathrm{0,0},\mathrm{1,1},\mathrm{1,2},\mathrm{2,2},2\)} and the weights \(\{1, \frac{1+\sqrt{2}}{3}, \frac{1+\sqrt{2}}{3},1, \frac{1+\sqrt{2}}{3},\frac{1+\sqrt{2}}{3},1\}\) in degree-3 NURBS in Section 3.1 (Fig. 18).

Fig. 18
figure 18

Circular and new pattern toolpath comparison

Full size image
$$\stackrel{\rightharpoonup}{A^{\prime}}=\frac{\sum_{i=0}^{6}{N}_{i,3}(u){w}_{i}^{\prime}\stackrel{\rightharpoonup}{{P}_{i}}}{\sum_{i=0}^{6}{N}_{i,3}(u){w}_{i}^{\prime}}=\sum_{i=0}^{6}{H}_{i,3}(u)\stackrel{\rightharpoonup}{{P}_{i}}$$
(45)
$${H}_{i,3}(u) =\frac{{N}_{i,3}(u){w}_{i}^{\prime}}{\sum_{i=0}^{6}{N}_{i,3}(u){w}_{i}^{\prime}}$$
(46)
$${\stackrel{\rightharpoonup}{A^{\prime}}}_{n\times 1}={H}_{n\times 7}{\stackrel{\rightharpoonup}{P}}_{7\times 1}$$
(47)
$${\stackrel{\rightharpoonup}{P}}_{7\times 1}={({H}_{7\times n}^{T}{H}_{n\times 7})}^{-1}{H}_{7\times n}^{T}{\stackrel{\rightharpoonup}{A^{\prime}}}_{n\times 1}$$
(48)

We generate the new tool path based on the new control points \(\stackrel{\rightharpoonup}{{P}^{1}}\) by Eq. (49).

$${{C}^{\prime}}_{A}\left(u\right)=\frac{\sum_{i=0}^{6}{N}_{i,3}\left(u\right){w}_{i}^{\prime}\stackrel{\rightharpoonup}{{P}_{i}}}{\sum_{i=0}^{6}{N}_{i,3}\left(u\right){w}_{i}^{\prime}}, 0\le \mathrm{u}\le 1$$
(49)

In Fig. 19, we compare the curve-fitting result with the curve created from the engangment angle planning. The NURBS curve with p = 3 from the curve fitting matches quite well with the green one which was built from the engangment angle planning.

Fig. 19
figure 19

Curve fitting result: the green curve is the original curve from engagement angle planning; the red curve is the curve from curve fitting

Full size image

Based on [19], we calculate the radius of curvature to find the trodoidal radius of the new trochoidal path:

$${R\mathrm{^{\prime}}}_{previous}=\frac{\Vert {\dot{{C}^{\mathrm{^{\prime}}}}}_{A}(u)\times {\ddot{C}\mathrm{^{\prime}}}_{A}(u)\Vert }{{\Vert {\dot{{C}^{\mathrm{^{\prime}}}}}_{A}(u)\Vert }^{3}}={R\mathrm{^{\prime}}}_{troch}+{R}_{tool}$$
(50)
$${R^{\prime}}_{troch}= \frac{\Vert {\dot{{C}^{\prime}}}_{A}(u)\times {\ddot{C}^{\prime}}_{A}(u)\Vert }{{\Vert {\dot{{C}^{\prime}}}_{A}(u)\Vert }^{3}}-{R}_{tool}$$
(51)

The result of the tool paths is shown in Fig. 20, where the blue curve is generated by circular model and the green one is generated by the proposed new pattern model. In the figure, the green curve has more cutting area compared with the blue one to impove the cutting efficiency.

Fig. 20
figure 20

Compare the tool paths between circular model and proposed new pattern model

Full size image

3.5 Tool path improvement in the non-active section

In the non-active section, we use the degree 3 NURBS curve to fit the section in the trochoidal path. As shown in Fig. 21, \({C}_{A,i}\left(\mathrm{u}\right)\) and \({C}_{A,i+1}\left(\mathrm{u}\right)\) are the tool paths of the active section. \({\stackrel{\rightharpoonup}{P}}_{{C}_{A},i\left(2\right)}\) and \({\stackrel{\rightharpoonup}{P}}_{{C}_{A},i+1\left(0\right)}\) are the end points of each curve. \({\stackrel{\rightharpoonup}{S}}_{{C}_{A},i\left(2\right)}\) and \({\stackrel{\rightharpoonup}{S}}_{{C}_{A},i+1\left(0\right)}\) are the end slopes of each curve. We recalculate the control points of the NURBS in the non-active section.

Fig. 21
figure 21

The toolpath by NURBS in non-active section

Full size image
$${P}_{0}={P}_{{C}_{A}\left(u\right)}\left(1\right)$$
(52)
$${P}_{1 }= \frac{3{P}_{0} + {S}_{{C}_{A}(u)}(1)}{3}$$
(53)
$${P}_{2}= \frac{3{P}_{3} - {S}_{{C}_{A}(u+1)}(0)}{3}$$
(54)
$${P}_{3}={P}_{{C}_{A}\left(u+1\right)}\left(0\right)$$
(55)

The knots of curve \(U=\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{1,1},\mathrm{1,1}\right\}\) and the weights \(w= \left\{\mathrm{1,1},\mathrm{1,1}\right\}\). The NURBS of the non-active section is:

$${C}_{NA,i}\left(u\right)= \frac{\sum_{i=0}^{n}{N}_{i,3}(u){w}_{i}{\stackrel{\rightharpoonup}{P}}_{i}}{\sum_{i=0}^{n}{N}_{i,3}(u){w}_{i}} , 0\le \mathrm{u}\le 1$$
(56)

As shown in Fig. 22, we compare two tool paths by different methods. The green curve is our proposed method, and the red curve is the circle-based method. In terms of tool path length comparision, as shown in Table 1, the path length in the non-active section is 115.679 mm by our proposed method and 202.105 mm by traditional trochiodal path method. The path length in non-active section is reduced by 42.8%. The result shows our proposed method can significantly shorten the processing time compared with the circle-based method.

Fig. 22
figure 22

Compare the trochoidal paths by different methods. The green curve is our proposed method, and the red curve is the circle-based method

Full size image
Table 1 Compare the length of tool path from Fig. 22
Full size table

3.6 Cutting force simulation

In order to verify the proposed method can achieve the purpose of improving the cutting efficiency, we use the mechanistic model [29] to anaylze and simulate the cutting force to see whether the change of the cutting force conforms to the change of the engangment angle calculated by our algorithm. Before calculating the cutting force, we refer to [30] and use the APT model of a generalized cutter, with α = 0, β = 0, and R = 0, to define the geometric shape of a flat end mill in Fig. 23. When the cutter contacts with the workpiece, as shown in Eq. (57), the engangment angle \(\phi\) between the entry angle \({\theta }_{st}\) and the depature angle \({\theta }_{ex}\) is calculated.

Fig. 23
figure 23

Generalized cutting tool geometry (a) and the cutting angle convention (b)

Full size image
$${\theta }_{st}\le \phi \le {\theta }_{ex}$$
(57)

In cutting simulation, we adopt a direct computation of cutting force method [31] and analyze the cutting force of each point on the layer along the Z axis of the cutter. According to the trochoidal tool path trajectory, the differential rotating angle, and the instantaneous chip thickness, the instantaineous cutting force is evaluated using the following mechanistice model (Fig. 24) [29]:

Fig. 24
figure 24

Mechanics and kinematics of milling process [29]

Full size image
$$\left[\begin{array}{c}{dF}_{rj}(\phi ,z)\\ {dF}_{tj}(\phi ,z)\\ {dF}_{aj}(\phi ,z)\end{array}\right]= \left[\begin{array}{c}{K}_{re}\\ {K}_{te}\\ {K}_{ae}\end{array}\right] dS(z) + \left[\begin{array}{c}{K}_{rc}\\ {K}_{tc}\\ {K}_{ac}\end{array}\right]{h}_{j}(\phi ,z)dz$$
(58)

where \({K}_{rc}\)、\({K}_{tc}\)、\({K}_{ac}\) are cutting force coefficients due to the shear and \({K}_{re}\)、\({K}_{te}\)、\({K}_{ae}\) are the edge friction coefficients between the cutter and the workpiece in radial, tangential, and axial directions. Based on Eq. (58), we compare the simulated cutting forces between the circle-based tool path and our proposed NURBS-based tool path.

As shown in Fig. 25, under the same cutting shape by Fig. 22, our proposed path generation algorithm can maintain the maximum cutting efficiency for a longer period of time and improve the cutting efficiency compared with the traditional trochoidal machining path.

Fig. 25
figure 25

Comparing cutting forces under different toolpaths (a) Circular method (b) Our proposed method

Full size image

4 Experimental validation and discussion

4.1 Experiment setting

To verify the proposed method in this paper, we use Tongtai VC-608 3-axis machine tool for testing. The controller of the machine is the LNC M6800D. The tool we used is NACHI 2SE ϕ3mm end-mill tool. The dynamometer is Kistler type 9257B. The sampling rate is 200 Hz. The materal we use is aluminum alloy as shown in Table 2. We use the cutting parameters in the milling process suggested by the tool supplier[32]. The spindle speed is 5333 rpm, the feedrate is 350 mm/min, and the axial depth of cut is 3 mm. As shown in Fig. 26, the size of the test workpiece is 50.06 mm × 41.4 mm.

Table 2 The composition ratio of Al6061
Full size table
Fig. 26
figure 26

Pocketing case

Full size image

5 Result and discussion

We compare the proposed new trochoidal too path with the circular trochoidal tool path, as shown in Figs. 27 and 28. The total length of the tool path by our proposed method achieves a reduction of 22.5%, with anincrease of 1.2% in the active area, and a reduction of 47.2% in the non-active area. The total machining time of the tool path achieves a reduction of 17.4%. The detail results are listed in Table 3 and show that the cutting efficienty is increased by inceasing the total engagement area in the cutting region and reducing the tool path in the non-active area.

Fig. 27
figure 27

Circle-based trochoidal toolpath

Full size image
Fig. 28
figure 28

NURBS-based trochoidal tool path

Full size image
Table 3 Comparison of two different toolpaths
Full size table

The cutting force of the total path in the demonstration case is shown in Fig. 29. For the analysis of a single cycle, as shown in Fig. 30, we compare the cutting time to the non-cutting time in the NURBS trochoidal tool path and the circular trochoidal tool path. Table 4 shows the ratio of active time to non-active time; the circular model is 0.52 and the NURBS model is 1.34. The result shows that the NURBS trochoidal tool path improves the cutting efficiency by saving the non-cutting time significantly.

Fig. 29
figure 29

Cutting force during machining (a) Circle-based path (b) NURBS-based path

Full size image
Fig. 30
figure 30

Cutting force in a single cycle (a) Circle-based path (b)NURBS-based path

Full size image
Table 4 The cutting time and ratio of active and non-active area in a single trochoidal cycle
Full size table

Figure 31 shows two more pocketing cases with one island and two islands. As shown in Table 5, the result shows that the NURBS trochoidal tool path improves the cutting efficiency by saving the non-cutting time significantly, indicated by the ratio of the cutting path to the non-cutting path.

Fig. 31
figure 31

Pocketing cases (a) one island (b) two islands

Full size image
Table 5 Comparison of two different toolpaths in pocketing case with two islands
Full size table

6 Conclusions

In this paper, we propose a novel double-NURBS trochoidal path generation method. The proposed method has three characteristics:

  1. 1

    Using the double-NURBS model to represent the trochoidal tool path that combines the (medial-axis) guiding-curve tool path and the circular tool path with a degree-3 NURBS curve to maintain C2 continuity throughout the entire trochoidal tool path.

  2. 2

    By degree elevation of the degree-2 NURBS circle to a degree-3 NURBS curve, we increase the cutter-workpiece engagement bandwidth by modifying the front-end cutting curve and its control points. This increases the cutting efficiency while maintaining the C2 continuity to improve smooth tool path transition and reduce undesired vibration.

  3. 3

    For the back-end retraction tool path in the non-active region, we modify the degree-3 NURBS curve to shorten the travel distance to save non-active time. The reduction of time saving from a ratio of 0.52 to 1.34 is quite significant.

Compared with the traditional circular trochoidal tool path, the double-NURBS method we present has a reduction of 22.5% of the tool path length which has an increase of 1.2% in the active area and a reduction of 47.2% in the non-active area. The total cutting time is reduced by 17.4%.

Since the trochoidal machining path has non-cutting path for every cycle, it is known that trochoidal machining will not be suitable for the entire machining region. Hence good strategies need to be designed to integrate trochoidal tool path with other types of tool path such as pocket contouring path. This will be one of our future work directions. Other future work includes the feed rate optimization of the trochoidal tool path based on the cutting force constraints. This is because as the trochoidal radius varies along the guiding curve to approximate pocketing contours, cutting force becomes smaller as the trochoidal radius increases. If we are to maintain a steady cutting force (so a steady tool wear progress), we can actually speed up the feed rate and increase productivity. In our future work, we plan to integrate real-time cutting force prediction with optimized feed rate scheduling to maximize trochoidal milling productivity. This might be further integrated with the look-ahead function of a machine tool controller that is equipped with the NURBS interpolation capability.