Development of elastic–plastic model of additively produced titanium for personalised endoprosthetics

Abstract

This study presents a model for Ti6Al4V alloy produced by applying electron beam melting as continuum media with orthotropic elastic and plastic properties and its application in total hip replacement (THR). The model exhibits three Young’s moduli, three shear moduli, and three Poisson’s ratios as elastic properties and six coefficients describing the Hill yield criterion. Several uniaxial tension and torsion experiments and subsequent data processing were performed to evaluate the properties and coefficients. The typical values obtained for Young’s moduli, shear moduli, and Poisson’s ratio were 121–124 MPa, 37–42 MPa, and 0.25–0.26, respectively. A comparison of the experimental tension and torsion curves with those obtained by a finite element analysis revealed a good correlation with a maximum error of 9.5%. The finite element simulation of a personalised pelvic implant for THR manufactured from the obtained material proved the mechanical capability of the implant to successfully withstand the applied loads.

1 Introduction

Additive manufacturing is an advanced manufacturing technology that is rapidly gaining acceptance worldwide in recent times.

Additive technologies are finding an increasing number of applications, as they facilitate manufacturing products that are impossible or impractical to produce by using other methods owing to economic reasons. Growing production capabilities compel the markets to implement additive manufacturing as efficiently as possible to manufacture competitive products. It is postulated that superior products must possess optimal characteristics at each product life step, from development to manufacturing.

This paper describes a method for the construction of material models for parts typically produced by applying metal powder melting or sintering using layer-by-layer material techniques. The proposed method can easily obtain material models for further use in finite element simulations.

Owing to the constantly increasing complexity and required accuracy of design and production methods, it is necessary to use material models that are as close to reality as possible. Therefore, the aim of this study is to develop methods for preparing accurate mathematical models for materials manufactured from metal powders using electron beam melting (EBM).

The relevance of this study and the topic as a whole is confirmed in Lewandowski and Mohsen [1], Rosenthal et al. [2], Carroll et al. [3], Zhang et al. [4], Zhao et al. [5], Chen et al. [6], Ren et al. [7], and Ataee et al. [8], in which comprehensive testing and analyses of additively manufactured materials are reported.

In Lewandowski and Mohsen [1], an exhaustive review and compilation of approximately 200 different studies on the mechanical properties of additively produced materials is presented. The behaviour of Ti6Al4V alloy was comprehensively studied in the context of various technologies, such as EBM, selective laser melting (SLM), direct metal laser sintering, and laser engineered net shaping, both before and after heat treatment.

In Rosenthal et al. [2], the microstructure and mechanical properties of AlSi10Mg alloy produced by SLM technology were studied. One of the main conclusions of that study was that printed samples produced by this method exhibit explicit anisotropic properties.

In Carroll et al. [3], the influence of heat treatment on the mechanical behaviour of Ti6Al4V samples produced by direct energy deposition technology was evaluated. The results indicate that the mechanical properties depend on the production process adopted for producing the parts.

In Zhang et al. [4] and Zhao et al. [5], the microstructure of additively produced titanium samples and the mechanical properties of the material in different directions were investigated. Several mechanical tests were performed to obtain the mechanical parameters. A comparison of these properties in terms of the material orientation and production technology was presented. In Chen et al. [6], the anisotropic mechanical and electrochemical properties of Ti6Al4V samples printed using an SLM machine were investigated.

The mechanical properties of titanium-printed parts used in medical applications, such as endoprosthetic purposes, have also been studied [7, 8]. Research on the mechanical properties of martensite steel, MS1, has been conducted [9]. Elastic and plastic behaviours of samples printed in different directions were studied. Applications of laser powder bed fusion technology for Al alloy powders has increased over the last decade, with a focus on improving the strength of the components produced [10].

All these studies support the assumption that a study of the mechanical properties of additively produced metal materials is essential. However, no attempt was made in any of these studies to create a complete mathematical model of the observed materials for further use in finite element simulations.

Hip replacement is one of the most common surgical operations and is a fundamental task in orthopaedic biomechanics. During the initial installation of the implants, the structure is formed by a standard set of components of a certain size and shape. With an increase in the number of primary surgical interventions and follow-up periods, the number of audit operations increases. For revision interventions, it amounts to 20% of the total number of hip replacement operations. Unsatisfactory results of hip replacement are very often associated with aseptic loosening of the acetabular component or injuries.

Over the last decade, certain publications have reported the results of biomechanical studies of the “skeleton–endoprosthesis” system under the conditions of revision arthroplasty, associated with significant surgical intervention and individual implant selection. Thus, in Liu et al. and Dong et al. [11, 12], various implants made from conventional titanium alloy and their fixation in the pelvic bone were examined from biomechanical perspectives. In earlier works [13, 14], reconstruction of the acetabulum of the pelvis using implants made from autogenous biological materials taken from the fibula was discussed.

In Zhou et al. [15], a modular endoprosthesis of customised shape and size was designed to replace the destroyed half of the pelvis. The study presented a comparative analysis of the stress distributions between a healthy and restored pelvis in three static positions: sitting, standing on two legs, and standing on one leg on the injured side. The loads, regions of their application, and kinematic constraints on the degrees of freedom of the finite element model were similar to those described in Jia et al. [16].

In Wong et al. and Fu et al. [17, 18], a new approach was presented for the creation of implants, based on 3D printing technology, using additive layer manufacturing. The 3D-printed Ti6Al4V augmentation had a 1-mm layer of porous coating of the same material, and the rest of the augmentation was solid [18]. As stated in Colen et al. [19], this method is ideal for automatically manufacturing appropriate individual implants with porous layers for bone-implant interfaces to improve osseointegration and tissue regeneration within a porous scaffold [20]. The individual geometry of the acetabulum for each person, corresponding exactly to the damaged areas of the bone, was first designed and then 3D-printed.

The main goal of this study is to prepare models based on elastic and plastic anisotropic continuum media, which are closer to real life than their widely used elastic isotropic counterparts. We present the methodology developed for Ti6Al4V alloy as a representative of metallic materials and samples that are additively produced using an EBM machine. Furthermore, this article describes the features of the numerical modelling of a revision endoprosthesis replacement of the acetabulum component of a hip joint. The results of the finite element analysis (FEA) of the stress–strain state system formed by the human skeleton and hip endoprosthesis in a double-supported state are presented. Attention is mainly paid to the calculation of stresses in the pelvic component of the endoprosthesis under a static load on the implant, arising from the torque applied during the tightening of the screws into the bone and the person’s weight.

2 Mathematical model of the material

2.1 Methodology concept

The material model type should be selected depending on the intended material application. For example, a model for materials used in jet engines must include thermodynamic equations to describe the thermal processes. The most common applications of additively produced parts are structures or construction parts. Therefore, primary consideration should be given to the mechanical behaviour of the materials.

Another factor to be considered is the influence of the manufacturing process on the material properties, as the former has a significant effect on the material behaviour.

Because this study is devoted to the construction of a mathematical model of Ti6Al4V alloy produced on EBM machines, as well as to the subsequent utilisation of this model for FEA simulations of personalised endoprosthesis, a brief discussion of how this technology works is given as follows.

EBM is an additive manufacturing technology that requires electron beams to melt the metal powder. The process is almost the same as any classic additive manufacturing technology that uses powder as an expendable material. A part is constructed layer-by-layer by melting the material in specific areas, as defined by a 3D model. The beam scans the cross section of the part, after which, the platform moves down at a distance equal to the layer height, and a new layer of powder is added to the top of the printing area. The beam melting printing process is conducted in a vacuum environment, to facilitate the use of materials with a high affinity for oxygen. In addition, during the printing process, the printing area is maintained at a high temperature (700–1000 °C), which reduces the residual stresses in the printed parts. As the part is formed layer-by-layer, this process may strongly affect the material properties, especially its anisotropy.

First, the microstructure of Ti6Al4V alloy was investigated to determine the type of material behaviour. In this study, two cylindrical specimens (Fig. 4) were printed on an EBM machine in different orientations (Fig. 5). One specimen was printed such that the axis of the cylinder was aligned with the X-axis of the printer, whereas the other had its axis aligned with the Z-axis of the machine. An Arcam Q20 (Arcam AB) machine was used to print these samples and all other samples used in this study. The printing process had the following setup: scanning speed of 3 m/s, layer height of 0.09 mm, and EBM power of 3 kW. The electron beam was also used to preheat the powder by scanning the surface at a speed of up to 75,000 mm/s. Ti6Al4V powder was produced by LPW Technology Ltd. and had a particle size range of 45–100 μm.

The microstructure was studied using the сross section of these cylinders for further comparison. A Brilliant 220 (ATM GmbH) machine with a diamond cut-off wheel was used to perform a cut. Micro-sections were made along the cross-sectional plane after the cutting. The micro-sections were pressed into a thermoplastic material using an Opal 460 (ATM GmbH) press-in machine. Subsequent grinding and polishing of the micro-sections were performed on a Saphir 560 (ATM GmbH) installation, using abrasive wheels and diamond suspensions. The samples were then etched to reveal their microstructures.

On the slice images (Figs. 1 and 2) obtained using electronic microscopy, the specimen microstructure was observed. The metallographic analysis of the microstructure of the samples was performed using optical microscopy methods on a Leica DMI 5000 (Leica Microsystems) light optical microscope in 50 to 1000 × magnification range.

Fig. 1

Microstructure of Ti6Al4V specimen in YOZ plane

Fig. 2

Microstructure of Ti6Al4V specimen in XOY plane

The microstructure of the cross sections of the described specimens is shown in Figs. 1 and 2. It can be inferred that, in terms of the material behaviour, these structures might provide anisotropic properties of the material on a macroscale. This can be attributed to the differences in the structures observed in these figures. The microstructure in the XOY plane (Fig. 2.) is more uniform than that in the YOZ plane (Fig. 1). This can be explained by the fact that the layers are printed in the XOY plane, whereas the YOZ plane contains several printed layers.

Therefore, the proposed methodology is based on the assumption that layer-by-layer metal production technology provides orthotropic properties to the material and, hence, is focused on the orthotropic model of elastoplastic behaviour.

Generally, the proposed methodology consists of the following steps:

• 1) mathematical formulation of the material model based on continuum mechanics approaches;

• 2) identification of the equation material constants from experiments;

• 3) model verification.

2.2 Elasticity

The construction of the orthotropic elastoplastic model is a step-by-step process. First, let us introduce the elastic behaviour by Hooke’s law in tensor notation [21]:

$$ \boldsymbol{\sigma} =\mathrm{C} \cdotp \cdotp \boldsymbol{\varepsilon} $$

(1)

where σ is the Cauchy stress tensor; С is the elasticity tensor; and ε is the strain tensor.

Equation (1) can be presented in the inverse form by using the engineering constants and matrix notations:

$$ \left\{\begin{array}{c}{\varepsilon}_{xx}\\ {}{\varepsilon}_{yy}\\ {}{\varepsilon}_{zz}\\ {}{\gamma}_{xy}\\ {}{\gamma}_{xz}\\ {}{\gamma}_{yz}\end{array}\right\}=\left[S\right]\cdotp \left\{\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\sigma}_{zz}\\ {}{\sigma}_{xy}\\ {}{\sigma}_{xz}\\ {}{\sigma}_{yz}\end{array}\right\} $$

(2)

where [S] is the compliance tensor in matrix form.

$$ \left[S\right]=\left(\begin{array}{cc}\begin{array}{ccc}\frac{1}{E_x}& -\frac{\mu_{xy}}{E_x}& -\frac{\mu_{xz}}{E_x}\\ {}-\frac{\mu_{yx}}{E_y}& \frac{1}{E_y}& -\frac{\mu_{yz}}{E_y}\\ {}-\frac{\mu_{zx}}{E_z}& -\frac{\mu_{zy}}{E_z}& \frac{1}{E_z}\end{array}& 0\\ {}0& \begin{array}{ccc}\frac{1}{G_{xy}}& 0& 0\\ {}0& \frac{1}{G_{xz}}& 0\\ {}0& 0& \frac{1}{G_{yz}}\end{array}\end{array}\right) $$

(3)

The following notations are commonly used in Formula (3):

ε_ii—strain tensor components

σ_ii—stress tensor components

E_i—Young’s moduli

G_ij—shear moduli

μ_ij—Poisson’s ratios

In Eq. (3), there are 12 different material constants; however, only nine of them are independent. Therefore, to fully describe the elastic behaviour of the orthotropic material, it is sufficient to find the following nine constants: three Young’s moduli, three shear moduli, and three Poisson’s ratios.

2.3 Plasticity

The next step in the formulation of the proposed model is defining the yield criterion. Here, the widely used von Mises yield criterion cannot be used because the obtained values of yield stress would noticeably differ in different directions; instead, the Hill yield criterion can be used to describe the moment of transition to plasticity for orthotropic materials. This criterion can be expressed in multiple ways. In this study, the following equation was used [22]:

$$ {\sigma}_{eq}=\sqrt{\frac{3}{2\left(H+F+G\right)}\Big(H{\left({\sigma}_{xx}-{\sigma}_{yy}\right)}^2+F{\left({\sigma}_{yy}-{\sigma}_{zz}\right)}^2+}\overline{+G{\left({\sigma}_{zz}-{\sigma}_{xx}\right)}^2+2N{\sigma}_{xy}^2+2M{\sigma}_{xz}^2+2L{\sigma}_{yz}^2\Big)}\ge {\sigma}_y $$

(4)

where σ_eq is the equivalent stress; H, F, G, N, M, and L are the Hill coefficients of the material; and σ_y is the threshold (yield) stress.

The six material constants, H, F, G, N, M, and L, in the criterion represented by Eq. (4) can be calculated from the values of the yield stresses in different directions, including the rotations. This criterion allows us to define the transition to plasticity by one specific value of threshold stress, which is compared to the equivalent value calculated by Eq. (4). Therefore, to define the yield criterion, six values of yield stress (three tensile yield stresses and three torsion yield stresses) need to be determined.

The final step in the construction of the mathematical model of orthotropic elastoplasticity is to describe the plastic behaviour. Different techniques can be used for this. However, because the model is constructed for FEA simulations, the most convenient method is to use a stress–strain curve with several specific points. Let us assign the axes of this curve as follows: the abscissa is the equivalent of the stress, as calculated by Eq. (4), and the ordinate represents the plastic strain. Here, we assumed that the chosen axes should provide an alignment of the stress–strain curves of any type and load direction.

In line with this approach, one stress–strain curve should be sufficient to define the plastic behaviour of the material. However, it is preferable to have more than one curve to ensure that the hypothesis of curve alignment works well. Let us set the number of these curves as the number of experiments needed to obtain the required yield stresses because these experiments also include measurements in the plastic region. Therefore, in this study, six stress–strain curves were utilised.

3 Testing and experimental data processing

3.1 Testing description

Once the mathematical model is constructed, it is possible to formulate a set of material properties to be obtained. These properties can be found from several mechanical experiments: uniaxial tension in the three coordinate directions and uniaxial torsion around the three axes.

Uniaxial tension experiments can provide information regarding the Young modulus, Poisson ratio, and three yield curves. Specimens with a circular cross section were designed for these experiments according to USSR Standart 1497-84 [23] and Instron [24], and these are shown in Fig. 3.

Fig. 3

Uniaxial tension specimen (unit: mm)

Tension tests were performed using a Zwick Z250 machine (Zwick Roell Group). A Zwick LaserXtens HP laser extensometer was used to measure the transverse strain for the estimation of Poisson’s ratio. The uniaxial tension test had the following setup: preloading of 5 MPa, clamping pressure of 8 MPa, rate of stressing of 30 MPa/s, and rate of measurement of 0.0067 s⁻¹.

The torsion experiments provided information on the shear moduli and three left yield curves. Specimens with a circular cross section were designed for these experiments according to USSR Standart 3565-80 [25], and these are shown in Fig. 4.

Fig. 4

Uniaxial torsion specimen (unit: mm)

Torsion tests were performed on an Instron 8850 test machine. The uniaxial torsion test had the following setup: preloading of 2 Nm, clamping pressure of 4 MPa, rate of straining of 12°/min, and rate of measurement of 0.2 s⁻¹.

Three directions of loading for each load type were required because of their orthotropic properties. The direction of loading was aligned with the axes of the machine that produced samples. These axes were considered to be the axes of anisotropy of the material. Figure 5 shows an example of the torsion specimen orientation in the printing machine. The tension specimens were also oriented in the same way.

Fig. 5

Schematic of directional orientation of the torsion specimens

The results of the aforementioned tests were the well-known stress–strain (load-displacement) curves. As a next step, it was necessary to process the experimental data to obtain the desired properties from these curves.

These tests were sufficient to calculate all the constants and fully define the orthotropic elastoplastic material model. However, it was also imperative to minimise the influence of random factors, such as manufacturing defects. Therefore, statistical processing of the required values was performed by manufacturing a set of three specimens and testing them for each direction and type of loading.

3.2 Experimental data processing

The process of obtaining the Young modulus and tension yield stress in the same direction was performed iteratively, according to the process described in USSR Standart 1497-84 [23], Instron [24], and USSR Standart 3565-80 [25], and is as follows.

First, a linear section of the stress–strain curve was chosen. The borders of this section were determined based on the expected value of the yield stress, which is related to the yield stress of an analogous cast specimen. The lower bound was set to 10% of this value, and the upper bound was set to 85%, to exclude all the nonlinearities in the very beginning and end of the elastic region. A linear approximation of this section was performed using the least squares method. The coefficient of this approximation was a possible value of the Young modulus. Subsequently, the plastic strain value was calculated by subtracting the elastic strain from the total strain. The stress corresponding to a 0.2% plastic strain was a possible value for the yield stress. If this value was equal or sufficiently close to the expected yield stress value at the beginning of the process, we considered the obtained value as final. Otherwise, we repeated the process until the obtained yield stress value met the expected value. These iterations provided a close approximation of the desired values.

The described process was performed for each tested specimen. This means that there were three values each for both the Young modulus and tension yield stress for statistical purposes. The final values of these coefficients were calculated as the averages of the three values obtained.

The process of obtaining the Poisson ratio was also based on the results of the uniaxial tension tests. The Poisson ratio was calculated as a relation of the transverse strain to the axial strain measured in the elastic section of the stress–strain curve. Thus, the Poisson ratio in each direction also had three available values, from which an average value was calculated.

The aforementioned processing techniques are widely used. Additionally, the proposed material model type has no effect on these techniques. However, in several cases, it is impossible to use these methods easily owing to the assumption of orthotropic properties. In this study, these cases were connected with the torsion problem. For this reason, the processing of shear moduli and torsion yield stresses could not be performed in the same way.

As mentioned earlier, it is possible to obtain the value of shear moduli from the results of uniaxial torsion tests. This procedure is simple in the isotropic case [25]. The value of the shear modulus is calculated as the ratio of shear stress to shear strain in a linear part of the stress–strain curve. However, if the material is orthotropic, the stress–strain state of such specimens differs. Therefore, it is necessary to perform additional evaluations to determine the value of the shear modulus.

The following calculation is based on anisotropic models of continuum mechanics [21]. Let us assume that the values of the torque and twist angle are known from the experiments. First, uniaxial torsion is considered and performed along the Z axis (Fig. 6).

Fig. 6

Statement of torsion problem

Next, we should consider that there are two shear moduli which affect the stress–strain state during uniaxial torsion. In the considered case, these two modules are G_xz and G_yz. This means that the relation between the torque and twist angle includes both these modules. We can describe this relation using the following equation [21]:

$$ \varphi =\frac{Ml}{2{J}_p}\left(\frac{1}{G_{xz}}+\frac{1}{G_{yz}}\right) $$

(5)

The main problem here is the non-availability of two independent values from one equation based on the experimental data. Therefore, another variable, Bz, is introduced as follows:

$$ \frac{1}{B_z}=\frac{1}{2}\left(\frac{1}{G_{xz}}+\frac{1}{G_{yz}}\right) $$

(6)

This step allows us to obtain the value connected with the required shear moduli from one load-displacement curve. The procedure for obtaining the value of B_z is based on USSR Standart 3565-80 [25] and follows the previously described process of finding the Young moduli.

The next step is to calculate two more values of B from the torsion tests about X and Y axes. Thus, we have three values: B_x, B_y, and B_z, which are connected to the required shear moduli by Eq. (6) or similar. These equations form a nonlinear system with the following solution:

$$ \left\{\begin{array}{c}{G}_{xy}=\frac{B_x{B}_y{B}_z}{\left(-{B}_x{B}_y+{B}_x{B}_z+{B}_y{B}_z\right)}\\ {}{G}_{xz}=\frac{B_x{B}_y{B}_z}{\left({B}_x{B}_y-{B}_x{B}_z+{B}_y{B}_z\right)}\\ {}{G}_{yz}=\frac{B_x{B}_y{B}_z}{\left({B}_x{B}_y+{B}_x{B}_z-{B}_y{B}_z\right)}\end{array}\right. $$

(7)

Therefore, all the required shear moduli can be calculated according to the relationships in Eq. (7) by obtaining B_x, B_y, and B_z.

The next step of model construction is to obtain the three yield stresses, based on the results of the uniaxial torsion tests. Here, we continue following the idea that the orthotropic model makes it necessary to perform an additional investigation on torsion problems. The main aim of obtaining the yield stresses here is to obtain the plastic strain values from the experimental data and to determine the specific value of plastic strain that corresponds to the moment of transition to plasticity. However, because we have two different shear moduli affecting the stress–strain state, we can expect shear strain to have a distribution that differs from that in the isotropic case. We omit intermediate analytical calculations and present the strain distribution in a cross section of the specimen (Eq. (8)):

$$ {\displaystyle \begin{array}{c}{\gamma}_{xz}=-\frac{1}{\left(\frac{1}{G_{xz}}+\frac{1}{G_{yz}}\right)}\frac{2}{G_{yz}}\theta y,\\ {}{\gamma}_{yz}=\frac{1}{\left(\frac{1}{G_{xz}}+\frac{1}{G_{yz}}\right)}\frac{2}{G_{xz}}\theta \mathrm{x}.\end{array}} $$

(8)

Using these equations and the obtained values of shear moduli, we can find the required components of the strain tensor from the experimental data. This strain distribution can be depicted by the diagram presented in Fig. 7.

Fig. 7

Strain diagram of a cross section of the specimen

Next, we can find the plastic strain by subtracting the elastic strain from the total strain. To understand the idea of obtaining the yield stresses in this case, let us describe the process of transition to plasticity in this specimen. In the elastic region, the material behaviour followed the Hooke law: The shear stress distribution was axisymmetric, with its maximum value on the outer surface of the specimen. The shear strain distribution can be described by Eq. (8). As soon as the stress value equals the yield stress, the process of transition to plasticity begins. It begins from two zones, which correspond to the achieved yield stress. From this moment, the stress–strain state becomes different from that in the elastic case. Next, the stress value reaches the second yield stress value, and the entire outer surface of the specimen can be referred to as a plastic region. With a further increase in the stress, the plastic region propagates to the centre of the specimen. Finally, when the torque reaches a certain value, the entire specimen behaves according to the plastic law.

Subsequently, to obtain all the required yield stresses, we need to make one more assumption. Let us assume that when the stress value is between the two considered yield stresses, the stress–strain state changes so slightly that we can still use the elastic (Eq. (8)) to calculate the strain values. Otherwise, it would be necessary to introduce laws of flow plasticity theory for orthotropic cases and define them by using experimental data.

Using the analytical research results presented earlier, we can calculate the plastic strain values (${\gamma}_{xz}^p,{\gamma}_{yz}^p$). These values allow the definition of yield stresses as the value of shear stress when the plastic strain reaches 0.2%. This approach yields two yield stress values for each load direction:

${\sigma}_{xy}^y,{\sigma}_{xz}^y$—for torsion about the X-axis

${\sigma}_{xy}^y,{\sigma}_{yz}^y$—for torsion about the Y-axis

${\sigma}_{xz}^y,{\sigma}_{yz}^y$—for torsion about the Z-axis

Thus, each yield stress value is defined twice. The results of the experimental data revealed that these values might differ slightly from each other. This can be explained by the influence of the manufacturing process on the residual stresses, which strongly affect the yield stress values. This difference could be caused by a statistical spread of the measured values because the low repeatability of printing results is a well-known issue in additive manufacturing technologies. Based on these considerations, the smaller value is selected from the two values obtained for each yield stress. This solution is more conservative in terms of FEA simulations.

3.3 Obtained material properties

Tables 1 and 2 list several obtained values of material properties in the three principal directions of material symmetry.

Table 1 Material properties of Ti6Al4V alloy

Table 2 Parameters of Hill’s plasticity model of Ti6Al4V

The values summarised in Tables 1 and 2 show that the studied materials exhibit property variations in different directions. This means that our assumption of anisotropic behaviour of the material was validated and that the chosen model described the real-life material more closely than the widely used elastic isotropic assumption.

These constants were used in subsequent finite element simulations and analyses.

4 Material property simulations

4.1 Model description

The developed mathematical models of the studied material were verified against with the experimental data. All the experiments were conducted in SIMULIA Abaqus (Dassault Systèmes) using an orthotropic elastoplastic material. The modelling process is described in detail in the proposed method.

Figures 8 and 9 show the models used in the FEA to control the alignment of the obtained properties to the real-life material. In the modelling process, only the gauge section of a specimen was used to reduce the computational complexity.

Fig. 8

Tension model for finite element simulations

Fig. 9

Torsion model for finite element simulations

The tension model included 9600 linear hexahedral finite elements. The boundary conditions for the tension modelling are as follows:

• The flat side surfaces comply with symmetry conditions.

• The left end surface has zero displacement along normal direction.

• The opposite end surface has a nonzero displacement along normal direction.

The torsion model contained 44,500 linear hexahedral finite elements.

The boundary conditions for the tension modelling are as follows:

• One of the end surfaces has zero rotation along the normal direction.

• The opposite end surface has nonzero rotation along normal direction.

In the described boundary conditions, loading was applied as a displacement. This displacement was applied over 100 steps with a linear growth from 0.1 to 100% of its final value. The chosen type of loading provided the possibility of extracting the stress–strain curve with an adequate resolution to analyse the same and compare the results with the experimental data. This displacement was applied through a reference point connected to the end surface.

4.2 Results

Figures 10, 11, 12, 13, 14, and 15 show the FEA simulation results in comparison with the experimental data represented by the bottom and upper curves, respectively.

Fig. 10

Tension in Ti6Al4V specimen along the X-axis

Fig. 11

Tension in Ti6Al4V specimen along the Y-axis

Fig. 12

Tension in Ti6Al4V specimen along the Z-axis

Fig. 13

Torsion in Ti6Al4V specimen about the X-axis

Fig. 14

Torsion in Ti6Al4V specimen about the Y-axis

Fig. 15

Torsion in Ti6Al4V specimen about the Z-axis

The experimental data had the following average values of the standard deviation: Fig. 10: 16 MPa, Fig. 11: 9 MPa, Fig. 12: 15 MPa, Fig. 13: 0.9 Nm, Fig. 14: 0.9 Nm, and Fig. 15: 1.9 Nm. The axis notations in these graphs were chosen in accordance with the experimental data obtained from the tension and torsion tests.

Several conclusions can be drawn from these curves. First, in each loading case, good agreement between the two results can be observed in the linear region. This indicates the high accuracy of the proposed model in the elastic region. Furthermore, the point where a transition to plasticity occurs is also correctly predicted by the proposed model, as both the curves undergo a change in their slope almost concurrently. However, in the subsequent plasticity region, larger deviations are observed (Figs. 10, 11, and 13).

On the other hand, these deviations are not significant in Figs. 12, 14, and 15. This can be attributed to the fact that the constructed model did not adequately account for the influence of orthotropic properties on the plastic behaviour because it is based on a single plastic curve assumption. This is why some loading directions may have had a lower accuracy in the plastic region. However, because the main application of this model is meant to be the calculations of construction and medical components, the need for late plasticity region modelling does not arise.

5 Titanium hip implant simulation

5.1 Finite element model

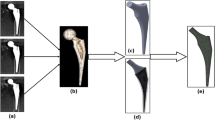
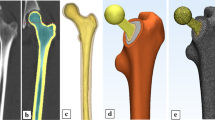
Geometric data were obtained from the surface models of the implant and screws, as well as a CT-based pelvic bone reconstruction for a patient treated at the federal state–funded institution “Russian Scientific Research Institute of Traumatology and Orthopaedics” named after R.R. Vreden. The analysed implant was a customised endoprosthesis of the hip joint, which is a replacement for a standard endoprosthesis [26].

The structure of the hip endoprosthesis element consisted of a stem inserted in the pelvic bone, a hemispherical cup, and a support flange attached to the ilium (Fig. 16). The external surface of the endoprosthesis in the bone contact area has a porous structure to improve osseointegration.

Fig. 16

Three-dimensional model of the restored hip joint system

Model development was performed in two steps. First, the MRI data were used to build the STL model in a 3D Slicer (Slicer Community). Second, the solid model was created in Altair Inspire (Altair Engineering) software on the basis of the surface model that had been previously built upon the STL model.

The developed finite element bone models, designed in SIMULIA Abaqus, consisted of two layers of finite elements with different properties: the outer cortical layer and the inner spongy layer (Fig. 17).

Fig. 17

Finite element model of the system “skeleton–hip implant”

The bone tissue was mathematically modelled as a homogeneous material with isotropic effective properties. Its Young’s modulus was set to 10 GPa for the compact bone and 0.5 GPa for the spongy bone, and the Poisson ratio was taken as 0.3 for both types of bones [27].

To describe the endoprosthesis material, an orthotropic model with elastic and plastic properties (Tables 1 and 2) was implemented in the implant finite element model by using the axes of the local coordinate system (XYZ), shown in Fig. 18, as the principal directions of the additive manufacturing process. Isotropic models of the remaining titanium components were employed with averaged values of the Young modulus of 123.4 GPa and Poisson ratio of 0.26. The outer porous layer of the implant stem and support flange were also considered solid and isotropic, with an effective Young’s modulus of 6.7 GPa and Poisson’s ratio of 0.26, obtained as a result of homogenisation [28].

Fig. 18

Primary directions of material anisotropy

The structure was subjected to static forces of the tightened screws and the weight of the patient. The static balance equations proved that in the two-leg standing position, gravity was balanced by the reaction of the support equal to half of the patient’s weight. The most convenient option was to apply the load to the end of the simplified hip bone model, while the upper part of the sacrum was fixed.

The load was applied in two steps. First, tightening of the screws was performed to produce forces that pulled the implant and the bone together. Two values equal to 150 and 300 N were considered. Second, the free ends of the leg models were subjected to longitudinal forces of 440 N, equivalent to a weight of 88 kg directed along the hips; the screw tightening was maintained as in the previous step.

5.2 Titanium implant stress analysis

The calculated stress–strain state for the titanium components of the biomechanical system are presented, taking into account the tightening force of the screws and the weight of the person. Figure 19 shows a general distribution of the equivalent von Mises stresses under a screw load of 300 N; the case of 150 N yielded an almost similar distribution, albeit with smaller peak values.

Fig. 19

Total stress distribution contours with a screw tightening force of 300 N; the range of displayed stresses is 1–50 MPa

In both the cases involving the screw tightening force, the stress concentration occurred at the boundary of the contact areas in the transition zone from porous to solid titanium, and were 206 and 297 MPa, respectively (Fig. 20). On the edges of the screw holes and at the transition point of the cup to the support flange, the stresses did not exceed 80–120 MPa on an average. Peak stresses of 130 and 230 MPa were observed near one of the holes.

Fig. 20

Stress distribution contours in the implant for a tightening force of 300 N

In the screws, at the points of interaction with the cortical layer of the bone and the implant, stress hikes in individual elements up to 312 and 527 MPa, respectively, was observed (Fig. 21). Large local stresses were possibly caused by a tight coupling between the model components. In other screws, the maximum stresses did not exceed 170 and 310 MPa on the screw heads.

Fig. 21

Stress distribution contours in the screws for a tightening force of 300 N

6 Discussion

To determine the relation between the material properties and manufacturing process, an analysis of the microstructure presented in Figs. 1 and 2 was performed, with a view to either prove or disprove the assumption of anisotropic material behaviour.

The microstructure of the additively produced material closely matched its cast counterpart; however, a detailed study revealed that crystallites in the YOZ plane had pronounced elongation in two directions. This may have been caused by the scanning strategy of the printing machine. This irregularity in the crystallite shape influences the material properties. This is confirmed by the perceptible differences, which can be observed in Tables 1 and 2. However, the degree of this influence was not as large as in other studies. For example, in [29], an analysis was performed for the same material as was considered in this study, and also for aluminium alloy AlSi10Mg. A comparison of these two materials in terms of microstructure and orthotropic properties revealed that aluminium exhibited more pronounced orthotropic properties than titanium. For example, the deviation of the Young modulus in the three directions was 1 GPa (0.9%) for titanium and 2.7 GPa (3.4%) for aluminium. For the shear modulus, these values were 2.1 GPa (5.1%) for titanium and 2.3 GPa (9.7%) for aluminium. This may have been caused by the fact that the aluminium samples were produced by SLM technology, which uses lower camera temperatures. This leads to a higher cooling rate, and thus, the structure becomes less stable and uniform.

The constructed model described the elastic behaviour with a high precision. This was indicated by the agreement in the linear part of the graphs. Furthermore, the constructed model enabled an accurate description of the transition to plasticity in terms of stress. This could be observed in the early plasticity parts of the graphs. However, the model had some deviations from the experiment in the region of high plastic strain. This may be attributed to the assumption of a single plastic curve. This assumption allowed for a proper and accurate description of the initial plasticity stage and early plasticity region. However, more assumptions need to be made to describe the later plasticity region.

This discussion has proved that additive manufacturing leads to changes in the material properties, thus causing material anisotropy.

Regarding the stress distribution in the complex “bone–implant” system, it should be noted that the maximum stresses occur in the group of titanium components at the moment of tightening the screws. It is correct from a biomechanical point of view, because when a person remains in a lying position, the pelvic bones do not experience any load. The increased stresses occur near the screw holes of the implant, and in the area where the implant contacts the bone.

The major stress concentration in the destroyed half of the pelvis takes place in the cortical layer around the holes for the titanium screws and is caused by the tension of titanium screws that attach the implant to the rest of the pelvis. However, the simulation showed that the peak values did not exceed the allowed limits for the cortical and spongy bones. Moreover, the stresses quickly decreased to less than 1 MPa away from the edges.

In the case of body weight loading, the stresses on the upper part of the destroyed pelvis region increased several times compared to the previous stage. Stress concentration was observed on the edges of the screw holes and on the edge of the hole for the implant stem. In this area, local biomedical problems are expected, as the maximum stresses on the edge exceed the permissible load. Under a screw load of 300 N, the maximum screw system stress increased from 434 to 527 MPa, as expected because, in the second stage, the weight of the person is also considered. However, a sufficient factor of safety equal to 1.7 was utilised. Increased stresses also occurred in the area near the screw holes (from 240 to 297 MPa), and the highest stresses occurred in the area of contact between the implant stem and the bone edge because of the direct support of the legs and implant.

7 Conclusions

The conclusions of this study are applicable to the research on material properties of additively produced parts, but not to the modelling method or the simulation based on this model. This implies that all the conclusions are part of the method, that is, the steps to be performed during the modelling. General conclusions, which can be drawn from this study, are as follows:

• The method comprises a detailed description of the modelling process for metal materials obtained using layer-by-layer technology.

• Each step of the modelling process was provided with an explanation and theoretical motivation. Specimens of additively produced Ti6Al4V alloy were used to demonstrate the method. The effectiveness of the approach was verified by conducting FEA simulations of all the mechanical tests performed. The average error in the elastic region for the considered directions and types of loading are as follows: tension X: 2%; tension Y: 1.9%; tension Z: 3.4%; torsion X: 3.5%; torsion Y: 4.7%; and torsion Z: 3.8%. These values represent the differences between the theoretical and experimental data. The corresponding values for the plastic area are as follows: tension X: 3.9%; tension Y: 2.7%; tension Z: 1.2%; torsion X: 9.5%; torsion Y: 0.5%; and torsion Z: 3.3%. These values indicate a high degree of conformity between the constructed model and experimental data.

• This method allows design engineers to easily understand the proposed modelling process and learn how to build high-fidelity models of additively produced materials.

• The results obtained by using this method have a significant dependence on the manufacturing process (printing machine and settings). This means that it is possible to have several different models of the same material if the specimens are produced on different machines.

• This method may be used as a basis for constructing even more complicated models, which can contain additional properties for special purposes.

We also examined the important problem of biomechanics of the reconstructed pelvis with an individual implant made from titanium powder using additive technologies. During the study, finite element models of the “skeleton–implant” system were developed. A theoretical assessment of the strength of the pelvic bones and individual hip joint endoprosthesis was performed. It was shown that both the cortical bone and the implant had adequate safety margins.