Modified iterative approach for predicting machined surface topography in ball-end milling operation

Abstract

Machined surface topography prediction is an important and useful tool for optimizing cutting parameters. However, accurate prediction of machined surface topography in ball-end milling operation has been extremely challenging, due to the complexity in tool-workpiece interaction induced by the trochoidal motion of cutting edge and computing burden. In this present research, a modified iterative approach was proposed to solve the intersections between the cutting-edge sweeping surface and the discrete Z-vector model of workpiece, which were used to predict the machined surface topography in ball-end milling operation. Firstly, the accurate model of cutting-edge sweeping surface was established utilizing homogeneous coordinate transformation, in which the tool runout was considered. Secondly, the cutting-edge sweeping surface was dispersed into a series of patches in accordance with equal parameter interval, and the in-cut patch was extracted by using the minimum and maximum axial immersion angle of the cutting edge. Thirdly, the intersection between each in-cut patch and discrete Z-vector was solved using the Newton’s method, which was used to update the endpoint of the corresponding discrete Z-vector. Finally, ball-end milling experiments of AISI P20 steel were carried out to validate the proposed approach as well as investigate the effect of cutting parameters on the machined surface topography and roughness. The predicted machined surface topography and roughness were in good agreement with the measured results. Moreover, the proposed approach needs less computing time than the traditional iterative approaches at the same predicting accuracy. This research also provides guidance for optimizing cutting parameters to control surface quality in ball-end milling operation.

1 Introduction

Ball-end milling operation plays an increasingly important role in the fields of aerospace and auto parts as well as molds, because it has excellent machining flexibility in curved surface machining, such as tool shape self-adaptability and simple programming [1]. Beňo et al [2] proposed a commonly accepted methodology for investigating the free-form process, in which the product was divided into fragmentation with defined measurability. The correlation between the roughness parameters of machined surface and the functional parameters of free-form surface has been established with the multivariate date treatments. The machining quality of ball-end milling operation largely relies on the machined surface topography, because the surface topography, as one of the significant roles in surface integrity, has a great impact on the performance and service life of the machined parts [3]. Accordingly, surface roughness is widely used as an index to evaluate the machined surface quality, in most cases, as a technical requirement for mechanical products [4]. Surface topography is the result of the relative motion of cutting tool and workpiece, which is mainly determined by the cutting parameters and tool geometry. Once the cutting tool of milling operation is determined, it is necessary to carefully select appropriate cutting parameters to achieve the desired machining quality [5]. However, cutting parameters are mainly selected by conducting trial-and-error testing in practice, which consumes masses of resources. Therefore, an accurate prediction of surface topography in ball-end milling operation is essential for investigating the machined surface topography and obtaining the optimal cutting parameters ahead of costly trials, which requires low budget in comparison with the high-cost cutting tests.

Currently there are three main methods for predicting the machined surface topography in milling operation, i.e., solid modeling, discretization, and iterative methods [6]. The solid modeling approach predicts the machined surface topography by Boolean subtraction operation between solid models for the volume swept by cutting tool and workpiece. For example, Imani et al. [7] and Liu et al. [8] developed in-process workpiece model by performing Boolean subtraction operation between solid workpiece model and a simplified solid cutting tooth model only containing the cutting edge and rake face. Nespor et al. [9] used an accurate solid cutting tooth model to simulate the surface topography after welding or brazing by means of re-contouring milling in regeneration of complex parts and investigated the correlation of weld size, tool deflection, chatter vibrations, and surface topography. Vakondios et al. [10] dispersed the simulation for micro-ball-end milling process into several repeated steps, and the workpiece was updated by the Boolean subtraction of accurate cutting tool model at each time step. The solid modeling approach can solve the contact area of the cutting tool and workpiece with high precision when an accurate solid model of cutting tool was adopted. However, the computation of the Boolean operation between the solid models is a difficult and computationally time-consuming task. The discretization approach adopted discrete models of the cutting-sweeping surface and workpiece for simulating the surface topography. Among others, the most widely used is the Z-buffer method for workpiece and the discrete point cloud model of cutting-edge sweeping surface. Some researchers studied the process mechanism for 3-axis and 5-axis milling process. For instance, Peng et al. [11] investigated the influence of the initial phase angle of cutter on surface micro-topography feature in micro-ball-end milling and controlled the initial phase angle of cutter and surface topography through the planning of noncutting tool path. Zhang et al. [12] correlated the surface roughness, the ratio, and product of the feed per tooth and radial depth of cut for reducing the surface roughness at constant material removal rate as well as investigated the amplitude parameters and power spectral density of machined surface in end milling process [13]. In addition, the effect of radius of corner and the cutting tool on the surface roughness has also been investigated [14]. Xu et al. [15] integrated the time-varying feed speed profile into the discrete point cloud model of cutting-edge sweeping surface for investigating the dynamic change of feed rate on the surface topography in high-speed milling along a curved path. The discretization approach has been applied extensively because of its strong expandability and robustness. However, to obtain higher simulation accuracy, the discretization size must be made smaller, which reduces the computational efficiency with the increase of the number of discrete elements to be simulated. In comparison with the discretization approach, the iterative approach calculates the intersections between the cutting-edge sweeping surface and workpiece by solving the system of nonlinear equations with numerical iterative methods. For example, Gao [16] and Zhang et al. [17] solved intersections between the cutting-edge sweeping surface and vertical reference line at the sample point of workpiece with Newton’s methods for simulating the surface topography in ball-end milling process. Li et al. [18] improved numerical iterative methods for developing a selection of initial values based on time-step algorithm. Lotfi et al. [19] investigated the effect of cutter deflection on surface topography. Liang et al. [20] investigated the chatter milling conditions on the surface topography with the numerical iterative method.

The surface topography prediction is an effective tool for optimizing the surface roughness and cutting parameters in milling operation. However, it can be clearly seen from the characteristics of the three mentioned-above methods that there are still some limitations of the predicting accuracy, calculating efficiency, and applications. Therefore, the main objective of the present research is to develop a modified iterative approach for predicting and investigating the surface topography and roughness in ball-end milling operation, which takes the advantage of both the discretization and iterative approaches. First, the modified iterative approach for predicting machined surface topography in ball-end milling operation was developed. Then, ball-end milling experiments of AISI P20 steel were carried to validate the proposed approach. Furthermore, the effect of tool orientation and feed per tooth as well as radial depth of cut on the machined surface topography and roughness were investigated. Finally, the proposed approach was evaluated by comparing with the traditional iterative approaches, which highlighted its computing efficiency.

2 Cutting-edge sweeping surface modeling

The cutting tool rotates around the axis of machine tool spindle and moves along a given tool path during the milling operation. The workpiece material is removed by the trochoidal moving cutting edge. Therefore, for predicting the machined surface topography formed by the residual workpiece material, the cutting-edge sweeping surface along a given tool path needs to be established first.

2.1 Coordinate system

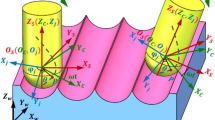
To obtain the accurate model of cutting-edge sweeping surface during ball-end milling operation, four space rectangular coordinate systems were established first as shown in Fig. 1.

Fig. 1

Coordinate system involved in ball-end milling operation as shown with the tilt angle β, yaw angle γ, and tool runout all are zero

Cutting tool coordinate system O_T-X_TY_TZ_T denotes a local coordinate system fixed on the cutting tool. The origin O_T is also placed at center of spherical part of the cutting tool. The Z_T-axis coincides with the tool axis. The X_T-axis has a radial direction and is tangent to the projection of the 1st cutting edge onto the plane perpendicular to tool axis at point O_T.

Spindle coordinate system O_S-X_SY_SZ_S indicates a local coordinate system fixed on the machine tool spindle. The origin O_S is set at the intersection of spindle axis and the X_TY_T plane. The Z_S-axis coincides with the spindle axis. The Y_S-axis is along the feed direction when the tilt angle and yaw angle are both zero.

Cutting location coordinate system O_L-X_LY_LZ_L represents a local coordinate system attached to the tool path. The origin O_L is placed at the CL point, which is also the center of spherical part of the cutting tool. The Y_L-axis is along the feed direction. The Z_L-axis is along the normal direction of design surface.

Workpiece coordinate system O-XYZ indicates a global coordinate fixed on the workpiece, in which the tool path is described. On basis of a set of kinematics transformation, the cutting-edge sweeping surface can be derived in O-XYZ.

2.2 Equation of cutting edge

As shown in Fig. 2, the ball-end milling cutter with constant lead and equal pitch angle is selected as the research object, which is used widely in practice. Only the cutting edge on the ball-end part of cutter is considered, as this is also the common case. As described in [21], the cutting-edge curve functions in terms of κ the Eq. (1).

$$ \Big\{{\displaystyle \begin{array}{c}\begin{array}{c}{x_{\mathrm{P}}}^{\mathrm{T}}={R}_0\cdot \sin \left(\kappa \right)\cdot \cos \left(\varphi \left(\kappa \right)+{\phi}_j\right)\\ {}{y_{\mathrm{P}}}^{\mathrm{T}}={R}_0\cdot \sin \left(\kappa \right)\cdot \sin \left(\varphi \left(\kappa \right)+{\phi}_j\right)\\ {}{z_{\mathrm{P}}}^{\mathrm{T}}=-{R}_0\cdot \cos \left(\kappa \right)\end{array}\\ {}\begin{array}{c}{\phi}_j=\left(j-1\right)2\pi /N\\ {}\varphi \left(\kappa \right)=\left(1-\cos \left(\kappa \right)\right)\tan \left({\beta}_0\right)\end{array}\end{array}}\operatorname{} $$

(1)

where R₀ is the tool radius, κ is the axial position angle, φ is the lag angle, β₀ is the nominal helix angle measured at the ball shank meeting boundary, ϕ_j is the radial position angle of cutting edge, j is the index of cutting edge, and N is the number of cutting teeth.

Fig. 2

a General view of cutting edge and b top view of cutting edge

2.3 Tool runout definition

Tool runout in the milling operation is almost inevitable due to the fabrication and installation errors of the cutting tool, which make the tool axis and spindle axis not coincide. As shown in Fig. 3, it is assumed that the tool axis has a parallel offset of magnitude ρ with respect to spindle axis. The O_T-X_TY_TZ_T rotates with the rotation of the cutting tool around the Z_S-axis. The homogeneous matrix T_T→S that transforms the coordinates of a point from coordinate system O_T-X_TY_TZ_T to the coordinate system O_S-X_SY_SZ_S can be expressed by Eq. (2) [15].

$$ {\boldsymbol{T}}_{T\to S}=\left[\begin{array}{cc}\begin{array}{cc}\cos \left(\alpha -\lambda \right)& \sin \left(\alpha -\lambda \right)\\ {}-\sin \left(\alpha -\lambda \right)& \cos \left(\alpha -\lambda \right)\end{array}& \begin{array}{cc}0& \rho \cdotp \cos \alpha \\ {}0& -\rho \cdotp \sin \alpha \end{array}\\ {}\begin{array}{cc}0& 0\\ {}0& 0\end{array}& \begin{array}{cc}1& 0\\ {}0& 1\end{array}\end{array}\right] $$

(2)

where α = ωt + α₀ is the phase angle of cutting tool and measured in the clockwise direction, ω is the angular speed of spindle, t is the machining time, α₀ is the initial phase angle of cutting tool, ρ is the eccentricity of cutting tool, and λ is the initial phase angle of cutting edge.

Fig. 3

Tool runout definition

2.4 Tool orientation

As shown in Fig. 4, the tool axis orientation in ball-end milling operation is defined by the tilt angle β and yaw angle γ as described in [22]. Therefore, the homogeneous matrix T_S→L that transforms the coordinates of a point from the coordinate system O_S-X_SY_SZ_S to the coordinate system O_L-X_LY_LZ_L can be expressed by the Eq. (3) [22].

$$ {\boldsymbol{T}}_{T\to S}=\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ {}0& \cos \beta \end{array}& \begin{array}{cc}0& 0\\ {}-\sin \beta & 0\end{array}\\ {}\begin{array}{cc}0& \sin \beta \\ {}0& 0\end{array}& \begin{array}{cc}\cos \beta & 0\\ {}0& 1\end{array}\end{array}\right]\left[\begin{array}{cc}\begin{array}{ccc}\cos \gamma & -\sin \gamma & 0\\ {}\sin \gamma & \cos \gamma & 0\\ {}0& 0& 1\end{array}& \begin{array}{c}0\\ {}0\\ {}0\end{array}\\ {}0\kern0.5em 0\kern0.5em 0& 1\end{array}\right] $$

(3)

Fig. 4

Tool orientation defined by tilt β and yaw γ angles

2.5 Tool path definition

As shown in Fig. 5, a simplified unidirectional tool path is taken as an example to carry out plane milling operation. The cutter feeds along the Y-axis direction; the step-over direction coincides with the X-axis. Therefore, the homogeneous matrix T_L→W that transforms the coordinates of a point from the coordinate system O_L-X_LY_LZ_L to coordinate system O-XYZ can be expressed by the Eq. (4) [18].

$$ {\boldsymbol{T}}_{L\to W}=\left[\begin{array}{cc}\begin{array}{ccc}1& 0& 0\\ {}0& 1& 0\end{array}& \begin{array}{c}\left(i-1\right)\cdotp {a}_{\mathrm{e}}\\ {} f\alpha /2\pi \end{array}\\ {}\begin{array}{ccc}0& 0& 1\\ {}0& 0& 0\end{array}& \begin{array}{c}H+{R}_0-{a}_p\\ {}1\end{array}\end{array}\right] $$

(4)

where i is the index of the tool path, a_e is the radial depth of cut, f is the feed per tool rotation, H is the height of cuboid workpiece blank, and a_p is the axial depth of cut.

Fig. 5

Sketch map of the simplified unidirectional tool path

By means of Eqs. (1)–(4), the surface swept by the j-th cutting edge can be derived and expressed by Eq. (5).

$$ \boldsymbol{P}\left(\kappa, \alpha \right)=\left[\begin{array}{c}{x}_{\mathrm{P}}\\ {}{y}_{\mathrm{P}}\\ {}\begin{array}{c}{z}_{\mathrm{P}}\\ {}1\end{array}\end{array}\right]={\boldsymbol{T}}_{\mathrm{L}\to \mathrm{W}}{\boldsymbol{T}}_{\mathrm{S}\to \mathrm{L}}{\boldsymbol{T}}_{\mathrm{T}\to \mathrm{S}}\left[\begin{array}{c}{x_{\mathrm{P}}}^T\\ {}{y_{\mathrm{P}}}^T\\ {}\begin{array}{c}{z_{\mathrm{P}}}^T\\ {}1\end{array}\end{array}\right] $$

(5)

where x_p, y_p, and z_p are the coordinates of a selected point P on the cutting edge in the workpiece coordinate system O-XYZ; P(κ, 𝛼) is the position vector of the point P in the workpiece coordinate system O-XYZ.

3 Surface topography prediction

The material removal process was simulated utilizing the discretization operation, in which the workpiece is represented by the discrete vectors parallel to the Z-axis. The discrete Z-vector model of the workpiece is then truncated by the cutting-edge sweeping surface along the tool path. The surface topography can be extracted by means of the endpoints of discrete Z-vectors. The focus of this paper is to calculate the intersection of the cutting-edge sweeping surface and the discrete Z-vectors.

3.1 Discrete Z-vector model of workpiece

The discrete Z-vectors were adopted to represent the workpiece as shown in Fig. 6, which can be obtained in the following three steps. First, a grid set was planned on the XY plane, and their grid points Q_a,b can be determined by the Eq. (6).

$$ {\boldsymbol{Q}}_{a,b}=\left(a\Delta x,b\Delta y,0\right),a=0,1,2,\cdots, b=0,1,2,\cdots $$

(6)

where a and b are the index of grid point and Δx and Δy are grid size in the X-axis and Y-axis directions, respectively.

Fig. 6

Discrete Z-vector model of workpiece

Then, a set of discrete vectors parallel to the Z-axis were established. The starting points of the discrete Z-vectors were associated with the grid points. The endpoints of the discrete Z-vectors were determined by the intersections of the vectors and the workpiece surface.

Finally, the workpiece surface was dispersed into a grid of points s_a,b by the endpoints of the discrete Z-vectors. The grid points s_a,b can be determined by Eq. (7).

$$ {\boldsymbol{s}}_{a,b}={\boldsymbol{Q}}_{a,b}+{h}_{a,b}\boldsymbol{k} $$

(7)

where h_a,b records the length of discrete Z-vector, initially it set to be H and will be updated using the intersection of the cutting-edge sweeping surface and the discrete Z-vectors after cutting, and k = (0, 0, 1) was the unit vector of the Z-axis.

3.2 Discretization of cutting-edge sweeping surface

As the calculation accuracy is controllable, the numerical iterative method was adopted to calculate the intersection between the cutting-edge sweep surface and the discrete Z-vectors. To determine the suitable initial value and improve the calculation efficiency, the cutting-edge sweep surface was dispersed into a series of patches with the equal parameter interval as shown in Fig. 7. Each patches F_r,s can be expressed as Eq. (8).

$$ {\boldsymbol{F}}_{r,s}=\boldsymbol{P}\left(\kappa, \alpha \right),r\Delta \kappa \le \kappa \le \left(r+1\right)\Delta \kappa, s\Delta \alpha \le \alpha \le \left(s+1\right)\Delta \alpha $$

(8)

where r and s are the index of patches (r = 0, 1, 2, …, s = 0, 1, 2, …) and Δκ and Δα are sizes of patches in the κ and α directions on the parameter planes.

Fig. 7

Discrete patch model of cutting-edge sweeping surface

3.3 Extraction of in-cut patches

To reduce a great number of non-contributing intersections operation between the cutting-edge sweeping surface and the discrete Z-vector, the in-cut patches in cutting-edge sweeping surface that contributes to the final surface topography was first roughly determined as shown in Fig. 8. According to this information, the in-cut patches can be determined by the minimum κ_min and maximum κ_max axial immersion angle of the cutting edge, which is determined by Eq. (9) and Eq. (10), respectively.

$$ {\kappa}_{\mathrm{min}}=\left\{\begin{array}{cc}0& \beta \le \mathit{\operatorname{arccos}}\left(1-{a}_{\mathrm{p}}/{R}_0\right)\\ {}\beta -\mathit{\operatorname{arccos}}\left(1-{a}_{\mathrm{p}}/{R}_0\right)& \beta >\mathit{\operatorname{arccos}}\left(1-{a}_{\mathrm{p}}/{R}_0\right)\end{array}\right. $$

(9)

$$ {\kappa}_{\mathrm{max}}=\beta +\mathit{\operatorname{arccos}}\left(1-{a}_{\mathrm{p}}/R\right) $$

(10)

Fig. 8

Illustration of in-cut cutting edge

For the implementation of the proposed approach, only the in-cut patches in CESS are attempted to intersect with the discrete Z-vectors. In comparison with the number of all patches, the number of the in-cut patches in CESS is much smaller, which greatly improves the efficiency of the simulating algorithm.

3.4 Calculation of intersection between in-cut patches and discrete Z-vector

As shown in Fig. 9, an in-cut patch F_r,s in cutting-edge sweeping surface was taken as an example to illustrate the calculation of intersection point of this in-cut patch and the discrete Z-vectors. First, it is needed to find the discrete Z-vector intersected with the patch F_r,s from all discrete Z-vectors {L_a,b} along the grid points. As described in [18, 23], the intersected discrete Z-vectors L_a,b can be determined by Eq. (11) and Eq. (12).

$$ \left\{\begin{array}{c}\min \left({x}_{{\mathrm{P}}_{r,s}},{x}_{{\mathrm{P}}_{r+1,s}},{x}_{{\mathrm{P}}_{r+1,s}+1},{x}_{{\mathrm{P}}_{r,s+1}}\right)\le {x}_{a,b}\le \max \left({x}_{{\mathrm{P}}_{r,s}},{x}_{{\mathrm{P}}_{r+1,s}},{x}_{{\mathrm{P}}_{r+1,s}+1},{x}_{{\mathrm{P}}_{r,s+1}}\right)\\ {}\min \left({y}_{{\mathrm{P}}_{r,s}},{y}_{{\mathrm{P}}_{r+1,s}},{y}_{{\mathrm{P}}_{r+1,s+1}},{y}_{{\mathrm{P}}_{r,s+1}}\right)\le {y}_{a,b}\le \max \left({y}_{{\mathrm{P}}_{r,s}},{y}_{{\mathrm{P}}_{r+1,s}},{y}_{{\mathrm{P}}_{r+1,s+1}},{y}_{{\mathrm{P}}_{r,s+1}}\right)\end{array}\right. $$

(11)

$$ \sum \boldsymbol{Area}\_\mathrm{tri}\left({{\boldsymbol{F}}_{r,s}}^{\prime },{\boldsymbol{Q}}_{a,b}\right)=\boldsymbol{Area}\_\boldsymbol{rect}\left({{\boldsymbol{F}}_{r,s}}^{\prime}\right) $$

(12)

where ΣArea_tri(F_r,s', Q_a,b) stands for area sum of four triangles which are formed by the point Q_a,b, and the projection of the four corner point of the patch F_r,s, on the XOY plane.

Fig. 9

Intersection of in-cut patches with the discrete Z-vectors

Once the intersected discrete Z-vector line is found, the parameter (κ_L, α_L) of intersection P_L can be calculated by the Newton’s method expressed by Eq. (13).

$$ \left[\begin{array}{c}{\kappa_L}^{k+1}\\ {}{\alpha_L}^{k+1}\end{array}\right]=\left[\begin{array}{c}{\kappa_L}^k\\ {}{\alpha_L}^k\end{array}\right]-{\left[\begin{array}{cc}\frac{{\partial x}_P}{\partial \kappa }& \frac{{\partial x}_P}{\partial \alpha}\\ {}\frac{{\partial y}_P}{\partial \kappa }& \frac{{\partial y}_P}{\partial \alpha}\end{array}\right]}^{-1}\left[\begin{array}{c}{x}_P-{x}_{a,b}\\ {}{y}_P-{y}_{a,b}\end{array}\right] $$

(13)

where k is the iteration ordinal number when calculating the intersection parameters between the discrete Z-vector and the in-cut patch, the iteration terminates when the difference between κ_L^k and κ_L^k+1, α_L^k and α_L^k+1, were all less than 10^-5, the initial value can be determined by Eq.(14).

$$ \left[\begin{array}{c}{\kappa_L}^0\\ {}{t_L}^0\end{array}\right]=0.5\left[\begin{array}{c}{\kappa}_{r,s}+{\kappa}_{r+1,s+1}\\ {}{t}_{r,s}+{t}_{r+1,s+1}\end{array}\right] $$

(14)

Once the parameters (κ_L, α_L) was obtained using Eq. (13), then it can be put into Eq. (5) to calculate the accurate intersection between the selected in-cut patch and the discrete Z-vector.

3.5 Procedure for surface topography generation

To have a clearer understanding of the procedure for the simulating of surface topography in milling process, the following steps were provided to illustrate.

• Step 1. Input the discrete Z-vector model of workpiece to be machined. Derive the transcendental equation of cutting-edge sweeping surface expressed by Eq. (5) with given cutting parameters, geometry parameters of cutting tool. Disperse the cutting-edge sweeping surface into a series of patches by the equal parameter interval.

• Step 2. Extract the in-cut patches in cutting-edge sweeping surface using the minimal κ_min and the maximum κ_max axial angle determined by the axial cutting depth and tilt angle as shown in Eqs. (9) and (10).

• Step 3. Determine the Z-vectors intersected with the selected in-cut patches using Eqs. (11) and (12), and solve the intersection with Newton’ methods using the Eqs. (13), (14), and (5). The endpoint of the intersected discrete Z-vector was updated using the intersected point.

• Step 4. Calculate the intersection between the in-cut patches in the surface swept by the next cutting edge and update the endpoint of the intersected discrete Z-vectors.

• Step 5. Repeat step 3 and 4 for all cutting edge.

• Step 6. Repeat step 3, 4, and 5 for all tool path.

• Step 7. Extract the final simulated surface topography and calculate the surface roughness using the endpoints of updated the discrete Z-vector model of the workpiece.

4 Experimental verification

4.1 Experimental procedure

The algorithm involved in this paper were coded in MATLAB language and implemented on a PC with an Intel 3.4 GHZ and 8.0G physical memory. To verify the validity of the proposed approach, ball-end milling experiments were carried out on a 3-axis CNC milling center (OKUMA-BYJC, DXR-460V), and a machine vise with adjustable inclination angle was used to change the tool orientation as shown in Fig. 10a. The workpiece material was AISI P20 steel, hardened and tempered to attain a hardness of 30~36HRC. The cutting tool was solid carbide ball-end milling cutter JH970100-TRIBON (Seco Company, Sweden) with 5 mm radius, two cutting teeth, and 30° helix angle. Dry milling method was employed. Constant cutting speed v_c = 94.2 m/min and yaw angle γ = 0° were adopted. Variated tilt angle β from 4 to 20°, feed rate f_z from 0.06 to 0.30 mm/tooth, and radial depth of cut a_e from 0.1 to 0.5 mm were adopted.

Fig. 10

Schematic diagram of milling test: a Experimental set up and cutting tool and (b) tool path and sampling area of surface roughness measurements

The topography and roughness of the machined surface were measured by Wyko NT9300 optical profiler (Veeco Instruments Inc., USA). As shown in Fig. 10b, the surface roughness measurement was carried out three times. Three rectangular sampling areas (1.5 mm × 1.44 mm) were evenly arranged along the feed direction on the machined surface; the average surface roughness of the sampling area was used as the roughness of the machined surface. The average roughness Sa represents the arithmetic mean of the absolute value of the height between each point on the measured surface and the reference plane of the sampling area, which can describe the height deviation of the whole surface. On the one hand, the average roughness Sa is generally used to describe the surface topography after machining and used as an index to evaluate the machining surface quality, i.e., the surface quality can be graded according to the average roughness Sa. One the other hand, the validity of the proposed model can be verified by comparing the predicted and measured Sa of the machined surface. Therefore, the average roughness Sa was adopted to evaluate the machined surface, and the Sa can be expressed as [24]

$$ Sa=\frac{1}{MN}\sum \limits_{m=1}^M\sum \limits_{n=1}^N\left|{Z}_{mn}\right| $$

(15)

where M and N are the number of sampling points along the feed and step-over direction, respectively, and Z_mn is the distance of the sampling point and the reference plane.

4.2 Predicting accuracy

Figure 11 shows a comparison between the predicted and measured topography of the machined surface in ball-end milling operation at different tilt angles. It can be observed that the machined surface topography is composed of a series of peaks and valleys that repeat periodically along the feed direction and step-over direction, respectively. The distance of the adjacent area peaks (or area valleys) in feed direction is 0.36 mm, which is equal to the product of the number of tooth and feed per tooth. Although each cutting edge can form a peak along the feed direction with the tool rotates once, the large tool runout (30 μm) makes only one peak can be retained. The distance of the adjacent area peaks (or area valleys) in step-over direction is 0.3 mm, which is equal to the radial depth of cut. This shows that these peaks and valleys formed by the residual material of the workpiece are intermittently removed by the cutting edge along the tool path. The tilt angles have no obvious effect on the distribution of the area peaks and area valleys, only maximum area peak height Sp and maximum area valley depth Sv. Comparing the predicted topography (Fig. 11a–c) and measured topography (Fig. 11d–f), respectively, and a good correspondence between them is observed.

Fig. 11

Machined surface topography at different tilt angles (feed per tooth f_z is 0.18 mm/tooth, and radial depth of cut a_e is 0.3 mm): a–c predicted; d–e measured

Figure 12 gives the comparison of the predicted and measured average roughness Sa at different tilt angles. According to the measured results, with the increase of tilt angle, it is clearly seen that the average roughness Sa reduces quickly and then begins to increase, but when the tilt angle is in a certain interval, according to our experiment, about from 8 to 16°, the roughness is almost unchanged but kept a stable value. The relative error between the predicted and measured surface roughness are all less than 20%, which indicate the proposed model has a high prediction accuracy.

Fig. 12

Relative error between the predicted and measured average roughness Sa at different tilt angles (feed per tooth f_z is 0.18 mm/tooth and radial depth of cut a_e is 0.3 mm)

Figure 13 shows the comparison between the predicted and measured topography of machined surface at different feed per tooth. Different from the tilt angle, the feed per tooth has a significant impact on the distribution of area peaks and area valleys along the feed direction, but the distances of the adjacent area peaks (or area valleys) is still equal to the product of the number of cutting tooth and feed per tooth. The maximum area peak height Sp and maximum area valley depth Sv increases with the increase of feed per tooth.

Fig. 13

Machined surface topography at different feed per tooth f_z (tilt angle β is 12°, and radial depth of cut a_e is 0.3 mm): a–c predicted; d–f measured

Figure 14 gives the comparison of the predicted and measured average roughness at different feed per tooth. Compared with the tilt angle, the average roughness Sa varies greatly as the feed per tooth increases. With the increase of feed per tooth, the average roughness Sa increases slowly, but after the feed per tooth reaches a certain value, according to our experiment, about 0.18 mm/tooth, the average roughness Sa increases quickly.

Fig. 14

Relative error between the predicted and measured average roughness Sa at different feed per tooth f_z (tilt angle β is 12°, and radial depth of cut a_e is 0.3 mm)

Figure 15 shows the comparison between the predicted and measured machined surface topography at different radial depth of cut. The radial depth of cut has a significant impact on the distribution of area peaks and area valleys along the step-over direction, but the distances of the adjacent area peaks (or area valleys) is still equal to the radial depth of cut. The maximum area peak height Sp and maximum area valley depth Sv increases with the increase of radial depth of cut.

Fig. 15

Machined surface topography at different radial depth of cut a_e (tilt angle β is 12° and feed per tooth f_z is 0.18 mm/tooth): a–c predicted; d–f Measured

Figure 16 gives the comparison of the predicted and measured average roughness Sa at different radial depth of cut. It is clearly seen that the predicted and measured average surface roughness Sa are both increased with the increase of the radial depth of cut and they show consistent change trend, and the rate of increase gradually becomes larger.

Fig. 16

Relative error between the predicted and measured surface roughness S_a at different radial depth of cut a_e (tilt angle β is 12°, and feed per tooth f_z is 0.18 mm/tooth)

4.3 Computing efficiency

To highlight the computing efficiency in predicting surface topography, the proposed approach is compared with the traditional iterative approaches described in ref. [17] and ref. [18]. Figure 17 illustrates the initial values determined in different approaches for solving the intersection of cutting-edge sweeping surface and discrete Z-vector. In the milling operation, due to only the intersection (P₁) of the in-cut cutting-edge sweeping surface (κ_min ≤ κ ≤ κ_max) and the discrete Z-vectors contribute to the surface topography, and the difference between the selected initial values and the parameters of intersection point (P₁) has significant effect on the efficiency and convergence for solving the intersection point using Newton’s methods. It can be seen that the initial values selected in the proposed approach are closer to the intersection than the approaches in ref. [17] and ref. [18], and only the initial values near the intersection (P₁) are extracted. In other words, a smaller amount and closer to intersection initial values than ref. [17] and ref. [18] are determined in the proposed approach, which all indicate that the proposed approaches will simulate the surface topography more efficiency. The difference between the initial values and the solutions is all determined by the discrete size of the in-cut cutting-edge sweeping surface in the developed method and Ref. [17]. The discrete size of the cutting-edge sweeping surface is smaller than the Ref. [17] in κ direction under the same discrete size in α direction. The initial values selected by the developed method are closer than by the Ref. [17]. The extreme value of cutting-edge sweeping surface is selected as the initial values in Ref. [18]; it can be clearly seen that it is farther to the solutions than the developed and Ref. [17]. In additions, the number of determined initial values in Ref. [18] is the largest.

Fig. 17

Schematic diagram of initial values selected in different approaches

A workpiece with the length of 1.5 mm and the width of 1.44 mm is established using the discrete Z-vectors with different grid sizes; different iterative approaches are used to simulate the surface topography. The cutting conditions and computation time of the numerical examples are listed in Table 1. It can be seen that the proposed approach needs less computation time than the approaches described in ref. [17] and ref. [18], which indicates the proposed approach is more efficient. Moreover, since the three mentioned-above approaches all calculate the intersections between cutting-edge sweeping surface and discrete Z-vectors using Newton’s methods, therefore, they have the same prediction accuracy under the same convergence accuracy.

Table 1 Computation time of the simulation process with different approaches

5 Conclusions

This paper presents a modified iterative approach to predict machined surface topography in ball-end milling operation. The accurate intersection of cutting-edge sweeping surface and the discrete Z-vectors of workpiece were calculated using the Newton’s method, which was used to update the in-process workpiece and extract surface topography. The approach was validated by experiments and numerical simulations. Following conclusions are drawn out.

• (1) The proposed approach is effective to predict the machined surface topography in ball-end milling operation based on the accurate intersection of the cutting-edge sweeping surface and the discrete Z-vectors of workpiece that was solved by Newton’s method.

• (2) The number of initial values has been reduced by the extracted in-cut patches in cutting-edge sweeping surface, and the quality of initial value can be well controlled by the size of the patches. This can greatly improve the computational efficiency.

• (3) Since the proposed approach is based on the attributes of the cutting-edge sweeping surface, in which the cutting-edge sweeping surface is derived by geometry parameters of cutting tool, tool orientation and cutting parameters along the tool path. It can be reliably used to predict machined surface topography for different cutting tools in milling operation.

• (4) Besides, the proposed approach is sometimes limited by the robustness, which is a common issue of all iterative approaches needed to be improved. This disadvantage may occur when tilt angle is small but can be overcome by adjusting the size of patches.