1 Introduction

Additive manufacturing (AM) can be defined as the process of producing parts from a three-dimensional data model, by joining or adding material using the layer-by-layer principle [1]. The physical AM process is relatively simple as it consists of only two steps: the generation of a single layer, with specific shape and thickness based on slice data coming from a 3D CAD model, and the joining of each new layer on top of the preceding one [2]. There are various AM processes and they can be classified according to the type of the energy source, the type and form of the material, and the bonding means and techniques that they use. The laser-powder bed fusion (L-PBF) processes, such as selective laser melting (SLM), are found and considered more promising than the solid-based ones [1]. AM is a revolutionizing product development and manufacturing technology that may reform the whole manufacturing industry. The rapid character of AM technology, the capability of building parts regardless of their shape complexity in a single step within an AM machine, and the inherent flexibility of the process make AM a promising manufacturing technique, competitive to the traditional subtractive and formative ones [3].

SLM is regarded as one of the most advanced AM techniques, with tremendous potential for producing complex, lightweight, high density (over 99%), and functionally optimized parts. The production of high-quality models, at reduced costs and lead times, is expected to benefit the medical, aerospace, and automotive industries [4]. SLM is a powder-based AM process, where a laser beam selectively melts metallic powder layers, forming a solid part on a base plate [5]. One additional advantage of SLM is its capability to utilize a variety of alloys as raw materials (powder bed). Specifically, in L-PBF processes, titanium (Ti)-, stainless steel (SS)–, nickel (Ni)-, aluminum (Al)-, lead (Pb)-, and niobium (Nb)-based alloys can be used [6]. During L-PBF, the interaction of the powder bed and the heat source is short due to the typically high scanning speeds of the laser beam, but due to the high energy densities, rapid heating and subsequent solidification is taking place. In the formed melt pool (MP), radial temperature gradients on the order of 102 to 104 K/mm can be developed between the center of the MP and the cooler solid-melt interface, while the cooling rates are estimated over 104 K/s [1]. Although the basic principle of SLM is quite simple, there are more than 130 parameters that affect the final quality of the produced part [7, 8].

The SLM system has non-linear response to the change of machining process, since complex physical mechanisms such as laser absorption; reflection and radiation; heat transfer in liquid, solid, and gas phases; phase transformations; fluid flow; and moving interface between the solid and liquid phases are taking place [9]. As the quality of the produced parts is strongly dependent on the optimized selection of machining parameters, the need of deep and clear understanding how the principal process parameters affect the SLM system arises. In the last years, many studies have been conducted in this field, both experimental and computational. Τhe melt pool (MP) characteristics and behavior have intense scientific interest; hence, extensive experimental research has been carried out for different materials and parameters [10,11,12,13]. The generation of a single-track MP can be considered the basic and primary mechanism in L-PBF, and its understanding and optimization are essential. After all, any part, regardless of its complexity or material, is produced by a number of single tracks and layers. The great number of different process parameters and materials, along with the increased costs of SLM machines and measurement equipment, i.e., high-speed cameras, thermocouples, thermal cameras, etc., raises the need to develop realistic and accurate simulation models of the process. At the same time, beyond the benefits in time and money saving, the difficulties of observing the process in real time and in situ, due to its rapid nature and the strictly controlled environment, can be overcome by using simulation models.

Gusarov et al. [14] presented a model for the laser–powder interaction zone based on the assumption of slow consolidation, as a single-line scan on a layer of unconsolidated powder. The model included heat transfer through radiation and conduction. The absorption due to radiation was approximated by a volumetric heat source, while the power density of the laser beam was modeled by a bell-like radial distribution. Besides other conclusions, calculations have shown that the total absorptivity of the powder-substrate system and the fraction of the radiation absorbed by the substrate dependent on the optical depth of the powder layer. Antony et al. [15] developed a finite element model (FEM) to determine the temperature field in a powder melting process. For the simulation of the heat source, a 2D surface Gaussian distribution was used. To estimate the effective thermal conductivity of the powder bed, the coexistence of solid material in a gaseous environment was taken into consideration and it was calculated using an empirical coefficient combining the conductivity of powder material and the conductivity of the gas phase. The FEM model was utilized for understanding the effect of process parameters on the geometric characteristics of a single track and to facilitate the creation of better quality melted tracks without unwanted phenomena.

Lee et al. [16] presented an extended 3D transient MP physics model to calculate the temperature field, fluid convection, and MP shape in the L-PBF of Inconel Alloy 718. The heat input from the laser beam approximated as a 2D Gaussian heat flux distribution, while the absorption coefficient was considered constant with a value of 0.38. Additionally, the convection coefficient and the emissivity were taken as constant values and not temperature-dependent. The model took into consideration the heat loss by evaporation and the existence of recoil pressure. Using the simulation results, solidification parameters, i.e., temperature gradients and solidification rate were computed and used to quantitatively assess the solidification microstructure. Heeling et al. [17] developed a simulation tool using a homogenized powder bed in its initial configuration, to achieve a balance between computational time and accurate results. A dynamic absorption model proposed by Gusarov et al. [18] was adopted, temperature-dependent material properties were used, while the powder bed thermal conductivity was handled separately since it does not follow the rule of mixtures. The recoil pressure and the evaporated material were calculated, too. Qian et al. [19] used the level set method to simulate the melting process of metal-based SLM. The assumptions that were made included a 2D Gaussian heat source with a constant absorptivity coefficient of 0.2, while the evaporation of material was neglected. Bian et al. [20], in order to simplify their model, adopted a stationary Gaussian laser beam profile, while the attenuation and scattering of the laser beam were ignored. Moreover, constant, and not temperature dependent, thermal and physical material properties and heat transfer coefficients were used. Similar simplifications about constant physical and thermal parameters and neglecting of the metal vaporization during SLM can be found in the work of Zhang et al. [21]. In their study, in order to calculate the laser absorption coefficient, a more sophisticated model was used, with multi-reflection phenomena taken into consideration, while the absorption rate was distinguished during absorption by the powder bed and by the substrate. The total absorption rate was estimated to be over 80%.

In another approach on the estimation of the laser–powder bed interaction, Tran et al. [22] presented a volumetric heat source model for the SLM process. A powder layer with various powder particle sizes was constructed using a modified sequential addition method. The absorptivity profile along the depth of the metal powder layer was calculated by means of Monte Carlo ray-tracing simulations. Those results, along with the calculations of the thermal conductivity of the powder bed in the pre-melted conditions, were used as inputs in a FEM simulation. The comparison of simulation results with results presented in the literature showed that taking into account the powder nature of the raw material and the multi-scattering of the laser beam along the powder bed depth can give accurate results, although, in some cases, there was deviation between simulation and experiment. In a bit different approach for modeling the laser beam, Bruna-Rosso et al. [23] implemented two different heat source models for modeling the laser beam, a “Goldak” [24] and a “Gusarov” [14] heat source. Although the simulation results were in a fair agreement with experimental ones, there was a need to calibrate heat source model parameters, and thus, for this kind of models, it is necessary to jointly use them with experiments for their proper modification.

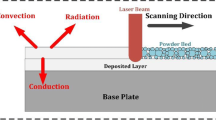
During L-PBF process depending on laser energy intensity value, the melt pool can be created with a different melting mode. For example, under low or moderate values of laser energy intensity, laser energy is absorbed mainly by the upper layers of the workpiece, no vaporization occurs, and heat transfer takes place primarily through conduction and convection in the molten pool, a mode named conduction or conductive mode [25, 26]. In conduction mode, the evolution and the final shape of the melt pool is caused by thermal conduction [25, 27,28,29,30], as the powder is melted due to the heat conduction effect, whereas the convection is found to be relatively weak in the melt pool [27, 31]. In low-energy density regime, the effect of fluid flow dynamics on the creation of the melt pool is lower, whereas the effect of heat conduction in the solid-state increases, being considered the dominant factor for the laser melting [32]. On the contrary, when laser energy intensity is high enough to lead to vaporization of the powder material, creating a dense plume, a recoil pressure occurs, larger than the surface tension and hydrostatic pressure of the liquid metal, forming a cavity on the molten material, a mode named keyhole mode [25, 27]. In the keyhole mode, where the fluid dynamics and recoil pressure dominate, a characteristic feature is the large penetration depth, small heat-affected zone (HAZ), and high energy efficiency but it is considered an unstable process with higher probability of defect occurrence than in conduction mode [32, 33]. In conduction mode, the molten pool is shallow and wider with a semi-circular, U-shape morphology with a small aspect ratio, below 0.5, and the heat input is better controlled [25,26,27, 29, 30, 34, 35]. Moreover, in this mode, the parts have higher density and generally better mechanical properties than in keyhole mode, with uniform microstructure and better formability [26, 31]. The boundary between the two modes is not strictly defined, but researchers have proposed that a certain laser power, laser power density [25, 28, 29], or normalized enthalpy value [28, 33] can define the limit between them. Furthermore, another indicator of the melting mode during SLM is the laser energy transfer efficiency, which is the ratio of the energy absorbed by the target material and the laser power of the source; if efficiency value is equal to the material absorptivity, then conduction mode melting occurs, whereas higher values of efficiency are associated with keyhole mode [34]. A transition mode is sometimes observed, between the two other modes, in which the most important factor for the determination of melt pool dimensions is the Marangoni force, which is the driving force for the developed fluid flow, rather than the conductive heat transfer or fluid dynamics and the recoil pressure [32].

The current paper, as a novelty, presents a general modeling methodology for SLM process under conduction mode, in which the boundary conditions and the necessary coefficients are based on robust theoretical background, so that the need for empirical coefficients is limited or even eliminated. At first, the absorption coefficient is calculated for the pre-melted phase as the result of the laser beam and the powder bed interaction and for the melted phase by utilizing the concept of electron-phonon-dominated optical conductivity and the Drude theory, thus adopting a volumetric Gaussian heat source with temperature-dependent absorption coefficient. The powder bed thermo-physical properties and the emissivity are estimated based on its porosity, while the temperature-dependent convection coefficient is derived from the calculation of the Nusselt number. The latent heat of melting and evaporation are taken into consideration, as well as the heat losses due to vaporization. Based on the aforementioned boundary conditions, a thermal transfer model is developed and solved. From the calculated temperature field, the dimension and characteristics of the MP can be estimated, along with its spatial and temporal evolution, as well as the shape of the MP. Simulation results are validated by comparison with experimental ones, under various process conditions. The various components of the SLM thermal model are depicted in detail in the flow chart of Fig. 1.

Fig. 1
figure 1

SLM model flow chart

Full size image

2 Modeling method

In the present work, a comprehensive 3D computational model for single-track SLM process is constructed, which is capable of predicting not only the depth of melt pool but also the shape of the resulting track due to the laser irradiation. In specific, a finite element thermal model is developed for the SLM process, incorporating various features, which render it capable to take into account several phenomena occurring during the SLM process. The laser beam is approached by a Gaussian volumetric moving heat source, while on the upper surface of the control volume, heat exchange occurs through convection and radiation and due to material vaporization. Throughout simulation, temperature-dependent material thermo-physical properties are taken into consideration, as well as the latent heats of melting and vaporization. Furthermore, for the powder bed domain, the properties are estimated according to the rule of mixtures or using analytical relations based on its porosity. Figure 2 presents a schematic representation of the basic feature of the SLM model. In order to ensure the validity of the model, data from single-track SLM experiments are considered [36] and a comparison between experimental and computational results is performed.

Fig. 2
figure 2

Schematic of SLM model features

Full size image

It is obvious that during the melting process, a velocity field with relatively low velocities is developed within the melt pool and in this region convection heat transfer takes place, apart from conductive heat transfer. However, the heat losses due to convection are not significant in every case of SLM process. The inclusion of fluid flow calculations in the SLM models is essential in order to predict the melt pool dimensions in cases where flow-related phenomena such as Marangoni flow are dominant, e.g., in the keyhole melting mode, but for the conduction melting mode the simulation results can be in good agreement with the experimental data without considering the flow-related phenomena [28]. When the effects of fluid flow are less significant, the inclusion of Marangoni effect can lead to overestimation of the melt pool dimensions [32]. Thus, various thermal models exist in the relevant literature, which were shown to predict melt pool dimensions with high degree of accuracy [16, 23, 37,38,39,40,41,42,43,44,45,46,47,48,49], as well as microstructure [50], onset of balling formation [37], and residual stresses [38], and some researchers noted that in some cases melt pool dimensions can be predicted even by using simplified thermal models such as the Rosenthal equation [38, 39, 50].

For example, Gusarov et al. [14] employed a thermal model for the selective laser melting of 316L steel powder in order to successfully predict cross-section dimensions of the melt pool as well as the morphology of produced tracks. They noted that according to the experimental results, the absorptivity did not increase significantly with temperature and thus Marangoni convection could be neglected because its contribution to heat transfer was rather low. Tran and Lo [22] aimed also to predict the geometry of melt pool region below the upper surface of the substrate by using a thermal model. They stated that in the region of melt pool, where conduction melting occurs, the effect of fluid flow on the formation of this region can be neglected, as the conductive heat transfer is the dominant factor that should be taken into consideration in order to predict the dimension of the melt pool. Their findings indicated that a high level of accuracy was obtained regardless of the assumption that the effect of recoil pressure and Marangoni convection on the creation of the melt pool was negligible, as, only if keyhole mode melting occurred, the accuracy could be significantly lower. Hodge et al. [40] developed a thermo-mechanical model in order to predict temperature field, melt pool dimensions, and other phenomena occurring during SLM and verified the validity of their model with results from previous works such as the work of Gusarov [14]. Moreover, Guo et al. [41] used a thermal model for SLM process of tungsten in order to predict temperature gradient and cooling rate, both in cases of conduction and keyhole mode melting and managed to explain successfully the phenomena occurring during the SLM experiments. Krakhmalev et al. [42] studied the microstructure of AISI 420 steel after SLM process and employed a thermal model in order to calculate the temperature field and re-melted depth of tracks. Their model did not include the heat losses due to the convection of the molten material, as during conductive model of melting these losses were assumed to have a negligible contribution.

Additionally, in the work of Kundakcioglu et al. [43], it was found that a thermal model was able to predict the melt pool cross-section depth and width with sufficient accuracy compared to experimental measurements for Inconel 625 and titanium workpieces. Metelkova et al. [38] pointed out that in the estimation of melt pool dimensions during conduction mode, the Rosenthal equation can be used, which does not include neither temperature-dependent properties nor fluid flow. The same statement was supported by the work of Promoppatum et al. [50], who noted that the natural convection in the liquid melt pool can be neglected without considerable alteration in the prediction of melt pool width. Moreover, Philo et al. [37] recently used a thermal model with an ablation module but without considering fluid flow and managed to achieve the prediction of melt pool profile even in keyhole mode.

2.1 Governing equations

In the thermal model of SLM process in conduction mode, the governing equation is the time-dependent 3D heat equation, formulated as follows:

$$ \rho {C}_p\frac{\partial T}{\partial t}-\nabla \cdot \left(k\nabla T\right)=\dot{Q} $$
(1)

where ρ represents the density (kg/m3), CP represents the specific heat (J/kgK), k represents the thermal conductivity (W/mK), and \( \dot{Q} \) represents the heat rate per unit volume (W/m3).

The boundary conditions of the governing equation include the heat transfer due to convection between the surrounding environment and the workpiece, and the radiative heat transfer, as well as the heat loss due to vaporization of the workpiece material, when temperature exceeds the boiling point. To specify the thermal boundary conditions, the following expression is employed:

$$ k\nabla T={q}_{conv}+{q}_{rad}+{q}_{abl} $$
(2)

where qconv, qrad, and qabl are the heat fluxes because of natural convection, radiation, and vaporization of the material, respectively.

2.2 Moving Gaussian volumetric heat source

The laser beam is approached with a moving volumetric heat source with Gaussian spatial distribution. Mathematically is represented as:

$$ Q\left(x,y,z,t\right)=\frac{P\eta}{2{\pi \sigma}_x{\sigma}_y}\cdot \frac{2}{\sqrt{2\pi }{\sigma}_z}\cdot {e}^{-\frac{1}{2}\left(\frac{{\left(x-{\upsilon}_Lt\right)}^2}{\sigma_x^2}+\frac{y^2}{\sigma_y^2}\right)}\cdot {e}^{-\frac{1}{2}\frac{{\left({d}_s+{d}_{pb}-z\right)}^2}{\sigma_z^2}} $$
(3)

with P as the nominal laser beam power, η as the absorption coefficient, υL as the laser beam velocity on x-axis, ds and dpd as the substrate and powder bed thicknesses respectively, and σx, σy, and σz as the standard deviation of Gaussian distribution on the respective axes. For the SLM laser beam, it can be considered that:

$$ {\displaystyle \begin{array}{l}{\sigma}_x={\sigma}_y=\frac{R_L}{2}\\ {}{\sigma}_z=\frac{d_{pb}}{3}\end{array}} $$
(4)

with RL as the laser spot radius. The Gaussian spatial distribution along the powder bed thickness approximates the multiple scattering and the consequent absorption of the laser beam by the powder particles.

2.2.1 Absorption coefficient

The interaction of the laser beam with the powder bed is divided into two phases: the pre-melted phase, where interaction between the electromagnetic wave and the solid particles of the powder bed occurs and the melted phase, during which the laser beam energy is absorbed by liquid material. The fundamental physical mechanism is different for each kind of interaction, thus different calculation methodology is appropriate. The main steps for this modeling approach are presented in Fig. 3.

Fig. 3
figure 3

Main steps for the absorption coefficient calculation

Full size image

For the pre-melted phase, the laser beam interacts with the solid particles of the powder bed and is either absorbed by the material or undergoes multiple reflections. As a consequence, the absorption coefficient must be calculated as the sum of the total reflections along the powder bed volume. The absorbed or reflected proportion of energy depends on the electromagnetic beam wavelength, the powder material’s optical constants, and the incident angle of laser beam. The absorption coefficient is calculated in respect to the incident angle (θ) by using the Fresnel equations [44]:

$$ {\displaystyle \begin{array}{l}{a}_s\left(\theta \right)=1-{\left|\frac{\cos \theta -{\left({n}^2-{\sin}^2\theta \right)}^{1/2}}{\cos \theta +{\left({n}^2-{\sin}^2\theta \right)}^{1/2}}\right|}^2\\ {}{a}_p\left(\theta \right)=1-{\left|\frac{n^2\cos \theta -{\left({n}^2-{\sin}^2\theta \right)}^{1/2}}{n^2\cos \theta +{\left({n}^2-{\sin}^2\theta \right)}^{1/2}}\right|}^2\end{array}} $$
(5)

where αs and αp refer to the absorption to S-polarized and P-polarized light, respectively, and n is the relative refractive index of the powder material. For 316L steel, the refractive index is n = 2.9613–4.0133i at the wavelength of 1070 nm [45], corresponding to Yb fiber laser. Solving the above equations for the pre-mentioned refractive index, the results that are depicted in Fig. 4 emerged.

Fig. 4
figure 4

Absorption, reflectance, and transmittance coefficients of 316L steel at 1070 nm wavelength of electromagnetic wave

Full size image

The absorption coefficient in respect to the incident angle can be approximated by the second order polynomial of Eq. 6, with R2 ≈ 1, and θ representing the incident angle in degrees:

$$ a\left(\theta \right)=-0.000046{\theta}^2+0.000006\theta +0.372491 $$
(6)

For modeling the powder material, the assumption of an ideal powder bed is made; thus, 3 layers of identical spheres in hexagonal close packing arrangement are used. This approach is not far from the actual setup of the powder bed fusion in SLM [46]. Using a ray-tracing computational module, the trajectories of an incident laser beam are calculated, see Fig. 5, and thereby, the incident angles along the laser beam path over the powder bed, considering the multiple scatterings. As the assumption of an ideal powder bed is made, the model presents symmetry, and, thus, can be solved for the quarter of a sphere. Using the calculated incident angles in Eq. 6, the total absorbance can be estimated, taking into account the energy that is absorbed due to multiple scattering.

Fig. 5
figure 5

Ray trajectories

Full size image

For powder particles with diameter 30.5 μm, and laser beam wavelength of 1070 nm, the mean total absorbance coefficient is computed as 58.66%. This result is in line with experimental measurements of Yan et al. [47], who have determined a 55% absorptivity coefficient for 316L powder.

When the powder bed material reaches a temperature above the melting point, the absorbance physical mechanism is different, since the laser beam “meets” a liquid material. For estimation of the absorbance during the melted phase, electron-phonon-dominated optical conductivity and the Drude theory was used. Based on the work of Siegel [48], the absorbance of iron at 1060-nm incident light wavelength, for temperatures above its melting point, is calculated by Eq. 7:

$$ \eta =0.0002485T-0.07833 $$
(7)

This approach has an upper temperature limit of two times the melting temperature. The total absorbance is mathematically expressed by Eq. 8:

$$ \eta =\left\{\begin{array}{c}0.5866\to T< Tm\\ {}0.0002485T-0.07833\to {T}_m<T<3622\\ {}0.82\to T>3622\end{array}\right|\Rightarrow {\eta}_{\mathrm{max}}=0.82 $$
(8)

Equation 8 indicates that the maximum absorbance is 82% for extremely high temperatures, a conclusion that is justified by the experimental measurements of Trapp et al. [49]. In their study, a similar high value of average absorbance was measured for high laser powers.

2.3 Thermo-physical properties and emissivity

The computational domain is composed of two main regions, namely the powder bed region and the solid substrate region, which is placed below the powder bed. Initial temperature in both regions is 293 K. For powder bed and substrate regions, material properties such as density, specific heat, and thermal conductivity are assumed as temperature-dependent and for the case of powder bed, phase-dependent as well. Thermo-physical properties and emissivity for both materials are defined as polynomials, with different expressions below and above the melting point, using appropriate formulas from the relevant literature for 316L steel.

2.3.1 Thermo-physical properties and emissivity for temperature below the melting point

The modeling of powder bed effective thermal conductivity kpb is complex, based on the Zehner and Schlunder model, taking into account free fluid radiation, and core heat transfer, as well as solid contact heat transfer terms [51]. Thus, it is expressed as follows:

$$ {k}_{pb}={k}_{ff}+{k}_{core}+{k}_{contact} $$
(9)
$$ {k}_{ff}={k}_g\left(1-\sqrt{1-\varphi}\right)\left(1+\frac{k_R}{k_g}\right)\left[\frac{W}{mK}\right] $$
(10)
$$ {k}_{core}={k}_g\sqrt{1-\varphi}\left\{\left(1-\phi \right)\right.\left[\frac{2}{1-\frac{B\cdot {k}_g}{k_s}}\left(\frac{B}{{\left(1-\frac{B\cdot {k}_g}{k_s}\right)}^2}\left(1-\frac{k_g}{k_s}\right)\ln \frac{k_g}{B\cdot {k}_s}-\frac{B+1}{2}-\frac{B-1}{1-\frac{B\cdot {k}_g}{k_s}}\right)+\frac{k_R}{k_g}\right]\left[\frac{W}{mK}\right] $$
(11)
$$ {k}_{contact}=\phi \frac{k_{sol. con}}{k_g}\left[\frac{W}{mK}\right] $$
(12)

where kff represents the free fluid radiation heat transfer, kcore represents the core heat transfer, kcontact represents the solid contact heat transfer, kg is the thermal conductivity of the continuous gas phase, kR is the part of thermal conductivity owing to radiation, φis the porosity of the powder bed, Β is the deformation parameter of the particle according to its geometry, ks is the thermal conductivity of solid, and ksol.con represents the solid contact conductivity. The deformation parameter B in the present case is expressed as follows:

$$ B\approx 1.25{\left(\frac{1-\varphi }{\varphi}\right)}^{\raisebox{1ex}{$10$}\!\left/ \!\raisebox{-1ex}{$9$}\right.} $$
(13)

The thermal conductivity part due to radiation is calculated as follows:

$$ {k}_R=\frac{4\cdot \varepsilon \cdot \sigma \cdot {\mathrm{T}}^3\cdot {d}_R}{1-0.132\cdot {\varepsilon}_{T<{T}_m}}\left[\frac{W}{mK}\right] $$
(14)

where ε is the emissivity of the powder bed, σ is the Stefan-Boltzmann constant equal to 5.6704 × 108 Wm2K−4, T represents the mean absolute temperature of the powder bed (K), and dR is the effective length for radiation between particles, equal to the particle diameter (m).

Emissivity of the powder bed is modeled using two different equations for temperatures below and above the melting point. For T < Tm the following expression is employed:

$$ {\varepsilon}_{T<{T}_m}={A}_H{\varepsilon}_H+\left(1-{A}_H\right){\varepsilon}_S $$
(15)

where εΗ is the emissivity of cavities (holes) of the powder bed, εS is the emissivity of solid particles in the powder bed, and AH is the area fraction of the surface that is occupied by the radiation emitting cavities. The area fraction can be calculated by the following expression:

$$ {A}_H=\frac{0.908\cdot {\varphi}^2}{1.908\cdot {\varphi}^2-2\cdot \varphi +1} $$
(16)

Moreover, the emissivity of the cavities can be expressed as a function of solid particle emissivity and bed porosity as follows:

$$ {\varepsilon}_H=\frac{\varepsilon_S\left[2+3.082{\left(\frac{1-\varphi }{\varphi}\right)}^2\right]}{\varepsilon_S\left[1+3.082{\left(\frac{1-\varphi }{\varphi}\right)}^2\right]+1} $$
(17)

Finally, the specific heat and the density of the powder bed is calculated based on the rule of mixtures, while for the solid state, the literature-recommended formulas are used [52].

2.3.2 Thermo-physical properties and emissivity for temperature above the melting point

For temperatures above the melting point, the powder bed has been transformed into a homogeneous liquid material, having the same properties with the melted substrate material.

Thermal conductivity of the melted material is expressed by Eq. 18 [52]:

$$ {k}_{T>{T}_m}=12.41+0.003279\cdot T\left[\frac{W}{mK}\right] $$
(18)

and the emissivity is expressed as follows [53]:

$$ {\varepsilon}_{T>{T}_m}=0.28\exp \left(\frac{-\left(T-{T}_m\right)}{55}\right)+0.087 $$
(19)

2.4 Convection heat flux

The convective heat transfer coefficient between the powder bed and thesurrounding environment is calculated, taking into account the Nusselt number of the flow field, as follows [54]:

$$ h(T)=\frac{Nu\left(T\hbox{'}\right)\cdot k(T)}{L}\left[\frac{W}{m^2K}\right] $$
(20)

where

$$ {\displaystyle \begin{array}{l} Nu(T)=0.54{\left( Gr\left(T\hbox{'}\right)\cdot \Pr \left(T\hbox{'}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}\\ {} and\\ {}T\hbox{'}=\frac{T_{\infty }+T}{2}\left[K\right]\end{array}} $$
(21)

Gr represents the Grashof number and Pr the Prandtl number.

2.5 Phase change and material ablation

Phase changes in both materials are taken into account by including the latent heat of the phase transition. The phase changes that can occur are solid to liquid and liquid to gas. In the case of powder bed material, porosity is taken into account, as well. The latent heat of melting and vaporization for 316L are 260 kJ/kg and 6090 kJ/kg respectively.

Finally, in order to model the heat produced during vaporization of the powder bed material when temperature reaches the boiling point, a heat flux is also defined, as follows [55]:

$$ {Q}_{abl}=\left[\left(1-{\beta}_R\right){\left(\frac{m}{2\cdot \pi \cdot {k}_B\cdot T}\right)}^{\frac{1}{2}}p(T)\right]\left(\int Cp(T) dT+{L}_m+{L}_v\right)\left[\frac{W}{m^2}\right] $$
(22)

where βR is equal to 0.95 as SLM is a weak evaporation process, while p(T) is calculated by the expression:

$$ p(T)={p}_o\cdot \exp \left[\frac{m\cdot {L}_v}{k_B\cdot {T}_V}\left(1-\frac{T_v}{T}\right)\right]\left[ Pa\right] $$
(23)

where m represents the mass per atom of a metal (kg), Lv represents the latent heat of evaporation (J/kg), Lm is the latent heat of melting (J/kg), and kB is the Boltzmann constant.

2.6 Computational domain and mesh

In order to reduce computational cost, the computational domain is cut along the symmetrical plane so that one-half of the real domain is solved, see Fig. 6. The domain consists of two sub-domains, one for the powder bed and one for the substrate. The depth of the substrate domain is 75 μm, while the substrate depth changes according to SLM parameters, i.e., laser power and speed, in order to avail sufficient depth for a fully developed thermal profile. The length of the powder bed and substrate domain is 5 mm, i.e., 2 mm longer than the laser path and the domain’s width is 0.5 mm. In the contact face of the powder bed and the substrate domain, a temperature and energy continuity boundary condition is used. Special mesh refinement has been performed near the melt pool area, which will be affected mainly by the laser irradiation during the SLM process, whereas the element size is larger in the rest of the powder bed and substrate regions, as these areas will not be significantly affected by thermal phenomena, see Fig. 6. The implicit time-dependent method of backward differentiation formula (BDF) was used, with maximum BDF order 2 and event tolerance 0.01. The computational time was set always greater than the real process time, providing an additional time frame of 0.003 s, in order for the temperature profile to be adequately developed. Finally, all the necessary temperature-dependent material properties and coefficients were defined as a function of temperature, based on literature data and/or calculations that took place prior to the simulation. The powder bed thermal conductivity, the convection coefficient, and the heat flux due to ablation were estimated for a wide range of temperatures and subsequently approximated by a polynomial.

Fig. 6
figure 6

Computational domain; mesh refinement is necessary, especially along the heat source path

Full size image

3 Results and discussion

For the validation of the model, experimental data for three different volumetric energy densities (VEDs) have been used [36]. The VED is defined as:

$$ VED=\frac{P}{\upsilon_L{R}_L{d}_{pb}}\left[\frac{J}{mm^3}\right] $$
(24)

The different sets of laser power and laser scanning speed of the simulations are presented in Table 1.

Table 1 Simulation parameters
Full size table

3.1 Track shape evolution

The track shape evolution and the formation of continuous tracks are a crucial parameter in AM. In SLM, the material has to be fully melted and uniformly spread on the substrate. Under certain process parameter values, namely laser power density and laser beam speed, irregularities in track morphology can appear, along with the balling effect. Balling effect is called the phenomenon where the molten metal breaks into droplets, forming separate beads in lieu of a continuous line. The volumetric energy density of the process and the Plateau-Rayleigh capillary instability of the melt pool are considered the essential causes of irregularities and balling formation in SLM. As the VED is decreased, the track morphology is shifted towards an irregular shape, until the balling regime is reached. This lower VED limit for the balling formation differs depending on the laser power and the powder bed thickness, but for a specific laser power and powder bed thickness, the crucial parameter is the scanning speed. Increase in the scanning speed results to an elongation of the melt pool, which loses its circular shape. When this elongation becomes too prominent, the Plateau-Rayleigh instability condition is satisfied, and instabilities in the melt pool appear, and thus, it breaks into droplets [36, 56]. The balling effect and the threshold of its formation depend on the geometrical and shape characteristics of the melt pool and namely the length-to-depth ratio [57, 58]. As a result, a modeling method that can accurately simulate the melt pool shape can predict the balling formation during the SLM process. This statement is also supported by the highly cited work of Gusarov et al. [14], who presented a purely thermal model and managed to predict melt pool dimensions during SLM, stating explicitly the prediction of balling formation with this model. There is an inherent difficulty in modeling of the irregularities and balling formation, as in the melt pool dynamics, other physical mechanisms, like Marangoni convection, are involved [59, 60]. Nevertheless, the current thermal model, through the analytical and extended definition of the material properties and boundary conditions, can predict the melt pool shape, along with the irregularities up to the onset of balling. The track shape is evaluated according to the substrate melt pool; as for the efficient joining of the molten powder material with the substrate or previous layers, a molten pool has to be formed. In a different case, when the molten powder material cannot develop, a sufficient bond with the substrate material or fails to wet the underlying substrate, defects can be formed [61].

In Figs. 7, 8, 9, and 10, the geometry and shape of the melt pool, as it has been formed during the whole process, is depicted. The temperatures that are presented refer to the maximum reached temperature in every melt pool point during the process. In other words, they are all the locations in the substrate where the value of temperature exceeded the melting point, for all the calculated moments up to a particular time step.

Fig. 7
figure 7

Comparison between experimental and simulation results

Full size image
Fig. 8
figure 8

Track shape evolution for P = 100 W and υL = 250 mm/s

Full size image
Fig. 9
figure 9

Track shape evolution for P = 100 W and υL = 300 mm/s

Full size image
Fig. 10
figure 10

Track shape evolution for P = 200 W and υL = 1000 mm/s

Full size image

In Fig. 7, the simulation results are juxtaposed with experimental ones. In the simulation results, the material volume of the substrate that has reached the melting point is presented, i.e., the melt pool. In agreement with the established theory, as the scanning speed increases, the track shape becomes irregular, with corrugated track sides, see Fig. 7a and b. It is obvious that the track morphology shifts towards to various ellipsoid formations separated by narrow tracks as the onset of balling formation is approached; however, disconnected balling formation is not observed, yet. For 200-W laser power and scan speed of 1000 mm/s, see Fig. 7c, the track is narrow, with ellipsoid formations; however, these formations are not totally disconnected from the track, in compliance with the characteristics of “irregular” tracks described in [36]. At the beginning and the end of the track, where the laser is turned on and off, respectively, there is an unstable state region with length of about 1 mm.

In Figs. 8 to 10, the track shape evolution is presented. For P = 100 W and υL = 250 mm/s, see Fig. 8, at first an unstable melt pool is formed with about 1.2 mm length. After that, there is a narrow “neck” formation, and, subsequently, there is an almost uniform melt pool. At the end of the track, there is again a “neck” before the instability of the track end.

For P = 100 W and υL = 300 mm/s, see Fig. 9, again at the beginning of the track, there is an unstable state, followed by a “neck” formation. After that, and as the VED has decreased, a melt pool zone with several ellipsoid formations is developed and is formed. The melt pool gradually loses its circularity, moving towards an elongated geometry. At the end of the track, instabilities are distinguished once more.

Finally, for P = 200 W, υL = 1000 mm/s, and VED = 48 J/mm3, see Fig. 10, the track shape is uniform but narrow, with small ellipsoid formations at the end of the track. The typical unstable formations at the beginning and at the end of the melt pool still exist.

In Fig. 11, the calculated widths and depths of the molten pools are presented, in juxtaposition with experimental results. Both, width and depth of the track, are not constant, with, especially the depth varying eminently. Nevertheless, a mean value for the melt pool depth can be estimated. In the simulations, as it can be also seen in experiments, the increase in laser speed from 250 to 300 mm/s results in higher molten pool depth, while the width does not change significantly. For laser speed 1000 mm/s, even though the laser power raised at 200 W, the track width and depth were reduced. It can be concluded that decrease in VED leads in lower aspect ratio of depth to width. This ratio is of high importance since it is directly related to the sufficient bond of layers. Extremely shallow depth may result to inadequate attachment of the new layer on the previous one, ensuing parts with defects and/or weak points. Hence, the machining parameters have to ensure the sufficient melt pool depth, along with the avoidance of keyhole formation. The melt pool has the characteristic U-shape morphology, with a small aspect ratio, i.e., lower than 0.5, indicating that SLM process is under conduction mode; thus, the current model is rightly adopted. Furthermore, the existence of unstable regions at the beginning and the end of the track, for all sets of parameters, raise the need of extra caution in planning of the process, while implying that for modeling, adequate track length has to be simulated for realistic and accurate results.

Fig. 11
figure 11

Width and depth of the melt pool

Full size image

3.2 Power losses during SLM process

By integrating the power fluxes from the top surface, the heat losses due to ablation, radiation, and convection can be calculated. The corresponding diagrams are presented in Fig. 12. It is concluded that the power losses coming from the material ablation are the highest, for all sets of processing parameters. For 100-W laser power, the maximum ablation power loss is approximately 2 W, while for 200 W it increases at 2.5 W. The power loss due to material ablation is the most mutable as it depends on the re-condensation of the material. On the other hand, the radiation power losses are similar and steady in all cases. They are in the range of 0.5 W and almost constant for the whole time of the process, while they are rapidly decreased when the laser beam is switched off. Taking in mind that the heat transfer due to radiation strongly depends on the temperature difference, it is a rational result that the radiation heat loss, which occurs while the laser beam is turned on, is more intense. Finally, for all sets of processing parameters, the heat losses due to convection are the lowest and almost constant, in the range of 0.1 to 0.2 W. It has to be mentioned that convection heat transfer depends on the fluid properties; thus, a different processing environment, for example with different gas velocity, will result to a change in the convection heat losses. At this point, an important clarification regarding the heat losses due to ablation has to be made. The heat losses due to ablation are proportional to ablated material volume, which strongly depends on the combination of process parameters. This dependence is mathematically expressed through the coefficient βR in Eq. 22. Hence, in modeling and result’s evaluation, it is always to be considered and re-estimated, keeping in mind that higher VED may lead to more intense material ablation, thus a lower coefficient βR.

Fig. 12
figure 12

Power losses due to material ablation, radiation, and convection for a P = 100 W and υL = 250 mm/s, b P = 100 W and υL = 300 mm/s, c P = 200 W and υL = 1000 mm/s

Full size image

3.3 Cooling and heating rates in the workpiece

Finally, remarks on the temperature rate, during different SLM conditions, can be made. In Fig. 13, the temperature profiles and the temperature rates are depicted, at the center cross-section, when the laser beam reaches the end of the track and is turned off. The maximum temperature rates are of the order of 105 K/s, with the areas on either side of the center having a temperature rate of an order lower, i.e., 104 K/s. These cooling and heating rates that emerged from simulation are in total agreement with bibliographic references [1]. Additionally, the importance of a detailed modeling of the powder thermal properties can be emphasized through those figures. It can be seen that at the boundaries of the molten material, namely, where the temperature is lower or equal to material melting point, the temperatures rates are extremely low. This rapid reduction in the temperatures rates is the result of the low thermal conductivity of the powder bed, forming some kind of heat barrier around the melt pool, with the thermal energy being transferred easier and faster to the substrate material through the melt pool. Thus, an anisotropic thermal system is developed, forming asymmetric melt pools with irregularities. The high temperatures rates that occur can explain the development of thermal residual stresses, which often result in defects like cracks, and/or the distortion of the component. Finally, according to the results of Fig. 13, for different VED, the cooling rate profiles differentiate; hence, it is feasible for an optimal set of parameters to be found, which limits areas with extremely uneven cooling rates, and/or high temperature gradients that may lead to unwanted results.

Fig. 13
figure 13

Temperature profile and temperature rate when the laser beam is turned off at the center cross-section for a P = 100 W and υL = 250 mm/s, b P = 100 W and υL = 300 mm/s, and c P = 200 W and υL = 1000 mm/s

Full size image

4 Conclusions

The current paper presents a complete and robust methodology for modeling the evolution and final shape of melt pool, as well as other thermal phenomena occurring during conduction mode SLM process. At first, the effective absorption coefficient of the laser beam incident is calculated using the Fresnel equations, taking into account the multiple scattering that the laser beam undergoes as it interacts with the powder material. For the melted phase of the material, the absorption coefficient was determined based on the electron-phonon-dominated optical conductivity and the Drude theory. Then, the thermo-physical properties of the powder bed were calculated; in order to determine the thermal conductivity of the powder bed, the Zehner and Schlunder model was used, while for the other material properties, analytical relations from the literature were adopted, both temperature- and phase-dependent. The convection coefficient was calculated based on the Nusselt number, according to the process parameters. Moreover, the energy loss due to ablated material was estimated, while the latent heats of melt and evaporation were taken into consideration. Finally, a moving volumetric Gaussian heat source was used, to simulate the laser beam.

Three simulations were run, for different volumetric energy densities, and the simulation results were compared and validated with experimental ones. The melt pool shape and its geometrical characteristics were calculated; the total heat losses owing to material ablation, radiation, and convection were estimated, as well as the heating and cooling rates. In brief, from the described study, it was deduced that:

  • The absorption coefficient of the powder bed, with the material remaining in a solid state and taking into consideration the multiple scatterings of the laser beam, was calculated as 58.66%. The coefficient increases gradually as the material melts, reaching up to 82%.

  • In numerical models of the SLM process, thermo-physical properties of the powder bed have to be calculated in respect to the powder characteristics, as they significantly differ from those of the solid material. Specifically, the thermal conductivity of the powder bed was found to be one order of magnitude lower than that of the solid material.

  • The melt pool formation, as well as the track shape, can be simulated by the presented model with a significant degree of accuracy. For different VED values, the track acquires different geometrical characteristics. For VED value of 97 J/mm3, a uniform melt pool was formed, while for 81 J/mm3, the melted pool developed ellipsoid formations and instabilities. For a VED value of 48 J/mm3, the melt pool was narrow, with a small zone of ellipsoid formations connected to the track. The above results were in line with experimental findings.

  • The nominal depth and width of the melt pool were estimated and it was found that they were in accordance with the experimentally measured values.

  • The heat losses due to material ablation are the highest, followed by the radiation losses which are almost constant, while the convection losses are, in all cases, considerably low.

  • From the obtained results, it is found that temperature rates of the order of 106 K/s occur during the SLM process at the time when laser beam is turned off, being in agreement with the relative literature.