1 Introduction

Owing to the unique characteristics of mechanical properties, aluminium alloy pipes are widely used in many fields, such as aerospace, automobile, architecture, and civil engineering. The pipe bending process plays an essential role in pipe formation. However, with the development of technology, this process is facing more and more requirements.

Over the years, many researchers have studied free bending process based on various methods. The free bending process was first proposed by Murata et al. [1], which was called the MOS-bending method. The bending radius of the pipes varies depending on the movement and rotation of the mobile die, which was applied for a patent by Murata [2]. It is a milestone in the history of the free bending process. Based on MOS, a new bending method, torque superposition spatial (TSS) bending, was proposed by Hermes et al. [3, 4]. This process could realise pipe production with arbitrary cross-sections and has an extensive application value. Since then, studies on the free bending process have become significant in pipe formation. Based on finite element method (FEM) analysis and process optimisation, He et al. [5] investigated the application of thin-walled pipes in the aerospace field and reviewed various pipe formation processes, TSS included. They concluded that the new processes contributed to the structure optimisation and production of lightweight pipes. Liang et al. [6] investigated the surface defects in the forming parts through the free bending process and concluded that the defects could be reduced, which validated the advantages of the new process. Li et al. [7] and Guo et al. [8] compared experimental and simulation results, and found that simulation could be used to guide the free bending process. According to Li et al. [9], the free bending process showed that the bending radii varied continuously. Guo et al. [10] established the CAD model and FE model to analyse the accuracy of pipe formation in the free bending process and investigated the deviation of bending radius and bending angle on account of the springback.

The springback after unloading is a factor that affects the accuracy of bent pipes and needs to be investigated in studies on pipe bending. Most studies on pipe springback during the bending process are based on classical springback theory. Qureshi et al. [11] established the analytic formulas of springback prediction and the distribution of residual stress of thin-walled aluminium alloy pipes and proposed a way for establishing an analytic model of springback prediction. E et al. [12] proposed a similar methodology on 1Cr18Ni9Ti pipe formation calculation and found that the springback angle is affected by the bending radius and bending angles. Through the FE model, Gu et al. [13] investigated the springback process of thin-walled aluminium alloy pipes in NC bending and found that the springback angle increases with the increase of Poisson’s ratio and bending radius. Megharbel et al. [14] modified the formulas proposed by Al-Qureshi and enhanced the springback prediction of strain-hardening materials. Xue et al. [15] studied the twist springback and concluded that more reliable results could be obtained if the surface-based hinge constraint in the FE model was used. Liao et al. [16] compared different hardening models to show their influence on springback prediction. Zhan et al. [17] established an analytic model for springback prediction based on the static equilibrium condition in NC bending and validated the methodology by comparing with FEM results. In studies on residual stress, the classical elastoplastic theory is often applied for springback prediction, which has broadened the development of pipe springback research.

Many studies have investigated the free bending process, especially the mechanical structure. However, few studies have investigated springback during the free bending process. Thus, in the present study, aluminium alloy pipes are used as the research object, and an analytic model for pipe bending springback prediction is proposed. Three process parameters, namely, friction, clearance, and bend-die section shape, are analysed to determine their influence on the springback. The model precision is validated by comparing the FE simulation and analytic results. The results showed that the strain neutral layer offset tends to move towards the material tensile direction, which is opposite to the traditional rotary bending process. Finally, the analytic model of pipe bending springback is optimised by the addition of a neutral layer offset variable.

2 Theoretical basis

2.1 Constitutive equations for FEM

When the metallic material reaches the yield point, hardening occurs, where the pipes deform plastically. The material hardening rules mainly include isotropic hardening, kinematic hardening, and distortional hardening [18]. In the classical elastic–plastic theory, isotropic hardening is always considered, whilst others are ignored. However, in realistic pipe production, the plastic deformation of the pipe is frequently complicated because the Bauschinger effect exists definitely and kinematic hardening occurs. Considering the complex deformation mechanism of metal materials, each effect of isotropic and kinematic hardening is hard to distinguish. Thus, the accurate description of the actual metal material plastic deformation plays an essential role in precise springback prediction.

In this model, based on the Helmholtz free energy, the state equations can be obtained by derivation considering the state variables of Cauchy stress \( \underline {\boldsymbol{\sigma}} \), kinematic hardening state variable \( \underline {\boldsymbol{X}} \) and isotropic hardening state variable R [19, 20]:

$$ \underline{\sigma}=\underline {\underline{\varLambda}}:\underline {\varepsilon^e}\kern0.40em $$
(1)
$$ \underline{X}=\frac{2}{3}C\underline{\alpha} $$
(2)
$$ R= Qr $$
(3)

where \( \underline {\underline {\boldsymbol{\varLambda}}} \) is the elastic stiffness matrix and C and Q are the kinematic hardening modulus and isotropic hardening modulus, respectively. After considering the yield surface distortion, the yield criterion f and the plastic potential F of the proposed FEM model are changed into:

$$ f\left(\underline{S},\underline{X},R\right)={\left\Vert {\underline{S}}_d-\underline{X}\right\Vert}_H-R-{\sigma}_y $$
(4)
$$ \mathrm{F}\left(\underline{S},\underline{X},R\right)={\left\Vert {\underline{S}}_d-\underline{X}\right\Vert}_H-R+\frac{3a}{4C}\underline{X}:\underline{X}+\frac{b}{2Q}{R}^2 $$
(5)

where σy is the initial yield strength. The initial anisotropy in the yield criterion and the plastic potential is Hill48, and the improved Francois model is used to describe the induced anisotropy (the original Francois model cannot adjust the distortion ratio of the yield surface in the vertical direction). To achieve the effect of controlling the yield surface distortion and realising the anisotropy, the distortion stress \( {\underline{S}}_d \) is used to replace the deviatoric stress tensor in the yield equation.

$$ {\underline{S}}_d=\underline{S}+\frac{{\underline{S}}_0:{\underline{S}}_0}{2{X}_{l1}\left(R+{\sigma}_y\right)}\underline{X} $$
(6)
$$ {\underline{S}}_d=\underline{S}+\frac{{\underline{S}}_0:{\underline{S}}_0}{2{X}_{l1}\left(R+{\sigma}_y\right)}\underline{X}-\frac{\underline{X}:\underline{X}}{2{X}_{l2}\left(R+{\sigma}_y\right)}{\underline{S}}_0\kern0.60em $$
(7)
$$ {\underline{S}}_0=\underline{S}-{\underline{S}}_x $$
(8)
$$ {\underline{S}}_x=\frac{\underline{S}:\underline{X}}{\underline{X}:\underline{X}}\cdotp \underline{X} $$
(9)

where \( {\underline{S}}_x \) indicates the part of stress contributed by the active slip system and \( {\underline{S}}_0 \) indicates the ones contributed by the potential slip system. Xl1 and Xl2 are the new material parameters of distortional hardening, which can control the yield surface distortion in parallel and perpendicular to the loading directions, respectively. The constitutive model of \( {\underline{S}}_d \) is one of the key issues in this study. Combined with the plastic flow rules and potential energy equation F, the plastic strain rate\( {\underline{D}}^p \), kinematic hardening strain rate \( \dot{\underset{\_}{\alpha }} \) and isotropic hardening strain rate \( \dot{r} \) can be obtained:

$$ {\underline{D}}^p=\dot{\lambda}\frac{\partial F}{\partial \underset{\_}{\sigma }}=\dot{\lambda}{\underline{n}}^p $$
(10)
$$ \dot{\underset{\_}{\alpha }}=-\dot{\lambda}\frac{\partial F}{\partial \underset{\_}{X}}=\dot{\lambda}\left({\underline{n}}^x-a\underline{\alpha}\right) $$
(11)
$$ \dot{r}=-\dot{\lambda}\frac{\partial F}{\partial R}=\dot{\lambda}\left({n}^r- br\right) $$
(12)

where \( \dot{\lambda} \) represents the strain rate. The normal tensor equation is based on the well-known generalised normality rule as follows:

\( \kern0.1em {\underline{n}}^p={\underline{n}}_d^p:\left[{\underline {\underline{I}}}^D+\frac{\underline{X}\otimes {\underline{S}}_0}{X_{l1}\left(R/+{\sigma}_y\right)}\right] \) (13)

$$ {\underline{n}}_d^p=\frac{{\underline {\underline{H}}}^p:\left({\underline{S}}_d-\underline{X}\right)}{{\left\Vert {\underline{S}}_d-\underline{X}\right\Vert}_p} $$
(14)
$$ {\underline{n}}^x={\underline{n}}_d^p-\frac{{\underline{S}}_0:{\underline{S}}_0\ }{2{X}_{l1}\left(R+{\sigma}_y\right)}{\underline{n}}_d^p+\frac{\left(\underline{S}:\underline{X}\right)\left(\underline{X}:{\underline{n}}_d^p\right)}{X_{l1}\left(\underline{X}:\underline{X}\right)\left(R+{\sigma}_y\right)}{\underline{S}}_0 $$
(15)
$$ {n}^r=\frac{\left({\underline{S}}_0:{\underline{S}}_0\right)\left({\underline{n}}_d^p:\underline{X}\right)}{2{X}_{l1}{\left(R+{\sigma}_y\right)}^2}+1 $$
(16)

By using the implicit method for local integration of constitutive equations, the Jacobi matrix can be obtained as follows:

$$ \underline {\underline{K}}=\underline {\underline{\varLambda}}-\left(\underline {\underline{\varLambda}}:{\underline{n}}^p\right)\otimes \frac{\underline {\underline{\varLambda}}:{\underline{n}}^p}{{\underline {\underline{H}}}_P} $$
(17)
$$ {\underline {\underline{H}}}_P={\underline{n}}^p:\underline {\underline{\varLambda}}:{\underline{n}}^p+\frac{2}{3}C{\underline{n}}^x:\left(a\underline{\alpha}-{\underline{n}}^x\right)+Q{n}^r\left( ar-{n}^r\right) $$
(18)

2.2 Analytic models

Based on the static equilibrium condition, one analytic model suited for the springback prediction in traditional pipe bending process has been given. This model is built for the rotary bending process. Thus, an enhancement will be proposed in this section to improve the suitability in the free bending process.

2.2.1 Model assumption

The bending deformation of the pipe is extremely complex in the formation process. The assumptions are proposed before establishing the model.

  1. (1)

    Young’s modulus in elastic–plastic deformation is defined as follows:

$$ E=\left\{\begin{array}{c}{E}_0,\sigma \le {\sigma}_s\\ {}{E}_v,\sigma >{\sigma}_s\end{array}\right. $$
(19)

where σ is the stress, σs is the yield stress, E0 is Young’s modulus in elastic deformation, and Ev is the equivalent modulus in a certain moment, which can be calculated using Eq. (20). Detailed discussion can be found in [21].

$$ {E}_v={E}_0-\left({E}_0-{E}_a\right)\left(1-{e}^{\xi \overline{\varepsilon}}\right) $$
(20)
  1. (2)

    The shear stress σij (i ≠ j) and the shear strain εij (i ≠ j) are neglected, whose functions can be as follows:

    $$ \left\{\begin{array}{c}{\sigma}_{ij}\ \left(i\ne j\right)=0,\kern0.5em i,j=1,2,3\\ {}{\varepsilon}_{ij}\ \left(i\ne j\right)=0,\kern0.5em i,j=1,2,3\ \end{array}\right. $$
    (21)
  2. (3)

    The section deformation is ignored. Thus, the stress in the pipe thickness direction σt and the strain in the circumferential direction εC are zero.

  3. (4)

    There is always volume constancy of the pipe during the formation process εx + εy + εz = 0.

  4. (5)

    The stress neutral layer coincides with the strain neutral layer. The pipe section always stays flat during the formation process. The friction between the bend die and pipe is ignored.

2.2.2 Model deduction

After unloading, residual stress and strain are present in the deformation section, and the bent pipe remains in a state of equilibrium, which has been given in Eq. (22). The springback model is established on the basis of this condition.

$$ {F}_{\theta }=0 $$
(22)

When an external load is applied, the wall thickness of the outside layer becomes thinner, and the inner layer becomes thicker. A strain neutral layer is formed during the pipe bending process. The bending moment reaches a balance on the strain neutral layer. Due to the asymmetric stress distribution, an offset occurs between the strain neutral layer and the geometrical neutral layer.

During loading, elastic deformation occurs firstly. With increasing external load, plastic deformation will appear. The outermost and innermost materials reach the yield condition firstly. Plastic deformation extends from the outer and inner layers to the middle layer, and no plastic deformation occurs on the neutral layer. The material near the neutral layer only occurs elastic deformation during the bending process. Thus, the cross-section can be divided into four deformation zones, namely, outer plastic deformation, outer elastic deformation, inner elastic deformation, and inner plastic deformation, as shown in Fig. 1.

Fig. 1
figure 1

Cross-section of the pipe

Full size image

In the elastic deformation zone, the stress–strain relationship follows generalised Hooke’s rule. The axial stress–strain relationship in the elastic deformation zone can be obtained using Eq. (23), where σθ and εθ represent the axial stress and axial strain, respectively.

$$ {\sigma}_{\theta }=\frac{E_0}{1-{\mu}^2}{\varepsilon}_{\theta } $$
(23)

In the plastic deformation zone, the stress–strain relationship can be expressed by Eq. (24) according to Hencky’s total strain.

$$ \left|{\sigma}_{\theta}\right|=\frac{2K}{\sqrt{3}}{\left(\frac{2}{\sqrt{3}}\left|{\varepsilon}_{\theta}\right|+b\right)}^n $$
(24)

The curvature radius of the neutral layer Rε can be calculated according to the literature [22], where Fθ is the axial force, y is the distance from the strain neutral layer, and De is the neutral layer offset.

$$ {F}_{\theta }={\int}_A\sigma \mathrm{d}A={\int}_AE\frac{y}{R_{\varepsilon }+y}\frac{\delta }{\mathrm{d}\varphi}\mathrm{d}A=0 $$
(25)
$$ {R}_{\varepsilon }=\frac{A}{\int_A\frac{\mathrm{d}A}{\rho +y}}=\sqrt{\rho^2-{r}^2} $$
(26)
$$ {D}_e=\rho -{R}_{\varepsilon } $$
(27)

Compared with the pure bending process, the pusher will apply additional axial compressive stress to the pipe during the free bending process. This additional stress will superimpose with the original compressive stress and tensile stress of the pipe. The additional compressive stress given by the axial pusher is offset by the tensile stress, which will make the bending neutral layer move towards the outer layer during the elastoplastic deformation stage. Thus, considering the effect of axial stress, the neutral layer offset can be optimised as follows:

$$ {\sigma}_{P1}=\frac{F_P}{2{A}_1} $$
(28)
$$ {\sigma}_{P2}=\frac{F_P}{2{A}_2} $$
(29)
$$ \lambda =\frac{\sigma_{P1}+{\sigma}_{P2}}{\sigma } $$
(30)
$$ {F}_{\theta }={\int}_A\left(1+\lambda \right)\sigma \mathrm{d}A=0 $$
(31)
$$ {R}_{\varepsilon}^{\prime }=\left(1+\lambda \right)\frac{A}{\int_A\frac{\mathrm{d}A}{\rho }}=\left(1+\lambda \right){R}_{\varepsilon } $$
(32)
$$ {D}_e=R-{R}_{\varepsilon}^{\prime } $$
(33)

where FP is the axial push force, σP1 and σP2 are the stress of the outer and inner deformation zones, respectively. A1 and A2 are the areas of the outer and inner deformation zones, respectively. λ is optimal coefficients.

Through the definition of strain and model assumptions, the thickness of the pipe after bending can be obtained using Eq. (34), where t0 represents the initial thickness of the pipe, t represents the thickness after bending, and ρ represents the bending radius before springback. When yielding occurs, the strain between the elastic deformation zone and the plastic deformation zone can be obtained using Eq. (35). Together with the geometrical relationship as shown in Fig. 1, the different deformation layer angle α and β can be obtained.

$$ t=\left\{\begin{array}{c}\frac{\left(\rho -{D}_e\right){t}_0}{\rho },\kern16.70003em \varphi =\frac{\pi }{2}\\ {}\frac{-\left(\rho +r\cos \varphi \right)+\sqrt{{\left(\rho +r\cos \varphi \right)}^2+4\cos \varphi {t}_0\left(\rho -{D}_e\right)}}{2\cos \varphi },\kern0.7em \varphi \ne \frac{\pi }{2}\end{array}\right. $$
(34)
$$ {\varepsilon}_s=\overset{\_\_}{\varepsilon_{\alpha }}=\frac{2}{\sqrt{3}}{\varepsilon}_{\alpha }=\frac{2}{\sqrt{3}}\ln \frac{\rho +{d}_1}{\rho -{D}_e} $$
(35)
$$ {d}_1=\left(\rho -{D}_e\right){e}^{\frac{\sqrt{3}}{2}{\varepsilon}_s}-\rho $$
(36)
$$ {y}_{\alpha }={d}_1=\left(r+{t}_{\alpha}\right)\cos \alpha $$
(37)
$$ {t}_{\alpha }=\frac{-\left(\rho +r\cos \alpha \right)+\sqrt{{\left(\rho +r\cos \alpha \right)}^2+4\cos \alpha {t}_0\left(\rho -{D}_e\right)}}{2\cos \alpha } $$
(38)
$$ \alpha =\operatorname{arccos}\frac{\left[\left(\rho -{D}_e\right){e}^{\frac{\sqrt{3}}{2}{\varepsilon}_s}-\rho \right]{e}^{\frac{\sqrt{3}}{2}{\varepsilon}_s}}{r{e}^{\frac{\sqrt{3}}{2}{\varepsilon}_s}+{t}_0} $$
(39)
$$ \beta =\operatorname{arccos}\frac{\left[\left(\rho -{D}_e\right){e}^{-\frac{\sqrt{3}}{2}{\varepsilon}_s}-\rho \right]{e}^{-\frac{\sqrt{3}}{2}{\varepsilon}_s}}{r{e}^{-\frac{\sqrt{3}}{2}{\varepsilon}_s}+{t}_0} $$
(40)

The axial stress–strain relationships in the elastic and plastic deformation zones are given in Eq. (41). After springback, the residual stress can be regarded as the result of the superposition of bending stress and axial stress and is calculated using Eq. (42), where Δσ represents residual axial stress during the springback. Together with the elastoplastic theory, the axial stress after springback can be regarded as elastic springback stress. Thus, through the axial stress–strain relationship in the elastic deformation zone, the axial stress after the springback can be obtained using Eq. (43), where ρe represents the springback radius and Δεθ represents the axial strain after springback.

$$ {\sigma}_{\theta }=\left\{\begin{array}{c}\frac{2K}{\sqrt{3}}{\left(\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n,\kern2.6em 0\le \varphi \le \alpha \\ {}\frac{E_0}{1-{\mu}^2}{\varepsilon}_{\theta },\kern6.699996em \alpha \le \varphi \le \beta \\ {}-\frac{2K}{\sqrt{3}}{\left(-\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n,\kern0.9000001em \beta \le \varphi \le \pi \end{array}\right. $$
(41)
$$ {\sigma}_{\theta}^r={\sigma}_{\theta }+\varDelta \sigma $$
(42)
$$ \varDelta {\sigma}_{\theta }=\frac{E}{1-{\mu}^2}\varDelta {\varepsilon}_{\theta }=\frac{E}{1-{\mu}^2}\ln \left(\frac{\rho_e-y}{\rho_e+{D}_e}\right) $$
(43)

Residual stress \( {\sigma}_{\theta}^r \) can be obtained using Eq. (44). The bent pipe remains in a load equilibrium state after springback, and its equilibrium relationship can be expressed using Eq. (45). The axial force equilibrium equation is given by Eq. (46), where C1 − C6 represent the sum of axial force in the deformation zone during bending and springback processes. The curvature radius relationship of the pipe before and after the springback is given in Eq. (48).

The length of the pipe remains constant before and after springback, and its relationship to length during springback can be expressed as Eq. (49), where θr represents the bending angle after springback. Through these equilibriums, the springback angle can be obtained using Eq. (50).

$$ {\sigma}_{\theta}^r=\left\{\begin{array}{c}\frac{2K}{\sqrt{3}}{\left(\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n+\frac{E_v}{1-{\mu}^2}\frac{-y-{D}_e}{\rho_e+{D}_e},\kern2.1em 0\le \varphi \le \alpha \\ {}\frac{E_0}{1-{\mu}^2}{\varepsilon}_{\theta}\left({\varepsilon}_{\theta }+\frac{-y-{D}_e}{\rho_e+{D}_e}\right),\kern5.599997em \alpha \le \varphi \le \beta \\ {}-\frac{2K}{\sqrt{3}}{\left(-\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n+\frac{E_v}{1-{\mu}^2}\frac{-y-{D}_e}{\rho_e+{D}_e},\kern0.9000001em \beta \le \varphi \le \pi \end{array}\right. $$
(44)
$$ {F}_{\theta }=\underset{0}{\overset{\pi }{\int }}{\sigma}_{\theta}^r\left({t}^2+2 tr\right){d}_{\varphi }=0 $$
(45)
$$ \frac{1}{\rho_e+{D}_e}=\frac{C_1+{C}_2+{C}_3}{C_4+{C}_5+{C}_6} $$
(46)
$$ \left\{\begin{array}{c}{C}_1=\underset{0}{\overset{\alpha }{\int }}\frac{2K\left({t}^2+2 tr\right)}{\sqrt{3}}{\left(\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n d\varphi \\ {}{C}_2=\underset{\alpha }{\overset{\beta }{\int }}\frac{E_0\left({t}^2+2 tr\right)}{1-{\mu}^2}{\varepsilon}_{\theta } d\varphi \\ {}{C}_3=\underset{\beta }{\overset{\pi }{\int }}-\frac{2K\left({t}^2+2 tr\right)}{\sqrt{3}}{\left(-\frac{2}{\sqrt{3}}{\varepsilon}_{\theta }+b\right)}^n d\varphi \\ {}{C}_4=\underset{0}{\overset{\alpha }{\int }}\frac{E_v\left({t}^2+2 tr\right)\left(y+{D}_e\right)}{1-{\mu}^2} d\varphi \\ {}{C}_5=\underset{\alpha }{\overset{\beta }{\int }}\frac{E_0\left({t}^2+2 tr\right)\left(y+{D}_e\right)}{1-{\mu}^2} d\varphi \\ {}{C}_6=\underset{\beta }{\overset{\pi }{\int }}\frac{E_v\left({t}^2+2 tr\right)\left(y+{D}_e\right)}{1-{\mu}^2}d\upvarphi \end{array}\right. $$
(47)
$$ \frac{1}{\rho_e^r}=\frac{1}{\rho -{D}_e}-\frac{1}{\rho_e+{D}_e} $$
(48)
$$ \left(\rho -{D}_e\right)\theta ={\rho}_e^r{\theta}^r $$
(49)
$$ \varDelta \theta =\theta -{\theta}^r=\frac{\rho -{D}_e}{\rho_e+{D}_e} $$
(50)

3 Simulation analysis of free bending processes

In this section, the springback of spatial free bending will be simulated through the commercial software ABAQUS. Parameters, such as friction, clearance between the bend dies and the pipe, and section shape of the mobile die will be separately investigated.

3.1 Treatment of the main technical problems in ABAQUS

3.1.1 Principle of the free bending process

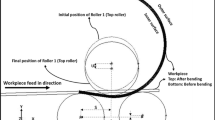
The pipe free bending process is more complicated than the traditional bending process, and its principle is shown in Fig. 2. The free bending process consists of three components: pusher, fixed die, and mobile die. Under the action of the pusher, the pipe loops through the fixed die and mobile die. The mobile die can move and rotate, and the free bending process can be realised by the movement and rotation of the mobile die. The pipe is bent by the thrust force of the pusher and the bending moment of the mobile die. The bending radius of the pipe depends on the distance L between the fixed and mobile dies, and the offset u of the mobile die. The bending radius ρ is obtained using Eq. (51), and the bending moment M is obtained using Eq. (52).

$$ \rho =\frac{1}{2}\times \left(u+\frac{L^2}{u}\right) $$
(51)
$$ M={F}_P\times u+F\cos \theta \times L $$
(52)
Fig. 2
figure 2

Sketch map of the free bending process

Full size image

3.1.2 Finite element simulation model

The simulation of pipe springback was conducted in ABAQUS. The aluminium alloy pipe 6061 with a diameter of 30 mm, and wall thickness of 2.0 mm was chosen. The constitutive model has been provided in Section 2.1. The tensile specimen is prepared along the axial and circumferential direction of the pipe, and the tensile test is conducted using a universal testing machine, as shown in Fig. 3. The basic mechanical properties are obtained, and they are applied for the parameter characterisation of the constitutive model. Furthermore, the free bending simulation is conducted to better understand the formation process. The model parameters of aluminium alloy pipe 6061 are shown in Table 1, and the experimental and simulation results are shown in Fig. 4.

Fig. 3
figure 3

Experiment setups: a axial tensile test, b ring hoop tension test, and c press bending test

Full size image
Table 1 Model parameters of aluminium alloy pipe 6061
Full size table
Fig. 4
figure 4

Experimental and simulation results: a axial tension, b ring hoop tension, and c press bending

Full size image

Through the comparison of simulation and experimental results, a good agreement can be found. Of note, the ring hoop tension strain is difficult to be measured, and its force–displacement curves are compared. Furthermore, the validity of the model was confirmed through comparison. Thus, the free bending process simulation was conducted with the model parameters given in Table 1.

The geometrical model of the free bending process consists of the pipe, pusher, fixed, and mobile dies, as shown in Fig. 5. The pipe is defined as deformable shell (S4R), and other parts are set as rigid shell type. The minimum mesh size is 1 mm.

Fig. 5
figure 5

Geometrical models of free bending processes

Full size image

Considering the realistic condition in the free bending process, the bending process is conducted before springback. Thus, the entire pipe formation process is divided into two projects, bending, and springback. For the bending project, two steps are established. The movement and rotary angle are calculated using Eq. (53), which is set in the first step. u and θ are the moving distance and rotation angle of the mobile die, respectively. ρ is the bending radius, and L is the distance between the fixed die and the mobile die. Then, in the second step, the mobile die is constrained in all freedom degrees, and the pipe is pushed to realise pipe bending. The fixed die is constrained in all freedom degrees in both steps. For springback project, a step is established. The ‘INP’ file is input in the project, and the final state of the pipe in the bending process is set as the initial state in the predefined field module. The mobile and fixed dies are removed, and the end of the pipe is constrained in all freedom degrees.

$$ \left\{\begin{array}{c}u=\rho -\sqrt{\rho^2-{L}^2}\\ {}\theta =\arcsin \frac{L}{\rho}\end{array}\right. $$
(53)

3.2 Influence of process parameters on pipe springback

To investigate the influence of process parameters on pipe springback, for the AL6061 pipe (diameter r is 30.0 mm, thickness t0 is 2.0 mm, bending radius ρ is 150.0 mm, bending angle θ is 120°), the simulation of the three process parameters (friction, clearance, mobile die section shape) is conducted, and the simulation results are analysed in this section.

On the symmetrical surface of the pipe, four nodes are chosen at the beginning and the end of the arc part. These nodes constitute vector \( \overrightarrow{ab} \) and vector \( \overrightarrow{cd} \) as shown in Fig. 6. The spatial angle between two vectors is considered as the bending angle of the pipe. The coordinate of the node can be obtained in the ‘INP’ file of the results in ABAQUS. The same nodes are chosen and calculated after springback, and the difference of the two angles is regarded as the springback angle.

Fig. 6
figure 6

Measurement of the springback angle

Full size image

3.2.1 Influence of friction on pipe springback

Friction exists between the mobile die and the pipe in the free bending process, which has significant influences on material flow. To study the influence of friction on pipe springback, five values of friction coefficient (0, 0.02, 0.04, 0.06, 0.08) are selected. The bending angle before and after springback is shown in Fig. 7.

Fig. 7
figure 7

Bending and springback angle with different friction coefficients

Full size image

The springback angle of the pipe ranges from 2.20 to 2.36°, which shows that friction has little influence on the springback in the free bending process, as shown in Fig. 7. When the friction coefficient is 0.04, the springback angle is the smallest, and pipe formation is most precise. However, the difference between the maximum and minimum springback angles is 0.16∘, which can be ignored.

3.3 Influence of clearance on pipe springback

Clearance exists between the mobile die and the pipe in the free bending process. To study the influence of clearance on pipe springback, five clearance values (0.1, 0.2, 0.3, 0.4, 0.5 mm) are selected. The bending and springback angles show different clearance values, as shown in Fig. 8.

Fig. 8
figure 8

Bending and springback angles with different clearance values

Full size image

The springback angle of the pipe ranges from 2.27 to 2.50° which shows that clearance has little influence on springback in the free bending process, as shown in Fig. 8. When the clearance is 0.2 mm, the springback angle is the smallest, and pipe formation is most precise. However, the difference between the maximum and minimum springback angles is 0.13∘, which can be ignored.

3.3.1 Influence of mobile die section shape on pipe springback

The shape of the section will directly affect the deformation behaviour of the pipe. Line contact between the mobile die and the pipe is applied in the free bending process. Thus, the section shape of the mobile die has significant influences on pipe formation. The parabolic section shape of the mobile die is selected in this paper, as shown in Fig. 9, where a is the section shape coefficient of the mobile die. To study the influence of mobile die section shape on pipe springback, five coefficient values (0.02, 0.04, 0.06, 0.08, 0.1) are selected, as shown in Fig. 9.

Fig. 9
figure 9

Section shape of mobile die

Full size image

The springback angle of the pipe ranges from 1.65 to 2.31°, which shows that the section shape of the mobile die has little influence on springback in the free bending process, as shown in Fig. 10. When the coefficient is 0.02, the springback angle is the smallest, and pipe formation is most precise. However, the difference between the maximum and minimum springback angles is 0.66∘, which can also be ignored.

Fig. 10
figure 10

Bending and springback angles with different section shapes

Full size image

4 Comparison between analytical and simulation results

In this section, the AL6061 pipe is selected as the research object to predict the springback angle based on the analytic model in Section 2.2. Furthermore, comparison between the analytical and simulation results is conducted to validate the accuracy of the analytic model.

4.1 Springback prediction of AL6061 pipe

Through the model assumption, the friction is ignored. Thus, the prediction springback angle of the pipe is calculated in the frictionless condition. The material property of AL6061 is shown in Table 2. According to Zhan et al. [17], the stable elastic modulus Ea for an infinitely large equivalent strain can be calculated by using the curve fitting algorithm. The initial thickness t0 and section radius r of the pipe are 2.0 mm and 13.0 mm, respectively. The springback of different bending angles with bending radius ρ = 150  mm and different bending radii with bending angle θ = 90° is analysed based on springback in Section 2.3, and the material parameters are shown in Table 2. The springback angle is calculated by MATLAB, and the calculation results are shown in Tables 3 and 4.

Table 2 Material parameters of AL6061
Full size table
Table 3 Springback angle of different bending angles
Full size table
Table 4 Springback angle of different bending radii
Full size table

4.2 Evaluation of the theoretical results

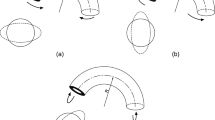
Through the FE simulation results, the neutral layer offset has a tendency to move towards the material compressed direction for rotary bending process, which is validated by E et al. [23] and FE simulation results (shown in Fig. 11a). However, the neutral layer offset has a tendency to move towards the material tensile direction for the free bending process (shown in Fig. 11b), which is beneficial to reduce the thinning ratio of the outer pipe wall thickness. This is because there is an axial force that acts on the pipe in the free bending process. Considering the effect of the axial force, the neutral layer offset is corrected by using Eqs. (28)–(33). To evaluate the validity of the model, the analysis, optimisation, and simulation results are compared with different bending conditions, as shown in Fig. 12. As shown in the figure, the variation tendency of the calculation results of the springback angle is in accordance with the simulation results. Obviously, the optimisation results considering axial force are closer to the simulation results, which can fully certify the accuracy of the springback prediction model in this study.

Fig. 11
figure 11

Neutral layer offset: a free bending process, b rotary bending process

Full size image
Fig. 12
figure 12

Springback angle with different bending conditions: a Springback angle of different bending angles, b springback angle of different bending radii

Full size image

5 Conclusions

This study investigated the springback of the pipe free bending process based on FEM and analytic methods. The influence of three process parameters (friction, clearance, and mobile die section shape) on the springback of pipe free bending was investigated and analysed. In particular, the neutral layer offset in the free bending process has its unique characteristics compared with the traditional pipe bending process. The conclusions are summarised as follows:

  1. (1)

    In the stress and strain analysis of springback in the free bending process, the distribution of stress and strain can be observed precisely based on the FEM, which provides a guiding significance for understanding the plastic deformation mechanism of pipe free bending.

  2. (2)

    In terms of the springback in the pipe free bending process, for the AL6061 pipe, the springback angle is predicted based on FEM and analytic methods. The process parameters (e.g. friction, clearance between mobile die and pipe, section shape of the mobile die) have a negligible influence on pipe springback. Comparatively, the minimum springback value was obtained when the friction coefficient was 0.04, the clearance was 0.2 mm, and the shape coefficient of the mobile die was 0.02. In terms of influence, the effects of clearance, friction, and section shape of the bend die decrease in turn.

  3. (3)

    The neutral layer offset has a tendency to move towards the material tensile direction in the free bending process, which is opposite to that in the rotary bending process.

  4. (4)

    Through the FEM simulation result, the analytical model for pipe free bending springback prediction is optimised by the addition of the neutral layer offset variable. The optimised analytical model has an appreciable guiding significance for the prediction of pipe free bending process.