1 Introduction

Due to their high efficiency and high torque density, permanent magnet synchronous motors (PMSM) have been widely used in various applications such as electric automobile, high-speed machine tool, and centrifugal compressor [1, 2]. Position sensors (such as encoders and resolvers) are typically used to obtain the real-time position information of rotor to control the PMSM. At the same time, the application of position sensors will result in higher system cost and larger volume, as well as related reliability problem. Therefore, different sensorless control methods of PMSM have been presented and studied for decades [3].

Recently, there are mainly two sensorless control methods for PMSM. One is to estimate the rotational speed of rotor through the back electromotive force (EMF), which is generally used for medium-speed and high-speed motors. The other is to estimate the rotor position by detecting the salient poles of motor rotor, which is generally used for stationary state or low speed. For the former, the methods generally include extended Kalman filtering (EKF) [4,5,6], model reference adaptive method (MRA) [7,8,9], sliding mode observer (SMO) [10, 11], and their improved methods. For the later, there are rotating high-frequency voltage injection method [12,13,14,15,16], pulse voltage injection method [17,18,19], and carrier frequency component method [20]. In addition, the robust controller design [21], saturated PID control [22], and the comparison between innovation method and existing methods [23] are all helpful for the sensorless control design of PMSM.

From the recent researches, it can be seen that when the motor runs above a certain speed, it is easy to detect its position, but it is difficult to estimate the position when starting at zero or low speed [24]. If the initial rotor position is unknown, the motor starting torque may be insufficient, or the rotor may even rotate reversely when starting. It is necessary to detect the initial position of the rotor before starting the motor, especially for the motor basing on vector control technique. Therefore, in many applications of sensorless control, the initial rotor position needs to be estimated before the motor is started.

Nowadays, the initial rotor position estimation method of PMSM has been investigated in many papers, and the related methods can be mainly summarized as follows:

  1. 1.

    The virtual high-frequency (HF) voltage pulsating injection method [24].

  2. 2.

    Multi-signal injection method [25].

  3. 3.

    Voltage vector injection method [18, 19].

  4. 4.

    Carrier signal injection method using zero-sequence voltage [16, 26].

    The above methods have estimated the initial position of rotor accurately, and these methods need complex calculation and a long estimation time. In this paper, a new estimation method of initial rotor position of SPMSM is presented based on voltage vector injection. Different from the traditional voltage vector injection method, which injects the voltage vector into the forward and backward positions of rotor, the proposed method injects the voltage vector into the A, B, and C phase axes of the motor stator. Then, the arcsine function of the response current of virtual q-axis corresponding to the three voltage vectors is solved out, and the average value of calculation results will be equal to the estimated initial position of the rotor, which is expressed as Δθ. Finally, two voltage vectors are injected into the estimated rotor position angle, Δθ and Δθ + π, respectively, and the polarity of the rotor N-pole will be determined by comparing the response currents of virtual d-axis at the initial position. At the end of this paper, the proposed method is verified by experimental test. As this method has the advantages such as not requiring a low-pass filter, reducing complexity of the system, and quickly estimating the initial rotor position, it has a great application prospect in the sensorless position estimation of SPMSM rotor.

2 Traditional rotor position estimation method based on voltage vector injection

The voltage equations of the PMSM in the dq-axis synchronous reference frame can be expressed as follows [12]:

$$ \Big\{{\displaystyle \begin{array}{l}{v}_{\mathrm{d}}=R{i}_{\mathrm{d}}+{L}_{\mathrm{d}}\frac{d}{dt}{i}_{\mathrm{d}}-{\omega}_{\mathrm{r}}{L}_{\mathrm{q}}{i}_{\mathrm{q}}\\ {}{v}_{\mathrm{q}}=R{i}_{\mathrm{q}}+{L}_{\mathrm{q}}\frac{d}{dt}{i}_{\mathrm{q}}-{\omega}_{\mathrm{r}}{L}_{\mathrm{d}}{i}_{\mathrm{d}}+{\omega}_{\mathrm{r}}{\varphi}_{\mathrm{m}}\end{array}} $$
(1)

where vd, vq, id, and iq are the stator voltages and currents of d-axis and q-axis, respectively, Ld and Lq are the inductances of d-axis and q-axis, R is the stator resistance, ωr is the rotor speed, and φm is the flux linkage of rotor permanent magnet.

The dq-axis synchronous reference frame can be transformed to αβ-axis stationary reference frame by anti-Park transformation, and Eq. (1) may be written as

$$ \left[\begin{array}{l}{v}_{\upalpha}\\ {}{v}_{\upbeta}\end{array}\right]=R\left[\begin{array}{l}{i}_{\upalpha}\\ {}{i}_{\upbeta}\end{array}\right]+\frac{d}{dt}{L}_{\mathrm{M}}\left[\begin{array}{l}{i}_{\upalpha}\\ {}{i}_{\upbeta}\end{array}\right]+\frac{d}{dt}{L}_{\mathrm{D}}\left[\begin{array}{cc}\cos 2{\theta}_{\mathrm{r}}& \sin 2{\theta}_{\mathrm{r}}\\ {}\sin 2{\theta}_{\mathrm{r}}& -\cos 2{\theta}_{\mathrm{r}}\end{array}\right]\left[\begin{array}{l}{i}_{\upalpha}\\ {}{i}_{\upbeta}\end{array}\right]+{\omega}_{\mathrm{e}}{\varphi}_{\mathrm{f}}\left[\begin{array}{l}-\sin {\theta}_{\mathrm{e}}\\ {}\cos {\theta}_{\mathrm{e}}\end{array}\right] $$
(2)
$$ {L}_{\mathrm{M}}=\frac{L_{\mathrm{d}}+{L}_{\mathrm{q}}}{2} $$
(3)
$$ {L}_{\mathrm{D}}=\frac{L_{\mathrm{d}}-{L}_{\mathrm{q}}}{2} $$
(4)

where subscripts α and β represent parameters in the αβ-axis stationary reference frame, LM is the average value of stator inductance, and LD is the difference of inductance between d-axis and q-axis.

When using the vector representation, Eq. (2) can be expressed as [18]:

$$ {\overline{v}}_{\upalpha \upbeta}=R{\overline{i}}_{\upalpha \upbeta}+\left({L}_{\mathrm{M}}\frac{d}{dt}{\overline{i}}_{\upalpha \upbeta}+{L}_{\mathrm{D}}\frac{d}{dt}{\overline{i}}_{\upalpha \upbeta}^{\ast }{e}^{j2{\theta}_{\mathrm{r}}}\right)+j2{\omega}_{\mathrm{r}}{L}_{\mathrm{D}}{\overline{i}}_{\upalpha \upbeta}^{\ast }{e}^{j2{\theta}_{\mathrm{r}}}+j{\omega}_{\mathrm{r}}{\varphi}_{\mathrm{m}}{e}^{j{\theta}_{\mathrm{r}}} $$
(5)

where \( {\overline{v}}_{\upalpha \upbeta} \) and \( {\overline{i}}_{\upalpha \upbeta} \) are the voltage and current vectors, \( {{\overline{i}}^{\ast}}_{\upalpha \upbeta} \) is the conjugate vector of \( {\overline{i}}_{\upalpha \upbeta} \), and θr is the rotor position angle.

When the PMSM is at standstill, the rotor speed equals zero, and the last two items in Eq. (5) associated with ωr may be eliminated. If an injection voltage \( {\overline{v}}_{\upalpha \upbeta}=R{\overline{i}}_{\upalpha \upbeta} \) is selected, the item \( R{\overline{i}}_{\upalpha \upbeta} \) also can be neglected, and Eq. (5) can be simplified as:

$$ {\overline{v}}_{\upalpha \upbeta}={L}_{\mathrm{M}}\frac{d}{dt}{\overline{i}}_{\upalpha \upbeta}+{L}_{\mathrm{D}}\frac{d}{dt}{\overline{i}}_{\upalpha \upbeta}^{\ast }{e}^{j2{\theta}_{\mathrm{r}}} $$
(6)

So the current vector in Eq. (6) can be expressed as

$$ \frac{d}{dt}{\overline{i}}_{\upalpha \upbeta}=\frac{1}{L_{\mathrm{M}}^2+{L}_{\mathrm{D}}^2}\left({L}_{\mathrm{M}}{\overline{v}}_{\upalpha \upbeta}-{L}_{\mathrm{D}}{\overline{v}}_{\upalpha \upbeta}^{\ast }{e}^{j2\theta}\right) $$
(7)

From Eq. (7), it can be seen that the part in the equation related to the rotor position will be eliminated for the non salient pole PMSM (Ld = Lq). So this method of voltage vector injection is suitable for salient pole PMSM, but not for non salient pole PMSM. In one switching period, the differential current di/dt in Eq. (7) may be approximated by Δi/Δt, which means that Eq. (7) can be expressed as:

$$ \varDelta {\overline{i}}_{\upalpha \upbeta}=\left({c}_1+{c}_2{e}^{j2\left({\theta}_{\mathrm{r}}-{\theta}_{\mathrm{u}}\right)}\right)\varDelta t{\overline{v}}_{\upalpha \upbeta} $$
(8)

where \( {c}_1=\frac{L_1}{\left({L}_{\mathrm{M}}^2-{L}_{\mathrm{D}}^2\right)} \),\( {c}_2=\frac{-{L}_2}{\left({L}_{\mathrm{M}}^2-{L}_{\mathrm{D}}^2\right)} \), θu is the angle of the voltage vector in the αβ reference frame.

By multiplying \( {e}^{-j{\theta}_{\mathrm{r}}} \) on both sides of Eq. (8), the following equation can be derived that

$$ \varDelta {\overline{i}}_{\hat{\mathrm{d}}\hat{\mathrm{q}}}=\varDelta {\overline{i}}_{\upalpha \upbeta}{e}^{-j{\hat{\theta}}_{\mathrm{r}}}=\left({c}_1+{c}_2{e}^{j2\left({\theta}_{\mathrm{r}}-{\hat{\theta}}_{\mathrm{r}}-{\theta}_{\mathrm{u}}\right)}\varDelta t{\overline{v}}_{\hat{\mathrm{d}}\hat{\mathrm{q}}}\right) $$
(9)

Figure 1 shows the diagram of the proposed injection voltage vector and actual voltage vector, in which the proposed injection method for position estimation injects two opposite voltage vectors on the estimated \( \hat{q} \)-axes. For example, in the first injection period, the voltage vector (vmejπ/2) is injected on the positive direction of \( \hat{q} \)-axis. Then, the second voltage vector (vme−jπ/2) on the negative direction of \( \hat{q} \)-axis is injected consequently in the following switching period. Assuming that various voltage errors \( \varDelta \overline{v} \) will not change during these two switching periods, the actual two voltage vectors injected to the PMSM may be expressed as:

$$ {\overline{v}}_{\hat{d}\hat{q}1}={v}_{\mathrm{m}}{e}^{j{\hat{\theta}}_{u1}}\approx {v}_{\mathrm{m}}{e}^{j\pi /2}-\varDelta \overline{v} $$
(10)
$$ {\overline{v}}_{\hat{d}\hat{q}2}={v}_{\mathrm{m}}{e}^{j{\hat{\theta}}_{u2}}\approx {v}_{\mathrm{m}}{e}^{- j\pi /2}-\varDelta \overline{v} $$
(11)
Fig. 1
figure 1

Real and estimated rotor coordinate system

Full size image

According to Eq. (9), the observed variations of resultant currents in the estimated d^q^ reference frame may be expressed as:

$$ \varDelta {\overline{i}}_{\hat{d}\hat{q}1}=\varDelta t{c}_1\left({v}_{\mathrm{m}}{e}^{j\pi /2}-\varDelta \overline{v}\right)+\varDelta t{c}_2{e}^{j2{\hat{\theta}}_{\mathrm{r}}}\ast {e}^{-j{\hat{\theta}}_{\mathrm{u}1}} $$
(12)
$$ \varDelta {\overline{i}}_{\hat{d}\hat{q}2}=\varDelta t{c}_1\left({v}_{\mathrm{m}}{e}^{- j\pi /2}-\varDelta \overline{v}\right)+\varDelta t{c}_2{e}^{j2{\hat{\theta}}_{\mathrm{r}}}\ast {e}^{-j{\hat{\theta}}_{\mathrm{u}1}} $$
(13)

As the angle Δθu1 is very close to zero, the real part of resultant current variation is obtained as follows [19].

$$ \operatorname{Re}\left(\varDelta {\overline{i}}_{\hat{d}\hat{q}1}-\varDelta {\overline{i}}_{\hat{d}\hat{q}2}\right)=2k\sin \left(2{\overset{\sim }{\theta}}_{\mathrm{r}}\right)\approx 4k{\tilde{\theta}}_{\mathrm{r}} $$
(14)

Similarly, two voltage vectors in opposite directions will be injected to the \( \hat{d} \)-axis, that is, one along the positive direction of \( \hat{d} \)-axis (vmej0) and another along the negative direction of \( \hat{d} \)-axis (vmejπ). By following the same calculation process described previously, the imaginary part of resultant current variation also can be obtained [19].

$$ \operatorname{Im}\left(\varDelta {\overline{i}}_{\hat{d}\hat{q}1}-\varDelta {\overline{i}}_{\hat{d}\hat{q}2}\right)=2k\sin \left(2{\overset{\sim }{\theta}}_{\mathrm{r}}\right)\approx 4k{\tilde{\theta}}_{\mathrm{r}} $$
(15)

3 Nonlinear saturated salient characteristics of SPMSM

It can be seen from the above principle analysis that the magnetic saturation effect of motor is one of the necessary conditions for the injection of the voltage vector. For SPMSM, it is generally considered that its dq-axis inductance is identical, that is, Ld = Lq. Actually, in the motor design, in order to improve the utilization of the equipment, the d-axis magnetic circuit of the PMSM is usually designed to be saturated as shown in Fig. 2 (Point A). It can be seen from Fig. 2 that magnetic field will be generated when a current is applied to the motor in the same direction as d-axis, and the magnetic flux change caused by current change is nonlinear due to the magnetic saturation effect. The magnetic flux of q-axis of the motor is not saturated and is not affected by the saturation salient effect. According to Eq. (16), the inductance L is the slope of the Ψ-i curve. Therefore, when the motor is energized to generate a magnetic flux in the same direction as the d-axis, a saturated salient effect occurs by the right side of point A, as shown in Fig. 2, which means Ld < Lq.

$$ L=\frac{d\varPsi}{d i} $$
(16)
Fig. 2
figure 2

Ψ-i characteristic curve of d-axis magnetic circuit of SPMSM

Full size image

4 4. Principle of the proposed voltage vector injection method

4.1 Principle of virtual voltage vector injection

The virtual d*q* reference frame is established by taking the injection direction of the voltage vector as the d*-axis. The angle between d*-axis and A phase axis of the stator winding is θ, and the angle between the d*-axis and d-axis of the rotor is Δθ, as shown in Fig. 3.

Fig. 3
figure 3

Relationship between different coordinate systems

Full size image

The voltage vectors injected into the virtual d∗q∗*-axis are expressed as:

$$ \Big\{{\displaystyle \begin{array}{l}{u}_{\mathrm{d}\ast }=U\\ {}{u}_{\mathrm{q}\ast }=0\end{array}} $$
(17)

where the superscript “*” represents the virtual reference frame.

So the voltage vectors on the actual dq-axis can be obtained as:

$$ \Big\{{\displaystyle \begin{array}{l}{u}_{\mathrm{d}}={u}_{\mathrm{d}\ast}\cos \varDelta \theta +{u}_{q\ast}\sin \varDelta \theta \\ {}{u}_{\mathrm{q}}={u}_{\mathrm{q}\ast}\cos \varDelta \theta -{u}_{\mathrm{d}\ast}\sin \varDelta \theta \end{array}} $$
(18)

Figure 4 shows the equivalent circuit diagram of SPMSM in dq and virtual d*q* reference frame, where Rd, Rq, Rd∗, and Rq∗ are the equivalent resistances and Ld, Lq, Ld∗, and Lq∗ are the equivalent inductances, respectively.

Fig. 4
figure 4

Equivalent circuit diagram of SPMSM. (a) Equivalent circuit diagram of SPMSM in d-axis; (b) equivalent circuit diagram of SPMSM in q-axis; (c) equivalent circuit diagram of SPMSM in d*-axis; (d) equivalent circuit diagram of SPMSM in q*-axis

Full size image

The resistance and inductance of SPMSM are identical in d- and q-axes, which means \( {R}_{\mathrm{d}}={R}_{\mathrm{q}}={R}_{{\mathrm{d}}^{\ast }}={R}_{{\mathrm{q}}^{\ast }}=R \), \( {L}_{\mathrm{q}}={L}_{{\mathrm{q}}^{\ast }}=L \). At the same time, as the proposed method is used to estimate the initial rotor position of the motor at standstill (ω = 0), and the mutual inductance effect of the motor circuit is ignored, the dq-axis equivalent circuits of SPMSM can be simplified as RL circuits, as shown in Fig. 5.

Fig. 5
figure 5

Simplified SPMSM equivalent circuit diagram. (a) Simplified circuit diagram of SPMSM in d-axis; (b) simplified circuit diagram of SPMSM in q-axis; (c) simplified circuit diagram of SPMSM in d*-axis; (d) simplified circuit diagram of SPMSM in q*-axis

Full size image

The voltage vector injection schematic is shown in Fig. 6, and the virtual q*-axis current is generated after voltage vector injection. As shown in Fig. 6(a), the injected voltage vector U can be decomposed into ud and uq in the dq synchronous reference frame, and id and iq are the response currents corresponding to ud and uq respectively. Because of the saturated salient effect, the response currents id and iq will vary in different proportions, as shown in Fig. 6(b). Figure 6(c) shows that the response current vector i is composed of id and iq, where current vector i can be decomposed into id* and iq* in virtual d*q* coordinate frame. This is the generation principle of response current in virtual d*- and q*-axes.

Fig. 6
figure 6

The voltage vector injection schematic

Full size image

Substituting Eq. (17) into Eq. (18), the following equation can be obtained as:

$$ \Big\{{\displaystyle \begin{array}{l}{u}_{\mathrm{d}}=U\cos \varDelta \theta \\ {}{u}_{\mathrm{q}}=-U\sin \varDelta \theta \end{array}} $$
(19)

According to the response current principle of RL circuit, the response current of the dq-axis after the voltage vector injection can be expressed as:

$$ \Big\{{\displaystyle \begin{array}{l}{i}_{\mathrm{d}}=\frac{u_{\mathrm{d}}}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\\ {}{i}_{\mathrm{q}}=\frac{u_{\mathrm{q}}}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{q}}}}\right)\end{array}} $$
(20)

The response currents of the virtual d*q* reference frame will be obtained.

$$ \Big\{{\displaystyle \begin{array}{l}{i}_{d\ast }={i}_{\mathrm{d}}\cos \varDelta \theta -{i}_{\mathrm{q}}\sin \varDelta \theta =\frac{U\cos \varDelta \theta}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\cos \varDelta \theta +\frac{U\sin \varDelta \theta}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{q}}}}\right)\sin \varDelta \theta \\ {}{i}_{q\ast }={i}_{\mathrm{d}}\sin \varDelta \theta +{i}_{\mathrm{q}}\cos \varDelta \theta =\frac{U\cos \varDelta \theta}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \varDelta \theta -\frac{U\sin \varDelta \theta}{R}\left(1-{e}^{\frac{- Rt}{L_{\mathrm{q}}}}\right)\cos \varDelta \theta \end{array}} $$
(21)

According to Eq. (21), the response current iq∗ of virtual q*-axis can be simplified as:

$$ {i}_{\mathrm{q}\ast }=\frac{U}{R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \varDelta \theta \cos \varDelta \theta =\frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \left(2\ast \varDelta \theta \right) $$
(22)

4.2 Response current after ABC three-phase voltage vector injection

Assuming that the angle between the injected voltage vector and the d-axis is less than π/2, so the component of the voltage vector in the d-axis will produce salient pole effect of saturation circuit, which results in Ld < Lq. And the following inequality is true.

$$ \frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)>0 $$
(23)

After the voltage vector injection of ABC three-phase axes, the corresponding response currents are obtained as follows:

$$ \Big\{{\displaystyle \begin{array}{l}{i}_{\mathrm{q}\mathrm{A}\ast }=\frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \left(2\ast \varDelta \theta \right)\\ {}{i}_{\mathrm{q}\mathrm{B}\ast }=\frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \left(2\ast \left(\varDelta \theta -120{}^{\circ}\right)\right)\\ {}{i}_{\mathrm{q}\mathrm{C}\ast }=\frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right)\sin \left(2\ast \left(\varDelta \theta +120{}^{\circ}\right)\right)\end{array}} $$
(24)

In order to obtain the rotor position angle Δθ by using iqA∗, iqB∗, and iqC∗ Eq. (24) can be simplified as:

$$ \Big\{{\displaystyle \begin{array}{l}{i}_{\mathrm{qA}\ast }=k\sin \left(2\ast \varDelta \theta \right)\\ {}{i}_{\mathrm{qB}\ast }=k\sin \left(2\ast \left(\varDelta \theta -120{}^{\circ}\right)\right)\\ {}{i}_{\mathrm{qC}\ast }=k\sin \left(2\ast \left(\varDelta \theta +120{}^{\circ}\right)\right)\end{array}} $$
(25)

where \( k=\frac{U}{2R}\left({e}^{\frac{- Rt}{L_{\mathrm{q}}}}-{e}^{\frac{- Rt}{L_{\mathrm{d}}}}\right) \).

According to Eq. (25), the rotor position angle under different response currents are expressed as:

$$ \Big\{{\displaystyle \begin{array}{l}\varDelta {\theta}_{\mathrm{A}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qA}\ast }}{k}\\ {}\varDelta {\theta}_{\mathrm{B}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qB}\ast }}{k}+120{}^{\circ}\\ {}\varDelta {\theta}_{\mathrm{C}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qC}\ast }}{k}+60{}^{\circ}\end{array}} $$
(26)

where ΔθA, ΔθB, and ΔθC are the calculated rotor position angles according to the A, B, and C phase response currents, respectively.

The average value of the obtained three position angles will be equal to the estimated initial position angle of the rotor, which is expressed as:

$$ \varDelta \theta =\frac{\varDelta {\theta}_{\mathrm{A}}+\varDelta {\theta}_{\mathrm{B}}+\varDelta {\theta}_{\mathrm{C}}}{3} $$
(27)

4.3 Rotor polarity identification

By analyzing Eqs. (26) and (27), the rotor position angle obtained by the first three voltage vector injections is between 0 and π, and it is necessary to determine the polarity of the rotor N-pole. Here, the voltage vector injection method is adopted, and by using the magnetic saturation phenomenon of the N-pole (the positive direction of the d-axis) of the SPMSM rotor, two voltage vectors are injected into the estimated rotor position angles corresponding to Δθ and Δθ + π, respectively. By comparing the virtual d*-axis response current after the injection of two voltage vectors, the polarity of the rotor N-pole can be determined.

4.4 Selection of injection period and sample point

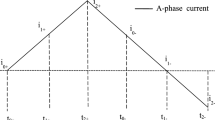
Figure 7 shows the injection period and sampling points of the proposed method. It can be seen that the proposed method in this paper injects five voltage vectors, the first voltage vector is injected into the A phase axis of motor stator, the second voltage vector is injected into B phase axis, and the third voltage vector is injected into C phase axis. Through the former three voltage vector injections, the corresponding response currents of virtual q*-axis are obtained, and the rotor position angles are estimated by solving the arcsine of response current. The fourth and fifth voltage vectors are injected in the estimated rotor position angle and its opposite direction angle, and the polarity of the rotor N-pole is determined.

Fig. 7
figure 7

Injection period and sampling points of the proposed method

Full size image

5 Experiment and analysis

An experimental test system based on the proposed voltage vector injection method is designed, as shown in Fig. 8. The test system consists of two identical permanent magnet synchronous motors, which are connected through a coupling. In the experiment, the test motor is used for voltage vector injection, and the load motor is used to control the rotor position of the test motor. In addition, the DSP controller (TMS320F28335) is selected to control and estimate the rotor position of test motor, and a three-phase inverter composed of three IGBT half bridges is chosen to drive the test motor. Computer 1 and the oscilloscope are used to obtain the motor three-phase current and calculate the dq axes current. Computer 2 is used to control the rotation of the load motor by a servo driver.

Fig. 8
figure 8

Experimental system

Full size image

The parameters of experimental motor are shown in Table 1. In the process of rotor position estimation, the value of injection voltage vector is 6.5 V, the PWM frequency of the inverter is 10 kHz, and one injection period is 8 ms, which is about equal to 80 times in PWM period. And the sampling point is selected at the midpoint of the 50th PWM period.

Table 1 Motor parameters
Full size table

5.1 Normalization of virtual q-axis current

According to Eq. (26), the arcsine function of the virtual q*-axis is solved to estimate the rotor position angle, but the coefficient k is a time-varying parameter and is difficult to get the accurate value. Therefore, the normalization of virtual q*-axis current is adopted before solving the arcsine function. The normalization equation may be expressed as follows.

$$ \Big\{{\displaystyle \begin{array}{l}\frac{i_{\mathrm{qA}\ast }}{k}\approx \frac{i_{\mathrm{qA}\ast }}{i_{\mathrm{qA}\mathrm{max}\ast }}\\ {}\frac{i_{\mathrm{qB}\ast }}{k}\approx \frac{i_{\mathrm{qB}\ast }}{i_{\mathrm{qB}\mathrm{max}\ast }}\\ {}\frac{i_{\mathrm{qC}\ast }}{k}\approx \frac{i_{\mathrm{qC}\ast }}{i_{\mathrm{qC}\mathrm{max}\ast }}\end{array}} $$
(28)

Then Eq. (26) can be expressed as:

$$ \Big\{{\displaystyle \begin{array}{l}\varDelta {\theta}_{\mathrm{A}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qA}\ast }}{i_{\mathrm{qA}\mathrm{max}\ast }}\\ {}\varDelta {\theta}_{\mathrm{B}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qB}\ast }}{i_{\mathrm{qB}\mathrm{max}\ast }}+120{}^{\circ}\\ {}\varDelta {\theta}_{\mathrm{C}}=\frac{1}{2}\arcsin \frac{i_{\mathrm{qC}\ast }}{i_{\mathrm{qC}\mathrm{max}\ast }}+60{}^{\circ}\end{array}} $$
(29)

For the voltage vector injection method proposed in this paper, Eq. (29) can be used to estimate the rotor position angle in the experimental test.

When the motor rotor is at different positions, the response currents of the virtual q*-axis are obtained by injecting voltage vectors into the three axes of A, B, and C, respectively, as shown in Fig. 9. It can be seen that the virtual q*-axis response currents of the three axes A, B, and C are sinusoidal wave of different phases, which verifies the correctness of Eq. (25). The maximum virtual q*-axis current of different phase axes, namely iqAmax∗, iqBmax∗, and iqCmax∗, are taken as current normalization parameters and obtained from sinusoidal wave of Fig. 9, which are shown in Table 2.

Fig. 9
figure 9

Virtual q-axis response current after ABC injection at different rotor positions

Full size image
Table 2 Normalized parameters of virtual q-axis current of experimental motor
Full size table

5.2 Initial rotor position estimation using the proposed voltage vector injection

In order to accurately estimate the rotor position, total 25 rotor position angles are chosen in the estimation and experiment. The purpose of choosing different rotor position angles is to illustrate the correctness of the estimated initial rotor position by the virtual voltage vector injection method. The 25 rotor position angles are from 0° to 360°, and the adjacent angle interval is 15°. In fact, as the virtual voltage vector injection method is based on the salient pole effect of PM rotor, there are four special angles of 0°, 90°, 180°, and 270°, which correspond to response current zero of q*-axis. As the estimation method of these rotor positions are similar, only five rotor positions are shown in the manuscript, which include two special angles (0° and 270°) and three arbitrary angles (45°, 75°, and 135°). So, 0°, 45°, 75°, 135°, and 270° of rotor position are displayed in Figs. 10, 11, 12, 13, and 14.

Fig. 10
figure 10

The response current at initial rotor position with 0°

Full size image
Fig. 11
figure 11

The response current at rotor position with 45°

Full size image
Fig. 12
figure 12

The response current at the 75° position of rotor

Full size image
Fig. 13
figure 13

The response current at the 135o position of rotor

Full size image
Fig. 14
figure 14

The current response when the rotor initial position is 270°

Full size image

The response current at the initial rotor position with 0° is shown in Fig. 10, and it can be seen that the response currents of virtual q*-axis, namely \( {i}_{{\mathrm{qA}}^{\ast }} \), \( {i}_{{\mathrm{qB}}^{\ast }} \), and \( {i}_{{\mathrm{qC}}^{\ast }} \), are 0.00439 A, 0.2157 A, − 0.2321 A at each sample point, respectively. According to Eq. (29), the rotor position angles are calculated to be the following: ΔθA = 0.5574°, ΔθB = 1.1434°, and ΔθC =  − 4.5339°. So, − 0.9444° can be obtained as the initial position angle of the rotor according to Eq. (27). By comparing the obtained values of the virtual d*-axis current between the fourth and fifth injections, it is determined that the estimated electrical angle is − 0.9444o, so the estimated error of electrical angle at the initial position with 0° is − 0.9444°.

The response current at the rotor position with 45° is shown in Fig. 11, it can be seen that \( {i}_{{\mathrm{qA}}^{\ast }} \), \( {i}_{{\mathrm{qB}}^{\ast }} \), and \( {i}_{{\mathrm{qC}}^{\ast }} \) equals 0.22565A, − 0.08439A, and − 0.0832A, respectively. And the calculated position angles are obtained as follows: ΔθA = 45°, ΔθB = 40.5321°, and ΔθC = 50.025°. Therefore, the estimated position angle of the rotor at 45° position is 45.1857°, and the estimated error of electrical angle at this position is −0.1857°.

Similarly, the response current at the 75° position of rotor is shown in Fig. 12, where \( {i}_{{\mathrm{qA}}^{\ast }} \), \( {i}_{{\mathrm{qB}}^{\ast }} \), and \( {i}_{{\mathrm{qC}}^{\ast }} \) equals 0.1358A, − 0.2245A, and 0.15259A, respectively. And the calculated position angles are as follows: ΔθA = 71.5°, ΔθB = 83.51°, and ΔθC = 75.707°. Therefore, the estimated position angle of the rotor with 75° is 76.906°, and the estimated error of electrical angle at this position is −1.906°.

The response current at the 135° position of rotor is shown in Fig. 13, where the response current of virtual q*-axis, \( {i}_{{\mathrm{qA}}^{\ast }} \), \( {i}_{{\mathrm{qB}}^{\ast }} \), and \( {i}_{{\mathrm{qC}}^{\ast }} \) equals − 0.24906A, 0.1411A, and 0.12865A, respectively. And the calculated position angles are as follows: ΔθA = 140.91°, ΔθB = 137.694°, and ΔθC = 136.97°. Therefore, the estimated position angle of the rotor under 135° is 138.525°, and the estimated error of electrical angle at this position is 3.525°.

The response current at the 270° position of rotor is shown in Fig. 14, where \( {i}_{{\mathrm{qA}}^{\ast }} \), \( {i}_{{\mathrm{qB}}^{\ast }} \), and \( {i}_{{\mathrm{qC}}^{\ast }} \) equals − 0.004169A, − 0.21816A, and 0.276A, respectively. And the calculated position angles are obtained as follows: ΔθA = 89.532°, ΔθB = 85.85°, and ΔθC = 95.262°. Therefore, the calculated position angle of the rotor is 90.215°. According to the value of the virtual d*-axis obtained by the fourth and fifth injections, the estimated position angle of the rotor under 270° is 270.215°, and the estimated error of electrical angle at this position is −0.215° .

As shown in Fig. 15, the estimation errors of different rotor position angles are calculated from 0° to 360°, which includes 25 points in all at the interval of 15°. It can be concluded that the maximum value of the estimation error of electrical angle is 3.722°, and the average error of electrical angle is 0.1845°. From Figs. 10, 11, 12, 13, and 14, it can be seen that the proposed method needs only 40 ms to complete the voltage vector injection and rotor position angle estimation.

Fig. 15
figure 15

Estimation errors under different rotor position angles

Full size image

In [17], the most fastest estimating time needs about 20 ms, but the smallest estimated errors are about 4°, 5.5°, and 5.5° for three different PMSM. In [24], the estimation time needs about 80 ms, and the estimated error of position angle is less than 1°. In addition, the method in references [17, 24] needs low-pass filter, which will increase the complexity of control system. So, the proposed method in this paper compromises the estimation time and accuracy. And the experimental results show that the proposed voltage vector injection method is feasible and effective, and has a high accuracy for the initial position estimation of the rotor. The comparisons are shown in Table 3.

Table 3 Comparisons with different methods
Full size table

6 Conclusions

In this paper, a novel method based on voltage vector injection is proposed for the initial rotor position estimation of SPMSM. Different from the traditional estimation method, the proposed estimation method does not need filtering or demodulation to deal with the current signal. The virtual d*q* reference frame is established in the A, B, and C phase axes, and the voltage vector is injected into the virtual d*-axis of the three-phase axes respectively. By solving the arcsine function of response current of the virtual q*-axis, a rotor position angle Δθ can be calculated, which is between 0 and π. Then, two voltage vectors are injected into the contrary position angles (Δθ∆θ and Δθ + π)∆θ + π, and the polarity of rotor N-pole is identified according to the magnitude of the response current, and the estimated rotor position is finally determined. The experimental results show that the maximum value of the estimation error of electrical angle is about 3.722°, and the average error of estimated electrical angle is about 0.1845°, which shows that the proposed voltage vector injection method is feasible and effective, and it has a high accuracy for the initial rotor position estimation of the PMSM.