Design complexity tradeoffs in topology optimization of forced convection laminar flow heat sinks

Abstract

This paper demonstrates that there is much more to gain from topology optimization of heat sinks than what is described by the so-called pseudo 3D models. The utilization of 3D effects, even for microchannel heat sinks is investigated and compared to state-of-the art industrial designs, for a microelectronic application. Furthermore, the use of design restrictions in the optimization framework demonstrates that the performances of microchannel heat sinks are highly dependent on the ability to provide complex refrigerant distribution and intricate flow paths through the heat sink. The topology optimized microchannel heat sinks are exported from a voxel mesh to bodyfitted mesh using Trelis Sculpt and imported into a commercial CFD software. A systematic comparison with the state-of-the art industrial design shows that the temperature elevation of the microelectronic chip can be reduced by up to 70%, using a 3D topology optimized microchannel heat sink. Restricting the design freedom, for example, by limiting the solid features to be unidirectional downgrades the performances of the optimized microchannel heat sinks but still outperforms the reference case, for a similar design complexity.

1 Introduction

The heat exchange in forced convection liquid cooled heat sinks may be increased by the application of topology optimization. However, compared to state-of-the art fin designs, often restrictions due to modeling resolution make it difficult to achieve better thermal performance under similar flow conditions. Furthermore, typical designs are pin-fins or plates which are manufactured very efficiently by skiving which enables wall thickness below 0.2 mm. This feature size is also close to current state of the art in SLM/SLS (Selective Laser Melting/Sintering) 3D printing which make realization of similar scale full freedom topology optimized designs applicable.

However, the design restrictions imposed due to e.g., milling or skiving might hinder secondary flow which has the potential to increase the heat transfer dramatically. This paper investigates the limitations imposed by using restrictive designs such as extruded 2D, e.g., skiving processes or 2.5D designs manufacturable by single direction milling processes where the potential gains from secondary fluid motion are not fully exploited and compare with large-scale full 3D optimized heat sinks. The optimized designs are benchmarked by the use of a commercial CFD software with reference to state-of-the-art cooling profiles from microelectronics where feature sizes/wall thickness approach 0.1 mm.

Topology optimization of fluid flow problems was first presented in the seminal paper considering Stokes flow by Borrvall and Petersson (2003) and later extended to Navier–Stokes flow (Gersborg-Hansen et al. 2005). The fundamental idea was to consider the plane flow between two plates. By locally varying the plate distance, the behavior of solid material was mimicked. This idea was later generalized by using the Brinkman model (Brinkman 1947) for porous flow. The ideas have extended into scalar transport problems in microreactors (Okkels and Bruus 2007) and microfluidic mixing (Andreasen et al. 2009) and naturally also applications to convective heat transfer in Dede (2012) and Yoon (2010) where in addition to a locally varying permeability also the conductive behavior changes between solid and fluid. For a general overview of topology optimization of heat transfer problems, one should consult the review by Dbouk (2017) or the more general review on fluid-based topology optimization (Alexandersen and Andreasen 2020).

As most heat transfer problems vary spatially they are true three dimensional in their nature, and this paper builds on the findings from optimization of 3D natural convection heat sinks (Alexandersen et al. 2016) and forced convection heat exchangers (Høghøj et al. 2020) and is inspired by the works on microchannel heat sinks in e.g., (Sun et al. 2020). However, as evident from these and other works, the synthesis of such full-scale designs by topology optimization is costly and often, especially for forced convection problems, the resolution of the domain is the limiting factor.

As a means to decrease the computational cost and exploit that many heat sinks do not extend much in an out-of-plane direction, the so-called pseudo 3D models have been exploited. They basically utilize upscaling where the out-of-plane flow and thermal profiles are predefined. By this assumption, a high 2D resolution of extruded fin designs can be obtained c.f. (Yan et al. 2019). In Zeng and Lee (2019), such a density-based topology optimization for microchannel heat sinks with fin thickness of 0.3mm is implemented. The optimized heat sinks, with extruded fins, are compared well to their experimental data, validating the approach for high performances heat sinks. The pseudo 3D models are also used for spider-web heat sinks (Han et al. 2021), multipass heat sinks (Li et al. 2021), or pin-fin heat exchangers (Haertel et al. 2018).

Other recent work e.g., Sun et al. (2020) focuses on exploiting the full freedom of 3D topology optimization for compact heat sinks. They showed that optimized designs take full advantage of fluid secondary motion in out-of-plane direction. However, they point out that the results of the optimization framework are very sensitive to the optimization parameters, especially at high pressure. Dilgen et al. (2018) introduced a two-equation turbulence model to enhance turbulent mixing at higher Reynolds number in both 2D and 3D designs. While turbulent designs show better performances at higher Reynolds number, laminar designs still perform well at similar flow rates. A further advantage of staying in the laminar flow regime is a more favorable flow vs pressure drop relation.

Works on experimental realization and testing cf. (Lazarov et al. 2018) show good correspondence between numerical and actual performance. However, for natural convection cooling, feature sizes are generally large to avoid excessive flow restriction due to the direct coupling between fluid flow and heat transfer. For forced convection heat sinks, the relation between thermal performance and feature size is different and intricate structures and thin features are generally improving the performance as smaller channels increase the flow velocity and thereby the heat exchange.

This poses a further challenge as generally topology optimization increases the design complexity and a complicated flow network often appears. Locally there may be very narrow channels which induce local transitions into the turbulent flow regime as flow rate remains constant. Transitions to turbulence are usually avoided in commercial designs as this changes the relation between flow and pressure drop significantly, as well as near-wall heat transfer.

The outline of the paper is that the model problem under consideration is presented in Sect. 2 with the modeling in Sect. 3. The optimization formulation is discussed in Sect. 4 with optimization results in Sect. 5. Section 5 also covers a methodology to post-process the obtained optimized designs in the commercial CFD software ANSYS CFX along with a quantitative comparison of the performance gap. The results are discussed and a conclusion is provided in Sect. 6.

2 Domain

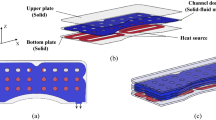
Modern microprocessors require substantial cooling of relatively small areas. The heat flux is on the order of 1–2 MW/m$^2$ and the heat sink typically extends over the entire processor area despite the heat input is mainly localized to the cores. Figure 1 shows a whole heat sink, where the heating cores of the processors are highlighted in orange. However, discretizing such a finely detailed structure with, e.g., 6 elements per fin width and perform topology optimization requires enormous computational resources. To save computational cost, a strip version of the heat sink which only represents a few fins is investigated, and symmetry conditions are applied on both lateral sides. This is an approximation that represents the center-most cores best while heat sink outer regions are not considered.

Figure 1 further shows the domain under investigation which is a microchannel heat sink containing in the reference configuration 5 plate fins for a total dimension of 24 $\times$ 2 $\times$ 4 mm (L $\times$ W $\times$ H) and a fin length of 20 mm. The base plate has a thickness of 1 mm for a fin height of 3 mm. The heat source is located at the center of the heat sink, with a length $L_s$ of 4 mm and a width $W_s$ of 2 mm. The coolant is a single-phase fluid which flows longitudinally inside the heat sink. It has the specificity of having a compact geometry with a high surface-to-volume ratio to increase the heat transfer with the smallest footprint as possible. The optimization is based on a reference geometry composed of a base plate and a succession of straight fins with a fin size and fin gap of 0.2mm.

Fig. 1

3D view of the full reference straight finned heatsink with the solid region in gray and the coolant side in blue while heating areas are orange. Below the strip domain is visualized

The problem is modeled such that the inflow which is in the positive y-direction is represented by a fully developed parabolic profile, while the outlet with zero pressure is modeled on the opposite face. The lateral sides parallel with the fins are modeled with symmetry conditions to mimic that this is only a strip of a larger heat sink. The bottom and top faces are modeled with no-slip conditions and all external faces are thermally isolated except for a localized heat input at the bottom plate and the in- and outlet.

3 Theory/Model

The forced convection heat sink can be modeled as a conjugate heat transfer problem where a mass transfer problem is coupled with a heat transfer problem. The properties of the fluid and solid are considered constant, the fluid flow is considered incompressible and laminar and the heat generated by the viscous dissipation is neglected. It is also assumed that forced convection is the predominant heat transfer phenomena in the fluid which leads to a one-way coupling of the mass and heat problems where the heat transfer is affected by the mass transfer but not opposite.

The governing equations in their non-dimensional form as well as the penalization model used for immersed boundary model are presented in the following. A unified computational domain $\varOmega =\varOmega ^s \cup \varOmega ^f$ is utilized where $\varOmega ^s$ denotes solid and $\varOmega ^f$ fluid. The methodology follows the developments in Alexandersen et al. (2016) and Høghøj et al. (2020) with the addition of a discontinuity stabilization scheme.

3.1 Mass transfer problem

The mass transfer problem is modeled using the steady-state incompressible Navier–Stokes equation with Brinkman penalization.

$$\begin{aligned}&{\frac{\partial u_i^*}{\partial x_i^*}=0,} \end{aligned}$$

(1)

$$\begin{aligned}&{u_i^*\frac{\partial u_j^*}{\partial x_i^*}-\frac{1}{Re}\frac{\partial }{\partial x_i^*}\left( \frac{\partial u_i^*}{\partial x_j^*}+\frac{\partial u_j^*}{\partial x_i^*}\right) +\frac{\partial P^*}{\partial x_i^*}+\alpha (\xi )u_i^*=0,} \end{aligned}$$

(2)

where $u ^*$ and $P ^*$ are the velocity and the pressure in their non-dimensional form and $\alpha$ is the inverse permeability coefficient. The Reynolds number, Re, corresponds to the ratio of inertial forces to viscous forces in the fluid flow. It is defined by the following equation:

$$\begin{aligned} Re=\frac{U \rho D_h}{\mu }, \end{aligned}$$

(3)

where U is the reference velocity (Here mean inflow velocity at the inlet), $\rho$ is the mass density, $D_h$ is the hydraulic diameter for a rectangular duct at the inlet, and $\mu$ is the dynamic viscosity. The state variables in dimensional form are shown in Table 1.

Table 1 State variable in dimensional form

The inverse permeability coefficient $\alpha ({{\textbf {x}}})$ is defined in the entire domain $\varOmega$ ideally taking the value zero in the fluid region and infinite in the solid region. This is however not feasible numerically and thus the inverse permeability is bounded as $\alpha \in [0; \alpha _{max}]$ where $\alpha _{max}$ is a sufficiently high number.

Concerning the boundary conditions, in-homogeneous Dirichlet conditions are applied for the velocity at the flow inlet and homogeneous Dirichlet conditions are used to model the pressure outlet. A symmetry condition is set to both lateral sides of the domain and the top and bottom walls are considered non-slip.

3.2 Heat transfer problem

The heat transfer is modeled using the steady-state convection–diffusion equation and non-dimensionalized by the thermal conductivity of the solid $k_s$.

$$\begin{aligned} Pe_s u_i^*\frac{\partial T^*}{\partial x_i^*}-\frac{\partial }{\partial x_i^*}\left( C_k({{\textbf {x}}})\frac{\partial T^*}{\partial x_j^*}\right) =q^*, \end{aligned}$$

(4)

where $T^*$ is the dimensionless Temperature normalized by the reference temperature $T_0$ = 1 ($T^*$=T), $Pe_s$ the solid Peclet number, $\overline{C_k}$ the thermal conductivity ratio, and $q^*$ a volumetric heat source. They are expressed by the following equation:

$$\begin{aligned}&Pe = \frac{\rho c_p U D_h}{k_s}, \end{aligned}$$

(5)

$$\begin{aligned}&\overline{C_k} = \frac{k_f}{k_s}, \end{aligned}$$

(6)

$$\begin{aligned}&Pe_s = \frac{Pe}{\overline{C_k}}, \end{aligned}$$

(7)

where Pe is the Peclet number which indicates the ratio of convective to diffusive heat transfer, $c_p$ is the heat capacity and $k_f$ is the thermal conductivity of the fluid. One can note that in case of null velocity, the convection–diffusion equation simplifies to the steady-state heat equation for pure conduction problems.

Similarly to the Brinkman penalization term in the mass transfer problem, the thermal conductivity ratio $C_k({{\textbf {x}}})$ is defined in the whole domain with the following values:

$$\begin{aligned} C_k({{\textbf {x}}}) = {\left\{ \begin{array}{ll} \overline{C_k} &{} \text {if } {{\textbf {x}}} \in \varOmega ^f \\ 1 &{} \text {if } {{\textbf {x}}} \in \varOmega ^s \end{array}\right. } \end{aligned}$$

(8)

At the flow inlet of the domain, homogeneous Dirichlet boundary condition is applied. A Neumann boundary condition is applied to the location of the heat source, whereas other boundaries are assumed adiabatic which is implicitly modeled in the finite element model in case no heat source is applied.

3.3 Finite element formulation

The state equations are numerically discretized using the Finite Element Method (FEM), elaborating on the implementations of Alexandersen et al. (2016). The mesh is fully structured with regular tri-linear hexahedral elements of the same dimensions.

The Pressure-Stabilizing/Petrov–Galerkin (PSPG) scheme is used to overcome the deficiency of using equal-order elements which is chosen to allow highest possible resolution. The Streamline–Upwind/Petrov–Galerkin (SUPG) scheme is applied to the mass and heat transfer problems in order to stabilize the solution where large convective gradients are present in the stream-wise direction. In addition, the Discontinuity-Capturing Directional Dissipation (DCDD) (Tezduyar et al. 2008) is used to stabilize the solution in the heat transfer problem for steep thermal gradients in the crosswind direction.

A weak coupling of the two problems leads to a sequential solving, also called the forward problem, where the state field of the mass transfer problem is plugged into the heat transfer problem. The mass transfer problem is solved iteratively by resolving the following non-linear residual equation.

$$\begin{aligned} \mathbf {R_{F}}=\mathbf {M_{F}}({\mathbf {u}},\alpha ){\mathbf {u}}-\mathbf {b_{F}}=0, \end{aligned}$$

(9)

where $\mathbf {M_{F}}$ is the system matrix for the mass transfer and contains the PSPG and SUPG stabilization terms. The vector ${\mathbf {u}}$ is composed of the velocity components in the three directions and the pressure, at each node. Finally, the vector $\mathbf {b_{F}}$ includes the applied boundary conditions.

Similar to the mass transfer problem, the heat transfer problem is defined by the following Eq.:

$$\begin{aligned} \mathbf {R_{T}}=\mathbf {M_{T}}({\mathbf {u}},C_k,{\mathbf {T}}){\mathbf {T}}-\mathbf {b_{T}}=0, \end{aligned}$$

(10)

where $\mathbf {M_{T}}$ is the system matrix for the heat transfer problem. One should note that the heat transfer state matrix has dependency on the temperature vector ${\mathbf {T}}$ due to the DCDD stabilization scheme, in addition to the SUPG stabilization term.

4 Topology optimization for conjugate heat transfer

The topology optimization problem is formulated as a minimization of an objective function $\phi$ subject to a number of constraints $g_j$. The design variable $\xi$ indicating either solid ($\xi =0$) or fluid ($\xi =1$) is relaxed from a discrete variable to a continuous variable, which allows to use gradient-based optimization algorithms. The optimization problem is solved using a nested formulation where the governing equations are solved for each optimization iteration:

$$\begin{aligned} \underset{\xi \in R^n}{\min }\quad&\phi (\xi ,{\mathbf {u}},{\mathbf {T}}) \\ \text {s.t.} \quad&\mathbf {R_F}=0 \\&\mathbf {R_T}=0 \\&g_j\le 0,\quad \forall j=1,...,m \\&0\le \xi _i \le 1, \quad \forall i=1,...,n \end{aligned}$$

The objective function for the microchannel heat sink is to minimize the average bottom temperature of the domain where the heat source is applied. One should note that the average temperature is computed on the whole bottom surface due to the presence of the base plate ensuring a good heat spread on the whole surface.

$$\begin{aligned} \phi =\frac{1}{\int _{bot} \,dA}\int _{bot} T \,dA. \end{aligned}$$

(11)

Choosing an integral form for the objective function allows to get a smoother optimization where a maximum temperature objective function would induce jumps and oscillating solutions due to its non-linearity.

A pressure constraint is applied to the inlet to control the pumping power required for cooling.

$$\begin{aligned} g_1=\frac{1}{\varDelta P^*\int _{In} \,dA}\int _{In} P \,dA - 1 \le 0, \end{aligned}$$

(12)

with $\varDelta P^*$ the non-dimensional maximum pressure drop. Parallel to the pressure constraint, a volume constraint allows to control the volume of the heat sink (footprint in cases where design is 2D extruded).

$$\begin{aligned} g_2=\frac{\int _{\varOmega _d} (1-\mathbf {\xi })\,dV}{\theta \int _{\varOmega _d} \,dV } - 1 \le 0, \end{aligned}$$

(13)

where $\theta$ is the volume fraction relative to the design domain $\varOmega _d$.

4.1 Design filtering and interpolation

A filtering of the design variable is necessary in topology optimization of heat transfer problems to avoid checkerboard patterns with a succession of solid/fluid cells. Moreover, a filter in combination with a projection can ensure a minimum thickness for the solid region (similar to a minimum fin thickness) or the fluid region as a minimum channel size (c.f. Guest et al. (2004) and Sigmund (2007)). Furthermore, filters and projection might also be used to enforce manufacturing constraints either explicitly (Gersborg and Andreasen 2011) or by use of multiple projections (Langelaar 2018). In this study, on top of the filter seen in Alexandersen et al. (2016) and Høghøj et al. (2020), two new additional filters are utilized and compared:

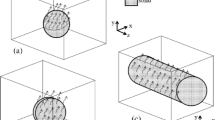
• For full freedom 3D design optimization, a PDE based filter is utilized (Lazarov and Sigmund 2011),

• For 2.5D machining, a single direction projection filter c.f. (Langelaar 2018) is used to “grow” solid exclusively in a single direction,

• a 2D extrusion filter where the solid material forms an extruded geometry from bottom to top.

A schematic view of the difference of the three filters is seen in Fig. 2.

Fig. 2

Three types of filter with a the 3D PDE filter, b the 2.5 milling filter, and c the 2D extrusion filter

For the PDE filter, the new filtered design variable ${\hat{\xi }}$ is found by resolving the following PDE.

$$\begin{aligned} -R^2\nabla ^2{\hat{\xi }}+{\hat{\xi }}=\xi , \end{aligned}$$

(14)

with

$$\begin{aligned} R=\frac{r}{2\sqrt{3}}, \end{aligned}$$

(15)

where r corresponds the physical filter radius c.f. Fig. 2a.

Finally, in order to get a sharper transition from solid to fluid, and to impose a length scale, a Heaviside projection (Wang et al. 2011) is used.

$$\begin{aligned} \tilde{\xi }({\hat{\xi }},\beta ,\eta )=\frac{\tanh (\beta \eta )+\tanh ([{\hat{\xi }}-\eta ]\beta )}{\tanh (\beta \eta )+\tanh ([1-\eta ]\beta )}, \end{aligned}$$

(16)

where $\beta$ is the steepness coefficient and $\eta$ the threshold.

The use of a continuous coefficient $\xi$ involves an interpolation of the inverse permeability coefficient $\alpha$ used in the mass transfer problem and the ratio of thermal conductivity $C_k$ used in the thermal transfer problem. The RAMP formulation (Stolpe and Svanberg 2001) is used for the inverse permeability coefficient.

$$\begin{aligned} \alpha (\xi )=\alpha _{max}\frac{1-\xi }{1+\xi q_{\alpha }}, \end{aligned}$$

(17)

where $\alpha _{max}$ is the maximum inverse permeability coefficient and $q_{\alpha }$ is the penalization coefficient controlling the steepness of the interpolation curve. A SIMP (Bendsøe 1989) style formulation is used for the thermal conductivity ratio.

$$\begin{aligned} C_k(\xi )=(1-\overline{C_k})(1-\xi )^{q_f}+\overline{C_k}, \end{aligned}$$

(18)

where $\overline{C_k}$ is the thermal conductivity ratio and $q_f$ is the penalization coefficient.

4.2 Sensitivities

Fig. 3

Sketch of the design domain with parabolic inlet profile on the left side, an uniform pressure distribution at the outlet, and a constant heat flow on the bottom part

The gradient-based optimization requires the sensitivities of the objective and constraint functions to steer the optimization algorithm. The sensitivities are found using the adjoint method in which the residuals (which are null by definition) multiplied by their respective Lagrangian multipliers are added to the objective function to form the Lagrangian function:

$$\begin{aligned} {\mathcal {L}}=\phi +\lambda _F^T\mathbf {R_F}+\lambda _T^T\mathbf {R_T}. \end{aligned}$$

(19)

By using the chain rule and choosing adequate expression for the Lagrangian multipliers, the sensitivities are found using the following relation:

$$\begin{aligned} \frac{d\phi }{d\xi }=\frac{\partial \phi }{\partial \xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }, \end{aligned}$$

(20)

with the Lagrangian multipliers being found solving the following adjoint problem sequence which exploits the one-way coupling:

$$\begin{aligned} \left( \frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\right) ^T\lambda _T=\left( -\frac{\partial \phi }{\partial {\mathbf {T}}}\right) ^T, \end{aligned}$$

(21)

$$\begin{aligned} \left( \frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}\right) ^T\lambda _F=-\left[ \left( \frac{\partial \phi }{\partial {\mathbf {u}}}\right) ^T+\left( \frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\right) ^T\lambda _T\right] . \end{aligned}$$

(22)

A detailed calculation of the sensitivities can be found in the appendix. The adjoint problem, also called the backward problem, is solved sequentially with the thermal adjoint solution required to solve the mass adjoint problem. Finally, it should be noted that the Dirichlet boundary conditions applied in the forward problem are also applied in the backward problem however, as homogeneous.

4.3 Continuation of optimization parameters

Due to the high non-linearity of the interpolation and projection functions, a continuation approach is employed. The steepness coefficient $\beta$ is set initially to 1 and doubled every 20 iterations to its final value of 64. The penalization coefficient $q_f$ is initially set to 1 and incremented by 1 each 40 iterations until its final value of 3. All other optimization parameters are set constant with $\eta$ = 0.5, $\alpha _{max}$ = $10^6$ and $q_{\alpha }$ = 100, unless otherwise noted.

4.4 Notes on implementation and run times

The numerical framework is based on the PETSc framework (Portable, Extensible Toolkit for Scientific Computation, version 3.15) (Balay et al. 1997) which allows a good scaling of the problem to get a fine resolution of both the fluid and solid domain. The work is based on the implementation of (Alexandersen et al. 2016) and the TopOpt in PETSc framework (Aage et al. 2015). The problems are solved using the DTU-HPC facility (DTU Computing Center 2021). Problems are solved using servers with 2 x Intel Xeon 2650v4 (2x12 cores), 256 GB RAM and interconnected with FDR Infiniband. Typically, 72 cores are used leading to design iteration times of 450 seconds.

5 Results

At first, a full freedom 3D optimized heat sink, obtained using the PDE filter and projection, is compared in terms of thermal performances and pressure drop with the reference case seen in Fig. 1. This allows to discuss the full potential of using a full freedom 3D topology optimization on a compact design such as a microchannel heat sink. The optimized geometry is then exported and meshed to be used in a commercial CFD software. This, allows to confirm the validity of our optimization framework in a standard simulation environment. Secondly, two variations of the heat sink optimization using different projection parameters $\eta$ are carried out, where using low threshold $\eta$ = 0.05 introduces a minimum feature size to the fluid region and using a high threshold $\eta$ = 0.95 introduces a minimum feature size to the solid region. This allows for a study on the influence of length scale on the heat sink design and corresponding performance. Finally, the results of a 2.5D optimized heat sink (using a machining filter) and a 2D heat sink (extrusion filter) are compared with the previous cases to show the effects of imposing designs restrictions on the performances of the heat sinks.

Fig. 4

Iso-contour of the optimized heat sink surface for $\xi$ = 0.85, $\overline{\varDelta P}$ = 62 Pa and using the PDE filter (3D)

5.1 Full freedom 3D optimized heat sink

The design domain of the optimization is shown in Fig. 3. The dimensions correspond to those of the reference design. A laminar velocity profile is set at the inlet, with a corresponding Reynolds number of Re = 50, a static pressure of 0 Pa is applied at the outlet, and the heat flux is set to 1.58MW/m$^2$ (which corresponds to the heat flux of a modern 10 cores CPU). One should note that the footprint of the power source is restricted to the size of a CPU core, which is closer to a real cooling application. The properties of the coolant of solid material are described in Table 2.

Table 2 Properties of solid material and refrigerant

Fig. 5

Optimized heat sink with slices through the domain showing temperature of the fluid & solid domain (up) and velocity and velocity streamlines (down), for the 3D optimized heat sink (inlet on left side) with $\overline{\varDelta P}$ = 62 Pa

Several optimized designs were generated using different non-dimensional pressure drops $\varDelta P^* = \{100, 200, 282\}$ corresponding to dimensional pressure drops $\overline{\varDelta P}=\{ 62, 124, 175\}$ Pa, and a maximum allowed solid volume fraction $\theta$ of 50% in the design domain. The mesh used in the optimization is structured with regular elements and has 4.2M elements (56 $\times$ 672 $\times$ 112) which corresponds to 21.7M DoF, for an element size of 35.7$\mu \text {m}$ in all directions. The resolution is chosen to facilitate easy interpolation between grid levels in when utilizing a solver setup employing a geometric multigrid preconditioned GMRES method. The PDE filter employs a radius of 5.6 elements which corresponds to the feature size of the reference design (0.2$\text {mm}$).

The final geometry of the 3D optimized heat sink (for $\overline{\varDelta P}$ = 62 Pa) is shown in Fig. 4. The evolution of the objective function and the constraint functions can be seen in the appendix.

The optimized design does not contain straight parallel channels, similar to the reference case in Fig. 1, but rather a succession of pins and fin-like objects of different sizes and cross-sections. The enhancement of the heat transfer generated by the complex material distribution is the result of many physical aspects. However, four main functions of the pin-fin-like objects can be pointed out due to their predominant effects on the heat transfer rate:

• Diffuse the heat in the whole domain by heat conduction through the many features (pins, unstructured fins) of the solid region,

• Accelerate the fluid in narrower regions/channels to locally increase the convective heat transfer by increasing the flow velocity,

• Create recirculation zones in the wake of the pins to improve the mixing and increase the heat transfer in the neighborhood regions,

• Destruction and re-initialization of the fluid boundary layer profile development, at each obstacle, similar to offset fins as pointed out by Qasem and Zubair (2018), providing an increase in local heat transfer while keeping a low pressure loss.

Furthermore, the material is distributed to split the flow at several locations to get a better heat transfer distribution along the length of the heat sink. At the entrance of the heat sink, a part of the cold refrigerant is pushed toward the bottom where the heat source is located, whereas a part of the refrigerant stays near the top of the domain. Toward half the length of the heat sink, the heated refrigerant is pushed toward the top and replaced by the colder upper stream to get a better heat transfer overall. This may explain the presence of free-floating material in the top of the domain, which is thermally insulated from the fixed solid region but leads the flow toward the bottom region. One should note that the current design shows a more complex structure when compared to similar topology optimized heat sinks found in the literature such as in the work of Sun et al. (2020). This can be mainly explained by the presence of a fixed solid region at the bottom, diffusing the heat more evenly in the whole geometry and a finer mesh resolution which allows thinner structures and channels to be created. The temperature field of the fluid part, as well as the solid part of the 3D optimized heat sink is shown in Fig. 5. Furthermore, the in-plane (X-Z) velocity is shown at different cross-sections along the flow path, as well as velocity streamlines. Fig. 5 clearly shows that several regions with high flow velocity are located close to the bottom surface, where colder flow is dragged from the top side of the heat sink to increase cooling close to the heating element. It can also be observed that the amount of solid material decreases along the flow path, due to the heating of the refrigerant. As the flow heats up, its cooling capacity decreases, making the presence of material downstream less relevant. Its performance comparison with the reference model is shown in Fig. 6. To get a fair comparison between the reference and the three optimized designs, the geometry of the reference heat sink is simulated in our PETSc optimization framework. However, the response of the reference design is computed using a higher resolution (80 $\times$ 672 $\times$ 112) to represent the fin width in an integer number of elements while maintaining the same solver settings.

Fig. 6

Objective (average bottom temperature) vs pressure drop for the reference and three 3D optimized designs

The optimized 3D designs outperform the reference model for all cases. This is expected since the reference design with straight parallel fins does not initiate secondary motion in the fluid region and generates a relatively high pressure drop due to the constant narrow cross-section of the channels. Even so the flow in the optimized heat sink often changes direction which also induces friction and momentum losses, the relaxation of the free-flow cross-section combined with a reduction in the solid-fluid interface area of 46% (for $\overline{\varDelta P}$ = 62 Pa) allows to decrease the viscous losses overall. However, the results of the optimization framework are subject to some flow leakage and artificial higher heat transfer rate at the fluid/solid boundary due to the material interpolation used in the immersed method. Therefore, when comparing the performances of all optimized designs, the geometries are exported, meshed, and simulated in a commercial CFD software (ANSYS CFX) to avoid numerical artifacts due to the immersed method and to get results representing manufacturing ready components.

5.2 Post evaluation by commercial CFD solver

The designs of the 3D optimized models were evaluated using a commercial CFD software with the same boundary conditions as for the optimization framework c.f. Fig. 1. The procedure for exporting the designs is as follows: An STL file of the isosurface at a specified threshold is created using ParaView. Next, a structured mesh is created using the meshing software Trelis with the same grid size as the original. The mesh is then carved using Trelis Sculpt to create a volume mesh with large structured regions and only adapted elements along the solid–fluid interface. This mesh is then imported to Ansys CFX where the post analysis is performed. The main difference lies in the physical representation of the border between the fluid and solid regions in the CFD model, avoiding fluid leakage in the solid part and artificial heat diffusion in the transitional solid interface. The results are presented in Fig. 7.

Fig. 7

Objective in function of the pressure drop with optimization framework (PETSc based) and commercial CFD solver (ANSYS CFX). Arrows and corresponding values indicate maximum allowed pressure drop during the optimization

For a threshold value of $\xi = 0.5$, the results of the CFD models do not fully coincide with those of the optimization framework. A custom threshold value for each case is therefore determined by varying $\xi$ in the export until the pressure drop of both models is similar. This leads to the following values $\xi = \{0.85, 0.90, 0.90\}$ for $\overline{\varDelta P}=\{ 62, 124, 175\}$ Pa, respectively. Fig. 8 represents the change in the location of the solid–fluid interface depending on the threshold value.

A higher value of $\xi$ expands the volume of the solid region, narrowing the flow channels with the consequence of higher flow velocity and an increase in the pressure drop, as seen in Fig. 8. One should note that the interpolation function used to create the smooth surface seen in Fig. 8 has the benefits to create high-quality bodyfitted meshes. Therefore, a better representation of the solid–fluid interface has been prioritized over using a threshold of the “raw data” with the aim to minimize the numerical diffusion due to a poor representation of the regions boundary, crucial to correctly estimate the heat transfer from the solid’s surface to the fluid’s surface.

Figure 7 also shows that for a pressure drop larger than 62 Pa, the optimization framework overestimates the cooling performance. This can be explained by two main factors: (1) As the overall pressure drop increases, the fluid is more inclined to flow through the porous solid region, especially at low thickness solid regions. (2) The application of a filter and a projection with finite $\beta$ cannot avoid generating a “grey border” between the solid and fluid regions which locally increases heat diffusion, as shown in Fig. 8. Besides, high speed flow in narrow channels, high crosswind thermal gradients, poor mesh resolution, and numerical solver properties constitute sources of discrepancies between the two models. In order to get reliable results with the optimization framework, all following optimized designs are generated using a pressure drop constraint of $\overline{\varDelta P}$ = 62 Pa, due to the low deviation observed in Fig. 7.

Fig. 8

Different stages of mesh extrusion from raw design to CFD commercial software

5.3 Projection direction

Fig. 9

Iso-contour of the optimized heat sink surface for $\xi$ = 0.95, with $\eta$ = 0.05, $\overline{\varDelta P}$ = 62 Pa and using the PDE filter (3D)

Fig. 10

Iso-contour of the optimized heat sink surface for $\xi$ = 0.95, with $\eta$ = 0.95, $\overline{\varDelta P}$ = 62 Pa and using the PDE filter (3D)

Fig. 11

Optimized heat sink surface for $\xi$ = 0.95, subdivided into its two main geometries: the large tree-structure (top) and the corral-like shaped fins (bottom)

The projection parameter $\eta$ defines the projection direction either to the fluid region ($\eta$ = 0.05) or to the solid region ($\eta$ = 0.95). To investigate the influence of the projection direction on the final design and performances, two new geometries have been optimized, with the exact same boundary conditions as for $\eta$ = 0.5. The two designs are shown in Figs. 9 and 10 for $\eta$ = 0.05 and $\eta$ = 0.95, respectively.

When compared with the original optimized heat sink shown in Fig. 4, the two new geometries exhibit larger feature sizes and a continuous solid region. In both designs, a tree-shaped structure is developing from the middle part of the heat sink (where the heat source is located), extending its geometry toward the top wall and spreading in two main branches toward the inlet and outlet regions (strictly for $\eta$ = 0.95). Similarly, to the previous design, the large tree-structure conducts the heat away from its source and pushes the flow toward the bottom part. Furthermore, smaller corral-like shapes are present along the flow path, creating recirculation zones and ensuring thermal connection between the bottom plate and the top part of the heat sink. A representation of the structure layout is shown in Fig. 11 where the heat sink is subdivided into two parts: the large tree shape structure and the corral-like shaped structure Thus, imposing a length scale, to either the fluid or the solid region, seems to help creating simpler designs as well as maintaining a well-connected solid body, which is beneficial for manufacturability. For the design where a length scale is imposed on the fluid, the intricate flow patterns may be better resolved. The thermal and velocity fields of the two designs are shown in the appendix.

In terms of performances, the objective function for the fluid-oriented design ($\eta =0.05$) shows a marginal improvement of 2.3% (26.7 K), while a decrease in performance of 5.4% (28.8 K) is seen for the solid-oriented design ($\eta =0.95$), when compared with the original optimized geometry (27.3 K) at the same pressure drop. The small improvement is due to the better resolution of the flow in narrow channels by imposing a minimum number of cells in these regions. Concerning the solid-oriented geometry, the decrease in performances is largely owed to the higher minimum length scale of the solid region.

5.4 Restricted freedom 2.5D and 2D optimized heat sinks

New optimized heat sinks were generated using the milling filter (2.5D) and the extrusion filter (2D) and compared to the previous designs. The boundary conditions remain the same as for the previous iterations and a pressure drop of $\overline{\varDelta P}$ = 62 Pa is set for the constraint function. The optimized designs are shown in Figs. 12 and  13 for the 2.5D and 2D filters, respectively.

Fig. 12

Iso-contour of the optimized heat sink surface for $\xi$ = 0.70, $\overline{\varDelta P}$ = 62 Pa and using the milling filter (2.5D)

Fig. 13

Iso-contour of the optimized heat sink surface for $\xi$ = 0.87, $\overline{\varDelta P}$ = 62 Pa and using the extrusion filter (2D)

A summary of the optimization results is provided in Table 3, where the value of the objective function (in K) and the two constraint functions are given at the final iteration of the optimization. The constraint function $g_{1}$ is expressed as the average inlet pressure $P_{in}$ (in Pa) and the constraint function $g_{2}$ is expressed as the solid volume ratio SVR (in %).

Table 3 Results from the optimization framework for all designs

First of all, the complexity of the optimized geometries is greatly reduced when compared with the 3D optimized heat sinks. Both new designs generate pins and fins of different sizes, the 2.5D model having the particularity of producing variable cross-section fins along their height. Similarly to the 3D optimized design, the fins diffuse the heat in the whole domain space, accelerate the flow, generate recirculation zones, and disturb the boundary layer, but with a lower amplitude due to the design restriction. In Figs. 14 and 15, it can be clearly seen that the amount of vertical motion of the flow (in z-direction) decreases as the design freedom is further restricted during the optimization process. For the 2D optimized heat sink, the z-velocity component is negligible due to the uniform fins’ cross-section area as seen in Fig. 15, similar to the restrictions employed in pseudo 3D formulations (Yan et al. 2019).

Fig. 14

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 2.5D optimized heat sink (inlet on left side)

Fig. 15

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 2D optimized heat sink (inlet on left side)

Furthermore, the solid regions do not exhibit overhangs (or suspended material) due to the tool accessibility constraint imposed by the design filters, making it very difficult, if not impossible, to push the flow toward the bottom part of the heat sink where the heat source is located. Instead, both designs show an increase in material distribution at the center of the heat sink to increase the fins’ area as close as possible to the heat source. As seen in Table 3, one should note that the pressure constraint function of the 2.5D design was not reached which indicates that such design filter does not require a high pressure drop to perform well. Another remark is the sensibility of the 2D optimized model on its initial design. It appears that the solid part “grows” primarily from the prescribed initial solid regions and keeps some characteristics of the original designs (the staggered fins in this example) which indicates that the optimized design is in a local minimum. As pointed out by Haertel et al. (2018), one should make sure to test different initial designs configurations to avoid reaching poor local minimums and get more robust designs. For this example, three initial designs were tested: A single longitudinal central fin, 5 pins along the center-line, and 15 staggered thin pins, with the latter giving the best performances.

5.5 Performance benchmark

In order to quantify the limitation of such manufacturing filters on the optimization results, the performances of all optimized heat sinks are benchmarked with the reference heat sink. The heat sinks were simulated using ANSYS CFX, following the procedure described in the CFD validation section, for different inlet velocities corresponding to a range of Re = [25,300]. One should note that the range of the volume flow rate is low when compared to real electronic cooling applications, mainly to keep a laminar flow regime through the heat sinks, and so to showcase the applicability of this method. The flow is considered laminar in the CFD solver with a laminar inlet velocity parabolic profile and an average static pressure of 0 Pa at the outlet.

Fig. 16

Pressure drop in function of the Reynolds number, for all designs

Fig. 17

Value of the objective in function of the Reynolds number for all designs

Fig. 18

Value of the objective in function of the pressure drop, for all designs

Figure 16 represents the pressure drop in function of the Reynolds number, and Fig. 17 represents the value of the objective in function of the Reynolds number. To get a better overview, Fig. 18 summarizes the performances of each heat sink in terms of cooling capability in regard of the pressure drop. The closest to the bottom left a data point lies, the better the performances of the heat sink. The 3D optimized heat sink shows the best performances with the 2.5D, 2D, and reference design in hierarchical order. One should note that the 2.5D design exhibits better performances at lower pressure drops since the pressure constraint was never reached during the optimization. However, it should be pointed out that the flow conditions, in terms of volume flow rate, required to achieve similar objectives (or similar temperature range) differ for each designs. In that matter, the curve fitting tool from Matlab was used to create regression models for each optimized heat sinks using power laws, similar to forced flow convection in cylinder or ducts. Table 4 summarizes the coefficients and accuracy of the power law regression functions.

Table 4 Regression models of the optimized heat sinks using the power function $T = aP^{b}+c$

The regression models fit very well with $R^2>0.999$ for all cases, with an example of the 3D case shown in the appendix. Therefore, the value of the objective function for higher pressure, for the 2.5D and 2D designs, can be predicted with good confidence. Fig. 19 shows the value of the objective function, evaluated using the regression models, at the pressures found for the reference case.

Fig. 19

Value of the objective using regression models in function of the pressure drop, for all designs

The design models perform well at low pressure drop, for which they were designed for ($\overline{\varDelta P}$ = 62 Pa). The temperature elevation can be reduced by a maximum of 70% using the 3D optimized heat sink, for a same pressure drop, whereas the pressure drop can be reduced by a maximum of 90% using the 2.5D optimized heat sink, for a same temperature elevation. It should be pointed out that the optimized heat sinks perform well outside of their optimization range, showing a good flexibility to flow condition changes.

6 Discussion and conclusion

In this paper, microchannel heat sinks for microelectronic applications were generated using topology optimization and with the use of manufacturing filters. The optimization considered minimizes the average bottom temperature of the heat sink, while keeping a relatively low pressure drop. The mass transfer and the heat transfer problems were solved sequentially using the incompressible Navier–Stokes and Convection–Diffusion equations, respectively. A 2.5D milling filter and a 2D extrusion filter were applied in the optimization routine to restrict the design space freedom with the goal of improving manufacturability.

A performance benchmark of the optimized heat sinks and a reference straight microchannel heat sink, for a range of flow velocities, was carried out using strictly separated solid–fluid models using a commercial CFD software. The full freedom optimized heat sink showed the best performances of all designs, with a reduction as high as 70% in chip elevation temperature, for a same pressure drop, and a maximum reduction of 90% for the pressure drop for a same temperature elevation.

The use of design filters downgrades the performances of the optimized heat sinks, especially at higher pressure drop, where the level of restrictions is related to the decrease in performance. The lack of design freedom in the direction normal to the bottom and transverse to the main flow inhibits flow focusing near the heated surface and initiation of secondary flow which increase convective effects. On the other hand, both design-restricted heat sinks exhibit better performances, when compared to the reference case, with a similar design complexity. Despite their good performances in comparison with the reference geometry, the progress in SLM production technique and its reduction in cost makes 3D topology optimization a better candidate to fully exploit the intricate designs obtained with this method.

The comparison of the topology optimized designs with a commercial CFD software highlighted certain challenges to be discussed in further work for compact geometries. The large velocity and temperature gradients encountered in narrow regions, as well as a high pressure distribution along the flow stream direction, challenge the current density-based methodology and framework. The use of additional stabilization schemes in the cross-flow direction, as well as length scale on either the fluid or solid region, is not sufficient to maintain a good accuracy for post-processed validation. Future work should focus on limiting exploitation of artificial leakage and thereby parasitic heat transfer. Furthermore, sufficient resolution of internal flow channels seems to be of great importance to ensure consistency between density-based models and strictly separated solid–fluid models.

Appendices

Appendices

1.1 Sensitives for conjugate heat transfer

In the case of a conjugate heat transfer problem, the objective function is dependent on the density field $\xi$ but also on the velocity and pressure field ${\mathbf {u}}(\xi )$ and the temperature field ${\mathbf {T}}(\xi )$.

$$\begin{aligned} \phi =\phi ({\mathbf {u}}(\xi ),{\mathbf {T}}(\xi ),\xi ). \end{aligned}$$

(A.1.1)

Using the chain rule, the derivative of the objective function in respect to the density field is expressed by

$$\begin{aligned} \frac{d\phi }{d\xi }=\frac{\partial \phi }{\partial \xi }+\frac{\partial \phi }{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\frac{\partial \phi }{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }. \end{aligned}$$

(A.1.2)

The Lagrangian function ${\mathcal {L}}$ is introduced alongside the Lagrangian multipliers and their respective residual functions.

$$\begin{aligned} {\mathcal {L}}=\phi +\lambda _F^T\mathbf {R_F}+\lambda _T^T\mathbf {R_T}. \end{aligned}$$

(A.1.3)

The residual terms being by definition null or close to zero, the Lagrangian formulation is used to bypass the calculation of the difficult terms of Eq. A.1.2. Using the chain rule, the derivative of the Lagrangian function in respect to the density field is expressed by

$$\begin{aligned} \begin{aligned} \frac{d{\mathcal {L}}}{d\xi }=& \frac{\partial \phi }{\partial \xi }+\frac{\partial \phi }{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\frac{\partial \phi }{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }\\ &+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }\\ &+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\frac{d{\mathbf {u}}}{d\xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\frac{d {\mathbf {T}}}{d\xi }. \end{aligned} \end{aligned}$$

(A.1.4)

Since forced convection is the predominant heat transfer phenomena, there only exists a one-way coupling where the fluid residuals in respect of the temperature are assumed to be zero.

$$\begin{aligned} \frac{\partial \mathbf {R_F}}{\partial {\mathbf {T}}}=0. \end{aligned}$$

(A.1.5)

By regrouping the terms of Eq. A.1.4, the sensitivity of the Lagrangian function can be expressed as

$$\begin{aligned} \begin{aligned}\frac{d{\mathcal {L}}}{d\xi }=&\frac{\partial \phi }{\partial \xi }+\left( \frac{\partial \phi }{\partial {\mathbf {u}}}+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\right) \frac{d{\mathbf {u}}}{d\xi }\\&+\left( \frac{\partial \phi }{\partial {\mathbf {T}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\right) \frac{d {\mathbf {T}}}{d\xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }. \end{aligned} \end{aligned}$$

(A.1.6)

The terms $\frac{d{\mathbf {u}}}{d\xi }$ and $\frac{d{\mathbf {T}}}{d\xi }$, difficult to evaluate, can be carefully eliminated from Eq. A.1.4 by choosing the adequate Lagrangian multipliers fulfilling the following two equality functions.

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial {\mathbf {u}}}+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial {\mathbf {u}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {u}}}\right) =0, \end{aligned}$$

(A.1.7)

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial {\mathbf {T}}}+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial {\mathbf {T}}}\right) =0. \end{aligned}$$

(A.1.8)

After solving the so-called backward problem, the Lagrangian multipliers can be plugged back to the Eq. A.1.4 leading to the final equation:

$$\begin{aligned} \frac{d\phi }{d\xi }=\frac{\partial \phi }{\partial \xi }+\lambda _F^T\frac{\partial \mathbf {R_F}}{\partial \xi }+\lambda _T^T\frac{\partial \mathbf {R_T}}{\partial \xi }. \end{aligned}$$

(A.1.9)

1.2 Evolution of optimization

Figure 20 represents the variation of the objective function value and the constraint functions value in respect of the iteration number, for the 3D optimized model with $\eta = 0.5$.

Fig. 20

Value of the objective in function of the iteration number

First of all, the optimization terminates and is considered converged when the maximum amount of design change (or density change) becomes lower than 0.1%. The spikes and jumps in the evolution of the objective and constraint functions appear each time once the optimization parameter is subject to continuation. Overall, the optimization is rather smooth, expect for lower values of $\beta$ where the optimization takes several iterations to stabilize. Fig. 20 also shows that the pressure constraint leads the optimization, whereas a volume fraction of 50% appears to be too generous to get an optimized geometry at the current pressure drop. Fig. 21 represents the evolution of the material distribution of the optimized heat sink at different stages of the optimization process.

Fig. 21

Evolution of the design of the optimized heat sink at iteration 20, 40, 60, 80, and 100 (from bottom to top) for the 3D optimized heat sink with $\eta = 0.5$

1.3 Restricted optimized models

The temperature field, flow streamlines, and velocity profiles at different cross-sections of the optimized heat sinks are shown in Figs. 22 and 23. The flow field is similar with the non-projected 3D design, with the difference of having a single solid block with thicker features.

Fig. 22

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 3D optimized heat sink with $\eta = 0.05$ (inlet on left side)

Fig. 23

Optimized heat sink with slices through the design domain showing velocity and velocity streamlines (up) and Temperature of the solid domain (down), for the 2D optimized heat sink with $\eta = 0.95$ (inlet on left side)

1.4 Regression models

The values of the objective using the interpolation model are plotted along the results of the CFD simulations (Fig. 24).

Fig. 24

Objective function value vs the pressure drop for the CFD results and the interpolation model

The power law regression model can fit all the data points of the CFD simulations, making it reliable for predicting data outside of the current pressure range, as long as the flow remains laminar.