Distributed-parametric optimization approach for free-orientation of laminated shell structures with anisotropic materials

Abstract

In this study, we propose a distributed-parametric material orientation optimization method for the optimal design of laminated composite shell structures consisting of anisotropic materials. We consider the compliance as the objective function and minimize it under the state-equation constraint. The material orientation in all the layers is treated as the design variable. The optimal design problem is formulated as a distributed-parameter optimization problem based on the variational method, and the sensitivity function with respect to the material orientation variation is theoretically derived. The optimal orientation variations are determined using the H¹ gradient method with Poisson’s equation, where the derived sensitivity function is applied as the fictitious internal heat generation under the Robin condition to reduce the objective function while maintaining a smooth material orientation. With the proposed method, we can conventionally obtain the arbitrary optimal distribution of the material orientations of all the layers of complicated large-scale shell structures like aircraft or automotive bodies without design variable parameterization. The optimal results of the design examples show that the proposed optimization method can effectively obtain the optimal distribution of the material orientation in laminated shell structures.

1 Introduction

Shell structures have been used in a variety of industrial products. From an economic perspective, weight reduction is strictly required in the structural design of cars, aircraft, etc. Using composite materials such as carbon-fiber-reinforced plastics (CFRP) in shell structures is one of the solutions to meet the requirement of lightweight, since they have higher specific mechanical performances than metal. In particular, anisotropic materials are often used to design a specific stiff direction easily. From the manufacturing standpoint, the conventional distribution of material orientation is parallel, but new technologies such as automated fiber placement (AFP) have enabled the manufacture of curvilinear-distributed material orientation. The arbitrary optimal material distribution can develop the potential of CFRP. Therefore, the optimization method for material distribution with curvilinear orientation that considers continuous curves manufactured by AFP is required. This work focuses on the optimization of the material orientation for anisotropic shell structures, which would enable the full potential of CFRP.

In previous works to date, many optimization methods and their application techniques for material orientation optimization have been reported.

As one of the classical methods, Miki (1985) has developed a graphical laminate optimization method based on lamination parameters. This method has the advantage that a designer can easily visualize the entire design space. Hammer et al. (1997) proposed a composite material optimization method by optimizing the elemental lamination parameters, which are used to describe in-plane and bending stiffness of an element made from a symmetrical configuration of the composite material. These methods, which are based on the lamination parameters, have the drawback of imposing manufacturing constraints on the material orientation.

An intuitive approach to this design problem is based on the theoretical knowledge that higher stiffness is obtained by aligning the element material orientation along the principal stress directions. Suzuki and Kikuchi (1991) used this approach in calculating microstructure orientation angles in the homogeneous design method and obtaining the optimal topology distribution. Pederson (1989) have also used this idea in a strain-based approach for optimizing the material orientation, which led to significant improvements in the stiffness over the uniform material orientation. Temmen et al. (2006) introduced the optimality criteria method to align the elemental material orientation along the principal stress or strain directions and successfully improved the stiffness of a composite material. In this method, the material orientation was constantly updated for satisfying optimality criteria at each iteration step.

Sensitivity based approaches, which have mathematical backgrounds as well, can also be found in the literature. One of the earliest sensitivity-based methods was suggested by Hyer and Lee (1991). They used both a sensitivity analysis and a gradient-search technique to select material orientation in a number of regions of a plate and increase the buckling load relative to straight-line designs; however, the material orientation continuity was not satisfied. The main advantage of the gradient-based method is its efficiency in solving large-scale structures in contrast to optimality criteria methods or genetic algorithms (GAs). However, it may cause multiple local minimum solutions and it is highly dependent on the initial material orientation distribution. Thus, Stegmann and Lund (2005) suggested an alternative method called direct material optimization (DMO) method to solve a discrete optimization problem. In this method, the material orientation at any design point is represented as a weighted sum of several candidate orientations, and the weights are taken as design variables. The optimization algorithm is based on the gradient method, and the element-based penalization coefficient is used to force the candidate orientations to only one candidate. This method is an amelioration of the other alternative methods such as simple gradient methods that may cause multiple local minima. Bruyneel (2011) proposed a parameterization method to enhance mechanical properties called the shape functions with penalization (SFP), which is simpler than the DMO. This method can decrease the number of design variables for selecting the optimal material orientations with convergence speed and quality compared to the solutions of the DMO. Gao et al. (2012) proposed a parameterization method for the selection problem of material orientation called the bi-value coding parameterization (BCP), which generalized the concept of the shape function based on the SFP. These alternative SFP and BCP methods used weighted formulations to parameterize the different material orientations and to reduce the number of design variables. However, the results do not cover manufacturable continuous material orientation distribution (Nomura et al. 2015). As a further development approach, Kiyono et al. (2017) presented a material orientation optimization formulation (NDFO) considering the optimal selection of the discrete material orientation of each element. The proposed method was based on the normal distribution function, which has the advantage of requiring only one variable to select the optimal discrete orientation among the candidates. This method achieved the continuous material orientation by using the spatial filter suggested by Yin and Ananthasuresh (2001), but the continuity of the material orientation depended strongly on the filter radius compared to the element-based methods. The parametric method is effective for reducing the number of design variables and reducing the risk of obtaining local minimum solutions. However, the designer needs considerable parameterization knowledge and experience. Additionally, the optimal solution is strongly influenced by the design parameterization.

GA, which is another effective method to avoid the local minimum solutions, has been used to solve the optimization problem of material orientation such as stacking sequence (Le and Haftka 1993; Kogiso et al. 1994; Kim et al. 1999). Other researchers (Honda et al. 2013; Guanxin et al. 2016) also used GA as an optimization solver and the shape coefficients of a cubic path function. The cubic path function represents fiber paths as the design variables to be optimized to obtain the manufacturable continuous optimal fiber paths. As known widely, GA is expected to find some local minimum solutions and have the potential to obtain the global minimum solution, where sensitivity analysis is unnecessary. However, the application of GA to the practical structural problems is limited since FE analyses of large-scale structures with a large number of design variables, especially for every element in every layer of a laminated shell, results in a significant amount of calculation cost.

With these background and motivation, in this study, we propose a distributed-parametric optimization method for free-orientation and gradient-based material orientation optimization method for the optimal design of complicated-shape and large-scale laminated shell structures like automotive or aircraft body shell structures, consisting of anisotropic or locally orthotropic materials. “Distributed-parametric optimization method for free-orientation” in this paper means that the design variable parameterization to determine the material orientation in advance is unnecessary; that is, defining the candidate material orientations or polynomials to determine the design variables in advance is unnecessary. In other words, it means the design variables have the largest design freedom and the material orientation can be varied freely over the entire region. The design variable parameterization reduces the smaller design freedom and leads to a lower computational cost; however, the obtained mechanical performance can be limited since the optimal solution is highly dependent on the pre-defined parameters. To overcome this issue, we propose a distributed-parametric material orientation optimization method for the free-orientation design of laminated shell structures. It is a gradient method with a Laplacian smoother in the Hilbert space, which does not require any material orientation parameterization and makes it possible to design the smooth free-orientation that reduces the objective function. We consider the compliance as the objective function and minimize it under the state-equation constraint. The arbitrary and optimal material orientation distribution in each layer is then determined. Considering a distributed-parametric problem, or an enormous design degrees of freedom problem, it is not easy to control its behavior. Without a countermeasure, the problem may become ill-condition like in the case of the checkerboard problem of topology optimization or the jagging problem of shape optimization. In this study, the optimal design problem is formulated as a distributed-parameter optimization problem, and the sensitivity function with respect to the orientation variation is theoretically derived based on the classical variational method. The optimal orientation variations, which are the design variable functions, are determined based on the modern H¹ gradient method in a function space with Poisson’s equation. The H¹ gradient method has been developed for shape optimization of continua shell by the authors (Shimoda et al. 1998; Shimoda and Liu 2014). In this study, we have extended this method using Poisson’s equation for material orientation optimization. With this method, the material orientation can be optimized while avoiding the aforementioned ill-condition risk, or maintaining the smoothness of material orientation. The background and detail of this method will be explained in Sect. 4. The sensitivity function derived is used as the driving force via the internal heat generation in the method to vary the orientation to reduce the objective function while maintaining a smooth material orientation distribution. The arbitrary optimal and continuous orientation variations in each layer are conventionally determined as the temperature distribution from the fictitious heat transfer analysis. Thereby, with the proposed classical and modern conventional method, we can treat the material orientation optimization problem for complicated-shape and large-scale structures with enormous design variables efficiently without design parameterization. We can also obtain more easily the arbitrary optimal and continuous material orientation and minimize the compliance, simultaneously.

2 Formulation of material orientation optimization problem

2.1 Governing equation for a laminated shell structure

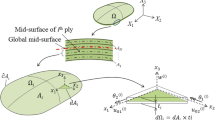
As shown in Fig. 1a, the i^th ply of a laminated shell structure has an initial design domain Ω_i, middle surface A_i with boundary ∂A_i, and thickness t_i. The bounded domain is composed of a set of infinitesimal flat surfaces. For simplicity, we assume that a laminated shell structure consists of N layers. In this paper, the subscripts of the Greek letters are expressed as α = 1, 2 and the tensor subscript notation uses Einstein’s summation convention and a partial differential notation with respect to the spatial coordinates (⋅)_,j = ∂(⋅)/∂x_j.

Fig. 1

Laminated shell with N layers as a set of infinitesimal flat surfaces. a Geometry of a laminated shell. b Local coordinate and DOF of flat surface of the i^th ply

The Reissner-Mindlin plate theory posits that

$$ {u}_{\alpha}^{(i)}\left({x}_1^{(i)},{x}_2^{(i)},{x}_3^{(i)}\right)\equiv {u}_{0\alpha}^{(i)}\left({x}_1^{(i)},{x}_2^{(i)}\right)-{x}_3^{(i)}{\theta}_{\alpha}^{(i)}\left({x}_1^{(i)},{x}_2^{(i)}\right), $$

(1)

$$ {u}_3^{(i)}\left({x}_1^{(i)},{x}_2^{(i)},{x}_3^{(i)}\right)\equiv {w}^{(i)}\left({x}_1^{(i)},{x}_2^{(i)}\right), $$

(2)

where ${\left\{{u}_{0\alpha}^{(i)}\right\}}_{\alpha =1,2},{w}^{(i)}$, and ${\left\{{\theta}_{\alpha}^{(i)}\right\}}_{\alpha =1,2}$ express in-plane displacement, out-of-plane displacement, and rotational angles of the mid-area of the i^th ply of the laminated shell structure, respectively. Then, the weak form state equation relative to ${\boldsymbol{u}}^{(i)}=\left({\boldsymbol{u}}_0^{(i)},{w}^{(i)},{\boldsymbol{\theta}}^{(i)}\right)\in U\kern0.5em \left(i=1,\cdots, N\right)$ can be expressed as (3) by substituting (4) and (5) into the variational equation for the three-dimensional linear elastic body, considering ${\sigma}_{33}^{(i)}=0$ and eliminating ${\varepsilon}_{33}^{(i)}$.

$$ a\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right)=l\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right),\kern1em \forall \left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\in \overline{U},\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right)\in U $$

(3)

where ${\boldsymbol{u}}^{(i)}={\left[{\boldsymbol{u}}_0^{(i)},{w}^{(i)},{\boldsymbol{\theta}}^{(i)}\right]}^T$ and $\left(\overline{\cdotp}\right)$ expresses a variation. In addition, the bilinear form a(⋅, ⋅) and linear form l(⋅) for the state variables (u₀, w, θ) are respectively defined as

$$ \kern0em {\displaystyle \begin{array}{l}a\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right)\\ {}=\sum \limits_{i=1}^N{\int}_{A_i}\Big\{{\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right){\boldsymbol{E}}^{B(i)}{\overline{\boldsymbol{\kappa}}}^{(i)}\left(\overline{\boldsymbol{\theta}}\right)+{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right){\boldsymbol{E}}^{M(i)}{\overline{\boldsymbol{\varepsilon}}}_0^{(i)}\left({\overline{\boldsymbol{u}}}_0\right)+{\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right){\boldsymbol{E}}^{C(i)}{\overline{\boldsymbol{\varepsilon}}}_0^{(i)}\left({\overline{\boldsymbol{u}}}_0\right)\\ {}\kern1em +{\overline{\boldsymbol{\kappa}}}^{(i)T}\left(\overline{\boldsymbol{\theta}}\right){\boldsymbol{E}}^{C(i)}{\boldsymbol{\varepsilon}}_0^{(i)}\left({\boldsymbol{u}}_0\right)+{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right){\boldsymbol{E}}^{C(i)}{\overline{\boldsymbol{\kappa}}}^{(i)}\left(\overline{\boldsymbol{\theta}}\right)+{\overline{\boldsymbol{\varepsilon}}}_0^{(i)T}\left({\overline{\boldsymbol{u}}}_0\right){\boldsymbol{E}}^{C(i)}{\boldsymbol{\kappa}}^{(i)}\left(\boldsymbol{\theta} \right)\\ {}+{\boldsymbol{\gamma}}^{(i)T}\left(w,\boldsymbol{\theta} \right){\boldsymbol{E}}^{S(i)}{\overline{\boldsymbol{\gamma}}}^{(i)}\left(\overline{w},\overline{\boldsymbol{\theta}}\right)\Big\}d{A}_i,\end{array}} $$

(4)

$$ {\displaystyle \begin{array}{l}l\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\\ {}=\sum \limits_{i=1}^N\left[{\int}_{A_i}\left({\boldsymbol{f}}^T{\overline{\boldsymbol{u}}}_0^{(i)}-{\boldsymbol{m}}^T{\overline{\boldsymbol{\theta}}}^{(i)}+q{\overline{w}}^{(i)}\right)d{A}_i+{\int}_{\partial {A}_i}\left({\boldsymbol{N}}^T{\overline{\boldsymbol{u}}}_0^{(i)}-{\boldsymbol{M}}^T{\overline{\boldsymbol{\theta}}}^{(i)}+Q{\overline{w}}^{(i)}\right)d{s}_i\right].\end{array}} $$

(5)

The external loadings relative to the local coordinate system (x₁, x₂, 0) are defined as f, m, q, N, M, and Q, which denote in-plane load, out-of-plane moment, out-plane load on the middle surface in-plane load, bending moment, and shearing force on the sub-boundaries respectively. The notations, E^B(i), E^M(i), E^C(i), and E^S(i)express the orthotropic elastic matrices with respect to bending, membrane, coupling, and shear component of the i^th ply, respectively. Additionally, ${\boldsymbol{\varepsilon}}^{(i)}={\left\{{\varepsilon}_{\alpha \beta}\right\}}_{\alpha, \beta =1,2}^{(i)},{\boldsymbol{\kappa}}^{(i)}={\left\{{\kappa}_{\alpha \beta}\right\}}_{\alpha, \beta =1,2}^{(i)},{\boldsymbol{\varepsilon}}_0^{(i)}={\left\{{\varepsilon}_{0\alpha \beta}\right\}}_{\alpha, \beta =1,2}^{(i)}$and ${\boldsymbol{\gamma}}^{(i)}={\left\{{\gamma}_{\alpha 3}\right\}}_{\alpha =1,2}^{(i)}$ express strain tensor, curvature tensor, in-plane strain tensor, and transverse shear strain on the middle surface of the i^th ply, respectively, and these are defined by the following equations:

$$ {\varepsilon}_{\alpha \beta}^{(i)}\overline{=}\frac{1}{2}\left({u}_{\alpha, \beta}^{(i)}+{u}_{\beta, \alpha}^{(i)}\right), $$

(6)

$$ {u}_{\alpha, \beta}^{(i)}={u}_{0\alpha, \beta}^{(i)}-{x}_3^{(i)}{\theta}_{\alpha, \beta}^{(i)}, $$

(7)

$$ {\gamma}_{\alpha}^{(i)}\overline{=}{w}_{,\alpha}^{(i)}-{\theta}_{\alpha}^{(i)}, $$

(8)

$$ {\kappa}_{\alpha \beta}^{(i)}\overline{=}\frac{1}{2}\left({\theta}_{\alpha, \beta}^{(i)}+{\theta}_{\beta, \alpha}^{(i)}\right), $$

(9)

$$ {\varepsilon}_{0\alpha \beta}^{(i)}\overline{=}\frac{1}{2}\left({u}_{0\alpha, \beta}^{(i)}+{u}_{0\beta, \alpha}^{(i)}\right). $$

(10)

The displacement continuity between each layer is fulfilled as

$$ {\boldsymbol{u}}^{(i) bottom}={\boldsymbol{u}}^{\left(i-1\right) top}, $$

(11)

where (⋅)^(i)bottom and (⋅)^{(i − 1)top} indicates the value on the bottom surface of the i^th ply and the top surface of the (i − 1)^th ply, respectively.

It will be noted that $\overline{U}$ and U in (3) are the space of the kinematically admissible displacements, which are given by the following equation.

$$ \overline{U}=\left\{\left({\overline{u}}_{01}^{(i)},{\overline{u}}_{02}^{(i)},{\overline{w}}^{(i)},{\overline{\theta}}_1^{(i)},{\overline{\theta}}_2^{(i)}\right)\in {\left({H}^1\left({A}_i\right)\right)}^5\left(i=1,\cdots, N\right)|\ {\overline{u}}_{01}^{(i)}={\overline{u}}_{02}^{(i)}={\overline{w}}^{(i)}={\overline{\theta}}_1^{(i)}={\overline{\theta}}_2^{(i)}=0\ on\ the\ Dirichlet\ boundaries\ \right\}, $$

(12)

$$ U=\left\{\left({u}_{01}^{(i)},{u}_{02}^{(i)},{w}^{(i)},{\theta}_1^{(i)},{\theta}_2^{(i)}\right)\in {\left({H}^1\left({A}_i\right)\right)}^5,\left(i=1,\cdots, N\right)| satisfying\ the\ Dirichlet\ condition\; on\; each\ subboundary\right\}, $$

(13)

where H¹(=W^{1, 2}) is the Sobolev space of square integrable and differentiable of order 1.

2.2 Compliance minimization problem

Using the state equation as the constraint condition, and the compliance as the objective function to be minimized, a distributed-parameter optimization problem for determining the optimal material orientation is formulated as

$$ \mathrm{Find}\kern0.5em \delta {\varphi}^{(i)}\left(\boldsymbol{x}\right) $$

(14)

$$ \mathrm{that}\ \mathrm{minimizes}\kern0.5em l\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right) $$

(15)

$$ \mathrm{subject}\ \mathrm{to}\kern0.5em \mathrm{Eq}.(3) $$

(16)

where δφ⁽ⁱ⁾(x), (x ∈ A_i) is the variation of the x in the material orientation of the i^th ply from its original material orientation φ⁽ⁱ⁾(x), and the updated material orientation ${\varphi}_s^{(i)}\left(\boldsymbol{x}\right)$ is described as ${\varphi}_s^{(i)}\left(\boldsymbol{x}\right)={\varphi}^{(i)}\left(\boldsymbol{x}\right)+\delta {\varphi}^{(i)}\left(\boldsymbol{x}\right)$ (shown in Fig. 2).

Fig. 2

Variation of material orientation of orthotropic material of the i^th ply

2.3 Sensitivity analysis

The Lagrange multiplier method is used to transform this constrained material orientation optimization problem to a non-constrained material orientation optimization problem. Letting $\left({\overline{\boldsymbol{u}}}_0^{(i)},{\overline{w}}^{(i)},{\overline{\boldsymbol{\theta}}}^{(i)}\right)$ denote the Lagrange multiplier of the state equation, the Lagrange functional L associated with this problem is expressed as

$$ {\displaystyle \begin{array}{l}L\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right)\\ {}=l\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right)+l\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)-a\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right).\end{array}} $$

(17)

Using the design field δφ⁽ⁱ⁾(x) to represent the amount of the material orientation variation, the first variation δL of the Lagrange functional L can be expressed as

$$ {\displaystyle \begin{array}{c}\delta L=l\left({{\boldsymbol{u}}^{\prime}}^{(1)},{{\boldsymbol{u}}^{\prime}}^{(2)},\cdots, {{\boldsymbol{u}}^{\prime}}^{(N)}\right)+l\left({{\overline{\boldsymbol{u}}}^{\prime}}^{(1)},{{\overline{\boldsymbol{u}}}^{\prime}}^{(2)},\cdots, {{\overline{\boldsymbol{u}}}^{\prime}}^{(N)}\right)\\ {}-a\left(\left({{\boldsymbol{u}}^{\prime}}^{(1)},{{\boldsymbol{u}}^{\prime}}^{(2)},\cdots, {{\boldsymbol{u}}^{\prime}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right)\\ {}-a\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({{\overline{\boldsymbol{u}}}^{\prime}}^{(1)},{{\overline{\boldsymbol{u}}}^{\prime}}^{(2)},\cdots, {{\overline{\boldsymbol{u}}}^{\prime}}^{(N)}\right)\right)+{\left\langle {G}_{\varphi}^{(i)},\delta {\varphi}^{(i)}\right\rangle}_{\varphi}\end{array}} $$

(18)

$$ {\displaystyle \begin{array}{l}\kern0em \\ {}\begin{array}{l}{\left\langle {G}_{\varphi}^{(i)},\delta {\varphi}^{(i)}\right\rangle}_{\varphi }=\sum \limits_{i=1}^N{\int}_{A_i}{G}_{\varphi}^{(i)}\delta {\varphi}^{(i)}d{A}_i\\ {}=\sum \limits_{i=1}^N{\int}_{A_i}\Big\{{\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{B(i)}}{\partial \varphi }{\overline{\boldsymbol{\kappa}}}^{(i)}\left(\overline{\boldsymbol{\theta}}\right)+{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right)\frac{\partial {\boldsymbol{E}}^{M(i)}}{\partial \varphi }{\overline{\boldsymbol{\varepsilon}}}_0^{(i)}\left({\overline{\boldsymbol{u}}}_0\right)+{\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\overline{\boldsymbol{\varepsilon}}}_0^{(i)}\left({\overline{\boldsymbol{u}}}_0\right)\\ {}\kern2em +{\overline{\boldsymbol{\kappa}}}^{(i)T}\left(\overline{\boldsymbol{\theta}}\right)\frac{\partial {\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\boldsymbol{\varepsilon}}_0^{(i)}\left({\boldsymbol{u}}_0\right)+{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right)\frac{\partial {\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\overline{\boldsymbol{\kappa}}}^{(i)}\left(\overline{\boldsymbol{\theta}}\right)+{\overline{\boldsymbol{\varepsilon}}}_0^{(i)T}\left({\overline{\boldsymbol{u}}}_0\right)\frac{\boldsymbol{\partial}{\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\boldsymbol{\kappa}}^{(i)}\left(\boldsymbol{\theta} \right)\\ {}+{\boldsymbol{\gamma}}^{(i)T}\left(w,\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{S(i)}}{\partial \varphi }{\overline{\boldsymbol{\gamma}}}^{(i)}\left(\overline{w},\overline{\boldsymbol{\theta}}\right)\Big\}\delta {\varphi}^{(i)}d{A}_i,\end{array}\end{array}} $$

(19)

where (⋅)^′ indicates the first variation with respect to the design field δφ⁽ⁱ⁾(x).

The optimality conditions of the Lagrange function L with respect to the state variable ${\boldsymbol{u}}^{(i)}=\left({\boldsymbol{u}}_0^{(i)},{w}^{(i)},{\boldsymbol{\theta}}^{(i)}\right)$ and the adjoint variable ${\overline{\boldsymbol{u}}}^{(i)}=\left({\overline{\boldsymbol{u}}}_0^{(i)},{\overline{w}}^{(i)},{\overline{\boldsymbol{\theta}}}^{(i)}\right)$ are respectively expressed below:

$$ a\left(\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{\prime (1)},{{\overline{\boldsymbol{u}}}^{\prime}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{\prime (N)}\right)\right)=l\left({\overline{\boldsymbol{u}}}^{\prime (1)},{\overline{\boldsymbol{u}}}^{\prime (2)},\cdots, {\overline{\boldsymbol{u}}}^{\prime (N)}\right),\left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right)\in U,\forall \left({\overline{\boldsymbol{u}}}^{\prime (1)},{\overline{\boldsymbol{u}}}^{\prime (2)},\cdots, {\overline{\boldsymbol{u}}}^{\prime (N)}\right)\in \overline{U}, $$

(20)

$$ {\displaystyle \begin{array}{l}a\left(\left({{\boldsymbol{u}}^{\prime}}^{(1)},{{\boldsymbol{u}}^{\prime}}^{(2)},\cdots, {{\boldsymbol{u}}^{\prime}}^{(N)}\right),\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\right)=l\left({{\boldsymbol{u}}^{\prime}}^{(1)},{{\boldsymbol{u}}^{\prime}}^{(2)},\cdots, {{\boldsymbol{u}}^{\prime}}^{(N)}\right),\\ {}\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right)\in \overline{U},\forall \left({{\boldsymbol{u}}^{\prime}}^{(1)},{{\boldsymbol{u}}^{\prime}}^{(2)},\cdots, {{\boldsymbol{u}}^{\prime}}^{(N)}\right)\in U.\end{array}} $$

(21)

(20) is the governing equation for the state variable ${\boldsymbol{u}}^{(i)}=\left({\boldsymbol{u}}_0^{(i)},{w}^{(i)},{\boldsymbol{\theta}}^{(i)}\right),\kern0.36em \left(i=1,2,3,\cdots, N\right)$ and coincides with the state (3). (21) is the adjoint equation for the adjoint variable ${\overline{\boldsymbol{u}}}^{(i)}=\left({\overline{\boldsymbol{u}}}_0^{(i)},{\overline{w}}^{(i)},{\overline{\boldsymbol{\theta}}}^{(i)}\right),\kern0.36em \left(i=1,2,3,\cdots, N\right)$.

When (20) and (21) are satisfied, (18) becomes

$$ \delta L={\left\langle {G}_{\varphi}^{(i)},\delta {\varphi}^{(i)}\right\rangle}_{\varphi }. $$

(22)

Considering the following self-adjoint relationship between (20) and (21),

$$ \left({\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{(N)}\right)=\left({\overline{\boldsymbol{u}}}^{(1)},{\overline{\boldsymbol{u}}}^{(2)},\cdots, {\overline{\boldsymbol{u}}}^{(N)}\right), $$

(23)

the material orientation sensitivity function (or material orientation gradient function) ${G}_{\varphi}^{(i)}$ of this problem is then simply derived as

$$ {\displaystyle \begin{array}{l}{G}_{\varphi}^{(i)}={\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{B(i)}}{\partial \varphi }{\boldsymbol{\kappa}}^{(i)}\left(\boldsymbol{\theta} \right)+{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right)\frac{\partial {\boldsymbol{E}}^{M(i)}}{\partial \varphi }{\boldsymbol{\varepsilon}}_0^{(i)}\left({\boldsymbol{u}}_0\right)+2{\boldsymbol{\kappa}}^{(i)T}\left(\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\boldsymbol{\varepsilon}}_0^{(i)}\left({\boldsymbol{u}}_0\right)\\ {}+2{\boldsymbol{\varepsilon}}_0^{(i)T}\left({\boldsymbol{u}}_0\right)\frac{\partial {\boldsymbol{E}}^{C(i)}}{\partial \varphi }{\boldsymbol{\kappa}}^{(i)}\left(\boldsymbol{\theta} \right)+{\boldsymbol{\gamma}}^{(i)T}\left(w,\boldsymbol{\theta} \right)\frac{\partial {\boldsymbol{E}}^{S(i)}}{\partial \varphi }{\boldsymbol{\gamma}}^{(i)}\left(w,\boldsymbol{\theta} \right).\end{array}} $$

(24)

The components of the stiffness matrices on the right side of (24) will be shown concretely in the next section. Each term involving curvature strain, in-plane strain, and the transverse shear strain in (24) is calculated by (20) or (21), and the finite element method is used to solve those equations. The derived material orientation sensitivity function ${G}_{\varphi}^{(i)}$ will be applied to the proposing H¹ gradient method with Poisson’s equation as an internal heat generation.

3 Stress–strain relations for orthotropic Mindlin–Reissner plates

For an orthotropic lamina, the stress–strain relation in the principal material direction (shown in Fig. 3) is given by the following matrix equation with six independent components (Gürdal et al. 1999):

$$ \left\{\begin{array}{l}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\tau}_{23}\\ {}{\tau}_{31}\\ {}{\tau}_{12}\end{array}\right\}=\left[\begin{array}{l}{Q}_{11}\kern0.5em {Q}_{12}\kern0.5em 0\kern0.5em \begin{array}{cc}\kern0.36em 0& \kern0.24em 0\end{array}\\ {}\begin{array}{ccc}{Q}_{12}& {Q}_{22}& \begin{array}{ccc}0& \kern0.36em 0& \kern0.24em 0\end{array}\end{array}\\ {}\begin{array}{ccc}\kern0.24em 0& \kern0.48em 0& \begin{array}{ccc}\;{Q}_{44}& 0& \kern0.24em 0\end{array}\end{array}\\ {}\begin{array}{ccc}\kern0.24em 0& \kern0.48em 0& \begin{array}{ccc}\kern0.24em 0&\;{Q}_{55}& 0\end{array}\end{array}\\ {}\kern0.24em \begin{array}{ccc}0& \kern0.48em 0& \begin{array}{ccc}\kern0.24em 0& \kern0.36em 0&\;{Q}_{66}\end{array}\end{array}\end{array}\right]\left\{\begin{array}{l}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\gamma}_{23}\\ {}{\gamma}_{31}\\ {}{\gamma}_{12}\end{array}\right\}. $$

(25)

Fig. 3

Variation of material orientation of orthotropic material of the i^th ply

Note that notation i, which indicates i^th ply of lamina in previous section, is not shown in this section for simplicity. The shear strain is expressed as the engineering shear strain. Each component of the Q_ij is a function of the orthotropic material constants, E₁, E₂, v₁₂, v₂₁, G₁₂, G₁₃, and G₂₃, and defined as

$$ {\displaystyle \begin{array}{l}{Q}_{11}=\frac{E_1}{1-{\nu}_{12}{\nu}_{21}}\kern0.36em ,{Q}_{22}=\frac{E_2}{1-{\nu}_{12}{\nu}_{21}},{Q}_{12}=\frac{\nu_{21}{E}_1}{1-{\nu}_{12}{\nu}_{21}}=\frac{\nu_{12}{E}_2}{1-{\nu}_{12}{\nu}_{21}},\\ {}{Q}_{44}={G}_{23},{Q}_{55}={G}_{13},{Q}_{66}={G}_{12}.\end{array}} $$

(26)

Because the orthotropic plates are rotated with respect to a reference coordinate system x − y (shown in Fig. 3), the principal directions of the orthotropic material must be transformed to match the reference axes. The transformed stress–strain relation is given by

$$ \left\{\begin{array}{l}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\tau}_{yz}\\ {}{\tau}_{xz}\\ {}{\tau}_{xy}\end{array}\right\}=\left[\begin{array}{l}{\overline{Q}}_{11}\kern0.62em {\overline{Q}}_{12}\kern0.62em 0\kern0.5em \begin{array}{cc}\kern0.36em 0& \kern0.24em {\overline{Q}}_{16}\end{array}\\ {}\begin{array}{ccc}{\overline{Q}}_{12}&\;{\overline{Q}}_{22}& \begin{array}{ccc}\;0& \kern0.36em 0& \kern0.24em {\overline{Q}}_{26}\end{array}\end{array}\\ {}\begin{array}{ccc}\kern0.24em 0& \kern0.6em 0& \begin{array}{ccc}\kern0.24em {\overline{Q}}_{44}& {\overline{Q}}_{45}& 0\end{array}\end{array}\\ {}\begin{array}{ccc}\kern0.24em 0& \kern0.6em 0& \begin{array}{ccc}\kern0.24em {\overline{Q}}_{45}& {\overline{Q}}_{55}& 0\end{array}\end{array}\\ {}\kern0.24em \begin{array}{ccc}{\overline{Q}}_{16}& {\overline{Q}}_{26}& \begin{array}{ccc}\;0& \kern0.36em 0& \kern0.24em {\overline{Q}}_{66}\end{array}\end{array}\end{array}\right]\left\{\begin{array}{l}{\varepsilon}_{xx}\\ {}{\varepsilon}_{yy}\\ {}{\gamma}_{yz}\\ {}{\gamma}_{xz}\\ {}{\gamma}_{xy}\end{array}\right\}, $$

(27)

where the transformed stiffness matrix ${\overline{Q}}_{ij}$ is given by

$$ {\displaystyle \begin{array}{l}{\overline{Q}}_{11}={U}_1+{U}_2\cos 2\varphi +{U}_3\cos 4\varphi, {\overline{Q}}_{22}={U}_1-{U}_2\cos 2\varphi +{U}_3\cos 4\varphi, {\overline{Q}}_{12}={U}_4-{U}_3\cos 4\varphi \\ {}{\overline{Q}}_{16}=\frac{1}{2}{U}_2\sin 2\varphi +{U}_3\sin 4\varphi, {\overline{Q}}_{26}=\frac{1}{2}{U}_2\sin 2\varphi -{U}_3\sin 4\varphi, {\overline{Q}}_{66}={U}_5-{U}_3\cos 4\varphi \\ {}{\overline{Q}}_{44}={Q}_{44}{\cos}^2\varphi +{Q}_{55}{\sin}^2\varphi, {\overline{Q}}_{45}=\frac{1}{2}\sin 2\varphi \left({Q}_{55}-{Q}_{44}\right),\end{array}} $$

(28)

and the elastic invariant U_i  (i = 1, 2, ⋯, 5) is given by

$$ {\displaystyle \begin{array}{l}{U}_1=\frac{1}{8}\left(3{Q}_{11}+3{Q}_{22}+2{Q}_{12}+4{Q}_{66}\right),{U}_2=\frac{1}{2}\left({Q}_{11}-{Q}_{22}\right),{U}_3=\frac{1}{8}\left({Q}_{11}+{Q}_{22}-2{Q}_{12}-4{Q}_{66}\right)\\ {}{U}_4=\frac{1}{8}\left({Q}_{11}+{Q}_{22}+6{Q}_{12}-4{Q}_{66}\right),{U}_5=\frac{1}{8}\left({Q}_{11}+{Q}_{22}-2{Q}_{12}+4{Q}_{66}\right).\end{array}} $$

(29)

We consider the stress–strain relations of the laminates of the orthotropic plate layers. The stress–strain relation with respect to the bending and membrane stiffness of each layer applies a reduced stiffness of (27) and the stress in the i^th layer can be expressed in terms of the reduced stiffness of that particular layer as

$$ \left\{\begin{array}{l}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\tau}_{xy}\end{array}\right\}=\left[\begin{array}{ccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}\\ {}{\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{26}\\ {}{\overline{Q}}_{16}& {\overline{Q}}_{26}& {\overline{Q}}_{66}\end{array}\right]\left(\left\{\begin{array}{l}{\varepsilon}_{0 xx}\\ {}{\varepsilon}_{0 yy}\\ {}{\gamma}_{xy}\end{array}\right\}+{x}_3\left\{\begin{array}{l}{\kappa}_{xx}\\ {}{\kappa}_{yy}\\ {}{\kappa}_{xy}\end{array}\right\}\right), $$

(30)

where ${\boldsymbol{\varepsilon}}_0^{(i)}$ and κ⁽ⁱ⁾ are the in-plane strain tensor and the curvature tensor in the middle surface of the i^th ply, respectively. Furthermore, the stress–strain relation with respect to the shear stiffness of each layer applies a reduced stiffness of (27), and the stress in the i^th ply can be expressed in terms of the reduced stiffness of that particular layer as

$$ \left\{\begin{array}{l}{\tau}_{yz}\\ {}{\tau}_{xz}\end{array}\right\}=\left[\begin{array}{cc}{\overline{Q}}_{44}& {\overline{Q}}_{45}\\ {}{\overline{Q}}_{45}& {\overline{Q}}_{55}\end{array}\right]\left\{\begin{array}{l}{\gamma}_{yz}\\ {}{\gamma}_{xz}\end{array}\right\}. $$

(31)

The stress resultants, moment resultants, and transverse shear resultants per unit width of the cross section acting at a point in the laminate are obtained by the through-the-thickness integration of the stresses in each layer. Finally, the stiffness matrices E^B(i), E^M(i), E^C(i), and E^S(i)on the right side of (24) can be obtained as follows:

$$ {\displaystyle \begin{array}{l}{\left\{{E}_{\alpha \beta \gamma \delta}^M\right\}}_{\alpha, \beta, \gamma, \delta =1,2}={\int}_{-{t}_i/2}^{t_i/2}\left[\begin{array}{ccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}\\ {}{\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{26}\\ {}{\overline{Q}}_{16}& {\overline{Q}}_{26}& {\overline{Q}}_{66}\end{array}\right]d{x}_3,\\ {}{\left\{{E}_{\alpha \beta \gamma \delta}^C\right\}}_{\alpha, \beta, \gamma, \delta =1,2}={\int}_{-{t}_i/2}^{t_i/2}\left[\begin{array}{ccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}\\ {}{\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{26}\\ {}{\overline{Q}}_{16}& {\overline{Q}}_{26}& {\overline{Q}}_{66}\end{array}\right]{x}_3d{x}_3,\\ {}{\left\{{E}_{\alpha \beta \gamma \delta}^B\right\}}_{\alpha, \beta, \gamma, \delta =1,2}={\int}_{-{t}_i/2}^{t_i/2}\left[\begin{array}{ccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}\\ {}{\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{26}\\ {}{\overline{Q}}_{16}& {\overline{Q}}_{26}& {\overline{Q}}_{66}\end{array}\right]{x}_3^2d{x}_3,\\ {}{\left\{{E}_{\alpha \beta}^S\right\}}_{\alpha, \beta =1,2}={\int}_{-{t}_i/2}^{t_i/2}\left[\begin{array}{cc}{\overline{Q}}_{44}& {\overline{Q}}_{45}\\ {}{\overline{Q}}_{45}& {\overline{Q}}_{55}\end{array}\right]d{x}_3.\end{array}} $$

(32)

Thus, the material orientation sensitivity function ${G}_{\varphi}^{(i)}$ is obtained by the derivative of (32) with respect to material orientation φ⁽ⁱ⁾.

Each term of the material orientation sensitivity function ((24)) derived in the previous section can be obtained by calculating the first variation of (32). Finally, we derive the first variation of stiffness matrix ${\overline{Q}}_{ij}$as follows:

$$ {\displaystyle \begin{array}{l}{\overline{Q}}_{11}^{\prime }=-2{U}_2\sin 2\varphi -4{U}_3\sin 4\varphi, {\overline{Q}}_{22}^{\prime }=2{U}_2\sin 2\varphi -4{U}_3\sin 4\varphi, {\overline{Q}}_{12}^{\prime }=4{U}_3\sin 4\varphi \\ {}{\overline{Q}}_{16}^{\prime }={U}_2\cos 2\varphi +4{U}_3\cos 4\varphi, {\overline{\;Q}}_{26}^{\prime }={U}_2\cos 2\varphi -4{U}_3\cos 4\varphi, {\overline{Q}}_{66}^{\prime }=4{U}_3\sin 4\varphi \\ {}{\overline{Q}}_{44}^{\prime }=-{Q}_{44}\sin 2\varphi +{Q}_{55}\sin 2\varphi, {\overline{Q}}_{45}^{\prime }=\cos 2\varphi \left({Q}_{55}-{Q}_{44}\right).\end{array}} $$

(33)

4 H¹ gradient method for free-material orientation optimization

The free-orientation optimization method consists of three main processes: (1) derivation of the gradient function mentioned in Sect. 2, (2) numerical calculation of the gradient function, and (3) H¹ gradient method for determining the optimal orientation variation and updating. The H¹ gradient method is a gradient method in Hilbert space and is theoretically possible to treat infinite design degrees of freedom. The original H¹ gradient method called traction method at first was proposed for shape optimization of a linear elastic structure by Azegami and Wu (1994), Azegami et al. (1997), and Shimoda and Liu (2014) further extended it for the free-form optimization of shells, where the optimal distribution of the vector design variable can be determined. In addition, the H¹ gradient method is extended to size optimization (Ikeya et al. 2016) and topology optimization with SIMP method (Azegami et al. 2011; Nakayama and Shimoda 2016). The extended H¹ gradient method can determine the optimal distribution of the scalar design variable. The main advantages of the H¹ gradient method are that it can determine the smooth distribution of the design variables and decrease the objective function simultaneously without any design variable parameterization.

In this paper, we develop a novel H¹ gradient method with Poisson’s equation for determining the optimal material orientation distribution based on the extended H¹ gradient method for thickness (Ikeya et al. 2016). The formulation of H¹ gradient method for thickness can be used for material orientation since both of the design variables on thickness and material orientation are scalar variables. With the proposed method, optimal material orientation distribution can be conventionally determined while maintaining the smooth distribution of the design variables and does not require any design variable parameterization.

The concept illustration of the developed H¹ gradient method for material orientation optimization in the present work is shown in Fig. 4. When the state equations and the adjoining equations are satisfied, the perturbation expansion ΔL of the Lagrange functional L can be expressed as

$$ \varDelta L=\left\langle {G}_{\varphi}^{(i)},\varDelta s\delta {\varphi}^{(i)}\right\rangle . $$

(34)

where Δs is a sufficient small positive value.

Fig. 4

Schematic diagram of H¹ gradient method with Poisson’s equation for optimizing the material orientation

To obtain the optimal material orientation variation field δφ⁽ⁱ⁾(x) of the i^th ply, the following weak-formed Poisson’s equation for δφ⁽ⁱ⁾(x) is introduced as

$$ {\displaystyle \begin{array}{l}b\left(\delta {\varphi}^{(1)},{v}^{(1)},\cdots, \delta {\varphi}^{(N)},{v}^{(N)}\right)+{\alpha}_{\varphi}\left\langle \delta {\varphi}^{(i)},{v}^{(i)}\right\rangle =-\left\langle {G}_{\varphi}^{(i)},{v}^{(i)}\right\rangle, \forall {v}^{(i)}\in {C}_{\varphi },\delta {\varphi}^{(i)}\in {C}_{\varphi },\\ {}b\left(\delta {\varphi}^{(1)},{v}^{(1)},\cdots, \delta {\varphi}^{(N)},{v}^{(N)}\right)=\sum \limits_{i=1}^N{\int}_{A_i}\delta {\varphi}_{,i}^{(i)}{k}_{ij}{v}_{,j}^{(i)}d{A}_i,\end{array}} $$

(35)

where δφ⁽ⁱ⁾(x) denotes the material orientation field. The notations α_φ(>0) and k_ij are equivalent to the heat transfer coefficient and the thermal conductivity matrix in the heat transfer analysis, respectively. C_φ is the function space of the kinematically admissible temperatures that satisfy the Dirichlet conditions for material orientation variation δφ⁽ⁱ⁾(x), and Cv is defined as

$$ {C}_v=\left\{{v}^{(i)}\in {H}^1|\ {v}^{(i)}=0 on\ the\ Dirichlet\ boundaries\right\}. $$

(36)

The Dirichlet conditions of (Cφ) can be arbitrarily defined by only considering the design requirement for the material orientations.

Substituting (35) into (34) and considering the arbitrariness of v⁽ⁱ⁾ in (35), we obtain

$$ \varDelta L=\left\langle {G}_{\varphi}^{(i)},\varDelta s\delta {\varphi}^{(i)}\right\rangle =-\varDelta s\left(b\left(\delta {\varphi}^{(1)},\delta {\varphi}^{(1)},\cdots, \delta {\varphi}^{(N)},\delta {\varphi}^{(N)}\right)+{\alpha}_{\varphi}\left\langle \delta {\varphi}^{(i)},\delta {\varphi}^{(i)}\right\rangle \right). $$

(37)

Furthermore, considering the positive definitiveness of α_φ〈δφ⁽ⁱ⁾, δφ⁽ⁱ⁾〉 > 0 and b(δφ⁽¹⁾, v⁽¹⁾, ⋯, δφ^(N), v^(N)) > 0 in (37), we have ΔL < 0. This relationship holds true in a piecewise convex design space. As above-mentioned, the gradient function is not applied directly to update the material orientation variation but rather is replaced by a fictitious internal heat generation. This makes it possible both to reduce the objective functional and to maintain the smoothness of the design variable distribution, simultaneously. α_φ has a role of smoothing filter for controlling the influence range of the shape gradient function at a point. With larger α_φ, the influence area of the material orientation sensitivity function is smaller. With smaller α_φ, the influence area of the material orientation sensitivity function is larger, and then the material orientation distribution becomes smoother, or the curvature change of the material orientation flow becomes smaller. Generally, there is a trade-off relationship between them. This value is empirically defined based on the numerical experiment in advance, which will be shown in Sect. 5.2.1.

Figure 5 shows the schematic flowchart of the optimization system developed in this study. The material orientation optimization process is summarized as (1) stiffness analysis by (20) and evaluation of objective function; (2) calculation of material orientation sensitivity function by (24); (3) the negative material orientation gradient function $-{G}_{\varphi}^{(i)}$ is applied layer by layer as a distributed internal heat generation to a fictitious elastic shell structure to the design surface of the i^th ply. The material orientation variation field δφ(x) is calculated as the temperature field of Poisson’s equation; (4) updating of the material orientation by using δφ(x).

Fig. 5

Flowchart of optimization process

This process is repeated until the optimal material orientation distribution is obtained. A commercial FEM code is used for the processes in yellow. The optimization system can be easily constructed in combination with a commercial FEA code because the proposed method does not need to manipulate the stiffness matrix in each process. We use MSC/NASTRAN in this study. The proposed method can therefore be applied to practical and actual design works.

5 Numerical results

The proposed distributed-parametric optimization method for free-orientation is applied to design a single-layer rectangular plate, a single-layer square plate, and three-layer hemi-cylindrical shell to verify the effectiveness of the material orientation optimization method for laminated anisotropic shell structures. The following constants are used in all design examples. Young’s moduli of each orthotropic element E₁ and E₂ are 210 and 21 GPa, respectively except for Sects. 5.2.4 and 5.4.2. In Sect. 5.2.4, the influence of the ratio E₁ : E₂ on both the compliance and the obtained material orientation is studied for various ratios. Transverse elasticity modulus G₁₂ = 65 GPa and Poisson’s ratio v₁₂ = 0.3. The thickness of each layer is set to 1 mm. The ratio of heat transfer coefficient α_φ to the thermal conductivity coefficient k in the thermal conductivity matrix k_ij in the H¹ gradient method with Poisson’s equation is set to α_φ : k = 1 : 4 except for Sect. 5.2.1, where the influence of the ratio α_φ : k to both the compliance and the obtained material orientation is studied for various ratios. With the aim of a completely free design of material orientation, the Dirichlet conditions (or δφ⁽ⁱ⁾(x) = 0) are not applied in the H¹ gradient method in all the design examples shown in this paper.

5.1 A single-layer rectangular plate

Figure 6a shows the boundary condition of a single-layer rectangular plate and its initial material orientation of E₁ distributing in the parallel direction of the y-axis. The design domain is a rectangle of size 1 : 3 and consists of 1200 triangular elements. One side of the plate is clamped and a concentrated shear force is applied at the center of the opposite side. The obtained arbitrary and optimal material orientation of E₁ is shown in Fig. 6b. The iteration history of compliance and the comparison of initial and optimal strain energy density distribution are shown in Fig. 7. The obtained optimal material orientation shows the combination of maximum and minimum principal stress directions and maintains the smooth distribution. The compliance is reduced by about 90% and the strain energy density distribution is more homogeneous than the initial distribution as shown in Fig. 7c. One of the intuitive ideas generally known to improve the stiffness is to distribute the material orientation in the principal stress directions that results in an improvement of the stiffness. The principal direction of the initial state is shown in Fig. 8 to compare with the optimized material orientation distribution. The red arrows indicate the maximum principal directions, and blue arrows indicate the minimum principal directions. Both of the two principal stress directions and optimal material orientation distribution show some similarity. However, we can see the difference of distribution around the middle axis. We confirmed that the compliance of the optimal distribution obtained with the proposed method was 3% lower than the one obtained with the principal stress approach.

Fig. 6

Boundary condition and comparison of material orientations of E₁

Fig. 7

Iteration history of compliance and comparison of strain energy density distribution

Fig. 8

Distributions of maximum and minimum principal stress direction of the initial model

5.2 Single-layer square plate

In this subsection, the influence of the ratio of the heat transfer coefficient α_φ to the heat conduction coefficient k in the H¹ gradient method with Poisson’s equation, the mesh dependency, and the influence of Young’s moduli ratio of E₁ to E₂ are studied through numerical experiments with a single-layer square plate, where L = 100 mm and all-sides are clamped and a downward force of 10 N is applied at the center of the plate as shown in Fig. 9a. For benchmarking, some results obtained through the proposed method are compared to those obtained with other comparable methods.

Fig. 9

Definition of the single-layer square plate problem

5.2.1 Influence of ratio of α _φ : k in H¹ gradient method with Poisson’s equation

As stated in Sect. 4, α_φ has a role of smoother of the material orientation. We study the influence of α_φ on both the obtained material orientation and the compliance, varying the ratio of α_φ to k. As shown in Fig. 9a, the FE model is discretized to 6400 triangular elements. The initial material orientation E₁ is set parallel to the x-axis, and the quarter symmetric condition for material orientation is applied to the square plate as shown in Fig. 9b.

Figure 10 compares the material orientations obtained for the various ratios of α_φ : k, where the orientations of E₁ over the quarter part (upper left section of the plate) are shown. The compliances normalized to that of the initial material orientation are compared in Fig. 11. Different material orientations are obtained by varying the magnitude of α_φ. The material orientation shows a complex pattern with large curvatures when α_φ = 1. The compliance decreases by about 37% when α_φ = 1. With smaller α_φ, the material orientation flow curvature and curvature change are reduced, and the material orientation flow shows nearly straight lines, and the compliance reduction becomes smaller. By setting production-related constraints on the maximum curvature or the curvature distribution of the material orientation, we can define the magnitude of α_φ. In this paper, we use α_φ = 1 (α_φ : k = 1 : 4), since the compliance obtained shows the smallest value, and the material orientation is smooth.

Fig. 10

Comparison of obtained material orientation distributions for various α_φ : k

Fig. 11

Comparison of compliances for various α_φ : k

5.2.2 Benchmarking

The result obtained through the proposed method is here compared to those obtained with the so-called continuous fiber angle optimization (CFAO), the BCP, and the NDFO methods. Note that all the comparison results are quoted from Kiyono et al. (2017). The CFAO (Stegmann and Lund 2005; Nomura et al. 2015) changes the material orientation at the centers of finite elements continuously and independently. It is also known to present the multiple local minima problem, where the optimal solution is highly dependent on the initial material orientation. The BCP (Gao et al. 2012) and the NDFO (Kiyono et al. 2017) methods were proposed to avoid the local minima problem as alternatives to the CFAO.

With the same single-layer square plate and the boundary condition as Fig. 9a, the 45^° symmetry condition for the material orientation is applied to the design domain as shown in Fig. 12. The initial material orientation E₁ is set parallel to the x-axis as shown in Fig. 12. The material constants are changed to compare with those methods as follows: the original values of the Young’s moduli E₁, E₂, and the transverse elasticity modulus are 135 GPa, 10 GPa, and 65 GPa, respectively. The initial material orientation is required in both the CFAO and the G₁₂proposed method to obtain the optimal solution. In contrast, the BCP and the NDFO methods require the candidates of the material orientation for optimization procedure. Figure 13 shows the optimal results by using the CFAO, BCP, NDFO, and the proposed methods. In addition, Fig. 14 shows the comparison of the initial compliance for the CFAO and the proposed methods, and the final compliance in each method.

Fig. 12

Forty-five degree symmetric condition for material orientation design of square plate problem

Fig. 13

Comparison of optimal results for each method

Fig. 14

Comparison of compliances for each method

The comparison results of optimal material orientation follow the similar pattern in the center region and outside region. In the center region, the material orientations are radially arranged as circles. In the CFAO result, the final compliance is lower than the BCP since the CFAO has larger design freedom. However, some of the material orientations have been wrongly oriented and the continuous material orientation has not been satisfied. In the NDFO result, it has the lowest compliance of all comparison results and presents more organized material orientation distribution. Figure 13c shows the optimal result, which is simply obtained by the NDFO. The rest of the results show the optimal result, which are obtained by the NDFO with the material orientation continuity represented as NDFO-C. (Kiyono et al. 2017) The NDFO-C uses the filter for the material orientation continuity, which is a spatial filter based on the projection technique. In this method, the material orientation continuity is smoother with larger filter radius; however, there is a constraint in the arrangement of the material orientation, the compliance in Fig. 13d, e is greater than the NDFO result.

With all these results as a comparison, the optimal result obtained by the proposed method has the lowest compliance in all cases while maintaining the continuous material orientation distribution. The optimal material orientation distribution follows the similar pattern in the center region and outside region except each corner region where lower sensitivity is calculated. The proposed method and the CFAO have the largest design freedom, hence having the biggest potential for minimizing the compliance. The differential between the proposed method and the CFAO is the material orientation continuity, which is important not only for manufacturing issues, but also to avoid the stress concentrations at discontinuous orientations. Therefore, the comparisons can be summarized as follows. The main advantages for the proposed method are distributed-parametric optimization method for free-orientation, solving a large-scale structure efficiency and reducing the compliance while maintaining the smooth material orientation. On the other hand, the disadvantage is that the proposed method has a potential to obtain a local optimal solution, and it is dependent on the initial material orientation since it is a gradient-based method. However, this disadvantage could be solved by changing the initial material orientation distribution.

5.2.3 Mesh dependency

As mesh dependency is one of the common issues for the structural optimization techniques with finite element method, we study here the influence of the level of mesh refinement to the optimal material orientation. Figure 15a, b has the same design domain and boundary conditions as those in Fig. 12, but the number of elements is reduced to 1600 elements and 400 elements, respectively. By comparing to Figs. 13f, and 15a, b shows that although the smoothness, or continuity, seems to be poor due to the decrease of the number of elements, the material orientation distribution follows almost the same pattern. The initial and optimal compliances in Fig. 15a, b are almost similar with (0.99, 0.40) and (0.98, 0.42), respectively. It is confirmed that the smooth material orientation distribution can be obtained even for a coarse mesh model with the proposed method.

Fig. 15

Comparison of optimal results according to the number of elements

5.2.4 Influence of Young’s moduli ratio of E ₁ and E ₂

We study the influence of Young’s moduli ratio of E₁ to E₂ on the optimal material distribution with the same single-layer square plate shown in Fig. 9a. Four different ratios of 1:1, 5:1, 10:1, 100:1 are compared, assuming G₁₂ is constant. The original value of E₁ and G₁₂ are 210 and 65 GPa, respectively. Note that the quarter symmetric condition is applied to the square plate this time. Figure 16 shows the optimized material orientation distribution of each Young’s moduli ratio, and all of the optimal results express the same tendency as forming the closed shape material orientation around the load point. This comparison result shows the utility of the proposed method to optimize the orthotropic material with any Young’s moduli ratio. For example, extending this idea to manufacture the composite materials with unidirectional tapes (UD-tapes) when we calculate the optimization problem with a much larger ratio of E₁ than E₂.

Fig. 16

Comparison of optimized material orientation for each Young’s moduli ratio

5.3 Three-layer hemi-cylindrical shell

We optimize a three-layer hemi-cylindrical laminated shell structure as shown in Fig. 17. The quarter symmetric condition is applied to the design domain according to the gray area in Fig. 17, and the quarter part is discretized to 720 triangular elements. The initial material orientation of E₁ in each layer is distributed in the direction parallel to the x-axis. The obtained optimal orientation of E₁ in each layer of a quarter of the shell structure is shown in Fig. 18. As shown in Fig. 18, each layer has a different optimal material orientation of E₁ while maintaining the smooth distribution. The compliance is reduced by approximately 65%. Therefore, we can obtain the arbitrary and optimal material orientation of each layer of a laminated shell structure and minimize the compliance simultaneously.

Fig. 17

Boundary condition of stiffness analysis and initial material orientation of E₁ of hemi-cylindrical shell with three layers

Fig. 18

Optimal material orientation of E₁ of each layer

5.4 Applicative numerical problems

5.4.1 Fuselage-like shell structure

We optimize a fuselage-like shell structure of an airplane composed of anisotropic materials as an applicative design problem. Figure 19a shows a simplified model of a fuselage part of an airplane with three layers, which is reinforced by longitudinal U-stiffeners as shown in Fig. 19b. The design domain is discretized to 3640 triangular elements. The boundary condition and the initial material orientation of E₁ in each layer are distributed in the direction parallel to the x-axis as shown in Fig. 19a. The two corners of one side and the center of the opposite side are pinned, and a distributed load of 150 N is applied at the center of the surface. The optimal results of the shell surface and longitudinal U-stiffeners in each layer are shown in Figs. 20 and 21, respectively. We observed that each layer has a different optimal material orientation distribution while maintaining the continuity. The compliance of the laminated shell structure is decreased by 45% by arbitrarily optimizing the material orientation in each layer.

Fig. 19

Simplified model of a fuselage of airplane with three layers reinforced by longitudinal U-stiffeners

Fig. 20

Optimal material orientation of E₁ of each layer of hemi-cylindrical shell surface

Fig. 21

Optimal material orientation of E₁ of each layer of longitudinal U-stiffeners

5.4.2 Yacht sail

Another applicative design problem is the optimization of a simplified model of a yacht sail as shown in Fig. 22a. The design domain is discretized to 911 triangular elements. The materials used in sails, as of today, are polymers and plastic fibers in general. For the advanced yacht such as racing yacht, more contributions to the lower weight and higher intensity are required. The high intensity material such as carbon fiber can meet those requirements, so optimization of the material orientation of the sail is important. In this design problem, the sail is assumed to be a linear elastic material for simplicity and we use Young’s moduli ratio of E₁ and E₂ as 100:1 and assume that manufacture of the fiber in the sail with unidirectional tapes (UD-tapes). Before optimizing the material orientation, we determined the curvature of the sail by solving a numerical form-finding problem for the minimal surface of membrane structures (Shimoda and Yamane 2015). The area constraint of the sail was set as 101% and the optimal shape of the sail is shown in Fig. 22b. Then, we optimize the material orientation in the optimal shape, in which the initial material orientation distributes to the z-axis direction. The boundary condition is shown in Fig. 22b, where three corners and one side are simply supported. A surface load is applied on all elements for simulating the wind power to propel yacht. Figure 23a shows the optimal material orientation of E₁ in each mesh, and Fig. 23b shows the continuous fibers connected by a line among the material orientation of each element. The continuous connected line indicates the path to tape the fiber with UD-tapes, though some un-continuous lines occur due to the difference of the angle of the material orientation among the elements. The compliance is decreased by about 80% by optimizing the material orientation smoothly. Thus, we can confirm the utility of the proposed method for optimizing the fiber path such as UD-tapes in the simplified model of a sail.

Fig. 22

Boundary condition of a simplified model of a sail of yacht

Fig. 23

Optimal material orientation of E₁

6 Conclusions

In this paper, we proposed a distributed-parametric optimization method for free-orientation based on the variational method and a novel H¹ gradient method with Poisson’s equation. The H¹ gradient method with Poisson’s equation determines the arbitrary and smooth optimal distributions of the material orientation of the laminated anisotropic shell structures, which enables to develop the potential of the CFRP. Considering compliance as an objective function, the optimization problem was formulated and the sensitivity function for material orientation variation was derived. The validity and practicality of the proposed optimization method were verified by several design examples involving realistic structures such as the fuselage of an airplane and a yacht sail. The influence of the ratio α_φ : k on the proposed H¹ gradient method, the benchmarking with other comparable methods, the mesh dependency, and the influence of Young’s moduli ratio of E₁ to E₂ on the obtained results were also investigated and discussed.

It is generally known that the optimization problem for the material orientation has multiple local minima. Our results may also be one of the multiple local minimum solutions since our proposed method is based on the gradient method. However, a value exists to determine one of them for the engineering and industrial design, especially for large-scale design problems with material orientation of every element in every layer of a complicated-shape.