Efficient design optimization strategy for structural dynamic systems using a reduced basis method combined with an equivalent static load

Abstract

This paper presents an efficient structural design optimization strategy that combines the reduced basis method (RBM) with the equivalent static load (ESL). In dynamic response optimization using ESL, the computation of a static system optimization is repeatedly executed under multiple static loads. In this process, we propose parametrizing the static system and employing the RBM with global proper orthogonal decomposition (POD). In general, the snapshots for the sampling procedure under multiple loads increase proportionally to the number of loads, which results in an inefficient computational procedure. Thus, we propose taking snapshots with a proper orthogonal mode (POM) of the multiple loads rather than for the multiple loads themselves. The number of snapshots then decreases, and the original system can be efficiently reduced. We directly employ the framework of the proposed RBM with the POM of multiple loads to ESL-based design optimization, and the results indicate that the proposed method is more efficient than conventional ESL-based optimization as well as a full order model. Various numerical examples, including comparisons of relative errors and the dynamic response optimizations, support the strength of the proposed strategy.

1 Introduction

Structural design optimization for dynamic systems requires extensive computational resources because transient analyses and design variable updates require repetitive computations. Even though high performance computers with large quantities of storage can cope with the massive computational burden, the CAD models and finite element mesh models continue to increase in size. In other words, high-fidelity, full-sized models are still problematic for the computational mechanics of dynamic system optimization. As a consequence, various studies have focused on developing efficient design optimization of large-scale dynamic systems (e.g., Feng et al. 1977; Chahande and Arora 1994; Park 2011).

Design optimization using the equivalent static load (ESL) efficiently optimizes various large-scale structures under dynamic loads. Choi and Park (1999) proposed an ESL-based dynamic response optimization method, and many studies since then carried out using the ESL, i.e., design optimization of a linear dynamic system (Kang et al. 2001; Choi and Park 2002), nonlinear dynamic response problems (Kim and Park 2010), the design of an elastic-plastic material, and shape and topology optimization problems (Park et al. 2005; Lee and Park 2015). The general design optimization of the dynamic response requires a transient analysis during the design variable update. ESL-based design optimization repeats the design optimization of a static problem several times until convergence of the design variables by transforming the dynamic problem to a static one with multiple loads. Thus, major time is saved by decreasing the number of repetitive computations. However, the size of the system matrix (i.e., mass, damping, and stiffness matrix) does not change. In other words, there is no ‘order reduction’ of the dynamic system.

On the other hand, a reduced-order model (ROM) is an attractive, popular approach that commonly requires significant computational resources for the analysis and design of large-scale dynamic systems. In fact, since the ROM can be employed in most fields requiring big-sized data, it has a wide range of applications such as computational fluid dynamics (Willcox and Peraire 2002), vibration/acoustic systems (Davidsson and Sandberg, 2006), microelectromechanical systems (Liang et al. 2002), molecular systems (Hoang et al. 2016), weather prediction (Daescu and Navon 2008), etc. (Antoulas 2005). For a design problem in computational structural dynamics, the model order reduction can be applied to significantly relieve the computational burden in a design optimization problem that requires iterative and repetitive computations. The order reduction techniques are introduced in discrete governing equations to obtain reduced, small-sized system matrices that can be used in the optimization procedures, for example, computing nonlinear constraint functions and design sensitivities. As a consequence, even though all processes of the design optimization using the ROM are the same as those using the full order model (FOM), the computational time is greatly reduced since the size of the vectors and matrices decreases.

Actually, numerous methods have been developed to achieve design optimization in conjunction with reduced order modelling, such as, surrogate-based design optimization (Queipo et al. 2005; Forrester and Keane 2009), interpolation-based ROM adaption methods (Amsallem et al. 2015; Zahr and Farhat 2015), ROM-based combined with substructuring schemes (Kim and Cho 2007; Lee and Cho 2017), etc. (see, e.g. Shan and Wang 2010). Among these theories, research has been actively conducted on parameterized ROM since Balmès (1996) employed the reduced basis method (RBM) to project the FOM to a generalized coordinate system generated by considering a change in the system parameters. To be specific, Balmès derived the reduced basis of a parameter-dependent system by displacement snapshots obtained by solving the FOM changes in the parameter of a structure within a certain range. The proper orthogonal decomposition (POD) is employed in the displacement snapshots to obtain the reduced basis. Basically, if the parameter of a structure changes, the FOM has to be reconstructed. Then, the computational time increases as the number of finite elements increases. For a conventional finite element procedure, the system matrices are integrated whenever the value of the parameter changes, which results in a great increase in the computational time. However, if the FOM is projected to the space generated by considering the changes in the parameter, the computational time decreases significantly since the reconstruction process is executed in a reduced space. Therefore, the ROM derived by the RBM is very efficient and useful in structural design optimization. After Balmès, many researchers developed various methods, i.e., real-time solution strategies (Prud’homme et al. 2002), a posterior error estimation (Veroy 2003), an extension to non-affine parameterization case (Grepl et al. 2007) and certified reduced basis method (Quarteroni et al. 2011).

Although both the ESL and ROM have the same purpose that efficiently manages large-scale dynamic systems, the ways of acquiring the efficiency of the computation are different from each other. Whereas the ESL-based method decreases the number of repetitive computations, the ROM reduces the size of the system. Therefore, we expect the efficiency to increase to a higher level by combining reduced order modelling with ESL-based design optimization, and such work is comparatively recent. Kim et al. (2014) introduced degree-of-freedom-based (DOF-based) system reduction to decrease the computational burden of the dynamic response optimization. However, even though ESL-based design optimization combined with DOF-based reduction is more efficient than a conventional ESL-based method, the projector of the DOF-based reduction should be computed whenever the parameter changes since most of the DOF-based reduction methods reduce the FOM depending on the dynamic characteristics of the system (O’Callahan 1989; Friswell et al. 1995). Therefore, we need to develop a strategy that does not compute the basis whenever the values of the parameter are updated.

The main idea of the proposed method is to apply the RBM to an ESL-based approach to execute an efficient structural design optimization for dynamic systems. Since the system matrices have the size of the FOM during conventional ESL-based design optimization, we can improve the efficiency of the optimization by employing model order reduction to full-sized matrices. In ESL-based optimization, the external load is represented by multiple column vectors rather than a single vector. However, the RBM is not applicable to the multiple loading conditions. Therefore, in this paper, we propose calculating the proper orthogonal modes (POM) of the external loads, which makes it possible to employ the RBM in reduction and parameterization of the system under multiple loads. Fortunately, the meaning of the POM of the external loads in the ESL-based approach is the same as the POM of the acceleration vectors multiplied by the mass matrix, which is calculated naturally during the transient analysis in the ESL-based approach. As a consequence, few additional computations are required to obtain the POM of the external loads.

This paper is organized as follows. In Section 2, we introduce the global-POD method to employ the RBM in the problem with multiple loads. Then, the POM for the external loads is derived for multiple loads in general. In Section 3, a strategy is proposed for structural optimization by combining the multiple-load RBM with the ESL-based approach. In Section 4, we verify the accuracy and efficiency of the proposed optimization strategy by dealing with some numerical examples providing related discussions. In Section 5, we finish our paper with the conclusion and suggestions for further research.

2 Reduced basis method for multiple loads

To combine the RBM with ESL-based design optimization, we first need to derive the RBM for use under multiple loads. In this section, we introduce a global-POD method to compute the POM of the external load.

2.1 Reduced basis method and global proper orthogonal decomposition

For the RBM, we have to define the operating point at which the displacement snapshots are obtained. The operating points are in a design space, such that,

(1)

where is the set of the feasible design variables, μ is a vector of design parameters, N_p is the size of parameter, and ‘lb’ and ‘ub’ represent ‘lower bound’ and ‘upper bound’ of the design variables, respectively. The set of operating points can be defined as

(2)

where N_s denotes the number of operating points and μ_i is expressed as

$$ {\boldsymbol{\mu}}_i={\left[{\mu}_i^1\kern0.5em {\mu}_i^2\kern0.5em \cdots \kern0.5em {\mu}_i^{N_p}\right]}^T. $$

(3)

For example, if we have three different samples of the elastic modulus, N_s = 3, and if two different areas of a structure have each modulus, N_p = 2.

For multiple loads, the RHS of the static finite element equation becomes multiple column vectors as follows:

$$ \mathbf{K}\left(\boldsymbol{\mu} \right)\mathbf{U}\left(\boldsymbol{\mu} \right)=\mathbf{F}, $$

(4)

where

$$ \mathbf{K}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{N\times N},\mathbf{U}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{N\times {N}_f}, $$

(5)

and $\mathbf{F}\in {\mathbf{\mathbb{R}}}^{N\times {N}_f}$. K represents a stiffness matrix, U and F are the column matrices of displacements and forces, respectively. N_f is the number of loads, and N represents the size of the FOM, which is determined by the FE discretization of the system. The displacement snapshot at the operating point μ_i and the load f_j is obtained as

$$ {\mathbf{u}}_j\left({\boldsymbol{\mu}}_i\right)={\mathbf{K}}^{-1}\left({\boldsymbol{\mu}}_i\right){\mathbf{f}}_j,\left\{\begin{array}{l}i=1,2,\cdots, {N}_s\\ {}j=1,2,\cdots, {N}_f\end{array}\right., $$

(6)

where ${\boldsymbol{\mu}}_i\in {S}_{\mu}^{N_p}$, and u_j and f_j are the column vectors of U and F, respectively. For multiple loads, the displacement is not only a function of the parameter, but also a function of the loading. Thus, we introduce the global-POD method (Taylor 2001; Amsallem 2010) employed for the matrix of the displacement snapshots. The corresponding j-th snapshot matrix is constructed under the j-th load, such that

$$ {\mathbf{X}}_j=\left[{\mathbf{u}}_j\left({\boldsymbol{\mu}}_1\right)\kern0.5em {\mathbf{u}}_j\left({\boldsymbol{\mu}}_2\right)\kern0.5em \cdots \kern0.5em {\mathbf{u}}_j\left({\boldsymbol{\mu}}_{N_s}\right)\right]\in {\mathrm{\mathbb{R}}}^{N\times {N}_s}. $$

(7)

In this work, we did not used any weight to each snapshot since we used a uniform time step in the transient analysis (see, Section 3–3 for details). By allocating X_j side by side, the total snapshot matrix can be constructed, and the POD is successively employed to the snapshot matrix $\widehat{\mathbf{X}}$ in a global manner:

$$ {\displaystyle \begin{array}{c}\widehat{\mathbf{X}}=\left[{\mathbf{X}}_1\kern0.5em {\mathbf{X}}_2\kern0.5em \cdots \kern0.5em {\mathbf{X}}_{N_f}\right]\\ {}={\boldsymbol{\Phi} \boldsymbol{\Sigma} \mathbf{A}}^T.\end{array}} $$

(8)

where Φ is the proper orthogonal mode (POM), Σ is a diagonal matrix of singular values, and A is the right singular vector. In (8), $\widehat{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{N\times {N}_g}$, and N_g = N_s × N_f. Thus, N_g number of displacement snapshots are obtained. Then, a low-dimensional global approximation space can be spanned by the snapshots in (6), such that

$$ {W}_{N_p}=\mathrm{span}\left\{{\zeta}_i\equiv \mathbf{u}\left({\boldsymbol{\mu}}_i\right),i=1,2,\cdots {N}_s\right\}. $$

(9)

Various approaches can efficiently extract the reduced basis. In this work, we used a sampling strategy with replacement based on the greedy sampling strategy. After constructing the RB space based on the first sample that is randomly selected in a predefined parameter set, we compute the errors of the RB space over the whole parameter set. And then we choose the second sample that generates the maximum of error. Details can be found in literatures (Rozza et al. 2008, Quarteroni et al. 2011). We employed the classical POD method after determining the number of samples via the error comparison of the greedy algorithm (see, Section 4 for details).

From the Φ matrix in (8), R number of modes can be selected, which is determined by introducing the numerical rank of the snapshot matrix $\widehat{\mathbf{X}}$. In practice, the singular values in Σ represent energies of the corresponding modes. Thus, if we select the R modes that have the largest singular values, the summation of selected singular values becomes the energy of the ROM. Details of the entire procedures of the POD and SVD are well explained in the literature (see, e.g., Buljak 2011). The selected modes are the reduced basis as follows:

$$ \mathbf{T}=\left[{\phi}_1\kern0.5em {\phi}_2\kern0.5em \cdots \kern0.5em {\phi}_R\right]\in {\mathrm{\mathbb{R}}}^{N\times R},R\le {N}_g. $$

(10)

Note that the projection T does not depend on the parameter μ. Then, the displacement of the FOM can be approximated as

$$ \mathbf{u}\left(\boldsymbol{\mu} \right)\approx \mathbf{T}\overline{\mathbf{v}}\left(\boldsymbol{\mu} \right). $$

(11)

To obtain the reduced system, the stiffness matrix is parameterized as follows:

$$ \mathbf{K}\left(\boldsymbol{\mu} \right)=\sum \limits_{i=1}^{N_s}{w}_i\left(\boldsymbol{\mu} \right){\mathbf{K}}_i, $$

(12)

where K_i = K(μ_i) and is computed at the operating points. In general, the interpolation of (12) should be conducted in the tangent space since the stiffness K is the symmetric positive-definite matrix manifolds (see, e.g., Amsallem 2010). Substituting Eqs. (11) and (12) into (4), and multiplying T^T to the left of (4) yields

$$ \overline{\mathbf{K}}\left(\boldsymbol{\mu} \right)\overline{\mathbf{V}}\left(\boldsymbol{\mu} \right)=\overline{\mathbf{F}}, $$

(13)

where

$$ \overline{\mathbf{K}}\left(\boldsymbol{\mu} \right)=\sum \limits_{i=1}^{N_s}{w}_i\left(\boldsymbol{\mu} \right){\mathbf{T}}^T{\mathbf{K}}_i\mathbf{T}, $$

(14)

$$ \overline{\mathbf{F}}=\kern0.5em {\mathbf{T}}^T\mathbf{F}, $$

(15)

where

$$ \overline{\mathbf{K}}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{R\times R},\overline{\mathbf{V}}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{R\times {N}_f},\overline{\mathbf{F}}\in {\mathrm{\mathbb{R}}}^{R\times {N}_f} $$

(16)

Thus, for a new operating point ${\boldsymbol{\mu}}^{\ast}\notin {S}_{\mu}^{N_p}$, the following reduced system can be solved with a much smaller resource for the computation than that of the FOM, such that

$$ \overline{\mathbf{V}}\left({\boldsymbol{\mu}}^{\ast}\right)={\overline{\mathbf{K}}}^{-1}\left({\boldsymbol{\mu}}^{\ast}\right)\overline{\mathbf{F}}. $$

(17)

Finally, the displacement is recovered by the projection matrix T as given by (11).

2.2 Proper orthogonal mode of multiple loads

To employ the global POD to the FOM, we have to take displacement snapshots under a multiple loading condition as shown in (6). However, the computational resources for solving (6) depend on the number of loads. Therefore, we propose reducing the number of multiple loads. To do so, we calculate the POM of the external force by applying the POD to multiple load vectors. In fact, various researches have been carried out regarding the POD of the loads (Tamura et al. 1999; Chen and Kareem 2005). In the present study, we can directly employ the previously reported cases except the one that we cannot uniquely determine the eigenvectors during the POD computations. If the mode of loads is not available, we have no choice but to solve (6) without any reduction in the external loads. For the ESL, the POM of the loads has an obvious meaning. Therefore, by computing the POM of the ESL, we can handle (6) without many computational resources. The detailed procedure related to the ESL will be handled in Section 3. To obtain the POM of the loads, the snapshot matrix and the SVD of the external forces are written as

$$ \mathbf{F}={\boldsymbol{\Phi}}_{\mathbf{F}}{\boldsymbol{\Sigma}}_{\mathbf{F}}{\mathbf{A}}_{\mathbf{F}}^T, $$

(18)

where

$$ {\boldsymbol{\Phi}}_{\mathbf{F}}=\left[{\gamma}_1\kern0.5em {\gamma}_2\kern0.5em \cdots \kern0.5em {\gamma}_{N_{\gamma }}\right]\in {\mathbf{\mathbb{R}}}^{N\times {N}_{\gamma }},{N}_{\gamma}\le {N}_f. $$

(19)

In (19), N_γ denotes the number of modes, which is smaller than N_f if the rank of F is smaller than N_f. In addition, since Φ_F follows the properties of the SVD, the lower modes contain the most energy of the external forces. Therefore, by selecting R_γ < N_γ basis from Φ_F, we can obtain the POM of the external force, $\boldsymbol{\Gamma} \in {\mathbf{\mathbb{R}}}^{N\times {R}_{\gamma }}$. Finally, by replacing f_j by γ_j in (6), we compute the N_s × R_γ number of displacement snapshots.

The remaining parts are the same as the procedure from (12) to (15). The computational gain of introducing the POM of external load is that (i) the initial sampling time is reduced since the number of computations for the displacement snapshots is reduced from N_f to R_γ; and (ii) the size of the snapshot matrix $\widehat{\mathbf{X}}$ in (8) is also reduced, which results in a fast computation of the POM Φ.

3 Structural optimization strategy using reduced equivalent static load

3.1 Design optimization for dynamic responses

In this chapter, we propose an optimization strategy for a structure under a dynamic load based on the finite element framework. To this end, the parameter that is also a design variable of the structure should be expressed in the equation of motion. A parameter dependent on the equation of motion of the FE discretized system that consists of symmetric positive-definite matrices is expressed as

$$ \mathbf{M}\left(\boldsymbol{\mu} \right)\ddot{\mathbf{u}}\left(t;\boldsymbol{\mu} \right)+\mathbf{C}\left(\boldsymbol{\mu} \right)\dot{\mathbf{u}}\left(t;\boldsymbol{\mu} \right)+\mathbf{K}\left(\boldsymbol{\mu} \right)\mathbf{u}\left(t;\boldsymbol{\mu} \right)=\mathbf{f}(t), $$

(20)

where t is the time variable in a bounded interval [t₀, T], and,

$$ {\displaystyle \begin{array}{l}\mathbf{M}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{N\times N},\\ {}\mathbf{f}:\left[{t}_0,T\right]\to {\mathrm{\mathbb{R}}}^N,\end{array}}\kern0.5em {\displaystyle \begin{array}{l}\mathbf{C}:{\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^{N\times N},\\ {}\mathbf{u}:\left[{t}_0,T\right]\times {\mathrm{\mathbb{R}}}^{N_p}\to {\mathrm{\mathbb{R}}}^N.\end{array}} $$

(21)

The optimization problem is stated as ‘find the optimal design, μ^∗’, that satisfies

(22)

where $\mathcal{W}$(μ) is a cost function, for example, a total weight of the structure. ℱ is the set of the feasible design variable defined as expressed in (1). In this study, the constraints involve the design variable and the displacement field. Therefore, the j-th inequality constraint is expressed as

$$ {c}_j\left(\boldsymbol{\mu}, \mathbf{u}\left(t;\boldsymbol{\mu} \right)\right)\le 0,j=1,2,\cdots, {N}_{const}. $$

(23)

For example, we require the maximum displacement to be less than the allowed limit, such that

$$ {c}_1=\max \left(\left|\mathbf{u}\left(t;\boldsymbol{\mu} \right)\right|\right)-\underline {\mathbf{u}}\le 0. $$

(24)

Also, the maximum stress constraint is expressed as

$$ {c}_2=\max \left(\left|\boldsymbol{\upsigma} \left(t;\boldsymbol{\mu} \right)\right|\right)-\underline {\boldsymbol{\upsigma}}\le 0. $$

(25)

For the characteristic of the dynamics, the first natural frequency condition is assigned:

$$ {c}_3={\underline{\omega}}_1-{\omega}_1\left(\boldsymbol{\mu} \right)\le 0. $$

(26)

In this work, we considered the above three constraints in the numerical examples as considered in the previous works (Kang et al. 2001; Choi and Park 2002). In addition, various strategies for the computation of constraints in a transient response, we recommend to read an article of Kang et al. (2006).

The dynamic equation in (20) is solved using time-discretized methods, explicitly or implicitly. The initial condition and the external dynamic force are assumed to be independent to the design variables. The external force is discretized with respect to the time as follows:

$$ {\mathbf{f}}_i=\mathbf{f}\left({t}_i\right),i=1,2,\cdots, {N}_T. $$

(27)

Thus, the displacement field at each time step can be obtained by solving (20). After the displacement solution is obtained, the column vectors of the external force and the displacement are written as

$$ {\displaystyle \begin{array}{l}\mathbf{F}=\left[{\mathbf{f}}_1\kern0.5em {\mathbf{f}}_2\kern0.5em \cdots \kern0.5em {\mathbf{f}}_{N_T}\right],\\ {}\mathbf{U}=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_{N_T}\end{array}\right],\end{array}} $$

(28)

where u_i = u(t_i). Even though we used the subscript of u to represent the number of multiple loads in (6), there is no confusion in the proposed method since the number of time steps is equal to the number of ESL. Finally, the displacement solution obtained and the design variable are substituted to the constraints shown in (23).

3.2 Equivalent static load for dynamic response optimization

The ESL is a static load set that makes the same displacement field as that under a dynamic load. Thus, the optimization algorithm using ESL executes static optimizations with multiple times instead of solving the dynamic equation at every design update.

From (20), the inertia and damping parts are moved to the RHS. Then, the sum of the RHS is an equivalent load set such that

$$ {\displaystyle \begin{array}{c}\mathbf{K}\left(\boldsymbol{\mu} \right)\mathbf{u}\left(t;\boldsymbol{\mu} \right)=\mathbf{f}(t)-\mathbf{M}\left(\boldsymbol{\mu} \right)\ddot{\mathbf{u}}\left(t;\boldsymbol{\mu} \right)-\mathbf{C}\left(\boldsymbol{\mu} \right)\dot{\mathbf{u}}\left(t;\boldsymbol{\mu} \right)\\ {}={\mathbf{f}}_{eq}\left(t;\boldsymbol{\mu} \right).\end{array}} $$

(29)

In other words, after executing the transient analysis of (20), we obtain the time-dependent displacement u_i, velocity ${\dot{\mathbf{u}}}_i$, and acceleration ${\ddot{\mathbf{u}}}_i$, and then we calculate f_eq by the RHS of (29). As a result of the transient analysis, the column vectors of the displacement U, and the ESL F are computed by multiplying the stiffness matrix with the displacement U. Thus, (29) can be changed as follows:

$$ \mathbf{K}\left(\boldsymbol{\mu} \right)\mathbf{U}\left(\boldsymbol{\mu} \right)={\mathbf{F}}_{eq}\left(\boldsymbol{\mu} \right). $$

(30)

Note that the ESL is calculated after obtaining the displacement field from the time integration.

The main characteristic of the design optimization using the ESL is that updating the design variable in a stiffness matrix is discriminated to that of the design variable of the ESL. Therefore, we divide the design variables in (30) into μ and $\widehat{\boldsymbol{\mu}}$. During static optimization, $\widehat{\boldsymbol{\mu}}$ is fixed while only μ varies. Thus, the static solution can be represented as

$$ \mathbf{U}\left({\boldsymbol{\mu}}^{m,k}\right)={\mathbf{K}}^{-1}\left({\boldsymbol{\mu}}^{m,k}\right){\mathbf{F}}_{eq}\left({\widehat{\boldsymbol{\mu}}}^m\right), $$

(31)

where the superscript k denotes the iteration of the design variable for the static optimization. The superscript m represents the update of the ESL. Therefore, during the static optimization process, m is fixed. Initially, all variables are the same, as follows:

$$ {\boldsymbol{\mu}}^{1,1}={\widehat{\boldsymbol{\mu}}}^1={\boldsymbol{\mu}}_{ini}. $$

(32)

After the first static optimization, μ^1,k is converged to the optima μ^1,∗ which is the initial design variable of the second static optimization process such that

$$ {\boldsymbol{\mu}}^{m+1,1}={\widehat{\boldsymbol{\mu}}}^{m+1}={\boldsymbol{\mu}}^{m,\ast },\kern0.72em m\ge 1. $$

(33)

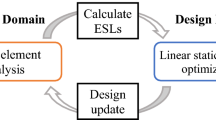
The overall process of the conventional ESL-based method is presented in Fig. 1. To sum up, there are two loops for the design optimization, and we update the design variables with the current optimum design for the new ESL from transient analysis. In details, the index for the inner loop is k, which is design optimization update for a static problem with multiple loads.

Fig. 1

Dynamic response optimization process using ESL

After finding the optimal solution of the static design optimization, a transient analysis is executed by using the optimum to update the ESL. Then, the next static optimization starts with the updated loading condition (updated ESL). This process is represented by the index m, which indicates the outer loop for the update of the ESL. As a consequence, the converged solution of the outer loop becomes the final optimum of the design optimization for dynamics. Also, we represented the flow chart of the proposed method in Fig. 2, and we explained the computational procedure in algorithm 1.

Fig. 2

Dynamic response optimization process using ESL combined with RBM

In the previous works of ESL (Choi and Park 1999; Kang et al. 2001; Choi and Park 2002), the convergence criteria were set as the convergence of the ESL, which is physically the same criteria as the convergence of the design variables under the assumption of a linear elastic material.

3.3 Combining the ESL-based optimization with the RBM

In the Section 2–3, we proposed to calculate the POM of the external loads to employ the RBM to the problem with a multiple loading condition. Therefore, by replacing the multiple loads with the ESL, we can compute the POM of the ESL. As a consequence, the global-POD method combined with the RBM can be employed for static optimization using the ESL. The combination of two methods can reduce the computational costs of the ESL-based optimization algorithm. In fact, since the ESL is a superposition of inertia, damping, and external forces, we can regard the mode of the ESL as a kind of the mode of forces. As shown in Section 2–2, the mode of the loads exists in most cases, the mode of the ESL can also be obtained. The good point of this method is that the inertia and damping forces are necessarily computed during the time integration to update the ESL. Thus, the POM of the ESL is easily obtained without additional, heavy computations. However, since we compute the ESL by multiplying the stiffness matrix by the displacement vector, we obtain the POM of the ESL by applying the POD to the ESL directly. In other words, each column of the ESL is regarded as a snapshot. Then, by the POM of the ESL, we can approximate the ESL efficiently. The snapshots matrix is written as

$$ {\displaystyle \begin{array}{c}{\mathbf{F}}_{eq}=\left[{\mathbf{f}}_{eq,1}\kern0.5em {\mathbf{f}}_{eq,2}\kern0.5em \cdots \kern0.5em {\mathbf{f}}_{eq,{N}_T}\right]\\ {}={\boldsymbol{\Phi}}_{eq}{\boldsymbol{\Sigma}}_{eq}{\mathbf{A}}_{eq}^T.\end{array}} $$

(34)

From Φ_eq, the POM of the ESL is obtained as follows:

$$ {\boldsymbol{\Gamma}}_{eq}=\left[{\gamma}_1\kern0.5em {\gamma}_1\kern0.5em \cdots \kern0.5em {\gamma}_{R_{\gamma }}\right],{R}_{\gamma }<{N}_{\gamma}\le {N}_T. $$

(35)

The rest of the procedure is exactly the same as with Eqs. (6)–(8). The displacement snapshots are obtained by the mode of the ESL, such that

$$ \mathbf{U}\left({\boldsymbol{\mu}}_i\right)={\mathbf{K}}^{-1}\left({\boldsymbol{\mu}}_i\right){\boldsymbol{\Gamma}}_{eq},i=1,2,\cdots, {N}_s. $$

(36)

Applying the POD to the snapshots as in (8) gives the reduced basis T of the static problems as follows:

$$ \overline{\mathbf{V}}\left({\boldsymbol{\mu}}_i\right)={\overline{\mathbf{K}}}^{-1}\left({\boldsymbol{\mu}}_i\right){\overline{\mathbf{F}}}_{eq}, $$

(37)

where

$$ {\overline{\mathbf{F}}}_{eq}={\mathbf{T}}^T{\mathbf{F}}_{eq}. $$

(38)

Compared to the previously developed-optimization method using the RBM (Veroy 2003; Lei et al. 2013), the proposed one does not distinguish off-line and on-line stages. Rather, the displacement snapshots are computed as the ESL is updated. Considering the characteristics of the structural design optimization, excluding the computation at the off-line stage is controversial because the purpose of the optimizations is to quickly and efficiently find an optimal solution within limited resources. In the following section, we evaluate the performance of the proposed method by executing the design optimization for some structural examples.

4 Numerical results

We evaluate the proposed method by analyzing and optimizing the structural dynamics of several designs. In the present paper, we used MATLAB 2017b under Windows 10 with an Intel i5 CPU running at 3.5 GHz. For the transient analysis, a Newmark-Beta scheme was chosen to solve the time-dependent equation under a certain initial condition.

4.1 Example 1. Box-type structure with stiffeners

For the first example, we selected a box-type structure with stiffeners shown in Fig. 3, which is similar with the box-beam model (Balmès 1996), and we added stiffeners (#2 and #4) between the ribs (#5 and #6) and the clamped end. The left side is clamped, and a sinusoidal dynamic load F(t) = 50sin(πt/1.25) is applied to the right free-end, (3,0,0.1) (m) position. The material was set to aluminum with elastic modulus E = 72 GPa, density ρ = 2823 Kg/m³, and the Poisson’s ratio ν = 0.33. The number of subdomains is set to ‘6’, and we set the same parameters for the upper and lower skins to retain the convergence during the optimization (for parameters #1 and #3 in Fig. 3). The structure is discretized using a four-node Mixed Interpolation of Tensorial Components (MITC4) shell element (Dvorkin and Bathe 1984). Since we used the same elements for both FOM and ROM, the proposed method is applicable to other FE cases that have a basic FE routine. The FE model has 176 elements and 193 nodes, with a total of 1158 DOFs. Using a Newmark-Beta scheme, we set 500 time steps within [0, 5] sec. In this condition, we computed the relative errors of the displacement vectors. We set the upper and lower bounds of the parameters in (1) to μ_lb = 0.005(m) and μ_ub = 0.012(m), respectively.

Fig. 3

Clamped box-type structure with stiffeners under a tip dynamic load f(t)

For μ_ini = 0.01(m), we obtained the ESL shown in (29), which consists of 501 load vectors. We then computed 34 POMs of the ESL by applying the POM to the ESL. Fig. 4 represents the distribution of the singular values of the ESL. The magnitudes of the singular values after the 34th decrease remarkably, and 34 modes have 99.997% energy of the full ESL. In the design domain, we first employ the greedy algorithm (Rozza et al. 2008) to determine the number of the operating points, which are 3⁶ = 729 samples computed by the permutations of 6 parameters, each with 3 levels. In Fig. 5, the error decreases monotonically depending on the increase in the number of modes, obtained by following computation:

$$ error=\frac{\left\Vert \mathbf{U}\left(\boldsymbol{\mu} \right)-\overline{\mathbf{V}}\left(\boldsymbol{\mu} \right)\right\Vert }{\left\Vert \mathbf{U}\left(\boldsymbol{\mu} \right)\right\Vert }. $$

(39)

Fig. 4

Singular values of the ESL for initial thicknesses of a box-type structure with stiffeners

Fig. 5

Relative error depending on the number of modes obtained by the greedy algorithm

In the present study, we used 28 operating points, as shown in Table 1. A combination with a repetition of ‘k’ parameters, each with ‘n’ levels, becomes _n + k-1C_k. For the present example, there are 6 parameters (μ₁, μ₂, …, μ₆), and we sample each parameter with 3 levels (t₁, t₂, t₃). Therefore, _3 + 6-1C₆ = 8!/(2! × 6!) = 28 samples were determined, which includes the variation in all parameters, decreasing the number of operating points. For each mode of the ESL, we took 34 snapshots by setting 28 operating points. Thus, a total number of 952 snapshots was obtained, and we then computed 102 modes from the snapshots by the POD. This set based on a combination with repetition is valid for the approach that computes the modes from snapshots since extrapolation with snapshots significantly decreases the accuracy. However, the one using modes does not (Kerschen et al. 2005). After determining the number of operating points, we fixed these during the design optimization process.

Table 1 Sampling strategy of a combination with repetition

Regarding the accuracy and reproducibility of the proposed ROM, we compared the tip displacement of the proposed method to that of the FOM under the ESL. After constructing the ROM, the displacement vectors were calculated with a random parameter μ = (0.0117, 0.0075, 0.0058, 0.0071, 0.0092, 0.0099) $\notin {S}_{\mu}^{N_p}$, which is the extrapolation of the operating points. Fig. 6a represents the tip displacement, and Fig. 6b shows the relative errors of the FOM and ROMs. The errors were obtained by changing the size of reduced basis T, from R = 20 to R = 100, which is the same as the size of the ROM. As expected, the ROM shows a good agreement with the FOM as the number of modes increases. From the results, we can decide how many modes should be chosen to satisfy the accuracy required, which is also represented by the magnitude of the accumulated singular values in (8). (e.g., Kerschen et al. 2005)

Fig. 6

Comparisons of the FOM and ROM (100 POMs). (a) Tip displacement. (b) Relative error

Fig. 7a represents the averaged relative errors of the displacement vectors depending on the size of the reduced basis. We first generated 1000 random samples within the design domain, which also includes extrapolations of the operating points. Then, we computed the relative errors of the 2-norm of the displacement vectors and averaged with respect to 1000 samples. During the computation, we changed the size of the reduced basis from 10 to 300. Therefore, we can observe the accuracy of the displacement that depends on the size of the ROM. Fig. 7b shows the distributions of the singular values of the snapshot matrix. Considering that a singular value represents the energy of its mode, both Figs. 7a and b have very similar shapes as each other. Since there is no direct connection between the averaged error and the singular values, the magnitudes in the y-axis of both graphs are not correlated with each other.

Fig. 7

Similarity between the error with respect to the number of basis and the distribution of singular values. (a) Averaged error for 1000 random samples. (b) Magnitudes of singular values

For this example, we conducted a design optimization by setting the thicknesses of the box-shell to become design variables. For a constrained nonlinear optimization, we used sequential quadratic programming (SQP) to compute the gradients using the finite difference method. The convergence tolerance of the design variables, objective function, and constraints was set to 1e-4. Table 2 shows the details and the results of the optimization. The optimal thicknesses of each method are presented in Fig. 8. We also presented the % errors of the optima in Table 3, and they are in great agreement with each other, which means the proposed ROMs are sufficient to solve the design optimization of the dynamic problems similar to the present conditions. For the ‘ESL’ and proposed ‘ESL w Param.’, we employed an additional reduction of the full-transient analysis that is essential to generate the ESL. Since there is no change in the ESL during the inner loop of the static optimization, we can save much of the computation time by performing the modal transient analysis. A similar approach has already been employed for ESL-based optimization with a degrees of freedom-based model reduction technique, and its performance was verified using various examples (Kim et al. 2014). In the present study, we applied the Lanczos method. Thus ‘ESL-M’ reduced the transient analysis by modal reduction, and ‘ESL-M w Param.’ combined both ‘ESL-M’ and ‘ESL w Param.’

Table 2 Constraints obtained at the initial and optima of the FOM and ROMs for a box-type structure with stiffeners

Fig. 8

Comparison of optimal thicknesses of the FOM and ROMs

Table 3 Comparison of errors of the optimal thicknesses

For the efficiency, we first checked the total optimization time of each method, as shown in Fig. 9. All methods using the ESL save a lot of time compared to those with the FOM. For the ‘ESL’, ‘ESL-M’, ‘ESL w Param.’, and ‘ESL-M w Param.’, computation times of each method are reduced to 13.24%, 9.15%, 5.72%, and 2.99%, respectively, compared with that of the FOM. For the proposed method, the total time includes the off-line procedure of the parameterization and the generation of a reduced basis whenever the ESLs are updated. Fig. 10 shows the computational times for the methods in further detail. First of all, for ‘ESL w Param.’ and ‘ESL-M w Param.’, almost no time was consumed for the matrix generation since the stiffness matrix was parameterized. Also, the static optimization time is faster than with the other two methods. In the 4th graph of Fig. 10, ‘ROM construction’ includes the step of taking snapshots, employing the global POD and computing ESLs, which is an essential procedure for the proposed method. For the time consumed in the transient analysis, ‘ESL-M’ and ‘ESL-M w Param.’ are small compared to the other two methods. However, an eigen-analysis using the Lanczos method is required to execute the modal reduction. As a consequence, the proposed methods, ‘ESL w Param.’ and ‘ESL-M w Param.’, that use the reduced basis and the parameterization are more efficient than that reducing the dynamics of the structure, ‘ESL-M’. Although the degrees of efficiency of the methods can vary from those of the present example when other structures in different environments are analyzed, the trends shown in Fig. 10 are certainly maintained.

Fig. 9

Comparison of computation time of the FOM and ROMs

Fig. 10

Details of the computation time of the ROMs

4.2 Example 2. Wing box model

Another example to verify the proposed method is a wing box model with 20 subdomains, as shown in Fig. 11, which is a complexified model of the wing shown in the previous work (Kim and Cho 2007; Kim et al. 2014). To view the inside of the wing box, the configuration was plotted separately. In fact, all components are connected exactly including the upper and lower skins. The FE model has 12,560 elements and 12,073 nodes, with a total of 72,438 DOFs. For a realistic demonstration of the proposed optimization, we performed aerodynamic-structure coupled analysis and design optimization by coupling the wing FE model with a doublet lattice method (Albano and Rodden 1969; Giesing et al. 1972). Since we adapt the DLM to compute a lift acting on the entire wing surface, we used 300 panels for the aerodynamic analysis as shown in Fig. 12. For all aerodynamic panels, one panel exactly fits to 4 × 4 = 16 structural elements. Thus, we bilinearly transformed the lift obtained to the nodal forces of each element. Also, we simply computed the configuration of deformed panel by selecting the structural nodes coinciding with the panel. To perform a gust response, we introduced a spatially distributed, ‘1-cosine’ discrete gust model (Su and Cesnik 2011), such that,

$$ {W}_g\left(r,\eta, t\right)=\frac{A_c}{2}\left[1-\cos \left(\frac{2\pi t}{t_g}\right)\right]\sqrt{{\left({A}_E\cos \eta \right)}^2+{\left({A}_N\sin \eta \right)}^2}, $$

(40)

$$ {\displaystyle \begin{array}{l}{A}_E(r)=\sin \left(\frac{\pi }{2}\left[1-{\left(\frac{r}{r_0}\right)}^{n_E}\right]\right),\\ {}{A}_N(r)=\sin \left(\frac{\pi }{2}\left[1-{\left(\frac{r}{r_0}\right)}^{n_N}\right]\right),0<r\le {r}_0.\end{array}} $$

(41)

where subscripts E and N represent east and north directions, respectively. n_E and n_N are parameters to adjust the spatial distribution of the gust, r₀ is the radius of the gust region, r is the distance from one point within the gust region to the gust center, and η represents the orientation angle of the point with respect to the east direction. A_c denotes the amplitude at the gust center, which is defined by (Valente et al. 2017),

$$ {A}_c={U}_{ref}{F}_g{\left(\frac{H}{106.68}\right)}^{1/6} $$

(42)

where H is the distance for the gust to reach its peak velocity, U_ref denotes the reference gust velocity in equivalent air speed, and F_g is the flight profile alleviation factor. Considering the wing size, we employed a cruise flight condition presented in Valente et al. (2017), which is shown in Table 4. Thus the 1-cosine gust profile of the gust center is presented as shown in Fig. 13. The gust region is represented in Fig. 12. G_P is the position of the gust center, and the dotted line is a flight direction. In Fig. 14, spatial distributions of the gust speed with respect to time are plotted, which are applied to the panels. By employing the gust model to the DLM, we can obtain nodal forces that are calculated by the lift of collocation points as shown in Fig. 15. As a result, the load in (20) becomes not only a function of the time, but also a function of a displacement, expressed as f(t,u; μ). Therefore, we updated the positon of the panels and computed the aerodynamic forces at every time step.

Fig. 11

Wing box model with 20 design variables

Fig. 12

Panel geometry for DLM and gust region

Table 4 Flight conditions and gust modelling

Fig. 13

1-cosine gust profile

Fig. 14

Time-dependent, spatial distribution of the gust

Fig. 15

Time-dependent lift obtained by coupled DLM-structure analysis

Regarding the configuration of the wing structure, we set the 20 design variables to be the thicknesses of the upper skins (subdomain # 11~15) and lower skins (subdomain # 16~20), ribs (subdomain # 6~10) and spars (subdomain # 1~5). We used the same material properties as the one used in example 1. For all design variables, we used μ_ub = 0.013 (m), μ_lb = 0.001 (m), and μ_ini = 0.007 (m). For the initial thicknesses, we executed the transient analysis with 1000 time steps within [0, 2] sec. In Fig. 16, we represented the displacements of the tip and center of the wing, respectively. Since the wing shows a geometrically linear deformation, there is no drastic change of the deformation in the transient response.

Fig. 16

Transient responses obtained at the tip and center of the wing box

For 1000 ESLs, we obtained the 144 modes of the ESL by considering the singular values of the ESL matrix. In Fig. 17(a), we plotted the distribution of the singular values, which shows a different shape as that presented in Fig. 7b. Whereas the singular values in Fig. 7b decrease monotonically since the change in the displacement is continuous with respect to the variation in the parameters, those in Fig. 17(a) have a sharp decrease around the 550th mode because the lower order modes have most energy of the dynamic response. If we use all 550 modes, all the ESL can be considered during the analysis. However, the efficiency decreases drastically since the total numbers of the snapshot increases rapidly. Therefore, we used 144 modes to contain 95% energy of the load to the mode of the ESL based on the cumulative distribution of the singular values shown in Fig. 17(b). With these modes, we computed snapshots at 231 operating points, which is determined by the combination with a repetition as presented in example 1. However, if the number of design variable increases, the total numbers of the snapshot could be larger than the number of DOFs, which results in a decrease in the efficiency. Thus, in this example, we employed a common mode to compute the global POD. This common mode was originally used for ROM adaptation (Amsallem 2010; Amsallem and Farhat 2011), in particular, for the congruence transformation of the interpolation-based ROM. By taking snapshots for each mode of the ESL, we computed the POMs relevant to the mode of the ESL, not making the global snapshot matrix directly. And then we obtained the global snapshot matrix that consists of the modes, not the displacement snapshots. By applying the SVD to the snapshot matrix of the modes, we obtained 186 common modes, which contain 99.99% energy of the snapshot matrix of the modes and is the same as the size of the reduced system matrices.

Fig. 17

Singular values of the ESL for initial thicknesses of a wing box model. (a) Distribution of the singular values of the ESL. (b) Cumulative distribution of the singular values

Table 5 shows the details of the constraints and the optima of each method, and in Fig. 18, we present the optimal thicknesses of various approaches. As is expected, all thicknesses of each method show a great agreement with each other. For the ‘ESL-M’, ‘ESL w Param.’, and ‘ESL-M w Param.’, 4.32%, 5.01%, and 4.06% averaged errors are observed compared with the optimum of the original ESL method. The results also represent the weights of each optima have slight differences compared to those obtained by the original ESL-based optimization. Considering that the optima obtained by the original ESL method is almost the same as that obtained by the FOM, the accuracy of the proposed ROM can be guaranteed. In Figs. 19, 20, and 21, we plotted the histories of the objective function and design variables for each ESL-based method. Since the optimal thicknesses of each method are similar with each other, there is almost no difference in the objective functions during the iterations. By observing a trend in thickness in Figs. 19 and 20, there are little difference between the methods. After the 15th iteration, the design variables seem to be near to a local minimum. From the histories obtained, we verified that the proposed method shows a good agreement with the original ESL method.

Table 5 Constraints obtained at the initial and optima of the FOM and ROMs for a wing box structure

Fig. 18

Comparison of optimal thicknesses of the FOM and ROMs

Fig. 19

Comparison of objective function histories

Fig. 20

Histories of design variables of the FOM and ROMs. (a) Spars (b) Ribs

Fig. 21

Histories of design variables of the FOM and ROMs. (a) Upper skins (b) Lower skins

Fig. 22 shows the computational time for each method for 1 update of the ESL. Unlike the example 1, the computation of the aerodynamic lift is included. Note that the computation time of the DLM is smaller than that of the structural FE, since we used large-size panels compared with the structure elements. For all methods, the DLM computations are the same with each other. Thus, except the DLM of entire time, we can observe the actual difference between the ESL-based methods.

Fig. 22

Comparison of computation times of the ROMs

By comparing the results in Fig. 10, the proposed method maintains computational efficiency even though the number of design variables increases. However, the time of ROM construction increased, since the complexity of the ESL is increased. In fact, identifying the external forces is important, especially for the problems related to aero and fluid dynamics. In the present study, we verified that employing the mode of the ESL to the RBM is possible and efficient. Thus, applications of the proposed method to various loading conditions can be remained for future development.

Basically, the parameterized methods have to obtain snapshots by changing the design variables. In that process, as the number of design variable increases, the number of initial samples also increases. Therefore, the efficiency of the parameterized model could decrease. However, since the increase in the DOF depending on the refinement of a mesh configuration is generally more common than the increase in the number of design variables, we can acquire greater efficiency by using the proposed method as the size of the dynamic system increases.

5 Conclusions

We have developed a ROM by combining the RBM for multiple loads with an ESL-based method, and we proposed a new strategy for the dynamic response optimization of the structures in the FE framework. To this end, we suggested (i) using the RBM under multiple loading condition by calculating the POM of multiple loads, (ii) employing the global POD method to snapshots obtained at the operating points that are selected using a simple method, and (iii) combining the proposed ROM with the design optimization using the ESL method. There is a clear reason for proposing a strategy that consists of various approaches rather than a single one. When reducing a dynamic system for efficient optimization, we need to consider both the dynamics of the target structure and the variation in the design parameters. Consequently, the final reduced system should contain the above two characteristics, and the proposed method naturally comprises two individual reduction methods for the dynamic responses and the parameter changes.

There are two major contributions of the present work. First, in the sampling process, we proposed using the POM of the ESL that has an apparent physical meaning. As the ESL is generated by multiplying the stiffness matrix to the acceleration vectors, the meaning of the ESL-mode is similar to that of the second derivative of the displacement. For general multiple loading cases in which the mode of the load does not have any specific meaning, we cannot guarantee the efficiency of the RBM during sampling. Second, we employed the ROM for the static optimization part that was not reduced in the previous methods of the ESL-based design optimization. We use numerical examples to verify the two contributions and the efficiency and accuracy that are essential for computations using ROMs. In fact, the present work is suitable to design the optimization of a large-scale dynamic system and we expect that the proposed method will also work for such a case. In addition, further research is needed to combine the RBM with the ESL methods for nonlinearities of the static and dynamic systems.