1 Introduction

The wood material presents a very high variability in terms of mechanical properties. This variability comes from several factors. In particular, many studies have shown the existing correlation between density and mechanical properties (Rohanovà et al. 2011; Wang et al. 2008; Hanhijarvi et al. 2008; Johansson et al. 1992). The density can vary across species and between individuals of the same species and even within the same tree. Moreover, for structural application, local singularities in timber are present such as knots, grain angle or the presence of juvenile or reaction wood. These singularities have a strong influence on the final mechanical properties of the board. Indeed, several studies (Hanhijarvi et al. 2008; Piter et al. 2004; Riberholt and Madsen 1979) showed that the first stage of the failure of timber occurs most likely in areas where the knots are concentrated (in fact the presence of the largest knot or group of knots) and that the knottiness can be a good indicator of the mechanical properties. The grain angle also explains the reduction of wood strength (Brannstrom et al. 2008; Bano et al. 2011; Olsson et al. 2013; Viguier et al. 2015), in particular the deviation of the fibres around knots, which is the result of simultaneous secondary growth of the trunk and branch. The variation in grain angle influences the mechanical properties of timber, as the maximum strength of timber occurs when the load is parallel to the fibres direction and decreases non-linearly when the angle formed by the fibres increases (Bergman et al. 2010).

However, since 2012, on the European market, wood used for structural purpose has to be graded according to strength and it has to be CE marked to ensure the designer that the product meets the standards specifications. This grading must guarantee three properties: density, modulus of elasticity (MOE) and bending strength sometimes called modulus of rupture (MOR). Because of the wide variability, the grading is based on so-called characteristic values that are fifth percentile for density and MOR and mean value for the MOE. There are two ways to perform the grading: visual or machine grading. It is well known that visual methods lead to a large proportion of downgraded boards (Roblot et al. 2008).

Main techniques used so far to perform machine grading are based on the existing correlation between the modulus of elasticity and bending strength. The modulus of elasticity can be determined on a global or local level but it is known that local MOE measures may give better predictors of bending strength than what global MOE does (Oscarsson et al. 2014). The methods used on those two levels are:

  • on a global level: these techniques are based on elastic modulus estimation by vibration methods (van de Kuilen 2002; Biechele et al. 2011) or using its relationship with the velocity of a wave (Rajeshwar et al. 1997). These methods are extremely dependent on the correlation between MOE and MOR and only take partially into consideration local singularities (Olsson et al. 2012).

  • on a local level: the local estimation of the modulus of elasticity can be obtained with flat wise bending machines (machines stress rating), which consist of deflecting a piece of timber over a given span at a certain interval (Biechele et al. 2011). There are also ways to measure singularities that affect the mechanical properties such as knot (Roblot et al. 2010; Oh et al. 2009) or grain deviation (Simonaho et al. 2004). The local modulus of elasticity can be calculated using grain angle information and mechanical modelling (Olsson et al. 2013). There are also machines on the market today that combine vibration methods and X-ray measurements.

The aim of this study is to propose a fast way to use local data (X-ray measurements and grain angle) to perform strength grading while remaining feasible in an industrial context, meaning at high-speed (about 200–300 m/min). This is done by means of mechanical modelling on the basis of non-destructive measurements. Moreover, the proposed model is analyzed on the basis of the prediction quality of the mechanical properties and on the results of the grading process according to EN 14081 (CEN 2009, 2011, 2012a, 2013). The proposed grading method is then compared to existing methods on two species used in timber structure in France (spruce and Douglas fir).

2 Materials and methods

2.1 Sampling

The sample is composed of 437 spruce boards (Picea abies) and 805 Douglas fir boards (Pseudotsuga menziesii) sawn from approximatively 45 years old tree harvested in French forest. The different boards were dried to about 12% moisture content. The mean moisture content is respectively equal to 11.3 and 11.45% for spruce and Douglas fir. Three different sections were chosen: 40 \(\times\) 100 mm\(^2\) (137 and 235 for spruce and Douglas fir, respectively), 50 \(\times\) 150mm\(^2\) (150 and 278) and 65 \(\times\) 200mm\(^2\) (150 and 292). The length of all boards is about 4 m.

2.2 Non-destructive measurements

2.2.1 Stiffness measurements

Two different non-destructive methods were used to estimate the modulus of elasticity of the boards on a global level.

  • One using the relationship between the speed of an ultrasonic wave along the board and its Young’s modulus. The modulus of elasticity is then calculated using Eq. 1.

  • One other using the relationship between the resonance frequency of the boards under longitudinal vibration and its Young’s modulus. The modulus of elasticity is then calculated using Eq. 2.

    $$\begin{aligned} E_{sound}=\rho \times \left( \frac{l}{t_{sound}}\right) ^2 \end{aligned}$$
    (1)

    where: \(E_{sound}\): estimation of the MOE, \(\rho\): density, l: board’s length, \(t_{sound}\): travel time of the ultrasonic wave

    $$\begin{aligned} E_{vib}=4\rho f^2 l^2 \end{aligned}$$
    (2)

    where: \(E_{vib}\): estimation of the MOE, \(\rho\): density, l: board’s length, f: first natural frequency under longitudinal vibration

2.2.2 Local measurements

All boards were passed through a scanner dedicated to mechanical grading to obtain different local data such as density, grain angle and knottiness. The following coordinate system has been considered: x-direction along the length and y-direction along the height.

2.2.2.1 Density measurement

In addition to a global weighing and measuring that gives the average density, the density of boards was measured locally. This measurement is performed by a scanner equipped with an X-ray imaging system. Assuming that the grey levels of thereby provided images are proportional to the acquired corresponding light intensities, they can easily and accurately be converted into local density maps. Under this condition, the Beer–Lambert’s law can be applied to determine the density for each pixel of the densities maps (Kim et al. 2006). The final expression of the local density \(\rho (x,y),\) averaged through the thickness of the board, is given by Eq. 3, where t represents the thickness of the board, \(a_\rho\) and \(b_\rho\) are linear calibration coefficients, G is the corresponding image pixel’s grey level, and x and y are the local coordinates. The resolution in x and y directions is 10 and 2 mm, respectively.

$$\begin{aligned} \rho (x,y) \times t(x,y) = a_\rho \times ln(G(x,y)) + b_\rho \end{aligned}$$
(3)

The actual values of \(a_\rho\) and \(b_\rho\) depend on several factors, but can easily be determined by scanning and weighing a batch of boards. These two parameters are in fact the linear regression coefficients between mean value of ln(G) of the boards, calculated on the images and their mean densities multiplied by their respective thickness.

2.2.2.2 Grain angle measurement

The grain angle was measured using the tracheid’s effect (Olsson et al. 2013; Simonaho et al. 2004), by projecting a laser line on the surface of the boards. Due to the wood’s anisotropic light diffusion properties, the observed pattern on the surface of the board is elliptic. The ellipses main axis is oriented in the same direction as the fibre orientation, or more exactly in the same direction as the projection of the grain angle on the surface of the board. Consequently, the measure of the grain angle can be obtained thanks to a Principal Component Analysis applied on the ellipse binarized image. The evolution of grain angle of the whole surface of each board can be obtained by illuminating the wood surface by laser dots along a line that is perpendicular to the main direction of the board, as shown in Fig. 1. The measurement has been made on the two wide faces of each board (not on the narrow faces).

Fig. 1
figure 1

Actual technology used in the scanner (top) and illustration of the grain angle measurements (bottom)

Full size image
2.2.2.3 Knottiness calculation

The characterization of the knottiness was made by calculating the Knot Depth Ratio (KDR). This value represents the local knot thickness divided by the thickness of the board (Oh et al. 2009). The resolution is the same as for the density measurement. This method relies on the fact that the knot density is higher than the clear wood density. The KDR is equal to 0 in clear wood and 1 when at a given position the thickness of the board is composed entirely of knot. The KDR is calculated using Eq. 4 where \(\rho _{cw}\) and \(\rho _{knot}\) are the clear wood and knot density, respectively, \(f_1\) represents the clear wood density variability within a board (\(f_1=1+(std(\rho _{cw}))/(mean(\rho _{cw}))\)) and \(f_2\) is the ratio between \(\rho _{knot}\) and \(\rho _{cw}.\) Finally \(\rho (x,y)\) is the locally measured density. The \(f_1\) parameter is useful in order to limit oversensing due to the natural variability of density.

$$\begin{aligned} \begin{array}{ll} KDR(x,y) &{} = 0 \quad if \quad \rho (x,y)< f_1 \times \rho _{cw} \\ KDR(x,y) &{} = \frac{\rho (x,y)-\rho _{cw}}{\rho _{knot}-\rho _{cw}} \quad if \quad f_1 \times \rho _{cw}< \rho (x,y) < f_2 \times \rho _{cw} \\ KDR(x,y) &{} = 1 \quad if \quad \rho (x,y)> f_2 \times \rho _{cw} \\ \end{array} \end{aligned}$$
(4)

In order to determine those parameters (\(f_1,\) \(f_2,\) \(\rho _{cw}\) and \(\rho _{knot})\) a first image processing step is used to separate knotty areas from clear wood ones. For each board, \(\rho _{knot}\) can be calculated as the mean of the density measured in knotty areas, \(\rho _{cw}\) as the mean density of clear wood areas and \(f_1,\) \(f_2\) are calculated using the previously defined formulas. Finally, the different parameters for each species are taken as the mean of the values found on each board of the studied batches. Knot density is then assumed to be constant and proportional to clear wood density within a batch.

2.2.2.4 Illustration of the data obtained from the scanner

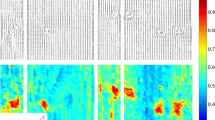
An example of the grain angle and density measurements on a board is shown in Fig. 2. This figure shows that because of the density variation there are clear wood areas where the KDR values are not equal to 0. Nevertheless, the values of the KDR are very low in those areas, and have only a slight influence on the outcome of the modelling. A strong grain angle deviation around the knots is also observable.

Fig. 2
figure 2

Photographs of top and bottom faces and model’s input data maps; from top to bottom, density, knot depth ratio and grain angle of top and bottom faces

Full size image

2.3 Destructive tests

The different boards have been destructively tested in bending. These destructives tests have been performed according to EN 408 (CEN 2012b). The critical cross-section was chosen visually and placed between the loading heads. Bending tests were performed using a distance equal to 18 times the specimen’s height between the supports and 6 times between the loading heads. The bending test performed was an edgewise bending test and the tension edge was selected at random. The global modulus of elasticity is calculated using Eq. 5 where b and h are respectively the thickness and the height of boards, a is equal to 6 × h and l is the span. \(F_2-F_1\) is an increment of load on the regression line (on the load vs displacement curve) with a correlation coefficient of 0.99 or better, and \(w_2-w_1\) is the increment of global displacement corresponding to \(F_2-F_1.\) The bending strength is calculated according to Eq. 6 where \(F_{max}\) is the maximum load during the bending test. The boards having a moisture content in the range 8 to 18 %, their modulus of elasticity has been adjusted to 12 % moisture content according to EN 384 (1% change for every percentage point difference in moisture content). For bending strength no adjustment has been made according to EN 384.

$$\begin{aligned} E_{m,g} =\frac{3al^2-4a^3}{4bh^3 \frac{w_2-w_1}{F_2-F_1}} \end{aligned}$$
(5)
$$\begin{aligned} \sigma _m =\frac{3F_{max}a}{bh^2} \end{aligned}$$
(6)

According to EN 384 (CEN 2010) some adjustments have been made on the modulus of elasticity and bending strength. To determine the sample mean of modulus of elasticity for strength grading purpose, the mean global MOE shall be corrected using Eq. 7 which includes an adjustment to a pure bending modulus of elasticity. The bending strength is adjusted to boards of 150 mm height by dividing \(\sigma _m\) by \(k_h\) with \(k_h=\left( \frac{150}{h}\right) ^{0.2}\) in order to take into account size effects.

$$\begin{aligned} \bar{E} = 1.3 \times \left[ \sum E_{{m,g}_i}/n\right] - 2690 \end{aligned}$$
(7)

2.4 Mechanical modelling

The following model is based on the theory of linear elasticity considering each pixel as a single element with its own mechanical properties, depending on the measured singularities (\(\rho ,\) KDR, grain angle). Since the destructive tests have been made according to EN 408, the span depends on the height of each board. Consequently, for certain boards (those with a lower height), the span is not equal to their full length. For the calibration of the model (Sects. 2.4.1, 2.4.2), the considered length depends on the height of the boards (18 times the specimen’s height between the supports and 6 times between the loading heads). In other terms, only a part of the different images is considered. However, for strength grading purpose (Sect. 2.4.3) the estimation of the mechanical properties must be representative of the entire board, in this case the full-length (4 m) is considered.

2.4.1 Estimation of the MOE

2.4.1.1 Estimation of the local modulus of elasticity

The first step is to assign a modulus of elasticity E(x, y) to each element of the board. E(x, y) has been chosen according to the local density and the local grain angle. Concerning the dependency on the local density, a linear relationship between E(x, y) and \(\rho\)(x,y) has been chosen. In addition, the influence of the local grain angle is taken into account by using a function based on the Hankinson formula (Bergman et al. 2010). Finally, the local modulus of elasticity E(x, y) is calculated using Eq. 8.

$$\begin{aligned} E(x,y) = \left( g_1 + g_2 \times (\rho (x,y) - g_3 ) \right) \times \frac{H[\theta _{top}(x,y)]+H[\theta _{bot}(x,y)]}{2} \end{aligned}$$
(8)

where:

  • \(g_1\) \(g_2\) and \(g_3\) are the coefficient of the linear relationship between E(x,y) and \(\rho (x,y)\)

  • \(\theta _{top}(x,y)\) and \(\theta _{bot}(x,y)\) are the values of grain angle measured respectively on top and bottom faces

  • \(H(\theta )\) is a function giving the reduction factor between the modulus of elasticity parallel to the grain (which is in practice the modulus of elasticity determined by the linear relationship with the density) and the modulus of elasticity at the measured grain angle value

The \(H(\theta )\) function is given by Eq. 9 where \(E_0\) is the modulus of elasticity determined thanks to the linear relationship with the density, k a coefficient representing the ratio \(E_{90}\)/\(E_0\) with \(E_{90}\) the modulus of elasticity perpendicular to the grain, and n a constant.

$$\begin{aligned} H(\theta )= \frac{E(\theta )}{E_0} = \frac{k}{sin^n(\theta )+kcos^n(\theta )} \end{aligned}$$
(9)

Note that the reduction due to the grain angle is taken as the mean of the reduction induced by the grain angle on each wide face of the boards. Those different steps on a spruce board are given in Fig. 3.

Fig. 3
figure 3

Illustration of the local modulus of elasticity computation along the beam

Full size image
2.4.1.2 Estimation of the effective bending stiffness

The effectiveness of the calculation of the effective bending stiffness to predict the bending strength of timber has already been proven in Olsson et al. (2013). It was therefore chosen to be used. The presence of knots within the thickness of the boards is taken into account by reducing the local thickness using Eq. 10. The \(\alpha\) parameter has been added in order to allocate a given weight to the knottiness. Considering this reduction of thickness and the previous local modulus of elasticity, an effective bending stiffness \((EI)_{ef}\) can now be calculated for each section (i.e along the total height at a given x position) along the sollicited part of the board, using Eq. 11.

$$\begin{aligned} t(x,y)= 1 - \alpha \times KDR(x,y) \end{aligned}$$
(10)
$$\begin{aligned} (EI)_{ef}(x)= \sum _{j=1}^{n_{elements}} (E(x,j)I(x,j)+E(x,j)A(x,j)a(x,j)^2) \end{aligned}$$
(11)

where E(x, j) , A(x, j) , I(x, j) and a(x, j) are respectively: the modulus of elasticity, the area, the second moment of area, and the distance from the neutral fibre of each element at a given x position. \(n_{elements}\) is the total number of elements along the total height of each section and j is the index of the elements along the y direction. The effective bending stiffness is calculated for each segment i of the board along the x direction. The length of those segments corresponds to the resolution of the images along the x axis.

2.4.1.3 Estimation of the MOE

In this section, the deflection at mid-span in the case of a four-point bending test \(\left(v(\frac{l}{2})\right)\) of the degraded boards is calculated in order to obtain \(E_{model}\) which can be assimilated to an equivalent of \(E_{m,g}.\) The deflection at mid-span \(\left(v(\frac{l}{2})\right)\) of the degraded boards can be calculated using the principle of virtual work. See Eq. 12 where \(M_{f}(i)\) is the bending moment during a four-point bending test, \(M_{v}(i)\) is the bending moment induced by an unitary load at mid-span, \((EI)_{ef}(i)\) is the effective bending stiffness of each segment i and \(\Delta l\) the length of each segment (\(\Delta l\) = 1cm which corresponds to the resolution of the images along x direction). These variables are described in Fig. 4.

Fig. 4
figure 4

Definition of the variables used in the MOE estimation

Full size image
$$\begin{aligned} v\left(\frac{l}{2}\right) = \sum _{i=1}^{n_{segment}} \frac{M_{f}(i) M_{v}(i)}{(EI)_{ef}(i)} \Delta l \end{aligned}$$
(12)

The modulus of elasticity is then calculated by application of beam theory in 4-point bending using Eq. 13, where F is the load which induced the previous bending momentum \(M_{f},\) l is the span, I the second moment of inertia of the actual board and the deflection term is the one calculated with the principle of virtual work on the degraded board (Eq. 12).

$$\begin{aligned} E_{model} = \frac{23 F l^3}{648 I v\left(\frac{l}{2}\right)} \end{aligned}$$
(13)

2.4.2 Estimation of the MOR

In the following part, note that the difference of rupture behaviour existing in compression and tension is not taken into account. Making this differentiation could be dangerous since after the grading process it is not possible to know which side of the different boards will be solicited during their use.

2.4.2.1 Stress calculation

The normal stress at each element is calculated using Eq. 14, where E(x, y) is the local modulus of elasticity defined previously, \(M_{f}\) is the bending momentum, a(x, y) is the distance between the neutral axis of each element and the neutral axis of the board and \(h_e\) is the height of each element (\(h_e\) is actually constant and equal to 2 mm which is the resolution of the images along the y direction). Note that the term a(x, y) is variable along the x direction (at a given y position of the board) since the neutral axis of the board is dependent on the KDR due to the reduced thickness of the degraded board.

$$\begin{aligned} \sigma (x,y)=\frac{E(x,y)a(x,y)M_{f}(x)}{(EI)_{ef}(x)}+ \frac{E(x,y)(h_e/2)M_{f}(x)}{(EI)_{ef}(x)} \end{aligned}$$
(14)
2.4.2.2 Admissible strength estimation

An estimation of the admissible strength of each element is calculated according to Eq. 15. It depends on the modulus of elasticity (linearly with the K parameter) and the grain angle using the same H function as in Eq. 9 with a different set of parameters, since the grain angle influence is not the same, according to the studied property (Bergman et al. 2010).

$$\begin{aligned} \sigma _{lim}(x,y)=K\times E(x,y) \times \frac{H[\theta _{top}(x,y)]+H[\theta _{bot}(x,y)]}2 \end{aligned}$$
(15)
2.4.2.3 Estimation of the MOR

Finally, the estimation of the modulus of rupture consists in finding the bending momentum for which the calculated stress \(\sigma (x,y)\) of a N percentage of the total elements (those between the supports) reaches the admissible strength \(\sigma _{lim}(x,y).\) The modulus of rupture is then calculated using Eq. 16 where \(M_{f_{lim}}\) is the ultimate bending momentum, I the modulus of inertia of the actual board and h is the height of the board.

$$\begin{aligned} \sigma _{model}= \frac{M_{f_{lim}}}{I/h/2} \end{aligned}$$
(16)
2.4.2.4 Model parameters

Several parameters were defined to take into account the different singularities; the optimal values obtained for those parameters are the results of an optimization using the simplex method; the objective function is the minimum of the root mean square error between the prediction and the destructive results. Those parameters needed to be optimized in conditions as close as possible to reality, so the actual test has been modeled. However, in practice for strength grading, indicating properties representative of the entire board must be defined.

2.4.3 Calculation of indicating properties

2.4.3.1 IPMOEmodel

The calculation of \(IPMOE_{model}\) follows exactly the same steps as those described previously to calculate \(E_{model}\) but in this case the span is the entire board (i.e the length is equal to 4m) and not only the part of the boards that was actually loaded.

2.4.3.2 IPMORmodel

The calculation of the \(IPMOR_{model}\) is based on the same principle used in the calculation of \(\sigma _{model},\) but this time the entire board is considered. Since the percentage of the broken surface (N, Table 3) is optimized for a length equal to 18 times the height of the board, \(M_{f_{lim}}\) is calculated within a window (with a length equal to 18 times the height of the board) moving along the entire board. The bending momentum is constant in each window. The calculation of \(IPMOR_{model}\) is then conducted with the minimum of \(M_{f_{lim}}\) from all windows. The stress fields (for the board presented in Fig. 2) for the actual bending momentum and for a constant bending momentum can be seen in Fig. 5.

Fig. 5
figure 5

From top to bottom: local modulus of elasticity; effective bending stiffness along the board; bending momentum used for the \(\sigma _{model}\) calculation; normal stress under the bending momentum of the actual four-point bending test; bending momentum used for the \(IPMOR_{model}\) determination and normal stress under the constant bending momentum. The different fields correspond to the data of the board presented in Fig. 2

Full size image

2.5 Machine grading and efficiency

Strength grading was made according to EN 14081 standards. Two commonly used grade combinations were chosen, C30/C18/Reject and C24/Reject. The indicating properties for the vibration and ultrasound methods are taken as the MOE predictions described previously (directly equal to \(E_{vib}\) and \(E_{sound}\)).

The starting point of the method described in EN 14081 is to build a size matrix which is a double entry table comprising optimal grade vs. assigned grade. In order to obtain the optimal grading, all the pieces shall be sorted into the highest possible grades that are graded together, such that they meet the required values for the grade. Optimal grading is made on the basis of the mechanical properties obtained during the four-point bending test according to the algorithm described in EN 14081-2 (part 6.2.4.5). The assigned grade of each board is obtained by following the method described in EN 14081-2 as well (part 6.2.4.6).

Basically, the method consists in finding indicative properties threshold values; boards with indicating properties higher than these thresholds must fulfill the requirements of the limits defined for each grade in EN 338. This standard requires that the fifth percentiles of density, the fifth percentiles of modulus of rupture \(f_{05}\) and the average modulus of elasticity (\(\bar{E}\)) of the selected boards must be above the given limits in EN 338 for the grade considered.

Moreover, grading has to fulfil the cost matrix method defined in EN 14081-2. This method requires in particular the construction of the size matrix. An example is given in Table 1a. The terms on the diagonal represent well graded boards, i.e boards assigned (with the machine) to the same grade as in the case of optimal grading. The upper part of the matrix represents downgraded boards, i.e boards that are assigned to a lower grade than their optimal grade. Then, the lower part of the matrix represents the upgraded boards, i.e boards that are graded in a higher grade than their optimal grade. Finally, a global cost matrix is calculated by dividing each cell of the size matrix by the total number of boards on the assigned grade and by multiplying it by the corresponding term in a so called elementary cost matrix. The upper part of the elementary cost matrix describes the cost of downgraded boards and the lower part the safety risk of upgraded boards. Since upgraded boards might represent a danger, the number of upgraded boards is limited by the previously cited standards by considering that the settings of the machine are valid if the terms of the lower part of the global cost matrix are lower than 0.2. These matrixes are described in Table 1.

In order to characterize the performance of the studied grading machines, different index were calculated:

  • The index of accuracy is equal to the well graded boards’ percentage \(\left(\frac{75+17+5}{201}\right) \times 100 = 48\%\) in the case of Table 1).

  • Selling price: represents the ratio between the selling prices of the batch of boards graded by machine and the batch of boards optimally graded. The following prices were taken as 100, 200, 220 and 240 euros.m\(^{-3}\) respectively for Reject, C18, C24, and C30 quality. Those prices are representative of the French market price and are based on surveys of industrial partners. The Selling price is equal to \(\frac{78\times 240 +48\times 220 + 75 \times 100}{171\times 240 +18\times 220 + 12 \times 100} \times 100 = 80\%\) in the case of Table 1.

  • The index of efficiency is the application of the method described by Roblot et al. (2013).

To compute the index of efficiency, the first step is to compute a so-called efficiency size matrix which presents the repartition of the boards between grades, but wrongly upgraded boards are moved to the correct grade. A global efficiency matrix is then built based on the method used for the global cost matrix described in EN 14081. The difference stands in the calculation of the efficiency elementary cost matrix. In this case the efficiency elementary cost matrix is computed by dividing the elementary cost matrix of EN 14081 by the maximum value of the upper part of the diagonal. This maximum is 4.5 and corresponds to a C50 board rejected from C14 grade. The complementary to one is finally taken in order to get higher weights for well graded boards and lower for downgraded boards. The different matrixes calculated according to Roblot et al. and EN 14081 are given in Table 1. The index of efficiency is the sum of global efficiency matrix divided by the number of grades \(\frac{1+0.55+0.60+0.41+0+0.15}{3}\times 100= 90.33\%\) for Table 1 data.

Table 1 Cost matrix method and computation of the index of efficiency
Full size table

3 Results and discussions

3.1 Destructives tests

The measured and calculated properties of the different boards for each species, i.e density, modulus of elasticity and bending strength are presented in Table 2. Mechanical and physical properties are higher for Douglas fir than for spruce. The mean density is on average 19% higher for Douglas fir than for spruce, nearly the same percentage can be observed on the \(E_{m,g}\) and the 5% percentile of \(\sigma _{m}\) is 24% higher for Douglas fir than for spruce. The correlations between density and both \(E_{m,g}\) and \(\sigma _{m}\) for the two species are in the same range (slightly lower in the case of density and MOR for Douglas fir). The coefficient of determination between \(E_{m,g}\) and \(\sigma _{m}\) is considerably higher for spruce than for Douglas fir (0.71 compared to 0.58).

Table 2 Minimum, mean, maximum, 5% percentiles values, standard deviations, coefficient of variation, and coefficient of determination for different properties measured
Full size table

3.2 Non-destructive measurements

3.2.1 Density measurements

The comparison between the average density measured by simply measuring and weighing the boards and the average density measured by X-ray scanning highlights the very good accuracy of this method. Indeed the coefficients of determination are respectively equal to 0.99 and 0.96 for spruce and Douglas fir. The accuracy is slightly better in the case of spruce despite the fact that the calibration has been carried out on the two species.

3.2.2 Knotiness measurements

The first image processing used to compute the KDR gives the following results: the average clear wood density is equal to 383 and 475 \(\mathrm{kg}\,\mathrm{m}^{-3}\) respectively for spruce and Douglas fir and 770 and 817 \(\mathrm{kg}\,\mathrm{m}^{-3}\) concerning the average knot density. The mean values of the \(f_1\) parameters (the ones used in the analytical model) are nearly the same for spruce as for Douglas fir (1.11 and 1.13, respectively). The \(f_2\) parameters are quite different (2.03 and 1.75) between the two species showing that the difference between clear wood density and knot density is higher in the case of spruce than for Douglas fir. Finally, the mean KDR is higher in the case of Douglas fir (0.43) than for spruce (0.32) and indicates the potentially higher nodosity of Douglas fir compared to spruce.

3.2.3 Stiffness measurements

The vibratory method estimates highly accurately the MOE for both spruce and Douglas fir with a high coefficient of determination (0.85 and 0.80, respectively). Concerning the correlation with the MOR, the results are consistent with those observed with destructive values, i.e. a better correlation for spruce than for Douglas fir (0.58 compared to 0.44). It seems that the ultrasound method gives lower results independently of the species. Indeed, the coefficients of determination between \(E_{sound}\) and \(E_{m,g}\) are respectively equal to 0.76 and 0.68 for spruce and Douglas fir. The ones between \(E_{sound}\) and \(\sigma _{m}\) are respectively equal to 0.48 and 0.34. Those results are consistent with a previous study (Wang et al. 2008).

3.3 Mechanical modelling

3.3.1 Mechanical properties prediction

As stated earlier, different parameters have been defined to consider the different singularities depending on the species; the optimal values obtained for those parameters are described in Table 3. The parameters of the linear relationship between density and modulus of elasticity might appear different depending on the species but they describe nearly the same relationship. Concerning the \(\alpha\) parameters which in fact reflect the influence of the knottiness, it seems to take a greater value for the bending strength prediction. Concerning the parameters of grain angle they are consistent with the literature. The K parameters represent the relationship between MOE and MOR for wood without defects, it can be considered acceptable for example that for a board with a MOE equal to 10,000 MPa the corresponding MOR is equal to approximatively 50 MPa. Concerning the last parameter N, it is there expressed as a percentage of the \(<<\) broken \(>>\) surface based on the total surface of the board. It corresponds to a surface equal to approximatively 38 and 49 cm\(^2\) for spruce and Douglas fir, respectively.

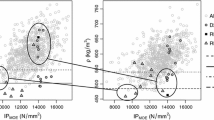
Table 3 Model parameters for the two species
Full size table

The relationships between \(E_{model}\) (Eq. 13) and the measured global MOE as defined in Eq. 5, and between \(\sigma _{model}\) (Eq. 16) and the measured MOR (Eq. 6) are presented in Fig. 6. The coefficient of determination between \(E_{model}\) and \(E_{m,g}\) is lower than the one between \(E_{vib}\) and \(E_{m,g}\) but the correlation is quite good and even better than the one observed for the ultrasound method \(E_{sound}\) for both spruce and Douglas fir. The root mean square error between \(E_{model}\) and \(E_{m,g}\) is equal to 1188 (13% of the mean value) and 1224 MPa (11% of the mean value) respectively for spruce and Douglas fir. Concerning the MOR, it can be seen that taking into account the different measured singularities improves a lot the prediction. The results are better for spruce than for Douglas fir; it can be explained by the higher intrinsic correlation between \(\rho\) and \(\sigma _m\) and \(E_{m,g}\) and \(\sigma _m\) (Table 2). The root mean square error between \(\sigma _{model}\) and \(\sigma _m\) is equal to 6.5 MPa (21% of the mean value) and 7.9 MPa (22% of the mean value) respectively for spruce and Douglas fir. Concerning the computational time, it is about 72s for the batch of spruce boards and 137 s for the batch of Douglas fir boards on a personal computer.

Fig. 6
figure 6

Comparison of predicted and tested values of the modulus of elasticity and bending strength in the case of spruce and Douglas fir

Full size image

3.3.2 Indicating properties

The coefficients of determination between \(IPMOE_{model}\) and \(E_{m,g}\) are respectively equal to 0.78 for spruce and 0.74 in the case of Douglas fir. The ones between \(IPMOR_{model}\) and \(\sigma _m\) are respectively equal to 0.66 for spruce and 0.53 for Douglas fir. The coefficients of determination are lower in the case of the two indicating properties:

  • 0.78 compared to 0.79 and 0.74 compared to 0.75 for \(E_{m,g}\)

  • 0.66 compared to 0.68 and 0.53 compared to 0.58 for \(\sigma _m\)

Those results are due to the fact that the computation of the Indicating Properties includes parts of the boards that were not actually sollicited during the four-point bending tests.

3.4 Grading efficiency

Grading results for the different methods and the C24/Reject combination in the case of Douglas fir are presented in Table 4. As a reminder when grading by machines, the required characteristic value on the 5th percentile bending strength must be divided by the factor \(k_v\) which is equal to 1.12 for grades with \(f_{m,k}\) equal or less than 30 MPa and 1 for other grades (EN 14081-2 part 6.2.2 and EN 384). The required average modulus of elasticity is equal to the required average MOE of the grade times 0.95 (EN 14081-2 part 6.2.4.5). By taking into account those adjustments, the requirements for the C24 grade are respectively equal to 21.4 MPa, 10,450 MPa and 350 kg\(^{-3}\) for the 5th percentile MOR, the mean MOE and the 5th percentile MOR. The MOR is clearly the discriminating property in this combination (bold values in Table 4 are very close to the requirements), so it explains why the methods with the higher correlation with the MOR give the better results.

Table 4 Grading results in the case of Douglas fir for the C24/Reject combination
Full size table

Grading results of the different methods presented in this study and for the chosen grade combinations are given in Fig. 7. On the basis of the optimal grading (i.e. made according to the destructive test results) Douglas fir has better mechanical properties than spruce; this is consistent with the observation of the previously established characteristics values. The studied spruce batch has a lower proportion of C30 boards than the Douglas fir batch; the grading process by machine gives almost the same proportion of C30 boards for both species. As an example, for the model and the C30/C18/Reject combination, 32% of spruce timber is graded C30 compared to 39% actually present in the batch, while for the case of Douglas fir the proportion is only 26% compared to 70%. Whatever the machines used, spruce is better valued than Douglas fir. This difference is much less visible for lower grade, but this fact is visible by considering the average efficiency of all machines and all the grade combination, that is about 96% for spruce and just over 90% for Douglas fir. The correlation of the ultrasound method with MOE and MOR was lower, the results show that it is also on average the least efficient machine to perform mechanical grading on the two batches of boards.

Fig. 7
figure 7

Strength grading results of every machine and every grade combination tested for Spruce (top) and Douglas fir (bottom)

Full size image

Table 5 shows the gain (in %) observed by using the developed model in comparison to the other two methods studied in terms of efficiency, accuracy and selling prices. For all three criteria and any combination of grade tested, the use of the model is always an improvement in the case of Douglas fir, while the improvement is only consistently greater in terms of accuracy for grade combination containing C30 in the case of spruce. Note that despite this difference, the use of the proposed model is still favourable to grade a larger number of boards in higher grade. The fact that the improvement is greater in the case of Douglas fir is due to the fact that the consideration of the local defects in the case of Douglas fir greatly improves the correlation with \(\sigma _m\) compared to the methods that measure a global MOE, while in the case of spruce, these methods take advantage of the better correlation between \(E_{m,g}\) and \(\sigma _m.\)

Table 5 Gain or loss (in %) observed using the proposed model compared to existing methods
Full size table

4 Conclusion

This study shows that it is possible to develop a mechanical model using local information (measured by a scanner dedicated to mechanical grading) to perform strength grading in an industrial context instead of global information. Indeed, the model allows to handle a speed of about 1600 m/min (with a personal computer) and is therefore not a limiting factor when comparing this rate to the acquisition speed of the scanner, which is approximatively 200 m/min. In addition, this method gives better results (in terms of efficiency, accuracy and economic valorisation) than two commonly used methods which consist of a non-destructive measurement of the global elastic modulus. It was also shown that the application of this method is more efficient in the case of Douglas fir than for spruce, and that this difference is probably due to the lower natural correlation between the MOE and MOR, and also that bigger knots are present in the case of Douglas fir. Taking into account Douglas fir local singularities strongly improves the correlation between the MOR prediction and the actual MOR which leads to better results on the strength grading. In order to improve the models performance, other kind of singularities, such as juvenile or compression wood, could be taken into account. For example, the linear relationship between the density and the modulus of elasticity could be changed in areas where there is juvenile wood which has a lower modulus of elasticity than mature wood (Moore et al. 2009).