Generalized Fourier Transforms Associated with the Oscillator Representation

Abstract

By identifying the Fourier transform $\mathcal {F}$ with an operator in the oscillator representation of the metaplectic group ${\widetilde{Sp}(2n,\mathbb {R})}$, the twofold cover of the symplectic group $Sp(2n,\mathbb {R})$, we study generalized Fourier transforms inspired by the work of De Bie, Oste and Van der Jeugt. We obtain several families of operators $\mathcal {T}$’s that have the important properties similar to $\mathcal {F}$ using various dual pair correspondences.

1 Introduction

The Fourier transform is a powerful tool in harmonic analysis with wide applications. For instance, it plays a pivotal role in the recent progress on the spherical packing problem as it can simultaneously diagonalize translations and make periodic structures easier to understand [1]. There are several conventions to define the Fourier transform over $\mathbb {R}^n$. Let $L^p({\mathbb {R}}^n)$ denotes the space of all p-th power Lebesgue integrable functions on ${\mathbb {R}}^n$ for $1\le p<\infty$. Throughout this paper, the Fourier transform of $f\in L^1(\mathbb {R}^n)\cap L^2(\mathbb {R}^n)$ is given by

$$\begin{aligned} (\mathcal {F}f)(y)=\frac{1}{(2\pi )^{n/2}}\int _{\mathbb {R}^n} e^{-i\langle x, y\rangle } f(x) d x, \end{aligned}$$

where $\langle x, y\rangle$ is the standard inner product on $\mathbb {R}^n$. The inverse Fourier transform $\mathcal {F}^{-1}$ of $f\in L^1(\mathbb {R}^n)\cap L^2(\mathbb {R}^n)$ is given by

$$\begin{aligned} \left( \mathcal {F}^{-1} f\right) (y)=\frac{1}{(2\pi )^{n/2}}\int _{\mathbb {R}^n} e^{i\langle x, y\rangle } f(x) d x, \end{aligned}$$

which is indeed the inverse of $\mathcal {F}$ as a consequence of the Fourier inverse theorem. It follows that $\mathcal {F}$ is a unitary operator on $L^2(\mathbb {R}^n)$, with respect to the inner product $\langle f,g \rangle =\int _{\mathbb {R}^n}f(x)\overline{g(x)}dx$. The Schwartz space $\mathcal {S}(\mathbb {R}^n)$ is a dense subspace of $L^2(\mathbb {R}^n)$ and the action of $\mathcal {F}$ on $L^2(\mathbb {R}^n)$ is extended from its action on $\mathcal {S}(\mathbb {R}^n)$. In addition, $\mathcal {F}$ is a homeomorphism of $\mathcal {S}(\mathbb {R}^n)$ onto itself (cf. [11]). For convenience, we specify the underlying space of $\mathcal {F}$, as well as the generalized operators we will construct in this paper, to be $\mathcal {S}(\mathbb {R}^n)$.

In the framework of the oscillator representation, the Fourier transform $\mathcal {F}$ is expressed by

(1.1)

with an element in $\mathfrak {sl}(2,\mathbb {R})$ that is embedded into ${\mathfrak {sp}}(2n,\mathbb {R})$ in a dual pair $(O(n),\mathfrak {sl}(2,\mathbb {R}))$. De Bie, Oste and Van der Jeugt [2] have obtained a class of generalized Fourier transforms as exponential of elements in the universal enveloping algebra $\mathcal {U}(\mathfrak {sl}(2,\mathbb {R}))$ by determining their series expansions. In this paper, we construct generalized Fourier transforms by a different approach.

To illuminate our idea, we recall the basic concepts of the dual pair correspondence. Following Howe, we define a reductive dual pair in $Sp(2n,\mathbb {R})$ to be a pair of closed reductive subgroups $G,G'$ of $Sp(2n,\mathbb {R})$ such that G and $G'$ are centralizers of each other. The dual pair correspondence can be obtained by the following consideration. Denote by $\mathbb {D}(\mathbb {R}^n)$ the Weyl algebra of polynomial coefficient differential operators on $\mathbb {R}^n$ (cf. [3, p. 278]). Let G be a reductive algebraic subgroup of $GL(n,\mathbb {R})$ (cf. [7, p. 446]). Then G acts on $\mathcal {S}(\mathbb {R}^n)$ by

$$\begin{aligned} \rho (g)f(x)=f(g^{-1}x). \end{aligned}$$

Let $\mathbb {D}(\mathbb {R}^n)^G$ be the commutant of G in $\mathbb {D}(\mathbb {R}^n)$. If the generators of $\mathbb {D}(\mathbb {R}^n)^G$ span a Lie algebra $\mathfrak {g}'$, then it is the Lie algebra of $G'$ in a dual pair $(G,G')$. In this case there is a correspondence of representations between G and $\mathfrak {g}'$ (cf. [3], Sect. 9.2.1).

We can easily construct the following four families of dual pairs with m, n, p, q positive integers:

• (i) $(O(n),Sp(2m,\mathbb {R}))\subset Sp(2nm,\mathbb {R})$,

• (ii) $(U(n),U(m))\subset Sp(2nm,\mathbb {R})$,

• (iii) $(O(p,q),Sp(2m,\mathbb {R}))\subset Sp(2(p+q)m,\mathbb {R})$,

• (iv) $(U(p,q),U(m))\subset Sp(2(p+q)m,\mathbb {R})$.

In this paper we are only concerned with the case $m=1$ for the construction of generalized Fourier transforms.

A very important property of Fourier transform $\mathcal {F}$ is that it commutes with the standard action of the orthogonal group O(n) on $\mathcal {S}(\mathbb {R}^n)$. In other words, $\mathcal {F}$ is O(n)-equivariant. In case $G=O(n)$ the other party in the dual pair is $\mathfrak {g}'=\mathfrak {sl}(2,\mathbb {R})$. The Fourier transform $\mathcal {F}$ in the oscillator representation has the following $O(n)\times \mathfrak {sl}(2,\mathbb {R})$-module decomposition [9]

$$\begin{aligned} \mathcal {F}\simeq \sum _{k=0}^{\infty }Id|_{\mathcal {H}_k} \otimes T_k, \end{aligned}$$

(1.2)

where $\mathcal {H}_k$ is the space of harmonic polynomials homogeneous of degree k and $T_k$ is the Hankel transform. This leads us to consider the generalized Fourier transforms in the dual pair $(O(n),\mathfrak {sl}(2,\mathbb {R}))$.

We note that a key technique in our approach is Schur’s lemma. The discrete decomposition as above (1.2) is crucial. It is natural to consider the dual pair $(O(p,q),\mathfrak {sl}(2,\mathbb {R}))$ ($p+q=n$). However, our approach fails in this case, since the decomposition of the oscillator representation is not discrete [4, 10]. Nevertheless, we are able to deal with another two pairs (U(n), U(1)) and (U(p, q), U(1)) due to the discrete decompositions of the oscillator representation.

We are very grateful to Hendrik De Bie for his insightful comments. We also thank the referee for very helpful remarks.

2 Fourier Transform and the Oscillator Representation

In this section, we recall the basic properties of the Fourier transform $\mathcal {F}$ in the framework of the oscillator representation.

Proposition 2.1

$\mathcal {F}$ has the following properties:

• (i) $\mathcal {F}$ is $O(n)-equivariant,$ i.e.

  $$\begin{aligned} \mathcal {F}(gf)=g(\mathcal {F}f),\forall f\in \mathcal {S}(\mathbb {R}^n), g\in O(n). \end{aligned}$$

• (ii) Write $\partial _j$ for $\frac{\partial }{\partial x_j}$. Then

  $$\begin{aligned} \mathcal {F}\circ x_j= & {} i\partial _j \circ \mathcal {F}, \,\,\mathcal {F}\circ \partial _j=i x_j \circ \mathcal {F}\\ \mathcal {F}^{-1} \circ x_j= & {} -i\partial _j \circ \mathcal {F}^{-1},\,\, \mathcal {F}^{-1} \circ \partial _j=-i x_j \circ \mathcal {F}^{-1}. \end{aligned}$$

• (iii) Let ${\tilde{f}}$ be the reflection of f, i.e. ${\tilde{f}}(x)=f(-x),\forall x\in \mathbb {R}^n.$ Then

  $$\begin{aligned} \mathcal {F}^2f=\mathcal {F}^{-2}f={\tilde{f}},\forall f\in \mathcal {S}(\mathbb {R}^n). \end{aligned}$$

These properties are obtained by straightforward calculation [11, Chapter I §2].

Recall that the Schwartz space on $\mathbb {R}^n$ is defined by is

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)=\left\{ f\in C^{\infty }(\mathbb {R}^n): \sup _{x\in \mathbb {R}^n}|x^{\alpha }D^{\beta }f(x)|<\infty , \forall \alpha ,\beta \in \mathbb {N}^n \right\} \end{aligned}$$

where $x^{\alpha }D^{\beta }=x_1^{\alpha _1}\ldots x_n^{\alpha _n}\frac{\partial ^{|\beta |}}{\partial x_1^{\alpha _1}\ldots \partial x_n^{\alpha _n}}$. When $n=1$, $\mathcal {S}(\mathbb {R})$ is space of the oscillator representation of $\mathfrak {sl}(2,\mathbb {R})$ and is denoted by $\omega$. Set

$$\begin{aligned} SL(2,\mathbb {R})=\left\{ \begin{bmatrix} a&\quad b\\ c&\quad d \\ \end{bmatrix}\Big | a,b,c,d\in \mathbb {R} \text{ satisfying } ad-bc=1\right\} . \end{aligned}$$

The group $SL(2,\mathbb {R})$ has fundamental group $\mathbb {Z}$ and thus has a unique (up to isomorphism) connected twofold cover, denoted by $\widetilde{SL}(2,\mathbb {R})$. The Lie algebra $\mathfrak {sl}(2,\mathbb {R})$ has a natural basis:

$$\begin{aligned} e^+=\begin{bmatrix} 0&\quad 1\\ 0&\quad 0 \\ \end{bmatrix}, \text { } e^-=\begin{bmatrix} 0&\quad 0\\ -1&\quad 0 \\ \end{bmatrix}, \text { } h=\begin{bmatrix} 1&\quad 0\\ 0&\quad -1 \\ \end{bmatrix} \end{aligned}$$

with commutator relations

$$\begin{aligned}{}[h,e^+]=2e^+,[h,e^-]=-2e^-,[e^+,e^-]=h. \end{aligned}$$

The group SO(2) is a maximal compact subgroup of $SL(2,\mathbb {R})$, and its Lie algebra is $\mathfrak {k}_0=\mathfrak {so}(2,\mathbb {R})$. The complexification $\mathfrak {k}=(\mathfrak {k}_0)_{\mathbb {C}}$ is spanned by

Then together with

$$\begin{aligned} n^+=\frac{1}{2}\left( h+i\left( e^-+e^+\right) \right) ,n^-=\frac{1}{2}\left( h-i\left( e^-+e^+\right) \right) , \end{aligned}$$

form another basis for $\mathfrak {sl}(2,\mathbb {R})$, with the similar commutation relations as $\{h,e^+,e^-\}$.

The oscillator representation $(\omega ,\mathcal {S}(\mathbb {R}))$ of $\mathfrak {sl}(2,\mathbb {R})$ is given by

$$\begin{aligned} \omega (e^+)=\frac{i}{2}x^2, \text { } \omega (e^-)=\frac{i}{2}\frac{d^2}{dx^2}, \text { } \omega (h)=x\frac{d}{dx}+\frac{1}{2}. \end{aligned}$$

The Lie algebra action exponentiates to a unitary representation of $\widetilde{SL}(2,\mathbb {R})$ on $L^2(\mathbb {R})$ [5, Theorem 2.1.2].

Set $a=x+\frac{\partial }{\partial x},a^+=x-\frac{\partial }{\partial x}$. Then acts on $\mathcal {S}(\mathbb {R})$ diagonally by

which is known as the Hermite operator (see [5, p. 103]). Set

$$\begin{aligned} v_{j}:=(a^+)^{j}e^{-\frac{r^2}{2}}, \text { for }j\in \mathbb {Z}_{\ge 0}. \end{aligned}$$

Then $\{v_j\}$ forms an orthogonal -eigenbasis.

Lemma 2.2

[5, Chapter III §2.1] Set

$$\begin{aligned} V_{\frac{1}{2}}=Span\{v_{2j}|j\in \mathbb {N}\} \text { and } V_{\frac{3}{2}}=Span\{v_{2j+1}|j\in \mathbb {N}\}. \end{aligned}$$

Then $V_{\frac{1}{2}}$ and $V_{\frac{3}{2}}$ are irreducible lowest weight modules of $\mathfrak {sl}(2,\mathbb {R})$ with lowest weights $\frac{1}{2}$ and $\frac{3}{2}$ respectively, and the oscillator representation is decomposed as

$$\begin{aligned} \mathcal {S}(\mathbb {R})\simeq V_{\frac{1}{2}}\oplus V_{\frac{3}{2}}. \end{aligned}$$

Let $v_j^*\in \mathcal {S}(\mathbb {R})^*$ be the dual basis of $v_j$. Then $\mathcal {S}(\mathbb {R})^*_{adm}={\text {Span}}\left\{ v_j^*|j\in \mathbb {Z}\right\}$, the admissible dual of $(\omega ,\mathcal {S}(\mathbb {R}))$, can be identified with the -finite vectors in $\mathcal {S}(\mathbb {R})$ with $\mathfrak {sl}(2,\mathbb {R})$-action given by

$$\begin{aligned} \omega ^*(e^+)=-\frac{i}{2}x^2, \text { } \omega ^*(e^-)=-\frac{i}{2}\frac{d^2}{dx^2}, \text { } \omega ^*(h)=x\frac{d}{dx}+\frac{1}{2}. \end{aligned}$$

The representation $(\omega ^n,\mathcal {S}(\mathbb {R}^n))$ of $\mathfrak {sl}(2,\mathbb {R})$ is the $n-$fold tensor power of $(\omega ,\mathcal {S}(\mathbb {R}))$, where $\mathcal {S}(\mathbb {R})^{\otimes n}$ is identified with $\mathcal {S}(\mathbb {R}^n)$ and the action is given by

$$\begin{aligned} \omega ^n(e^+)=\frac{i}{2}r^2, \text { } \omega ^n(e^-)=\frac{i}{2}\Delta , \text { } \omega ^n(h)=E+\frac{n}{2}. \end{aligned}$$

Here $r^2= \sum _{j=1}^n x_j^2$ is the multiplication by $r^2$, $\Delta = \sum _{j=1}^n \left( \frac{\partial }{\partial x_j}\right) ^2$ is the Laplace operator and $E=\sum _{j=1}^n x_j\frac{\partial }{\partial x_j}$. When there is no confusion on the action, we omit $\omega ^n$.

Set $a_j=x_j+\frac{\partial }{\partial x_j},a_j^+=x_j-\frac{\partial }{\partial x_j}$. Then

For $\beta =(\beta _1,\ldots ,\beta _n)\in \mathbb {N}_+^n$, set

$$\begin{aligned} v_{\beta }=\left( a_1^+\right) ^{\beta _1}\ldots \left( a_n^+\right) ^{\beta _n}v_{0}\text { with }v_{0}=e^{-\frac{1}{2}r^2}. \end{aligned}$$

By computation, $v_{\beta }=P_{\beta }(x_1,\ldots ,x_n)v_{0}$, where $P_{\beta }$ are the well-known Hermite polynomials. And $v_{\beta }$ are known as Hermite functions. Moreover, $\{v_{\beta }|\beta \in \mathbb {N}^n\}$ forms an orthogonal eigenbasis for $\mathcal {S}(\mathbb {R}^n)$, because

where $|\beta |=\sum _{j=1}^n \beta _j$, for all $\beta \in \mathbb {N}^n$. It follows that

In addition, by comparing their actions on the basis (cf. [5], p. 121), we conclude that

(2.1)

The action of $\mathcal {F}$ on the basis of $\mathcal {S}(\mathbb {R}^n)$ spanned by $v_\beta$’s indicates that the intertwining relation in (ii) of Proposition 2.1 characterize $\mathcal {F}$. We make the precise statement in the following proposition [9, Propositions 1.2.1 and 1.2.2].

Proposition 2.3

Suppose $\mathcal {T}$ is a continuous operator on $\mathcal {S}(\mathbb {R}^n)$.

• (i) The condition

  $$\begin{aligned} \mathcal {T}\circ x_j=i\partial _j \circ \mathcal {T}\text { and }\mathcal {T}\circ \partial _j=i x_j \circ \mathcal {T}\ (1\le i\le n) \end{aligned}$$

  (2.2)

  implies that $\mathcal {T}$ is a multiple of $\mathcal {F}.$

• (ii) The condition

  $$\begin{aligned} \mathcal {T}\circ x_ix_j=-\partial _i\partial _j \circ \mathcal {T}\text { and }\mathcal {T}\circ \partial _i\partial _j=- x_ix_j \circ \mathcal {T}(1\le i,j\le n) \end{aligned}$$

  (2.3)

  implies that $\mathcal {T}=a\mathcal {F}+b\mathcal {F}^{-1}$ for some $a,b\in \mathbb {C}$.

Proof

These two facts are consequences of straightforward calculations. We include these calculations, since this is the simplest case for our approach of using the dual pair correspondence and Schur’s lemma.

• (i) The condition $\mathcal {T}\circ x_j=i\partial _j \circ \mathcal {T}\text { and } \mathcal {T}\circ \partial _j=i x_j \circ \mathcal {T}\ (1\le j\le n)$ implies that

  $$\begin{aligned} \mathcal {T}\circ a_j^+=\mathcal {T}\circ (x_j-\partial _j)=(i\partial _j-ix_j)\circ \mathcal {T}=-ia_j^+\circ \mathcal {T}. \end{aligned}$$

  We have $\mathcal {T}v_{0}=c v_{0}$ for some $c\in \mathbb {C}$, because for $1\le j\le n$

  $$\begin{aligned} \partial _j \frac{\mathcal {T}v_{0}}{v_{0}}= & {} \partial _j \left( \mathcal {T}\left( e^{-\frac{r^2}{2}}\right) e^{\frac{r^2}{2}}\right) \\= & {} (\partial _j\mathcal {T})\left( e^{-\frac{r^2}{2}}\right) e^{\frac{r^2}{2}}+x_j\mathcal {T}\left( e^{-\frac{r^2}{2}}\right) e^{\frac{r^2}{2}}\\= & {} 0, \end{aligned}$$

  since $\partial _j\mathcal {T}\big (e^{-\frac{r^2}{2}}\big )=-i\mathcal {T}\big (x_je^{-\frac{r^2}{2}}\big )=i\mathcal {T}\big (\partial _j\big (e^{-\frac{r^2}{2}}\big )\big )=-x_j\mathcal {T}(e^{-\frac{r^2}{2}})$. It follows that

  $$\begin{aligned} \mathcal {T}v_{\beta }= & {} \mathcal {T}\left( \left( a_1^+\right) ^{\beta _1}\ldots \left( a_n^+\right) ^{\beta _n}v_{0}\right) \\= & {} (-i)^{|\beta |}\left( a_1^+\right) ^{\beta _1}\ldots \left( a_n^+\right) ^{\beta _n}\mathcal {T}v_{0}\\= & {} (-i)^{|\beta |}cv_{\beta } \end{aligned}$$

  for all $\beta \in \mathbb {N}^n$. Therefore, .

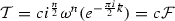• (ii) Note that $\{x_{i}\partial _j+\frac{1}{2}\delta _i^j,x_ix_j,\partial _i\partial _j|1\le i,j\le n\}$ forms a basis of the Lie algebra isomorphic to $\mathfrak {sp}(2n,\mathbb {R})$ via the map $\psi$

  $$\begin{aligned} x_{i}\partial _j+\frac{1}{2}\delta _i^j\mapsto & {} e_{i,j}-e_{n+j,n+i},\\ x_ix_j\mapsto & {} e_{i,j+n}+e_{j,i+n},\\ \partial _i\partial _j\mapsto & {} -e_{i+n, i}-e_{j+n,i}. \end{aligned}$$

  Here $e_{i,j}$ is the matrix whose (i, j)th entry is 1 and 0’s elsewhere. Set

  $$\begin{aligned} V_{even}={\text {Span}}\{v_{\beta }:|\beta | \text { is even}\}, \ V_{odd}={\text {Span}}\{v_{\beta }:|\beta | \text { is odd}\}. \end{aligned}$$

  Then both $V_{even}$ and $V_{odd}$ are irreducible $\mathfrak {sp}(2n,\mathbb {R})$-modules, and

  $$\begin{aligned} \mathcal {S}(\mathbb {R}^n)=V_{even}\oplus V_{odd}. \end{aligned}$$

  It follows from the condition

  $$\begin{aligned} \mathcal {T}\circ x_ix_j=-\partial _i\partial _j \circ \mathcal {T}\text { and }\mathcal {T}\circ \partial _i\partial _j=- x_ix_j \circ \mathcal {T}\ (1\le i,j\le n) \end{aligned}$$

  that

  $$\begin{aligned} \mathcal {T}\circ \left( x_{i}\partial _j+\frac{n}{2}\delta _i^j\right) =\mathcal {T}\circ [x_ix_j,\partial _i\partial _j]=-\left( x_{i}\partial _j+\frac{n}{2}\delta _i^j\right) \circ \mathcal {T}. \end{aligned}$$

  Note that $\mathcal {F}$ has the similar property. It follows that $\mathcal {T}\mathcal {F}$ commutes with action of each element in $\mathfrak {sp}(2n,\mathbb {R})$. By Schur’s lemma, there exist $c_1,c_2\in \mathbb {C}$ such that

  $$\begin{aligned} \mathcal {T}\mathcal {F}|_{V_{even}}=c_1{\text {Id}}, \ \ \mathcal {T}\mathcal {F}|_{V_{odd}}=c_2{\text {Id}}. \end{aligned}$$

  Let $a=\frac{c_1+c_2}{2}, b=\frac{c_1-c_2}{2}$. Note that $\mathcal {F}^2|_{V_{even}}={\text {Id}},\ \mathcal {F}^2 |_{V_{odd}}=-{\text {Id}}$. It follows that

  $$\begin{aligned} \mathcal {T}\mathcal {F}=a\mathcal {F}^2+b{\text {Id}}. \end{aligned}$$

  Thus, $\mathcal {T}=a\mathcal {F}+b\mathcal {F}^{-1}$.

$\square$

Remark 2.4

In the proof of (ii) of Proposition 2.3, $\mathcal {S}(\mathbb {R}^n)$ is a module (not irreducible) for the symplectic Lie algebra ${\mathfrak {sp}}(2n,\mathbb {R})$ generated by $\{x_ix_j, \partial _i\partial _j\}$. It can be shown that this module is actually a representation for the twofold cover of the symplectic group $Sp(2n,\mathbb {R})$ and is called the oscillator representation. One can make $\mathcal {S}(\mathbb {R}^n)$ a simple module for either the Lie superalgebra $\mathfrak {osp}(1|2n)$ generated by $\{x_j,\partial _j\}$ or the Weyl algebra $\mathbb {D}(\mathbb {R}^n)$. Then one can deduce (i) of Proposition 2.3 by the Schur’s lemma.

We write $I_n$ for the n by n identity matrix. Set

$$\begin{aligned} J_n=\begin{bmatrix} 0&\quad I_{n}\\ -I_{n}&\quad 0 \end{bmatrix}\in Sp(2n,\mathbb {R}). \end{aligned}$$

Recall that the metaplectic group ${\widetilde{Sp}(2n,\mathbb {R})}$ is a two-fold cover of the symplectic group $Sp(2n,\mathbb {R})$. There exists a unique central element $\xi _0$ of order 2 and an exact sequence of Lie groups:

$$\begin{aligned} 1\rightarrow \{I_{2n},\xi _0\}\rightarrow {\widetilde{Sp}(2n,\mathbb {R})}\rightarrow {Sp(2n,\mathbb {R})}\rightarrow 1. \end{aligned}$$

The oscillator representation mentioned above for ${\mathfrak {sp}}(2n,\mathbb {R})$ is actually a unitary representation for ${\widetilde{Sp}(2n,\mathbb {R})}$. There is an element $\omega _0'\in {\widetilde{Sp}(2n,\mathbb {R})}$ such that $\omega _0'$ corresponds to $J_n$ under the covering map and $i^{\frac{n}{2}} \mathcal {F}^{-1} (\text {mod }\{I_{2n},\xi _0\})$ is equal to the action of $\omega '_0$ in the oscillator representation (cf. [9] p. 21).

We now extend our consideration to the indefinite Fourier transform $\mathcal {F}_{p,q}$ and their corresponding elements in the metaplectic group ${\widetilde{Sp}(2n,\mathbb {R})}$ associated with the oscillator representation.

Let p, q be two positive integers such that $p+q=n$. Consider the indefinite bilinear form of signature (p, q) on $\mathbb {R}^{p+q}$:

$$\begin{aligned} \langle x,x'\rangle _{p,q}:=\sum _{j=1}^p x_jx_j'-\sum _{j=p+1}^{p+q} x_jx_j',\forall x,x'\in \mathbb {R}^{p+q}, \end{aligned}$$

and define Fourier transforms $\mathcal {F}_{p,q}$ by

$$\begin{aligned} (\mathcal {F}_{p,q} f)(y)=\frac{1}{(2\pi )^{(p+q)/2}}\int _{\mathbb {R}^{p+q}} e^{-i\langle x, y\rangle _{p,q}} f(x) d x. \end{aligned}$$

Then one has

$$\begin{aligned} i^{\frac{p-q}{2}} \mathcal {F}_{p,q}^{-1} (\text {mod }\{I_{2n},\xi _0\}) =J_{p,q}=\begin{bmatrix} 0&\quad I_{p,q}\\ -I_{p,q}&\quad 0 \end{bmatrix}\in Sp(2(p+q),\mathbb {R}), \end{aligned}$$

where $I_{p,q}=\begin{bmatrix}I_p&\quad 0\\0&\quad -I_q\end{bmatrix}$ (cf [5]). One may use another indefinite bilinear form of signature (p, q) on $\mathbb {R}^{p+q}$ in different order of variables. The resulting Fourier transform is different, but conjugate to $\mathcal {F}_{p,q}$ by an element in ${\widetilde{Sp}(2n,\mathbb {R})}$.

The tensor product $\omega ^p\otimes \omega ^{q*}$ can be identified with $\mathcal {S}(\mathbb {R}^{p+q})$ (cf. [5, Chapter III §2.3]), that is

$$\begin{aligned} \mathcal {S}(\mathbb {R}^p)\widehat{\otimes } \mathcal {S}(\mathbb {R}^q) \cong \mathcal {S}(\mathbb {R}^{p+q}). \end{aligned}$$

Then the representation $(\omega ^{p,q},\mathcal {S}(\mathbb {R}^{p+q}))$$\simeq (\omega ^p\otimes \omega ^{q*},\mathcal {S}(\mathbb {R}^p)\widehat{\otimes } \mathcal {S}(\mathbb {R}^q))$ of $\mathfrak {sl}(2,\mathbb {R})$ is given by

$$\begin{aligned} \omega ^{p,q}(e^+)=\frac{i}{2}r_{p,q}, \text { } \omega ^{p,q}(e^-)=\frac{i}{2}\Delta _{p,q}, \text { } \omega ^{p,q}(h)=E+\frac{n}{2}. \end{aligned}$$

(2.4)

Here

$$\begin{aligned} r_{p,q}=\left( r_p^2-r_q^2\right) =\sum _{j=1}^p x_j^2-\sum _{j=1}^{q} x_{j+p}^2 \end{aligned}$$

is the standard indefinite metric of signature (p, q), and

$$\begin{aligned} \Delta _{p,q}=(\Delta _p-\Delta _q)=\sum _{j=1}^p \frac{\partial ^2}{\partial x_j^2}-\sum _{j=1}^{q} \frac{\partial ^2}{\partial x_{j+p}^2} \end{aligned}$$

is called the indefinite Laplacian when $q>0$. It follows that

Denote $\frac{1}{2}(r^2_{p,q}-\Delta _{p,q})$ by . For $\beta \in \mathbb {N}^{p},\gamma \in \mathbb {N}^{q}$, recall from section 2 that $u_{\beta },w_{\gamma }$ are the bases for $\mathcal {S}(\mathbb {R}^p)$ and $\mathcal {S}(\mathbb {R}^q)$ respectively. Then $\{v_{\beta ,\gamma }:=u_{\beta } w_{\gamma } ^*|\beta \in \mathbb {N}^{p},\gamma \in \mathbb {N}^{q}\}$ forms an orthogonal eigenbasis for $\mathcal {S}(\mathbb {R}^{p+q})$. By comparing the actions of and $\mathcal {F}_{p,q}$ on the basis of $\mathcal {S}(\mathbb {R}^{p+q})$, we conclude that

Denote by $\varpi _{p,q}$. Then

$$\begin{aligned} \varpi _{p,q} (\text {mod} \{I_{2n},\xi _0\})=J_{p,q} \end{aligned}$$

and

$$\begin{aligned} \varpi _{p,q}=\varpi _{q,p}^{-1},\ \varpi _{p,q}\varpi _{s,t}=\varpi _{s,t}\varpi _{p,q}\text { and }\varpi _{p,q}^2=\varpi _{s,t}^2. \end{aligned}$$

Let $\Gamma$ be the finite abelian group generated by all $\varpi _{p,q}$. It is clear that $\Gamma$ is actually generated by $\varpi _{p,q}$ with $p=0,1,\ldots ,$$[\frac{p+q+1}{2}]$.

3 Generalized Fourier Transforms in $(O(n),\mathfrak {sl}(2,\mathbb {R}))$-Pair

The conditions (2.2) and (2.3) both give characterizations of the Fourier transform. For generalized Fourier transforms, we consider the following weaker condition called the Helmholtz relations

$$\begin{aligned} \mathcal {T}\circ r^2=-\Delta \circ \mathcal {T}\text { and }\mathcal {T}\circ \Delta =- r^2 \circ \mathcal {T}. \end{aligned}$$

It is readily to verify that $\{\Delta ,r^2, [\Delta ,r^2]\}$ forms a basis of a Lie algebra isomorphic to $\mathfrak {sl}(2,\mathbb {R})$. Both $r^2$ and $\Delta$ are O(n)-invariant. It leads us to consider the decomposition of $\mathcal {S}(\mathbb {R}^n)$ into a direct sum of irreducible $O(n)\times \widetilde{SL}(2,\mathbb {R})-$modules. We obtain some generalized Fourier transforms according to this decomposition.

Denote by $\mathcal {P}(\mathbb {R}^n)$ the space of all polynomials on $\mathbb {R}^n$ with complex coefficients, $\mathcal {P}_k(\mathbb {R}^n)$ the subspace of homogeneous polynomials in $\mathcal {P}(\mathbb {R}^n)$ of degree k, and

$$\begin{aligned} \mathcal {H}_k(\mathbb {R}^n)=\{f\in \mathcal {P}_k(\mathbb {R}^n):\Delta f=0\} \end{aligned}$$

the space of homogeneous harmonic polynomials of degree k. Recall that $e^-=\frac{i}{2}\Delta$. Then $\mathcal {H}_k(\mathbb {R}^n)$ consists of $e^--$null vectors.

Set $\tilde{\mathcal {H}}_k(\mathbb {R}^n):=\mathcal {H}_k(\mathbb {R}^n)e^{-\frac{r^2}{2}}$. Then it is clear that $\tilde{\mathcal {H}}_k(\mathbb {R}^n)$ is the space of $n^--$null vectors with eigenvalue $\frac{n}{2}+k.$ Therefore, each function $\phi \in \tilde{\mathcal {H}}_k(\mathbb {R}^n)$ generates a $\mathfrak {sl}(2,\mathbb {R})$ module isomorphic to $V_{\frac{n}{2}+k}$, the lowest weight module with lowest weight $\frac{n}{2}+k.$ This isomorphism defines an embedding

$$\begin{aligned} i_{\phi }:V_{\frac{n}{2}+k}\rightarrow \mathcal {S}(\mathbb {R}^n). \end{aligned}$$

By Corollary 2.1.3 in Chapter II of [5], we have a decomposition

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)\simeq (V_{\frac{1}{2}}\oplus V_{\frac{1}{2}+1})^{\otimes n}\simeq \sum _{k\ge 0}a(n,k)V_{\frac{n}{2}+k}, \end{aligned}$$

where the multiplicity $a(n,k)=\Big (\begin{matrix} n+k-1\\ k \end{matrix}\Big )-\Big (\begin{matrix} n+k-3\\ k-2 \end{matrix}\Big )$ is the same as the dimension of $\mathcal {H}_k(\mathbb {R}^n).$ Furthermore, the following result holds.

Proposition 3.1

[5, Chapter III, Theorem 2.4.4] For $n\ge 2,$ we have a decomposition of

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)\simeq \sum _{k=0}^{\infty }(\tilde{\mathcal {H}}_k(\mathbb {R}^n)\otimes V_{\frac{n}{2}+k})^- \end{aligned}$$

(3.1)

into irreducible $O(n)\times \widetilde{SL}(2,\mathbb {R})-$modules. Here the “–” indicates closure in $\mathcal {S}(\mathbb {R}^n)$.

• (i) The $O(n)\times \widetilde{SL}(2,\mathbb {R})-$intertwining map

  $$\begin{aligned} \tilde{\mathcal {H}}_k(\mathbb {R}^n)\otimes V_{\frac{n}{2}+k}\rightarrow & {} \mathcal {S}(\mathbb {R}^n)\\ \phi \otimes v\mapsto & {} i_{\phi }(v) \end{aligned}$$

  defines an isomorphism of $O(n)\times \widetilde{SL}(2,\mathbb {R})-$modules.

• (ii) $\tilde{\mathcal {H}}_k(\mathbb {R}^n)$ is an irreducible $O(n)-$module. In particular, $\tilde{\mathcal {H}}_k(\mathbb {R}^n)$ are non-isomorphic O(n)-modules for different k.

Remark 3.2

• (i) Note that $\tilde{\mathcal {H}}_k(\mathbb {R}^n)\cong \mathcal {H}_k(\mathbb {R}^n)$ as O(n)-modules and we write $\mathcal {H}_k$ for $\mathcal {H}_k(\mathbb {R}^n)$. Therefore, we have the following decomposition for polynomials [5, Theorem on p. 118]:

  $$\begin{aligned} \mathcal {P}(\mathbb {R}^n)|_{O(n)\times \widetilde{SL}(2,\mathbb {R})}\simeq \sum _{k=0}^{\infty }\mathcal {H}_k \otimes V_{\frac{n}{2}+k}. \end{aligned}$$

  (3.2)

• (ii) The decomposition (3.2) describes the correspondence for the $(O(n), \mathfrak {sl}(2,\mathbb {R}))$-pair.

Note that $V_{\frac{n}{2}+k}$ is $O(n)-$invariant. Denote by $\mathfrak {J}(\mathbb {R}^n)$ the space of O(n) invariant functions in $\mathcal {S}(\mathbb {R}^n)$. Thus, we have the following decomposition

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)=\sum _{k=0}^{\infty }\mathcal {H}_k(\mathbb {R}^n)\cdot \mathfrak {J}(\mathbb {R}^n). \end{aligned}$$

This leads us to consider the map

$$\begin{aligned} \alpha _k:\mathcal {H}_k(\mathbb {R}^n)\otimes \mathcal {S}(\mathbb {R}_+)\rightarrow \mathcal {S}(\mathbb {R}^n),f\otimes \psi \mapsto f(x)\psi (r^2). \end{aligned}$$

Let $\rho _k$ be the representation of $\mathfrak {sl}(2,\mathbb {R})$ on $\mathcal {S}(\mathbb {R}_+)$ defined by

$$\begin{aligned} \alpha _k(f\otimes \rho _k(X) \psi )=X(\alpha _k(f\otimes \psi )),\forall X\in \mathfrak {sl}(2,\mathbb {R}). \end{aligned}$$

By [5, Chapter IV, Lemma 1.2.2], $\rho _k$ is explicitly given by:

$$\begin{aligned} h\mapsto 2r\frac{d}{dr}+k+\frac{n}{2},\ e^+\mapsto \frac{ir}{2},\ e^-\mapsto 2i\left[ \left( k+\frac{n}{2}\right) \frac{d}{dr}+r\frac{d^2}{dr^2}\right] . \end{aligned}$$

Proposition 3.3

(Bochner’s Relations) [5, Chapter IV, Theorem 1.2.4]

If $g(x)=f(x)\psi (r^2)$ for some $f\in \mathcal {H}_k(\mathbb {R}^n)$ and $\psi \in \mathcal {S}(\mathbb {R}_+)$, then

$$\begin{aligned} (\mathcal {F}g) (y)=f(y)T_k (\psi )(r^2), \end{aligned}$$

where

Remark 3.4

This proposition is a well-known fact in analysis. Here the $T_k$’s are in fact the Hankel transforms [11, Chapter IV,Theorem 3.10].

The above proposition shows that $\mathcal {F}$ acts on each summand $\mathcal {H}_k\otimes V_{k+\frac{n}{2}}$ by $Id\otimes T_k$. In view of the decomposition (3.2), we have

$$\begin{aligned} \mathcal {F}\simeq \sum _{k=0}^{\infty }Id|_{\mathcal {H}_k} \otimes T_k. \end{aligned}$$

(3.3)

Now we consider bounded operators on $\mathcal {S}(\mathbb {R}^n)$ that share some of the properties of $\mathcal {F}$.

Theorem 3.5

Let $\mathcal {T}$ be a bounded operator on $\mathcal {S}(\mathbb {R}^n)$ satisfying the following conditions:

• (i) $\mathcal {T}$ is $O(n)-equivariant,$ i.e.

  $$\begin{aligned} \mathcal {T}(gf)=g(\mathcal {T}f),\forall f\in L^2(\mathbb {R}^n), g\in O(n); \end{aligned}$$

• (ii) $\mathcal {T}\circ r^2=-\Delta \circ \mathcal {T}$ and $\mathcal {T}\circ \Delta =- r^2 \circ \mathcal {T}$;

• (iii) $\mathcal {T}^4=Id$.

Then in view of (3.2)

$$\begin{aligned} \mathcal {T}=\sum _{k=0}^{\infty }c_k(Id|_{\mathcal {H}_k} \otimes T_k), \end{aligned}$$

where $c_k=\pm i$ or $\pm 1$, for $k\in \mathbb {Z}_{\ge 0}$.

Proof

Assume that $c_k$’s are complex number such that $|c_k|=1$. Then an operator of the form $\sum _{k=0}^{\infty }c_k(Id \otimes T_k)$ is unitary and therefore bounded. It is easy to check that such an operator satisfies (i)–(iii). We now prove any $\mathcal {T}$ under conditions (i)–(iii) can be written in this form with $c_k$’s being fourth roots of unit. Set $\widetilde{\mathcal {T}}=\mathcal {T}\circ \mathcal {F}^{-1}$. Then $\widetilde{\mathcal {T}}$ is O(n)-equivariant, because both $\mathcal {T}$ and $\mathcal {F}^{-1}$ are O(n)-equivariant. On the other hand, $\mathcal {F}^{-1}$ satisfies the Helmholtz relations too, so

$$\begin{aligned} \widetilde{\mathcal {T}}\circ r^2=r^2\circ \widetilde{\mathcal {T}} \hbox {and }\widetilde{\mathcal {T}}\circ \Delta =\Delta \circ \widetilde{\mathcal {T}}. \end{aligned}$$

It follows that $\widetilde{\mathcal {T}}$ commutes with $\mathfrak {sl}(2,\mathbb {R})$ generated spanned by $\{r^2,\Delta ,[r^2,\Delta ]\}$, and thus commutes with $O(n)\times \widetilde{SL}(2,\mathbb {R})$.

Recall from (3.2) that $\mathcal {S}(\mathbb {R}^n)$ is decomposed into irreducible representations of $O(n)\times \widetilde{SL}(2,\mathbb {R})$, where all the summands are not isomorphic to each other. By Schur’s Lemma, $\widetilde{\mathcal {T}}$ preserves each summand and acts as scalar on each of them, i.e. $\widetilde{\mathcal {T}}|_{ \mathcal {H}_k\otimes V_{k+\frac{n}{2}}}=c_k\in \mathbb {C}$, $\forall k\ge 0.$

Since $\mathcal {F}$ on $\mathcal {S}(\mathbb {R}^n)$ decomposes into $\mathcal {F}\simeq \sum _{k=0}^{\infty }Id \otimes T_k$, it follows that

$$\begin{aligned} \mathcal {T}=\widetilde{\mathcal {T}}\circ \mathcal {F}=\sum _{k=0}^{\infty }c_k(Id|_{\mathcal {H}_k} \otimes T_k). \end{aligned}$$

As $\mathcal {F}^{-1}$ and $\mathcal {T}$ both have order 4, we have $\widetilde{\mathcal {T}}^4=Id$ and thus $c_k=\pm i$ or $\pm 1$ for all k. $\square$

Although each $c_k$ take only four different values, the sequence $(c_0,c_1,\ldots )$ is uncountable. Thus, Theorem 3.5 describes uncountably many operators that generalize the Fourier transform. Note that

$$\begin{aligned} \mathcal {F}v_{\beta }=(-i)^{\beta }v_{\beta }\implies \mathcal {F}|_{ \mathcal {H}_k\otimes V_{k+\frac{n}{2}}}=(-i)^k. \end{aligned}$$

Then $\mathcal {T}$ in Theorem 3.5 can be determined more explicitly if it satisfies a certain periodicity condition. Denote by $C_4=\{\pm 1,\pm i\}=\langle i \rangle$ the cyclic group of order 4 generated by i.

Corollary 3.6

If the map $k\mapsto c_k$ defines a group homomorphism from $\mathbb {Z}$ to $C_4$, then $\mathcal {T}$ is in $\{Id, \mathcal {F},\mathcal {F}^2,\mathcal {F}^3=\mathcal {F}^{-1}\}$.

Proof

If the map $k\mapsto c_k$ defines a group homomorphism from $\mathbb {Z}$ to $C_4$, then

$$\begin{aligned} c_{k+4}=c_{k},c_0=1,c_{k+l}=c_kc_l, \forall \ k,l\in \mathbb {Z}. \end{aligned}$$

Therefore, $\mathcal {T}$ is determined by $c_1$. There are four possibilities:

Thus, the corollary follows. $\square$

Remark 3.7

The standard eigenfunction basis of the Fourier transform given by the Hermite functions in (2.1) of [2] are eigenfunctions of the generalized Fourier transform $\mathcal {T}$ in Theorem 3.5. Therefore, $\mathcal {T}$ is an integral transform as shown in [2, Proposition 2.3]:

$$\begin{aligned} (\mathcal {T}f)(y)=\frac{1}{(2\pi )^{n/2}}\int _{\mathbb {R}^n} K_n(x,y) f(x) d x, \end{aligned}$$

where

$$\begin{aligned} K_n(x,y)=2^\lambda \Gamma (\lambda )\sum _{k=0}^\infty c_k (k+\lambda )z^{-\lambda }J_{k+\lambda }(z)C_k^\lambda (w). \end{aligned}$$

Here we adopt the notations $\lambda ={(n-2)/2}, z=|x||y|,w=\langle x,y\rangle /z$ and $J_{k+\lambda }$ are the Bessel functions while $C^\lambda _k$ denote the Gegenbauser or ultraspherical polynomials in [2, Proposition 2.3].

4 Generalized Fourier Transforms in (U(n), U(1))-Pair

In this section, we consider another dual pair (U(n), U(1)) in the seesaw pairs with $O(n)\times \widetilde{SL}(2,\mathbb {R})$. Recall that $(G,G')$ is a reductive dual pair in $Sp(2n,\mathbb {R})$ if $G,G'$ are closed reductive subgroups of $Sp(2n,\mathbb {R})$ such that G and $G'$ are centralizers of each other. Let K be a maximal compact subgroup of G, and let $H'$ be the centralizer of K in $Sp(2n,\mathbb {R})$. Then $(K,H')$ forms another dual pair in $Sp(2n,\mathbb {R})$. In this situation, $(G,G')$ and $(K,H')$ form seesaw pairs (cf. [3], p. 400).

Note that is a maximal compact subgroup of $G=SL(2,\mathbb {R})$ and U(n) is the centralizer of U(1) in $Sp(2n,\mathbb {R})$, so we get the following seesaw pairs (cf. [8])

Let $\widetilde{U(1)}$ be the inverse image of U(1) in $\widetilde{SL}(2,\mathbb {R})$. Each $V_{k+\frac{n}{2}}$, lowest weight module of $\mathfrak {sl}(2,\mathbb {R})$, can be decomposed into $\widetilde{U(1)}-$types of $\widetilde{SL}(2,\mathbb {R})$:

$$\begin{aligned} V_{k+\frac{n}{2}}=\sum _{l=0}^{\infty }W_{k+\frac{n}{2}+2l}. \end{aligned}$$

By substituting the above formula into formula (3.2), we get

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)\simeq \sum _{k=0}^{\infty }\sum _{l=0}^{\infty }\mathcal {H}_k\otimes W_{k+\frac{n}{2}+2l}. \end{aligned}$$

Set $\mathcal {L}_k=\sum _{l=0}^{[\frac{k}{2}]}\mathcal {H}_{k-2l}$. We note there is a U(n)-module isomorphism from $\mathcal {L}_k$ to $\mathcal {P}_k$ the space of homogeneous polynomials of degree k, since

$$\begin{aligned} \mathcal {P}_k=\sum _{l=0}^{[\frac{k}{2}]}r^{2l}\mathcal {H}_{k-2l}. \end{aligned}$$

It follows that we have the following (U(n), U(1))-pair correspondence.

Proposition 4.1

We have a decomposition of $\mathcal {S}(\mathbb {R}^n)$ into irreducible $U(n)\times \widetilde{U(1)}-$ modules:

$$\begin{aligned} \mathcal {S}(\mathbb {R}^n)|_{U(n)\times \widetilde{U(1)}}\simeq \sum _{k=0}^{\infty }\mathcal {L}_k\otimes W_{k+\frac{n}{2}}, \end{aligned}$$

(4.1)

Here $W_{k+\frac{n}{2}}$ is a one-dimensional weight space of with the weight $k+\frac{n}{2}$. We denote the action of $\widetilde{U(1)}$ on it by $\chi _k$ and write . It is clear that $S_k$ is simply multiplication by $(-i)^k$. In addition, the Fourier transform $\mathcal {F}$ decomposes into

$$\begin{aligned} \mathcal {F}\simeq \sum _{k=0}^{\infty }Id|_{\mathcal {L}_k}\otimes S_k. \end{aligned}$$

Now we consider the generalized Fourier transforms in the setting of the (U(n), U(1))-pair. Recall that by the end of Sect. 2 we defined $\Gamma$ to be the finite abelian group generated by $\varpi _{p,q}$ corresponding to the indefinite Fourier transforms $\mathcal {F}_{p,q}$.

Theorem 4.2

Let $\mathcal {T}$ be a bounded operator on $\mathcal {S}(\mathbb {R}^n)$ satisfying the following conditions:

• (i) $\mathcal {T}$ is $O(n)-$equivariant and $\Gamma -$equivariant;

• (ii) $\mathcal {T}^4=Id$.

Then $\mathcal {T}$ is $U(n)-$equivariant, and in view of (4.1)

$$\begin{aligned} \mathcal {T}=\sum _{k=0}^{\infty }c_k Id|_{\mathcal {L}_k}\otimes S_k, \end{aligned}$$

where $c_k=\pm 1, \pm i$.

Moreover, the Helmholtz relations

$$\begin{aligned} \mathcal {T}\circ r^2=-\Delta \circ \mathcal {T}\text { and } \mathcal {T}\circ \Delta =- r^2 \circ \mathcal {T}\end{aligned}$$

imply that $\mathcal {T}$ is a multiple of $\mathcal {F}$ or $\mathcal {F}^{-1}$.

Proof

To show that $\mathcal {T}$ is $U(n)-$equivariant, it suffices to prove that O(n) and $\Gamma$ generate U(n). Let H be subgroup of U(n) generated by O(n) and $\Gamma$. Denote by Lie(H) the Lie algebra of H. The set

$$\begin{aligned} \mathcal {I}=\{iI_{s,t}:s=0,\ldots ,[(n+1)/2]\} \end{aligned}$$

is contained in Lie(H),  since H contains $\Gamma$. Consider the decomposition

$$\begin{aligned} \mathfrak {su}(n)=\mathfrak {k}_0\oplus i\mathfrak {p}_0=\mathfrak {so}(n)\oplus i\mathfrak {p}_0, \end{aligned}$$

where $\mathfrak {p}_0=$$\{X|X\in \mathfrak {g}\mathfrak {l}(n,\mathbb {R}),X=X^t,{\text {tr}}(X)=0\}.$ It follows that

$$\begin{aligned} \mathfrak {u}(n)=\mathfrak {su}(n)\oplus i\mathbb {R}I_n=\mathfrak {so}(n)\oplus i\mathfrak {p}_0\oplus i\mathbb {R}I_n. \end{aligned}$$

Since $\mathfrak {p}_0$ is an irreducible representation of $\mathfrak {so}(n)$, for any non-zero $iX\in i\mathfrak {p}_0,$$\mathfrak {so}(n)\cup \{iX\}$ generates $\mathfrak {su}(n)$. As $iI_{s,t}(s> 0)$ and $iI_n$ are in Lie(H), we can take $iX=iI_{s,t}+i(t-s)I_n$, and thus $Lie(H)=\mathfrak {u}(n)$. Then H contains an open neighborhood of 1 in U(n) and hence $H=U(n)$ (cf. [6, Cor. 2.10]).

Let $\widetilde{\mathcal {T}}=\mathcal {T}\circ \mathcal {F}^{-1}$. Since $\widetilde{\mathcal {T}}$ commutes with $\varpi _{n,0}$, we have $\widetilde{\mathcal {T}}$ is $\widetilde{U(1)}-$equivariant. So $\widetilde{\mathcal {T}}$ commutes with $U(n)\times \widetilde{U(1)}$. It follows from Schur’s Lemma that

$$\begin{aligned} \widetilde{\mathcal {T}}|_{ \mathcal {L}_k\otimes W_{k+\frac{n}{2}}}=c_k. \end{aligned}$$

Thus, $\mathcal {T}$ must be in the form given above and $c_k=\pm i$ or $\pm 1$ for all $k\ge 0$, because $\mathcal {T}$ and $\mathcal {F}$ both have order 4. In addition the Helmholtz relations imply that $\widetilde{\mathcal {T}}$ commutes with $\mathfrak {sp}(2n,\mathbb {R})$, since $\mathfrak {sp}(2n,\mathbb {R})$ is generated by $\mathfrak {u}(n)$ together with $\Delta$ and $r^2$. This implies that $\mathcal {T}$ is a linear combination of $\mathcal {F}$ and $\mathcal {F}^{-1}$ as we argued in the proof of Proposition 2.3. Then we deduce that $\mathcal {T}$ is a multiple $\mathcal {F}$ or $\mathcal {F}^{-1}$ by the condition that $T^4=Id$. $\square$

Remark 4.3

In the proof, it is enough to assume that $\mathcal {T}$ commutes with $\varpi _{n,0}$ and some $\varpi _{s,t}\ (0<s<n)$. Since Condition (ii) implies that $\mathcal {T}$ commutes with $\varpi _{n,0}$, ‘$\mathcal {T}$ is $\Gamma$-equivariant’ in Condition (i) may be replaced by a weaker condition that ‘$\mathcal {T}$ commutes with $\varpi _{s,t}$ for a positive integer s less than n’.

Remark 4.4

By a similar consideration mentioned in Remark 3.10, the generalized Fourier transform $\mathcal {T}=\sum _{k=0}^{\infty }c_k Id|_{\mathcal {L}_k}\otimes S_k$ in Theorem 4.2 coincides with the integral transform

$$\begin{aligned} (\mathcal {T}f)(y)=\frac{1}{(2\pi )^{n/2}}\int _{\mathbb {R}^n} K'_n(x,y) f(x) d x, \end{aligned}$$

where

$$\begin{aligned} K'_n(x,y)=2^\lambda \Gamma (\lambda )\sum _{k=0}^\infty c_k z^{-\lambda }J_{k+\lambda }(z) \sum _{l=0}^{[\frac{k}{2}]} (k-2l+\lambda )C_{k-2l}^\lambda (w). \end{aligned}$$

Here we adopt the notations $\lambda ={(n-2)/2}, z=|x||y|,w=\langle x,y\rangle /z$ and $J_{k+\lambda }$ are the Bessel functions while $C^\lambda _k$ denote the Gegenbauser or ultraspherical polynomials in [2, Prop. 2.3].

5 Generalized Fourier Transforms in (U(p, q), U(1))-Pair

It follows from the decomposition of $\omega ^p$ (resp. $\omega ^{q*}$) by $(O(p),SL(2,\mathbb {R}))$ (resp. $(O(q),SL(2,\mathbb {R}))$) duality that

$$\begin{aligned} \omega ^p\otimes \omega ^{q*}\simeq & {} \left( \sum _{k=0}^{\infty } \mathcal {H}_k \otimes V_{k+\frac{p}{2}}\right) \otimes \left( \sum _{l=0}^{\infty }\mathcal {H}_l^* \otimes V_{l+\frac{q}{2}}^*\right) \\\simeq & {} \sum _{k=0}^{\infty }\sum _{l=0}^{\infty } \mathcal {H}_k\otimes \mathcal {H}_l^*\otimes V_{k+\frac{p}{2}}\otimes V_{l+\frac{q}{2}}^*. \end{aligned}$$

There is a natural action of O(p, q) on $\mathcal {S}(\mathbb {R}^{p+q})$, and it commutes with the $\mathfrak {sl}(2,\mathbb {R})$ action defined by (2.4).

Because $V_{l+\frac{q}{2}}^*$ is a highest weight discrete series with highest weight $-l-\frac{q}{2}$, the representation $V_{k+\frac{p}{2}}\otimes V_{l+\frac{q}{2}}^*$ is a tensor product of a lowest weight discrete series and a highest weight discrete series. In this case, $V_{k+\frac{p}{2}}\otimes V_{l+\frac{q}{2}}^*$ contains a copy of direct integral, when k, l large enough. Furthermore, there is a direct integral decomposition of $L^2(\mathbb {R}^{p+q})$ into irreducible $O(p,q)\times \widetilde{SL}(2,\mathbb {R})-$modules (cf. [4] for details). Our argument of using Schur’s lemma cannot be applied to this direct integral decomposition. Nevertheless, we can use the decomposition (4.1) to get

$$\begin{aligned} \omega ^p\otimes \omega ^{q*}\simeq & {} \left( \sum _{k=0}^{\infty } \mathcal {L}_k \otimes W_{k+\frac{p}{2}}\right) \otimes \left( \sum _{l=0}^{\infty } \mathcal {L}_l^* \otimes W_{l+\frac{q}{2}}^*\right) \\\simeq & {} \sum _{k=0}^{\infty }\sum _{l=0}^{\infty } \mathcal {L}_k\otimes \mathcal {L}_l^*\otimes W_{k+\frac{p}{2}}\otimes W_{l+\frac{q}{2}}^*. \end{aligned}$$

Note that the group gives a maximal compact subgroup of $SL(2,\mathbb {R})$, with U(p, q) its centralizer. So the two dual pairs (O(p, q), U(1)) and (U(p, q), U(1)) form the seesaw pair:

Let $\mathfrak {L}_k=\sum _{l=0}^{\infty }\mathcal {L}_{k+l}\otimes \mathcal {L}_l^*.$ Since $W_{k+\frac{p-q}{2}}\simeq W_{k+l+\frac{p}{2}}\otimes W_{l+\frac{q}{2}}^*$ as $\widetilde{U(1)}$-modules, we have the following result.

Proposition 5.1

There is a multiplicity-free decomposition of $\mathcal {S}(\mathbb {R}^{p+q})$ into irreducible $U(p,q)\times \widetilde{U(1)}-$modules:

$$\begin{aligned} \mathcal {S}(\mathbb {R}^{p+q})|_{U(p,q)\times \widetilde{U(1)}}\simeq \sum _{k=-\infty }^{\infty }\mathfrak {L}_k\otimes W_{k+\frac{p-q}{2}}. \end{aligned}$$

(5.1)

In the above decomposition the indefinite Fourier transform is decomposed as

$$\begin{aligned} \mathcal {F}_{p,q}\simeq \sum _{k=-\infty }^{\infty }Id|_{\mathfrak {L}_k}\otimes S_{k}. \end{aligned}$$

Here $S_{k}$ is the action of on the weight space $W_{k+\frac{p-q}{2}}$, which is readily identified with the multiplication by $(-i)^{k}$.

Theorem 5.2

Let $\mathcal {T}$ be bounded operator on $\mathcal {S}(\mathbb {R}^n)$ satisfying the following conditions:

• (i) $\mathcal {T}$ is $O(p,q)-$equivariant and $\Gamma -$equivariant;

• (ii) $\mathcal {T}^4=Id$.

Then $\mathcal {T}$ is $U(p,q)-$equivariant, and in view of (5.1)

$$\begin{aligned} \mathcal {T}=\sum _{k=-\infty }^{\infty } c_k Id|_{\mathfrak {L}_k}\otimes S_{k}, \end{aligned}$$

where $c_k=\pm 1, \pm i$.

Morover, the Helmholtz relations

$$\begin{aligned} \mathcal {T}\circ r_{p,q}^2=-\Delta _{p,q} \circ \mathcal {T}\text { and } \mathcal {T}\circ \Delta _{p,q}=- r_{p,q}^2 \circ \mathcal {T}\end{aligned}$$

imply that $\mathcal {T}$ is a multiple of $\mathcal {F}_{p,q}$ or $\mathcal {F}_{p,q}^{-1}$.

Proof

The proof is similar to that of Theorem 4.2. For the $U(p,q)-$equivariance it suffices to prove that O(p, q) and $\Gamma$ generate U(p, q). Denote by H the subgroup of U(p, q) generated by O(p, q) and $\Gamma$, and by Lie(H) its Lie algebra. Consider the adjoint action of $\mathfrak {su}(p,q)$ when restricted to $\mathfrak {so}(p,q)$. We conclude that $Lie(H)= \mathfrak {u}(p,q)$, since some $iI_{s,t}(0<s\ne p)$ and $iI_{p,q}$ are in Lie(H). It follows that H contains an open neighborhood of 1 in U(p, q) and hence $H=U(p,q)$ (cf. [6, Cor. 2.10]).

Let $\widetilde{\mathcal {T}}=\mathcal {T}\circ \mathcal {F}^{-1}$. Since $\widetilde{\mathcal {T}}$ commutes with $\varpi _{p,q}$, we have $\widetilde{\mathcal {T}}$ is $\widetilde{U(1)}-$equivariant. So $\widetilde{\mathcal {T}}$ commutes with $U(p,q)\times \widetilde{U(1)}$. It follows from Schur’s Lemma that

$$\begin{aligned} \widetilde{\mathcal {T}}|_{ \mathfrak {L}_k\otimes W_{k+\frac{p-q}{2}}}=c_k. \end{aligned}$$

Thus, $\mathcal {T}$ must be in the form given by the theorem. Since both $\mathcal {T}$ and $\mathcal {F}$ have order 4, $c_k=\pm i$ or $\pm 1$ for all k. In addtion the Helmholtz relations imply that $\widetilde{\mathcal {T}}$ commutes with $\mathfrak {sp}(2n,\mathbb {R})$, since $\mathfrak {sp}(2n,\mathbb {R})$ is generated by $\mathfrak {u}(p,q)$ together with $\Delta _{p,q}$ and $r^2_{p,q}$. This forces $\mathcal {T}$ to be a linear cobmination of $\mathcal {F}$ and $\mathcal {F}^{-1}$ as we showed in the proof of Proposition 2.3. Then we deduce that $\mathcal {T}$ is a multiple of $\mathcal {F}_{p,q}$ or $\mathcal {F}_{p,q}^{-1}$. $\square$

Remark 5.3

It is readily checked that Condition (ii) implies that $\mathcal {T}$ commutes with $\varpi _{p,q}$. For the proof of the theorem it is enough to assume $\mathcal {T}$ to commute with $\varpi _{s,t}$ for a non-negative integer $s\ne p$. Therefore, ‘$\mathcal {T}$ is $\Gamma -$equivariant’ in Condition (i) may be replaced by a weaker condition that ‘$\mathcal {T}$ commutes with $\varpi _{s,t}$ for a non-negative integer $s<p$’.

How to relate the generalized Fourier transfroms in Theorem 5.2

$$\begin{aligned} \mathcal {T}=\sum _{k=-\infty }^{\infty } c_k Id|_{\mathfrak {L}_k}\otimes S_{k} \end{aligned}$$

to integral transforms is an interesting problem, which we are not able to give an easy solution here.