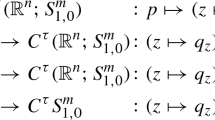Abstract
We prove the spectral invariance of the algebra of classical pseudodifferential boundary value problems on manifolds with conical singularities in the \(L_{p}\)-setting. As a consequence we also obtain the spectral invariance of the classical Boutet de Monvel algebra of zero order operators with parameters. In order to establish these results, we show the equivalence of Fredholm property and ellipticity for both cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Elliptic boundary value problems on manifolds with conical singularities have been studied since the 60’s, where the work of Kondratiev [15] stands out, see also Kozlov, Maz’ya and Rossmann [16] for a detailed presentation. The pseudodifferential analysis started with the work of Melrose and Mendoza [20, 21], Plamenevsky [22], and Schulze [33]. Algebras of pseudodifferential boundary value problems for conical singularities were constructed in the 90’s by Derviz [7] and Schrohe and Schulze [30, 31]. The latter approach combines elements of the Boutet de Monvel calculus [3] with the pseudodifferential analysis developed by Schulze [32, 33]. While initially only \(L_{2}\)-based Sobolev spaces were used, Coriasco, Schrohe and Seiler established the continuity also on Bessel potential and Besov spaces [5], see also [4], relying on work of Grubb and Kokholm [9, 13].
Our main result is the spectral invariance of the algebra developed in [31] in the \(L_{p}\)-setting, see Theorem 61. This algebra contains, after the composition with order reducing operators, the classical differential boundary value problems studied by Kondratiev [15], hence also their inverses, whenever these exist. As a by-product we obtain the spectral invariance of the algebra of zero order classical Boutet de Monvel operators with parameters in the \(L_{p}\)-setting, see Theorem 29. This algebra includes, after composition with order reducing operators, the differential boundary value problems studied by Agranovich and Vishik in [1], which were an important ingredient for the work of Kondratiev. Spectral invariance for the Boutet de Monvel algebra in the \(L_{2}\)-setting was shown by Schrohe for the larger class of SG operators [27, Theorem 3.27] and by Grubb [10, Theorem 1.14]. For the \(L_{p}\)-case, partial results were obtained by Grubb [10, Theorem 1.12].
It is an immediate consequence of Theorem 61 that the invertibility of a conically degenerate boundary value problem is to a large extent independent of the space it is considered on: It depends neither on the Sobolev regularity parameter s nor on \(1<p<\infty \). This is of great practical importance as it allows to check invertibility in the most convenient setting. A similar result holds for the Fredholm property, as we show in Corollary 50.
In order to demonstrate the applicability of these results, we study the Dirichlet realization \(\Delta _{\mathrm{Dir}}\) of the Laplacian on a 2-dimensional manifold with conical singularities, e.g. the closure of a plane domain with finitely many conical points. In applications, one is interested in the invertibility of \(\lambda -\Delta _{\mathrm{Dir}}, \lambda \notin \left. \right] -\infty ,0\left. \right] \), as an unbounded operator in the cone Sobolev space \({\mathcal {H}}^{s,\gamma }_p({\mathbb {D}})\) with domain
for different values of s and p; see Definition 37 for the definition of the spaces. We show that for \(s=0\) and \(p=2\), the invertibility can be checked by hand. The spectral invariance allows us to deduce the invertibility for all \(1<p<\infty \) and \(s>-\,2+1/p\).
This article extends the results of [28] to conical manifolds with boundary. The need to work with Besov spaces led to interesting new features. In Theorem 29, for example, we consider a zero order parameter-dependent operator \(A=\{A(\lambda ); \lambda \in \Lambda \}\) in Boutet de Monvel’s calculus. We show that the invertibility of \(A(\lambda )\) for each \(\lambda \) together with a norm estimate \(\Vert A(\lambda )^{-1}\Vert \le c\langle \lambda \rangle ^r\) for a constant \(c\ge 0\) and sufficiently small \(r>0\) implies that the inverse also is parameter-dependent of order zero. In particular, the operator norm will then be uniformly bounded. Similar effects can be observed when showing the equivalence of parameter-ellipticity and the Fredholm property with parameters.
This paper is a step toward the analysis of nonlinear partial differential equations on manifolds with boundary and conical singularities, see e.g. [24, 26] by Roidos and Schrohe, [34] by Shao and Simonett or [35] by Vertman for the case without boundary. A next step concerns the analysis of resolvents of closed extensions in the spirit of Gil et al. [8] or [29] in the case without boundary and Krainer [17] for conic manifolds with boundary.
2 Parameter-Dependent Boutet de Monvel Algebra
To make this article readable for non-experts, we briefly describe the parameter-dependent Boutet de Monvel algebra with classical symbols on compact manifolds with boundary in the \(L_{p}\)-setting. We first define several operator classes on the half-space \({\mathbb {R}}_{+}^{n}=\left\{ x\in {\mathbb {R}}^{n};\,x_{n}>0\right\} \).
The set of parameters of the operators and symbols will always be a conical open set \(\Lambda \subset {\mathbb {R}}^{l}\), that is, \(p\in \Lambda \) implies that \(tp\in \Lambda \) for \(t>0\). It can be the empty set, in which case we recover the usual symbols and operators. We write \({\mathbb {N}}_{0}:=\left\{ 0,1,2,\ldots \right\} \) and \({\mathbb {R}}^{2}_{++}={\mathbb {R}}_{+}\times {\mathbb {R}}_{+}\). For a Fréchet space W, the Schwartz space \({\mathcal {S}}\left( {\mathbb {R}}^{n},W\right) \) consists of all \(u\in C^{\infty }\left( {\mathbb {R}}^{n},W\right) \) such that \(\sup _{x\in {\mathbb {R}}^{n}}p\left( x^{\alpha }\partial _{x}^{\beta }u\left( x\right) \right) <\infty \) for every continuous seminorm p of W. We simply write \({\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \), if \(W=\mathbb {C}\). If \(\Omega \subset {\mathbb {R}}^{n}\) is an open set, \(C_{c}^{\infty }(\Omega )\) denotes the space of smooth functions with compact support in \(\Omega \). The operator of restriction of distributions defined in \({\mathbb {R}}^{n}\) to \(\Omega \) is denoted by \(r_{\Omega }:\mathcal {D}'\left( {\mathbb {R}}^{n}\right) \rightarrow \mathcal {D}'\left( \Omega \right) \). It allows us to define the spaces \({\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) =r_{{\mathbb {R}}_{+}^{n}}\left( {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \right) \) and \({\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\times \overline{{\mathbb {R}}_{+}^{n}}\right) =r_{{\mathbb {R}}_{+}^{n}\times {\mathbb {R}}_{+}^{n}}\left( {\mathcal {S}}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\right) \right) \). When \(n=1\), we also use the notation \({\mathcal {S}}_{+}={\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \) and \({\mathcal {S}}_{++}={\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\times \overline{{\mathbb {R}}_{+}}\right) ={\mathcal {S}}\left( \overline{{\mathbb {R}}_{++}^{2}}\right) \). The extension by zero of a function u defined in \(\Omega \) to \({\mathbb {R}}^{n}\) will be denoted by \(e_{\Omega }\):
If \(\Omega ={\mathbb {R}}_{+}^{n}\), we denote \(r_{{\mathbb {R}}^n_+}\) also by \(r^+\) and \(e_{{\mathbb {R}}_{+}^{n}}\) by \(e^{+}\). The open ball in \({\mathbb {R}}^{n}\) with the Euclidean norm whose center is x and radius is \(r>0\) will be denoted by \(B_{r}\left( x\right) \). Our convention for the Fourier transform is \({\mathcal {F}}u(\xi )=\hat{u}\left( \xi \right) =\int e^{-ix\xi }u(x)dx\). We shall often use the function \(\left\langle .\right\rangle :{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}\) defined by
and sometimes we use \(\left\langle \xi ,\lambda \right\rangle :=\sqrt{1+\left| \left( \xi ,\lambda \right) \right| ^{2}}\) and similar expressions, as well.
Finally, given two Banach spaces E an F, we denote by \({\mathcal {B}}\left( E,F\right) \) the bounded operators from E to F and use the notation \({\mathcal {B}}\left( E\right) :={\mathcal {B}}\left( E,E\right) \).
Definition 1
The space \(S^{m}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \) of parameter-dependent symbols of order \(m\in {\mathbb {R}}\) consists of all functions \(p\in C^{\infty }\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\times \Lambda \right) \) that satisfy
A symbol p defines a parameter-dependent pseudodifferential operator \(op\left( p\right) \left( \lambda \right) :{\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) by the formula:
We say that p is classical, if there are symbols \(p_{\left( m-j\right) }\in S^{m-j}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \), \(j\in {\mathbb {N}}_{0}\), such that
-
(1)
For all \(t\ge 1\) and \(\left| \left( \xi ,\lambda \right) \right| \ge 1\), we have \(p_{\left( m-j\right) }\left( x,t\xi ,t\lambda \right) =t^{m-j}p_{\left( m-j\right) }\left( x,\xi ,\lambda \right) \).
-
(2)
We have the asymptotic expansion \(p\sim \sum _{j=0}^{\infty }p_{\left( m-j\right) }\), i.e., \(p-\sum _{j=0}^{N-1}p_{\left( m-j\right) }\in S^{m-N}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \), for all \(N\in {\mathbb {N}}_{0}\).
This subset is denoted by \(S_{cl}^{m}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \). It is a Fréchet space with the natural seminorms.
Definition 2
Let \(p\in S_{cl}^{m}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \), \(m\in {\mathbb {Z}}\), be written as a function of \(\left( x',x_{n},\xi ',\xi _{n},\lambda \right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}\times {\mathbb {R}}^{n-1}\times {\mathbb {R}}\times \Lambda \). We say that it satisfies the transmission condition, if \(p\sim \sum _{j=0}^{\infty }p_{\left( m-j\right) }\) and if, for all \(k\in {\mathbb {N}}_{0}\) and for all \(\alpha \in {\mathbb {N}}_{0}^{n+l}\), we have
In this case, the operator \(P\left( \lambda \right) _{+}:=r^{+}op\left( p\right) \left( \lambda \right) e^{+}:{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\) is well defined.
Two more classes of functions are required. Our notation here follows Grubb [12].
Definition 3
We denote by \(S^{m}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\), \(m\in {\mathbb {R}}\), the space of all functions \(\tilde{f}\in C^{\infty }\left( {\mathbb {R}}^{n-1}\times \overline{{\mathbb {R}}_{+}}\times {\mathbb {R}}^{n-1}\times \Lambda \right) \) that satisfy:
The subset \(S_{cl}^{m}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\) consists of all \(\tilde{f}\) with an asymptotic expansion \(\tilde{f}\sim \sum _{j=0}^{\infty }\tilde{f}_{\left( m-j\right) }\), i.e. there are functions \(\tilde{f}_{\left( m-j\right) }\in S^{m-j}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\), \(j\in {\mathbb {N}}_{0}\), such that \(\tilde{f}-\sum _{j=0}^{N-1}\tilde{f}_{\left( m-j\right) }\in S^{m-N}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\) for all \(N\in {\mathbb {N}}_{0}\), and
Similarly, \(S^{m}({\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda )\) denotes all \(\tilde{g}\in C^{\infty }\left( {\mathbb {R}}^{n-1}\times \overline{{\mathbb {R}}^{2}_{++}}\times {\mathbb {R}}^{n-1}\times \Lambda \right) \) with
Write \(\tilde{g}\in S_{cl}^{m}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda ),\) if \(\tilde{g}\sim \sum _{j=0}^{\infty }\tilde{g}_{\left( m-j\right) }\) with \(\tilde{g}_{\left( m-j\right) }\in S^{m-j}({\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda )\) such that \(\tilde{g}-\sum _{j=0}^{N-1}\tilde{g}_{\left( m-j\right) }\) belongs to \(S^{m-N}({\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda )\), for all \(N\in {\mathbb {N}}_{0}\), and
We may now define the operators that, together with the pseudodifferential ones, appear in the Boutet de Monvel calculus: the Poisson, trace and singular Green operators. We will always restrict ourselves to the classical elements. The notation \(\gamma _{j}:{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}({\mathbb {R}}^{n-1})\), \(j\in {\mathbb {N}}_{0}\), indicates the operator \(\gamma _{j}u\left( x'\right) =\lim _{x_{n}\rightarrow 0}D_{x_{n}}^{j}u\left( x',x_{n}\right) \) as well as its extension to Sobolev, Bessel and Besov spaces.
Definition 4
Let \(\lambda \in \Lambda , m\in {\mathbb {R}}\) and \(d\in {\mathbb {N}}_0\).
-
(1)
A classical parameter-dependent Poisson operator of order m is an operator family \(K\left( \lambda \right) :{\mathcal {S}}({\mathbb {R}}^{n-1})\rightarrow {\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\) associated with \(\tilde{k}\in S_{cl}^{m-1}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\) of the form
$$\begin{aligned} K\left( \lambda \right) u\left( x',x_{n}\right) =\left( 2\pi \right) ^{1-n}\int _{{\mathbb {R}}^{n-1}}e^{ix'\xi '}\tilde{k}(x',x_{n},\xi ',\lambda )\hat{u}\left( \xi '\right) d\xi ', \end{aligned}$$(2.1)For \(\tilde{k}\sim \sum _{j=0}^{\infty }\tilde{k}_{\left( m-1-j\right) }\), we define \(\tilde{k}_{\left( m-1\right) }\left( x',\xi ',D_{n},\lambda \right) :\mathbb {C}\rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \) by
$$\begin{aligned} \tilde{k}_{\left( m-1\right) }\left( x',\xi ',D_{n},\lambda \right) \left( v\right) =v\tilde{k}_{\left( m-1\right) }\left( x',x_{n},\xi ',\lambda \right) . \end{aligned}$$ -
(2)
A classical parameter-dependent trace operator of order m and class d is an operator family \(T\left( \lambda \right) :{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}({\mathbb {R}}^{n-1})\) of the form
$$\begin{aligned} T\left( \lambda \right) =\sum _{j=0}^{d-1}S_{j}\left( \lambda \right) \gamma _{j}+T'\left( \lambda \right) , \end{aligned}$$where \(S_{j}\left( \lambda \right) \) is a parameter-dependent pseudodifferential operator of order \(m-j\) on \({\mathbb {R}}^{n-1}\) and \(T'\left( \lambda \right) :{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}({\mathbb {R}}^{n-1})\) is of the form
$$\begin{aligned} T'(\lambda )u\left( x'\right) =\left( 2\pi \right) ^{1-n}\int _{{\mathbb {R}}^{n-1}}e^{ix'\xi '}\int _{{\mathbb {R}}_{+}}\tilde{t}\left( x',x_{n},\xi ',\lambda \right) \left( {\mathcal {F}}_{x'\rightarrow \xi '}u\right) \left( \xi ',x_{n}\right) dx_{n}d\xi ' \end{aligned}$$(2.2)with \(\tilde{t}\in S_{cl}^{m}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\). For \(\tilde{t}\sim \sum _{j=0}^{\infty }\tilde{t}_{\left( m-j\right) }\) we define \(\tilde{t}_{\left( m\right) }\left( x',\xi ',D_{n},\lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \rightarrow \mathbb {C}\) by
$$\begin{aligned} \tilde{t}_{\left( m\right) }\left( x',\xi ',D_{n},\lambda \right) u=\int _{{\mathbb {R}}_{+}}\tilde{t}_{\left( m\right) }\left( x',x_{n},\xi ',\lambda \right) u\left( x_{n}\right) dx_{n}. \end{aligned}$$ -
(3)
A classical parameter-dependent singular Green operator of order m and class d is an operator family \(G\left( \lambda \right) :{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\) of the form
$$\begin{aligned} G\left( \lambda \right) =\sum _{j=0}^{d-1}K_{j}'\left( \lambda \right) \gamma _{j}+G'\left( \lambda \right) , \end{aligned}$$where \(K_{j}'\) are Poisson operators of order \(m-j\) and \(G'\left( \lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \) is an operator of the form
$$\begin{aligned} G'\left( \lambda \right) u(x)&=(2\pi )^{1-n}\int _{{\mathbb {R}}^{n-1}}e^{ix'\xi '}\int _{{\mathbb {R}}_{+}}\tilde{g}(x',x_{n},y_{n},\xi ',\lambda ) \nonumber \\&\quad \times \left( {\mathcal {F}}_{x'\rightarrow \xi '}u\right) \left( \xi ',y_{n}\right) dy_{n}d\xi ', \end{aligned}$$(2.3)where \(\tilde{g}\in S_{cl}^{m-1}({\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda )\). We define the operator \(g_{\left( m-1\right) }\left( x',\xi ',D_{n},\lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \) by
$$\begin{aligned}&{g_{\left( m-1\right) }\left( x',\xi ',D_{n},\lambda \right) u\left( x_{n}\right) }\\&\quad =\sum _{l=0}^{d-1}\tilde{k}'_{l\left( m-l-1\right) }\left( x',x_{n},\xi ',\lambda \right) D_{x_{n}}^{l}u\left( 0\right) \\&\quad \quad \,+\int _{{\mathbb {R}}_{+}}\tilde{g}_{\left( m-1\right) }\left( x',x_{n},y_{n},\xi ',\lambda \right) u\left( y_{n}\right) dy_{n}. \end{aligned}$$
Remark 5
With a symbol \(p\in S_{cl}^{m}\left( {\mathbb {R}}^{n}\times \mathbb {{\mathbb {R}}}^{n},\Lambda \right) \) that satisfies the transmission condition, we associate the operator \(p_{\left( m\right) +}\left( x',0,\xi ',D_{n},\lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \) defined by:
Definition 6
Let \(n_{1}, n_{2}, n_{3}\) and \(n_{4}\in {\mathbb {N}}_{0}\). The set of classical parameter-dependent Boutet de Monvel operators on \({\mathbb {R}}_{+}^{n}\), denoted by \({\mathcal {B}}_{n_{1},n_{2},n_{3},n_{4}}^{m,d}\left( {\mathbb {R}}^{n},\Lambda \right) \) for \(m\in {\mathbb {Z}}\) and \(d\in {\mathbb {N}}_{0}\), or just by \({\mathcal {B}}^{m,d}\left( {\mathbb {R}}^{n},\Lambda \right) \), consists of all operators A given by
where \(P_{+}\) is a pseudodifferential operator of order m satisfying the transmission condition, G is a singular Green operators of order m and class d, K is a Poisson operator of order m, T is a trace operator of order m and class d and S is a pseudodifferential operator of order m. All are parameter-dependent in the respective classes.
The following algebra is also useful to prove spectral invariance:
Definition 7
Let \(n_{1}\), \(n_{2}\), \(n_{3}\), \(n_{4}\in {\mathbb {N}}_{0}\) and \(1<p<\infty \). We define the set \(\tilde{{\mathcal {B}}}_{n_{1},n_{2},n_{3},n_{4}}^{p}\left( {\mathbb {R}}^{n},\Lambda \right) \), also denoted by \(\tilde{{\mathcal {B}}}^{p}\left( {\mathbb {R}}^{n},\Lambda \right) \), as the set of all operators A of the form (2.4), where: \(P_{+}\) is of order 0, G is of order 0 and class 0, K is of order \(\frac{1}{p}\), T is of order \(-\frac{1}{p}\) and class 0 and S is of order 0. All are parameter-dependent in the respective classes.
Definition 8
With \(A\in {\mathcal {B}}_{n_{1},n_{2},n_{3},n_{4}}^{m,d}\left( {\mathbb {R}}^{n},\Lambda \right) \), we associate the operator-valued principal boundary symbol \(\sigma _{\partial }\left( A\right) \), defined on \({\mathbb {R}}^{n-1}\times \left( \left( {\mathbb {R}}^{n-1}\times \Lambda \right) \backslash \left\{ 0\right\} \right) \). The operator
is given by
where the entries are the matrix version of the operators in Definition 4 and Remark 5.
Similarly, with \(A\in \tilde{{\mathcal {B}}}_{n_{1},n_{2},n_{3},n_{4}}^{p}\left( {\mathbb {R}}^{n},\Lambda \right) \), we associate an operator \(\sigma _{\partial }\left( A\right) \left( x',\xi ',\lambda \right) \) acting as in (2.5), given as
Let now M be a manifold with boundary, \(E_{0}\) and \(E_{1}\) two complex hermitian vector bundles over M and \(F_{0}\) and \(F_{1}\) two complex hermitian vector bundles over \(\partial M\). Let \(U_{j}\subset M\), \(j=1,\ldots ,N\), be open cover of M consisting of trivializing sets for the vector bundles, \(\Phi _{1}\), ..., \(\Phi _{N}\in C^{\infty }\left( M\right) \) be a partition of unity subordinate to \(U_{1}\), ..., \(U_{N}\) and \(\Psi _{1}\), ...,\(\Psi _{N}\in C^{\infty }\left( M\right) \) be supported in \(U_{j}\) such that \(\Psi _{j}\Phi _{j}=\Phi _{j}\).
A linear operator \(A\left( \lambda \right) {:}\,C^{\infty }\left( M,E_{0}\right) \oplus C^{\infty }\left( \partial M,F_{0}\right) \rightarrow C^{\infty }\left( M,E_{1}\right) \oplus C^{\infty }\left( \partial M,F_{1}\right) \) can always be written as
Using the above definitions, we define the Boutet de Monvel algebra on M:
Definition 9
A family \(A\left( \lambda \right) {:}\,C^{\infty }\left( M,E_{0}\right) \oplus C^{\infty }\left( \partial M,F_{0}\right) \rightarrow C^{\infty }\left( M,E_{1}\right) \oplus C^{\infty }\left( \partial M,F_{1}\right) \), \(\lambda \in \Lambda \), is called a parameter-dependent Boutet de Monvel operator of order \(m\in {\mathbb {Z}}\) and class \(d\in {\mathbb {N}}_{0}\), if
-
(1)
The operators \(\Psi A\left( \lambda \right) \Phi {:}\,{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) ^{n_{1}}\oplus {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) ^{n_{2}}\rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) ^{n_{3}}\oplus {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) ^{n_{4}}\) belong to \({\mathcal {B}}^{m,d}\left( {\mathbb {R}}^{n},\Lambda \right) \) after localization.
-
(2)
The Schwartz kernels of the operators \(\sum _{j=1}^{N}\Phi _{j}A\left( \lambda \right) \left( 1-\Psi _{j}\right) \) belong to
$$\begin{aligned} \begin{pmatrix} {\mathcal {S}}\left( \Lambda ,C^{\infty }\left( M\times M,Hom\left( \pi _{2}^{*} E_{0},\pi _{1}^{*}E_{1}\right) \right) \right) &{} \quad {\mathcal {S}}\left( \Lambda ,C^{\infty }\left( M\times \partial M,Hom\left( \pi _{2}^{*}F_{0},\pi _{1}^{*}E_{1}\right) \right) \right) \\ {\mathcal {S}}\left( \Lambda ,C^{\infty }\left( \partial M\times M,Hom\left( \pi _{2}^{*}E_{0},\pi _{1}^{*}F_{1}\right) \right) \right) &{} \quad {\mathcal {S}}\left( \Lambda ,C^{\infty }\left( \partial M\times \partial M,Hom\left( \pi _{2}^{*}F_{0},\pi _{1}^{*}F_{1}\right) \right) \right) \end{pmatrix}, \end{aligned}$$
where Hom indicates the space of homomorphisms and \(\pi _{i}:M\times M\rightarrow M\) is given by \(\pi _{i}\left( x_{1},x_{2}\right) =x_{i}\) for \(i=1,2\).
If \(\partial M=\emptyset \), the algebra reduces to the classical parameter-dependent pseudodifferential operators. The above definition is independent of the partitions of unity and trivializing sets we choose.
A central notion is parameter-ellipticity:
Definition 10
Given a parameter-dependent Boutet de Monvel operator \(A\in {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( M,\Lambda \right) \) we define:
-
(1)
The interior principal symbol \(\sigma _{\psi }(A)\in C^{\infty }((T^{*}M\times \Lambda )\backslash \left\{ 0\right\} ,Hom(\pi _{T^{*}M\times \Lambda }^{*}E_{0},\)\(\pi _{T^{*}M\times \Lambda }^{*}E_{1}))\), where \(\pi _{T^{*}M\times \Lambda }:T^{*}M\times \Lambda \rightarrow M\) is the canonical projection. It is the principal symbol of the pseudodifferential operator part of the operator A.
-
(2)
The boundary principal symbol \(\sigma _\partial (A)\). For \((z,\lambda )\in \left( T^{*}\partial M\times \Lambda \right) \backslash \left\{ 0\right\} \) we let
$$\begin{aligned} \sigma _{\partial }\left( A\right) \left( z\right) \left( \lambda \right) :\pi _{T^{*}\partial M\times \Lambda }^{*} \begin{pmatrix} \left. E_{0}\right| _{\partial M}\otimes {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \\ \oplus \\ F_{0} \end{pmatrix} \rightarrow \pi _{T^{*}\partial M\times \Lambda }^{*} \begin{pmatrix} \left. E_{1}\right| _{\partial M}\otimes {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \\ \oplus \\ F_{1} \end{pmatrix}, \end{aligned}$$
where \(\pi _{T^{*}\partial M\times \Lambda }:\left( T^{*}\partial M\times \Lambda \right) \backslash \left\{ 0\right\} \rightarrow \partial M\) is the canonical projection. After localization, it corresponds to the symbol in Definition 8.
We say that \(A\left( \lambda \right) \) is parameter-elliptic if both symbols are invertible. With obvious changes, we can also define parameter-ellipticity, interior and boundary principal symbols of operators \(A\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \).
The parameter-dependent pseudodifferential operators defined above are a particular version of the more general calculus introduced by Grubb in [11], and by Grubb [10] and Grubb and Kokholm in [13], for the \(L_{p}\) case. In these references, pseudodifferential symbols \(p\in S_{1,0}^{m,\nu }\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},{\mathbb {R}}_{+}\right) \) of order \(m\in {\mathbb {R}}\) and regularity \(\nu \in {\mathbb {R}}\) are used. These are functions \(p\in C^{\infty }\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\times \overline{{\mathbb {R}}_{+}}\right) \) that satisfy the estimates:
Similar estimates are used to define the boundary terms. This more general parameter-dependent calculus, as well as its notion of parameter-ellipticity [11, Chapter 3], can be reduced to ours by considering \(\nu =+\infty \). Therefore many results of our calculus can be deduced from this more general one. Our simplified version of the parameter-dependent calculus coincides with the one used by Schrohe and Schulze [30, 31]. It is easier to handle and very suitable for the study of conical singularities, which is our main concern.
The above operators act continuously on Bessel and Besov spaces. First we fix a dyadic partition of unity \(\left\{ \varphi _{j};\,j\in {\mathbb {N}}_{0}\right\} \).
Definition 11
Let \(\varphi _{0}\in C_{c}^{\infty }({\mathbb {R}}^{n})\) be supported \(\left\{ \xi ;\,\left| \xi \right| <2\right\} , 0\le \varphi _{0}\le 1\) and \(\varphi _{0}\left( \xi \right) =1\) in a neighborhood of the closed unit ball. Define \(\varphi _{j}\in C_{c}^{\infty }({\mathbb {R}}^{n})\), \(j\ge 1\), by \(\varphi _{j}\left( \xi \right) =\varphi _{0}\left( 2^{-j}\xi \right) -\varphi _{0}\left( 2^{-j+1}\xi \right) \).
Remark 12
We use the following notation: \(K_{j}:=\left\{ \xi \in {\mathbb {R}}^{n};2^{j-1}\le \left| \xi \right| \le 2^{j+1}\right\} \), for \(j\ge 1\), and \(K_{0}:=\left\{ \xi \in {\mathbb {R}}^{n};\left| \xi \right| \le 2\right\} .\) The above definition implies that \(\text{ supp }\left( \varphi _{j}\right) \subset \text {interior}\left( K_{j}\right) \), for \(j\ge 0\). Moreover, we see that \(\varphi _{j}\left( \xi \right) =\varphi _{1}\left( 2^{-j+1}\xi \right) \), for \(j\ge 2\) and \(\sum _{j=0}^{\infty }\varphi _{j}\left( \xi \right) =1\), \(\xi \in {\mathbb {R}}^{n}\).
Definition 13
For each \(s\in {\mathbb {R}}\), we define the operator \(\left\langle D\right\rangle ^{s}:{\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) \rightarrow {\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) \) as the pseudodifferential operator with symbol \(\xi \in {\mathbb {R}}^{n}\mapsto \left\langle \xi \right\rangle ^{s}\). Moreover, we write \(\varphi _{j}(D)u=op(\varphi _{j})u\).
-
(1)
The Bessel potential space \(H_{p}^{s}\left( {\mathbb {R}}^{n}\right) =\left\{ u\in {\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) ;\,\left\langle D\right\rangle ^{s}u\in L_{p}\left( {\mathbb {R}}^{n}\right) \right\} \), for \(1<p<\infty \) and \(s\in {\mathbb {R}}\), is the Banach space with norm \(\left\| u\right\| _{H_{p}^{s}\left( {\mathbb {R}}^{n}\right) }:=\left\| \left\langle D\right\rangle ^{s}u\right\| _{L_{p}\left( {\mathbb {R}}^{n}\right) }\).
-
(2)
The Besov space \(B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \), for \(s\in {\mathbb {R}}\) and \(1<p<\infty \), is the Banach space of all tempered distributions \(f\in {\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) \) that satisfy:
$$\begin{aligned} \left\| f\right\| _{B_{p}^{s}\left( {\mathbb {R}}^{n}\right) }:=\left( \sum _{j=0}^{\infty }2^{jsp}\left\| \varphi _{j}\left( D\right) f\right\| _{L_{p}\left( {\mathbb {R}}^{n}\right) }^{p}\right) ^{\frac{1}{p}}<\infty . \end{aligned}$$
For an open set \(\Omega \subset {\mathbb {R}}^{n}\), we define the Bessel potential spaces \(H_{p}^{s}\left( \Omega \right) \), as the set of restrictions of \(H_{p}^{s}\left( {\mathbb {R}}^{n}\right) \) to \(\Omega \) with norm
Similarly, we define the Besov spaces \(B_{p}^{s}\left( \Omega \right) \). Together with partition of unity and local charts, this leads to the spaces \(H_{p}^{s}\left( M\right) \), \(H_{p}^{s}\left( M,E\right) \), \(B_{p}^{s}\left( \partial M\right) \) and \(B_{p}^{s}\left( \partial M,E\right) \), where E is a vector bundle over M or \(\partial M\).
Remark 14
Let \(s\in {\mathbb {R}}, 1<p<\infty \) and \(\frac{1}{p}+\frac{1}{q}=1\).
-
(1)
There are continuous inclusions \(C_{c}^{\infty }\left( {\mathbb {R}}^{n}\right) \hookrightarrow {\mathcal {S}}({\mathbb {R}}^{n})\hookrightarrow B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \hookrightarrow {\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) \). Moreover the spaces \(C_{c}^{\infty }\left( {\mathbb {R}}^{n}\right) \) and \({\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) are dense in \(B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \). The same can be said of \(H_{p}^{s}\left( {\mathbb {R}}^{n}\right) \).
-
(2)
The dual of \(B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \) is \(B_{q}^{-s}\left( {\mathbb {R}}^{n}\right) \), where the identification is given by the \(L_{2}\) scalar product. Again the same holds for \(H_{p}^{s}\left( {\mathbb {R}}^{n}\right) \) and \(H_{q}^{-s}\left( {\mathbb {R}}^{n}\right) \).
-
(3)
A pseudodifferential operator with symbol \(a\in S^{m}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\right) \) extends to continuous operators \(op(a):H_{p}^{s}\left( {\mathbb {R}}^{n}\right) \rightarrow H_{p}^{s-m}\left( {\mathbb {R}}^{n}\right) \) and \(op(a):B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \rightarrow B_{p}^{s-m}\left( {\mathbb {R}}^{n}\right) \) for all \(s\in {\mathbb {R}}\).
-
(4)
The following interpolation holds: \(\left( L_{p}\left( {\mathbb {R}}^{n}\right) ,H_{p}^{1}\left( {\mathbb {R}}^{n}\right) \right) _{\theta ,p}=B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \), for all \(0<\theta <1\), where \(\left( X,Y\right) _{\theta ,p}\) denotes the real interpolation space of the interpolation couple \(\left( X,Y\right) \), as in Lunardi [19].
-
(5)
If M is a compact manifold (with or without boundary) and E is a vector bundle over M, then \(H_{p}^{s}(M,E)\hookrightarrow H_{p}^{s'}(M,E)\) and \(B_{p}^{s}(M,E)\hookrightarrow B_{p}^{s'}(M,E)\) are compact inclusions, whenever \(s>s'\).
-
(6)
The trace functional \(\gamma _{0}:{\mathcal {S}}({\mathbb {R}}^{n})\rightarrow {\mathcal {S}}({\mathbb {R}}^{n-1})\) extends to a continuous and surjective map \(\gamma _{0}:H_{p}^{s}({\mathbb {R}}^{n})\rightarrow B_{p}^{s-\frac{1}{p}}({\mathbb {R}}^{n-1})\) when \(s>\frac{1}{p}\).
-
(7)
The Besov spaces do not depend on the choice of the dyadic partition of unity; different partitions yield equivalent norms.
Remark 15
We recall some notions from vector-valued harmonic analysis; see for instance Denk and Kaip [6]. A Banach space G is a UMD space if, for some \(p\in \left. \right] 1,\infty \left[ \right. \), the Hilbert transform H, given by
extends to a bounded operator in \({\mathcal {B}}\left( L_{p}\left( {\mathbb {R}},G\right) \right) \). The Banach space has property \((\alpha )\) if there exists a constant \(C>0\) such that for all \(n\in {\mathbb {N}}\), for all \(\left( \alpha _{ij}\right) _{i,j=1,\ldots ,n}\subset \mathbb {C}\) with \(\left| \alpha _{ij}\right| \le 1\), and for all \(\left( x_{ij}\right) _{i,j=1,\ldots ,n}\subset G\), we have
where \(r_{j}\left( t\right) =\text {sign}\left( \sin \left( 2^{k}\pi t\right) \right) , j\in {\mathbb {N}}\), are the Rademacher functions. These properties allow the extension of important theorems of classical harmonic analysis to the vector valued case.
If G is a UMD space with property \(\left( \alpha \right) \), we can define, using Bochner integrals, \(B_{p}^{s}\left( {\mathbb {R}}^{n},G\right) \) and \(H_{p}^{s}\left( {\mathbb {R}}^{n},G\right) \) in the same way as before, see, for instance, [2, 6]. It is worth noting that \(B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \) and \(B_{p}^{s}\left( \partial X,E\right) \) are UMD spaces with the property \(\left( \alpha \right) \) for all \(s\in {\mathbb {R}}\) and \(1<p<\infty \). Later, we also use that \(B_{p}^{s}\left( {\mathbb {R}},G\right) \subset H_{p}^{1}\left( {\mathbb {R}},G\right) :=\left\{ u\in L_{p}\left( {\mathbb {R}},G\right) ;\,\frac{du}{dt}\in L_{p}\left( {\mathbb {R}},G\right) \right\} \), for all \(0<s<1\).
Let us now state the following properties of composition, adjoints and continuity of Boutet de Monvel operators [9, 11, 13, 23].
Theorem 16
-
(1)
(Composition) Let \(A\in {\mathcal {B}}_{E_{1},F_{1},E_{2},F_{2}}^{m,d}\left( M,\Lambda \right) \), \(B\in {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m',d'}\left( M,\Lambda \right) \). Then \(AB\in {\mathcal {B}}_{E_{0},F_{0},E_{2},F_{2}}^{m+m',d''}\left( M,\Lambda \right) \), where \(d'':=\max \left\{ m'+d,d'\right\} \). Similarly, if \(A\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{2},F_{2}}^{p}\left( M,\Lambda \right) \) and \(B\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \), then \(AB\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{2},F_{2}}^{p}\left( M,\Lambda \right) \).
-
(2)
(Adjoint) Let \(A\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \). Then \(A^{*}\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{q}\left( M,\Lambda \right) \), where \(\frac{1}{p}+\frac{1}{q}=1\) and \(A^{*}\) is the only operator that satisfies, for every \(u\in C^{\infty }\left( M,E_{0}\right) \oplus C^{\infty }\left( \partial M,F_{0}\right) \) and \(v\in C^{\infty }\left( M,E_{1}\right) \oplus C^{\infty }\left( \partial M,F_{1}\right) \), the relation
$$\begin{aligned} \left( A\left( \lambda \right) u,v\right) _{L_{2}(M,E_{1})\oplus L_{2}(M,F_{1})}=\left( u,A^{*}\left( \lambda \right) v\right) _{L_{2}(M,E_{0})\oplus L_{2}(M,F_{0})}. \end{aligned}$$ -
(3)
(Continuity) An operator \(A\in {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( M,\Lambda \right) \) induces bounded operators \(A\left( \lambda \right) :H_{p}^{s}\left( M,E_{0}\right) \oplus B_{p}^{s-\frac{1}{p}}\left( \partial M,F_{0}\right) \rightarrow H_{p}^{s-m}\left( M,E_{1}\right) \oplus B_{p}^{s-m-\frac{1}{p}}\left( \partial M,F_{1}\right) \) for all \(s>d-1+\frac{1}{p}\). Similarly \(A\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \) induces bounded operators \(A\left( \lambda \right) :H_{p}^{s}\left( M,E_{0}\right) \oplus B_{p}^{s}\left( \partial M,F_{0}\right) \rightarrow H_{p}^{s}\left( M,E_{1}\right) \oplus B_{p}^{s}\left( \partial M,F_{1}\right) \), \(\forall s>-1+\frac{1}{p}\).
-
(4)
(Fredholm property) If \(A\in {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( M,\Lambda \right) \), \(d=\max \left\{ m,0\right\} \), is parameter-elliptic, then there exists a \(B\in {\mathcal {B}}_{E_{1},F_{1},E_{0},F_{0}}^{-m,d'}\left( M,\Lambda \right) \), \(d'=\max \left\{ -m,0\right\} \), such that
$$\begin{aligned} AB-I\in {\mathcal {B}}_{E_{1},F_{1},E_{1},F_{1}}^{-\infty ,d'}\left( M,\Lambda \right) \,\,\,\,\,\text{ and }\,\,\,\,\,BA-I\in {\mathcal {B}}_{E_{0},F_{0},E_{0},F_{0}}^{-\infty ,d}\left( M,\Lambda \right) . \end{aligned}$$(2.6)
As a consequence, \(A\left( \lambda \right) \) is a Fredholm operator of index 0 for each \(\lambda \in \Lambda \), and there exists a constant \(\lambda _{0}>0\) such that \(A\left( \lambda \right) \) is invertible, if \(\left| \lambda \right| \ge \lambda _{0}\).
Similarly, if \(A\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \) is parameter-elliptic, then there exists a \(B\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( M,\Lambda \right) \) such that Eq. (2.6) holds for \(d=d'=0\).
2.1 The Equivalence Between Ellipticity and Fredholm Property
In this section, we prove that the Fredholm property together with some growth condition on \(\lambda \) implies parameter-dependent ellipticity. The use of Besov spaces makes the proofs a little more elaborate than e.g. the proof in the parameter-independent \(L_{2}\)-case studied by Rempel and Schulze [23]. To make it clearer, we first study the pseudodifferential term on Besov spaces and then the boundary terms.
2.1.1 Pseudodifferential Operators with Parameters on a Manifold Without Boundary Acting on Besov Spaces
In this section, we prove the following theorem:
Theorem 17
Let M be a compact manifold without boundary, E and F be vector bundles over M. Let \(A\left( \lambda \right) {:}\,C^{\infty }\left( M,E\right) \rightarrow C^{\infty }\left( M,F\right) \), \(\lambda \in \Lambda \), be a classical parameter-dependent pseudodifferential operator of order 0. Then the following conditions are equivalent:
-
(i)
A is parameter-elliptic.
-
(ii)
There exist uniformly bounded operators \(B_{j}\left( \lambda \right) {:}\,B_{p}^{0}(M,F)\rightarrow B_{p}^{0}(M,E)\), \(\lambda \in \Lambda \), \(j=1\) and 2, such that
$$\begin{aligned} B_{1}\left( \lambda \right) A\left( \lambda \right) =1+K_{1}\left( \lambda \right) \,\text{ and }\,A\left( \lambda \right) B_{2}\left( \lambda \right) =1+K_{2}\left( \lambda \right) . \end{aligned}$$where \(K_{1}\left( \lambda \right) :B_{p}^{0}(M,E)\rightarrow B_{p}^{0}(M,E)\) and \(K_{2}\left( \lambda \right) :B_{p}^{0}(M,F)\rightarrow B_{p}^{0}(M,F)\) are compact operators for every \(\lambda \in \Lambda \) and \(\lim _{\left| \lambda \right| \rightarrow \infty }K_{j}\left( \lambda \right) =0\).
-
(iii)
There exist bounded operators \(B_{j}\left( \lambda \right) :B_{p}^{0}(M,F)\rightarrow B_{p}^{0}(M,E)\), \(\lambda \in \Lambda , j=1\) and 2, such that
$$\begin{aligned} B_{1}\left( \lambda \right) A\left( \lambda \right) =1+K_{1}\left( \lambda \right) \,\text{ and }\,A\left( \lambda \right) B_{2}\left( \lambda \right) =1+K_{2}\left( \lambda \right) . \end{aligned}$$where \(K_{1}\left( \lambda \right) {:}\,B_{p}^{0}(M,E)\rightarrow B_{p}^{0}(M,E)\) and \(K_{2}\left( \lambda \right) {:}\,B_{p}^{0}(M,F)\rightarrow B_{p}^{0}(M,F)\) are compact operators for every \(\lambda \in \Lambda \). Moreover, \(\lim _{\left| \lambda \right| \rightarrow \infty }K_{j}\left( \lambda \right) =0\) and there exist \(M\in {\mathbb {N}}_{0}\) and \(C>0\) such that \(\left\| B_{j}\left( \lambda \right) \right\| _{{\mathcal {B}}\left( B_{p}^{0}(M,F),B_{p}^{0}(M,E)\right) }\le C\left\langle \ln \left( \lambda \right) \right\rangle ^{M}\), for \(j=1\) and 2.
The third item also holds if \(\left\| B_{j}\left( \lambda \right) \right\| _{{\mathcal {B}}\left( B_{p}^{0}(M,F),B_{p}^{0}(M,E)\right) }\le C\left\langle \lambda \right\rangle ^{r}\), for some sufficiently small r, as a careful study of our proof shows.
We note that \(A\left( \lambda \right) B_{2}\left( \lambda \right) =1+K_{2}\left( \lambda \right) \) is equivalent to \(B_{2}\left( \lambda \right) ^{*}A\left( \lambda \right) ^{*}=1+K_{2}\left( \lambda \right) ^{*}\), where \(*\) indicates the adjoint. This is the condition that we shall need. Obviously condition i) implies that \(\text{ dim }\left( E\right) =\text{ dim }\left( F\right) \).
If (i) holds, then we can find a parametrix to \(A\left( \lambda \right) \) by Theorem 16(4) so that (ii) is true, and (ii) trivially implies (iii). So we only need to prove that (iii) implies (i).
Definition 18
Let \(s>0\), \(0<\tau <\frac{1}{3}\) and \((y,\eta )\in {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\). We define the operator \(R_{s}(y,\eta ){:}\,{\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \), also denoted just by \(R_{s}\), by
Below we collect some well-known facts about the operators \(R_{s}\). The items 1, 2, 4, 5 and 6 can be found in [23, 28]. As we are dealing also with Besov spaces, some estimates must be done more carefully. The third item was not proven in the previous references. Statement 7 is stronger than usual. Both are necessary, as \(R_{s}\) is not an isometry in the space \(B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \).
Lemma 19
The operator \(R_{s}=R_{s}\left( y,\eta \right) \) has the following properties:
-
(1)
\(\left\| R_{s}u\right\| _{L_{p}\left( {\mathbb {R}}^{n}\right) }=\left\| u\right\| _{L_{p}\left( {\mathbb {R}}^{n}\right) }\) for all \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \).
-
(2)
\(\lim _{s\rightarrow \infty }R_{s}u=0\) weakly in \(L_{p}\left( {\mathbb {R}}^{n}\right) \) for all \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \).
-
(3)
\(R_{s}:B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \rightarrow B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \) is continuous for all \(s>0\) and \(\left\| R_{s}u\right\| _{B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) }\le C_{\theta }\left( 1+s\left\langle \eta \right\rangle \right) ^{\theta }\left\| u\right\| _{H_{p}^{1}\left( {\mathbb {R}}^{n}\right) }\), for every \(\theta \in \left. \right] 0,1\left[ \right. \), \(s\ge 1\) and \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \). The constant \(C_{\theta }\) depends on \(\theta \), but not on y, \(\eta \) or s.
-
(4)
The operator \(R_{s}\) is invertible. Its inverse is given by
$$\begin{aligned} R_{s}^{-1}u\left( x\right) =s^{-\frac{\tau n}{p}}e^{-is\left( y+s^{-\tau }x\right) \eta }u\left( y+s^{-\tau }x\right) . \end{aligned}$$ -
(5)
The Fourier transform of \(R_{s}u\) is given by
$$\begin{aligned} {\mathcal {F}}\left( R_{s}u\right) \left( \xi \right) =s^{\frac{\tau n}{p}-n\tau }e^{-iy\left( \xi -s\eta \right) }\hat{u}\left( s^{-\tau }\left( \xi -s\eta \right) \right) . \end{aligned}$$ -
(6)
Let \(a\in S^{m}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \). Then
$$\begin{aligned} R_{s}^{-1}op(a)\left( s\lambda \right) R_{s}u(x)=op(a_{s})\left( \lambda \right) u(x), \end{aligned}$$where \(a_{s}(x,\xi ,\lambda )=a\left( y+s^{-\tau }x,s\eta +s^{\tau }\xi ,s\lambda \right) \).
-
(7)
Let \(a\in S_{cl}^{0}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \) be classical, \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \), \(\lambda \in \Lambda \) with \(\left( \eta ,\lambda \right) \ne \left( 0,0\right) \) and \(0<r<\tau \). Then
$$\begin{aligned} \lim _{s\rightarrow \infty }s^{r}\left\| op(a)\left( s\lambda \right) R_{s}u-a_{(0)}(y,\eta ,\lambda )R_{s}u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }=0. \end{aligned}$$(2.7)
Proof
(1), (4) and (5) are just simple computations, and (6) follows from (4), (5) and the definition of pseudodifferential operators.
In order to prove (2), we just have to note that \(\lim _{s\rightarrow \infty }\int _{{\mathbb {R}}^{n}}R_{s}u\left( x\right) v\left( x\right) dx=0\) for all \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) and \(v\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \). The proof follows then from the fact that \(L_{p}({\mathbb {R}}^{n})'\simeq L_{q}\left( {\mathbb {R}}^{n}\right) \), for \(\frac{1}{p}+\frac{1}{q}=1\), and that \(R_{s}\) is an isometry.
(3) The operator \(R_{s}:B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \rightarrow B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \) is continuous for all \(s\in {\mathbb {R}}\), as \(R_{s}\) is the composition of dilatation, translation and multiplication by \(e^{is\eta x}\). The estimate follows by interpolation. In fact, for \(s\ge 1\), it is easy to see that \(\left\| R_{s}u\right\| _{H_{p}^{1}\left( {\mathbb {R}}^{n}\right) }\le \left( 1+s\left\langle \eta \right\rangle \right) \left\| u\right\| _{H_{p}^{1}\left( {\mathbb {R}}^{n}\right) }\). As \(\left( L_{p}\left( {\mathbb {R}}^{n}\right) ,H_{p}^{1}\left( {\mathbb {R}}^{n}\right) \right) _{\theta ,p}=B_{p}^{\theta }\left( {\mathbb {R}}^{n}\right) \), we conclude (see Lunardi [19, Corollary 1.1.7]) that there exists a constant \(C_{\theta }\) such that
(7) This is the longest statement we need to prove. We divide the proof into several steps. Our first goal is the \(L_p\)-convergence:
In a first step let us show that, for every \(\left( x,\xi \right) \in {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\),
Let \(\chi :{\mathbb {R}}^{n}\times \Lambda \rightarrow \mathbb {C}\) be a smooth function that is equal to 0 in a neighborhood of the origin and equal to 1 outside a closed ball centered at the origin that does not contain \(\left( \eta ,\lambda \right) \). For \(s\ge 1\), we have
where we have used Peetre’s inequality. Since \(a_{\left( 0\right) }\left( y,s\eta ,s\lambda \right) =a_{\left( 0\right) }\left( y,\eta ,\lambda \right) \),
The estimates (2.10) and (2.11) imply (2.9) for \(\tau <\frac{1}{3}\).
In a second step we are going to show the pointwise convergence of the integrand of (2.8) for all \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) and all \(x\in {\mathbb {R}}^{n}\). We know that
The integrand goes to zero, as we have seen in Eq. (2.9). Moreover
is integrable with respect to \(\xi \), so that the dominated convergence theorem applies.
In the third step we will finally prove (2.8). It is enough to show that the integrand is dominated. Indeed, integration by parts shows that
For \(\sigma =0\), we recall (2.9); for \(\sigma \ne 0\), we use that \(r+2\tau \left| \sigma \right| -\left| \sigma \right| <0\) and obtain
As \(\xi \mapsto \langle \xi \rangle ^{M}\hat{u}\left( \xi \right) \) is integrable for all \(M>0\), (2.12) can be estimated by \(\tilde{C}_{\lambda ,\eta ,\gamma }\left\langle x\right\rangle \). Hence, for arbitrary N,
The dominated convergence then shows the desired \(L_p\)-convergence.
Our next goal is to show \(L_p\)-convergence of the derivative:
Let us first observe that
Using Eq. (2.8) and the fact that \(r<\tau \), we conclude that
and
for all \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \). Hence
Equations (2.8) and (2.14) imply (2.13).
In order to finish the proof of item (7), choose \(\theta >0\) such that \(\theta +r<\tau \). Then item (3) implies that
As the last term goes to zero, we obtain (2.7). \(\square \)
Corollary 20
Let \(a\in S_{cl}^{0}({\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda )\) satisfy the transmission condition and \(u\in {\mathcal {S}}({\overline{{\mathbb {R}}_{+}^{n}}})\). Then
for \(\left( y,\eta ,\lambda \right) \in \overline{{\mathbb {R}}_{+}^{n}}\times \left( \left( {\mathbb {R}}^{n}\times \Lambda \right) \backslash \left\{ 0\right\} \right) \) and \(0<r<\tau \), where \(R_{s}=R_{s}\left( y,\eta \right) \).
Proof
We use that \(r^{+}:L_{p}\left( {\mathbb {R}}^{n}\right) \rightarrow L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \) is continuous, that \(R_{s}:L_{p}\left( {\mathbb {R}}^{n}\right) \rightarrow L_{p}\left( {\mathbb {R}}^{n}\right) \) is an isometry mapping \(C_{c}^{\infty }({\mathbb {R}}_{+}^{n})\) to \(C_{c}^{\infty }({\mathbb {R}}_{+}^{n})\), and Eq. (2.8). \(\square \)
In order to control the action of \(R_{s}\) on Besov spaces, we recall the equivalence of Besov norm and \(L_{p}\) norm on certain subsets of \({\mathcal {S}}({\mathbb {R}}^{n})\), see e.g. [18].
Lemma 21
(Besov space property) There is a constant \(C>0\) such that
for all \(u\in {\mathcal {S}}'\left( {\mathbb {R}}^{n}\right) \) with \(\text{ supp }\, {\mathcal {F}}(u)\subset \cup _{k=m}^{m+2}K_{k}\) for some \(m\ge 0\). Here C does not depend on m. In particular, under these circumstances, \(u\in L_{p}\left( {\mathbb {R}}^{n}\right) \) if and only if \( u\in B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \).
The number 2 could be replaced by a different one. We recall that the sets \(K_{j}\) were defined in Remark 12.
Proof
As \(\varphi _{j}(\xi )=\varphi _{1}(2^{-j+1}\xi )\) for \(j\ge 1\), and \(u=\sum _{j=m-1}^{m+3}\varphi _{j}(D)u\), the estimate
implies the result. \(\square \)
The operator \(R_{s}\) has important properties when acting on functions whose Fourier transform is supported in \(\tilde{K}:=\left\{ \xi \in {\mathbb {R}}^{n};\,\frac{1}{2}<\left| \xi \right| <1\right\} \).
Lemma 22
There is a constant \(s_{0}>0\), that depends only on \(\eta \), for which the operator \(R_{s}=R_{s}\left( y,\eta \right) \) has the following properties:
-
(1)
If \(u\in {\mathcal {S}}'({\mathbb {R}}^{n})\) and \(\text{ supp }\,({\mathcal {F}}u)\subset \tilde{K}\), then, for every \(s\ge s_0\), there is an \(m\in {\mathbb {N}}_{0}\) that depends on s, such that \(\text{ supp }\,{\mathcal {F}}\left( R_{s}u\right) \subset \cup _{k=m}^{m+2}K_{k}\).
-
(2)
There exists a constant \(C>0\) such that \(C^{-1}\left\| u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }\le \left\| R_{s}u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }\le C\left\| u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }\) for all \(s>s_{0}\) and all \(u\in B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \) with \(\text{ supp }\left( {\mathcal {F}}u\right) \subset \tilde{K}\).
-
(3)
For \(u\in {\mathcal {S}}({\mathbb {R}}^{n})\) with \(\text{ supp }({\mathcal {F}}u)\subset \tilde{K}\), \(\lim _{s\rightarrow \infty }R_{s}u=0\) weakly in \(B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \).
Proof
-
(1)
By item (5) of Lemma 19, \({\mathcal {F}}\left( R_{s}u\right) \left( \xi \right) =0\), unless \(\frac{1}{2}<\left| s^{-\tau }\left( \xi -s\eta \right) \right| <1\). If \(\eta =0\), this means that \(\frac{1}{2}s^{\tau }<\left| \xi \right| <s^{\tau }\). If \(\eta \ne 0\), choose \(s_{0}>0\) such that \(2s^{\tau }<s\left| \eta \right| \), for \(s>s_{0}\). Then \(\text{ supp }\, {\mathcal {F}}\left( R_{s}\left( u\right) \right) \subset \left\{ \xi ;\frac{1}{2}s\left| \eta \right|<\left| \xi \right| <2s\left| \eta \right| \right\} \), for \(s>s_{0}\). The result now follows easily.
-
(2)
As \(\text{ supp }\,{\mathcal {F}}(R_{s}u)\subset \cup _{k=m}^{m+2}K_{k}\) and \(\text{ supp }\left( {\mathcal {F}}\left( u\right) \right) \subset \tilde{K}\), the result follows from Lemma 21 and the fact that \(R_{s}\) is an isometry in \(L_{p}\left( {\mathbb {R}}^{n}\right) \).
-
(3)
From item (2) of Lemma 19, we know that
$$\begin{aligned} \lim _{s\rightarrow \infty }\int _{{\mathbb {R}}^{n}}R_{s}u\left( x\right) v\left( x\right) dx=0,\,v\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) . \end{aligned}$$However, \(B_{q}^{0}\left( {\mathbb {R}}^{n}\right) \cong B_{p}^{0}\left( {\mathbb {R}}^{n}\right) '\), for \(\frac{1}{p}+\frac{1}{q}=1\), and \({\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) is dense in \(B_{q}^{0}\left( {\mathbb {R}}^{n}\right) \). As, by item 2), \(\left\| R_{s}u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }\) is uniformly bounded in s for all fixed \(u\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) such that \(\text{ supp }\left( {\mathcal {F}}u\right) \subset \tilde{K}\), the result follows.
\(\square \)
We now prove Theorem 17. The next simple lemma will be useful:
Lemma 23
Let E and F be Banach spaces and \(E'\) and \(F'\) be their dual spaces. If \(A{:}\,E\rightarrow F\) is a bounded linear operator such that A is injective, has closed range and its adjoint \(A^{*}{:}\,F'\rightarrow E'\) is also injective, then A is an isomorphism.
Proof
Suppose that the range \(R\left( A\right) \) of A is a proper subset of F. By the Hahn-Banach Theorem, there is an \(f\in F^{*}\), \(f\ne 0\), such that \(\left. f\right| _{R\left( A\right) }=0\). This implies that \(A^{*}\left( f\right) =f\circ A=0\). As \(A^{*}:F'\rightarrow E'\) is injective, we conclude that \(f=0\), which is a contradiction. \(\square \)
Proof
(of Theorem 17)
As it suffices to prove the implication (iii) \(\implies \) (i), consider \(A\left( \lambda \right) \), \(B\left( \lambda \right) \) and \(K\left( \lambda \right) \) as in (iii). Our aim is to prove that the principal symbol \(p_{\left( 0\right) }\left( z,\lambda \right) \) of A is invertible for every \(\left( z,\lambda \right) \in \left( T^{*}M\times \Lambda \right) {\backslash }\left\{ 0\right\} \). We focus on a trivializing coordinate neighborhood U containing \(x=\pi (z)\). We choose smooth functions \(\Phi , \Psi \) and \({\mathrm {H}}\) supported in U such that \(\Phi \) equals 1 near x and \(\Psi \Phi = \Phi \), \({\mathrm {H}}\Psi =\Psi \). Denote by \(\tilde{A}(\lambda )\in {\mathcal {B}}(B^0_p({\mathbb {R}}^n)^{N_1}, B^0_p({\mathbb {R}}^n)^{N_2})\) and \(\tilde{B}(\lambda )\in {\mathcal {B}}(B^0_p({\mathbb {R}}^n)^{N_2}, B^0_p({\mathbb {R}}^n)^{N_1})\) the operators \({\mathrm {H}} A(\lambda )\Psi \) and \(\Phi B(\lambda ){\mathrm {H}}\) in local coordinates. Then our assumptions imply that there are compact operators \(\tilde{K}(\lambda )\), tending to zero in \({\mathcal {B}}(B^0_p({\mathbb {R}}^n)^{N_1})\) as \(|\lambda |\rightarrow \infty \) such that
where \(\tilde{\Phi }\) is \(\Phi \) in local coordinates. Here we use the fact that \(\tilde{B}(\lambda )\) has logarithmic growth and that \(\Phi B(\lambda ){\mathrm {H}}^2A(\lambda ) \Psi \) differs from \(\Phi B(\lambda )A(\lambda )\mathrm \Psi \) by a compact operator whose norm tends to zero as \(|\lambda | \rightarrow \infty \).
Denote by \((y,\eta ,\lambda )\in {\mathbb {R}}^n\times ({\mathbb {R}}^n\times \Lambda )\setminus \{0\}\) the point corresponding to \((z,\lambda )\) and fix an element \(u=cv\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) ^{N_{1}}\), where \(c\in {\mathbb {C}}^{N_{1}}\) and \(0\ne v\in {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) with \(\text{ supp }\left( {\mathcal {F}}v\right) \subset \left\{ \xi ;\,\frac{1}{2}<|{\xi }|<1\right\} \). Equation (2.15) together with item (ii) of Lemma 22 implies that
We claim that \(\lim _{s\rightarrow \infty }\Vert \tilde{K}\left( s\lambda \right) R_{s}u\Vert _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) ^{ N_{1}}}=0\): Indeed \(\Vert \tilde{K}\left( s\lambda \right) \Vert _{{\mathcal {B}}(B_{p}^{0}\left( {\mathbb {R}}^{n})^{ N_{1}}\right) }\rightarrow 0\) for \(\lambda \ne 0\), and \(\Vert R_{s}u\Vert _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) ^{ N_{1}}}\le C\left\| u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) ^{N_{1}}}\). For \(\lambda =0\), we use that \(\tilde{K}\left( 0\right) \) is compact and the third item of Lemma 22, which implies that \(\lim _{s\rightarrow \infty }R_{s}u=0\) weakly in \(B_{p}^{0}\left( {\mathbb {R}}^{n}\right) ^{N_{1}}\).
Since \(\tilde{\Phi }\in C_{c}^{\infty }\left( {\mathbb {R}}^{n}\right) \) is equal to 1 in a neighborhood of y, \(\lim _{s\rightarrow \infty }(1-\tilde{\Phi })R_{s}(y,\eta )u=0\) in the topology of \({\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \) and, therefore, also in the topology of \(B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \). We moreover estimate
Item 7 of Lemma 19 implies that \(\lim _{s\rightarrow \infty }s^{r}\Vert \tilde{A}\left( s\lambda \right) R_{s}u-p_{\left( 0\right) }\left( y,\eta ,\lambda \right) R_{s}u\Vert _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) ^{N_{2}}}=0\) for r sufficiently small. By assumption, \(\Vert \tilde{B}(s\lambda )\Vert _{{\mathcal {B}}(B_{p}^{0}({\mathbb {R}}^{n})^{N_{2}},B_{p}^{0}({\mathbb {R}}^{n})^{N_{1}})} \le \tilde{C}\langle \ln (s\lambda )\rangle ^{M}\). Taking s sufficiently large, we conclude that
Hence, for sufficiently large s, we have
As \(v\ne 0\), this clearly implies that \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) \) is injective.
An analogous argument applies to the adjoint operator. We conclude that \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) ^{*}\), that is, the adjoint of \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) \) and the principal symbol of \(A\left( \lambda \right) ^{*}\), is also injective. Lemma 23 then tells us that \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) \) is an isomorphism and, in particular, that \(N_{2}=N_{1}\). Therefore \(A\left( \lambda \right) \) is an elliptic operator. \(\square \)
2.1.2 Boutet de Monvel Operators with Parameters Acting on \(L_{p}\)-Spaces
Theorem 24
Let M be a compact manifold with boundary \(\partial M\). Let \(E_{0}\) and \(E_{1}\) be vector bundles over M, \(F_{0}\) and \(F_{1}\) be vector bundles over \(\partial M\) and \(A\in \tilde{{\mathcal {B}}}^p_{E_{0},F_{0},E_{1},F_{1}}\left( M,\Lambda \right) \). Then the following conditions are equivalent:
-
(i)
The operator \(A\left( \lambda \right) \) is an elliptic parameter-dependent operator.
-
(ii)
We find bounded operators \(B_{1}\left( \lambda \right) {:}\,L_{p}\left( M,E_{0}\right) \oplus B_{p}^{0}\left( M,F_{0}\right) \rightarrow L_{p}\left( M,E_{1}\right) \oplus B_{p}^{0}\left( M,F_{1}\right) \) and \(B_{2}\left( \lambda \right) {:}\,L_{p}\left( M,E_{1}\right) \oplus B_{p}^{0}\left( M,F_{1}\right) \rightarrow L_{p}\left( M,E_{0}\right) \oplus B_{p}^{0}\left( M,F_{0}\right) \) such that
$$\begin{aligned} B_{1}\left( \lambda \right) A\left( \lambda \right) =1+K_{1}\left( \lambda \right) \,\,\,\text {and}\,\,\,A\left( \lambda \right) B_{2}\left( \lambda \right) =1+K_{2}\left( \lambda \right) ,\,\lambda \in \Lambda , \end{aligned}$$where the \(B_{j}\left( \lambda \right) \) are uniformly bounded in \(\lambda \) and \(K_{1}\left( \lambda \right) {:}\,L_{p}\left( M,E_{0}\right) \oplus B_{p}^{0}\left( M,F_{0}\right) \rightarrow L_{p}\left( M,E_{0}\right) \oplus B_{p}^{0}\left( M,F_{0}\right) \) and \(K_{2}\left( \lambda \right) {:}\,L_{p}\left( M,E_{1}\right) \oplus B_{p}^{0}\left( M,F_{1}\right) \rightarrow L_{p}\left( M,E_{1}\right) \oplus B_{p}^{0}\left( M,F_{1}\right) \) are compact and \(\lim _{\left| \lambda \right| \rightarrow \infty }K_{j}\left( \lambda \right) =0\), \(j=1,2\).
-
(iii)
Condition ii) holds with the uniform boundedness of the \(B_{j}\left( \lambda \right) \) replaced by the condition that, for \(j=1,2\) and some \(M\in {\mathbb {N}}_0\),
$$\begin{aligned} \left\| B_{j}\left( \lambda \right) \right\| _{{\mathcal {B}}\left( L_{p}\left( M,E_{1}\right) \oplus B_{p}^{0}\left( M,F_{1}\right) ,L_{p}\left( M,E_{0}\right) \oplus B_{p}^{0}\left( M,F_{0}\right) \right) }\le C\left\langle \ln \left( \lambda \right) \right\rangle ^{M}. \end{aligned}$$
Remark 25
Let \(A^{*}\left( \lambda \right) \) be the adjoint operator of \(A\left( \lambda \right) \). Theorem 16 tells us that \(A\left( \lambda \right) B_{2}\left( \lambda \right) =1+K_{2}\left( \lambda \right) \) is equivalent to
which is the condition that we will need later.
Again a standard parametrix construction shows that (i) implies (ii). As (ii) implies (iii) trivially, we only have to prove that (iii) implies (i).
We fix a point \(\left( y,\eta \right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}^{n-1}\) and a constant \(0<\tau <\frac{1}{3}\). For every \(s>0\), we define the isometries \(R_{s}=R_{s}\left( y,\eta \right) {:}\,L_{p}\left( {\mathbb {R}}^{n-1}\right) \rightarrow L_{p}\left( {\mathbb {R}}^{n-1}\right) \), \(S_{s}{:}\,L_{p}\left( {\mathbb {R}}_{+}\right) \rightarrow L_{p}\left( {\mathbb {R}}_{+}\right) \) and \(R_{s}\otimes S_{s}{:}\,L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \rightarrow L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \) by
The following simple proposition will be useful. It is very similar to the results we have already seen.
Proposition 26
The operator \(R_{s}\otimes S_{s}{:}\,L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \rightarrow L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \) satisfies:
-
(1)
\(\left\| R_{s}\otimes S_{s}u\right\| _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }=\left\| u\right\| _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }\), \(u\in L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \).
-
(2)
\(\lim _{s\rightarrow \infty }R_{s}\otimes S_{s}u=0\) in the weak topology of \(L_{p}\left( {\mathbb {R}}_{+}^{n}\right) \).
Proof
-
(1)
Is easily verified.
-
(2)
Due to the first item and the fact that \(L_{q}\left( {\mathbb {R}}_{+}^{n}\right) \cong L_{p}\left( {\mathbb {R}}_{+}^{n}\right) '\), it is enough to prove that if \(u\left( x\right) =u_{1}\left( x'\right) u_{2}\left( x_{n}\right) \) and \(v\left( x\right) =v_{1}\left( x'\right) v_{2}\left( x_{n}\right) \), where \(u_{1},v_{1}\in C_{c}^{\infty }\left( {\mathbb {R}}^{n-1}\right) \) and \(u_{2},v_{2}\in C_{c}^{\infty }\left( \overline{{\mathbb {R}}_{+}}\right) \), then
$$\begin{aligned}&{\lim _{s\rightarrow \infty }\int _{{\mathbb {R}}_{+}^{n}}R_{s}\otimes S_{s}u\left( x\right) v\left( x\right) dx}\\&\quad =\lim _{s\rightarrow \infty }\left( \int _{{\mathbb {R}}^{n-1}}R_{s}u_{1}\left( x'\right) v_{1}\left( x'\right) dx'\right) \left( \int _{{\mathbb {R}}_{+}}S_{s}u_{2}\left( x_{n}\right) v_{2}\left( x_{n}\right) dx_{n}\right) =0. \end{aligned}$$A simple computation shows that both terms on the right hand side go to zero as \(s\rightarrow \infty \).
\(\square \)
Proposition 27
Let \(0<r<\tau \) and let \(v\in {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) be such that \({\mathcal {F}}\left( v\right) \) has compact support. Denote by \(C\left( s\right) \) a function such that \(\lim _{s\rightarrow \infty }C\left( s\right) =0\). Then
-
(1)
(Pseudodifferential operator in the interior) Let \(p\in S_{cl}^{0}\left( {\mathbb {R}}^{n}\times {\mathbb {R}}^{n},\Lambda \right) \) satisfy the transmission condition and \(p\sim \sum _{j\in {\mathbb {N}}_{0}}p_{\left( -j\right) }\) be its asymptotic expansion. Then
$$\begin{aligned}&{s^{r}\Big \Vert op\left( p\right) \left( s\lambda \right) \left( R_{s}v\otimes S_{s}w\right) }\\&\quad -R_{s}\otimes S_{s} \Big (\frac{v\left( x'\right) }{2\pi }\int _{{\mathbb {R}}}e^{ix_{n}\xi _{n}}p_{\left( 0\right) }\left( y,x_{n},\eta ,\xi _{n},\lambda \right) {\mathcal {F}}_{x_{n}\rightarrow \xi _{n}}\left( e^{+}w\right) \left( \xi _{n}\right) d\xi _{n}\Big )\Big \Vert _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }\\&\qquad \le C\left( s\right) \left\| w\right\| _{L_{p}\left( {\mathbb {R}}_{+}\right) }, \quad w\in {\mathcal {S}}(\overline{{\mathbb {R}}_{+}}). \end{aligned}$$ -
(2)
(Singular Green operators) Let \( S_{cl}^{-\,1}({\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda ) \ni \tilde{g}\sim \sum _{j\in {\mathbb {N}}_{0}}\tilde{g}_{\left( -1-j\right) }\) and \(G\left( \lambda \right) :{\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\rightarrow {\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\) be defined by (2.3). Then, for \(w\in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \),
$$\begin{aligned}&{s^{r}\Big \Vert G\left( s\lambda \right) \left( R_{s}v\otimes S_{s}w\right) }\\&\quad -R_{s}\otimes S_{s}\Big (v(x')\int _{{\mathbb {R}}_{+}}\tilde{g}_{\left( -1\right) }\left( y,x_{n},y_{n},\eta ,\lambda \right) w(y_{n})dy_{n}\Big )\Big \Vert _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }\\&\qquad \le C\left( s\right) \Vert w\Vert _{L_{p}\left( {\mathbb {R}}_{+}\right) }. \end{aligned}$$ -
(3)
(Trace operators) Let \(S_{cl}^{-\frac{1}{p}}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda )\ni \tilde{t}\sim \sum _{j\in {\mathbb {N}}_{0}}\tilde{t}_{\left( -\frac{1}{p}-j\right) }\) and \(T\left( \lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) be defined by (2.2). Then for \(w\in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \),
$$\begin{aligned}&s^{r}\,\,\,\,\,\Big \Vert T\left( s\lambda \right) \left( R_{s}v\otimes S_{s}w\right) -R_{s}\Big (v\left( x'\right) \int _{{\mathbb {R}}_{+}}\tilde{t}_{\left( -\frac{1}{p}\right) }\left( y,x_{n},\eta ,\lambda \right) w\left( x_{n}\right) dx_{n}\Big )\Big \Vert _{B_{p}^{0}({\mathbb {R}}^{n-1})}\\&\quad \le C\left( s\right) \left\| w\right\| _{L_{p}\left( {\mathbb {R}}_{+}\right) }. \end{aligned}$$ -
(4)
(Poisson operators) Let \(S_{cl}^{\frac{1}{p}-1}({\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda ) \ni \tilde{k} \sim \sum _{j\in {\mathbb {N}}_{0}}\tilde{k}_{\left( \frac{1}{p}-1-j\right) }\) and \(K\left( \lambda \right) :{\mathcal {S}}({\mathbb {R}}^{n-1})\rightarrow {\mathcal {S}}(\overline{{\mathbb {R}}_{+}^{n}})\) be defined by (2.1). Then for \(w\in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \),
$$\begin{aligned} \lim _{s\rightarrow \infty }s^{r}\left\| K\left( s\lambda \right) \left( R_{s}v\right) -R_{s}\otimes S_{s}\left( \tilde{k}_{\left( \frac{1}{p}-1\right) }\left( y,x_{n},\eta ,\lambda \right) v\left( x'\right) \right) \right\| _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }=0. \end{aligned}$$
Proof
The items (1), (2) and (4) extend the results in [23, Section 2.3.4.2]. They can be obtained by replacing the operators \(R_{s}\) and \(S_{s}\) in [23] by the definitions given here and arguing similarly as for the third item.
The third item is more delicate, as the limit is taken in the Besov space: Let q be such that \(\frac{1}{p}+\frac{1}{q}=1\). Using item 4, 5 and 6 of Lemma 19, we find that
Fix \(\left( y,\eta ,\lambda \right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}^{n-1}\times \Lambda \) such that \(\left( \eta ,\lambda \right) \ne \left( 0,0\right) \). We will use the simple fact that if \(v\in {\mathcal {S}}({\mathbb {R}}^{n-1})\) is such that \(\text {supp}\,({\mathcal {F}}(v))\) is compact, then for all \(\theta \in \left. \right] 0,1\left[ \right. \) and for all \(\xi '\in \text {supp}\left( {\mathcal {F}}\left( v\right) \right) \), there is a \(s_{0}>0\) such that
The constant C does not depend on \(\theta \), \(s\ge s_{0}\) and \(\xi '\in \text {supp}\left( {\mathcal {F}}\left( v\right) \right) \).
We start by establishing \(L_p\)-convergence: let \(0<r<\tau \) and \(v\in {\mathcal {S}}({\mathbb {R}}^{n-1})\) with \(\text {supp}\left( {\mathcal {F}}(v)\right) \) compact. Then, for all \(w\in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \), we have
where \(C\left( s\right) \) is a constant that depends on s, \(\left( y,\eta ,\lambda \right) \) and v but not on w. Moreover, \(\lim _{s\rightarrow \infty }C\left( s\right) =0\).
We divide the proof into s, always assuming that \(s\ge s_{0}\). First we see that
In a first step we will prove that, for all \(\left( x',x_{n},\xi '\right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}_{+}\times {\mathbb {R}}^{n-1}\) and \(M\in {\mathbb {N}}_{0}\), there is a constant that depends on \(\eta , \lambda \) and M such that
Let us fix a function \(\chi \in C^{\infty }\left( {\mathbb {R}}^{n-1}\times \Lambda \right) \) that is zero near the origin and equal to 1 outside a closed ball that does not contain \(\left( \eta ,\lambda \right) \). We note that
for \(\xi '\in \text {supp}\left( {\mathcal {F}}\left( v\right) \right) .\) We now study the term
Using the fact that \(s^{-\frac{1}{q}}\tilde{t}_{\left( -\frac{1}{p}\right) }\left( y,\frac{x_{n}}{s},s\eta ,s\lambda \right) =\tilde{t}_{\left( -\frac{1}{p}\right) }\left( y,x_{n},\eta ,\lambda \right) \), and a Taylor expansion we conclude that the expression (2.20) is smaller or equal to
As \(0<r<\tau <\frac{1}{3}\), we conclude that \(-1+r<r-\tau \) and \(r+\tau -1<r-\tau \). Hence (2.18) follows from the estimates of (2.19) and (2.21).
In a second step we will next show that the limit of Eq. (2.17) as \(s\rightarrow \infty \) is zero. This is true, as it is smaller than or equal to
In a third step we want to prove that, for all \(M\in {\mathbb {N}}_{0}\), the expression (2.17) is bounded by \(C_{M}\left\langle x'\right\rangle ^{-M}\), for a constant \(C_{M}>0\). Then Lebesgue’s dominated convergence theorem will imply that (2.17) holds. In order to do that, we note that
is a linear combination of terms of the form
If \(\sigma =0\), we have already proven that the above expression is smaller than \(C_{\eta ,\lambda ,M}\left\langle x_{n}\right\rangle ^{-M}s^{r-\tau }\). For \(\sigma \ne 0\), we estimate
Hence \(\big |s^{r-\frac{1}{q}}D_{\xi '}^{\sigma }\left( \tilde{t}\left( y+s^{-\tau }x',\frac{x_{n}}{s},s\eta +s^{\tau }\xi ',s\lambda \right) \right) \big |\le C_{\eta ,\lambda ,M}\left\langle x_{n}\right\rangle ^{-M}s^{r-\tau }\). The result now follows easily.
We will next establish the \({L_p}\)-convergence of the derivative. Let \(0<r<\tau \) and \(v\in {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) with \(\text {supp}\left( {\mathcal {F}}\left( v\right) \right) \) compact. Then, for all \(w\in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) \), we have
where \(C\left( s\right) \) is a constant that depends on s, \(\left( y,\eta ,\lambda \right) \) and v but not on w. Moreover, \(\lim _{s\rightarrow \infty }C\left( s\right) =0\).
Let us first fix a notation. We denote by \(\left( \partial _{x_{j}}T\right) \left( \lambda \right) \), \(j=1,\ldots ,n-1\), the operator:
Now, let us first observe that, for \(j=1,\ldots ,n-1\),
Using Eq. (2.17) and the fact that \(r<\tau \), we conclude that
and
The expressions (2.24), (2.25) and (2.26) imply that
Finally, (2.23) is a consequence of Eqs. (2.27) and (2.17).
We are now in the position to prove item 3. Choose \(0<\theta<\theta +r<\tau \). Then
\(\square \)
We also need to understand the action of the singular Green and trace operators on the operators \(R_{s}=R_{s}\left( y,\eta \right) \) for \(\left( y,\eta \right) \in \overline{{\mathbb {R}}_{+}^{n}}\times {\mathbb {R}}^{n}\). Notice that \(\left( y,\eta \right) \in \overline{{\mathbb {R}}_{+}^{n}}\times {\mathbb {R}}^{n}\) instead of \({\mathbb {R}}^{n-1}\times {\mathbb {R}}^{n-1}\) as in the previous proposition.
Proposition 28
Let \(R_{s}=R_{s}\left( y,\eta \right) \), where \(\eta =\left( \eta ',\eta _{n}\right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}\) and \(y=\left( y',0\right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}\). For \(u\in C_{c}^{\infty }\left( {\mathbb {R}}_{+}^{n}\right) \) the following properties hold:
-
(1)
(Green) For \(\tilde{g}\in S_{cl}^{-1}\left( {\mathbb {R}}^{n-1},{\mathcal {S}}_{++},\Lambda \right) \) define \(G\left( \lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \rightarrow {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \) by Eq. (2.3). Then \(\lim _{s\rightarrow \infty }s^{r}\left\| G\left( s\lambda \right) R_{s}\left( e^{+}u\right) \right\| _{L_{p}\left( {\mathbb {R}}_{+}^{n}\right) }=0\) for all \(r>0\).
-
(2)
(Trace) For \(\tilde{t}\in S_{cl}^{-\frac{1}{p}}\left( {\mathbb {R}}^{n-1},{\mathcal {S}}_{+},\Lambda \right) \) define \(T\left( \lambda \right) :{\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}^{n}}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) by Eq. (2.2). Then \(\lim _{s\rightarrow \infty }s^{r}\left\| T\left( s\lambda \right) R_{s}\left( e^{+}u\right) \right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n-1}\right) }=0\) for all \(r>0\).
Proof
The proof is analogous to that of Proposition 27. Let us sketch the proof of (2) as (1) is similar.
Let \(\frac{1}{p}+\frac{1}{q}=1\), \(R_{s}^{-1}:=R_{s}^{-1}\left( y',\eta '\right) :{\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) and \(R_{s}:=R_{s}\left( y,\eta \right) :{\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \rightarrow {\mathcal {S}}\left( {\mathbb {R}}^{n}\right) \). Using item 6 of Lemma 19 in \(\left( x',\xi '\right) \) and the definition of \(R_{s}\), we obtain that
Now, we note that
On the support of u, we have \(x_{n}\ge R>0\) for a certain constant \(R>0\). Hence
As \(2\tau -1<0\), we can always choose \(N\in {\mathbb {N}}_{0}\) so large that, for all \(\left( x',x_{n},\xi ',\lambda \right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}_{+}\times {\mathbb {R}}^{n-1}\times \Lambda \) such that \(x_{n}\ge R\) and for all \(r>0\), we have
For large \(N\in {\mathbb {N}}_{0}\), the dominated convergence theorem implies that
Now, to finish the proof, we just study \(L_{p}\) and \(H_{p}^{1}\) convergence. Using integration by parts in the expression \(x'^{\gamma }R_{s}^{-1}T\left( s\lambda \right) \left( R_{s}u\right) \left( x'\right) \), we see that we can dominate \(R_{s}^{-1}T\left( s\lambda \right) \left( R_{s}u\right) \left( x'\right) \) by \(\left\langle x'\right\rangle ^{-N}\) for every N. Hence
If we take derivatives of first order in \(x'\), we find that
The estimate of the norm of \(R_{s}\) on Besov space and the same argument with interpolation of Proposition 27 lead us to the conclusion that
\(\square \)
Finally, we prove the main Theorem of this sub-section.
Proof
(of Theorem 24) Let \(A=\left( \begin{array}{cc} P_{+}+G &{} K\\ T &{} S \end{array}\right) \in \tilde{{\mathcal {B}}}^{p}_{E_{0},F_{0},E_{1},F_{1}}\left( M,\Lambda \right) \) and \(B_{1}\), \(B_{2}\), \(K_{1}\) and \(K_{2}\) be as in Theorem 24, (iii). Write \(B_{1}=\left( \begin{array}{cc} B_{11} &{} B_{12}\\ B_{21} &{} B_{22} \end{array}\right) \) and decompose similarly \(K_1\).
Next we choose smooth functions \(\Phi , \Psi \) and \({\mathrm {H}}\), supported in a trivializing neighborhood U of \(x=\pi (z)\), such that \(\Phi \) equals 1 near x and \(\Psi \Phi = \Phi \), \({\mathrm {H}}\Psi =\Psi \). We denote by \(\tilde{P}_+(\lambda ), \tilde{G}(\lambda ) \in {\mathcal {B}}(L_p({\mathbb {R}}^n_+)^{n_1}, L_p({\mathbb {R}}^n_+)^{n_3})\), \(\tilde{T}(\lambda ) \in {\mathcal {B}}(L_p({\mathbb {R}}^n_+)^{n_1},B^0_p({\mathbb {R}}^{n-1})^{n_4})\), \(\tilde{B}_{11}(\lambda )\in {\mathcal {B}}(L_p({\mathbb {R}}^n_+)^{n_3}, L_p({\mathbb {R}}^n)^{n_1})\) and \(\tilde{B}_{12}(\lambda )\in {\mathcal {B}}(B^0_p({\mathbb {R}}^{n-1})^{n_4}, L_p({\mathbb {R}}^n_+)^{n_1})\) the operators \({\mathrm {H}} P_+(\lambda )\Psi \), \({\mathrm {H}} G(\lambda )\Psi \), \(\Phi B_{11}(\lambda ){\mathrm {H}}\), \({\mathrm {H}} T(\lambda ) \Psi \), and \(\Phi B_{12}(\lambda ){\mathrm {H}}\) in local coordinates.
The identity \(B_{1}A=I+K_{1}\) implies that
where \(\tilde{\Phi }\) is the function \(\Phi \) in local coordinates and \(\tilde{K}(\lambda )\) is the operator which collects the terms arising from the localizations of \(\Phi K_{11}(\lambda ){\mathrm {H}}\), \(\Phi B_{11}(\lambda )(1-{\mathrm {H}}^2)(P_+(\lambda )+ G(\lambda ))\Psi \) and \(\Phi B_{12}(\lambda ) (1-{\mathrm {H}}^2) T(\lambda )\Psi \). As the latter two operators have smooth integral kernels, with seminorms rapidly decreasing with respect to \(\lambda \), \(\tilde{K}(\lambda )\) is compact and its norm tends to zero as \(|\lambda |\rightarrow \infty \).
The interior principal symbol In order to prove the invertibility of the interior principal symbol \(p_{\left( 0\right) }\left( z,\lambda \right) :\pi _{T^{*}M\times \Lambda }^{*}\left( E_{0}\right) \rightarrow \pi _{T^{*}M\times \Lambda }^{*}\left( E_{1}\right) \) for \((z,\lambda )\in \left( T^{*}M\times \Lambda \right) \backslash \left\{ 0\right\} \), fix \(u=cv\in C_{c}^{\infty }({\mathbb {R}}_{+}^{n})^{n_{1}}\), where \(c\in {\mathbb {C}}^{n_{1}}\) and \(0\ne v\in C_{c}^{\infty }({\mathbb {R}}_{+}^{n})\). Denote by \((y,\eta )\in \overline{{\mathbb {R}}}^n_+\times {\mathbb {R}}^n\) the point corresponding to z in local coordinates. For \(R_{s}=R_{s}\left( y,\eta \right) \) we note that \(R_s(e^+u)\in C^\infty _c({\mathbb {R}}^n_+)\), since \(\text {supp} \,R_s (e^+u) \subset {\mathbb {R}}^n_+\). In particular \(\Vert u\Vert _{L_{p}({\mathbb {R}}_{+}^{n})^{n_{1}}}=\Vert r^{+}R_{s}(e^{+}u)\Vert _{L_{p}({\mathbb {R}}_{+}^{n})^{n_{1}}}\). Hence we obtain from (2.28)
On the right hand side of Eq. (2.29), we estimate
and note that Corollary 20 implies that
We claim that also \(\tilde{K}(s\lambda )R_s(e^+u)\) tends to zero: For \(\lambda =0\) we infer this from the fact that \(\tilde{K}(0)\) is compact, while \(R_s(e^+u)\) weakly tends to zero. For \(\lambda \not =0\) the norm of \(\tilde{K}(s\lambda )\) tends to zero as \(s\rightarrow \infty \), whereas \(R_s(e^+u)\) is bounded. Finally, it is easy to check that \(\lim _{s\rightarrow \infty }(1-\tilde{\Phi })R_{s}(e^{+}u)=0\) in \({\mathcal {S}}\left( {\mathbb {R}}^{n}\right) ^{ n_{1}}\) and therefore also in \(L_{p}\left( {\mathbb {R}}_{+}^{n}\right) ^{ n_{1}}\).
If we assume, for an instant, that also the second summand on the right hand side of (2.29) tends to zero as \(s\rightarrow \infty \), then, taking s sufficiently large, the boundedness of \(R_{s}\), Inequality (2.30) and Eq. (2.29) imply together with the assumption that \(\Vert \tilde{B}_{11}(s\lambda )\Vert _{{\mathcal {B}}(L_{p}({\mathbb {R}}_{+}^{n})^{n_{3}},L_{p}({\mathbb {R}}_{+}^{n})^{ n_{1}})}\le C\langle \text {ln}(s\lambda )\rangle ^{M}\), that
Hence \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) \) is injective. The same argument, applied to the adjoint operator, shows the injectivity of \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) ^{*}\) and thus the invertibility of \(p_{\left( 0\right) }\left( y,\eta ,\lambda \right) \). In particular, \(n_{1}=n_{3}\). In order to establish the convergence to zero of the second summand in (2.29), we distinguish two cases.
Case 1\(x\notin \partial M\). Then U can be taken as a subset of the interior of M. According to the rules of the calculus, \(\tilde{T}(s\lambda )\) and \(\tilde{G}(s\lambda )\) are regularizing elements in their respective classes; in particular, they are compact. For \(\lambda \ne 0\), their operator norms are rapidly decreasing as \(s\rightarrow \infty \). Arguing as for \(\tilde{K}\) above, we obtain the assertion from the assumptions on B.
Case 2\(x\in \partial M\) Here, statements (1) and (2) of Proposition 28 assert that, for every \(r>0\), the norms of \(s^r\tilde{G}(s\lambda )R_s(e^+u) \) and \(s^r\tilde{T}(s\lambda ) R_s(e^+u) \) go to zero in the corresponding spaces as \(s\rightarrow \infty \). The assertion then follows from the fact that the norm of \(B(s\lambda )\) grows at most logarithmically in s by assumption.
The boundary principal symbol We have to show that, for any given \(\left( z,\lambda \right) \in \left( T^{*}\partial M\times \Lambda \right) \backslash \{0\}\), \(\sigma _\partial (A)(z,\lambda )\) is invertible in
Let \(\tilde{B}\) and \(\tilde{A}\) be the operators \({\mathrm {H}}A\Psi \) and \(\Phi B {\mathrm {H}}\) in local coordinates, respectively. Write the principal boundary symbol of \(\tilde{A}\) in the form
and let \(\left( y,\eta \right) \in {\mathbb {R}}^{n-1}\times {\mathbb {R}}^{n-1}\) be the point that corresponds to z in local coordinates.
Fix a function \(0\ne u'\in {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) with \(\text{ supp }\left( {\mathcal {F}}u'\right) \subset \left\{ \xi ;\,\frac{1}{2}<|{\xi }|<1\right\} \). For \(u=\left( u_{1},\ldots ,u_{n_{1}}\right) \in {\mathcal {S}}\left( \overline{{\mathbb {R}}_{+}}\right) ^{n_{1}}\) and \(v=\left( v_{1},\ldots ,v_{n_{3}}\right) \in {\mathbb {C}}^{n_{2}}\), not both zero, denote by \(u'\otimes u\) and \(u'\otimes v\) the functions \({\mathbb {R}}_{+}^{n}\ni \left( x',x_{n}\right) \mapsto \left( u'\left( x'\right) u_{1}\left( x_{n}\right) ,\ldots ,u'\left( x'\right) u_{n_{1}}\left( x_{n}\right) \right) \) and \({\mathbb {R}}^{n-1} \ni x' \mapsto \left( u'\left( x'\right) v_{1},\ldots ,u'\left( x'\right) v_{n_{2}}\right) \), respectively. According to Lemmas 19, 21 and 22 there are constants such that
Writing \(\left\| .\right\| _{L_{p}B_{p}^{0}}\) for the norm in \(L_{p}({\mathbb {R}}_{+}^{n})^{ n_{1}}\oplus B_{p}^{0}({\mathbb {R}}^{n-1})^{ n_{2}}\), in analogy with Eq. (2.28) conclude from the identity \(B_1A=I+K_1\) that
Let us first consider the case where \(\lambda \ne 0\). We infer from Proposition 27 and the fact that the norm of \(\tilde{B}(s\lambda )\) is \(O(\langle \ln (s\lambda )\rangle ^M)\) that the first summand on the right hand side is \(o(\Vert (u'\otimes u )\oplus (u'\otimes v)\Vert )\). The same is true for the third summand, since the norm of \(\tilde{K}(s\lambda )\) tends to zero as \(s\rightarrow \infty \). The fourth summand tends to zero in \({\mathcal {S}}(\overline{{\mathbb {R}}^n_+})^{n_1} \oplus {\mathcal {S}}({\mathbb {R}}^{n-1})^{n_2}\), a fortiori in the \(L_pB^0_p\)-norm. Taking s sufficiently large, we may achieve that the sum of the first, the third and the fourth summand is \(\le \frac{1}{2} (\Vert (u'\otimes u )\oplus (u'\otimes v)\Vert )\). From the boundedness of \(\tilde{B}(s\lambda )\), \(R_s\) and \(S_s\) for this fixed value of s, we conclude that, with norms taken in \(L_{p}\left( {\mathbb {R}}_{+}\right) ^{n_{1}}\oplus {\mathbb {C}}^{n_{2}}\) and \(L_{p}\left( {\mathbb {R}}_{+}\right) ^{n_{3}}\oplus {\mathbb {C}}^{n_{4}}\),
In case \(\lambda =0\), we obtain the same conclusion using the compactness of \(\tilde{K}\left( 0\right) \).
Hence the operator from Eq. (2.31) is injective and has closed range. As the same can be said of the adjoint, we conclude from Lemma 23 that the principal boundary symbol is an isomorphism. \(\square \)
2.2 The Spectral Invariance of the Parameter-Dependent Boutet de Monvel Algebra
Theorem 29
Let \(A\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \) be a parameter-dependent operator. Suppose that, for each \(\lambda \in \Lambda \), the operator
is invertible. If there are constants \(C>0\) and \(M\in {\mathbb {N}}_{0}\) such that
then \(A\left( \lambda \right) ^{-1}\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( M,\Lambda \right) \).
Proof
By Theorem 24A is parameter-elliptic. Hence we find a parametrix \(B\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( M,\Lambda \right) \) and \(K_{1}\in {\mathcal {B}}_{E_{1},F_{1},E_{1},F_{1}}^{-\infty ,0}\left( M,\Lambda \right) \) and \(K_{2}\in {\mathcal {B}}_{E_{0},F_{0},E_{0},F_{0}}^{-\infty ,0}\left( M,\Lambda \right) \) such that \(AB=I+K_{1}\) and \(BA=I+K_{2}\). We conclude that
As \(K_{2}B\in {\mathcal {B}}_{E_{1},F_{1},E_{0},F_{0}}^{-\infty ,0}\left( M,\Lambda \right) \), \(A\left( \lambda \right) ^{-1}\) grows at most as \(\left\langle \ln \left( \lambda \right) \right\rangle ^{M}\) in \(\lambda \) and \(K_{j}\left( \lambda \right) \), \(j=1,2\), are integral operators with smooth kernels whose derivatives decay rapidly with respect to \(\lambda \), we see that \(K_{2}A^{-1}K_{1}\in {\mathcal {B}}_{E_{1},F_{1},E_{0},F_{0}}^{-\infty ,0}\left( M,\Lambda \right) \) and \(A^{-1}\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( M,\Lambda \right) \). \(\square \)
The above theorem establishes spectral invariance for the \(\tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( M,\Lambda \right) \) calculus. When \(\Lambda =\emptyset \), that is, the algebra is independent of parameters, we can use order reducing operators and argue as in the proof of Corollary 50, to prove spectral invariance of the Boutet de Monvel calculus of integer order in the \(L_{p}\)-setting.
In [10, Theorem 1.12] Grubb proved that the inverse of elliptic elements of Boutet de Monvel algebra belongs again to the algebra. This was done for a larger algebra that allows the treatment on some non-compact manifolds. For the class of operators defined here, our result is stronger, as it does not assume ellipticity.
3 Boundary Value Problems on Manifolds with Conical Singularities
In this section, we provide the definitions and results concerning manifolds with boundary and conical singularities that we shall need. Details can be found in [30, 31].
Definition 30
A compact manifold with boundary and conical singularities of dimension n is a triple \(\left( D,\Sigma ,{\mathcal {F}}\right) \) formed by:
-
(1)
A compact Hausdorff topological space D.
-
(2)
A finite subset \(\Sigma \subset D\), which we call conical points, such that \(D\backslash \Sigma \) is an n-dimensional smooth manifold with boundary.
-
(3)
A set of functions \({\mathcal {F}}_{\sigma }=\left\{ \varphi :U_{\sigma }\rightarrow X_{\sigma }\times \left[ \right. 0,1\left[ \right. /X_{\sigma }\times \left\{ 0\right\} ,\,\sigma \in \Sigma \right\} \) such that:
-
(i)
The sets \(U_{\sigma }\subset D\) are open and disjoint sets. Moreover, each \(U_{\sigma }\) is a neighborhood of \(\sigma \in \Sigma \).
-
(ii)
\(X_{\sigma }\) is a compact smooth manifold with boundary for each \(\sigma \in \Sigma \).
-
(iii)
The function \(\varphi _{\sigma }:U_{\sigma }\rightarrow X_{\sigma }\times \left[ \right. 0,1\left[ \right. /X_{\sigma }\times \left\{ 0\right\} \) is a homeomorphism, \(\varphi _{\sigma }(\sigma )=X_{\sigma }\times \left\{ 0\right\} /X_{\sigma }\times \left\{ 0\right\} \) and \(\varphi _{\sigma }:U_{\sigma }\backslash \left\{ \sigma \right\} \rightarrow X_{\sigma }\times \left. \right] 0,1\left[ \right. \) is a diffeomorphism.
-
(i)
Remark 31
For each \(\sigma \in \Sigma \), we could use a different function \(\tilde{\varphi }_{\sigma }:U_{\sigma }\rightarrow X_{\sigma }\times \left[ \right. 0,1\left[ \right. /X_{\sigma }\times \left\{ 0\right\} \) with the same properties as in item iii), as long as, for each \(\sigma \),
extends to a diffeomorphism \(\tilde{\varphi }_{\sigma }\circ \varphi _{\sigma }^{-1}:X_{\sigma }\times \left. \right] -1,1\left[ \right. \rightarrow X_{\sigma }\times \left. \right] -1,1\left[ \right. \). These are the changes of variables that we allow to do near the singularities.
For the analysis of the typical (pseudo-) differential boundary value problems on these manifolds, we introduce the Fuchs type boundary value problems on a manifold with corners \({\mathbb {D}}\). It is obtained by gluing the sets \(X_{\sigma }\times \left[ \right. 0,1\left[ \right. \) in place of \(U_{\sigma }\), using the functions \(\varphi _{\sigma }\). In this way, the singularities are identified with the sets \(X_{\sigma }\times \left\{ 0\right\} \). The above remark ensures that the use of different functions \(\tilde{\varphi }_{\sigma }\) instead of \(\varphi _{\sigma }\) leads to diffeomorphic manifolds with corners. In order to avoid unnecessary complications with the notation, we shall consider manifolds with just one point singularity. A neighborhood of the conical point will always be identified with \(X\times \left[ \right. 0,1\left[ \right. /X\times \left\{ 0\right\} \) and a neighborhood of the corner will always be identified with \(X\times \left[ \right. 0,1\left[ \right. \), where X is a compact manifold with boundary. For a finite number of singularities the definitions and arguments are analogous.
We will denote by \(\text {int}\left( {\mathbb {D}}\right) \) the manifold with boundary \({\mathbb {D}}\backslash \left( X\times \left\{ 0\right\} \right) \). By \(\text {int}\left( \mathbb {B}\right) \), we denote the boundary of \(\text {int}\left( {\mathbb {D}}\right) \). In a neighborhood of the singularity, it can be identified with \(\partial X\times \left. \right] 0,1\left[ \right. \). Finally \(\mathbb {B}\) is the manifold with boundary given by \(\text {int}\left( \mathbb {B}\right) \cup \left( \partial X\times \left\{ 0\right\} \right) \). In particular, in a neighborhood of the singularity, it can be identified with \(\partial X\times \left[ \right. 0,1\left[ \right. \). We will also use \(2{\mathbb {D}}\) to denote a manifold with boundary in which \({\mathbb {D}}\) is embedded. The boundary of \(2{\mathbb {D}}\) is \(2\mathbb {B}\), a manifold without boundary.
We divide our presentation into two parts. First we define the classes of functions and distributions and then the operators. The operators acting on a neighborhood of the singularity will be defined as operators on \(X\times \left. \right] 0,1\left[ \right. \). We denote by \(E_{0}\) and \(E_{1}\) two vector bundles over \({\mathbb {D}}\) and by \(F_{0}\) and \(F_{1}\) two vector bundles over \(\mathbb {B}\). Let \(\pi _{X}:X\times \left[ \right. 0,1\left[ \right. \rightarrow X\) be the projection operator, then there are vector bundles \(E_{0}'\) and \(E_{1}'\) over X such that \(E_{0}\) and \(E_{1}\) can be identified with \(\pi _{X}^{*}\left( E_{0}'\right) \) and \(\pi _{X}^{*}\left( E_{1}'\right) \), respectively. Similarly, if \(\pi _{\partial X}:\partial X\times \left[ \right. 0,1\left[ \right. \rightarrow \partial X\) is the projection operator, then there are vector bundles \(F_{0}'\) and \(F_{1}'\) over \(\partial X\) such that \(F_{0}\) and \(F_{1}\) can be identified with \(\pi _{\partial X}^{*}\left( F_{0}'\right) \) and \(\pi _{\partial X}^{*}\left( F_{1}'\right) \), respectively. \(E_{0}\) will denote \(E_{0}\) and \(E_{0}'\) and the same will be done for \(E_{1}\), \(F_{0}\) and \(F_{1}\). We also denote by \(2E_{0}\), \(2F_{0}\), ...the vector bundles over \(2{\mathbb {D}}\) and \(2\mathbb {B}\), whose restriction to \({\mathbb {D}}\) and \(\mathbb {B}\) are \(E_{0}\) and \(F_{0}\).
Finally, a cut-off function \(\omega \in C_{c}^{\infty }\left( \overline{{\mathbb {R}}_{+}}\right) \) is a smooth nonnegative function that is equal to 1 in a neighborhood of 0 and equal to 0, outside \(\left[ 0,1\right] \).
3.1 Classes of Functions and Distributions
In the following sections, X is a manifold endowed with a Riemannian metric and with boundary \(\partial X\). All vector bundles are assumed to be hermitian. We use the notation \(X^{\wedge }:={\mathbb {R}}_{+}\times X\) and \(\partial X^{\wedge }:={\mathbb {R}}_{+}\times \partial X\) and we will denote by \(E, E_{0}\) and \(E_{1}\) vector bundles over X or \({\mathbb {D}}\) and by \(F, F_{0}\) and \(F_{1}\) vector bundles over \(\partial X\) or \({\mathbb {B}}\). The vector bundles \(E, E_{0}, E_{1}, F, F_{0}\) and \(F_{1}\) will also refer to the pullback bundles in \(X\times {\mathbb {R}}, X^{\wedge }, \partial X\times {\mathbb {R}}\) and \(\partial X^{\wedge }\). Finally we denote by \(C^{\infty }(X,E,F)\) the set \(C^{\infty }\left( X,E\right) \oplus C^{\infty }\left( \partial X,F\right) \).
Definition 32
Let W be a Fréchet space and \(\gamma \in {\mathbb {R}}\). We define the Fréchet space \({\mathcal {T}}_{\gamma }\left( {\mathbb {R}}_{+},W\right) \) as the space of all functions \(\varphi \in C^{\infty }\left( {\mathbb {R}}_{+},W\right) \) that satisfy
for all \(k.\,l\in {\mathbb {N}}_{0}\) and for all continuous seminorms p of W. We write \({\mathcal {T}}_{\gamma }\left( {\mathbb {R}}_{+}\right) \) when \(W={\mathbb {C}}\).
Definition 33
Let \(\omega \in C^{\infty }\left( \left[ \right. 0,1\left[ \right. \right) \) be a cut-off function. The space of functions \(C_{\gamma }^{\infty }\left( {\mathbb {D}}\right) \), \(\gamma \in {\mathbb {R}}\), consists of all functions \(u\in C^{\infty }\left( \text {int}\left( {\mathbb {D}}\right) \right) \) such that \(\omega u\in {\mathcal {T}}_{\gamma -\frac{n}{2}}\left( X^{\wedge }\right) \). Similarly, \(C_{\gamma }^{\infty }\left( \mathbb {B}\right) \) are all the functions \(u\in C^{\infty }\left( \text {int}\left( \mathbb {B}\right) \right) \) such that \(\omega u\in {\mathcal {T}}_{\gamma -\frac{n-1}{2}}\left( \partial X^{\wedge }\right) \).
Definition 34
Let \(X=\cup _{j=1}^{M}U_{j}\) be a cover of X consisting of trivializing sets and \(\varphi _{j}:U_{j}\subset X\rightarrow V_{j}\subset \overline{{\mathbb {R}}_{+}^{n}}\) be coordinate charts and \(\left( \psi _{j}\right) _{j=1}^{M}\) be a partition of unity subordinate to \(U_{j}\), \(j=1,\ldots ,M\). The space \(H_{p}^{s}\left( X\times {\mathbb {R}},E\right) \) is defined as the set of distributions \({\mathcal {D}}'\left( {\mathbb {R}}\times X,E\right) \) such that \(\left( t,x\right) \in {\mathbb {R}}\times {\mathbb {R}}_{+}^{n}\mapsto \left( \psi _{j}u\right) \left( t,\varphi _{j}^{-1}\left( x\right) \right) \) belong to \(H_{p}^{s}\left( {\mathbb {R}}\times {\mathbb {R}}_{+}^{n},{\mathbb {C}}^{N}\right) \), where N is the dimension of E, with norm given by:
The space \({\mathcal {H}}_{p}^{s,\gamma }\left( X^{\wedge },E\right) \) is the space of all distributions \(u\in \mathcal {D}'\left( X^{\wedge },E\right) \) such that \(u\left( t,x\right) =t^{-\frac{n+1}{2}+\gamma }v\left( \ln \left( t\right) ,x\right) \), where \(v\in H_{p}^{s}\left( X\times {\mathbb {R}},E\right) \). Its norm is given by \(\left\| u\right\| _{{\mathcal {H}}_{p}^{s,\gamma }\left( X^{\wedge },E\right) }:=\left\| v\right\| _{H_{p}^{s}\left( X\times {\mathbb {R}},E\right) }\).
Similarly, using the space \(B_{p}^{s}\left( {\mathbb {R}}^{n},{\mathbb {C}}^{N}\right) \) instead of \(H_{p}^{s}\left( {\mathbb {R}}\times {\mathbb {R}}_{+}^{n},{\mathbb {C}}^{N}\right) \), we define the space \(B_{p}^{s}\left( \partial X\times {\mathbb {R}},F\right) \), where N is the dimension of F. Associated to it is the space \({\mathcal {B}}_{p}^{s,\gamma }\left( \partial X^{\wedge },F\right) \) of all distributions \(u\in \mathcal {D}'\left( \partial X^{\wedge },F\right) \) such that \(u\left( t,x\right) =t^{-\frac{n}{2}+\gamma }v\left( \text {ln}\left( t\right) ,x\right) ,\) where \(v\in B_{p}^{s}\left( \partial X\times {\mathbb {R}},F\right) \). Its norm is given by \(\left\| u\right\| _{{\mathcal {B}}_{p}^{s,\gamma }\left( \partial X^{\wedge },F\right) }:=\left\| v\right\| _{B_{p}^{s}(\partial X\times {\mathbb {R}},F)}\!.\)
Remark 35
The above definition implies \(u\mapsto \left\| t\partial _{t}u\right\| _{L_{p}\left( X^{\wedge },E,dx\frac{dt}{t}\right) }+\left\| u\right\| _{L_{p}\left( {\mathbb {R}}_{+},H_{p}^{1}\left( X,E\right) ,\frac{dt}{t}\right) }\) is an equivalent norm for \({\mathcal {H}}_{p}^{1,\frac{n+1}{2}}\left( X^{\wedge },E\right) \).
Finally, we need Bessel and Besov spaces with asymptotics. First let us define asymptotic types.
Definition 36
We say that \(P=\left\{ \left( p_{j},m_{j},L_{j}\right) ;\,j\in \left\{ 1,\ldots ,M\right\} \right\} \) is an asymptotic type for \(C^{\infty }\left( X,E\right) \) with weight \(\left( \gamma ,k\right) \in {\mathbb {R}}\times {\mathbb {N}}_{0}\) if \(p_{j}\in {\mathbb {C}}\), \(\frac{n+1}{2}-\gamma -k<\text {Re}\left( p_{j}\right) <\frac{n+1}{2}-\gamma \), are distinct numbers, \(m_{j}\in {\mathbb {N}}_{0}\) and \(L_{j}\subset C^{\infty }\left( X,E\right) \) are finite dimensional spaces. The set of all asymptotic types is denoted by \(As\left( X,E,\gamma ,k\right) \). Similarly, we say that \(Q=\left\{ \left( p_{j},m_{j},L_{j}\right) ;\,j\in \left\{ 1,\ldots ,M\right\} \right\} \) is an asymptotic type for \(C^{\infty }\left( \partial X,F\right) \) with weight \(\left( \gamma ,k\right) \in {\mathbb {R}}\times {\mathbb {N}}_{0}\) and write \(Q\in As\left( \partial X,F,\gamma ,k\right) \), if \(p_{j}\in {\mathbb {C}}\), \(\frac{n}{2}-\gamma -k<\text {Re}\left( p_{j}\right) <\frac{n}{2}-\gamma \), are distinct numbers, \(m_{j}\in {\mathbb {N}}_{0}\) and \(L_{j}\subset C^{\infty }\left( \partial X,F\right) \) are finite dimensional spaces.
Definition 37
The Bessel potential and Besov space with asymptotics, respectively, are defined as follows:
-
(1)
Let \(P=\left\{ \left( p_{j},m_{j},L_{j}\right) ;\,j\in \left\{ 1,\ldots ,M\right\} \right\} \in As\left( X,E,\gamma ,k\right) \). We define
$$\begin{aligned}{\mathcal {H}}_{p,P}^{s,\gamma }\left( {\mathbb {D}},E\right) =\cap _{\epsilon >0}{\mathcal {H}}_{p}^{s,\gamma +k-\epsilon }\left( {\mathbb {D}},E\right) \oplus \mathcal {E}_{P}\left( X\right) ,\end{aligned}$$where \(\mathcal {E}_{P}:=\left\{ X^{\wedge }\ni \left( t,x\right) \mapsto \omega \left( t\right) \sum _{j=1}^{M}\sum _{k=0}^{m_{j}}t^{-p_{j}}\ln ^{k}\left( t\right) v_{jk}\left( x\right) ,\,v_{jk}\in L_{j}\right\} \).
-
(2)
Let \(\tilde{P}=\{ (\tilde{p}_{j},\tilde{m}_{j},\tilde{L}_{j});\,j\in \{ 1,\ldots ,M\} \} \in As \left( \partial X,F,\gamma ,k\right) \). We define
$$\begin{aligned}{\mathcal {B}}_{p,\tilde{P}}^{s,\gamma } \left( \mathbb {B},F\right) =\cap _{\epsilon >0}{\mathcal {B}}_{p}^{s,\gamma +k-\epsilon }\left( \mathbb {B},F\right) \oplus \mathcal {E}_{\tilde{P}}\left( \partial X\right) ,\end{aligned}$$where \(\mathcal {E}_{\tilde{P}} :=\big \{\partial X^{\wedge }\ni \left( t,x\right) \mapsto \omega \left( t\right) \sum _{j=1}^{M}\sum _{k=0}^{\tilde{m}_{j}}t^{-\tilde{p}_{j}}\ln ^{k}\left( t\right) v_{jk}\left( x\right) ,\,v_{jk}\in \tilde{L}_{j}\big \} \) and \(\omega \) is a cut-off function.
Remark 38
-
(1)
The scalar product of \(L_{2}\left( \partial X^{\wedge },F,dx\frac{dt}{t}\right) \) allows the identification \({\mathcal {B}}_{p}^{s,\frac{n}{2}}\left( \partial X^{\wedge },F\right) '\cong {\mathcal {B}}_{q}^{-s,\frac{n}{2}}\left( \partial X^{\wedge },F\right) \), \(\frac{1}{p}+\frac{1}{q}=1\). As \({\mathcal {B}}_{p}^{s,\gamma }\left( \partial X^{\wedge },F\right) =t^{\gamma -\frac{n}{2}}{\mathcal {B}}_{p}^{s,\frac{n}{2}}\left( \partial X^{\wedge },F\right) \) and \({\mathcal {B}}_{q}^{-s,-\gamma }\left( \partial X^{\wedge },F\right) =t^{-\gamma -\frac{n}{2}}{\mathcal {B}}_{q}^{-s,\frac{n}{2}}\left( \partial X^{\wedge },F\right) \), we conclude that \({\mathcal {B}}_{p}^{s,\gamma }\left( \partial X^{\wedge },F\right) '\cong {\mathcal {B}}_{q}^{-s,-\gamma }\left( \partial X^{\wedge },F\right) \), if we use the scalar product of \(L_{2}\left( \partial X^{\wedge },F,t^{n-1}dtdx\right) \).
-
(2)
In the same way, \({\mathcal {H}}_{p}^{s,\frac{n+1}{2}}\left( X^{\wedge },E\right) '\cong {\mathcal {H}}_{q}^{-s,\frac{n+1}{2}}\left( X^{\wedge },E\right) \), if we use the scalar product of \(L_{2}\left( X^{\wedge },E,dx\frac{dt}{t}\right) \), and \({\mathcal {H}}_{p}^{s,\gamma }\left( X^{\wedge },E\right) '\cong {\mathcal {H}}_{q}^{-s,-\gamma }\left( X^{\wedge },E\right) \), if we use that of \(L_{2}\left( X^{\wedge },E,t^{n}dtdx\right) \).
Definition 39
Let \(s,\gamma \in {\mathbb {R}}\) and \(1<p<\infty \).
-
(1)
We define \({\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}},E\right) \) as the space of all distributions \(u\in H_{p,\mathrm{loc}}^{s}\left( \text {int}\left( {\mathbb {D}}\right) ,E\right) \) such that, for any cut-off function \(\omega \), here considered as a function on \({\mathbb {D}}\), we have \(\omega u\in {\mathcal {H}}_{p}^{s,\gamma }\left( X^{\wedge },E\right) \). Its norm is given by
$$\begin{aligned} \left\| u\right\| _{{\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}},E\right) }:=\left\| \omega u\right\| _{{\mathcal {H}}_{p}^{s,\gamma }\left( X^{\wedge },E\right) }+\left\| \left( 1-\omega \right) u\right\| _{H_{p,\mathrm{loc}}^{s}\left( \text {int}\left( {\mathbb {D}}\right) ,E\right) }. \end{aligned}$$ -
(2)
Similarly, we obtain \({\mathcal {B}}_{p}^{s,\gamma }\left( \mathbb {B},F\right) \) from \({\mathcal {B}}_{p}^{s,\gamma }\left( \partial X^{\wedge },F\right) \) and \(B_{p,\mathrm{loc}}^{s}\left( \text {int}\left( \mathbb {B}\right) ,F\right) \).
3.2 Classes of Operators
We are going to use the natural identification
and write \(\Gamma _{\sigma }:=\left\{ z\in {\mathbb {C}};\,Re\left( z\right) =\sigma \right\} \). The latter set will be obviously identified with \({\mathbb {R}}\), when it is convenient to do so.
Definition 40
The weighted Mellin transform is the continuous linear operator \({\mathcal {M}}_{\gamma }:{\mathcal {T}}_{\gamma }\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E,F\right) \right) \rightarrow {\mathcal {S}}\left( \Gamma _{\frac{1}{2}-\gamma },C^{\infty }\left( X,E,F\right) \right) \) defined by
It is an invertible operator, whose inverse is given by
Definition 41
For \(m\in {\mathbb {Z}}\) and \(d\in {\mathbb {N}}_{0}\), \(M{\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X,{\mathbb {R}}_{+};\Gamma _{\gamma }\right) \) is the space of all functions \(h\in C^{\infty }\left( {\mathbb {R}}_{+},{\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X,\Gamma _{\gamma }\right) \right) \) that satisfy
for all continuous seminorms p of \({\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X,\Gamma _{\gamma }\right) \). In a similar way we define \(M\tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,{\mathbb {R}}_{+};\Gamma _{\gamma }\right) \).
To a function in \(M{\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X,{\mathbb {R}}_{+};\Gamma _{\gamma }\right) \) or \(M\tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,{\mathbb {R}}_{+};\Gamma _{\gamma }\right) \) we associate the Mellin operator
by
We also need to define the discrete Mellin asymptotic types:
Definition 42
A discrete Mellin asymptotic type of order \(d\in {\mathbb {N}}_{0}\) is a set
where \(p_{j}\in {\mathbb {C}}\) satisfy \(Re\left( p_{j}\right) \rightarrow \pm \,\infty \) as \(j\rightarrow \mp \,\infty \), \(m_{j}\in {\mathbb {N}}_{0}\) and \(L_{j}\) are finite-dimensional subspaces of operators of finite rank in \({\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{-\infty ,d}\left( X\right) \). The collection of all these asymptotic types is denoted by \(As\left( {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{-\infty ,d}\left( X\right) \right) \). Moreover, we let \(\pi _{{\mathbb {C}}}P:=\left\{ p_{j}:\,j\in {\mathbb {Z}}\right\} \subset {\mathbb {C}}\).
The asymptotic types are used to define the following meromorphic functions.
Definition 43
The space \(M_{P\,E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) \), \(P\in As\left( {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{-\infty ,d}\left( X\right) \right) \), is the space of all meromorphic functions \(a:{\mathbb {C}}\backslash \pi _{{\mathbb {C}}}P\rightarrow {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) \) such that:
-
(i)
For every \(p_{j}\in \pi _{{\mathbb {C}}}P\), there is a neighborhood of \(p_{j}\) where a can be written as
$$\begin{aligned} a\left( z\right) =\sum _{k=0}^{m_{j}}\nu _{jk}\left( z-p_{j}\right) ^{-k-1}+a_{0}\left( z\right) . \end{aligned}$$Above, \(a_{0}\) is a holomorphic function near \(p_{j}\), with values in \({\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) \) and \(\nu _{jk}\in L_{j}\), for \(k=0,\ldots ,m_{j}\).
-
(ii)
For every \(N\in {\mathbb {N}}_{0}\), the function \(\gamma \in \left[ -N,N\right] \mapsto a_{N}\left( \gamma +i\,\cdot \right) \in {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X,{\mathbb {R}}\right) \) is continuous, where
$$\begin{aligned} a_{N}\left( z\right) :=a\left( z\right) -\sum _{\left| Re\left( p_{j}\right) \right| \le N}\sum _{k=0}^{m_{j}}\nu _{jk}\left( z-p_{j}\right) ^{-k-1}. \end{aligned}$$
For \(P\in As\left( {\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{-\infty ,0}\left( X\right) \right) \), we can also define \(\tilde{M}_{P\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( X\right) \) replacing \({\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) \) by \(\tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X\right) \). When \(P=\emptyset \), we also use the notations \(M_{{\mathcal {O}}\,E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) \) and \(\tilde{M}_{{\mathcal {O}}\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( X\right) \).
The last operator that we need are the Green ones.
Definition 44
We define \(C_{G\,E_{0},F_{0},E_{1},F_{1}}^{d}\left( {\mathbb {D}};\gamma ,\gamma ',k\right) \) as the space of operators of the form
where, for each \(\mathcal {G}_{j}\), there exist asymptotic types \(P\in As\left( X,E_{1},\gamma ',k\right) \) and \(P'\in As\left( X,E_{0},-\gamma ,k\right) \), \(Q\in As\left( \partial X,F_{1},\gamma '-\frac{1}{2},k\right) \) and \(Q'\in As\left( \partial X,F_{0},-\gamma -\frac{1}{2},k\right) \), such that \(\mathcal {G}_{j}\) and its formal adjoint with respect to \({\mathcal {H}}_{2}^{0,0}\left( {\mathbb {D}},E_{j}\right) \oplus {\mathcal {B}}_{2}^{-\frac{1}{2},-\frac{1}{2}}\left( \mathbb {B},F_{j}\right) \), \(j=0,1\), define continuous operators:
for all \(r\in {\mathbb {R}}\), \(s>-1+\frac{1}{p}\) on the left hand side and \(s>-1+\frac{1}{q}\) on the right hand side. Near the boundary \({\mathbb {B}}\) of \({\mathbb {D}}\), the operators \(D^{j}\) coincide with \(\left( -i\partial _{\nu }\right) ^{j}\) where \(\partial _{\nu }\) is the normal derivative.
Similarly, \(\tilde{C}_{G\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}};k\right) \) denotes the space of all operators \(\mathcal {G}\) for which there exist asymptotic types \(P\in As\left( X,E_{1},\frac{n+1}{2},k\right) \), \(P'\in As\left( X,E_{0},\frac{n+1}{2},k\right) \), \(Q\in As\left( \partial X,F_{1},\frac{n}{2},k\right) \) and \(Q'\in As\left( \partial X,F_{0},\frac{n}{2},k\right) \), such that \(\mathcal {G}\) and its formal adjoint \(\mathcal {G}^{*}\) with respect to \({\mathcal {H}}_{2}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{j}\right) \oplus {\mathcal {B}}_{2}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{j}\right) \), \(j=0,1\), define continuous operators:
for all \(r\in {\mathbb {R}}\), \(s>-1+\frac{1}{p}\) on the left hand side and \(s>-1+\frac{1}{q}\) on the right hand side.
It is an immediate consequence of the embedding properties for cone Sobolev spaces that, for \(r\in {\mathbb {R}}\), \(s>d+1/p-1\) and arbitrary \(r',s'\in {\mathbb {R}}\), an operator
is compact. An analogous statement applies to operators in \(\tilde{C}_{G\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}};k\right) \).
Finally, we can define the cone algebra for boundary value problems.
Definition 45
For \(\gamma \in {\mathbb {R}}\), \(m\in {\mathbb {Z}}, d\in {\mathbb {N}}_{0}\) and \(k\in {\mathbb {N}}_{0}\) we define the space \(C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \) of all operators \(A:C_{\gamma }^{\infty }\left( {\mathbb {D}},E_{0}\right) \oplus C_{\gamma -\frac{1}{2}}^{\infty }\left( {\mathbb {B}},F_{0}\right) \rightarrow C_{\gamma -m}^{\infty }\left( {\mathbb {D}},E_{1}\right) \oplus C_{\gamma -m-\frac{1}{2}}^{\infty }\left( {\mathbb {B}},F_{1}\right) \) of the form
where \(\omega _{1},\,\ldots ,\,\omega _{4}\in C^{\infty }\left[ \right. 0,1\left[ \right. \) are cut-off functions. The operator \(A_{M}\) is a Mellin operator: \(A_{M}=t^{-m}op_{M}^{\gamma -\frac{n}{2}}\left( h\right) \), with \(h\in C^{\infty }(\overline{{\mathbb {R}}_{+}},M_{O\,E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( X\right) )\). The operator \(A_{\psi }\) is a Boutet de Monvel operator \(A_{\psi }\in {\mathcal {B}}_{2E_{0},2F_{0},2E_{1},2F_{1}}^{m,d}\left( 2{\mathbb {D}}\right) \). The operator M is a smoothing Mellin operator: \(M=\omega _{0}\left( \sum _{l=0}^{k-1}t^{-m+l}op_{M}^{\gamma _{l}-\frac{n}{2}}\left( h_{l}\right) \right) \omega _{1}\) with \(h_{l}\in M_{P_{l}\,E_{0},F_{0},E_{1},F_{1}}^{-\infty ,d}\left( X\right) \), \(\pi _{{\mathbb {C}}}P_{l}\cap \Gamma _{\frac{n+1}{2}-\gamma _{l}}=\emptyset \), and \(\gamma -l\le \gamma _{l}\le \gamma \). The operator G is a Green operator: \(G\in C_{G\,E_{0},F_{0},E_{1},F_{1}}^{d}\left( {\mathbb {D}};\gamma ,\gamma -m,k\right) \).
Similarly, the algebra \(\tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) is defined as the space of all continuous operators \(A:C_{\frac{n+1}{2}}^{\infty }\left( {\mathbb {D}},E_{0}\right) \oplus C_{\frac{n}{2}}^{\infty }\left( {\mathbb {B}},F_{0}\right) \rightarrow C_{\frac{n+1}{2}}^{\infty }\left( {\mathbb {D}},E_{1}\right) \oplus C_{\frac{n}{2}}^{\infty }\left( {\mathbb {B}},F_{1}\right) \) of the form (3.1), where \(A_{M}=op_{M}^{\frac{1}{2}}\left( h\right) \), with \(h\in C^{\infty }\left( \overline{{\mathbb {R}}_{+}},\tilde{M}_{O\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( X\right) \right) \), \(A_{\psi }\in \tilde{{\mathcal {B}}}_{2E_{0},2F_{0},2E_{1},2F_{1}}^{p}\left( 2{\mathbb {D}}\right) \), \(M=\omega _{0}\left( \sum _{l=0}^{k-1}t^{l}op_{M}^{\gamma _{l}-\frac{n}{2}}\left( h_{l}\right) \right) \omega _{1}\) with \(h_{l}\in M_{P_{l}\,E_{0},F_{0},E_{1},F_{1}}^{-\infty ,0}\left( X\right) \), \(\pi _{{\mathbb {C}}}P_{l}\cap \Gamma _{\frac{n+1}{2}-\gamma _{l}}=\emptyset \), and \(\frac{n+1}{2}-l\le \gamma _{l}\le \frac{n+1}{2}\), and \(G\in \tilde{C}_{G\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \).
Definition 46
(Ellipticity) Using the notation of Definition 45, we say that \(A\in C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \), \(d\le \max \{0,m\}\), is elliptic if:
-
(1)
Outside the singularity \(X\times \left\{ 0\right\} \), A is an elliptic Boutet de Monvel operator in \({\mathcal {B}}_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( \text {int}\left( {\mathbb {D}}\right) \right) \): Its interior symbol and boundary symbol are invertible at each point.
-
(2)
Its conormal symbol \(\sigma _{M}\left( A\right) \left( z\right) :=h\left( 0,z\right) +h_{0}\left( z\right) :H_{p}^{s}\left( X,E_{0}\right) \oplus B_{p}^{s-\frac{1}{p}}\left( X,F_{0}\right) \rightarrow H_{p}^{s-m}\left( X,E_{1}\right) \oplus B_{p}^{s-\frac{1}{p}-m}\left( X,F_{1}\right) \), \(s>d-1+\frac{1}{p}\), is invertible for each \(z\in \Gamma _{\frac{n+1}{2}-\gamma }\) and its inverse belongs to \(B_{E_{1},F_{1},E_{0},F_{0}}^{-m,d'}(X,\Gamma _{\frac{n+1}{2}-\gamma })\), \(d'=\max \{-m,0\}\).
Similarly, we say that \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) is an elliptic operator if, outside the singularity \(X\times \left\{ 0\right\} \), A is an elliptic operator in \(\tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( \text {int}\left( {\mathbb {D}}\right) \right) \) and its conormal symbol \(\sigma _{M}\left( A\right) \left( z\right) :=h\left( 0,z\right) +h_{0}\left( z\right) :H_{p}^{s}\left( X,E_{0}\right) \oplus B_{p}^{s}\left( X,F_{0}\right) \rightarrow H_{p}^{s}\left( X,E_{1}\right) \oplus B_{p}^{s}\left( X,F_{1}\right) \) is invertible for each \(z\in \Gamma _{\frac{n+1}{2}}\), \(s>d-1+\frac{1}{p}\), and its inverse belongs to \(\tilde{B}_{E_{1},F_{1},E_{0},F_{0}}^{p}(X,\Gamma _{\frac{n+1}{2}})\).
Remark 47
Definition 46 follows [31]. Instead one might ask that
-
(1)
The principal pseudodifferential symbol \(\sigma _\psi (A)\) is invertible on \(T^*(\text {int}\,{\mathbb {D}})\setminus \{0\}\) and, in local coordinates \((t,x,\tau ,\xi )\) for the cotangent space in a collar neighborhood of the conical point, \(t^m \sigma _\psi (A)(t,x, \tau /t, \xi )\) is smoothly invertible up to \(t=0\).
-
(2)
The boundary principal symbol \(\sigma _\partial (A)\) is invertible on \(T^*(\text {int}\, {{\mathbb {B}}})\setminus \{0\}\) and, in local coordinates \((t,y, \tau , \eta ) \) for the cotangent space in a collar neighborhood of the conical point, \(t^m \sigma _\partial (A)(t,y, \tau /t, \eta )\) is smoothly invertible up to \(t=0\).
-
(3)
The conormal symbol is pointwise invertible.
See [14, Section 6.2.1] for details.
Proposition 48
The operators in \(C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \) and \(\tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) have the following properties:
-
(1)
If \(B\in C_{E_{0},F_{0},E_{1},F_{1}}^{m_{0},d_{0}}\left( {\mathbb {D}},\left( \gamma ,\gamma -m_{0},k\right) \right) \) and \(A\in C_{E_{1},F_{1},E_{2},F_{2}}^{m_{1},d_{1}}\left( {\mathbb {D}},\left( \gamma -m_{0},\gamma -m_{2},k\right) \right) \) then \(AB\in C_{E_{0},F_{0},E_{2},F_{2}}^{m_{2},d_{2}}\left( {\mathbb {D}},\left( \gamma ,\gamma -m_{2},k\right) \right) \), where \(m_{2}:=m_{0}+m_{1}\) and \(d_{2}:=\max \left\{ m_{0}+d_{1},d_{0}\right\} \). If \(B\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) and \(A\in \tilde{C}_{E_{1},F_{1},E_{2},F_{2}}^{p}\left( {\mathbb {D}},k\right) \), then \(AB\in \tilde{C}_{E_{0},F_{0},E_{2},F_{2}}^{p}\left( {\mathbb {D}},k\right) \).
-
(2)
If \(A\in C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \), then A extends to a continuous operator:
$$\begin{aligned} A:\begin{array}{c} {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}},E_{0}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s-\frac{1}{p},\gamma -\frac{1}{2}}\left( {\mathbb {B}},F_{0}\right) \end{array}\rightarrow \begin{array}{c} {\mathcal {H}}_{p}^{s-m,\gamma -m}\left( {\mathbb {D}},E_{1}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s-m-\frac{1}{p},\gamma -m-\frac{1}{2}}\left( {\mathbb {B}},F_{1}\right) \end{array},\,\,s>d-1+\frac{1}{p}. \end{aligned}$$If \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \), then A extends to a continuous operator:
$$\begin{aligned} A:\begin{array}{c} {\mathcal {H}}_{p}^{s,\frac{n+1}{2}}\left( {\mathbb {D}},E_{0}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s,\frac{n}{2}}\left( {\mathbb {B}},F_{0}\right) \end{array}\rightarrow \begin{array}{c} {\mathcal {H}}_{p}^{s,\frac{n+1}{2}}\left( {\mathbb {D}},E_{1}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s,\frac{n}{2}}\left( {\mathbb {B}},F_{1}\right) \end{array},\,\,s>-1+\frac{1}{p}. \end{aligned}$$ -
(3)
If \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \), then its formal adjoint with respect to the inner product in \({\mathcal {H}}_{2}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{j}\right) \oplus {\mathcal {B}}_{2}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{j}\right) \) belongs to \(\tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{q}\left( {\mathbb {D}},k\right) \), for \(\frac{1}{p}+\frac{1}{q}=1\). If A is elliptic, so is its adjoint.
-
(4)
If \(A\in C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \) is elliptic, \(d:=\max \left\{ m,0\right\} \), then there is an operator \(B\in C_{E_{1},F_{1},E_{0},F_{0}}^{-m,d'}\left( {\mathbb {D}},\left( \gamma -m,\gamma ,k\right) \right) \), \(d':=\max \left\{ -m,0\right\} \), such that
$$\begin{aligned}&BA-I\in C_{G\,E_{0},F_{0},E_{0},F_{0}}^{d}\left( {\mathbb {D}},\left( \gamma ,\gamma ,k\right) \right) ;\\&AB-I\in C_{G\,E_{1},F_{1},E_{1},F_{1}}^{d'}\left( {\mathbb {D}},\left( \gamma -m,\gamma -m,k\right) \right) . \end{aligned}$$Similarly, if \(\tilde{A}\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) is elliptic, then there is an operator \(\tilde{B}\in \tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \), such that
$$\begin{aligned} \tilde{B}\tilde{A}-I\in \tilde{C}_{G\,E_{0},F_{0},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \,\,\,\text {and}\,\,\,\tilde{A}\tilde{B}-I\in \tilde{C}_{G\,E_{1},F_{1},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) . \end{aligned}$$In particular, A and \(\tilde{A}\) are then Fredholm operators.
-
(5)
(Existence of order reducing operators) For \(m\in {\mathbb {Z}}\), \(m'\in {\mathbb {R}}\) and \(\gamma \in {\mathbb {R}}\), there are elliptic operators \(A\in C_{E_{0},E_{0}}^{m,0}\left( {\mathbb {D}},\left( \gamma ,\gamma -m,k\right) \right) \) and \(B\in C_{F_{0},F_{0}}^{m',0}\left( {\mathbb {B}},\left( \gamma -\frac{1}{2},\gamma -m'-\frac{1}{2},k\right) \right) \), such that \(A:{\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}},E_{0}\right) \rightarrow {\mathcal {H}}_{p}^{s-m,\gamma -m}\left( {\mathbb {D}},E_{0}\right) \) and \(B:{\mathcal {B}}_{p}^{s-\frac{1}{p},\gamma -\frac{1}{2}}\left( {\mathbb {B}},F_{0}\right) \rightarrow {\mathcal {B}}_{p}^{s-m'-\frac{1}{p},\gamma -m'-\frac{1}{2}}\left( {\mathbb {B}},F_{0}\right) \) are invertible for all \(s>-1+\frac{1}{p}\), see [14, Section 6.4].
3.3 The Equivalence Between the Fredholm Property and the Ellipticity
Theorem 49
Let \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \). Then the following conditions are equivalent:
-
(i)
A is elliptic.
-
(ii)
\(A:\begin{array}{c} {\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{0}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{0}\right) \end{array}\rightarrow \begin{array}{c} {\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{1}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{1}\right) \end{array}\) is Fredholm.
That (i) implies (ii) follows from the existence of a parametrix of an elliptic operator, as it is stated in item (4) of Proposition 48. It remains to prove that (ii) implies (i). If A is Fredholm, then condition (1) of Definition 46 holds by Theorem 24. In fact, the proof of Theorem 24 is local, so it applies in this context. In the next two subsections, we will show that condition (2) of Definition 46 holds. We rely on the arguments in [28, Section 3.1]; however, the Besov space estimates need more attention. Before, however, we note the following consequence.
Corollary 50
For \(A\in C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}({\mathbb {D}},\gamma , \gamma -m, k)\), \(m\in {\mathbb {Z}}\), \(d\le \max \{m,0\}\), \(p\in \, ]1,\infty [\), \(s\in {\mathbb {Z}}\), \(s\ge d\), the following are equivalent:
-
(i)
A is elliptic.
-
(ii)
$$\begin{aligned} A:\begin{array}{c} {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}},E_{0}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s-\frac{1}{p},\gamma -\frac{1}{2}}\left( {\mathbb {B}},F_{0}\right) \end{array}\rightarrow \begin{array}{c} {\mathcal {H}}_{p}^{s-m,\gamma -m}\left( {\mathbb {D}},E_{1}\right) \\ \oplus \\ {\mathcal {B}}_{p}^{s-m-\frac{1}{p},\gamma -m-\frac{1}{2}}\left( {\mathbb {B}},F_{1}\right) \end{array}\text { is Fredholm.} \end{aligned}$$(3.2)
In particular, the Fredholm property is independent of p and s, subject to the condition \(s\in {\mathbb {Z}}\), \(s\ge d\). The same is then true for the kernel and the index.
Proof
According to item (4) of Proposition 48, ellipticity implies the Fredholm property. In order to see the converse, we note that, by item 5 of Proposition 48, we find operators \(P^{-s}\in t^{-s}C_{E_0,E_0}^{-s,0}({\mathbb {D}},\frac{n+1}{2}, \frac{n+1}{2}+s,k)\) and \(Q^{s-m}\in t^{s-m} C^{s-m,0}_{E_1,E_1}({\mathbb {D}},\frac{n+1}{2}, \frac{n+1}{2}-s+m,k)\) defined on \({\mathbb {D}}, \tilde{P}^{-s+1/p}\in t^{-s+1/p} C^{-s+1/p}_{F_0,F_0}({{\mathbb {B}}},\frac{n}{2}, \frac{n}{2}+s-\frac{1}{p},k)\) and \(\tilde{Q}^{s-m+1/p}\in t^{s-m+1/p} C^{s-m+1/p}_{F_1,F_1}({{\mathbb {B}}},\frac{n}{2}, \frac{n}{2}-s+m-\frac{1}{p}, k)\), defined on \({\mathbb {B}}\), such that \(P^{-s}:{\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{0}\right) \rightarrow {\mathcal {H}}_{p}^{s,\frac{n+1}{2}}\left( {\mathbb {D}},E_{0}\right) \), \(\tilde{P}^{-s+\frac{1}{p}}:{\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{0}\right) \rightarrow {\mathcal {B}}_{p}^{s-\frac{1}{p},\frac{n}{2}}\left( {\mathbb {B}},F_{0}\right) \), \(Q^{s-m}:{\mathcal {H}}_{p}^{s-m,\frac{n+1}{2}}\left( {\mathbb {D}},E_{1}\right) \rightarrow {\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{1}\right) \), and \(\tilde{Q}^{s-m+\frac{1}{p}}:{\mathcal {B}}_{p}^{s-m-\frac{1}{p},\frac{n}{2}}\left( {\mathbb {B}},F_{1}\right) \rightarrow {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{1}\right) \) are invertible. Here we use that \(s\in {\mathbb {Z}}\). Since A is a Fredholm operator, the operator \(\tilde{A}\in \tilde{C}^p_{E_0,F_0,E_1,F_1}({\mathbb {D}},k)\), defined by
is a Fredholm operator in \({\mathcal {B}}({\mathcal {H}}_{p}^{0,\frac{n+1}{2}}({\mathbb {D}},E_{0})\oplus {\mathcal {B}}_{p}^{0,\frac{n}{2}}({\mathbb {B}},F_{0}), {\mathcal {H}}_{p}^{0,\frac{n+1}{2}}({\mathbb {D}},E_{1}) \oplus {\mathcal {B}}_{p}^{0,\frac{n}{2}}({\mathbb {B}},F_{1}))\). By Theorem 49, \(\tilde{A}\) is elliptic, hence so is A. As a consequence, the Fredholm property is independent of p and s.
Suppose A is elliptic and \(u\in {\mathcal {H}}_{p}^{s,\gamma }({\mathbb {D}},E_{0})\oplus {\mathcal {B}}_{p}^{s-\frac{1}{p},\gamma -\frac{1}{2}}({\mathbb {B}},F_{0})\) belongs to the kernel of A. Then the existence of a parametrix and the mapping properties of the Green operators imply that, for some \(\epsilon >0\) and all \(t\in {\mathbb {R}}\), \(u\in {\mathcal {H}}_{p}^{t,\gamma +\epsilon }({\mathbb {D}},E_{0})\oplus {\mathcal {B}}_{p}^{t-\frac{1}{p},\gamma +\epsilon -\frac{1}{2}}({\mathbb {B}},F_{0})\). Thus u also is an element of \( {\mathcal {H}}_{q}^{t,\gamma }({\mathbb {D}},E_{0})\oplus {\mathcal {B}}_{q}^{t-\frac{1}{p},\gamma -\frac{1}{2}}({\mathbb {B}},F_{0})\) for \(1<q<\infty \) and \(t\in {\mathbb {R}}\) and belongs to the kernel of A on that space. This shows the independence of the kernel on s and p.
We next consider the formal adjoint \({\tilde{A}}'\) of \(\tilde{A}\) in the sense of item 3) of Proposition 48, which is an elliptic element of \(\tilde{C}^q_{E_1,F_1,E_0,F_0}({\mathbb {D}},k)\), where \(1/p+1/q=1\). Its extension to an operator in \({\mathcal {B}}({\mathcal {H}}_{q}^{0,\frac{n+1}{2}}({\mathbb {D}},E_{1})\oplus {\mathcal {B}}_{q}^{0,\frac{n}{2}}({\mathbb {B}},F_{1}), {\mathcal {H}}_{q}^{0,\frac{n+1}{2}}({\mathbb {D}},E_{0}) \oplus {\mathcal {B}}_{q}^{0,\frac{n}{2}}({\mathbb {B}},F_{0}))\) furnishes the adjoint to the operator \(\tilde{A}\) acting as in (3.3). The index of \(\tilde{A}\) then is the difference of the kernel dimensions of \(\tilde{A}\) and \({\tilde{A}}'\). By the same argument as above, these are independent of p and q. Hence the index of \(\tilde{A}\) is independent of p and the index of A is independent of s and p. \(\square \)
3.4 Besov-Space Preliminaries
Given dyadic partitions of unity \(\left\{ \varphi _{j}\right\} _{j\in {\mathbb {N}}_{0}}\subset C_{c}^{\infty }({\mathbb {R}})\) and \(\left\{ \tilde{\varphi }_{j}\right\} _{j\in {\mathbb {N}}_{0}}\subset C_{c}^{\infty }({\mathbb {R}}^{n-1})\) of \({\mathbb {R}}\) and \({\mathbb {R}}^{n-1}\), respectively, we define a dyadic partition of unity \(\left\{ \psi _{j}\right\} _{j\in {\mathbb {N}}_{0}}\subset C_{c}^{\infty }({\mathbb {R}}^{n})\) of \({\mathbb {R}}^{n}\) by
Then \(\text {supp}\left( \psi _{0}\right) \subset \left\{ \left( t,x\right) \in {\mathbb {R}}^{n};\left\| \left( t,x\right) \right\| _{N}<2\right\} \) and \(\text {supp}\left( \psi _{j}\right) \subset \{ \left( t,x\right) \in {\mathbb {R}}^{n};\)\(2^{j-1}<\left\| \left( t,x\right) \right\| _{N}<2^{j+1}\}\), for \(j\ge 1\). Here \(\left\| \left( t,x\right) \right\| _{N}\) denotes the norm
where \(\left| x\right| \) denotes the Euclidean norm of \(x\in {\mathbb {R}}^{n-1}\) and \(\left| t\right| \) denotes the modulus of \(t\in {\mathbb {R}}\).
Item 8 of Remark 14 implies that we can choose the following norm for \(B_{p}^{s}\left( {\mathbb {R}}^{n}\right) \):
The next spaces are very useful for computations.
Definition 51
Let G be a Banach space that is a UMD Banach space with the property \(\left( \alpha \right) \). We define \({\mathcal {B}}_{p}^{s,\frac{1}{2}}\left( {\mathbb {R}}_{+},G\right) \) as the space of all \(u\in {\mathcal {D}}'\left( {\mathbb {R}}_{+},G\right) \) such that \(\left( {\mathbb {R}}\ni t\mapsto u\left( e^{-t}\right) \right) \in B_{p}^{s}\left( {\mathbb {R}},G\right) \) and \({\mathcal {H}}_{p}^{s,\frac{1}{2}}\left( {\mathbb {R}}_{+},G\right) \) as the set of all \(u\in {\mathcal {D}}'\left( {\mathbb {R}}_{+},G\right) \) such that \(\left( {\mathbb {R}}\ni t\mapsto u\left( e^{-t}\right) \right) \in H_{p}^{s}\left( {\mathbb {R}},G\right) \). In particular, \({\mathcal {H}}_{p}^{0,\frac{1}{2}}\left( {\mathbb {R}}_{+},G\right) =L_{p}\left( {\mathbb {R}}_{+},G,\frac{dt}{t}\right) \) and \({\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},G\right) =\left\{ u\in L_{p}\left( {\mathbb {R}}_{+},G,\frac{dt}{t}\right) ;\,t\partial _{t}u\in L_{p}\left( {\mathbb {R}}_{+},G,\frac{dt}{t}\right) \right\} \).
Proposition 52
There is a constant \(C>0\) such that
for all \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( \partial X,F\right) \right) \).
Proof
In order to prove the proposition, we fix a constant \(\theta \in \left. \right] 0,1\left[ \right. \) and a constant \(C_{\theta }>1\) such that \(j+1\le C_{\theta }2^{\theta j}\), for all \(j\in {\mathbb {N}}_{0}\). The Hölder inequality implies that, for every non-negative real numbers \(a_{0}, \ldots , a_{j}\), we have
Now, let us first prove that \(\left\| u\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }\le C\left\| u\right\| _{H_{p}^{1}\left( {\mathbb {R}},B_{p}^{0}\left( {\mathbb {R}}^{n-1}\right) \right) }\):
Choosing \(\theta <1\), we conclude that
Using a change of variable \(t\mapsto e^{-t}\), we obtain that
where \({\mathcal {B}}_{p}^{0,\gamma }({\mathbb {R}}_{+}^{n})=\left\{ v\left( \ln \left( t\right) ,x\right) ;\,v\in B_{p}^{0}\left( {\mathbb {R}}^{n}\right) \right\} \). Finally, using partition of unity and localization, we obtain the assertion. \(\square \)
For the following proposition we write \({\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) :={\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( X^{\wedge },E_{j}\right) \oplus {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( \partial X^{\wedge },F_{j}\right) \) and \({\mathcal {HB}}_{pE_{j},F_{j}}\left( {\mathbb {D}}\right) :={\mathcal {H}}_{p}^{0,\frac{n+1}{2}}\left( {\mathbb {D}},E_{j}\right) \oplus {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {B}},F_{j}\right) \), for \(j=0,1\). We denote by \(K_{j}\), \(j\in {\mathbb {N}}_{0}\), the sets introduced in Remark 12 for \(n=1\).
Proposition 53
There exists a constant C, independent of m, such that for all \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+}\right) \) and all \(v\in C^{\infty }\left( X,E,F\right) \) with \(supp(\tau \mapsto ({\mathcal {M}}_{\frac{1}{2}}u)(i\tau ))\subset K_{m}\)
In order to make the proof more transparent, we first prove the following lemma.
Lemma 54
There exists a constant \(C>0\), independent of m, such that for \(u\in {\mathcal {S}}\left( {\mathbb {R}}\right) \) and \(v\in {\mathcal {S}}({\mathbb {R}}^{n-1})\) with \(\text {supp}\left( {\mathcal {F}}u\right) \subset K_{m}\).
Proof
Let \(\left( t,x\right) \in {\mathbb {R}}\times {\mathbb {R}}^{n-1}\) and \(C>0\) such that \(\left\| \varphi _{k}\left( D_{t}\right) u\right\| _{L_{p}\left( {\mathbb {R}}\right) }\le C\left\| u\right\| _{L_{p}\left( {\mathbb {R}}\right) }\) and \(\left\| \tilde{\varphi }_{k}\left( D_{x}\right) u\right\| _{L_{p}\left( {\mathbb {R}}^{n-1}\right) }\le C\left\| u\right\| _{L_{p}\left( {\mathbb {R}}^{n-1}\right) }\) for all \(k\in {\mathbb {N}}_{0}\) and for all Schwartz functions u. This constant exists, as we have seen in the proof of Lemma 21. In particular, \(\left\| \varphi _{k}\left( D_{t}\right) \tilde{\varphi }_{j}\left( D_{x}\right) \left( u\right) \right\| _{L_{p}\left( {\mathbb {R}}\times {\mathbb {R}}^{n-1}\right) }\le C^{2}\left\| u\right\| _{L_{p}\left( {\mathbb {R}}\times {\mathbb {R}}^{n-1}\right) }\), for all \(k,j\in {\mathbb {N}}_{0}\) and \(u\in {\mathcal {S}}({\mathbb {R}}\times {\mathbb {R}}^{n-1})\).
Using the conventions \(\varphi _{k}=0\), \(\tilde{\varphi }_{k}=0\), \(\psi _{k}=0\) and \(K_{k}=\emptyset \), whenever \(k\le -1\), we see that
On the other hand, with \(\Vert \cdot \Vert \) denoting the norm in \(L_p({\mathbb {R}}^n)\),
We have used in (1) that \(\text {supp}\left( {\mathcal {F}}u\right) \subset K_{m}\) and, therefore, we have
We have used in (2) that for \(j\in \left\{ 0,\ldots ,m+1\right\} \) and \(k\in \left\{ m-1,\ldots ,m+1\right\} \)
\(\square \)
Proof
(of Proposition 53) Let \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+}\right) \), \(v\in {\mathcal {S}}\left( {\mathbb {R}}^{n-1}\right) \) and suppose that \(\text {supp}\big (\tau \mapsto {\mathcal {M}}_{\frac{1}{2}}u\left( i\tau \right) \big )\subset K_{m}, m\in {\mathbb {N}}_0\). Define \(\tilde{u}\in {\mathcal {S}}\left( {\mathbb {R}}\right) \) by \(\tilde{u}\left( t\right) =u\left( e^{-t}\right) \). Hence \({\mathcal {F}}_{t\rightarrow \xi }\tilde{u}\left( \xi \right) ={\mathcal {F}}_{t\rightarrow \xi }\left( u\left( e^{-t}\right) \right) \left( \xi \right) ={\mathcal {M}}_{\frac{1}{2}}u\left( i\xi \right) \). Therefore, there is a constant \(m\in {\mathbb {N}}_{0}\) such that \(\text {supp}\left( {\mathcal {F}}\tilde{u}\right) \subset K_{m}\). Hence, Lemma 54 implies that
As \(\left\| \tilde{u}\otimes v\right\| _{B_{p}^{0}\left( {\mathbb {R}}^{n}\right) }=\left\| u\otimes v\right\| _{{\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {R}}^{n}_+\right) }\), we conclude that
The general result follows using a partition of unity. \(\square \)
3.5 Proof of the Invertibility of the Conormal Symbol
We notice that \({\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{j},F_{j}\right) \right) \) is a dense space of \({\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \).
Definition 55
Let W be a Fréchet space, \(\epsilon >0\), \(\tau _{0}\in {\mathbb {R}}\). We define \(T_{\epsilon }:{\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \rightarrow {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \) and \(R_{\epsilon ,\tau _{0}}:{\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \rightarrow {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \) by \(T_{\epsilon }u(t)=u\left( \frac{t}{\epsilon }\right) \) and \(R_{\epsilon ,\tau _{0}}u(t)=\epsilon ^{\frac{1}{p}}t^{-i\tau _{0}}u\left( t^{\epsilon }\right) \).
The above operators are invertible: \(T_{\epsilon }^{-1}=T_{\frac{1}{\epsilon }}\) and \(R_{\epsilon ,\tau _{0}}^{-1}=R_{\frac{1}{\epsilon },-\frac{\tau _{0}}{\epsilon }}\). The next proposition is analogous to Lemma 19.
Proposition 56
For an UMD Banach space W with the property (\(\alpha \)), the operators \(T_{\epsilon },R_{\epsilon ,\tau _{0}}:{\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \rightarrow {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \) have the following properties:
-
(1)
\(T_{\epsilon }\) extends to an isometry
$$\begin{aligned} T_{\epsilon }:{\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \rightarrow {\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) . \end{aligned}$$If \(W=C^{\infty }\left( X,E_{j},F_{j}\right) \), \(j=0,1\), then the operator \(T_{\epsilon }\) extends to an isometry \(T_{\epsilon }:{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \rightarrow {\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \).
-
(2)
For all \(\varepsilon >0\), \(R_{\epsilon ,\tau _{0}}\) extends to a bijective continuous map
$$\begin{aligned} R_{\epsilon ,\tau _{0}}:{\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) \rightarrow {\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) . \end{aligned}$$There exists a \(C\ge 0\) with \(\left\| R_{\epsilon ,\tau _{0}}\right\| _{{\mathcal {B}}({\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) )}\le C\left( 1+\left| \tau _{0}\right| \right) \), \(\epsilon <1\).
-
(3)
-
(i)
Let \(h\in M\tilde{B}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,{\mathbb {R}}_{+};\Gamma _{0}\right) \cap C\left( \overline{{\mathbb {R}}_{+}},\mathcal {\tilde{B}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,\Gamma _{0}\right) \right) \) and \(h_{0}(z):=h(0,z)\). For any \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) \) we then have
$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left\| op_{M}^{\frac{1}{2}}\left( h\right) T_{\epsilon }u-T_{\epsilon }op_{M}^{\frac{1}{2}}\left( h_{0}\right) u\right\| _{{\mathcal {HB}}_{pE_{1},F_{1}}\left( X^{\wedge }\right) }=0. \end{aligned}$$ -
(ii)
Let \(h\in \tilde{B}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,\Gamma _{0}\right) \) and \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) \). Then
$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\left\| op_{M}^{\frac{1}{2}}\left( h\right) R_{\epsilon ,\tau _{0}}u-R_{\epsilon ,\tau _{0}}h\left( i\tau _{0}\right) u\right\| _{{\mathcal {HB}}_{pE_{1},F_{1}}\left( X^{\wedge }\right) }=0. \end{aligned}$$
-
(i)
Proof
(1) Since \(\left\| T_{\epsilon }u\right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }=\left\| u\right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }\) and \(\left\| \left( t\partial _{t}\right) \left( T_{\epsilon }u\right) \right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }=\left\| t\partial _{t}u\right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }\), we conclude that \(\left\| T_{\epsilon }u\right\| _{{\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) }=\left\| u\right\| _{{\mathcal {H}}_{p}^{1,\frac{1}{2}}\left( {\mathbb {R}}_{+},W\right) }\).
In order to show that \(T_{\epsilon }:{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \rightarrow {\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \) is an isometry, it remains to prove that \(T_{\epsilon }:{\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( \partial X^{\wedge },F_{j}\right) \rightarrow {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( \partial X^{\wedge },F_{j}\right) \) is an isometry. This follows with a partition of unity and the fact that \(T_{\epsilon }:{\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {R}}_{+}^{n}\right) \rightarrow {\mathcal {B}}_{p}^{0,\frac{n}{2}}\left( {\mathbb {R}}_{+}^{n}\right) \) given by \(T_{\epsilon }u\left( t,x\right) =u\left( \frac{t}{\epsilon },x\right) \) is an isometry. In fact, if \(v\left( s,x\right) =u\left( e^{-s},x\right) \), then \(\left( T_{\epsilon }u\right) \left( e^{-s},x\right) =v\left( s+\ln \left( \epsilon \right) ,x\right) \). Hence
(2) It is easy to see that \(\left\| R_{\epsilon ,\tau _{0}}u\right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }=\left\| u\right\| _{L_{p}\left( {\mathbb {R}}_{+},W,\frac{dt}{t}\right) }.\) As \(t\partial _{t}\left( R_{\epsilon ,\tau _{0}}u\right) =\left( -i\tau _{0}\right) R_{\epsilon ,\tau _{0}}u+\epsilon R_{\epsilon ,\tau _{0}}\left( t\partial _{t}u\right) \), we conclude that
(3.i) We first show \(\mathbf {L}_p\)-convergence: For \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) ,\)
The proof here is exactly the same as the proof of [28, Lemma 3.9]. It relies on the fact that \( T_{\epsilon }^{-1}op_{M}^{\frac{1}{2}}\left( h\right) T_{\epsilon }=op_{M}^{\frac{1}{2}}\left( h_{\epsilon }\right) , \) where \(h_{\epsilon }\left( t,z\right) =h\left( \epsilon t,z\right) \), and on Lebesgue’s dominated convergence theorem.
Next we establish the \(\mathbf {L_p}\)-convergence of the derivative:
This follows almost immediately from the fact that
Using (3.5), the fact that \(T_{\epsilon }\) are isometries and Proposition 52, we conclude that, as \(\epsilon \rightarrow 0\),
(3.ii) It is straightforward to check that \(R_{\epsilon ,\tau _{0}}^{-1}op_{M}^{\frac{1}{2}}\left( h\right) R_{\epsilon ,\tau _{0}}=op_{M}^{\frac{1}{2}}\left( h_{\epsilon }\right) \), where \(h_{\epsilon }\left( z\right) =h\left( \epsilon z+i\tau _{0}\right) \). Repeating the previous arguments, we conclude that
Moreover, \(\left( -t\partial _{t}\right) op_{M}^{\frac{1}{2}}\left( h\left( \epsilon z+i\tau _{0}\right) \right) u=op_{M}^{\frac{1}{2}}\left( h\left( \epsilon z+i\tau _{0}\right) \right) \left( -t\partial _{t}u\right) \). Hence
Finally, using Proposition 52 and item 2, we conclude that, as \(\epsilon \rightarrow 0\),
\(\square \)
The next lemma is analogous to Lemma 22.
Lemma 57
The operators \(T_{\epsilon }\) and \(R_{\epsilon ,\tau _{0}}\) satisfy the following properties:
-
(1)
If \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+}\right) \) with \(\text{ supp }({\mathcal {M}}_{\frac{1}{2}}u)\subset \left\{ \xi \in \Gamma _{0};\,\left| \xi \right| \le \frac{1}{2}\right\} \), \(v\in C^{\infty }\left( X,E_{j},F_{j}\right) \) and \(\epsilon <1\), then \(\text{ supp }({\mathcal {M}}_{\frac{1}{2}}\left( R_{\epsilon ,\tau _{0}}u\right) )\subset K_{m}\), where \(K_{0}:=\left\{ \xi \in \Gamma _{0};\left| \xi \right| \le 2\right\} \), \(K_{j}:=\left\{ \xi \in \Gamma _{0};2^{j-1}\le \left| \xi \right| \le 2^{j+1}\right\} \), \(j\in {\mathbb {N}}_{0}\backslash \left\{ 0\right\} \). The number \(m\in {\mathbb {N}}_{0}\) is equal to 0 if \(\left| \tau _{0}\right| +\frac{1}{2}<2\) and, for \(\left| \tau _{0}\right| +\frac{1}{2}>2\), m is the smallest number such that \(2^{m-1}<\left| \tau _{0}\right| -\frac{1}{2}<\left| \tau _{0}\right| +\frac{1}{2}<2^{m+1}\). Hence \(m\le C\left\langle \ln \left( \tau _{0}\right) \right\rangle \).
-
(2)
There is a constant \(C>0\) such that for all \(\epsilon <1\), \(v\in C^{\infty }\left( X,E_{j},F_{j}\right) \) and \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+}\right) \) with \(\text{ supp }({\mathcal {M}}_{\frac{1}{2}}u)\subset \left\{ \xi \in {\mathbb {R}};\,\left| \xi \right| \le \frac{1}{2}\right\} \)
$$\begin{aligned}&{\frac{1}{C\left\langle \ln \tau _{0}\right\rangle }\left\| u\otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }}\\&\quad \le \left\| R_{\epsilon ,\tau _{0}}\left( u\otimes v\right) \right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }\le C\left\langle \ln \tau _{0}\right\rangle \left\| u\otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }. \end{aligned}$$ -
(3)
For all \(u\in {\mathcal {T}}_\frac{1}{2}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{j},F_{j}\right) \right) \), we have \(\lim _{\epsilon \rightarrow 0}T_{\epsilon }\left( u\right) =0\) weakly in \({\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \).
Proof
-
(1)
An easy computation shows that \({\mathcal {M}}_{\frac{1}{2}}\left( R_{\epsilon ,\tau _{0}}u\right) (z)=\epsilon ^{\frac{1}{p}-1}{\mathcal {M}}_{\frac{1}{2}}u\left( \frac{z}{\epsilon }-\frac{i\tau _{0}}{\epsilon }\right) \). When \(\epsilon <1\), this means that, if \(x\in {\mathbb {R}}\) is such that \({\mathcal {M}}_{\frac{1}{2}}\left( R_{\epsilon ,\tau _{0}}u\right) \left( ix\right) \ne 0\), then \(\tau _{0}-\frac{1}{2}<x<\tau _{0}+\frac{1}{2}\), which implies that \(\text {supp}({\mathcal {M}}_{\frac{1}{2}}\left( R_{\epsilon ,\tau _{0}}u\right) )\) is contained in some ball of radius \(\frac{1}{2}\).
-
(2)
As \(\text{ supp }({\mathcal {M}}_{\frac{1}{2}}u)\subset K_{0}\), Proposition 53 implies that
$$\begin{aligned}&{\left\| u\otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }\le C_{1}\left\| u\otimes v\right\| _{L_{p}\left( {\mathbb {R}}_{+},L_{p}\left( X,E_{j}\right) \oplus B_{p}^{0}\left( \partial X,F_{j}\right) ;\frac{dt}{t}\right) }}\\&\quad = C_{1}\left\| \left( R_{\epsilon ,\tau _{0}}u\right) \otimes v\right\| _{L_{p}\left( {\mathbb {R}}_{+},L_{p}\left( X,E_{j}\right) \oplus B_{p}^{0}\left( \partial X,F_{j}\right) ;\frac{dt}{t}\right) }\nonumber \\&\quad \le C_{2}\left\langle \ln \tau _{0}\right\rangle \left\| \left( R_{\epsilon ,\tau _{0}}u\right) \otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) } \nonumber \end{aligned}$$and
$$\begin{aligned}&\left\| \left( R_{\epsilon ,\tau _{0}}u\right) \otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }\le C_{3}\left\langle \ln \tau _{0}\right\rangle \left\| \left( R_{\epsilon ,\tau _{0}}u\right) \right. \\&\quad \left. \otimes v\right\| _{L_{p}\left( {\mathbb {R}}_{+},L_{p}\left( X,E_{j}\right) \oplus B_{p}^{0}\left( \partial X,F_{j}\right) ;\frac{dt}{t}\right) }\\&\quad = C_{3}\left\langle \ln \tau _{0}\right\rangle \left\| u\otimes v\right\| _{L_{p}\left( {\mathbb {R}}_{+},L_{p}\left( X,E_{j}\right) \oplus B_{p}^{0}\left( \partial X,F_{j}\right) ;\frac{dt}{t}\right) }\\&\quad \le C_{4}\left\langle \ln \tau _{0}\right\rangle \left\| u\otimes v\right\| _{{\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) }. \end{aligned}$$ -
(3)
We identify the dual of \({\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \) with \({\mathcal {HB}}_{qE_{j},F_{j}}\left( X^{\wedge }\right) \), where \(\frac{1}{p}+\frac{1}{q}=1\), using the scalar product \(L_{2}\left( {\mathbb {R}}_{+},L_{2}\left( X,E_{j}\right) \oplus L_{2}\left( \partial X,F_{j}\right) ,\frac{dt}{t}\right) \). As \(T_{\epsilon }\) is an isometry in \({\mathcal {HB}}_{pE_{j},F_{j}}\left( X^{\wedge }\right) \), it is enough to prove that
$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\int _{{\mathbb {R}}_{+}}\left\langle u(t/\epsilon ),v(t)\right\rangle _{L_{2}\left( X,E_{j}\right) \oplus L_{2}\left( \partial X,F_{j}\right) }\frac{dt}{t}=0 \end{aligned}$$for all \(u,v\in C_{c}^{\infty }\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{j},F_{j}\right) \right) \). But this is true. In fact, let \(a,b,R>0\) be such that \(\text {supp}\left( u\right) \subset \left[ 0,R\right] \) and \(\text {supp}\left( v\right) \subset \left[ a,b\right] \), then, for \(\epsilon <\frac{a}{R}\), we have \(\text {supp}\left( T_{\epsilon }u\right) \cap \text {supp}\left( v\right) =\emptyset \). Hence we obtain the result.
\(\square \)
Lemma 58
Let \(h\in \tilde{{\mathcal {B}}}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( X,\Gamma _{0}\right) \) and suppose that there is a constant \(c>0\) such that, for each \(u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) \), we have
Then, for every \(v\in C^{\infty }\left( X,E_{0},F_{0}\right) \) and \(\tau \in {\mathbb {R}}\), we have
for some constant C independent of v.
Proof
Let \(0\ne u\in {\mathcal {T}}_{\frac{1}{2}}\left( {\mathbb {R}}_{+}\right) \), be a function with \(\text {supp}({\mathcal {M}}_{\frac{1}{2}}\left( u\right) )\subset \left\{ z\in \Gamma _{0};\left| z\right| <\frac{1}{2}\right\} \) and \(v\in C^{\infty }\left( X\right) \). Then item 2 of Lemma 57 implies that
As \(\lim _{\epsilon \rightarrow 0}\big \Vert op_{M}^{\frac{1}{2}}\left( h\right) R_{\epsilon ,\tau _{0}}\left( u\otimes v\right) -h\left( i\tau _{0}\right) \left( u\otimes v\right) \big \Vert _{{\mathcal {HB}}_{pE_{1,}F_{1}}\left( X^{\wedge }\right) }=0\), we see again from Lemma 57 that
where \(\left( u\otimes h\left( i\tau _{0}\right) v\right) (t,x):=u(t)\left( h\left( i\tau _{0}\right) v\right) (x)\). Now, it is easy to conclude that
\(\square \)
We finish with the following proposition that proves the invertibility of the conormal symbol.
Proposition 59
Let \(A\in \tilde{C}^{p}\left( {\mathbb {D}};k\right) \) be a Fredholm operator in the space
Then the conormal symbol is invertible on \(\Gamma _{0}\), and its inverse is an element of \(\tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( X,\Gamma _{0}\right) \).
Proof
We are going to consider operators given as
where \(P\in \tilde{{\mathcal {B}}}_{2E_{0},2E_{1},2F_{0},2F_{1}}^{p}\left( 2{\mathbb {D}}\right) \), \(G\in \tilde{C}_{{\mathcal {O}}\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \), and \(h\left( t,z\right) =a\left( t,z\right) +\tilde{a}\left( z\right) \) with functions \(a\in C^{\infty }\left( \overline{{\mathbb {R}}_{+}},\tilde{M}_{{\mathcal {O}}\,E_{0},F_{0},E_{1},F_{1}}^{p}\left( X\right) \right) \) and \(\tilde{a}\in M_{P\,E_{0},F_{0},E_{1},F_{1}}^{-\infty }\left( X\right) \) for some asymptotic type P with \(\pi _{{\mathbb {C}}}P\cap \Gamma _{0}=\emptyset \). In particular, \(h_{0}\left( z\right) :=h\left( 0,z\right) =\sigma _{M}^{0}\left( A\right) \left( z\right) \).
Let us first prove that for all \(u\in {\mathcal {HB}}_{pE_{0},F_{0}}\left( X^{\wedge }\right) \)
It suffices to show this for \(u\in C_{c}^{\infty }\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) \). We find operators \(B_{1}\in {\mathcal {B}}\left( {\mathcal {HB}}_{pE_{1},F_{1}}\left( {\mathbb {D}}\right) \!,{\mathcal {HB}}_{pE_{0},F_{0}}\left( {\mathbb {D}}\right) \right) \) and \(K_{1}\in {\mathcal {B}}\left( {\mathcal {HB}}_{pE_{0},F_{0}}\left( {\mathbb {D}}\right) \!,{\mathcal {HB}}_{pE_{0},F_{0}}\left( {\mathbb {D}}\right) \right) \), where \(K_{1}\) is compact, such that \(B_{1}A-1=K_{1}\). Let us choose \(\sigma \) and \(\sigma _{1}\) in \(C_{c}^{\infty }\left( \left[ \right. 0,1\left[ \right. \right) \) such that \(\sigma \sigma _{1}=\sigma \), \(\sigma _{1}\omega _{1}=\sigma _{1}\) and \(\sigma _{1}\omega =\sigma _{1}\). Then
As the supports of \(\sigma \) and \(1-\sigma _{1}\) are disjoint, the operator \(\left( 1-\sigma _{1}\right) A\sigma \) is a Green operator and therefore compact. Hence
where \(K_{2}\) is a compact. Using Eq. (3.6) for \(A\sigma \), we conclude that \(\sigma =Bop_{M}^{\frac{1}{2}}\left( h\right) \sigma -K\), where \(B=\sigma _{1}B_{1}\sigma _{1}\) and \(K=\sigma _{1}\left( K_{2}-B_{1}\sigma _{1}G\right) \sigma \) is compact.
Now let \(u\in C_{c}^{\infty }\left( {\mathbb {R}}_{+},C^{\infty }\left( X,E_{0},F_{0}\right) \right) \). We know that \(T_{\epsilon }\left( u\right) =\sigma T_{\epsilon }\left( u\right) \), when \(\epsilon \) is small. As \(\sigma =Bop_{M}^{\frac{1}{2}}\left( h\right) \sigma -K\), we have that, for \(\epsilon \) sufficiently small,
As \(T_{\epsilon }u\) weakly tends to zero and K is compact, \(\lim _{\epsilon \rightarrow 0}\left\| KT_{\epsilon }\left( u\right) \right\| _{{\mathcal {HB}}_{pE_{0},F_{0}}\left( X^{\wedge }\right) }=0\). Using that \(T_{\epsilon }\) is an isometry and item 3.(ii) of Proposition 56, we conclude that Inequality (3.7) holds. This result together with Lemma 58 implies that
for some constant C independent of v.
As \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}};k\right) \) is Fredholm, so is \(A^{*}\in \tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{q}\left( {\mathbb {D}};k\right) \). The above argument implies that \(\sigma _{M}^{0}\left( A^{*}\right) \left( z\right) =h\left( i\tau \right) ^{*}\) also satisfies an estimate as (3.8), for q instead of p, where \(\frac{1}{p}+\frac{1}{q}=1\). Hence, for all \(\tau \in {\mathbb {R}}\), \(h\left( i\tau \right) \) is injective, has closed range and the same is true for its adjoint. Lemma 23 implies that \(h\left( i\tau \right) \) is bijective and
Theorem 29 implies that \(h_{0}^{-1}\in \tilde{{\mathcal {B}}}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( X,\Gamma _{0}\right) \). \(\square \)
3.6 Spectral Invariance of Boundary Value Problems with Conical Singularities
Once we know the equivalence of Fredholm property and ellipticity, we can establish the spectral invariance.
Theorem 60
Let \(A\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \). Suppose that, for each \(\lambda \in \Lambda \), the operator
is invertible. Then \(A^{-1}\in \tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \).
Proof
The operator A is invertible, hence it is Fredholm and there are operators \(B\in \tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \), \(K_{1}\in \tilde{C}_{G\,E_{1},F_{1},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) and \(K_{2}\in \tilde{C}_{G\,E_{0},F_{0},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \) such that \(AB=I+K_{1}\) and \(BA=I+K_{2}\). These identities imply that
As \(B\in \tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \), \(K_{2}B\in \tilde{C}_{G\,E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \) and \(K_{2}A^{-1}K_{1}\) belongs to \(\tilde{C}_{G\,E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \), we obtain the result. \(\square \)
Theorem 61
Let \(A\in C_{E_{0},F_{0},E_{1},F_{1}}^{m,d}\left( {\mathbb {D}},(\gamma ,\gamma -m,k)\right) \), where \(m\in {\mathbb {Z}}, d=\max \left\{ m,0\right\} \). Suppose that there is an \(s\in {\mathbb {Z}}, s\ge d\) such that
is invertible. Then, \(A^{-1}\in C_{E_{1},F_{1},E_{0},F_{0}}^{-m,d'}\left( {\mathbb {D}},(\gamma -m,\gamma ,k)\right) \) , where \(d':=\max \left\{ -m,0\right\} \). In particular, for all \(s>d-1+\frac{1}{q}\) and \(1<q<\infty \) the operator A is invertible in \({\mathcal {B}}\big ({\mathcal {H}}_{q}^{s,\gamma }\left( {\mathbb {D}},E_{0}\right) \oplus {\mathcal {B}}_{q}^{s-\frac{1}{p},\gamma -\frac{1}{2}}\left( {\mathbb {B}},F_{0}\right) ,{\mathcal {H}}_{q}^{s-m,\gamma -m}\left( {\mathbb {D}},E_{1}\right) \oplus {\mathcal {B}}_{q}^{s-m-\frac{1}{q},\gamma -m-\frac{1}{2}}\left( {\mathbb {B}},F_{1}\right) \big )\).
Proof
As in the proof of Corollary 50 we consider the operator \(\tilde{A}\in \tilde{C}_{E_{0},F_{0},E_{1},F_{1}}^{p}\left( {\mathbb {D}},k\right) \) defined by (3.3). As A is invertible, so is \(\tilde{A}\). We infer from Theorem 60 that \((\tilde{A})^{-1}\) belongs to \(\tilde{C}_{E_{1},F_{1},E_{0},F_{0}}^{p}\left( {\mathbb {D}},k\right) \) and hence \(A^{-1}\in C_{E_{1},F_{1},E_{0},F_{0}}^{-m,d'}\left( {\mathbb {D}},(\gamma -m,\gamma ,k)\right) \). \(\square \)
4 Application: The Dirichlet Laplacian
In order to illustrate the applicability of Theorem 61, we show how it can be used to study the spectrum of the Dirichlet Laplacian.
We consider a two-dimensional manifold with conical singularities D, for example the closure of a domain in \({\mathbb {R}}^2\), which has a smooth boundary apart from a finite set of conical points. Let \({\mathbb {D}}\) be the associated manifold with corners introduced in Definition 30, \({{\mathbb {B}}}\) its boundary and X be the union of the connected components of the cross-sections of each conical point. Working on \({\mathbb {D}}\) is analytically simpler; it amounts to introducing polar coordinates near the conical singularities. As before, we write \(t\in [0,1]\) for the variable that represents the distance to the conical points.
We will consider a particular instance of the Dirichlet problem on D; see also [5, Section 6] for more background on the Dirichlet problem on manifolds with boundary and conical singularities. Since \(\dim {\mathbb {D}}=2\), we have \(n=1\) in the notation of the previous section.
Denote by \(\Delta \) the Laplace-Beltrami operator on \({\mathbb {D}}\) with respect to a straight conically degenerate metric on \({\mathbb {D}}\), i.e. a Riemannian metric on \({\mathbb {D}}\), which near \(t=0\) takes the form
for a (non-degenerate) Riemannian metric h on X that does not depend on t. By \(\gamma _0\) denote the trace on \({\mathbb {B}}\) of a function defined in \({\mathbb {D}}\). We consider the operator
for suitable parameters \(s,\gamma \) and p. Let \(Q\in C_{{\mathbb {C}},{\mathbb {C}}}^{2,0}\left( {\mathbb {B}},\left( \gamma +\frac{3}{2},\gamma -\frac{1}{2},k\right) \right) \) be an invertible operator as in Proposition 48, (5). Then \(\left( {\begin{array}{c}\Delta \\ Q\gamma _0\end{array}}\right) \) is an operator in \(C^{2,0}_{{{\mathbb {C}}},0,{{\mathbb {C}}}, {{\mathbb {C}}}}({\mathbb {D}}, (\gamma +2,\gamma , k))\) for arbitrary k.
For the above metric, the Laplace–Beltrami operator near \(t=0\) is of the form
where \(\Delta _X\) is the Laplacian on the 1-dimensional manifold X.
We will next check the ellipticity conditions for \({\mathscr {A}}\). The analysis can be found in [5, Section 6.1]. It is easy to see that the principal pseudodifferential symbol and the principal boundary symbol are elliptic in the sense of Remark 47. The conormal symbol of \({\mathscr {A}}\) is
where \(\gamma _{0,X}\) is the trace operator for functions defined on X to functions on \(\partial X\). Note that here \(\partial X\) consists of finitely many points, so that \(H^{3/2}(\partial X)\) is just \({{\mathbb {C}}}^{2N}\), where N is the number of components of cross sections of all conical points. We denote by \(0>\lambda _1>\lambda _2>\ldots \) the different eigenvalues of the Dirichlet problem for the Laplacian on X. Let \(q_j^\pm = \pm \sqrt{-\lambda _j}\). Then the conormal symbol will be invertible for all \(z\in {{\mathbb {C}}} \setminus \{q_j^\pm ;j=1,2,\ldots \}. \) In this case, the operator \({\mathscr {A}}\) in (4.1) will be a Fredholm operator whenever \(1<p<\infty \) and \(s>-2+1/p\), due to Proposition 48. 4).
We will now consider the realizations of the Laplace operator with Dirichlet conditions on \({\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \). Let \(C_{c}^{\infty }\left( {\mathbb {D}}\right) \) be the set of smooth functions on \({\mathbb {D}}\) supported in \(\text {int}\left( {\mathbb {D}}\right) \) and \(C_{c}^{\infty }\left( {\mathbb {D}}\right) _{\gamma _{0}}=\big \{ u\in C_{c}^{\infty }\left( {\mathbb {D}}\right) _{\gamma _{0}};\,\gamma _{0}\left( u\right) =0\big \}\). To the Laplace operator with Dirichlet conditions \(\Delta :C_{c}^{\infty }\left( {\mathbb {D}}\right) _{\gamma _{0}}\rightarrow C_{c}^{\infty }\left( {\mathbb {D}}\right) \), we can associate two important closed extensions: the minimal and maximal realization. The maximal realization is the Laplace operator \(\Delta _{\text {Dir,max}}:{\mathscr {D}}_{p}^{s,\gamma }\left( \Delta _{\text {Dir,max}}\right) \subset {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \rightarrow {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \) with the domain \({\mathscr {D}}_{p}^{s,\gamma }\left( \Delta _{\text {Dir,max}}\right) =\left\{ u\in {\mathcal {H}}_{p}^{s+2,\gamma }\left( {\mathbb {D}}\right) ;\,\gamma _{0}\left( u\right) =0\,\text { and }\,\Delta u\in {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \right\} \).
The minimal realization \(\Delta _{\text {Dir,min}}\) is the closure of the operator \(\Delta :C_{c}^{\infty }\left( {\mathbb {D}}\right) _{\gamma _{0}}\subset {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \rightarrow {\mathcal {H}}_{p}^{s,\gamma }\left( {\mathbb {D}}\right) \). Its domain is denoted by \({\mathscr {D}}_{p}^{s,\gamma }\left( \Delta _{\text {Dir,min}}\right) \). It is clear that \(\Delta _{\text {Dir,min}}\subset \Delta _{\text {Dir,max}}\). The closed extensions of the Dirichlet Laplacian are therefore precisely those with a domain between that of the minimal and that of the maximal realization.
Instead of \({\mathscr {A}}\), we will study the realization \(\Delta _{{\mathrm{Dir}}}\), acting like \(\Delta \) on the domain
It is well-known that the Fredholm property and the invertibility of the realization \(\Delta _{{\mathrm{Dir}}}\) are equivalent to that of the operator \({\mathscr {A}}\) in (4.1); a proof can be found in [5, Section 8].
In applications to nonlinear partial differential equations like the Cahn-Hilliard equation or the porous medium equation one is often interested in realizations with particular weights \(\gamma \), for example, because the functions in the domain should be bounded near the singular set.
We shall explain this briefly. For \(q\in \{q_j^\pm ; j=1,2,\ldots \}\), let \({\mathscr {E}}_q = \{\omega t^{-q}e; e\in E_q\}\), where \(\omega \) is an arbitrary cut-off function near \(\partial {\mathbb {D}}\) and \(E_q\) is the eigenspace of the Laplace operator with Dirichlet conditions acting on X, \(\Delta _{X,{{\mathrm{Dir}}}}\), with respect to the eigenvalue \(\lambda _j\).
For \(v\in {\mathscr {E}}_{q_j^\pm }\), the function \(\Delta v\) is smooth and vanishes near \(t=0\), so it is an element of \({\mathcal {H}}^{\infty ,\infty }_2({\mathbb {D}})\). Moreover v satisfies the Dirichlet boundary condition.
It was shown in [5, Proposition 6.1]Footnote 1 that the domain of the maximal extension of the Laplacian with Dirichlet boundary condition in the space \({\mathcal {H}}^{s,\gamma }_p({\mathbb {D}})\), \(s>-2+1/p\), is
Here \(I_\gamma =\ ]-1-\gamma , 1-\gamma [\ \cap \{ q_j^\pm ; j=0,1,\ldots \}.\) Moreover, it can be shown that \(\Delta _{{\mathrm{Dir}}}=\Delta _{\text {Dir,min}}\), whenever \(-1-\gamma \) is not one of the \(q_j^\pm \). In particular, in this case, \({\mathscr {D}}_p^{s,\gamma }(\Delta _{{{\mathrm{Dir}}},\min })= {\mathcal {H}}^{s+2,\gamma +2}_p({\mathbb {D}})_{\mathrm{Dir}}\).
In general, we know from [5, Theorem 4.13] that
As in [24, 26] we choose the weight \(\gamma \) of the form
(note that \(q_1^-\) is negative). Then \(-1-\gamma = -\delta \in \ ]q_1^-,0[\) equals none of the \(q^\pm _j\).
We will now study the spectrum of \(\Delta _{{\mathrm{Dir}}}\).
Proposition 62
For \(s=0\) and \(p=2\) the unbounded operator \(\lambda -\Delta _{\mathrm{Dir}}\) in \({\mathcal {H}}^{0,\gamma }_2({\mathbb {D}})\) with domain (4.2) is invertible provided \(\lambda \notin \left. \right] -\infty ,0\left. \right] \).
Proof
We first note that \(\Delta :C_{c}^{\infty }\left( {\mathbb {D}}\right) \rightarrow C_{c}^{\infty }\left( {\mathbb {D}}\right) \) is a non-positive symmetric operator when we consider the scalar product given by \({\mathcal {H}}_{2}^{0,0}\left( {\mathbb {D}}\right) \). Therefore we can define its Friedrichs extension \(\Delta _{\text {Dir,F}}\). Similarly as in the proof of [25, Theorem 4.1] we relate our operator to the Friedrichs extension, whose domain has been determined in [5, Theorem 6.4]:
Step 1. We first check injectivity: Suppose \(u\in {\mathcal {H}}^{2,\gamma +2}_2({\mathbb {D}})_{{\mathrm{Dir}}}\) and \((\lambda -\Delta )u=0\). The fact that \(\Delta u = \lambda u\in {\mathcal {H}}^{2,\gamma +2}_2({\mathbb {D}})\) implies that u is in the maximal domain of \(\Delta _{\mathrm{Dir}}\) in \({\mathcal {H}}^{2,\gamma +2}_2({\mathbb {D}})\), which, according to (4.3)/(4.4) is given by
We observe that \(I_{\gamma +2} = \,]-2-\delta ,-\delta [\,\cap \{q_j^-;j=1,2,\ldots \},\) and \(\gamma +4 = 3+\delta >3\). Hence u actually is in the domain of the Friedrichs extension. As the Friedrichs extension has no spectrum outside \(\left. \right] -\infty ,0\left. \right] \), we conclude that \(u=0\).
Step 2. Since \(\Delta _{\mathrm{Dir}}\) is a Fredholm operator, it has closed range. Therefore to prove that \(\lambda -\Delta _{\mathrm{Dir}}\) is surjective, it is enough to prove that its adjoint is injective, see Lemma 23. This is the content of the next step.
Step 3. As the scalar product of \({\mathcal {H}}_{2}^{0,0}\left( {\mathbb {D}}\right) \) can be used to identify the dual of \({\mathcal {H}}_{2}^{0,\gamma }\left( {\mathbb {D}}\right) \) with \({\mathcal {H}}_{2}^{0,-\gamma }\left( {\mathbb {D}}\right) \), we can consider the adjoint \(\Delta _{\mathrm{Dir}}^*\) of \(\Delta _{\mathrm{Dir}}\) as an unbounded operator on \({\mathcal {H}}_2^{0,-\gamma }({\mathbb {D}})\). Noting that the domain (4.2) is actually the minimal domain, that the adjoint boundary condition to the Dirichlet boundary condition is again the Dirichlet boundary condition and that \(\Delta \) is symmetric, the domain of the adjoint can be determined from [5, Theorem 4.6] (or [5, Theorem 6.3]):
The last inclusion follows from (4.4). Since \(I_{-\gamma } = \, ]-2+\delta ,\delta [\,\cap \, \{q_j^\pm ; j=1,2,\ldots \}\) and \(\delta < q_1^+\), we see that \(I_{-\gamma }\) contains only the \(q^-_j\) with \(-2+\delta<q_j^-<0\).
Suppose \(u\in {\mathscr {D}}^{0,-\gamma }_2(\Delta _{\mathrm{Dir}}^*)\) with \((\lambda -\Delta )u=0\). Write \(u=v+w\) with \(v\in {\mathcal {H}}^{2,2-\gamma }_2({\mathbb {D}})_{\mathrm{Dir}} \) and \(w\in \bigoplus _{q\in I_{-\gamma }}{\mathscr {E}}_q\). Since \((\lambda -\Delta )v = -\lambda w -\Delta w, \Delta w\in {\mathcal {H}}^{\infty ,\infty }_2({\mathbb {D}})\) and \(\lambda w \in {\mathcal {H}}^{\infty , 1+\delta }_2({\mathbb {D}})\) (this follows from the fact that \(t^{-q} \in {\mathcal {H}}^{\infty ,\mu }_p({\mathbb {D}})\) if and only if \(\mathfrak {R}(q)<1-\mu \)), we see that
This implies that v is in the domain of the Friedrichs extension, and so is w, as \({\mathcal {H}}_{2}^{2,1}\left( {\mathbb {D}}\right) \cap {\mathscr {D}}_{2}^{0,0}\left( \Delta _{\text {Dir,max}}\right) \subset {\mathscr {D}}\left( \Delta _{\text {Dir,F}}\right) \), where \({\mathscr {D}}\left( \Delta _{\text {Dir,F}}\right) \) is the domain of the Friedrichs extension. This was shown in the proof of Theorem 6.4 of [5]. Since the Friedrichs extension has no spectrum outside \(\left. \right] -\infty ,0\left. \right] \), we conclude that \(u=0\). Therefore \(\lambda -\Delta ^{*}_{{\mathrm{Dir}}}\) is injective. \(\square \)
Theorem 63
For \(1<p<\infty \) and \(s>-2+1/p\) the unbounded operator \(\lambda -{\Delta }_{\mathrm{Dir}}\) in \({\mathcal {H}}^{s,\gamma }_p({\mathbb {D}})\) with domain (4.2) is invertible whenever \(\lambda \notin \left. \right] -\infty ,0\left. \right] \).
Proof
According to [5, Section 8], the invertibility of
is equivalent to that of
In Proposition 62 we have shown invertibility of (4.6) for \(s=0\) and \(p=2\). Hence we obtain invertibility of (4.7) for this case. According to Theorem 61 the inverse is an element in \(C^{-2,0}_{{{\mathbb {C}}}, {{\mathbb {C}}}, {{\mathbb {C}}}, 0}({\mathbb {D}},(\gamma , \gamma +2,k))\) for arbitrary k. It therefore also furnishes the inverse for arbitrary p and \(s>-2+1/p\). As a consequence we also obtain the invertibility of \(\Delta _{\mathrm{Dir}}\) in (4.6) for these values of s and p. \(\square \)
Notes
The result is stated for \(s=0\) but extends to other values of s.
References
Agranovich, M.S., Visik, M.I.: Elliptic problems with a parameter and parabolic problems of general type. Usp. Mat. Nauk. 19.3(117), 53–161 (1964)
Amann, H.: Anisotropic Function Spaces and Maximal Regularity For Parabolic Problems. Part 1, Function Spaces. Jindřich Nečas Center for Mathematical Modeling Lecture Notes, vol. 6. Matfyzpress, Prague (2009)
Boutet de Monvel, L.: Boundary problems for pseudodifferential operators. Acta Math. 126(1–2), 11–51 (1971)
Coriasco, S., Schrohe, E., Seiler, J.: Bounded \(H_\infty \)-calculus for differential operators on conic manifolds with boundary. Commun. Partial Differ. Equ. 32(1–3), 229–255 (2007)
Coriasco, S., Schrohe, E., Seiler, J.: Realizations of differential operators on conic manifolds with boundary. Ann. Glob. Anal. Geom. 31(3), 223–285 (2007)
Denk, R., Kaip, M.: General Parabolic Mixed Order Systems in \({L_p}\) and Applications. Operator Theory: Advances and Applications, vol. 239. Birkhäuser/Springer, Cham (2013)
Derviz, A.O.: An algebra generated by general pseudodifferential boundary value problems in a cone. In: Nonlinear Equations and Variational Inequalities. Linear Operators and Spectral Theory (Russian), Probl. Mat. Anal., vol. 11, pp. 133–161, 251. Leningrad. Univ., Leningrad, 1990. Translated in J. Soviet Math. 64, no. 6, 1313–1330 (1993)
Gil, J.B., Krainer, T., Mendoza, G.A.: Resolvents of elliptic cone operators. J. Funct. Anal. 241(1), 1–55 (2006)
Grubb, G.: Pseudodifferential boundary problems in \(L_p\) spaces. Commun. Partial Differ. Equ. 15(3), 289–340 (1990)
Grubb, G.: Parameter-elliptic and parabolic pseudodifferential boundary problems in global \(L_p\) Sobolev spaces. Math. Z. 218(1), 43–90 (1995)
Grubb, G.: Functional Calculus of Pseudodifferential Boundary Problems. Progress in Mathematics, vol. 65, 2nd edn. Birkhäuser Boston, Inc., Boston (1996)
Grubb, G.: Distributions and Operators. Graduate Texts in Mathematics, vol. 252. Springer, New York (2009)
Grubb, G., Kokholm, N.J.: A global calculus of parameter-dependent pseudodifferential boundary problems in \(L_p\) Sobolev spaces. Acta Math. 171(2), 165–229 (1993)
Harutyunyan, G., Schulze, B.-W.: Elliptic Mixed, Transmission and Singular Crack Problems. EMS Tracts in Mathematics, vol. 4. European Mathematical Society (EMS), Zürich (2008)
Kondrat’ev, V.A.: Boundary value problems for elliptic equations in domains with conical or angular points. Trudy Mosk. Mat. Obš. 16, 209–292 (1967)
Kozlov, V.A., Maz’ya, V.G., Rossmann, J.: Elliptic Boundary Value Problems in Domains with Point Singularities. Mathematical Surveys and Monographs, vol. 52. American Mathematical Society, Providence (1997)
Krainer, T.: Resolvents of elliptic boundary problems on conic manifolds. Commun. Partial Differ. Equ. 32(1–3), 257–315 (2007)
Leopold, H.-G., Schrohe, E.: Spectral invariance for algebras of pseudodifferential operators on Besov–Triebel–Lizorkin spaces. Manuscr. Math. 78(1), 99–110 (1993)
Lunardi, A.: Interpolation Theory. Lecture Notes: Scuola Normale Superiore di Pisa (New Series), 2nd edn. Pisa, Edizioni della Normale (2009)
Melrose, R.: Transformation of boundary problems. Acta Math. 147(3–4), 149–236 (1981)
Melrose, R., Mendoza, G.: Elliptic operators of totally characteristic type. MSRI preprint (1983)
Plamenevskiĭ, B.A.: Algebras of Pseudodifferential Operators. Mathematics and its Applications (Soviet Series), vol. 43. Kluwer Academic Publishers Group, Dordrecht (1989)
Rempel, S., Schulze, B.-W.: Index Theory of Elliptic Boundary Problems. Reprint of the 1982 edition. North Oxford Academic Publishing Co., Ltd., London (1985)
Roidos, N., Schrohe, E.: The Cahn–Hilliard equation and the Allen–Cahn equation on manifolds with conical singularities. Commun. Partial Differ. Equ. 38(5), 925–943 (2013)
Roidos, N., Schrohe, E.: Bounded imaginary powers of cone differential operators on higher order Mellin–Sobolev spaces and applications to the Cahn–Hilliard equation. J. Differ. Equ. 257, 611–637 (2014)
Roidos, N., Schrohe, E.: Existence and maximal \(L^p\)-regularity of solutions for the porous medium equation on manifolds with conical singularities. Commun. Partial Differ. Equ. 41(9), 1441–1471 (2016)
Schrohe, E.: Fréchet algebra techniques for boundary value problems on noncompact manifolds: Fredholm criteria and functional calculus via spectral invariance. Math. Nachrichten 199(1), 145–185 (1999)
Schrohe, E., Seiler, J.: Ellipticity and invertibility in the cone algebra on \(L_p\)-Sobolev spaces. Integral Equ. Oper. Theory 41(1), 93–114 (2001)
Schrohe, E., Seiler, J.: The resolvent of closed extensions of cone differential operators. Can. J. Math. 57, 771–811 (2005)
Schrohe, E., Schulze, B.-W.: boundary value problems in Boutet de Monvel‘s algebra for manifolds with conical singularities. I. In: Pseudodifferential Calculus and Mathematical Physics, vol. 5, pp. 97–209. Akademie Verlag, Berlin (1994)
Schrohe, E., Schulze, B.-W.: Boundary value problems in Boutet de Monvel’s algebra for manifolds with conical singularities. II. In: Boundary value problems, Schrödinger operators, deformation quantization, vol. 8, math. Top, pp. 70–205. Akademie Verlag, Berlin (1995)
Schulze, B.-W.: Pseudodifferential Operators on Manifolds with Singularities. Studies in Mathematics and its Applications, vol. 24. North-Holland Publishing Co., Amsterdam (1991)
Schulze, B.-W.: Boundary Value Problems and Singular Pseudodifferential Operators. Pure and Applied Mathematics (New York). Wiley, Chichester (1998)
Shao, Y., Simonett, G.: Continuous maximal regularity on uniformly regular Riemannian manifolds. J. Evol. Equ. 14(1), 211–248 (2014)
Vertman, B.: The biharmonic heat operator on edge manifolds and non-linear fourth order equations. Manuscr. Math. 149(1–2), 179–203 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Ruzhansky.
Pedro T. P. Lopes was partially supported by FAPESP (Processo Número 2016/07016-8).
Rights and permissions
About this article
Cite this article
Lopes, P.T.P., Schrohe, E. Spectral Invariance of Pseudodifferential Boundary Value Problems on Manifolds with Conical Singularities. J Fourier Anal Appl 25, 1147–1202 (2019). https://doi.org/10.1007/s00041-018-9607-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00041-018-9607-5
Keywords
- Boundary value problems
- Manifolds with conical singularities
- Pseudodifferential analysis
- Spectral invariance