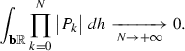Generalized Riesz Products on the Bohr Compactification of ${\mathbb {R}}$

Abstract

We study a class of generalized Riesz products connected to the spectral type of some class of rank one flows on ${\mathbb {R}}$. Applying Kac’s central limit theorem, we exhibit a large class of singular generalized Riesz products on the Bohr compactification of ${\mathbb {R}}$.

1 Introduction

The purpose of this paper is to extend and to study the notion of generalized Riesz product in the setting of the Bohr compactification of ${\mathbb {R}}$. This notion was formulated in the same manner as Peyrière in [11]. Therein, the authors proved that the spectral type of some class of rank one flows is given by some kind of generalized Riesz product on ${\mathbb {R}}$ normalized by some class of kernels. Here, following Peyrière’s suggestion [23], we give an alternative extension using the Bohr compactification of ${\mathbb {R}}$.

It is usual that the extension of some notions from the periodic setting to the almost periodic ones requires the consideration of the Bohr compactification of ${\mathbb {R}}$, which plays in the almost periodic case the same role played by the torus ${\mathbb {T}}\mathop {=}\limits ^\mathrm{{def}}\{t \in {\mathbb {C}},|t|=1\}$ in the periodic case. As opposed to the torus, the Bohr compactification is often a non-separable compact topological space and this lack of separability is a source of difficulties in trying to adapt the arguments from the periodic context to the almost periodic one. Peyrière also mentioned those difficulties in [23].

Our analysis is also motivated by the recent growing interest in the problem of the flat polynomials in the real setting suggested in [24]. It turns out that the main idea developed in [24] can not be adapted in ours. For a recent account on the problem of the flat polynomials we refer the reader to [26].

The paper is organized as follows. In Sect. 2, we recall some standard facts on almost periodic functions and the Bohr compactification of ${\mathbb {R}}$. In Sect. 3, we introduce generalized Riesz products on the Bohr compactification of ${\mathbb {R}}$ and state our main result concerning the singularity of a large class of these generalized Riesz products. In Sect. 4, we summarize and extend the relevant material on Kakutani’s criterion and Bourgain’s criterion on the singularity of the generalized Riesz products introduced in Sect. 3. In Sect. 5, we state and prove the central limit theorem due to M. Kac. Finally, in Sect. 6, we apply Kac’s central limit theorem to prove our main result.

2 The Bohr Compactification of ${\mathbb {R}}$

The Bohr compactification of ${\mathbb {R}}$ is based on the theory of almost periodic functions initiated by H. Bohr [3] in connection with the celebrated Riemann’s $\zeta$-function. In this section we are going to recall the basic ingredients of this theory. For the classical presentation we refer the reader to [1, 3, 18], Chap V. Section 2].

The space of all almost periodic functions is denoted by ${\mathcal {AP}}({\mathbb {R}})$. It is well known that ${\mathcal {AP}}({\mathbb {R}})$ is a subspace of the space of bounded continuous functions on ${\mathbb {R}}$. An important characterization of almost periodic functions is due to Bohr and it can be stated as follows

Theorem 2.1

(Bohr) A bounded continuous function $f$ is almost periodic function if, and only if, $f$ is uniformly approximated by finite linear combinations of functions in the set $\left\{ \cos (tx),\sin (tx)\right\} _{t \in {\mathbb {R}}}$.

We will denote by ${\mathbf {b}}{\mathbb {R}}$ the Bohr compactification of ${\mathbb {R}}$, and by $C({\mathbf {b}}{\mathbb {R}})$ the space of continuous functions on ${\mathbf {b}}{\mathbb {R}}$. We remind that one can define ${\mathbf {b}}{\mathbb {R}}$ as follows:

Theorem 2.2

[13] The group ${\mathbb {R}}$, equipped with the usual addition operation, may be embedded as a dense subgroup of a compact abelian group ${\mathbf {b}}{\mathbb {R}}$ such that ${\mathcal {AP}}({\mathbb {R}})$ is the family of all restrictions functions $f_{|{\mathbb {R}}}$ to ${\mathbb {R}}$ of functions $f \in C({\mathbf {b}}{\mathbb {R}})$. The operator $f \longmapsto f_{|{\mathbb {R}}}$ is an isometric $\star$-isomorphism of $C({\mathbf {b}}{\mathbb {R}})$ onto ${\mathcal {AP}}({\mathbb {R}})$. Moreover, the addition operation $+:{\mathbb {R}}\times {\mathbb {R}}\longrightarrow {\mathbb {R}}$ extends uniquely to the continuous group operation of ${\mathbf {b}}{\mathbb {R}}$, $+:{\mathbf {b}}{\mathbb {R}}\times {\mathbf {b}}{\mathbb {R}}\longrightarrow {\mathbf {b}}{\mathbb {R}}.$ The group ${\mathbf {b}}{\mathbb {R}}$ is called the Bohr compactification of ${\mathbb {R}}$.

For simplicity of notation, for any $f$ in ${\mathcal {AP}}({\mathbb {R}})$, we use the same letter $f$ for its canonical extension to ${\mathbf {b}}{\mathbb {R}}$. We denote by $h$ the Haar measure on ${\mathbf {b}}{\mathbb {R}}$, normalized to be a probability measure, and by $dt$ the usual Lebesgue measure on ${\mathbb {R}}$.

It is obvious that the continuous characters of ${\mathbf {b}}{\mathbb {R}}$ are the functions ${e^{i\lambda .}}:{\mathbf {b}}{\mathbb {R}}\longrightarrow {\mathbb {T}}$. For $f \in {\mathcal {AP}}({\mathbb {R}})$ we denote by $\int _{{\mathbf {b}}{\mathbb {R}}} f(t) dh(t)$ the asymptotic mean value of $f$, given by

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} f(t) dh(t) =\lim _{T \longrightarrow +\infty } \frac{1}{2T}\int _{-T}^{T}f(t) dt. \end{aligned}$$

Following [18], for any $f\in {\mathcal {AP}}({\mathbb {R}})$, we put

$$\begin{aligned} \widehat{f}\big (\{\lambda \}\big )=\int _{{\mathbf {b}}{\mathbb {R}}} f(t) e^{-i\lambda t} dh(t). \end{aligned}$$

$\big (\widehat{f}\big (\{\lambda \}\big )\big )_{\lambda \in {\mathbb {R}}}$ are the Fourier coefficients of $f$ relative to orthonormal family ${\{e^{i \lambda t}\}_{\lambda \in {\mathbb {R}}}}$; the inner product is given by

$$\begin{aligned} \langle f, g\rangle = \int _{{\mathbf {b}}{\mathbb {R}}} {f}(t) {\overline{g}}(t) dh(t). \end{aligned}$$

Furthermore, for any $p \ge 1$, we denote by $\Vert \cdot \Vert _p$ the norm in $L^p({\mathbf {b}}{\mathbb {R}},h)$. We remind that the sequence of probability measures $(\mu _n)$ on ${\mathbf {b}}{\mathbb {R}}$ converge in the weak-$\star$ topology to some probability measure $\mu$ if, for any $\lambda \in {\mathbb {R}}$,

3 Generalized Riesz Products on ${\mathbf {b}}{\mathbb {R}}$

Riesz products was introduced in [28]. Therein, F. Riesz construct a continuous measure on the torus whose Fourier coefficients do not vanish at infinity. Roughly speaking, Riesz products are measures on ${\mathbb {T}}$ which are constructed inductively. This powerful construction can be used to produce examples of measures with desired properties. Later, Riesz’s construction was extended in [29], p.208].

As shown in [21] Riesz products can be realized as a spectral type of some dynamical systems. Specific Riesz products are the right tool to describe the spectrum of a class of dynamical systems arising from the substitution [25, 27]. A large class of Riesz products was realized in [15] as the maximal spectral type of the unitary operator associated to a non-singular dynamical system and a cocycle over it. In [4], the author established a connection between some class of generalized Riesz products on the circle and the maximal spectral type of rank one maps. Alternative proofs were given in [6, 20, 22].

Generalized Riesz products analogous to Peyrière–Riesz products were realized in [11] as a spectral type of some class of rank one flows.

Here, our aim is to extend the notion of generalized Riesz products to ${\mathbf {b}}{\mathbb {R}}$. Let $(p_k)_{k \in {\mathbb {N}}}$ be a sequence of positive integers greater than $2$ and $\Big ((s_{k,j})_{j=0, \cdots ,p_k}\Big )_{k \ge 0}$ be a sequence of finite sequence of positive real numbers with $s_{k,0}=0$ for any $k \in {\mathbb {N}}$. Put

$$\begin{aligned} P_k(t)=\frac{1}{\sqrt{p_k}}\sum _{j=0}^{p_k-1} e^{i t(jh_k+\overline{s_{k,j}})} , \end{aligned}$$

(1)

where $\overline{s_{k,0}}=0,$ and $\overline{s_{k,j}}=\sum _{l=0}^{j}{s}_{k,l},~1 \le j \le p_k-1$. The sequence $(h_k)$ is defined inductively by

$$\begin{aligned} h_0=1\, \mathrm{and}\, h_{k+1}=p_k h_k +\sum _{l=0}^{p_k-1}{s}_{k,l}=p_kh_k+\overline{s_{k,p_k-1}}. \end{aligned}$$

(2)

For $p,q \in \{0,\cdots ,p_k-1\}$, we introduce the following sequence of positive real numbers

$$\begin{aligned} \overline{s_{k,p,q}}=\sum _{j=\min (p,q)+1}^{\max (p,q)}s_{k,j}=(\overline{s_{k,p}}-\overline{s_{k,q}})~\mathrm{sgn}(p-q). \end{aligned}$$

Finally, for any real number $t$, we set $e(t)=e^{it}.$

Theorem 3.1

(Generalized Riesz Products on ${\mathbf {b}}{\mathbb {R}}$) Let $(P_n)_{n \in {\mathbb {N}}}$ be a family of trigonometric polynomials given by (1) and $\sigma _n=\displaystyle {\mathop {{\prod }}_{k=0}^{n}\big |P_k(t)\big |^2} \,dh(t)$, $n=0,1,2,\cdots$. Then $(\sigma _n)_{n \ge 0}$ converge in the weak-$\star$ topology to some probability measure $\sigma$ on ${\mathbf {b}}{\mathbb {R}}$. $\sigma$ will be denoted by

$$\begin{aligned} \displaystyle {\mathop {{\prod }}_{k=0}^{\infty }\bigg |P_k(t)\bigg |^2}. \end{aligned}$$

Proof

Let $R_n(t)=\big |P_{0}(t) \cdots P_n(t)\big |^2$. Then $\sigma _n= R_n(t)dh(t)$, and by the definition of $P_n$, we have

$$\begin{aligned} \big |P_n(t)\big |^2=1+\Delta _n(t)\,\,{\mathrm{with}}\,\,\Delta _n(t) =\frac{1}{p_n}\sum _{p \ne q} e\bigg (\big ((p-q)h_n+\overline{s_{n,p,q}}~\mathrm{sgn}(p-q)\big )t\bigg ). \end{aligned}$$

Hence, obviously

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} \big |P_n(t)\big |^2 dh(t)=1. \end{aligned}$$

Put

$$\begin{aligned} W_n=\{(b-a)h_{n}+\overline{s_{n,b}}-\overline{s_{n,a}} \mid b\ne a \in \{0,\cdots ,p_{n}-1\}\}. \end{aligned}$$

By expanding the product of the $\left| P_{k}(t)\right| ^2$, we can write

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} R_n(t) dh(t)-1, \end{aligned}$$

as a sum of terms of the type

$$\begin{aligned} \frac{1}{p_0 \cdots p_n}\int _{{\mathbf {b}}{\mathbb {R}}} e \left( \sum _{j=1}^n \epsilon _jw_j t \right) dh(t), \end{aligned}$$

where each $\epsilon _j$ is 0 or 1 (not all $=0$) and each $w_j$ belongs to $W_j$. To show that $\displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} R_n(t) dh(t)-1=0$, it is sufficient to prove that each of these terms is null. For that, it is sufficient to prove that each of the numbers $\sum _{j=1}^k \epsilon _jw_j$ has absolute value ${\ge }{1}$.

We consider one of these expressions $\sum _{j=1}^n \epsilon _jw_j$ and denote by $j_0$ the greater index $j$ such that $\epsilon _j\ne 0$. Then, we have

$$\begin{aligned} \left| \sum _{j }\epsilon _j w_j\right| \ge \left| w_{j_0}\right| -\sum _{j<j_0} \left| w_{j}\right| . \end{aligned}$$

Moreover, for all $j$,

$$\begin{aligned} h_{j}\le \left| w_{j}\right| \le (p_{j}-1)h_{j}+\overline{s_{j,p_{j}-1}}. \end{aligned}$$

Hence, to conclude, it is sufficient to prove that

$$\begin{aligned} h_{{j_0}}-\sum _{j=0}^{j_0-1}\big ((p_{j}-1)h_{j}+\overline{s_{j,p_{j}-1}}\big )\ge 1. \end{aligned}$$

The equality

$$\begin{aligned} h_{n}=p_{n-1}h_{n-1}+\overline{s_{n-1,p_{n-1}-1}} \end{aligned}$$

implies by induction

$$\begin{aligned} h_{n}-\sum _{k=0}^{n-1}(p_{k}-1)h_{k}+\overline{s_{k,p_{k}-1}}=1, \end{aligned}$$

whence

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} R_n(t) dh(t)=1. \end{aligned}$$

(3)

Thus $\sigma _n$ is a probability measure on ${\mathbf {b}}{\mathbb {R}}$. In addition, for any $t \in {\mathbb {R}}$, we have

$$\begin{aligned} R_{n+1}(t)=R_n(t)|P_n(t)|^2=R_n(t)+R_n(t)\Delta _n(t), \end{aligned}$$

since $\widehat{R_{n}}$ and $\widehat{\Delta _{n}}$ are $\ge 0$ on ${\mathbb {R}}$

$$\begin{aligned} \widehat{\sigma _{n+1}}\big (\lambda \big )= & {} \widehat{R_{n+1}}\big (\{\lambda \})\\= & {} \widehat{R_{n}}\big (\{\lambda \})+ \widehat{R_n}*\widehat{\Delta _n}(\lambda )\\\ge & {} \widehat{R_{n}}\big (\{\lambda \})= \widehat{\sigma _n}\big (\lambda \big ). \end{aligned}$$

Consequently the limit $r_{\lambda }$ of the sequence $(\widehat{\sigma _n}\big (\lambda \big ))$ exists. Now, since ${\mathbf {b}}{\mathbb {R}}$ is a compact space, and $(\sigma _n)$ is a sequence of probability measures on ${\mathbf {b}}{\mathbb {R}}$, we can extract a subnet $(\sigma _{n_k})$ which converges weakly to some probability measure on ${\mathbf {b}}{\mathbb {R}}$. This gives that the limit of $(\sigma _n)$ exists in the weak-$\star$ topology and the proof is complete. $\square$

The proof above is largely inspired by Lemma 2.1 in [20]; it gives more, namely, the polynomials $P_n$ given in (1) can be chosen with positive coefficients and satisfying

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} \bigg |P_n(t)\bigg |^2 dh(t)=1\,\,\mathrm{and}\,\,\int _{{\mathbf {b}}{\mathbb {R}}} \mathop {{\prod }}_{j=1}^{n}\bigg |P_j(t)\bigg |^2 dh(t)=1. \end{aligned}$$

We further mention that we have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} \mathop {{\prod }}_{j=1}^{k}\bigg |P_{n_j}(t)\bigg |^2 dh(t)=1, \end{aligned}$$

(4)

for any given sequence of positive integers $n_1<n_2<\cdots <n_k,~~k \in {\mathbb {N}}^*$. The proof is the same as the proof of (3).

We are now able to formulate our main result.

Theorem 3.2

(Main result) Let $(p_m)_{m \in {\mathbb {N}}}$ be a sequence of positive integers greater than $1$ and $((s_{m,j})_{j=0}^{p_m-1})_{m \in {\mathbb {N}}}$ be a sequence of positive real numbers. Defining $(h_m)$ as in (2) and assuming that there exists a sequence of positive integers $m_1<m_2<\cdots ,$ such that, the numbers $h_{m_j},s_{m_j,0},\cdots ,s_{m_j,{p_{m_j}-1}},$ $j=1,2, \cdots ,$ are rationally independent. Then the generalized Riesz product

$$\begin{aligned} \mu =\displaystyle {\prod _{k=0}^{+\infty }\big |P_k(t)\big |^2} \end{aligned}$$

where $P_k$ is given by (1), is singular with respect to the Haar measure on ${\mathbf {b}}{\mathbb {R}}$.

We recall that the real numbers $\lambda _1,\lambda _2,\cdots ,\lambda _r$, $r \ge 2$, are rationally independent if they are linearly independent over ${\mathbb {Z}}$ , i.e. for all $n_1,\cdots ,n_r \in {\mathbb {Z}},$

$$\begin{aligned} n_1\lambda _1+\cdots +n_r\lambda _r=0 \Longrightarrow n_1=\cdots =n_r=0. \end{aligned}$$

We say that the set of real number $\big \{\lambda _n,~~n \ge 1~\big \}$ is rationally independent if for any finite subsequence $m_1,m_2,\cdots , m_r$, the real numbers $\lambda _{m_1},\lambda _{m_2},\cdots ,\lambda _{m_r}$ are rationally independent.

4 On Kakutani’s Criterion and Bourgain’s Singularity Criterion in the Setting of Generalized Riesz Products on ${\mathbf {b}}{\mathbb {R}}$

The famous dichotomy theorem of Kakutani has a rather long history. In his 1948 paper [17], Kakutani established a purity law for infinite product measures. More precisely, he proved that if $\displaystyle {\mathbb {P}}=\bigotimes _{i=1}^{+\infty }{\mathbb {P}}_i$ and $\displaystyle {\mathbb {Q}}=\bigotimes _{i=1}^{+\infty }{\mathbb {Q}}_i$ are infinite product measures, where ${\mathbb {P}}_i, {\mathbb {Q}}_i$ are probability measures such that ${\mathbb {P}}_i$ is absolutely continuous with respect to ${\mathbb {Q}}_i$, for each positive integer $i$. Then

$$\begin{aligned} {\mathbb {P}}\ll {\mathbb {Q}}~\mathrm{or}~ {\mathbb {P}}\perp {\mathbb {Q}}~\mathrm{according}\, \mathrm{as}~ \displaystyle \prod _{i} \int \bigg (\frac{d{\mathbb {P}}_i}{d{\mathbb {Q}}_i}\bigg ) d{\mathbb {Q}}_i ~\mathrm{converges~ or~ diverges.} \end{aligned}$$

There are a several proofs of Kakutani’s criterion in literature (see [5] and the references therein). For a proof based on the Hellinger’s integral we refer the reader to [8], p. 60].

Here, applying Bourgain’s methods combined with the central limit tools introduced in [12], we obtain a new extension of Kakutani’s theorem in the setting of generalized Riesz products on ${\mathbf {b}}{\mathbb {R}}$. Indeed, we will see that the independence along subsequences allows us to prove the singularity.

We start by stating and proving the Bourgain’s singularity criterion in the setting of ${\mathbf {b}}{\mathbb {R}}$. We remind that this criterion in the periodic setting follows from the initial remarks in the proof of Proposition 1 in [4], Equations (2.15) and (2.22)].

Theorem 4.1

(${\mathbf {b}}{\mathbb {R}}$ version of Bourgain’s criterion) The following are equivalent

• (i)

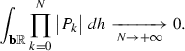
• (ii) $\mu$ is singular with respect to the Haar measure.

• (iii) $\inf \left\{ \displaystyle \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} {{\prod _{\ell =1}^L\big | {P_{n_\ell }}\big |\;}} dh\;:\; L\in {{\mathbb {N}}},~n_1<n_2<\ldots <n_L\right\} =0.$

Proof

$(i)\Longrightarrow (ii)$: it suffices to show that for any $\epsilon >0$, there is a Borel set $E \subset {\mathbf {b}}{\mathbb {R}}$ with $h(E)<\epsilon$ and $\mu (E^c)<\epsilon$. Let $0<\epsilon <1$, by $(i)$ there exists $N_0$ such that

$$\begin{aligned} \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} {\prod _{k=0}^{N_0}|P_k|} \;dh<\epsilon ^2. \end{aligned}$$

The set $E=\left\{ \lambda \in {\mathbf {b}}{\mathbb {R}}\;:\;{\prod _{k=0}^{N_0}|P_k(\lambda )|} \ge \epsilon \right\}$ satisfies:

$$\begin{aligned} h(E)\le \frac{1}{\epsilon }\left\| {\prod _{k=0}^{N_0}P_k}\right\| _1\le \epsilon ^2/\epsilon =\epsilon , \end{aligned}$$

and, since $E^c$ is an open set, it follows by the portmanteau theorem that

$$\begin{aligned} \mu (E^c)\le & {} \liminf _{M\rightarrow +\infty }\int _{E^c}{\prod _{k=0}^{M}|P_k|^2}\; dh\\\le & {} \liminf _{M\rightarrow +\infty }\int _{E^c}{\prod _{k=0}^{N_0}|P_k|^2 \prod _{k=N_0+1}^{M}|P_k|^2}\;dh\\\le & {} \epsilon ^2 \lim _{M\rightarrow +\infty } \int _{{\mathbf {b}}{\mathbb {R}}}{\prod _{k=N_0+1}^{M}|P_k|^2}\; dh= \epsilon ^2 <\epsilon . \end{aligned}$$

For $(ii) \Longrightarrow (i)$: given $0<\epsilon <1$, there exists a continuous function $\varphi$ on ${\mathbf {b}}{\mathbb {R}}$ such that:

$$\begin{aligned} 0\le \varphi \le 1,\qquad \mu (\{\varphi \ne 0\})\le \epsilon \qquad (*)\qquad \hbox {and}\quad h(\{\varphi \ne 1\})\le \epsilon \qquad (**). \end{aligned}$$

Indeed, by hypothesis, there exists a Borel set $E \subset {\mathbf {b}}{\mathbb {R}}$ such that $\mu (E)=h(E^c)=0.$ Let $K \subset E$ be a compact set such that $h(K^c) < \epsilon$. Since $\mu (K)=0$, we can choose a compact set $L \subset K^c$, such that $\mu (L^c) <\epsilon$. Then, by Urysohn’s Lemma [10], pp.47], there exists a continuous function $\varphi ~~:{\mathbf {b}}{\mathbb {R}}\rightarrow [0,1]$, taking the value $0$ at all points of $L$, and the value $1$ at all points of $K$. It is easy to check that $\varphi$ satisfy $(*)$ and $(**)$.

Let $f_N=\displaystyle {\prod _{k=1}^N |P_k|}$. By Cauchy–Schwarz inequality, we have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} f_N\ dh= & {} \displaystyle \int _{\{\varphi \ne 1\}} f_N\ dh+ \int _{\{\varphi = 1\}} f_N\ dh\\\le & {} h(\{\varphi \ne 1\})^{1/2}\left( \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} f_N^2\ dh\right) ^{1/2} + \left( \displaystyle \int _{\{\varphi = 1\}} f_N^2\ dh\right) ^{1/2} h(\{\varphi = 1\})^{1/2}\\\le & {} \sqrt{\epsilon } + \left( \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} f_N^2\, \varphi \ dh\right) ^{1/2}. \end{aligned}$$

Since $\mu$ is the weak limit of $f_N^2 dh$, we obtain

$$\begin{aligned} \lim _{N\rightarrow \infty } \int _{{\mathbf {b}}{\mathbb {R}}} f_{N}^2\, \varphi \ dh=\int _{{\mathbf {b}}{\mathbb {R}}} \varphi \ d\mu \le \mu (\{\varphi \ne 0\})\le \epsilon . \end{aligned}$$

Thus, $\limsup \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} f_N\ dh\le 2 \sqrt{\epsilon }$. Since $\epsilon$ is arbitrary, we get $\displaystyle \lim _{N\rightarrow \infty } \displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} f_{N}\ dh=0.$

Now $(i)$ obviously implies $(iii)$ and by a simple application of Cauchy–Schwarz inequality, $(iii)$ implies $(i)$. Indeed, consider $n_1<n_2<\ldots <n_L$, $N\ge n_L$ and denote $\mathcal {N}=\left\{ n_1<n_2<\ldots <n_L\right\}$ with $\mathcal {N}^c$ its complement in $\left\{ 1,\cdots ,N\right\}$. Then

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}\prod _{k=0}^{N}|P_k|\ dh= & {} \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N}|P_k|^{\frac{1}{2}} \times \prod _{k\in \mathcal N^c}|P_k|^{\frac{1}{2}}\prod _{k=0}^N|P_k|^{\frac{1}{2}}\ dh\\\le & {} \left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N}|P_k|\ dh\right) ^{\frac{1}{2}}\left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N^c}|P_k|\times \prod _{k=0}^N|P_k|\ dh\right) ^{\frac{1}{2}} \\\le & {} \left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N}|P_k|\ dh\right) ^{\frac{1}{2}}\left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N^c}|P_k|^2\ dh\right) ^{\frac{1}{4}}\left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k=0}^N|P_k|^2\ dh\right) ^{\frac{1}{4}}. \end{aligned}$$

Therefore

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}\prod _{k=0}^{N}|P_k|\ dh\le & {} \left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N}|P_k|\ dh\right) ^{\frac{1}{2}}\left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N^c}|P_k|^2\ dh\right) ^{\frac{1}{4}}\left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k=0}^N|P_k|^2\ dh\right) ^{\frac{1}{4}}\\= & {} \left( \int _{{\mathbf {b}}{\mathbb {R}}} \prod _{k\in \mathcal N}|P_k|\ dh(t)\right) ^{\frac{1}{2}}. \end{aligned}$$

The last equality follows from (4). $\square$

From now, let us fix a sequence ${\mathcal {M}}$ of positive integers for which the set $\big \{h_m,s_{m,0},\cdots ,s_{m,p_m-1},~~m\in {\mathcal {M}}\}$ is linearly independent over the rational numbers. Let $\ k \in {{\mathbb {N}}}$ and let ${\mathcal {N}}=\left\{ n_1<n_2<\ldots <n_k\right\}$ be a subsequence of ${\mathcal {M}}$. Put

$$\begin{aligned} Q_k\left( t\right) =\mathop {{\prod }}_{i=1}^k {P_{n_i}(t)}. \end{aligned}$$

Our strategy in the proof of our main theorem is to construct a subsequence $\left\{ n_1<n_2<\ldots \right\}$ of ${\mathcal {M}}$ for which the Bourgain’s criterion (Theorem 4.1) holds.

Having in mind applications beyond the context of this paper, we state and prove a sufficient condition for the existence of an absolutely continuous component with respect to the Haar measure for a given Riesz product on ${\mathbf {b}}{\mathbb {R}}$. In the case of the torus, the result is due to Mélanie Guenais [14].

Proposition 4.2

If $\displaystyle \sum _{k=1}^{+\infty }\sqrt{1-\bigg (\int _{{\mathbf {b}}{\mathbb {R}}}{|P_k|\;}dh\bigg )^2}<\infty$, then $\mu$ admits an absolutely continuous component.

Proof

Write $v_k^2=1-\Vert P_k\Vert ^2$. Then $\sum _{k=1}^\infty v_k < \infty$, equivalently $\prod _{k=1}^\infty \Vert P_k\Vert _1 >0$. For all functions $f,g \in L^2({\mathbf {b}}{\mathbb {R}}, dh)$, Cauchy-Schwarz inequality gives

$$\begin{aligned} \mid \Vert f\cdot g\Vert _1 - \Vert f\Vert _1 \Vert g\Vert _1\mid \le (\Vert f\Vert _2^2 -\Vert f\Vert _1^2)^{1/2} (\Vert g\Vert _2^2 -\Vert g\Vert _1^2)^{1/2}. \end{aligned}$$

Fix an integer $n_0 > 1$ and let $k > n_0$. Then

$$\begin{aligned}&\left| \Big \Vert \prod _{j=n_0}^k P_j\Big \Vert _1 - \Big \Vert \prod _{j=n_0}^{k-1}P_j \Big \Vert _1\Vert P_k\Vert _1\right| \\&\quad \le \left( \Big \Vert \prod _{j=n_0}^{k-1}P_j\Big \Vert _2^2 - \Big \Vert \prod _{j=n_0}^{k-1} P_j\Big \Vert _1^2\right) ^{1/2} \bigg (\Vert P_k\Vert _2^2 - \Vert P_k\Vert _1^2\bigg )^{1/2}\\&\quad \le v_k. \end{aligned}$$

hence

$$\begin{aligned} \left| \left\| \prod _{j=n_0}^k P_j\right\| _1 - \left\| \prod _{j=n_0}^{k-1}P_j \right\| _1\Vert P_k\Vert _1\right| \le v_k, \end{aligned}$$

and this gives

$$\begin{aligned} \left| \left\| \prod _{j=n_0}^{k-1} P_j\right\| _1\Vert P_k\Vert _1 - \left\| \prod _{j=n_0}^{k-2}P_j \right\| _1\Vert P_{k-1}\Vert _1\Vert P_k\Vert _1\right| \le v_{k-1}\Vert P_k\Vert _1 \le v_{k-1},\\ \begin{array}{ccc} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots \\ \end{array}\\ \left| \left\| \prod _{j=n_0}^{n_0+1} P_j\right\| _1\prod _{j=n_0+2}^{k}\Vert P_j\Vert _1 - \prod _{j=n_0}^{k}\Vert P_j\Vert _1\right| \le v_{n_0+1}, \end{aligned}$$

since, for any $j \in {\mathbb {N}}$, $\Vert P_j\Vert _1\le 1$ by (4). On adding the above inequalities:

$$\begin{aligned} \left| \left\| \prod _{j=n_0}^kP_j\right\| _1 - \prod _{j=n_0}^k\Vert P_j\Vert _1\right| \le \sum _{j=n_0}^kv_j. \end{aligned}$$

Since $\prod _{j=1}^\infty \Vert P_j\Vert _1 > 0$ and $\sum _{j=1}^\infty v_k < \infty$, we see that $\displaystyle \limsup _{k\rightarrow \infty }\Vert \prod _{j=1}^k P_j\Vert _1 > 0$. Whence, by Bourgain’s criterion for singularity (Theorem 4.1), we see that $\mu$ is not singular to Haar measure on ${\mathbf {b}}{\mathbb {R}}$. $\square$

5 On Kac’s Central Limit Theorem

Kac’s central limit theorem in the setting of ${\mathbf {b}}{\mathbb {R}}$ is stated and proved in [16]. For the sake of completeness we prove it here using standard probability arguments.

We will need the following classical central limit theorem [9], p.81]. For our purpose, we state it in the following form

Theorem 5.1

(Complex CLT) Let $(Z_k)_{k \in {\mathbb {N}}}$ be a sequence of independent and identically distributed complex random variables. Suppose that the real and imaginary parts of $Z_1$ have variance $\frac{1}{2}$ and covariance $0$. Then, the sequence of random variables

$$\begin{aligned} \left( \frac{1}{\sqrt{n}}\sum _{k=1}^{n} Z_{k}\right) _{n\ge 1} \end{aligned}$$

converges in distribution to the complex gaussian measure $\mathcal N_{{\mathbb {C}}}(0,1)$ on ${\mathbb {C}}$.

Now let us state and prove Kac’s central limit theorem.

Theorem 5.2

(Kac’s CLT [16]) Let $(\lambda _n)_{n \in {\mathbb {N}}}$ be a sequence of rationally independent real numbers. Then the functions $\cos (\lambda _n t)+i\sin (\lambda _n t), n=1,\cdots$, are stochastically independent and identically distributed under the Haar measure of ${\mathbf {b}}{\mathbb {R}}$ and converges in distribution to the complex gaussian measure $\mathcal N_{{\mathbb {C}}}(0,1)$ on ${\mathbb {C}}$.

Proof

By Theorem 5.1, it suffices to prove that the random variables $e(\lambda _n t)$, $n=1,\cdots$ are stochastically independent and identically distributed under the Haar measure of ${\mathbf {b}}{\mathbb {R}}$. For that, notice that for any positive integer $k$ and for a given positive integers $l_1,l_2,\cdots , l_k$, we have

$$\begin{aligned}&\int _{{\mathbf {b}}{\mathbb {R}}}\bigg (e(\lambda _1 t)\bigg )^{l_1} \bigg (e(\lambda _2 t)\bigg )^{l_2} \cdots \bigg (e(\lambda _k t)\bigg )^{l_k} dh(t) \\&\quad = \int _{{\mathbf {b}}{\mathbb {R}}}e\bigg (\big (\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k\big ) t\bigg ) dh(t) \\&\quad = \int _{{\mathbf {b}}{\mathbb {R}}}\bigg (e(\lambda _1 t)\bigg )^{l_1}dt \int _{{\mathbf {b}}{\mathbb {R}}} \bigg (e(\lambda _2 t)\bigg )^{l_2}dt \cdots \int _{{\mathbf {b}}{\mathbb {R}}}\bigg (e(\lambda _k t)\bigg )^{l_k} dh(t). \end{aligned}$$

Indeed, $\displaystyle \int _{{\mathbf {b}}{\mathbb {R}}}e\big ((\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k) t\big ) dh(t)=1$ is equivalent to $\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k=0$, and by assumption, this is equivalent to $l_1=l_2=\cdots =l_k=0$. Therefore, if $\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k=0$, then

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}e\big ( (\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k) t\big ) dh(t)=1 =\prod _{j=1}^{k}\int _{{\mathbf {b}}{\mathbb {R}}}\bigg (e(\lambda _j t)\bigg )^{0}dh(t), \end{aligned}$$

and if $\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k \ne 0$, then

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}e\big ((\lambda _1l_1+\lambda _2l_2+\cdots +\lambda _kl_k) t \big ) dh(t)=0= \prod _{j=1}^{k}\int _{{\mathbf {b}}{\mathbb {R}}}e(\lambda _j l_j t)dh(t). \end{aligned}$$

Hence, the random variables $e(\lambda _n t),$ $n=1,\cdots$, are stochastically independent under the Haar measure on ${\mathbf {b}}{\mathbb {R}}$. It remains to prove that $e(\lambda _n t),$ $n=1,\cdots$, are identically distributed.

Let $s_1,s_2 \in {\mathbb {R}}$ and let us compute the characteristic function of the random variable $e( \lambda t)$, with $\lambda \in \{\lambda _n,~~n=1,2,\cdots \}$. We have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}e\bigg (\mathrm{Re}\big ((s_1+is_2).e(-\lambda t)\big )\bigg ) dh(t)= & {} \sum _{n=0}^{+\infty } \frac{i^n}{n!}\int _{{\mathbf {b}}{\mathbb {R}}}\bigg (\mathrm{Re}\big ((s_1+is_2).e(-\lambda t)\big )\bigg )^n dh(t)\\= & {} \sum _{n=0}^{+\infty } \frac{i^n}{n!}\int _{{\mathbf {b}}{\mathbb {R}}}\bigg (s_1\cos (\lambda t)+s_2 \sin (\lambda t)\bigg )^n dh(t). \end{aligned}$$

Write

$$\begin{aligned} \cos (\lambda t)=\frac{1}{2}\bigg (e(\lambda t)+e(-\lambda t)\bigg ),~~~~ \sin (\lambda t)=\frac{1}{2i}\bigg (e(\lambda t)-e(-\lambda t)\bigg ), \end{aligned}$$

and notice that we have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}e(\alpha t)dh(t)= \lim _{T \longrightarrow + \infty }\frac{1}{2T}\int _{-T}^{T} e(\alpha t)dt={\left\{ \begin{array}{ll} 1 \quad \mathrm{if}~\alpha =0,\\ 0 \quad \mathrm{if~not.} \end{array}\right. } \end{aligned}$$

Therefore

$$\begin{aligned}&\int _{{\mathbf {b}}{\mathbb {R}}}\bigg (s_1\cos (\lambda t)+s_2 \sin (\lambda t)\bigg )^n dh(t)\\&\quad =\sum _{k=0}^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{(s_2+is_1)^k (-s_2+is_1)^{n-k}}{(2i)^n}\left( \int _{{\mathbf {b}}{\mathbb {R}}} e\left( (2k-n) \lambda t\right) dh(t)\right) . \end{aligned}$$

Whence

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}\bigg (s_1\cos (\lambda t)+s_2 \sin (\lambda t)\bigg )^n dh(t) ={\left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}n\\ \frac{n}{2}\end{array}}\right) (-1)^{\frac{n}{2}}\frac{(s_2^2+s_1^2)^{{\frac{n}{2}}}}{(2i)^n} &{}\text {if n~is~even,}\\ 0&{}\text {if}~ n~\mathrm{is~odd}.\nonumber \end{array}\right. } \end{aligned}$$

We thus get

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}e\bigg (\mathrm{Re}\big ((s_1+is_2).e(-\lambda t)\big )\bigg ) dh(t)= & {} \sum _{l=0}^{+\infty } \frac{(-1)^l}{4^l(l!)^2}(s_1^2+s_2^2)^l=J_0(|s_1+is_2|)\\= & {} \frac{1}{\pi }\int _{0}^{\pi }\cos \bigg (|s_1+is_2|.\sin (t)\bigg ) dt, \end{aligned}$$

where $J_0$ is the familiar Bessel function. We conclude that the hypotheses of central limit theorem 5.1 are satisfied, and the sequence

$$\begin{aligned} \left( \frac{1}{\sqrt{n}}\sum _{k=1}^{n} e(\lambda _k t)\right) _{n\ge 1} \end{aligned}$$

converges in distribution to the complex gaussian measure $\mathcal N_{{\mathbb {C}}}(0,1)$ on ${\mathbb {C}}$. In particular, by Theorem 5.3 below,

$\square$

It is well-known that the convergence in distribution or probability does not in general imply that the moments converge (even if they exist). The useful condition to ensure the convergence of the moments is the uniform integrability. Indeed, we have

Theorem 5.3

If the sequence of random variables $\{X_n\}$ converges in distribution to some random variable $X$ and if for some $p>0$, $\displaystyle \sup _{n \in {\mathbb {N}}} \big ({\mathbb {E}}(|X_n|^{p})\big ) =M <+\infty$, then for each $r<p$,

$$\begin{aligned} \lim _{n \longrightarrow +\infty }{\mathbb {E}}\bigg (\big |X_n\big |^r\bigg )={\mathbb {E}}\bigg (\big |X\big |^r\bigg ). \end{aligned}$$

For the proof of Theorem 5.3 we refer to [2], pp. 32–33] or [7], p. 100]. We remind that the condition

$$\begin{aligned} \sup _{ n \in {\mathbb {N}}}\bigg ({\mathbb {E}}\big (\big |X_n\big |^{1+\varepsilon }\big )\bigg ) < +\infty , \end{aligned}$$

for some $\varepsilon$ positive, implies that $\{X_n\}$ are uniformly integrable.

Notice that our proof yields that for any sequence $(\lambda _j)_{j \in {\mathbb {N}}}$ of rationally independent numbers, we have

(5)

6 Proof of the Main Result (Theorem 3.2)

Using the analogue of Féjer’s lemma combined with the CLT methods introduced in [12], we will give a direct proof of the singularity of a large class of generalized Riesz products on ${\mathbf {b}}{\mathbb {R}}$. Therefore, our strategy is slightly different from the strategy used by many authors in the case of the torus [4, 12, 19, 20]. More precisely, they showed that the weak limit point of the sequence $\left( \left| |P_m|^2-1\right| \right)$ is bounded below by a positive constant and it is well-known that this implies the singularity of the generalized Riesz products (see for instance [12] or [19]).

Let us start our proof with the following analogue of Féjer’s lemma [29], Theorem 4.15, p. 52]

Lemma 6.1

Under the notations of Theorem 3.2, let $n_1<n_2<\cdots <n_k \in {\mathcal {M}}$ and $Q=\prod _{j=1}^{k}P_{n_j}$. Then, for any $m > n_k$, $m\in {\mathcal {M}}$, we have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} {|Q| \big | {P_m} \big |} dh= \bigg (\int _{{{\mathbf {b}}{\mathbb {R}}}} {|Q|} dh\bigg ) \bigg (\int _{{\mathbf {b}}{\mathbb {R}}}{|P_m|} dh\bigg ). \end{aligned}$$

Proof

By our assumption $\big (h_k, (s_{k,p_k-1})\big )_{k \in {\mathcal {M}}}$ are rationally independent. Hence, by Kac’s theorem (Theorem 5.2), for $m>{n_k}$, $m\in {\mathcal {M}}$, $Q$ and $P_m$ are stochastically independent since $Q$ is the sum of the random variables $e(\lambda t)$ with $\lambda \in \{jh_{n_i}+\overline{s_{n_i,j}}, j=0,\cdots ,p_{n_i}-1,i=1,\cdots ,k\}$ and $P_m$ is the sum of the random variables $e(\lambda t)$ with $\lambda \in \{jh_{m}+\overline{s_{m,j}}, j=0,\cdots ,p_{m}-1\}$. $\square$

Proof of Theorem 3.2

By application of Lemma 6.1 combined with (5), we proceed inductively to construct a subsequence $\{n_k\}$ of ${\mathcal {M}}$ such that, for any $k \ge 1$, we have

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}} { \mathop {{\prod }}_{j=1}^{k+1} \big |{P_{n_j}}\big |} dh\le \frac{51}{100}\sqrt{\pi }\int _{{\mathbf {b}}{\mathbb {R}}} { \mathop {{\prod }}_{j=1}^{k} \big |{P_{n_j}}\big |} dh. \end{aligned}$$

(6)

Denote $u_k=\displaystyle \int _{{\mathbf {b}}{\mathbb {R}}} { \mathop {{\prod }}_{j=1}^{k} \big |{P_{n_j}}\big |} dh$. Since $\displaystyle \frac{51}{100}\sqrt{\pi }<1$, the sequence $(u_k)$ will be decreasing with limit $0$. Hence, $\mu$ is singular with respect to the Haar measure by Bourgain’s criterion (Theorem 4.1).

By our assumption combined with Theorem 5.2, $(P_m)_{m \in {\mathcal {M}}}$ converges in distribution to the complex gaussian measure $\mathcal N_{{\mathbb {C}}}(0,1)$. Hence, from Theorem 5.3 applied with $p=2$ and $r=1$ we get

$$\begin{aligned} \lim _{\overset{m\longrightarrow +\infty }{m\in {\mathcal {M}}}}\int _{{\mathbf {b}}{\mathbb {R}}}{|P_m|}dh= \int _{{\mathbb {C}}} \big |z\big | d{\mathcal N_{{\mathbb {C}}}(0,1)}(z)=\frac{\sqrt{\pi }}{2}. \end{aligned}$$

(7)

Recall that the density of the standard complex normal distribution $\mathcal N_{{\mathbb {C}}}(0,1)$ is given by

$$\begin{aligned} f(z) = \frac{1}{\pi } e^{-|z|^2}. \end{aligned}$$

Let us assume that we have already construct $n_1<n_2<n_3<\cdots <n_k$ satisfying $u_k \le \frac{51}{100}\sqrt{\pi } u_{k-1}$. By (7) there exists $m>n_k$, $m\in {\mathcal {M}}$, such that

$$\begin{aligned} \Big |\int _{{\mathbf {b}}{\mathbb {R}}}{|P_m|}dh-\frac{\sqrt{\pi }}{2}\Big | < \frac{\sqrt{\pi }}{100}. \end{aligned}$$

Therefore, by Lemma 6.1, we can write

$$\begin{aligned} \int _{{\mathbf {b}}{\mathbb {R}}}{{|Q| |P_m|}} dh\le \frac{51\sqrt{\pi }}{100} \int _{{\mathbf {b}}{\mathbb {R}}}{|Q|} dh, \end{aligned}$$

and set $n_{k+1}=m$. This implies that the inequality (6) holds which finish the proof of the theorem. $\square$

Remark 6.2

The argument in the above proof strongly depends on the assumption that along subsequence the set of positive real numbers $\big \{h_m,s_{m,0},\cdots ,s_{m,p_m-1},~~~~m\ge 1\big \}$ is linearly independent over the rationales. In the general case, one may use the methods of [4, 19], [20] and [12] to establish the singularity of a large class of generalized Riesz products on ${\mathbf {b}}{\mathbb {R}}$, in particular when $(p_m)$ is bounded. In a forthcoming paper, we will see how to extend classical results from the torus and real line settings to the Riesz products on ${\mathbf {b}}{\mathbb {R}}$.

In view of (5) one may ask

Question 1

Let $n \in {\mathbb {N}}^*$ and put

$$\begin{aligned} J_{\lambda ,n}= \left\{ P \in {\mathcal {P}}~:~P(t)=\sum _{k=0}^{n}a_k e^{i \lambda _k t}, a_0=1,~a_k \in \{0,1\} \right\} , \end{aligned}$$

where ${\mathcal {P}}$ is the subspace of polynomials on ${\mathbf {b}}{\mathbb {R}}$. The polynomials in $J_{\lambda ,n}$ are called Newman polynomials. Is it true that have for any increasing sequence $(\omega _j)_{j \in {\mathbb {N}}}$ of real numbers, we have

$$\begin{aligned} {\sup _{n \ge 1}}\bigg \{{\sup _{P \in J_{\omega , n}}}\bigg (\frac{\big \Vert P(t)\big \Vert _1}{\big \Vert P(t)\big \Vert _2}\bigg )\bigg \}<1? \end{aligned}$$

In the contrast of the previous question, one may ask

Question 2

Does there exist a sequence of $L^1$-flat Newman polynomials on ${\mathbf {b}}{\mathbb {R}}$? That is, does there exist a sequence of polynomials $P_n \in J_{\lambda ,n}$ such that

$$\begin{aligned} \lim _{n \longrightarrow +\infty } \frac{\big \Vert P_n(t)\big \Vert _1}{\big \Vert P_n(t)\big \Vert _2}=1? \end{aligned}$$