Analytic Monotone Pseudospectral Interpolation

Abstract

In the paper we construct an analytic pseudospectral interpolant to a monotone interpolating table. The approximant is a sum of a linear function and a trigonometric polynomial of degree depending on the number and variation of the interpolating conditions. In the case when the interpolating cites are equidistant exact interpolation is obtained. In all of the other cases the error of approximation is shown to decrease geometrically fast with respect to the degree of the trigonometric polynomial. The least degree of the interpolating polynomial is discussed. Applications in signal processing including numerical examples are considered.

1 Introduction

Any $2\pi$-periodic function, $f$, with a bounded variation $\int _0^{2\pi }|f'(t)|\; dt$ can be expanded into an infinite series in terms of the bi-orthogonal systems $e^{is\theta (t)}$ and $\theta '(t)e^{is\theta (t)}, s\in \mathbb {Z}$. For a phase function $\theta$ with a positive continuous $\theta '$ on $[0,2\pi ]$ the series is

$$\begin{aligned} f(t)=\sum _{s=-\infty }^\infty c_se^{is\theta (t)},\;\;\;c_s=\frac{1}{2\pi }\int _0^{2\pi }\theta '(t)f(t)e^{is\theta (t)}\; dt. \end{aligned}$$

(1.1)

The convergence is uniform on $[0,2\pi ]$. The series (1.1) can be obtained from the classical Fourier series of $f(\theta ^{-1}(t))$, where $\theta ^{-1}$ is the inverse of $\theta$ on the interval $[0,2\pi ]$. There are many similarities between the series (1.1) and the Fourier series expansion of $f$, provided that the function $\theta '$ is $2\pi -$periodic. In particular it is interesting to estimate how much the analytic signal of $\cos s \theta , s>0$, defined as $A\cos s\theta =\cos s\theta +iH\cos s\theta$ differs from the quadrature signal $e^{is\theta }, s>0$ for a given phase function $\theta$. For a $2\pi -$periodic function, $f$, the conjugate operator $H$ is $Hf(t)=\frac{1}{2\pi }\int _0^{2\pi }f(x)\cot \frac{t-x}{2}\; dx$.

In practice one may know or approximate the zeros of a real-valued function $\cos s\tilde{\theta }$ for an unknown $\tilde{\theta }$. Then an interpolating function of the form $\cos s\theta$ has to have a phase function $\theta$ that takes values $\theta _j=\frac{2m+1}{2s}\pi , m=0,1,\ldots ,2s-1$ at the known zeros and $\theta '>0$. Instead of directly constructing $\theta$, one can construct first $\theta ^{-1}$ by interpolating at the equidistant points $\theta _j$. Interpolation at the zeros of $\cos st$ is known as pseudospectral and hence we call the functions constructed in the paper pseudospectral interpolants. The case of equidistant interpolation is considered in details in Sect. 4.

To measure the deviation of the quadrature signal $e^{is\theta }$ from the analytic signal $A\cos s\theta ,\; s\in \mathbb {N}$ we use the point-wise estimate, see [3] and the references within,

$$\begin{aligned} \left| e^{is\theta }-A\cos s\theta \right| \le \frac{1}{\pi }\sum _{n=-\infty }^{-1}\left| \int _0^{2\pi }e^{is\theta (t)-int}\; dt\right| . \end{aligned}$$

The convergence of the above series depends on the properties of $\theta$. In particular, it depends on the rate of decay with respect to $s>0$ and $n<0$ of the function

$$\begin{aligned} F(s,n)(\theta )=\int _{0}^{2\pi }e^{is\theta (t)}e^{-int}\; dt. \end{aligned}$$

It is well known, see [1], that the rate of decay depends on the smoothness of $\theta$. Summing up the desirable properties of $\theta$ we formulate the problem:

Given an interpolating table $U=(x_j,y_j)_{j=1}^M$, with constrains $0=x_1<x_2< \ldots <x_{M-1}<x_M=2\pi$ and $y_1<y_2< \ldots <y_{M-1}<y_M$, construct a smooth interpolant or approximant that preserves the monotonicity of the data.

The problem of interpolating $U$ by algebraic polynomials is best known from the works of Passow and Raymon [13] and Iliev [10]. The authors estimate the least degree of the algebraic interpolating polynomial. The estimates are in terms of

$$\begin{aligned} \Delta (y)= & {} \max _j(y_j-y_{j-1}), \delta (y)=\min _j(y_j-y_{j-1}),\\ \delta (x)= & {} \min _j |x_j-x_{j-1}|,\Sigma =\max _j\left| \frac{y_j-y_{j-1}}{x_j-x_{j-1}} \right| . \end{aligned}$$

In [13], it is shown that the degree is no less than $C\frac{\Sigma }{\delta (y)}$, and in [10] in the case when $\delta (x)\ge c_0\frac{1}{M}$ the degree is no less than $\frac{C}{\delta (x)}\ln \Big (e+\frac{\Delta (y)}{\delta (y)}\Big )$, where $C$ and $c_0$ are absolute constants. The constructions of such algebraic interpolants involve solving large linear systems.

The problem has been intensively studied for the Sobolev classes $W^k[a,b]=\{f|f^{(k)}\in C[a,b]\}$, where $C[a,b]$ is the space of the continuous functions equipped with the norm $\Vert f\Vert _{C[a,b]}=\max _{x\in [a,b]}|f(x)|$. For practical applications the most interesting cases are when $k\le 3$, then the interpolants are spline functions, cubic or quadratic with extra nodes. The first algorithm, for $k=1$, was introduced by Fritsch and Carlson, [8], and later improved in [9]. Schumaker was the first to introduce extra nodes in [14]. In Sect. 2 we construct a spline interpolant with continuous $k$-th derivative for any integer $k$.

To construct an increasing phase function with all of its derivatives periodic we relax the interpolation conditions, namely we construct an analytic, monotone, and periodic function $f$ such that $|f(x_j)-y_j|<\epsilon (M), j=1,\ldots ,M$, for some function $\epsilon (M)\rightarrow 0$ as $M\rightarrow \infty$. The functions $\epsilon (M)$ used in the paper are either $M^{-k}$ for a natural $k$, or $q^M$ with $0<q<1$. The resulting interpolants or approximants are either algebraic polynomials, $P_n$, or linear functions, $L$, plus trigonometric polynomials, $T_n$. In both cases the least possible degree $n^*$ is either an absolute constant, or $\ln M$, multiple of the least degree in [10]. A numerical method for constructing such a function is based on trigonometric interpolation at equally spaced nodes known as pseudospectral method, [1]. In Sect. 3 analytic pseudospectral interpolants are obtained by using trigonometric approximation and the case of equidistant interpolation nodes is studied. In Sect. 5 the function $F(s,n)(\theta )$ is estimated an algorithm based on the results is presented. Three numerical examples for quadrature signal $e^{is\theta }$ are considered in Sect. 6.

Throughout the paper $i^2=-1$, $\left[ x\right]$ is the least integer bigger than or equal to $x$, ${ 2k-1 \atopwithdelims ()\left[ \frac{2k-1}{2}\right] }={ 2k-1 \atopwithdelims ()k-1}$, and $C$ stands for an absolute constant.

2 Smooth Monotone Interpolation

In the current section we construct increasing interpolating splines of arbitrary smoothness $k$. The first step in the construction of monotone splines usually is to assign slopes at the interpolating points, (similar to the constructions in [8, 14]). These slopes can be adjusted latter, if necessary. We start by constructing a piece-wise linear monotone function with break points $t_j = \frac{x_{j-1}+x_j}{2},\quad j=2,\ldots ,M$. Let $I_j=[x_{j-1},x_j),j=2,\ldots ,M$, $J_1=[x_1,t_2),J_j=[t_j,t_{j+1}),j=2,\ldots , M-1, J_M=[t_M,x_M]$. The slopes $s_j$ at the points $x_j$ have to satisfy the monotone conditions

$$\begin{aligned} 0< s_j\le & {} \min \left( \frac{y_j-y_{j-1}}{x_j-x_{j-1}},\frac{y_{j+1}-y_j}{x_{j+1}-x_j} \right) , j=2,\ldots ,M-1;\\ 0< s_1\le & {} \frac{y_2-y_1}{x_2-x_1},\;\;\;\;0< s_M\le \frac{y_M-y_{M-1}}{x_M-x_{M-1}}. \end{aligned}$$

The slopes will remain unchanged. A more detailed discussion on the selection of the initial function is in the next section. Let $\eta =\min _j|s_j|$ and $\chi _\alpha$ be the characteristic function of the interval $[-\alpha ,\alpha ]$.

For $t\in J_j$, let $R_j(t)=s_j(t-x_j)+y_j$, then

$$\begin{aligned} f_0(t)=\sum _{j=1}^M R_j(t)\chi _{J_j}(t) \end{aligned}$$

is monotone piece-wise linear interpolant to $U$ with points of discontinuity at all of the $t$’s.

The smoothness of the interpolant is further increased by repeated running average. The uniform $B$-splines for fixed $k$ and $\alpha$ are defined as $k-$fold convolution of $\chi _\alpha$, namely

$$\begin{aligned} B_{\alpha ,k}(t)=\frac{1}{(2\alpha )^{k+1}}\underbrace{\chi _\alpha *\chi _\alpha *\ldots *\chi _\alpha }_{k+1 \text { factors }}(t). \end{aligned}$$

For $S_j(t)=R_{j-1}(t)\chi _{(-\infty ,t_{j-1}]}+R_j(t)\chi _{(t_{j-1},\infty )}(t)$, and $\alpha _j\le \frac{|I_j|}{2(k+1)}, j=2,\ldots ,M$ we define the splines

$$\begin{aligned} f_k(t)=\sum _{j=2}^M (S_j*B_{\alpha _j,k}(t))\chi _{I_j}(t). \end{aligned}$$

From the definition and the finite support of the $B$ splines it is clear that the properties of $f_k$ on $I_j$ depend only on the properties of $S_j$ and hence we can restrict our attention to a single interval $I_j$. For $\alpha _j<\frac{|I_j|}{2(k+1)}$ we will show in Corollary 1 that in neighborhoods of the end points of $I_j=[x_{j-1},x_j)$ the spline $f_k$ is identical to $S_j$, around $x_{j-1}$, and to $S_{j+1}$, around $x_j$. In particular $f_k'(x_j)=s_j$ and $f^{(m)}(x_j)=0$ for $m>1$.

The finite difference operator is defined as

$$\begin{aligned} \Delta _{\alpha }^k g(t)=\sum _{m=0}^k(-1)^m {k\atopwithdelims ()m}g(t+(k-2m)\alpha ). \end{aligned}$$

In the next lemma we consider $t\in I_2$ and use the notations $S=S_2,I=I_2, \tau =t_2,\alpha =\alpha _2$, and $B_k=B_{\alpha _2,k}$ but the results hold for any interval $I=I_j$ with the corresponding $S_j$ and $\alpha _j$.

Lemma 1

For any natural $k$ the function $b_k(t)=S*B_k(t)$ is such that $b_k(t)=S(t)$ for $t\in (-\infty ,\tau -(k+1)\alpha ]\cup [\tau +(k+1)\alpha ,\infty )$, $b_k\in C^k$, $b_k'>0$, and

$$\begin{aligned} \Vert b_k^{(k)}\Vert _C < \left( \frac{2\alpha k}{|I|}+3\right) {k \atopwithdelims ()\left[ \frac{k}{2}\right] }\frac{y_1-y_0}{(2\alpha )^k}. \end{aligned}$$

(2.1)

Proof

From the definition of $B_k$, it follows that it is non-zero only on the interval $[t-(k+1)\alpha , t+(k+1)\alpha ]$, i.e. the value of $b_k(t)$ depends only on the values of $t$ from the interval $[t-(k+1)\alpha ,t+(k+1)\alpha ]$.

We consider three cases for $t$. First, let $t\le \tau -(k+1)\alpha$, then it is clear that $b_k$ is the linear function $R_0$ and hence $b_k(t)=S(t)$. Similarly we have $b_k(t)=S(t)$ for $t\ge \tau +(k+1)\alpha$. Thus $b_k$ is infinitely times differentiable, $b_k'=s_0>0$ or $b_k'=s_1>0$, $b_k^{(k)}=0, k>1$ and the lemma is proved for $t\notin (\tau -(k+1)\alpha ,\tau +(k+1)\alpha )$. To the rest of the proof we consider $t\in [\tau -(k+1)\alpha ,\tau +(k+1)\alpha ].$

For $k>1$ the spline $B_{k-1}$ is continuous and from the definition of $B_k$ we have that $B_k'(t)=\frac{1}{2\alpha }(B_{k-1}(t+\alpha )- B_{k-1}(t-\alpha ))$. Hence $b_k'(t)= \frac{1}{2\alpha }( S(t+\alpha )- S(t-\alpha ))*B_{k-1}(t)$. Since $S$ is monotone by construction and $B_{k-1}\ge 0$, it follows that $b_k'(t)>0$ for any real $t$.

By iterative differentiation, it follows that

$$\begin{aligned} B_k^{(k-1)}(t)=\frac{1}{(2\alpha )^{k-1}}\Delta ^{k-1}_{\alpha } B_1(t), \end{aligned}$$

and hence $b_k^{(k-1)}(t)=(S*B_k)^{(k-1)}(t)=S*B_k^{(k-1)}(t)=\frac{1}{(2\alpha )^{k-1}}\Delta _{\alpha }^{k-1} S*B_1(v)$. Since $S*\chi _\alpha$ is continuous and $S*B_1(v)=\frac{1}{(2\alpha )^2}\int _{v-\alpha }^{v+\alpha } S*\chi _\alpha (v_1)\;dv_1$ we get that $(S*B_1)'(v)=\frac{1}{(2\alpha )^2}\int _{-\alpha }^{\alpha } (S(v+v_1+\alpha )-S(v+v_1-\alpha ))\; dv_1$. Summing up we obtain that $b_k\in C^k$ and

$$\begin{aligned} |b_k^{(k)}(t)|=\frac{1}{(2\alpha )^{k+1}}\left| \int _{-\alpha }^{\alpha } \Delta _{\alpha }^k S(v+t)\;dv\right| \le \frac{\Vert \Delta _{\alpha }^k S\Vert _{C(I)}}{(2\alpha )^{k}}. \end{aligned}$$

(2.2)

Let $u=u(t)$ be the index for which

$$\begin{aligned} \Delta _{\alpha }^k S(t)=\sum _{i=0}^u (-1)^i{ k\atopwithdelims ()i} R_1(t+(k-2i)\alpha )+ \sum _{i=u+1}^k (-1)^i{ k\atopwithdelims ()i} R_0(t+(k-2i)\alpha ), \end{aligned}$$

i.e. the largest natural $u$ that satisfies $t+(k-2u)\alpha < \tau$, then $u=\left[ \frac{k}{2}+\frac{t-\tau }{2\alpha }\right] -1$. Since both $R_0$ and $R_1$ are linear, then $\Delta _\alpha ^k R_1=\Delta _\alpha ^k R_0=0$ and it follows that

$$\begin{aligned} \Delta _\alpha ^k S(t)= & {} \sum _{i=0}^u (-1)^i{ k\atopwithdelims ()i} (R_1(t+(k-2i)\alpha )-R_0(t+(k-2i)\alpha ))\\= & {} \sum _{i=u+1}^k (-1)^i{ k\atopwithdelims ()i} (R_0(t+(k-2i)\alpha )-R_1(t+(k-2i)\alpha )). \end{aligned}$$

The function $Q(i)=R_1(t+(k-2i)\alpha )-R_0(t+(k-2i)\alpha )$ is linear with respect to $i$ and

$$\begin{aligned} Q(i)=-(s_1-s_0)2\alpha i+ s_1(t-x_1+k\alpha )-s_0(t-x_0+k\alpha ) +y_1-y_0. \end{aligned}$$

Let $A=-(s_1-s_0)2\alpha$ and $B=s_1(t-x_1+k\alpha )-s_0(t-x_0+k\alpha ) +y_1-y_0$. WLOG we can assume $u\le \left[ \frac{k}{2}\right]$. From the identities ${ k \atopwithdelims ()i} i=k{k-1 \atopwithdelims ()i-1}$ and ${k \atopwithdelims ()i}={k-1 \atopwithdelims ()i}+{ k-1 \atopwithdelims ()i-1}$ it follows that

$$\begin{aligned} |\Delta _{\alpha }^k S(t)|= & {} |\sum _{i=0}^u (-1)^i{ k\atopwithdelims ()i}( Ai+B)|=|kA \sum _{i=1}^u (-1)^i{ k-1 \atopwithdelims ()i-1}+B \sum _{i=0}^u (-1)^i{ k\atopwithdelims ()i}|\\= & {} |Ak{k-2 \atopwithdelims ()u} +B { k-1 \atopwithdelims ()u}|\le |A|k{k-2 \atopwithdelims ()u} +|B| { k-1 \atopwithdelims ()u}. \end{aligned}$$

Since $t\in [\tau -(k+1)\alpha ,\tau +(k+1)\alpha ]$ we have that $|t-x_q+k\alpha |\le |I|$ for $q=0,1$. From the definition of $s_0$ and $s_1$ it follows that $0<s_0,s_1\le \frac{y_1-y_0}{|I|}$ and hence the inequalities $|s_1-s_0|\le \frac{y_1-y_0}{|I|}$ and $|s_1(t-x_1+k\alpha )-s_0(t-x_0+k\alpha )|<2(y_1-y_0)$ hold true. Summing up we get that

$$\begin{aligned} |\Delta _{\alpha }^k S(t)|\le {k-2 \atopwithdelims ()u}\frac{2\alpha k}{|I|}(y_1-y_{0}) + { k-1 \atopwithdelims ()u}3(y_1-y_0). \end{aligned}$$

Finally, the binomial coefficients ${K \atopwithdelims ()u}$ are increasing for $u\le \left[ \frac{K}{2}\right]$ and hence

$$\begin{aligned} |\Delta _{\alpha }^k S(t)|\le \left( \frac{2\alpha k}{|I|}+3\right) {k \atopwithdelims ()\left[ \frac{k}{2}\right] }(y_1-y_0) \end{aligned}$$

which combined with (2.2) completes the proof of the lemma. $\square$

The estimate (2.1) holds on $I_j$ with any choice of $\alpha _j< |I_j|/2(k+1)$. The restriction on $\alpha _j$ is necessary for $f_k$ to satisfy the interpolation condition at $x_j$. The uniform estimate for $\Vert f_k^{(k)} \Vert _{C[0,2\pi ]}$ depends on the minimum of the $\alpha _j$ which is smaller than $\frac{\delta (x)}{2(k+1)}$. It is clear that if such $\alpha$ is used on all of the intervals the uniform estimate stays unchanged. An interpolant that has the same smoothing window, $\alpha '$, on any $I_j$, and satisfies (2.2) for the $k-$th derivative is the function

$$\begin{aligned} G_k(t,\alpha ')=\left( \sum _{j=2}^M S_j\chi _{I_j}(t)\right) *B_{\alpha ',k}(t), \end{aligned}$$

where $\alpha '=\frac{(k-1)^{-1+1/k}}{6}\delta (x)$. For $k>3$ the inequality $k+1<3(k-1)^\frac{k-1}{k}$ holds and hence $\alpha '<\frac{\delta (x)}{2(k+1)}$. The choice of $\alpha '$ simplifies the expressions in the proofs in the next sections.

Corollary 1

The functions $f_k$ and $G_k$ are such that

• (i) $f_k,G_k\in C^k$ and $f_k'>0$, $G_k'>0$ . For any $\alpha \in \left( 0,\frac{\delta (x)}{2(k+1)}\right)$ the following hold true:

• (ii) $f_k(t)=G_k(t)=S_j(t)=s_j(t-x_j)+y_j$ for $t\in (x_j-\frac{|\delta (x)|}{2}+(k+1)\alpha ' , x_j+\frac{|\delta (x)|}{2}-(k+1)\alpha ' )$. Hence $f_k(x_j)=y_j,f'_k(x_j)=s_j$ and $f^{(m)}(x_j)=0$ for $j=1,\ldots ,M$, $m>1$;

• (iii) $\max (\Vert f_k^{(k)} \Vert _{C[0,2\pi ]},\Vert G_k^{(k)} \Vert _{C[0,2\pi ]}) \le {k \atopwithdelims ()\left[ \frac{k}{2}\right] }\frac{4\Delta (y)(k+1)^k}{\delta (x)^k}$. In particular for $k>3$ and $\alpha '=\frac{(k-1)^{-1+1/k}}{6}\delta (x)$ we have that $\max (\Vert f_k^{(k)} \Vert _{C[0,2\pi ]},\Vert G_k^{(k)} \Vert _{C[0,2\pi ]}) \le 12{k \atopwithdelims ()\left[ \frac{k}{2}\right] }\frac{\Delta (y)}{\delta (x)}\left( \frac{3(k-1)}{\delta (x)}\right) ^{k-1}$.

Proof

The properties (i) and (iii) follow from Lemma 1 and the definition of $\alpha '$. For (ii) it is enough to notice that the support of $B_{\alpha ',k}$ is the interval $(-(k+1)\alpha ',(k+1)\alpha ')$ and since $\alpha '<\frac{|I_j|}{2(k+1)}$, it follows that on the stated interval $f_k(t)=S_j(t)$.

In the next section we extend the construction to analytic functions by convolving $f_k$ with trigonometric polynomials. The convolution with a trigonometric polynomial results in a periodic function but a periodic sequence $y_j$ cannot be monotone. For a function $g$ let $L(g,t)=\frac{g(2\pi )-g(0)}{2\pi }t+g(0)$ and $Pg(t)=g(t)-L(g,t)$. Clearly $Pg(0)=Pg(2\pi )=0$. The analytic pseudospectral interpolant will be $L$ plus a trigonometric approximating polynomial to $Pf_k$. In order to get full advantage of trigonometric approximation we set the slopes $s_1=s_M=\min (s_1,s_M)$ and extend $Pf_k(t+2\pi )=Pf_k(t),$ periodically on the whole real line. From (ii) and $x_0=0,x_M=2\pi$ it follows that $Pf_k(0)=Pf_k(2\pi )=0$, $Pf_k'(0)=Pf_k'(2\pi )=s_1-\frac{y_M-y_1}{2\pi }$, and $Pf_k^{(m)}(0)=Pf_k^{(m)}(2\pi )=0 , m>1$ i.e. $Pf_k$ is periodic and continuous along with all of its derivatives. $\square$

3 Analytic Monotone Approximation

The Fourier series of an integrable function $f$ on the interval $[0,2\pi ]$ is defined as

$$\begin{aligned} f(t)=a_0+\sum _{j=1}^\infty (a_j\cos jt+b_j\sin jt), \end{aligned}$$

where the Fourier coefficients are

$$\begin{aligned} a_0\!=\!\frac{1}{2\pi }\int _0^{\pi } f(x)\; dx,\;\; a_j\!=\!\frac{1}{\pi }\int _0^{2\pi } f(x)\cos jx\; dx,\;\; b_j\!=\!\frac{1}{\pi }\int _0^{2\pi } f(x)\sin jx\; dx. \end{aligned}$$

The $r$-th Dirichlet sum is

$$\begin{aligned} S_r(f,t)\!=\!\frac{1}{2\pi }f\!*\!D_r(t)\!=\!\frac{1}{2\pi }\!\int _0^{2\pi } \!\!f(x)D_r(t-x)\; dx\!=\!a_0\!+\!\sum _{j=1}^r (a_j\cos jt\!+\!b_j\sin jt), \end{aligned}$$

where $D_r(t)=1+2\sum _{j=1}^r \cos rt =\frac{\sin (r+\frac{1}{2})t}{\sin {\frac{t}{2}}}$ is the $r-$th Dirichlet kernel. The Vallée Poussin sums are defined as $V_{m,n}=\frac{1}{n-m}\sum _{r=m}^{n-1} S_r=f*v_{m,n}$, where $v_{m,n}=\frac{1}{n-m}\sum _{r=m}^{n-1} \frac{D_r}{2\pi }$. The error of the best trigonometric approximation of a continuous $2\pi -$periodic function by trigonometric polynomials of degree less than or equal to $n-1$ is $E_{n-1}(g)=\min \Vert g-\tau _{n-1}\Vert _C$. In [7] a near best polynomial for the trigonometric approximation to a periodic function $g\in C^k[0,2\pi ]$ is obtained,

$$\begin{aligned} E_{n-1}(g)\le \frac{5}{{\left( \begin{array}{c}k\\ \left[ \frac{k}{2}\right] \end{array}\right) }}w_k\left( g,\frac{2\pi }{n}\right) \le \frac{5}{{\left( \begin{array}{c}k\\ \left[ \frac{k}{2}\right] \end{array}\right) }}\left( \frac{2\pi }{n}\right) ^k\Vert g^{(k)}\Vert _C, \end{aligned}$$

where $w_k(g,\alpha )=\Vert \Delta _\alpha ^k g\Vert _{C[0,2\pi ]}$. The near best polynomial that provides the equality is $V_{\frac{8}{9}n,n}=g*v_{\frac{8}{9}n,n}=\frac{9}{n}\sum _{r=\frac{8}{9}n}^n S_r$.

Next we consider approximation of $Pf_k$, defined in Sect. 2, by trigonometric polynomials. In the case of equidistant $x$’s it is well known that the numerically computed Dirichlet sums interpolate $U$ for an appropriate choice of the parameters. The process is known as pseudospectral Fourier analysis, see [1]. We first consider arbitrary points $0=x_1<x_2<\ldots <x_M=2\pi$ and the approximating polynomial $V_{\frac{8}{9}n,n}$. The resulting function is neither interpolant nor with positive first derivative but it has the fastest convergence rate which allows by controlling the number of smoothing repetitions, $k$, and $n$ to obtain a good monotone pseudospectral interpolant. The error of approximation of $Pf_k'$ has to be smaller than the minimum of the first derivative of the function $f_k$ which is independent on $k$ and equal to $\eta =\min _{t\in [0,2\pi ]}|f_k'(t)|=\min _j \frac{s_j}{2}$. Let $\alpha =\frac{(k-1)^{-1+1/k}}{6}\delta (x)$, see Corollary 1, then we show that for any $n\ge n^*= \left[ \frac{6e\pi }{\delta (x)}\left( \ln \frac{180\Delta (y)}{\eta \delta (x)}+1\right) \right] =O\Big ( \frac{1}{\delta (x)}\ln \frac{\Delta (y)}{\eta \delta (x)}\Big )$, there exits a trigonometric approximating polynomial of degree $n$ such that, it plus $L(Pf_k,t)$ is a monotone function.

Theorem 1

The function $f(t)=Pf_k*v_{\frac{8}{9}n,n}(t)+L(Pf_k,t)$ is analytic on $[0,2\pi ]$ and is increasing for any $n\ge n^*$ and any integer $k> 2$ from the interval $\left( \ln \frac{180\Delta (y)}{\eta \delta (x)}+1,\left[ \frac{\delta (x)}{6\pi e}n\right] \right]$. In case $k=\left[ \frac{\delta (x)}{6\pi e}n\right]$ we have that $\max _j |f(x_j)-y_j|< 20\Delta y\left( \frac{1}{3e} \right) ^{\left[ \frac{\delta (x)}{6\pi e}n\right] }$.

Proof

The polynomial $Pf_k'*v_{\frac{8}{9}n,n}$ is a near best trigonometric approximant to $Pf'_k$. From [7], it follows that

$$\begin{aligned} |Pf_k(t)-Pf_k*v_{\frac{8}{9}n,n}(t)|\le & {} \frac{5}{{ \left( \begin{array}{c}k\\ \left[ \frac{k}{2}\right] \end{array}\right) }}\left( \frac{2\pi }{n}\right) ^k\Vert f_k^{(k)}\Vert _C\end{aligned}$$

(3.1)

$$\begin{aligned} |Pf'_k(t)-Pf_k'*v_{\frac{8}{9}n,n}(t)|\le & {} \frac{5}{{\left( \begin{array}{c} k-1\\ \left[ \frac{k-1}{2}\right] \end{array}\right) }}\left( \frac{2\pi }{n}\right) ^{k-1}\Vert f_k^{(k)}\Vert _C. \end{aligned}$$

(3.2)

From Corollary 1 and the inequality ${ \left( \begin{array}{c}k-1\\ \left[ \frac{k-1}{2}\right] \end{array}\right) }\ge \frac{2}{3}{ \left( \begin{array}{c}k \\ \left[ \frac{k}{2}\right] \end{array}\right) }$, it follows that

$$\begin{aligned} E_{n-1}(Pf'_k)<90\frac{\Delta (y)}{\delta (x)}\left( \frac{6\pi (k-1)}{n\delta (x)}\right) ^{k-1}. \end{aligned}$$

In order $f'>0$ we require $n$ and $k$ to be such that $E_{n-1}(P'f_k)<\frac{\eta }{2}$ which is equivalent to

$$\begin{aligned} \left( \frac{6\pi (k-1)}{n\delta (x)}\right) ^{k-1}<\frac{\eta \delta (x)}{180\Delta (y)}. \end{aligned}$$

Let $R=\frac{\eta \delta (x)}{180\Delta (y)}, \beta =\frac{6\pi }{\delta (x)}$, and $h(n,s)=\left( \beta \frac{s}{n}\right) ^s$, then the above inequality is $h(n,s)<R$ for $s=k-1$. We first determine the least $n$ for which the inequality holds. Solving it for $n$ we get that $n>\beta s R^{-1/s}$ or in logarithmic form $\ln n>\ln \beta s-\frac{\ln R}{s}$. The minimum of the function on the right with respect to $s$ is attained at $s=-\ln R>0$ and hence $n>-e\beta \ln R$. By substituting $R,\beta$, and $s$ and taking into account that $k$ and $n$ have to be integer we obtain that $k>\ln \frac{180\Delta (y)}{\eta \delta (x)}$ and hence the estimate for the minimum degree is $n^*$.

The minimum of $h(n,s)$ with respect to $s$ is attained at $s=\frac{n}{e\beta }$ and the inequality for that $s$ is $h(n,\frac{n}{e\beta })= \left( \frac{1}{e}\right) ^{\frac{n}{e\beta }}<R$. Solving it we obtain the same estimate $n^*$.

For a fixed $n$ the derivative of $\ln h(n,s)$ with respect to $s$, $(\ln \frac{s\beta }{n}+1)/h(n,s)$, is negative for $-\log R\le s \le \frac{n}{e\beta }$ and hence for any $n>\beta s R^{-1/s}$ and any $-\log R\le k-1 \le \frac{n}{e\beta }$ the function $f$ is increasing.

For $k=\left[ \frac{\delta (x)}{6\pi e}n\right]$ from

$$\begin{aligned} E_{n-1}(Pf_k)\le 20\Delta (y)\left( \frac{2\pi (k+1)}{n\delta (x)}\right) ^k, \end{aligned}$$

we obtain that

$$\begin{aligned} E_{n-1}(Pf_{k})< 20\Delta (y) \left( \frac{1}{3e} \right) ^{\left[ \frac{\delta (x)}{6\pi e}n\right] }. \end{aligned}$$

The proof of the theorem is complete. $\square$

Next we consider pseudospectral monotone algebraic polynomials on $[0,1]$. The interpolating points, $0=x_1<\cdots <x_M= 1$, have to be first transformed to $X_j=\frac{M-1}{M+1}x_j+\frac{1}{M+1}, j=1,\ldots ,M$ and two additional points included $X_{0}=0, X_{M+1}=1$ with corresponding $y_0=2y_1-y_2<y_1$ and $y_{M+1}=2y_M-y_{M-1}>y_M$ added to $y_1,\ldots ,y_M$. For the transformed table $\tilde{\eta }=\frac{M+1}{M-1}\eta =\frac{M+1}{M-1}\min _j\frac{s_j}{2}$ and $\delta (X)=\frac{M-1}{M+1}\delta (x)$. Let $z_j=\arccos (X_j), j=0,\ldots ,M+1$ then $0=z_{M+1}<z_M<\cdots <z_1<z_0=\frac{\pi }{2}$. After reflecting the table $(z_j,y_{M+1-j})_{j=0}^{M+1}$ with respect to the $y$-axis and considering the $\pi$-periodic extension we obtain a table that is even with respect to the $z$ values. By using Theorem 1 with $k=\left[ \ln 180\frac{\Delta (y)\Delta (z)}{\delta (y)\delta (z)}\right] +1$ and $P_n(x)=Pf_{k+1}*v_{\frac{8n}{9},n}\left( \arccos (x)\right)$ we can formulate the following corollary.

Corollary 2

For any $n\ge n^*= \left[ \frac{6e\pi (M+1)}{\delta (x)(M-1)} \left( \ln 180\frac{\Delta (y)\Delta (z)}{\delta (y)\delta (z)}+1\right) \right]$ the polynomial $P_n$ is increasing on $[0,1]$ and for $n=n^*$ we have that

$$\begin{aligned} \max _j |P(x_j)-y_j|<\frac{\delta (y)}{12e \ln \left( 180e\frac{\Delta (y)\Delta (z)}{\delta (y)\delta (z)}\right) }<\frac{\delta (y)}{200}. \end{aligned}$$

Proof

The new interpolation table $(z_j,y_j)$ is $2\pi$-periodic and have $4M+5$ interpolating points on $[0,2\pi ]$. By using Lemma 1, with $s_{0}=s_{M+1}=0$ we construct the periodic functions $f_k$, and notice that due to the extension of the data $Pf_k=f_k$. The original interpolating points $x_1,\ldots ,x_M$ are transformed to points on the interval $[z_M,z_1]$ and hence the degree of the trigonometric polynomial depends only on the sign of the derivative of the approximant on that interval. From Theorem 1 we obtain the pseudospectral interpolant $\tilde{f}$ that is decreasing on $[z_M,z_1]$. The pseudospectral interpolating algebraic monotone polynomial is obtained by changing the variable in $\tilde{f}(z)$ to $x=\cos z$ in the even function $\tilde{f}$. The algebraic degree is $\tilde{n}^*= \left[ \frac{6e\pi }{\delta (z)}\ln \frac{180e\Delta (y)}{\eta (z)\delta (z)} \right]$.

Let $\delta (z)=|z_{r+1}-z_r|$ then $\delta (X)\le |X_{r+1}-X_r|=|\cos z_{r+1}-\cos z_r|=2|\sin \frac{z_{r+1}-z_r}{2}\sin \frac{z_{r+1}+z_r}{2}|<|z_{r+1}-z_r|=\delta (z)$ and hence $\frac{1}{\delta (z)}<\frac{M+1}{(M-1)\delta (x)}$. Since $\eta (z)=\frac{y_{k+1}-y_k}{z_{k+1}-z_k}<\frac{\delta (y)}{\Delta (z)}$ then we obtain the estimate for $n^*$. The two error estimates follow from Theorem 1 for $(z_j,y_j)_{j=1}^M$.

For $n=n^*$ from the proof of Theorem 1, it follows that

$$\begin{aligned} |P(x_j)-y_j|<\Vert Pf_k-Pf_k*v_{\frac{8n}{9},n}\Vert _C\le \frac{\pi \eta }{n}. \end{aligned}$$

Let $\delta (y)=y_{k+1}-y_k$ then $\eta \delta (x)\le \frac{\delta (y)}{2(x_{k+1}-x_k)}\delta (x)\le \frac{\delta (y)}{2}$. Finally, since $\Delta (y)>\delta (y)$, $\frac{M-1}{M+1}<1$ and by substituting $n^*$ in the above inequality we obtain the stated in the case $n^*$. $\square$

In the case when $\Delta (z)<c_0\delta (z)$ for some real $c_0$ we see that $n^*$ is asymptotically equal to the least degree of the exact interpolant, obtained in [10, 13]. A trivial case is when $x_j=\cos \frac{(j-1)\pi }{M-1}, j=1,\ldots , M$ are the Chebyshev points, then $\Delta (z)=\delta (z)$. In the next section we consider interpolation at equidistant nodes.

4 Pseudospectral Interpolation and Positive Kernels

In this section we consider the special case of equidistant interpolation nodes $x_j=j\frac{2\pi }{2M+1}, j=0,1,\ldots ,2M$. The case of even number of nodes can be treated similarly.

The Fourier coefficients of a function are numerically computed by using the Discrete Fourier Transform( DFT). DFT of a sequence $y_j, j=0,\ldots , 2M$ is defined by the formulas

$$\begin{aligned} Y_j=\sum _{m=0}^{2M}y_me^{-i m x_j},\quad j=0,\ldots ,2M, \end{aligned}$$

and the Inverse DFT( IDFT) by the formulas

$$\begin{aligned} y_j=\frac{1}{2M}\sum _{m=0}^{2M}Y_me^{i m x_j},\quad j=0,\ldots ,2M. \end{aligned}$$

The corresponding Lagrange interpolating trigonometric polynomial, see [1], is

$$\begin{aligned} T_M(y,t)=\frac{1}{2M}\sum _{j=0}^{2M}Y_je^{i jt}. \end{aligned}$$

The polynomial $T_{NM}$ interpolates the table $(x_j,y_j)_{j=0}^{2M}$ for any integer $N$. A lower bound for $N$ such that $\Vert f_k'-T_{NM}'\Vert _C<\frac{\eta }{2}$ is provided in Theorem 2.

For a periodic function $g\in C^1$ and its trigonometric interpolant $T_n$ at the points $z_j=\frac{2\pi }{2n+1}j, j=0,\ldots , 2n$ the following holds true.

Proposition 1

For $g$ and $T_n$ as above we have that $\Vert g'-T_n'\Vert _C < 2\ln n (E_{n-1}(g')+nE_{n-1}(g)).$

Proof

The proof is a combination of the estimates $\Vert g-S_{n-1}\Vert _C\le 2\ln n E_{n-1}(g)$, see [5], $\Vert S_{n-1}-T_n\Vert _C\le 2 \ln n E_{n-1}(g)$, see [6], and the Bernstein’s inequality for trigonometric polynomials. Indeed, since $S_{n-1}'$ is a Dirichlet sum of $f'$ we have that

$$\begin{aligned} \Vert g'-T_n'\Vert _C< & {} \Vert g'-S_{n-1}'\Vert _C+\Vert S_{n-1}'-T_n'\Vert _C < 2\ln n E_{n-1}(g')+n\Vert S_{n-1}-T_n\Vert _C \\< & {} 2\ln n (E_{n-1}(g')+nE_{n-1}(g)). \end{aligned}$$

$\square$

The proof of Theorem 1 can be modified in the case to estimate the minimum $n$ such that $f(t)=T_n(Pf_k,t)+L(f,t)$ is increasing. For technical reasons the minimum $n^*$ is estimated in case the DFT is computed by using less than $10^9$ points.

Theorem 2

For the table $U=(x_j,y_j)_{j=0}^{2M}$ the function $f$, obtained in Theorem 1, with $k^*=\left[ 5+\ln \frac{\Delta (y)}{\delta (y)}\right]$ and $n^*=\left[ 6e k^*\right] M$, interpolates $U$, is increasing, and is analytic on $[0,2\pi ]$.

Proof

The interpolation follows from the properties of DFT. Since $x_j$ are equidistant then $\delta (x)=\frac{\pi }{M}$ and $\eta =\frac{\delta (y)}{\pi }M$. From Proposition 1, (3.1), and (3.2) we have that

$$\begin{aligned} \Vert Pf_k'-T_n'(Pf_k)\Vert _C<\frac{\eta }{2} \end{aligned}$$

is equivalent to the condition

$$\begin{aligned} (120+80\pi )\frac{\Delta (y)}{\delta (y)}(6M(k-1))^{k-1}\ln n <n^{k-1}. \end{aligned}$$

By taking the $k-1$ root from both sides and minimizing the function on the right with respect to $k$ as in the proof of Theorem 1 we get the minimum at $k=\ln \left( (120+80\pi )\frac{\Delta (y)}{\delta (y)}\ln n \right)$. Since $n<10^9$ it follows that $\ln \ln n<2.22$ and hence $k<5+\ln \frac{\Delta (y)}{\delta (y)}$. By taking into account that $k^*$ and $n^*$ are integer we obtain the estimates stated in the theorem. $\square$

In Sect. 2 we constructed a family of increasing functions $f_k\in C^k$ that interpolate the table $U$. In order to construct analytic functions in the general case we relaxed the approximation conditions and in Sect. 3 showed that the analytic function $f(t)=Pf_k*V_{\frac{8}{9}n,n}(t)+L(Pf_k,t)$ approximates the values $y_j$ with a geometrically decreasing error with respect to $n$ if $k=\left[ \frac{\delta (x)}{6\pi e} n\right]$. In the case when $\Delta (x)<c_0\delta (x)$ for a real $c_0$, the minimum degree, $n^*$ of the trigonometric polynomial $Pf_k*v_{\frac{8}{9}n,n}(t)$ is of the same order as the one for the algebraic interpolant from [10, 13]. In the beginning of the current section in the case of equidistant nodes we studied the convolution with $S_n$ in lieu of $v_{\frac{8}{9}n,n}$. The advantage of using $S_n$ is that it can be numerically computed by using the DFT resulting in exact interpolant with complexity of computations $O\left( M\ln \frac{\Delta (y)}{\delta (y)}\ln \left( M\ln \frac{\Delta (y)}{\delta (y)}\right) \right)$. The complexity of the corresponding spline methods which is $O(M)$. Next we discuss an alternative approach to obtain increasing approximants.

The Jackson’s kernels are

$$\begin{aligned} J_{n,r}(t)=\lambda _{n,r}\left( \frac{\sin \frac{nt}{2}}{\sin \frac{t}{2}}\right) ^{2r}, \end{aligned}$$

where $\lambda _{n,r}$ is a real constant such that $\Vert J_{n,r}\Vert _2=1$. The convolution of a step function and $J_{n,r}$ is used to construct a basis of increasing polynomials in [10]. From the Korovkin’s theorem for positive linear operators, see [4, 12], and later generalized in [5], it follows that $\Vert g-g*J_{n,r}\Vert _C\ge O(n^{-2})$ and the best order of approximation, $n^{-2}$, is achieved for $r=2$. By using the technique of the previous sections we can prove the following lemma.

Lemma 2

The function $f(t)=Pf_k*\frac{1}{2\pi }J_{n,2}(t)+L(f_0,t)$ is analytic, $f'>0$, and

$$\begin{aligned} \Vert f_{k+1}-f\Vert _C\le \frac{C}{n^2}, \end{aligned}$$

where $C$ depends only on $f$. $\square$

Although the monotonicity is preserved we do not have interpolation to $U$ and the error is of a relatively low order $n^{-2}$ for large $n$. On the other hand for smaller $n$( less than $100$, for example) we have that $n^{-2}<0.9675^{2\pi n }$. The magnitude of $n$ could be used to decide which kernel provides a smaller $n^*$.

5 Quadrature vs. Analytic Signal

The functions constructed in the previous sections have properties that make them good candidates for phase functions of the system $e^{is\theta (t)}, s\in \mathbb {N}$. In that case the analytic phase $\theta (t)=T_m(t)+t$, where $T_m$ is a trigonometric polynomial of degree $m$. Furthermore $\theta '=T_m'+1>0$ and hence $\frac{1}{\theta '(x+iy)}$ is holomorphic in a strip $|y|<1/\tau$ for some $\tau >0$. The conjugate function of a $2\pi -$periodic real-valued function $g$ is defined by the conjugate operator $Hg(t)=\frac{1}{2\pi }\int _0^{2\pi } g(x)\cot \frac{t-x}{2}\; dx$, see [3]. In this section we estimate how much $\sin s\theta$ and $\cos s\theta$ deviate correspondingly from $H\cos s\theta$ and $H\sin s\theta$ for $s>0$. Since $e^{is\theta }-A\cos s\theta =i(\sin s\theta -H\cos s\theta )$ and $-ie^{is\theta }+A\sin s\theta =i(\cos s\theta -H\sin s\theta )$ it suffices to consider the deviation of the quadrature signal $e^{is\theta }$ from the analytic signal $A\cos s\theta (t)=\cos s\theta (t)+iH\cos s\theta (t)$. The measure we use is the point-wise estimate, see [3] and the references within,

$$\begin{aligned} |e^{is\theta }-A\cos s\theta |\le \frac{1}{\pi }\sum _{n=-\infty }^{-1}\left| \int _0^{2\pi }e^{is\theta (t)-int}\; dt\right| . \end{aligned}$$

Our first result is an auxiliary lemma for the behavior of the function

$$\begin{aligned} F(s,n)(\theta )=\int _{0}^{2\pi }e^{is\theta (t)}e^{-int}\; dt=\int _{0}^{2\pi }e^{i(sT_m(t)+st-nt)}\; dt, \end{aligned}$$

for $s>1$ and $n<-1$.

Lemma 3

The following estimates hold true

• (i) $|F(s,n)(\theta )|\le Ce^{-\tau |n|}$ for a fixed $s\in \mathbb {N}$ when $n\rightarrow -\infty$;

• (ii) $|F(s,n)(\theta )|\le Ce^{-\tau _1|s|}$, for some $\tau _1>0$ and a fixed negative integer $n$ when $s\rightarrow \infty$;

• (iii) $\sum _{n=-\infty }^{-1}|F(s,n)(\theta )|\le \frac{1}{s^2}\int _0^{2\pi }\left( \frac{|T_m^{(4)}|}{3(T_m'+1)^3} + \frac{5|T_m^{(3)}T_m''|}{2(T_m'+1)^4}+\frac{3(T_m'')^2}{(T_m'+1)^5}\right) dt$ for any $s\in \mathbb {N}$.

Proof

Part one and part two follow from the well known rate of convergence of holomorhic functions, see [2]. Indeed, $e^{is\theta }$ is entire function and since $\theta '>0$ on $[0,2\pi ]$ then, it follows that the inverse function $\theta ^{-1}$ on $[0,2\pi ]$ is holomorphic in a strip $|y|<1/\tau ^*$ for some $\tau ^*>0$. By changing the variable $t=\theta (t)$ in (ii) we have that

$$\begin{aligned} F(s,n)(\theta )=\int _0^{2\pi } \frac{e^{-in\theta ^{-1}(t)}}{\theta '(\theta ^{-1}(t))}e^{ist}\;dt, \end{aligned}$$

and the estimate follows with $\tau _1=\min (\tau ,\tau ^*)$.

For part three let $\phi _n(t)=i(sT_m(t)+st-nt)$ then from the periodicity of $\phi _n'(t)=i(sT'_m(t)+s-n)$ we have that

$$\begin{aligned} F(s,n)(\theta )= & {} \int _0^{2\pi }\frac{de^{\phi _n(t)}}{\phi _n'(t)}=-\int _0^{2\pi }\left( \frac{1}{\phi _n'(t)}\right) 'e^{\phi _n(t)}\; dt\\= & {} \int _0^{2\pi }\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\right) '\right) 'e^{\phi _n(t)}\; dt\\= & {} -\int _0^{2\pi }\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\right) '\right) '\right) 'e^{\phi _n(t)}\; dt . \end{aligned}$$

Direct calculations show that

$$\begin{aligned}&\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\right) '\right) '\right) '\\&\quad =\frac{1}{s^3}\left( \frac{T_m^{(4)}}{(T_m'+1-\frac{n}{s})^4}-\frac{10T_m^{(3)}T_m''}{(T_m'+1-\frac{n}{s})^5}+\frac{15(T_m'')^3}{(T_m'+1-\frac{n}{s})^6}\right) \end{aligned}$$

and for a fixed $t$

$$\begin{aligned}&\sum _{n=-\infty }^{-1} \left| \left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\left( \frac{1}{\phi _n'(t)}\right) '\right) '\right) '\right| \\&\quad \le \sum _{n=-\infty }^{-1} \frac{|T_m^{(4)}|}{s^3(T_m'+1-\frac{n}{s})^4}+\sum _{n=-\infty }^{-1} \frac{10|T_m^{(3)}T_m''|}{s^3(T_m'+1-\frac{n}{s})^5}+\sum _{n=-\infty }^{-1} \frac{15(T_m'')^2}{s^3(T_m'+1-\frac{n}{s})^6} \\&\quad \le \int _{0}^\infty \frac{|T_m^{(4)}|\;du}{s^2(T_m'+1+u)^4} +\int _{0}^\infty \frac{10|T_m^{(3)}T_m''|\; du}{s^2(T_m'+1+u)^5}+\int _{0}^\infty \frac{15|(T_m'')^2|\; du}{s^2(T_m'+1+u)^6} \\&\quad \le \frac{|T_m^{(4)}|}{3s^2(T_m'+1)^3} + \frac{5|T_m^{(3)}T_m''|}{2s^2(T_m'+1)^4}+\frac{3(T_m'')^2}{s^2(T_m'+1)^5}. \end{aligned}$$

The estimate in (iii) follows from $|e^{\phi _n}|=1$ and integration on $[0,2\pi ]$. $\square$

The functions $\theta =T_m+L$ interpolate the table $U=(x_j,y_j)_{j=1}^M$. In the next corollary the deviation between the quadrature and the analytic signals is presented in terms of $U$. The degree of the trigonometric polynomial $T_m$ is $m=O( \frac{1}{\delta (x)}\ln \frac{\Delta (y)}{\eta \delta (x)})$, $T'_m+1\ge \frac{\eta }{2}$ and by applying the Bernstein’s inequality to $T_m$ we have the following corollary.

Corollary 3

$|e^{is\theta (t)}-A\cos s\theta (t)|\le \frac{C}{s^2\eta ^5}\left( \frac{1}{\delta (x)}\ln \frac{\Delta (y)}{\eta \delta (x)}\right) ^4$.

The corollary shows that the method agrees with the observation that the smaller the variation of the slopes $s_j$, the better approximation of the analytic by the quadrature signal. In particular if $\Delta (y)=\delta (y)$, i.e. a constant instantaneous frequency, it is easy to follow that we obtain the classical Fourier series $e^{ist}$.

To illustrate the results we propose an algorithm to construct the interpolant in the case of equidistant interpolation nodes. The case is special for many reasons, data can be taken at equal intervals, provides uniform $\alpha$, and from computational point of view DFT’s complexity is $O(n\log _2 n)$. Furthermore $f_k$ can be obtained as a $k-$folded convolution of $f_0$ with $B_k$.

Let the Fourier transform of $f$ be $\hat{f}(\xi )=\frac{1}{2\pi }\int _0^{2\pi }f(t)e^{-i\xi t}\; dt$ and sinc${\xi }=\frac{\sin \xi }{\xi }$, then $\hat{f}_k(\xi )= \text{ sinc }^{k+1} (\alpha '\xi )\hat{f}_0(\xi )$, and $\hat{f}=\chi _{[-n^*,n^*]}\hat{f}_{k^*}$, $k^*=\left[ \frac{n^*}{6Me} \right]$. Summing up the above we propose the following numerical algorithm for constructing $f$ in the case of equidistant nodes.

Procedure $pIn(x,y)$

Step 1. Initialize $p_j=j\frac{2\pi }{2n^*+1}, j=0,1,\ldots , 2n^*$

Step 2. Construct $f_0$, then $Pf_0=f_0-L(f_0)$, and compute $DFT(Pf_0)$.

Step 3. Compute $DFT(f)=DFT(Pf_0)(\xi )\text{ sinc }^{k^*+1} (\alpha '\xi )$ at all $p_j$.

Step 4. Construct the interpolant $f=IDFT(DFT(f))+L(f_0)$. End.

Since the convolution is commutative operator we first truncated the Fourier series of $f_0$. The complexity of the proposed algorithm is $O(n^*\log _2 n^*)$ and is comparable to the complexity of $DFT$. In case of arbitrary interpolation nodes Step 3. has to be modified for each of the sub intervals.

6 Numerical Examples

We conclude the paper with three numerical examples. The estimates obtained in Theorems 1,2 are asymptotically good but for small numbers of interpolating points (less than 12) they provide unnecessary large values for $n^*>\frac{6e\pi (\ln (180)+1)}{\delta (x)}>300$. In order to obtain a smaller value we use $n^*$ as an upper bound and apply the procedure $pIn$ first with $b=0, e=n^*$, and $n_0=(b+e)/2$. If the resulting $\theta '$ is positive next we set $e=(b+e)/2$, otherwise (if $\theta '$ changes sign) we set $b=(b+e)/2$. Next we apply $pIn$ with the new $b$ and $e$ and $n_1=(b+e)/2$. The procedure is repeated $r$ times until $\theta '>0$ for $n_r$ and changes sign for $n_{r+1}=n_r/2$. The worst case is to reach the value $n^*$ in $r=\log _2 n^*$ iterations. The smoothing step was fixed to $k^*=6$ with corresponding window length $\alpha _6=\frac{|I_j|}{15}$. The question of the practical realization for the least $n^*$ will be studied independently. The software MatLab was used for the computations and visualization with a scale from $0$ to $2\pi$ with a step $2\pi /2^{-14}$. The first two examples are the case of interpolation at odd number of equidistant nodes. In Example 1 we consider $7$ nodes and the $3$ interpolating nodes in Example 2 are among $\frac{2k}{7}\pi , k=0,1,\ldots ,7$.

Example 1

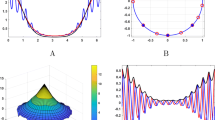
The first example represents interpolation of the parabola $y=x+x(2\pi -x)/7$ at the points $x_j=\frac{2j\pi }{7}, j=0,1,\ldots ,7$. The least degree of the trigonometric polynomial $T_m$ is $18$. In Fig. 1a the circles are the interpolating points, the dashed line is the parabola, and the continuous line is the pseudospectral interpolant. Fig 1b shows $\cos \theta$ (the dashed line), $\sin \theta$ (the tick line), and the conjugate of the cosine, $H\cos \theta$ (the dotted line).

Fig. 1

Parabolic instantaneous frequency

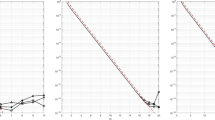
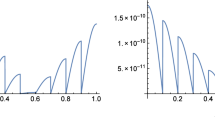
The Fourier spectrum ( DFT) of $\cos \theta$ is plotted in Fig. 2a. The dotted line represents the negative frequencies. In Fig. 2b the spectrum of $\cos s\theta$ for $s=1$ (the darker line) and $s=50$ (the lighter line) are superimposed.

Fig. 2

Fourier Spectrum

Example 2

The pseudospectral interpolation of the table with $x=(0,\frac{6\pi }{7} ,\frac{8\pi }{7} , 2\pi )$ and $y=(0,\frac{\pi }{6},\frac{11\pi }{6},2\pi )$ is constructed by using the same setting as in Example 1. The least degree of the trigonometric polynomial $T_m$ is $m=52$. In Fig. 3a the circles are the interpolating points and the continuous line is the pseudospectral interpolant. Figure 3b shows $\cos \theta$ (the dashed line), $\sin \theta$ (the tick line), and the conjugate of the cosine, $H\cos \theta$ (the dotted line).

Fig. 3

Interpolating table of a big variation

The spectrum of $\cos \theta$ is plotted in Fig. 4a. The dotted line represents the negative frequencies. In Fig. 4b the spectrum of $\cos s\theta$ for $s=1$ (the darker line) and $s=50$ ( the lighter line) are superimposed.

Fig. 4

Fourier Spectrum

Example 3

The third example illustrates interpolation at arbitrary points. By using Matlab the following interpolating table, Fig. 5a, was randomly generated

$$\begin{aligned} x= & {} (0, \; 0.1685 , \; 0.6421 ,\; 3.4579 , \; 3.6609 , \;3.8349 ,\; 4.3065 , \; 4.6351 ,\\&4.7994 ,\; 4.8831 , \; 5.6127 , \; 6.0763 , \; 6.2111 ,\; 6.2832) \end{aligned}$$

and

$$\begin{aligned} y= & {} (0 , \; 0.0395, \; 0.0931 , \; 0.5248, \; 0.8764,\; 1.2304 ,\; 1.8342 , \; 2.3010, \\&2.7693, \; 3.0967 , \; 4.0252 , \; 4.3471 , \; 6.1420 , \; 6.2832). \end{aligned}$$

In $Step 2$ of $pIn$ the points $x$ were used for the set of interpolating cites. The minimum degree of the polynomial $T_m$ is $m=84$. Figure 5b shows $\cos \theta$ (the dashed line), $\sin \theta$ (the tick line), and the conjugate of the cosine, $H\cos \theta$ (the dotted line).

Fig. 5

Randomly generated instantaneous frequency

The spectrum of $\cos \theta$ is plotted in Fig. 6a. The dotted line represents the negative frequencies. In Fig. 6b the spectrum of $\cos s\theta$ for $s=1$ (the darker line) and $s=50$ (the lighter line) are superimposed.

Fig. 6

Fourier Spectrum

From the examples we see that the spectrum for $s=1$ is centered at $1$ and is decreasing exponentially fast as the frequency approaches $\pm \infty$ which agrees with Lemma 2. Furthermore we see that the approximation of the analytic signal by the quadrature is improving significantly when $s$ increases.