The Mystery of Gabor Frames

Abstract

This is a survey about the theory of Gabor frames. We review the structural results about Gabor frames over a lattice and then discuss the few known results about the fine structure of Gabor frames. We add a new result about the relation between properties of the window and properties of the frame set and conclude with a vision of how a more complete theory of the fine structure might look like.

1 Introduction

The defining problem of Gabor analysis is to determine pairs $(g,\Lambda )$ consisting of an $L^2$-function $g$ and a lattice $\Lambda \subseteq {\mathbb {R}^{2d}}$ such that the set of functions $\mathcal {G}(g,\Lambda ) = \{e^{2\pi i \lambda _2 t} g(t-\lambda _1) : (\lambda _1, \lambda _2) \in \Lambda \}$ constitutes a frame for $L^2(\mathbb {R}^d )$. Denoting $z=(x,\xi ) \in \mathbb {R}^d\times \mathbb {R}^d$ for a point in time–frequency space and using the notation

$$\begin{aligned} \pi (z)f(t) = M_\xi T_x g(t) = e^{2\pi i \xi \cdot t} g(t-x), \qquad x,\xi ,t\in \mathbb {R}^d, \end{aligned}$$

for the time–frequency shift by $z$, the set $\mathcal {G}(g,\Lambda )$ is called a frame if there exist two positive constants $A,B>0$ such that

$$\begin{aligned} A\Vert f\Vert _2^2 \le \sum _{\lambda \in \Lambda } |\langle f, \pi (\lambda ) g\rangle |^2 \le B \Vert f\Vert _2^2 \qquad \text { for all } f \in L^2(\mathbb {R}^d ). \end{aligned}$$

(1)

Of course, the frame property of a Gabor family $\mathcal {G}(g,\Lambda )$ depends on the properties of the “window function” $g$ and on the lattice $\Lambda$. Gabor analysis investigates the question for which window functions $g\in L^2(\mathbb {R}^d)$ and which lattices $\Lambda \subseteq {\mathbb {R}^{2d}}$ the set $\mathcal {G}(g,\Lambda )$ is a frame.

Formally, the goal is to completely understand and describe the set of lattices for which $\mathcal {G}(g,\Lambda )$ is a frame. We call this the full frame set and denote it by

$$\begin{aligned} \mathcal {F}_{\mathrm {full}} (g) = \{\Lambda \subseteq {\mathbb {R}^{2d}}: \mathcal {G}(g,\Lambda )\, \text { is a frame}\} . \end{aligned}$$

(2)

The problem of Gabor frames is fundamental in time–frequency analysis, because Gabor frames are applied in several different disciplines. Gabor frames are used as a tool for the characterization of smoothness properties and phase space concentration [25, 30, 36], for the study of pseudodifferential operators [37] and, of course, in signal processing [30, 31]. They arise in complex analysis [68, 77] and in non-commutative geometry [66, 72]. Since the series expansion corresponding to a Gabor frame can be interpreted as a sum of local Fourier series, Gabor frames arise in many engineering contexts. To mention two important applications, Gabor frames are used in speech processing and in the analysis of music signals [19] (under the name “phase vocoder”) and in wireless transmission with OFDM [9, 53, 79, 80].

A variation of (2) is to consider only rectangular lattices $\Lambda = \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$ with positive lattice parameters $\alpha ,\beta >0$ and to investigate when $\mathcal {G}(g,\Lambda )$ is a frame. We will denote the corresponding set of lattice parameters $\alpha , \beta >0$ by

$$\begin{aligned} \mathcal {F}(g) = \{ (\alpha ,\beta ) \in \mathbb {R}_+ ^2: \mathcal {G}(g, \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d) \text { is a frame}\} , \end{aligned}$$

(3)

and simply call it the frame set (or the reduced frame set, if we want to distinguish it from the full frame set).

The frame set for the Gaussian window was already determined in 1992 in the celebrated results of Lyubarski [68] and Seip [77]. Since then Gabor theory has advanced significantly, and we now have a beautiful structure theory and know many characterizations of Gabor frames. However, there has been little progress on the original question of how to determine which windows and lattices generate a Gabor frame. The frame set $\mathcal {F}(g)$ is known for a small class of functions; for general window functions the set $\mathcal {F}(g)$ remains as mysterious as ever.

The goal of this survey is to describe the state-of-the-art of Gabor analysis. For this purpose we will distinguish between the coarse structure of Gabor frames and their fine structure. The coarse structure refers to the general properties of the frame set and the characterization of Gabor frames, and contains results that hold for every window (or at least every “nice” window). The fine structure refers to the relation between the properties of a fixed window (or class of windows) and the corresponding frame set. The fine structure is hardly explored and poorly understood. At this time the fine structure of Gabor frames is rather mysterious; we therefore feel justified to speak of the mystery of Gabor frames.

The richness and beauty of the general theory is in striking contrast to the paucity of precise, explicit results about the frame set. Our ignorance of the fine structure is stunning. In the “normal” evolution of a mathematical subject the understanding of the basic examples leads to mathematical statements and to conjectures for the open questions. Surprisingly, within the last 25 years only a single conjecture about the frame set has been stated by Daubechies [15]. This conjecture has been disproved, forgotten, and then only recently revived [48]. We feel that mathematical research thrives through its open problems, therefore a second goal of this survey is the (explicit) formulation of open problems and some conjectures.

Although this is a survey of known results, it offers several new aspects. The material is presented from the point of view of the fine structure. We reorganize the duality theory of Gabor frames and try to give short proofs (or at least the ideas of the proofs). These proofs use only the Poisson summation formula and should be more accessible than the original literature.

As a new result, we will characterize those windows for which the frame set omits a horizontal line and is contained in $\{ (\alpha , \beta ) \subseteq \mathbb {R}_+ ^2: \alpha \beta <1, \beta \ne \beta _0, \alpha >0\}$ for some $\beta _0 >0$. This result might serve as a model for the formulation of other statements about the fine structure and comes with a message: To understand Gabor frames, we need to understand better the obstructions to Gabor frames. We have to complement the question “When is $\mathcal {G}(g,\Lambda )$ a frame?” by the question “What prevents $\mathcal {G}(g,\Lambda )$ from generating a frame?”

The survey is organized as follows: In Sect. 2 we review the general properties of the frame set and discuss a long list of characterizations for Gabor frames. This covers the coarse structure. In Sect. 3 we review for which windows the frame set is known and discuss the interaction between properties of the window and properties of the corresponding frame set. This covers the fine structure of Gabor frames. In Sect. 4 we formulate a number of open questions and conjectures.

1.1 Tools

Lattices. We parametrize lattices by a choice of a basis or equivalently by the choice of an invertible real-valued $2d\times 2d$-matrix $A$. Every lattice $\Lambda \subseteq {\mathbb {R}^{2d}}$ in time–frequency space has the form $\Lambda = A {\mathbb {Z}^{2d}}$. The generating matrix is not unique, as every matrix of the form $A' = A Z$ for an invertible integer-valued $2d\times 2d$-matrix $Z$ generates the same lattice. In mathematical notation, the set of all lattices in ${\mathbb {R}^{2d}}$ is $\mathrm {GL}(2d,\mathbb {R})/ \mathrm {SL}(2d,\mathbb {Z})$ and it inherits a topology from $\mathrm {GL}(2d,\mathbb {R})$. The volume of $\Lambda$ is given by $\mathrm {vol}(\Lambda )= |\det A |$, and its density is $\mathrm {vol}(\Lambda )^{-1}$.

Function Spaces. Fix a non-zero Schwartz function $g\in \mathcal {S}(\mathbb {R}^d)$. Then the modulation space $M^p(\mathbb {R}^d)$ for $1\le p\le \infty$ is defined by the norm

$$\begin{aligned} \Vert f\Vert _{M^p} ^p = \mathop \int _{\mathbb {R}^d}\limits \mathop \int _{\mathbb {R}^d}\limits |\langle f,M_\xi T_x g\rangle | ^p \, dxd\xi \, , \end{aligned}$$

with the usual adjustment for $p=\infty$. The definition of $M^p(\mathbb {R}^d)$ is independent of the choice of $g\in \mathcal {S}(\mathbb {R}^d)$. Also, $M^2(\mathbb {R}^d) = L^2(\mathbb {R}^d)$.

The modulation spaces are the standard spaces in time–frequency analysis and arise naturally in many problems. Although frame theory is an $L^2$-theory, we will need the two spaces $M^1(\mathbb {R}^d)$ and $M^\infty (\mathbb {R}^d)$. In a sense $M^1(\mathbb {R}^d)$ is the largest space of reasonable window functions for Gabor frames and arises also as the canonical space of test functions for time–frequency analysis. Its dual space $M^\infty (\mathbb {R}^d)$ is the natural space of distributions in time–frequency analysis. Thus in time–frequency analysis the pair $(M^1, M^\infty )$ is the appropriate substitute for the usual pair $(\mathcal {S}, \mathcal {S}' )$ in analysis. See [22] for the original publication on modulation spaces, [23] for a historical survey, and [36] for a systematic introduction.

In some arguments we will use the Poisson summation formula

$$\begin{aligned} \sum _{k\in \mathbb {Z}^d} f(k) = \sum _{k\in \mathbb {Z}^d} \hat{f}(k). \end{aligned}$$

For $f\in M^1(\mathbb {R}^d)$, the Poisson formula holds with absolute convergence of both sums [21, 35].

Sometimes we will use the Wiener amalgam space $W(\mathbb {R}^d) = W(L^\infty , L^1)(\mathbb {R}^d)$ which is defined by the norm $\Vert f\Vert _W = \sum _{k\in \mathbb {Z}^d} \sup _{t\in [0,1]^d} |f(k+t)|$. Certain results also hold for windows in $W(\mathbb {R}^d)$ instead of $M^1(\mathbb {R}^d)$.

Operators related to a Gabor family. Fix a non-zero $g\in L^2(\mathbb {R}^d)$. The short-time Fourier transform $V_gf$ of $f\in L^2(\mathbb {R}^d)$ with respect to the “window” $g$ is the function of $2d$ variables $z=(x,\xi ) \in \mathbb {R}^d\times \mathbb {R}^d$ given by

$$\begin{aligned} V_gf (x,\xi ) = \mathop \int _{\mathbb {R}^d}\limits f(t) \bar{g}(t-x) \, e^{-2\pi i x\cdot t} \, dt = \langle f, \pi (z) g\rangle . \end{aligned}$$

By duality, the short-time Fourier transform is always defined when $g\in M^1(\mathbb {R}^d)$ and $f\in M^\infty (\mathbb {R}^d)$, or when $(f,g) \in \mathcal {S}'(\mathbb {R}^d) \times \mathcal {S}(\mathbb {R}^d)$.

Let $\mathcal {G}(g,\Lambda )= \{ \pi (\lambda )g, \lambda \in \Lambda \}$ be a Gabor family with a window $g\in L^2(\mathbb {R}^d)$ and a lattice $\Lambda \subseteq {\mathbb {R}^{2d}}$. Associated to $\mathcal {G}(g,\Lambda )$ are the following canonical operators: the coefficient operator or analysis operator maps functions or distributions on $\mathbb {R}^d$ to functions on $\Lambda$ (“sequences”)

$$\begin{aligned} C_{g,\Lambda } f = \Big ( \langle f, \pi (\lambda )g\rangle \Big ) _{\lambda \in \Lambda } = V_gf |_\Lambda . \end{aligned}$$

(4)

The synthesis operator maps functions on $\Lambda$ to functions or distributions on $\mathbb {R}^d$ by

$$\begin{aligned} D_{g,\Lambda }c = \sum _{\lambda \in \Lambda } c_\lambda \pi (\lambda ) g \, , \end{aligned}$$

(5)

and the frame operator maps functions on $\mathbb {R}^d$ to functions or distributions on $\mathbb {R}^d$ by

$$\begin{aligned} S_{g,\Lambda } f = \sum _{\lambda \in \Lambda } \langle f, \pi (\lambda )g\rangle \, \pi (\lambda )g \,. \end{aligned}$$

(6)

We note that formally $C_{g,\Lambda }$ and $D_{g,\Lambda }$ are adjoint to each other, and that $S_{g,\Lambda } = D_{g,\Lambda } C_{g,\Lambda }$. A Gabor family $\mathcal {G}(g,\Lambda )$ is called a Bessel family if $C_{g,\Lambda }$ is bounded from $L^2(\mathbb {R}^d)$ to $\ell ^2(\Lambda )$, or, equivalently, if $D_{g,\Lambda }$ is bounded from $\ell ^2(\Lambda )$ to $L^2(\mathbb {R}^d)$. Furthermore, $\mathcal {G}(g,\Lambda )$ is a frame if the frame operator $S_{g,\Lambda }$ is bounded and invertible on $L^2(\mathbb {R}^d)$ or equivalently, $C_{g,\Lambda }$ is bounded above and below on $L^2(\mathbb {R}^d)$. Similarly, $\mathcal {G}(g,\Lambda )$ is a Riesz sequence if $D_{g,\Lambda }$ is bounded above and below on $\ell ^2(\Lambda )$.

The invertibility of the Gabor frame operator $S_{g,\Lambda }$ implies the existence of a dual window $\gamma = S_{g,\Lambda } ^{-1}g$ in $L^2(\mathbb {R}^d)$ and a corresponding Gabor expansion for arbitrary functions $f\in L^2(\mathbb {R}^d)$, namely,

$$\begin{aligned} f&=S_{g,\Lambda } ^{-1}S_{g,\Lambda } f= \sum _{\lambda \in \Lambda } \langle f, \pi (\lambda )g\rangle \pi (\lambda )\gamma \nonumber \\&= S_{g,\Lambda } S_{g,\Lambda } ^{-1}f = \sum _{\lambda \in \Lambda } \langle f, \pi (\lambda )\gamma \rangle \pi (\lambda )g . \end{aligned}$$

(7)

Both series converge unconditionally in $L^2(\mathbb {R}^d)$.

The following lemma summarizes the boundedness properties of the canonical operators.

Lemma 1.1

Assume that $g\in M^1(\mathbb {R}^d)$ and $1\le p\le \infty$. Then $C_{g,\Lambda }$ is bounded from $M^p(\mathbb {R}^d)$ into $\ell ^p (\Lambda )$, $D_{g,\Lambda }$ is bounded from $\ell ^p (\Lambda )$ into $M^p(\mathbb {R}^d)$, and the frame operator $S_{g,\Lambda }$ is bounded on $M^p(\mathbb {R}^d)$.

See [25] and [36, Cor. 12.1.12] for proofs. The boundedness on $L^2(\mathbb {R}^d)$ holds under a weaker condition on $g$: if $g$ is in the amalgam space $W(\mathbb {R}^d)$, then $S_{g,\Lambda }$ is bounded on $L^2(\mathbb {R}^d)$ [81].

2 The Coarse Structure of Gabor Frames

In this section we review the general properties of the frame set and describe several characterizations of Gabor frames. These results constitute the canon of Gabor analysis and have been described many times. From our point of view they deal with the coarse structure of Gabor frames.

2.1 General Properties of the Frame Set

Given a lattice $\Lambda = A{\mathbb {Z}^{2d}}$ and a window $g\in L^2(\mathbb {R}^d)$, we consider the general Gabor family $\mathcal {G}(g, \Lambda ) = \{ \pi (\lambda )g: \lambda \in \Lambda \}$ and ask when $\mathcal {G}(g,\Lambda )$ is a frame.

The coarse structure of Gabor frames can be summarized as follows.

Theorem 2.1

If $g\in M^1(\mathbb {R}^d)$, then $\mathcal {F}_{\mathrm {full}} (g)$ is an open subset of $\{ \Lambda : \mathrm {vol} (\Lambda ) <1\}$ and contains a neighborhood of $\mathbf {0}$.

Likewise, $\mathcal {F}(g)$ is open in $\{ (\alpha , \beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1\}$ and contains a neighborhood of $(0,0)$ in $\mathbb {R}_+ ^2$.

Although Theorem 2.1 is simple and short, it is the synthesis of four different directions of research on Gabor frames. In fact, the theorem combines the density theorem, the Balian-Low theorem, the theorem on the existence of Gabor frames, and perturbation results. Let us discuss these aspects in more detail. For a detailed exposition and complete references we refer to the books and surveys [10, 30, 31, 36, 51, 52].

(a) The density condition gives a necessary condition for a lattice to generate a Gabor frame. The general density theorem holds for arbitrary windows $g\in L^2(\mathbb {R}^d)$ and asserts that necessarily $\mathrm {vol}(\Lambda )\le 1$ whenever $\mathcal {G}(g,\Lambda )$ is a frame. Clearly $\mathrm {vol}(\Lambda )= 1$ is possible. The density theorem is a form of the uncertaintly principle and asserts that the time–frequency shifts of a given window must cover phase-space densely enough [15, 70]. There are many different proofs of the density theorem ranging from elementary calculations with the Poisson summation formula [59] to the language of non-commutative geometry [66]. For a detailed history and list of references we refer to the survey of Heil [51]. Let us mention that the density theorem does not require the lattice structure and also holds for non-uniform Gabor frames [70].

(b) The formulation of Theorem 2.1 contains a subtle point: the critical density is $\mathrm {vol}(\Lambda )= 1$. There exist Gabor frames at the cricital density; for instance, if $g = \chi _{[0,1]^d}$ and $\Lambda = {\mathbb {Z}^{2d}}$, then $\mathcal {G}(g,\Lambda )$ is even an orthonormal basis for $L^2(\mathbb {R}^d)$. However, the characteristic function decays only like $\mathcal {O}(|\xi |^{-1})$ in the frequency variable and $\chi \not \in M^1(\mathbb {R}^d )$. As soon as a mild decay and/or smoothness condition is imposed on the window $g$, the inequality in the necessary density condition is strict. If $g\in M^1(\mathbb {R}^d)$ and $\mathcal {G}(g,\Lambda )$ is a frame, then $\mathrm {vol}\, (\Lambda ) <1$ [4, 15, 65]. This is the so-called Balian-Low-Theorem; see [7, 13] for two surveys and [27, 41] for the multivariate case. To put it differently, if $\mathcal {G}(g,\Lambda )$ is a frame and $\mathrm {vol} (\Lambda ) =1$ (in particular, if $\mathcal {G}(g,\Lambda )$ is an orthonormal basis), then $g\not \in M^1(\mathbb {R}^d)$. Historically, the impossibility to produce orthonormal bases of time–frequency shifts with good time–frequency localization was the first strong argument for using frames in analysis.

In the context of time–frequency analysis the condition $g\in M^1(\mathbb {R}^d)$ is natural, but the Balian-Low theorem holds under even weaker conditions. For instance, if $g$ is continuous and $g\in W(\mathbb {R}^d)$, then $\mathcal {F}(g) \subseteq \{ (\alpha ,\beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1\}$ [7].

(c) The search for sufficient conditions is more difficult and has lead to numerous results [8, 15, 24, 32, 73, 82]. In a nutshell, these conditions say that sampling the phase-space densely enough is sufficient to obtain a Gabor frame. In Theorem 2.1 this is expressed by saying that $\mathcal {F}(g)$ contains a neighborhood of the origin. This class of results yields qualitative statements and asserts the existence of Gabor frames. However, these results do not give any hint as to which lattices generate a Gabor frame.

In general there is a huge gap between the necessary conditions of the density theorem and these sufficient conditions.

Let us also mention a different type of existence result: Bekka [6] showed that for a given lattice $\Lambda \subseteq {\mathbb {R}^{2d}}$ with $\mathrm {vol}\, (\Lambda ) \le 1$ there always exists a window $g\in L^2(\mathbb {R}^d)$, such that $\mathcal {G}(g,\Lambda )$ is a frame.

(d) The openness of $\mathcal {F}(g)$ can be viewed as a strong perturbation result. To put it differently, assume that $g\in M^1(\mathbb {R}^d)$ and $\Lambda = A{\mathbb {Z}^{2d}}$ and $\mathcal {G}(g,\Lambda )$ is a frame. If $\Vert B-A\Vert <\epsilon$, where $\epsilon >0$ is sufficiently small, then $\mathcal {G}(g, B{\mathbb {Z}^{2d}})$ is also a frame [27]. This is a remarkable result, because the points of $A{\mathbb {Z}^{2d}}$ and of $B{\mathbb {Z}^{2d}}$ may be far apart. A version for non-uniform Gabor frames has been derived only recently [3], and it is still an open problem how to formulate a reasonable notion for the deformation of a Gabor frame. A general result is forthcoming in [47]. The assumption $g\in M^1(\mathbb {R}^d)$ is crucial in Theorem 2.1. For arbitrary windows the frame set $\mathcal {F}(g)$ is not open [57]. Indeed, this is already the case for the characteristic function $g= \chi _{[0,1]} \not \in M^1(\mathbb {R})$.

Finally, we state some of the invariance properties of the frame set. These help sometimes to fix convenient normalizations. We use $D_t f(x) = t^{-d/2} f(x/t)$ for the dilation, and $\mu (\mathcal {A})$ for the metaplectic operator that is defined by the commutation relation $\mu (\mathcal {A}) \pi (z) \mu (\mathcal {A})^{-1}= \pi (\mathcal {A}z)$ for $z\in {\mathbb {R}^{2d}}$, where $\mathcal {A}$ a symplectic matrix on ${\mathbb {R}^{2d}}$. See [34, 36] for the definition and properties of metaplectic operators.

Lemma 2.2

Let $g\in L^2(\mathbb {R}^d)$. Then for all $z\in {\mathbb {R}^{2d}}$, all $t\in \mathbb {R}_+$, and all symplectic $2d\times 2d$-matrices $\mathcal {A}$ we have

$$\begin{aligned}&\mathcal {F}(\pi (z) g) = \mathcal {F}(g) \, , \\&\mathcal {F}(\hat{g}) = \{ (\beta , \alpha ): (\alpha , \beta )\in \mathcal {F}(g)\} \, ,\\&\mathcal {F}(D_t g) = \{ (t \alpha , \tfrac{\beta }{t} ): (\alpha , \beta )\in \mathcal {F}(g)\} \, , \\&\mathcal {F}_{\mathrm {full}} (\mu (\mathcal {A}) g) = \{ \mathcal {A}\Lambda :\Lambda \in {\mathcal {F}_{\mathrm {full}}}_f (g)\}. \end{aligned}$$

Proof

We only prove the last identity. By the definition of metaplectic operators, $\mu (\mathcal {A}) \pi (\lambda )g = \pi (\mathcal {A}\lambda ) \mu (\mathcal {A})g$, and therefore

$$\begin{aligned} \mu (\mathcal {A}) \mathcal {G}(g, \Lambda ) = \mathcal {G}(\mu (\mathcal {A})g, \mu (\mathcal {A}) \Lambda ). \end{aligned}$$

Since the frame property of $\mathcal {G}(g,\Lambda )$ is preserved by unitary operators, $\mathcal {G}(g,\Lambda )$ is a frame if and only if $\mathcal {G}(\mu (\mathcal {A})g, \mu (\mathcal {A}) \Lambda )$ is a frame, as claimed. $\square$

2.2 Criteria for Gabor Frames

To determine whether or not a given lattice generates a Gabor frame $\mathcal {G}(g,\Lambda )$, one may try to apply one of many known criteria for Gabor frames. In the following we present the most important and useful such criteria, and in some cases we sketch the proofs.

Let $\mathcal {J}$ denote the symplectic matrix $\mathcal {J}= \Big ( \begin{array}{ll} 0 &{} I \\ -I &{} 0 \end{array} \Big )$. Then the adjoint lattice of $\Lambda = A{\mathbb {Z}^{2d}}$ is defined as

$$\begin{aligned} \Lambda ^\circ = \mathcal {J}(A^{-1})^T {\mathbb {Z}^{2d}}. \end{aligned}$$

The adjoint lattice is determined by the commutation property

$$\begin{aligned} \Lambda ^{\circ }= \{ z\in {\mathbb {R}^{2d}}: \pi (z) \pi (\lambda ) = \pi (\lambda ) \pi (z) \,\, \forall \lambda \in \Lambda \}. \end{aligned}$$

For a rectangular lattice $\Lambda = \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$, the adjoint lattice is given by $\Lambda ^\circ = \tfrac{1}{\beta } \mathbb {Z}^d\times \tfrac{1}{\alpha } \mathbb {Z}^d$.

2.2.1 Criteria for Arbitrary Lattices

Theorem 2.3

(Duality Theory) Assume that $g\in L^2(\mathbb {R}^d)$ and $\Lambda \subseteq {\mathbb {R}^{2d}}$ is a lattice. Then the following are equivalent:

• (i) $\mathcal {G}(g,\Lambda )$ is a frame for $L^2(\mathbb {R}^d)$.

• (ii) $\mathcal {G}(g, \Lambda ^{\circ })$ is a Bessel family and there exists a dual window $\gamma \in L^2(\mathbb {R}^d)$ such that both $\mathcal {G}(g, \Lambda )$ and $\mathcal {G}(\gamma , \Lambda ^\circ )$ are Bessel families and

  $$\begin{aligned} \langle \gamma , \pi (\mu )g\rangle = \mathrm {vol}\, (\Lambda ) \delta _{\mu ,0} \qquad \forall \mu \in \Lambda ^{\circ }. \end{aligned}$$

  (8)

  The biorthogonality condition (8) characterizes all possible dual windows of $\mathcal {G}(g,\Lambda )$.

• (iii) $\mathcal {G}(g , \Lambda ^{\circ })$ is a Riesz basis for a subspace of $L^2(\mathbb {R}^d)$.

This fundamental duality theory goes back to Daubechies et al. [16], Janssen [54], and Ron–Shen [73]. The formulation for arbitrary lattices is due to Feichtinger and Kozek [28]. The biorthogonality conditions were originally discovered in the engineering literature [83].

In the following we sketch the simple proof of Feichtinger and Luef [29] that is based on a careful interpretation of an idea of Rieffel [72]. The proof is elementary and requires only a few basic properties of the short-time Fourier transform and the Poisson summation formula.

Proof

The idea is to apply Poisson’s summation formula to the function $F(z) = \, |\langle f, \pi (Az)g\rangle |^2$. To do this, we need to calculate the Fourier transform of $F$, or more generally, of a product of two short-time Fourier transforms. This can be done in a straightforward manner with two standard formulas for the short-time Fourier transform, namely the covariance property and the orthogonality relations. These are

$$\begin{aligned} V_{\pi (w)g} \big (\pi (w)f \big )(z) = e^{2\pi i z \cdot \mathcal {J}w } V_gf( z), \qquad w,z\in {\mathbb {R}^{2d}}\, , \end{aligned}$$

(9)

and

$$\begin{aligned} \langle V_{g}f, V_{\gamma }h \rangle _{{\mathbb {R}^{2d}}} = \langle f, h\rangle _{\mathbb {R}^d} \, \overline{\langle g, \gamma \rangle }_{\mathbb {R}^d} , \qquad f, g, h,\gamma \in L^2(\mathbb {R}^d). \end{aligned}$$

(10)

The first identity follows from the elementary calculation of the commutator $\pi (w)^{-1}\pi (z) \pi (w)$, the orthogonality relations follows immediately from Plancherel’s theorem for the Fourier transform, since $V_gf(x,\xi ) = (f \, T_x \bar{g})\, \widehat{} \, (\xi )$ (see [15] or [36, Thm. 3.2.1]).

Since by (9)

$$\begin{aligned} V_{\gamma }h(z) e^{2\pi i z\cdot \zeta } = V_{\gamma }h (z) e^{2\pi i z\cdot ( - \mathcal {J}^2\zeta ) } = V_{\pi (-\mathcal {J}\zeta )\gamma } (\pi (-\mathcal {J}\zeta )h) (z) \, , \end{aligned}$$

we obtain the following formula for the Fourier transform of two short-time Fourier transforms:

$$\begin{aligned} \Big ( V_{g}f \, \overline{V_{\gamma }h} \Big ) \, \widehat{\,}\, (\zeta )&= \mathop \int _{{\mathbb {R}^{2d}}}\limits V_{g}f (z)\, \overline{V_{\gamma }h (z)} e^{-2\pi i z\cdot \zeta } \, dz \nonumber \\&= \mathop \int _{{\mathbb {R}^{2d}}}\limits V_{g}f (z)\, \overline{V_{\pi (-\mathcal {J}\zeta )\gamma } (\pi (-\mathcal {J}\zeta )h) (z)} \, dz \nonumber \\&= \langle f, \pi (-\mathcal {J}\zeta ) h\rangle \, \overline{\langle g, \pi (-\mathcal {J}\zeta ) \gamma \rangle } \nonumber \\&= V_g \gamma (\mathcal {J}z) \, \overline{V_fh(\mathcal {J}z)} . \end{aligned}$$

(11)

Set $F(z) = V_{g}f(z) \, \overline{V_{\gamma }h(z)}$, and recall that $\Lambda = A {\mathbb {Z}^{2d}}$ and $\Lambda ^{\circ }= \mathcal {J}(A^{-1})^T {\mathbb {Z}^{2d}}$. Using the Poisson summation formula and (11), we obtain that

$$\begin{aligned} \sum _{\lambda \in \Lambda } V_{g}f(\lambda ) \, \overline{V_{\gamma }h(\lambda )}&= \sum _{k\in {\mathbb {Z}^{2d}}} F(Ak) \nonumber \\&= |\det A|^{-1}\sum _{k\in {\mathbb {Z}^{2d}}} \widehat{F}\big ( (A^{-1})^T k \big ) \nonumber \\&= |\det A|^{-1}\sum _{k\in {\mathbb {Z}^{2d}}} V_g \gamma \big ( \mathcal {J}(A^{-1})^T k \big ) \, \overline{V_fh\big (\mathcal {J}(A^{-1})^T k \big )} \nonumber \\&= \mathrm {vol}\, (\Lambda )^{-1}\sum _{\mu \in \Lambda ^{\circ }} V_g\gamma (\mu ) \, \overline{ V_fh(\mu )} . \end{aligned}$$

(12)

The application of the Poisson summation formula is justified under mild conditions. For instance, (12) holds when $f,h \in M^1(\mathbb {R}^d)$ and $g,\gamma \in L^2(\mathbb {R}^d)$ or when $g,\gamma \in M^1(\mathbb {R}^d)$ and $f,h \in L^2(\mathbb {R}^d)$. See [12, Thm. 5.2] for the relevant properties of the short-time Fourier transform. Equation (12) is sometimes called the fundamental identity of Gabor analysis [29, 30].

We are now ready to prove the duality theorem.

(i) $\Rightarrow$ (ii) If $\mathcal {G}(g,\Lambda )$ is a frame, then there exists a dual window $\gamma \in L^2(\mathbb {R}^d)$, e.g., $\gamma = S_{g,\Lambda } ^{-1}g$, such that $\mathcal {G}(\gamma , \Lambda )$ is a Bessel family and

$$\begin{aligned} f = \sum _{\lambda \in \Lambda } \langle f, \pi (\lambda ) g\rangle \pi (\lambda ) \gamma . \end{aligned}$$

(13)

In a weak formulation, this means

$$\begin{aligned} \langle f, h \rangle = \sum _{\lambda \in \Lambda } V_gf (\lambda ) \overline{V_\gamma h (\lambda )} \, \end{aligned}$$

for all $f, h\in L^2(\mathbb {R}^d)$. If $f,h \in M^1(\mathbb {R}^d)$, then the fundamental identity (12) applies, and we have

$$\begin{aligned} \langle f, h \rangle = \mathrm {vol}\, (\Lambda )^{-1}\sum _{\mu \in \Lambda ^{\circ }} \, V_g\gamma (\mu ) \overline{V_fh(\mu )} . \end{aligned}$$

(14)

Now replace the pair $f,h\in M^1(\mathbb {R}^d)$ by $\pi (z) f, \pi (z)h \in M^1(\mathbb {R}^d)$ and use (9) once more, then we obtain

$$\begin{aligned} \langle f, h \rangle = \mathrm {vol}\, (\Lambda )^{-1}\sum _{\mu \in \Lambda ^{\circ }} V_g\gamma (\mu ) \, \overline{V_fh(\mu )} \, e^{- 2\pi i \mu \cdot \mathcal {J}z} \, \quad z\in {\mathbb {R}^{2d}}. \end{aligned}$$

The Fourier series on the right-hand side is constant, therefore its coefficients must satisfy the relations

$$\begin{aligned} \mathrm {vol}\, (\Lambda )^{-1}V_g\gamma (\mu ) \overline{V_fh(\mu )} = \langle f,h\rangle \, \delta _{\mu ,0}, \quad \text { for } \mu \in \Lambda ^{\circ }. \end{aligned}$$

This holds for all $f,h \in M^1(\mathbb {R}^d)$, whence we obtain the biorthogonality relations

$$\begin{aligned} \mathrm {vol}\, (\Lambda )^{-1}V_g\gamma (\mu ) = \delta _{\mu ,0}, \quad \text { for } \mu \in \Lambda ^{\circ }. \end{aligned}$$

(ii) $\Rightarrow$ (i)  Conversely, if $\gamma$ satisfies the biorthogonality relations, we can read the fundamental identity (12) backwards and find that every $f$ possesses a Gabor expansion (13). Since $\mathcal {G}(\gamma , \Lambda )$ is a Bessel family, we deduce that

$$\begin{aligned} \Vert f\Vert _2^2 \le C \sum _{\lambda \in \Lambda } |\langle f, \pi (\lambda ) g\rangle |^2 \quad \text { for all } f\in L^2(\mathbb {R}^d). \end{aligned}$$

(ii) $\Rightarrow$ (iii) If $\gamma$ is a dual window, then, for an appropriate phase factor $c$ with $|c| =1$, we have

$$\begin{aligned} \langle \pi (\nu )\gamma , \pi (\mu )g\rangle = \langle \gamma , \pi (\nu )^{-1}\pi (\mu )g\rangle = c \langle \gamma , \pi (\mu -\nu ) g\rangle = c \, \mathrm {vol}\, (\Lambda ) \delta _{\mu -\nu , 0} .\end{aligned}$$

(15)

Since by assumption $\mathcal {G}(\gamma , \Lambda ^{\circ })$ is a Bessel family, (15) asserts that $\mathcal {G}(\gamma , \Lambda ^{\circ })$ is dual to $\mathcal {G}(g,\Lambda ^{\circ })$, whence $\mathcal {G}(g, \Lambda ^{\circ })$ must be a Riesz sequence.

(iii) $\Rightarrow$ (ii)  Since $\mathcal {G}(g, \Lambda ^{\circ })$ is a Riesz sequence, there exists a dual basis $\{e_\nu : \nu \in \Lambda ^{\circ }\}$ in the closed span such that $\langle e_\nu , \pi (\mu )g\rangle = \delta _{\mu ,\nu }$ for all $\mu , \nu \in \Lambda ^{\circ }$. Now take the dual window $\gamma$ to be $\mathrm {vol} \, (\Lambda )^{-1}\, e_0$. $\square$

For a rigorous proof the above sketch needs to be expanded as follows. In the implication (i) $\Rightarrow$ (ii) we have shown the biorthogonality relations, but we still need to verify that $\mathcal {G}(\gamma , \Lambda ^{\circ })$ is a Bessel family. Likewise, in the implication (ii) $\Rightarrow$ (i) we start with the Bessel family $\mathcal {G}(\gamma , \Lambda ^{\circ })$ and derive the Gabor expansion (13), but we still need that $\mathcal {G}(g,\Lambda )$ is a Bessel family. These details are clarified in a technical lemma: Let $f\in L^2(\mathbb {R}^d)$. Then $\mathcal {G}(f , \Lambda )$ is a Bessel family, if and only if $\mathcal {G}(f , \Lambda ^{\circ })$ is a Bessel family. For more information we refer to the original literature [29, 33, 70].

In our description of the coarse structure we have omitted the analogous definitions and results for Gabor Riesz sequences. Let

$$\begin{aligned} \mathcal {R}_{\mathrm {full}} (g) = \{\Lambda \subseteq {\mathbb {R}^{2d}}: \mathcal {G}(g,\Lambda )\text { is a Riesz sequence} \}\, \end{aligned}$$

and $\mathcal {R}(G) = \{(\alpha ,\beta )\in \mathbb {R}_+ ^2: \mathcal {G}(g, \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d) \text { is a Riesz sequence} \}$. In view of the duality theory, it is clear that Gabor Riesz sequences need not be investigated separately. The results are as follows.

Corollary 2.4

Let $g\in M^1(\mathbb {R}^d)$. Then $\mathcal {R}_{\mathrm {full}}(g) \subseteq \{ \Lambda \subseteq {\mathbb {R}^{2d}}: \mathrm {vol}(\Lambda )> 1\}$ and $\mathcal {R}(g) \subseteq \{ (\alpha ,\beta ) \subseteq \mathbb {R}_+ ^2: \alpha \beta >1\}$. Furthermore $\mathcal {R}(g)$ is open in $\mathrm {GL}(2d, \mathbb {R})$ and contains a neighborhood of $\infty$. (This means that there exists a compact set $K \subseteq \mathrm {GL}(2d, \mathbb {R})$ such that $A\not \in K$ implies that $\Lambda =A{\mathbb {Z}^{2d}}\in \mathcal {R}(g)$.)

2.2.2 Criteria for Rectangular Lattices

If $\Lambda = \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$ is a rectangular lattice, then $\mathcal {G}(g,\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d)$ is a set that is invariant under the shifts $T_{\alpha k}, k\in \mathbb {Z}^d$, and separately under the shifts $M_{\beta l}, l\in \mathbb {Z}^d$. In the language of approximation theory, $\mathcal {G}(g,\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d)$ is a shift-invariant system with generators $M_{\beta l}g$. The resulting additional invariance properties imply special characterizations of Gabor frames, see  [70].

The pre-Gramian matrix $P=P(x)$ is defined by the entries

$$\begin{aligned} P(x)_{jk} = \bar{g}(x+j\alpha - \tfrac{k}{\beta }), \qquad j,k \in \mathbb {Z}^d. \end{aligned}$$

(16)

The Ron–Shen matrix is $G(x) = P(x)^* P(x)$, whose entries are

$$\begin{aligned} G(x)_{kl} = \sum _{j\in \mathbb {Z}^d} \bar{g}(x+j\alpha - \tfrac{l}{\beta }) \, g(x+j\alpha - \tfrac{k}{\beta }), \qquad k,l \in \mathbb {Z}^d. \end{aligned}$$

(17)

Theorem 2.5

Let $g\in L^2(\mathbb {R}^d)$ and $\Lambda = \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$ for $\alpha , \beta >0$. Then the following conditions are equivalent

• (i) The Gabor family $\mathcal {G}(g, \alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d)$ is a frame for $L^2(\mathbb {R}^d)$.

• (ii) The Gabor family $\mathcal {G}(g, \tfrac{1}{\beta } \mathbb {Z}^d\times \tfrac{1}{\alpha } \mathbb {Z}^d)$ is a Riesz sequence in $L^2(\mathbb {R}^d)$.

• (iii) There exist $A,B >0$ such that

  $$\begin{aligned} A\Vert c\Vert _2^2 \le \sum _{j\in \mathbb {Z}^d} \big | \sum _{k\in \mathbb {Z}^d} c_k \bar{g}(x+j\alpha - \tfrac{k}{\beta })\big |^2 \le B \Vert c\Vert _2^2 \, , \quad \text {a.e.} \,\, x\in \mathbb {R}^d, c\in \ell ^2(\mathbb {Z}^d) . \end{aligned}$$

  (18)

• (iv) There exist $A,B >0$ such that the spectrum of almost every Ron–Shen matrix $G(x)$ is contained in the interval $[A,B]$:

  $$\begin{aligned} \sigma (G(x)) \subseteq [A,B] \qquad \text {a.e. } x\in \mathbb {R}^d. \end{aligned}$$

Proof

The equivalence (i) $\Leftrightarrow$ (ii) is part of Theorem 2.3.

(iii) $\Leftrightarrow$ (iv)  Since $\sum _{j\in \mathbb {Z}^d} \big | \sum _{k\in \mathbb {Z}^d} c_k \bar{g}(x+j\alpha - \tfrac{k}{\beta })\big |^2 = \Vert P(x) c\Vert _2^2 = \langle P^*(x) P(x) c, c \rangle = \langle G(x) c, c \rangle$, conditions (iii) and (iv) express the same estimates in different notation.

(iii) $\Rightarrow$ (ii) Assume that (18) holds. For arbitary $c = (c_{kl})_{k,l \in \mathbb {Z}^d}\in \ell ^2({\mathbb {Z}^{2d}})$ we introduce the trigonometric series $p_k(x) = \sum _{l\in \mathbb {Z}^d} c_{kl} e^{2\pi i l\cdot x/\alpha }$. Then $p_k$ is periodic with period $\alpha$ and is square-integrable over $[0,\alpha ]^d$ with local $L^2$-norm

$$\begin{aligned} \mathop \int \limits _{[0,\alpha ] ^d} |p_k(x)|^2 \, dx = \alpha ^d \sum _{l\in \mathbb {Z}^d} |c_{kl}|^2 . \end{aligned}$$

We now write

$$\begin{aligned} \sum _{k,l \in \mathbb {Z}^d} c_{kl} M_{\tfrac{l}{\alpha }} T_{\tfrac{k}{\beta }}g = \sum _{k\in \mathbb {Z}^d} p_k T_{\tfrac{k}{\beta }}g \end{aligned}$$

and then estimate its $L^2$-norm. We use the “periodization trick” to express an integral over $\mathbb {R}^d$ as an integral over its periodized version and the assumption (18)

$$\begin{aligned} \Big \Vert \sum _{k,l \in \mathbb {Z}^d} c_{kl} M_{\tfrac{l}{\alpha }} T_{\tfrac{k}{\beta }}g\Big \Vert _2^2&= \mathop \int \limits _{\mathbb {R}^d} \Big |\sum _{k\in \mathbb {Z}^d} p_k(x) g(x-\tfrac{k}{\beta })\Big | ^2 \, dx \\&= \mathop \int \limits _{[0,\alpha ]^d} \sum _{j\in \mathbb {Z}^d} \Big |\sum _{k\in \mathbb {Z}^d} p_k(x) g(x+\alpha j-\tfrac{k}{\beta })\Big | ^2 \, dx \\&\ge \mathop \int \limits _{[0,\alpha ]^d} A \Big ( \sum _{k\in \mathbb {Z}^d} |p_k(x)|^2 \Big ) \, dx \\&= A \alpha ^d \sum _{k\in \mathbb {Z}^d} \sum _{l\in \mathbb {Z}^d} |c_{kl}|^2. \end{aligned}$$

Since the upper estimate is similar, we have proved that $\mathcal {G}(g, \tfrac{1}{\beta } \mathbb {Z}^d\times \tfrac{1}{\alpha } \mathbb {Z}^d)$ is a Riesz sequence in $L^2(\mathbb {R}^d)$.

(ii) $\Rightarrow$ (iii)  By assumption there exist constants $A,B >0$, such that for every sequence $a = (a_{kl}) \in \ell ^2({\mathbb {Z}^{2d}})$ (or every finite sequence $a$)

$$\begin{aligned} A\Vert a\Vert _2^2 \le \Vert \sum _{k,l \in \mathbb {Z}^d} a_{kl} M_{\tfrac{l}{\alpha } } T_{\tfrac{k}{\beta } } g \Vert _2^2 \le B \Vert a\Vert _2^2. \end{aligned}$$

We choose $a$ as a tensor product $a_{kl} = b_l c_k$ for $b,c \in \ell ^2(\mathbb {Z}^d)$ and set $p(x) = \sum _{l\in \mathbb {Z}^d} b_l e^{2\pi i k\cdot x / \alpha }$. Then we obtain that

$$\begin{aligned} \frac{A}{\alpha ^d}\, \Vert c \Vert _2^2 \mathop \int \limits _{[0,\alpha ]^d} |p(x)|^2\, dx&= A \Vert b\Vert _2^2 \, \Vert c\Vert _2^2 \\&\le \Vert \sum _{k,l \in \mathbb {Z}^d} c_k b_l M_{\tfrac{l}{\alpha }} T_{\tfrac{k}{\beta }} g\Vert _2^2 \\&= \mathop \int _{\mathbb {R}^d}\limits \Big | p(x) \Big ( \sum _{k\in \mathbb {Z}^d} c_k g(x-\tfrac{k}{\beta }) \Big ) \Big |^2 \, dx \\&= \mathop \int \limits _{[0,\alpha ] ^d} |p(x)|^2 \, \sum _{j\in \mathbb {Z}^d} \Big | \sum _{k\in \mathbb {Z}^d} c_k g(x+\alpha j-\tfrac{k}{\beta }) \Big |^2 \, dx \, . \end{aligned}$$

This inequality holds for all $p\in L^2([0,\alpha ]^d)$ and $c\in \ell ^2(\mathbb {Z}^d)$ and therefore implies that

$$\begin{aligned} \sum _{j\in \mathbb {Z}^d} \Big | \sum _{k\in \mathbb {Z}^d} c_k g(x+\alpha j-\tfrac{k}{\beta }) \Big |^2 \ge \frac{A}{\alpha ^d} \Vert c \Vert _2^2 \end{aligned}$$

for almost every $x\in [0,\alpha ]^d$. (For the spectrum of multiplication operators see [11, p. 198, Exercise 3].) This is the lower bound in condition (iii). The upper bound is obtained analogously. $\square$

The inequalities in (18) have been the master tool of Janssen to determine the frame set of the exponential functions [56, 58].

For rectangular lattices $\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$ with rational volume $\alpha \beta \in \mathbb {Q}$ (“rational lattices”) one often encounters the Zeevi–Zibulski criterium using a vector-valued Zak transform [84, 85].

For most applications the conditions of Daubechies et al. [17] on “painless non-orthogonal expansions” are perfectly sufficient.

Corollary 2.6

Let $g\in L^\infty (\mathbb {R}^d)$ with ${{\mathrm{supp}}}g \subseteq [-L/2,L/2]^d$ and choose $\alpha <L, \beta < 1/L$. If  $0 < \inf _{t\in \mathbb {R}^d} \sum _{k\in \mathbb {Z}^d} |g(t-\alpha k)|^2$, then $\mathcal {G}(g,\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d)$ is a frame for $L^2(\mathbb {R}^d)$.

Proof

Since $\beta ^{-1}>L$, distinct translates $T_{k/\beta }g$ and $T_{l/\beta }g$ with $k\ne l$ have disjoint support. Therefore the entries of the Ron–Shen matrix simplify to

$$\begin{aligned} G(x)_{kl}&= \sum _{j\in \mathbb {Z}^d} \bar{g}(x+\alpha j - \tfrac{l}{\beta }) g(x+\alpha j - \tfrac{k}{\beta }) \\&= \sum _{j\in \mathbb {Z}^d} |g(x+\alpha j - \tfrac{k}{\beta })|^2 \, \delta _{k,l}\,. \end{aligned}$$

Hence $G(x)$ is a diagonal matrix for every $x$. Set $A = \inf _{x\in \mathbb {R}^d} \sum _{j\in \mathbb {Z}^d} |g(x+\alpha j - \tfrac{k}{\beta })|^2$ and $B = \sup _{x\in \mathbb {R}^d} \sum _{j\in \mathbb {Z}^d} |g(x+\alpha j - \tfrac{k}{\beta })|^2 \,$; then the spectrum of $G(x)$ on $\ell ^2(\mathbb {Z})$ is containly in $[A,B]$ uniformly for all $x$. Since $A>0$ by assumption, $\mathcal {G}(g,\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d)$ is a frame according to Theorem 2.5(ii). $\square$

2.2.3 Criteria for Windows in $M^1$

The previous criteria worked for windows in $L^2(\mathbb {R}^d)$. If the window is in the smaller space $M^1(\mathbb {R}^d)$, then additional criteria can be formulated [38]. The advantage of these criteria is that they do not require inequalities as in the definition of Gabor frames. The invertibility of the frame operator is replaced by its injectivity, albeit on a larger space of distributions.

Theorem 2.7

Assume that $g\in M^1(\mathbb {R}^d)$. Then the following are equivalent.

• (i) $\mathcal {G}(g,\Lambda )$ is a frame for $L^2(\mathbb {R}^d)$.

• (ii) The analysis operator $C_{g,\Lambda }$ is one-to-one on $M^\infty (\mathbb {R}^d)$, i.e., if $f\in M^\infty (\mathbb {R}^d)$ and $\langle f, \pi (\lambda )g\rangle = 0$ for all $\lambda \in \Lambda$, then $f = 0$ in $M^\infty (\mathbb {R}^d)$.

• (iii) Duality: The synthesis operator $D_{g,\Lambda ^{\circ }}$ is one-to-one on $\ell ^\infty (\Lambda ^{\circ })$, i.e., if $c = (c_\mu )_{\mu \in \Lambda ^{\circ }} \in \ell ^\infty (\Lambda ^{\circ })$ and $\sum _{\mu \in \Lambda ^{\circ }} c_\mu \pi (\mu ) g = 0$ in $M^\infty (\mathbb {R}^d)$, then $c = 0$.

Formulated differently, (ii) says that $\Lambda$ is a set of uniqueness for the space of short-time Fourier transforms on $M^\infty (\mathbb {R}^d)$, and (iii) says that the time–frequency shifts $\pi (\mu )g, \mu \in \Lambda ^{\circ }$, are $\ell ^\infty$-linearly independent.

Condition (iii) is to be understood as follows: For $c\in \ell ^\infty (\Lambda ^{\circ })$ the sum $\sum _{\mu \in \Lambda ^{\circ }} c_\mu \pi (\mu )g$ is in $M^\infty (\mathbb {R}^d)$ by Lemma 1.1 and converges in the weak$^*$ topology. Thus $\sum _{\mu \in \Lambda ^{\circ }} c_\mu \pi (\mu )g= 0$ means that

$$\begin{aligned} \sum _{\mu \in \Lambda ^{\circ }} c_{\mu } \langle \pi (\mu ) g, f\rangle = 0 \, \end{aligned}$$

(19)

for all $f\in M^1(\mathbb {R})$. Since $\mu \mapsto \big (\langle \pi (\mu )g,f\rangle \big )_{\mu \in \Lambda ^{\circ }} \in \ell ^1(\Lambda ^{\circ })$ by Lemma 1.1, the sum in (19) converges absolutely.

If $\mathcal {G}(g,\Lambda )$ is not a frame, then the kernel of the synthesis operator is non-trivial. We note the following elementary property.

Lemma 2.8

Let $g\in M^1(\mathbb {R}^d)$, let $\Lambda$ be a lattice in ${\mathbb {R}^{2d}}$, and set

$$\begin{aligned} V_{\Lambda ^{\circ }} = \mathrm {ker}\, _{\ell ^{\infty } } D_{g,\Lambda ^{\circ }}= \{ c\in \ell ^\infty (\Lambda ^{\circ }): \sum _{\mu \in \Lambda ^{\circ }} c_\mu \pi (\mu ) g = 0\}. \end{aligned}$$

Then $V_{\Lambda ^{\circ }}$ is weak$^*$-closed in $\ell ^\infty (\Lambda ^\circ )$, and is invariant with respect to the twisted translation $c \rightarrow T_\mu c, (T_\mu c)_{\lambda } = e^{2\pi i \mu _1\cdot (\mu _2-\lambda _2)} c_{\lambda -\mu }$.

Theorem 2.7 is part of a long list of conditions that characterize a Gabor frame. Conceptually they are easier to handle than the criteria in Sects. 2.2.1 and 2.2.2, since the invertibility of an operator is usually harder to verify than its injectivity. Theorem 2.7 has been used successfully in several problems involving Gabor frames [20].

Whereas the duality theory (Theorem 2.3) and its corollaries require only the Poisson summation formula for their proof, Theorem 2.7 is deeper. The proof requires a non-commutative version of Wiener’s theorem for twisted convolution [43] and methods from abstract harmonic analysis [38]. See [39] for an extended survey and discussion.

Surprisingly, the equivalence of conditions (i) and (ii) in Theorem 2.7 does not require the lattice structure and also holds for non-uniform Gabor frames [47].

To summarize, the results in Sect. 2 provide a beautiful theory of the structure of Gabor frames. The manifold characterizations of Gabor frames provide tools for checking whether a Gabor family $\mathcal {G}(g,\Lambda )$ is a frame or not. It is fair to say that this part of Gabor analysis is well understood and reasonably complete. We refer to this set of results as the coarse structure of Gabor frames.

2.3 Outside $M^1$

In the formulation of the results for the frame set we have restricted ourselves to window functions in $M^1(\mathbb {R}^d)$. This is certainly the canonical choice in the context of time–frequency analysis, since time–frequency analysis deals with the properties of functions and distributions in terms of their time–frequency concentration and thus requires a suitable space of test functions and distributions.

However, Gabor frames are an object in the Hilbert space $L^2(\mathbb {R}^d)$ and thus one may strive for more generality. Indeed, many $L^2$-results have been formulated under weaker conditions on the window. In particular the treatment of rectangular lattices and the Balian-Low theorem can be worked out under the hypothesis that either $g$ or $\hat{g}$ belong to the amalgam space $W(L^\infty , L^1)$ [7].

In our opinion, the world of Gabor frames outside $M^1(\mathbb {R}^d)$ is a world of pathologies. The most striking result in this direction is Janssen’s tie [57]. Janssen investigated the frame set $\mathcal {F}(g)$ for the simplest possible window function, namely the characteristic function $\chi _{[0,1]}$. The main insight of this example is that the frame set is extremely complicated: neither is it open nor does it contain a neighborhood of $(0,0)$ [26], quite in contrast to the properties of $\mathcal {F}(g)$ for $M^1$-windows. Janssen left many white spots on the tie, where he could not determine whether $\mathcal {G}(\chi _{[0,1]}, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is a frame or not; he observed that the frame property seems to depend on number theoretic properties of $\alpha , \beta$. After contributions in [49, 50], the picture of Janssen’s tie was completed by the stunning work of Dai and Sun [14]. Based on the analysis of a dynamical system associated to a lattice $\alpha \mathbb {Z}\times \beta \mathbb {Z}$, they developed a decision tree with many branches that let one determine in principle when $\mathcal {G}(\chi _{[0,1]}, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is a frame.

3 The Fine Structure of Gabor Frames

The fine structure of Gabor frames tries to explain the relation between the window $g$ and the frame set $\mathcal {F}(g)$. This relation is not understood and remains mysterious. In this section, we present the known results on the fine structure and add a small new result.

The original problem of Gabor analysis is hardly touched by the existing theory. Clearly, none of the characterizations of Sect. 2 provides an answer to the principal question whether a given Gabor family $\mathcal {G}(g,\Lambda )$ is a frame or not. At best, these characterizations serve as a tool for the investigation of the fine structure. For the study of the frame set other ingredients are necessary. So far these have been complex analysis, or approximation theory, or simply hard work. Currently we lack good methods to treat the fine structure of general window classes. Our analysis and tools are based on a case-by-case treatment of examples.

In the following, we restrict ourselves to the one-dimensional case, as all known results are for windows of one variable. The lattices in the time–frequency plane are therefore $A \mathbb {Z}^2$ for an invertible $2\times 2$-matrix $A$. (We note that every matrix acting on $\mathbb {R}^2$ is a multiple of a symplectic matrix; probably this simplifies the analysis a bit.)

3.1 Early Examples of the Fine Structure

In the first 25 years of Gabor analysis, from [17] in 1986 to 2011, the frame set was determined for precisely six (=6) functions, up to trivial modifications such as scaling and time–frequency shifts.

Theorem 3.1

• (i) Let $g(t)=e^{-a t^2}$ where $a>0$. Then the (full) frame set is

  $$\begin{aligned} \mathcal {F}_{\mathrm {full}} (g) = \{ \Lambda \subset \mathbb {R}^2: \mathrm {vol}(\Lambda )< 1\}. \end{aligned}$$

• (ii) Let $g$ be $g(t) = (e^{at} + e^{-at})^{-1}$, $g(t)= e^{-a |t|}$, or $g(t) = (1+4a t^2)^{-1}$ where $a>0$. Then the (reduced) frame set is

  $$\begin{aligned} \mathcal {F}(g) = \{ (\alpha ,\beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1\}. \end{aligned}$$

• (iii) Let $g$ be either $g(t) = e^{-at} \chi _{\mathbb {R}_+} (t)$ or $g(t) = (1+2\pi i a t)^{-1}$ where $a>0$. Then the reduced frame set is $\mathcal {F}(g) = \{ (\alpha ,\beta ) \in \mathbb {R}_+ ^2: \alpha \beta \le 1\}$

We note that in Theorem 3.1, the necessary density condition on $\Lambda$ is also sufficient for $\mathcal {G}(g,\Lambda )$ to be a frame.

The celebrated characterization of Gabor frames with a Gaussian window (i) is due to Lyubarski [68] and Seip [77]. Let us emphasize that the Gaussian is the only function for which the full frame set is known. The case of the hyperbolic secant (ii) was reduced to the case of the Gaussian by Janssen and Strohmer [60], and the two exponential functions in (ii) and (iii) were analyzed by Janssen [56, 58]. They used Theorem 2.5 and a remarkable factorization property of the Zak transform of $g$. The case of the Poisson kernel follows from invariance under the Fourier transform (Lemma 2.2).

It is instructive to review briefly the proof idea for the Gaussian $g(t) = 2^{1/4}\, e^{-\pi t^2}$. The starting point is the following easy calculation of the short-time Fourier transform with Gaussian window

$$\begin{aligned} \langle f, \pi (x,-\xi )g \rangle&= 2^{1/4} \mathop \int \limits _{\mathbb {R}} f(t) e^{-\pi (t-x)^2} e^{2\pi i \xi t} \, dt \\&= 2^{1/4} \mathop \int \limits _{\mathbb {R}} f(t) e^{2\pi t (x+i\xi )} e^{-\pi t^2} \, dt \,\, e^{-\pi x^2}. \end{aligned}$$

By writing a point $(x,\xi )$ in the time–frequency plane $\mathbb {R}^2$ as a complex number $z=x+i\xi$, we discover a complex structure in the short-time Fourier transform of $f$ with respect to the Gaussian. Let

$$\begin{aligned} B f(z)=F(z)= 2^{1/4}e^{-\pi z^2 /2}\mathop \int \limits _{\mathbb {R}} f(t)e^{-\pi t^2}\, e^{2\pi t z} dt, \, \qquad z\in \mathbb {C}\, , \end{aligned}$$

be the Bargmann transform of $f$. Then

$$\begin{aligned} V_g f(x,-\xi ) = e^{\pi i x\xi } Bf(z) e^{-\pi |z|^2/2}. \end{aligned}$$

(20)

It follows from the definition that $Bf$ is an entire function. Moreover, the Bargmann transform is unitary from $L^2(\mathbb {R})$ onto the Fock space $\mathcal {F}$ of entire functions with finite norm $\Vert F\Vert _{\mathcal {F}} = \int _{\mathbb {C}} |F(z)|^2 e^{-\pi |z|^2} \, dz$ [34]. We can therefore reformulate the frame property as a sampling property for the Fock space: $\mathcal {G}(g,\Lambda )$ is a frame for $L^2(\mathbb {R}^d)$ if and only if

$$\begin{aligned} \sum _{\lambda \in \overline{\Lambda }} |F(\lambda )|^2 e^{-\pi |\lambda |^2} \asymp \mathop \int \limits _{\mathbb {C}} |F(z)|^2 \, e^{-\pi |z|^2} \, dz \end{aligned}$$

(21)

for all $F\in \mathcal {F}$. The identity (20) translates the problem from Gabor analysis into a problem of complex analysis. Proving sampling inequalities in the style of (21) is a central problem in complex analysis, and thus complex analysis comes with a large and powerful toolbox [64, 78]. In fact, Seip and Lyubarsky solved the problem of Gabor frames with the Gaussian even for non-uniform Gabor frames. We note that the results on the coarse structure of Gabor frames played only an auxiliary role in their solution.

Perhaps the main point is that the determination of the frame set for the Gaussian became possible only through the interaction of two different mathematical disciplines.

Unfortunately, the use of complex methods seems to be restricted to the Gaussian window. It can be shown that the Gaussian is the only window whose short-time Fourier transform has analytic properties [2].

3.2 Gabor Frames with Totally Positive Functions

Early on, Daubechies conjectured that $\mathcal {F}(g) = \{ (\alpha ,\beta )\in \mathbb {R}_+ ^2: \alpha \beta <1\}$ whenever $g$ is a positive function in $L^1$ with positive Fourier transform in $L^1$ [15, p. 981]. This conjecture was soon disproved by Janssen in [55], and then forgotten. Only recently, Daubechies’s conjecture was taken up again. The key observation justifying a new attempt was the observation that the Gaussian, the hyperbolic secant, and the exponential functions are totally positive functions. This fact led to the study of Gabor frames with totally positive window functions.

A function on $\mathbb {R}$ is called totally positive if for every two sets of increasing real numbers $x_1<x_2<\cdots <x_N$ and $y_1<y_2<\cdots <y_N$ , $N\in \mathbb {N}$, the determinant of the matrix $\left[ g(x_j-y_k)\right] _{1\le j,k \le N}$ is non-negative. The concept of total positivity is well-known in approximation theory and statistics [61, 74, 76]. Totally positive functions are completely characterized by a factorization of their Fourier–Laplace transforms [75].

A particular class of totally positive functions are the totally positive functions of finite type. These are defined by a factorization of their Fourier transform as follows:

$$\begin{aligned} \hat{g}(\xi ) = \prod _{j=1}^{M}(1+2\pi i \delta _j \xi )^{-1}\end{aligned}$$

(22)

for real, non-zero parameters $\delta _j \in \mathbb {R}$ and $M\in \mathbb {N}$. The number $M$ is called the type of $g$. If $M\ge 2$, then $g$ is in $M^1(\mathbb {R})$; if $M=1$, then $g(t) = \delta ^{-1}e^{-t/\delta } \chi _{\mathbb {R}^+} (\delta t)$ is a one-sided exponential and not in $M^1(\mathbb {R})$.

If we take total positivity as the appropriate notion of positivity, then Daubechies’ conjecture is true.

Theorem 3.2

[48] Assume that $g\in L^2(\mathbb {R})$ is a totally positive function of finite type $M \ge 2$. Then $\mathcal {F}(g)= \{ (\alpha , \beta ) \in \mathbb {R}_+^2: \alpha \beta <1\}$. In other words, $\mathcal {G}(g, \alpha \mathbb {R}\times \beta \mathbb {R})$ is a frame if and only if $\alpha \beta <1$.

Note again that the necessary density condition is also sufficient for the frame property in this case.

Theorem 3.2 increases the number of functions with known frame set from six to an uncountable set that can be parametrized by countably many real parameters. Using a partial fraction decomposition of the product in (22) and the inverse Fourier transform, one sees that the totally positive functions of finite type are special linear combinations of exponential functions. Among these are the truncated power functions $g(t) = e^{-t} t^r \chi _{\mathbb {R}_+}(t)$ for $r\in \mathbb {N}$, or the functions $g(t) = (e^{-at} - e^{-bt}) \chi _{\mathbb {R}^+}(t)$ and $g(t) = e^{at} \chi _{\mathbb {R}_+}(-t) + e^{-bt} \chi _{\mathbb {R}_+}(t)$ for $a,b>0$.

Using Lemma 2.2, we obtain the following corollary.

Corollary 3.3

Let $g$ be a finite product of the form (22) with $M\ge 2$. Then $\mathcal {F}(g) = \{ (\alpha , \beta ) \in \mathbb {R}_+^2: \alpha \beta <1\}$.

The corollary covers the Poisson kernel and its powers $g(t) = (1+4\pi ^2 t^2)^{-n}$ for $n\in \mathbb {N}$.

Thus, as in the case of the Gaussian, the complete characterization of the frame set requires an additional ingredient and the input from a different mathematical area. For totally positive functions, the connection is with approximation theory.

Let us briefly sketch the idea of the proof of Theorem 3.2. Consider the finite sections

$$\begin{aligned} Q_{jk}(x) = g(x+\alpha j - \tfrac{k}{\beta } ), \qquad j_0 \le j \le j_0 +L-1, k_0 \le k \le k_0 +N-1 \, , \end{aligned}$$

of the pre-Gramian for judiciously chosen indices $j_0,k_0 \in \mathbb {Z}$ and $L\ge N$ large enough. By properties of total positivity and the so-called Schoenberg–Whitney conditions [76], $Q$ possesses a square submatrix with positive determinant. This means that $Q$ has maximum rank, and thus

$$\begin{aligned} \sum _{j=j_0 } ^{j_0 + L-1} \big | \sum _{k=k_0 }^{k_0 +N-1} c_k \bar{g}(x+j\alpha - \tfrac{k}{\beta })\big |^2 \ge B_{L,N} \Vert c\Vert _2^2 \end{aligned}$$

for all finite sequences $c$. One can therefore hope that the lower bound $B_{L,N}$ is independent of the dimensions of the matrix $Q$ and thus verify the criterium of Theorem 2.5(iii). The actual proof in [48] is rather tricky and constructs a dual window with compact support from which the uniform lower bounds follow.

Totally positive functions constitute an important function class in approximation theory and statistics. The convolution of totally positive functions is again totally positive; every totally positive function decays exponentially fast, and thus for numerical purposes behaves like a compactly supported function. Furthermore, a user is not obliged to make a subtle choice for the lattice parameters; every lattice with the necessary density will generate a Gabor frame. Finally, totally positive functions can be written explicitly: using partial fractions and an inverse Fourier transform, one can show [5] that every totally positive function of finite type with distinct parameters $\delta _j \ne \delta _k$ in the Fourier transform (22) can be written as

$$\begin{aligned} g(x) = \sum _{i=1}^m \left( \frac{1}{|\delta _i|} e^{-\frac{x}{\delta _i}} h(x \delta _i) \prod _{k = 1,\, k\ne i}^m \left( 1-\frac{\delta _k}{\delta _i}\right) ^{-1}\right) \, , \end{aligned}$$

(23)

where $h$ is the Heaviside function $h(x) = 1,$ if $x>0$, $h(0) = 1/2$, and $h(x) = -1$, if $x<0$. See also [63].

For all these reasons one may hope that Theorems 3.1 and  3.2 will also have practical consequences.

3.3 Obstructions

In all known examples of frame sets the frame property was completely characterized by the density of the lattice: the necessary density condition $\alpha \beta <1$ is also sufficient for $\alpha \mathbb {Z}\times \beta \mathbb {Z}$ to generate a frame (with Gaussian window or a totally positive window). Next we will discuss the known obstructions and interpret them as results about the fine structure of the frame set. We restrict to the one-dimensional case, although the results are simple enough to allow for multivariate extensions.

3.3.1 Support Properties

An obvious property is the support property. If ${{\mathrm{supp}}}g \subseteq [0,L]$, then $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ cannot be a frame for $\alpha > L$, because the $\alpha$-translates of $g$ do not cover the real line. We include a simple result.

Lemma 3.4

Let $g\in M^1(\mathbb {R})$ with ${{\mathrm{supp}}}g \subseteq [0,L]$. Then

$$\begin{aligned} \mathcal {F}(g) \subseteq \{ (\alpha ,\beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1, \text { and } \alpha < L\}. \end{aligned}$$

(24)

Proof

Let $\alpha \ge L$. Since $g\in M^1(\mathbb {R})$, $g$ is continuous, we have $g(0) = g(L) = 0$. Let $f= \delta _0 \in M^\infty (\mathbb {R})$. Then $\langle f, M_{\beta l}T_{\alpha k} g\rangle = g(-\alpha k) = 0$ for all $k, l\in \mathbb {Z}$ by the support property. By Theorem 2.7(ii), $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame, and thus $(\alpha , \beta ) \not \in \mathcal {F}(g)$. $\square$

More generally, we need the covering condition $\alpha \mathbb {Z}+ {{\mathrm{supp}}}\, g = \mathbb {R}$ as a necessary condition on the translation parameter $\alpha$. One might expect that the inclusion (24) implies that ${{\mathrm{supp}}}\, g \subseteq [c,c+L]$ for some $c\in \mathbb {R}$. This is not true, as is shown by Example 3.9.

3.3.2 Uniform Partitions of Unity

The following theorem (the only new contribution of this survey) seems to be the first result that characterizes a property of the frame set $\mathcal {F}(g)$ by a property of the window $g$.

Theorem 3.5

For a non-zero $g\in M^1(\mathbb {R})$ the following statements are equivalent.

• (i) $\mathcal {G}(\alpha \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame for all $\alpha >0$. (i’) There exists a sequence $\alpha _n >0$ with $\lim _{n\rightarrow \infty } \alpha _n = 0$ such that $\mathcal {G}(g, \alpha _n \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame for all $n\in \mathbb {N}$.

• (ii) There exists $\xi \in [0,\beta )$ such that

  $$\begin{aligned} \sum _{k\in \mathbb {Z}} g(x-\tfrac{k}{\beta }) e^{2\pi i k\xi /\beta } = 0 \qquad \text { for all }\,\, x \in \mathbb {R}. \end{aligned}$$

  (25)

• (iii) There exists a $\xi \in [0,\beta )$ such that $\hat{g}(\beta k +\xi ) =0$ for all $k\in \mathbb {Z}$.

Proof

(ii) $\Rightarrow$ (i) Assume that $\sum _{k\in \mathbb {Z}} e^{2\pi i k\xi /\beta } \, g(x-\tfrac{k}{\beta }) = 0$ for all $x\in \mathbb {R}$. Set $c_{kl} = 0$ for $l\ne 0$ and $c_{k,0} = e^{2\pi i k\xi /\beta }$. Then $c \in \ell ^\infty (\mathbb {Z}^2)$ and

$$\begin{aligned} \sum _{k,l\in \mathbb {Z}} c_{kl} M_{l/\alpha } T_{k/\beta } g = \sum _{k\in \mathbb {Z}} c_{k,0} T_{k/\beta } g = \sum _{k\in \mathbb {Z}} e^{2\pi i k\xi /\beta } \, g( \cdot -\tfrac{k}{\beta }) = 0 \, , \end{aligned}$$

where the latter sum converges even pointwise. Thus condition (iii) of Theorem 2.7 is violated, and therefore $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame for arbitrary $\alpha >0$.

(i), (i’) $\Rightarrow$ (ii)    Conversely, assume that $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ fails to be a frame for some $\beta >0$ and all $\alpha >0$ (a sequence $\alpha _n$ tending to $0$, respectively). Again by Theorem 2.7, there exist $c^\alpha = (c^\alpha _{kl})_{k,l\in \mathbb {Z}} \in \ell ^\infty (\mathbb {Z}^2)$ such that

$$\begin{aligned} \sum _{k,l\in \mathbb {Z}} c^\alpha _{kl} M_{l/\alpha } T_{k/\beta }g = 0 \qquad \text { in } M^\infty (\mathbb {R}). \end{aligned}$$

(26)

We may assume that $\Vert c^\alpha \Vert _\infty = 1$. By Lemma 2.8, we may assume in addition that $|c^\alpha _{0,0}| \ge 1/2$. Since the unit ball of $\ell ^\infty (\mathbb {Z}^2)$ is weak$^*$-compact and metrizable, there exists a sequence $\alpha _n >0$ with $\lim _{n\rightarrow \infty } \alpha _n = 0$, such that $c^{\alpha _n} \xrightarrow {w^*} c \in \ell ^\infty (\mathbb {Z}^2)$. Therefore $c\ne 0$, and for fixed $k\in \mathbb {Z}$ the sequence $(c_{kl}^{\alpha _n} )_{l\in \mathbb {Z}}$ converges weak$^*$ to $(c_{kl})_{l\in \mathbb {Z}}$.

Claim We may choose $c$ to have the form $c_{kl} = \mu _k \delta _{l,0}$.

To prove the claim, let $f\in M^1(\mathbb {R})$ be arbitrary and split the double sum in (26) as follows

$$\begin{aligned} \sum _{k,l\in \mathbb {Z}} \!c_{kl}^\alpha \langle M_{l/\alpha } T_{k/\beta } g, f \rangle \!=\! \sum _{k \in \mathbb {Z}} c_{k,0}^\alpha \langle T_{k/\beta } g, f \rangle \!+\! \sum _{k,l\in \mathbb {Z}, l\ne 0 }\!\! c_{kl}^\alpha \langle M_{l/\alpha } T_{k/\beta } g, f \rangle \!=\! I_\alpha \!+\! II_\alpha . \end{aligned}$$

As $\alpha _n \rightarrow 0$, we have $I_{\alpha _n} \rightarrow \sum _{k\in \mathbb {Z}} c_{k,0} \langle T_{k/\beta }g, f\rangle$, because $c^{\alpha _n} \xrightarrow {w^*} c$ and the sequence $k \mapsto \langle T_{k/\beta } g, f\rangle$ is in $\ell ^1(\mathbb {Z})$.

For the second term we use that

$$\begin{aligned} |II_\alpha | \le \Vert c^\alpha \Vert _\infty \, \sum _{k,l\in \mathbb {Z}, l\ne 0} |\langle M_{l/\alpha } T_{k/\beta } g, f \rangle |. \end{aligned}$$

By assumption $\Vert c^\alpha \Vert _\infty =1$. Since $f,g\in M^1(\mathbb {R})$, the short-time Fourier transform $V_gf$ is in $M^1(\mathbb {R}^2)$, and thus in $W(\mathbb {R}^2)$ by [36, Prop. 12.1.11]. This property implies that $II_{\alpha _n }\rightarrow 0$ for $\alpha _n \rightarrow 0$. Since this is true for all $f\in M^1(\mathbb {R})$, we have shown that

$$\begin{aligned} 0= \sum _{k,l\in \mathbb {Z}} c^{\alpha _n} _{kl} M_{l/\alpha } T_{k/\beta } g \xrightarrow {w^*} \sum _{k\in \mathbb {Z}} c _{k,0} T_{k/\beta } g. \end{aligned}$$

So, we have shown that assumption (i) implies the identity

$$\begin{aligned} \sum _{k\in \mathbb {Z}} \mu _k T_{k/\beta } g = 0 \quad \text { in } M^\infty (\mathbb {R}). \end{aligned}$$

(27)

for some non-zero $(\mu _k) \in \ell ^\infty (\mathbb {Z})$. Since $g\in M^1(\mathbb {R})$, this sum converges uniformly on compact sets and makes sense pointwise.

Now let $V$ be the subspace of $\ell ^\infty (\mathbb {Z})$ defined by

$$\begin{aligned} V = \{ \nu \in \ell ^\infty (\mathbb {Z}): \sum _{k\in \mathbb {Z}} \nu _k g(x-k/\beta ) = 0, \,\, \forall x\in \mathbb {R}\} . \end{aligned}$$

We have shown that $V\ne \{0\}$. Clearly, $V$ is a weak$^*$-closed, translation-invariant subspace of $\ell ^\infty (\mathbb {Z})$ as in Lemma 2.8. By a Tauberian theorem of Wiener [62, 71], $V$ contains a sequence $\nu$ of the form $\nu _k = e^{2\pi i \xi k/\beta }$ for some $\xi \in \mathbb {R}$. This means that $\sum _{k\in \mathbb {Z}} e^{2\pi i k\xi /\beta } \, g(x-\frac{k}{\beta }) = 0$ for all $x \in \mathbb {R}$, as claimed.

The equivalence (ii) $\Leftrightarrow$ (iii) follows from Poisson’s summation formula. $\square$

Remark

Since the dual version of Wiener’s Lemma above may not be as standard as the $\ell ^1$-version, we give a short argument. Let $V\ne \{0\}$ be a weak $^*$-closed, translation-invariant subspace of $\ell ^\infty (\mathbb {Z})$. Then $V$ contains a sequence $\nu$ with entries $\nu _k = e^{2\pi i k \xi }$ for some $\xi \in \mathbb {R}$. The annihilator $V^\perp = \{ c \in \ell ^1(\mathbb {Z}): \sum _{k\in \mathbb {Z}} c_k \nu _k = 0 \, \text { for all } \nu \in V\}$ is a translation-invariant subspace of $\ell ^1(\mathbb {Z})$ and hence an ideal. Since $V\ne \{0\}$, $V^\perp$ is a proper closed ideal. By Wiener’s Theorem (in the precise formulation [62, VIII.6.7]) there exists a $\xi \in \mathbb {R}$, such that $\hat{c} (\xi ) = \sum _{k\in \mathbb {Z}} c_k e^{2\pi i k\xi } = 0$ for all $c \in V^\perp$. This implies that the sequence $\nu$ with $\nu _k = e^{2\pi i k\xi }$ is in $V$.

Remark

Recall that the Zak transform of $g$ (with respect to a parameter $\beta$) is defined by

$$\begin{aligned} Z_{\frac{1}{\beta } } g(x,\xi ) = \sum _{k\in \mathbb {Z}} g(x-\tfrac{k}{\beta }) e^{2\pi i k\xi /\beta }. \end{aligned}$$

As is well known, the properties of the Zak transform $Zg$ are closely related to the frame properties of a Gabor set $\mathcal {G}(g,\alpha \mathbb {Z}\times \beta \mathbb {Z})$. Theorem 3.5 is another example of such a connection.

To put the statement slightly differently, $\mathcal {F}(g) \subseteq \{ (\alpha , \beta )\in \mathbb {R}_+ ^2: \alpha \beta <1, \beta \ne \beta _0, \alpha >0\}$ if and only if there exists $\xi \in \mathbb {R}$ such that $Z_{1/\beta _0 } g(x,\xi ) = 0$ for all $x\in \mathbb {R}$. This means that the zero set of the Zak transform of $g$ contains a horizontal line. Since $Z_{1/\beta } (M_{-\xi } g)(x, 0 ) = e^{-2\pi i x\xi } Z_{1/\beta } g(x, \xi )$, this means that the periodization of a modulation of $g$ vanishes identically.

Corollary 3.6

Let $g\in M^1(\mathbb {R})$.

Assume that $g$ generates a partition of unity, i.e., there exists $\gamma >0$ such that

$$\begin{aligned} \sum _{k\in \mathbb {Z}} g(t-\gamma k) = a \qquad \text {for all } \, t \in \mathbb {R}. \end{aligned}$$

Then $\mathcal {G}(g,\alpha \mathbb {Z}\times \frac{n}{\gamma } \mathbb {Z})$ is not a frame for every $\alpha >0$ and $n = 2, 3 , 4 , \dots$.

Thus $\mathcal {F}(g) \subseteq \{ (\alpha ,\beta )\in \mathbb {R}_+ ^2: \alpha \beta <1, \beta \ne \tfrac{n}{\gamma } \, \text { for } n=2, 3, \dots \}$.

Proof

The assumption implies that for all $n\in \mathbb {N}, n\ge 2$,

$$\begin{aligned} \sum _{k\in \mathbb {Z}} e^{2\pi i k/n} g(t- \gamma k /n)&= \sum _{j=0}^{n-1} \sum _{l\in \mathbb {Z}} e^{2\pi i \tfrac{ln+j}{n}} g(t-\gamma \tfrac{ln+j}{n}) \\&= \sum _{j=0}^{n-1} e^{2\pi i \tfrac{j}{n}} \sum _{l\in \mathbb {Z}} g(t-\gamma \tfrac{j}{n} - \gamma l) = a \sum _{j=0}^{n-1} e^{2\pi i \tfrac{j}{n}} = 0 . \end{aligned}$$

By Theorem 3.5, $\mathcal {G}(g, \alpha \mathbb {Z}\times \tfrac{n}{\gamma } \mathbb {Z})$ fails to be a frame for all $\alpha \!>\!0$ and $n\!=\!2,3,\dots$.

$\square$

The corollary was first observed in [18] and rediscovered in [42]. It is easy to formulate a statement for more general windows.

Using Lemma 2.2, similar statements hold when $\hat{g}$ satisfies a partition of unity property.

Corollary 3.7

Assume that $g\in M^1(\mathbb {R}^d)$ and $g(k/\gamma ) = 0$ for all $k\in \mathbb {Z}$, or, equivalently, $\sum _{k\in \mathbb {Z}} \hat{g}(\xi - k\gamma ) = 0$ for all $\xi \in \mathbb {R}$.

Then $\mathcal {G}(g, \tfrac{n}{\gamma }\mathbb {Z}\times \beta \mathbb {Z})$ is not a frame for all $\beta >0$ and all $n\in \mathbb {N}$.

Proof

Theorem 3.5 and Corollary 3.6 imply that $\mathcal {G}(\hat{g}, \beta \mathbb {Z}\times \tfrac{n}{\gamma }\mathbb {Z})$ is not a frame for every $\beta >0$ and $n\in \mathbb {N}$. Hence by Lemma 2.2 $\mathcal {G}(g, \tfrac{n}{\gamma } \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame for every $\beta >0$ and $n\in \mathbb {N}$. $\square$

3.3.3 Symmetry

Proposition 3.8

If $g$ is an odd function in $M^1(\mathbb {R})$ and $\alpha \beta = 1 - \tfrac{1}{n}$ for $n=2,3, \dots$, then $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame.

Therefore $\mathcal {F}(g) \subseteq \{ (\alpha , \beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1, \alpha \beta \ne 1-\tfrac{1}{n} , n=2, 3, \dots \}$.

Proof

By a change of variables $t \rightarrow \alpha t$ and by using the dilated window $g(\alpha t)$, we may assume without loss of generality that $\alpha =1$. According to Theorem 2.7(iii), we need to find a sequence $c \in \ell ^\infty (\mathbb {Z}^2)$ such that

$$\begin{aligned} \sum _{k,l\in \mathbb {Z}} c_{kl} \langle M_l T_{k/\beta } g, f\rangle = 0. \end{aligned}$$

(28)

for all $f\in M^1(\mathbb {R})$.

To apply the Poisson summation formula to the sum over $l$, we choose $c_{kl} = d_k$ independently of $l$. Then

$$\begin{aligned} \sum _{l\in \mathbb {Z}} \langle M_l T_{k/\beta } g, f\rangle = \sum _{l\in \mathbb {Z}} (T_{k/\beta } g \cdot \bar{ f} ) \,\widehat{} \, (l) = \sum _{l\in \mathbb {Z}} (T_{k/\beta } g \cdot \bar{ f} ) (l ) \, , \end{aligned}$$

so the double sum in (28) becomes

$$\begin{aligned} \sum _{k,l\in \mathbb {Z}} c_{kl} \langle M_l T_{k/\beta } g, f\rangle = \sum _{k,l\in \mathbb {Z}} d_k (T_{k/\beta } g \cdot \bar{ f} ) (l ) = \sum _{l\in \mathbb {Z}} \Big ( \sum _{k\in \mathbb {Z}} d_k g(l-\tfrac{k}{\beta } \Big ) \bar{f}(l) =0. \end{aligned}$$

We try to determine a sequence $d \in \ell ^\infty (\mathbb {Z})$ such that this sum vanishes for all $f\in M^1(\mathbb {R})$. By choosing $f\in M^1(\mathbb {R})$ with support in $[l-\tfrac{1}{2}, l+\tfrac{1}{2}]$, we see that (28) implies that

$$\begin{aligned} \sum _{k\in \mathbb {Z}} d_k g\big (l-\tfrac{k}{\beta }\big ) = 0 \quad \text { for all } l\in \mathbb {Z}. \end{aligned}$$

(29)

Substituting $\beta = 1 - \tfrac{1}{n}$, we have $g(l-\tfrac{n}{n-1}k)$ in the sum. This suggests splitting the sum into residues modulo $n-1$, i.e., $k=(n-1)s+j$:

$$\begin{aligned} \sum _{k\in \mathbb {Z}} d_k g(l-\tfrac{k}{\beta }) = \sum _{j=0}^{n-2} \sum _{s\in \mathbb {Z}} d_{(n-1)s+j} g\big ( l-ns - \frac{n}{n-1}j\big ). \end{aligned}$$

As a further simplification we now assume that the sequence $d\in \ell ^\infty (\mathbb {Z})$ depends only on the coset modulo $n-1$, i.e., $d_{(n-1)s+j} = \delta _j$ for $j=0, \dots , n-2$. Thus we need to find $n-1$ numbers $\delta _j\in \mathbb {C}$ such that

$$\begin{aligned} \sum _{j=0}^{n-2} \delta _j \sum _{s\in \mathbb {Z}} g(ns +l + \tfrac{n}{n-1}j) = 0. \end{aligned}$$

(30)

Note that we may replace the sum $\sum _{j=0}^{n-2}$ by a sum over arbitrary $n-1$ coset representatives of $\mathbb {Z}_{n-1}$.

Now let $A$ be the matrix with entries

$$\begin{aligned} A_{lj} = \sum _{s\in \mathbb {Z}} g(ns +l + \tfrac{n}{n-1}j) \, \quad l,j\in \mathbb {Z}. \end{aligned}$$

(31)

Then $A_{lj}$ is periodic with period $n$ in $l$ and with period $n-1$ in $j$ and therefore A is effectively an $n\times (n-1)$-matrix. Hence (30) can be abbreviated as $A\delta = 0$ for some non-zero vector $\delta \in \mathbb {C}^{n-1}$.

Now let us assume that $g$ is odd. Then $A$ possesses additional symmetries. It follows immediately from the definition (31) and the periodicity that

$$\begin{aligned} A_{-l,-j} = A_{n-l, n-1-j} = - A_{l,j} \, \quad \forall j,l\in \mathbb {Z}. \end{aligned}$$

(32)

Claim These symmetry properties imply that $A\delta =0$ possesses a non-trivial solution $\delta \ne 0$.

Let us argue explicitly and distinguish between the cases $n$ even and $n$ odd.

Let $n=2n_0$ be even. We choose the representatives $\{j : |j| < n_0\}$ for $\mathbb {Z}_{n-1}$ and $\{0, \dots , 2n_0-1\}$ for $\mathbb {Z}_n$ and assume that $\delta$ is an even sequence $\delta _{-j}=\delta _j$. Then, by the symmetry (32), the equations for $l$ and $-l$ coincide:

$$\begin{aligned} \sum _{j=-n_0+1}^{n_0-1} A_{lj}\delta _j&= A_{l,0} \delta _0 + \sum _{j=1}^{n_0-1} (A_{lj} +A_{l,-j}) \delta _j\\&= - A_{-l,0} \delta _0 -\sum _{j=1}^{n_0-1} (A_{-l,j} +A_{-l,-j}) \delta _j. \end{aligned}$$

In addition, since $A_{0,0}=0$, $A_{n_0,0} = - A_{n-n_0, 0} = - A_{n_0,0} = 0$, $A_{0,j} + A_{0,-j}=0$, and $A_{n_0,j} +A_{n_0,-j} = A_{n_0,j} +A_{n-n_0,-j} = 0$, the equations for $l=0$ and $l=n_0$ are identically zero. Consequently, the linear equation $A\delta =0$ consists only of $n_0-1$ equations (for $l=1, \dots , n_0-1$) in $n_0$ variables $\delta _j, j=0, \dots , n_0-1$, and thus must have a non-trivial solution.

Similarly, if $n=2n_0+1$ is odd, we choose the representatives $\{l = -n_0, \dots , n_0\}$ for $\mathbb {Z}_{n}$ and $\{-n_0+1, \dots , n_0\}$ for $\mathbb {Z}_{n-1}$. By symmetry (32) we obtain that $A_{0,0} = - A_{0,0}$ and

$$\begin{aligned} A_{-l,n_0} = A_{-l,n_0 - (2n_0+1-1) } = A_{-l,-n_0}= -A_{l,n_0}. \end{aligned}$$

Thus $A_{0,n_0} = A_{0,0}=0$. We choose $\delta _j = \delta _{-j}$ for $j=1, \dots , n_0 - 1$, so that $\delta$ consists of $n_0 +1$ independent parameters. The equations for $l=0$ and $l=n_0$ are identically zero and the equations for $l$ and $-l$, $l=1, \dots , n_0$ coincide. Consequently, the linear equation $A\delta =0$ consists only of $n_0$ equations (for $l=1, \dots , n_0$) in $n_0+1$ variables $\delta _j, j=0, \dots , n_0$, and thus must have a non-trivial solution. $\square$

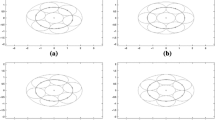
The proof of Proposition 3.8 is an interpretation of Lyubarski and Nes [67] in the light of Theorem 2.7. Where they use a Zak transform criterion for Gabor frames, we use the criterion without inequalities (at the cost of windows in $M^1$ rather than $L^2$). Our approach gives hope of discovering additional general obstructions to Gabor frames several examples of possible frames sets are illustrated in Fig. 1.

Fig. 1

Four examples of possible frame sets. (a) general properties according to Theorem 2.1; (b) frame set of a compactly supported function (Lemma 3.4); (c) frame set of a function satisfying a partition of unity condition (Corollary 3.6); (d) frame set of an odd function (Proposition 3.8). Dashed lines and the region above the hyperbola $\alpha \beta =1$ do not belong to the frame set. The interior of the rectangle at the origin always belongs to the frame set. For the remaining part under the hyperbola general statements are possible only for few window classes

Example 3.9

It is clear that one may create arbitrarily complicated obstruction patterns by combining various effects. For instance, set

$$\begin{aligned} g(t) = (\chi _{[0,1]}*\chi _{[0,1]})(t) - (\chi _{[0,1]}*\chi _{[0,1]})(t+2). \end{aligned}$$

Then $g$ is in $M^1(\mathbb {R})$, $g$ is odd, $\sum _{k\in \mathbb {Z}} g(t-2k) = 0$ and $\sum _{k\in \mathbb {Z}} g(t-k) = 0$, and, for every $\alpha \ge 2$, we have $g(\alpha k) = 0$ for all $k\in \mathbb {Z}$. Therefore $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ with $\alpha \beta <1$ is not a frame when either

• (a) $\alpha \beta = 1- n^{-1}$ for $n=2,3,\dots$ (Proposition 3.8), or when

• (b) $\beta = n/2$ for $n\in \mathbb {N}$ and $\alpha >0$ arbitrary (Corollary 3.6), or when

• (c) $\alpha \ge 2$ and $\beta >0$ arbitrary (Corollary 3.7).

At first glance the last property looks surprising, but it can be easily confirmed with Theorem 2.7(ii). Choosing the point measure $\delta _0\in M^\infty (\mathbb {R})$, we have

$$\begin{aligned} \langle \delta _0 , M_{\beta l} T_{\alpha k} g\rangle = g(-\alpha k) = 0 \end{aligned}$$

for all $k,l\in \mathbb {Z}$ precisely when $\alpha \ge 2$.

4 Open Problems, Conjectures, and a Vision

Conjectures are usually based on a sufficient supply of examples that lead to the formulation of general results. To make a conjecture based on a single example of a frame set, as was done by Daubechies in 1992, is rather daring and requires a superb intuition. In 2014 the situation is slightly different, as we now have an uncountable supply of examples of frame sets. So it is less daring and should be easier to make up a new set of conjectures about the frame set.

In this section we discuss some open problems and associated conjectures on the fine structure of Gabor frames.

We start with a bold speculation. In all examples so far the frame set is the largest set compatible with the density theorem, and the necessary density condition for a lattice is also sufficient to generate a frame. To put it differently, for totally positive functions of finite type there is no good reason or no “obstruction” that would exclude a particular lattice from generating a frame.

On the other hand, there exist obstructions of an algebraic nature that exclude certain pairs of $(g,\Lambda )$ from generating a Gabor frame, namely, symmetry and support properties and partition-of-unity conditions, and possibly other obstructions.

Based on these results, we now make a big leap and formulate the following vision.

For a window $g\in M^1(\mathbb {R})$ the frame set $\mathcal {F}(g)$ is the maximal set in $\{ (\alpha , \beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1\}$ that is compatible with the obstructions.

 $\mathcal {F}_{\mathrm {full} } (g)$ is maximal in $\{ \Lambda : \mathrm {vol}\, \Lambda <1\}$.

To put it differently, for $\mathcal {G}(g, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ not to be a frame, some (algebraic) obstructions on $g$ and $\Lambda$ must conspire. In Sect. 3.3 we have seen examples of such obstructions.

The above formulation can hardly be called a conjecture. It is almost tautological, because at this time the term “obstruction” has no precise meaning. It is better to consider the formulation a vague dream about the mystery of Gabor frames, a dream, whose formulation became possible only after Theorem 3.2.

Let us take the dream as a challenge and a guideline to ask the right questions.

• What are other possible obstructions to the Gabor frame property?

• How can one prove generic results in Gabor analysis?

• Which mathematical methods could play a role in the investigation of the fine structure of Gabor frames?

To make the dream more concrete, one should first consider special classes of windows and work on specific conjectures. The open problems and conjectures below are difficult enough for a start.

(A) Totally positive functions again: In view of Theorem 3.2 the following conjecture seems natural.

Conjecture 4.1

If $g$ is a totally positive function other than the one-sided exponential, then the frame set is $\mathcal {F}({g})= \{ (\alpha , \beta ) \in \mathbb {R}_+^2: \alpha \beta <1\}$.

Currently this statement is known to be true for the Gaussian, the hyperbolic secant, and for totally positive functions of finite type. There is no reason (no clear obstruction) why the extension of Theorem 3.2 to arbitrary totally positive functions should fail. However, since the proof of Theorem 3.2 is tailored to totally positive functions of finite type, the proof of the full conjecture will require additional methods.

The factorization property of totally positive functions also leads to questions of a basic nature: Assume that the frame set is known for two ”nice” functions $g$ and $h$, what can be said about the frame set of $gh$ and $g*h$? Except for a negative result in [18] nothing seems to be known about this question.

(B) Hermite functions: Let $h_n(t) =$ be the $n$-th Hermite function defined by

$$\begin{aligned} h_n(t) = e^{ \pi t^2} \frac{d^n}{dx ^n} e^{ -2\pi t^2} \end{aligned}$$

for $n\in \mathbb {N}\cup \{0\}$. In [44, 45] we proved that for every lattice $\Lambda \subseteq \mathbb {R}^2$ with $\mathrm {vol}\, (\Lambda ) < \tfrac{1}{n+1}$ the Gabor family $\mathcal {G}(g,\Lambda )$ is a frame. At that time we even conjectured this condition to be necessary and sufficient, because this statement is true for the case of the Gaussian window $h_0$ and we had a version of Proposition 3.8 for $n=2$. Thanks to [67] we now know that for odd indices $n$ the frame set does not include the hyperbolas $\alpha \beta = 1 - N^{-1}$ for $N=2,3, \dots$. So much for bold conjectures!

In the absence of additional obstructions, or, more precisely, as long as we do not discover other types of obstructions, the next best conjecture for Hermite functions is as follows.

Conjecture 4.2

For even Hermite functions,

$$\begin{aligned} \mathcal {F}(h_{2n } ) = \{ (\alpha , \beta ): \alpha \beta <1\}. \end{aligned}$$

For odd Hermite functions,

$$\begin{aligned} \mathcal {F}(h_{2n +1 } ) = \{ (\alpha , \beta ): \alpha \beta <1, \alpha \beta \ne 1 - \frac{1}{N}, N=2,3,\dots \}. \end{aligned}$$

For $h_1$, the article [67] cites some numerical evidence for this conjecture.

(C) $B$-splines: Let $\chi = \chi _{[0,1]}$ be the characteristic function of the interval $[0,1]$ and let $b_n = \chi *\dots *\chi$ ($n+1$-times) be the B-spline of order $n$. Then $b_n\in M^1(\mathbb {R})$ for $n\ge 1$ and ${{\mathrm{supp}}}\, b_n = [0,n+1]$. The $B$-splines are prototypes for painless non-orthogonal expansions. Indeed, if $\alpha < n+1$ and $\beta < (n+1)^{-1}$, then $\mathcal {G}(b_n, \alpha \mathbb {Z}\times \beta \mathbb {Z})$ is a frame by Theorem 2.6. On the other hand, $b_n$ generates a partition of unity, $\sum _{k\in \mathbb {Z}} b_n (t-k) = \mathrm {const}$, so the Gabor family $\mathcal {G}(b_n, \alpha \mathbb {Z}\times N \mathbb {Z})$ is not a frame for $N =2, 3, \dots$ and all $\alpha >0$ by Corollary 3.6. Furthermore, interpreting a result about sampling in shift-invariant spaces from [1], the Gabor family $\mathcal {G}(b_n, \alpha \mathbb {Z}\times \mathbb {Z})$ is a frame for all $\alpha <1$.

Since there do not seem to be any further obstructions, we may turn the vision expressed above into the following conjecture.

Conjecture 4.3

$\mathcal {F}(b_n) = \{ (\alpha , \beta ) \in \mathbb {R}_+ ^2: \alpha \beta <1, \alpha < n+1, \beta \ne 2, 3, \dots \}$

Using Theorem 2.5(iii) it is easy to give some sufficient conditions for $(\alpha , \beta )$ to be in the frame set, but the difficult problem is to show that all rectangular lattices not excluded by the partition-of-unity condition belong to the frame set.

The comparison between $B$-splines and Hermite functions shows certain analogies: to both $s_n$ and $h_n$ one can associate the polynomial degree $n$, the hyperbolas $\alpha \beta = 1-N^{-1}$ for Hermite functions correspond to the horizontal lines $(\alpha , N)$, and in both cases $N=2,3, \dots$. Is this just a superficial analogy or is there something to learn?

With the above open problems and conjectures we have only touched the tip of an iceberg. Of course, all of these questions and related conjectures can be formulated for Gabor frames in higher dimensions and for the full (rather than the reduced) frame set.

In higher dimensions many more complications have to be expected, the frame set is not even known for the multivariate Gaussian $g(t) = e^{-\pi t\cdot t}, t\in \mathbb {R}^d$. Preliminary results have been obtained in [40, 69]. In [46] a family of non-separable lattices $\Lambda _n \subseteq \mathbb {R}^4$ is constructed, such that $\mathrm {vol}\, (\Lambda _n) = 1 - n^{-2} <1$ and $\mathcal {G}(g, \Lambda _n)$ fails to be a frame for $L^2(\mathbb {R}^2)$. These examples should alert us when trying to generalize results about the fine structure of Gabor frames to higher dimensions.

As for the vision that inspires these conjectures, let us add some final words. One reason for optimism comes from the characterization of Gabor frames without using the frame inequalities in Theorem 2.7, that is, $\mathcal {G}(g,\alpha \mathbb {Z}\times \beta \mathbb {Z})$ is not a frame if and only if there exists a bounded sequence $(c_{kl} )\in \ell ^\infty ( \mathbb {Z}^2)$ on the adjoint lattice $\beta ^{-1}\mathbb {Z}\times \alpha ^{-1}\mathbb {Z}$, such that $\sum _{k,l \in \mathbb {Z}} c_{k,l} M_{\frac{l}{\alpha }} T_{\frac{k}{\beta }} g = 0$ in $M^\infty$. Whereas the injectivity of an operator is stable under perturbations, the existence of a non-trivial kernel of an operator is highly sensitive to perturbations. There must be a good reason for the existence of such a kernel. Indeed, for the obstructions mentioned in Sect. 3.3 we have described the kernel explicitly in this way. We may hope to relate a non-trivial kernel to algebraic properties of $g$.