Construction of Wavelet Sets Using Integral Self-Affine Multi-tiles

Abstract

Gabardo and Yu first considered using integral self-affine tiles in the Fourier domain to construct wavelet sets and they produced a class of compact wavelet sets with certain self-similarity properties. In this paper, we generalize their results to the integral self-affine multi-tiles setting. We characterize some analytic properties of integral self-affine multi-tiles under certain conditions. We also consider the problem of constructing (multi)wavelet sets using integral self-affine multi-tiles.

1 Introduction

In this paper, we denote |K| as the Lebesgue measure of a measurable set $K\subset\mathbb{R}^{n}$. For two measurable sets $E, F\subseteq\mathbb{R}^{n}$, we write E≅F if their symmetric difference i.e. (F∖E)∪(E∖F) has zero Lebesgue measure. We will denote by $M_{n}(\mathbb{Z})$ the set of n×n matrices with integer entries.

An n×n real matrix is called expansive if all its eigenvalues have moduli greater than one. A finite collection of essentially disjoint sets $K_{i}\subseteq \mathbb{R}^{n}, 1\le i \le M$, that are either compact or empty, is said to be a (B,Γ)-self-affine collection if there is an expansive matrix $B\in M_{n}(\mathbb{Z})$ and finite (possibly empty) sets $\varGamma_{ij}\subseteq\mathbb{Z}^{n}, \ i,j=1,\dots,M$, such that

$$ BK_i=\bigcup_{j=1}^{M}( \varGamma_{ij}+K_j)\quad \text{for}\ i=1,\dots,M, $$

(1.1)

and for any i,j,k∈{1,…,M}

$$ (\beta+K_i)\cap(\gamma+K_j) \cong\emptyset\quad \text{for} \ \beta\in\varGamma_{ki}, \ \gamma\in \varGamma_{kj} \ \text{and} \ i\ne j \ \text{or} \ \beta\ne\gamma. $$

(1.2)

The set Γ:={Γ _ij }_1≤i,j≤M is called a collection of digit sets. Γ is called a standard collection of digit sets if for each j∈{1,…,M}, $\mathcal{D}_{j}:=\bigcup_{i=1}^{M}\varGamma_{ij}$ is a complete set of coset representatives for the group $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$. This definition is the analogue of that of the standard digit set introduced in [7, 13].

If $\varLambda\subseteq\mathbb{Z}^{n}$, a measurable set $K\subset \mathbb{R}^{n}$ is said to Λ-tile $\mathbb{R}^{n}$ or to be a Λ-tiling set, if $\bigcup_{\ell\in\varLambda}(K+\ell)\cong \mathbb{R}^{n}$ and (K+ℓ ₁)∩(K+ℓ ₂)≅∅ for ℓ ₁,ℓ ₂∈Λ and ℓ ₁≠ℓ ₂.

Let $K:=\bigcup_{i=1}^{M}K_{i}$. If K Λ-tiles $\mathbb{R}^{n}$ and a finite collection of sets $\{ K_{i}\subset\mathbb{R}^{n}, 1\le i\le M\}$ form a (B,Γ)-self-affine collection, we call K an integral self-affine Λ-tiling set with M prototiles or an integral self-affine multi-tile for short. Particularly, in the case where M=1, K is an integral self-affine Λ-tiling set with one tile, (1.1) has exactly one solution [11]. In such a case, we say that K is an integral self-affine tile. Thus integral self-affine tiles are a special class of integral self-affine multi-tiles. Self-affine tiles have been extensively studied (see e.g. [8, 13–15]) and they have been shown to be closely related to wavelet theory [7, 8, 12]. In view of this, it is of interest to study integral self-affine multi-tiles and their connection with wavelet theory.

In contrast to the one tile case, there may exist several solutions of the set Eq. (1.1) when some prototiles are allowed to be empty. The theory of self-affine multi-tiles is much less understood because of their complicated structure. Gröchenig and Hass in [9] gave a detailed description on integral self-affine multi-tiles. They constructed and classified the general solutions of (1.1) and derived a necessary condition for a solution of (1.1) to be a $\mathbb{Z}^{n}$-tiling set. Furthermore, they established the relationship between the theory of multi-wavelets and the theory of self-affine multi-tiles. Flaherty and Wang showed in [4] how integral self-affine multi-tiles can be used to construct Haar-type multi-wavelets. Their results extended the work in [7] to higher multiplicity. Similar to the result in [7], Gröchenig and Hass [9] showed that a multi-resolution analysis [3, 17] for $L^{2}(\mathbb{R}^{n})$ is generated by the characteristic functions $\chi_{K_{i}}$, i=1,2,…,M, if and only if $K=\bigcup_{i=1}^{M}K_{i}$ is an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles and each prototile K _i ,1≤i≤M, has positive Lebesgue measure.

The main purpose of this paper is to construct wavelet sets using integral self-affine multi-tiles.

Let A be an expanding matrix in $M_{n}(\mathbb{Z})$. An A-dilation wavelet is a measurable function $\psi\in L^{2}(\mathbb{R}^{n})$ such that the set

$$\begin{aligned} \bigl\{ \lvert \det A\rvert^{\frac{j}{2}}\psi\bigl(A^jx-k\bigr):\ j \in\mathbb{Z},\ k\in\mathbb{Z}^n\bigr\} \end{aligned}$$

forms an orthonormal basis for $L^{2}(\mathbb{R}^{n})$. The Fourier transform of any function $f\in L^{1}(\mathbb{R}^{n})\cap L^{2}(\mathbb{R}^{n})$ is defined by

$$\begin{aligned} \mathcal{F}(f) (\xi)=\hat{f}(\xi)=\int_{\mathbb{R}^n}e^{-2\pi ix\cdot\xi}f(x) \, dx, \end{aligned}$$

where x⋅ξ is the standard inner product of the vectors $x,\xi\in\mathbb{R}^{n}$. The inverse Fourier transform will be denoted as $\mathcal{F}^{-1}$. An A-dilation wavelet set is a measurable set $Q\subseteq\mathbb{R}^{n}$ such that $\mathcal{F}^{-1}(\chi_{Q})$ is an A-dilation wavelet.

Gabardo and Yu [6] first considered using integral self-affine tiles in the Fourier domain to construct wavelet sets. The wavelet sets they constructed are finite unions of integer translates of integral self-affine tiles. However, many wavelet sets are derived from integral self-affine multi-tiles, not integral self-affine tiles. For example, all wavelet sets given in Sect. 3 of [10], are finite unions of integer translates of integral self-affine collection and they cannot be written as finite unions of integer translates of integral self-affine tiles. Another interesting example is the well-known Shannon wavelet whose corresponding wavelet set is $Q=[-1,-\frac{1}{2}]\cup[\frac{1}{2},1]$, which is a finite union of an integral self-affine collection {K ₁,K ₂}, where $K_{1}:=[-\frac{1}{2},0]$ and $K_{2}:=[0,\frac{1}{2}]$, i.e. Q=(K ₁+1)∪(K ₂−1). Obviously, K=K ₁∪K ₂ is a self-affine $\mathbb{Z}$-tiling set with 2 prototiles. Thus integral self-affine multi-tiles can provide a nice framework in which the known examples of wavelet sets appear naturally and also constitute a new tool with the help of which new examples can be created.

The paper is organized as follows. In Sect. 2, we characterize some properties of integral self-affine multi-tiles. In Sect. 3, we provide some sufficient conditions for constructing wavelet sets using integral self-affine multi-tiles. Comparing to the case of integral self-affine tiles, it is more restrictive to construct wavelet sets using integral self-affine multi-tiles. In Sect. 4, we consider constructing multi-wavelet sets using integral self-affine multi-tiles.

2 Properties of Integral Self-Affine Multi-tiles

Throughout this paper, we will limit our discussion to expanding matrices $A\in M_{n}(\mathbb{Z})$. We let B=A ^t and S={1,2,…,M}. In the following, we will always assume that $K=\bigcup_{i=1}^{M}K_{i}$, where the unions are essentially disjoint and |K _i |>0 for each i∈S, and that the sets K _i , i∈S, satisfy (1.1) and (1.2). We call such set K a self-affine tiling set with M prototiles. By our assumption and the result in [10] (see Proposition 1), each K _i ,i∈S can be represented as

$$\begin{aligned} K_i= \Biggl\lbrace x\in\mathbb{R}^n:x=\sum _{k=1}^{\infty}B^{-k} \epsilon_k,\ \epsilon_k\in\varGamma_{\rho_k\rho_{k+1}}\ne \emptyset, \ {\rm{for \ some}} \ \rho_k\in S \ {\rm{and}} \ \rho_1=i \Biggr\rbrace . \end{aligned}$$

(2.1)

In addition, if K is a $\mathbb{Z}^{n}$-tiling set, we call K an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles. Gröchenig and Hass [9] showed that a necessary condition for K to be an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles is that Γ={Γ _ij ,i,j=1,…,M} be a standard collection of digit sets. Lemma 2.1 below is covered by a much more general result in [16]. We state it here for later use.

Lemma 2.1

Let K be a self-affine tiling set with M prototiles. Given any x∈K, if V is a neighborhood of x, then |V∩K|>0.

Lemma 2.2

If K is an integral self-affine $\mathbb{Z}^{n}$-tiling set, then K contains a neighborhood of 0 if and only if $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$.

Proof

Suppose that $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$. This implies that 0∈K. If 0 is an interior point of K, then K contains a neighborhood of 0. If 0 is the boundary point of K, then there exists $j\in\mathbb{Z}^{n}\setminus\{0\}$ such that 0∈K+j since K is a $\mathbb{Z}^{n}$-tiling set. This implies that −j∈K, contradicting the fact that $K\cap\mathbb{Z}^{n}=\lbrace0\rbrace$.

Conversely, suppose that K contains a neighborhood of 0. Assume that $0\ne\ell\in K\cap\mathbb{Z}^{n}$. Then ℓ∈K∩(K+ℓ) since 0∈K. Let U be a neighborhood of 0 with U⊆K. Then U+ℓ is a neighborhood of ℓ and U+ℓ⊆K+ℓ. By Lemma 2.1, |(K+ℓ)∩K|≥|(U+ℓ)∩K|>0 which contradicts the fact that (K+ℓ)∩K≅∅. Therefore, $K\cap\mathbb{Z}^{n}=\lbrace0\rbrace$. □

If K is an integral self-affine tiling set with M prototiles as above, there exists $\varGamma_{ij}^{m}\subset\mathbb{Z}^{n}$ satisfying

$$\begin{aligned} B^mK_i=\bigcup_{j=1}^{M} \bigl(K_j+ \varGamma_{ij}^m\bigr). \end{aligned}$$

(2.2)

Indeed, it follows from (1.1) that we can take $\varGamma_{ij}^{1}=\varGamma_{ij}$. Using (1.1) to each prototile K _j , we have

$$\begin{aligned} B^2K_i&=\bigcup_{j=1}^{M} (BK_j+B\varGamma_{ij})= \bigcup_{j=1}^{M}\bigcup_{\ell=1}^{M} \bigl(K_j+(\varGamma_{\ell j}+B\varGamma_{i\ell})\bigr)\\ &=\bigcup_{j=1}^{M} \Biggl(K_j+ \bigcup_{\ell=1}^{M} (\varGamma_{\ell j}+B \varGamma_{i\ell})\Biggr). \end{aligned}$$

Thus we can define

$$\begin{aligned} \varGamma_{ij}^2=\bigcup_{\ell=1}^{M}(\varGamma_{\ell j}+B \varGamma_{i\ell}). \end{aligned}$$

(2.3)

Inductively, we obtain

$$\begin{aligned} \varGamma_{ij}^m=\bigcup_{\ell=1}^{M}\bigl(\varGamma_{\ell j}+B \varGamma_{i\ell}^{m-1}\bigr),\quad m\ge 2. \end{aligned}$$

(2.4)

Defining

$$\begin{aligned} \mathcal{D}_j:=\bigcup_{i=1}^{M} \varGamma_{ij}\quad {\rm{and}}\quad \mathcal{D}_j^m:= \bigcup_{i=1}^{M}\varGamma_{ij}^m, \end{aligned}$$

(2.5)

the corresponding self-affine multi-tile $K= \bigcup_{i=1}^{M}K_{i}$ satisfies

$$\begin{aligned} BK=\bigcup_{i=1}^M BK_i=\bigcup_{i=1}^M\bigcup_{j=1}^M (K_j+ \varGamma_{ij}) =\bigcup_{j=1}^M (K_j+\mathcal{D}_j), \end{aligned}$$

(2.6)

and

$$\begin{aligned} B^mK=\bigcup_{i=1}^M B^mK_i=\bigcup_{i=1}^M \bigcup_{j=1}^M \bigl(K_j+ \varGamma_{ij}^m\bigr) =\bigcup _{j=1}^M \bigl(K_j+\mathcal{D}_j^m \bigr). \end{aligned}$$

(2.7)

Theorem 2.3

Let K be an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles and $0\in\mathcal{D}_{j}$ for each j∈S. Then K contains a neighborhood of 0 if and only if $\bigcup_{m\geqslant 0}\bigcup_{i=1}^{M}\varGamma_{ij}^{m}=\mathbb{Z}^{n}$, where $\varGamma_{ij}^{m}$ is defined by (2.2).

Proof

Suppose that K contains a neighborhood of 0. Then $\bigcup_{m\geqslant 1}B^{m} K=\mathbb{R}^{n}$ since B is expansive (see [14]). By the definition of $\varGamma_{ij}^{m}$, we obtain

$$\begin{aligned} \bigcup_{m\geqslant 1}B^m K =& \bigcup_{m\geqslant 1}\bigcup_{i=1}^{M}B^m K_i =\bigcup_{m\geqslant 1}\bigcup_{i=1}^{M}\bigcup_{j=1}^{M} \bigl(K_j+\varGamma_{ij}^m\bigr) \\ =&\bigcup_{j=1}^{M} \Biggl(K_j+\bigcup_{m\geqslant 1}\bigcup_{i=1}^{M} \varGamma_{ij}^m\Biggr). \end{aligned}$$

(2.8)

Thus, we have

$$\begin{aligned} \bigcup_{j=1}^{M} \Biggl(K_j+\bigcup_{m\geqslant1}\bigcup_{i=1}^{M}\varGamma_{ij}^m \Biggr) =\mathbb{R}^n. \end{aligned}$$

(2.9)

Since $\bigcup_{m\geqslant1}\bigcup_{i=1}^{M}\varGamma_{ij}^{m}\subseteq\mathbb{Z}^{n}$ and $K= \bigcup_{j=1}^{M}K_{j}$ is a $\mathbb{Z}^{n}$-tiling set, it follows that $\bigcup_{m\geqslant1}\bigcup_{i=1}^{M}\varGamma_{ij}^{m}=\mathbb{Z}^{n}$.

Conversely, suppose that $\bigcup_{m\geqslant1}\bigcup_{i=1}^{M}\varGamma_{ij}^{m}=\mathbb{Z}^{n}$. Define $\mathcal{D}_{j}^{m}, m\ge1$ as in (2.5), then using (2.4) and (2.5), we have that

$$\begin{aligned} \mathcal{D}_j^m=\bigcup_{i=1}^{M}\varGamma_{ij}^m = \bigcup_{i=1}^{M}\bigcup_{\ell=1}^{M} \bigl(\varGamma_{\ell j}+B \varGamma_{i\ell}^{m-1}\bigr) =\bigcup_{\ell=1}^{M} \bigl(\varGamma_{\ell j}+B \mathcal{D}_{\ell}^{m-1}\bigr). \end{aligned}$$

(2.10)

In particular, taking m=2, (2.10) gives

$$\begin{aligned} \mathcal{D}_j^2=\bigcup_{i=1}^{M}\varGamma_{ij}^2 = \bigcup_{\ell=1}^{M} (\varGamma_{\ell j}+B \mathcal{D}_{\ell}). \end{aligned}$$

(2.11)

By assumption, $0\in\mathcal{D}_{j}$ for each j∈S, it follows from (2.11) that $\mathcal{D}_{j}\subseteq\mathcal{D}_{j}^{2}$. Suppose that $\mathcal{D}_{j}^{m}\subseteq\mathcal{D}_{j}^{m+1}$, j∈S, for m≥1. Then we deduce from (2.10) and our assumption that

$$\begin{aligned} \mathcal{D}_j^{m+2}= \bigcup_{\ell=1}^{M} \bigl(\varGamma_{\ell j}+B\mathcal{D}_{\ell}^{m+1}\bigr) \supseteq \bigcup_{\ell=1}^{M} \bigl( \varGamma_{\ell j}+B\mathcal{D}_{\ell}^{m}\bigr) = \mathcal{D}_j^{m+1}. \end{aligned}$$

This shows that $\mathcal{D}_{j}^{m}\subseteq\mathcal{D}_{j}^{m+1}$ for each j∈S and for any m≥1. Since K is a $\mathbb{Z}^{n}$-tiling set and $\bigcup_{m\geqslant1} \bigcup_{i=1}^{M}\varGamma_{ij}^{m}=\mathbb{Z}^{n}$, (2.7) and (2.8) show that

$$\begin{aligned} \bigcup_{m\geqslant 1}B^m K= \bigcup_{j=1}^{M} \biggl(K_j+ \bigcup_{m\geqslant1}\mathcal{D}_j^m \biggr)=\mathbb{R}^n. \end{aligned}$$

(2.12)

Let V be a compact set containing a neighborhood of 0. Define

$$S_i:= \bigl\{ k\in\mathbb{Z}^n:\bigl\lvert (K_i+k)\cap V\bigr\rvert >0 \bigr\} , \quad i\in S. $$

Since S _i ⊂V−K _i , S _i is bounded and so is $\bigcup_{s\in S_{i}} (K_{i}+s)$. Hence, there exists r _i >0 such that

$$\bigcup_{s\in S_i} (K_i+s) \subseteq B(0,r_i) \quad {\rm{and}} \quad V\subseteq \bigcup _{i=1}^M \bigcup_{s\in S_i} (K_i+s)\subseteq \bigcup_{i=1}^MB(0,r_i). $$

Since the sets K _i +s,s∈S _i , are measure disjoint, the number of elements in S _i is at most $\frac{\lvert B(0,r_{i})\rvert}{\lvert K_{i}\rvert}$. The inclusion $\mathcal{D}_{j}^{m}\subseteq \mathcal{D}_{j}^{m+1}$, j∈S and the fact that $\bigcup_{m\geqslant1} \bigcup_{i=1}^{M}\varGamma_{ij}^{m}= \bigcup_{m\geqslant1}\mathcal{D}_{j}^{m}=\mathbb{Z}^{n}$ imply that for each j∈S, there is $M_{j}\in\mathbb{N}$ such that $S_{j}\subseteq\mathcal{D}_{j}^{M_{j}}$. Let M=max_1≤j≤M M _j . Then, we have

$$V\subseteq \bigcup_{i=1}^M (K_i+S_i)\subseteq \bigcup_{i=1}^M \bigl(K_i+\mathcal{D}_i^M\bigr) =B^MK. $$

This proves that K contains B ^−M V, a neighborhood of 0. □

Theorem 2.4 and Corollary 2.5 below provide a sufficient condition for K to be a self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles. Theorem 2.4 in the single tile case is proved in [13] and its proof can also be applied to the multi-tile case directly. So we omit the proof of Theorem 2.4 here.

Theorem 2.4

Let K be an integral self-affine tiling set with M prototiles K ₁,…,K _M , and let Γ={Γ _ij ,i,j=1,…,M} be a standard collection of digit sets. Then |K| is a positive integer and K satisfies $\sum_{k\in\mathbb{Z}^{n}}\chi_{K}(x-k)=\lvert K\rvert$.

By Theorem 2.4, we get the following corollary.

Corollary 2.5

Let K be an integral self-affine tiling set with M prototiles and suppose that Γ={Γ _ij ,i,j=1,…,M} is a standard collection of digit sets. If $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$, then K is a $\mathbb{Z}^{n}$-tiling set.

Proof

Since $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$, then 0∈K and 0∉K+ℓ for $\ell\in\mathbb{Z}^{n}\setminus\{0\}$. This implies that $\sum_{\ell\in\mathbb{Z}^{n}}\chi_{K}(x-\ell)=\chi_{K}(x)=1$ if x belongs to a sufficiently small neighborhood of 0. On the other hand, since $\sum_{\ell\in\mathbb{Z}^{n}}\chi_{K}(x-\ell)=\lvert K\rvert$ for a.e. $x\in\mathbb{R}^{n}$ by the previous result, it follows that |K|=1 and thus K is a $\mathbb{Z}^{n}$-tiling set. □

Combining all the previous results, we obtain the following.

Proposition 2.6

Let K be an integral self-affine Λ-tiling set with M prototiles, where $\varLambda\subseteq\mathbb{Z}^{n}$, and let Γ={Γ _ij ,i,j=1,…,M} be a standard collection of digit sets. Assume that $0\in\mathcal{D}_{j}$ for each j∈S, then the following conditions are equivalent.

• (i) $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$.

• (ii) |K|=1 and K contains a neighborhood of 0.

• (iii) $\bigcup_{m\ge0} \bigcup_{i=1}^{M}\varGamma_{ij}^{m}=\mathbb{Z}^{n}$.

3 Construction of Single Wavelet Sets Using Integral Self-Affine Multi-tiles

In this section, we will always assume that $K=\bigcup_{i=1}^{M}K_{i}$, where the unions are essentially disjoint, is an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles, which satisfies (1.1) and (1.2). Then Γ={Γ _ij ,i,j=1,…,M} is a standard collection of digit sets.

Gabardo and Yu introduced in [6] a method for the construction of single wavelet sets using integral self-affine tiling set with one tile. The wavelet sets they constructed have the general form Q=C ⁻¹⋃ _ℓ∈L (K+ℓ), where C is an integral matrix commuting with B and L is a finite subset of $\mathbb{Z}^{n}$. In this section, we will extend their results to the integral self-affine multi-tiles setting and construct the wavelet sets with the form

$$\begin{aligned} Q=C^{-1} \bigcup_{i=1}^M \bigcup_{\ell\in L_i} (K_i+\ell), \end{aligned}$$

(3.1)

where C is an n×n integral matrix commuting with B, K ₁,…,K _M are M-prototiles associated with an integral self-affine multi-tile and L _i , i=1,…,M are finite subsets of $\mathbb{Z}^{n}$. Lemma 3.1 provides a necessary condition for Q defined by (3.1) to be an A-dilation wavelet set.

Lemma 3.1

If there is a nonsingular integral matrix C commuting with B such that Q defined by (3.1) is an A-dilation wavelet set, then for each i∈S, L _i must be a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$.

Proof

Since Q is a wavelet set, $\bigcup_{k\in\mathbb{Z}^{n}}(Q+k)\cong\mathbb{R}^{n}$ by Proposition 3.2. We have, using (3.1), that

$$\mathbb{R}^n\cong C \bigcup_{k\in\mathbb{Z}^n}(Q+k)= \bigcup_{k\in\mathbb{Z}^n} \bigcup_{i=1}^M \bigcup_{\ell\in L_i}(K_i+\ell+Ck). $$

The fact that K is a $\mathbb{Z}^{n}$-tiling set implies that $\bigcup_{z\in\mathbb{Z}^{n}} \bigcup_{\ell\in L_{i}}(\ell+Cz)=\mathbb{Z}^{n}$. This proves that for each i∈S, L _i is a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$. □

For the case where K is an integral self-affine $\mathbb{Z}^{n}$-tiling set with one tile, if Q defined by (3.1) is an A-dilation wavelet set, then $\lvert \det C\rvert\in(q-1)\mathbb{Z}$, where q=|detB| (see Proposition 4.1 in [6]). However, this does not hold any more for the case where K is an integral self-affine $\mathbb{Z}^{n}$-tiling set with at least two prototiles, as shown in Example 3.3 below.

Next, we give a sufficient condition for the set Q defined by (3.1) to be an A-dilation wavelet set. We need first to state the following criterion of Dai, Larson and Speegle [2] for a measurable set $Q\subseteq \mathbb{R}^{n}$ to be an A-dilation wavelet set.

Proposition 3.2

A measurable set $Q\subseteq \mathbb{R}^{n}$ is an A-dilation wavelet set if and only if Q satisfies the following two tiling conditions:

• (i) $\bigcup_{j\in\mathbb{Z}}B^{j}Q\cong\mathbb{R}^{n} \ and\ B^{i}Q\cap B^{j}Q\cong\emptyset \ for \ i\ne j$,

• (ii) $\bigcup_{k\in\mathbb{Z}^{n}} (Q+k)\cong\mathbb{R}^{n} \ and \ Q\cap (Q+\ell)\cong\emptyset \ for \ \ell\ne 0$.

Theorem 3.3

Suppose C is a nonsingular integral matrix which commutes with B and satisfies |detC|=q−1, where q=|detB|. If, for each i∈S, $0\in \mathcal{D}_{i}$, $L_{i}=\mathcal{D}_{i}\setminus \lbrace 0\rbrace$ is a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$, and $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$, then the set Q defined by (3.1) is an A-dilation wavelet set.

Proof

We deduce from (2.6) and $L_{i}=\mathcal{D}_{i}\setminus\lbrace 0\rbrace$ that

$$\begin{aligned} Q=C^{-1} \bigcup_{i=1}^M \bigcup_{\ell\in L_i} (K_i+\ell)=C^{-1}(BK \setminus K). \end{aligned}$$

(3.2)

Equation (3.2) implies that $\lvert Q\rvert=\frac{1}{\lvert\det C\rvert}(\lvert\det B\rvert-1)\lvert K\rvert=1$ since |detC|=|detB|−1 and |K|=1. By assumption, for each i∈S, L _i is a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$ and the set $K= \bigcup_{i=1}^{M}K_{i}$ is a $\mathbb{Z}^{n}$-tiling set, we have

$$\begin{aligned} \begin{aligned}[b] \bigcup_{z\in\mathbb{Z}^n}(Q+z)&= C^{-1} \bigcup_{z\in\mathbb{Z}^n} \bigcup_{i=1}^{M} \bigcup_{\ell\in L_i}(K_i+\ell+Cz) \\ &=C^{-1} \bigcup_{i=1}^{M} \bigcup_{z\in\mathbb{Z}^n}(K_i+z)\cong \mathbb{R}^n.\end{aligned} \end{aligned}$$

(3.3)

Equation (3.3) and the fact that |Q|=1 show that Q is a $\mathbb{Z}^{n}$-tiling set. It follows from (3.2) that B ^m Q=C ⁻¹(B ^m+1 K∖B ^m K) and $\lbrace B^{m} Q,m\in\mathbb{Z} \rbrace$ is an essencially disjoint family, i.e B ^m Q∩B ⁿ Q≅∅ for $m,n\in\mathbb{Z}$ and m≠n. It is left to prove that $\bigcup_{m\in \mathbb{Z}}B^{m}Q\cong\mathbb{R}^{n}$. The condition $K\cap \mathbb{Z}^{n}=\lbrace 0\rbrace$ implies that K contains a neighborhood of 0 by Lemma 2.2. Then $\bigcup_{m\in \mathbb{Z}}B^{m}K= \mathbb{R}^{n}$ since B is expansive. Moreover, lim _m→∞|B ^−m K|=lim _m→∞|detB|^−m=lim _m→∞ q ^−m=0 since |K|=1 and q>1. For any s∈K∖{0}, there exists m≥0 such that s∈B ^−m K, but s∉B ^−(m+1) K. Thus s∈C⋃ _k≥1 B ^−k Q, which implies that K⊆C⋃ _k≥1 B ^−k Q. Since for each j∈S, $0\in\mathcal{D}_{j}$, it follows from (2.6) that K⊂BK. Since $\bigcup_{m\in \mathbb{Z}}B^{m}K= \mathbb{R}^{n}$ and K⊂BK, we have thus

$$\begin{aligned} C \bigcup_{k=0}^{\infty} B^kQ = \bigcup_{k=0}^{\infty} \bigl(B^{k+1}K\setminus B^kK\bigr) = \mathbb{R}^n \setminus K. \end{aligned}$$

(3.4)

The inclusion K⊆C⋃ _k≥1 B ^−k Q together with (3.4) shows that $C \bigcup_{m\in\mathbb{Z}}B^{m}Q=\mathbb{R}^{n}$ and thus that $\bigcup_{m\in \mathbb{Z}}B^{m}Q=\mathbb{R}^{n}$. □

It has been proved in [6] that the conditions in Theorem 3.3 are necessary and sufficient for the set Q=C ⁻¹⋃ _ℓ∈L (K+ℓ) to be an A-dilation wavelet set when K is an integral self-affine $\mathbb{Z}^{n}$-tiling set with one tile. However, they are not necessary for the set Q defined by (3.1) to be an A-dilation wavelet set if the corresponding set K is an integral self-affine $\mathbb{Z}^{n}$-tiling set with at least two prototiles, as illustrated by the following example.

Example 3.1

In dimension one, consider the set K=[0,1] associated with the dilation A=2. Then B=A ^t=2. Let $K_{1}=[0,\frac{1}{2}],\ K_{2}=[\frac{1}{2},1]$. Then we have

$$BK_1=[0,1]=K_1\cup K_2, \qquad BK_2=[1,2]=(K_1+1)\cup(K_2+1). $$

Thus Γ ₁₁={0},Γ ₁₂={0},Γ ₂₁={1},Γ ₂₂={1}. For j=1,2, $\mathcal{D}_{j}:= \bigcup_{i=1}^{2}\varGamma_{ij}=\lbrace 0,1\rbrace$ is a complete set of coset representatives for the group $\mathbb{Z}/2\mathbb{Z}$ and $0\in\mathcal{D}_{j}$. Moreover, the set $Q:=(K_{1}-1)\cup K_{2}=[-1,-\frac{1}{2}]\cup[\frac{1}{2},1]$ is the Shannon wavelet set.

In Example 3.1, the set K is an integral self-affine $\mathbb{Z}$-tiling set with 2 prototiles. q=2, C=1=q−1. However, $L_{1}=\lbrace -1\rbrace=\mathcal{D}_{1}\setminus\{0\}, \ L_{2}=\lbrace 0\rbrace=\mathcal{D}_{2}\setminus\{1\}$ are both complete sets of coset representatives for $\mathbb{Z}/C\mathbb{Z}$ but $K\cap\mathbb{Z}^{n}=\lbrace 0,1\rbrace\ne\{0\}$.

There are many examples of wavelet sets in the form of (3.1) that have appeared in the literature (see e. g. [10]). We can show that there exists, for each example of MRA wavelet set appeared in [10], a corresponding integral self-affine multi-tile set K which can be used to generate the wavelet set using the method of Theorem 3.3. Before proceeding to give some new examples, we need to introduce one lemma which is used to characterize the integer points of an integral self-affine set associated with an integral expansive matrix B and the digit set $\mathcal{D}\subset\mathbb{Z}^{n}$ when $\mathcal{D}$ contains a complete set of coset representatives for $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$ and which has been proved in [5].

Lemma 3.4

Let B be an n×n integral expansive matrix and K be a self-affine set which satisfies that $BK= \bigcup_{i=1}^{M} (K+d_{i})$, where $\mathcal{D}:=\{d_{1},d_{2},\ldots,d_{M}\}\subseteq\mathbb{Z}^{n}$ contains a complete set of coset representatives for $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$. Then $K\cap\mathbb{Z}^{n}=-S$, where S=⋃S _i and S _i is defined as follows:

$$S_0:=\Biggl\{ k\in\mathbb{Z}^n:\bigl(I-B^m \bigr)k= \sum_{i=0}^{m-1}B^id_i, \ d_i\in\mathcal{D},\ \textit{for some} \ m\geqslant 1\Biggr\} $$

and, for any j≥0,

$$S_{j+1}:=\bigl\{ x\in\mathbb{Z}^n: B(-x)=d-s,\ \textit{for some} \ d\in\mathcal{D} \ \textit{and some} \ s\in S_j \bigr\} . $$

Example 3.2

Let and B=A ^t. Consider the set K=K ₁∪K ₂ which satisfies the following set equation:

$$\begin{aligned} BK_1 =&K_1\cup K_2, \\ BK_2 =&\biggl(K_1+\binom{1}{0}\biggr)\cup \biggl(K_2+\binom{0}{1}\biggr). \end{aligned}$$

Thus

$$\begin{aligned} \varGamma_{11}=\biggl\lbrace \binom{0}{0}\biggr\rbrace ,\qquad \varGamma_{12}=\biggl\lbrace \binom{0}{0}\biggr\rbrace ,\qquad \varGamma_{21}=\biggl\lbrace \binom{1}{0}\biggr\rbrace ,\qquad \varGamma_{22}=\biggl\lbrace \binom{0}{1}\biggr\rbrace . \end{aligned}$$

Furthermore, $\mathcal{D}_{1}=\varGamma_{11}\cup\varGamma_{21}=\bigl\{\binom{0}{0}, \binom{1}{0}\bigr\}$ and $\mathcal{D}_{2}=\varGamma_{12}\cup\varGamma_{22}=\bigl\{\binom{0}{0}, \binom{0}{1}\bigr\}$ are both a complete set of coset representatives for the group $\mathbb{Z}^{2}/B\mathbb{Z}^{2}$. This implies that $\bigcup_{\ell\in\mathbb{Z}^{2}} (K+\ell)=\mathbb{R}^{n}$ (see Theorem 1.2 in [9]). Let $x\in K\cap\mathbb{Z}^{2}$. It follows from (2.1) that $x\in K^{\prime}\cap\mathbb{Z}^{2}$, where K′ is defined by

$$K^{\prime}:= \Biggl\{ \sum_{j=1}^{\infty}B^{-j} \delta_{j},\ \delta_j\in\biggl\{ \binom{0}{1}, \binom{0}{0}, \binom{1}{0}\biggr\} \Biggr\} . $$

Using Lemma 3.4, we obtain that

$$\begin{aligned} K^{\prime}\cap\mathbb{Z}^2= \biggl\{ \binom{0}{0}, \binom{0}{1}, \binom{0}{-1}, \binom{1}{0}, \binom{-1}{0}, \binom{1}{-1}, \binom{-1}{-1} \biggr\} . \end{aligned}$$

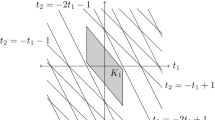
The set K′ and its integer points are depicted in Fig. 1.

Fig. 1

K′ and its integer points $\binom{0}{0}$, $\binom{0}{1}$, $\binom{0}{-1}$, $\binom{1}{0}$, $\binom{-1}{0}$, $\binom{1}{-1}$, $\binom{-1}{-1}$ (dark points)

Furthermore, we have

$$\begin{aligned} &\binom{0}{-1}=\sum_{i=1}^{\infty}B^{-i} \varepsilon_i,\quad {\rm{where}} \ \varepsilon_i= \begin{cases} \binom{0}{1}, \ {\rm{if}} \ i=3k+1 \ {\rm{or}} \ 3k+2 \ {\rm{for}} \ k\ge 0 \ {\rm{and}} \ k\in\mathbb{Z},\\ \binom{1}{0}, \ {\rm{if}} \ i=3k \ {\rm{for}} \ k\ge 1 \ {\rm{and}} \ k\in\mathbb{Z}. \end{cases} \\ &\binom{1}{0}=\sum_{i=1}^{\infty}B^{-i} \delta_i, \quad {\rm{where}} \ \delta_i=\begin{cases} \binom{0}{1}, \ {\rm{if}} \ i=3k+1 \ {\rm{or}} \ 3k+3 \ {\rm{for}} \ k\ge 0 \ {\rm{and}} \ k\in\mathbb{Z},\\ \binom{1}{0}, \ {\rm{if}} \ i=3k+2 \ {\rm{for}} \ k\ge 0 \ {\rm{and}} \ k\in\mathbb{Z}. \end{cases}\\ &\binom{-1}{0}=B^{-1}\binom{1}{0}+B^{-1} \binom{0}{-1}=B^{-1}\binom{1}{0}+\sum _{i=2}^{\infty}B^{-i}\varepsilon_{i-1}, \\ &\binom{-1}{-1}=B^{-1}\binom{1}{0}+B^{-1} \binom{1}{0}= B^{-1}\binom{1}{0}+\sum _{i=2}^{\infty}B^{-i}\delta_{i-1}, \\ &\binom{0}{1}=B^{-1}\binom{-1}{-1}=B^{-2} \binom{1}{0}+\sum_{i=3}^{\infty}B^{-i} \delta_{i-2}, \\ &\binom{1}{-1}=B^{-1}\binom{0}{1}+B^{-1} \binom{0}{1}=B^{-1}\binom{0}{1}+B^{-3} \binom{1}{0}+\sum_{i=4}^{\infty}B^{-i} \delta_{i-3}. \end{aligned}$$

By the representations obtained above for the elements $\binom{-1}{0}$, $\binom{1}{0}$, $\binom{0}{1}$, $\binom{0}{-1}$, $\binom{-1}{-1}$, $\binom{1}{-1}$ and (2.1), we conclude that none of them belong to $K\cap\mathbb{Z}^{2}$. Therefore, $K\cap\mathbb{Z}^{2}=\{0\}$. It follows from Proposition 2.6 that K is an integral self-affine $\mathbb{Z}^{2}$-tiling set with 2 prototiles. The sets K ₁ and K ₂ are depicted in Fig. 2 and the set K and its integer translations $K+\binom{0}{1}$, $K+\binom{1}{0}$ are depicted in Fig. 3. Let C be a two dimensional identity matrix. Then we conclude from Theorem 3.3 that $Q:=C^{-1} \bigcup_{j=1}^{2} (K_{j}+L_{j}) = \bigl(K_{1}+\binom{1}{0}\bigr)\cup\bigl(K_{2}+\binom{0}{1}\bigr)$, where $L_{j}=\mathcal{D}_{j}\setminus\{0\}$, is an A-dilation wavelet set. The set Q and its integer translations $Q+\binom{0}{-1}, Q+\binom{-1}{0}$ are depicted in Fig. 4. The set Q and its B-dilations B ⁻¹ Q,BQ are depicted in Fig. 5.

Fig. 2

K ₁ (gray) and K ₂ (black)

Fig. 3

K, $K+\binom{0}{1}$ and $K+\binom{1}{0}$ (dark … light)

Fig. 4

Q, $Q+\binom{0}{-1}$ and $Q+\binom{-1}{0}$ (dark … light)

Fig. 5

Q, B ⁻¹ Q and BQ (dark … light)

It has been shown in [5] that no single self-affine tile can yield a wavelet set associated with the matrix . However, an example given in [10] illustrates that some A-dilation wavelet sets can be constructed by an integral self-affine multi-tile K which is defined by

$$K=\text{conv} \biggl\{ \binom{1/2}{1/2}, \binom{1/2}{-1/2}, \binom{-1/2}{1/2}, \binom{-1/2}{-1/2} \biggr\} , $$

where conv(K) denotes the convex hull of K. It is easy to check that K is an integral self-affine $\mathbb{Z}^{2}$-tiling set with 8 prototiles . This again demonstrates that integral self-affine multi-tiles are useful for constructing many new examples of wavelet sets. We now state a more general theorem for the construction of wavelet sets using integral self-affine multi-tiles. This result generalizes Theorem 4.5 in [6], with the difference that the conditions for the theorem to hold are now sufficient, but no longer necessary. Theorem 3.3 is a particular case of it obtained by taking S _j ={0} for all j=1,…,M, below.

Theorem 3.5

Let C be an n×n nonsingular integral matrix which commutes with B. If $K\cap\mathbb{Z}^{n}=\lbrace 0\rbrace$ and for each j=1,…,M, there exists a finite set $S_{j}\subset\mathbb{Z}^{n}$ satisfying

• (i) $\lbrace0\rbrace\subset S_{j}\subset \bigcup_{i=1}^{M}(\varGamma_{ij}+BS_{i})$,

• (ii) $L_{j}:= \bigcup_{i=1}^{M}(\varGamma_{ij}+BS_{i})\setminus S_{j}$ is a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$.

Then $Q:=C^{-1} \bigcup_{i=1}^{M}(K_{i}+L_{i})$ is an A-dilation wavelet set.

Proof

Since, for each j∈S, L _j is a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$ and the set K is a $\mathbb{Z}^{n}$-tiling set, then we have

$$\begin{aligned} \bigcup_{k\in\mathbb{Z}^n} (Q+k) =&C^{-1} \bigcup_{k\in\mathbb{Z}^n} \bigcup _{j=1}^M(K_j+L_{j}+Ck) \\ =&C^{-1} \bigcup_{k\in\mathbb{Z}^n} \bigcup _{j=1}^M(K_j+k) \cong \mathbb{R}^n, \end{aligned}$$

(3.5)

and

$$\begin{aligned} \lvert Q\rvert=\lvert \det C\rvert^{-1} \sum _{j=1}^M \lvert \det C\rvert \lvert K_j \rvert= \sum_{j=1}^M\lvert K_j \rvert=1. \end{aligned}$$

(3.6)

It follows from (3.5) and (3.6) that Q is a $\mathbb{Z}^{n}$-tiling set. Let $W=\bigcup_{i=1}^{M}(K_{i}+S_{i})$. By the definition of Q and L _j , j∈S, we have

$$\begin{aligned} C^{-1}(BW\setminus W) =&C^{-1}\Biggl[B \bigcup _{i=1}^M(K_i+S_i) \bigg\backslash \bigcup_{i=1}^M (K_i+S_i)\Biggr] \\ =&C^{-1}\Biggl[ \bigcup_{i=1}^M \bigcup_{j=1}^M (K_j+ \varGamma_{ij}+BS_i)\bigg\backslash \bigcup _{j=1}^M(K_j+S_j)\Biggr] \\ =&C^{-1} \bigcup_{j=1}^M \Biggl(K_j+\Biggl( \bigcup_{i=1}^M( \varGamma_{ij}+BS_i)\Big\backslash S_j\Biggr)\Biggr) \\ =&C^{-1} \bigcup_{j=1}^M (K_j+L_j)=Q. \end{aligned}$$

(3.7)

Thus B ^m Q=C ⁻¹(B ^m+1 W∖B ^m W) and $\lbrace B^{m}Q\rbrace_{m\in\mathbb{Z}}$ is an essentially disjoint family. Now we only need to prove that $\bigcup_{m\in\mathbb{Z}}B^{m}Q\cong\mathbb{R}^{n}$. The fact that $K\cap\mathbb{Z}^{n}=\lbrace0\rbrace$ implies that K contains a neighborhood of 0 by Lemma 2.2. Since for each i∈1,…,M, 0∈S _i , K⊂W. Thus W contains a neighborhood of 0 and $\bigcup_{m\in\mathbb{Z}}B^{m}W=\mathbb{R}^{n}$. An argument similar to the one given in Theorem 3.3 shows that $\bigcup_{m\in\mathbb{Z}}B^{m}Q=\mathbb{R}^{n}$. □

Example 3.3

In dimension one, consider the set $K=[-\frac{1}{2},\frac{1}{2}]$ associated with the dilation A=3. Let $K_{1}=[-\frac{1}{2},0], \ K_{2}=[0,\frac{1}{2}]$. Then B=A ^t=3 and we have

$$\begin{aligned} BK_1&=3K_1=\biggl[-\frac{3}{2},0\biggr]= \bigl(K_1+\lbrace -1,0\rbrace \bigr)\cup(K_2-1), \\ BK_2&=3K_2=\biggl[0,\frac{3}{2} \biggr]=(K_1+ 1)\cup\bigl(K_2+\lbrace 0,1 \rbrace\bigr). \end{aligned}$$

Thus Γ ₁₁={−1,0},Γ ₁₂={−1},Γ ₂₁={1},Γ ₂₂={0,1}. Let

$$S_1= \lbrace -3,-2,-1,0,4 \rbrace,\qquad S_2= \lbrace -4,-3,-2,-1,0,1,3,4 \rbrace. $$

Then we obtain

$$\begin{aligned} S_1&= \lbrace -3,-2,-1,0,4 \rbrace \\ &\subset \bigcup_{i=1}^2( \varGamma_{i1}+BS_i)= (\varGamma_{11}+BS_1) \cup(\varGamma_{21}+BS_2) \\ &=\bigl( \lbrace-1,0 \rbrace+3 \lbrace-3,-2,-1,0,4 \rbrace\bigr)\cup\bigl( \lbrace1 \rbrace+3 \lbrace-4,-3,-2,-1,0,1,3,4 \rbrace\bigr) \\ &= \lbrace -11,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,4,10,11,12,13 \rbrace, \\ S_2&= \lbrace-4, -3,-2,-1,0,1,3,4 \rbrace \\ &\subset \bigcup_{i=1}^2( \varGamma_{i2}+BS_i)= (\varGamma_{12}+BS_1) \cup(\varGamma_{22}+BS_2) \\ &= \bigl( \lbrace-1 \rbrace+3 \lbrace-3,-2,-1,0,4 \rbrace \bigr)\cup \bigl( \lbrace0,1 \rbrace+3 \lbrace-4,-3,-2,-1,0,1,3,4 \rbrace \bigr) \\ &= \{-12,-11,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,3,4,9,10,11,\\ &\quad \ \ 12,13 \}. \end{aligned}$$

Define

$$\begin{aligned} L_1:={}& \bigcup_{i=1}^2( \varGamma_{i1}+BS_i)\Big\backslash S_1= \lbrace-11,-10,-9,-8,-7,-6,-5,-4,1,10,11,12,13\rbrace,\\ L_2:={}& \bigcup_{i=1}^2( \varGamma_{i2}+BS_i)\Big\backslash S_2\\ ={}& \lbrace -12,-11,-10,-9,-8,-7,-6,-5,9,10,11,12,13\rbrace. \end{aligned}$$

Then L ₁ and L ₂ are both complete sets of coset representatives for the group $\mathbb{Z}/13\mathbb{Z}$. It follows from Theorem 3.5 that the set

$$Q:=13^{-1}\Biggl(3 \bigcup_{i=1}^2K_i+S_i \Biggr)\bigg\backslash \Biggl( \bigcup_{i=1}^2K_i+S_i \Biggr) =13^{-1} \bigcup_{i=1}^2(K_i+L_i) $$

is a 3-dilation wavelet set.

In Example 3.3, the set K is an integral self-affine $\mathbb{Z}$-tiling set with 2 prototiles and $\lvert \det C\rvert\notin (3-1)\mathbb{Z}$ since |detB|=3 and |detC|=13. This shows that the last statement of Proposition 4.1 in [6] can not be extended to multi-tiles.

Example 3.4

In dimension two, consider the set $K=\mathrm{conv} \bigl\{\binom{\frac{1}{2}}{\frac{1}{2}}, \binom{\frac{1}{2}}{-\frac{1}{2}}, \binom{-\frac{1}{2}}{-\frac{1}{2}}, \binom{-\frac{1}{2}}{\frac{1}{2}} \bigr\}$ associated with the matrix . Then . Let

$$\begin{aligned} K_1 =&\mathrm{conv} \biggl\lbrace \binom{0}{0}, \binom{1/2}{0}, \binom{1/2}{1/2}, \binom{0}{1/2} \biggr\rbrace , \\ K_2 =&\mathrm{conv} \biggl\{ \binom{-1/2}{0}, \binom{-1/2}{1/2}, \binom{0}{1/2}, \binom{0}{0} \biggr\} , \\ K_3 =&\mathrm{conv} \biggl\lbrace \binom{0}{0}, \binom{-1/2}{0}, \binom{-1/2}{-1/2}, \binom{0}{-1/2} \biggr\rbrace ,\\ K_4 =&\mathrm{conv} \biggl\lbrace \binom{0}{0}, \binom{1/2}{0}, \binom{1/2}{- 1/2}, \binom{0}{-1/2} \biggr\rbrace . \end{aligned}$$

Then (see Fig. 6), we have

$$\begin{aligned} BK_1 =&K_1\cup\biggl(K_4+ \binom{0}{1}\biggr),\qquad BK_2= \biggl(K_1+ \binom{0}{-1}\biggr)\cup K_4, \\ BK_3 =&\biggl(K_2+\binom{0}{-1}\biggr)\cup K_3, \qquad BK_4=K_2\cup \biggl(K_3+\binom{0}{1}\biggr). \end{aligned}$$

Thus

$$\begin{aligned} \varGamma_{11} =&\biggl\lbrace \binom{0}{0}\biggr\rbrace ,\qquad \varGamma_{12}=\emptyset, \qquad \varGamma_{13}=\emptyset,\qquad \varGamma_{14}=\biggl\lbrace \binom{0}{1}\biggr\rbrace ,\\ \varGamma_{21} =& \biggl\lbrace \binom{0}{-1}\biggr\rbrace ,\qquad \varGamma_{22}=\emptyset,\qquad \varGamma_{23}=\emptyset,\qquad \varGamma_{24}=\biggl\lbrace \binom{0}{0}\biggr\rbrace , \\ \varGamma_{31} =& \emptyset,\qquad \varGamma_{32}=\biggl\lbrace \binom{0}{-1}\biggr\rbrace ,\qquad \varGamma_{33}=\biggl\lbrace \binom{0}{0}\biggr\rbrace ,\qquad \varGamma_{34}=\emptyset,\\ \varGamma_{41} =&\emptyset,\qquad \varGamma_{42}=\biggl\lbrace \binom{0}{0}\biggr\rbrace ,\qquad \varGamma_{43}=\biggl\lbrace \binom{0}{1}\biggr\rbrace ,\qquad \varGamma_{44}=\emptyset. \end{aligned}$$

And

$$\begin{aligned} \mathcal{D}_1 =& \bigcup_{i=1}^4 \varGamma_{i1}= \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ) \right\rbrace,\qquad \mathcal{D}_2= \bigcup _{i=1}^4\varGamma_{i2} = \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ) \right\rbrace, \\ \mathcal{D}_3 =& \bigcup_{i=1}^4 \varGamma_{i3} = \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ 1\end{matrix} \right ) \right\rbrace, \qquad \mathcal{D}_4= \bigcup _{i=1}^4\varGamma_{i4} = \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ 1\end{matrix} \right ) \right\rbrace. \end{aligned}$$

Obviously, K is a $\mathbb{Z}^{2}$-tiling set. Note that for each j∈{1,2,3,4}, $0\in\mathcal{D}_{j}$ and $\mathcal{D}_{j}$ is a complete set of coset representatives for the group $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$. Hence, K is an integral self-affine $\mathbb{Z}^{2}$-tiling set with 4 prototiles which satisfies that $K\cap\mathbb{Z}^{2}=\{0\}$. Let

$$\begin{aligned} S_1 =& \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}-1\\ -1\end{matrix} \right ) \right\rbrace, \qquad S_2= \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ) \right\rbrace, \\ S_3 =& \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix} 0\\ 1\end{matrix} \right ) \right\rbrace,\qquad S_4= \left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ 1\end{matrix} \right ) \right\rbrace. \end{aligned}$$

Then, we have

$$\begin{aligned} &\begin{aligned}\left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ) \right\}&\subseteq S_1\subseteq \bigcup_{i=1}^4\varGamma_{i1}+BS_i=BS_1 \cup \left (\begin{matrix}0\\ -1\end{matrix} \right )+BS_2\\ &= \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ),\left (\begin{matrix}-1\\ -2\end{matrix} \right ), \left (\begin{matrix}-1\\ -1\end{matrix} \right ) \right\},\end{aligned} \\ &\begin{aligned} \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ) \right\}&\subseteq S_2\subseteq \bigcup_{i=1}^4\varGamma_{i2}+BS_i =\left (\begin{matrix}0\\ -1\end{matrix} \right )+BS_3\cup BS_4\\&= \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ),\left (\begin{matrix}1\\ -1\end{matrix} \right ), \left (\begin{matrix}1\\ 0\end{matrix} \right ) \right\}, \\ \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ) \right\}&\subseteq S_3\subseteq \bigcup_{i=1}^4\varGamma_{i3}+BS_i =BS_3\cup \left (\begin{matrix}0\\ 1\end{matrix} \right )+BS_4= \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}0\\ 1\end{matrix} \right ),\left (\begin{matrix}1\\ 0\end{matrix} \right ), \left (\begin{matrix}1\\ 1\end{matrix} \right ) \right\},\end{aligned} \\ &\begin{aligned} \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ) \right\}&\subseteq S_4\subseteq \bigcup_{i=1}^4\varGamma_{i4}+BS_i =\left (\begin{matrix}0\\ 1\end{matrix} \right )+BS_1\cup BS_2\\ &= \left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ),\left (\begin{matrix}0\\ 1\end{matrix} \right ), \left (\begin{matrix}-1\\ -1\end{matrix} \right ), \left (\begin{matrix}-1\\ 0\end{matrix} \right ) \right\}.\end{aligned} \end{aligned}$$

Define $L_{j}=\bigcup_{i=1}^{4}\varGamma_{ij}+BS_{i}\setminus S_{j}, \ j=1,2,3,4$. Then

$$\begin{aligned} L_1 =& \left\lbrace \left (\begin{matrix}0\\ -1\end{matrix} \right ), \left (\begin{matrix}-1\\ -2\end{matrix} \right ) \right\rbrace, \qquad L_2= \left\lbrace \left (\begin{matrix}1\\ -1\end{matrix} \right ), \left (\begin{matrix}1\\ 0\end{matrix} \right ) \right\rbrace,\\ L_3 =& \left\lbrace \left (\begin{matrix}1\\ 0\end{matrix} \right ), \left (\begin{matrix} 1\\ 1\end{matrix} \right ) \right\rbrace, \qquad L_4= \left\lbrace \left (\begin{matrix}-1\\ -1\end{matrix} \right ), \left (\begin{matrix}-1\\ 0\end{matrix} \right ) \right\rbrace. \end{aligned}$$

Let . Then C=B, where B=A ^t and obviously, it commutes with the matrix B. It is easy to check that for each j=1,2,3,4, L _j is a complete set of coset representatives for the group $\mathbb{Z}^{2}/C\mathbb{Z}^{2}$. It follows from Theorem 3.5 that $Q:=C^{-1} \bigcup_{i=1}^{4}(K_{i}+L_{i})$ is an A-dilation wavelet set. The set Q and its integer translations $Q+\binom{1}{0}, Q+\binom{1}{-1}$ are depicted in Fig. 7. The set Q and its B-dilations BQ,B ⁻¹ Q are depicted in Fig. 8.

Fig. 6

K _i and its B-dilations BK _i , i=1,2,3,4

Fig. 7

Q and its integer translations $Q+\binom{1}{0}, Q+\binom{1}{-1}$

Fig. 8

Q and its B-dilations BQ,B ⁻¹ Q

4 Construction of Multi-wavelet Sets Using Integral Self-Affine Multi-tiles

A finite set $\psi=\{\psi^{1},\dots,\psi^{M}\}\subset L^{2}(\mathbb{R}^{n})$ is called an A-dilation orthonormal multi-wavelet if the system

$$\begin{aligned} \bigl\{ \lvert \det A\rvert^{\frac{j}{2}}\psi^{\ell}{ \bigl(A^j\cdot-k\bigr)}:j\in\mathbb{Z},\ k\in\mathbb{Z}^n,\ \ell=1,\dots, M \bigr\} \end{aligned}$$

is an orthonormal basis for $L^{2}(\mathbb{R}^{n})$. A measurable set Q is called a multi-wavelet set of order M if $Q= \bigcup_{i=1}^{M}Q_{i}$ for some essencially disjoint sets $Q_{i}\subset\mathbb{R}^{n},\ 1\le i\le M$, with the property that the finite collection $\{\mathcal{F}^{-1}(\chi_{Q_{1}}),\dots, \mathcal{F}^{-1}(\chi_{Q_{M}}) \}$ is an A-dilation orthonormal multi-wavelet.

Bownik, Rzeszotnik and Speegle [1] characterized all multi-wavelet sets using the following theorem.

Theorem 4.1

A measurable set Q is an A-dilation multi-wavelet set of order M if and only if

• (i) $\sum_{k\in\mathbb{Z}^{n}}\chi_{Q}(\xi+k)=M \ a.e. \ \xi\in\mathbb{R}^{n}$,

• (ii) $\sum_{j\in\mathbb{Z}}\chi_{Q}(B^{j}\xi)=1 \ a.e. \ \xi\in\mathbb{R}^{n}$.

The condition (ii) above is equivalent to the condition (i) of Proposition 3.2. Bownik, Rzeszotnik and Speegle ([1], Sect. 3) showed the connection between generalized scaling sets and multi-wavelet sets. Definition 4.1 and Lemma 4.2 below show that A-dilation generalized scaling sets and A-dilation multi-wavelet sets are determined by one another.

Definition 4.1

For fixed $L\in\mathbb{N}$, a set $K\subset\mathbb{R}^{n}$ is called a generalized scaling set of order L associated with a dilation A if $\lvert K\rvert=\frac{L}{q-1}$ and BK∖K is a multi-wavelet set of order L associated with the dilation A, where B=A ^t and q=|detA|.

Lemma 4.2

[1]

A measurable set $Q\subset\mathbb{R}^{n}$ is an A-dilation multi-wavelet set of order L if and only if the set $K:= \bigcup_{j=1}^{\infty}B^{-j}Q$ is an A-dilation generalized scaling set of order L.

Theorem 4.3 below, taken from [1] presents a criterion for a measurable set $K\subset\mathbb{R}^{n}$ to be an A-dilation generalized scaling set.

Theorem 4.3

[1]

A measurable set $K\subset\mathbb{R}^{n}$ is an A-dilation generalized scaling set of order L if and only if

• (i) $\lvert K\rvert=\frac{L}{q-1}$,

• (ii) K⊂BK,

• (iii) lim _m→∞ χ _K (B ^−m ξ)=1 for a.e. $\xi\in\mathbb{R}^{n}$,

• (iv) $\sum_{d\in\mathcal{D}} D(\xi+B^{-1}d)=D(B\xi)+L$ a.e., where $D(\xi)= \sum_{k\in\mathbb{Z}^{n}}\chi_{K}(\xi+k)$ and $\mathcal{D}$ is a set of coset representatives for the group $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$.

Theorem 4.4

Let K be an integral self-affine $\mathbb{Z}^{n}$-tiling set with M prototiles which satisfies (1.1) and (1.2), where, for each j∈S, $0\in \mathcal{D}_{j}:= \bigcup_{i=1}^{M}\varGamma_{ij}$. In addition, let us assume that $K\cap\mathbb{Z}^{n}=\lbrace0\rbrace$. Then K is an A-dilation generalized scaling set of order q−1, where A=B ^t and q=|detB|.

Proof

Since for each j∈S, $0\in \mathcal{D}_{j}$, it follows from (2.6) that K⊆BK. K contains a neighborhood of 0 using Proposition 2.6 since $K\cap\mathbb{Z}^{n}=\{0\}$. Thus we have $\bigcup_{m\in\mathbb{Z}}B^{m}K=\mathbb{R}^{n}$ since B is expansive. The facts that K⊆BK and $\bigcup_{m\in\mathbb{Z}}B^{m}K=\mathbb{R}^{n}$ imply that lim _m→∞ χ _K (B ^−m ξ)=1 for a.e. $\xi\in\mathbb{R}^{n}$. Define $D(\xi):= \sum_{k\in\mathbb{Z}^{d}}\chi_{K}(\xi+k)$. Then D(ξ)=1 for a.e. $\xi\in\mathbb{R}^{n}$ and |K|=1 since K is a $\mathbb{Z}^{n}$ tiling set. This shows that $\sum_{d\in\mathcal{D}}D(\xi+B^{-1}d)=\lvert \det B\rvert=q$ if $\mathcal{D}$ is a set of coset representatives for the group $\mathbb{Z}^{n}/B\mathbb{Z}^{n}$. Therefore, we have

$$\sum_{d\in\mathcal{D}}D\bigl(\xi+B^{-1}d\bigr)=D(B \xi)+(q-1). $$

By Theorem 4.3, K is an A-dilation generalized scaling set of order q−1. □

The following example can be easily deduced from Theorem 3.3 in [1].

Example 4.1

In dimension two, consider the unite square $K=[-\frac{1}{M},\frac{M-1}{M}]\times[-\frac{1}{M},\frac{M-1}{M}]$ associated with the matrix , where M≥2 and N≥2. Then K must be an integral self-affine multi-tile associated with the matrix B=A ^t=A since the set $[-\frac{1}{M},\frac{M-1}{M}]$ is an integral self-affine multi-tile associated with the dilation N. It follows from Theorem 4.4 that K is an A-dilation generalized scaling set of order N ²−1.

In Theorem 4.4, if we let $Q:= \bigcup_{j=1}^{M} (K_{j}+L_{j})$, where $L_{j}=\mathcal{D}_{j}\setminus\{0\}$, then Q=BK∖K and Q is an A-dilation multi-wavelet set of order q−1 by Definition 4.1. If q=2, then the wavelet set Q must be an A-dilation MRA wavelet set which has been extensively studied in [5]. We can also construct an A-dilation multi-wavelet set starting with a given A-dilation wavelet set.

Lemma 4.5

Let Q be an A-dilation wavelet set. If C is an n×n nonsingular integral matrix commuting with B, where B=A ^t, then CQ is an A-dilation multi-wavelet set of order |detC|.

Proof

Let $\mathcal{D}^{\prime}$ be a complete set of coset representatives for the group $\mathbb{Z}^{n}/C\mathbb{Z}^{n}$. By assumption that Q is an A-dilation wavelet set, then the set Q satisfies (i) and (ii) of Proposition 3.2. Therefore, we have, using (i) of Proposition 3.2, that

$$\begin{aligned} \sum_{j\in\mathbb{Z}}\chi_{CQ} \bigl(B^j\xi\bigr)= \sum_{j\in\mathbb{Z}} \chi_{Q}\bigl(C^{-1}B^j\xi\bigr) = \sum _{j\in\mathbb{Z}}\chi_{Q}\bigl(B^jC^{-1} \xi\bigr)=1\quad \mbox{a.e.} \ \xi\in\mathbb{R}^n. \end{aligned}$$

(4.1)

Using (ii) of Proposition 3.2, we have $\sum_{k\in\mathbb{Z}^{n}}\chi_{Q}(\xi+k)=1$ for a.e. $\xi\in\mathbb{R}^{n}$ and thus

$$\begin{aligned} \begin{aligned}[b] \sum_{k\in\mathbb{Z}^n}\chi_{CQ}(\xi+k) &= \sum_{t\in\mathcal{D}^{\prime}} \sum_{k\in\mathbb{Z}^n} \chi_{CQ}(\xi+Ck+t) \\ &= \sum_{t\in\mathcal{D}^{\prime}} \sum_{k\in\mathbb{Z}^n} \chi_Q\bigl(C^{-1}\xi+C^{-1}t+k\bigr) \\ &=\lvert \det C\rvert\quad {\rm{for}} \ \mbox{a.e.} \ \xi\in\mathbb{R}^n.\end{aligned} \end{aligned}$$

(4.2)

By (4.1), (4.2) and using Theorem 4.1, we obtain that CQ is an A-dilation multi-wavelet set of order |detC|. □

Similarly, we have the following result.

Proposition 4.6

If Q is an A-dilation multi-wavelet set of order M and C is an n×n nonsingular integral matrix commuting with B, where B=A ^t, then CQ is an A-dilation multi-wavelet set of order |detC|M.

The previous result raises a natural question: given an A-dilation multi-wavelet set of order M, can we find a nonsingular integral matrix C with |detC|=M which commutes with the matrix B, where B=A ^t, such that C ⁻¹ Q is an A-dilation wavelet set. The answer turns out to be negative. The following example shows that the existence of an A-dilation multi-wavelet set $Q\subset\mathbb{R}^{2}$ of order 2 and for which we cannot find a 2×2 nonsingular integral matrix C such that C ⁻¹ Q is an A-dilation wavelet set.

Example 4.2

Let and B=A ^t. Consider the set K=K ₁∪K ₂ which satisfies the following set equation:

$$\begin{aligned} BK_1 =&\left(K_1+\left\{\left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}1\\ -1\end{matrix} \right )\right\}\right)\cup \left(K_2+ \left\{\left (\begin{matrix}1\\ -1\end{matrix} \right ), \left (\begin{matrix}1\\ 0\end{matrix} \right )\right\}\right), \\ BK_2 =&\left(K_1+\left (\begin{matrix}0\\ -1\end{matrix} \right )\right)\cup K_2. \end{aligned}$$

Thus

$$\begin{aligned} \varGamma_{11} =&\left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}1\\ -1\end{matrix} \right )\right\rbrace,\qquad \varGamma_{12}=\left\lbrace \left (\begin{matrix}1\\ -1\end{matrix} \right ),\left (\begin{matrix}1\\ 0\end{matrix} \right )\right\rbrace,\\ \varGamma_{21} =&\left \lbrace \left (\begin{matrix}0\\ -1\end{matrix} \right )\right\rbrace,\qquad \varGamma_{22}=\left\lbrace \left (\begin{matrix}0\\ 0\end{matrix} \right )\right\rbrace. \end{aligned}$$

Furthermore, $\mathcal{D}_{1}=\varGamma_{11}\cup\varGamma_{21}=\bigl\{\binom{0}{0}, \binom{1}{-1}, \binom{0}{-1}\bigr\}$ and $\mathcal{D}_{2}=\varGamma_{12}\cup\varGamma_{22}=\bigl\{\binom{0}{0}, \binom{1}{-1}, \binom{1}{0}\bigr\}$ are both a complete set of coset representatives for the group $\mathbb{Z}^{2}/B\mathbb{Z}^{2}$. This implies that $\bigcup_{\ell\in\mathbb{Z}^{2}} (K+\ell)=\mathbb{R}^{n}$ (see Theorem 1.2 in [9]). Let $x\in K\cap\mathbb{Z}^{2}$. It follows from (2.1) that $x\in K^{\prime}\cap\mathbb{Z}^{2}$, where K′ is defined by

$$K^{\prime}:= \Biggl\{ \sum_{j=1}^{\infty}B^{-j} \delta_{j},\ \delta_j\in\left\{\left (\begin{matrix}0\\ -1\end{matrix} \right ), \left (\begin{matrix}0\\ 0\end{matrix} \right ), \left (\begin{matrix}1\\ 0\end{matrix} \right ), \left (\begin{matrix}1\\ -1\end{matrix} \right )\right\} \Biggr\} . $$

Using Lemma 3.4, we obtain that $K^{\prime}\cap\mathbb{Z}^{2}= \{\binom{0}{0}, \binom{0}{1} \}$. The set K′ and its integer points are depicted in Fig. 9. Moreover, the identity $\binom{0}{1}=\sum_{i=1}^{\infty}B^{-i}\binom{1}{0}$ implies that $\binom{0}{1}\notin K\cap\mathbb{Z}^{2}$. Therefore, $K\cap\mathbb{Z}^{2}=\{0\}$. It follows from Proposition 2.6 that K is an integral self-affine $\mathbb{Z}^{2}$-tiling set with 2 prototiles. The sets K ₁ and K ₂ are depicted in Fig. 10 and the set K and its integer translations $K+\binom{1}{0}, K+\binom{0}{1}$ are depicted in Fig. 11.

Fig. 9

K′ and its integer points $\binom{0}{0}$, $\binom{0}{1}$ (dark points)

Fig. 10

K ₁ (gray) and K ₂ (black)

Fig. 11

K, $K+\binom{0}{1}$ and $K+\binom{1}{0}$ (dark … light)

It follows from Theorem 4.4 that K is an A-dilation generalized scaling set of order 2. Therefore, $Q:=BK\setminus K= \bigcup_{j=1}^{2} (K_{j}+L_{j})$, where $L_{j}=\mathcal{D}_{j}\setminus\{0\}$, is an A-dilation multi-wavelet set of order 2. Assume that there exists a nonsingular 2×2 integral matrix C which commutes with the matrix B such that $\widetilde{Q}:=C^{-1}Q=C^{-1}(BK\setminus K)=C^{-1} \bigcup_{j=1}^{2}(K_{j}+L_{j})$ is an A-dilation wavelet set. Then the matrix C has a general form with $a,b\in\mathbb{Z}$ and |detC|=2. Furthermore, for each j∈{1,2}, $L_{j}=\mathcal{D}_{j}\setminus\lbrace0\rbrace$ is a complete set of coset representatives for the group $\mathbb{Z}^{2}/C\mathbb{Z}^{2}$ by Lemma 3.1. Hence, for each j∈{1,2}, there must exist ℓ _j ∈L _j such that $\ell_{j}\in C\mathbb{Z}^{2}$ and the difference of any two elements in L _j is not in $C\mathbb{Z}^{2}$. In our case,

$$\begin{aligned} L_1= \left\lbrace \left (\begin{matrix}1\\ -1\end{matrix} \right ), \left (\begin{matrix}0\\ -1\end{matrix} \right ) \right\rbrace, \qquad L_2= \left\lbrace \left (\begin{matrix}1\\ -1\end{matrix} \right ), \left (\begin{matrix}1\\ 0\end{matrix} \right ) \right\rbrace. \end{aligned}$$

By the definition of L ₁ and L ₂, $\binom{1}{-1}\in C\mathbb{Z}^{2}$. This implies that $a,b\in2\mathbb{Z}$, which contradicts the fact that detC=a ²+2b ²=2. Therefore, there does not exist a nonsingular matrix C commuting with B such that $\widetilde{Q}=C^{-1}Q$ is an A-dilation wavelet set.