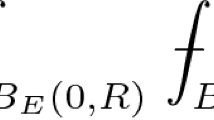L ^p,q-Boundedness of Bergman Projections in Homogeneous Siegel Domains of Type II

Abstract

In this paper, we generalize to homogeneous Siegel domains of second kind the L ^p-continuity properties of the Bergman projection. Precisely, we give an improvement of the index p using Fourier analysis as in the case of convex homogeneous tube type domains (Nana and Trojan in Ann. Scuola Norm. Sup. Pisa Cl. Sci. (5) X:477–511, 2011).

1 Introduction

Let n≥3, D be a domain in $\mathbb{C}^{n}$ and dv the Lebesgue measure defined in $\mathbb{C}^{n}$. We denote by P the Bergman projection i.e., the orthogonal projection of the Hilbert space L ²(D,dv) onto its closed subspace A ²(D,dv) consisting of holomorphic functions on D. It is well-known that P is an integral operator defined in L ²(D,dv) whose kernel B(⋅,⋅), called the Bergman kernel is the reproducing kernel of A ²(D,dv). In this work, we consider the case where D is a homogeneous Siegel domain of second kind and we are interested with the values of p≥1 such that the Bergman projection P can be extended as a bounded operator on L ^p(D,dv).

The L ^p-boundedness of Bergman projections on homogeneous Siegel domains, or special cases of these, has been studied by many authors. In [1], D. Békollé and A. Bonami considered the tube domain over the forward light cone; they obtained some sufficient conditions, using Schur’s Lemma, which are also necessary for the operator with positive Bergman kernel |B(⋅,⋅)|. On the other hand, D. Békollé and A. Temgoua in [3] generalized results in [1] to the case of homogeneous Siegel domains of type II, symmetric or not; again they applied Schur’s Lemma to the operator with positive Bergman kernel. Later, considering tube domains over symmetric cones, the authors of [4, 5] and [7] found values of p for which the Bergman projection is bounded whereas the operator with positive Bergman kernel is not bounded. Moreover, D. Debertol in [9] obtained a generalization of this result for general weighted measures. Following this direction, authors of [15] extended the result to tube domains over convex homogeneous cones. Also, using a different method, J. Gonessa in his PhD thesis [14], gave an improvement of the indices of p obtained by authors of [3], for the Pyateckii-Shapiro domain, a non symmetric homogeneous Siegel domain of type II, associated to the spherical cone of $\mathbb{R}^{3}$.

In this paper, we extend to all homogeneous Siegel domains of second kind results of [14] and [15]. The optimal range of L ^p boundedness for P is still an open question, with additional partial results known only in the case of tube domains over light cones [7, 12].

This paper is divided in 6 sections. In Sect. 2, we deeply rely on [3, 13, 16] and [15] to give a brief description of homogeneous Siegel domains and state our results. In Sect. 3, we recall some useful results about homogeneous cones, such as the Whitney decomposition and state some theorems and propositions which are helpful to carry out computations in the paper. Section 4 deals with Bergman spaces. In Sects. 5 and 6, we give the proofs of the results announced in the second section.

2 Statement of the Results

In this section, we recall the description of a homogeneous cone within the framework of T-algebra. Next, we introduce homogeneous Siegel domains of second kind and state our results.

2.1 Homogeneous Cones

We use the same notations as in [8] and [15]. Consider a (real) matrix algebra $\mathcal{U}$ of rank r with canonical decomposition

$$\mathcal{U}=\bigoplus_{1\leq i,j\leq r}\mathcal{U}_{ij} $$

such that $\mathcal{U}_{ij}\mathcal{U}_{jk}\subset\mathcal{U}_{ik}$ and $\mathcal{U}_{ij}\mathcal{U}_{\ell k}=0$ if j≠ℓ. We assume that $\mathcal{U}$ has the structure of T-algebra (in the sense of [16]) in which an involution is given by x↦x ^⋆. This structure implies that the subspaces $\mathcal{U}_{ij}$ satisfy: $\mathcal {U}_{ii}=\mathbb{R}c_{i}$ where $c_{i}^{2}=c_{i}$ and $\mbox{dim}\,\mathcal{U}_{ij}=n_{ij}=n_{ji}$. Also, the matrix

$${\bf e}=\sum_{j=1}^rc_j $$

is a unit element for the algebra $\mathcal{U}$. These concepts have a clear meaning in the special example $\mathcal{U}=\mbox{Sym}(r,\,\mathbb {R})$. (See [15, Example 2.8, p. 484].)

Let ρ be the unique isomorphism from $\mathcal{U}_{ii}$ onto $\mathbb{R}$ with ρ(c _i )=1 for all i=1,…,r. We shall consider the subalgebra

$$\mathcal{T}=\bigoplus_{1\leq i\leq j\leq r}\mathcal{U}_{ij} $$

of $\mathcal{U}$ consisting of upper triangular matrices and let

$$H=\{t\in\mathcal{T}:\rho(t_{ii})>0,i=1,\ldots,r\} $$

be the subgroup of upper triangular matrices whose diagonal elements are positive.

Denote by V the vector space of “Hermitian matrices” in $\mathcal{U}$

$$V=\{x\in\mathcal{U}: x^\star=x\}. $$

If we set

$$n_i=\sum_{j=1}^{i-1}n_{ji},\quad\quad m_i=\sum_{j=i+1}^{r}n_{ij}, $$

then

(1)

The vector space V becomes Euclidean with the inner product

$$(x|y)={\rm tr}(xy^\star) $$

where

$${\rm tr}(x)=\sum_{i=1}^r\rho(x_{ii}). $$

Next, we define

$$\varOmega =\{ss^\star,\,s\in H\}. $$

By a theorem of Vinberg [16, p. 384], Ω is an open convex homogeneous cone with no straight lines, in which the group H acts simply and transitively via the transformations

(2)

Thus, to every element y∈Ω corresponds a unique t∈H such that

$$y=\pi(t)[{\bf e}]=t\cdot{\bf e}. $$

We shall assume that Ω is irreducible, and hence ${\rm rank}(\varOmega )=r$. All homogeneous convex cones can be constructed in this way [16, p. 397].

As in [15], we denote by Q _j the fundamental rational functions in Ω given by

$$Q_j(y)=\rho(t_{jj})^2,\quad{\rm when}\ y=t\cdot{\bf e}\in \varOmega . $$

These are denoted χ _j in [13].

We consider the matrix algebra with involution $\mathcal{U}'$ which differs from $\mathcal{U}$ only on its grading, and we put

$$\mathcal{U}'_{ij}=\mathcal{U}_{r+1-i,\,r+1-j}\quad(i,j=1,\ldots,r). $$

It is proved in [16] that $\mathcal{U}'$ is also a T-algebra and V′=V where V′ is the subspace of $\mathcal{U}'$ consisting of Hermitian matrices. The corresponding homogeneous cone coincides with the dual cone of Ω, namely

$$\varOmega ^*=\{\xi\in V': (x|\xi)>0,\,\forall x\in\overline{\varOmega}\setminus\{ 0\}\}. $$

One also has

$$\varOmega ^*=\{t^\star t:t\in H\}. $$

(see [16, p. 390]).

For ξ=t ^⋆ t∈Ω ^∗, we shall define

$$Q_j^*(\xi)=\rho(t_{jj})^2. $$

In the notation of [13], this corresponds to

$$Q_j^*(\xi)=\chi^*_{r-j+1}(\xi). $$

In the sequel, we will use the following notations: for all x∈Ω, ξ∈Ω ^∗ and $\alpha =( \alpha _{1}, \alpha _{2},\ldots, \alpha _{r})\in\mathbb{R}^{r}$,

$$Q^ \alpha (x)=\prod_{j=1}^rQ_j^{ \alpha _j}(x)\quad\mbox{and}\quad (Q^*)^{ \alpha }(\xi)=\prod_{j=1}^r(Q_j^{*})^{ \alpha _j}(\xi). $$

In the notations of [13], these functions correspond to

$$Q^ \alpha (x)=(x)^\alpha \quad\mbox{and}\quad (Q^*)^{ \alpha }(\xi )=(\xi)_*^{\alpha ^*},\quad{\rm with\ }\alpha ^*=( \alpha _r, \alpha _{r-1},\ldots, \alpha _1). $$

We put $\tau=(\tau_{1},\tau_{2},\ldots,\tau_{r})\in\mathbb{R}^{r}$ with

$$\tau_i=1+\frac{1}{2}(m_i+n_i). $$

Let y∈Ω, we have for j=1,…,r

(3)

Therefore, for any s∈H,

(4)

since

(5)

(See [16, p. 388].) The above properties are also valid if we replace Q _j by $Q_{j}^{*}$ and x∈Ω by ξ∈Ω ^∗.

2.2 Homogeneous Siegel Domains

Let $V^{\mathbb{C}}=V+iV$ be the complexification of V. Then each element of $V^{\mathbb{C}}$ is identified with a vector in $\mathbb{C}^{n}$. The coordinates of a point $z\in\mathbb{C}^{n}$ are arranged in the form

(6)

where

(7)

and

(8)

For all j=1,…,r we denote e _jj =z, where z _jj =1 and the other coordinates are equal to zero and we denote

$$e=\sum_{j=1}^re_{jj}=(1,0,1,\ldots,0,1). $$

Let $m\in\mathbb{N}$. For each row vector $u\in\mathbb{C}^{m}$, we denote u′ the transpose of u. Given m×m Hermitian matrices $\widetilde {H}_{1},\ldots,\widetilde{H}_{n}$, we define a Ω-Hermitian, homogeneous form $F:\mathbb{C}^{m}\times\mathbb{C}^{m}\to\mathbb{C}^{n}$ as

(9)

such that

• (i) $F(u,u)\in\overline{\varOmega }$;

• (ii) F(u,u)=0 if and only if u=0;

• (iii) for every t∈H, there exists $\tilde{t}\in GL(m,\mathbb{C} )$ such that $t\cdot F(u,u)=F(\tilde{t}u,\tilde{t}u)$.

The point set

(10)

in $\mathbb{C}^{n+m}$ is called a Siegel domain of the second kind over Ω.

Using (6), we write

$$F(u,u)=(F_{11}(u,u),F_{2}(u,u),F_{22}(u,u),\ldots,F_{r}(u,u),F_{rr}(u,u)) $$

where for i=1,…,r and j=2,…,r,

$$F_{ii}(u,u)=uH_{i}\bar{u}',\,F_j(u,u)=(F_{1j}(u,u),\ldots,F_{j-1,j}(u,u)) $$

and for 1≤i<j≤r and t=1,…,n _ij ,

$$F_{ij}(u,u)=(F_{ij}^{(1)}(u,u),\ldots,F_{ij}^{(n_{ij})}(u,u)),\quad F_{ij}^{(t)}(u,u)=uH_{ij}^{(t)}\bar{u}'. $$

The space $\mathbb{C}^{m}$ decomposes into direct sum of subspaces $\mathbb{C} ^{b_{1}}\oplus\cdots\oplus\mathbb{C}^{b_{r}}$ on which are concentrated the Hermitian forms F _jj , that is, with appropriate coordinates we have for i=1,…,r,

(11)

where $0_{(b_{k})}$ and $I_{(b_{k})}$ denote respectively the null matrix and the identity matrix of the vector space $\mathbb{C}^{b_{k}}$ for all k=1,…,r. (See for instance [17, pp. 127–129].)

In the sequel, we denote b the vector

$$b=(b_1,b_2,\ldots,b_r)\in\mathbb{N}^r $$

and $D=\{(z,\,u)\in\mathbb{C}^{n}\times\mathbb{C}^{m}:\Im m\,z-F(u,\, u)\in\varOmega \}$ is the Siegel domain of second kind associated to the open convex homogeneous cone Ω and to the Ω-Hermitian, homogeneous form F.

For each (z, u)∈D,

$$Q^{-2\tau-b}(\Im m\,z-F(u,\,u))dv(z)dv(u) $$

is the invariant measure with respect to the group of automorphisms of D. (See [13, p. 56].) Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in\mathbb{R}^{r}$, we denote by $L_{\nu}^{p}(D),1\leq p\leq\infty$, the Lebesgue space $L^{p}(D,Q^{\nu-\frac{b}{2}-\tau}(\Im m\,z-F(u,\,u))dv(z)dv(u))$.

Recall that if m=0, the domain D is a tube type Siegel domain or a Siegel domain of first kind, denoted T _Ω , associated with the cone Ω, considered by authors of [15].

For all (z,u)∈D, we shall consider the measure

$$dV_\nu(z,u)=Q^{\nu-\frac{b}{2}-\tau}(\Im m\,z-F(u,\,u))dv(z)dv(u) $$

with the convention that if y=ℑm  z,

$$dV_\nu(y,u)=Q^{\nu-\frac{b}{2}-\tau}(y-F(u,\,u))dydv(u) $$

where dv is the Lebesgue measure on $\mathbb{C}^{\ell}$ where ℓ=n or ℓ=m.

The weighted Bergman space $A_{\nu}^{p}(D)$ is the closed subspace of $L_{\nu}^{p}(D)$ consisting of holomorphic functions. In order to have a non-trivial subspace, we take $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in\mathbb{R}^{r}$ such that $\nu_{i}>\frac{m_{i}+b_{i}}{2}, i=1,\ldots,r$.¹

The orthogonal projection of the Hilbert space $L_{\nu}^{2}(D)$ on its closed subspace $A_{\nu}^{2}(D)$ is the weighted Bergman projection P _ν . We recall that P _ν is defined by the integral

$$P_\nu f(z,\,u)=\int_{D}B_\nu((z,\,u),(w,\,t))f(w,\,t)dV_\nu(w,t),\quad (z,\,u)\in D, $$

where for suitable constant d _ν, b ,

$$B_\nu((z,\,u),(w,\,t))=d_{\nu,\,b} Q^{-\nu-\frac{b}{2}-\tau}\left (\frac{z-\bar{w}}{2i}-F(u,\,t)\right) $$

is the weighted Bergman kernel i.e., the reproducing kernel of $A_{\nu}^{2}(D)$. (See [3, Proposition II.5].)

Let us now introduce mixed normed spaces. For 1≤p,q≤∞, let $L_{\nu}^{p,q}(D)$ be the space of functions f on D such that

$$\|f\|_{L_\nu^{p,q}(D)}:=\left(\int_{\mathbb{C}^m}\int_{\varOmega +F(u,u)}\left (\int_V |f(x+iy,\,u)|^pdx\right)^{\frac{q}{p}}dV_\nu(y,u)\right )^{\frac{1}{q}} $$

is finite (with obvious modification if p=∞). As before, we call $A_{\nu}^{p,q}(D)$ the closed subspace of $L_{\nu}^{p,q}(D)$ consisting of holomorphic functions. Note that for p=q, the space $L_{\nu}^{p,q}(D)$ coincides with the space $L_{\nu}^{p}(D)$.

The unweighted case corresponds to $\nu=\tau+\frac{b}{2}$.

In this paper, we discuss boundedness of P _ν on $L_{\nu}^{p,q}(D)$. The case p=2 being of special interest. This is due the fact that, this induces us to use Fourier transform in the x variables and consequently focus on L ²-norms in these variables. We shall start by obtaining the boundedness of the weighted Bergman projection from the operator with positive Bergman kernel $P_{\nu}^{+}$ defined on $L_{\nu}^{2}(D)$ by

$$P_\nu^+ f(z,\,u)=\int_{D}|B_\nu((z,\,u),(w,\,t))|f(w,\,t)dV_\nu(w,t). $$

We prove the following:

Theorem 2.1

Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu _{r})\in\mathbb{R}^{r}$ such that $\nu_{i}>\frac{m_{i}+n_{i}+b_{i}}{2}, i=1,\ldots,r$. The operator $P_{\nu}^{+}$ is bounded on $L_{\nu}^{p,q}(D)$ when

$$1+\max_{1\leq i\leq r}\frac{\frac{n_i}{2}}{\nu_i-\frac {m_i}{2}-\frac{b_i}{2}}<q<1+\min_{1\leq i\leq r}\frac{\nu_i-\frac {m_i}{2}-\frac{b_i}{2}}{\frac{n_i}{2}}. $$

Hence P _ν is bounded for this range of q.

Recall that for p=q, this theorem has been proved by D. Békollé and A. Temgoua in [3]. Next, we shall focus on the case p=2 to prove the following:

Theorem 2.2

Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu _{r})\in\mathbb{R} ^{r}$ such that $\nu_{i}>\frac{m_{i}+b_{i}}{2}, i=1,\ldots,r$. The weighted Bergman projector P _ν is bounded on $L_{\nu}^{2,q}(D)$ when

$$2\left(1+\max_{1\leq i\leq r}\frac{\frac{n_i}{2}}{\nu_i-\frac {m_i}{2}-\frac{b_i}{2}}\right)<q<2\left(1+\min_{1\leq i\leq r}\frac {\nu_i-\frac{m_i}{2}-\frac{b_i}{2}}{\frac{n_i}{2}}\right). $$

Our main result is the following theorem, which gives an improvement of the index obtained in [3, Theorem II.7].

Theorem 2.3

Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in\mathbb{R}^{r}$ such that $\nu_{i}>\frac{m_{i}+n_{i}+b_{i}}{2}, i=1,\ldots,r$. The Bergman projector P _ν extends to a bounded operator on $L_{\nu}^{p}(D)$ for

$$1+\max_{1\leq i\leq r}\frac{\frac{n_i}{2}}{\nu_i-\frac{m_i}{2}-\frac{b_i}{2}+\frac {n_i}{2}}<p<1+\min_{1\leq i\leq r}\frac{\nu_i-\frac{m_i}{2}-\frac{b_i}{2}+\frac {n_i}{2}}{\frac{n_i}{2}}. $$

To prove this result, we shall proceed as in [2, 6, 15] and conclude by interpolation using Theorems 2.1 and 2.2. Note that in the case of symmetric Siegel domain of tube type T _Ω , which Debertol considered, the necessary condition of the $L_{\nu}^{2,q}(T_{\varOmega})$-boundedness of the weighted Bergman projector P _ν has been left open. In [15], authors gave necessary conditions for the $L_{\nu}^{p}(T_{\varOmega})$-boundedness of the operator $P_{\nu}^{+}$ and the $L_{\nu}^{2,q}(T_{\varOmega})$-boundedness of the weighted Bergman projector P _ν ; they indicated that they don’t understand why they seem not to be sharp. We are still looking for examples of open convex homogeneous cones for which these necessary conditions do not coincide with the sufficient conditions. This is motivated by the fact that for the case of rank 2 and the Vinberg cone [2] and its dual, the sufficient conditions above are also necessary. Moreover, for general symmetric cones, if we assume that $\nu=(\nu,\ldots,\nu)\in\mathbb{R}^{r}$, then these sufficient conditions are also necessary. (See [6, Theorem 4.10].)

3 Some Useful Results in a Convex Homogeneous Cone

In this section, we recall some important facts about homogeneous cones such as the Riemannian structure that yields an isometry between the cone and its dual and the Whitney decomposition of the cone. Most of these results have been established in [2, 6] and [15].

3.1 The Riemannian Structure Ω and Its Dual

Following [15], let d and d _∗ denote the Riemannian distances in Ω and Ω ^∗ which are invariant under the action of G(Ω) and G(Ω ^∗) respectively, i.e.

$$d(gx,gy)=d(x,y)\quad \mbox{and}\quad d_*(g^*\xi,g^*\eta)=d_*(\xi,\eta)\quad \forall g\in G(\varOmega ). $$

Recall from [15] (see also [10, Chap. I]) that there is a bijection from Ω to Ω ^∗ given by

$$x=t\cdot{\bf e}\in\varOmega \mapsto x'=t^{\star-1}\cdot{\bf e}\in \varOmega ^*, $$

such that x″=x. This is an isometry for the Riemannian distances [2]

$$d_*(x',\,y')=d(x, y). $$

We also use that [15, p. 489]

(12)

3.2 The Invariant Measure on Ω and the Whitney Decomposition

Since we have also this identification Ω ^∗≡H′⋅e, we deduce from (4), that the measure

$$dm(x)=Q^{-\tau}(x)dx\quad({\rm resp.}\ dm_*(\xi)=(Q^*)^{-\tau }(\xi)d\xi) $$

is H-invariant on Ω (resp. H′-invariant on Ω ^∗).

Lemma 3.1

Given λ>0, there is a constant C=C(λ)>0 such that:

• (i) if d(y, t)≤λ then $\frac{1}{C}\leq\frac{Q_{j}(y)}{Q_{j}(t)}\leq C$ for all j=1,…,r and y, t∈Ω;

• (ii) if d _∗(ξ, η)≤λ then $\frac{1}{C}\leq\frac{Q_{j}^{*}(\xi)}{Q_{j}^{*}(\eta)}\leq C$ for all j=1,…,r and ξ, η∈Ω ^∗.

Let λ>0,y∈Ω (resp. ξ∈Ω ^∗) and d (resp. d _∗) the G(Ω)-invariant (resp. G(Ω ^∗)-invariant ) distance defined in Ω (resp. Ω ^∗). We denote by

$$B_\lambda (y)=\{x\in\varOmega : d(y,\,x)<\lambda \} $$

and

$$B_\lambda ^{*}(\xi)=\{\eta\in\varOmega ^*: d_*(\eta,\,\xi)<\lambda \} $$

the d-ball (resp. d _∗-ball) centered at the point y (resp. ξ) with the radius λ.

We give now the Whitney decomposition of the cone Ω, which is obtained, for instance, as in Lemma 3.5 of [2].

Lemma 3.2

There exists a sequence {y _j } _j of points of Ω such that the following three properties hold:

• (i) the balls $B_{\frac{1}{2}}(y_{j})$ are pairwise disjoint;

• (ii) the balls B ₁(y _j ) form a covering of Ω;

• (iii) there is an integer N=N(Ω) such that every y∈Ω belongs to at most N balls B ₁(y _j ).

Remark 3.3

This lemma is also true for the dual cone Ω ^∗.

Definition 3.4

A sequence {y _j } in Ω as in Lemma 3.2 is called a lattice of Ω. In this case, the sequence $\{ y_{j}'\}$ is also a lattice in Ω ^∗, called the dual lattice.

The family {B ₁(y _j )} _j (resp. $\{B_{1}^{*}(y_{j}')\}_{j}$) is called the Whitney decomposition of the cone Ω (resp. Ω ^∗).

We will need the following results whose proofs can be found in [15].

Lemma 3.5

Let y ₀∈Ω, ξ ₀∈Ω ^∗; then

(13)

Proposition 3.6

Let y ₀∈Ω, ξ ₀∈Ω ^∗. There is a constant γ=γ(Ω, Ω ^∗)≥1 such that

Corollary 3.7

Let y ₀∈Ω. There is a constant γ>0 such that

$$\frac{1}{\gamma}\leq(y|\xi)\leq\gamma,\quad\forall y\in B_1(y_0),\,\xi\in B_1^*(y'_0). $$

The following results hold if Ω is substituted by Ω ^∗, provided the roles of m _j and n _j are reversed.

Corollary 3.8

[15] Let $\nu=(\nu_{1},\ldots,\nu_{r})\in\mathbb{R}^{r}$ such that $\nu_{j}>\frac{m_{j}}{2}, j=1,\ldots,r$. Then

$$\int_\varOmega e^{-(\xi|y)}Q^{\nu-\tau}(y)dy=\varGamma _{\varOmega }(\nu )(Q^*)^{-\nu }(\xi),\quad \xi\in\varOmega ^*, $$

where Γ _Ω (ν) denotes the gamma integral [13] in the cone Ω.

Remark 3.9

Using the corollary above, one can extend Q ^∗ as an analytic function in V′+iΩ ^∗. More precisely, if ζ∈V′+iΩ ^∗ and $\nu _{j}>\frac{m_{j}}{2}, j=1,\ldots,r$, we set

(14)

Lemma 3.10

[15, Lemma 4.19]

Let $\mu=(\mu_{1},\mu _{2},\ldots,\mu_{r})\in\mathbb{R}^{r}$ and $\lambda =(\lambda _{1},\lambda _{2},\ldots, \lambda _{r})\in\mathbb{R}^{r}$.

For all y∈Ω, the integral

$$J_{\mu\lambda }(y)=\int_\varOmega Q^\mu(y+v) Q^{\lambda -\tau}(v) dv $$

is finite if and only if

In this case, there is a positive constant M _λμ such that

$$J_{\mu\lambda }(y)=M_{\lambda \mu}Q^{\mu+\lambda }(y). $$

Lemma 3.11

[15, Lemma 4.20]

Let $\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{r})\in\mathbb{R}^{r}$.

The integral

(15)

converges if and only if $\alpha _{j}>1+n_{j}+\frac{m_{j}}{2}, j=1,\ldots,r$. In this case, there is a positive constant c _α such that

4 The Bergman Spaces

Here, we recall some basic facts about Bergman spaces. Once we have the preliminary results above, the proof of all these results are basically the same as those obtained in the papers [2, 5] and [15]. The reader can look at these papers to have more details of proofs omitted here. Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in \mathbb{R}^{r}$ such that $\nu_{j}>\frac{m_{j}+b_{j}}{2}, j=1,\ldots,r$. Following [3], we shall denote $L_{(-\nu)}^{2}(\varOmega ^{*}\times\mathbb{C}^{m})$ the Hilbert space of functions $g:\varOmega ^{*}\times\mathbb{C}^{m}\to\mathbb{C}$ such that:

• (i) for all compact subset K ₁ of $\mathbb{C}^{n}$ contained in Ω ^∗ and for all compact subset K ₂ of $\mathbb{C}^{m}$, the mapping u↦g(⋅,u) is holomorphic on K ₂ with values in L ²(K ₁,−ν), where

  $$L^2(K_1,-\nu)=\biggl\{f:K_1\to\mathbb{C}:\int_{K_1}|f(\xi)|^2(Q^*)^{-\nu +\frac {b}{2}}(\xi)d\xi<\infty\biggr\}; $$

• (ii) the function $g\in L^{2}(\varOmega ^{*}\times\mathbb{C}^{m},\, (Q^{*})^{-\nu +\frac{b}{2}}(\xi) e^{-2(F(u,\,u)|\xi)}d\xi dv(u))$.

We then define by

$$L g(z,\,u)=(2\pi)^{-\frac{n}{2}}\int_{\varOmega ^*}e^{i(z|\xi)}g(\xi ,\, u)d\xi $$

the “Laplace transform” of any function $g \in L_{(-\nu)}^{2}(\varOmega \times \mathbb{C}^{m})$. Now, we recall the Plancherel-Gindikin result found in [3, Theorem II.2] which is a generalization of the Paley-Wiener Theorem [15, Theorem 5.1].

Theorem 4.1

Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in\mathbb{R}^{r}$ with $\nu_{j}>\frac{m_{j}+b_{j}}{2}, j=1,\ldots,r$. A function G belongs to $A_{\nu}^{2} (D)$ if and only if G=Lg, with $g\in L_{(-\nu)}^{2}(\varOmega ^{*}\times\mathbb{C}^{m})$. Moreover there is a positive constant e _ν,b such that

(16)

The following results can be proved with standard arguments; see [15].

Proposition 4.2

The Bergman space $A_{\nu}^{p,q}(D)$ is a Banach space.

Lemma 4.3

Let $\nu=(\nu_{1},\ldots,\nu_{r})\in\mathbb{R}^{r}$ and $\mu=(\mu_{1},\ldots,\mu_{r})\in\mathbb{R}^{r}$ such that $\nu_{j}>\frac{m_{j}+b_{j}}{2}, j=1,\ldots,r$ and $\mu_{j}>\frac{m_{j}+b_{j}}{2}, j=1,\ldots,r$. The subspace $A_{\nu}^{p,q}(D)\cap A_{\mu}^{s,r}(D)$ of the Bergman spaces $A_{\nu}^{p,q}(D)$ and $A_{\mu}^{s,r}(D)$ is dense in each of them.

5 Proof of Theorem 2.1

In order to prove Theorem 2.1, we follow the scheme of [2, Proof of Theorem 6.2]. Let $\nu=(\nu_{1},\nu_{2},\ldots,\nu_{r})\in \mathbb{R}^{r}$ such that $\nu_{j}>\frac{m_{j}+b_{j}}{2}, j=1,\ldots,r$.

We shall denote $U=\{(t,u): u\in\mathbb{C}^{m}, t\in\varOmega +F(u,u)\}$. We define $L_{\nu}^{q}(U)$ as the set of all $g:U\to\mathbb{C}$ with norm given by

We will state that the $L_{\nu}^{p,q}(D)$-boundedness of the operator $P_{\nu}^{+}$ is related to the $L^{q}_{\nu}(U)$-boundedness of an integral operator T with positive kernel on U. We will need this result:

Lemma 5.1

([13], p. 58)

For all ξ∈Ω ^∗,

(17)

As a consequence, we have the following:

Proposition 5.2

Let $u,s\in\mathbb{C}^{m}; y\in\varOmega +F(u,u)$ and t∈Ω+F(s,s). For $\lambda =(\lambda _{1},\lambda _{2},\ldots,\lambda _{r})\in\mathbb{R}^{r}$, the integral

$$I_\lambda (y,u,t)=\int_{\mathbb{C}^m}Q^{-\lambda }(y+t+F(s,s)-2\Re e\,F(u,s))dv(s) $$

converges if $\lambda _{j}-b_{j}>\frac{n_{j}}{2},\,j=1,\ldots,r$. In this case, there is a positive constant C _λ such that

(18)

Proof

By Corollary 3.8, we write

$$Q^{-\lambda }(y+t+F(s,s)-2\Re e\,F(u,s))\,{=}\,c_\lambda \int_{\varOmega ^*}e^{-(y+t+F(s,s)-2\Re e\,F(u,s))|\xi)}(Q^*)^{\lambda -\tau}(\xi )d\xi $$

Now, since 2ℜe  F(u,s)=F(s,s)+F(u,u)−F(u−s,u−s), using Fubini’s Theorem, (17) and Corollary 3.8 , we get

 □

Next, we shall use this notation: for all $u,s\in\mathbb{C}^{m}$,

$$A=\Re e\,F(u,s). $$

Also we shall denote

$$f_{y,u}(x)=f(x+iy,u). $$

Thus, for $f\in L_{\nu}^{p,q}(D)$, using Minkowski’s inequality for integrals, Young’s inequality and Lemma 3.11, we get

where for $s\in\mathbb{C}^{m}$ and t∈Ω+F(s,s),

$$g(t,s)=\|f_{t,s}\|_p $$

and T is the integral operator with positive kernel defined on $L^{q}_{\nu}(U)$ by

(19)

It is easy to verify that T is a self-adjoint operator. To prove Theorem 2.1, it suffices therefore to prove the boundedness of the operator on $L^{q}_{\nu}(U)$. We put

$$q_\nu=1+\min_{1\leq i\leq r}\frac{\nu_i-\frac{m_i}{2}-\frac {b_i}{2}}{\frac{n_i}{2}}. $$

Theorem 5.3

Let $\nu=(\nu_{1},\ldots,\nu_{r})\in\mathbb{R}^{r}$ such that $\nu_{j}>\frac{m_{j}+n_{j}+b_{j}}{2}, j=1,\ldots,r$. The operator T is bounded on $L_{\nu}^{q}(U)$ when $q'_{\nu}<q<q_{\nu}$.

Proof

We will use Schur’s Lemma (see [11]). The kernel of the operator T relative to the measure dV _ν (t,s) is given by

$$N(y,u;t,s)= Q^{-\nu-\frac{b}{2}}(y-2A+t) $$

and it is positive. By Schur’s Lemma, it is sufficient to find a positive and measurable function φ defined on U such that

(20)

and

(21)

We take as test functions φ(t, s)=Q ^γ(t−F(s, s)) where $\gamma=(\gamma_{1},\ldots,\gamma_{r})\in\mathbb{R}^{r}$ has to be determined. The left-hand side of (20) equals

$$K(t,s)=\int_\varOmega \left(\int_{\mathbb{C}^m} Q^{-\nu-\frac {b}{2}}(y+F(u,u)-2A+t)dv(u)\right)Q^{\gamma q+\nu-\frac{b}{2}-\tau}(y)dy. $$

Using (18), we get

(22)

An application of Lemma 3.10 gives that (22) holds whenever

Likewise, (21) holds when

For these intervals to be non-empty, we need $\nu_{j}>\frac {m_{j}+n_{j}+b_{j}}{2}, j=1,\ldots,r$.

The identities (20) and (21) are simultaneously satisfied if any γ _j ,j=1,…,r, satisfies the following condition

(23)

The intersection in (23) is not empty if $\frac{-\nu_{j}+\frac{m_{j}}{2}+\frac{b_{j}}{2}}{q'}<\frac{-\frac {n_{j}}{2}}{q}$ and $\frac{-\nu_{j}+\frac{m_{j}}{2}+\frac{b_{j}}{2}}{q}<\frac{-\frac {n_{j}}{2}}{q'}$; that is for any j=1,…,r,

$$\frac{\nu_j+\frac{-m_j-b_j+n_j}{2}}{\nu_j-\frac {m_j+b_j}{2}}<q<\frac{\nu_j+\frac{-m_j-b_j+n_j}{2}}{\frac{n_j}{2}} $$

i.e. for any j=1,…,r,

$$1+\frac{\frac{n_j}{2}}{\nu_j-\frac{m_j}{2}-\frac {b_j}{2}}<q<1+\frac{\nu_j-\frac{m_j}{2}-\frac{b_j}{2}}{\frac{n_j}{2}}. $$

 □

6 Proofs of Theorems 2.2 and 2.3

In this section, we will use the Plancherel-Gindikin Theorem (Theorem 4.1) to prove that the “Laplace transform” is an isomorphism between $A _{\nu}^{2,q}(D)$ and the space $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$ to be defined below. This will lead us to the proof of Theorem 2.2. We shall then obtain the proof of Theorem 2.3 by interpolation. The results here are the analogues of those in the papers [2, 4, 6] and [15]. We will give only statements of the proofs that emphasize differences.

In the sequel, we consider the following disjoint covering of the cone Ω ^∗

$$E_1^*=B_1^*,\quad\quad E_j^*=B_j^*\setminus\bigcup_{k=1}^{j-1}B_k^*,\quad j=2,\ldots. $$

where $B_{j}^{*}=B_{1}^{*}(y'_{j})$ and $\{y'_{j}\}$ is the dual of the lattice {y _j }. We have $\varOmega ^{*}=\bigcup_{j} E_{j}^{*}$ and

$$|E_j^*|\sim|B_j^*|\sim{(Q^*)^{\tau}(y'_j)}. $$

We shall need the following definitions:

Definition 6.1

Let $j\in\mathbb{N}^{*}$. We say that a function g belongs to $L^{2,q}(E_{j}^{*}\times\mathbb{C}^{m})$ if g is measurable and satisfies

$$\|g\|_{L^{2,q}(E_j^*\times\mathbb{C}^m)}^q:=\int_{\mathbb {C}^m}\left(\int _{E_j^*}e^{-2(F(u,u)|\xi)}|g(\xi,u)|^2d\xi\right)^{\frac{q}{2}}dv(u) $$

is finite.

Definition 6.2

Let q≥1 and {ξ _j } a lattice in Ω ^∗. We denote by $\beta_{\nu}^{q}(\varOmega ^{*}\times \mathbb{C} ^{m})$ the space of all functions $g\in L^{2,q}(E_{j}^{*}\times\mathbb{C}^{m})$ so that

$$\|g\|_{\beta_\nu^q(\varOmega ^*\times\mathbb{C}^m)}^q:=\sum _j(Q^*)^{-\nu+\frac {b}{2}}(\xi_j)\|g\|_{L^{2,q}(E_j^*\times\mathbb{C}^m)}^q $$

is finite.

We say that a sequence {λ _j } _j belongs to $l_{\nu}^{q}$ if it satisfies

$$\sum_j|\lambda _j|^q(Q^*)^{-\nu+\frac{b}{2}}(\xi_j)<+\infty. $$

Lemma 6.3

The space $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$ is a Banach space.

Proof

Just remark that $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})=l_{\nu}^{q}(L^{2,q}(E_{j}^{*}\times\mathbb{C}^{m}))$. □

Remark 6.4

Let {a _j } _j a positive sequence. Then

(24)

and

(25)

6.1 The Boundedness of the Bergman Projector P _ν on $L_{\nu}^{2,q}(D)$

We shall show that the “Laplace transform” L is isomorphically bounded from $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb {C}^{m})$ onto $A_{\nu}^{2,q}(D)$.

Theorem 6.5

Let q≥1. For all $G\in A_{\nu}^{2,q}(D)$, there is a unique function $g\in\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$ such that G=Lg and

$$\|g\|_{\beta_\nu^q(\varOmega ^*\times\mathbb{C}^m)}\leq C\|G\|_{A_\nu ^{2,q}(D)}. $$

Proof

By density (see Corollary 4.3), take $G\in A_{\nu}^{2,q}(D)\cap A_{\nu}^{2,2}(D)$. By the Plancherel-Gindikin Theorem (Theorem 4.1), there exists a function $g\in L_{\left(-\nu\right)}^{2}(\varOmega^{*}\times\mathbb{C}^{m})$ such that

$$G(x+iy,u)= L g(x+iy,u)=(2\pi)^{-\frac{n}{2}}\int_{\varOmega^*}g(\xi ,u)e^{i(x+iy|\xi)}d\xi. $$

By Plancherel’s formula,

Since by Corollary 3.7, $\frac{1}{\gamma}\leq(y|\xi)\leq \gamma$ when $y\in B_{j},\,\xi\in B_{j}^{*}$, we see that

using in the last two inequalities (13) and (12). For general $G\in A_{\nu}^{2,q}$, one proceeds by density as in [4, Paragraph 4.1], completing the proof of the theorem. □

We prove now the converse of the previous theorem.

Theorem 6.6

Assume 1≤q<2q _ν . Given $g\in\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$, then $L g\in A_{\nu}^{2,q}(D)$ and

$$\| L g\|_{A_\nu^{2,q}(D)} \leq C\|g\|_{\beta_\nu^q(\varOmega ^*\times \mathbb{C}^m)}. $$

Proof

For every $u\in\mathbb{C}^{m}$ and y∈Ω+F(u,u), write

$$G(x+iy,u)=G_{y,u}(x)= L g(x+iy,u).$$

The function x↦G _y,u (x) is the inverse Fourier transform of the function

$$\xi\mapsto\psi_{y,u}(\xi)=g(\xi,u)e^{-(y|\xi)}.$$

By Plancherel’s formula,

By (ii) of Lemma 3.2 and Proposition 3.6, we deduce that

(26)

First assume that 1≤q≤2. Put for each $j\in\mathbb{N}^{*}$,

$$G_j(u)=\int_{E_j^*}e^{-2(F(u,u)|\xi)}|g(\xi,u)|^2d\xi. $$

Since $\frac{q}{2}\leq1$, we deduce from the inequality (24), and Corollary 3.8 that

Assume next that 2≤q<2q _ν . Let $\rho=\frac{q}{2}$ and $\alpha =(\alpha _{1},\ldots,\alpha _{r})\in\mathbb{R}^{r}$. By Hölder’s inequality,

From (26), it follows that

(27)

From (13), (ii) of Lemma 3.1, Proposition 3.6 and (iii) of Lemma 3.2 , we have

We deduce from Corollary 3.8 that

$$\sum_je^{-2\gamma(y|\xi_j)}(Q^*)^{\alpha\rho'}(\xi_j)\leq C_{\alpha \rho}Q^{-\alpha \rho'}(y) $$

whenever $\alpha _{j}\rho'>\frac{n_{j}}{2}, j=1,\ldots,r$.

So for $\alpha _{j}\rho'>\frac{n_{j}}{2}, j=1,\ldots,r$, from inequality (27) we obtain:

Moreover, if

$$-\alpha _j\rho+\nu_j-\frac{b_j}{2}>\frac{m_j}{2},\quad j=1,\ldots,r,$$

by (14), we have

$$\int_\varOmega e^{-2\gamma(y|\xi_j)}Q^{-\alpha \rho+\nu-\frac {b}{2}-\tau }(y)dy=c_{\alpha \gamma\nu \rho}(Q^*)^{\alpha\rho-\nu+\frac{b}{2}}(\xi_j); $$

it follows that,

Therefore, the conclusion follows if we choose α ₁,…,α _r such that

$$\alpha _j\rho'>\frac{n_j}{2}, \quad\quad-\alpha _j\rho+\nu_j-\frac {b_j}{2}>\frac {m_j}{2}, \quad j=1,\ldots,r. $$

Each parameter α _j ,j=1,…,r must lie in $]\frac{n_{j}}{2\rho'},\frac{\nu_{j}-\frac{m_{j}}{2}-\frac {b_{j}}{2}}{\rho}[$ which is a non-empty interval if q<2q _ν . □

We have proved that the “Laplace transform” L maps $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$ isomorphically onto $A_{\nu}^{2,q}(D)$ whenever 1≤q<2q _ν . Let us now consider the operator R=L ⁻¹ P _ν . We will now show that the operator R is bounded from $L_{\nu}^{2,q}(D)$ to $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$.

Let $\phi\in L_{\nu}^{2}(D)$; by the Plancherel-Gindikin theorem, $G\in A_{\nu}^{2}(D)$ if and only if G=Lg with $g\in L_{(-\nu)}^{2}(\varOmega ^{*}\times\mathbb{C}^{m})$. The self-adjointness of P _ν implies

$$\langle P_\nu\phi, G\rangle_{A_\nu^2(D)}=\langle\phi, G\rangle_{L_\nu^2(D)}=\langle\phi, L g\rangle_{L_\nu^2(D)}. $$

Now, by the Plancherel formula and Fubini’s theorem

(28)

where $\mathcal{F}$ is the Fourier transform. Therefore, for $g\in L_{(-\nu)}^{2}(\varOmega ^{*}\times\mathbb{C}^{m})$, equality (28) and the polarization of isometry (16) in the Plancherel-Gindikin theorem imply that

(29)

Comparing (28) and (29), if R=L ⁻¹ P _ν , we get

We have the following lemma:

Lemma 6.7

If q≥2, then R extends into a bounded operator from $L_{\nu}^{2,q}(D)$ to $\beta_{\nu}^{q}(\varOmega ^{*}\times \mathbb{C}^{m})$ i.e.,

$$\|R\phi\|_{\beta_\nu^q(\varOmega ^*\times\mathbb{C}^m)}\leq C\|\phi \|_{L_\nu^{2,q}(D)}. $$

Proof

By Hölder’s inequality and Corollary 3.8, we write

hence,

By Lemma 3.1, Fubini’s theorem and Proposition 3.6,

where the last inequality follows from Hölder’s inequality and Corollary 3.8. Therefore, by (25) and Plancherel’s formula,

 □

6.2 Proof of Theorem 2.2

Put

$$Q_\nu=2q_\nu=2\left(1+\min_{1\leq j\leq r}\frac{\nu_j-\frac {m_j}{2}-\frac{b_j}{2}}{\frac{n_j}{2}}\right). $$

Assume that 2≤q<Q _ν . By Lemma 6.7, the operator R is bounded from $L_{\nu}^{2,q}(D)$ to $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C} ^{m})$ and according to the Theorem 6.6, the “Laplace transform” L is bounded from $\beta_{\nu}^{q}(\varOmega ^{*}\times\mathbb{C}^{m})$ to $A_{\nu}^{2,q}(D)$. We conclude that the Bergman projector P _ν =L∘R is bounded from $L_{\nu}^{2,q}(D)$ to $A_{\nu}^{2,q}(D)$. We obtain the other part by self-adjointness of P _ν .  □

6.3 Proof of Theorem 2.3

Theorem 6.8

Let $\nu=(\nu_{1},\ldots,\nu _{r})\in\mathbb{R} ^{r}$ such that

$$\nu_j>\frac{m_j+n_j+b_j}{2},\quad j=1,\ldots,r.$$

The Bergman projector P _ν extends to a bounded operator from $L_{\nu}^{p,q}(D)$ to $A_{\nu}^{p,q}(D)$ if

or

Proof

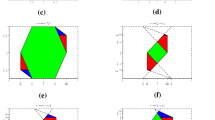
For a fixed $\nu=(\nu_{1},\ldots,\nu_{r})\in\mathbb{R}^{r}$ that satisfies $\nu_{j}>\frac{m_{j}+n_{j}+b_{j}}{2}, j=1,\ldots,r$ let us consider the following picture

By interpolation, P _ν is bounded on $L_{\nu}^{p,q}(D)$ for $(\frac{1}{p},\,\frac{1}{q})$ in the interior of the hexagon of vertices

$$A\left(0,\frac{1}{q_\nu}\right),\quad\quad D\left(\frac{1}{2},\,\frac{1}{Q_\nu}\right),\quad\quad E\left(1,\,\frac{1}{q_\nu}\right) $$

and their symmetric points with respect to $(\frac{1}{2},\,\frac{1}{2})$. □

Theorem 2.3 is the particular case p=q of Theorem 6.8. It is important to say that, for the dual cone Ω ^∗, we obtain

$$q_\nu=1+\min_{1\leq j\leq r}\frac{\nu_j-\frac{n_j}{2}-\frac {b_j}{2}}{\frac{m_j}{2}}. $$