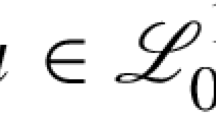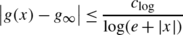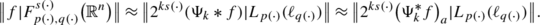Spaces of Variable Smoothness and Integrability: Characterizations by Local Means and Ball Means of Differences

Abstract

We study the spaces $B^{s(\cdot)}_{p(\cdot),q(\cdot)}(\mathbb {R}^{n})$ and $F^{s(\cdot)}_{p(\cdot),q(\cdot)}(\mathbb{R}^{n})$ of Besov and Triebel-Lizorkin type as introduced recently in Almeida and Hästö (J. Funct. Anal. 258(5):1628–2655, 2010) and Diening et al. (J. Funct. Anal. 256(6):1731–1768, 2009). Both scales cover many classical spaces with fixed exponents as well as function spaces of variable smoothness and function spaces of variable integrability.

The spaces $B^{s(\cdot)}_{p(\cdot),q(\cdot)}(\mathbb{R}^{n})$ and $F^{s(\cdot)}_{p(\cdot),q(\cdot)}(\mathbb{R}^{n})$ have been introduced in Almeida and Hästö (J. Funct. Anal. 258(5):1628–2655, 2010) and Diening et al. (J. Funct. Anal. 256(6):1731–1768, 2009) by Fourier analytical tools, as the decomposition of unity. Surprisingly, our main result states that these spaces also allow a characterization in the time-domain with the help of classical ball means of differences.

To that end, we first prove a local means characterization for $B^{s(\cdot)}_{p(\cdot),q(\cdot)}(\mathbb{R}^{n})$ with the help of the so-called Peetre maximal functions. Our results do also hold for 2-microlocal function spaces $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ which are a slight generalization of generalized smoothness spaces and spaces of variable smoothness.

1 Introduction

Function spaces of variable integrability appeared in a work by Orlicz [41] already in 1931, but the recent interest in these spaces is based on the paper of Kováčik and Rákosnik [32] together with applications in terms of modelling electrorheological fluids [45]. A fundamental breakthrough concerning spaces of variable integrability was the observation that, under certain regularity assumptions on p(⋅), the Hardy-Littlewood maximal operator is also bounded on L _p(⋅)(ℝⁿ), see [14]. This result has been generalized to wider classes of exponents p(⋅) in [11, 40] and [15].

Besides electrorheological fluids, the spaces L _p(⋅)(ℝⁿ) possess interesting applications in the theory of PDE’s, variational calculus, financial mathematics and image processing. A recent overview of this vastly growing field is given in [17].

Sobolev and Besov spaces with variable smoothness but fixed integrability have been introduced in the late 60s and early 70s in the works of Unterberger [57], Višik and Eskin [58], Unterberger and Bokobza [56] and in the work of Beauzamy [7]. Leopold studied in [33] Besov spaces where the smoothness is determined by a symbol a(x,ξ) of a certain class of hypoelliptic pseudodifferential operators. In the special case a(x,ξ)=(1+|ξ|²)^σ(x)/2 these spaces coincide with spaces of variable smoothness $B^{\sigma(x)}_{p,p}(\mathbb{R}^{n})$.

A more general approach to spaces of variable smoothness are the so-called 2-microlocal function spaces $B^{\boldsymbol{w}}_{p,q}(\mathbb{R}^{n})$ and $F^{\boldsymbol{w}}_{p,q}(\mathbb{R}^{n})$. Here the smoothness in these spaces gets measured by a weight sequence $\boldsymbol{w}=(w_{j})_{j=0}^{\infty}$. Besov spaces with such weight sequences appeared first in the works of Peetre [42] and Bony [9]. Establishing a wavelet characterization for 2-microlocal Hölder-Zygmund spaces in [24] it turned out that 2-microlocal spaces are well adapted in connection to regularity properties of functions [25, 35, 37]. Spaces of variable smoothness are a special case of 2-microlocal function spaces and in [34] and [8] characterizations by differences have been given for certain classes of them.

The theories of function spaces with fixed smoothness and variable integrability and function spaces with variable smoothness and fixed integrability finally crossed each other in [16], where the authors introduced the function spaces of Triebel-Lizorkin type with variable smoothness and simultaneously with variable integrability. It turned out that many of the spaces mentioned above are really included in this new structure, see [16] and references therein. The key point to merge both lines of investigation was the study of traces. From Theorem 3.13 in [16]

one immediately understands the necessity to take all exponents variable assuming p(⋅) or s(⋅) variable. So the trace embeddings may be described in a natural way in the context of these spaces. Furthermore, this was complemented in [59] by showing, that the classical Sobolev embedding theorem

holds also in this scale of function spaces if the usual condition is replaced by its point-wise analogue

Finally, Almeida and Hästö managed in [1] to adapt the definition of Besov spaces to the setting of variable smoothness and integrability and proved the Sobolev and other usual embeddings in this scale.

The properties of Besov and Triebel-Lizorkin spaces of variable smoothness and integrability known so far give a reasonable hope that these new scales of function spaces enjoy sufficiently many properties to allow a local description of many effects, which up to now could only be described in a global way. Subsequently, for the spaces $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ there is a characterization by local means given in [30]. This characterization still works with Fourier analytical tools but the analyzing functions $k_{0},k\in\mathcal{S}(\mathbb{R}^{n})$ are compactly supported in the time-domain and we only need local values of f around x∈ℝⁿ to calculate the building blocks k(2^−j,f)(x). This is in sharp contrast to the definition of the spaces by the decomposition of unity, cf. Definitions 1 and 3. For the spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ we will prove a local means assertion of this type in Sect. 3 which will be helpful later on.

The main aim of this paper is to present another essential property of the function spaces from [16] and [1]. We prove the surprising result that these spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb {R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ with variable smoothness and integrability do also allow a characterization purely in the time-domain by classical ball means of differences.

The paper is organized as follows. First of all we provide all necessary notation in Sect. 2. Since the proofs for spaces of variable smoothness and 2-microlocal function spaces work very similar (see Remark 2) we present our results for both scales. The proof for the local means characterization will be given in Sect. 3 in terms of 2-microlocal function spaces and we present the version for spaces of variable smoothness in Sect. 3.2. In Sect. 4 we prove the characterization by ball means of differences for $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb {R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and the version for 2-microlocal function spaces will be given in Sect. 4.5.

2 Notation

In this section we collect all the necessary definitions. We start with the variable Lebesgue spaces L _p(⋅)(ℝⁿ). A measurable function p:ℝⁿ→(0,∞] is called a variable exponent function if it is bounded away from zero, i.e. if $p^{-}=\operatornamewithlimits{ess-inf}_{x\in\mathbb{R}^{n}}p(x)>0$. We denote the set of all variable exponent functions by $\mathcal{P}(\mathbb{R}^{n})$. We put also $p^{+}=\operatornamewithlimits{ess-sup}_{x\in\mathbb{R}^{n}}p(x)$.

The variable exponent Lebesgue space L _p(⋅)(ℝⁿ) consists of all measurable functions f for which there exist λ>0 such that the modular

is finite, where

If we define $\mathbb{R}^{n}_{\infty}=\{x\in\mathbb{R}^{n}:p(x)=\infty\}$ and $\mathbb{R}^{n}_{0}=\mathbb{R}^{n}\setminus\mathbb{R}^{n}_{\infty}$, then the Luxemburg norm of a function f∈L _p(⋅)(ℝⁿ) is given by

If p(⋅)≥1, then it is a norm otherwise it is always a quasi-norm.

To define the mixed spaces ℓ _q(⋅)(L _p(⋅)) we have to define another modular. For $p,q\in\mathcal{P}(\mathbb {R}^{n})$ and a sequence $(f_{\nu})_{\nu\in\mathbb{N}_{0}}$ of L _p(⋅)(ℝⁿ) functions we define

(1)

If q ⁺<∞, then we can replace (1) by the simpler expression

The (quasi-)norm in the ℓ _q(⋅)(L _p(⋅)) spaces is defined as usual by

It is known, cf. [1, 31], that ℓ _q(⋅)(L _p(⋅)) is a norm if q(⋅)≥1 is constant almost everywhere (a.e.) on ℝⁿ and p(⋅)≥1, or if 1/p(x)+1/q(x)≤1 a.e. on ℝⁿ, or if 1≤q(x)≤p(x)≤∞ a.e. on ℝⁿ. Surprisingly enough, it turned out in [31] that the condition min(p(x),q(x))≥1 a.e. on ℝⁿ is not sufficient for ℓ _q(⋅)(L _p(⋅)) to be a norm. Nevertheless, it was proven in [1] that it is a quasi-norm for every $p,q\in\mathcal {P}(\mathbb{R}^{n})$.

For the sake of completeness, we state also the definition of the space L _p(⋅)(ℓ _q(⋅)), which is much more intuitive then the definition of ℓ _q(⋅)(L _p(⋅)). One just takes the ℓ _q(x) norm of $(f_{\nu}(x))_{\nu\in\mathbb{N}_{0}}$ for every x∈ℝⁿ and then the L _p(⋅)-norm with respect to x∈ℝⁿ, i.e.

$$\bigl\Vert{f_\nu}\vert{{L_{p(\cdot)}(\ell_{q(\cdot)})}}\bigr \Vert= \bigl\|\bigl\Vert{f_\nu(x)}\vert{\ell_{q(x)}}\bigr\Vert \big|L_{{p(\cdot)}} \bigr\|.$$

It is easy to show [16] that L _p(⋅)(ℓ _q(⋅)) is always a quasi-normed space and it is a normed space, if min(p(x),q(x))≥1 holds point-wise.

The summation in the definition of the norms of ℓ _q(⋅)(L _p(⋅)) and L _p(⋅)(ℓ _q(⋅)) can also be taken for ν∈ℤ. It always comes out of the context over which interval the summation is taken. Occasionally, we may indicate it by $\Vert{(f_{\nu})_{\nu=-\infty }^{\infty}}\vert{{\ell_{q(\cdot)}(L_{p(\cdot)})}}\Vert$.

By $\hat{f}=\mathcal{F}f$ and $f^{\vee}=\mathcal{F}^{-1}f$ we denote the usual Fourier transform and its inverse on $\mathcal{S}(\mathbb{R}^{n})$, the Schwartz space of smooth and rapidly decreasing functions, and on $\mathcal{S}'(\mathbb{R}^{n})$, the dual of the Schwartz space.

2.1 Spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})$

The definition of Besov and Triebel-Lizorkin spaces of variable smoothness and integrability is based on the technique of decomposition of unity exactly in the same manner as in the case of constant exponents.

Definition 1

Let $\varphi_{0}\in\mathcal{S}(\mathbb{R}^{n})$ with φ ₀(x)=1 for |x|≤1 and $\operatorname{supp}\varphi_{0}\subseteq\{x\in\mathbb{R}^{n}:|x|\leq 2\}$. For j≥1 we define

One may verify easily that

$$\sum_{j=0}^\infty\varphi_j(x)=1\quad\text{for all}\ x\in\mathbb{R}^n.$$

The following regularity classes for the exponents are necessary to make the definition of the spaces independent on the chosen decomposition of unity.

Definition 2

Let g∈C(ℝⁿ).

• (i) We say that g is locally log-Hölder continuous, abbreviated $g\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$, if there exists c _log(g)>0 such that

  

  (2)

  holds for all x,y∈ℝⁿ.

• (ii) We say that g is globally log-Hölder continuous, abbreviated g∈C ^log(ℝⁿ), if g is locally log-Hölder continuous and there exists g _∞∈ℝ such that

  

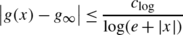
  holds for all x∈ℝⁿ.

Remark 1

With (2) we obtain

This implies that all functions $g\in C^{\log}_{\mathit{loc}}(\mathbb {R}^{n})$ always belong to L _∞(ℝⁿ).

If an exponent $p\in\mathcal{P}(\mathbb{R}^{n})$ satisfies 1/p∈C ^log(ℝⁿ), then we say it belongs to the class $\mathcal{P}^{\log}(\mathbb{R}^{n})$. We recall the definition of the spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$, as given in [16] and [1].

Definition 3

(i) Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with 0<p ⁻≤p ⁺<∞, 0<q ⁻≤q ⁺<∞ and let $s\in C^{\log}_{\mathit{loc}}(\mathbb {R}^{n})$. Then

(ii) Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ and let $s\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$. Then

The subscript φ at the norm symbolizes that the definition formally does depend on the resolution of unity. From [30] and [1] we have that the definition of the spaces $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})$ and $B^{s(\cdot)}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})$ is independent of the chosen resolution of unity if $p,q\in\mathcal{P}^{\log}(\mathbb {R}^{n})$ and $s\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$. That means that different start functions φ ₀ and $\tilde{\varphi }_{0}$ from Definition 1 induce equivalent norms in the above definition. So we will suppress the subscript φ in the notation of the norms.

Let us comment on the conditions on $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ for the Triebel-Lizorkin spaces. The condition 0<p ⁻≤p ⁺<∞ is quite natural since there exists also the restriction p<∞ in the case of constant exponents, see [51] and [63]. The second one, 0<q ⁻≤q ⁺<∞, is a bit unnatural and comes from the use of the convolution Lemma 21 [16, Theorem 3.2]. There is some hope that this convolution lemma can be generalized and the case q ⁺=∞ can be incorporated in the definition of the F-spaces.

The Triebel-Lizorkin spaces with variable smoothness have first been introduced in [16] under much more restrictive conditions on s(⋅). These conditions have been relaxed in [30] in the context of 2-microlocal function spaces (see the next subsection).

Besov spaces with variable p(⋅),q(⋅) and s(⋅) have been introduced in [1].

Both scales contain as special cases a lot of well known function spaces. If s,p and q are constants, then we derive the well known Besov and Triebel-Lizorkin spaces with usual Hölder and Sobolev spaces included, see [51] and [52]. If the smoothness s∈ℝ is a constant and $p\in\mathcal {P}^{\log}(\mathbb{R}^{n})$ with p ⁻>1, then $F^{s}_{{p(\cdot)},2}(\mathbb{R}^{n})=\mathcal{L}^{s}_{p(\cdot)}(\mathbb {R}^{n})$ are the variable Bessel potential spaces from [2] and [23] with its special cases $F^{0}_{{p(\cdot)},2}(\mathbb{R}^{n})=L_{p(\cdot)}(\mathbb{R}^{n})$ and $F^{k}_{{p(\cdot)},2}(\mathbb{R}^{n})=W^{k}_{p(\cdot)}(\mathbb{R}^{n})$ for k∈ℕ₀, see [16].

Taking s∈ℝ and q∈(0,∞] as constants we derive the spaces $F^{s}_{{p(\cdot)},q}(\mathbb{R}^{n})$ and $B^{s}_{{p(\cdot)},q}(\mathbb {R}^{n})$ studied by Xu in [61] and [62].

Furthermore it holds $F^{s(\cdot)}_{{p(\cdot)},{p(\cdot)}}(\mathbb {R}^{n})=B^{s(\cdot)}_{{p(\cdot)},{p(\cdot)}}(\mathbb{R}^{n})$ and $B^{s(\cdot)}_{\infty,\infty}(\mathbb{R}^{n})$ equals the variable Hölder-Zygmund space $\mathcal{C}^{s(\cdot)}(\mathbb{R}^{n})$ introduced in [3, 4] and [44] with 0<s ⁻≤s ⁺≤1, see [1].

2.2 2-Microlocal Spaces

The definition of Besov and Triebel-Lizorkin spaces of variable smoothness and integrability is a special case of the so-called 2-microlocal spaces of variable integrability. As some of the results presented here get proved in this more general scale, we present also the definition of 2-microlocal spaces. It is based on the dyadic decomposition of unity as presented above combined with the concept of admissible weight sequences.

Definition 4

Let α≥0 and let α ₁,α ₂∈ℝ with α ₁≤α ₂. A sequence of non-negative measurable functions $\boldsymbol{w}=(w_{j})_{j=0}^{\infty}$ belongs to the class $\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$ if and only if

• (i) there exists a constant C>0 such that

  

• (ii) and for all j∈ℕ₀ and all x∈ℝⁿ we have

  

Such a system $(w_{j})_{j=0}^{\infty}\in\mathcal{W}^{\alpha}_{\alpha _{1},\alpha_{2}}$ is called an admissible weight sequence.

Finally, here is the definition of the spaces under consideration.

Definition 5

Let $\boldsymbol{w}=(w_{j})_{j\in\mathbb{N}_{0}}\in\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$. Further, let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ (with p ⁺,q ⁺<∞ in the F-case), then we define

and

The independence of the decomposition of unity for the 2-microlocal spaces from Definition 5 follows from the local means characterization (see [30] for the Triebel-Lizorkin and Sect. 3 for the Besov spaces).

The 2-microlocal spaces with the special weight sequence

(3)

have first been introduced by Peetre in [42] and by Bony in [9]. Later on, Jaffard and Meyer gave a characterization in [24] and [25] with wavelets of the spaces $C^{s,s'}_{x_{0}}=B^{\boldsymbol{w}}_{\infty,\infty}(\mathbb{R}^{n})$ and $H^{s,s'}_{x_{0}}=B^{\boldsymbol{w}}_{2,2}(\mathbb{R}^{n})$ with the weight sequence (3). It turned out that spaces of this type are very useful to study regularity properties of functions. Subsequently, Lévy-Véhel and Seuret developed in [35] the 2-microlocal formalism and studied the behavior of cusps, chirps and fractal functions with respect to the spaces $C^{s,s'}_{x_{0}}$.

A first step to a more general weight sequence w has been taken by Moritoh and Yamada in [38] and wider ranges of function spaces have been studied by Xu in [60] and by Andersson in [5].

The above definition for 2-microlocal weight sequences was presented by Besov in [8] and also in [30] by Kempka.

A different line of study for spaces of variable smoothness—using different methods—are the spaces of generalized smoothness introduced by Goldman and Kalyabin in [20, 21, 26] and [27]. A systematic treatment of these spaces based on differences has been given by Goldman in [22], see also the survey [29] and references therein.

Later on, spaces of generalized smoothness appeared in interpolation theory and have been investigated in [10, 36] and [39]. For further information on these spaces see the survey paper [19] where also a characterization by atoms and local means for these spaces is given.

From the definition of admissible sequences, d ₁ σ _j ≤σ _j+1≤d ₂ σ _j , it follows directly that the spaces of generalized smoothness $B^{(\sigma_{j})}_{p,q}(\mathbb{R}^{n})$ and $F^{(\sigma _{j})}_{p,q}(\mathbb{R}^{n})$ of Farkas and Leopold [19] and $B^{(s,\Psi)}_{p,q}(\mathbb{R}^{n})$ and $F^{(s,\Psi )}_{p,q}(\mathbb{R}^{n})$ from Moura [39] are a special subclass of 2-microlocal function spaces with $2^{\alpha_{1}}=d_{1}$, $2^{\alpha_{2}}=d_{2}$ and α=0.

In a different approach Schneider in [48] studied spaces of varying smoothness. Here the smoothness at a point gets determined by a global smoothness s ₀∈ℝ and a local smoothness function s(⋅). These spaces can not be incorporated into the scale of 2-microlocal function spaces, but there exist some embeddings.

Remark 2

Surprisingly, these 2-microlocal weight sequences are directly connected to variable smoothness functions s:ℝⁿ→ℝ if we set

(4)

If $s\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$ (which is the standard condition on s(⋅)), then $\boldsymbol{w}=(w_{j}(x))_{j\in\mathbb{N}_{0}}=(2^{js(x)})_{j\in \mathbb{N}_{0}}$ belongs to $\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$ with α ₁=s ⁻ and α ₂=s ⁺. For the third index α we use Lemma 19 with m=0 and obtain α=c _log(s), where c _log(s) is the constant for s(⋅) from (2). That means that spaces of variable smoothness from Definition 3 are a special case of 2-microlocal function spaces from Definition 5. Both types of function spaces are very closely connected and the properties used in the proofs are either

(5)

for |x−y|≤c2^−k. This property follows directly either from the definition of $s\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$ or from Definition 4.

Nevertheless there exist examples of admissible weight sequences which can not be expressed in terms of variable smoothness functions. For example the important and well studied case of the weight sequence w from (3) can not be expressed via (4) if s′≠0. Another example are the spaces of generalized smoothness which can not be identified as spaces of variable smoothness.

Since spaces of variable smoothness are included in the scale of 2-microlocal function spaces all special cases of the previous subsection can be identified in the definition of 2-microlocal spaces.

Although the 2-microlocal spaces include the scales of spaces of variable smoothness, we will give some of our proofs in the notation of variable smoothness, since this notation is more common. We will then reformulate the results in terms of 2-microlocal spaces, the proof works then very similar; we just have to use (5).

3 Local Means Characterization

The main result of this section is the local means characterization of the spaces $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$. For the spaces $F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ there already exists a local means characterization [30, Corollary 4.7]. We shall first give the full proof for the 2-microlocal spaces and later on (in Sect. 3.2) we restate the result also for spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})$.

The crucial tool will be the Peetre maximal operator, as defined by Peetre in [42]. The operator assigns to each system $(\Psi_{k})_{k\in\mathbb{N}_{0}}\subset\mathcal{S}(\mathbb {R}^{n})$, to each distribution $f\in\mathcal{S}'(\mathbb {R}^{n})$ and to each number a>0 the following quantities

(6)

We start with two given functions $\psi_{0},\psi_{1}\in\mathcal{S}(\mathbb{R}^{n})$. We define

Furthermore, for all j∈ℕ₀ we write $\Psi_{j}=\hat{\psi_{j}}$. The main theorem of this section reads as follows.

Theorem 6

Let $\boldsymbol{w}=(w_{k})_{k\in\mathbb{N}_{0}}\in\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$, $p,q\in\mathcal{P}^{\log}(\mathbb {R}^{n})$ and let a>0, R∈ℕ₀ with R>α ₂. Further, let ψ ₀,ψ ₁ belong to $\mathcal{S}(\mathbb {R}^{n})$ with

(7)

and

(8)

(9)

for some ε>0. For $a>\frac{n+c_{\mathrm{log}}(1/q)}{p^{-}}+\alpha$ and all $f\in\mathcal{S}'(\mathbb{R}^{n})$ we have

Remark 3

• (i) The proof relies on [46] and will be shifted to the next section. Moreover, Theorem 6 shows that the definition of the 2-microlocal spaces of variable integrability is independent of the resolution of unity used in the Definition 5.

• (ii) The conditions (7) are usually called moment conditions while (8) and (9) are the so called Tauberian conditions.

• (iii) If R=0, then there are no moment conditions (7) on ψ ₁.

• (iv) The notation c _log(1/q) stands for the constant from (2) with 1/q(⋅).

Next we reformulate the abstract Theorem 6 in the sense of classical local means (see Sects. 2.4.6 and 2.5.3 in [52]). Since the proof is the same as the one from Theorem 2.4 in [30] we just state the result.

Corollary 1

There exist functions $k_{0},k\in\mathcal{S}(\mathbb{R}^{n})$ with $\operatorname{supp}k_{0},\operatorname{supp}k\subset\{x\in \mathbb{R}^{n}:|x|<1\}$ and $D^{\beta}\hat{k}(0)=0$ for all 0≤|β|<α ₂ such that for all $f\in\mathcal{S}'(\mathbb{R}^{n})$

is an equivalent norm on $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})$.

The building blocks get calculated by

and similarly for k ₀(1,f)(x).

A similar characterization for $F^{\boldsymbol{w}}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})$ and details how these functions $k_{0},k\in\mathcal{S}(\mathbb{R}^{n})$ can be constructed can be found in [30].

3.1 Proof of Local Means

The proof of Theorem 6 is divided into three parts. The next section is devoted to some technical lemmas needed later. Section 3.1.2 is devoted to the proof of Theorem 12, which gives an inequality between different Peetre maximal operators. Finally, Sect. 3.1.3 proves the boundedness of the Peetre maximal operator in Theorem 13. These two theorems combined give immediately the proof of Theorem 6.

3.1.1 Helpful Lemmas

Before proving the local means characterization we recall some technical lemmas, which appeared in the paper of Rychkov [46]. For some of them we need adapted versions to our situation.

The first lemma describes the use of the so called moment conditions.

Lemma 7

([46], Lemma 1)

Let $g,h\in\mathcal{S}(\mathbb{R}^{n})$ and let M∈ℕ₀. Suppose that

Then for each N∈ℕ₀ there is a constant C _N such that

where g _t (x)=t ⁻ⁿ g(x/t).

The next lemma is a discrete convolution inequality. We formulate it in a rather abstract notation and point out later on the conclusions we need.

Lemma 8

Let $X\subset\{(f_{k})_{k\in\mathbb{Z}}:f_{k}:\mathbb{R}^{n}\to[-\infty ,\infty]\ \mathit{measurable}\}$ be a quasi-Banach space of sequences of measurable functions. Further we assume that its quasi-norm is shift-invariant, i.e. it satisfies

For a sequence of non-negative functions (g _k ) _k∈ℤ∈X and δ>0 we denote

Then there exists a constant c>0 depending only on δ and X such that for every sequence (g _k ) _k∈ℤ

Proof

Since X is a quasi-Banach space, there exists a r>0 such that ∥⋅|X∥ is equivalent to some r-norm, cf. [6, 43]. We have then the following

Now taking the power 1/r yields the desired estimate. □

The spaces L _p(⋅)(ℓ _q(⋅)) and ℓ _q(⋅)(L _p(⋅)) are quasi-Banach spaces which fulfill the conditions of Lemma 8. Therefore, we obtain the following

Lemma 9

Let $p,q\in\mathcal{P}(\mathbb{R}^{n})$ and δ>0. Let (g _k ) _k∈ℤ be a sequence of non-negative measurable functions on ℝⁿ and denote

Then there exist a constants C ₁,C ₂>0, depending on p(⋅),q(⋅) and δ, such that

Remark 4

Of course, Lemma 9 holds true also if the indices k and ν run only over natural numbers.

Since the maximal operator is in general not bounded on ℓ _q(⋅)(L _p(⋅)) (see [1, Example 4.1]) we need a replacement for that. It turned out that a convolution with radial decreasing functions fits very well into the scheme. A careful evaluation of the proof in [1, Lemma 4.7] together with Lemma 19 gives us the following convolution inequality.

Lemma 10

Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with p(⋅)≥1 and let η _ν,m (x)=2^nν(1+2^ν|x|)^−m. For all m>n+c _log(1/q) there exists a constant c>0 such that for all sequences $(f_{j})_{j\in\mathbb{N}_{0}}\in{\ell_{q(\cdot)}(L_{p(\cdot)})}$ it holds

The last technical lemma is overtaken literally from [46].

Lemma 11

([46], Lemma 3)

Let 0<r≤1 and let $(\gamma_{\nu})_{\nu\in\mathbb{N}_{0}}$, $(\beta_{\nu})_{\nu\in\mathbb{N}_{0}}$ be two sequences taking values in (0,∞). Assume that for some N ⁰∈ℕ₀,

(10)

Furthermore, we assume that for any N∈ℕ

holds, then for any N∈ℕ

holds with the same constants C _N .

3.1.2 Comparison of Different Peetre Maximal Operators

In this subsection we present an inequality between different Peetre maximal operators. Let us recall the notation given before Theorem 6. For two given functions $\psi_{0},\psi_{1}\in\mathcal{S}(\mathbb {R}^{n})$ we define

Furthermore, for all j∈ℕ₀ we write $\Psi_{j}=\hat{\psi _{j}}$ and in an analogous manner we define Φ _j from two starting functions $\phi_{0},\phi_{1}\in\mathcal{S}(\mathbb{R}^{n})$. Using this notation we are ready to formulate the theorem.

Theorem 12

Let $\boldsymbol{w}=(w_{j})_{j\in\mathbb{N}_{0}}\in\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$, $p,q\in\mathcal{P}(\mathbb{R}^{n})$ and a>0. Moreover, let R∈ℕ₀ with R>α ₂,

(11)

and for some ε>0

(12)

(13)

then

holds for every $f\in\mathcal{S}'(\mathbb{R}^{n})$.

Remark 5

Observe that there are no restrictions on a>0 and $p,q\in\mathcal {P}(\mathbb{R}^{n})$ in the theorem above.

Proof

We have the fixed resolution of unity from Definition 1 and define the sequence of functions $(\lambda_{j})_{j\in\mathbb{N}_{0}}$ by

It follows from the Tauberian conditions (12) and (13) that they satisfy

$$\sum_{j=0}^\infty\lambda_j(x)\phi_j(x)=1,\quad x\in\mathbb{R}^n, $$

(14)

$$\lambda_j(x)=\lambda_1\bigl(2^{-j+1}x\bigr),\quad x\in\mathbb{R}^n,\ j\in\mathbb{N}, $$

(15)

and

$$\operatorname{supp}\lambda_0\subset\bigl\{x\in\mathbb {R}^n:|x|\leq\varepsilon \bigr\}\quad\text{and}\quad\operatorname{supp}\lambda_1\subset \bigl\{x\in \mathbb{R}^n:\varepsilon/2\leq|x|\leq2\varepsilon\bigr\}. $$

(16)

Furthermore, we denote $\Lambda_{k}=\hat{\lambda_{k}}$ for k∈ℕ₀ and obtain together with (14) the following identities (convergence in $\mathcal{S}'(\mathbb{R}^{n})$)

(17)

We have

(18)

where

$$I_{\nu,k}:=\int_{\mathbb{R}^n}\bigl|(\Psi_\nu\ast\Lambda_k) (z)\bigr|\bigl(1+\bigl|2^kz\bigr|^a\bigr)dz.$$

According to Lemma 7 we get

(19)

Namely, we have for 1≤k<ν with the change of variables 2^k z↦z

Similarly, we get for 1≤ν<k with the substitution 2^ν z↦z

M can be taken arbitrarily large because Λ₁ has infinitely many vanishing moments. Taking M=2a+|α ₁|+1 we derive (19) for the cases k,ν≥1 with k≠ν. The missing cases can be treated separately in an analogous manner. The needed moment conditions are always satisfied by (11) and (16). The case k=ν=0 is covered by the constant c in (19).

Furthermore, we have

We put this into (18) and get

Multiplying both sides with w _ν (x) and using

leads us to

This inequality together with (17) gives for δ:=min(1,R−α ₂)>0

Taking the ℓ _q(⋅)(L _p(⋅)) norm and using Lemma 9 yields immediately the desired result. □

3.1.3 Boundedness of the Peetre Maximal Operator

We will present a theorem which describes the boundedness of the Peetre maximal operator. We use the same notation introduced at the beginning of the last subsection. Especially, we have the functions $\psi_{k}\in\mathcal{S}(\mathbb{R}^{n})$ and $\Psi_{k}=\hat{\psi}_{k}\in\mathcal{S}(\mathbb{R}^{n})$ for all k∈ℕ₀.

Theorem 13

Let $(w_{k})_{k\in\mathbb{N}_{0}}\in\mathcal{W}^{\alpha}_{\alpha _{1},\alpha_{2}}$, a>0 and $p,q\in\mathcal{P}^{\log}(\mathbb {R}^{n})$. For some ε>0 we assume $\psi_{0},\psi_{1}\in \mathcal{S}(\mathbb{R}^{n})$ with

For $a>\frac{n+c_{\log}(1/q)}{p^{-}}+\alpha$

holds for all $f\in\mathcal{S}'(\mathbb{R}^{n})$.

Remark 6

Observe that in the theorem above no moment conditions on ψ ₁ are stated but this time there are restrictions on a and p(⋅),q(⋅).

Proof

As in the last proof we find the functions $(\lambda_{j})_{j\in\mathbb {N}_{0}}$ with the properties (15), (16) and

Instead of (17) we get the identity

(20)

where

The Ψ _k,ν are defined similarly. For k≥1 and ν∈ℕ₀ we have Ψ _k,ν =Ψ _k+ν and with the notation

we get ψ _k (2^−ν x)ψ _ν (x)=σ _k,ν (x)ψ _k+ν (x). Hence, we can rewrite (20) as

(21)

For k≥1 we get from Lemma 7

(22)

for all k,ν∈ℕ₀ and arbitrary large M∈ℕ. For k=0 we get the estimate (22) by using Lemma 7 with M=0. This together with (21) gives us

(23)

For fixed r∈(0,1] we divide both sides of (23) by (1+|2^ν(x−y)|^a) and we take the supremum with respect to y∈ℝⁿ. Using the inequalities

and

$$\frac{(1+|2^{k+\nu}(x-z)|^a)^{1-r}}{(1+|2^{\nu}(x-z)|^a)}\leq\frac{2^{ka}}{(1+|2^{k+\nu}(x-z)|^a)^{r}},$$

we get

(24)

Now, we apply Lemma 11 with

N=M+n−a, C _N =C _M +n−a and N ⁰ in (10) equals the order of the distribution $f\in\mathcal{S}'(\mathbb{R}^{n})$.

By Lemma 11 we obtain for every N∈ℕ, x∈ℝⁿ and ν∈ℕ₀

(25)

provided that $(\Psi_{\nu}^{*}f)_{a}(x)<\infty$.

Since $f\in\mathcal{S}'(\mathbb{R}^{n})$, we see that $(\Psi_{\nu}^{*}f)_{a}(x)<\infty$ for all x∈ℝⁿ and all ν∈ℕ₀ at least if a>N ⁰, where N ⁰ is the order of the distribution. Thus we have (25) with C _N independent of $f\in\mathcal {S}'(\mathbb{R}^{n})$ for a≥N ⁰ and therefore with C _N =C _N,f for all a>0 (the right side of (25) decreases as a increases). One can easily check that (25) with C _N =C _N,f implies that if for some a>0 the right side of (25) is finite, then $(\Psi_{\nu}^{*}f)_{a}(x)<\infty$. Now, repeating the above argument resurrects the independence of C _N . If the right side of (25) is infinite, there is nothing to prove. More exhaustive arguments of this type have been used in [54] and [47].

We point out that (25) holds also for r>1, where the proof is much simpler. We only have to take (23) with a+n instead of a, divide both sides by (1+|2^ν(x−y)|^a) and apply Hölder’s inequality with respect to k and then z.

Multiplying (25) by w _ν (x)^r we derive with the properties of our weight sequence

(26)

for all x∈ℝⁿ, ν∈ℕ₀ and all N∈ℕ.

Now, we choose r=p ⁻ and we have r(a−α)>n+c _log(1/q). We denote $g^{r}_{k+\nu}(z)=|(\Psi_{k+\nu}\ast f)(z)|^{r}w_{k+\nu}(z)^{r}$ then we can rewrite (26) by

(27)

For fixed N>0 with δ=N+α ₁>0 we apply the $\ell_{\frac {q(\cdot)}{r}}(L_{\frac{p(\cdot)}{r}})$ norm and derive from (27)

Now application of Lemma 9 and Lemma 10 (r(a−α)>n+c _log(1/q)) on the formula above give us

which proves the theorem. □

3.2 Local Means Characterization of $B^{s(\cdot)}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{s(\cdot )}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$

In this section we reformulate the local means characterization for $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ from above and for $F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ from Corollary 4.7 in [30] in terms of variable smoothness. If we have a variable smoothness function $s\in C_{\mathit{loc}}^{\log}(\mathbb{R}^{n})$ given, then w _j (x)=2^js(x) defines an admissible weight sequence $\boldsymbol{w}\in\mathcal{W}^{\alpha}_{\alpha _{1},\alpha_{2}}$ with α ₁=s ⁻, α ₂=s ⁺ and α=c _log(s), cf. Remark 2. Here, we denote by c _log(s) the constant in (2) for s(⋅).

Theorem 14

Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ (p ⁺,q ⁺<∞ in the F-case) and $s\in C_{\mathit{loc}}^{\log }(\mathbb{R}^{n})$. Further let a>0, R∈ℕ₀ with R>s ⁺ and let ψ ₀,ψ ₁ belong to $\mathcal{S}(\mathbb {R}^{n})$ with

and

for some ε>0.

• 1. For $a>\frac{n+c_{\log}(1/q)}{p^{-}}+c_{\log}(s)$ and all $f\in \mathcal{S}'(\mathbb{R}^{n})$ we have

  

• 2. For $a>\frac{n}{\min(p^{-},q^{-})}+c_{\log}(s)$ and all $f\in \mathcal{S}'(\mathbb{R}^{n})$ we have

  

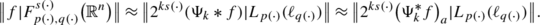
Remark 7

During the referee process of this work, there appeared in [18] a characterization by local means and a characterization by atoms for $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$. The author moved the smoothness sequence 2^ks(⋅) into the Peetre maximal operator (6) and modified it to

For this modified Peetre maximal operator he obtained in [18, Theorem 2] an equivalence of the norms similar to our Theorem 14 for $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$. The advantage of his method is that the condition on a>0 weakens to $a>\frac{n}{p^{-}}$.

4 Ball Means of Differences

This section is devoted to the characterization of Besov and Triebel-Lizorkin spaces $B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ by ball means of differences. In the case of constant indices p,q and s, this is a classical part of the theory of function spaces. We refer especially to [51, Sect. 2.5] and references given there. It turns out that, under the restriction

$$ s>\sigma_{p}=n \biggl(\frac{1}{\min(p,1)}-1\biggr)$$

(28)

in the B-case and

$$ s>\sigma_{p,q}=n \biggl(\frac{1}{\min(p,q,1)}-1\biggr)$$

(29)

in the F-case, Besov and Triebel-Lizorkin spaces with constant indices may be characterized by expressions involving only the differences of the function values without any use of Fourier analysis. This was complemented in [49] and [50] by showing that these conditions are also indispensable. Of course, we are limited by (28) and (29) also in the case of variable exponents.

The characterization by (local means of) differences for 2-microlocal spaces with constant p,q>1 was given by Besov [8] and a similar characterization for Besov spaces with p=q=∞ and the special weight sequence from (3) was given by Seuret and Levy Véhél in [34]. We refer to [19] and [28] for the treatment of spaces of generalized smoothness.

Our approach follows essentially [51] with some modifications described in [53]. The main obstacle on this way is the unboundedness of the maximal operator in the frame of L _p(⋅)(ℓ _q(⋅)) and ℓ _q(⋅)(L _p(⋅)) spaces, cf. [16, Sect. 5] and [1, Example 4.1]. This is circumvented by the use of convolution with radial functions in the sense of [16] and [1] together with a certain bootstrapping argument, which shall be described in detail below.

The plan of this part of the work is as follows. First we give in Sect. 4.1 the necessary notation. We state the main assertions of this part in Sect. 4.2. Then we prove in Sect. 4.3 a certain preliminary version of these assertions. In Sect. 4.4 we prove a characterization by ball means of differences for spaces with q∈(0,∞] constant (where the maximal operator is bounded) and use this together with our preliminary characterization from Sect. 4.3 to conclude the proof. Finally, in Sect. 4.5 we will present the ball means of differences characterization also for the 2-microlocal function spaces $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and $F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$ and in Sect. 4.6 we present separately some useful Lemmas, not to disturb the main proofs of this part.

4.1 Notation

Let f be a function on ℝⁿ and let h∈ℝⁿ. Then we define

$$\Delta^1_h f(x)=f(x+h)-f(x),\quad x\in\mathbb{R}^n.$$

The higher order differences are defined inductively by

$$\Delta^M_h f(x)=\Delta^1_h \bigl(\Delta^{M-1}_h f\bigr)(x), \quad M=2,3,\dots $$

This definition also allows a direct formula

$$ \Delta^M_h f(x):=\sum_{j=0}^M (-1)^j\binom{M}{j}f\bigl(x+(M-j)h\bigr).$$

(30)

By ball means of differences we mean the quantity

$$d^M_{t}f(x)=t^{-n}\int_{|h|\le t}\bigl|\Delta^M_{h}f(x)\bigr| dh =\int_B \bigl|\Delta^M_{th}f(x)\bigr|dh,$$

where B={y∈ℝⁿ:|y|<1} is the unit ball of ℝⁿ, t>0 is a real number and M is a natural number.

Let us now introduce the (quasi-)norms, which shall be the main subject of our study. We define

(31)

and its partially discretized counterpart

The norm $\|f|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb {R}^{n})\|^{**}$ admits a direct counterpart also for Besov spaces, namely

(32)

Finally, we shall use as a technical tool also the analogues of (31)–(32) with the integration over t restricted to 0<t<1. This leads to the following expressions

4.2 Main Theorem

Using the notation introduced above, we may now state the main result of this section.

Theorem 15

(i) Let $p,q\in\mathcal{P}^{\log}(\mathbb {R}^{n})$ with p ⁺,q ⁺<∞ and $s\in C^{\mathrm{log}}_{\mathit{loc}}(\mathbb{R}^{n})$. Let M∈ℕ with M>s ⁺ and let

$$ s^->\sigma_{p^-,q^-}\cdot\biggl[1+\frac{c_{\mathrm{log}}(s)}{n}\cdot\min\bigl(p^-,q^-\bigr) \biggr].$$

(33)

Then

$$F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr )=\bigl\{f\in L_{p(\cdot)}\bigl(\mathbb{R}^n\bigr)\cap\mathcal {S}'\bigl(\mathbb{R}^n\bigr):\bigl\|f|F^{s(\cdot)}_{{p(\cdot )},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|^*<\infty\bigr\}$$

and $\|\cdot|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb {R}^{n})\|$ and $\|\cdot|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})\|^{*}$ are equivalent on $F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$. The same holds for $\|f|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})\|^{**}$.

(ii) Let $p,q\in\mathcal{P}^{\log}(\mathbb {R}^{n})$ and $s\in C^{\mathrm{log}}_{\mathit{loc}}(\mathbb{R}^{n})$. Let M∈ℕ with M>s ⁺ and let

$$ s^->\sigma_{p^-}\cdot\biggl[1+\frac{c_{\mathrm{log}}(1/q)}{n}+\frac{c_{\mathrm{log}}(s)}{n}\cdot p^- \biggr].$$

(34)

Then

$$B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr )=\bigl\{f\in L_{p(\cdot)}\bigl(\mathbb{R}^n\bigr)\cap\mathcal {S}'\bigl(\mathbb{R}^n\bigr):\bigl\|f|B^{s(\cdot)}_{{p(\cdot )},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|^{**}<\infty\bigr\}$$

and $\|\cdot|B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}(\mathbb {R}^{n})\|$ and $\|\cdot|B^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})\|^{**}$ are equivalent on $B^{s(\cdot )}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$.

Remark 8

Let us comment on the rather technical conditions (33) and (34).

• If min(p ⁻,q ⁻)≥1, then (33) becomes just s ⁻>0. Furthermore, if p, q and s are constant functions, then (33) coincides with (29).

• If p ⁻≥1, then (34) reduces also to s ⁻>0 and in the case of constant exponents we again recover (28).

As indicated already above, the proof is divided into several parts.

4.3 Preliminary Version of Theorem 15

This subsection contains a preliminary version of Theorem 15 (Lemma 16). Its proof represents the heart of the proof of Theorem 15. For better lucidity, it is again divided into more parts.

Lemma 16

Under the conditions of Theorem 15, the following estimates hold for all $f\in L_{p(\cdot)}(\mathbb{R}^{n})\cap\mathcal{S}'(\mathbb{R}^{n})$:

(35)

(36)

(37)

(38)

Proof

Part I. First we prove (35) and (36). We discretize the inner part of ∥⋅∥^∗ and obtain

(39)

If 2^−k−1≤t≤2^−k, then 2^ks(x)q(x)≤t ^−s(x)q(x)≤2^{(k+1)s(x)q(x)} and

$$2^{kn}\int_{2^{-(k+1)}B}\bigl|\Delta_\varkappa^M f(x)\bigr|d\varkappa\lesssim t^{-n}\int_{tB}\bigl|\Delta_\varkappa^M f(x)\bigr|d\varkappa\lesssim 2^{(k+1)n}\int_{2^{-k}B}\bigl|\Delta_\varkappa^M f(x)\bigr|d\varkappa.$$

Plugging these estimates into (39), we may further estimate

The estimate from below follows in the same manner. Finally, the proof of (36) is almost the same.

Part II. This part is devoted to the proof of the left hand side of (37). It is divided into several steps to make the presentation clearer.

Step 1. First, we point out that the estimate

$$\bigl\Vert{f}\vert{L_{p(\cdot)} \bigl(\mathbb{R}^n\bigr)}\bigr\Vert\lesssim \bigl\Vert{f}\vert{B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl (\mathbb{R}^n\bigr)}\bigr\Vert $$

follows from the characterization of $B^{s(\cdot)}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})$ in terms of Nikol’skij representations (cf. Theorem 8.1 of [1]). We refer also to Remark 2.5.3/1 in [51]. The extension to F-spaces is then given by the simple embedding

$$\bigl\Vert{f}\vert{L_{p(\cdot)} \bigl(\mathbb{R}^n\bigr)}\bigr\Vert\lesssim \bigl\Vert{f}\vert{B^{s(\cdot)-\varepsilon}_{p(\cdot),p(\cdot)}\bigl(\mathbb{R}^n\bigr)}\bigr\Vert\lesssim \bigl\Vert{f}\vert{F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl (\mathbb{R}^n\bigr)}\bigr\Vert $$

with ε>0 chosen small enough.

Step 2. Let $(\varphi_{j})_{j\in\mathbb{N}_{0}}$ be the functions used in Definition 3. We use the decomposition

$$f=\sum_{l=-\infty}^\infty f_{(k+l)},\quad k\in\mathbb{Z},$$

where $f_{(k+l)}=(\varphi_{k+l}\hat{f})^{\vee}$, or =0 if k+l<0 and get

If q(x)≤1 then we proceed further

If q(x)>1, we use Minkowski’s inequality

We split in both cases

$$ \sum_{l=-\infty}^\infty \cdots=I+II=\sum_{l=-\infty}^0 \cdots+ \sum _{l=1}^\infty\cdots $$

(40)

Step 3. We estimate the first summand with l≤0.

We use Lemma 22 in the form

$$\bigl|\Delta^M_h f_{(k+l)}(x)\bigr|\le C\max \bigl(1,|bh|^a\bigr)\cdot\min \bigl(1,|bh|^M\bigr)P_{b,a}f_{(k+l)}(x),$$

where a>0 is arbitrary, b=2^k+l and

$$P_{b,a}f(x)=\sup_{z\in\mathbb{R}^n}\frac{|f(x-z)|}{1+|bz|^a}.$$

Furthermore, we use this estimate with 2^−k h instead of h. We obtain

(41)

The last inequality follows from max(1,|b2^−k h|^a)≤1 (recall that l≤0 and |h|≤1) and min(1,|b2^−k h|^M)≤2^lM.

If q(x)≤1, we estimate the first sum in (40)

where the last estimate makes use of M>s ⁺, q ⁻>0 and the fact that f _(k+l)=0 for k+l<0.

If q(x)>1, we proceed in a similar way to obtain

We have used in the last estimate again M>s ⁺ and the definition of f _(k+l).

Hence,

$$I^{1/q(x)}\lesssim \Biggl(\sum_{k=0}^\infty 2^{ks(x)q(x)}P^{q(x)}_{2^{k},a}f_{(k)}(x) \Biggr)^{1/q(x)}$$

holds for all x∈ℝⁿ.

Finally, we obtain

(42)

where we used the boundedness of Peetre maximal operator as described in Theorem 14 for a>0 large enough.

Step 4. We estimate the second summand in (40) with l>0. If min(p ⁻,q ⁻)>1, then we put λ=1. Otherwise we choose real parameters 0<λ<min(p ⁻,q ⁻) and a>0 such that

$$a>\frac{n}{\min(p^-,q^-)}+c_{\mathrm{log}}(s)$$

and a(1−λ)<s ⁻. Due to (33), this is always possible.

We start again with estimates of the ball means of differences. We use Lemma 22 and (30) to obtain

(43)

where the constants c _j,M are given by (30).

We shall deal in detail only with the term with j=1. The term with j=0 is much simpler to handle (as there the integration over h∈B immediately disappears) and this case reduces essentially to Hölder’s inequality and boundedness of the Peetre maximal operator. The terms with 2≤j≤M may be handled in the same way as the one with j=1.

We use Lemma 20 with r=λ in the form

$$\bigl|f_{(k+l)}(y)\bigr|^\lambda\lesssim \bigl(\eta_{k+l,2m}*|f_{(k+l)}|^\lambda\bigr)(y),$$

with m>max(n,c _log(s)), Lemmas 23 and 19 to get

(44)

We insert (44) into (43) and arrive at

(45)

If q(x)>1, we proceed further with the use of Hölder’s inequality

If q(x)≤1, we obtain in a similar way

and further (with use of Lemma 24)

If we denote

$$F(x):= \Biggl(\sum_{k=0}^\infty \bigl(2^{ks(x)}P_{2^{k},a}f_{(k)}(x) \bigr)^{q(x)}\Biggr)^{1/q(x)},\quad x\in\mathbb{R}^n$$

and

$$B_{k+l}(x):=\bigl|2^{(k+l)s(x)}f_{(k+l)}(x)\bigr|,\quad x\in\mathbb{R}^n$$

we get for δ:=−1/2⋅(a(1−λ)−s ⁻)>0

$$ II^{1/q(x)}\lesssim F(x)^{1-\lambda}\cdot\sum _{l=1}^\infty2^{-l\delta} \Biggl(\sum _{k=0}^\infty\bigl(\eta_{k,m}*B_{k+l}^\lambda \bigr)^{q(x)/\lambda}(x) \Biggr)^{\lambda/q(x)}.$$

(46)

We use $\|F_{1}^{1-\lambda}F_{2}^{\lambda}\|_{p(\cdot)}\le2\|F_{1}\|_{p(\cdot)}^{1-\lambda}\|F_{2}\|_{p(\cdot)}^{\lambda}$, cf. [17, Lemma 3.2.20], and suppose that the L _p(⋅)-(quasi-)norm is equivalent to an r-norm with 0<r≤1. Together with Lemma 21 we arrive at

(47)

which finishes the proof.

Part III. We prove the right hand side of (37). We follow again essentially [51, Sect. 2.5.9] with some modifications as presented in [53]. Roughly speaking, compared to the case of constant exponents, only minor modifications are necessary.

Let $\psi\in C^{\infty}_{0}(\mathbb{R}^{n})$ with ψ(x)=1, |x|≤1 and ψ(x)=0, |x|>3/2. We define

$$\varphi_0(x)=(-1)^{M+1}\sum_{\mu=0}^{M-1}(-1)^\mu\binom{M}{\mu }\psi \bigl((M-\mu)x\bigr).$$

It follows that $\varphi_{0}\in C^{\infty}_{0}(\mathbb{R}^{n})$ with φ(x)=0, |x|>3/2 and φ(x)=1, |x|<1/M. We also put φ _j (x)=φ ₀(2^−j x)−φ ₀(2^−j+1 x) for j≥1. This is the decomposition of unity we used in the definition of $\|f|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot )}}(\mathbb{R}^{n})\|$, cf. Definition 3. Recall that due to [16] and [30], this (quasi-)norm of $\|f|F^{s(\cdot )}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})\|$ does not depend on the choice of the decomposition of unity.

We observe that

$$\varphi_0(x)=(-1)^{M+1}\bigl(\Delta_x^M\psi(0)-(-1)^M\bigr),$$

and

(48)

Furthermore, a straightforward calculation shows that

(49)

holds for every j∈ℕ₀. We denote $g=\hat{\psi}\in \mathcal{S}(\mathbb{R}^{n})$ and obtain

(50)

The rest of this part consists essentially of using the property of $g\in\mathcal{S}(\mathbb{R}^{n})$ to come from (50) to ∥⋅∥^∗∗.

We denote

$$I_0:=B, \qquad I_u:=2^uB\setminus2^{u-1}B,\quad u\in\mathbb{N}$$

and use |g(h)|≤c2^−ur,h∈I _u with r taken large enough (recall that $g\in\mathcal{S}(\mathbb{R}^{n})$) and estimate

(51)

We put

$$G_j(x):=2^{js(x)}\bigl| \bigl(\mathcal{F}^{-1}\bigl(\Delta_{2^{-j}\xi}^M\psi (0)\bigr)\mathcal{F}f\bigr)(x)\bigr|,\quad j\in\mathbb{N}_0$$

and

$$g_k(x):=2^{ks(x)}2^{kn}\int_{2^{-k}B} \bigl|\Delta^M_{h}f(x)\bigr|dh,\quad k\in \mathbb{Z}.$$

Using (48), (49) and (51), we obtain the estimate

(52)

Choosing r>s ⁺+n and applying Lemma 9 then finishes the proof.

Part IV. The proof of the left hand side of (38) follows in the same manner as in Part II. We shall describe the necessary modifications. First, let us mention, that the condition q ⁺<∞ was used only in the application of Lemma 21. In the rest of the arguments also the case q(x)=∞ may be incorporated with only slight change of notation.

Let us put

$$f^{(k)}(x):=2^{ks(x)}\int_B \bigl|\Delta^M_{2^{-k}h}f(x)\bigr|dh, \quad x\in \mathbb{R}^n.$$

We obtain (in analogue to (40))

We estimate the first sum using (41) and get

$$f^{(k),I}\lesssim\sum_{l=-\infty}^0 2^{l(M-s^+)}g^1_{k+l}=\sum _{u=0}^k 2^{(u-k)(M-s^+)}g^1_u\le\sum_{u=0}^\infty2^{-|u-k|(M-s^+)}g^1_u,$$

where $g^{1}_{u}:=2^{us(x)}P_{2^{u},a}f_{(u)}(x)$. The application of Lemma 9 and Theorem 14 with a>0 large enough gives

To estimate f ^(k),II, we proceed as in the Step 4 of Part II. If p ⁻>1, we choose again λ=1, otherwise we take 0<λ<p ⁻ and

$$a>\frac{n+c_{\mathrm{log}}(1/q)}{p^-}+c_{\mathrm{log}}(s)$$

such that a(1−λ)<s ⁻. This is possible due to (34).

We use (44) with m>max(n+c _log(1/q),c _log(s)) to get

(53)

where $g^{2}_{k+l}(x):=|2^{(k+l)s(x)}f_{(k+l)}(x)|$. We take the ℓ _q(⋅)(L _p(⋅)) (quasi-)norm of the last expression—and assume that it is equivalent to some r-norm. This gives for δ:=s ⁻−a(1−λ)>0 the following estimate

(54)

We have used Lemma 10 and Lemma 25.

Part V. The right hand side inequality of (38) follows also along the same line as in Part III. We just combine (52) with the choice r>s ⁺+n and apply Lemma 9. □

4.4 Proof of Theorem 15

This section is devoted to the proof of Theorem 15. We start with the case of constant q. In that case, the usual Hardy-Littlewood maximal operator

$$Mf(x)=\sup_{r>0}\frac{1}{|B(x,r)|}\int_{B(x,r)}\bigl|f(y)\bigr|dy$$

is bounded on ℓ _q (L _p(⋅)) and L _p(⋅)(ℓ _q ). Indeed, the following lemma is a consequence of [12] and [17, Theorem 4.3.8].

Lemma 17

• (i) Let $p\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with 1<p ⁻≤p ⁺<∞ and 1<q<∞. Then

  $$\bigl\Vert{(M f_j)_{j=-\infty}^\infty}\vert{L_{p(\cdot)}(\ell _q)}\bigr\Vert\lesssim\bigl\Vert{(f_j)_{j=-\infty}^\infty}\vert {L_{p(\cdot)}(\ell_q)}\bigr\Vert $$

  for all $(f_{j})_{j=-\infty}^{\infty}\in L_{p(\cdot)}(\ell_{q})$.

• (ii) Let $p\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with p ⁻>1 and 0<q≤∞. Then

  $$\bigl\Vert{(M f_j)_{j=-\infty}^\infty}\vert{\ell_q(L_{p(\cdot )})}\bigr\Vert\lesssim\bigl\Vert{(f_j)_{j=-\infty}^\infty}\vert {\ell_q(L_{p(\cdot)})}\bigr\Vert $$

  for all $(f_{j})_{j=-\infty}^{\infty}\in\ell_{q}(L_{p(\cdot)})$.

Proof of Theorem 15

With the help of Lemma 17, we prove Theorem 15 for q constant. In view of Lemma 16, it is enough to prove

$$ \bigl\|f|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl (\mathbb{R}^n\bigr)\bigr\|^{**}\lesssim\bigl\|f|F^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|$$

(55)

and a corresponding analogue for the B-spaces.

Part I. In this part we point out the necessary modifications in the proof of Lemma 16 to obtain a characterization by ball means of differences for $B^{s(\cdot)}_{{p(\cdot)},q}(\mathbb {R}^{n})$ and $F^{s(\cdot)}_{{p(\cdot)},q}(\mathbb{R}^{n})$. The proof follows the scheme of Part II of the proof of Lemma 16. We start with $\sum_{k=-\infty}^{\infty}$ instead of $\sum_{k=0}^{\infty}$. With this modification the Steps 1–3 go through without any other changes and we obtain (42) again (just recall that f _(k)=0 if k<0).

Due to the boundedness of the maximal operator there is no need for the use of r-trick and convolution with η _ν,m . The analogue of (43), (44) and (45) now reads as follows:

where we used Hölder’s regularity of s(⋅), see (5). As a consequence, we obtain

$$II^{1/q(x)}\lesssim F(x)^{1-\lambda}\cdot\sum_{l=1}^\infty2^{-l\delta}\Biggl(\sum_{k=-l}^\infty\bigl(M B_{k+l}^\lambda\bigr)^{q(x)/\lambda}(x) \Biggr)^{\lambda/q(x)}$$

instead of (46). The rest then follows in the same manner with the help of Lemma 17 and the proof of (55) is finished.

The proof of

$$\bigl\|f|B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|^{**}\lesssim \bigl\|f|B^{s(\cdot)}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb {R}^n\bigr)\bigr\|$$

follows along the same lines. Especially, we get

instead of (53). The rest follows again by Lemma 17.

Part II. Finally, we present how the characterization for q constant can help us to improve on the case of variable exponent q(⋅).

In view of Lemma 16, it is enough to show that

But this is a consequence of

where ε>0 is small enough and we used the differences characterization for fixed q and a trivial embedding theorem.

The same arguments apply for the Besov spaces and the proof is finished. □

Remark 9

The somewhat complicated proof of Theorem 15 would work more direct and simpler if we could use versions of Lemmas 10 and 21 in (47) and (54) where the ℓ _q(⋅) summation runs over ν∈ℤ.

For Triebel-Lizorkin spaces there seems to exist such an extension [13], but for Besov spaces the proof of Lemma 10 in [1] seems to be to customized to the situation ν∈ℕ₀.

4.5 Ball Means of Differences for 2-Microlocal Spaces

As already remarked in Sect. 2.2 all the proofs for spaces of variable smoothness do also serve for 2-microlocal spaces. One just has to use the definition of admissible weight sequences and the property (5), see Remark 2.

First of all we give the notation for the (quasi-)norms. For simplicity we just use the discrete versions, although it is also possible to give continuous versions of 2-microlocal weights, see [55, Definition 4.1]. In analogy to the spaces of variable smoothness we introduce the following norms

and

$$\bigl\Vert{f}\vert{F^{\boldsymbol{w}}_{{p(\cdot )},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)}\bigr\Vert^{**}=\bigl \Vert{f}\vert{L_{p(\cdot)}\bigl(\mathbb{R}^n\bigr)}\bigr\Vert +\bigl\Vert{\bigl(w_k(x)d_{2^{-k}}^Mf(x) \bigr)_{k=-\infty}^\infty }\big\vert{{L_{p(\cdot)}(\ell_{q(\cdot)})}}\bigr\Vert.$$

Finally, the preceding calculations show that the following theorem is true.

Theorem 18

(i) Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with p ⁺,q ⁺<∞ and $\boldsymbol{w}\in\mathcal{W}^{\alpha}_{\alpha _{1},\alpha_{2}}$. Let M>α ₂ and

$$ \alpha_1>\sigma_{p^-,q^-}\cdot \biggl[1+\frac{\alpha}{n}\cdot\min\bigl(p^-,q^-\bigr) \biggr].$$

(56)

Then

$$F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr )= \bigl\{f\in L_{{p(\cdot)}}\bigl(\mathbb{R}^n\bigr):\bigl\|f|F^{\boldsymbol {w}}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|^{**}<\infty \bigr\}$$

and $\|\cdot|F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})\|$ and $\|\cdot|F^{\boldsymbol{w}}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})\|^{**}$ are equivalent on $F^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$.

(ii) Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ and $\boldsymbol{w}\in\mathcal{W}^{\alpha}_{\alpha_{1},\alpha_{2}}$. Let M>α ₂ and

$$ \alpha_1>\sigma_{p^-}\cdot \biggl[1+\frac{c_{\mathrm{log}}(1/q)}{n}+\frac{\alpha}{n}\cdot p^-\biggr].$$

(57)

Then

$$B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr )=\bigl\{f\in L_{{p(\cdot)}}\bigl(\mathbb{R}^n\bigr):\bigl\|f|B^{\boldsymbol {w}}_{{p(\cdot)},{q(\cdot)}}\bigl(\mathbb{R}^n\bigr)\bigr\|^{**}<\infty \bigr\}$$

and $\|\cdot|B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})\|$ and $\|\cdot|B^{\boldsymbol{w}}_{{p(\cdot )},{q(\cdot)}}(\mathbb{R}^{n})\|^{**}$ are equivalent on $B^{\boldsymbol{w}}_{{p(\cdot)},{q(\cdot)}}(\mathbb{R}^{n})$.

Remark 10

Again, if min(p ⁻,q ⁻)≥1 in the F-case, or p ⁻≥1 in the B-case, then the conditions (56) and (57) simplify to α ₁>0. In the case of constant exponents p,q we obtain similar results to [8] and [34].

4.6 Lemmas

The following lemma is a variant of Lemma 6.1 from [16].

Lemma 19

Let $s\in C^{\log}_{\mathit{loc}}(\mathbb{R}^{n})$ and let R≥c _log(s) , where c _log(s) is the constant from (2) for s(⋅). Then

$$2^{\nu s(x)}\eta_{\nu,m+R}(x-y)\le c\,2^{\nu s(y)}\eta_{\nu,m}(x-y)$$

holds for all x,y∈ℝⁿ and m∈ℕ₀.

Lemma 20

Let r>0, ν≥0 and m>n. Then there exists c>0, which depends only on m,n and r, such that for all g∈S′(ℝⁿ) with $\operatorname{supp}\hat{g}\subset\{\xi\in\mathbb{R}^{n}:|\xi |\le2^{\nu+1}\}$, we have

$$\bigl|g(x)\bigr|\le c \bigl(\eta_{\nu,m}*|g|^r(x)\bigr)^{1/r},\quad x\in\mathbb{R}^n.$$

The following lemma is the counterpart to Lemma 10 for Triebel-Lizorkin spaces.

Lemma 21

([16], Theorem 3.2)

Let $p,q\in\mathcal{P}^{\log}(\mathbb{R}^{n})$ with 1<p ⁻≤p ⁺<∞ and 1<q ⁻≤q ⁺<∞. Then the inequality

holds for every sequence $(f_{\nu})_{\nu\in\mathbb{N}_{0}}$ of $L_{1}^{loc}(\mathbb{R}^{n})$ functions and m>n.

The following lemma is well known (cf. [51]). We sketch its proof for the sake of completeness.

Lemma 22

Let a,b>0, M∈ℕ and h∈ℝⁿ. Let f∈S′(ℝⁿ) with $\operatorname{supp}\hat{f}\subset\{\xi\in \mathbb{R}^{n}:|\xi|\le b\}$. Then there is a constant C>0 independent of f,b and h, such that

$$\bigl|\Delta^M_h f(x)\bigr|\le C\max \bigl(1,|bh|^a\bigr)\cdot\min \bigl(1,|bh|^M\bigr)P_{b,a}f(x)$$

holds for every x∈ℝⁿ.

Proof

The estimate

holds for all the admissible parameters even without the assumption on $\hat {f}$.

Hence we need to prove only

$$ \bigl|\Delta^M_h f(x)\bigr|\le C\max \bigl(1,|bh|^a\bigr)\cdot|bh|^M\cdot P_{b,a}f(x).$$

(58)

Using the Taylor formula for the (analytic) function f, we obtain by direct calculation

If $\operatorname{supp}\hat{g}\subset\{\xi\in\mathbb{R}^{n}:|\xi|\le 1\}$, then this may be combined with the Nikol’skij inequality, cf. [51, Sect. 1.3.1], in the form

$$\sup_{|\alpha|=M}\sup_{z\in\mathbb{R}^n}\frac{|(D^\alpha g)(x-z)|}{1+|z|^a}\lesssim\sup_{z\in\mathbb{R}^n}\frac{|g(x-z)|}{1+|z|^a}$$

to obtain

$$ \bigl|\Delta^M_h g(x)\bigr|\le c'' |h|^M \max\bigl(1,|h|^a\bigr)\cdot\sup_{z\in\mathbb{R}^n}\frac{|g(x-z)|}{1+|z|^a}.$$

(59)

If $\operatorname{supp}\hat{f}\subset\{\xi\in\mathbb{R}^{n}:|\xi|\le b\}$, we define g(x)=f(x/b), apply (59) together with $\Delta_{h}^{M}f(x)=\Delta_{bh}^{M}g(bx)$ and obtain

$$\bigl|\Delta^M_h f(x)\bigr|\lesssim|bh|^M\max \bigl(1,|bh|^a\bigr)\sup_{z\in\mathbb {R}^n}\frac{|g(bx-z)|}{1+|z|^a}.$$

From this (58) follows and the proof is then complete. □

The following lemma resembles Lemma A.3 of [16].

Lemma 23

Let k∈ℤ, l∈ℕ₀ and m>n. Then

$$\eta_{k+l,m}* \bigl[2^{kn}\chi_{2^{-k}B}\bigr]\lesssim\eta_{k,m}.$$

Proof

Using dilations, we may suppose that k=0. If |x|≤2, then

$$\int_{\{y:|x-y|\le1\}}2^{nl} \bigl(1+2^l|y|\bigr)^{-m}dy \le \int_{y\in\mathbb{R}^n}2^{nl} \bigl(1+2^l|y|\bigr)^{-m}dy \lesssim \bigl(1+|x|\bigr)^{-m}.$$

If |x|>2 and |x−y|≤1, we obtain 1+2^l|y|≳1+2^l|x| and 2^nl(1+2^l|x|)^−m≲(1+|x|)^−m. This immediately implies that

 □

Remark 11

Another way, how to prove Lemma 23 is to use the inequality χ _B (x)≤2^m η _0,m (x) and apply Lemma A.3 of [16].

The following Lemma is quite simple and we leave out its proof.

Lemma 24

Let 0<q<∞, δ>0 and let (a _l ) _l∈ℕ be a sequence of non-negative real numbers. Then

$$\Biggl(\sum_{l=1}^\infty2^{-l\delta q}a_l \Biggr)^{1/q}\lesssim\sum _{l=1}^\infty2^{-l\delta/2}a_l^{1/q},$$

where the constant involved depends only on δ and q.

Finally, we shall need a certain version of Hölder’s inequality for ℓ _q(⋅)(L _p(⋅)) spaces.

Lemma 25

Let $p,q\in\mathcal{P}(\mathbb{R}^{n})$ and let 0<λ<1. Then

$$ \bigl\|f_k\cdot g_k|{\ell_{q(\cdot)}(L_{p(\cdot)})}\bigr\|\le 2^{1/q^-} \bigl\|f_k^{1/(1-\lambda)}|{\ell_{q(\cdot)}(L_{p(\cdot)})}\bigr\|^{1-\lambda}\cdot \bigl\|g_k^{1/\lambda}|{\ell_{q(\cdot)}(L_{p(\cdot)})}\bigr\|^\lambda $$

(60)

holds for all sequences of non-negative functions $(f_{k})_{k\in\mathbb {N}_{0}}$ and $(g_{k})_{k\in\mathbb{N}_{0}}$.

Proof

Due to the homogeneity, we may assume that

$$\bigl\Vert{f_k^{1/(1-\lambda)}}\vert{{\ell_{q(\cdot)}(L_{p(\cdot )})}}\bigr\Vert=\bigl\Vert{g_k^{1/\lambda}}\vert{{\ell_{q(\cdot )}(L_{p(\cdot)})}}\bigr\Vert=1.$$

Then for every ε>0, there exist two sequences of positive real numbers $(\lambda_{k})_{k\in\mathbb{N}_{0}}$ and $(\mu_{k})_{k\in\mathbb {N}_{0}}$, such that

$$\sum_{k=0}^\infty\lambda_k < 1+\varepsilon, \qquad \sum_{k=0}^\infty\mu_k < 1+\varepsilon $$

and

$$\varrho_{{p(\cdot)}} \biggl(\frac{f_k^{1/(1-\lambda)}}{\lambda _k^{1/q(\cdot)}} \biggr)\le1,\qquad \varrho_{{p(\cdot)}} \biggl(\frac{g_k^{1/\lambda}}{\mu_k^{1/q(\cdot)}}\biggr)\le1.$$

We put

$$c:=2^{1/q^-}\quad\text{and}\quad\gamma_k:=\frac{\lambda_k+\mu _k}{2}\ge\frac{\lambda_k+\mu_k}{c^{q(x)}}$$

and use the Young inequality in the form

$$\bigl[f_k(x)g_k(x)\bigr]^{p(x)}\le(1-\lambda)f_k(x)^{p(x)/(1-\lambda)}+\lambda g_k(x)^{p(x)/\lambda}$$

to obtain

Furthermore, the estimate

$$\sum_{k=0}^\infty\gamma_k<\frac{2(1+\varepsilon)}{2}=1+\varepsilon $$

finishes the proof of (60) with the constant $c=2^{1/q^{-}}$. □