New Stability and Stabilization Conditions of Switched Systems with Mode-Dependent Average Dwell Time

Abstract

In this paper, the problems of stability and stabilization for switched systems with mode-dependent average dwell time (MDADT) switching are revisited and discussed in both continuous-time and discrete-time contexts. By introducing a class of quasi-alternative switching signals, some improved stability conditions of switched systems with MDADT are obtained. In our switching design strategy, slow switching and fast switching are, respectively, used among stable subsystems and unstable subsystems. Then, based on the stability result, stabilization conditions for switched linear systems comprising uncontrollable subsystems are presented to guarantee the underlying system to be exponentially stable. The criteria obtained for the considered switched linear systems are all provided in terms of a set of linear matrix inequalities. To illustrate the advantages of our established results, a numerical example is finally given.

1 Introduction

The past a few decades have witnessed the rapid developments of both theories and applications of switched systems. Because switched systems can provide a general framework for modeling a lot of complex systems, they have been found wide application backgrounds such as power electronics, flight control systems, network control systems and process control systems. Switched system that can be viewed as a higher-level abstraction of hybrid systems consists of a family of continuous-time or discrete-time subsystems and a switching signal orchestrating the switching among them.

Due to numerous applications, the basic stability analysis and some other control issues for switched systems have been broadly addressed in the last a few years [2, 4, 6, 7, 14–17, 29, 32]. Among these studies, major efforts are devoted to robust control [25], $H_{\infty }$ filtering [18], and particularly stability analysis [3, 10, 26, 34]. As far as the stability of switched systems is concerned, there are two main methods that have been presented in the literature: the common Lyapunov function (CLF) approach and multiple Lyapunov functions (MLF) approach. Regarding the CLF method [1, 5], it requires that all subsystems share a single Lyapunov function, i.e., switched systems are stable under arbitrary switching. However, many practical switched systems fail to preserve stability under arbitrary switching signals and may be stable under constrained switching signals. For switched systems under constrained switching, it has been shown that MLFs have the advantage of extra flexibility in system analysis and synthesis [21, 22]. Typical constrained switching signals generally include dwell time (DT), average dwell time (ADT) and mode-dependent average dwell time (MDADT). A minimum time interval called DT is first introduced for switched systems such that the system is stable if a switching signal dwells on each mode not less than a specified constant. However, in many practical switched systems, specifying a fixed dwell time may be restrictive. The concept of average dwell time extending the concept of DT allows the possibility of dwell time being less than a given constant. The ADT switching signal has been found important not only in theory but also in practice, and many sound results have been obtained for analysis and synthesis of switched systems by using ADT switching signals [8, 13, 28, 30]. Yet, it should be noted that there still exist some restrictions by using ADT, mainly because of its mode-independent property. That is, the average dwell time is the same for all subsystems. Therefore, the authors of [33] proposed a new switching signal called mode-dependent average dwell time. It has been shown in [11, 19, 20, 27, 31] that MDADT switching is more applicable in practice than ADT switching. It is worth pointing out that, although the authors in [33] have investigated stabilization of switched systems with MDADT switching, the corresponding results require that all subsystems are controllable.

However, almost all the aforementioned works are focused on switched systems composed of stable subsystems. It should be pointed out that switched systems with unstable subsystems also have numerous practical backgrounds. For example, both stable and unstable operations inevitably exist in asynchronous switching control systems; recoverable and unrecoverable malfunctions always happen in complex dynamical network systems; supervisory control plant may be temporarily unstable with inadequacy controllers. Furthermore, controller failures, uncontrollable/unobservable modes, and sensor faults are often encountered in real plants, which may lead to switched system models with unstable subsystems. Therefore, it is of fundamental importance to numerous applications but theoretically challenging to carry out studies of switched systems with unstable subsystems. The stability analysis of switched linear systems composed of both Hurwitz stable and unstable subsystems under ADT switching has been studied in [23]. By adopting an MLF approach, the authors of [20] investigated stability problem of continuous-time switched systems with unstable subsystems under MDADT switching. Then, the authors of [24] extended the results in [20] to the discrete-time context. Based on piecewise Lyapunov-like function and minimum dwell time approaches, the problems of exponential stability and asynchronous stabilization for a class of switched nonlinear systems have been studied in [12]. Although these works all concerned switched systems with partial unstable modes, there still leave some room for improvements. For instance, the lower bound of ADT obtained in [23] is conservative and the method can only deal with switched linear systems; in [20, 24], the used Lyapunov function for unstable subsystems is common which will increase the conservativeness; the piecewise Lyapunov-like functions in [12] are too complicated. In this paper, in order to solve the aforementioned problems, the quasi-alternative switching signal with MDADT property is combined with an MLF approach. The methods are also utilized to stabilize switched linear systems with both controllable and uncontrollable subsystems.

In this paper, the problems of stability and stabilization for switched systems with a new class of switching signals will be studied in both continuous-time and discrete-time cases. A class of quasi-alternative switching signals is proposed which is efficient for stability analysis and stabilization design for switched systems comprising unstable subsystems. Then, improved stability and stabilization conditions of switched systems under our proposed quasi-alternative switching signal with MDADT property are derived. In our switching scheme, the slow switching is adopted for stable subsystems, and the fast switching is adopted for unstable subsystems. However, it should be pointed out that the so-called fast switching is not necessarily faster than the so-called slow switching. The switching behaviors are different from some traditional switching behaviors which activate the stable subsystems for a sufficient long time to absorb the state divergence caused by unstable subsystems. Moreover, numerically easily verified stabilization conditions of the corresponding switched systems are formulated in terms of a set of linear matrix inequalities.

The remainder of the paper is organized as follows. Section 2 reviews some necessary definitions on stability and stabilization of switched systems. In Sect. 3, stability criteria for switched nonlinear systems with proposed switching signals are derived, upon which some improved conditions for stability and stabilization of switched linear systems are also developed. Section 4 provides a numerical example to demonstrate the feasibility and effectiveness of the proposed techniques, and Sect. 5 concludes the paper.

1.1 Notations

In this paper, the used notations are standard. ${\mathbb {R}}$ and ${\mathbb {R}}^{n}$ denote the sets of the real numbers and n-dimensional Euclidean space, respectively, ${\mathbb {Z^{+}}}$ represents the set of positive integers; the notation $\Vert \cdot \Vert$ refers to the Euclidean norm. ${\mathcal {C}}^{1}$ denotes the set of continuously differentiable functions, and a function $\alpha$: $[0,\infty ) \rightarrow [0,\infty )$ is said to be of class $\mathrm{{\mathcal {K}}}$ if it is continuous, strictly increasing, and $\alpha (0)=0$. Class $\mathrm{{\mathcal {K}}}_{\infty }$ denotes the subset of $\mathrm{{\mathcal {K}}}$ consisting of all those functions that are unbounded. In addition, the notation $P > 0({\ge }0)$ means that P is a real symmetric and positive definite (semi-positive definite) matrix.

2 Problem Formulation and Preliminaries

Consider the following switched linear systems,

$$\begin{aligned} \delta x(t) = {A_{\sigma (t)}}x(t)+B_{\sigma (t)}u(t), \quad x({t_0}) = {x_0},\quad t \ge {t_0}, \end{aligned}$$

(1)

where $x(t) \in {\mathbb {R}}^{n}$, $u(t) \in {\mathbb {R}}^{m}$, $x_{0}$ and $t_{0}\ge 0$ denote the state vector, control input, initial state and initial time, respectively; the symbol $\delta$ denotes the derivative operator in the continuous-time case $(\delta x(t) = \dot{x}(t))$ and the shift forward operator in the discrete-time case $(\delta x(t) = x(t + 1))$; $\sigma (t)$ represents a switching signal which is a piecewise constant function from the right of time and takes its values in the finite set ${\mathfrak {L}}=\{1,2,\ldots ,m \}$, where $m >1$ is the number of subsystems. Moreover, $A_{r}, \forall r \in {\mathfrak {L}}$ is either Hurwitz stable or unstable. Without lose of generality, we assume that ${\mathfrak {L}}={\mathfrak {S}}\bigcup {\mathfrak {U}}$, where ${\mathfrak {S}}=\{1,2,\ldots ,s \}$ and ${\mathfrak {U}}=\{s+1,\ldots ,m \}$, i.e., there are s stable subsystems and $m-s$ unstable subsystems. When $t \in [t_{k},t_{k+1}), \ \forall k \in {\mathbb {Z^{+}}}$, we say the $\sigma (t_{k})$th mode is active. Let $\{A_{r} \in {\mathbb {R}}^{n\times n}, B_{r} \in {\mathbb {R}}^{n\times m}, r \in {\mathfrak {L}}\}$ be a family of constant matrices describing subsystems.

Next, some definitions are presented, which are necessary for later developments of the main results.

Definition 1

[9] The equilibrium $x=0$ of switched system (1) is globally uniformly exponentially stable (GUES) under a certain switching signal $\sigma (t)$, if for $u(t)=0$ there exists positive numbers $\lambda >0, \alpha >0$, (resp., $0<\nu <1$) such that $\left\| {x(t)} \right\| \le \lambda {\mathrm{e}^{ - \alpha (t - {t_0})}}\left\| {x({t_0})} \right\|$, (resp., $\left\| {x(t)} \right\| \le \lambda {\nu ^{ - (t - {t_0})}}\left\| {x({t_0})} \right\| )$, $\ \forall t\ge t_{0}$ with any initial conditions $x(t_{0})$.

Definition 2

For any time interval $[t_{1}, t_{2}]$, denote $N_{\sigma p}(t_{2}, t_{1})$ as the numbers of the pth subsystem being activated, and $T_{p}(t_{2}, t_{1})$ as the overall running time of the pth subsystem, $p \in {\mathfrak {S}}$. We can find two constants $N_{0p}$ and $\tau _\mathrm{ap}$ satisfying

$$\begin{aligned} N_{\sigma p}(t_{2},t_{1}) \le N_{0p}+\frac{T_{p}(t_{2},t_{1})}{\tau _\mathrm{ap}}, \quad \forall t_{2}\ge t_{1}\ge 0. \end{aligned}$$

(2)

where $\tau _\mathrm{ap}$ is called the slow mode-dependent average dwell time (SMDADT) of the switching signal $\sigma (t)$.

In this paper, we also define another type of MDADT called fast MDADT (FMDADT) in the following.

Definition 3

For any time interval $[t_{1}, t_{2}]$, denote $N_{\sigma q}(t_{2}, t_{1})$ as the numbers of the qth subsystem being activated, and $T_{q}(t_{2}, t_{1})$ as the overall running time of the qth subsystem, $q \in {\mathfrak {U}}$. We can find two constants $N_{0q}$ and $\tau _{aq}$ satisfying

$$\begin{aligned} N_{\sigma q}(t_{2},t_{1}) \ge N_{0q}+\frac{T_{q}(t_{2},t_{1})}{\tau _{aq}}, \quad \forall t_{2}\ge t_{1}\ge 0. \end{aligned}$$

(3)

where $\tau _{aq}$ is called the fast mode-dependent average dwell time (FMDADT) of the switching signal $\sigma (t)$.

Remark 1

It can be seen that the difference between Definitions 2 and 3 lies the inequalities in (2) and (3). Although the appearance difference is slight, the basic idea behind is thoroughly different. The traditional SMDADT in Definition 2 requiring $N_{\sigma p}(t_{2},t_{1}) \le N_{0p} +\frac{t_{2}\,-\,t_{1}}{\tau _{a}} \Longleftrightarrow \frac{T_{p}(t_{2}, t_{1})}{N_{\sigma p(t_{2},t_{1})}-\,N_{0p}}\ge \tau _\mathrm{ap}, \ \forall t_{2}\ge t_{1}\ge 0$ is called slow switching (in average sense), which means that average time among the intervals associated with the pth subsystem is larger than $\tau _\mathrm{ap}$. By resorting to this SMDADT to achieve stabilization, the basic idea is to allow the transient effect to dissipate after each switching. In this framework, the energy decrement of Lyapunov function during dwelling on stable subsystems can compensate possible energy increment at the switching instance and/or during dwelling at unstable subsystems. However, Definition 3 requires $N_{\sigma q}(t_{2},t_{1}) \ge N_{0q} +\frac{t_{2}\,-\,t_{1}}{\tau _{a}} \Longleftrightarrow \frac{T_{q}(t_{2}, t_{1})}{N_{\sigma q(t_{2},t_{1})}-N_{0q}}\le \tau _{aq}, \ \forall t_{2}\ge t_{1}\ge 0$. It is called fast switching (in average sense), since the average time among the intervals associated with the qth subsystem is no more than $\tau _{aq}$. The basic idea of using the FMDADT is to compensate the state divergence via dwelling at appropriate unstable subsystems, but obviously the dwell time cannot be too big. Therefore, in order to achieve stabilization, we will apply the SMDADT to stable subsystems and FMDADT to unstable subsystems in this paper.

3 Main Results

In this section, we consider the problems of stability and stabilization for switched linear systems described in the previous section.

3.1 Stability Analysis

Although the FMDADT defined in Definition 3 has been applied to switched systems comprising unstable subsystems with a degree of flexibility in system analysis and synthesis in [20], they only applied the common Lyapunov function, which leaves much room for improvements. As illustrated in Remark 3 of [20], there still exist some technical difficulties in exploring multiple Lyapunov functions to solve the considered problems. Thus, in order to solve these technical difficulties, we first introduce a class of quasi-alternative switching signals.

Definition 4

Suppose that a switching law $\sigma (t)$ satisfies the following conditions:

• (1) If $\sigma (t_{k}) \in {\mathfrak {S}}$, then $\sigma (t_{k+1}) \in {\mathfrak {L}}$;

• (2) If $\sigma (t_{k}) \in {\mathfrak {U}}$, then $\sigma (t_{k+1}) \in {\mathfrak {S}}$;

The switching signal $\sigma (t)$ satisfying the above conditions is called a quasi-alternative switching signal.

Remark 2

Definition 4 implies that a switched system cannot directly switches from an unstable mode to another unstable mode. If condition (1) is changed as: “If $\sigma (t_{k}) \in {\mathfrak {S}}$, then $\sigma (t_{k+1}) \in {\mathfrak {U}}$”, Definition 4 implies that $\sigma (t)$ is an alternative switching signal, i.e., stable subsystems and unstable subsystems alternately switch to each other.

Next, we are in a position to provide the first version of stability conditions for switched nonlinear systems

$$\begin{aligned} \delta x(t) = f_{\sigma (t)}(x(t)), \end{aligned}$$

(4)

in the following Lemmas by designing quasi-alternative switching signals with MDADT property.

Lemma 1

Consider continuous-time switched nonlinear system (4), $\sigma (t) \in {\mathfrak {L}}$, and let $\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {S}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in {\mathfrak {U}}$. Suppose that there exist two sets of ${\mathcal {C}}^{1}$ nonnegative functions $V_{p}(x(t)): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, p\in {\mathfrak {S}}$ and $V_{q} (x(t)): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, q\in {\mathfrak {U}}$, two class ${\mathcal {K}}_{\infty }$ functions $\alpha _{1}$ and $\alpha _{2}$, such that

$$\begin{aligned} \alpha _{1}(\Vert x(t) \Vert ) \le V_{p} (x(t))\le & {} \alpha _{2}(\Vert x(t) \Vert ),\quad \forall p \in {\mathfrak {S}},\end{aligned}$$

(5)

$$\begin{aligned} \alpha _{1}(\Vert x(t) \Vert ) \le V_{q} (x(t))\le & {} \alpha _{2}(\Vert x(t) \Vert ), \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(6)

$$\begin{aligned} \dot{ V_{p}}(x(t))\le & {} \eta _{p} V_{p}(x(t)), \quad \forall p \in {\mathfrak {S}}, \end{aligned}$$

(7)

$$\begin{aligned} \dot{ V_{q}}(x(t))\le & {} \eta _{q} V_{q}(x(t)), \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(8)

$$\begin{aligned} V_{p}(x(t_{k}))\le & {} \mu _{p} V_{r}(x(t^{-}_{k})), \quad \forall p \in {\mathfrak {S}}, \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(9)

$$\begin{aligned} V_{q}(x(t_{k}))\le & {} \mu _{q} V_{p}(x(t^{-}_{k})), \quad \forall p \in {\mathfrak {S}}, \forall q \in {\mathfrak {U}}. \end{aligned}$$

(10)

Then switched system (4) is GUES for any quasi-alternative switching signals with MDADT

$$\begin{aligned} \left\{ \begin{array}{l} {\tau _\mathrm{ap}} \ge \frac{{ - ln{\mu _p}}}{{{\eta _p}}},\quad \forall p \in {\mathfrak {S}},\\ {\tau _{aq}} \le \frac{{ - ln{\mu _q}}}{{{\eta _q}}}, \quad \forall q \in {\mathfrak {U}}. \end{array} \right. \end{aligned}$$

(11)

Proof

Without loss of generality, we denote $t_{1},t_{2},\ldots ,t_{k},t_{k+1},\ldots ,t_{N_{{\sigma (T,0)}}}$ as the switching times on time interval [0, T ]. Then we consider the function

$$\begin{aligned} W(t) = {\mathrm{e}^{ - \eta _{\sigma (t)} t}}{V_{\sigma (t)}}(x(t)). \end{aligned}$$

(12)

It is clear that this function is piecewise differentiable along solutions of (4). When $t \in [t_{k},t_{k+1})$, we get from (7), (8), (12) that

$$\begin{aligned} \dot{W}(t)= & {} - {\eta _{\sigma ({t_k})}}\mathrm{{ }}{\mathrm{e}^{ - {\eta _{\sigma ({t_k})}}t}}{V_{\sigma ({t_k})}}(x(t)) + \mathrm{{ }}{\mathrm{e}^{ - {\eta _{\sigma ({t_k})}}t}}{{\dot{V}}_{\sigma ({t_k})}}(x(t))\nonumber \\\le & {} - \eta _{\sigma ({t_k})} {\mathrm{e}^{ - \eta _{\sigma ({t_k})} t}}{V_{\sigma ({t_k})}}(x(t)) + {\mathrm{e}^{ - \eta _{\sigma ({t_k})} t}}\eta _{\sigma ({t_k})} V_{\sigma ({t_k})}(x(t))\nonumber \\= & {} 0. \end{aligned}$$

(13)

Thus W(t) is nonincreasing when $t \in [t_{k},t_{k+1})$. This together with (9), (10), (12) gives that

$$\begin{aligned} W(t_{k+1})= & {} {\mathrm{e}^{ - \eta _{\sigma \left( t_{k+1}\right) } t_{k+1}}} {V_{\sigma \left( t_{k+1}\right) }}(x\left( t_{k+1}\right) )\nonumber \\\le & {} \mu _{\sigma \left( t_{k+1}\right) }{\mathrm{e}^{ - \eta _{\sigma \left( t_{k+1}\right) } t_{k+1}}}{V_{\sigma \left( t_{k}\right) }}\left( x\left( t_{k+1}\right) \right) \nonumber \\= & {} {\mu _{\sigma ({t_{k + 1}})}}{\mathrm{e}^{ - {\eta _{\sigma ({t_{k + 1}})}} {t_{k + 1}} + {\eta _{\sigma ({t_k})}}{t_{k + 1}}}}{W}\left( x\left( t_{k + 1}^ - \right) \right) \nonumber \\\le & {} {\mu _{\sigma ({t_{k + 1}})}}{\mathrm{e}^{ - ({\eta _{\sigma ({t_{k + 1}})}} - {\eta _{\sigma ({t_k})}}){t_{k + 1}}}}W(x({t_k}))\nonumber \\\le & {} {\mu _{\sigma ({t_{k + 1}})}}{\mu _{\sigma ({t_k})}} {\mathrm{e}^{ - [({\eta _{\sigma ({t_{k + 1}})}} - {\eta _{\sigma ({t_k})}}){t_{k + 1}}\,+\,({\eta _{\sigma ({t_k})}}\,-\,{\eta _{\sigma ({t_{k - 1}})}}){t_k}]}}W(x({t_{k - 1}}))\nonumber \\&\ldots \nonumber \\\le & {} \prod \limits _{i = 0}^k {{\mu _{\sigma ({t_{i + 1}})}}} \exp \left\{ - \left[ \left( {\eta _{\sigma ({t_{k + 1}})}} - {\eta _{\sigma ({t_k})}}\right) {t_{k + 1}} + \left( {\eta _{\sigma ({t_k})}} - {\eta _{\sigma ({t_{k - 1}})}}\right) {t_k}\right. \right. \nonumber \\&\left. \left. + \cdots + ({\eta _{\sigma ({t_1})}}- {\eta _{\sigma ({t_0})}}){t_1}\right] \right\} W(x({t_0})). \end{aligned}$$

(14)

Then, from (12) and (14), one can obtain that

$$\begin{aligned} {\mathrm{e}^{ - {\eta _{\sigma ({T^ - })}}T}}W(x({T^ - }))\le \prod \limits _{i = 0}^{{N_\sigma } - 1} {{\mu _{\sigma ({t_{i + 1}})}}} {\mathrm{e}^{\sum \limits _{i = 0}^{{N_\sigma } - 1} { -\left( {\eta _{\sigma \left( {t_{i + 1}}\right) }} - {\eta _{\sigma ({t_i})}}\right) {t_i}} }}{V_{\sigma ({t_0})}}(x({t_0})). \end{aligned}$$

(15)

Moreover, it can be derived from (2), (3) and (15) that

$$\begin{aligned} {V_{\delta ({T^ - })}}(x(T))\le & {} \prod \limits _{p = 1}^s {\mu _p^{{N_{\sigma p}}}} \prod \limits _{q = s + 1}^m {\mu _q^{{N_{\sigma q}}}} {\mathrm{e}^{\left( \sum \limits _{p = 1}^s { {\eta _p}{T_p}(T,0)}\,+\,\sum \limits _{q = s + 1}^m { {\eta _q}{T_q}(T,0)} \right) }}{V_{\sigma (0)}}(x(0))\nonumber \\\le & {} \prod \limits _{p = 1}^s {\mu _p^{\left( {N_{0p}} + \frac{{{T_p}(T,0)}}{{{\tau _\mathrm{ap}}}}\right) }} \prod \limits _{q = s + 1}^m {\mu _q^{\left( {N_{0q}} + \frac{{{T_q}(T,0)}}{{{\tau _{aq}}}}\right) }}\nonumber \\&\times \,{\mathrm{e}^{\left( \sum \limits _{p = 1}^s { {\eta _p}{T_p}(T,0)}\,+\, \sum \limits _{q = s + 1}^m { {\eta _q}{T_q}(T,0)} \right) }} {V_{\sigma (0)}}(x(0))\nonumber \\= & {} {\mathrm{e}^{\left( \sum \limits _{p = 1}^s \left( {N_{0p}} + \frac{{{T_p}(T,0)}}{{{\tau _\mathrm{ap}}}}\right) \ln {\mu _p}\,+\sum \limits _{q = s+1}^{m} \left( {N_{0q}} + \frac{{{T_q}(T,0)}}{{{\tau _{aq}}}}\right) \ln {\mu _q}\right) }}\nonumber \\&\times \, {\mathrm{e}^{\left( \sum \limits _{p = 1}^s { {\eta _p}{T_p}(T,0)}\,+ \sum \limits _{q = s + 1}^m { {\eta _q}{T_q}(T,0)} \right) }} \times {V_{\sigma (0)}}(x(0))\nonumber \\\le & {} {\mathrm{e}^{\left( \sum \limits _{p = 1}^s {N_{0p}}\ln {\mu _p} + \sum \limits _{q = s+1}^{m} {N_{0q}}\ln {\mu _q}\right) }}\nonumber \\&\times \,{\mathrm{e}^{\left( \sum \limits _{p = 1}^s \left( {\eta _p} + \frac{{\ln {\mu _p}}}{\tau _\mathrm{ap}}\right) {T_p}(T,0)\,+ \sum \limits _{q = s + 1}^m \left( {\eta _q} + \frac{{\ln {\mu _q}}}{\tau _{aq}}\right) {T_q}(T,0)\right) }} {V_{\sigma (0)}}(x(0)). \end{aligned}$$

(16)

By (16), it can be got that, if $\tau _\mathrm{ap}, p \in {\mathfrak {S}}$ and $\tau _{aq}, q \in {\mathfrak {U}}$ satisfy the conditions in (11), then

$$\begin{aligned} {V_{\delta ({T^ - })}}(x(T)) \le \lambda {\mathrm{e}^{ - \alpha (T - {t_0})}} {V_{\sigma (0)}}(x(0)), \end{aligned}$$

where $\lambda = {\mathrm{e}^{(\sum \nolimits _{p = 1}^{s} {{N_{0p}}\ln {\mu _{p}} + } \sum \nolimits _{q = s + 1}^m {{N_{0q}}\ln {\mu _q})} }}, -\alpha ={\max _{(p,q) \in ({\mathfrak {S}} \times {\mathfrak {U}})}}\{ ({\eta _{p}} + \frac{{\ln {\mu _{p}}}}{{{\tau _\mathrm{ap}}}}),({\eta _{q}} + \frac{{\ln {\mu _q}}}{{{\tau _{aq}}}})\}$, which associated with Definition 1 verifies that ${V_{\delta ({T^ - })}}(x(T))$ exponentially converges to zero as $T \rightarrow \infty$. Finally, we conclude that switched nonlinear system (4) is GUES under quasi-alternative switching signals satisfying (11) if the conditions (5)–(10) hold. This completes the proof. $\square$

Lemma 2

Consider discrete-time switched nonlinear system (4), $\sigma (t) \in {\mathfrak {L}}$, and let $-1<\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {S}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in {\mathfrak {U}}$. Suppose that there exist two sets of ${\mathcal {C}}^{1}$ nonnegative functions $V_{p}(x(t)): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, p\in {\mathfrak {S}}$ and $V_{q}(x(t)): {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, q\in {\mathfrak {U}}$, two class ${\mathcal {K}}_{\infty }$ functions $\alpha _{1}$ and $\alpha _{2}$, such that

$$\begin{aligned} \alpha _{1}(\Vert x(t) \Vert ) \le V_{p} (x(t))\le & {} \alpha _{2}(\Vert x(t) \Vert ), \quad \forall p \in {\mathfrak {S}},\end{aligned}$$

(17)

$$\begin{aligned} \alpha _{1}(\Vert x(t) \Vert ) \le V_{q} (x(t))\le & {} \alpha _{2}(\Vert x(t) \Vert ), \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(18)

$$\begin{aligned} \triangle V_{p}(x(t))\le & {} \eta _{p} V_{p}(x(t)), \quad \forall p \in {\mathfrak {S}}, \end{aligned}$$

(19)

$$\begin{aligned} \triangle V_{q}(x(t))\le & {} \eta _{q} V_{q}(x(t)), \quad \forall p \in {\mathfrak {U}}, \end{aligned}$$

(20)

$$\begin{aligned} V_{p}(x\left( t_{k}\right) )\le & {} \mu _{p} V_{r}(x(t^{-}_{k})), \quad \forall q \in {\mathfrak {S}}, \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(21)

$$\begin{aligned} V_{q}(x\left( t_{k}\right) )\le & {} \mu _{q} V_{p}(x(t^{-}_{k})), \quad \forall p \in {\mathfrak {S}}, \forall q \in {\mathfrak {U}}. \end{aligned}$$

(22)

Then switched system (4) is GUES for any quasi-alternative switching signals with MDADT

$$\begin{aligned} \left\{ \begin{array}{l} {\tau _\mathrm{ap}} \ge \frac{{ - ln{\mu _p}}}{{{1+\eta _p}}}, \quad \forall p \in {\mathfrak {S}},\\ {\tau _{aq}} \le \frac{{ - ln{\mu _q}}}{{{1+\eta _q}}}, \quad \forall q \in {\mathfrak {U}}. \end{array} \right. \end{aligned}$$

(23)

Proof

The proof of Lemma 2 is similar to that of Lemma 1. We omit it here. $\square$

Fig. 1

Evolution of Energy Function

Remark 3

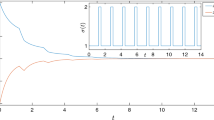
Some of previous results such as [28] required that the abstract energy functions of a system increase and decrease in the same interval, and the overall energy should decrease. However, the energy of a Lyapunov function in this paper can increase during the whole running time, as shown in Fig. 1. From (9) (or (21) in the discrete-time case), one can obtain that $\frac{V_{p}(x(t_{k}))}{ V_{r}(x(t^{-}_{k}))} \le \mu _{p}>1, \ \forall q \in {\mathfrak {S}}, \forall r \in {\mathfrak {L}}, \ \ p\ne r$, i.e., when a subsystem switches to a stable subsystem, the energy is allowed to increase at the switching instance. Yet, from (10) (or (22) in the discrete-time case), one can obtain that $\frac{V_{q}(x(t_{k}))}{ V_{p}(x(t^{-}_{k}))} \le \mu _{p}<1, \ \forall q \in {\mathfrak {U}}, \forall p \in {\mathfrak {S}}$, i.e., when a system switches to an unstable subsystem, the energy must decrease at the switching instance to compensate the divergence of the state trajectory. These also can be seen in Fig. 1.

Remark 4

In Lemma 1 and Lemma 2, based on multiple Lyapunov functions, two sets of quasi-alternative switching signals with MDADT property are designed in both continuous-time and discrete-time cases to ensure the GUES of a given switched system whose subsystems may not be stable. Compared with Lemma 1 of [20] and Lemma 2 of [24] that the Lyapunov functions for unstable subsystems are common, we utilize multiple Lyapunov functions with our proposed quasi-alternative switching signals, which can reduce the conservatism of the results. In fact, note in Lemma 1 of [20] that for unstable subsystems, $\tau _{a}^{c} \le \frac{{ - \ln {\mu _{c}}}}{{{\eta _{c}}}}$, where $\tau _{a}^{c}$ denotes the MDADT for all unstable subsystems, while in Lemma 1 of this paper ${\tau _{aq}} \le \frac{{ - ln{\mu _{q}}}}{{{\eta _{q}}}}, \forall q \in {\mathfrak {U}}$, i.e., each unstable subsystem also has its own ADT. Thus, it can be concluded that Lemma 1 (or Lemma 2 in the discrete-time context) presents a more general stability condition than Lemma 1 of [20] (resp., Lemma 2 of [24] ) which corresponds to the special case of $\mu _{c}=\mu _{q}, \eta _{c} =\eta _{q}, \tau _a^c={\tau _{aq}}, \forall q \in {\mathfrak {U}}$. This fact implies that our result has the advantages of relatively less conservativeness and extra flexibility in system analysis and synthesis.

Remark 5

Different from Lemma 3 (or Lemma 4 in the discrete-time case) of [33], unstable subsystems are considered in Lemma 1 (resp., Lemma 2). For stable subsystems, it also applies the slow switching scheme (Definition 2). But for unstable subsystems, it adopts the fast switching scheme (Definition 3). Such a switching strategy can guarantee to dwell on stable subsystems long enough to compensate possible energy increments at the switching instance and during dwelling on unstable subsystems, and avoid dwelling on unstable subsystems too long. Anyway, it should be pointed out that the dwell time on stable subsystems is not required to be bigger than that on unstable subsystems. In fact, if a switched system is composed of stable subsystems, Lemma 1 ( Lemma 2 in the discrete-time case) will reduce to Lemma 3 (resp., Lemma 4) of [33].

Next, the following two theorems for switched linear system (1) can be given on the basis of Lemmas 1 and 2. Theorem 1 corresponds to the continuous-time version, and Theorem 2 corresponds to the discrete-time version.

Theorem 1

Consider switched linear system (1) when $u(t)=0$, and let $\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {S}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in {\mathfrak {U}}$ be given constants. If there exists a set of matrices $P_{p}>0, P_{q}>0, \ p \in {\mathfrak {S}}, q \in {\mathfrak {U}}$, such that

$$\begin{aligned} A^{T}_{p}P_{p}+P_{p}A_{p}\le & {} \eta _{p} {P_{p}}, \quad \forall p \in {\mathfrak {S}}, \end{aligned}$$

(24)

$$\begin{aligned} A^{T}_{q}P_{q}+P_{q}A_{q}\le & {} \eta _{q} {P_{q}}, \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(25)

$$\begin{aligned} {P_{p}}\le & {} \mu _{p} {P_{r}}, \quad \forall q \in {\mathfrak {S}}, \quad \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(26)

$$\begin{aligned} {P_{q}}\le & {} \mu _{q} {P_{p}}, \quad \forall p \in {\mathfrak {S}}, \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(27)

then, the system is GUES for any quasi-alternative switching signals with MDADT satisfying (11).

Proof

Construct a multiple Lyapunov function for continuous-time switched system (1) in the form of

$$\begin{aligned} {V_{\sigma (t)}}(x(t)) = \left\{ {\begin{array}{*{20}{c}} {x(t)^{T}{P_{p}}x(t)},\quad \sigma (t)=p \in {\mathfrak {S}}\\ {x(t)^{T}{P_{q}}x(t)} \quad \sigma (t)=q \in {\mathfrak {U}}, \end{array}} \right. \end{aligned}$$

(28)

where $P_{p}>0, P_{q}>0, \ p \in {\mathfrak {S}}, q \in {\mathfrak {U}}$ are positive definite matrixes satisfying (24)–(27).

In the sequel, one can obtain from (24)–(27) that $\forall (p,q) \in {\mathfrak {S}}\times {\mathfrak {U}}$,

$$\begin{aligned} {{\dot{V}}_p}(x(t)) - {\eta _p}{V_p}(x(t))= & {} {x^T}(t)(A_p^T{P_p} + {P_p}{A_p} - {\eta _p}{P_p})x(t), \\\le & {} 0 , \quad p \in {\mathfrak {S}}, \\ {{\dot{V}}_q}(x(t)) - {\eta _q}{V_p}(x(t))= & {} {x^T}(t)(A_q^T{P_q} + {P_q}{A_q} - {\eta _q}{P_q})x(t), \\\le & {} 0, \quad q \in {\mathfrak {U}}. \\ {V_p}(x(t)) - {\mu _p}{V_r}(x(t))= & {} {x^T}(t)({P_p} - {\mu _p}{P_r})x(t), \\\le & {} 0, \quad p \in {\mathfrak {S}}, \quad r \in {\mathfrak {L}}, \quad p\ne r. \\ {V_q}(x(t)) - {\mu _q}{V_p}(x(t))= & {} {x^T}(t)({P_q} - {\mu _q}{P_p})x(t), \\\le & {} 0, \quad p \in {\mathfrak {S}}, \quad q \in {\mathfrak {U}}. \end{aligned}$$

Finally, one can readily conclude by Lemma 1 that switched system (1) is GUES for any quasi-alternative switching signals with MDADT satisfying (11). $\square$

Theorem 2

Consider switched linear system (1) when $u(t)=0$, and let $-1<\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {S}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in {\mathfrak {U}}$ be given constants. If there exists a set of matrices $P_{p}>0, P_{q}>0, \ p \in {\mathfrak {S}}, q \in {\mathfrak {U}}$, such that

$$\begin{aligned} A^{T}_{p}P_{p}A_{p}-P_{p}\le & {} \eta _{p} {P_p}, \quad \forall p \in {\mathfrak {S}}, \end{aligned}$$

(29)

$$\begin{aligned} A^{T}_{q}P_{q}A_{q}-P_{q}\le & {} \eta _{q} {P_q}, \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(30)

$$\begin{aligned} {P_{p}}\le & {} \mu _{p} {P_{r}}, \quad \forall p \in {\mathfrak {S}}, \quad \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(31)

$$\begin{aligned} {P_{q}}\le & {} \mu _{q} {P_{p}}, \quad \forall p \in {\mathfrak {S}}, \quad \forall q \in {\mathfrak {U}}, \end{aligned}$$

(32)

then, the system is GUES for any quasi-alternative switching signals with MDADT satisfying (23).

Proof

The proof of Theorem 2 is similar to that of Theorem 1. We omit it here. $\square$

Remark 6

In Theorems 1 and 2, based on multiple quadric Lyapunov functions, sufficient conditions ensuring the asymptotic stability of switched linear systems with unstable subsystems are proposed in both continuous-time and discrete-time contexts. More important, the obtained stability conditions are formulated in terms of linear matrix inequalities, which compared with Lemmas 1 and  2 have the advantage of being efficiently solved by LMI toolbox or Sedumi & Yalmip in Matlab.

3.2 Controller Design

In this subsection, the problem of controller design for switched system (1) with MDADT switching is presented. Unlike some control methods requiring all subsystems are controllable, we only require the existence of at least one controllable subsystem. Without loss of generality, we assume that $\{A_{p} \in {\mathbb {R}}^{n\times n}, B_{p} \in {\mathbb {R}}^{n\times m}, p \in {\mathfrak {C}}\}$ are controllable subsystems, where ${\mathfrak {C}}=\{1,2,\ldots ,s\}$, and $\{A_{q} \in {\mathbb {R}}^{n\times n}, q \in {\mathfrak {B}}\}$ are subsystems that cannot be stabilized, where ${\mathfrak {B}}=\{s+1,s+2,\ldots ,m\}$. Our objective is to design p controllers to ensure switched system (1) to be GUES with MDADT switching. In this subsection, the state feedback is considered with $u(t)=K_{p}x(t), p \in {\mathfrak {C}}$, where $K_{p}$ is the controller gain to be determined. Then closed-loop system (1) can be obtained as follows:

$$\begin{aligned} \delta x(t) = \left\{ {\begin{array}{*{20}{l}} {{A_p}x(t) + {B_p}{K_p}x(t)},&{} \quad \forall p \in {\mathfrak {C}},\\ {{A_q}x(t)}, &{}\quad \forall q \in {\mathfrak {B}}. \end{array}} \right. \end{aligned}$$

(33)

However, it should be pointed out that if the $A_{p}, \ \forall p \in {\mathfrak {C}}$ itself is a Hurwitz matrix, the controller gain $K_{p}$ is chosen as 0.

Theorem 3

Consider switched linear system (33), and let $\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {C}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in \mathfrak {P}$ be given constants. If there exists a set of matrices $Q_{r}>0,\ r \in {\mathfrak {L}}$, and $R_{p}, \ p \in {\mathfrak {C}}$ such that

$$\begin{aligned} Q_{p}A^{T}_{p}+A_{p}Q_{p}+R_{p}^{T}B_{p}^{T}+B_{p}R_{p}\le & {} \eta _{p} {Q_p}, \quad \forall p \in {\mathfrak {C}}, \end{aligned}$$

(34)

$$\begin{aligned} Q_{q}A^{T}_{q}+A_{q}Q_{q}\le & {} \eta _{q} {Q_q}, \quad \forall q \in {\mathfrak {B}}, \end{aligned}$$

(35)

$$\begin{aligned} {Q_{r}}\le & {} \mu _{p} {Q_{p}}, \quad \forall p \in {\mathfrak {C}}, \quad \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(36)

$$\begin{aligned} {Q_{p}}\le & {} \mu _{q} {Q_{q}}, \quad \forall p \in {\mathfrak {C}}, \quad \forall q \in {\mathfrak {B}}, \end{aligned}$$

(37)

then, there is a set of stabilizing controllers such that the system is GUES for any quasi-alternative switching signals with MDADT satisfying (11). Moreover, if a feasible solution of (34)–(37) exists, the controller gains are given by

$$\begin{aligned} K_{p}=R_{p}Q_{p}^{-1}. \end{aligned}$$

(38)

Proof

When $\sigma (t) \in {\mathfrak {S}}$, perform a congruence transformation to (34) via $Q_{p}^{-1}$. Then by (38), one can obtain that

$$\begin{aligned} A_{p}^{T}Q_{p}^{ - 1} + Q_{p}^{ - 1}{A_{p}} + K_{p}^{T}B_{p}^{T}Q_{p}^{ - 1} + Q_{p}^{ - 1}{B_{p}}{K_{p}} \le {\eta _{p}}Q_{p}^{ - 1}, \quad \forall p \in {\mathfrak {C}}, \end{aligned}$$

(39)

which is equivalent to

$$\begin{aligned} {({A_{p}} + {B_{p}}{K_{p}})^{T}}Q_{p}^{ - 1} + Q_{p}^{ - 1}({A_{p}} + {B_{p}}{K_{p}}) \le {\eta _{p}}Q_{p}^{ - 1}, \quad \forall p \in {\mathfrak {C}}. \end{aligned}$$

(40)

Then, by Schur complement theorem, we can get that (36) is equivalent to

$$\begin{aligned} {Q_{p}}^{-1}\le & {} \mu _{p} {Q_{r}}^{-1}, \quad \forall p \in {\mathfrak {C}}, \quad \forall r \in {\mathfrak {L}}, \quad p\ne r. \end{aligned}$$

(41)

Similarly, when $\sigma (t) \in {\mathfrak {U}}$, it can be derived that (36) and (38) are also equivalent to the following inequalities, respectively,

$$\begin{aligned}&A^{T}_{q}Q_{q}^{-1}+Q_{q}^{-1}A_{q} \le \eta _{q} {Q_q}^{-1}, \quad \forall p \in {\mathfrak {B}}, \end{aligned}$$

(42)

$$\begin{aligned}&{Q_{q}}^{-1} \le \mu _{q} {Q_{p}}^{-1}, \quad \forall p \in {\mathfrak {C}}, \quad \forall q \in {\mathfrak {B}}. \end{aligned}$$

(43)

Finally, by Theorem 1 and letting $P_{p}=Q_{p}^{-1}$, we can conclude that, if (40)–(43) hold, switched system (33) is GUES for any quasi-alternative switching signal with MDADT satisfying (11). This completes the proof. $\square$

Theorem 4

Consider switched linear system (33), and let $-1<\eta _{p}<0$, $\mu _{p}>1, p \in {\mathfrak {C}}$ and $\eta _{q}>0$, $0<\mu _{q}<1, q \in {\mathfrak {B}}$ be given constants. If there exists a set of matrices $Q_{r}>0,\ r \in {\mathfrak {L}}$, and $R_{p}, \ p \in {\mathfrak {C}}$ such that

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} { - {Q_{p}}}&{}\quad {{A_{p}}{Q_{p}} + {B_{p}}{R_{p}}}\\ *&{}\quad { - (1 + {\eta _{p}}){Q_{p}}} \end{array}} \right] \le 0, \quad \forall p \in {\mathfrak {C}}, \end{aligned}$$

(44)

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} { - {Q_{q}}}&{}\quad {{A_{q}}{Q_{q}}}\\ *&{}\quad { - (1 + {\eta _{q}}){Q_{q}}} \end{array}} \right] \le 0, \quad \forall q \in {\mathfrak {B}},\end{aligned}$$

(45)

$$\begin{aligned}&{Q_{r}} \le \mu _{p} {Q_{p}}, \quad \forall p \in {\mathfrak {C}}, \quad \forall r \in {\mathfrak {L}}, \quad p\ne r, \end{aligned}$$

(46)

$$\begin{aligned}&{Q_{p}} \le \mu _{q} {Q_{q}}, \quad \forall p \in {\mathfrak {C}}, \quad \forall q \in {\mathfrak {B}}, \end{aligned}$$

(47)

then there is a set of stabilizing controllers such that the system is GUES for any quasi-alternative switching signals with MDADT satisfying (23). Moreover, if a feasible solution of (44)–(47) exists, the controller gains are given by

$$\begin{aligned} K_{p}=R_{p}Q_{p}^{-1}. \end{aligned}$$

(48)

Proof

The proof of Theorem 4 is similar to that of Theorem 3. We omit it here. $\square$

Remark 7

Formulated in terms of linear matrix inequalities, the above theorems provide stabilization criteria for switched linear systems under MDADT switching. Compared with Theorems 3 and 4 of [33] where the subsystems are all controllable, uncontrollable subsystems are considered in Theorems 3 and 4, by adopting the fast switching scheme. Unlike the traditional switching behaviors using a longer dwell time on controlled stable subsystems to guarantee the system to be asymptotically stable, the switching behaviors in Theorems 3 and 4 do not necessarily dwell on controlled stable subsystems a “sufficient long time,” which will be illustrated by an example in the following section.

4 A Numerical Example

We provide the following numerical example in this section to verify our main results developed in this paper.

Example 1

Consider the continuous-time switched linear system (1) consisting of four subsystems and assume that the third and fourth subsystems are uncontrollable. The corresponding subsystem matrices are given below:

$$\begin{aligned} {A_1}= & {} \left[ {\begin{array}{*{20}{c}} { - 10.11}&{}\quad {10.32}\\ {\mathrm{{ }} - 8.60}&{}\quad {8.81} \end{array}} \right] ,\quad {B_1} = \left[ {\begin{array}{*{20}{c}} { - 2.2}\\ {0.8} \end{array}} \right] ,\quad {A_2} = \left[ {\begin{array}{*{20}{c}} {11.12}&{}\quad { - 13.32}\\ {11.10}&{}\quad { - 13.30} \end{array}} \right] ,\\ {B_2}= & {} \left[ {\begin{array}{*{20}{c}} {3.4}\\ { - 1.2} \end{array}} \right] ,\quad {A_3} = \left[ {\begin{array}{*{20}{c}} {9.72}&{}\quad { - 9.69}\\ {12.92}&{}\quad { - 12.89} \end{array}} \right] ,\quad {A_4} = \left[ {\begin{array}{*{20}{c}} {10.24}&{}\quad { - 10.23}\\ {13.64}&{}\quad { - 13.63} \end{array}} \right] .\mathrm{{ }} \end{aligned}$$

The eigenvalues of $A_{1}$ are $\lambda _{11} = -1.51$ and $\lambda _{12}= 0.21$, the eigenvalues of $A_{2}$ are $\lambda _{21} = 0.02$ and $\lambda _{22}= -2.2$, the eigenvalues of $A_{3}$ are $\lambda _{31} = 0.03$ and $\lambda _{32}= -3.2$, and the eigenvalues of $A_{4}$ are $\lambda _{41} = 0.01$ and $\lambda _{42}= -3.4$. It can be seen that none of these matrices is Hurwitz stable. Besides, one can easily check that $\{A_{p} \in {\mathbb {R}}^{2\times 2}, B_{p} \in {\mathbb {R}}^{2\times 1}, p =1,2\}$ are controllable.

Fig. 2

State responses of the first subsystem

Next, we are interested in designing a set of controllers and a quasi-alternative switching signal $\sigma (t)$ with property (2) and (3) to asymptotically stabilize the system. By using Theorem 3, if we choose $\mu _{1} = 2.9, \ \eta _{1}= -1.0$, $\mu _{2} = 2.3, \ \eta _{2}= -3.1$, $\mu _{3} = 0.44, \ \eta _{3}= 3.0$, $\mu _{4} = 0.51, \ \eta _{4}= 1.3$, the feasible solutions are obtained as follows:

$$\begin{aligned} {Q_{1}}= & {} \left[ {\begin{array}{*{20}{c}} { 77.0146 }&{}\quad {69.8370}\\ {69.8370}&{}\quad { 65.1947} \end{array}} \right] ,\quad {Q_{2}} = \left[ {\begin{array}{*{20}{c}} {83.2764}&{}\quad {77.1246}\\ { 77.1246 }&{}\quad { 73.6036} \end{array}} \right] ,\\ {Q_{3}}= & {} \left[ {\begin{array}{*{20}{c}} { 190.6688 }&{}\quad {176.4114}\\ {176.4114}&{}\quad {168.1891} \end{array}} \right] ,\quad {Q_{4}} = \left[ {\begin{array}{*{20}{c}} { 180.3970}&{}\quad {169.1126}\\ { 169.1126}&{}\quad {163.0650} \end{array}} \right] ,\\ {R_1}= & {} \left[ {\begin{array}{*{20}{c}} {6.5871}&\quad {- 13.5623} \end{array}} \right] ,\quad {R_2} = \left[ {\begin{array}{*{20}{c}} {- 18.2149}&\quad { - 3.7398\mathrm{{ }}} \end{array}} \right] ,\\ {K_1}= & {} {R_1}Q_1^{ - 1} = \left[ {\begin{array}{*{20}{c}} {9.5768}&\quad { - 10.4667} \end{array}} \right] ,\quad {K_2} = {R_2}Q_2^{ - 1} = \left[ {\begin{array}{*{20}{c}} { - 5.8056}&\quad {6.0325} \end{array}} \right] . \end{aligned}$$

Fig. 3

State responses of the second subsystem

Fig. 4

State responses of the switched linear system under quasi-alternative switching signal with MDADT

Applying the obtained controllers to the first and second subsystems, respectively, the corresponding state responses of the subsystems under initial state condition $x(0) = [2 \ -2]^{T}$ are shown in Figs. 2 and 3, in which we can see that the closed-loop subsystems are asymptotically stable. Then, one can obtain that the requirements of MDADT for subsystems $A_{i}, i=1,2,3,4$ are:

$$\begin{aligned} {\tau _{a1}} \ge \frac{{\ln {\mu _1}}}{{{\eta _1}}}= & {} \frac{{ - \ln 2.9}}{{ - 1.0}} = 1.065,\\ {\tau _{a2}} \ge \frac{{\ln {\mu _2}}}{{{\eta _2}}}= & {} \frac{{ - \ln 2.3}}{{ - 3.1}} = 0.269,\\ {\tau _{a3}} \le \frac{{\ln {\mu _3}}}{{{\eta _3}}}= & {} \frac{{ - \ln 0.44}}{{ 3.0}} =0.274,\\ {\tau _{a4}} \le \frac{{\ln {\mu _4}}}{{{\eta _4}}}= & {} \frac{{ - \ln 0.51}}{{ 1.3}} = 0.518. \end{aligned}$$

From the requirements of MDADT, we can see that the MDADT of the fourth subsystem can be larger than that of the second subsystem, i.e., the MDADT of unstable subsystems can be larger than that of stable subsystems, which means that some stable subsystems cannot run a “sufficient long time” to guarantee the system to be asymptotically stable.

Furthermore, we generate one possible quasi-alternative switching sequence (4,2,1,3,2,3,2,1,4,1,3,2,4,...) with MDADT property ($\tau _{a1}=1.2>1.065$, $\tau _{a2}=0.3>0.269$, $\tau _{a3}=0.2<0.274$, $\tau _{a4}=0.5<0.518$). The corresponding state responses of the system under initial state condition $x(0) = [2 \ -2]^{T}$ are shown in Fig. 4, from which we can see that the switched linear system is stable under MDADT switching.

5 Conclusions

The problems of stability and stabilization for switched systems comprising unstable subsystems are studied in both continuous-time and discrete-time contexts by using a new class of switching signals. The proposed switching signal is very efficient for analysis and design for switched systems comprising unstable subsystems. The stability results for switched systems comprising unstable subsystems are first derived on the basis of our proposed switching signals. Moreover, based on the obtained results, improved stabilization conditions are also established, which concern with uncontrollable subsystems. Finally, a numerical example is provided to verify the advantages of the proposed approach. By our proposed idea, extending the results of this paper to switched positive systems, or to switched systems with time-delay, will be considered in our future works.