1 Introduction

A switched system is a type of hybrid dynamical system that combines discrete states and continuous states. Typically, it consists of a number of subsystems and a switching signal, which defines a specific subsystem being activated during a certain interval. Many dynamical systems can be modeled as such switched systems [5, 20, 21]. Recently, switched positive systems, whose states and outputs are non-negative whenever the initial conditions and inputs are non-negative, have been investigated by many researchers due to their broad applications in communication networks [31], the viral mutation dynamics under drug treatment [9], formation flying [12], and systems theory [1, 13, 14, 29, 30]. Moreover, recently Kaczorek [15] has presented some results on 2-D positive switched systems, which has made much contribution to the system theory. A switched positive system means a switched system in which each subsystem itself is a positive system. It should be pointed out that studying the switched positive systems is more challenging than that of general switched systems and positive systems because, in order to obtain some results, one has to combine both of their features [2, 4, 6, 17, 18, 22, 27].

In practice, delays are universal in real engineering processes and have very complex impact on system dynamics. Hence, it is theoretically challenging and of fundamental importance to study time-delay systems. Although many results have been reported for these systems [7, 16, 24, 25, 34–36], until recently the switched positive liner systems with time delays have been investigated [23, 37].

On the other hand, in actual operation, the states of the systems are not all measurable, thus it is necessary to design state observers for the systems. The developed observer design techniques for non-positive dynamical systems may not be applicable when dealing with positive dynamical systems, since it is often necessary to impose a positive constraint on the designed observers for positive dynamical systems. In other words, the straightforward application of available observer designs to positive dynamical systems could produce meaningless state estimation if there was no non-negative restriction on the state estimation. Some recent results on the positive observer designs for positive linear systems have appeared [8, 11, 19, 28, 29, 32], and some sufficient conditions for the existence of positive linear observers have been established. However, to the best of our knowledge, the problem of positive observer design for switched positive systems has not been fully investigated, especially for switched positive systems with time-varying delays, which is quite an important issue. This motivates us to carry out present work.

In this paper, we are interested in designing positive switched observers for a class of switched positive linear systems with time-varying delays. The main contributions of this paper can be summarized as follows: (i) sufficient conditions for the existence of positive switched observers for the considered systems are given; and (ii) all the proposed conditions are expressed in terms of concise LMIs, and the observer gain matrices can be easily obtained by an effective algorithm.

The rest of the paper is organized as follows. In Sect. 2, system formulation and some necessary definitions and lemmas are given. In Sect. 3, based on average dwell time approach and LMIs technology, sufficient conditions for the existence of positive switched observers, which guarantee that the error switched systems are exponentially stable, are established. An example is provided to illustrate the efficiency of the proposed method in Sect. 4. Conclusions are given in Sect. 5.

Notation

In this paper, A⪰0 (⪯0,≻0,≺0) means that all elements of matrix A are non-negative (non-positive, positive, negative); A≻B (A⪰B) implies A−B≻0(A−B⪰0). A T denotes the transpose of matrix A;R(R +) is the set of all real (positive) numbers; \(R^{n}(R_{ + }^{n})\) is an n-dimensional real (positive) vector space; R n×k is the set of real n×k matrices.

2 Problem Statements and Preliminaries

Consider the following switched linear systems with time-varying delays:

$$ \left\{ \begin{array} {l} \dot{x}(t) = A_{\sigma (t)}x(t) + A_{d\sigma (t)}x\bigl(t - d(t)\bigr) + B_{\sigma (t)}u(t), \\ \noalign{\vspace*{3pt}} x(t) = \varphi(t),\quad t \in [ - \tau,0], \\ \noalign{\vspace*{3pt}} y(t) = C_{\sigma (t)}x(t), \\ \end{array} \right. $$
(1)

where x(t)∈R n and y(t)∈R l denote the state and the measured output, respectively; u(t)∈R w is the control input; \(\sigma(t):[0,\infty) \to\underline{M} = \{ 1,2, \ldots,m \} \) is a piecewise constant function of time, called a switching signal; m is the number of subsystems; A p ,A dp ,B p and \(C_{p}, \forall p \in\underline{M}\), are constant matrices with appropriate dimensions; d(t) denotes the time-varying delay satisfying \(0 \le d(t) \le\tau, \dot{d}(t) \le d\), where τ and d are known constants; and φ(t) is a continuous vector-valued initial function defined on interval [−τ,0].

Definition 1

[3]

System (1) is said to be positive if, for any switching signal σ(t), initial condition φ(t)⪰0,t∈[−τ,0] and all input u(t)⪰0, the corresponding trajectory x(t)⪰0 and y(t)⪰0 for all t≥0.

Definition 2

[26]

A is called a Metzler matrix, if the off-diagonal entries of matrix A are non-negative.

The following lemma can be obtained from Lemma 3 in [27] and Proposition 1 in [28].

Lemma 1

System (1) is positive if and only if A p are Metzler matrices, and \(A_{dp} \succeq 0,\allowbreak B_{p} \succeq 0,C_{p} \succeq 0, \forall\sigma(t) = p \in\underline{M}\).

Remark 1

It should be stressed here that, when φ(t)⪰0,t∈[−τ,0] and u(t)⪰0 are not satisfied, x(t) may not stay positive even if the conditions of Lemma 1 hold. In other words, φ(t)⪰0,t∈[−τ,0] and u(t)⪰0 are essential for the positivity of system (1). In the real world, these are often guaranteed by the features of practical physical systems.

Definition 3

[33]

System (1) is said to be exponentially stable under switching signal σ(t), if for initial conditions x(t)=φ(t),t∈[−τ,0], there exist constants α>0,β>0 such that the solution of the system satisfies \(\| x(t) \| \le\alpha\| x(t_{0}) \|_{C}e^{ - \beta (t - t_{0})},\forall t \ge t_{0}\), where \(\| x(t_{0}) \|_{C} = \sup_{ - \tau \le \theta \le 0}\{ \| x(\theta) \|,\| \dot{x}(\theta) \| \}\).

Definition 4

[10]

For a switching signal σ(t) and any T 2≥T 1≥0, let N σ(t)(T 1,T 2) be the switching number of σ(t) over the interval [T 1,T 2). If N σ(t)(T 1,T 2)≤N 0+(T 2−T 1)/T a holds for T a >0,N 0≥0, then T a is called an average dwell time and N 0 is called a chattering bound.

As commonly used in the literature, we choose N 0=0 in this paper.

The objective of this paper is to design an observer for switched positive system (1) such that the state of the designed observer converges to that of the system and has the positivity.

3 Positive Observer Design

In this section, we consider the problem of observer design for switched positive system (1). The observer structure which will be adopted for system (1) is of the form

$$ \left\{ \begin{array} {l} \dot{\hat{x}}(t) = A_{\sigma (t)} \hat{x}(t) + A_{d\sigma (t)}\hat{x}\bigl(t - d(t)\bigr) + B_{\sigma (t)}u(t) + L_{\sigma (t)}\bigl(y(t) - \hat{y}(t)\bigr), \\ \noalign{\vspace*{3pt}} \hat{x}(t) = 0,\quad t \in [ - \tau,0], \\ \noalign{\vspace*{3pt}} \hat{y}(t) = C_{\sigma (t)}\hat{x}(t), \\ \end{array} \right. $$
(2)

or, equivalently,

$$ \left\{ \begin{array} {l} \dot{\hat{x}}(t) = (A_{\sigma (t)} - L_{\sigma (t)}C_{\sigma (t)})\hat{x}(t) + A_{d\sigma (t)}\hat{x}\bigl(t - d(t) \bigr)\\ \quad {} + B_{\sigma (t)}u(t) + L_{\sigma (t)}C_{\sigma (t)}x(t), \\ \noalign{\vspace*{3pt}} \hat{x}(t) = 0,\quad t \in [ - \tau,0], \\ \noalign{\vspace*{3pt}} \hat{y}(t) = C_{\sigma (t)}\hat{x}(t), \\ \end{array} \right. $$
(3)

where \(\hat{x}(t) \in R^{n}\) is the estimated state vector of \(x(t), \hat{y}(t) \in R^{l}\) is the observer output, L p ∈R n×l is the observer gain matrix to be determined later; we let \(\bar{A}_{p} = A_{p} - L_{p}C_{p}, p \in\underline{M}\).

Remark 2

For a non-positive system, it is only required that the state of the designed observer converges to that of the considered system. However, this requirement for positive switched system (1) is not sufficient; we should also guarantee the positivity of the estimated state \(\hat{x}(t)\) of system (2) or (3) (see [11, 29–33]). To this end, it is naturally required, according to Lemma 1, that \(\bar{A}_{p}\) are Metzler matrices, and \(A_{dp} \succeq 0,\allowbreak B_{p} \succeq 0,L_{p}C_{p} \succeq 0,p \in\underline{M}\).

Define \(\tilde{x}(t) = x(t) - \hat{x}(t)\) the estimated error of the system; then we can obtain the following error switched system:

$$ \left\{ \begin{array} {l} \dot{\tilde{x}}(t) = (A_{\sigma (t)} - L_{\sigma (t)}C_{\sigma (t)})\tilde{x}(t) + A_{d\sigma (t)}\tilde{x}\bigl(t - d(t)\bigr), \\ \noalign{\vspace*{3pt}} \tilde{x}(t) = \varphi(t),\quad t \in [ - \tau,0]. \\ \end{array} \right. $$
(4)

Moreover, from Lemma 1, the error dynamic system (4) is a positive switched system if \(\bar{A}_{p} = A_{p} - L_{p}C_{p}\) are Metzler matrices, \(A_{dp} \succeq 0, L_{p}C_{p} \succeq 0, \sigma(t) = p \in\underline{M}\), for any initial condition φ(t)⪰0,t∈[−τ,0].

Remark 3

As stated in [31], one can find that the positivity requirement on the estimated error \(\tilde{x}(t)\) is not introduced only for the purpose of consistence with the state observer case, but also facilitates the synthesis of the desired positive observer. Although this requirement may cause a certain conservatism, it is noted that the positivity of the estimated error \(\tilde{x}(t)\) will not affect that of the estimated state \(\hat{x}(t)\). If the initial condition \(\tilde{x}(t) \succeq 0\ ( t \in[ - \tau,0 ] )\) does not hold, then the estimated error \(\tilde{x}(t)\ (t \ge 0)\) may not stay positive, but \(\hat{x}(t)\) will still remain positive for all t≥0. On the other hand, one can easily check that the error satisfies \(\tilde{x}(t) \preceq 0\) whenever \(\tilde{x}(t) \preceq 0, t \in[ - \tau,0 ]\ (\tilde{x}(t) \succeq 0\) whenever \(\tilde{x}(t) \succeq 0, t \in[ - \tau,0 ])\).

Before giving the main results, we first present a stability criterion which will be essential for our later development based on the following non-switched positive system:

$$ \left\{ \begin{array} {l} \dot{x}(t) = Ax(t) + A_{d}x\bigl(t - d(t) \bigr), \\ \noalign{\vspace*{3pt}} x_{\theta } = \varphi(\theta),\quad \theta\in[ - \tau,0 ], \\ \end{array}\right. $$
(5)

where A is a Metzler matrix and A d ⪰0 with appropriate dimensions, d(t) denotes the time-varying delay satisfying \(0 \le d(t) \le\tau,\dot{d}(t) \le d\).

Choose the co-positive type Lyapunov–Krasovskii functional candidate for system (5) as follows:

$$ V\bigl(t,x(t)\bigr) = V_{1}\bigl(t,x(t)\bigr) + V_{2} \bigl(t,x(t)\bigr) + V_{3}\bigl(t,x(t)\bigr) $$
(6)

where

$$V_{1}\bigl(t,x(t)\bigr) = x^{T}(t)v, $$
$$V_{2}\bigl(t,x(t)\bigr) = \int_{t - d(t)}^{t} e^{\lambda ( - t + s)}x^{T}(s)\upsilon \,ds, $$
$$V_{3}\bigl(t,x(t)\bigr) = \int_{{-}\tau }^{0} \int_{t + \theta }^{t} e^{\lambda ( - t + s)}\dot{x}^{T}(s) \vartheta \,ds \,d\theta, $$

and \(v, \upsilon,\vartheta\in R_{ + }^{n}\). For the sake of simplicity, V(t,x(t)) is written as V(t) in this paper.

Lemma 2

For a given positive scalar λ, if there exist vectors \(v, \upsilon, \vartheta\in R_{ + }^{n}\) and ς∈R n such that

$$ \stackrel{\frown}{\varPsi} = \operatorname{diag} \bigl\{ \stackrel{\frown}{\psi}_{1}, \stackrel{\frown}{\psi}_{2}, \ldots, \stackrel{\frown}{\psi}_{n}, \stackrel{\frown}{\psi}'_{1}, \stackrel{\frown}{\psi}'_{2}, \ldots, \stackrel{\frown}{\psi}'_{n},\stackrel{\frown}{\psi}''_{1}, \stackrel{\frown}{\psi}''_{2}, \ldots, \stackrel{\frown}{\psi}''_{n} \bigr\} \preceq 0 , $$
(7)

where

$$\stackrel{\frown}{\psi}_{r} = \lambda v_{r} + a_{r}^{T}(v + \tau\vartheta) + \upsilon_{r} + \varsigma_{r}, \quad\stackrel{\frown}{\psi}'_{r} = a_{dr}^{T}v - (1 - d)e^{ - \lambda \tau }\upsilon_{r} + \tau a_{dr}^{T}\vartheta - \varsigma_{r}, $$
$$\stackrel{\frown}{\psi}''_{r} = - e^{ - \lambda \tau }\vartheta_{r} - \varsigma_{r}, \quad r \in \underline{N} = \{ 1,2, \ldots,n \} $$

with a r (a dr ) representing the rth column vector of matrix A(A d ), and v=[v 1,v 2,…,v n ]T, υ=[υ 1,υ 2,…,υ n ]T, ϑ=[ϑ 1,ϑ 2,…,ϑ n ]T, ς=[ς 1,ς 2,…,ς n ]T, v r (υ r ,ϑ r ,ς r ) being the rth element of the vector v(υ,ϑ,ς), then along the trajectory of system (5) we have

Proof

Along the trajectory of system (5) with the co-positive type Lyapunov–Krasovskii functional (6), we have

$$\dot{V}_{1}(t) = \dot{x}^{T}(t)v = x^{T}(t)A^{T}v + x^{T}\bigl(t - d(t)\bigr)A_{d}^{T}v, $$
(8)

Using Leibniz–Newton formula, one can have

$$ \int_{t - d(t)}^{t} \dot{x}(s)\,ds = x(t) - x\bigl(t - d(t)\bigr). $$
(9)

Furthermore, from (9), the following equation can be obtained for any vector ς∈R n:

$$ \biggl[x(t) - x\bigl(t - d(t)\bigr) - \int_{t - d(t)}^{t} \dot{x}(s) \,ds\biggr]^{T}\varsigma = 0. $$
(10)

Adding this to the right-hand side of (8) yields

(11)

On the other hand, from (7), one can obtain

$$ \lambda v + A^{T}(v + \tau\vartheta) + \upsilon + \varsigma \preceq 0, $$
(12)
$$ A_{d}^{T}v - (1 - d)e^{ - \lambda \tau }\upsilon + \tau A_{d}^{T}\vartheta - \varsigma \preceq 0, $$
(13)
$$ - e^{ - \lambda \tau }\vartheta - \varsigma \preceq 0. $$
(14)

Substituting (12)–(14) into (11), we have

$$\dot{V}(t) \le - \lambda V(t). $$

Then, along the trajectory of system (5), we have \(V(t) \le e^{ - \lambda (t - t_{0})}V(t_{0})\). □

This completes the proof.

We are now in a position to deal with the design problem of the observer for system (1). The following theorem proposes a design scheme to choose the suitable observer gain matrices L p which can guarantee the positivity and exponential stability of error switched system (4).

Theorem 1

Consider switched positive system (1); if there exist \(v_{p}, \upsilon_{p},\vartheta_{p} \in R_{ + }^{n},\varsigma_{p} \in R^{n}\) and \(h_{p} \in R^{l}, \forall p \in\underline{M}\), such that

  1. (1)

    \(\bar{A}_{p} = A_{p} - L_{p}C_{p}\) are Metzler matrices, and A dp ⪰0,L p C p ⪰0;

  2. (2)

    for a given positive scalar λ,

    $$ \varPsi_{p} = \operatorname{diag} \bigl\{ \psi_{p1}, \psi_{p2}, \ldots, \psi_{pn}, \psi'_{p1}, \psi'_{p2}, \ldots, \psi'_{pn},\psi''_{p1}, \psi''_{p2}, \ldots, \psi''_{pn} \bigr\} \preceq 0 $$
    (15)

    where

    $$\psi_{pr} = \lambda v_{pr} + a_{pr}^{T}(v_{p} + \tau\vartheta_{p}) - c_{pr}^{T}h_{p} + \upsilon_{pr} + \varsigma_{pr}, $$
    $$\psi'_{pr} = a_{dpr}^{T}v_{p} - (1 - d)e^{ - \lambda \tau }\upsilon_{pr} + \tau a_{dpr}^{T} \vartheta_{p} - \varsigma_{pr}, $$
    $$\psi''_{pr} = - e^{ - \lambda \tau } \vartheta_{pr} - \varsigma_{pr},\quad r \in\underline{N} = \{ 1,2, \ldots,n \}, $$

    v pr (υ pr ,ϑ pr ,ς pr ,h pr ) is the rth element of the vector v p (υ p ,ϑ p ,ς p ,h p ) for any \(p \in\underline{M}\) and \(r \in\underline{N}\); and v p =[v p1,v p2,…,v pn ]T, υ p =[υ p1,υ p2,…,υ pn ]T, ϑ p =[ϑ p1,ϑ p2,…,ϑ pn ]T, ς p =[ς p1,ς p2,…,ς pn ]T, h p =[h p1,h p2,…,h pn ]T, \(h_{p} = L_{p}^{T}(v_{p} + \tau\vartheta_{p})\); a pr (a dpr ,c pr ) represents the rth column vector of matrix A p (A dp ,C p ); then the system (2) is a positive observer for system (1) with the following average dwell time scheme:

    $$ T_{a} > T_{a}^{*} = \ln\mu / \lambda , $$
    (16)

    where the parameter μ≥1 satisfies

    $$ v_{i} \preceq \mu v_{j},\qquad \upsilon_{i} \preceq \mu\upsilon_{j},\qquad \vartheta_{i} \preceq \mu \vartheta_{j},\quad \forall(i, j) \in\underline{M} \times\underline{M}. $$
    (17)

Proof

It follows from Lemma 1 and condition (1) that the system (2) is positive. Then we construct the multiple co-positive type Lyapunov–Krasovskii functional for system (4) as follows:

(18)

For \(\forall\sigma(t) = p \in\underline{M}\), by substituting \(h_{p} = L_{p}^{T}(v_{p} + \tau\vartheta_{p})\) and \(\bar{A}_{p} = A_{p} - L_{p}C_{p}\) into (15), one can obtain that

$$ \bar{A}_{p}^{T}(v_{p} + \tau\vartheta_{p}) + \lambda v_{p} + \upsilon_{p} + \varsigma_{p} \preceq 0, $$
(19)
$$ A_{dp}^{T}(v_{p} + \tau\vartheta_{p}) - (1 - d)e^{ - \lambda \tau }\upsilon_{p} - \varsigma_{p} \preceq 0, $$
(20)
$$ - e^{ - \lambda \tau }\vartheta_{p} - \varsigma_{p} \preceq 0. $$
(21)

By Lemma 2, it is not difficult to obtain

$$ \dot{V}_{p}(t) + \lambda V_{p}(t) \le 0, \quad \forall p \in \underline{M}. $$
(22)

Denote t 1,…,t k as the switching instants during the interval [t 0,t). Then for any t∈[t k ,t k+1), it holds that

$$ V_{\sigma (t)}(t) \le e^{ - \lambda (t - t_{k})}V_{\sigma (t_{k})}(t_{k}). $$
(23)

On the other hand, one can straightforwardly obtain from (17) and (18) that

$$ V_{\sigma (t_{k})}(t_{k}) \le\mu V_{\sigma (t_{k}^{ - })}\bigl(t_{k}^{ - } \bigr). $$
(24)

Then it follows from (16), (23), and (24) that

(25)

Denoting \(\varepsilon_{1} = \min_{(r,p) \in \underline{N} \times \underline{M} }\{ v_{pr} \} , \varepsilon_{2} = \max_{(r,p) \in \underline{N} \times \underline{M} }\{ v_{pr} \}, \varepsilon_{3} = \max_{(r,p) \in \underline{N} \times \underline{M} }\{ \upsilon_{pr} \}, \varepsilon_{4} = \max_{(r,p) \in \underline{N} \times \underline{M} }\{ \vartheta_{pr} \}\), it yields

$$ V_{\sigma (t)}(t) \ge\varepsilon_{1}\bigl\| \tilde{x}(t) \bigr\|, $$
(26)
$$ V_{\sigma (t_{0})}(t_{0}) \le\varepsilon_{2} \bigl\| \tilde{x}(t_{0}) \bigr\| + \varepsilon_{3}e^{ - \lambda \tau }\int _{t{}_{0} - \tau }^{t_{0}} \bigl\| \tilde{x}(s) \bigr\|\,ds + \varepsilon_{4}\tau e^{ - \lambda \tau }\int_{t{}_{0} - \tau }^{t_{0}} \bigl\| \dot{\tilde{x}}(s) \bigr\|\, ds. $$
(27)

Combining (25)–(27), we obtain

(28)

Thus, by denoting α=ε 2/ε 1+(ε 3/ε 1)τe −λτ+(ε 4/ε 1)τ 2 e −λτ,β=λ−lnμ/T a , it can be seen from (28) that \(\| \tilde{x}(t) \| \le\alpha e^{ - \beta (t - t_{0})}\| \tilde{x}(t_{0}) \|_{C}, \forall t \ge t_{0}\), where \(\| \tilde{x}(t_{0}) \|_{C} = \sup_{ - \tau \le \theta \le 0}\{ \| \tilde{x}(\theta) \|,\| \dot{\tilde{x}}(\theta) \| \}\).

Therefore, error system (4) is exponentially stable, which implies that the state \(\hat{x}(t)\) of system (2) converges to that of system (1). Then, we can conclude that system (2) is the positive observer of system (1).

This completes the proof. □

Remark 4

From Theorem 1 it is easy to see that a smaller λ will be favorable to the solvability of inequality (15). First, we can assign a value to λ; if (15) has no feasible solution for the assigned λ, we can change the parameter λ to be smaller. Following this guideline, a solution to the matrix inequality (15) can be found.

Remark 5

We first get the solutions of \(v_{p}, \upsilon_{p}, \vartheta_{p},\varsigma_{p}, h_{p},p \in\underline{M}\) by solving the LMI (15), then the observer gain matrices L p can be obtained by substituting v p ,ϑ p ,h p into \(h_{p} = L_{p}^{T}(v_{p} + \tau\vartheta_{p})\). By adjusting the parameter λ, we can find the feasible solutions such that condition (1) and condition (2) in Theorem 1 are both satisfied.

The procedure of observer design can be given as follows.

Algorithm 1

Step 1.:

Choose a parameter λ>0; one can obtain the solutions of v p ,υ p ,ϑ p ,ς p ,h p by solving the LMI (15);

Step 2.:

By the equation \(h_{p} = L_{p}^{T}(v_{p} + \tau\vartheta_{p})\) with the obtained v p ,ϑ p ,h p , one can get A p −L p C p ,∀p∈M;

Step 3.:

Check the condition (1) in Theorem 1. If it holds, enter the next step; else return to Step 1;

Step 4.:

The observer gain matrices L p are obtained.

When the time delay of system (1) is constant, that is, d(t)=τ, where τ is a known constant, we can obtain the following result.

Corollary 1

Consider switched positive system (1) with constant time-delay τ. If there exist \(v_{p}, \upsilon_{p},\vartheta_{p} \in R_{ + }^{n},\varsigma_{p} \in R^{n}\) and \(h_{p} \in R^{l}, \forall p \in\underline{M}\), such that

  1. (1)

    \(A_{p} - L_{p}C_{p}, \forall p \in\underline{M}\) are Metzler matrices, and \(A_{dp} \succeq 0,L_{p}C_{p} \succeq 0, \forall p \in\underline{M}\);

  2. (2)

    for a given positive scalar λ,

    $$\tilde{\varPsi}_{p} = \operatorname{diag} \bigl\{ \psi_{p1}, \psi_{p2}, \ldots,\psi_{pn},\tilde{\psi}'_{p1}, \tilde{\psi}'_{p2}, \ldots,\tilde{\psi}'_{pn}, \psi''_{p1},\psi''_{p2}, \ldots,\psi''_{pn} \bigr\} \preceq 0 $$

    where

    $$\tilde{\psi}'_{pr} = a_{dpr}^{T}v_{p} - e^{ - \lambda \tau }\upsilon_{pr} + \tau a_{dpr}^{T} \vartheta_{p} - \varsigma_{pr},\quad r \in\underline{N} = \{ 1,2, \ldots,n \}, $$

    ψ pr and \(\psi ''_{pr}\) have been defined in Theorem 1.

Then the system (2) with constant time-delay τ is a positive observer for the system with the average dwell time scheme (16), where μ≥1 satisfies (17).

Proof

Let d(t)=τ. Following the proof line of Theorem 1, one can obtain the Corollary 1. It is omitted here. □

4 Numerical Example

Consider system (1) with the following parameters:

Let u(t)=|sin(2t)|,λ=0.5,τ=0.4,d=0.8. Solving the matrix inequalities (15) in Theorem 1 gives rise to

By \(h_{p} = L_{p}^{T}(v_{p} + \tau\vartheta_{p}), p = 1,2\), we can get

$$L_{1} = \left[ \begin{array}{c@{\quad }c} 0.4915 & 2.1338 \\ 0.6292 & 2.7317 \\\end{array} \right],\qquad L_{2} = \left[ \begin{array}{c@{\quad }c} 3.6741 & - 0.6430 \\ 3.7977 & - 0.6646 \\\end{array} \right]. $$

Obviously, the condition (1) in Theorem 2 holds, i.e. A p −L p C p are Metzler matrices, and A dp ⪰0,L p C p ⪰0,p=1,2.

Then, from (16) and (17), we can obtain μ=1.4968 and \(T_{a}^{*} = 0.8067\). Therefore, there exists a positive observer for the system with the average dwell time \(T_{a} > T_{a}^{*} = 0.8067\).

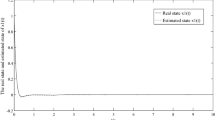
The simulation results are shown in Figs. 1–3, where the initial state of the system is x(t)=[0 0]T,t∈[−τ,0),x(0)=[0.5 0.6]T, and the initial state of the observer is \(\hat{x}(t) = [0\ 0 ]^{T}, t \in [ - \tau,0]\). Figure 1 shows the switching signal. From Fig. 1, one can get that T a >0.8067. Figure 2 shows the actual states and their estimation, and the estimated error states are shown in Fig. 3. From Figs. 2–3 it is not hard to find that the state of the designed observer not only possesses the positivity, but also approximates that of the original system (1). This demonstrates the effectiveness of the proposed approach.

Fig. 1
figure 1

Switching signal

Full size image
Fig. 2
figure 2

State response of the system and its estimation

Full size image
Fig. 3
figure 3

Estimated errors: \(\tilde{x}_{1}\) solid line, \(\tilde{x}_{2}\) dashed line

Full size image

5 Conclusions

In this paper, we have studied the positive observer design problem for a class of switched positive linear systems with time-varying delays. Sufficient conditions for the existence of positive observers are established, and the observer gain matrices can be obtained easily through the solutions of LMIs. Moreover, the state of the designed observer not only remains the positivity, but also converges to that of the original system. Finally, an illustrative example is provided to show the effectiveness and applicability of the proposed method.