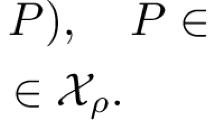Traveling wave solutions in a modified Leslie–Gower model with diffusion and chemotaxis

Abstract

In this paper, we study the existence and minimal wave speed of traveling wavefronts and the existence of periodic waves for a modified Leslie–Gower model with diffusion and chemotaxis. The existence of traveling wavefronts is proved by applying the perturbation method. Our approach is based on an abstract formulation of the wave profile as a solution of an operational equation in a certain Banach space, coupled with the Fredholm theory and the Banach contraction mapping principle. Moreover, we study the minimal wave speed of traveling wavefronts by using the standard stability analysis, and investigate the existence condition of periodic waves when traveling wavefronts disappears. Some numerical simulations are presented to illustrate our main results.

1 Introduction

In order to describe the reduction of the predator population is related to the per capita availability of its preferred food, Leslie and Gower [15] proposed the following predator–prey model:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\textrm{d} u}{\textrm{d} t}= u \left( a_1-q_1 u-\theta _1 v\right) ,\\ \frac{\textrm{d} v}{\textrm{d} t}= v \left( a_2-\theta _2 \frac{v}{u}\right) . \end{array}\right. \end{aligned}$$

(1.1)

Whereafter, Korobeinikov [13] proved global stability of the coexisting equilibrium of system (1.1) by introducing a Lyapunov function. Since the Leslie–Gower model has been proposed, numerous modified models were considerd. For example, Chen et al. [3] investigated a Leslie–Gower predator–prey model incorporating a prey refuge and showed that the unique positive equilibrium is globally stable, which means that for this ecosystem, prey refuge has no influence on the persistent property of the system. Nindjin et al. [17] discussed a Leslie–Gower model with time delay and obtained a sufficient condition for global stability of the positive equilibrium. In particularly, so as to show that the predator can switch over to other populations in the case of severe scarcity, Alaoui and Okiye [1] added two positive constant $K_1$ and $K_2$ into system (1.1), where $K_1$ (respectively, $K_2$) measures the extent to which environment provides protection to prey u (respectively, to predator v), i.e., they considered the following system with modified Leslie–Gower functional response:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\textrm{d} u}{\textrm{d} t}= u \left( a_1-q_1 u-\frac{\theta _1 v}{u+K_1}\right) , \\ \frac{\textrm{d} v}{\textrm{d} t}= v \left( a_2- \frac{\theta _2 v}{u+K_2}\right) , \end{array}\right. \end{aligned}$$

(1.2)

and obtained boundedness of solutions, existence of an attracting set and global stability of the coexisting interior equilibrium. In addition, for the sake of describe the spatial diffusion of populations, Du and Hsu [6] proposed the following reaction–diffusion model with Leslie–Gower reaction terms:

$$\begin{aligned} \left\{ \begin{array}{l} u_t=d_1 \Delta u+u\left( a_1-q_1 u-\theta _1 v\right) , \\ v_t=d_2 \Delta v+v\left( a_2-\frac{\theta _2 v}{u}\right) . \end{array}\right. \end{aligned}$$

(1.3)

and demonstrated some special behavior of steady-state solutions of system (1.3) due to the introduction of spatial heterogeneity. Based on the above diffusion model, Zou and Guo [26] considered Leslie–Gower predator–prey system with cross-diffusion and proved the global existence and boundedness of solutions. Pal et al. [19] showed interacting prey-predator reaction–diffusion model with modified Leslie–Gower type and investigated Hopf bifurcations of steady states. Cheng et al. [4] focused on the free boundary problems for a Leslie–Gower predator–prey model with radial symmetry in a higher dimensional environment and proved the spreading-vanishing dichotomy.

In nature, species exist in heterogeneous environments and migrate to adapt to this environment. Usually, animals slow their migration when food resources are abundant, but they move diligently when food is consumed. Therefore, for purpose of describe this phenomenon, many researchers studied the predator–prey system with chemotaxis and found that the prey-taxis can induce complex spatiotemporal dynamics as the values of prey-taxis change [2, 14, 23]. In especially, Qiu and Guo [20, 21] added the chemotaxis term and positive constant K into system (1.3) and investigated local and global structure of nonconstant positive steady states of the following modified Leslie–Gower model with diffusion and chemotaxis:

$$\begin{aligned} \left\{ \begin{array}{l} u_t=d_1 \Delta u+a_1 u\left( 1-b_1u-r_1 v\right) , \\ v_t=d_2 \Delta v+\beta \nabla \cdot (v \nabla u)+a_2 v\left( 1-\frac{r_2 v}{u+K}\right) , \end{array}\right. \end{aligned}$$

(1.4)

where u and v are the density of prey and predator at at position $x\in {\mathbb {R}}^{N}$ and time t, respectively. $\Delta$ and $\nabla$ are the Laplacian and the gradient operators with respect to x, respectively. $d_1$ and $d_2$ are the diffusion coefficient of prey and predator, respectively. $\beta$ is the chemotactic sensitivity. $a_1$ and $a_2$ denote the growth rates of prey and predator, respectively. $b_1$ measures the strength of competition among individuals of species u. $r_1$ measures the strength of competition among individuals of species u and v. $r_2$ is a measure of the food quantity that the prey provides converted to predator birth. K measures the extent to which environment provides protection to predator v. The aforementioned constants are all positive.

Traveling wave solutions has been widely studied as a type of steady-state solutions due to its shift invariance while the existence is the prime problem in the study of traveling wave solutions compared with other qualitative properties. Cheng and Yuan [5] studied the existence and stability of the invasion traveling waves for the nonlocal Leslie–Gower predator–prey model without chemotaxis term. Tian et al. [24, 25] added the diffusion term in system (1.2) and obtained traveling wavefronts by using the upper and lower solutions method. In especially, Guo and Cheng [10, 11] discussed the existence of forced waves for a Leslie–Gower prey-predator model under shifting environment by constructing appropriate upper and lower solutions combined with the monotone iteration scheme. The result showed that there exists a forced wave with the speed in keeping with the habitat changing speed and the asymptotical behavior of traveling wave fronts in two tails.

However, to the best of our knowledge, there are no results on traveling wave solutions in the Leslie–Gower model when both the nonlinear chemotaxis term and the nonzero kinetic term are present, even for the modified Leslie–Gower system with Lotka-Volterra type [8, 9]. The main difficulty is that, on the one hand, the classical phase plane analysis (or the shooting method) seems not to work due to the existence of chemotaxis term; on the other hand, when the reaction term is not zero, we cannot develop the ideas in [12, 22] to express the wave profile u in terms of v. As such, we will comprehensively consider the influence of diffusion and chemotaxis on the dynamic behavior of the population model in this paper, especially on the existence and minimal wave speed of traveling wavefront solutions and the existence of periodic wave solutions. Firstly, we study the existence of traveling wavefronts of system (1.4) by applying the perturbation method [7]. Compared with the traditional upper and lower solutions method proving the existence of traveling wavefronts of reaction–diffusion equation, our method does not need to judge whether the reaction term of the equation is quasi-monotone. Our approach relates the existence of traveling wavefront solutions of system (1.4) to the existence of heteroclinic connecting orbits of an associated differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{u}}(t)=- a_1 u\left( 1-b_1u-r_1v \right) , \\ {\dot{v}}(t)=- a_2 v\left( 1-\frac{r_2v}{u+K}\right) , \end{array}\right. \end{aligned}$$

(1.5)

which has four equilibria $O = (0,0)^{T}$, $E_1=(\frac{1}{b_1},0)^T$, $E_2=(0,\frac{K}{r_2})^T$, $E_{*} = (u_{*},v_{*})^{T}$, where $u_{*} = \frac{r_2-r_1K}{r_1+b_1r_2}$ and $v_{*} = \frac{1+b_1K}{r_1+b_1r_2}$. In ecology, the most interesting question is the coexistence of multiple populations. For that reason, we always assume that the $r_2>r_1K$ hold. Moreover, the proof of this approach is based on an abstract formulation of the wave profile as a solution of an operator equation in a certain Banach space, coupled with an index formula of the associated Fredholm operator, some careful estimation of the nonlinear perturbation and the Banach contraction mapping principle. Nonetheless, the deficiency of the perturbation method proving the existence of traveling wavefronts is that the wave speed must be sufficiently large. To determine the minimum wave speed for which there exist traveling wavefronts, we use the standard stability analysis to study the minimal wave speed of traveling wavefronts and obtain that traveling wavefront solutions exist when the wave speed is greater than a certain critical value (i.e., the minimal wave speed) and disappears otherwise. Moreover, we also investigate the existence condition of periodic waves when traveling wavefronts disappears. Our results suggest that, on the one hand, when the extent to which environment provides protection to predator is sufficiently large and the wave speed is equal to zero, periodic waves exists; on the other hand, when the wave speed is not equal to zero, even if very small, periodic waves disappear.

This paper is organized as follows. Section 2 is devoted to the existence of the heteroclinic solutions of system (1.5). In Sect. 3, we transform system (1.4) into an operator equation involving a linear operator and a nonlinear perturbation. Section 4 is devoted to the study of the properties of L and ${\mathcal {H}}$ introduced in Sect. 3. The existence of traveling wavefront solutions is given in Sect. 5. Section 6 is provided the minimal wave speed of traveling wavefronts and discussed the existence condition of periodic waves. Finally in Sect. 7, our main result is illustrated by some numerical simulations.

2 Heteroclinic solutions of system (1.5)

In this section, we consider the existence of heteroclinic solutions of system (1.5) connecting $E_{*}$ to O. For system (1.5), we have the following lemma.

Lemma 2.1

System (1.5) has a family of heteroclinic solutions $U_*(t)=\left( u_*(t), v_*(t)\right) ^T: {\mathbb {R}} \rightarrow {\mathbb {R}}^2$ from $E_*$ to O. Namely, system (1.5) has a family of solutions $U_*(t)$ defined for $t \in {\mathbb {R}}$ such that $U_*(-\infty )=E_*$ and $\ U_*(+\infty )=O.$

Proof

Introducing the variable $t=-s$, system (1.5) can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{u}}(s)=a_1u\left( 1-b_1u-r_1v \right) , \\ {\dot{v}}(s)=a_2 v\left( 1-\frac{r_2v}{u+K}\right) . \end{array}\right. \end{aligned}$$

(2.1)

Linearizing system (2.1) around $O=(0,0)^T$ yields

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{u}}(s)=a_1u, \\ {\dot{v}}(s)=a_2v. \end{array}\right. \end{aligned}$$

It is easy to know that O is unstable. Furthermore, considering the following Lyapunov function:

$$\begin{aligned} V(u,v)=u-u_*-u_*\ln \frac{u}{u_*}+v-v_*-v_*\ln \frac{v}{v_*}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned}&V\left( u_*, v_*\right) =0, \quad \frac{\partial V(u, v)}{\partial u} =\left( 1-\frac{u_*}{u}\right) , \quad \frac{\partial V(u, v)}{\partial v}=\left( 1-\frac{v_*}{v}\right) , \\&\frac{\partial ^2 V(u, v)}{\partial u^2}=\frac{ u_*}{u^2}, \quad \frac{\partial ^2 V(u, v)}{\partial v^2}=\frac{ v_*}{v^2}, \quad \frac{\partial ^2 V(u, v)}{\partial u \partial v}=0. \end{aligned} \end{aligned}$$

Hence V(u, v) is positive definite in ${\mathbb {R}}_{+}^2$. Furthermore, it is easy to verify that as (u, v) approaches the boundary of ${\mathbb {R}}_{+}^2$, we have $V(u,v) \rightarrow +\infty$. Calculating the derivative of along the solution of system (2.1), we obtain

$$\begin{aligned} \begin{aligned} \frac{d V}{d t}&=\left( 1-\frac{u_*}{u}\right) \left( 1-b_1 u-r_1 v\right) a_1 u+\left( 1-\frac{v_*}{v}\right) \left( 1-\frac{r_2 v}{u+K}\right) a_2 v \\&=-a_1 b_1\left( u-u_*\right) ^2-a_1 r_1\left( v-v_*\right) \left( u-u_*\right) +a_2\left( v-v_*\right) \left( \frac{r_2\left( v_*-v\right) +\left( u-u_*\right) }{u+K}\right) \\&=-a_1 b_1\left( u-u_*\right) ^2-a_2 r_2 \frac{\left( v-v_*\right) ^2}{u+K}-\left( a_1 r_1-\frac{a_2}{u+K}\right) \left( v-v_*\right) \left( u-u_*\right) \\&=\left( u-u_*,v-v_*\right) \left( \begin{array}{cc} -a_1b_1 &{} \frac{a_2}{u+K} \\ -a_1r_1 &{} -\frac{a_2r_2}{u+K} \end{array}\right) \left( \begin{array}{c} u-u_* \\ v-v_* \end{array}\right) . \end{aligned} \end{aligned}$$

It follows

$$\begin{aligned} \begin{aligned} \left| \begin{array}{cc} -a_1b_1 &{} \frac{a_2}{u+K} \\ -a_1r_1 &{} -\frac{a_2r_2}{u+K} \end{array}\right| =\frac{a_1a_2(r_1+b_1r_2)}{u+K}>0, \end{aligned} \end{aligned}$$

that ${\dot{V}}(u,v)$ is negative definite. From the Lyapunov stability theorem, we know that the unique positive equilibrium $E_*=\left( u_*, v_*\right) ^T$ of system (2.1) is globally uniformly asymptotically stable, i.e., all solutions $E(s)=(u(s), v(s))$ of system (2.1) with the initial condition $E(0) \ge 0$ satisfy $E(s) \rightarrow E_*$ as $s \rightarrow +\infty$.

Due to the global attractivity of $E_*$ and the instability of O, one readily gets the desired heteroclinic solution connecting O to $E_*$, i.e., system (2.1) has a heteroclinic solution ${\bar{E}}(s)=\left( {\bar{u}}(s), {\bar{v}}(s)\right) ^T: {\mathbb {R}} \rightarrow {\mathbb {R}}^2$ from O to $E_{*}$ such that ${\bar{E}}(-\infty )=O$ and ${\bar{E}}(+\infty )=E_*$. Consequently, system (1.5) has a heteroclinic solution $U_*(t)=\left( u_*(t), v_*(t)\right) ^T: {\mathbb {R}} \rightarrow {\mathbb {R}}^2$ from $E_*$ to O such that $U_*(-\infty )=E_*$ and $U_*(+\infty )=O$. This completes the proof. $\square$

3 Operator equation

Our main idea in studying the existence of traveling wavefront solutions of system (1.4) is to convert the differential equation for a traveling wave into an equivalent operator equation in a suitable Banach space. For convenience of further discussion, we firstly introduce some notations. Let $C=C({\mathbb {R}}, {\mathbb {R}}^2)$ be continuous function space equipped with the supremum norm and $C_0=\left\{ \psi \in C: \lim _{z \rightarrow \pm \infty } \psi (z)=0\right\}$.

Introducing the traveling wave variable $z=\nu \cdot x-c t$ and $u(x, t)={\tilde{u}}(z), v(x, t)={\tilde{v}}(z)$ with a unit vector $\nu$, then system (1.4) can be rewrittem as follows:

$$\begin{aligned} \left\{ \begin{array}{l} d_1\ddot{{\tilde{u}}}(z)+a_1{\tilde{u}}(z)\left( 1-b_1{\tilde{u}}(z)-r_1{\tilde{v}}(z)\right) +c\dot{{\tilde{u}}}(z)=0, \\ d_2 \ddot{{\tilde{v}}}(z)+ \beta \left( \dot{{\tilde{v}}}(z)\dot{{\tilde{u}}}(z)+{\tilde{v}}(z) \ddot{{\tilde{u}}}(z)\right) +a_2{\tilde{v}}(z)\left( 1-\frac{r_2{\tilde{v}}(z)}{{\tilde{u}}(z)+K}\right) +c\dot{{\tilde{v}}}(z)=0. \end{array}\right. \end{aligned}$$

(3.1)

Let further ${\mathcal {U}}(z)={\tilde{u}}(c z), {\mathcal {V}}(z)={\tilde{v}}(c z)$ and $\varepsilon =\frac{1}{c^2}$. we rewrite system (3.1) as

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon d_1 \ddot{{\mathcal {U}}}(z)+a_1{\mathcal {U}}(z)\left( 1-b_1{\mathcal {U}}(z)-r_1{\mathcal {V}}(z)\right) +\dot{{\mathcal {U}}}(z)=0, \\ \varepsilon d_2 \mathcal {\ddot{V}}(z)+\varepsilon \beta \left( \mathcal {{\dot{V}}}(z)\mathcal {{\dot{U}}}(z)+{\mathcal {V}}(z) \mathcal {\ddot{U}}(z)\right) +a_2{\mathcal {V}}(z)\left( 1-\frac{r_2{\mathcal {V}}(z)}{{\mathcal {U}}(z)+K}\right) +\dot{{\mathcal {V}}}(z)=0. \end{array}\right. \end{aligned}$$

(3.2)

Obviously, when c is large, $\varepsilon$ is small. If $\varepsilon$=0, then Eq. (3.2) reduces to Eq. (1.5). We further transform Eq. (3.2) by introducing the variable $W(z)=\left( w_1(z), w_2(z)\right) ^T$, where $w_1(z)={\mathcal {U}}(z)-u_*(z), w_2(z)={\mathcal {V}}(z)-v_*(z)$ for $z \in {\mathbb {R}}$ and $\left( u_*, v_*\right)$ is the heteroclinic solution in Lemma 2.1, then we obtain the following equation for W from Eq. (3.2):

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon d_1 \ddot{w}_1(z)+{\dot{w}}_1(z)-w_1(z) = -w_1(z)-{\mathcal {I}}_1 W(z)-M_1(\varepsilon , z, W), \\ \varepsilon d_2 \ddot{w}_2(z)+{\dot{w}}_2(z)-w_2(z) = -w_2(z)-{\mathcal {I}}_2 W(z)-M_2(\varepsilon , z, W), \end{array}\right. \end{aligned}$$

(3.3)

where the linear operator ${\mathcal {I}}_i(i = 1, 2)$ and the nonlinear operator $M_i(i = 1, 2)$ are defined as

$$\begin{aligned} \begin{aligned}&{\mathcal {I}}_1 W(z)=a_1\left[ 1-2b_1u_*(z)-r_1v_*(z)\right] w_1(z)-a_1r_1u_*(z)w_2(z),\\ {}&{\mathcal {I}}_2 W(z)=a_2\frac{r_2v_*^2(z)}{(u_*(z)+K)^2}w_1(z)+a_2\left( 1-\frac{2r_2v_*(z)}{u_*(z)+K}\right) w_2(z), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} M_1(\varepsilon , z,W)=&\varepsilon d_1 \ddot{u}_*(z)-a_1\left[ b_1w_1(z)+r_1w_2(z)\right] w_1(z), \\ M_2(\varepsilon , z, W)=&\varepsilon \beta [\left( {\dot{w}}_2(z)+{\dot{v}}_*(z)\right) \left( {\dot{w}}_1(z) +{\dot{u}}_*(z)\right) +(w_2(z)+v_*(z))(\ddot{w}_1(z)+\ddot{u}_*(z))] \\&+a_2[w_2(z)+v_*(z)]\left( 1-\frac{r_2(w_2(z)+v_*(z))}{w_1(z)+u_*(z)+K}\right) +\varepsilon d_2 \ddot{v}_*(z)-{\mathcal {I}}_2 W(z)\\&-a_2v_*(z)\left( 1-\frac{r_2v_*(z)}{u_*(z)+K}\right) . \end{aligned} \end{aligned}$$

Noticing that for each $i=1,2$, the equation $\varepsilon d_i \lambda ^2+\lambda -1=0$ has two zeros $\lambda _{i 1}(\varepsilon )$ and $\lambda _{i 2}(\varepsilon )$ with

$$\begin{aligned} \lambda _{i 1}(\varepsilon )=\frac{-1-\sqrt{1+4 \varepsilon d_i}}{2 \varepsilon d_i}<0,\ \ \ \lambda _{i 2}(\varepsilon )=\frac{-1+\sqrt{1+4 \varepsilon d_i}}{2 \varepsilon d_i}>0. \end{aligned}$$

For each $i \in \{1,2\}, j \in \{1,2\}$ and $\varepsilon >0$, let $p_{i j}(\varepsilon , t)=\frac{e^{\lambda _{i j}(\varepsilon ) t}}{\sqrt{1+4 \varepsilon d_i}}.$ Then W(z) is a bounded solution of Eq. (3.3) if and only if W(z) solves

$$\begin{aligned}{}[L W](z)={\mathcal {H}}(\varepsilon , z, W), \quad z \in {\mathbb {R}}, \end{aligned}$$

(3.4)

where the linear operator $L: C_0 \rightarrow C_0$ and the nonlinear operator ${\mathcal {H}}=\left( {\mathcal {H}}_1, {\mathcal {H}}_2\right) ^T:(0,\infty )\times {\mathbb {R}} \times C_0 \rightarrow {\mathbb {R}}^2$ are defined as

$$\begin{aligned}{}[L W](z)=\left( \begin{array}{c} \begin{aligned} w_1(z)-\int \limits _z^{+\infty } e^{(z-t)}\left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] \textrm{d} t \\ w_2(z)-\int \limits _z^{+\infty } e^{(z-t)}\left[ w_2(t)+{\mathcal {I}}_2 W(t)\right] \textrm{d} t \end{aligned} \end{array}\right) , \end{aligned}$$

(3.5)

and

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_1(\varepsilon , z, W)=&\int \limits _z^{+\infty }\left[ p_{12}(\varepsilon , z-t) -e^{(z-t)}\right] \left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] +p_{12}(\varepsilon , z-t) M_1(\varepsilon , t, W) \textrm{d} t \\&+\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t)\left[ w_1(t)+{\mathcal {I}}_1 W(t)+M_1(\varepsilon , t, W)\right] \textrm{d} t, \\ {\mathcal {H}}_2(\varepsilon , z, W)=&\int \limits _z^{+\infty }\left[ p_{22}(\varepsilon , z-t) -e^{(z-t)}\right] \left[ w_2(t)+{\mathcal {I}}_2 W(t)\right] +p_{22}(\varepsilon , z-t) M_2(\varepsilon , t, W) \textrm{d} t \\&+\int \limits _{-\infty }^z p_{21}(\varepsilon , z-t)\left[ w_2(t)+{\mathcal {I}}_2 W(t)+M_2(\varepsilon , t, W)\right] \textrm{d} t,\\ \end{aligned} \end{aligned}$$

respectively. By this means, we show that system (1.4) has a traveling wavefront solution $\gamma (z): {\mathbb {R}} \rightarrow {\mathbb {R}}^2$ connecting $E_*$ to O if and only if Eq. (3.4) has a solution $W\in C_0$. Therefore, our goal is to show the existence of solution of Eq. (3.4). We shall achieve this by using the Banach fixed point theorem. For this purpose, we need further detailed properties of the linear operator L and the nonlinear operator ${\mathcal {H}}$.

4 Properties of L and ${\mathcal {H}}$

The purpose of this section is to obtain the detailed properties of the linear operator L and the nonlinear operator ${\mathcal {H}}$.

4.1 Properties of L

Let ${\mathcal {N}}(L)$ denotes the null space of L. By the definition (3.5), we know that $L W=0$ if and only if

$$\begin{aligned} \left( \begin{array}{l} {w}_1(z) \\ \\ {w}_2(z) \end{array}\right) =\left( \begin{array}{c} \displaystyle \int \limits _z^{+\infty } e^{(z-t)}\left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] \textrm{d} t \\ \displaystyle \int \limits _z^{+\infty } e^{(z-t)}\left[ w_2(t)+{\mathcal {I}}_2 W(t)\right] \textrm{d} t \end{array}\right) . \end{aligned}$$

(4.1)

By differentiating Eq. (4.1), we see that $L W=0$ if and only if

$$\begin{aligned} \left( \begin{array}{l} {\dot{w}}_1(z) \\ \\ {\dot{w}}_2(z) \end{array}\right) =-\left( \begin{array}{c} {\mathcal {I}}_1 W(z) \\ \\ {\mathcal {I}}_2 W(z) \end{array}\right) . \end{aligned}$$

(4.2)

Equation (4.2) can be rewritten as the following equation

$$\begin{aligned} {\dot{W}}(z)=A(z) W(z), \end{aligned}$$

where

$$\begin{aligned} A(z)=\left( \begin{array}{cc} -a_1\left[ 1-2b_1u_*(z)-r_1v_*(z)\right] &{} a_1r_1u_*(z) \\ \\ -a_2\frac{r_2v_*^2(z)}{\left( u_*(z)+K\right) ^2} &{} -a_2\left( 1-\frac{2r_2v_*(z)}{u_*(z)+K}\right) \end{array}\right) . \end{aligned}$$

Now, we define a linear operator $T: C^1 \rightarrow C$ by

$$\begin{aligned} (T W)(z)={\dot{W}}(z)-A(z) W(z). \end{aligned}$$

So, $L W=0$ if and only if $T W=0$, i.e., we have the following result.

Lemma 4.1

${\text {dim}} {\mathcal {N}}(L)={\text {dim}} {\mathcal {N}}(T)$, where ${\mathcal {N}}(T)$ denotes the null space of T.

Furthermore, we define the formal adjoint equation of $T W=0$ as

$$\begin{aligned} {\dot{\phi }}(z)+A^*(z) \phi (z)=0, \end{aligned}$$

(4.3)

where

$$\begin{aligned} A^*(z)=\left( \begin{array}{cc} -a_1\left[ 1-2b_1u_*(z)-r_1v_*(z)\right] &{} -a_2\frac{r_2v_*^2(z)}{(u_*(z)+K)^2} \\ \\ a_1r_1u_*(z) &{} -a_2\left( 1-\frac{2r_2v_*(z)}{u_*(z)+K}\right) \end{array}\right) . \end{aligned}$$

By using the variation of constants formula, we obtain the following result on the solution to the formal adjoint equation of $T W=0$.

Lemma 4.2

If $\phi \in C^1$ is a solution of equation (4.3), then $\phi =0$.

Proof

Let $\phi$ be an arbitrary bounded solution of Eq. (4.3), then we have

$$\begin{aligned} {\dot{\phi }}(z)=-A^*(z) \phi (z). \end{aligned}$$

The limiting equation of the above equation as $z \rightarrow +\infty$ is

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\phi }}_1(z)=a_1\phi _1(z), \\ {\dot{\phi }}_2(z)=a_2\phi _2(z). \end{array}\right. \end{aligned}$$

Obviously, every nonzero solution of the above equation grows exponentially as $z \rightarrow +\infty$. Therefore, every bounded solution of Eq. (4.3) is identically equal to zero. This completes the proof. $\square$

Lemma 4.3

${\mathcal {R}}(T)=C$, where ${\mathcal {R}}(T)$ denotes the range of T.

Proof

It follows from the Fredholm theorem that ${\mathcal {R}}(T)=\{\phi \in C: \int \limits _{-\infty }^{\infty } h(t) \phi (t) \textrm{d} t=0.$ for an arbitrary bounded solution $\phi (\cdot )$ of Eq. (4.3)}. In view of Lemma 4.2, we have ${\mathcal {R}}(T)=C$. This completes the proof. $\square$

Next, we shall prove that ${\mathcal {R}}(L)=C_0$, where ${\mathcal {R}}(L)$ denotes the range of L. That is, for each $R=\left( r_1, r_2\right) ^T \in$ $C_0$, we need to show that there exists $W \in C_0$ such that $L W=R$, or equivalently,

$$\begin{aligned} \left( \begin{array}{l} w_1(z) \\ \\ w_2(z) \end{array}\right) -\left( \begin{array}{c} \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] \textrm{d} t \\ \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ w_2(t)+{\mathcal {I}}_2 W(t)\right] \textrm{d} t \end{array}\right) =\left( \begin{array}{c} r_1(z) \\ \\ r_2(z) \end{array}\right) , \end{aligned}$$

(4.4)

has a solution in $C_0$. To this end, we let $G(z)=W(z)-R(z)=\left( g_1(z), g_2(z)\right) ^T$. Upon a substitution, we obtain the following equation for G

$$\begin{aligned} \left( \begin{array}{l} g_1(z) \\ \\ g_2(z) \end{array}\right) =\left( \begin{array}{c} \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ g_1(t)+{\mathcal {I}}_1 G(t)\right] \textrm{d} t \\ \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ g_2(t)+{\mathcal {I}}_2 G(t)\right] \textrm{d} t \end{array}\right) +\left( \begin{array}{c} \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ r_1(t)+{\mathcal {I}}_1 R(t)\right] \textrm{d} t \\ \displaystyle \int \limits _{z}^{+\infty } e^{(z-t)}\left[ r_2(t)+{\mathcal {I}}_2 R(t)\right] \textrm{d} t \end{array}\right) . \end{aligned}$$

Differentiating the above equation yields that

$$\begin{aligned} \left( \begin{array}{l} {\dot{g}}_1(z) \\ \\ {\dot{g}}_2(z) \end{array}\right) =-\left( \begin{array}{c} {\mathcal {I}}_1 G(z)+r_1(z)+{\mathcal {I}}_1 R(z) \\ \\ {\mathcal {I}}_2 G(z)+r_2(z)+{\mathcal {I}}_2 R(z) \end{array}\right) . \end{aligned}$$

Thus, we get

$$\begin{aligned} (T G)(z)=Y(z) \triangleq -\left( \begin{array}{c} r_1(z)+{\mathcal {I}}_1 R(z) \\ \\ r_2(z)+{\mathcal {I}}_2 R(z) \end{array}\right) . \end{aligned}$$

(4.5)

From the expression of ${\mathcal {I}}_i(i=1,2)$, we obtain $Y(z) \in C_0$. For Eq. (4.5), we get the following result.

Lemma 4.4

Let $Y \in C_0$ be given. If $\psi$ is a bounded solution of the equation $T \psi =Y$, then $\psi \in C_0^1$.

Proof

From Lemma 4.3, we know that for any $Y \in C_0$, there exists a function $\psi \in C^1$ satisfying $T \psi =Y$, that is

$$\begin{aligned} {\dot{\psi }}(z)-A(z) \psi (z)=Y(z). \end{aligned}$$

(4.6)

When $z \rightarrow +\infty$ Eq. (4.6) asymptotically tends to

$$\begin{aligned} {\dot{\psi }}(z)=\left( \begin{array}{c} - a_1 \psi _1(z) \\ \\ - a_2 \psi _2(z) \end{array}\right) . \end{aligned}$$

(4.7)

We know that the $\omega$-limit set of every bounded solution to Eq. (4.7) is just the point $\psi =0$. As $z \rightarrow -\infty$ Eq. (4.6) asymptotically tends to

$$\begin{aligned} \left( \begin{array}{cc} \dot{\psi _1}(z) \\ \\ \dot{\psi _2}(z) \end{array}\right) =\left( \begin{array}{cc} a_1b_1u_* &{} a_1r_1u_* \\ \\ -\frac{a_2}{r_2} &{} a_2 \end{array}\right) \left( \begin{array}{cc} \psi _1(z) \\ \\ \psi _2(z) \end{array}\right) . \end{aligned}$$

(4.8)

It is obvious that any bounded solution to Eq. (4.8) is the zero solution. Therefore, from Theorem 1.8 in [16], we conclude that every bounded solution component of Eq. (4.6) satisfies $\lim _{|z| \rightarrow +\infty } \psi (z)=0$, i.e., $\psi \in C_0^1$. This completes the proof. $\square$

In view of Lemma 4.4, Eq. (4.5) has a solution $G \in C_0^1$. Consequently, $W=G+R \in C_0$ is a solution of Eq. (4.4). Hence, we can get the following result.

Lemma 4.5

${\mathcal {R}}(L)=C_0$, where ${\mathcal {R}}(L)$ denotes the range of L.

4.2 Properties of ${\mathcal {H}}$

Next, we study the properties of ${\mathcal {H}}(\varepsilon , z, W)$. For ${\mathcal {H}}_1(\varepsilon , z, W)$, we have

$$\begin{aligned} {\mathcal {H}}_1(\varepsilon , z, W) \le \left| {\mathcal {H}}_{11}(\varepsilon , z, W)\right| +\left| {\mathcal {H}}_{12}(\varepsilon , z, W)\right| +\left| {\mathcal {H}}_{13}(\varepsilon , z, W)\right| , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}_{11}(\varepsilon , z, W)=\int \limits _{z}^{+\infty }\left[ p_{12}(\varepsilon , z-t) -e^{(z-t)}\right] \left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] \textrm{d} t, \\&{\mathcal {H}}_{12}(\varepsilon , z, W)=\int \limits _{-\infty }^{z} p_{11}(\varepsilon , z-t) \left[ w_1(t)+{\mathcal {I}}_1 W(t)\right] \textrm{d} t, \\&{\mathcal {H}}_{13}(\varepsilon , z, W)=\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) {M}_1(\varepsilon , t, W) \textrm{d} t+\int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) {M}_1(\varepsilon , t, W) \textrm{d} t. \end{aligned} \end{aligned}$$

Lemma 4.6

For $W \in C_0$ and small $\varepsilon \ge 0$, we have

• (i) $\left| {\mathcal {H}}_{11}(\varepsilon , z, W)\right| =O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}$;

• (ii) $\left| {\mathcal {H}}_{12}(\varepsilon , z, W)\right| =O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}$;

• (iii) $\left| {\mathcal {H}}_{13}(\varepsilon , z, W)\right| =O\left( \varepsilon \right) +O\left( \Vert W\Vert _C^2\right) +O\left( \varepsilon \Vert W\Vert _C^2\right) , \quad \varepsilon \rightarrow 0^{+}$.

Proof

(i) For $z \in {\mathbb {R}}$ and $\varepsilon \ge 0$, we have

$$\begin{aligned} \begin{aligned}&\int \limits _{z}^{+\infty }\left| p_{12}(\varepsilon , z-t)-e^{(z-t)}\right| \textrm{d} t \\&\quad = \frac{1}{\sqrt{1+4 \varepsilon d_1}} \int \limits _{z}^{+\infty }\left| e^{\lambda _{12}(\varepsilon )(z-t)}-\sqrt{1+4 \varepsilon d_1} e^{(z-t)}\right| \textrm{d} t \\&\quad =\frac{1}{\sqrt{1+4 \varepsilon d_1}} \int \limits _{z}^{+\infty }\left| e^{\lambda _{12}(\varepsilon )(z-t)}\left( 1-\sqrt{1+4 \varepsilon d_1}\right) +\sqrt{1+4 \varepsilon d_1}\left( e^{\lambda _{12}(\varepsilon )( z-t)}-e^{(z-t)}\right) \right| \textrm{d} t \\&\qquad \le \frac{\sqrt{1+4 \varepsilon d_1}-1}{\sqrt{1+4 \varepsilon d_1}} \int \limits _{z}^{+\infty } e^{\lambda _{12}(\varepsilon )(z-t)} \textrm{d} t+\int \limits _{z}^{+\infty }\left| e^{\lambda _{12}(\varepsilon )(z-t)}-e^{(z-t)}\right| \textrm{d} t. \end{aligned} \end{aligned}$$

Since $\lambda _{12}(\varepsilon )< 1$, for $z \le t$, we obtain

$$\begin{aligned} \left| e^{\lambda _{12}(\varepsilon )(z-t)}-e^{(z-t)}\right| =e^{\lambda _{12}(\varepsilon )(z-t)}-e^{(z-t)}. \end{aligned}$$

It follows from inequality and equality that

$$\begin{aligned} \int \limits _{z}^{+\infty }\left| p_{12}(\varepsilon , z-t)-e^{(z-t)}\right| \textrm{d} t \le \frac{\sqrt{1+4 \varepsilon d_1}-1}{\sqrt{1+4 \varepsilon d_1}}\left( \frac{1}{\lambda _{12}(\varepsilon )}\right) +\left[ \frac{1}{\lambda _{12}(\varepsilon )}-1\right] . \end{aligned}$$

Noticing that $\lambda _{12}(\varepsilon ) \rightarrow 1$ as $\varepsilon \rightarrow 0^{+}$, we obtain from the above inequality that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^{+}} \int \limits _{z}^{+\infty }\left| p_{12}(\varepsilon , z-t)-e^{(z-t)}\right| \textrm{d} t=0. \end{aligned}$$

Next let $K_{11}=1+\Vert {\mathcal {I}}_1\Vert _{{\mathcal {L}}\left( C_0, C_0\right) }$. Then we have

$$\begin{aligned} \begin{aligned} \left| {\mathcal {H}}_{11}(\varepsilon , z, W)\right|&\le K_{11} \int \limits _{z}^{+\infty }\left| p_{12}(\varepsilon , z-t)-e^{(z-t)}\right| \textrm{d} t\Vert W\Vert _C \\&\quad =O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

(ii) In view of $\lambda _{11}(\varepsilon ) \rightarrow -\infty$ as $\varepsilon \rightarrow 0^{+}$, we obtain

$$\begin{aligned} \begin{aligned} \left| {\mathcal {H}}_{12}(\varepsilon , z, W)\right|&\le K_{11} \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) \textrm{d} t\Vert W\Vert _C \\&=-\frac{K_{11}}{\lambda _{11}(\varepsilon ) \sqrt{1+4 \varepsilon d_1}}\Vert W\Vert _C=O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

(iii) Noticing that $\ddot{u}_*$ is bounded in C. Moreover, in view of $\lambda _{12}(\varepsilon ) \rightarrow 1$ as $\varepsilon \rightarrow 0^{+}$, there are constants $\varepsilon ^*>0$ and $K_{12}>0$ such that $\left| \displaystyle \int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) \textrm{d} t\right| \le K_{12}$ for all $\varepsilon \in \left[ 0, \varepsilon ^*\right]$. Hence, we can get

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t)\varepsilon d_1\ddot{u}_*(z) \textrm{d} t+\int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) \varepsilon d_1 \ddot{u}_*(z)\textrm{d} t\right| \\&\le \varepsilon d_1\left| \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) \textrm{d} t\right| \left\| \ddot{u}_*\right\| _C+\varepsilon d_1 \left| \int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) \textrm{d} t\right| \left\| \ddot{u}_*\right\| _C \\&\le \varepsilon d_1 \left( \frac{1}{|\lambda _{11}(\varepsilon )|}+K_{12}\right) \left\| \ddot{u}_*\right\| _C\\&= O(\varepsilon ), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Let ${\tilde{M}}_{1}(\varepsilon , t, W)=-a_1b_1w_1^2(t)-a_1r_2w_1(t)w_2(t).$ For ${\tilde{M}}_{1}(\varepsilon , t, W)$, we know that there is some $K_{13}>0$ such that $\left| {\tilde{M}}_{1}(\varepsilon , t, W)\right| \le K_{13}\Vert W\Vert _C^2$. Thus, we have

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) {\tilde{M}}_{1}(\varepsilon , t, W) \textrm{d} t\right| +\left| \int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) {\tilde{M}}_{1}(\varepsilon , t, W) \textrm{d} t\right| \\&\le \left| \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) \textrm{d} t\right| K_{13}\Vert W\Vert _C^2+\left| \int \limits _z^{+\infty } p_{12}(\varepsilon , z-t) \textrm{d} t\right| K_{13}\Vert W\Vert _C^2 \\&\le \frac{K_{13}\Vert W\Vert _C^2}{|\lambda _{11}(\varepsilon )|}+K_{12} K_{13}\Vert W\Vert _C^2\\&=O\left( \Vert W\Vert _C^2\right) +O\left( \varepsilon \Vert W\Vert _C^2\right) , \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

The proof is completed. $\square$

Next, we estimate ${\mathcal {H}}_2(\varepsilon , z, W)$. For ${\mathcal {H}}_2(\varepsilon , z, W)$, we get

$$\begin{aligned} {\mathcal {H}}_2(\varepsilon , z, W) \le \left| {\mathcal {H}}_{21}(\varepsilon , z, W)\right| +\left| {\mathcal {H}}_{22}(\varepsilon , z, W)\right| +\left| {\mathcal {H}}_{23}(\varepsilon , z, W)\right| , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}_{21}(\varepsilon , z, W)=\int \limits _{z}^{+\infty }\left[ p_{22}(\varepsilon , z-t) -e^{(z-t)}\right] \left[ w_2(t)+{\mathcal {I}}_2 W(t)\right] \textrm{d} t, \\&{\mathcal {H}}_{22}(\varepsilon , z, W)=\int \limits _{-\infty }^{z} p_{21}(\varepsilon , z-t)\left[ w_2(t) +{\mathcal {I}}_2 W(t)\right] \textrm{d} t, \\&{\mathcal {H}}_{23}(\varepsilon , z, W)=\int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) {M}_2(\varepsilon , t, W) \textrm{d} t+\int \limits _z^{+\infty } p_{22}(\varepsilon , z-t) {M}_2(\varepsilon , t, W) \textrm{d} t, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&{M}_2(\varepsilon , t, W)={M}_{21}(\varepsilon , t, W)+{M}_{22}(\varepsilon , t, W) +{M}_{23}(\varepsilon , t, W)+{M}_{24}(\varepsilon , t, W),\\&{M}_{21}(\varepsilon , t, W)=\varepsilon d_2 \ddot{v}_*(t) +\varepsilon \beta [{\dot{v}}_*(t){\dot{u}}_*(t)+v_*(t)\ddot{u}_*(t)],\\&{M}_{22}(\varepsilon , t, W)= \varepsilon \beta [{\dot{w}}_2(t){\dot{w}}_1(t) +{\dot{v}}_*(t){\dot{w}}_1(t)+w_2(t)\ddot{w}_1(t)+{v}_*(t)\ddot{w}_1(t)],\\&{M}_{23}(\varepsilon , t, W)= \varepsilon \beta [{\dot{u}}_*(t){\dot{w}}_2(t)+\ddot{u}_*(t)w_2(t)],\\&{M}_{24}(\varepsilon , t, W)= a_2r_2\left( \frac{2w_2(t)v_*(t)+v_*^2(t)}{u_*(t)+K} -\frac{v_*^2(t)w_1(t)}{(u_*(t)+K)^2}-\frac{\left( w_2(t)+v_*(t)\right) ^2}{w_1(t)+u_*(t)+K}\right) .\\ \end{aligned} \end{aligned}$$

For ${\mathcal {H}}_{21}(\varepsilon , z, W)$ and ${\mathcal {H}}_{22}(\varepsilon , z, W)$, similar prove to Lemma 4.6, we can get the following result.

Lemma 4.7

• (i) $\left| {\mathcal {H}}_{21}(\varepsilon , z, W)\right| =O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}$.

• (ii) $\left| {\mathcal {H}}_{22}(\varepsilon , z, W)\right| =O\left( \varepsilon \Vert W\Vert _C\right) , \quad \varepsilon \rightarrow 0^{+}$.

Next, we study the properties of ${\mathcal {H}}_{23}(\varepsilon , z, W)$. For ${\mathcal {H}}_{23}(\varepsilon , z, W)$, we obtain

$$\begin{aligned} {\mathcal {H}}_{23}(\varepsilon , z, W) \le \left| \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) {M}_2(\varepsilon , t, W) \textrm{d} t\right| +\left| \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t) {M}_2(\varepsilon , t, W) \textrm{d} t\right| . \end{aligned}$$

For $\left| \displaystyle \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t){M}_{21}(\varepsilon , t, W) \textrm{d} t\right| + \left| \displaystyle \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t){M}_{21}(\varepsilon , t, W) \textrm{d} t\right|$, noticing that $\ddot{v}_*$, ${\dot{v}}_*$, ${\dot{u}}_*$, $v_*$ and $\ddot{u}_*$ are bound in C, we get

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) {M}_{21}(\varepsilon , t, W) \textrm{d} t \right| +\left| \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t) {M}_{21}(\varepsilon , t, W) \textrm{d} t \right| \\&\quad \le \frac{\varepsilon }{\sqrt{1+4 \varepsilon d_2}}\left[ \frac{1}{\lambda _{22}(\varepsilon )}-\frac{1}{\lambda _{21}(\varepsilon )}\right] \left[ d_2\left\| \ddot{v}_*\right\| _C+ \beta \left( \Vert {\dot{v}}_*\Vert _C\Vert {\dot{u}}_*\Vert _C+\Vert v_*\Vert _C\Vert \ddot{u}_*\Vert _C\right) \right] \\ {}&\qquad = O(\varepsilon ), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

In order to estimate $\left| \displaystyle \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t){M}_{22}(\varepsilon , t, W) \textrm{d} t\right| + \left| \displaystyle \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t){M}_{22}(\varepsilon , t, W) \textrm{d} t\right|$, let us return to the integral form of $w_1$ in Eq. (3.5), then we have

$$\begin{aligned} \begin{aligned} w_1(z)=&\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t)\left[ w_1(t)+{\mathcal {I}}_1 W(t)+M_1(\varepsilon , t, W)\right] \textrm{d} t \\&+\int \limits _z^{+\infty }p_{12}(\varepsilon , z-t)\left[ w_1(t)+{\mathcal {I}}_1 W(t)+ M_1(\varepsilon , t, W)\right] \textrm{d} t.\\ \end{aligned} \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \begin{aligned} {\dot{w}}_1(z)=&\lambda _{11}(\varepsilon )\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t)\left[ w_1(t)+{\mathcal {I}}_1 W(t) +M_1(\varepsilon , t, W)\right] \textrm{d} t\\&+\lambda _{12}(\varepsilon ) \int \limits _z^{+\infty }p_{12}(\varepsilon , z-t)\left[ w_1(t)+{\mathcal {I}}_1 W(t) + M_1(\varepsilon , t, W)\right] \textrm{d} t, \\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \ddot{w}_1(z)=&\lambda _{11}^2(\varepsilon )\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t)\left[ w_1(t) +{\mathcal {I}}_1 W(t)+M_1(\varepsilon , t, W)\right] \textrm{d} t\\&+\lambda _{12}^2(\varepsilon ) \int \limits _z^{+\infty }p_{12}(\varepsilon , z-t)\left[ w_1(t) +{\mathcal {I}}_1 W(t)+ M_1(\varepsilon , t, W)\right] \textrm{d} t \\&- \frac{1}{\varepsilon d_1}\left[ w_1(z)+{\mathcal {I}}_1 W(z)+M_1(\varepsilon , z, W)\right] . \end{aligned} \end{aligned}$$

Then, we get

$$\begin{aligned} \begin{aligned} |{\dot{w}}_1(z)|\le&\left| \lambda _{11}(\varepsilon )\right| \int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) \left| w_1(t)+{\mathcal {I}}_1 W(t)+ M_1(\varepsilon , t, W)\right| \textrm{d} t \\&+\lambda _{12}(\varepsilon ) \int \limits _z^{+\infty }p_{12}(\varepsilon , z-t)\left| w_1(t)+{\mathcal {I}}_1 W(t) + M_1(\varepsilon , t, W)\right| \textrm{d} t \\ \le&2\left[ K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right] , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |\ddot{w}_1(z)|\le&\lambda _{11}^2(\varepsilon )\int \limits _{-\infty }^z p_{11}(\varepsilon , z-t) \left| w_1(t)+{\mathcal {I}}_1 W(t)+M_1(\varepsilon , t, W)\right| \textrm{d} t\\&+ \lambda _{12}^2(\varepsilon ) \int \limits _z^{+\infty }p_{12}(\varepsilon , z-t)\left| w_1(t) +{\mathcal {I}}_1 W(t)+ M_1(\varepsilon , t, W)\right| \textrm{d} t \\&+ \frac{1}{\varepsilon d_1}\left| w_1(z)+{\mathcal {I}}_1 W(z)+M_1(\varepsilon , z, W)\right| \\ \le&\frac{2}{\varepsilon d_1}\left[ K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right] . \end{aligned} \end{aligned}$$

(4.9)

From the definition of ${M}_{22}(\varepsilon , t, W)$, we have

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t){M}_{22}(\varepsilon , t, W) \textrm{d} t\right| \\ \le&\varepsilon \beta \left( \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{w}}_2(t){\dot{w}}_1(t) \textrm{d} t\right| +\left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{v}}_*(t){\dot{w}}_1(t) \textrm{d} t\right| \right) \\&+\varepsilon \beta \left( \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) w_2(t)\ddot{w}_1(t)\textrm{d} t\right| +\left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) v_*(t)\ddot{w}_1(t)\textrm{d} t\right| \right) . \end{aligned} \end{aligned}$$

For $\varepsilon \beta \left| \displaystyle \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{w}}_2(t){\dot{w}}_1(t) \textrm{d} t\right|$, we have

$$\begin{aligned} \begin{aligned}&\varepsilon \beta \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{w}}_2(t){\dot{w}}_1(t) \textrm{d} t\right| \\ \le&\varepsilon \beta \left( \left| w_2(z){\dot{w}}_1(z)\right| +\left| \int \limits _{z}^{+\infty }|\lambda _{22}(\varepsilon )|p_{22}(\varepsilon ,z-t)w_2(t){\dot{w}}_1(t) \textrm{d} t\right| +\left| \int \limits _{z}^{+\infty }p_{22}(\varepsilon ,z-t)w_2(t)\ddot{w}_1(t)\textrm{d} t\right| \right) \\ \le&4 \varepsilon \beta \Vert W\Vert _C\left( K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right) +\varepsilon \beta \left| \int \limits _{z}^{+\infty }p_{22}(\varepsilon ,z-t)\textrm{d} t\right| \left| w_2(z)\right| \left| \ddot{w}_1(z)\right| \\ \le&\beta \left( 4 \varepsilon +\frac{2 }{\lambda _{22}(\varepsilon ) d_1}\right) \Vert W\Vert _C\left( K_{11}\Vert W\Vert _C + \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right) \\ =&O(\varepsilon \Vert W\Vert _C)+O(\Vert W\Vert ^2_C)+O(\Vert W\Vert ^3_C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Moreover, for $\varepsilon \beta \left( \left| \displaystyle \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{v}}_*(t){\dot{w}}_1(t) \textrm{d} t\right| +\left| \displaystyle \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) w_2(t)\ddot{w}_1(t) \textrm{d} t\right| \right)$, we yield

$$\begin{aligned} \begin{aligned}&\varepsilon \beta \left( \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) {\dot{v}}_*(t){\dot{w}}_1(t) \textrm{d} t\right| +\left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) w_2(t)\ddot{w}_1(t) \textrm{d} t\right| \right) \\ \le&\varepsilon \beta \left( \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) \textrm{d} t\right| \Vert {\dot{v}}_*(t)\Vert _C|{\dot{w}}_1(t)| +\left| \int \limits _{z}^{+\infty }p_{22}(\varepsilon ,z-t)\textrm{d} t\right| |w_2(z)||\ddot{w}_1(z)|\right) \\ \le&\frac{2\beta }{\lambda _{22}(\varepsilon )}\left( \varepsilon \Vert {\dot{v}}_*(t)\Vert _C +\frac{1}{d_1}\Vert W\Vert _C \right) \left[ K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right] \\ =&O(\varepsilon ^2)+O(\varepsilon \Vert W\Vert _C)+O(\varepsilon \Vert W\Vert ^2_C)+O(\Vert W\Vert ^2_C)+O(\Vert W\Vert ^3_C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Here, we should pay special attention to $\varepsilon \beta \left| \displaystyle \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) v_*(t)\ddot{w}_1(t) \textrm{d} t\right|$. More precisely, we can’t estimate it by using directly the inequality (4.9). Using integrals by parts, we have

$$\begin{aligned} \begin{aligned}&\varepsilon \beta \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon ,z-t) v_*(t)\ddot{w}_1(t) \textrm{d} t\right| \\ \le&\varepsilon \beta \left( \left| v_*(z){\dot{w}}_1(z)\right| +\left| \int \limits _{z}^{+\infty }|\lambda _{22}(\varepsilon )|p_{22}(\varepsilon ,z-t)v_*(t){\dot{w}}_1(t) \textrm{d} t\right| +\left| \int \limits _{z}^{+\infty }p_{22}(\varepsilon ,z-t){\dot{v}}_*(t){\dot{w}}_1(t)\textrm{d} t\right| \right) \\ \le&4 \varepsilon \beta \Vert v_*(z)\Vert _C\left( K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right) +\varepsilon \beta \left| \int \limits _{z}^{+\infty }p_{22}(\varepsilon ,z-t)\textrm{d} t\right| \left| {\dot{v}}_*(t)\right| \left| {\dot{w}}_1(z)\right| \\ \le&2\varepsilon \beta \left( 2 \Vert v_*(z)\Vert _C +\frac{1}{\lambda _{22}(\varepsilon ) }\Vert {\dot{v}}_*(t)\Vert _C\right) \left( K_{11}\Vert W\Vert _C+ \varepsilon d_1 \Vert \ddot{u}_*\Vert _C + K_{13}\Vert W\Vert ^2_C\right) \\ =&O(\varepsilon ^2)+O(\varepsilon \Vert W\Vert _C)+O(\varepsilon \Vert W\Vert ^2_C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \begin{aligned} \left| \int \limits _{-\infty }^{z} p_{21}(\varepsilon ,z-t){M}_{22}(\varepsilon , t, W)\textrm{d} t\right| =O(\varepsilon ^2 )+O( \varepsilon \Vert W\Vert _C)+O(\varepsilon \Vert W\Vert ^2_C)+O(\varepsilon \Vert W\Vert ^3_C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Next, we estimate $\left| \displaystyle \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t){M}_{23}(\varepsilon , t, W) \textrm{d} t \right| + \left| \displaystyle \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t){M}_{23}(\varepsilon , t, W) \textrm{d} t\right|$, then we have

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon , z-t) {M}_{23}(\varepsilon , t, W) \textrm{d} t\right| \\ \le&\varepsilon \beta \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon , z-t) {\dot{u}}_*(t){\dot{w}}_2(t) \textrm{d} t\right| +\varepsilon \beta \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon , z-t) \ddot{u}_*(t)w_2(t) \textrm{d} t\right| \\ \le&\varepsilon \beta \left( \left| {\dot{u}}_*(z)w_2(z)\right| +\left| \lambda _{22}(\varepsilon )\right| \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon , z-t) {\dot{u}}_*(t)w_2(t)\textrm{d} t\right| \right) \\&+2\varepsilon \beta \left| \int \limits _{z}^{+\infty } p_{22}(\varepsilon , z-t) \ddot{u}_*(t)w_2(t)\textrm{d} t\right| \\ \le&2 \varepsilon \beta \left( \Vert {\dot{u}}_*\Vert _C+\frac{\Vert \ddot{u}_*\Vert _C}{|\lambda _{22}(\varepsilon )|}\right) \Vert W\Vert _C\\ =&O(\varepsilon \Vert W\Vert _C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Similarly, we can get

$$\begin{aligned} \begin{aligned} \left| \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) {M}_{23}(\varepsilon , t, W) \textrm{d} t\right| =O(\varepsilon \Vert W\Vert _C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

For ${M}_{24}(\varepsilon , t, W)$, we have the following result.

Lemma 4.8

Let $B(\varrho )$ be the open ball in $C_0$ with radius $\varrho$ and centered at the origin, then for each $W \in B(\varrho )$ and $\varepsilon \in [0,1]$, there is $\varpi >0$ such that

$$\begin{aligned} \left| {M}_{24}(\varepsilon , t, W)\right| \le \varpi \Vert W\Vert _C^2. \end{aligned}$$

Proof

Since ${M}_{24}(\varepsilon , t, W)$ is $C^k$-smooth $(k \ge 2)$, we see that $\frac{\partial {M}_{24}(\varepsilon , t, W)}{\partial W}$ and $\frac{\partial ^2 {M}_{24}(\varepsilon , t, W)}{\partial W^2}$ are continuous in $W \in B(\varrho )$. Moreover,

$$\begin{aligned} \begin{aligned} {M}_{24}(\varepsilon , t, 0)&=a_2r_2\left( \frac{v_*^2(t)}{u_*(t)+K}-\frac{v_*^2(t)}{u_*(t)+K}\right) \equiv 0, \\ \frac{\partial {M}_{24}(\varepsilon , t, 0)}{\partial W}&= a_2r_2\left( \frac{2v_*(t)}{u_*(t)+K}-\frac{v_*^2(t)}{\left( u_*(t)+K\right) ^2} -\frac{2v_*(t)\left( u_*(t)+K\right) -v_*^2(t)}{\left( u_*(t)+K\right) ^2}\right) \equiv 0. \end{aligned} \end{aligned}$$

Hence, we have $\left| {M}_{24}(\varepsilon , t, W)\right| \le \varpi \Vert W\Vert _C^2$ uniformly for $\varepsilon \in [0,1]$. This completes the proof. $\square$

It follows Lemma 4.8 that

$$\begin{aligned} \begin{aligned}&\left| \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) {M}_{24}(\varepsilon , t, W) \textrm{d} t \right| +\left| \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t) {M}_{24}(\varepsilon , t, W) \textrm{d} t \right| \\&\le \left[ \int \limits _{-\infty }^z p_{21}(\varepsilon , z-t) \textrm{d} t + \int \limits _z^{+\infty } p_{22}(\varepsilon , z-t) \textrm{d} t \right] \varpi \Vert W\Vert _C^2 \\&\le \frac{1}{\sqrt{1+4 \varepsilon d_2 }}\left[ \frac{1}{\lambda _{22}(\varepsilon )} -\frac{1}{\lambda _{21}(\varepsilon )}\right] \varpi \Vert W\Vert _C^2\\&=O\left( \Vert W\Vert _C^2\right) , \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

Finally, we have

$$\begin{aligned} \left| {\mathcal {H}}_1(\varepsilon , z, W)\right| =O(\varepsilon )+O\left( \varepsilon \Vert W\Vert _C\right) +O\left( \Vert W\Vert _C^2\right) +O\left( \varepsilon \Vert W\Vert _C^2\right) , \quad \varepsilon \rightarrow 0^{+}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \left| {\mathcal {H}}_2(\varepsilon , z, W)\right| =&O(\varepsilon )+ O(\varepsilon \Vert W\Vert _C)+O(\Vert W\Vert ^2_C)\\&+O(\varepsilon \Vert W\Vert ^2_C)+O(\Vert W\Vert ^3_C)+O(\varepsilon \Vert W\Vert ^3_C), \quad \varepsilon \rightarrow 0^{+}. \end{aligned} \end{aligned}$$

5 Existence of traveling wavefront solutions

This section is devoted to prove the existence of traveling wavefronts by using the Banach fixed point theorem.

Theorem 5.1

There is a sufficiently large constant $c^*>0$ such that for any $c>c^*$, system (1.4) has a traveling wavefront solution $\kappa (z)=\left( \kappa _1(z), \kappa _2(z)\right) ^T$ connecting $E_*$ to O, where $\kappa _1(z)=u(x, t)$, $\kappa _2(z)=v(x, t)$. That is,

$$\begin{aligned} \kappa (-\infty )\triangleq \lim _{z\rightarrow -\infty }\kappa (z) =E_*,\hspace{0.4cm} \kappa (+\infty )\triangleq \lim _{z\rightarrow +\infty }\kappa (z)=O. \end{aligned}$$

Proof

Let Z be the subspace in $C_0$ such that

$$\begin{aligned} C_0=Z \oplus {\mathcal {N}}(L). \end{aligned}$$

It is well known that $Z \subseteq C_0$ is a Banach space. Let $S=\left. L\right| _Z$ be the restriction of L to Z, then $S: Z \rightarrow C_0$ is one-to-one and onto. Due to the Banach inverse operator theorem, $S^{-1}: C_0 \rightarrow Z$ is a bounded linear operator. Let $\left\| S^{-1}\right\| =\left\| S^{-1}\right\| _{{\mathcal {L}}\left( C_0, Z\right) }$.

For each $W \in C_0$, there are unique $\psi \in {\mathcal {N}}(L)$ and $\phi \in Z$ such that $W=\phi +\psi$. Hence W is a solution of Eq. (3.4) if and only if

$$\begin{aligned} L \phi ={\mathcal {H}}(\varepsilon , \cdot , \phi +\psi ), \end{aligned}$$

or, equivalently, if and only if $\phi$ is a solution of the equation

$$\begin{aligned} \phi =S^{-1} {\mathcal {H}}(\varepsilon , \cdot , \phi +\psi ). \end{aligned}$$

(5.1)

It follows from Sect. 4 that there are $\varrho>0, \varepsilon ^*>0$ and $0<\varpi <1$ such that for all $\varepsilon \in \left( 0, \varepsilon ^*\right]$ and $W, \phi , \psi \in B(\varrho ) \subset C_0$,

$$\begin{aligned} \Vert {\mathcal {H}}(\varepsilon , \cdot , W)\Vert _C \le \frac{1}{3\left\| S^{-1}\right\| }\left( \Vert W\Vert _{C}+\varrho \right) , \end{aligned}$$

(5.2)

and

$$\begin{aligned} \Vert {\mathcal {H}}(\varepsilon , \cdot , \psi )-{\mathcal {H}}(\varepsilon , \cdot , \phi )\Vert _C \le \frac{\varpi }{\left\| S^{-1}\right\| }\Vert \psi -\phi \Vert _C. \end{aligned}$$

(5.3)

For each fixed $\psi \in {\mathcal {N}}(L) \cap \overline{B(\varrho )}$, inequality (5.2) implies that

$$\begin{aligned} \left\| S^{-1} {\mathcal {H}}(\varepsilon , \cdot , \phi +\psi )\right\| _C \le \frac{1}{3}\left( \Vert \phi +\psi \Vert _C+\varrho \right) \le \varrho , \quad \varepsilon \in \left( 0, \varepsilon ^*\right] , \quad \phi \in Z \cap \overline{B(\varrho )}. \end{aligned}$$

Therefore, together with inequality (5.3) we see that the mapping ${\mathcal {F}}:(Z \cap \overline{B(\varrho )}) \times ({\mathcal {N}}(L) \cap \overline{B(\varrho )}) \times \left( 0, \varepsilon ^*\right] \rightarrow$ $Z \cap \overline{B(\varrho )}$ given by

$$\begin{aligned} {\mathcal {F}}(\phi , \psi , \varepsilon )=S^{-1} {\mathcal {H}}(\varepsilon , \cdot , \phi +\psi ), \end{aligned}$$

is a uniform contraction mapping of $\phi \in Z \cap \overline{B(\varrho )}$. Hence, for each $(\psi , \varepsilon ) \in ({\mathcal {N}}(L) \cap \overline{B(\varrho )}) \times \left( 0, \varepsilon ^*\right]$, there is a unique fixed point $\phi _{(\psi , \varepsilon )}$ of the mapping ${\mathcal {F}}(\cdot , \psi , \varepsilon )$. In other words, $\phi _{(\psi , \varepsilon )}$ is the unique solution in $Z \cap \overline{B(\varrho )}$ of Eq. (5.1). Thus, for fixed $\varepsilon \in \left( 0, \varepsilon ^*\right] , W_{(\psi , \varepsilon )}=\phi _{(\psi , \varepsilon )}+\psi$ is a solution of Eq. (3.4). Hence, system (1.4) has a traveling wavefront solution $\kappa =W+U_{*}$. $\square$

6 Minimal wave speed and periodic waves

In this section, we study the minimal wave speed of traveling wavefronts by using the standard stability analysis [18] and discussed the existence condition of periodic waves when traveling wavefronts disappears.

6.1 Minimal wave speed of traveling wavefronts

For ease of analysis, we shall consider the space domain as ($-\infty$,+$\infty$). Introducing the traveling wave variable $z=x-c t$ and $u(x, t)=U(z), v(x, t)=V(z)$. Specifically, we assume that the wave speed $c \ge 0$ and impose the following boundary conditions:

$$\begin{aligned} \left\{ \begin{array} { l } { U ( - \infty ) = \frac{r_2-r_1K}{r_1+b_1r_2}, } \\ \\ { V ( - \infty ) = \frac{1+b_1K}{r_1+b_1r_2}, } \end{array} \text{ and } \left\{ \begin{array}{l} U(+\infty )=0, \\ \\ V(+\infty )=0. \end{array}\right. \right. \end{aligned}$$

(6.1)

Substituting our proposed solution of the traveling wave form into the system (1.4), we thus have

$$\begin{aligned} \left\{ \begin{array}{l} d_1\ddot{U}(z)+a_1U(z)\left( 1-b_1U(z)-r_1V(z)\right) +c{\dot{U}}(z)=0, \\ d_2 \ddot{V}(z)+ \beta \left( {\dot{V}}(z){\dot{U}}(z)+V(z) \ddot{U}(z)\right) +a_2V(z)\left( 1-\frac{r_2V(z)}{U(z)+K}\right) +c{\dot{V}}(z)=0. \end{array}\right. \end{aligned}$$

(6.2)

System (1.4) has the spatially homogeneous solutions (0, 0) and $\left( \frac{r_2-r_1K}{r_1+b_1r_2}, \frac{1+b_1K}{r_1+b_1r_2}\right)$. To consider the connection between these two solutions, we first linearize the ODE system (6.2) at the origin (0, 0). Let $U^{\prime }=X, V^{\prime }=Y$; we study the following linear system of (U, X, V, Y):

$$\begin{aligned} \left( \begin{array}{c} U^{\prime } \\ X^{\prime } \\ V^{\prime } \\ Y^{\prime } \end{array}\right) =\left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ -\frac{a_1}{d_1} &{} -\frac{c}{d_1} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} -\frac{a_2}{d_2} &{} -\frac{c}{d_2} \end{array}\right) \left( \begin{array}{c} U \\ X \\ V \\ Y \end{array}\right) . \end{aligned}$$

(6.3)

The characteristic equation of the coefficient matrix is

$$\begin{aligned} \Delta (\lambda )=\left( \lambda ^2+\frac{c}{d_1} \lambda +\frac{a_1}{d_1}\right) \left( \lambda ^2+\frac{c}{d_2} \lambda +\frac{a_2}{d_2}\right) , \end{aligned}$$

(6.4)

where $\lambda$ is the eigenvalue. To make sure that there exists a positive solution going out from an unstable manifold of the origin and connecting the other equilibrium $\left( \frac{r_2-r_1K}{r_1+b_1r_2}, \frac{1+b_1K}{r_1+b_1r_2}\right)$, we need to exclude the spiral case to require and assume $a_2 d_2>a_1 d_1$, we thus get

$$\begin{aligned} c \ge c^{*}=2\sqrt{a_2 d_2}. \end{aligned}$$

(6.5)

Now we assume the existence of wave solutions, we want to derive the selection of the wave speed c from the initial condition at infinity. Suppose the initial condition to system (1.4) is

$$\begin{aligned} \left\{ \begin{array}{l} u(x, 0) \sim A e^{-\xi x}, \\ v(x, 0) \sim B e^{-\xi x}, \end{array}\right. \end{aligned}$$

as $x \rightarrow \infty$, where u(x, t) and v(x, t) have the same decaying coefficient $\xi >0$ and A, B are positive constants. If we look for a traveling wave solution of (1.4) in the form (the leading edge form)

$$\begin{aligned} \left\{ \begin{array}{l} u(x, t)=A e^{-\xi (x-c t)}, \\ v(x, t)=B e^{-\xi (x-c t)}, \end{array}\right. \end{aligned}$$

(6.6)

and substitute (6.6) into the second equation of system (1.4), this gives the dispersion relation between the wave speed c and the decay rate $\xi$:

$$\begin{aligned} c=d_2 \xi +\frac{a_2}{\xi }. \end{aligned}$$

(6.7)

Formula (6.7) provides a direct formula to estimate the wave speed. It is easy to determine from (6.7) that $c_{\min }=2 \sqrt{a_2 d_2}$ when $\xi =\sqrt{\frac{a_2}{d_2}}$, which agrees with the value obtained by (6.5). Now consider $\min \left\{ e^{-\xi x}, e^{-\sqrt{\frac{a_2}{d_2}} x}\right\}$ for x large and positive. It follows that

$$\begin{aligned} \xi <\sqrt{\frac{a_2}{d_2}} \Rightarrow e^{-\xi x}>e^{-\sqrt{\frac{a_2}{d_2}} x}. \end{aligned}$$

Then the velocity of propagation with asymptotic initial behavior will depend on the leading edge of the wave, and the wave speed c is given by (6.7). On the other hand, if $\xi >\sqrt{\frac{a_2}{d_2}}$, then $e^{-\xi x}$ is below $e^{-\sqrt{\frac{a_2}{d_2} x}}$ and the front takes the minimal wave speed $c=2 \sqrt{a_2 d_2}$. We thus conjecture that the asymptotic wave speed of the traveling wave solution of (6.6) is given by

$$\begin{aligned} c^{*}= {\left\{ \begin{array}{ll}d_2 \xi +\frac{a_2}{\xi }, &{} \text{ if } 0<\xi \le \sqrt{\frac{a_2}{d_2}}, \\ 2 \sqrt{a_2 d_2}, &{} \text{ if } \xi \ge \sqrt{\frac{a_2}{d_2}}.\end{array}\right. } \end{aligned}$$

(6.8)

6.2 Existence condition of periodic waves

When wave speed $c>c^{*}$, the traveling wavefront solution exists, otherwise it disappears. Now we discuss the existence of periodic waves for system (6.2) when traveling wavefront solution disappears. Linearizing it around the equilibrium $(u_*,v_*)=\left( \frac{r_2-r_1K}{r_1+b_1r_2}, \frac{1+b_1K}{r_1+b_1r_2}\right)$, we get the system

$$\begin{aligned} \left( \begin{array}{c} U^{\prime } \\ X^{\prime } \\ V^{\prime } \\ Y^{\prime } \end{array}\right) =\left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ -\frac{a_1(1-2b_1u_*-r_1v_*)}{d_1} &{} -\frac{c}{d_1} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \frac{a_1\beta v_*\left( 1-2b_1u_*-r_1v_*\right) }{d_1d_2} &{} \frac{c\beta v_*}{d_1d_2} &{} -\frac{a_2u_*+a_2K-2r_2v_*}{(u_*+K)d_2} &{} -\frac{c}{d_2} \end{array}\right) \left( \begin{array}{c} U \\ X \\ V \\ Y \end{array}\right) . \end{aligned}$$

(6.9)

and the characteristic equation is given by

$$\begin{aligned} \lambda ^4+\left( \frac{c}{d_1}+\frac{c}{d_2}\right) \lambda ^3+\left( M+\frac{c^2}{d_1d_2}+N\right) \lambda ^2 +\left( \frac{c}{d_1}M+\frac{c}{d_2}N\right) \lambda +NM=0. \end{aligned}$$

(6.10)

where $M=\frac{a_2u_*+a_2K-2r_2v_*}{(u_*+K)d_2}$ and $N=\frac{a_1\left( 1-2b_1u_*-r_1v_*\right) }{d_1}$.

We suppose that there exist periodic solutions near the positive equilibria and assume that the characteristic equation has purely imaginary roots $\lambda _{1,2}= \pm \omega i$. Plugging them into (6.10) gives a necessary condition $c=0$. In this case, (6.10) reduces to

$$\begin{aligned} \lambda ^4+\left( M+N\right) \lambda ^2+MN=0. \end{aligned}$$

(6.11)

Further analysis of (6.11) on the existence of purely imaginary roots requires that

$$\begin{aligned} a_2d_1+a_1d_2>\frac{2d_1r_1v_*}{u_*+K}+a_1d_2\left( 2b_1u_*+r_1v_*\right) . \end{aligned}$$

(6.12)

Substitute $(u_*,v_*)=\left( \frac{r_2-r_1K}{r_1+b_1r_2}, \frac{1+b_1K}{r_1+b_1r_2}\right)$ into inequality (6.12). We get

$$\begin{aligned} K>\frac{2(r_1+b_1r_2)d_1r_1}{a_2d_1r_1b_1+a_2d_1b_1^2r_2-a_1d_2b_1^2r_2}. \end{aligned}$$

(6.13)

This means that when $c=0$ and K is sufficiently large, system (6.2) may have periodic waves near the positive equilibrium $\left( \frac{r_2-r_1K}{r_1+b_1r_2}, \frac{1+b_1K}{r_1+b_1r_2}\right)$.

7 Numerical simulations

In this section, we illustrate our results by showing some numerical simulations. Here, we consider the case of a one-dimensional spatial domain. Moreover, in order to better elucidate the influence of chemotaxis on the existence of traveling wave solution, we take numerical simulation for the cases of the chemotactic sensitivity $\beta =0$ and $\beta \ne 0$, respectively. Namely, we consider the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll}u_t=d_1 \frac{\partial ^2u}{\partial x^2}+a_1u\left( 1-b_1u-r_1 v\right) , \\ v_t=d_2 \frac{\partial ^2v}{\partial x^2} +\beta \frac{\partial }{\partial x}\left( v \frac{\partial u}{\partial x}\right) +a_2v\left( 1-\frac{r_2 v}{u+K}\right) , \end{array}\right. } \end{aligned}$$

(7.1)

with the initial condition $u(x,0) =u_*-0.001$, $v(x,0) =v_*-0.001$ and the parameters $d_1 =0.2,d_2=0.4,a_1=1,a_2=1,b_1=1,r_1=0.5,r_2=5,K=5.$ Hence, system (7.1) have the coexistence steady state solution $E_*=(\frac{4989}{11000},\frac{11989}{11000})^T.$ The limit system of system (7.1) is

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{u}}(z)=-u(1-u-0.5v),\\ {\dot{v}}(z)=-v\left( 1-\frac{5v}{u+5}\right) . \end{array}\right. } \end{aligned}$$

(7.2)

The numerical heteroclinic solution of system (7.2) connecting $E_*$ to O is shown by red dashed line in Fig. 1.

Fig. 1

Solution of system (7.2) and solutions of system (7.3) with $\beta =0.24$ and $\beta =0$

Moreover, system (7.1) can be rewritten as the perturbation equation of system (7.2) by the same transformation as (3.2), i.e,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{u}}(z)=-0.2 \varepsilon \ddot{u}(z)-u(z)\left( 1-u(z)-0.5v(z)\right) , \\ {\dot{v}}(z)=-0.4 \varepsilon \ddot{v}(z)-\beta \varepsilon \left( {\dot{v}}(z){\dot{u}}(z)+v(z) \ddot{u}(z)\right) -v(z)\left( 1-\frac{5v(z)}{u(z)+5}\right) . \end{array}\right. } \end{aligned}$$

(7.3)

Letting the wave speed $c=3$, we have $\varepsilon =\frac{1}{c^2}=\frac{1}{9}.$ The numerical solutions of system (7.3) with the chemotactic sensitivity $\beta =0$ and $\beta =0.24$ are shown by blue dashed and green solid line in Fig. 1, respectively. It can be clearly seen from Fig. 1 that system containing chemotaxis have greater perturbation.

By translating back to the original variable, the three-dimensional numerical traveling wavefront solution of system (7.1) with the chemotactic sensitivity $\beta =0.24$ connecting $E_*$ to O is shown in Fig. 2.

Fig. 2

Traveling wavefront solution of system (7.1) with $\beta =0.24$

Based on Eq. (6.8), we have the minimum wave speed $c^{*}=2\sqrt{0.4}\approx 1.265$. We can see from Fig. 3a that the positive solution of system (7.3) disappears when $c = 0.7 < c^{*}$. In contrast, when $c = 1.4 > c^{*}$, the positive solution of system (7.3) exists (see Fig. 3b).

Fig. 3

Solutions of system (7.3) with $c=0.7$ and $c=1.4$

Now we discuss the numerical simulation of periodic wave solution of system (7.1) bifurcating from the positive equilibrium. To satisfy the inequality (6.13), we reselect parameters values $d_1 =0.2,d_2=0.4,\beta =6,a_1=20,a_2=8,b_1=0.32,r_1=0.5,r_2=5,K=5.$ Substituting the traveling wave transform $z=x-ct$ into system (7.1), we obtain

$$\begin{aligned} \left\{ \begin{array}{l} 0.2\ddot{u}(z)+20u(z)\left( 1-0.32u(z)-0.5v(z)\right) +c{\dot{u}}(z)=0, \\ 0.4 \ddot{v}(z)+ 6 \left( {\dot{v}}(z){\dot{u}}(z)+v(z) \ddot{u}(z)\right) +8v(z)\left( 1-\frac{5v(z)}{u(z)+5}\right) +c{\dot{v}}(z)=0. \end{array}\right. \end{aligned}$$

(7.4)

The numerical periodic solution of system (7.4) with $c=0$ bifurcating from the positive equilibrium is shown in Fig. 4a. When the wave speed is very small (say, $c=0.1$), but not equal to zero, the periodic solutions of system (7.4) disappear (see Fig. 4b).

Fig. 4

Solutions of system (7.4) bifurcating from $E_*$ with $c=0$ and $c=0.1.$

8 Conclusion

This paper study the existence and minimal wave speed of traveling wavefronts and the existence of periodic waves for a modified Leslie–Gower model with diffusion and chemotaxis. The existence of the wavefronts solution is proved by the perturbation method, and the minimal wave speed of traveling wavefronts is given by standard stability analysis. Moreover, the existence condition of the periodic waves is discussed when the traveling wavefronts disappears. When $c=0$ and K is sufficiently large, the system would have periodic waves near the positive equilibrium. In other words, when the protection to the predator provided by the environment is sufficiently large and the wave speed is equal to zero, the periodic waves exists. On the other hand, when the wave speed is not equal to zero, the periodic waves disappear, even if the wave speed is sufficiently small.

In this paper, we pay attention to the local diffusion. However, it is clear that local diffusion does not apply to all biological models, such as embryonic development, the cell density involved is not small, and long-distance interaction and non-local consumption of resources. Therefore, it is an interesting question whether our method can also be applied to the traveling waves of non-local diffusion models. These issues will be our follow-up work.