1 Introduction

Concrete is a multiphase and multiscale composite material that plays a fundamental and pivotal role in shaping our built environment, providing stability, durability, and versatility in a wide range of construction projects. Research in concrete technology is crucial to promote sustainability, enhance safety, and hence turns out to be of prominent interest for the construction industry. Concrete properties stem from its highly heterogeneous microstructure, including constituents of diverse typologies with various sizes and shapes which are subjected to chemical-physical processes not only during curing but along the entire service life, depending on the water-to-cement ratio and other possible additives as well as on the environmental conditions (in primis the history of temperature and of relative humidity, but also the possible diffusion of aggressive compounds). At the macroscale, the mechanical behavior of concrete results to be extremely complex, characterized by the superposition of an instantaneous response, which can be modeled by nonlinear elasticity, plasticity and damage, leading to hysteresis under cyclic loading, and of deferred phenomena, such as shrinkage and creep. A network of very small cracks, not visible by eyes, is usually present in concrete as a consequence of the cement hydration, shrinkage and loading.

The most recent research topics on concrete concern the study of supplementary cementitious materials, also of nanometer size, the long-term chemical physical deterioration processes and self-healing provisions. Materials like fly ash, slag and silica fume can be added to concrete, in order to improve some of its features and reduce its carbon footprint [1,2,3], contributing to more sustainable and environmentally friendly construction practices. As an alternative, the mechanical properties and the longevity of the material can be enhanced also by incorporating nanomaterials, see, e.g., [4, 5]. Nanoparticles are much smaller in size than conventional concrete constituents, and hence they fill in the gaps between larger particles, improving packing and the overall strength with it, and reducing permeability and porosity. Furthermore, nanomaterials such as nano-silica or nanotubes have a high surface-to-volume ratio [6], allowing for a better bonding with cement particles and favoring the chemical reactivity. Nanomaterials can contribute to mitigate early-age cracking in concrete by reducing the heat of hydration, controlling the formation of micro-cracks and improving the curing process. After decades of services life, chemical physical processes, such as the alkali silica reaction and the sulfate attack, promoted by specific ions already present in the constituents or diffusing from outside, accomplices the environmental conditions, can cause local swelling phenomena in the concrete elements endowed by cracking, with a correlated decrease in mechanical stiffness and strength, see e.g. [7,8,9,10]. Research on self-healing concrete focuses on strategies to repair cracks autonomously, mimicking the behavior of biological tissues, such as bone (see, e.g., [11,12,13]). Key aspects of this research are the development of healing agents that react and seal the crack, such as bacteria, polymers or organic and inorganic materials. At the same time, concrete-based materials with ultra-high-performance are being conceived, characterized by exceptional strength and durability, e.g., see [14,15,16].

In this scenario, computer simulations and digital modeling can play an increasing role in designing and optimizing the concrete structures, allowing one to carry out virtual tests very rapidly and at low costs, and contributing to a better understanding of the complex mechanisms which turn out to be multiphase and multiscale. This knowledge allows researchers for a more sustainable design, reduced construction costs, improved safety, enhanced durability, ultimately leading to better-engineered structures [17,18,19,20,21]. Moreover, due to a widespread use of cementitious materials in civil engineering, macroscopic models are supposed to be used also by not specialized personnel, implemented in commercial software, and hence they must be conceived as a compromise between simplicity and accuracy, hopefully including a low number of parameters to identify.

From a modeling perspective, the behavior of concrete poses numerous challenges. Crucial issues concern its nonlinear behavior [22,23,24,25,26] even under small strains, the dissipative effects stemming from its microstructure in both elastic and plastic regime [27,28,29,30,31], and the evolution of cracks [32]. Recent studies have explored innovative approaches using material particles akin to swarm robotics, offering promising computational efficiency [33, 34]. As an alternative to Cauchy media, generalized continua have been investigated, see e.g. [35,36,37,38,39,40,41]. Among them, Cosserat-type models account for the presence of stiff aggregates, and higher gradient continua can address strong heterogeneities (see, e.g., [42,43,44,45,46,47]). Furthermore, due to the presence of voids generated during the curing process and of micro-cracks, concrete can be treated as a porous material (see, e.g., [48,49,50]). In particular, micro-cracks affect concrete behavior by introducing asymmetry in its mechanical response and generating internal friction under cyclic loads.

In modeling the hysteresis cycles, commonly adopted viscous models rest on a linearization of the dissipative actions. Alternatively, Coulomb-type friction between bumpy surfaces in the micro-cracks can be used, providing a response nearly independent of the frequency. Rheological models and thermodynamic frameworks with diffusive internal variables are also employed to address dissipation in solid materials. Finally, it is important to acknowledge ongoing research efforts related to plasticity and damage evolution [51,52,53]. Variational formulations are favored for their logical consistency and ability to minimize unnecessary assumptions [54,55,56,57].

This work aims at investigating from the numerical standpoint the role played in concrete beams by the existing micro-cracks as a possible source of dissipation, especially during cyclic loading. To this purpose, an enhanced version of the Timoshenko beam model is proposed [58, 59], inspired by a 3D continuum formulation endowed with a Coulomb-like dissipation potential (see, e.g., [60, 61]), which turns out to predict more effectively the hysteresis cycles under moment and shear actions. The paper is organized as follows. Section 2 is devoted to the postulation of the elastic energy and of a Rayleigh dissipation potential for the beam and to the variational deduction of the governing equations. Details for the finite element implementation in COMSOL Multiphysics are outlined in Sect. 3. In Sect. 4, numerical results are discussed, at varying the model parameters. Section 4 outlines the pros and cons of the proposed approach and presents future developments.

A punctualization about the notation. Since a 1D description is considered in what follows, for the sake of brevity the first spatial derivative with respect to the x-coordinate of a function a(x, t) is denoted by the symbol \(a'=\partial a/\partial x\), while \({\dot{a}}=\partial a/\partial t\) indicates the first derivative of the same function with respect to time t. This notation is extended in a consistent way to the higher order derivatives.

2 Beam model with micro-slips and friction

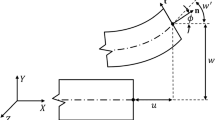
Let us consider a 1D model of a cementitious structural element in the plane xy, lying along the x-axis in its undeformed configuration and whose length is indicated by L. For the sake of simplicity, we will not introduce a curvilinear abscissa, although the results to be discussed hold for any curved plane beam. As well known, in the standard Timoshenko model, the cross sections remain plane during the deformation process but the orthogonality assumption between the longitudinal beam line and the cross section is not retained: the effect of shear, implying also warping, is accounted for by an equivalent rotation with respect to the neutral axis. Hence, the cross section can translate and rotate around the neutral axis. We assume that at the considered scale a random distribution of micro-cracks variously oriented is in place [62]. Let us introduce a further kinematic descriptor aiming to describe, as a volume average, sliding between pairs of rough surfaces inside the micro-cracks, see, e.g., [29]. Neglecting the axial strain, the complete set of kinematic descriptors is constituted of the three functions v(x), \(\varphi (x)\) and \(\gamma (x)\), representing in turn the transverse displacement (along y) of the beam longitudinal axis and hence of the centroid, the cross section rotation around the neutral axis and an average relative sliding between the pairs of faces constituting the distribution of micro-cracks. Under small displacements, rotations and strains, the current configuration of the beam is specified by the vector map \(\varvec{\chi }_{t}\) depending on the generic abscissa \(x\in [0,L]\) and on the time variable t, as illustrated in Fig. 1. By symbols

$$\begin{aligned} \varvec{\chi }_{t}(x):= {\left\{ \begin{array}{ll} {\varvec{r}}(t)\equiv (x, y=v(x,t)) \\ \varphi =\varphi (x,t)\\ \gamma = \gamma (x,t) \end{array}\right. }\,\,. \end{aligned}$$
(1)

Vector \({\varvec{r}}(x,t)\) specifies the position of the cross section centroid along the loading history, and \(\varphi (x,t)\) \([\textrm{rad}]\) and \(\gamma (x,t)\) \([\textrm{L}]\) indicate the slope of the cross section and the average microscopic sliding in the sense explained above.

Fig. 1
figure 1

Macroscopic kinematic descriptors of the beam

Full size image

To seek the equilibrium configuration, a generalized version of the principle of virtual work is considered herein. This principle states that, for any virtual perturbation of the equilibrium configuration, the virtual variation of the elastic energy within the system, say \(\delta {\mathcal {W}}^{\textrm{el}}\), must equal the virtual work made by the external forces acting on the system plus any other virtual dissipation, indicated in turn by \(\delta {\mathcal {W}}^{\,\textrm{ext}}\) and \(\delta {\mathcal {D}}^{\,\textrm{diss}}\). One has

$$\begin{aligned} \delta {\mathcal {W}}^{\,\textrm{el}}(t) = \delta {\mathcal {W}}^{\,\textrm{ext}}(t)+ \delta {\mathcal {D}}^{\,\textrm{diss}}(t), \end{aligned}$$
(2)

for each time instant t. Quasi-static conditions are assumed herein, neglecting the inertial effects. We postulate the following expression of the elastic energy based on the above mentioned kinematic fields, namely

$$\begin{aligned} {\mathcal {W}}^{\,\textrm{el}}&=\int \limits _0^L\frac{1}{2}\text {k}_b \left( \varphi '\right) ^2\,\text {d}x+\int \limits _0^L \frac{1}{2}\text {k}_s\left( v'-\varphi \right) ^2\,\text {d}x \nonumber \\&\quad +\int \limits _0^L \frac{1}{2}\text {k}_{m1}\, \gamma ^2\,\text {d}x + \int \limits _0^L \frac{1}{4}\text {k}_{m2} \,\gamma ^4\,\text {d}x - \int \limits _0^L\alpha _b \,\gamma \, \varphi ' \,\text {d}x - \int \limits _0^L\alpha _s \,\gamma \left( v'-\varphi \right) \,\text {d}x\,\,. \end{aligned}$$
(3)

The arguments of the integrals represent an energy density (per unit length), i.e. with the dimension of a force: the material parameters have the meaning of generalized stiffnesses. In particular, symbols \(\text {k}_b\) \([\textrm{FL}^{2}]\), \(\text {k}_s\) \([\textrm{F}]\), \(\text {k}_{m1}\) \([\textrm{F}/\textrm{L}^{2}]\) and \(\text {k}_{m2}\) \([\textrm{F}/\textrm{L}^{4}]\) denote direct stiffnesses associated with diverse deformation mechanisms, while \(\alpha _b\) and \(\alpha _s\) (in turn with dimensions \([\textrm{F}]\) and \([\mathrm {F/L}]\)) govern their coupling. Parameters \(\text {k}_{m1}\) and \(\text {k}_{m2}\) control the energy stored by the micro-cracks. From the theoretical standpoint, the stored energy of Eq. (3) must be positive defined and strictly convex, to ensure existence and uniqueness of the minimum point. As well known, for quadratic forms these two properties coincide. If we neglect for a while the quartic contribution of the micro-slip, the coefficient matrix of the quadratic form Eq. (3) can be easily specified. Through the Sylvester’s theorem, the admissible set of parameters can be specified through the constraints \(\text {k}_b>0\), \(\text {k}_s>0\), \(\text {k}_b\,\text {k}_s \text {k}_{m1}>\text {k}_s\,\alpha _b^{2}+\text {k}_b\,\alpha _s^{2}\,\). All these parameters can be estimated on the basis of suitable experimental data, or through a micro–macro identification strategy, see e.g. [63,64,65,66,67]. Furthermore, if we assume both the coefficients of the micro-slips \(\text {k}_{m1}\) \(\text {k}_{m2}\) to be nonnegative, the nonlinear elastic contribution corresponding to the average micro-slip turns out to be positive defined and strictly convex, exhibiting two coinciding real minimum points in the origin and other two complex conjugates. If we image to integrate such a polynomial expression in \(\gamma \), the odd terms cannot be included since they would provide non-symmetric contributions to the elastic energy, which in this circumstance does not appear mechanically based.

The first two contributions of the energy in Eq. (3), representing bending and shear, coincide with those of the standard Timoshenko model. The first two addends along the second row, which exhibit a polynomial dependence (quadratic and quartic) on \(\gamma \), govern the amount of elastic energy stored by the pairs of surfaces constituting the distribution of micro-cracks. In fact, from a geometric standpoint, the lips of a micro-crack, which exhibit bumps or asperities, interact with each other. When these asperities come into contact, similarly to the teeth of a saw profile, they can bend like cantilevers, and hence, their relative sliding induces a fully reversible amount of deformation energy. Experimental studies, see, e.g., [68], stated that in cement-based materials sliding of micro-cracks can induce a macroscopic nonlinear response, even under small displacements and strains. The last two contributions of Eq. (3) govern the mutual energy between the beam bending and the relative slip of the asperities within the micro-cracks, as well as between the macroscopic shear distortion of the beam and the asperity deformation. To clarify this concept, let us indicate by \({\textbf{n}}\) and \({\textbf{m}}\) the unit vectors normal and tangential to an ideally flat micro-crack. Locally, one would expect that the Cauchy stress component \(\sigma _{nm}=\varvec{\sigma }:{\textbf{n}}\otimes {\textbf{m}}\) were responsible for the relative sliding of the opposite surfaces, while the stress component \(\sigma _{nn}=\varvec{\sigma }:{\textbf{n}}\otimes {\textbf{n}}\), if compressive, caused the unilateral closure of that crack and an increase in the frictional dissipation as stated by Coulomb. Due to the random orientation of the micro-cracks within the bulk, we reasonably expect that both the shear action and the bending moment contribute to such a relative sliding, i.e. to \(\sigma _{nm}\), although not everywhere one has \(\sigma _{nn}<0\) and the frictional dissipation occurs. Therefore, we assume that coupling occurs between the micro-slips and both the shear deformation and the bending curvature.

By differentiating the energy in Eq. (3) with respect to the kinematic descriptors, we obtain the dual generalized stresses of the beam

$$\begin{aligned} M(x,t)&=\frac{\partial {\mathcal {W}}^{\,\textrm{el}}}{\partial \,\varphi '}=\text {k}_b\varphi '-\alpha _b\gamma \,\,\, ,\,\,\,T(x,t)=\frac{\partial {\mathcal {W}}^{\textrm{el}}}{\partial \,(v'-\varphi )}=\text {k}_s\left( v'-\varphi \right) -\alpha _s\gamma ,\nonumber \\ {\mathfrak {T}}(x,t)&=\frac{\partial {\mathcal {W}}^{\,\textrm{el}}}{\partial \,\gamma }=\text {k}_{m1}\, \gamma +\text {k}_{m2} \,\gamma ^3-\alpha _b \,\varphi '-\alpha _s\left( v'-\varphi \right) \nonumber \\&=\left( \text {k}_{m1}-\frac{\alpha _b^{2}}{\text {k}_b}-\frac{\alpha _s^{2}}{\text {k}_s}\right) \, \gamma +\text {k}_{m2} \,\gamma ^3- \frac{\alpha _b}{\text {k}_b}\,M-\frac{\alpha _s}{\text {k}_s}\,T\,\,\,. \end{aligned}$$
(4)

The virtual work made by the inner forces is straightforwardly computed by the first variation of the elastic energy (3) as:

$$\begin{aligned} \delta {\mathcal {W}}^{\,\textrm{el}}= & {} \int \limits _0^L \text {k}_b \varphi '\,\delta \varphi '\, \text {d}x+\int \limits _0^L \text {k}_s\left( v'-\varphi \right) \delta \left( v'-\varphi \right) \, \text {d}x\nonumber \\{} & {} + \int \limits _0^L \text {k}_{m1} \gamma \,\delta \gamma \, \text {d}x + \int \limits _0^L \text {k}_{m2} \gamma ^3\,\delta \gamma \, \text {d}x\nonumber +\\{} & {} - \int \limits _0^L \alpha _b \left( \varphi '\,\delta \gamma + \gamma \, \delta \varphi ' \right) \,\text {d}x - \int \limits _0^L \alpha _s \left[ \left( v'-\varphi \right) \,\delta \gamma + \gamma \, \left( \delta v' - \delta \varphi \right) \right] \,\text {d}x\,, \end{aligned}$$
(5)

where symbol \('\) denotes as usual the derivative with respect to the spatial coordinate x. Integrating by parts and applying the fundamental lemma of the integral calculus (as 1D counterpart of the divergence theorem), the contributions of the internal elastic energy can be grouped on the basis of the kinematic descriptor appearing as test function,

$$\begin{aligned} \delta {\mathcal {W}}^{\,\textrm{el}}= & {} - \int \limits _0^L \Big [\,\left( \text {k}_b \varphi '\right) '+\text {k}_s\left( v'-\varphi \right) -\left( \alpha _b \gamma \right) ' - \alpha _s \gamma \,\Big ]\,\delta \varphi \, \text {d}x + \left[ \left( \text {k}_b \varphi ' - \alpha _b \gamma \right) \,\delta \varphi \right] _0^L\nonumber \\{} & {} + \int \limits _0^L \Big [\,\text {k}_{m1} \gamma + \text {k}_{m2} \gamma ^3 - \alpha _b\, \varphi ' -\alpha _s \left( v'-\varphi \right) \,\Big ]\,\delta \gamma \, \text {d}x+ \nonumber \\{} & {} -\int \limits _0^L \Big \{\,\Big [\text {k}_s\left( v'-\varphi \right) \,\Big ]' -\left( \alpha _s \, \gamma \right) ' \,\Big \}\delta v\, \text {d}x + \Big [\,\Big \{\text {k}_s\left( v'-\varphi \right) - \alpha _s \gamma \,\Big \}\delta v\,\Big ]_0^L\,, \end{aligned}$$
(6)

being as usual \([a(x)]_0^L=a(L)-a(0)\). The above equations describes the conservative part of the system. To simulate the dissipation mechanisms at the macroscale due to microscopic tangential slip with friction, in the spirit of Hamilton–Rayleigh principle a dissipation potential is introduced, see, e.g., [69]. A nonnegative Rayleigh function can be postulated as follows:

$$\begin{aligned} {\mathfrak {R}}(x,t)=\frac{\zeta }{\eta }\,\ln \left[ \cosh (\eta \,{\dot{\gamma }})\right] \,\vert \varphi ' \vert \,\ge 0\,, \end{aligned}$$
(7)

having the dimension of a power density, namely \([\textrm{F}/t]\). Symbol \({\dot{\gamma }}\) \([\textrm{L}/t]\) denotes as usual the time derivative of the average slip in argument, being the product \(\eta \,{\dot{\gamma }}\) non-dimensional, and \(\zeta \) has dimension \([\textrm{F}]\). By differentiating the Rayleigh potential \({\mathfrak {R}}\) in Eq. (7) with respect to the average slip rate \({\dot{\gamma }}\), by changing the sign we obtain the dual friction force density, exerted between the opposite faces of the micro-cracks

$$\begin{aligned} \tau _{\textrm{diss}}=-\frac{\partial \, {\mathfrak {R}}}{\partial \,{\dot{\gamma }}}=-\zeta \,\tanh \left[ \eta \,{\dot{\gamma }}\right] \,\vert \varphi ' \vert \,, \end{aligned}$$
(8)

having dimension \([\textrm{F}/\textrm{L}]\). As anticipated in Eq. (2), we can take into account the virtual work carried out by the friction force density at the level of the micro-cracks, as follows:

$$\begin{aligned} \delta {\mathcal {D}}^{\textrm{diss}}(t) = -\int \limits _0^L \text {d}x\,\,\zeta \vert \varphi '(x,t) \vert \tanh [\,\eta \,{\dot{\gamma }}(x,t)] \,\delta \gamma \,\,. \end{aligned}$$
(9)

Basically, any friction force can be described through a standard Coulomb behavior. However, due to the non-Lipschitz continuity of the forcing term, including the signum function, the uniqueness of the solution would be lost. To overcome this drawback, the hyperbolic function \(\tanh [\eta \,{\dot{\gamma }}]\), with asymptotes \(\pm 1\) for \(\eta {\dot{\gamma }}\rightarrow \pm \infty \), can be utilized to mimic the Coulomb behavior while avoiding the aforementioned issue, assuming \(\eta \) sufficiently large, see e.g. [70, 71]. This approach turns out to work effectively in a variety of applications: moreover, it introduces a viscous behavior for small velocities \({\dot{\gamma }}\), which plays a stabilization role in several contexts, without mentioning that \(\eta \) can be tuned on the basis of the experimental data. The appearance in Eq. (9) of the derivative of the cross section rotation in absolute value, \(\vert \varphi ' \vert \), is related to the fact that, by increasing the bending curvature, compressive states become more significant at least in one part of the cross section, favoring the closure of the micro-cracks. The intensity of the friction force is governed also by the parameter \(\zeta \), independent of the term \(\vert \varphi ' \vert \). For a comprehensive description of the dissipation in a Lagrangian approach, the reader is referred to [69, 72].

The external virtual work, including the distributed forces \(b_y\) in the y-direction and the moment per unit length \(\mu \), is expressed as:

$$\begin{aligned} \delta {\mathcal {W}}^{\,\textrm{ext}}(t)&= \int \limits _0^L\,\text {d}x \,\,b_y(x,t) \, \delta v +\int \limits _0^L\,\text {d}x\,\, \mu (x,t)\, \delta \varphi \nonumber \\&\quad +F_{y0}(t) \,\delta v(0,t) + W_{0}(t) \,\delta \varphi (0,t) +F_{y}(t) \,\delta v(L,t) + W_{L}(t) \,\delta \varphi (L,t)\,\,\, ,\,\,\forall \,t, \end{aligned}$$
(10)

where concentrated vertical forces \(F_y\) and moments W can be applied at both the ends of the beam, at each instant t. We remark that Eq. (6) cannot provide any boundary condition for \(\gamma \) since this variable does not appear under a spatial derivative.

By substituting into Eqs. (2) the expressions in Eqs. (6), (9) and (10), by the fundamental lemma of the variational calculus the governing equations in strong form are as follows

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} -\left[ \text{ k}_s\left( v'-\varphi \right) \right] '+\left( \alpha _s \, \gamma \right) ' =-T'=b_y(x,t)\\ \quad \text{ k}_{m1} \gamma + \text{ k}_{m2} \gamma ^3 - \alpha _b\, \varphi ' -\alpha _s \left( v'-\varphi \right) ={\mathfrak {T}}=-\zeta \vert \varphi ' \vert \tanh [\,\eta \,{\dot{\gamma }}]\\ -\left[ \left( \text{ k}_b \varphi '\right) '+\text{ k}_s\left( v'-\varphi \right) -\left( \alpha _b \gamma \right) ' - \alpha _s \gamma \right] =-M'-T= \mu (x,t)\,\,\,\,\,. \end{array}\right. } \end{aligned} \end{aligned}$$
(11)

to hold \(\forall \,x\in ]0,L[\) and \(\forall \,t\,\). At the beam ends, with abscissae \(x=0\) and \(x=L\), values of v(0, t), v(L, t) and \(\varphi (0,t)\), \(\varphi (L,t)\) can be prescribed (essential boundary conditions), or, dually, the history of the shear force T(0, t), T(L, t) and of the bending moment M(0, t), M(L, t) (natural boundary conditions) in equilibrium with the external loading Eq. (10). Initial conditions at \(t=0\) must be considered, assuming for instance \(v(x,0)=\varphi (x,0)=\gamma (x,0)=0\), \(\forall \,x\in ]0,L[\).

The above equalities in Eq. (11), endowed by the boundary and the initial conditions, represent a system of nonlinear partial differential equations dependent on space and time, i.e., within the strip \([0,L]\times [0,t]\). The second equation from above includes first order derivatives as maximum order, and exhibits a nonlinear dependence on the micro-crack slip \(\gamma \), which appears at the maximum power 3, and on time also, through the slip rate \({\dot{\gamma }}\). The remaining equations are linear in the derivatives: In the first equation, an equivalent or effective distributed transversal loading can be considered, equal to \(b_{y}-(\alpha _{s} \gamma )'\), while in the last equation an equivalent or effective moment per unit length can be specified, namely \(\mu -(\alpha _{b} \gamma )'-(\alpha _{s} \gamma )\). If we assume the coupling stiffnesses \(\alpha _{b}\) and \(\alpha _{s}\) to vanish, the second equation becomes decoupled from the remaining ones and the standard Timoshenko beam model is retrieved.

It is worth noting that the average micro-slips can affect both the shear action and the bending moment: it acts like a microrotation of the generic cross section. If we differentiate the constitutive relationships for the shear actions and the bending moment in Eq. (4), in the absence of distributed loading one obtains

$$\begin{aligned} T' = \text {k}_s \left( v''-\varphi '\right) -\alpha _s \gamma ', \qquad M' = \text {k}_b \varphi '' - \alpha _b \gamma '\,. \end{aligned}$$
(12)

Hence, at locations where the moment is constant with the abscissa and the shear action T is null, namely \(M=c\) and \(T=0\), one has

$$\begin{aligned} \text {k}_s \left( v'-\varphi \right) =\alpha _s \gamma , \qquad \text {k}_b \varphi '' =\alpha _b \gamma '\,. \end{aligned}$$
(13)

Concentrated jumps in the diagram of the shear action cause cusps in the plots of \(\gamma \) (with right and left derivatives tending to \(\pm \,\infty \)), while angular points for T or M cause angular points in turn for \(v'-\varphi \) and \(\gamma \), and for \(\varphi '\) and \(\gamma \).

3 Virtual tests

To assess the dissipative behavior of a cementitious material under small displacements and strains, we make reference to standard experimental configurations under bending, commonly referred to as three-point and four-point bending tests. The sample has a rectangular parallelepiped shape, with sides \(d\times d\times L\), and is placed on two supports located symmetrically with respect to the beam center, at a distance \(\ell \) from each other: a vertical force is applied at the center, for the three-point test, or at two specific locations on the top for the four-point bending test (see Figs. 2, 3). Due to the presence of unilateral constraints, exclusively alternating (i.e. pulsating, with non-null mean value) loading cycles have been applied, besides a monotonic history. The preliminary numerical exercises discussed in what follows are intended to provide a basis for the model validation, and the reference for an experimental campaign on course.

Fig. 2
figure 2

Experimental configuration for three-point bending test and sample geometry

Full size image
Fig. 3
figure 3

Experimental configuration for the four-point bending, and sample geometry

Full size image

The 1D finite element analyses are carried out by the commercial software COMSOL Multiphysics [73], which enables the direct implementation of the weak formulation Eq. (2) through a package for partial differential equations. Since the proposed model includes the first gradient of the three kinematic descriptors, see Eq. (5), it represents a higher order model of first grade: hence, \(C^{0}\) conformity at for the finite element discretization is sufficient, guaranteed by standard Lagrangian quadratic polynomials as shape functions. The adopted discretization consists of 121 quadratic finite elements, each one including three nodes, corresponding to 720 overall degrees of freedom when considering the nodal values for the three fields and the constraints. An implicit time integration scheme has been utilized, referred to as backward differentiation formula (BDF) method. For further details on the numerical implementation even under geometric nonlinearity, we forward the interested reader to [74,75,76,77,78,79].

Fig. 4
figure 4

Profiles of the shear force T, in (a) and (b), and of the bending moment M, in (c) and (d), concerning the three-point bending test (first column) and the four-point bending configuration (second column)

Full size image

We have assumed Young’s modulus E=31.45 (GPa), and Poisson ratio \(\nu =0.15\). The standard bending stiffness can be retrieved as \(\text {k}_b=E\,J\), being J the second inertia moment of the cross section, while for the shear stiffness one has \(\text {k}_s=5/6\,G_c\,d^2\), where \(G_c=E/[2\,(1+\nu )]\) is the shear modulus. The set of parameter values needed for the simulations is reported in the synoptic Table 1. Alternatively, these parameters can be identified through micro–macro-approaches, or on the basis of experimental data through the minimization of a suitable discrepancy norm. Instead of lengthy minimization procedures requiring numerous forward analyses, artificial neural networks (ANN), once trained and tested on the basis of synthetic data corrupted by noise, can provide very rapidly at negligible cost the solution of the inverse problem in terms of parameter estimates, see, e.g., [80,81,82,83,84]. As external loading an alternating force with a sinusoidal trend was considered, namely

$$\begin{aligned} f(t)=\frac{F_0}{2}\Big [\,1-\cos \left( 2\pi f_q\, t\right) \,\Big ]\,. \end{aligned}$$
(14)

The amplitude was assumed as \(F_0=4.5\) (kN) for the three-point bending test, and one half of it for the four-point bending configuration. The frequency \(f_q\) was set to 10 (Hz).

3.1 Discussion of the results

In this section, the response of the proposed beam model is analyzed critically and comparatively when subjected to three- and four-point bending tests. Parameters, assumed as in Table 1, have been selected by trial and error to fit preliminary data on plain concrete samples. Moreover, we assess the resulting dissipation during cyclic loading.

The diagrams of the generalized stresses of the beam, namely the bending moment M and the shear action T, evaluated at the force peak, are drawn in Fig. 4: those in the first column concern the three-point bending test and those in the second column the four-point bending configuration. All of them can be computed on the basis of equilibrium conditions in the isostatic structural schemes.

Figure 5 shows a complete hysteresis cycle, consisting of a loading and an unloading branch, in terms of vertical force and displacement of the application point for the two configurations. The dissipated energy, corresponding to the area within the cycle for the three-point bending test, and to the double of it for the four bending configuration (in which two identical forces are applied), has been computed by numerical quadrature: the energy loss amounts to \(6.212 \times 10^{-4}\) (J) and to \(4.445 \times 10^{-4}\) (J) for three- and four-point bending tests, respectively.

Fig. 5
figure 5

Hysteresis cycle under three-point bending test, in (a), and four-point bending test, in (b). Beam geometry and model parameters are assumed as in Table 1

Full size image

The spatial profile of the three kinematical descriptors is depicted in Fig. 6: they are evaluated at the force peak, corresponding to the time instant \(t=0.05\) (s). Along the beam axis, run by abscissa x, we report the transverse displacement v (i.e., the deformed configuration), the slope of the cross section \(\varphi \), and the average sliding at the level of the micro-cracks \(\gamma \). In the synoptical view of Fig. 6, arranged as a \(3\times 2\) matrix, the first column concerns the three-point bending test, the second column the four-point configuration. In the first row, showing the vertical displacement profiles, the location of the hinges is marked by circles \(\circ \) along the curve, while the loading application points are marked by rhombs \(\diamond \). By visual inspection, spatial profiles of the variables v and \(\varphi \) coincide with those expected by the standard Timoshenko model. For the assigned parameter set of Table 1, the intensity of average micro-slip \(\gamma \) approximately follows the profile of the bending moment. Moreover, the plot of \(\gamma \) exhibits angular points and cusps at locations where the shear action undergoes jumps.

Fig. 6
figure 6

Three point bending (in the first column) and four-point bending configurations (in the second column). Profiles along the beam axis, evaluated at the force peak (time instant \(t=0.05\) (s)), of the three field variables: the transverse displacement, v, (a) and (b); the slope of the cross section, \(\varphi \), (c) and (d); and the relative sliding at the level of micro-cracks, \(\gamma \), (e) and (f). In plots (a) and (b), the locations of the supports are marked by circles \(\circ \), while the application points of the force by rhombs \(\diamond \)

Full size image

To favor a huge comprehension of the proposed model, Figs. 7 and 8 depict the time histories of the relative micro-slip \(\gamma \) and of the density of friction force \(\tau _{\textrm{diss}}=-\zeta \vert \varphi ' \vert \tanh [\,\eta \,{\dot{\gamma }}\,]\), evaluated at the application point of the external force for both the test configurations. It is worth noting that the time response of these quantities is nonlinear with respect to the evolution of the loading multiplier, varying according to the law in Eq. (14).

To assess the role played by the amplitude of the friction force, we have run several analyses by scaling the parameter \(\zeta \) in Eq. (8) through a factor q. Figure 9 shows the energy lost by the system along one complete cycle at varying the scale factor through the values \(q=(0.25, 0.5, 1, 2, 4)\). As a result, we have obtained for the dissipated energy values in the interval \([3.1 \times 10^{-4}, 6.2\times 10^{-4}]\) (J) for the three-point bending test, and slightly smaller values, within the interval \([1.9 \times 10^{-4}, 4.7\times 10^{-4}]\) (J), for the four-point configuration. The dotted lines indicate regression curves fitting these data, relevant to each test configuration. The observed trends are qualitatively similar, revealing the presence of a maximum of the dissipated energy. This behavior typically denotes the presence of two conflicting features. In fact, on the one hand, when the amplitude of the friction force density is low, there is less dissipation within a hysteresis cycle. On the other hand, if the amplitude of the friction force exceeds a threshold, the average relative sliding inside the distribution of micro-cracks cannot increase, and with it the dissipation necessarily decreases. Therefore, it is possible to select a value of the friction coefficient as the point which maximizes the dissipated energy.

To assess the role played by the coupling parameters, we have increase the value of the coefficient \(\alpha _b\) in Table 1 by 30% and 60%. Figure 10 shows the hysteresis cycles predicted by the finite element analyses for the selected configurations. In particular, for the three-point bending test, starting from \(6.212 \times 10^{-4}\) (J) the dissipated energy is increased up to 0.0011 (J) and 0.0019 (J), respectively. Similarly, in the four-point configuration, for the same percentage increment of the parameter \(\alpha _b\), starting from \(4.445 \times 10^{-4}\) (J) the dissipated energy is increased up to \(8.136 \times 10^{-4}\) (J) and 0.0014 (J), in the order for the two levels of considered increase.

Table 1 Beam geometry and model parameters used as a reference in the numerical exercises
Full size table
Fig. 7
figure 7

Time history of the micro-slip \(\gamma \) for the three-point bending test evaluated at the middle point, in (a), and for the four-point bending test evaluated at one loading point, in (b)

Full size image
Fig. 8
figure 8

Time history of the friction force density, \(\tau _{\textrm{diss}}=-\zeta \vert \varphi ' \vert \tanh [\,\eta \, {\dot{\gamma }}\,]\), evaluated at the middle point of the beam in the three-point bending configuration, in (a), and at one of the force application points for the four-point bending test, in (b)

Full size image
Fig. 9
figure 9

Dissipated energy at varying the scaling factor q (multiplying parameter \(\zeta \)), for the three-point bending test, in (a), and for the four-point configuration, in (b). The dashed line indicate a regression curve, interpolating the results of the simulations marked by red circles \(\circ \)

Full size image
Fig. 10
figure 10

Hysteresis cycles in the three-point bending test, when scaling the coupling stiffness \(\alpha _b\) by factors 1.3 and 1.6, in (a) and (c), respectively, and in the four-point bending test, in (b) and (d) with the same scaling

Full size image
Fig. 11
figure 11

Distribution of the micro-crack average sliding \(\gamma \) along the beam for the three-point bending test, in (a), and for the four-point configuration, in (b), relevant to \(\alpha _{s}=2.5\times 10^7\) (N/m). For this value of \(\alpha _{s}\), the profile of \(\gamma \) turns out to be non-symmetric with respect to the center of the beam, exhibiting a stronger dependence on the sign of the shear action T

Full size image
Fig. 12
figure 12

Distribution of the dissipated power density \({\mathfrak {R}}\) for the three-point bending test, in (a), and for the four-point configuration, in (b), relevant to \(\alpha _{s}=2.5\times 10^7\) (N/m). For this value of \(\alpha _{s}\), the distribution of the power density turns out to be non-symmetric with respect to the center of the beam, exhibiting a stronger dependence on the sign of the shear action T

Full size image

The same analysis has been carried out for the coupling coefficient \(\alpha _s\). However, since this coefficient affects less the overall behavior, the changes in percentage observed with respect to the reference set of parameters are negligible. In the case of the three-point bending test, the 30% increase in this coupling stiffness results into an energy loss of \(6.215 \times 10^{-4}\) (J), and a 60% increase causes a dissipation of \(6.219 \times 10^{-4}\) (J). In the four-point bending test, a 30% increase corresponds to an energy loss of \(4.449 \times 10^{-4}\) (J), while the 60% increase gives rise to a dissipation of \(4.453 \times 10^{-4}\) (J). After that, we increased the value of \(\alpha _s\) by five times. Firstly, we have obtained hysteresis cycles very close to those provided by the reference parameters of Table 1, confirming that the impact of \(\alpha _s\) is less significant with respect to \(\alpha _b\). The energy loss for the three-point and four-point bending configurations amounts to \(6.314 \times 10^{-4}\) (J) and \(4.534\times 10^{-4}\) (J), respectively. Secondly, analyzing the distribution of the average sliding \(\gamma \) at the peak, as shown in Fig. 11, due to the linear coupling between \(\gamma \) and the shear deformation \((v'-\varphi )\), one can easily recognize an increase of the average sliding in one side of the beam and the opposite behavior in the remaining part, so that the distribution of the average sliding of micro-cracks turns out to be not symmetric. This asymmetric behavior can be noticed also for the distribution of the dissipated power density, as reported in Fig. 12.

Fig. 13
figure 13

Hysteresis cycles in the three-point bending test, for \(\text {k}_{m2}=0\) (N/m\(^4\)) and \(\text {k}_{m2}=1\times 10^{20}\) (N/m\(^4\)), in (a) and (c) respectively, and in the four-point bending test, in (b) and (d) with the corresponding values of \(\text {k}_{m2}\) on the same row

Full size image

Let us consider the stiffness \(\text {k}_{m2}\), multiplying \(\gamma ^{4}\) in the expression of elastic energy Eq. (3). Figure 13 shows the hysteresis cycles corresponding to \(\text {k}_{m2}=0\) (N/m\(^4\)) (subfigures (a) and (b)) and \(\text {k}_{m2}=1\times 10^{20}\) (N/m\(^4\)) (subfigures (c) and (d)). The first and second column of the composite figure correspond in the order to the three-point and to the four-point bending test. When we set \(\text {k}_{m2}=0\) (N/m\(^4\)), we obtain for the three-point bending test an energy loss of \(6.212 \times 10^{-4}\) (J), while for the four-point bending test the dissipated energy per cycle amount to \(4.445 \times 10^{-4}\) (J), almost unchanged with respect to the above mentioned cases, with parameters corresponding to Table 1. By setting \(\text {k}_{m2}=1\times 10^{20}\) (N/m\(^4\)), for the three-point bending test the energy loss in the loading–unloading cycle amounts to \(3.423\times 10^{-4}\) (J), while for the four-point configuration equals \(2.605\times 10^{-4}\) (J). Thus, a higher stiffness of the asperities inside the micro-cracks leads to a substantial decrease of the dissipation.

4 Closing remarks and future prospects

In this study, a novel beam model especially suitable for cementitious structural elements is outlined, which generalizes the standard Timoshenko beam by a high order strategy. In the mechanical formulation, an additional kinematic descriptor has been considered, which represents an average sliding between the pairs of rough surfaces constituting a density of micro-cracks. Such a distributions of micro-cracks, randomly oriented within the beam volume, is assumed to remain constant during the entire loading process. The additional field variable, rooted in the meso-structure, generates both an elastic energy and a nonlinear dissipation, defined through a smooth Rayleigh potential which induces a Coulomb- like friction force with a viscous dependence on the rate of deformation. The expression of the stored energy associated with these micro-slips has been enriched up to include a quartic term, and represents the conservative part of the system. The coefficients weighting the diverse contributions are subjected to constraints, deduced by the Sylvester criterion, to guarantee positive definition and strict convexity of the energy functional. This formulation, deduced by a variational approach based on the principle of virtual work in the spirit of Hamilton–Rayleigh approach, provides a simple but effective framework to describe dissipative mechanisms in cementitious elements, which imply an energy loss during cycling loading. The response of the extended Timoshenko beam can be described through a system of three nonlinear partial different equations, depending on space and time, endowed by boundary and initial conditions: at the beam ends, one can prescribe the history of the transversal displacement and of the rotation of the cross section (but not the average sliding), or, alternatively, of their dual actions, while at the initial time instant the three fields are assumed to be null along the entire beam.

Starting from the weak formulation of this model, 1D finite element analyses have been carried out by COMSOL Multiphysics, describing the three-point and the four-point bending tests as reference configurations under alternating cycles. At varying the governing parameters, the extended beam model turns out to describe in a satisfactory manner hysteresis cycles, in agreement with literature data (see, e.g., [85, 86]) and with preliminary experiments carried out by the authors on plain concrete samples. The nonlinear relationship between the amplitude of the frictional force and the energy loss during the hysteresis cycles has been investigated, revealing the existence of a critical intensity at which the dissipation is maximized.

The proposed model is expected to provide useful insights for the optimal design of cementitious structural elements, particularly in those applications where both the energy dissipation and the mechanical stiffness represent critical factors. For instance, in the seismic structural design, building materials must be able of dissipating the highest amount of energy without decreasing the mechanical stiffness; analogous considerations can be referred to structures subjected to dynamic impact. The present formulation allows one to compare the dissipation capabilities of cementitious elements, for instance, at varying the typology and the percentage of additives.

As a possible improvement, the interactions among the micro-cracks can be investigated on a statistical basis, deducing the energy dissipated by friction. As discussed in [87, 88], for moderate crack densities, the interaction effects inside the population of cracks can be approximated assuming that the influence of the deformation at one crack on the stress field in the neighborhood of another crack remains spatially uniform (Kachanov model). This model would allow to provide through a micro–macro-approach estimations of the coupling stiffnesses in Eq. (3), to be compared with those identified by inverse analyses on the basis of experimental data at the macroscale. Moreover, by properly describing the growth of the population of micro-cracks as well as the propagation and coalescence of cracks (see, e.g., [89]), also damage and fatigue phenomena can be modeled.

In this scenario, robust identification procedures are required, exploiting sensitivity analysis to realize non-trivial tests and selecting a suitable discrepancy function to minimize. For instance, the response in terms of displacements and rotations predicted by the proposed model can be validated experimentally by means of full-field measurements, see, e.g., [90, 91]. As well known, kinematic data within a region of interest can be obtained through multiscale digital image correlation (DIC) techniques by processing digital images monitoring the sample deformation during the tests. Such images can be provided by a single optical camera, and in this case they provide information about plane displacements over the outer flat surface of the sample (2D DIC); alternatively, three dimensional tomographic reconstructions can be acquired within a X-ray tomograp coupled with an “in situ” mechanical apparatus, and in this case they provide information about three dimensional displacements within the bulk of the sample (3D-Volume DIC). As measurable quantities in the identification procedures one could process also the temperature fields provided, for instance, by a thermal imaging camera, since the temperature distribution over the outer surface is expected to be correlated with the dissipated power density generated by the micro-slips. Moreover, recourse can be made to micro–macro computational strategies starting from simplified mechanical assumptions on the meso-structure, apt to compute the stiffnesses appearing in the expression of the energy Eq. (3).