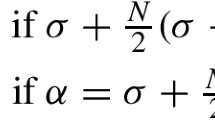Global existence and boundedness in a chemotaxis model with singular sensitivity and nonlocal term

Abstract

The chemotaxis system

$$\begin{aligned} \left\{ \begin{aligned}&u_t=\Delta u-\chi \nabla \cdot \left( \frac{u}{v}\nabla v\right) + u^{\alpha }\left( \gamma -\mu \int \limits _{\Omega }u^{\beta }\right) ,{} & {} x\in \Omega ,t>0,\\&v_t=\epsilon \Delta v-v+u,{} & {} x\in \Omega ,t>0, \end{aligned}\right. \end{aligned}$$

is considered under homogeneous Neumann boundary conditions in smoothly bounded domain $\Omega \subseteq \mathbb {R}^n$, $n\ge 2$, with constants $0<\epsilon <1$, $0<\chi <1-\epsilon$. It is asserted that the problem possesses a uniquely global classical solution whenever the numbers $\alpha , \beta$ satisfy $1<\alpha <2$, $\beta >\frac{n}{2}+\alpha -1$ or $\alpha \ge 2$, $\beta >\frac{n}{2}(\alpha -1)+1$. Moreover, it is shown that if $1<\alpha <2$, $\beta >\max \{\frac{n}{2}+\alpha -1, \frac{(\alpha -1)(1-\epsilon )}{(2-\alpha )\chi }+1\}$ and $\gamma >0$ is sufficiently large, then the global-in-time solution is uniformly bounded. In addition, we get similar results for the case of $n=1$, which is worth mentioning that the requirement for $\epsilon$ and $\chi$ is very weak in the global existence result.

1 Introduction

We consider the fully parabolic chemotaxis model with singular sensitivity and nonlocal logistic-type source given by

$$\begin{aligned} \left\{ \begin{aligned}&u_t=\Delta u-\chi \nabla \cdot (u\phi (v)\nabla v)+ f(u),{} & {} x\in \Omega ,t>0,\\&v_t=\epsilon \Delta v-v+u,{} & {} x\in \Omega ,t>0,\\&\frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,{} & {} x\in \partial \Omega ,t>0,\\&(u,v)(x,0)=\left( u_0(x),v_0(x)\right) ,{} & {} x\in \Omega , \end{aligned}\right. \end{aligned}$$

(1.1)

in a smooth bounded domain $\Omega \subseteq \mathbb {R}^n$, $n\ge 2$, with positive parameters $\epsilon , \chi$. Assume that the initial data in (1.1) are such that

$$\begin{aligned} \begin{aligned} \left\{ {\begin{array}{ll} {u_0} \in {C^{\theta }}\left( {\bar{\Omega } } \right) ,&{}\quad ~ \theta \in (0,1), \;{u_0} \ge 0\;\text {and }{u_0} \not \equiv 0, \\ {v_0} \in {W^{1,\infty }}\left( \Omega \right) ,&{}\quad \;{v_0}>0\;\text {in } \bar{\Omega }. \end{array}} \right. \end{aligned} \end{aligned}$$

(1.2)

In this framework, the system (1.1) can be viewed as a variant of the classical Keller–Segel system [12] obtained upon the choices $\epsilon =1$, $\chi =1$, $\phi (v)=1$ and $f=0$, which are used to model aggregation phenomena in situations where cells are attracted by a signal they themselves emit. Such chemotaxis processes are known to play an important role in various biological contexts [10], and accordingly, a considerable literature is devoted to their theoretical understanding. Results of which we refer to [9, 11, 16,17,18,19, 26, 27] and the references therein.

It has been studied widely with respect to global existence of solutions for the singular chemotaxis model with the choices $f=0$, $\phi (v)=\frac{1}{v}$ and $\epsilon =1$ corresponding to (1.1), that is,

$$\begin{aligned} \left\{ \begin{aligned}&u_t=\Delta u-\chi \nabla \cdot \left( \frac{u}{v}\nabla v\right) ,{} & {} x\in \Omega ,t>0,\\&v_t=\Delta v-v+u,{} & {} x\in \Omega ,t>0,\\&\frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,{} & {} x\in \partial \Omega ,t>0,\\&(u,v)(x,0)=\big (u_0(x),v_0(x)\big ),{} & {} x\in \Omega . \end{aligned}\right. \end{aligned}$$

(1.3)

The solution of (1.3) is global [23] and bounded [5] if $\chi <\sqrt{2/n}$. In addition, if the second equation is replaced by $\tau v_t=\Delta v-v+u$ with $\tau >0$ sufficiently small, then in radially symmetric settings the unique global classical solution exists and remains uniformly bounded in time for arbitrary $\chi >0$ [6]. In recent years, a large amount of research has been carried out toward the blow-up prevention by logistic source in various chemotaxis models. For example, consider the chemotaxis model (1.1) with logistic source $f(u)=\gamma u-\mu u^k$, $k>1$. The parabolic–parabolic system (1.1) with $k=2$ and $n=2$ was considered in [31], where it was obtained that there exists a unique globally bounded classical solution whenever $\gamma >\chi ^2/4$, $0<\chi \le 2$ or $\gamma >\chi -1$, $\chi >2$. In the higher dimensions, global weak solutions for $k=2$ and classical solutions for $k > 2$ have been established in [4]. It is known from [32] that the system (1.1) admits globally bounded classical solutions whenever $k>3(n+2)/(n+4)$, $n\ge 3$ and $\gamma , \chi$ satisfy $\chi ^2<\{2(\gamma +\gamma ^2)/k, 4/k(k-1)(k-2)\}$. For $n\ge 2$, $k>1$, the system possesses a globally bounded classical solution provided $0<\epsilon <1$, $0<\chi <1-\epsilon$ [30]. This assumption could be further relaxed in the sense that requiring $0<\chi <\min \{1/2, 1/\sqrt{2(n-1)}\}$ is sufficient to allow for corresponding global existence and boundedness in [29].

To study the properties of solutions for this chemotaxis system due to the complicated interplay emanating from the nonlinear reduced consumption effect and the singular chemotactic mechanism, a chemotaxis consumption system has been proposed in [12] i.e.

$$\begin{aligned} \left\{ \begin{aligned}&u_t=\Delta u-\chi \nabla \cdot \left( \frac{u}{v}\nabla v\right) + g(u),{} & {} x\in \Omega ,t>0,\\&v_t=\epsilon \Delta v-vu,{} & {} x\in \Omega ,t>0,\\&\frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,{} & {} x\in \partial \Omega ,t>0,\\&(u,v)(x,0)=\big (u_0(x),v_0(x)\big ),{} & {} x\in \Omega . \end{aligned}\right. \end{aligned}$$

(1.4)

In the case of $g=0$, for $n=2$, the literature [24] provides a result on global existence within a suitably generalized solution concept. In a radially symmetric setting, a normalized solution has been constructed for $n\ge 2$ [28]. Moreover, the normalized solution solves (1.4) classically in $(\bar{\Omega }\backslash \{0\})\times [0, \infty )$ [28]. In the case of $g=\gamma u-\mu u^k$, it is proved in [33] that there exists a global classical solution if $k>1$ for $n = 1$ or $k>1+n/2$ for $n\ge 2$, and the asymptotic behavior of solutions with $n=2$ is determined. More results on chemotaxis consumption model have been obtained in [13, 15, 22].

However, a new difficulty arises if such singular chemotaxis models are combined with the effect of nonlocal term. Mathematical models with nonlocal terms can predict the aggregation behavior of a disassociated adhesive cell population in response to the adhesive forces generated through binding in the process of cell–cell adhesion. See [1, 8, 20, 21] for the references. Recently, it is considered in [2] that under the conditions $\tau =0$, $\chi =1$, $\phi (v)=1$, $f(u)=u^{\alpha }\left( 1-\int \limits _{\Omega }u^{\beta }\textrm{d}x\right)$, the system (1.2) has a unique classical solution which is globally bounded if $2\le \alpha <1+2\beta /n$ or $1\le \alpha<2, (n+2)(2-\alpha )/n<1+2\beta /n-\alpha$. The same conclusion is established for the full parabolic version in [3].

Throughout this paper, we assume $\phi (v)=\frac{1}{v}$ and $f(u)=u^{\alpha }\Big (\gamma -\mu \int \limits _{\Omega }u^{\beta }\textrm{d}x\Big )$ with $\alpha >1$, $\beta >1$ in (1.1). We pay attention to the influence of singular sensitivity and nonlocal term on the behavior of solutions of (1.1). Our main results are as follows:

Theorem 1.1

Let $n\ge 2$ and $\Omega \subseteq \mathbb {R}^n$ be a smooth bounded domain. Suppose that $0<\epsilon <1$ and $0<\chi <1-\epsilon$. If $\alpha , \beta$ satisfy

$$\begin{aligned}&1<\alpha <2, \beta >\frac{n}{2}+\alpha -1, \end{aligned}$$

(1.5)

or

$$\begin{aligned}&\alpha \ge 2, \beta >\frac{n}{2}(\alpha -1)+1, \end{aligned}$$

(1.6)

then for any pair $(u_0,v_0)$ satisfying (1.2), the system (1.1) has a global classical solution.

Theorem 1.2

Let $n\ge 2$ and $\Omega \subseteq \mathbb {R}^n$ be a smooth bounded domain. Suppose that $0<\epsilon <1$, $0<\chi <1-\epsilon$ and that

$$\begin{aligned}&1<\alpha <2, \beta >\max \left\{ \frac{n}{2}+\alpha -1, \frac{(\alpha -1)(1-\epsilon )}{(2-\alpha )\chi }+1\right\} , \end{aligned}$$

(1.7)

then for initial data $(u_0,v_0)$ satisfying (1.2), there exists $\gamma _0>0$ with the property that if $\gamma >\gamma _0$, the global classical solution of (1.1) is bounded.

Theorem 1.3

Let $\Omega \subseteq \mathbb {R}$ be a smooth bounded domain. Suppose that $\chi >0$ and $\epsilon >0$. If

$$\begin{aligned}&1\le \alpha <2,~\beta \ge 1, \end{aligned}$$

(1.8)

or

$$\begin{aligned}&\alpha \ge 2, \beta >\alpha -1, \end{aligned}$$

(1.9)

then for any choice of $u_0$ and $v_0$ complying with (1.2), the problem (1.1) possesses a global classical solution.

Moreover, assume that $0<\epsilon <1$, $0<\chi <1-\epsilon$ and that

$$\begin{aligned}&1<\alpha <2, \beta >\frac{(\alpha -1)(1-\epsilon )}{(2-\alpha )\chi }+1, \end{aligned}$$

(1.10)

then for any pair $(u_0,v_0)$ satisfying (1.2), there exists $\gamma _1>0$ with the property that if $\gamma >\gamma _1$, then the global classical solution of (1.1) is bounded.

The rest of this paper is organized as follows. In Sect. 2, we present some preliminaries. In Sect. 3, we present the proof of Theorem 1.1. In Sect. 4, we prove Theorem 1.2. In Sect. 5, we prove Theorem 1.3.

2 Preliminaries

Let us start by recalling a basic statement asserting local well-posedness of solutions to problem (1.1), which can be proved by well-established fixed point arguments (see [25]).

Lemma 2.1

Let $n\ge 1$ and $\Omega \subseteq \mathbb {R}^n$ be a smooth bounded domain. Suppose that the parameters $\chi , \epsilon , \alpha , \beta$ are positive constants and that $u_0, v_0$ fulfill (1.2). Then there exist a maximal $T\in [0, \infty )$ and a uniquely determined pair (u, v) of nonnegative functions

$$\begin{aligned}&u\in C^0\Big (\bar{\Omega }\times [0, T)\Big )\cap C^{2,1}\Big (\bar{\Omega }\times (0, T)\Big ),\\&v\in C^0\Big (\bar{\Omega }\times [0, T)\Big )\cap C^{2,1}\Big (\bar{\Omega }\times (0, T)\Big )\cap L_{loc}^{\infty }\Big ((0,T),W^{1, \infty }(\Omega )\Big ), \end{aligned}$$

that solve (1.1) in the classical sense in $\Omega \times [0, T)$. Moreover,

$$\begin{aligned}&if~T<\infty ,~then~\Vert u\Vert _{L^{\infty }(\Omega )} + \Vert v\Vert _{W^{1,\infty }(\Omega )} \rightarrow \infty ~as~t\rightarrow T. \end{aligned}$$

We can obtain a lower bound for v related to t since we assume $v_0$ to be strictly positive.

Lemma 2.2

Let (u, v) be the solution of (1.1), then for any choice of $u_0$ and $v_0$ fulfilling (1.2) we have

$$\begin{aligned}&v(x,t) \ge \left( \inf \limits _{x\in \Omega }v_0\right) e^{-T}=:M_0(T),~for~all~ t\in (0, T). \end{aligned}$$

(2.1)

Proof

Define $\underline{v}=\left( \inf \limits _{x\in \Omega }v_0\right) e^{-t}$. We observe that $\underline{v}$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\underline{v}_t\le \epsilon \Delta \underline{v}-\underline{v}+u,{} & {} x\in \Omega ,t>0,\\&\frac{\partial \underline{v}}{\partial \nu }=0,{} & {} x\in \partial \Omega ,\\&\underline{v}(x,0)\le v_0,{} & {} x\in \Omega . \end{aligned}\right. \end{aligned}$$

From the comparison principle of the heat equation, we deduce

$$\begin{aligned}&v\ge \left( \inf \limits _{x\in \Omega }v_0\right) e^{-t}. \end{aligned}$$

This lemma is completed. $\square$

The following regularity properties of v in dependence on boundedness features of u will be used frequently on the proof of the global existence of solutions. This is a well-known result that can be founded in [23], for instance.

Lemma 2.3

Let $1\le r, \theta \le \infty$. Then for each solution of (1.1) with initial data fulfilling (1.2) we have the following properties:

• (i) If $\frac{n}{2}\left( \frac{1}{\theta }-\frac{1}{r}\right) <1$, then there exists $M_1>0$ independent of T such that

  $$\begin{aligned}&\Vert v\Vert _{L^r(\Omega )}\le M_1\left( 1+\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^\theta (\Omega )}\right) ,\quad \forall t\in (0, T). \end{aligned}$$

  (2.2)

• (ii) If $\frac{1}{2}+\frac{n}{2}\left( \frac{1}{\theta }-\frac{1}{r}\right) <1$, then there exists $M_2>0$ independent of T such that

  $$\begin{aligned}&\Vert \nabla v\Vert _{L^r(\Omega )}\le M_2\left( 1+\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^\theta (\Omega )}\right) ,\quad \forall t\in (0, T). \end{aligned}$$

  (2.3)

Proof

According to a variation-of-constants representation associated with the second equation in (1.1), we thus have

$$\begin{aligned} v(t)=e^{t(\epsilon \Delta -1)}v_0-{\int \limits _{0}}^{t}e^{(t-s)(\epsilon \Delta -1)}u(x,s)\textrm{d}s. \end{aligned}$$

By known smoothing estimates for the Neumann heat semigroup $(e^{\tau \Delta })_{\tau \ge 0}$ in $\Omega$, cf. [7], we thus finish this lemma. $\square$

We can estimate the mass of u from the first equation of (1.1).

Lemma 2.4

Let $\gamma >0$, $\mu >0$, $\alpha \ge 1$ and $\beta \ge 1$. Assume that initial data $u_0$, $v_0$ are as in (1.2). It holds that

$$\begin{aligned}&\int \limits _{\Omega } u \le M_3,\quad ~for~all~ t\in (0, T) \end{aligned}$$

(2.4)

with $M_3=\max \left\{ \int \limits _{\Omega } u_0, |\Omega |^{1-\frac{1}{\beta }}\right\}$. Moreover,

$$\begin{aligned}&\int \limits _{\Omega } v \le \max \left\{ \int \limits _{\Omega } v_0, M_3\right\} ,\quad ~for~all~ t\in (0, T). \end{aligned}$$

(2.5)

Proof

Integrating the first equation of (1.1) and from the Hölder inequality, we obtain

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u \le \int \limits _{\Omega }u^{\alpha }\left[ \gamma -|\Omega |^{1-\beta }\mu \left( \int \limits _{\Omega }u\right) ^{\beta }\right] , \end{aligned} \end{aligned}$$

which implies (2.4) by a straightforward ODE analysis.

From the second equation of (1.1), we have

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }v+\int \limits _{\Omega }v=\int \limits _{\Omega }u, \end{aligned}$$

which yields (2.5) by a comparison. $\square$

3 Global existence of solutions

To arrive at the $L^p$-estimation of u, the key step is to build the weighted integral $\int \limits _{\Omega }u^{p}v^{-q}$ with some $p>1$, $q>0$ to be determined in [23]. We should deal with a differential inequality on $\int \limits _{\Omega }u^{p}v^{-q}$. For convenience, we define

$$\begin{aligned} q_1(p)=:&\frac{\frac{\chi (1-\epsilon )p}{2}+\epsilon -\sqrt{\epsilon ^2+p\epsilon \chi (1-\epsilon -\chi )}}{{\frac{(\epsilon -1)^2p+4\epsilon }{2(p-1)}}} \end{aligned}$$

(3.1)

and

$$\begin{aligned} q_2(p)=:&\frac{\frac{\chi (1-\epsilon )p}{2}+\epsilon +\sqrt{\epsilon ^2+p\epsilon \chi (1-\epsilon -\chi )}}{\frac{(\epsilon -1)^2p+4\epsilon }{2(p-1)}}. \end{aligned}$$

(3.2)

Lemma 3.1

Let $q_1(p)$, $q_2(p)$ be as in (3.1) and (3.2). Assume that $0<\epsilon <1$ and $0<\chi <1-\epsilon$.

• (i) If $\alpha , \beta >1$ satisfy (1.5), then there exists $p>\frac{n}{2}$ such that

  $$\begin{aligned}&\frac{p+\alpha -1-\beta }{2-\alpha }<q_2(p). \end{aligned}$$

  (3.3)

  Moreover, we can find q satisfying

  $$\begin{aligned}&\frac{p+\alpha -1-\beta }{2-\alpha }<q<q_2(p). \end{aligned}$$

  (3.4)

• (ii) If $\alpha , \beta >1$ satisfy (1.6), then there exists $\frac{n}{2}<p <\beta -\alpha +1$ such that

  $$\begin{aligned}&q_1(p)<\frac{\beta -p-\alpha +1}{\alpha -2}. \end{aligned}$$

  (3.5)

  Moreover, we can find q satisfying

  $$\begin{aligned}&q_1(p)<q<\frac{\beta -p-\alpha +1}{\alpha -2}. \end{aligned}$$

  (3.6)

Proof

For (i), in view of (1.5) we can find $\frac{n}{2}<\beta +1-\alpha$. Since $(2-\alpha )q_2(p)>0$, we see that there is $p>\frac{n}{2}$ such that

$$\begin{aligned}&\frac{n}{2}<p<\beta +1-\alpha +(2-\alpha )q_2(p), \end{aligned}$$

which shows (3.3).

Now we prove the term (ii). Since

$$\begin{aligned}&\sqrt{\epsilon ^2+p\epsilon \chi (1-\epsilon -\chi )}<\frac{(1-\epsilon )(1-\epsilon -\chi )p}{2}+\epsilon , \end{aligned}$$

it is seen that

$$\begin{aligned}&q_1(p)<q<q_2(p)<p-1. \end{aligned}$$

(3.7)

So we only need to prove

$$\begin{aligned}&p-1<\frac{\beta -p-\alpha +1}{\alpha -2}, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&p<\frac{\beta -1}{\alpha -1}. \end{aligned}$$

The condition (1.6) entails that there is $\frac{n}{2}<p<\frac{\beta -1}{\alpha -1}$ such that the inequality (3.5) holds. $\square$

Lemma 3.2

Let $n\ge 2$, $0<\epsilon <1$ and $0<\chi <1-\epsilon$.

• (i) If $1<\alpha <2$, then for all $p>1$, each

  $$\begin{aligned}&\max \left\{ q_1(p), \frac{p+\alpha -1-\beta }{2-\alpha }\right\}<q<q_2(p), \end{aligned}$$

  (3.8)

  one can find constant $M_4$ independent of T such that

  $$\begin{aligned}&\int \limits _{\Omega }u^{p}v^{-q}\le M_4,~for~all~t\in (0, T). \end{aligned}$$

  (3.9)

• (ii) If $\alpha \ge 2$, then for all $\frac{n}{2}<p<\beta -\alpha +1$, each

  $$\begin{aligned}&q_1(p)<q<\frac{\beta -p-\alpha +1}{\alpha -2}, \end{aligned}$$

  (3.10)

  one can find constant $M_5>0$ independent of T such that

  $$\begin{aligned}&\int \limits _{\Omega }u^{p}v^{-q}\le M_5,~for~all~t\in (0, T). \end{aligned}$$

  (3.11)

Proof

For the sake of simplicity, we just prove the term (i). With $p, q>0$ to be determined, a direct computation with (1.1) shows

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p}v^{-q}+\int \limits _{\Omega }u^{p}v^{-q}\nonumber \\&\quad =-p(p-1)\int \limits _{\Omega }u^{p-2}v^{-q}|\nabla u|^2+[(1+\epsilon )pq+p(p-1)\chi ]\int \limits _{\Omega }{u^{p-1}}v^{-q-1}\nabla u\cdot \nabla v\nonumber \\&\qquad -[\chi pq+\epsilon q(q+1)]\int \limits _{\Omega }u^{p}v^{-q-2}|\nabla v|^2-q\int \limits _{\Omega }u^{p+1}v^{-q-1}\nonumber \\&\qquad +p\gamma \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}-p\mu \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\int \limits _{\Omega }u^{\beta }+(q+1)\int \limits _{\Omega }u^{p}v^{-q}. \end{aligned}$$

(3.12)

By Young’s inequality, we know

$$\begin{aligned}&[(1+\epsilon )pq+p(p-1)\chi ]\int \limits _{\Omega }{u^{p-1}}v^{-q-1}\nabla u\nabla v-p(p-1)\int \limits _{\Omega }u^{p-2}v^{-q}|\nabla u|^2\nonumber \\&\qquad -[\chi pq+\epsilon q(q+1)]\int \limits _{\Omega }u^{p}v^{-q-2}|\nabla v|^2\nonumber \\&\quad \le \Big \{\frac{[(1+\epsilon )pq+p(p-1)\chi ]^2}{4p(p-1)}-\chi pq-\epsilon q(q+1)\Big \}\int \limits _{\Omega }u^{p}v^{-q-2}|\nabla v|^2. \end{aligned}$$

(3.13)

Thanks to (3.8), we see

$$\begin{aligned}&\frac{[(1+\epsilon )pq+p(p-1)\chi ]^2}{4p(p-1)}-\chi pq-\epsilon q(q+1)\le 0. \end{aligned}$$

(3.14)

Combining (3.12), (3.13) and (3.14), we find

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p}v^{-q}+\int \limits _{\Omega }u^{p}v^{-q}&\le -q\int \limits _{\Omega }u^{p+1}v^{-q-1}+(q+1)\int \limits _{\Omega }u^{p}v^{-q}+p\gamma \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\nonumber \\&\quad -p\mu \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\int \limits _{\Omega }u^{\beta }. \end{aligned}$$

(3.15)

A direct calculation shows

$$\begin{aligned} \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}&=\left( \int \limits _{\Omega }[u^{p+1}v^{-q-1}]^{\frac{q}{q+1}}u^{\frac{(\alpha -2)q+p+\alpha -1}{q+1}}\right) ^{\frac{\beta (q+1)}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\\&\quad \times \left( \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\right) ^{\frac{(\alpha -2)q+p+\alpha -1}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\\&\le \left( \int \limits _{\Omega }u^{(\alpha -2)q+p+\alpha -1}\right) ^{\frac{\beta }{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\left( \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\right) ^{\frac{(\alpha -2)q+p+\alpha -1}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\\&\quad \times \left( \int \limits _{\Omega }u^{p+1}v^{-q-1}\right) ^{\frac{\beta q}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\nonumber \end{aligned}$$

by the Hölder inequality. From (3.8), we can find $p>1$, $q>0$ such that

$$\begin{aligned}&(\alpha -2)q+p+\alpha -1<\beta . \end{aligned}$$

(3.16)

It is immediate that $\frac{p-q}{(\alpha -2)q+p+\alpha -1}=\frac{p-q}{p-q+(\alpha -1)(q+1)}$. Moreover, due to (3.6) we know $p-q>0$, which along with $\alpha >1$ shows that

$$\begin{aligned}&0<\frac{p-q}{(\alpha -2)q+p+\alpha -1}<1. \end{aligned}$$

(3.17)

We therefore may invoke Hölder’s and Young’s inequality combining (3.16) and (3.17) to see that

$$\begin{aligned} (p\gamma +1)\int \limits _{\Omega }u^{p+\alpha -1}v^{-q}&\le (p\gamma +1)|\Omega |^{\frac{\beta (q+1)}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\left( \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}\int \limits _{\Omega }u^{\beta }\right) ^{\frac{(\alpha -2)q+p+\alpha -1}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\nonumber \\&\quad \times \left( \int \limits _{\Omega }u^{p+1}v^{-q-1}\right) ^{\frac{\beta q}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}\nonumber \\&\le p\mu \int \limits _{\Omega }u^{p+\alpha -1}v^{-q} \int \limits _{\Omega }u^{\beta }+C_1\left( \int \limits _{\Omega }u^{p+1}v^{-q-1}\right) ^{\frac{q}{q+1}}\nonumber \\&\le p\mu \int \limits _{\Omega }u^{p+\alpha -1}v^{-q} \int \limits _{\Omega }u^{\beta }+\frac{q}{2}\int \limits _{\Omega }u^{p+1}v^{-q-1}+C_2, \end{aligned}$$

(3.18)

and

$$\begin{aligned} (q+1)\int \limits _{\Omega }u^{p}v^{-q}&=(q+1)\int \limits _{\Omega }\left( u^{p+\alpha -1}v^{-q}\right) ^{\frac{p-q}{(\alpha -2)q+p+\alpha -1}}\Big (u^{p+1}v^{-q-1}\Big )^{\frac{q(\alpha -1)}{(\alpha -2)q+p+\alpha -1}}\nonumber \\&\le \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}+C_3\int \limits _{\Omega }\Big (u^{p+1}v^{-q-1}\Big )^{\frac{q}{q+1}}\nonumber \\&\le \int \limits _{\Omega }u^{p+\alpha -1}v^{-q}+\frac{q}{2}\int \limits _{\Omega }u^{p+1}v^{-q-1}+C_4, \end{aligned}$$

(3.19)

where

$$\begin{aligned} C_1&=\frac{\beta (p\gamma +1)(q+1)q^{\frac{p-q}{(\alpha -1)(q+1)}}|\Omega |^{\frac{\beta (q+1)}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}}{(\beta +\alpha -2)q+\beta +p+\alpha -1}\\&\cdot \left( \frac{[(\alpha -2)q+p+\alpha -1](p\gamma +1)|\Omega |^{\frac{\beta (q+1)}{(\beta +\alpha -2)q+\beta +p+\alpha -1}}}{[(\beta +\alpha -2)q+\beta +p+\alpha -1]p\mu }\right) ^{\frac{(\alpha -2)q+p+\alpha -1}{\beta (q+1)}+1},\\ C_2&=\frac{1}{2}\left( \frac{2C_1}{q+1}\right) ^{q+1},~C_3=\frac{(\alpha -1)(q+1)q}{p-q+(\alpha -1)(q+1)}\left( \frac{q(p-q)}{(\alpha -2)q+p+\alpha -1}\right) ^{\frac{p-q}{(\alpha -1)(q+1)}},\\ C_4&=\frac{1}{2}\left( \frac{2C_3}{q+1}\right) ^{q+1}. \end{aligned}$$

By virtue of (3.15), we can now combine (3.18) with (3.19) to achieve the inequality

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p}v^{-q}+\int \limits _{\Omega }u^{p}v^{-q}&\le C_2+C_4. \end{aligned}$$

A standard ODE comparison argument implies (3.9). $\square$

Based on the weighted integral $\int \limits _{\Omega }u^{p}v^{-q}$, we will get the $L^p$-boundedness of u under suitably coefficient $p>1$, $q>0$.

Lemma 3.3

Let $n\ge 2$, $0<\epsilon <1$ and $0<\chi <1-\epsilon$. If the condition (1.5) or (1.6) assumed in Theorem 1.1 holds, then there exist $p_0>\frac{n}{2}$ and $M_6>0$ independent of T such that

$$\begin{aligned} \int \limits _{\Omega }u^{p_0}\le M_6, ~for~all~t\in (0, T). \end{aligned}$$

Proof

According to Lemma 3.1, we pick p, q satisfying (3.8) or (3.10) such that

$$\begin{aligned} \int \limits _{\Omega }u^{p}v^{-q}&\le M_4+M_5. \end{aligned}$$

(3.20)

Taking $p_0\in (\frac{n}{2},p)$, from Hölder’s inequality and (3.20) we obtain

$$\begin{aligned} \int \limits _{\Omega }u^{p_0}&=\int \limits _{\Omega }u^{p_0}v^{-\frac{qp_0}{p}}v^{\frac{qp_0}{p}}\\&\le \left( \int \limits _{\Omega }u^{p}v^{-q}\right) ^{\frac{p_0}{p}}\left( \int \limits _{\Omega }v^{\frac{qp_0}{p-p_0}}\right) ^{\frac{p-p_0}{p}}\\&\le (M_4+M_5)^{\frac{p_0}{p}}\Vert v\Vert _{L^{\frac{qp_0}{p-p_0}}(\Omega )}^{\frac{qp_0}{p}}. \end{aligned}$$

In view of (2.2), we find

$$\begin{aligned} \int \limits _{\Omega }u^{p_0}&\le M_1(M_4+M_5)^{\frac{p_0}{p}}\left( 1+\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\right) ^{\frac{qp_0}{p}}. \end{aligned}$$

By (3.7), we see $q<p$, hence,

$$\begin{aligned} \sup \limits _{t\in (0,T)}\int \limits _{\Omega }u^{p_0}&\le C_5+C_5\left( \sup \limits _{t\in (0, T)}\int \limits _{\Omega }u^{p_0}\right) ^{\frac{q}{p}}\\&\le \frac{1}{2}\sup \limits _{t\in (0,T)}\int \limits _{\Omega }u^{p_0}+C_5\left( 1+\left( \frac{2C_5q}{p}\right) ^{\frac{q}{p-q}}\frac{p-q}{p}\right) , \end{aligned}$$

where $C_5=M_1(M_4+M_5)^{\frac{p_0}{p}}2^{\frac{qp_0}{p}}$. Obviously, this lemma is completed by taking

$$\begin{aligned}&M_6=2C_5\left( 1+\left( \frac{2C_5q}{p}\right) ^{\frac{q}{p-q}}\frac{p-q}{p}\right) . \end{aligned}$$

$\square$

Furthermore, we proceed to turn this into an estimate in $L^{\infty }$ norm of u in the case of $1\le \alpha <2$ by straightforward iteration.

Lemma 3.4

Let $n\ge 2$, $\chi >0$ and $\epsilon >0$. Assume that the initial functions $u_0, v_0$ fulfill (1.2) and that $\alpha , \beta$ satisfy (1.5). Suppose that there exists $p_0>\frac{n}{2}$ such that

$$\begin{aligned} u\in L^\infty ((0,T); L^{p_0}(\Omega )). \end{aligned}$$

Then there exists $M_7(T)>0$ such that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )}\le M_7, ~for~all ~t\in (0, T). \end{aligned}$$

Proof

In the case of $\frac{n}{2}<p_0\le n$, observing that $\alpha <2$ we infer that $p_0>\frac{n(\alpha -1)}{2}$, and therefore, we can choose $p_0<p_1< \min \{\frac{np_0}{2n-2p_0}, \frac{np_0}{\alpha n-2p_0}\}$, $\frac{np_1}{n+p_1}<r_1<\min \{\frac{np_0}{2n-p_0}, p_0\}$, $r_2=\frac{p_0}{\alpha }$. Use (2.3) to obtain

$$\begin{aligned} \left\| \frac{u}{v}\nabla v\right\| _{L^{r_1}(\Omega )}&\le M^{-1}_0\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\Vert \nabla v\Vert _{L^{\frac{p_0r_1}{p_0-r_1}}(\Omega )}\nonumber \\&\le M^{-1}_0M_2\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\left( 1+\Vert u\Vert _{L^{p_0}(\Omega )}\right) . \end{aligned}$$

(3.21)

By means of the variation-of-constants representation for u, we can obtain

$$\begin{aligned} \begin{aligned} u(t)&=e^{(\Delta -1)t}u_0+{\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}u-\chi {\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}\nabla \cdot \left( \frac{u}{v}\nabla v\right) +\gamma {\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}u^{\alpha }\\&\quad -\mu {\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}\left( u^{\alpha }\int \limits _{\Omega }u^\beta \right) \\&\le u_0+{\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}u-\chi {\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}\nabla \cdot \left( \frac{u}{v}\nabla v\right) +\gamma {\int \limits _{0}}^{t}e^{(\Delta -1)(t-s)}u^{\alpha }. \end{aligned} \end{aligned}$$

(3.22)

According to known smoothing estimates for the Neumann heat semigroup $\{e^{\Delta t}\}_{t\ge 0}$ in $\Omega$ [26], we can choose $C_6>0$ such that

$$\begin{aligned} \begin{aligned} \Vert u\Vert _{L^{p_1}(\Omega )}&\le \Vert u_0\Vert _{L^{p_1}(\Omega )}+C_6{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{p_0}-\frac{1}{p_1}\right) }\right] e^{-(t-s)}\Vert u\Vert _{L^{p_0}(\Omega )}\\&\quad +C_6\chi {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{n}{2}\left( \frac{1}{r_1}-\frac{1}{p_1}\right) }\right] e^{-(\lambda _1+1)(t-s)}\left\| \frac{u}{v}\nabla v\right\| _{L^{r_1}(\Omega )}\\&\quad +C_6\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{r_2}-\frac{1}{p_1}\right) }\right] e^{-(t-s)}\Vert u^{\alpha }\Vert _{L^{r_2}(\Omega )}. \end{aligned} \end{aligned}$$

which together with (3.21) shows

$$\begin{aligned} \begin{aligned} \Vert u\Vert _{L^{p_1}(\Omega )}&\le \Vert u_0\Vert _{L^{p_1}(\Omega )}+C_6{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{p_0}-\frac{1}{p_1}\right) }\right] e^{-(t-s)}\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\\&\quad +C_6\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{r_2}-\frac{1}{p_1}\right) }\right] e^{-(t-s)}\sup \limits _{t\in (0, T)}\Vert u\Vert ^{\alpha }_{L^{p_0}(\Omega )}\\&\quad +C_6\chi M^{-1}_0M_2\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}(1+\Vert u\Vert _{L^{p_0}(\Omega )})\\&\qquad \times {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{n}{2}\left( \frac{1}{r_1}-\frac{1}{p_1}\right) }\right] e^{-(\lambda _1+1)(t-s)}. \end{aligned} \end{aligned}$$

(3.23)

Since ${\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{r_2}-\frac{1}{p_1}\right) }\right] e^{-(\lambda _1+1)(t-s)}$ and ${\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2}\left( \frac{1}{p_0}-\frac{1}{p_1}\right) }\right] e^{-(t-s)}$ as well as ${\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{n}{2}\left( \frac{1}{r_1}-\frac{1}{p_1}\right) }\right] e^{-(\lambda _1+1)(t-s)}$ are finite, consequently, we have

$$\begin{aligned} \begin{aligned} \Vert u\Vert _{L^{p_1}(\Omega )}\le C_7,~for~all~t\in (0,T) \end{aligned} \end{aligned}$$

(3.24)

with some $C_7>0$.

In the case $p_0>n$, considering $\alpha <2$ we know $p_0>\frac{\alpha n}{2}$. Hence, it is possible to pick $n<r_3=p_0$, $\frac{n}{2}<r_4=\frac{p_0}{\alpha }$. We may invoke (2.3) to see

$$\begin{aligned} \begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )}&\le \Vert u_0\Vert _{L^{\infty }(\Omega )}+C_6{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2p_0}}\right] e^{-(t-s)}\Vert u\Vert _{L^{p_0}(\Omega )}\\&\qquad +C_6\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2r_4}}\right] e^{-(t-s)}\Vert u^{\alpha }\Vert _{L^{r_4}(\Omega )}\\&\qquad +C_6\chi M^{-1}_0{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{n}{2r_3}}\right] e^{-(\lambda _1+1)(t-s)}\Vert u\nabla v\Vert _{L^{r_3}(\Omega )}\\&\quad \le \Vert u_0\Vert _{L^{\infty }(\Omega )}+C_6{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2p_0}}\right] e^{-(t-s)}\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\\&\qquad +C_6\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{n}{2r_4}}\right] e^{-(t-s)}\sup \limits _{t\in (0, T)}\Vert u\Vert ^{\alpha }_{L^{p_0}(\Omega )}\\&\qquad +C_6\chi M^{-1}_0 {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{n}{2r_3}}\right] e^{-(\lambda _1+1)(t-s)}\sup \limits _{t\in (0, T)}\Vert u\Vert _{L^{p_0}(\Omega )}\Vert \nabla v\Vert _{L^{{\infty }}(\Omega )}. \end{aligned} \end{aligned}$$

In the case of $\frac{n}{2}<p_1\le n$, we fix $\eta >0$ small such that $p_1>\frac{n}{2}+\eta$. For $k=0, 1, 2\ldots$, we define

$$\begin{aligned} p_{k+1}=\left\{ \begin{aligned}&\frac{np_k}{2(n-p_k+\eta )},{} & {} \quad if ~p_k\le n,\\&\infty ,{} & {} \quad if~p_k >n. \end{aligned} \right. \end{aligned}$$

We see that $p_{k+1}>p_k$ for all $k\ge 0$. Successive applications of (3.23) and (3) to $p_1=p_{k+1}$ and $p_0=p_{k}$ show that u is bounded in $L^{\infty }\left( (0,T), L^{p_k}(\Omega )\right)$ for all k and hence, in particular, in $L^{\infty }\left( (0,T), L^{\infty }(\Omega )\right)$ for all sufficiently large k. $\square$

We will give an estimate in $L^\infty$ norm of the first solution component for $\alpha \ge 2$ by a recursive argument.

Lemma 3.5

Let $n\ge 2$, $\chi >0$ and $\epsilon >0$. Assume that the initial functions $u_0, v_0$ fulfill (1.2). Suppose that $\alpha , \beta$ satisfy (1.6) and that there exists $p_0>\frac{n}{2}$ satisfying

$$\begin{aligned} u\in L^\infty ((0,T); L^{p_0}(\Omega )). \end{aligned}$$

Then there exists $M_{8}(T)>0$ such that

$$\begin{aligned} \Vert u(t)\Vert _{L^{\infty }(\Omega )}\le M_{8}, ~for ~ all ~t\in (0, T). \end{aligned}$$

Proof

We pick $0<s<2$ sufficiently close to 2 and define $p_k=\frac{2^k}{s^k}p_{0}$, $k\ge 1$. Taking $p_ku^{p_k-1}$ as a test function for the first equation in (1.1) and integrating by parts, we obtain

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p_k}+\int \limits _{\Omega }u^{p_k}+\frac{p_k(p_k-1)}{2}\int \limits _{\Omega }u^{p_k-2}|\nabla u|^2+\frac{2(p_k-1)}{p_k}\int \limits _{\Omega }|\nabla u^{\frac{p_k}{2}}|^2\nonumber \\&\quad =\chi p_k(p_k-1)\int \limits _{\Omega }\frac{u^{p_k-1}}{v}\nabla u\cdot \nabla v+\int \limits _{\Omega }u^{p_k}+p_k\gamma \int \limits _{\Omega }u^{p_k+\alpha -1}-\mu p_k\int \limits _{\Omega }u^{p_k+\alpha -1}\int \limits _{\Omega }u^{\beta }. \end{aligned}$$

(3.25)

From the Gagliardo–Nirenberg inequality, we infer that there is a constant $C_{GN}>0$ such that

$$\begin{aligned} \int \limits _{\Omega }u^{p_k}&\le 4C^2_{GN}\left( \Vert \nabla u^{\frac{p_k}{2}}\Vert ^{2a}_{L^{2}(\Omega )}\Vert u^{\frac{p_k}{2}}\Vert ^{2(1-a)}_{L^{\frac{2p_{k-1}}{p_k}}(\Omega )}+\Vert u^{\frac{p_k}{2}}\Vert ^{2}_{L^{\frac{2p_{k-1}}{p_k}}(\Omega )}\right) , \end{aligned}$$

where $a=\left( \frac{1}{s}-\frac{1}{2}\right) \left( \frac{1}{s}-\frac{n-2}{2n}\right) ^{-1}\in (0,1)$. Upon an application of Young’s inequality, we derive

$$\begin{aligned} \int \limits _{\Omega }u^{p_k}&\le \frac{(p_k-1)}{p_k}\int \limits _{\Omega }|\nabla u^{\frac{p_k}{2}}|^2+C_8\left( \int \limits _{\Omega }u^{p_{k-1}}\right) ^{\frac{p_k}{p_{k-1}}}, \end{aligned}$$

(3.26)

where $C_8=4C^2_{GN}\left[ (1-a)\left( \frac{4C^2_{GN}p_0a}{p_0-1}\right) ^{\frac{a}{1-a}}+1\right]$.

We now employ Young’s inequality to estimate

$$\begin{aligned} \chi p_k(p_k-1)\int \limits _{\Omega }\frac{u^{p_k-1}}{v}\nabla u\cdot \nabla v&\le \frac{ p_k(p_k-1)}{2}\int \limits _{\Omega }u^{p_k-2}|\nabla u|^2+\frac{\chi ^2 p_k(p_k-1)}{2M^2_0}\int \limits _{\Omega }u^{p_k}|\nabla v|^2. \end{aligned}$$

(3.27)

Recalling $p_{k-1}\ge p_0>\frac{n}{2}$ and $\beta >\frac{n(\alpha -1)}{2}$, we fix

$$\begin{aligned}&n<p^*<\min \left\{ \frac{np_0}{n-p_0}, \frac{2\beta }{\alpha -1}\right\} . \end{aligned}$$

(3.28)

From the Hölder inequality, we have

$$\begin{aligned} \frac{\chi ^2 p_k(p_k-1)}{2M^2_0}\int \limits _{\Omega }u^{p_k}|\nabla v|^2&\le \frac{\chi ^2 p_k(p_k-1)}{2M^2_0}\left( \int \limits _{\Omega }|\nabla v|^{p^*}\right) ^{\frac{2}{p^*}}\left( \int \limits _{\Omega }u^{\frac{p_kp^*}{p^*-2}}\right) ^{\frac{p^*-2}{p^*}}\nonumber \\&=\frac{\chi ^2 p_k(p_k-1)}{2M^2_0}\Vert \nabla v\Vert ^{2}_{L^{p^*}(\Omega )}\Vert u^{\frac{p_k}{2}}\Vert ^{2}_{L^{\frac{2p^*}{p^*-2}}(\Omega )}. \end{aligned}$$

(3.29)

Considering (3.28) and applying Hölder’s inequality and Cauchy’s inequality, we derive

$$\begin{aligned} p_k\gamma \int \limits _{\Omega }u^{p_k+\alpha -1}&=p_k\gamma \left( \int \limits _{\Omega }u^{p_k+\alpha -1}\right) ^{\lambda }\left( \int \limits _{\Omega }u^{p_k}u^{\alpha -1}\right) ^{1-\lambda }\nonumber \\&\le p_k\gamma \left( \int \limits _{\Omega }u^{p_k+\alpha -1}\int \limits _{\Omega }u^{\beta }\right) ^{\lambda }\left( \int \limits _{\Omega }u^{\frac{p_k\beta }{\beta -\alpha +1}}\right) ^{\frac{(\beta -\alpha +1)(1-\lambda )}{\beta }}\nonumber \\&\le p_k\mu \int \limits _{\Omega }u^{p_k+\alpha -1}\int \limits _{\Omega }u^{\beta }+C_9p_k\left( \int \limits _{\Omega }u^{\frac{p_kp^*}{p^*-2}}\right) ^{\frac{p^*-2}{p^*}}\nonumber \\&=p_k\mu \int \limits _{\Omega }u^{p_k+\alpha -1}\int \limits _{\Omega }u^{\beta }+C_9p_k\Vert u^{\frac{p_k}{2}}\Vert ^{2}_{L^{\frac{2p^*}{p^*-2}}(\Omega )}, \end{aligned}$$

(3.30)

where $\lambda =\frac{\alpha -1}{\beta +\alpha -1}$, $C_9=\gamma (1-\lambda )|\Omega |^{\frac{2}{p^*}}\left( \lambda \gamma \mu ^{-1}\right) ^{\frac{\lambda }{1-\lambda }}$.

Here the Gagliardo–Nirenberg inequality provides $C_{GN}>0$ fulfilling

$$\begin{aligned} \Vert u^{\frac{p_k}{2}}\Vert ^2_{L^{\frac{2p^*}{p^*-2}}(\Omega )}&\le 4C^2_{GN}\left( \Vert \nabla u^{\frac{p_k}{2}}\Vert ^{2b}_{L^{2}(\Omega )}\Vert u^{\frac{p_k}{2}}\Vert ^{2(1-b)}_{L^{\frac{2p_{k-1}}{p_k}}(\Omega )}+\Vert u^{\frac{p_k}{2}}\Vert ^{2}_{L^{\frac{2p_{k-1}}{p_k}}(\Omega )}\right) , \end{aligned}$$

(3.31)

where $b=\left( \frac{1}{s}-\frac{p^*-2}{2p^*}\right) \left( \frac{1}{s}-\frac{(n-2)_{+}}{2n}\right) ^{-1}\in (0,1)$. In view of (3.30) and (3.31), we find that

$$\begin{aligned} p_k\gamma \int \limits _{\Omega }u^{p_k+\alpha -1}&\le p_k\mu \int \limits _{\Omega }u^{p_k+\alpha -1}\int \limits _{\Omega }u^{\beta }+\frac{(p_k-1)}{2p_k}\int \limits _{\Omega }|\nabla u^{\frac{p_k}{2}}|^2\nonumber \\&+C_{10}p^\frac{1}{1-b}_k\Vert u\Vert ^{p_k}_{L^{p_{k-1}}(\Omega )}, \end{aligned}$$

(3.32)

where $C_{10}=4C_7C^2_{GN}\left[ \left( \frac{8bC_7C^2_{GN}p_0}{p_0-1}\right) ^{\frac{b}{1-b}}(1-b)+1\right]$. We employ Young’s inequality and make use of (2.3), (3.29) as well as (3.31) to see

$$\begin{aligned} \frac{\chi ^2 p_k(p_k-1)}{2M^2_0}\int \limits _{\Omega }u^{p_k}|\nabla v|^2&\le C_{11}p^2_k\Vert \nabla u^{\frac{p_k}{2}}\Vert ^{2b}_{L^{2}(\Omega )} \Vert u\Vert ^{p_k(1-b)}_{L^{p_{k-1}}(\Omega )}+C_{11}p^2_k\Vert \nabla u^{\frac{p_k}{2}}\Vert ^{2b}_{L^{2}(\Omega )}\Vert u\Vert ^{2+p_k(1-b)}_{L^{p_{k-1}}(\Omega )}\nonumber \\&\quad +C_{11}p^2_k\Vert u\Vert ^{p_k}_{L^{p_{k-1}}(\Omega )}+C_{11}p^2_k\Vert u\Vert ^{2+p_k}_{L^{p_{k-1}}(\Omega )}\nonumber \\&\le \frac{(p_k-1)}{2p_k}\int \limits _{\Omega }|\nabla u^{\frac{p_k}{2}}|^2+C_{12}p^{\frac{2}{1-b}}_k\Vert u\Vert ^{\frac{2}{1-b}+p_k}_{L^{p_{k-1}}(\Omega )}\nonumber \\&\quad +C_{11}p^2_k\Vert u\Vert ^{2+p_k}_{L^{p_{k-1}}(\Omega )}+\left( C_{11}p^2_k+C_{12}p^{2+\frac{2b}{1-b}}_k\right) \Vert u\Vert ^{p_k}_{L^{p_{k-1}}(\Omega )} \end{aligned}$$

(3.33)

where $C_{11}=\frac{4C^2_{GN} \chi ^2M_3}{2M^2_0}$, $C_{12}=C_9(1-b)\left( \frac{4p_0bC_9}{p_0-1}\right) ^{\frac{b}{1-b}}$. To simplify this, observing $\frac{2}{1-b}+p_k>\max \{2+p_k, p_k\}$, combining (3.25), (3.26), (3.27), (3.32) and (3.33) we see that there is a constant $C_{13}=\max \{C_8, C_{10}, 2C_{11}, 2C_{12}\}$ independent of k such that

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p_k}+\int \limits _{\Omega }u^{p_k}&\le C_{13}p^{\frac{2}{1-b}}_k\Vert u\Vert ^{\frac{2}{1-b}+p_k}_{L^{p_{k-1}}(\Omega )}. \end{aligned}$$

(3.34)

Let us define

$$\begin{aligned} A_k:=\sup \limits _{t\in (0, T)}\Vert u(\cdot ,t)\Vert _{L^{p_k}(\Omega )}. \end{aligned}$$

Now by an ODE comparison, the ODI (3.34) warrants that

$$\begin{aligned} A_k&\le \max \left\{ \Vert u_0\Vert _{L^{p_k}(\Omega )}, C^{p^{-1}_k}_{13}p_0^{p^{-1}_k}\left( \frac{2}{s}\right) ^{2k(1-b)^{-1}p^{-1}_k}A^{1+\frac{2}{(1-b)p_k}}_{k-1}\right\} . \end{aligned}$$

(3.35)

Therefore, in the case when

$$\begin{aligned} \Vert u_0\Vert _{L^{p_k}(\Omega )}\ge&C^{p^{-1}_k}_{13}p_0^{p^{-1}_k}\left( \frac{2}{s}\right) ^{2k(1-b)^{-1}p^{-1}_k}A^{1+\frac{2}{(1-b)p_k}}_{k-1},~\forall k\ge 1, \end{aligned}$$

then we have $\Vert u\Vert _{L^{\infty }(\Omega )}\le \Vert u_0\Vert _{L^{\infty }(\Omega )}$. Otherwise, (3.35) entails

$$\begin{aligned} A_k&\le C^{p^{-1}_k}_{13}p_0^{p^{-1}_k}\left( \frac{2}{s}\right) ^{2k(1-b)^{-1}p^{-1}_k}A^{1+\frac{2}{(1-b)p_k}}_{k-1},\end{aligned}$$

which by a well-known inductive argument shows that with $h_k=1+\frac{2}{(1-b)p_k}$ we have

$$\begin{aligned} A_k&\le C^{p^{-1}_k+\sum _{j=0}^{k-2} {p^{-1}_{k-j-1}\prod _{i=k-j}^kh_i}}_{13}p_0^{p^{-1}_k+\sum _{j=0}^{k-2} {p^{-1}_{k-j-1}\prod _{i=k-j}^kh_i}}\\&\quad \times \left( \frac{2}{s}\right) ^{{2(1-b)^{-1}k}{p^{-1}_k}+\sum _{j=0}^{k-2} {2(1-b)^{-1}(k-j-1)p^{-1}_{k-j-1}\prod _{i=k-j}^kh_i}}A_{k-1}^{\prod _{i=1}^kh_i}. \end{aligned}$$

Since

$$\begin{aligned} \ln \left( \prod _{i=1}^kh_j\right)&\le \sum _{i=1}^k\frac{2}{(1-b)p_k}=\frac{2}{(1-b)p_0}\sum _{i=1}^k\left( \frac{s}{2}\right) ^i\le \frac{2s}{(2-s)(1-b)p_0}, \end{aligned}$$

together with the Dirichlet discriminant method we obtain

$$\begin{aligned}&\sum _{j=0}^{k-2} {p^{-1}_{k-j-1}\prod _{i=k-j}^kh_i}<\infty , \end{aligned}$$

and

$$\begin{aligned}&\sum _{j=0}^{k-2} {2(1-b)^{-1}(k-j-1)p^{-1}_{k-j-1}\prod _{i=k-j}^kh_i}<\infty . \end{aligned}$$

Hence, $\Vert u\Vert _{L^{\infty }(\Omega )}$ is bounded from above by a constant independent of k. This clearly proves this lemma. $\square$

Now we prove Theorem 1.1.

Proof

Having the above estimates at hand, Theorem 1.1 directly results from Lemmas 3.4 and 3.5. $\square$

4 Boundedness of the solution

The intention of this section is to derive a positive uniform-in-time lower bound for v to arrive at the global boundedness of solutions of (1.1). Based on the linear parabolic theory, the pointwise lower bound on the chemical v can be measured by the mass of cells u. In fact, we can obtain the uniform estimation of $\int \limits _{\Omega }u^\beta$.

Lemma 4.1

Let $n\ge 2$, $0<\epsilon <1$ and $0<\chi <1-\epsilon$. If $\alpha , \beta$ satisfy (1.7), then we have

$$\begin{aligned}&\int \limits _{\Omega }u^{\beta }\le M_6,~for~all~t\in (0, T), \end{aligned}$$

(4.1)

where $M_6$ is as in Lemma 3.3.

Proof

A observation shows that

$$\begin{aligned}&q_2(\beta )\ge \left( \frac{\chi (1-\epsilon )\beta }{2}+2\epsilon \right) \left( \frac{(\epsilon -1)^2\beta +4\epsilon }{2(\beta -1)}\right) ^{-1}. \end{aligned}$$

(4.2)

Due to our restriction $0<\chi <1-\epsilon$, we know

$$\begin{aligned}&\left( \frac{\chi (1-\epsilon )\beta }{2}+2\epsilon \right) \left( \frac{(\epsilon -1)^2\beta +4\epsilon }{2(\beta -1)}\right) ^{-1}>\frac{\chi (\beta -1)}{1-\epsilon }. \end{aligned}$$

(4.3)

The condition (1.7) implies

$$\begin{aligned}&\frac{\chi (\beta -1)(2-\alpha )}{1-\epsilon }>\alpha -1. \end{aligned}$$

(4.4)

Combining (4.2), (4.3) and (4.4) shows that

$$\begin{aligned}&(2-\alpha )q_2(\beta )>\alpha -1. \end{aligned}$$

which is equivalent to

$$\begin{aligned}&\beta <\beta -\alpha +1+(2-\alpha )q_2(\beta ). \end{aligned}$$

Taking $p>\beta$ closed to $\beta$, based on the continuous dependency of parameters p it is possible to pick p to ensure (3.4). Therefore, by a similar proof of (i) in Lemma 3.2 we get (3.9). According to $p>\beta >\frac{n}{2}$ and Lemma 3.3, we finish the proof. $\square$

The key point of the lower bound of $\int \limits _{\Omega }u$ is to control the integral $\int \limits _{\Omega }u^{r}v^{\theta }$ for suitable $r, \theta \in (0, 1)$, which has been used in [14]. The result is embedded in the following lemma.

Lemma 4.2

Let $n\ge 2$, $0<\epsilon <1$ and $0<\chi <1-\epsilon$. Assume that initial data $u_0$, $v_0$ satisfy (1.2) and that $\alpha , \beta$ satisfy (1.7), then there exists $\gamma _0>0$ with the property that if $\gamma >\gamma _0$, then for $0<r<1$, $\theta _{-}<\theta <\min \{1, \theta _{+}\}$, there exists some constant $M_{9}>0$ independent of T such that

$$\begin{aligned}&\int \limits _{\Omega }u^{r}v^{\theta }\ge M_{9},~for~all~ t\in (0, T), \end{aligned}$$

(4.5)

where

$$\begin{aligned} \theta _{\pm }&=\left( \frac{\chi (1-\epsilon )r}{2}+\epsilon \pm \sqrt{\epsilon ^2+p\epsilon \chi (1-\epsilon -\chi )}\right) \cdot \left( \frac{(\epsilon -1)^2r+4\epsilon }{2(1-r)}\right) ^{-1}. \end{aligned}$$

Proof

We differentiate the term $\int \limits _{\Omega }u^{r}v^{\theta }$ to obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{r}v^{\theta }&=r(1-r)\int \limits _{\Omega }u^{r-2}v^{\theta }|\nabla u|^2-[(1+\epsilon )r\theta +r(1-r)\chi ]\int \limits _{\Omega }{u^{r-1}}v^{\theta -1}\nabla u\cdot \nabla v \\&\quad +[\chi r\theta +\epsilon \theta (1-\theta )]\int \limits _{\Omega }u^{r}v^{\theta -2}|\nabla v|^2+\theta \int \limits _{\Omega }u^{r+1}v^{\theta -1} \\&\quad +r\gamma \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }-r\mu \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }\int \limits _{\Omega }u^{\beta }-\theta \int \limits _{\Omega }u^{r}v^{\theta }. \end{aligned}$$

We furthermore note that by means of Young’s inequality

$$\begin{aligned}&r(1-r)\int \limits _{\Omega }u^{r-2}v^{\theta }|\nabla u|^2-[(1+\epsilon )r\theta +r(1-r)\chi ]\int \limits _{\Omega }{u^{r-1}}v^{\theta -1}\nabla u\cdot \nabla v\\&\quad +[\chi r\theta +\epsilon \theta (1-\theta )]\int \limits _{\Omega }u^{r}v^{\theta -2}|\nabla v|^2\\&\ge \left\{ \chi r\theta +\epsilon \theta (1-\theta )-\frac{r[(1+\epsilon )\theta +(1-r)\chi ]^2}{4(1-r)}\right\} \int \limits _{\Omega }u^{r}v^{-\theta -2}|\nabla v|^2; \end{aligned}$$

therefore, the inequality $\theta _{-}<\theta <\theta _{+}$ ensures

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{r}v^{\theta }+\theta \int \limits _{\Omega }u^{r}v^{\theta }\ge&\theta \int \limits _{\Omega }u^{r+1}v^{\theta -1}+r\gamma \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }-r\mu \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }\int \limits _{\Omega }u^{\beta }. \end{aligned}$$

In virtue of lemma 4.1, we have

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{r}v^{\theta }+\theta \int \limits _{\Omega }u^{r}v^{\theta }\ge&\theta \int \limits _{\Omega }u^{r+1}v^{\theta -1}+r(\gamma -\mu M_5)\int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }. \end{aligned}$$

(4.6)

By Hölder’s inequality, one can derive

$$\begin{aligned} \int \limits _{\Omega }u^{r}v^{\theta }&\le |\Omega |^{\frac{(1-\theta )(\alpha -1)}{r+\alpha -1}}\left( \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }\right) ^{\frac{r}{r+\alpha -1}}\left( \int \limits _{\Omega }v\right) ^{\frac{\theta (\alpha -1)}{r+\alpha -1}}. \end{aligned}$$

(4.7)

From (2.5) and (4.7), we know

$$\begin{aligned} \int \limits _{\Omega }u^{r+\alpha -1}v^{\theta }\ge&|\Omega |^{-\frac{(1-\theta )(\alpha -1)}{r}}\Bigg (\int \limits _{\Omega }v_0+M_3\Bigg )^{-\frac{\theta (\alpha -1)}{r}}\Bigg (\int \limits _{\Omega }u^{r}v^{\theta }\Bigg )^{\frac{r+\alpha -1}{r}}. \end{aligned}$$

(4.8)

Letting $\gamma$ be large enough satisfying $\gamma >\mu M_5$ and then combining (4.6) and (4.8) show

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{r}v^{\theta }+\theta \int \limits _{\Omega }u^{r}v^{\theta }\ge&C_{14}\left( \int \limits _{\Omega }u^{r}v^{\theta }\right) ^{\frac{r+\alpha -1}{r}}, \end{aligned}$$

(4.9)

where $C_{14}=r(\gamma -\mu M_5)|\Omega |^{-\frac{(1-\theta )(\alpha -1)}{r}}\left( \int \limits _{\Omega }v_0+M_3\right) ^{-\frac{\theta (\alpha -1)}{r}}$.

Next we claim $\int \limits _{\Omega }u^{r}_0v^{\theta }_0$ has a lower bound. By the definition of (1.2), we know $\int \limits _\Omega {u_0}>0$ and there are constants $C_{15}, C_{16}>0$ such that $\Vert u_0\Vert _{L^{\infty }(\Omega )}\le C_{15}$ and $\inf \limits _{x\in \Omega }v_0(x)>C_{16}$. For $m\in (0,1)$, we thus have

$$\begin{aligned} \int \limits _\Omega {u_0}&=\int \limits _{\Omega }({u_0}^{r}{v_0}^{\theta })^{m}\cdot ({u_0}^{1-rm}{v_0}^{-m\theta }) \\&\le \left( \int \limits _{\Omega }{u_0}^{r}{v_0}^{\theta }\right) ^{m}\cdot \left( \int \limits _{\Omega }{u_0}^{\frac{1-rm}{1-m}}{v_0}^{\frac{-m\theta }{1-m}}\right) ^{1-m} \\&\le {C_{15}^{1-rm}}{C_{16}^{-m\theta }}|\Omega |^{1-m}\left( \int \limits _{\Omega }{u_0}^{r}{v_0}^{\theta }\right) ^{m}, \end{aligned}$$

which implies

$$\begin{aligned} \int \limits _{\Omega }{u_0}^{r}{v_0}^{\theta }\ge C_{17}, \end{aligned}$$

(4.10)

where $C_{17}=\left( |\Omega |^{m-1} C_{15}^{rm-1}{C_{16}^{m\theta }}\right) ^{\frac{1}{m}}$. Therefore, based on the principle of comparison of ordinary differential equation for (4.9) and (4.10) we have

$$\begin{aligned} \int \limits _{\Omega }u^{r}v^{\theta }\ge&\max \left\{ C_{17}, \left( \frac{\theta }{C_{14}}\right) ^{\frac{r}{\alpha -1}} \right\} . \end{aligned}$$

Letting $M_{9}=\max \left\{ C_{17}, \left( \frac{\theta }{C_{14}}\right) ^{\frac{r}{\alpha -1}} \right\}$ establishes (4.5). $\square$

Taking $r=1-\theta$, we can obtain the lower bound of $\int \limits _{\Omega }u$.

Lemma 4.3

Let $n\ge 2$, $0<\epsilon <1$ and $0<\chi <1-\epsilon$. Assume that initial data $u_0$, $v_0$ satisfy (1.2). If $\alpha , \beta$ satisfy (1.7), then there exists some constant $M_{10}>0$ independent of T such that

$$\begin{aligned}&\int \limits _{\Omega }u\ge M_{10},~for~all~t\in (0, T). \end{aligned}$$

(4.11)

Proof

We fix $\theta _{-}<\theta <\min \{1, \theta _{+}\}$ and take $r=1-\theta$ in (4.5) to estimate

$$\begin{aligned}&M_{9}\le \int \limits _{\Omega }u^{1-\theta }v^\theta \le \int \limits _{\Omega }u\int \limits _{\Omega }v,~ t\in (0,T), \end{aligned}$$

Using (2.5), we get

$$\begin{aligned}&M_{9}\le \int \limits _{\Omega }u^{1-\theta }v^\theta \le \left( M_3+\int \limits _{\Omega }v_0\right) \int \limits _{\Omega }u,~ t\in (0,T), \end{aligned}$$

which directly yields (4.11) with $M_{10}=M_{9}\left( M_3+\int \limits _{\Omega }v_0\right) ^{-1}$. $\square$

Now we establish the uniformly lower bound estimate for v. In view of the local existence lemma in Lemma 2.1, it is routine to check that there is $t_0\in (0, T)$ such that $v(x,t)\ge \frac{1}{2} \inf \limits _{x\in \Omega }v_0(x)$ for all $x\in \Omega$ and $t\in (0, t_0]$. So we only need to derive the uniform lower bound of v for $t_0<t<T$.

Lemma 4.4

Assume the conditions in Lemma 4.3 hold. Then there is $M_{11}>0$ independent of T such that

$$\begin{aligned}&v\ge M_{11},~for~all~t\in (0, T). \end{aligned}$$

(4.12)

Proof

Applying the Neumann heat semigroup $\{e^{(\epsilon \triangle -1)t}\}_{t\ge 0}$ and (4.11), we obtain from the second equation of (1.1) and the positivity of $v_0$,

$$\begin{aligned} \begin{aligned} v(t)&=e^{(\epsilon \Delta -1)(t-t_0)}v_0-{\int \limits _{t_0}}^{t}e^{(\epsilon \triangle -1)(t-s)}u(x,s)\textrm{d}s\\&\ge {\int \limits _{t_0}}^{t}\frac{1}{4\pi (t-s)}e^{-(t-s)-\frac{|diam\Omega |^2}{4(t-s)}}\Big (\int \limits _{\Omega }u(x,s)\textrm{d}x\Big )\textrm{d}s\\&\ge M_{10}{\int \limits _{0}}^{t_0}\frac{1}{4\pi \sigma }e^{-\sigma -\frac{|diam\Omega |^2}{4\sigma }}d\sigma , ~(x,t)\in \Omega \times (t_0, T). \end{aligned} \end{aligned}$$

Taking $M_{11}=\max \left\{ M_{10}{\int \limits _{0}}^{t_0}\frac{1}{4\pi \sigma }e^{-\sigma -\frac{(diam\Omega )^2}{4\sigma }}d\sigma , \frac{1}{2} \inf \limits _{x\in \Omega }v_0(x)\right\}$, the inequality (4.12) yields. $\square$

In light of Lemmas 3.1–3.3, we obtain the time-independent bounds for u in $L^{p_0}(\Omega )$ for some $p_0>\frac{n}{2}$. Notice that the uniformly positive lower bound of v is essential to deal with improving the regularity from $L^{p_0}(\Omega )$ to $L^{\infty }(\Omega )$ in Lemma 3.4. For completeness, we provide a lemma in the following.

Lemma 4.5

Let $n\ge 2$, $\chi >0$ and $\epsilon >0$. Assume that the initial functions $u_0, v_0$ fulfill (1.2) and that $\alpha , \beta$ satisfy (1.5). Suppose that there exist $p_0>\frac{n}{2}$ such that

$$\begin{aligned} u\in L^\infty ((0,T); L^{p_0}(\Omega )). \end{aligned}$$

Then there exists $M_{12}>0$ independent of T such that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )}\le M_{12},~for~all~t\in (0, T). \end{aligned}$$

Proof

By changing $M_0$ by $M_{11}$ in Lemma 3.4, this lemma follows immediately. $\square$

Without any further difficulties, Lemma 4.5 guarantees Theorem 1.2.

5 Existence and boundedness for 1-d

We proceed to establish the regularity in $L^{\infty }$ in the case of $1\le \alpha <2$.

Lemma 5.1

Let $\chi ,\epsilon >0$, $1\le \alpha <2$ and $\beta \ge 1$. Suppose that the initial functions $u_0, v_0$ fulfill (1.2). Then there exists $M_{14}(T)>0$ such that $\Vert u\Vert _{L^{\infty }(\Omega )}\le M_{14},~for~all~t\in (0, T)$.

Proof

Applying the variation in constants formula to the first equation of (1.1) and according to the properties of the Neumann semigroup, for any $r_1>1$, $r_2=\frac{1}{\alpha }$,

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )}&\le \Vert u_0\Vert _{L^{\infty }(\Omega )}+\chi M^{-1}_0{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{1}{2r_1}}\right] \Vert u v_x\Vert _{L^{r_1}(\Omega )}\textrm{d}s\\&\quad +\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2r_2}}\right] \Vert u\Vert ^{\alpha }_{L^{1}(\Omega )}\textrm{d}s. \end{aligned}$$

Taking $1<r_1<r<\infty$, by Hölder’s inequality we have

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )}&\le \Vert u_0\Vert _{L^{\infty }(\Omega )}+\chi M^{-1}_0{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{1}{2r_1}}\right] \textrm{d}s\sup \limits _{t\in (0,T)}\Vert v_x\Vert _{L^{r}(\Omega )}\Vert u\Vert _{L^{\frac{rr_1}{r-r_1}}(\Omega )}\\&\quad +\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2r_2}}\right] \Vert u\Vert ^\alpha _{L^{1}(\Omega )}\textrm{d}s. \end{aligned}$$

From (2.3) and (2.4), we have

$$\begin{aligned}&\Vert u\Vert _{L^{\infty }(\Omega )}\le \Vert u_0\Vert _{L^{\infty }(\Omega )}+C_{1}\Vert u\Vert ^{\frac{rr_1-r+r_1}{rr_1}}_{L^{\infty }(\Omega )}+C_{2}, \end{aligned}$$

where

$$\begin{aligned}&C_{1}=\chi M^{-1}_0M_3(1+M_1)|\Omega |^{\frac{rr_1-r+r_1}{rr_1}}{\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2}-\frac{1}{2r_1}}\right] \textrm{d}s,\\&C_{2}=M^\alpha _1\gamma {\int \limits _{0}}^{t}\left[ 1+(t-s)^{-\frac{1}{2r_2}}\right] \textrm{d}s. \end{aligned}$$

Notice $\frac{rr_1-r+r_1}{rr_1}<1$, by Young’s inequality we find

$$\begin{aligned}&\Vert u\Vert _{L^{\infty }(\Omega )}\le 2\Vert u_0\Vert _{L^{\infty }(\Omega )}+C_{3}, \end{aligned}$$

where $C_{3}=2C_{2}+2C_{1}\frac{r-r_1}{rr_1}\left( \frac{2C_{1}(rr_1-r+r_1)}{r-r_1}\right) ^{\frac{rr_1-r+r_1}{r-r_1}}$. We finish the proof of Lemma 5.1 by taking $M_{11}=2\Vert u_0\Vert _{L^{\infty }(\Omega )}+C_{3}$. $\square$

We will give an estimation in $L^\infty (\Omega \times (0, T))$ for $\alpha \ge 2$ by a recursive argument.

Lemma 5.2

Let $\chi ,\epsilon >0$, $\alpha \ge 2$ and $\beta >\alpha -1$. Suppose that the initial functions $u_0, v_0$ fulfill (1.2). Then there exists $M_{15}(T)>0$ such that $\Vert u\Vert _{L^{\infty }(\Omega )}\le M_{15},~for~all~t\in (0, T)$.

Proof

The proof is similar to Lemma 3.11. We only point out the difference. We pick $0<s<2$ and define $p_k=\frac{2^k}{s^k}$, $k\ge 0$. Taking $p_ku^{p_k-1}$ ($k\ge 1$) as a test function for the first equation in (1.1) and integrating by parts, we obtain

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t}\int \limits _{\Omega }u^{p_k}\textrm{d}x+\int \limits _{\Omega }u^{p_k}\textrm{d}x+\frac{p_k(p_k-1)}{2}\int \limits _{\Omega }u^{p_k-2}|u_x|^2\textrm{d}x+\frac{2(p_k-1)}{p_k}\int \limits _{\Omega }\left| u^{\frac{p_k}{2}}\right| ^2_x\textrm{d}x\nonumber \\&\quad =\chi p_k(p_k-1)\int \limits _{\Omega }\frac{u^{p_k-1}u_xv_x}{v}\textrm{d}x+\int \limits _{\Omega }u^{p_k}\textrm{d}x+p_k\gamma \int \limits _{\Omega }u^{p_k+\alpha -1}\textrm{d}x-\mu p_k\int \limits _{\Omega }u^{p_k+\alpha -1}\textrm{d}x\int \limits _{\Omega }u^{\beta }\textrm{d}x. \end{aligned}$$

(5.1)

Recalling $\beta >\alpha -1$, we fix

$$\begin{aligned}&2<p^*<\frac{2\beta }{\alpha -1}. \end{aligned}$$

(5.2)

Combining (5.1), (3.26), (3.27), (3.32) and (3.33), we proceed in quite the same manner as Lemma 3.5 to produce Lemma 5.2. $\square$

Now we begin with proving Theorem 1.3.

Proof

Having these preliminaries at hand, we can give the existence of solution by Lemmas 5.1 and 5.2. The lower bound of v result from Lemmas 4.1–4.4. Using a similar reasoning as Theorem 1.2, we therefore obtain Theorem 1.3. $\square$