1 Introduction

Stress concentration around small holes in an elastic material has been a lasting topic in the theory of elasticity and in the failure analysis of perforated structures. Classical analytic results in this topic may be found in [1] for circular cylindrical hole, in [2, 3] for elliptical cylindrical hole, in [4] for spheroidal hole and in [5] for general ellipsoidal hole. While the majority of researchers focused on forward problems of the stress concentration around holes in which the geometry of the holes is specified in advance and the objective is to determine the stress field around the holes, a few researchers endeavored to solve the inverse problem as to the identification of special configurations of the holes that minimize the stress concentration. For example, Cherepanov [6] considered a remotely-loaded elastic plane containing holes whose boundary undergoes a uniform pressure, and introduced the concept of ‘equally strong’ holes in which the resulting hoop stress remains constant on the entire boundary of the holes; he also devised a novel method to determine the shapes of such holes (including both single and multiple interacting cases). In contrast to [6], Bjorkman & Richards [7] considered similar cases but introduced a different concept of ‘harmonic’ holes in which the resulting mean stress remains constant in the entire medium surrounding the hole. Coincidentally, from a mathematical point of view, the concept of ‘equally strong’ holes is exactly equivalent to that of ‘harmonic’ holes when the boundary of the holes is subjected to a uniform pressure (including the traction-free case). In particular, it was proved rigorously by Wheeler [8] and Banichuk [9] for plane deformations and by Wheeler & Kunin [10] for three-dimensional deformations that the configuration of a hole designed based on the ‘equally strong’ or ‘harmonic’ concept is indeed optimal leading to minimum stress concentration around the hole. The ‘equally strong’ or ‘harmonic’ concept was later extended to the cases of an elastic matrix enveloping small rigid or elastic inclusions (see, for example, [11,12,13]). In the case of a perfectly bonded inclusion-matrix interface, Wheeler and his coauthor [11, 12] showed that the harmonic shape for a single rigid inclusion must be ellipsoidal (three-dimensional deformations) or elliptical (plane deformations) when the far-field loading is uniform, while Wang and Schiavone [13] identified a large family of harmonic shapes for two interacting elastic inclusions in plane deformations for a certain linear type of far-field loadings. In the case of an imperfect inclusion-matrix interface (for example, involving spring-type interfaces or interface coatings), however, it is possible to make an elastic inclusion of certain specified shapes (for example, circular, spherical and hypotrochoidal shapes) harmonic by selecting related material constants appropriately [14,15,16]. In addition to the above-mentioned pieces of research based on classical linear elasticity theories, the study of the ‘equally strong’ or ‘harmonic’ concept in finite deformations attracted also some attention. For example, in the case of a particular class of compressible hyperelastic materials under finite plane deformations, the design of harmonic holes, harmonic rigid inclusions and harmonic coated elastic inclusions were explored in [17,18,19,20], respectively.

In this paper, we aim to re-examine the design of ‘harmonic’ holes under similar conditions (i.e. uniform far-field loading and uniform pressure exerted on the boundary of the hole) but incorporating the change in the direction of the internal pressure in the hole during deformation (which was neglected in [6, 7]), leading to some refined results which are more applicable to the design of stress-concentration-minimizing holes inside a soft elastic medium. In fact, when the medium surrounding the hole is soft, the pressure acting on the boundary of the hole would undergo an appreciable directional change (as the normal to the boundary of the hole changes) during deformation and this directional change may alter the local stress distribution significantly [21, 22]. Here, it is worth mentioning that although a soft elastic medium indicates relatively large deformations, the use of the classical linear elasticity theory in corresponding mechanical analysis still provides the possibility of yielding acceptably accurate results (for example, it is demonstrated in [23] for a soft silicone gel containing liquid inclusions that the local deformations predicted by the linear elasticity theory agree overall well with experimental results even when the far-field strain reaches 20%).

The paper is arranged as follows. In Sect. 2, we describe the modified harmonic-hole problem from a physical point of view, while in Sect. 3 we formulate this problem mathematically, solve it using the complex variable method and obtain the desired shape of the harmonic hole. In Sect. 4, we illustrate the differences between the modified solution and the classical solution relative to the remote loading and internal pressure.

2 Problem statement

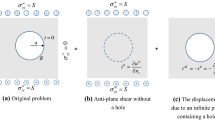
We refer to a rectangular xy coordinate system and consider a hole surrounded by an infinite elastic solid under plane deformation (see Fig. 1). The solid undergoes a uniform biaxial tension/compression remotely (denoted by \(\sigma _{{xx}}^{\infty }\) and \(\sigma _{{yy}}^{\infty }\)) and a uniform pressure (denoted by \(P_{0}\)) on its internal boundary (i.e. the boundary of the hole). The hole is called a harmonic hole if the mean stress (referred to as the average of all the normal stress components) in the entire solid remains constant. The harmonic-hole problem has been solved in [7] with the use of the classical boundary condition in which the directional change of the pressure in the hole during deformation is ignored. Here, we aim to revisit this problem when a modified boundary condition incorporating the directional change of the internal pressure is used.

Fig. 1
figure 1

Perforated elastic solid under internal pressure and far-field loading

Full size image

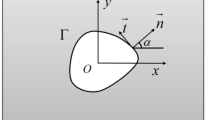
The notation is introduced as follows. The shear modulus and Poisson’s ratio of the solid are represented by G and \(\nu \), respectively. The region occupied by the perforated solid is denoted by S, while the boundary of the hole is denoted by L. The initial normal and tangent to L are denoted by n and t. The rectangular components of the stress and displacement in the solid are represented, respectively, by (\(\sigma _{{xx}}, \sigma _{{ yy}}, \sigma _{{xy}}\)) and (\(u_{{x}},u_{{y}}\)). With reference to the local n-t coordinate system, the corresponding components of the stress and displacement around the hole are denoted by (\(\sigma _{{nn}}, \sigma _{{tt}},\sigma _{{nt}}\)) and (\(u_{{n}}, u_{{t}}\)).

Following the concept introduced in [21], we represent a modified Piola-type boundary condition on L accounting for the directional change of internal pressure during deformation, as

$$\begin{aligned} \sigma _{{nn}} =-P_{0} (1+\varepsilon _{{tt}} ),\,\sigma _{{nt}} =-P_{0} \omega ,\hbox { on }L\hbox {,} \end{aligned}$$
(1)

where \(\varepsilon _{{tt}}\) and \(\omega \) denote the stretching strain and the rotation angle of an infinitesimal element of the curve L during deformation. It is seemingly more reasonable to remove \(\varepsilon _{{tt}}\) from Eq. (1), although for the current harmonic-hole problem, the boundary condition would become ill-posed and admit no solution for the shape of the hole if \(\varepsilon _{{tt}}\) is removed (because in this case the traction induced by the internal pressure may be not self-equilibrated). The stretching strain and rotation angle introduced from Eq. (1) are defined, in terms of the local displacement, by

$$\begin{aligned} \varepsilon _{{tt}} =\frac{\textrm{d}u_{{t}} }{\textrm{d}s}+u_{{n}} k,\,\omega =ku_{{t}} -\frac{\textrm{d}u_{{n}} }{\textrm{d}s},\hbox { on }L, \end{aligned}$$
(2)

where ds is the length of an infinitesimal element of L and k is the curvature of L. The harmonic-hole problem seeks to identify an appropriate shape of the hole such that the resulting stress field in the solid determined from Eq. (1) meets

$$\begin{aligned} \sigma _{{xx}} +\sigma _{{yy}} =\sigma _{{xx}}^{\infty } +\sigma _{{yy}}^{\infty } ,\hbox { in entire }S. \end{aligned}$$
(3)

We present an analytic treatment of this inverse problem in next Section.

3 Solving process

We formulate the harmonic-hole problem using the complex variable formalism which states that the rectangular components of the stress and displacement in the solid can be represented in terms of two complex analytic functions \(\varphi (z)\) and \(\psi (z)\) (where \(z=x+iy\) and i is the imaginary unit) as [3]

$$\begin{aligned} \left. {{\begin{array}{*{20}c} {\sigma _{{xx}} +\sigma _{{yy}} =2\left[ {{\varphi }'(z)+\overline{{\varphi }'(z)} } \right] ,} \\ {\sigma _{{yy}} -\sigma _{{xx}} +2i\sigma _{{xy}} =2\left[ {\bar{{z}}{\varphi }''(z)+{\psi }'(z)} \right] ,} \\ \end{array} }} \right\} z\in S, \end{aligned}$$
(4)
$$\begin{aligned} u_{{x}} +iu_{{y}} =\frac{\kappa \varphi (z)-z\overline{{\varphi }'(z)} -\overline{\psi (z)} }{2G},\quad z\in S, \end{aligned}$$
(5)

where

$$\begin{aligned} \kappa =\left\{ {{\begin{array}{*{20}c} {3-4\nu ,\hbox { plane strain};} \\ {{(3-\nu )} \big / {(1+\nu )},\hbox { plane stress.}} \\ \end{array} }} \right. \end{aligned}$$
(6)

Directly representing the boundary condition (1) in terms of the boundary values of \(\varphi (z), \psi (z)\) and their derivatives on L will lead to very complicated and lengthy expressions, reducing the possibility of attaining a closed-form solution to the shape of the hole. In [21], however, the authors established an integral-form boundary condition which is equivalent to Eq. (1) but allows for a quite simple complex variable representation (see Sects. 2 and 3 and especially Sections 2.1 and 3.1 there). Consequently, following Eq. (21) in [21] we are able to represent the boundary condition (1) as

$$\begin{aligned} \varphi (t)+t\overline{{\varphi }'(t)} +\overline{\psi (t)} =-P^{*}\left[ {\kappa \varphi (t)-t\overline{{\varphi }'(t)} -\overline{\psi (t)} } \right] -P_{0} t+C,\quad t\in L, \end{aligned}$$
(7)

where C is a certain constant of integration and

$$\begin{aligned} P^{*}={P_{0} } \big / {(2G)}. \end{aligned}$$
(8)

The presence of the uniform far-field loading allows us to decompose \(\psi (z)\) into

$$\begin{aligned} \psi (z)=\Gamma _{2} z+\psi _{0} (z),\quad z\in S, \end{aligned}$$
(9)

where \(\psi _{0} (z)\) is a new complex analytic function (we stipulate, without loss of generality, that \(\lim \limits _{\left| z \right| \rightarrow \infty } \psi _{0} (z)=0)\) and

$$\begin{aligned} \Gamma _{2} ={(\sigma _{{yy}}^{\infty } -\sigma _{{xx}}^{\infty } )} \big / 2. \end{aligned}$$
(10)

On the other hand, the essential indicator for a harmonic hole described in Eq. (3) necessitates

$$\begin{aligned} \varphi (z)\equiv \Gamma _{1} z,\quad z\in S, \end{aligned}$$
(11)

with

$$\begin{aligned} \Gamma _{1} ={(\sigma _{{xx}}^{\infty } +\sigma _{{yy}}^{\infty })} \big / 4. \end{aligned}$$
(12)

Here, we simply let the imaginary part of \(\Gamma _{1}\) be zero and remove an arbitrary constant from the right side of Eq. (11) as they play no role in determining the stress field in the solid. Substituting Eqs. (9) and (11) into the conjugate of Eq. (7) we arrive at

$$\begin{aligned} (1-P^{*})\psi _{0} (t)=(P^{*}-1)\Gamma _{2} t-\left[ {\left( {2+(\kappa -1)P^{*}} \right) \Gamma _{1} +P_{0} } \right] \bar{{t}}+C,\quad t\in L, \end{aligned}$$
(13)

which imposes some constraints on the shape of the hole. We disregard an impractical case in which the internal pressure approaches twice the shear modulus of the solid (i.e. \(P^{*}=1\)), because this case violates the setting of small deformations too excessively.

For an arbitrarily-shaped hole bounded by a simple closed curve L, there always exists a conformal mapping function that maps the corresponding region S onto the exterior of a unit circle in an imaginary plane. This mapping function is represented as [3]

$$\begin{aligned} z=\omega (\xi )=z_{0} +R\left( {\xi +\sum \limits _{j=1}^\infty {\alpha _{j} \xi ^{-j}} } \right) ,\quad \left| \xi \right| \ge 1,\quad z\in S, \end{aligned}$$
(14)

where \(z_{0}\) is a complex constant determining the overall position of the hole, R is a positive constant setting roughly the size of the hole while \(\alpha _{j}\) (\(j=1,2,...\)) are a group of complex constants specifying the shape of the hole. When the variable \(\xi \) moves on the unit circle (denoted by \(\sigma =e^{i\theta }\) (\(0\le \theta <2\pi \))) in the \(\xi \)-plane, Eq. (14) maps coincidentally the curve L onto the unit circle, i.e.

$$\begin{aligned} t=\omega (\sigma )=z_{0} +R\left( {\sigma +\sum \limits _{j=1}^\infty {\alpha _{j} \sigma ^{-j}} } \right) ,\quad t\in L. \end{aligned}$$
(15)

Since Eq. (14) is conformal, \(\psi _{0} (z)\) may be treated as being analytic in the exterior of the unit circle in the \(\xi \)-plane. Consequently, \(\psi _{0} (z)\) can be expanded into

$$\begin{aligned} \psi _{0} (z)=\sum \limits _{j=1}^\infty {c_{j} \xi ^{-j}} ,\quad z\in S, \end{aligned}$$
(16)

whose boundary value on L is

$$\begin{aligned} \psi _{0} (t)=\sum \limits _{j=1}^\infty {c_{j} \sigma ^{-j}} ,\quad t\in L, \end{aligned}$$
(17)

where \(c_{j}\) are a group of complex constant coefficients. Substituting Eqs. (15) and (17) into Eq. (13), the left side appears to be a power series in \(\sigma \) with only negative exponents while the right side becomes formally a power series in \(\sigma \) with both negative and positive exponents. Consequently, to meet Eq. (13), one has to require that

$$\begin{aligned} \alpha _{1} =\frac{(P^{*}-1)\Gamma _{2} }{\left[ {2+(\kappa -1)P^{*}} \right] \Gamma _{1} +P_{0} },\quad \alpha _{2} =\alpha _{3} =\cdots =0, \end{aligned}$$
(18)

to eliminate at the right side the polynomial in \(\sigma \) with positive exponents.

Now it turns out from Eqs. (15) and (18) that the harmonic hole is of elliptical shape whose axes are parallel to the x- and y-axis, respectively. The aspect ratio of the elliptical shape, defined by the ratio of the semi-axis in the x-direction to that in the y-direction, is

$$\begin{aligned} r^{*}=\frac{1+\alpha _{1} }{1-\alpha _{1} }, \end{aligned}$$
(19)

and particularly it approaches the classical counterpart obtained in [7] when \(P^{*}\) is negligibly small. If the solid is taken as an incompressible soft material (\(\nu =0.5\)) and subjected to plane strain deformations, the first part of Eq. (18) reduces to

$$\begin{aligned} \alpha _{1} =\frac{(P^{*}-1)\Gamma _{2} }{2\Gamma _{1} +P_{0} }. \end{aligned}$$
(20)

Here, since the validity of the mapping function is premised on that all the roots of \({\omega }'(\xi )\) fall within the unit circle (i.e. equivalently \({\omega }'(\xi )\ne 0\) for \(\left| \xi \right| \ge 1)\), we have to require \(\left| {\alpha _{1} } \right| <1\) which leads to

$$\begin{aligned} \left| {(1-P^{*})(\sigma _{{xx}}^{\infty } -\sigma _{{yy}}^{\infty } )} \right| <\left| {2P_{0} +\left[ {1+{(\kappa -1)P^{*}} \big / 2} \right] (\sigma _{{xx}}^{\infty } +\sigma _{{yy}}^{\infty } )} \right| . \end{aligned}$$
(21)

4 Discussion

In the classical solution for the design of a harmonic hole [7], the aspect ratio of the (elliptical) hole does not depend on the magnitude of the internal pressure and the remote loading if the ratios between them are fixed. However, in the current modified solution, the aspect ratio of the harmonic hole relies nonlinearly on the magnitude of the internal pressure and/or the remote loading even if the ratios between them are fixed. In fact, one may simplifies Eq. (19) into

$$\begin{aligned} r^{*}=\frac{1+\left[ {2+(\kappa -1)P^{*}} \right] r_{1} +(P^{*}-1)r_{2} }{1+\left[ {2+(\kappa -1)P^{*}} \right] r_{1} -(P^{*}-1)r_{2} }, \end{aligned}$$
(22)

where \(r_{1}\) and \(r_{2}\) representing the ratios between the remote loading and the internal pressure are defined by

$$\begin{aligned} r_{1} ={\Gamma _{1} } \big / {P_{0} },\quad r_{2} ={\Gamma _{2} } \big / {P_{0} }. \end{aligned}$$
(23)

Consequently, it is seen from Eq. (22) that for given \(r_{1}\) and \(r_{2}\), the aspect ratio \(r^{*}\) still changes with varying magnitude of the internal pressure and the remote loading (because of the essential parameter \(P^{*}\)). A specific illustrative example is presented in Fig. 2 to show the dependence of the aspect ratio on the magnitude of the internal pressure and remote loading.

Fig. 2
figure 2

Aspect ratio of the elliptical harmonic hole in a soft solid relative to the magnitude of the internal pressure and external loading for fixed ratios between the pressure and loading (\(G=1\) MPa, \(\nu =0.47\))

Full size image

We continue to illustrate specific differences between the current modified solution and the classical solution in determining the aspect ratio of the harmonic hole as either the internal pressure or the remote loading increases. Detailed results are presented in Figs. 3 and 4. It is observed from these figures that the directional change of the pressure (which is the essential feature of the current modified solution as opposed to the classical counterpart) mainly plays the role of rounding the harmonic hole (making it closer to a circle).

Fig. 3
figure 3

Aspect ratio of the elliptical harmonic hole in a soft solid relative to the internal pressure for given external loading (\(G=1\) MPa, \(\nu =0.47\))

Full size image
Fig. 4
figure 4

Aspect ratio of the elliptical harmonic hole in a soft solid relative to the external for given internal pressure (\(G=1\) MPa, \(\nu =0.47\))

Full size image

The current modified solution differs also from the classical counterpart in the limiting cases when the internal pressure is much larger or smaller than the remote loading. To demonstrate such differences clearly, we first rewrite Eq. (22) as

$$\begin{aligned} r^{*}=\frac{1+2r_{1} -r_{2} +{\left[ {(\kappa -1)\Gamma _{1} +\Gamma _{2} } \right] } \big / {(2G)}}{1+2r_{1} +r_{2} +{\left[ {(\kappa -1)\Gamma _{1} -\Gamma _{2} } \right] } \big / {(2G)}}, \end{aligned}$$
(24)

or

$$\begin{aligned} r^{*}=\frac{{P_{0} } \big / {\sigma _{\max } }+\left[ {2+(\kappa -1)P^{*}} \right] {\Gamma _{1} } \big / {\sigma _{\max } }+(P^{*}-1){\Gamma _{2} } \big / {\sigma _{\max } }}{{P_{0} } \big / {\sigma _{\max } }+\left[ {2+(\kappa -1)P^{*}} \right] {\Gamma _{1} } \big / {\sigma _{\max } }-(P^{*}-1){\Gamma _{2} } \big / {\sigma _{\max } }}, \end{aligned}$$
(25)

where \(\sigma _{\textrm{max}}\) is the maximum of \(\left| {\sigma _{{xx}}^{\infty } } \right| \) and \(\left| {\sigma _{{yy}}^{\infty } } \right| \). Then, for the limiting cases the current modified solution leads to

$$\begin{aligned} r^{*}=\left\{ {{\begin{array}{*{20}c} {\frac{1+{\left[ {(\kappa -1)\Gamma _{1} +\Gamma _{2} } \right] } \big / {(2G)}}{1+{\left[ {(\kappa -1)\Gamma _{1} -\Gamma _{2} } \right] } \big / {(2G)}},\hbox { for }P_{0} \gg \sigma _{\max } ;} \\ {\frac{\left[ {2+(\kappa -1)P^{*}} \right] \Gamma _{1} +(P^{*}-1)\Gamma _{2} }{\left[ {2+(\kappa -1)P^{*}} \right] \Gamma _{1} -(P^{*}-1)\Gamma _{2} },\hbox { for }\sigma _{\max } \gg P_{0} .} \\ \end{array} }} \right. \end{aligned}$$
(26)

while the classical solution in [7] leads to

$$\begin{aligned} r^{*}=\left\{ {{\begin{array}{*{20}c} {1,\hbox { for }P_{0} \gg \sigma _{\max } ;} \\ {{\sigma _{{xx}}^{\infty } }\big / {\sigma _{{yy}}^{\infty } },\hbox { for }\sigma _{\max } \gg P_{0} .} \\ \end{array} }} \right. \end{aligned}$$
(27)

5 Conclusions

We examine the plane deformation of a hole embedded in an elastic solid. The solid is subjected to a far-field biaxial tension/compression while the boundary of the hole undergoes a uniform pressure. We seek to identify the harmonic shape of the hole leading to a constant mean stress in the entire solid under a modified boundary condition accounting for deformation-induced change in the direction of the pressure inside the hole. We show that as opposed to the classical harmonic shape of the hole (corresponding to the classical boundary condition), the modified harmonic shape here continues to be elliptical with, however, its aspect ratio changed. We illustrate the differences between the classical and modified harmonic shapes via a few numerical examples. We organize the main findings as follows:

  1. 1.

    The aspect ratio of the modified harmonic shape relies on the magnitude of the far-field loading and the internal pressure even when the ratios between the far-field loading and internal pressure are fixed. This phenomenon never happens for the classical harmonic shape.

  2. 2.

    In most cases, the directional change in the internal pressure during deformation plays the role of rounding the harmonic shape, leading to that the modified harmonic shape as opposed to the classical counterpart is closer to a circle.