1 Introduction

Most recently, Li et al. [1] have investigated the integrability, modulational instability (MI), and mixed localized wave solutions for the generalized nonlinear Schrödinger (NLS) equation

$$\begin{aligned} i\frac{\partial u}{\partial t}+\frac{\partial ^{2}u}{\partial x^{2}} +2\left| u\right| ^{2}u+4\beta ^{2}\left| u\right| ^{4}u-4i\beta \left( \frac{\partial \left| u\right| ^{2}}{\partial x} \right) u-4i\alpha \left( \frac{\partial u}{\partial x}-i\alpha u\right) =0, \end{aligned}$$
(1)

where \(u=u(x,t)\) is a complex function of space variable x and time variable t, and \(\alpha \) and \(\beta \) are real constant coefficients. For studying Liouville integrability of Eq. (1), authors have introduced the following spectral problems

$$\begin{aligned} \frac{\partial \Phi }{\partial x}=M\Phi ,\frac{\partial \Phi }{ \partial t}=N\Phi , \end{aligned}$$
(2)

in which \(\Phi =\left( \varphi ,\psi \right) ^{T}\) is the vector eigenfunction with complex components \(\varphi \) and \(\psi \), M and N are the matrices

$$\begin{aligned} M=\left( \begin{array}{cc} -i\xi +i\beta \left| u\right| ^{2}+i\alpha &{} u \\ -u^{*} &{} i\xi -i\beta \left| u\right| ^{2}-i\alpha \end{array} \right) ,N=\left( \begin{array}{cc} N_{11} &{} N_{12} \\ -N_{12}^{*} &{} -N_{11} \end{array} \right) , \end{aligned}$$
(3)

with

$$\begin{aligned} N_{11}=-2i\xi ^{2}+4i\beta ^{2}\left| u\right| ^{4}+i\left| u\right| ^{2}+4i\alpha \beta \left| u\right| ^{2}+\beta \left( u \frac{\partial u^{*}}{\partial x}-u^{*}\frac{\partial u}{\partial x} \right) ,\text { }N_{12}=2\xi u+2\beta \left| u\right| ^{2}u+2\alpha u+i\frac{\partial u}{\partial x}, \end{aligned}$$

where \(u^{*}\) is the complex conjugate of u, \(a_{j},\) \(b_{j},\) and \( c_{j}\) are complex functions, and \(\xi \) is a complex spectral parameter. For constructing analytical solutions of Eq. (1) by means of the generalized (\(n,N-n\))-fold Darboux transformation (DT), authors have first built the following seed solution and studied its modulational instability

$$\begin{aligned} u_{0}\left( x,t\right) =c\exp \left[ i\left( \kappa x+\omega t\right) \right] ,\text { }\omega =2c^{2}-\kappa ^{2}+4\beta ^{2}c^{4}+4\alpha \left( \kappa -\alpha \right) , \end{aligned}$$
(4)

c and \(\kappa \) being two arbitrary real parameters. In the following, we first investigate in the correct manner the MI of the plane wave solution (4) of the generalized NLS Eq. (1) and then carry out the correct integration of the differential system (2) for \(\xi _{j}=Z\) when using the plane wave solution (4) as the seed solution.

2 Baseband modulational instability of the plane wave solution (4)

For investigating the (baseband) MI of the generalized NLS Eq. (1), Li et al. [1] have perturbed the plane wave solution (4) as follows

$$\begin{aligned} u\left( x,t\right) =\left( \varepsilon Q+c\right) \exp \left[ i\left( \kappa x+\omega t\right) \right] , \end{aligned}$$
(5)

where \(\varepsilon \) is the small perturbation and Q is the perturbation function having the form

$$\begin{aligned} Q\left( x,t\right) =F\cos \left[ \Theta x-\Omega t\right] +iG\sin \left[ \Theta x-\Omega t\right] , \end{aligned}$$
(6)

where F and G are amplitudes of the perturbation eigenmode, and the propagation parameters \(\Theta \) and \(\Omega \) are real and complex quantities, respectively. Substituting Eq. (5) into Eq. (1) and linearizing the resulting equation with respect to \(\varepsilon \), authors found the following equation for the perturbation function

$$\begin{aligned} i\frac{\partial Q}{\partial t}+\frac{\partial ^{2}Q}{\partial x^{2}} +2c^{2}\left( 1+4c^{2}\beta ^{2}\right) Q+2c^{2}\left( 1+4\beta ^{2}c^{2}\right) Q^{*}+2\left( ia-2i\beta ^{2}c^{2}-2\kappa \right) \frac{\partial Q}{\partial x}-4i\beta ^{2}c^{2}\frac{\partial Q^{*}}{ \partial x}=0. \end{aligned}$$
(7)

Equation (7) obviously contains an error because the first derivative of each of Q and \(Q^{*}\) was supposed to come with the pure imaginary number i. The correct equation for the perturbation function Q is as follows

$$\begin{aligned} i\frac{\partial Q}{\partial t}+\frac{\partial ^{2}Q}{\partial x^{2}} +2c^{2}\left( 1+4c^{2}\beta ^{2}\right) Q+2c^{2}\left( 1+4\beta ^{2}c^{2}\right) Q^{*}+2i\left( \kappa -2\beta c^{2}-2\alpha \right) \frac{\partial Q}{\partial x}-4i\beta c^{2}\frac{ \partial Q^{*}}{\partial x}=0. \end{aligned}$$
(8)

Asking that Eq. (6) satisfies Eq. (7), authors obtained the following linear algebraic system for parameters F and G

$$\begin{aligned} \left[ \left( 4c^{2}+16c^{4}\beta ^{2}-\Theta \right) F+\left( \Omega -2\kappa \Omega -8\beta ^{2}c^{2}\Omega -4\alpha \Theta \right) G\right] \cos \left[ \Theta x-\Omega t\right]= & {} 0, \end{aligned}$$
(9a)
$$\begin{aligned} \left[ \left( \Omega -2\kappa \Theta \right) F-\Theta ^{2}G\right] \sin \left[ \Theta x-\Omega t\right]= & {} 0, \end{aligned}$$
(9b)

leading to the following condition for the existence of nontrivial solutions for F and G

$$\begin{aligned} \Omega =4\beta ^{2}c^{2}\Theta +2\kappa \Theta +4\alpha \Theta \pm 2\Theta \sqrt{4\beta ^{2}c^{4}-4c^{4}\beta ^{2}-c^{2}+\frac{\Theta ^{2}}{4}}. \end{aligned}$$
(10)

Either ansatz (6) for the perturbation function Q is not correct, or the mathematical calculations that gave system (9a) and (9b) were not correct. Indeed, ansatz (6) can be correct only if \(\cos \left[ \Theta x-\Omega t\right] \) and \(\sin \left[ \Theta x-\Omega t\right] \) appearing there are just symbolic representations of complex functions. It should be noted that for any real quantity A,

$$\begin{aligned} \cos \left[ iA\right] =\cosh \left[ A\right] \text { and }\sin \left[ iA \right] =i\sinh \left[ A\right] \end{aligned}$$

so that the complex conjugate of \(\cos \left[ \Theta x-\Omega t\right] \) and \(\sin \left[ \Theta x-\Omega t\right] \) is

$$\begin{aligned} \cos ^{*}\left[ \Theta x-\Omega t\right] =\cos \left[ \Theta x-\Omega ^{*}t\right] \text { and }\sin ^{*}\left[ \Theta x-\Omega t\right] =\sin \left[ \Theta x-\Omega ^{*}t\right] , \end{aligned}$$

where \(\Omega ^{*}\) is the complex conjugate of the modulation frequency \(\Omega .\) Inserting Eq. (6) into Eq. (7) will then lead to a linear algebraic system containing \(\cos \left[ \Theta x-\Omega t\right] ,\) \(\sin \left[ \Theta x-\Omega t\right] ,\) \(\cos \left[ \Theta x-\Omega ^{*}t\right] ,\) and \(\sin \left[ \Theta x-\Omega ^{*}t\right] ,\) which will be naturally different from system (9a) and (9b). Therefore, even if the perturbation Eq. (7) was correct, system (9a) and (9b) is not correct. I have realized that in their calculations, authors have considered \(\cos \left[ \Theta x-\Omega t\right] \) and \(\sin \left[ \Theta x-\Omega t\right] \) as real functions of x and t. I have also realized that authors of work [1] have considered parameters F and G of the perturbation eigenmode as real quantities. When studying the MI, a number of researchers also considered the perturbation in form (6) with real F and G, and this is not correct at all [2,3,4]. They generally use such a perturbation because they assume that for complex quantity \(\Omega \),

$$\begin{aligned} \exp \left[ i\left( \Theta x-\Omega t\right) \right] =\cos \left( \Theta x-\Omega t\right) +i\sin \left( \Theta x-\Omega t\right) , \end{aligned}$$

instead of

$$\begin{aligned} \exp \left[ i\left( \Theta x-\Omega t\right) \right] =\left[ \cos \left( \Theta x-{\text {Re}}\left[ \Omega \right] t\right) +i\sin \left( \Theta x-{\text {Re}}\left[ \Omega \right] t\right) \right] \exp \left[ \text {Im}\left[ \Omega \right] t\right] . \end{aligned}$$
Fig. 1
figure 1

(Color online) Modulation instability gain spectrum as per equation (14) for different values amplitude c of the carrier wave

Full size image

The correct way of investigating the MI of the generalized NLS Eq. (1) is to seek the perturbation function Q as [5,6,7]

$$\begin{aligned} Q\left( x,t\right) =F\exp \left[ i\Theta x+i\Omega t\right] +G^{*}\exp \left[ -i\Theta x-i\Omega ^{*}t\right] , \end{aligned}$$
(11)

where F and G are complex parameters so that \(\left| F\right| +\left| G\right| >0\), \(\Theta \) and \(\Omega \) are, respectively, the real wavenumber and the complex angular frequency of the modulation, and star \((*)\) stands for the complex conjugate. When using Eq. (11) for the perturbation function, some scientists take G instead of \(G^{*} \), which really speaking cannot lead to the desired results (the consider F and G as real parameters, and this contradicts the fact that F and G will be found as nontrivial solution of a linear algebraic system with complex coefficients whose solutions are complex numbers) [8, 9]. Inserting Eq. (11) into Eq. (8) yields the following linear algebraic system for F and G

$$\begin{aligned}{} & {} \left( \begin{array}{cc} 2c^{2}\left( 1+4c^{2}\beta ^{2}\right) -\Omega -2\left( \kappa -2\beta c^{2}-2\alpha \right) \Theta -\Theta ^{2} &{} 2c^{2}\left( 1+4\beta ^{2}c^{2}\right) +4\beta c^{2}\Theta \\ -4\beta c^{2}\Theta +2c^{2}\left( 1+4\beta ^{2}c^{2}\right) &{} 2c^{2}\left( 1+4c^{2}\beta ^{2}\right) +\Omega +2\left( \kappa -2\beta c^{2}-2\alpha \right) \Theta -\Theta ^{2} \end{array} \right) \nonumber \\{} & {} \times \left( \begin{array}{c} F \\ G \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \end{array} \right) . \end{aligned}$$
(12)

The condition for the existence of nontrivial solutions F and G is obtained by imposing to the determinant of system (12) to be zero:

$$\begin{aligned} \Omega =\Theta \left( 4\alpha +4c^{2}\beta -2\kappa \pm 2i\sqrt{ c^{2}-\frac{\Theta ^{2}}{4}}\right) . \end{aligned}$$
(13)

The corresponding modulation instability gain spectrum is therefore

$$\begin{aligned} \Gamma \left( \Theta ;c\right) =2\left| \Theta \right| \sqrt{c^{2}- \frac{\Theta ^{2}}{4}} \end{aligned}$$
(14)

and depends only on the modulation wavenumber \(\Theta \) and amplitude c of the carrier wave; its evolution as a function of the modulation wavenumber \( \Theta \) is depicted in Fig. 1. Equation (13) means that the zero amplitude (\(c=0\)) wave is stable under modulation, while any nonzero amplitude \(\left( c\ne 0\right) \) plane wave will be unstable under modulation. This result is in agreement with that obtained by Kengne and Liu for a NLS equation with self-steepening and self-frequency shift that generalizes Eq. (1) [10].

3 Taylor series expansions for solution of Lax pair (3)

Using the plane wave solution \(u_{0}\left( x,t\right) \) given by Eq. (4) as a seed solution, Li et al. [1] found one basic solution of Eq. (2) with data (3) as

$$\begin{aligned} \Phi =\left( \begin{array}{c} \exp \left[ X\right] \left( T_{1}\exp \left[ Y\right] +T_{2}\exp \left[ -Y \right] \right) \\ \exp \left[ -X\right] \left( T_{1}\tau _{+}\exp \left[ Y\right] +T_{2}\tau _{-}\exp \left[ -Y\right] \right) \end{array} \right) , \end{aligned}$$
(15a)

where \(T_{1}\) and \(T_{2}\) are arbitrary constants, and X, Y, and \(\tau _{\pm }\) are given as

$$\begin{aligned} X= & {} \frac{i}{2}\left[ \kappa x+\left( 2c^{2}-\kappa ^{2}+4\beta ^{2}c^{4}+4\alpha \left( \kappa -\alpha \right) \right) t\right] , Y=\frac{\sqrt{H}}{2}\left[ x+\left( 2\beta c^{2}-\kappa +2\xi +2\alpha \right) t+\theta \left( \varepsilon \right) \right] , \nonumber \\ \theta \left( \varepsilon \right)= & {} \sum _{j=0}^{N}\left( p_{j}+iq_{j}\right) \varepsilon ^{2j},\text { }\tau _{\pm }=\frac{i\left( \kappa +2\xi -2\beta c^{2}-2\alpha \right) \pm \sqrt{H}}{2c}, \nonumber \\ H= & {} \left( -2\beta c^{2}+2\alpha -2ic-\kappa -2\xi \right) \left( -2\beta c^{2}-2\alpha -2ic+\kappa +2\xi \right) , \end{aligned}$$
(15b)

\(p_{j}\) and \(q_{j}\) are arbitrary real parameters, and \(\varepsilon \) is a small parameter. In Ref. [1], authors have denoted \(Z=\beta c^{2}+\alpha -\frac{\kappa }{2}+ic\) and by inserting \(\xi =\) \(\xi _{j}=Z\), \( T_{1}=-T_{2}=1/\varepsilon ,\) and \(c=1\) into Eq. (15a), they found that polynomial functions of x and t form vector \(\Phi .\) In the following, we show that by taking the complex spectral parameter as \(\xi =\) \(\xi _{j}=Z=\beta c^{2}+\alpha -\frac{\kappa }{2}+ic,\) Eq. (15a) will no longer give a basic solution of Eq. (2) when \(u_{0}\left( x,t\right) \) is used as a seed solution.

When using \(u_{0}\left( x,t\right) \) as the seed solution for Eq. (1), the first system of Eq. (2) with data (3) becomes

$$\begin{aligned} \frac{\partial \varphi }{\partial x}= & {} i\left( -\xi +\beta c^{2}+\alpha \right) \varphi +c\psi \exp \left[ i\left( \kappa x+\omega t\right) \right] , \end{aligned}$$
(16a)
$$\begin{aligned} \frac{\partial \psi }{\partial x}= & {} -c\exp \left[ -i\left( \kappa x+\omega t\right) \right] \varphi +i\left( \xi -\beta c^{2}-\alpha \right) \psi , \end{aligned}$$
(16b)

which is linear differential system with variable coefficients. Solving Eq. (16b) and substituting the result in Eq. (16a) yield the following second-order linear differential equation in \(\varphi \)

$$\begin{aligned} \frac{\partial ^{2}\varphi }{\partial x^{2}}-i\kappa \frac{\partial \varphi }{\partial x}+\left[ \left( \alpha -\xi +c^{2}\beta \right) ^{2}-\kappa \left( \alpha -\xi +c^{2}\beta \right) +c^{2}\right] \varphi =0, \end{aligned}$$
(16c)

whose characteristic equation reads

$$\begin{aligned} \left( \lambda -\frac{i\kappa }{2}\right) ^{2}+\left( \xi -\beta c^{2}-\alpha +\frac{\kappa }{2}-ic\right) \left( \xi -c^{2}\beta -\alpha +ic+ \frac{\kappa }{2}\right) =0. \end{aligned}$$
(16d)

The condition \(\left( \xi -\beta c^{2}-\alpha +\frac{\kappa }{2}-ic\right) \left( \xi -c^{2}\beta -\alpha +ic+\frac{\kappa }{2}\right) \ne 0\) leads to the basic solution (3.6) of Ref. [1]. If \(\xi =\beta c^{2}+\alpha - \frac{\kappa }{2}+ic\), the characteristic Eq. (16d) will admit only one solution \(\lambda =\frac{i\kappa }{2}\), and the general solution of Eq. (16c) will be

$$\begin{aligned} \varphi \left( x,t\right) =\left( C_{1}+C_{2}x\right) \exp \left[ \frac{ i\kappa }{2}x\right] , \end{aligned}$$

where \(C_{1}\) and \(C_{2}\) are two constants (with respect to variable x) of integration, but functions of variable t. The general solution of the first of system (2) with data (3) under the condition \(\xi =\beta c^{2}+\alpha -\frac{\kappa }{2}+ic\) is then

$$\begin{aligned} \Phi \left( x,t\right) =\left( \begin{array}{c} \varphi \left( x,t\right) \\ \psi \left( x,t\right) \end{array} \right) =\left( \begin{array}{c} \left( C_{1}+C_{2}x\right) \exp \left[ \frac{i\kappa }{2}x\right] \\ \left( -C_{1}+\left( \frac{1}{c}-x\right) C_{2}\right) \exp \left[ -i\left( \frac{\kappa }{2}x+\omega t\right) \right] \end{array} \right) , \end{aligned}$$
(17)

where \(C_{1}\) and \(C_{2}\) are two arbitrary complex functions of variable t to be defined by imposing to Eq. (17) to satisfy Eq. (2), and \( \omega \) is given in Eq. (4). Imposing thus to Eq. (17) to satisfy the second equation in Eq. (2) when \(\xi =Z=\beta c^{2}+\alpha -\frac{\kappa }{2}+ic,\) we obtain the following basic solution

$$\begin{aligned} \Phi \left( x,t\right) =\left( \begin{array}{c} \varphi \left( x,t\right) \\ \psi \left( x,t\right) \end{array} \right) \left( \begin{array}{c} \frac{D_{+}}{2C_{21}}C_{10}\exp \left[ \frac{i\kappa }{2}x+\frac{\Delta _{+}}{2}t\right] +\frac{D_{-}}{2C_{21}}C_{20}\exp \left[ \frac{i\kappa }{2}x+\frac{\Delta _{-}}{2}t\right] \\ \frac{\Delta _{1-}}{2cC_{21}}C_{10}\exp \left[ -i\frac{\kappa }{2}x-i\left( \frac{i\Delta _{+}}{2}+\omega \right) t\right] \frac{\Delta _{1+} }{2cC_{21}}C_{20}\exp \left[ -i\frac{\kappa }{2}x-i\left( \frac{i\Delta _{-}}{2}+\omega \right) t\right] \end{array} \right) , \nonumber \\ \end{aligned}$$
(18)

where \(C_{10}\) and \(C_{20}\) are arbitrary complex constants, and \(\Delta _{\pm }\ne 0,\) \(D_{\pm },\) \(\Delta _{1\pm },\) and \(C_{21}\) are constants given as

$$\begin{aligned} D_{+}= & {} i\left( 2c^{2}+4c^{4}\beta ^{2}-\left( 2\alpha -\kappa \right) ^{2}\right) +\Delta _{+}, \\ D_{-}= & {} i\left( 2c^{2}+4c^{4}\beta ^{2}-\left( 2\alpha -\kappa \right) ^{2}\right) +\Delta _{-}, \\ \Delta _{1-}= & {} 4ic^{5}\beta ^{2}+4c^{2}\beta \left( \kappa +2c^{2}\right) +10ic^{3}-8c^{4}-4c^{2}\kappa -ic\left( 2\alpha -\kappa \right) ^{2}+c\Delta _{-}, \\ \Delta _{1+}= & {} 4ic^{5}\beta ^{2}+4c^{2}\beta \left( \kappa +2c^{2}\right) +10ic^{3}-8c^{4}-4c^{2}\kappa -ic\left( 2\alpha -\kappa \right) ^{2}+c\Delta _{+}, \\ C_{21}= & {} \frac{c\left( 12ic^{2}-2i\left( 2\alpha -\kappa \right) ^{2}+8ic^{4}\beta ^{2}-8c^{3}-4c\kappa +\beta \left( 4c\kappa +8c^{3}\right) \right) }{2}, \\ \Delta _{\pm }= & {} \pm \sqrt{F}, \\ F= & {} 4c^{4}\left( 8\kappa -16\alpha -13\right) -\left( 2\alpha -\kappa \right) ^{4}+4c^{2}\left( 6\alpha -7\kappa \right) \left( 2\alpha -\kappa \right) \\{} & {} \quad +16c^{2}\beta \left( 4c^{2}\alpha -\kappa ^{2}-4c^{4}+2\kappa \left( \alpha -2c^{2}\right) \right) -16c^{8}\beta ^{4}\\{} & {} +8c^{4}\beta ^{2}\left( 2c^{2}+4\kappa +\left( 2\alpha -\kappa \right) ^{2}\right) +8ic\left( \left( 2\alpha -\kappa +2c^{2}\beta \right) \left( 6c^{2}+4c^{4}\beta ^{2}-\left( 2\alpha -\kappa \right) ^{2}\right) \right. \\{} & {} \quad \left. +2c^{2}\left( \beta \kappa -2c^{2}-\kappa +2\beta c^{2}\right) \right) . \end{aligned}$$
Fig. 2
figure 2

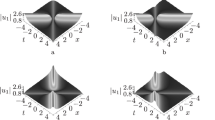
(Color online) Spatiotemporal evolution of nonlinear waves generated with the help of the \(\left( 1,0\right) -\)soliton solution of Eq. (1), obtained by the means of the generalized perturbation \( (1,0)-\)fold DT for \(\alpha =3,\) \(\beta =0.5,\) \(\kappa =1\), and three different values of the seed solution parameter c, and namely \(c=0.1,\) \(c=0.2,\) \(c=1.51,\) and \(c=2.0 \) for panels (a), (b), (c), and (d), respectively

Full size image

In the case when \(\Delta _{\pm }=0,\) the components of the basic solution \( \Phi \left( x,t\right) =\left( \varphi \left( x,t\right) ,\psi \left( x,t\right) \right) ^{T}\) are found to be

$$\begin{aligned} \varphi \left( x,t\right)= & {} \left[ \frac{i\left( 2c^{2}+4c^{4}\beta ^{2}-\left( 2\alpha -\kappa \right) ^{2}\right) }{2C_{21}} C_{10}+\frac{2+i\left( 2c^{2}+4c^{4}\beta ^{2}-\left( 2\alpha -\kappa \right) ^{2}\right) t}{2C_{21}}C_{20}\right] \exp \left[ \frac{i\kappa }{2}x\right] , \nonumber \\ \psi \left( x,t\right)= & {} \left[ \frac{4ic^{5}\beta ^{2}+4c^{2}\beta \left( \kappa +2c^{2}\right) -8c^{4}-4c^{2}\kappa +10ic^{3}-ic\left( 2\alpha -\kappa \right) ^{2}}{2cC_{21}}C_{10}\right. \\{} & {} \left. +\frac{\left[ 4ic^{5}\beta ^{2}+4c^{2}\beta \left( \kappa +2c^{2}\right) +10ic^{3}-8c^{4}-4c^{2}\kappa -ic\left( 2\alpha -\kappa \right) ^{2}\right] t-2c}{2cC_{21}}C_{20}\right] \exp \left[ -i\left( \frac{\kappa }{2}x+\omega t\right) \right] , \nonumber \end{aligned}$$
(19)

where \(C_{10}\) and \(C_{20}\) are free constants of integration. In equations (18) and (19), \(\omega \) is the same as that of Eq. (4). The vector basic solution (18) is a combination of exponential functions of x and t,  while components \(\varphi \left( x,t\right) \) and \( \psi \left( x,t\right) \) of the basic solution given by Eq. (19) are the combinations of polynomial functions and exponential functions of x and t. These two basic solutions are absent from the work of Ref. [1]. The above two basic solutions (18) and (19) will obviously lead to two different Taylor series expansions.

Because these solutions do not contain \(\xi ,\) it is preferable to consider the constants of integration \(C_{10}\) and \(C_{20}\) as functions of a tiny parameter \(\epsilon \) and expand functions \(\varphi \left( x,t\right) \) and \( \psi \left( x,t\right) \) in Taylor series around \(\epsilon =0\). By taking for example \(C_{10}=-C_{20}=\ln \left( e+\epsilon \right) ,\) we obtain, respectively, the following Taylor expansions of the basic solutions (18) and (19)

$$\begin{aligned} \Phi \left( x,t;\epsilon \right) =\Phi _{0}\left( x,t\right) \left( 1+\frac{1 }{e}\epsilon -\frac{1}{2e^{2}}\epsilon ^{2}+\cdots \right) , \end{aligned}$$
(20a)

and

$$\begin{aligned} \Phi \left( x,t;\epsilon \right) =\Phi _{0}\left( x,t\right) \left( 1+\frac{1 }{e}\epsilon -\frac{1}{2e^{2}}\epsilon ^{2}+\cdots \right) , \end{aligned}$$
(20b)

where \(\Phi _{0}\left( x,t\right) \) is the vector function obtained from Eqs. (18) and (19) after taking \(C_{10}=1\) and \(C_{20}=-1\). Because none of the above vector functions \(\Phi \left( x,t\right) \) is formed of the polynomial functions of x and x, we conclude that using the generalized perturbation \((n,N-n)-\)fold DT under the condition \(\xi =\beta c^{2}+\alpha -\frac{\kappa }{2}+ic\) cannot lead to rogue wave solutions of Eq. (1). Indeed, as we can see from plots of Fig. 2, the structures of nonlinear waves generated with the use of the solution of Eq. (1) obtained by means of the generalized perturbation \( (1,0)-\)fold DT (see theorem 1 of Ref. [1]) differ from those of rogue waves.

4 Conclusion

In the present comment, we have provided the correct form of the perturbation function \(Q\left( x,t\right) \) which was supposed to be used instead of that given by Eq. (2.12) of Ref. [1] for studying the MI phenomenon of Eq. (1). Furthermore, we have built the correct basic solution of Lax pair (2.8) of Ref. [1] that corresponds to the eigenvalue \(\xi =\beta c^{2}+\alpha -\frac{\kappa }{2}+ic\). The obtained here basic solution is different from the one used in Ref. [1] by letting \(\xi =\beta c^{2}+\alpha -\frac{\kappa }{2}+ic\) in Eq. (3.6) of this same Ref. [1]. We have then showed that by using the built here basic solution, it will not be possible to get, by means of the generalized perturbation \((2,N-2)-\)fold DT, mixed interaction solutions between rogue waves and other nonlinear waves as those obtained in Ref. [1] by using the first Taylor expansion shown by Li et al. [1].