1 Introduction

As we know the classical heat conduction model along with the energy equation implies the instantaneous propagation of thermal waves which is physically unacceptable, many non-classical theories have been proposed to overcome the drawback of infinite propagation of heat conduction. The non-Fourier heat conduction model has attracted the interest of many researchers as these models offer a mean to understand the thermal interactions in scenarios involving high-speed energy transport, low temperatures and extremely high heat fluxes. The thermoelasticity theories have also been modified in many ways by introducing phase lags and/or by modifying constitutive equations. We must recall the Lord–Shulman [1] thermoelasticity theory which involves one relaxation parameter with heat flux as a modification to Fourier’s law which accounts for the finite propagation of thermal waves. In the early twentieth century, Green–Naghdi [2,3,4] has proposed three forms of thermoelasticity theory by involving a new constitutive variable \(\alpha \) known as thermal displacement which follows \(\dot{\alpha }=\theta \) in which the third one is the generalization of the first and second forms. Furthermore, Tzou [5] introduced a new constitutive variable known as phase-lag parameter to generalize the CV heat conduction model [6, 7] which is known as single-phase-lag model. Further, by involving two-phase-lag parameters of heat flux and temperature gradient, Tzou [8, 9] developed dual-phase-lag heat conduction theory.

The dual-phase-lag (DPL) model allows for the inclusion of time-dependent effects in heat conduction, such as propagation delays and finite thermal relaxation times. It provides a more accurate representation of heat conduction phenomena in situations where non-Fourier effects are significant, such as in high-speed heat transfer, transient heat conduction or at small length scales; hence, it is worth recalling some contributions in this direction. Kang et al. [10] predicted the existence of thermal waves in dual-phase-lag heat conduction by measuring the time lag ratio. The exponential stability, spatial behaviour of solutions in a semi-infinite cylinder and a result on domain of influence under DPL thermoelasticity were shown in reference [11]. Bazarra et al. [12] worked on a contact problem between a thermoelastic body with dual-phase-lag and a deformable obstacle to prove an existence and uniqueness result by applying the Faedo–Galerkin method and Gronwall’s inequality. Singh et al. [13] discovered the equations which governs the phenomena of transversely isotropic DPL two-temperature thermoelasticity for the surface wave. Furthermore, Jha and Oyelade [14] investigated the role of dual-phase-lag (DPL) heat conduction model on transient free convection flow in a vertical channel. Based on non-local heat conduction model with DPL, Gupta and Mukhopadhyay [15] studied the generalized thermoelasticity theory. Also, Morro et al. [16] established the decay, growth, continuous dependence and backward uniqueness results of an alternative formulation of dual-phase-lag model carried out by taking the heat conduction at low temperatures which is often modelled by accounting for space correlation through suitable approximations. Many more interesting results concerning the dual-phase-lag thermoelasticity theory can be found in references [17,18,19,20].

The theory of thermopiezoelectricity is the branch of applied mechanics which includes the thermal and mechanical influences on elastic bodies under the effect of mechanical loads and/or non-uniform temperature distributions in the presence of electric field. Thus, the interaction of three major fields: mechanical, thermal and electric, is observed as the response of piezothermoelastic materials. By smartly integrating sensing and actuating capabilities of this material, it is possible to design intelligent structures. Mindlin [21] was the first who provided the general three-dimensional basic governing equations of piezothermoelasticity. Afterwards, some mathematical models and general theorems of thermopiezoelectricity were given by Nowacki [22] which can be considered as the basis for several numerical methods. Yang and Batra [23] used two perturbation methods to study the effect of heat conduction on frequency shift of a freely vibrating linear piezoelectric body. Furthermore, three-dimensional Green’s functions for two-phase transversely isotropic piezothermoelastic media have been investigated by Leung [24]. Chen et al. [25] derived the general solution for transversely isotropic piezothermoelastic media. Kulikov and Plotnikova [26] studied an analytical approach to three-dimensional coupled thermoelectroelastic analysis of layered and functionally graded piezoelectric shells. In extended thermodynamics, Ghaleb [27] discussed fully coupled thermopiezoelasticity.

The quantitative modelling of the micro- and nanostructured materials has become a significant and intriguing task in materials research. Numerous experiments have demonstrated that materials exhibit different behaviours at the macro- and microscales, which leads to the emergence of size-dependent continuum theories incorporating couple stress parameters which results in couple stress theory. However, this theory poses some difficulties in the formulation due to the ambiguity in determining the spherical part of the couple stress tensor. Thus, Yang et al. [28] developed modified couple stress theory with the introduction of an equilibrium relation for the moments of the couple without explaining this ambiguity which allows couple stress tensor to be symmetric only. Consequently, the number of material length scale parameters is reduced to only one length scale parameter. This makes the modified couple stress theory smoother to implement than the classical couple stress or other non-classical elasticity theories. On the basis of modified couple stress theory, damping analysis was done by Asghari et al. [29] in functionally graded Timoshenko beams. However, Park and Gao [30] observed and analysed the effects of length scale parameter on the static behaviour of an Euler–Bernoulli microbeam by utilizing modified couple stress theory. Some relevant articles which show the application of MCST are [31,32,33]. It is worth mentioning that thermoelastic damping is the major mechanism responsible for energy loss in micro- and nanomechanical systems. Thus, damping analysis plays an important role in case of micro- and nanoelectromechanical devices which has many applications and importance in communication and sensing. Thermoelastic damping is obtained in terms of inverse quality factor which is a dimensionless parameter used to describe the quality performance of a micro- and nanoresonator. Zener [34, 35] was the first to obtain thermoelastic damping by applying the classical heat conduction theory. Duwel et al.[36] and Evoy et al. [37] presented new experimental data illustrating the importance of thermoelastic damping in MEMS and NEMS devices. Later on, TED in microbeam resonator was examined by Kakhki et al. [38] under modified coupled stress theory. The investigation of TED based on modified strain gradient elasticity and generalized thermoelasticity theories was done by Bostani and Mohammadi [39] in the microbeam resonators. The complex frequency approach to obtain the closed-form expression for frequency shift, \(Q^{-1}\), and attenuation was introduced by Lifshitz and Roukes [40]. This approach has found widespread application in the analysis of energy dissipation due to TED in various structures, like beams [41], plates [42], cylindrical shells[43] and rings [44]. Along with the above, one can also go through the articles [45,46,47,48,49,50].

The present work explains the damping analysis of a piezothermoelastic nanobeam resonator by utilizing modified couple stress theory under dual-phase-lag theory of thermoelasticity. In Sect. 2, we have mentioned the basic general equations for the anisotropic piezothermelastic material. In Sect. 3, the structure of the beam considered in the present scenario is explained and the problem is formulated with some assumptions. In Sect. 4, the time harmonic solution of the problem is considered and the equations for electric field, temperature and deflection of the beam have been obtained which governs the vibrations in piezothermoelastic beam resonator. Sect. 5 explains the different boundary conditions applied to the edges of the beam. The corresponding characteristic equation has been solved to obtain the complex roots. In Sect. 6, a closed-form analytical expression for TED in the form of inverse quality factor has been obtained while in Sect. 7, numerical results and discussion have been carried out by taking a piezothermoelastic material, lead zirconate titanate (PZT-5A) to understand the behaviour of damping factor numerically and graphically. At last, in Sect. 8, some important key findings regarding dual-phase-lag model, modified couple stress theory and piezoelectric material in the present scenario have been concluded which will help designers to optimize the performance of resonators.

2 Basic equations

The basic general equations for a linear homogeneous anisotropic piezothermoelastic solid medium in the absence of heat sources and body forces in the Cartesian coordinate systems followed from [51] and [52] can be given as follows:

Strain–stress–temperature and electric field relation:

$$\begin{aligned} \varrho _{ij}= & {} c_{ijkl}\varepsilon _{kl}-e_{ijk}E_{k}-b_{ij}\theta -\frac{1}{2}\epsilon _{ijk}m_{kl,l}, \end{aligned}$$
(1)
$$\begin{aligned} m_{ij}= & {} 2\mu l^{2}\kappa _{ij}, \end{aligned}$$
(2)
$$\begin{aligned} \kappa _{ij}= & {} \frac{1}{2}\left( \frac{\partial \varphi _{i}}{\partial x_{j}}+\frac{\partial \varphi _{j}}{\partial x_{i}}\right) , \end{aligned}$$
(3)
$$\begin{aligned} \varphi _{j}= & {} \frac{1}{2}\text {(curl(}u\text {))}_{j}, \end{aligned}$$
(4)

Energy equation:

$$\begin{aligned} -q_{i,i}=\rho \theta _{0}\dot{S}, \end{aligned}$$
(5)

Entropy equation:

$$\begin{aligned} \rho S=b_{ij}\varepsilon _{ij}+\tau _{i}E_{i}+r\theta , \end{aligned}$$
(6)

Gauss equation and electric field relations:

$$\begin{aligned}{} & {} \mathcal {F}_{i}=\zeta _{ij}E_{j}+e_{ijk}\varepsilon _{jk}+\tau _{i}\theta , \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \mathcal {F}_{i,i}=0,\\{} & {} E_{i}=-\psi _{,i},\nonumber \end{aligned}$$
(8)

Equation of motion:

$$\begin{aligned} \varrho _{ij,j}+\rho \ddot{u_{i}}=0, \end{aligned}$$
(9)

Heat conduction equation:

$$\begin{aligned} \begin{aligned} {{-k_{ij}\left( 1+\tau _{\theta }\frac{\partial }{\partial t}\right) \theta _{,~j}=\left( 1+\tau _{q}\frac{\partial }{\partial t}\right) q_{i}}}, \end{aligned} \end{aligned}$$
(10)

Strain–displacement relation:

$$\begin{aligned} \varepsilon _{ij}=\frac{1}{2}\left( u_{i,j}+u_{j,i}\right) , \end{aligned}$$
(11)

where \(q_{i}\) is the component of heat flux vector and s is the entropy per unit mass. \(\zeta _{ij},\) \(\tau _{i}\), \(b_{ij}\), \(e_{mij}\), \(\epsilon _{ijk}\), \(m_{kl,l}\) and \(\kappa _{ij}\) are the piezothermal moduli tensors, couple stress tensor and electric permittivity, respectively. \(\varepsilon _{ij}\) and \(\varrho _{ij}\) represent the components of the strain and stress tensors, respectively. The component of displacement vector is denoted by \(u_{i}\). The coefficient r indicates the measure of thermal effect, \(\tau _{q}\) and \(\tau _{\theta }\) are the time phase lags of heat flux and temperature gradient, and \(\theta \) and \(\theta _{0}\) are the absolute and reference temperature of the beam. The component of thermal conductivity is denoted as \(k_{ij}\), \(E_{i}\) is the component of electric field intensity, and \(\mathcal {F}_{i}\) and \(\psi _{i}\) are the components of the electric displacement and electric potential, respectively. Comma and dot over a variable represent the time and space derivatives, respectively.

3 Problem formulation and structure of the beam

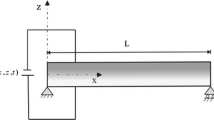
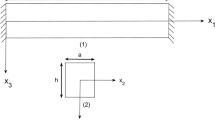
The current study assumes a piezothermoelastic beam having length L, thickness h and, width b. In equilibrium, the beam is maintained free from strain and stress and its temperature is kept at reference temperature \(\theta _{0}\). We have taken x axis along the beam length \(L(0\le x\le L)\), y axis along the beam width b(\(0\le y\le b\)) and z axis along the beam thickness h \((-h/2\le z\le h/2)\), respectively. Along the length, the beam is assumed to experience small-amplitude bending vibrations and linear Euler–Bernoulli beam theory has been utilized to explain the deflection of the beam. The beam displacements are therefore given as follows:

$$\begin{aligned} w(x,y,z,t)=w(x,t),\ \ u=-z\frac{\partial w}{\partial x},\ \ v=0,\ \frac{\partial w}{\partial z}=0. \end{aligned}$$
(12)

Furthermore, due to the slenderness of the PTE beam, the rotatory inertia, transverse shear strains and transverse shear deformations can be taken as negligible, as followed from Ugural and Tzou ([53, 54]). Since in-plane electric fields (\(E_{x}\text {and }E_{y}\)) are associated with the out-of-plane electric field (\(E_{z}\)) via Poisson effect which is negligible for bending vibrations of small-amplitude, in-plane electric fields can be disregarded. Hence, only out-of-plane electric field is considered for the present study. Further, the relation \(\mathcal {F}_{i}=\epsilon E_{i}\) implies \(\mathcal {F}_{x}=\mathcal {F}_{y}=0.\) Moreover, the normal stress along z- axis is assumed to be zero, i.e. \(\varrho _{zz}=0;\) thus, from Eq. (1), we have

$$\begin{aligned} b_{33}\theta =-c_{13}z\frac{\partial ^{2}w}{\partial x^{2}}+e_{33}\frac{\partial \psi }{\partial z}. \end{aligned}$$
(13)

And from Eq. (7), one can obtain

$$\begin{aligned} \mathcal {F}_{z}=-e_{31}z\frac{\partial ^{2}w}{\partial x^{2}}-\zeta _{33}\frac{\partial \psi }{\partial z}+\tau _{3}\theta . \end{aligned}$$
(14)

Putting Eq. (14) into Eq. (8) yields

$$\begin{aligned} e_{31}\frac{\partial ^{2}w}{\partial x^{2}}+\zeta _{33}\frac{\partial ^{2}\psi }{\partial z^{2}}=\tau _{3}\frac{\partial \theta }{\partial z}. \end{aligned}$$
(15)

Integrating the above equation with respect to z, we have

$$\begin{aligned} \frac{\partial \psi }{\partial z}=-\frac{e_{31}}{\zeta _{33}}z\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\tau _{3}\theta }{\zeta _{33}}+\psi _{0}. \end{aligned}$$
(16)

Substituting \(\theta \) from Eq. (13) into the above equation, we have

$$\begin{aligned} \frac{\partial \psi }{\partial z}=-Cz\frac{\partial ^{2}w}{\partial x^{2}}+\zeta _{33}^{*}\psi _{0},\ \text {with } {C}={\frac{e_{31}b_{33}+c_{13}\tau _{3}}{\zeta _{33}b_{33}-\tau _{3}e_{33}}} \text { and } {\zeta _{33}^{*}}={\frac{\zeta _{33}b_{33}}{\zeta _{33}b_{33}-\tau _{3}e_{33}}}. \end{aligned}$$
(17)

Solving the above by assuming that the major surfaces of the beam are shorted electrically, we have the following equation which shows the distribution of electric potential of the beam during vibration as:

$$\begin{aligned} \psi (x,z,t)=-\frac{C}{2}\left( z^{2}-\frac{h^{2}}{4}\right) \frac{\partial ^{2}w}{\partial x^{2}}+\zeta _{33}^{*}\psi _{0}z. \end{aligned}$$
(18)

Further, combining and manipulating Eqs. (10), (12), and (18), we have the following form:

$$\begin{aligned} \left( 1+\tau _{\theta }\frac{\partial }{\partial t}\right) \left( k_{11}\frac{\partial ^{2}\theta }{\partial x^{2}}+k_{33}\frac{\partial ^{2}\theta }{\partial z^{2}}\right) -\rho c_{e}\left( \frac{\partial }{\partial t}+\tau _{q}\frac{\partial ^{2}}{\partial t^{2}}\right) \theta +\theta _{0}b_{11}^{*}z\frac{\partial ^{2}}{\partial x^{2}}\left( \frac{\partial }{\partial t}+\tau _{q}\frac{\partial ^{2}}{\partial t^{2}}\right) w=0, \end{aligned}$$
(19)

where \(b_{11}^{*}=\) \(b_{11}-\tau _{3}C.\)

In terms of the components of bending moment due to classical stress (\(M_{c}\)) and couple stress (\(M_{s}\)), bending moment of cross section of the beam can be given as follows:

$$\begin{aligned} M= & {} M_{c}+M_{s}, \\ M_{c}= & {} \intop _{-h/2}^{h/2}b\varrho _{xx}z\textrm{d}z,\ \ M_{s}=\intop _{-h/2}^{h/2}bm_{xy}\textrm{d}z. \end{aligned}$$

Thus, M can be given as

$$\begin{aligned} M(x,t)&=-\overline{c}_{11}I\frac{\partial ^{2}w}{\partial x^{2}}-2\mu l^{2}A\frac{\partial ^{2}w}{\partial x^{2}}-b_{11}M_{\theta }, \end{aligned}$$
(20)

where \(\overline{c}_{11}=\) \(c_{11}+e_{31}C\), \(I=\frac{bh^{3}}{12}\), \(M_{\theta }=b\intop _{-h/2}^{h/2}\theta z\textrm{d}z\). Here, I denotes the moment of inertia of the cross section, \(M_{\theta }\) is the moment of beam which arises due to the thermal effects, and A is the cross-sectional area.

The equilibrium equation of transverse vibration of a beam is given as

$$\begin{aligned} \frac{\partial ^{2}M}{\partial x^{2}}-\rho A\frac{\partial ^{2}w}{\partial t^{2}}=0. \end{aligned}$$
(21)

Now, substituting M from Eq. (20) into the above equation takes the following form:

$$\begin{aligned} \overline{c}_{11}I\frac{\partial ^{4}w}{\partial x^{4}}+2\mu l^{2}A\frac{\partial ^{4}w}{\partial x^{4}}+b_{11}\frac{\partial ^{2}M_{\theta }}{\partial x^{2}}+\rho A\frac{\partial ^{2}w}{\partial t^{2}}=&0. \end{aligned}$$
(22)

4 Harmonic solution

In order to solve the system of Eqs. (18), (19), and (22), we consider the time harmonic solutions in the following way:

$$\begin{aligned} w(x,t)= & {} W(x)\ e^{(i\omega t)}, \end{aligned}$$
(23)
$$\begin{aligned} \psi (x,t)= & {} \varPhi (x)\ e^{(i\omega t)}, \end{aligned}$$
(24)
$$\begin{aligned} \theta (x,t)= & {} \varTheta (x)\ e^{(i\omega t)}. \end{aligned}$$
(25)

Using the above in Eqs. (19), (21) and (22), we obtain

$$\begin{aligned}{} & {} \widetilde{D}\frac{\partial ^{4}W}{\partial x^{4}}+2\mu l^{2}A\frac{\partial ^{4}W}{\partial x^{4}}+b_{11}\frac{\partial ^{2}M_{\theta _{0}}}{\partial x^{2}}-\rho A\omega ^{2}W=0, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \tau _{\theta }^{*}\left( k_{11}\frac{\partial ^{2}\varTheta }{\partial x^{2}}+k_{33}\frac{\partial ^{2}\varTheta }{\partial z^{2}}\right) -\rho c_{e}i\omega \tau _{q}^{*}\varTheta +\theta _{0}b_{11}^{*}\tau _{q}^{*}zi\omega \frac{\partial ^{2}}{\partial x^{2}}W=0, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \varPhi (x,z)=-\frac{C}{2}\left( z^{2}-\frac{h^{2}}{4}\right) \frac{\partial ^{2}W}{\partial x^{2}}+\zeta _{33}^{*}\psi _{0}z, \end{aligned}$$
(28)

where \(M_{\theta _{0}}=b\intop _{-h/2}^{h/2}\varTheta z\textrm{d}z,\) \(\tau _{\theta }^{*}=1+\tau _{\theta }(i\omega )\) and \(\tau _{q}^{*}=1+\tau _{q}(i\omega ).\)

Now, we attempt to find out a trial solution of Eq. (27) by assuming that the heat does not flow across the major surfaces of the beam, i.e. \(\frac{\partial \varTheta }{\partial z}=0\) at \(z=\pm h/2\), the temperature field is steady in the plane perpendicular to the thickness of the beam and the temperature gradient along the thickness direction of the beam in the cross-sectional plane is significantly larger when compared to those along the plane normal to it, i.e. \(\frac{\partial ^{2}\theta }{\partial x^{2}}\)= 0. Therefore, the trial solution can be taken as follows:

$$\begin{aligned} \begin{aligned} \varTheta (x,z)=\frac{b_{11}^{*}{{\theta }_{0}}}{\rho c_{e}}\left( z-\frac{\text{ sin }{(\beta z)}}{\beta \text{ cos } {(\frac{\beta h}{2})}}\right) \frac{\partial ^{2}W}{\partial x^{2}}. \end{aligned} \end{aligned}$$
(29)

Here, the value of \(\beta \) is still open to modifications.

Again using Eq. (29) into Eq. (27), we get

$$\begin{aligned}{} & {} \begin{aligned}{}&{} \frac{\partial ^{2}\varTheta }{\partial x^{2}}+\frac{k_{33}}{k_{11}}\left( \beta ^{2}+\frac{\rho c_{e}i\omega \tau _{q}^{*}}{k_{33}\tau _{\theta }^{*}}\right) \left( \frac{b_{11}^{*}\theta _{0}}{\rho c_{e}}\left( \frac{\text{ sin }{(\beta z)}}{\beta \text{ cos }{(\frac{\beta h}{2})}}\right) \frac{\partial ^{2}W}{\partial x^{2}}\right) =0, \end{aligned} \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \begin{aligned}{}&{} \frac{\partial ^{2}\varTheta }{\partial x^{2}}=-\frac{Kb_{11}^{*}\theta _{0}}{\rho c_{e}}\beta ^{*}\frac{\text{ sin }{(\beta z)}}{\beta \text{ cos }{(\frac{\beta h}{2})}}\frac{\partial ^{2}W}{\partial x^{2}}, \end{aligned} \end{aligned}$$
(31)

where \(\beta ^{*}=\beta ^{2}+\frac{\rho c_{e}i\omega \tau _{q}^{*}}{k_{33}\tau _{\theta }^{*}}\) and K=\(\frac{k_{33}}{k_{11}}\).

Further, \(M_{\theta _{0}}\) is calculated in the following form:

$$\begin{aligned} M_{\theta _{0}}= & {} b\intop _{-h/2}^{h/2}\varTheta z\textrm{d}z=b\frac{b_{11}^{*}\theta _{0}}{\rho c_{e}}\frac{\partial ^{2}W}{\partial x^{2}}\intop _{-h/2}^{h/2}\left( z^{2}-\frac{z\text {sin}{(pz)}}{p\text {cos}{(\frac{ph}{2})}}\right) \textrm{d}z, \\= & {} \frac{Ib_{11}^{*}\theta _{0}}{\rho c_{e}}(1+f(\beta ))\frac{\partial ^{2}W}{\partial x^{2}}, \end{aligned}$$

where \(f(\beta )=\frac{24}{(\beta h)^{3}}\left( \frac{\beta h}{2}-\text {tan}{(\frac{\beta h}{2})}\right) .\)

Therefore, one can find

$$\begin{aligned} \begin{aligned}{}&{} \frac{\partial ^{2}M_{\theta _{0}}}{\partial x^{2}}=\frac{Ib_{11}^{*}\theta _{0}}{\rho c_{e}}(1+f(\beta ))\frac{\partial ^{2}}{\partial x^{2}}\left( \frac{\partial ^{2}W}{\partial x^{2}}\right) .\\{}&{} \quad \text{ Also, }\quad \frac{\partial ^{2}M_{\theta _{0}}}{\partial x^{2}}=b\intop _{-h/2}^{h/2}\frac{\partial ^{2}\varTheta }{\partial x^{2}}z\text {d}z=-b \frac{Kb_{11}^{*}\theta _{0}}{\rho c_{e}}\frac{\beta ^{*}}{\beta \text{ cos }{(\frac{\beta h}{2})}}\left( \frac{\partial ^{2}W}{\partial x^{2}}\right) \intop _{-h/2}^{h/2}z\text{ sin } \beta z\text {d}z, \end{aligned}\end{aligned}$$
(32)

which implies

$$\begin{aligned} \frac{\partial ^{2}M_{\theta _{0}}}{\partial x^{2}}=\frac{KIb_{11}^{*}\theta _{0}\beta ^{*}f(\beta )}{\rho c_{e}}\frac{\partial ^{2}W}{\partial x^{2}}. \end{aligned}$$
(33)

Comparing Eqs. (32) and (33), we have

$$\begin{aligned} K\beta ^{*}f(\beta )\cong [1+f(\beta )]\frac{\partial ^{2}}{\partial x^{2}}. \end{aligned}$$
(34)

Putting the expression for \(\frac{\partial ^{2}M_{\theta _{0}}}{\partial x^{2}}\) in Eq. (26), one can obtain

$$\begin{aligned} \widetilde{D}\frac{\partial ^{4}W}{\partial x^{4}}+2\mu l^{2}A\frac{\partial ^{4}W}{\partial x^{4}}+\frac{b_{11}Ib_{11}^{*}\theta _{0}K\beta ^{*}f(\beta )}{\rho c_{e}}\frac{\partial ^{2}W}{\partial x^{2}}-\rho A\omega ^{2}W=0, \end{aligned}$$

Using the relation from Eq.(34), the above equation yields

$$\begin{aligned}{} & {} \widetilde{D}\frac{\partial ^{4}W}{\partial x^{4}}+2\mu l^{2}A\frac{\partial ^{4}W}{\partial x^{4}}+\frac{b_{11}Ib_{11}^{*}\theta _{0}(1+f(\beta ))}{\rho c_{e}}\frac{\partial ^{2}}{\partial x^{2}}\left( \frac{\partial ^{2}W}{\partial x^{2}}\right) -\rho A\omega ^{2}W=0, \nonumber \\{} & {} \quad \frac{\partial ^{4}W}{\partial x^{4}}\left( 1+2\mu l^{2}A+\frac{b_{11}^{*}Ib_{11}\theta _{0}\left( 1+f(\beta )\right) }{\widetilde{D}\rho c_{e}}\right) -\frac{\rho A\omega ^{2}W}{\widetilde{D}}=0, \nonumber \\{} & {} \quad \frac{\partial ^{4}W}{\partial x^{4}}-\frac{\rho A\omega ^{2}W}{d_{\omega }}=0, \end{aligned}$$
(35)

where \(d_{\omega }=\) \(\widetilde{D}\left( 1+2\mu l^{2}A+\frac{b_{11}^{*}Ib_{11}\theta _{0}\left( 1+f(\beta )\right) }{\widetilde{D}\rho c_{e}}\right) .\)

Now, substituting the values of \(\widetilde{D}=(c_{11}+e_{31}C)I\) and \(b_{11}^{*}=b_{11}-\tau _{3}C\) in \(d_{\omega }\), one can obtain the following expression:

$$\begin{aligned} d_{\omega }= & {} (c_{11}+e_{31}C)I\left( 1+2\mu l^{2}A+\frac{(b_{11}-\tau _{3}C)Ib_{11}\theta _{0}}{(c_{11}+e_{31}C)I\rho c_{e}}\left( 1+f(\beta )\right) \right) ,\nonumber \\ i.e. d_{\omega }= & {} c_{11}I\left( 1+N_{1}+N_{2}+\frac{b_{11}^{2}\theta _{0}-\tau _{3}b_{11}\theta _{0}C}{\rho c_{e}c_{11}}(1+f(\beta ))\right) , \nonumber \\ i.e. d_{\omega }= & {} D\left( 1+N_{1}+N_{2}+N_{3}(1+f(\beta ))-\frac{\tau _{3}b_{11}\theta _{0}N_{1}}{\rho c_{e}e_{31}}(1+f(\beta ))\right) , \end{aligned}$$
(36)

where \(D=c_{11}I,\ \ N_{3}=\frac{b_{11}^{2}\theta _{0}}{\rho c_{e}c_{11}}\ \ N_{1}=\frac{e_{31}C}{c_{11}},\) \(N_{2}=\frac{2\mu l^{2}A}{c_{11}I}\).

Equations (29), (28) and (35) clearly together govern the vibrations in piezothermoelastic resonator.

5 Application

Since W is the function of x only, we can write Eq. (35) in the following way:

$$\begin{aligned} \frac{\text {d}^{4}W}{\text {d}x^{4}}-\eta ^{4}W=0, \end{aligned}$$
(37)

where

$$\begin{aligned} \eta ^{4}=\frac{\rho A\omega ^{2}}{d_{\omega }}. \end{aligned}$$
(38)

The solution for the above equation with \(G_{i},i=1,2,3,4\) as integration constants can be given as

$$\begin{aligned} W(x)=G_{1}\text {sin}{\eta x}+{G_{2}\text {cos}{\eta x}+{G_{3}\text {sinh}{\eta x}+{G_{4}\text {cosh}{\eta x} }} }. \end{aligned}$$
(39)

To solve for constants, the edges of the beam are treated with three distinct set of boundary conditions which results in three distinct types of beams as explained in Set-1, Set-2 and Set-3 as follows:

Set-1: The boundary conditions for clamped–free (CF) beam are given as

$$\begin{aligned} W=0,\frac{\text {d}W}{\text {d}x}=0 \text { at } x=0, \frac{\text {d}^{2}W}{\text {d}x^{2}}=0, \frac{\text {d}^{3}W}{\text {d}x^{3}}=0 \text { at } x=L. \end{aligned}$$
(40)

Characteristic equation and characteristic roots (\(\eta _{n}\)) are therefore obtained as

$$\begin{aligned}{} & {} \text {cosh}{\eta L} \text { cos } {\eta L} =-1 \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \eta _{1}=\frac{1.8751}{L},\eta _{2}=\frac{4.6940}{L} \nonumber \\{} & {} \quad \eta _{n}^{CF}=\frac{1}{L}\left( \frac{2n-1}{2}\pi \right) ,\ \ \,n(\ge 3)\ \epsilon \ Z. \end{aligned}$$
(42)

Set-2: The boundary conditions for doubly clamped beam (CC) beam are as follows:

$$\begin{aligned} W=0,\frac{\text {d}W}{\text {d}{x}}=0 \text { at } x=0,\ \ \ W=0,\frac{\text {d}{W}}{\text {d}x}=0 \text { at } {x=L}. \end{aligned}$$

Characteristic equation and characteristic roots for this case are given by

$$\begin{aligned}{} & {} \text {cosh}{\eta L}\text {cos } {\eta L} =1 \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \eta _{1} =\frac{4.73004}{L},\eta _{2}=\frac{7.85320}{L}\nonumber \\{} & {} \eta _{n}^{CC}=\frac{1}{L}\left( \frac{2n+1}{2}\pi \right) ,\ \ \,n(\ge 3)\ \epsilon \ Z. \end{aligned}$$
(44)

Set-3: Doubly simply supported beam (SS) has the boundary conditions of the form

$$\begin{aligned} W=0,\frac{\text {d}^{2}W}{\text {d}{x^{2}}}=0 \text { at } x=0,\ \ \ W=0,\frac{\text {d}^{2}W}{\text {d}x^{2}}=0 \text { at } x=L. \end{aligned}$$

The corresponding characteristic equation and characteristic roots are obtained as

$$\begin{aligned}{} & {} \text {sinh}\eta L\text {sin } {\eta L} =0 \end{aligned}$$
(45)
$$\begin{aligned}{} & {} \eta _{1}=\frac{3.14159}{L},\eta _{2}=\frac{6.28318}{L} \nonumber \\{} & {} \eta _{n}^{SS}=\left( \frac{n\pi }{L}\right) ,\ \ \,n(\ge 3)\ \epsilon \ Z. \end{aligned}$$
(46)

In each case, Newton–Raphson method is utilized to find out the first two eigenvalues and general formulae for the roots of the characteristic equation numerically. The variation of temperature, the deflection and electric potential of the analysed beams can be obtained by using the expression of \(\eta _{n}\) in each case. These solutions agree well with the boundary conditions and the physical situation of the problem.

6 Inverse quality factor

Inverse quality factor to obtain thermoelastic damping in the analysed piezothermoelastic beam is given by

$$\begin{aligned} Q^{-1}&=2\left| \frac{\text {Img}(\omega _{n})}{\text {Re}(\omega _{n})}\right| , \end{aligned}$$
(47)

where \(\omega _{n}\) is the vibration frequency.

The vibration frequency of the piezothermoelastic nanobeam in the present context can be found from Eq. (38) as

$$\begin{aligned} \omega _{n}=q_{n}\sqrt{\frac{d_{\omega }}{\rho A}}=\omega _{0}\sqrt{1+N_{0}[1+f(\beta )]}, \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned} \mathcal {\omega }_{0}=~&{} \frac{q_{n}hR}{2}, R=\sqrt{\frac{c_{11}}{3\rho }\left( 1+N_{1}+\frac{24\mu l^{2}}{c_{11}h^{2}}\right) },\ N_{0}=\frac{N_{3}}{1+N_{1}+\frac{24\mu l^{2}}{c_{11}h^{2}}}\left( 1-\frac{C\tau _{3}}{b_{11}}\right) . \\ q_{n}=~&{} \eta _{n}^{2}\ \,\text{ for } \text{ the } \text{ sets } \text{1, } \text{2 } \text{ and } \text{3. } \end{aligned} \end{aligned}$$
(49)

Furthermore, usually, the temperature gradients along the thickness direction of the beam in the cross-sectional plane is significantly larger when compared to those along the planes normal to it; therefore, we consider \(\frac{\partial ^{2}\varTheta }{\partial x^{2}}\)= 0, and hence, for harmonic vibration, one can find

$$\begin{aligned} \beta ^{*}=0\Rightarrow \beta ^{2}=\frac{\rho c_{e}i\omega \tau _{q}^{*}}{k_{33}\tau _{\theta }^{*}},\ \ \ \tau _{\theta }^{*}=1+\tau _{\theta }(i\omega )\ \text {and }\tau _{q}^{*}=1+\tau _{q}(i\omega ). \end{aligned}$$

It is clear from above that the expression for \(\beta \) is complex in the form

$$\begin{aligned} \beta= & {} \sqrt{2}\beta _{0}\text {exp}\left( -\frac{i\gamma }{2}\right) , \nonumber \\ \text {where }\beta _{0}= & {} \sqrt{\frac{\rho c_{e}\omega }{2k_{33}}},\ \gamma =\text {tan}^{-1}\left( \frac{a_{2}}{\sqrt{1-a_{2}^{2}}}\right) ,\,\,a_{2}=\frac{1+\tau _{\theta }\tau _{q}\omega ^{2}}{1+\tau _{\theta }^{2}\omega ^{2}}. \end{aligned}$$
(50)

Replacing \(\omega \) by \(\omega _{0}\) in the expression of \(\beta \) as the dimensionless parameter \(N_{0}\) is much less than 1 for the considered material. Thus, we have \(f(\omega _{0})\) in place of \(f(\beta )\) in Eq. (49). Hence, expanding Eq. (48) up to the first order, we get

$$\begin{aligned} \begin{aligned} \omega _{n}^{2}=\omega _{0}^{2}\left( 1+{N_{0}}(1+f(\omega _{0})\right) . \end{aligned} \end{aligned}$$
(51)

Resolving \(\omega _{n}\) into real and imaginary parts by using a theorem of complex analysis [55], we have

$$\begin{aligned} \begin{aligned} \omega _{n}=&{} \pm \left[ \sqrt{\frac{x+\sqrt{x^{2}+y^{2}}}{2}+}i \text{ sgn }(y)\sqrt{\frac{-x+\sqrt{x^{2}+y^{2}}}{2}}\,\,\right] , \\\\ \text{ where },\ \ x=&{} 1+N_{0}(1+\text{ Re }f(\omega _{0})),\ y=N_{0}\text{ Img } f(\omega _{0}),\\ \\ \text{ Re }f(\omega _{0})=&{} \frac{6\text{ cos }\gamma _{0}}{\xi ^{2}}-\frac{6\sqrt{2}\cos \left( \frac{3\gamma _{0}}{2}\right) }{\xi ^{3}}\left( \frac{\sin \zeta +\text{ tan }\left( \frac{3\gamma _{0}}{2}\right) \sinh \zeta T^{*}}{\cos \zeta +\cosh \zeta T^{*}}\right) , \\ \text{ Img } f(\omega _{0})=&{} \frac{6\sqrt{2}\cos \left( \frac{3\gamma _{0}}{2}\right) }{\xi ^{3}}\left( \frac{\sin \zeta \tan \left( \frac{3\gamma _{0}}{2}\right) -\sinh \zeta T^{*}}{\cos \zeta +\cosh \zeta T^{*}}\right) -\frac{6\sin \alpha _{0}}{\xi ^{2}}, \end{aligned}\end{aligned}$$

where \(\xi =\beta _{0}h,\zeta =\sqrt{2}\xi \cos \frac{\gamma _{0}}{2},T^{*}=\tan \frac{\gamma _{0}}{2}.\)

7 Results and explanation

This section concerns with the illustration of the analytical results obtained in the previous section. For this, we use numerical data for the considered homogeneous transversely isotropic piezothermoelastic beam made up of the lead zirconate titanate (PZT-5A) material to study the thermoelastic damping in the context of DPL thermoelasticity theory by utilizing modified couple stress theory. We calculate the damping factor for the considered beam with three distinct boundary conditions using the formulae provided by Eq. (47). Inverse quality factor \((Q^{-1})\) is used to express the amount of thermoelastic damping for the piezothermoelastic beam. The impact of various factors on the variation of damping factor has been investigated. The physical data for the PZT-5A material have been followed from Grover and Sharma [56] which is as follows:

  • \(c_{11}=13.9\times 10^{10}\)Nm\(^{-2}\), \(c_{13}=7.54\times 10^{10}\,\)Nm\(^{-2}\), \(\rho =7.75\times 10^{3} \text {kg } \text {m}^{-3}\),

  • \(K_{33}^{*}=1.5\,\)Wm\(^{-1}\)K\(^{-1}\) s\(^{-1}\), \(K_{33}=1.5\,\)Wm\(^{-1}\) K\(^{-1}\), \(b_{11}=1.53\times 10^{6}\) NK\(^{-1}\)m\(^{-1}\),

  • \(T_{0}=298\) K, \(c=420\) JKg\(^{-1}\)K\(^{-1}\), \(e_{13}=-6.98\) \(\text {C}\text {m}^{-2}\)

  • \(\tau _{0}=2\times 10^{-8}\)s, \(e_{31}=-6.98\text {C}\text {m}^{-2}\), \(\tau _{3}=-452\times 10^{-6}\) CK\(^{-1}\) m\(^{-2}.\)

7.1 Effect of boundary conditions

Figure 1 shows the variation of thermoelastic damping in terms of inverse quality factor with respect to the thickness of the nanobeam for three distinct arrangements of the beam edges. As indicated by this figure, the damping factor of the nanobeam, under all the cases of boundary conditions, firstly increases with the increase in thickness and then decreases after achieving a peak value of the damping factor. The nature of variation of TED in all three cases is similar but shows a significant difference in the peak values of the damping factor. The thickness at which the vibrations suffer maximum damping is called the critical thickness of the beam. From the figure, it is clear that the peak values of both damping factor and the critical thickness are maximum for the clamped–free case while they are lowest in case of doubly clamped beam. This can be seen from graphical data as for CF nanobeam, the critical thickness and peak value of damping factor are 7.4nm and \(3.2\times 10^{-6}\), respectively, while for doubly clamped beam they are 3.8nm and \(0.466\times 10^{-6}\), respectively. Moreover, the critical thickness and peak value of damping factor for doubly simply supported beam are 5.01nm and \(0.986\times 10^{-6}\), respectively. Thus, it is concluded that the modelling of piezothermoelastic nanobeam resonator in the present scenario with doubly clamped boundary condition performs better as it gives a lower rate of energy dissipation as compared to the other boundary conditions.

Fig. 1
figure 1

Variation of TED with respect to the thickness of the beam under different boundary conditions

Full size image
Fig. 2
figure 2

TED versus thickness with and without piezoelectric effect for clamped–free nanobeam

Full size image
Fig. 3
figure 3

Variation of TED with respect to the thickness with and without piezoelectric effect for CC and SS nanobeams

Full size image

7.2 Effect of piezoelectricity

Fig. 2 shows the variation of inverse quality factor opposite to the thickness of the nanobeam with piezoelectric effect (WPE) and without piezoelectric effect (WOPE) in clamped–free boundary condition while Fig. 3 shows the same for doubly clamped and doubly simply supported boundary conditions of the nanobeam. The nature of variation of thermoelastic damping is same as explained in the above subsection. To see the piezoelectric effect on the damping factor, we have neglected the piezoelectric parameters and plotted the graph from where we can see that the peak value of the damping factor without piezoelectric effect is much higher (almost ten times) than the peak value of the damping factor with piezoelectric effect. It can also be seen from the data as the maximum value of damping factor WPE and WOPE is \(5.2\times 10^{-6}\) and \(0.49\times 10^{-6}\), respectively. Furthermore, the critical thickness does not show significant difference in both the cases as the critical thickness WPE is 7.3nm while WOPE is 7.5nm. Also, the extent of the piezoelectric beam up to which the vibrations of the beam experience the dissipation in energy is significantly less, i.e. the piezoelectric resonator earlier stops experiencing the energy dissipation in its vibrations with piezoelectric parameter. Furthermore, it can be observed from both the figures that piezoelectricity influences the inverse quality factor likewise for all the conditions imposed on the edge of the beam in the present study.

7.3 Temperature variation

Fig. 4 indicates the variation of damping factor in the form of inverse quality factor opposite to the thickness of the nanobeam w.r.t. different reference temperatures. The nature of inverse quality factor first increases with the increase in thickness and then starts decreasing after attaining the peak value of the damping factor at the point of critical thickness. Temperature changes can induce internal stresses within the material due to the differential expansion or contraction of different components and also can affect the polarization and alignment of the piezoelectric domains. The nature of variation of TED for all temperature variation is similar but shows a slight difference in the peak value of the damping factor. Hence, the thermal variation influences the peak value or the maximum value of the inverse quality factor in the manner that the lower the reference temperature, the lower is the peak value of the damping factor. From the graph, the respective values of maximum damping factor at distinct reference temperatures 298K, 305K and 312K are \(3.22\times 10^{-6},\) \(3.35\times 10^{-6}\) and \(3.42\times 10^{-6}\). Furthermore, Fig. 5 shows the influence of temperature variation on thermoelastic damping for the doubly clamped and doubly simply supported beam. From the figures, it is quite obvious that the variation of damping factor with the variation in temperature is similar for the doubly clamped and doubly simply supported boundary condition of the beam while the variation among all the boundary conditions are same as explained in Subsect. 7.1. Moreover, if we take more difference in temperature values, the change in the peak value of damping factor will be more significant.

Fig. 4
figure 4

TED versus thickness at different temperatures for clamped–free nanobeam

Full size image
Fig. 5
figure 5

TED versus thickness at different temperatures for CC and SS nanobeam, respectively

Full size image

7.4 MCST effect

Figure 6 reveals the change in damping factor with the increase in the thickness of the nanobeam for two cases: one under MCST (with modified couple stress parameter) and the other under classical elasticity theory (without modified couple stress parameter) in case of clamped–free nanobeam. From the figure, the variation of damping factor clearly shows that the thermoelastic damping first significantly increases and after attaining the peak value starts decreasing and tends to zero. The consideration of the microrotation of the particles of the taken material lessens down the maximum value of energy dissipated during vibration while the critical thickness of the beam shows slight difference. Thus, modified couple stress parameter helps to reduce the energy dissipation during the vibration of the beam. The graph for doubly clamped and doubly simply supported nanobeam will show similar behaviour and the variation among them is explained in Subsect. 7.1.

Fig. 6
figure 6

TED versus thickness with and without modified couple stress parameter for clamped–free case

Full size image

7.5 Effect of phase-lag parameters

7.5.1 When (\(\tau _{q}>\tau _{\theta }\))

Figure 7 mentions the behaviour of damping factor opposite to the thickness of the beam for the CF boundary condition when the phase lag of heat flux is greater than the phase lag of temperature gradient. The attached figure clearly shows a prominent effect of phase lags of heat flux and temperature gradient on thermoelastic damping. It can be observed from the figures that the peak value of TED increases rapidly with the increase in the values of phase-lag parameters of heat flux. This indicates that the quality factor decreases with an increase in the value of phase-lag parameters. It can be concluded that beam experiences dissipation in energy up to a less extent of the thickness of the nanobeam for smaller values of the phase-lag parameters and energy dissipation occurs slowly for small values of phase-lag parameters. It can also be observed from the graphical data, when the values of the phase-lag parameters are taken null, the peak value of the damping factor is \(1.9\times 10^{-7}\) while the peak value of thermoelastic damping in case of \(\tau _{q}=2\times 10^{-11}\)s and \(\tau _{\theta }=10^{-11}\)s is \(3.3\times 10^{-7}\) and in case of \(\tau _{q}=4\times 10^{-11}\)s and \(\tau _{\theta }=10^{-11}\)s is \(5.51\times 10^{-7}\). Moreover, when we take \(\tau _{q}=\tau _{\theta }=0\) (i.e. in the context of classical heat conduction model), and \(\tau _{q}=10^{-11},\tau _{\theta }=0\) (Lord–Shulman heat conduction model), the damping nature shows similar behaviour while further increase in \(\tau _{q}\) influences the peak value of TED and critical thickness of the nanobeam resonator significantly. This is an important observation of the present study.

Fig. 7
figure 7

TED versus thickness for different values of phase-lag parameters

Full size image

7.5.2 When (\(\tau _{q}<\tau _{\theta }\))

Figure 8 shows the change in the nature of damping factor with increase in the thickness of the beam in case of clamped–free boundary condition when \(\tau _{q}<\tau _{\theta }\). As we can see from the graph, it is clear that the thermoelastic damping first increases with the increment in the thickness of the beam and then decreases after attaining a maximum value and becomes zero afterwards. Also we can observe, with the increase in the phase lags of temperature gradient, the graph for damping factor starts having multiple peaks. Moreover, the maximum peak value of the damping factor as well as the sharpness of the graph at the point of critical thickness increases with the increase in the value of phase-lag parameter. For \(\tau _{\theta }=0=\) \(\tau _{q}\), there is only one peak attained by the graph which is obtained at the critical thickness of the 5nm as explained above. With a slight increase in phase-lag parameter of temperature gradient, i.e. for \(\tau _{\theta }=2\times 10^{-11}\)s, the peak value of the damping factor increases rapidly and the curve starts having multiple peaks with small amplitude at the thickness of 3nm, 8nm and 12.7nm. With further increase in the value of phase-lag parameter of temperature gradient, i.e. for \(\tau _{\theta }=3\times 10^{-11}\)s, the increment in peak value is higher and the number of peaks increases more with significant amplitude than the earlier at the point of thickness of 2.89nm, 7.86nm, 12.2nm and 16.7nm. Also, the sharpness of decline increases with the increase in phase lags, i.e. the peak value of the damping factor gets sharper with the increase in phase lags at the point of critical thickness. For \(\tau _{q}\)= \(\tau _{\theta }\), the damping nature shows similar behaviour as that of for \(\tau _{q}=\tau _{\theta }=0\).

Fig. 8
figure 8

TED versus thickness under the different values of phase lags of temperature gradient for CF nanobeam

Full size image

Moreover, as discussed above, we can conclude that with the increase in the phase lag of heat flux having value greater than the phase lag of temperature, the peak value of the damping factor as well as the critical thickness increases while with the increase in phase lag of temperature gradient having value greater than the phase lag of heat flux, not only the peak value of damping factor increases but also the graph starts having multiple peaks with less amplitude and decreases the extent of the thickness up to which the vibration suffers damping. Therefore, it can be concluded that the DPL model of piezothermoelastic nanobeam shows significant difference in the damping nature of the beam and thereby affecting the quality factor. Moreover, the critical thickness is much less in case of DPL theory.

7.6 Variation with Aspect ratio

Figure 9 displays the effect of aspect ratio (L/h) on the behaviour of thermoelastic damping with respect to the thickness of the beam for clamped–free boundary condition of the beam. We can observe from the graphical plot that the peak value of the damping factor remains same for all the distinct values of aspect ratio, but the critical thickness at which the maximum peak value is obtained shows a significant difference. With the increase in the value of aspect ratio, the critical thickness increases prominently as the critical thickness for the aspect ratio 15 is 313nm, the critical thickness for the aspect ratio 20 is 566nm, and for the aspect ratio 25, the critical thickness is 846nm. Moreover, the variation of TED with respect to the different values of aspect ratio for doubly clamped and doubly simply supported boundary condition of the nanobeam is almost the same.

Fig. 9
figure 9

Effect of Aspect ratio on inverse quality factor for CF nanobeam

Full size image
Fig. 10
figure 10

Effect of modes of vibration on inverse quality factor for CF nanobeam

Full size image

7.7 Variation with mode of vibration

Figure 10 shows the impact of distinct modes of vibration on the nature of thermoelastic damping for clamped–free boundary condition with respect to the thickness of the beam. From the graphs, it is clear that with the increase in modes of vibration, the critical thickness as well as the damping factor decreases. For the first mode of vibration, i.e. for the lowest frequency mode of vibration which represents the primary mode of oscillation of the beam, the peak value of the damping factor and critical thickness is \(4.75\times 10^{-7}\)and 4nm. For the second mode of vibration, 3nm and \(1.8\times 10^{-7}\) are the critical thickness and peak value of the damping factor, respectively, while for the third mode of vibration, the critical thickness is 2.5nm and the peak value of the damping factor is \(0.9\times 10^{-7}.\) Higher-order modes arise due to the increase in the frequency which includes additional nodal lines or points along the length of the beam.

8 Conclusion

The current study focuses on investigating the vibrations of a transversely isotropic piezothermoelastic nanobeam. The performance of the nanobeam is studied for its various boundary conditions such as clamped–free, doubly clamped and doubly simply supported configurations. The study incorporates the dual-phase-lag theory of thermoelasticity to analyse the behaviour of the nanobeam and modified couple stress theory is employed to consider the size effect of the nanobeam. The expression for the inverse quality factor is derived using the complex frequency approach. The effect of the different parameters has been thoroughly examined. The following are some notable findings and observations of the study.

  • All the figures demonstrate that the damping factor initially increases considerably and achieves a maximum peak which is followed by a sharp decline until it attains a stable nature to have zero damping.

  • The damping factor is dependent on all material parameters of the beam including the phase lags of temperature gradient and heat flux, characteristic of DPL theory.

  • Graphical representations for CC, SS and CF nanobeams indicate that the nature of TED is almost similar for all the cases. However, the major distinction among them is caused by the different values of critical thickness and the amplitude of the peak values of damping factor.

  • The magnitude of critical thickness and peak value of damping factor for doubly clamped beam is the lowest followed by the magnitudes for doubly simply supported and clamped–free beams, respectively.

  • The piezoelectric parameter decreases the amplitude of the damping factor, and the vibrations of the nanobeam suffer damping up to less extent of the thickness for all the three analysed beams, i.e. with the piezoelectric effect the energy loss reduces rapidly which can lead to reduced vibrations and better performance of the nanobeam.

  • The thermal variation influences the magnitude of peak value of the damping factor and critical thickness of the nanobeam in the manner that with the increment in reference temperature, the peak value of the damping factor decreases significantly while the critical thickness does not show noticeable difference.

  • The material length scale parameter effects the peak value of damping factor as well as the critical thickness of the nanobeam in a way that it decreases the peak value of damping factor and increases the value of critical thickness of the nanobeam.

  • The prominent effect of phase lags on the critical thickness and peak value of damping factor has been observed.

  • In case when \(\tau _{q}<\tau _{\theta }\), with the increase in phase lags of temperature gradient, the peak value of the damping factor as well as the sharpness of damping factor increases along with a decrease in critical thickness. Moreover, the curve starts having multiple peaks with the increase in phase lags and then reduces to zero.

  • In case when \(\tau _{q}>\tau _{\theta }\), the increment in the value of phase lag of heat flux increases the peak value of the damping factor as well as the critical thickness of the damping factor.

  • The increment in the aspect ratio (L/h) of the beam increases the critical thickness of the beam significantly while the peak value of the damping factor remains almost similar for all the boundary conditions of the beam.

  • The increment in the modes of vibration decreases the critical thickness as well as the peak value of the damping factor.

  • Thus, it is worth mentioning that the \(\tau _{q}\) and \(\tau _{\theta }\), which represent the phase-lag parameter of the heat flux and the temperature gradient, influence the transverse vibrations of piezothermoelastic nanobeam in a significant manner.