Abstract
This work considers the modeling of torsion in elastic shafts accounting for the non-uniform warping of the cross sections along them. In this paper, we present an analysis of (1) the original formulation of Timoshenko–Wagner–Kappus–Vlasov, consisting of the underlying Saint-Venant torsion but with a non-constant rate of twist defining the warping magnitude, and (2) the alternative formulation first considered by Reissner–Benscoter–Vlasov involving an independent field for the warping amplitude. The theoretical results presented here characterize the kinematically constrained character of the first of these formulations, noting in the process the anomalies resulting from the full restrainment of the warping at a cross section in this setting. New explicit expressions for the warping shear stress and other features are obtained in this context. The second formulation relaxes the constraint between warping and twisting, with the analyses presented here identifying explicitly for the first time how its enforcement can be achieved in a limit process controlled by a parameter depending on the cross-sectional geometry. Hence, it avoids the anomalies of the first formulation, but at the price to involve local stresses not in equilibrium, a situation that does not seem to be much present in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The torsion of shafts and, in a more general sense, of bars, beams, rods or columns is a problem of great practical importance whose understanding goes back to the fundamental work of Saint-Venant in [19]. In those early days of modern elasticity theory, Saint-Venant considered a prismatic three-dimensional solid and studied its deformation and state of stress, the so-called Saint-Venant problem, through what is now known as Saint-Venant semi-inverse method. In this way, he identified the warping of the shaft’s cross section out of its plane as a main characteristic of the torsion part of the problem for a general geometry of the cross section, extending the early results by Coulomb in [5] on the torsion of thin circular wires, where warping does not occur. We limit our comments and considerations in this paper to isotropic elastic solids in the infinitesimal deformation range.
The resulting problem and its solution is now well-known, covered in all textbooks on (or even just related to) elasticity theory; see e.g. [13, 24, 29] to cite just a few. The solution consists of the shaft’s plane cross sections rotating without distortion in their plane, the twist rotation around the shaft axis, with the section’s warping displacement in this axial direction proportional to the rate of this twist rotation along the shaft length. The actual distribution of this warping displacement on the cross section itself is given by the so-called Saint-Venant warping function, an harmonic function on the plane domain defined by the cross section in the homogeneous linear elastic case. We refer to this solution simply as Saint-Venant torsion.
This solution received a great deal of attention leading to a number of refinements and extensions, among which the classical treatment by Prandtl in [16] in terms of the alternative stress function and the well-known membrane analogy must be pointed out. This allowed the easy treatment of important practical cases like thin-walled sections where the effects of torsion are significant in general, as studied by Föppl in [7] for thin-walled sections with open (or simply-connected) topology, and in the classical work of Bredt in [3] for closed (or multiply-connected) hollow sections. In both cases, away from any wall ends, junctions or kinks, the dominant stress component follows the direction of the wall middle line, but the first case of open sections is known to lead in the limit of thin walls (i.e., neglecting second-order terms as in [15]) to a linear distribution of the shear stress through the thickness (centered so it vanishes along the wall’s middle line), whereas closed hollow sections result in a constant distribution instead. We refer to [8, 34] among others for monographs focused on thin-walled beams.
In Saint-Venant torsion, equilibrium considerations require the rate of twist giving the amplitude of the section’s warping to remain constant along the shaft length. This situation implies not only that no normal axial stresses appear (so only shear stresses on the cross section are involved), but it also restricts the exactness of this three-dimensional solution to configurations with such uniform warping along the length of the shaft. In particular, no supports restraining the warping of the section can be accounted for. The restrainment of the warping at a given cross section (by a support, stiffener or similar) creates a non-uniform distribution of this axial displacement of the cross sections along the shaft, and hence, it leads to normal axial strains and stresses, resulting in a different structural response of the shaft. Given the practical interest of these configurations, this clear limitation of pure Saint-Venant torsion, although local to those restraining conditions, motivated the development of extensions of this theory accommodating a non-uniform warping along the shaft, leading to the so-called torsion with restrained warping or simply, as it is often called in short, warping torsion, notwithstanding that the original Saint-Venant torsion does involve warping, even if just a uniform one; see e.g. [13, 14, 20] among many references in the field, including professional manuals like [21].
With this background in mind, the main objective here is to develop a structural model of the shaft (or, more generally, rod or other structural members in torsion) that incorporates the effects of restrained warping. The most important aspect in accomplishing this goal is to develop an appropriate approximation of the warping displacement of the cross sections, crucially identifying its link with the twisting of the shaft. In the process, the considered arguments must also identify both the resulting properties of the member at the global structural level, like its flexibility, as well as the normal and shear stresses involved in the approximation at the local level defined by a particular cross section, altogether pointing to the adequacy of the formulation based on the assumed approximation of the full three-dimensional elastic problem.
Historically, early treatments accommodating restrained warping in torsion were presented by Timoshenko in [25,26,27], with a focus on thin-walled sections and, in particular, on the observed bending of the flanges in these sections when warping is restrained; see the case of an I-beam discussed in [28, p. 213]. These early analyses were later extended and formalized by Wagner in [32] and Kappus in [11], where the main assumption underlying the final formulation was identified as simply assuming a non-constant rate of twist in the Saint-Venant torsion solution, including the use of that same harmonic Saint-Venant warping function over the cross section. These considerations are usually referred to as the Wagner assumption; see, e.g., [8, 9]. Hence, and as we explore in detail in this work, the amplitude of the warping is constrained to be the rate of twist of the cross sections along the shaft, a kinematic constraint in our point of view elaborated here.
Additional important contributions for this treatment of restrained warping were made in [9, 12, 31]. In particular, this last monograph by Vlasov has had a great influence in the field. Interestingly, Vlasov considered a different starting point when analyzing open thin-walled sections under torsion, namely the vanishing of the shear strain between the local tangential direction to the wall’s middle line (the idealization of the thin-walled section) and the axial direction of the shaft. This assumption/approximation is often referred to as the Vlasov assumption. Note that this situation is consistent with the centered linear distribution of the shear stress through the thickness indicated above for open thin-walled sections. This assumption can be seen to lead to the same kinematics encompassed by the Wagner assumption (see [8]), and it leads to an elegant treatment for thin-walled sections, incorporating the consideration of the so-called sectorial coordinate along the section’s middle line. This approach gives convenient explicit expressions for thin-wall limit estimates of the different section constants involved in the torsion problem, to the point that it has become an standard treatment in the field. Besides the excellent monograph by Vlasov itself, we refer to [8, 13, 34] among other volumes considering these developments in detail. Because of all these historic considerations, in this work we refer to this first approximation of torsion with restrained warping as the TWKV formulation for Timoshenko–Wagner–Kappus–Vlasov.
A clear alternative to the TWKV approach is provided by leaving the parameter controlling the amplitude of the restrained warping as an independent field along the shaft, sometimes in combination with distributions over the cross section itself different that the harmonic Saint-Venant warping function. This more general approximation was indeed considered early by Reissner in [17] as a general option, by Benscoter in [2] for multi-cell sections, and again by Vlasov in [31] for solid and closed thin-walled sections. Hence, we refer to the resulting formulation as the RBV formulation in this work. The direct link (or constraint) between the amplitude of the warping displacement and the rate of twist along the shaft is then relaxed. We shall see with the results presented in this work that it is precisely for this reason that this formulation is more appropriate for solid and hollow sections, whose response is far from the limit constrained kinematics, rather than the need to modify the aforementioned Vlasov assumption to accommodate the constant shear flow through the thickness in closed thin-walled sections. This relaxed treatment of restrained torsional warping makes this formulation also very appealing for the incorporation of torsion in general models of beams and rods; see, e.g., [18], among many others. This is especially the case in the geometrically nonlinear range, with a marked interest in accommodating it in computational models, as illustrated by [10, 23] to name just two more recent works.
The goal of the current paper is to analyze these two existing formulations in their fundamental assumptions and developments, identifying in the process their features as well as several limitations motivating the need of alternative treatments. In particular, we are interested in fully characterizing the constrained character of the original TWKV formulation as outlined above, and how the RBV relaxes the constraint involved. We shall see that a direct consequence of the constraint in the original TWKV formulation, is the appearance of stresses from purely static considerations (that is, with no associated strains), and hence in equilibrium by definition. But one should expect that this formulation, also for this reason, leads to an over-stiff prediction of the shaft’s structural response and, as discussed further below, in anomalies when the warping is to be fully restrained at a given section (briefly, no shear stresses nor torque associated with the twisting). While these anomalies are avoided by the RBV formulation, this formulation results, as shown in this paper, in stresses not in equilibrium.
An outline of the rest of the paper is as follows. Section 2 introduces the basic problem of a linear elastic prismatic shaft in torsion. More specifically, Sect. 2.1 includes a complete definition of the physical problem under study, with Sect. 2.3 summarizing the basic Saint-Venant solution of torsion with uniform warping, after considering the case of general warping and its associated anomalies in Sect. 2.2. The center of twist, ubiquitous in all the considerations in this work, is discussed in Sect. 2.4. Section 3 presents the TWKV formulation of restrained warping, identifying the governing equations in Sect. 3.1 and analyzing the role played by the additional warping stresses and their resultants, the so-called bimoment and bishear, in Sect. 3.2. Section 4 considers the RBV formulation, developing the governing equations in Sect. 4.1, with Sect. 4.2 identifying the limit process leading to the original constrained TWKV formulation. The aforementioned physically incorrect (non-equilibrated) stresses in the RBV formulation are studied in Sect. 4.3. Finally, we summarize in Sect. 6 all these results while drawing a number of concluding remarks.
2 The Saint-Venant problem in torsion
After defining the physical problem of interest, we summarize in this section basic fundamental results about its mathematical treatment.
2.1 The physical problem
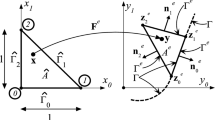
The problem of interest here consists of a straight shaft or, more generally, rod of constant cross section \(\Omega \subset {\mathbb {R}}^2\) and length L subjected to torsional loading; see Fig. 1 for a representative example. It depicts a prismatic shaft with an applied torque \(T_L\) and resulting rotation \(\phi _L\) at its free tip (free to warp), while the shaft is fixed at its root in both twisting and warping.
We consider a Cartesian coordinate system (x, y, z), with the coordinate z along the axis of the shaft and the points \((x,y) \in \Omega \) on a generic cross section \(\Omega \). We shall not assume the origin of this Cartesian system on the section \(\Omega \) to have a specific property (e.g., the centroid) nor the axis directions themselves (e.g., principal directions of inertia); see Remark 2.1. With this coordinate system in mind, we are interested in modeling the shear stresses \(\varvec{\tau }= [\tau _{xz}, \tau _{yz}]^T\) and the normal (axial) stress \(\sigma _z\) on the shaft’s cross sections created by the assumed torsional loading, the latter caused by the non-uniform warping of the sections.
We shall assume an isotropic linear elastic response for the material, and the standard infinitesimal assumption of small displacements and strains in all our developments in this paper. In this case, the stresses are given by \(\varvec{\tau }= G \varvec{\gamma }\) and \(\sigma _z= E \varepsilon _z\), in terms of the conjugate transverse shear strain \(\varvec{\gamma }= \left[ \gamma _{xz}, \gamma _{yz}\right] ^T\) and axial strain \(\varepsilon _z\). for the shear modulus \(G>0\) and the Young modulus \(E > 0\) (under the usual additional assumption of uniaxial normal stress in the beam/shaft response). An effective elastic modulus E (like the usual plane strain value \(E/(1-\nu ^2)\) for the Poisson’s ratio \(\nu \) of the material) can be considered alternatively, if preferred; see, e.g., [2]. To accommodate general composite sections, we consider moduli distributions of the form
for reference values \({\bar{E}}\) and \({\bar{G}}\), and (non-dimensional) distributions \(n_{_E}(x,y)\) and \(n_{_G}(x,y)\) on the cross section \(\Omega \).
As noted above, we focus our considerations to the effects of the assumed torsional loading on the shaft, namely twisting and warping of the cross sections. Axial or bending effects must not appear. Hence, the distribution of the normal stress \(\sigma _z\) along the axial direction needs to satisfy the relations
where \(x_{_{E}}:= x - {{\bar{x}}}_{_{E}}\) and \(y_{_{E}}:= y - {{\bar{y}}}_{_{E}}\) for the centroid \({{\bar{{\varvec{x}}}}}_{_{E}}= ({{\bar{x}}}_{_{E}},{{\bar{y}}}_{_{E}})\) of the Young’s modulus distribution \(n_{_E}(x,y)\); see Remark 2.1. Clearly, the use of this centroid in the relations (2) is not necessary because of the condition (2)\(_1\), corresponding to a zero resultant force on the cross sections \(\Omega \). Similarly, equations (2)\(_{2,3}\) imply the absence of bending moments on the cross sections.
Remark 2.1
For the sake of generality, we consider an independent distribution of the Young and shear moduli over the cross section \(\Omega \), and avoid the use of a prescribed centroid as the origin of the coordinate system. Even if this option would simplify some of the expressions below, its identification and use complicates, for example, the setting of the problem in the numerical simulations. In general, we have two different centroids, one associated with each distribution. In this way, we have the centroid \({{\bar{{\varvec{x}}}}}_{_{E}}= ({{\bar{x}}}_{_{E}},{{\bar{y}}}_{_{E}})\) with coordinates \({{\bar{x}}}_{_{E}}:= \int \limits _\Omega x\,n_{_E}(x,y)\,\mathrm{d}\Omega /A_{n_{_E}}\) and \({{\bar{y}}}_{_{E}}:= \int \limits _\Omega y\,n_{_E}(x,y)\,\mathrm{d}\Omega /A_{n_{_E}}\), where \(A_{n_{_E}}:= \int \limits _\Omega n_{_E}(x,y)\mathrm{d}\Omega \), for the Young modulus distribution \(n_{_E}(x,y)\). Similarly, we have the centroid \({{\bar{{\varvec{x}}}}}_{_{G}}= ({{\bar{x}}}_{_{G}},{{\bar{y}}}_{_{G}})\) associated with the shear modulus distribution \(n_{_G}(x,y)\) In the next section, we introduce a third point on the cross section \(\Omega \), the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}= ({{\bar{x}}}_{_{T}},{{\bar{y}}}_{_{T}})\) and follow a similar notation \({\varvec{x}}_{_{T}}= (x_{_{T}},y_{_{T}}) := (x-{{\bar{x}}}_{_{T}},y-{{\bar{y}}}_{_{T}})\). \(\square \)
2.2 Torsion with general warping
Following Saint-Venant’s semi-inverse method, we look for a solution of the problem at hand with the assumed three-dimensional displacements
along each of the Cartesian directions described above, in terms of two generalized displacements: the twist rotation \(\phi (z)\) along the shaft and the warping displacement \(w(x,y,z)\), both for the cross section at \(z \in [0,L]\) along the shaft. Physically, the formulas (3)\(_{1,2}\) correspond to an infinitesimal rotation of magnitude \(\phi (z)\) for the section \(\Omega \) at \(z\in [0,L]\) about the shaft’s axis direction at the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}:=({{\bar{x}}}_{_{T}},{{\bar{y}}}_{_{T}})\) (to be identified below), while the section remains rigid with no distortion in its plane. The axial displacement component (3)\(_3\) models a general out-of-plane warping of that section along that same shaft’s axial direction marked as z in our notation. Restraining the warping at \(z=0\) imposes \(w(x,y,0)=0\) for all points \((x,y)\in \Omega \) at the shaft’s root.
The infinitesimal strains associated with the displacement field (3) are
for the transverse shear strains, and
for the axial normal strain, all other components vanishing (this fact corresponding to the assumed no distortion of the section in its plane). Here we have denoted by \(\left( \cdot \right) ^\prime = {\partial (\cdot ) / \partial z}\) (so \(\phi ^\prime := \mathrm{d}\phi /\mathrm{d}z\)), and by \(\nabla (\cdot ) = [\partial (\cdot )/\partial x, \partial (\cdot )/ \partial y]^T\) the plane gradient operator associated with the considered Cartesian coordinates (x, y) in the section’s plane.
For the elastic shaft of interest here, the formulation of the boundary value problem is best obtained by considering the potential energy
for the shaft’s volume \(V = \Omega \times [0,L]\), the stored energy function \(\varPsi (\varepsilon _z,\varvec{\gamma }) = E\varepsilon _z^2/2 + G\varvec{\gamma }\cdot \varvec{\gamma }/2\) for the linear elastic case of interest (with the usual Euclidean inner product and norm \(\varvec{\gamma }\cdot \varvec{\gamma }= \Vert \varvec{\gamma }\Vert ^2\)), and the external potential
if a distributed torque \(t_{ex}(z)\) is applied along the shaft besides the aforementioned tip torque \(T_L\) at the end \(z= L\), otherwise free. We have tacitly assumed that this external loading is conservative for convenience in the presentation here, although this is not required in general treatments of the problem under consideration. As usual, what matters is not so much the actual variational functional (6) but the resulting governing equations below.
In this way, taking the variations of the potential energy (6) for all admissible variations (i.e. \(\delta \phi (0) = 0\) and \(\delta w(x,y,0) = 0\), corresponding to the assumed kinematic boundary condition at the root), we obtain
where we have introduced the resultant internal torque T(z) along the shaft, defined through the “arm function” \({\mathbb {J}}(x,y)\) in (4) around the section’s center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\). The variational equation (8) corresponds to the weak form of the balance of moment around the shaft’s axis, and it results in the strong form equation

after a standard use of integration by parts.
A similar argument reduces equation (9) to
for the boundary \(\partial \Omega \) of the plane domain \(\Omega \) defined by the cross section, with (outward) unit normal \(\varvec{\nu }\). We obtain then the (strong) equations
for all sections in [0, L], together with \(\sigma _z= 0\) at the end with free warping. For the linear elastic material model of interest, problem (12) reduces to

defining the characteristic Neumann type boundary condition on the boundary \(\partial \Omega \) of the cross section \(\Omega \) for the derivative along its normal direction \(\partial w/ \partial \nu := \nabla w\cdot \varvec{\nu }\). Assuming constant moduli \(G={\bar{G}}\) and \(E={\bar{E}}\) for the whole shaft, including over the cross section \(\Omega \) (i.e., assuming \(n_{_G}(x,y) = n_{_E}(x,y) = 1\)), the differential equation (13) reduces to
for the Laplace operator \(\Delta (\cdot ) = \nabla \cdot \nabla (\cdot )\) in the (x, y) plane of the section \(\Omega \). Still, we have a full three-dimensional problem for the warping displacement \(w(x,y,z)\).
Integration of equation (12) over the cross section \(\Omega \) readily leads to the relation
so \(\int \limits _\Omega \sigma _z\mathrm{d}\Omega = 0\) along the shaft, after imposing the boundary condition \(\sigma _z=0\) at the free end \(z=L\). Hence, the condition (2)\(_{1}\), the absence of an axial force in the shaft, is automatically satisfied. In the same way, multiplying equation (12) by \(x_{_{E}}\) and integrating, we obtain
with a similar expression multiplying by \(y_{_{E}}\). The final integrals correspond to the x and y components of the resultant shear force of the shear stresses \(\varvec{\tau }\) on the cross sections \(\Omega \) along the shaft [0, L]. Hence, imposing the conditions (2)\(_{2,3}\) on the distribution of the normal stress \(\sigma _z\) appearing on the cross sections due to torsional warping lead to the vanishing of that resultant force from equilibrium considerations.
Remark 2.2
Note that the above arguments, based on the assumed displacements (3), can be rephrased as finding the best approximate solution to the exact elasticity problem with those displacements, best in the sense of minimizing the (convex) functional (6). The resulting equations (10) and (12) correspond physically to the balance of moments and forces, respectively, along the axial direction z of the shaft. The problem at hand does not impose the other two partial differential equations of three-dimensional elasticity, which would reduce for the assumed non-zero stress components to \(\tau _{xz}^\prime = \tau _{yz}^\prime = 0\). This is a common situation in beam/rod models of structural mechanics and, in our case, can be traced back to the assumption of the cross section being rigid in its plane, an unphysical but a realistic and very useful approximation in typical applications. Similarly, our focus on the torsional response of the shaft, including the warping of the sections, allows us to consider only those equilibrium relations, global equilibrium in the transversal directions being imposed by the integral conditions (2)\(_{2,3}\) on all cross sections. \(\square \)
Remark 2.3
\({\underline{The \ torque \ anomaly}.}\) In fact, the assumed displacements (3) are not an appropriate option in general. We observe that, for a section at z for which \(w(x,y,z) = 0\) for all \((x,y)\in \Omega \), the shear stresses reduce to \(\varvec{\tau }= G\phi ^\prime (z){\mathbb {J}}\). Therefore, the boundary condition (12)\(_2\) of the boundary-value problem in the cross section plane \(\Omega \) implies
for a general section geometry (i.e., non-circular, so \({\mathbb {J}}\cdot \varvec{\nu }\ne 0\) at some point along \(\partial \Omega \)), hence implying \(\varvec{\tau }= 0\) altogether on the whole cross section. In fact, the boundary condition \(w(x,y,0) = 0\) for the restrained support at \(z=0\) is such a case and, as a consequence, no shear stresses would develop there and hence no torque, something physically unfeasible. This situation was denoted in [4] as “the torque anomaly,” although the authors proceeded with the consideration of the resulting three-dimensional equation (14) in the analysis of response of different sections to restrained warping, treating it as one more contradiction in the assumed structural approximation of the three-dimensional problem as noted in the previous remark. This anomaly can be traced back again to the inadequacy of the assumed rigid rotation of the cross section on its plane when the warping is restrained. Circular symmetric sections, or unrestrained warping of general sections (general warping but constant along the shaft’s axis), do not lead to this anomaly. One of the goals of this paper is to evaluate the avoidance of these difficulties by different additional approximations to the three-dimensional displacements (3) in its axial component \(w(x,y,z)\). \(\square \)
2.3 The Saint-Venant solution with unrestrained warping
The free out-of-plane warping of the cross section \(\Omega \) in the absence of normal axial stress \(\sigma _z\) is referred by unrestrained warping. With the considerations above, this situation occurs when \(\varepsilon _z=w^\prime (x,y,z) = 0\), in the isotropic case of interest, that is, for a constant warping displacement along the length of the shaft for all \(z\in [0,L]\). In this case, equation (12) is satisfied with shear stresses constant in z by considering the case \(\phi ^\prime (z)={\overline{\phi ^\prime }}=\) constant \(\forall z \in [0,L]\), that is, involving a constant rate of twist along the shaft. The resulting problem was first considered in this form in the classical work by Saint-Venant in [19].
For the linear elastic case, the warping displacement \(w(x,y,z)\) can then be written as
as a simple calculation shows. The new function \({W}_{\scriptscriptstyle {SV}}(x,y)\) defines the distribution of the warping displacement over the cross section \(\Omega \). This function will appear in all our developments below, and we refer to it as the Saint-Venant warping function. Noting the presence of the (non-dimensional) twist rotation \(\phi (z)\) and its derivative in the axial displacement (18), we observe that, in terms of units, \({W}_{\scriptscriptstyle {SV}}\sim (\hbox {length})^2\), that is, area.
Inserting relation (18) in the governing equation (13), we see that the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) is a solution of the problem

with the characteristic Neumann boundary condition along the boundary \(\partial \Omega \) of the section \(\Omega \). The problem (19) reduces to the standard Laplace equation (\(\Delta {W}_{\scriptscriptstyle {SV}}= 0\) in \(\Omega \)) for the case of constant shear modulus G in \(\Omega \) so \(n_{_G}(x,y)=1\), making the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) an harmonic function in this case; see many standard expositions on the subject, like [13, 14, 24, 29], among many others.
Continuing with the linear elastic response case, with stresses then given by \(\varvec{\tau }= G{\overline{\phi ^\prime }}\left[ \nabla {W}_{\scriptscriptstyle {SV}}+ {\mathbb {J}}\right] \) for a general distribution \(G = {\bar{G}}\,n_{_G}(x,y)\) of the shear modulus, the torque T(z) in (8) reads
for the Saint-Venant torsional constant J of the section \(\Omega \) defined by
for, again, \(x_{_{T}}= x-{{\bar{x}}}_{_{T}}\) and \(y_{_{T}}= y - {{\bar{y}}}_{_{T}}\). The constant torque distribution (20) corresponds to the solution of the differential equation (10) for a zero distributed torque \(t_{ex}(z) = 0\), thus leading to \(T(z) = T_L\), the torque applied at the shaft’s free end, identifying with this semi-inverse approach the Saint-Venant problem in torsion. Expression (21) for the Saint-Venant torsional constant J of the cross section \(\Omega \) in terms of the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) can be found in [14, 24], among others, for the case of constant elastic modulus.
Remark 2.4
We note the orthogonality relation
after the use of the divergence theorem and the governing equations (13) defining the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\). Then, a straightforward calculation shows that
giving an alternative expression for the Saint-Venant torsional constant J, an expression that explicitly shows \(J > 0\). Also, arguments similar to the ones behind the relation (16) show that
for the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) (nothing else but the zero resultant of the Saint-Venant stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\)). Combining all these results, we also have the alternative expression
recovering the standard expression (the integral in this expression) for the Saint-Venant torsional constant J when the shear modulus centroid is chosen as origin of the coordinate system (i.e., when \({{\bar{{\varvec{x}}}}}_{_{G}}= 0\)); see [24, p. 112]. This torsional constant seems to be dependent on the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\) (explicitly in this equation and, in principle, implicitly through the function \({W}_{\scriptscriptstyle {SV}}(x,y)\), solution of the boundary-value problem (19) involving this point in the “arm function” \({\mathbb {J}}\)), but this is not the case as shown next. \(\square \)
2.4 The center of twist
The above developments do not identify the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}= ({{\bar{x}}}_{_{T}},{{\bar{y}}}_{_{T}})\). In fact, such a point is not determined in the Saint-Venant’s torsion problem with unrestrained warping; see [24, p. 113]. As noted in this reference, different centers of twist lead to solutions differing by a rigid body displacement. Hence, the center of twist in actual realizations of the unrestrained Saint-Venant problem will be determined on how the shaft is supported at its ends; see also [13] in this respect.
Indeed, if we consider a different center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}^*=({{\bar{x}}}_{_{T}}^*,{{\bar{y}}}_{_{T}}^*)\), a straightforward calculation shows that
for the solutions \({W}_{\scriptscriptstyle {SV}}(x,y)\) and \({W}_{\scriptscriptstyle {SV}}^{*}(x,y)\) of the linear boundary-value problem (19) with respect to \({{\bar{{\varvec{x}}}}}_{_{T}}\) and \({{\bar{{\varvec{x}}}}}_{_{T}}^*\), respectively. In equation (26), we have used the shifted coordinates \((x_{_{E}},y_{_{E}}) = (x-{{\bar{x}}}_{_{E}},y-{{\bar{y}}}_{_{E}})\) for later convenience, since the terms involving the centroid \(({{\bar{x}}}_{_{E}},{{\bar{y}}}_{_{E}})\) of the Young modulus distribution \(n_{_E}(x,y)\) (or any other point for that matter) could have been lumped in the constant C in (26). This additional constant is a consequence of the arbitrariness of an additional constant into these functions given the presence of only their derivatives in the problem (19). This constant and the two additional linear terms in (26) are nothing else but the additional superposed rigid body displacement noted above.
The stresses arising from both functions coincide (that is, \(\varvec{\tau }= G{\overline{\phi ^\prime }}\big (\nabla {W}_{\scriptscriptstyle {SV}}+ {\mathbb {J}}\big ) =G{\overline{\phi ^\prime }}\big (\nabla {W}_{\scriptscriptstyle {SV}}^{*}+ {\mathbb {J}}^{*}\big )\)), and so is the Saint-Venant torsional constant \(J =J^*\), as a simple calculation shows using the expression (25) with the relation (26). Hence, the Saint-Venant torsion solution is independent of the center of twist, even for sections with general distribution of the shear modulus, a fact not often pointed out in the vast literature on the subject.
The arbitrariness of the constant C and the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}= ({{\bar{x}}}_{_{T}},{{\bar{y}}}_{_{T}})\) given by (26) (that is, three arbitrary values total) allows us to impose the three conditions
and
on the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\). Indeed, these conditions are satisfied by choosing the constant in (26) as \(C = -Q^*/ A_{n_{_E}}\) for \(Q^*:= \int \limits _\Omega n_{_E}(x,y)~{W}_{\scriptscriptstyle {SV}}^{*}(x,y)~\mathrm{d}\Omega \), and the center of twist given by
with
for the solution \({W}_{\scriptscriptstyle {SV}}^{*}(x,y)\) of the problem (19) with an arbitrary point \({{\bar{{\varvec{x}}}}}_{_{T}}^*\).
Expressions like (29) can be found in, e.g., [13, p. 120], and [14, p. 256], for the case of an homogeneous section. In the general case considered in this paper, the (so-far arbitrary) use of the distribution \(n_{_E}(x,y)\) for the Young modulus in (27) and (28) is required in the developments to follow for the case of restrained warping. The specific point identified by the relations (29) will be the center of twist in that case, as elaborated in the developments below. This point also corresponds to the shear center of the cross section \(\Omega \) as proposed by Trefftz in [30], a fact originally pointed out by [33]; see, e.g., [14, p. 254], for a detailed discussion (here we have presented it in a general non-centroidal coordinate system for inhomogeneous cross sections).
3 The Timoshenko–Wagner–Kappus–Vlasov (TWKV) approximation of restrained warping
The general treatment presented in Sect. 2 leads to the three-dimensional partial differential equation (13) for the three-dimensional function \(w(x,y,z)\). The goal in any structural mechanics treatment of the shaft of interest is to reduce the problem to an ordinary differential equation along its length \(z\in [0,L]\), while still accounting for its torsional/warping response at the section level \((x,y) \in \Omega \). In fact, this has been accomplished in the Saint-Venant solution presented in Sect. 2.3 since the warping displacement naturally reduces to \(w(x,y,z) = {\overline{\phi ^\prime }}~{W}_{\scriptscriptstyle {SV}}(x,y)\), for a constant rate of twist \({\overline{\phi ^\prime }}\) and, hence, only requiring the section function \({W}_{\scriptscriptstyle {SV}}(x,y)\). To accomplish this reduction in the general case of non-uniform rate of twist, the original TWKV formulation proceeds as follows.
3.1 The governing equations of the TWKV formulation
The older and more direct approximation for the non-constant warping along the shaft is to consider the axial displacement

that is, the Saint-Venant solution (18) with a general non-constant rate of twist \(\phi ^\prime (z)\). The form of the distribution of the axial displacement on a given section is assumed fixed and given by the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\), the solution problem (19). We choose the particular function \({W}_{\scriptscriptstyle {SV}}(x,y)\) satisfying the conditions (27) and (28), fixing then the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\) as discussed in Sect. 2.4. Hence, together with the lateral displacements (3)\(_{1,2}\) we have a single degree of freedom field, namely, the twist rotation \(\phi (z)\). As noted in the introduction, the resulting formulation was originally considered by [32] and [11] extending early considerations by Timoshenko in [25,26,27] and later considered in [31] for thin-walled sections, although starting from an alternative but equivalent assumption for these cross sections; see Sect. 1. The particular form (31) of the warping displacement corresponds to the Wagner assumption indicated in that section, as it can be found referred to in [2, 8, 9], among others.
The potential energy in this case reads then
where now
The potential of the external loading \(\Pi _{ext}(\phi )\) is still given by (7). Note that the formulation considered here, given by the warping displacement (31), assumes a fixed distribution of that warping displacement on any given cross section \(\Omega \), a distribution given by the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) simply modulated in amplitude by the derivative of the twist rotation \(\phi (z)\), the only generalized displacement in the theory at hand.
Taking the variation of the functional (32) leads to

for the Saint-Venant torque
and the so-called bimoment
following [31]; see Sect. 3.2 for an additional discussion of the terminology used here. In equation (35), different than the developments in the previous section, we have denoted by \(\varvec{\tau }_{\scriptscriptstyle {SV}}= \partial \varPsi / \partial \varvec{\gamma }= G\,\varvec{\gamma }\) the stresses arising from the strain energy of the material, given in terms of the shear strain \(\varvec{\gamma }\) in (33)\(_2\), and the corresponding resultant torque \(T_{\scriptscriptstyle SV}(z)\) (instead of simply \(\varvec{\tau }\) and T(z)), since additional shear stresses and torque are identified below in this formulation. Note that the balance of moments about the shaft’s axis (balance of torque) (34) involves both the torque \(T_{\scriptscriptstyle SV}(z)\) and the bimoment \(B_{\scriptscriptstyle W}(z)\), through different derivatives of the variation of the twist rotation \(\delta \phi (z)\).
For the linear elastic material of interest here, we have
which are in equilibrium by themselves (that is, \(\nabla \cdot \varvec{\tau }_{\scriptscriptstyle {SV}}=0\) in \(\Omega \) and \(\varvec{\tau }_{\scriptscriptstyle {SV}}\cdot \varvec{\nu }=0\) along \(\partial \Omega \)) by the equations (19) defining the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\). We also have
the first equality following from the divergence theorem and the equilibrium relations for \(\varvec{\tau }_{\scriptscriptstyle {SV}}\), with the appearance of the Saint-Venant torsional constant J following easily from the first expression in (23) in combination of those stresses. Hence, both the stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) and their resultant torque \(T_{\scriptscriptstyle SV}\) on a cross section \(\Omega \) follow the same expressions as for the Saint-Venant solution, even with a general (non-constant) rate of twist \(\phi ^\prime (z)\). In fact, combining equations (37) and (38) we obtain the alternative formula

showing more explicitly the relation between these shear stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) and its resultant torque \(T_{\scriptscriptstyle SV}\).
Similarly, from equation (36) combined with the stress \(\sigma _z= E\varepsilon _z\) for the axial strain (33)\(_1\), we obtain
for the bimoment, where we have introduced the parameter
another torsional constant of the section \(\Omega \). We note that, by definition, \(I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}>0\) and the “inertia nature” of its expression if \({W}_{\scriptscriptstyle {SV}}(x,y)\) is understood as a coordinate on the section \(\Omega \), the sectorial coordinate for thin-walled sections. Vlasov in [31] calls this section constant the “sectorial moment of inertia” for thin-walled sections, while the technical literature refers to it as the “warping constant” and it is often denoted by \(C_{\scriptscriptstyle W}\); see, e.g., [20, 21], among others.
For the fixed support at \(z=0\) with no rotation \(\phi (0)=0\), the restraining of the warping is easily enforced by imposing in (31) \(\phi ^\prime (0) = 0\). The corresponding admissible variations in (34) satisfy then \(\delta \phi (0) = 0\) and \(\delta \phi ^\prime (0) =0\). Integrating by parts twice in (34) results in the strong form of the governing equation
that is, the same equation as (10) (physically, the balance of moments about the axis of the shaft), but now with the internal (total) torque T(z) given by
the bishear, often called the warping torque too; see Sect. 3.2. In addition, we obtain the natural boundary condition \(B_{\scriptscriptstyle W}(L) = 0\) at the end \(z=L\) with no restraining of the warping and, similarly, with a reacting bimoment \(B_{\scriptscriptstyle W}(0)\) at the shaft’s root \(z=0\) where the warping is restrained.
Combining equations (43) with (40), we obtain
for the linear elastic case of interest, the latter expression assuming \({\bar{E}}I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\) constant in z. The differential equation (42) reads then

a fourth-order ordinary differential equation for the twist rotation distribution \(\phi (z)\), with the boundary conditions
or, alternatively, \(\phi (L) = \phi _L\) instead of the latter condition if the shaft is loaded by an imposed twist rotation \(\phi _L\) at that end. The condition (46)\(_3\) is given by the free warping at the tip of the shaft, corresponding to zero normal strain/stress by (33)\(_1\) and, consequently, to \(B_{\scriptscriptstyle W}(L) = 0\) by (36).
Remark 3.1
The introduction of the assumed displacements (3) with the axial displacement given by (31) for a fixed spatial distribution on \(\Omega \) (specifically, the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) for the assumed particular formulation) reduces the problem from a problem in three-dimensional elasticity to an structural mechanics theory for the shaft of interest, the latter in terms of the twist rotation field \(\phi (z)\) in this case. All the arguments in the above developments, and the ones below, involving particular stress distributions and other considerations at the section level \(\Omega \) must be understood as arguments to justify the connection of those two treatments, the approximation in the structural theory. In fact, the structural model can be simply characterized by the potential energy
in terms of the section constants J and \(I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\) for the linear elastic case considered here. The equality of this functional with the original (three-dimensional) functional (32) follows easily. Similarly, the governing weak equation (34), for the section resultant torques defined by (35) and (36), follows directly from the (one-dimensional) potential energy (47), and so is equation (45). \(\square \)
Remark 3.2
The functional (47) also indicates when to expect the effects of restrained warping to be less dominant, the second term in this expression, with the response of the shaft reducing to Saint-Venant torsion, the first term, in the limit. Indeed, factoring \(G\,J\) in (47), we can easily see that for long shafts, namely for
the underlying Saint-Venant torsion will dominate in the overall (global) structural response of the shaft. This also indicates that, in general, the effects of restrained warping are local in nature, as measured by the characteristic length \(L_T^{(TWKV)}\). However, note that general shafts, even such as (48), may require special practical considerations locally near restrained sections (by supports, stiffeners, or other conditions), hence the motivation behind this work in modeling its effects correctly. In the definition (48), we have introduced the trivial parameter \(\alpha ^{(TWKV)}= 1\) for later comparisons with other formulations. Similarly, for later use, the governing equation for the case shown in Fig. 1 (i.e., prismatic shaft with non-varying section constants, an imposed torque \(T_L\) at its end, and no distributed loading \(t_{ex}(z) = 0\)) can be reduced to the equation
and the non-dimensional derivatives \((\cdot )^{{\widetilde{\prime }}} = d(\cdot )/d\widetilde{z}\) with \(\widetilde{z}= z/L\). The limit marked by the condition (48), recovering Saint-Venant torsion, becomes also apparent in this expression, as it is the flexibility of the shaft \(f_{T}^{(SV)}\) given by this basic torsion solution. \(\square \)
3.2 The bimoment, the bishear, and the associated stresses in the TWKV formulation
As discussed in detail in [34] or [13], the bimoment \(B_{\scriptscriptstyle W}(z)\) can be understood physically as a couple of balanced moments acting on the cross section \(\Omega \), corresponding to the statically balanced distribution of the normal stress \(\sigma _z= E \phi ^{\prime \prime }(z){W}_{\scriptscriptstyle {SV}}(x,y)\), that is, with zero resultant force and moments by relations (2) after using the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) in the assumed warping displacement (31) normalized with the conditions (27) and (28). We refer also to [6] for a mathematical, more abstract, interpretation of the bimoment and bishear.
The typical illustration of this bimoment is an open thin-walled section, like a I-beam or channel section, warping with a pair of same but opposite moments bending the flanges. Hence, the appearance of the associated (same and opposite) shear forces acting along the flanges and creating a torque on the whole section, the bishear \(T_{\scriptscriptstyle W}(z)\); see, e.g., [13, p. 226], for details, including an illustrative figure for a channel section. In fact, this was how the incorporation of the effects of restrained warping in torsion was accomplished originally; see [26, 27]. This is why some authors have traditionally referred to the bishear \(T_{\scriptscriptstyle W}(z)\) as the flexural torque, as opposed to the twisting torque \(T_{\scriptscriptstyle SV}(z)\); see [31, 34]. Some other authors call \(T_{\scriptscriptstyle W}(z)\) the warping shear [13], the warping torque [8], or even the Vlasov torque in this last reference too, referring implicitly to restrained warping since the twisting torque \(T_{\scriptscriptstyle SV}(z)\) also involves (uniform) warping. We shall refer to \(T_{\scriptscriptstyle SV}(z)\) and \(T_{\scriptscriptstyle W}(z)\) as the Saint-Venant torque and the bishear, respectively. Their sum, the total internal torque \(T(z)\), is the one satisfying the balance (of moments) equation (42). The term bishear has been used in [23], motivated by the “transverse shear-type” role that \(T_{\scriptscriptstyle W}(z)\) plays for the bimoment \(B_{\scriptscriptstyle W}(z)\) in equation (43)\(_2\).
The assumed three-dimensional warping displacement (31) does not satisfy equations (13), so it is indeed an approximation of the problem described in Sect. 2.2 or, better, an alternative treatment of the torsional problem with restrained warping. It may appear that the torque anomaly described in Remark 2.3 still applies to this approximation since restraining the warping displacement at the support \(z=0\) also implies \(\phi ^\prime (0) = 0\) and, hence, zero shear strains \(\varvec{\gamma }\) by (33)\(_2\), zero stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) by (37), and zero resulting Saint-Venant torque \(T_{\scriptscriptstyle SV}(0)\) by (38). In fact, such observation can be found in [17], motivating somehow the alternative approximation discussed in Sect. 4. However, this torque is only part of the total torque \(T(0)\) appearing at that support, balancing by (42) the applied torsional loading on the shaft. In other words, the appearance of the bishear \(T_{\scriptscriptstyle W}(z)\) resolves the anomaly (at least partially since, again, the Saint-Venant part of the stress and torque still vanishes).
Still, the above developments do not identify a particular shear stress distribution due to this torque on the cross section \(\Omega \), say \(\varvec{\tau }_{\scriptscriptstyle {W}}\), but the illustrative case presented in the previous comments clearly points out to the existence of such stresses associated with the bending caused by the bimoment \(B_{\scriptscriptstyle W}(z)\) on parts of the section (e.g the flanges of an I-beam). We can proceed as follows to identify these stresses.
First, we note that the normal stress \(\sigma _z= E\varepsilon _z\) on the cross section can be written as

after combining (33)\(_1\) and (40). By equilibrium (i.e by equation (12)), these normal stresses identify the shear stresses \(\varvec{\tau }_{\scriptscriptstyle {W}}\) through the equation
By inspection, we can write these stresses as

for the function \({W}_{{\sigma }}(x,y)\) solution of the boundary-value problem

where the Saint-Venant \({W}_{\scriptscriptstyle {SV}}(x,y)\) enters this problem as data defining the new function \({W}_{{\sigma }}(x,y)\). The claim that the shear stresses (52) satisfy the equilibrium equations (51) for the normal stress \(\sigma _z\) in (50) follows easily by simply inserting them in those equations after noting that \(T_{\scriptscriptstyle W}(z) = - B_{\scriptscriptstyle W}^\prime (z)\) by (43). Note that we need here to assume that indeed the warping constant \(I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\) does not depend on z as in the prismatic shafts of interest here.
Up to an irrelevant constant the function \({W}_{{\sigma }}(x,y)\), the well-posedness of the Neumann problem (53) is assured after noting the compatibility condition
since the condition (27) is imposed on the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\). We fix the arbitrary constant in \({W}_{{\sigma }}(x,y)\) by requiring
following the same condition (27) for the original Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\).
The warping stresses \(\varvec{\tau }_{\scriptscriptstyle {W}}\), and their distribution function, have been studied in [8, 14, 34], being called sometimes as the complementary in [31] or secondary in [12, 13, 31] shear stresses. Their derivation from purely static (equilibrium) considerations like equation (51) and not from a material constitutive relation with associated strains clearly points their origin to the imposition of a kinematic constraint. This setting will become apparent in the alternative formulation considered in the next section.
The resultant torque of the stresses \(\varvec{\tau }_{\scriptscriptstyle {W}}\) in (52) is the bishear \(T_{\scriptscriptstyle W}\). Indeed, noting the result
after a repeated use of the divergence theorem, we have
as claimed. The total shear stress on the cross section \(\Omega \) is then given by
in equilibrium with the normal stress \(\sigma _z\) in (50) (that is, they satisfy (12)), and with the resultant torque \(T(z) = \int \limits _\Omega \varvec{\tau }\cdot {\mathbb {J}}\,\mathrm{d}\Omega = T_{\scriptscriptstyle SV}(z) + T_{\scriptscriptstyle W}(z)\) given by (44)\(_1\) for each cross section \(\Omega \) along \(z\in [0,L]\).
Furthermore, using the condition (28)\(_1\) on the Saint-Venant function \({W}_{\scriptscriptstyle {SV}}(x,y)\), we have
with a similar expression for the y-derivative, thus concluding
This result, together with the relation (24) for the Saint-Venant part \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) of the total stress \(\varvec{\tau }\) in (58), directly shows the vanishing of the total resultant tangential force \(\int \limits _\Omega \varvec{\tau }\mathrm{d}\Omega = 0\), also implied by the absence of bending contribution of the normal stresses \(\sigma _z\).
All these arguments indicate that, as noted above, even if the Saint-Venant component part of the stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) vanishes at a particular cross section because of the restraining of the warping (e.g., a fully fixed support), forcing the vanishing of the rate of twist too, the warping stress component \(\varvec{\tau }_{\scriptscriptstyle {W}}\) appears if needed from equilibrium considerations. The same arguments apply to their respective resultant torques, the Saint-Venant torque \(T_{\scriptscriptstyle SV}(z)\) and bishear \(T_{\scriptscriptstyle W}(z)\), with the former vanishing entirely in such a fully fixed cross section so the bishear is only determined by equilibrium considerations. The torque anomaly discussed in Remark 2.3 for the full three-dimensional treatment may be avoided then by the presence of the warping stress component \(\varvec{\tau }_{\scriptscriptstyle {W}}\) and the corresponding bishear \(T_{\scriptscriptstyle W}(z)\), but this constrained setting with a predetermined torque component may distort the distribution of this stress resultant and related bimoment \(B_{\scriptscriptstyle W}(z)\) along the shaft. It is for this reason that we think of the current TWKV formulation as resolving the original torque anomaly only partially, and refer to the new (constrained) situation characterized by a necessary vanishing of the Saint-Venant component of the shear stress and torque still as the torque anomaly. It has the same origin as in the full three-dimensional setting, namely, the direct control of the warping by the twisting (or rather, its rate), a kinematic constraint underlying the TWKV formulation identified below. As shown in the developments to follow, the other formulation considered in this work avoids the torque anomaly in its entirety by relaxing this constraint.
In this respect, it is worth emphasizing that, in contrast with the original Saint-Venant shear stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) produced by the twisting of the shaft (if not fully restrained by the warping) and obtained through the associated shear strains (33)\(_2\) by the constitutive relation of the material, the warping stresses \(\varvec{\tau }_{\scriptscriptstyle {W}}\) appear by equilibrium from the distribution of the normal stress \(\sigma _z\) distribution, with no direct use of the constitutive relation of the material. Note that the expression (52) depends at most on the non-dimensional distributions \(n_{_E}(x,y)\) and \(n_{_G}(x,y)\) of the material moduli. This situation points again to the origin of these stresses as coming from a kinematic constraint in the assumed displacement (31), a constraint fully characterized in the following section.
Remark 3.3
For later use, we also note that
with \(\varvec{\tau }_{\scriptscriptstyle {SV}}= \varvec{\tau }-\varvec{\tau }_{\scriptscriptstyle {W}}\) dropping after using the orthogonality relation (22). The identification of the last integral in (61) with \(\left( -I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\right) \) follows again from a straightforward use of the divergence theorem given the defining problems for both warping functions. Hence, we obtain the relation
an alternative expression for the bishear \(T_{\scriptscriptstyle W}(z)\). We note the consistency of this relation with the general expression
employed above for the total torque \(T(z)\) as the sum of the Saint-Venant \(T_{\scriptscriptstyle SV}(z)\) and warping (bishear) \(T_{\scriptscriptstyle W}(z)\) torques. \(\square \)
Remark 3.4
The conditions (2) are shown in Sect. 2.4 to determine a particular center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\) for the Saint-Venant torsional problem with unrestrained warping (\(\sigma _z=0\)), undefined otherwise and with an irrelevant definition in that problem. The need to impose those conditions, physical balance equations in the general problem involving restrained warping implies that the center of twist is precisely determined in this problem. This situation effectively decouples the torsional problem considered in this paper with the bending/transverse shear problem of the shaft, not considered here. It is then of no surprise that this particular center of twist, defined by the formulas (29), coincides with the shear center as defined by Trefftz in [30], who used this decoupling as the defining condition for the shear center. \(\square \)
4 The Reissner–Benscoter–Vlasov (RBV) approximation of restrained warping
As indicated in the previous section, the derivation of the restrained warping part \(\varvec{\tau }_{\scriptscriptstyle {W}}\) of the total shear stresses \(\varvec{\tau }\) on a cross section from purely static considerations of equilibrium (not involving any strains nor the material parameters per se) points to the presence of a constraint in the original TWKV formulation. Actually, this suspicion is corroborated by the governing differential equation (45) being of high order (fourth order to be precise), a usual feature of mechanical formulations were a hidden constraint is involved. In fact, the original motivation presented by Timoshenko [28], based on the aforementioned bending of the flanges in an I-beam, considers the (high-order) Euler–Bernoulli beam theory, with no transverse shear strain along those flanges when bending due to the restrained warping of the cross sections. Revisiting the original assumption in this formulation, namely equation (31) where the warping displacement is assumed proportional to the rate of twist \(\phi ^\prime (z)\), identifies the constraint connecting the amplitude of this displacement and the twisting of the shaft.
In a similar way, the equivalent Vlasov assumption considers directly the vanishing of the longitudinal shear strain along the middle line of open thin-walled cross sections. As noted above, this leads directly to the Wagner assumption (31), thus constraining the warping to the rate of twist of the section, besides the approximation of the Saint-Venant warping function with the sectorial coordinate along that middle lime for those cross sections.
4.1 The governing equations of the RBV formulation
With this insight, we can see that the motivation behind the alternative starting assumption

for a general function \(\lambda (z)\), thus considering a formulation based on two generalized displacements: the warping parameter \(\lambda (z)\) and the twist rotation \(\phi (z)\). As in the previous section, the distribution of the warping displacements on a cross section \(\Omega \) is given by the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\), defined by the boundary-value problem (19) on \(\Omega \) and the additional normalizing conditions (27) and (28), the latter with the proper choice of the center of twist. It is interesting to observe that
after using the definition (41) of the warping constant \(I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\). Equation (65) identifies the parameter \(\lambda (z)\) with a weighted average over the cross section of the warping displacement along the shaft.
The consideration of the independently scaled warping displacement (64) was originally considered by Reissner in [17] for a general section (in fact, without elaboration), by Benscoter in [2] for hollow multi-cell sections, and independently by Vlasov in [31] for general solid sections, the latter after considering the original TWKV formulation for open thin-walled sections. We refer to the final formulation as the Reissner–Benscoter–Vlasov or RBV formulation in short.
Note that the warping of all the sections in the shaft are assumed to be proportional to each other, of the same shape or form, only differing by their amplitude as defined by the unknown function \(\lambda (z)\). The use of alternative distributions, still constant along the shaft but based on other functions \(W(x,y)\), usually approximations of \({W}_{\scriptscriptstyle {SV}}(x,y)\), has been considered in [31].
Given the discussion above, we expect that the hidden constraint in the original TWKV formulation presented in the previous section is
This relation is clearly kinematic in nature, involving two kinematic fields: the warping amplitude \(\lambda (z)\) and the rate of twist \(\phi ^\prime (z)\). Given this, we refer to (66) as the warping-twist constraint, by which the twisting controls directly the warping. It is of interest then under what conditions this constraint is physically appropriate, motivating or not the use of this formulation in front of the original TWKV treatment. One clear motivation for considering this alternative treatment of the warping is the avoidance of a higher-order problem for the twist rotation \(\phi (z)\), as we will see below, at the price of solving for the additional degree of freedom \(\lambda (z)\).
The formulation based on the assumed axial displacement (64) can be derived in the same way as presented in the previous sections. We start then with the identification of the associated strains, namely
for the axial normal and transverse shear strains, respectively. The potential energy now reads
a two-field formulation in this case. For the representative problem of interest here, the essential boundary conditions on the generalized displacement fields read \(\phi (0)=0\) for the fixed rotation and \( \lambda (0) = 0\) for the restrained warping, at the support \(z=0\). The corresponding kinematically admissible variations \(\delta \phi (z)\) and \(\delta \lambda (z)\) are to satisfy then the same homogeneous boundary conditions. Crucially, restraining the warping involves the independent field \(\lambda (z)\) rather than the rate of twist \(\phi ^\prime (0)\) as the TWKV formulation does, with this rate left free in the current RBV formulation.
Taking variations of the functional (68), we obtain
after decomposing the integrations over the cross sections \(\Omega \) and along the shaft \(z\in [0,L]\) so, again,
and
the total internal torque, bishear and bimoment, respectively, with the stresses given now by
for the linear elastic case of interest. We then have the stresses in terms of the two unknown fields \(\phi (z)\) and \(\lambda (z)\), and now their first derivative only. We have reverted to our original consideration \(\varvec{\tau }= {\partial \varPsi /\partial \varvec{\gamma }}\) for the total shear stress \(\varvec{\tau }\) and its resultant torque T(z), since no additional stress nor torque appear explicitly in the development of this formulation, only separate components of these two quantities; see Sect. 4.2 for a connection with the developments in the previous section, including the separate shear stresses and torque identified in that case.
The strong form of the governing equations associated with (69) and (70) reads then
for all \(z\in [0,L]\), with the corresponding natural boundary conditions \(T(L)= T_L\) and \(B_{\scriptscriptstyle W}(L) = 0\) for the problem of interest here. As we would expect the same equilibrium equations as in the previous formulation apply, noting the role of T(z) in (71) as the total internal torque. Equation (74)\(_2\) corresponds to the balance of warping stress resultants, between the bishear \(T_{\scriptscriptstyle W}(z)\) and bimoment \(B_{\scriptscriptstyle W}(z)\).
To write the governing equations (74) in terms of the generalized displacements, it proves convenient to introduce the section constant
which we can also write as
an equality easily obtained from the defining problem (19) for \({W}_{\scriptscriptstyle {SV}}(x,y)\) in combination with the divergence theorem. With this notation at hand, inserting the stresses (73) in the relations (71), we obtain
for the bimoment \(B_{\scriptscriptstyle W}(z)\), and
for the total torque T(z) and the bishear \(T_{\scriptscriptstyle W}(z)\), where we have introduced the quantity \(\varpi (z) := \phi ^\prime (z) - \lambda (z)\), which we refer to as the “warping lag.” Clearly, \(\varpi (z)\) measures the extent that the warping-twist constraint (66) is not satisfied. We note the direct relation of this “generalized strain” with the bishear \(T_{\scriptscriptstyle W}(z)\) through the new torsional constant \(I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}\) in (78)\(_2\).
Inserting the relations (77)–(78) into the equations (74), we obtain the system of ordinary differential equations

a second-order system in terms of the structural fields \(\phi (z)\) and \(\lambda (z)\). The weak equations (69)–(70) in combination with the constitutive relations (77)–(78) are to be favored for a general numerical treatment of the problem at hand, especially for varying section parameters J, \(I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\) and \(I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}\) along the shaft’s length if such extension is considered.
As opposed to the fourth-order differential equation (45) on the twist rotation \(\phi (z)\) governing the original TWKV formulation, the current formulation results in the second-order system (79), but with the added field \(\lambda (z)\). We investigate next the connection of the two formulations.
4.2 The TWKV formulation as the constrained limit of the RBV formulation.
The structural formulation considered in this section is characterized by the potential energy (68) reduced to the (one-dimensional) axis to the shaft. In fact, the orthogonality of the two components of the shear strain (67)
given by relation (22) allows to write the functional (68) as
as a straightforward calculation shows, fully defined along the shaft’s length [0, L] with the proper use of the different torsional section constants. The weak equations (69) and (70), with the constitutive relations (71) and (72) for the different resultant torques, are easily obtained by considering the variations of the functional (81).
Comparing this functional with the potential energy (47) for the original TWKV formulation, based on the assumed axial displacement (31), we clearly see that the current formulation corresponds to a penalty treatment of the warping-twist constraint \(\varpi (z) = \lambda (z) - \phi ^\prime (z) = 0\) characteristic of that original formulation. In particular, factoring \({\bar{G}}J\) in (81), we readily identify the (penalty) parameter
recovering the original formulation when \(\kappa _t^{(RBV)}\rightarrow \infty \).
The parameter \(\kappa _t^{(RBV)}\) is clearly a property of the geometry of the cross section. Note that dimensionally
for a characteristic length of the cross section (say its height h), as a simple inspection of the definitions of these constants show. Thus, the TWKV is recovered in the limit \(\kappa _t^{(RBV)}\rightarrow \infty \), regardless of the length of the shaft.
We also observe that, as occurred for the TWKV formulation, the total torque (71)\(_1\) for this RBV formulation can also be written as
that is, following the same relation with the rate of twist \(\phi ^\prime (z)\) as in that formulation, but with the bishear \(T_{\scriptscriptstyle W}(z)\) given now by (71)\(_1\). Remember that the bishear had no constitutive relation in the TWKV formulation, being defined entirely by equilibrium considerations, as shown in Sect. 3.2. On the other hand, the bishear in the current formulation is given by the constitute relation (78), with
as \(\varpi \rightarrow 0\) for the limit case \(\kappa _t^{(RBV)}= I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}/J\rightarrow \infty \). Note that the section constant \(I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}\) never appeared in the original TWKV formulation. The classical role of the bishear \(T_{\scriptscriptstyle W}(z)\) as the Lagrange multiplier enforcing the warping-twist constraint \(\varpi (z) = 0\) in that original formulation becomes clear. In a related matter, note the appearance of the warping shear strain \(\varvec{\gamma }_{_{\scriptscriptstyle {W}}}\) in (80), a new component not present in the original TWKV formulation of the previous section.
Remark 4.1
As occurred with the TWKV formulation and given the locality of the effects of restrained warping observed in Remark 3.2, the current RBV formulation also predicts that the structural response of long shafts will be dominated by Saint-Venant torsion at the global level and, in this way, also recover the TWKV formulation in that limit. To quantify this limiting process, we consider again the case of a prismatic shaft with a single applied torque \(T_L\) considered in that remark, that is, the shaft depicted in Fig. 1. This allows to reduce the governing system of equations (79) to a single (high-order) equation, exactly like (49) but with the characteristic length \(L_T\) given now by
after eliminating the field \(\lambda (z)\) with some straightforward algebraic manipulations in this particular model problem; further details are omitted. Hence, long shafts in the sense of being dominated at the global structural level by Saint-Venant torsion (i.e., with flexibility close to the value \(f_{T}^{(SV)}\) in (49)) correspond to \(L \gg L_T^{(RBV)}\). The result (86) agrees with our previous considerations, namely that the TWKV formulation is recovered from the RBV formulation in the limit \(\kappa _t^{(RBV)}\rightarrow \infty \) and, in fact, tells us that
for real shafts not in that limit. Interestingly, this inequality is also controlled by the same parameter \(\kappa _t^{(RBV)}\) by (86), characterizing the two different limit processes that recover the TWKV formulation form the RBV formulation. In the process involving long shafts as marked by these characteristic lengths (or, more trivially, a negligible warping constant in (86)), both formulations recover effectively Saint-Venant torsion, involving no bishear nor any bimoment. \(\square \)
4.3 The stresses in the RBV formulation
The developments of the previous section show the clear connection of the TWKV and RBV formulations at the global structural level. However, the two formulations differ significantly at the local section level as it refers to the stresses involved in their development.
The normal stresses \(\sigma _z\) over the cross sections for the RBV formulation are obtained by combining equations (67)\(_1\) and (77) as

thus still possessing the same relation (50) for the TWKV formulation when written in terms of the bimoment \(B_{\scriptscriptstyle W}(z)\). Note, though, that each formulation will produce, in general, different diagrams of the bimoment \(B_{\scriptscriptstyle W}(z)\), and the different parts of the torque (the bishear \(T_{\scriptscriptstyle W}(z)\), in particular), along the shaft in a given problem.
Even then, the distribution of the shear stresses over a cross section predicted by the RBV formulation differs considerably to the one given by the TWKV formulation. The decomposition (84) for the total torque in the RBV formulation does translate in a similar decomposition for the total stresses (73), that is,
in terms of the warping lag \(\varpi (z)\). The calculations behind the relations (78) identify the resultant torque of these two stresses as \(T_{\scriptscriptstyle SV}(z)\) and \(T_{\scriptscriptstyle W}(z)\), respectively. In this respect, note that
as a straightforward calculation shows. An alternative expression of the shear stresses (89) is then given by
for the Saint-Venant component, like equation (39) for the TWKV formulation, and

after using the definition of each part of the torque in equation (78).
These stresses do resemble the stresses (58) for the TWKV formulation, but with a clear difference for the warping stress \(\varvec{\tau }_{\scriptscriptstyle {W}}\). The distribution of this stress on a typical section is given now by \(\nabla {W}_{\scriptscriptstyle {SV}}/I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}\) while it is given by \(\nabla {W}_{{\sigma }}/I_{\scriptscriptstyle {W}_{\scriptscriptstyle {SV}}}\) for the original TWKV formulation.
The main consequence of this result is that, in general, the stresses in the RBV formulation will not be in equilibrium, that is, they will not satisfy the relations (12), as they did in the TWKV formulation. A simple calculation shows that
which will not vanish unless \(T_{\scriptscriptstyle W}(z) = 0\) in general, that is, \(\varpi (z) = 0\). It is interesting to note that the non-equilibrium stress component \(\varvec{\tau }^{\scriptscriptstyle {noeq}}_{\scriptscriptstyle {W}}\) defined in this expression satisfies the relation
that is, it has a zero resultant torque. However, after using the relations (24) and (60), we have
in general, showing again the lack of equilibrium of the stresses underlying the RBV formulation. Note that this deficiency of the RBV formulation occurs even for prismatic shafts, involving a constant cross section and corresponding warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) in z along the shaft, the focus of this work. This is in contrast with the original TWKV formulation where any discrepancy from equilibrium is linked to a tapering of the shaft, in the geometry of the cross section or material distribution on it. This would affect, in particular, the section torsional constants along the shaft, being functions of z.
The imposition of no warping at the support \(z=0\) for the problem at hand in the RBV formulation is accomplished by setting \(\lambda (0) = 0\), leaving free \(\phi ^\prime (0)\). This allows a non-zero stress at that fixed end due to twisting, namely the Saint-Venant shear stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}(0)\) and the corresponding torque \(T_{\scriptscriptstyle SV}(0)\), resolving then the torque anomaly indicated in Remark 2.3 in its entirety, as opposed to the partial situation discussed at the end of Sect. 3.2 for the TWKV formulation. However, this is accomplished by considering stresses that are not in equilibrium.
In any case, as indicated several times above and, in particular, in Remark 2.2, the goal of any structural model is to capture the response of the structural member at the global (structural) level or scale, with necessarily a number of contradictions/anomalies at the local (section) level forced by the nature of the approximation. It is precisely the result (94) of vanishing torque associated with the non-equilibrium part of the stresses, hence not affecting the global torque balance at the structural level, that allows the RBV formulation to provide a good approximation of the structural response of the shaft. This situation explains, somehow, the wide use of this formulation in the literature, even in the nonlinear range as discussed in the introduction presented in Sect. 1. However, we think that this situation may be appropriate for elastic shafts as considered here, where the specific stress values on the cross section may not be of the importance when modeling inelastic responses, like plasticity or fracture. It is for this specific practical reason, besides the general goal to involve equilibrated stresses per se, that we are interested in developing an alternative unconstrained formulation free of torque anomalies while involving a better representation of the stresses at the local (section) level, as we undertake in follow-up publications.
Remark 4.2
The arguments presented in this section rigorously show that the total RBV stresses \(\varvec{\tau }\) are not equilibrium, in general, for any section inside the shaft. For a section with a fully restrained warping, say, the fixed support at \(z=0\), this situation becomes clear by noting that then \(\lambda (0) =0\), so the original expression (73) of the total shear stress reads then
that is, proportional to the “arm function” \({\mathbb {J}}(x,y)\) in (4)\(_2\). Hence, the stress vectors associated with the RBV shear stress vectors \(\varvec{\tau }= [\tau _{xz}, \tau _{yz}]^T\) will show a “rotational” pattern around the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\), regardless of the shape of the cross section. We illustrate this pattern in Sect. 5 with a characteristic example. Clearly, these stresses will not satisfy the equilibrium boundary conditions along the section boundary \(\partial \Omega \), at the least. \(\square \)
Remark 4.3
We note that the use of the orthogonality relation (22) and definition (75) for the section constant \(I_{\scriptscriptstyle \nabla {W}_{\scriptscriptstyle {SV}}}\) easily makes us conclude that the expressions (91)–(92) for the shear stress components in the RBV formulation are consistent with the general relation (63), also applicable to the original TWKV formulation. This equation gives the Saint-Venant \(T_{\scriptscriptstyle SV}(z)\) and warping (bishear) \(T_{\scriptscriptstyle W}(z)\) parts of the total torque \(T(z)\) in terms of the total shear stress \(\varvec{\tau }\) on the cross section and the gradient of the Saint-Venant warping function \(\nabla {W}_{\scriptscriptstyle {SV}}(x,y)\), on the cross section as well. \(\square \)
Remark 4.4
It is quite significant to note that the second warping function \({W}_{{\sigma }}(x,y)\), defining the warping shear stresses in the TWKV formulation, plays no role whatsoever in the current RBV formulation. In fact, the arguments in this section identify this situation as the source of the physically incorrect (non-equilibrated) final stresses. \(\square \)
Illustrative example. Composite cross section with relative dimensions (left), and tables with the computed positions of the (material) centroids \({{\bar{y}}}_{_{E}}\) and \({{\bar{y}}}_{_{G}}\), and the center of twist/shear center \({{\bar{y}}}_{_{T}}\) (top right), and the computed torsional constants (bottom right), all for \(h= 50\) cm and \(t= 0.04\,h = 2\) cm
5 An illustrative example
To illustrate the results obtained above for the stresses predicted by different formulations under study, we consider briefly a specific shaft with the cross section depicted in Fig. 2. We have explicitly considered the case of a composite section to illustrate the generality encompassed in this respect by the developments in this work. It consists an I-beam of height \(h=50\) cm and varying thickness (with the reference value \(t=2\) cm), made of a linear elastic material with Young modulus \(E_1= {\bar{E}}= 200\) GPa and Poisson’s ration \(\nu _1= 0.3\) (so \(G_1= {\bar{G}}= 76.92\) GPa), perfectly bonded at its top to a rectangular slab made of a linear elastic material with \(E_2= {\bar{E}}/10 = 20\) GPa and \(\nu _2= 0.20\), say, steel and concrete, respectively. Hence, we have the distributions \(n_{_{E_1}}= n_{_{G_1}}= 1.0\) for the thin-walled part of the section and \(n_{_{E_2}}= 0.10\) and \(n_{_{G_2}}= 0.108\bar{3}\) for the slab at the top.
To calculate the torsional constants involved in the two formulations of interest, and from them all the other features, we first obtain the warping functions \({W}_{\scriptscriptstyle {SV}}(x,y)\) and \({W}_{{\sigma }}(x,y)\) with a finite element approximation of the boundary-value problems (19) and (53). Figure 3 depicts the computed functions. It also depicts the assumed plane finite element mesh for the analysis of this fixed section, with proportionally spaced 4-node bilinear quadrilateral elements along different parts of the section. Our implementation also produces the centroids \({{\bar{{\varvec{x}}}}}_{_{E}}\) and \({{\bar{{\varvec{x}}}}}_{_{G}}\), and the center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}\) based on the computed Saint-Venant function following the considerations indicated in Sect. 2.4. Both functions are solved first for an arbitrary center of twist \({{\bar{{\varvec{x}}}}}_{_{T}}^*\) with a fixed value at a node, with the final functions and final center of twist obtained with the shifting given by relations (26) and (29), respectively. The first table in Fig. 2 includes the computed values of these specific points for their vertical positions (from the bottom of the section); symmetry considerations apply. Similarly, the second table in that figure also includes the computed torsional constants of interest here, all evaluated from their defining expressions above with the full \(2\times 2\) Gaussian quadrature for the finite elements considered.
Composite cross section: axial stress. Distribution of the end axial stress \(\sigma _z\) at the shaft root \(z=0\) for the considered cross section and shaft’s length \(L/h=5.0\). All values are normalized by the reference Young modulus as \(\sigma _z/{\bar{E}}\) and correspond to a unit rotation \(\phi _L= 1.0\) at the opposite tip of the shaft
Composite cross section: shear stresses. Distributions of the Saint-Venant shear stress \(\varvec{\tau }_{\scriptscriptstyle {SV}}\), the warping shear stress \(\varvec{\tau }_{\scriptscriptstyle {W}}\) and the total shear stress \(\varvec{\tau }\), all at the shaft root \(z=0\), for the considered cross section and shaft’s length \(L/h=5.0\). All values are normalized as \(\varvec{\tau }/{\bar{G}}\) and correspond to a unit rotation \(\phi _L= 1.0\) at the opposite tip of the shaft
The computed Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) in Fig. 3 (left plot) shows the dominance of the thin-walled part in the overall warping of the section, at least where this warping is not restrained. Note that both formulations define the warping displacement proportional to this function, by \(\phi ^\prime (z)\) or \(\lambda (z)\) for the TWKV or RBV formulations, respectively. As noted in Remark 4.1, the two formulations result in the differential equation (49) in the twist rotation \(\phi (z)\) with the proper combination of torsional constants for a prismatic shaft loaded by a tip torque \(T_L\) (or, equivalently, imposed tip twist rotation \(\phi _L\)) and fully fixed at its root. We solve this equation analytically, providing the distribution of the twist rotation \(\phi (z)\) along the shaft, and with it all the other quantities discussed in the paper; we refer to [1] for details. We shall focus here on the stresses only.
Both the TWKV and RBV formulations result in a normal stress \(\sigma _z\) proportional by the bimoment \(T_{\scriptscriptstyle W}(z)\) to the weighted Saint-Venant warping function in the form \(n_{_E}(x,y){W}_{\scriptscriptstyle {SV}}(x,y)\); see equations (50) and (88), respectively. Figure 4 shows contour plots of this stress at the root of the shaft for a shaft of length \(L/h = 5.0\), for the two formulations under study. The same pattern noted above for the function \({W}_{\scriptscriptstyle {SV}}(x,y)\) is recovered for the axial stress \(\sigma _z\). In particular, the plots in this figure indicate that the two flanges of the I-profile, the stiffer part of the composite section, take the main part of the normal stress \(\sigma _z\) in a basically linear and symmetric manner along each individual flange, especially the bottom one; see the warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) at the left plot of Fig. 3. This situation clearly illustrates the popular representation of the bimoment causing these stresses by two equal and opposite bending moments on the flanges, with the associated bishear identified with the torque of the associated same and opposite shear forces on the flanges; see e.g. [13, p. 226]. It was precisely this observation that motivated the original developments by Timoshenko for thin-walled sections; see [28, p. 213].
Comparing the two formulations, we can see that the differences in the axial stress distribution in Fig. 4 are small. This is due, in part, to the dominance of the thin-walled part of the section, as opposed to the less stiff (thick) solid slab at the top, making the warping kinematics closed to the constrained limit. However, this resemblance does not apply to the shear stresses at all.
Figure 5 shows the shear stresses at the shaft’s root \(z=0\) for, again, the shaft of length \(L/h = 5.0\). We include the Saint-Venant component \(\varvec{\tau }_{\scriptscriptstyle {SV}}\), the warping component \(\varvec{\tau }_{\scriptscriptstyle {W}}\) and the total shear stress \(\varvec{\tau }= \varvec{\tau }_{\scriptscriptstyle {SV}}+ \varvec{\tau }_{\scriptscriptstyle {W}}\), all for the two formulations under study. We have depicted the stress vector of each of these components, on top of contour plots of its magnitude. The stress vectors sit at the quadrature points of the underlying 2D finite element meshes, where the gradients of the warping functions can be accurately evaluated, gradients that define these stresses as obtained in the paper.
Composite cross section: 3D shaft. Three-dimensional finite element solution for shafts with \(L/h=5.0\), showing the contours of the axial displacement \(u_z\) on top of the 3D deformed configuration of the shaft (left), and the elevation plot of the resulting warping at the shaft’s tip \(z=L\) (right)
Composite cross section: stresses. Normal and shear stresses in the three-dimensional finite element solution at the shaft root \(z=0\) for the shaft of length \(L/h=5.0\). Values are normalized as \(\varvec{\tau }/{\bar{G}}\) and \(\sigma _z/{\bar{E}}\), and they correspond to the case with a unit rotation \(\phi _L= 1.0\) at the opposite tip of the shaft
We first observe that the Saint-Venant shear stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) for the TWKV formulation vanish at that support with no warping, an illustration of the torque anomaly noted in the paper, and so is its associated torque \(T_{\scriptscriptstyle SV}(0)\). This formulation relies completely on the warping stresses \(\varvec{\tau }_{\scriptscriptstyle {W}}\) and the resultant bishear \(T_{\scriptscriptstyle W}(0)\). Recall that this component of the stress is proportional to \(n_{_G}(x,y)\nabla {W}_{{\sigma }}(x,y)\) in this formulation as given by equation (52), with the higher stress level occurring at the top flange of the (stiffer) I-profile.
This situation is to be contrasted to the stress distribution obtained by the RBV formulation. The Saint-Venant stresses \(\varvec{\tau }_{\scriptscriptstyle {SV}}\) do not vanish in this case, avoiding then the torque anomaly. The pattern of this stress component is actually similar to the observed total stress in the TWKV formulation, loading the top flange too. Unfortunately, the non-equilibrium warping stress component \(\varvec{\tau }_{\scriptscriptstyle {W}}\) (proportional now to \(n_{_G}(x,y)\nabla {W}_{\scriptscriptstyle {SV}}(x,y)\), equation (92)) pollutes the total shear stress \(\varvec{\tau }\), resulting in the incorrect “rotational” pattern of the stress vectors around the center of twist, as obtained in Remark 4.2. This pattern can be easily recognized in the total stress \(\varvec{\tau }\) shown in Fig. 5 for the RBV formulation. Given the value \({{\bar{y}}}_{_{T}}\) in the first table of Fig. 2, the center of twist is close to the top flange. As a consequence, it is now the opposite bottom flange that exhibits the higher stress level. The incorrectness of this situation can be inferred by the stress vectors not following the outer boundary of the section, as it happens in the equilibrated stresses of the TWKV formulation.
To verify these stress patterns, we have included in Figs. 6 and 7 the solutions obtained via full three-dimensional finite elements, that is, for the shaft treated as a full 3D solid, in its kinematics and material response. Figure 6 shows the considered mesh (involving the QM1/E12 enhanced brick elements in [22] for their good response in shear) and the computed warping displacement at the free tip \(z=L\), while the displacements at that end are imposed to a unit rotation \(\phi _L= 1.0\) using the distribution (3)\(_{1,2}\), all displacement components fixed at the root. Figure 7 shows the shear and normal stress components obtained at the root of the shaft. Note that these values are now the projected values to the nodes from the 3D quadrature points of the volume elements, and so are the stress vectors shown.
The results shown in these figures confirm the conclusions drawn above from the purely structural models. In particular, the warping displacement in Fig. 6 matches well the Saint-Venant warping function \({W}_{\scriptscriptstyle {SV}}(x,y)\) in Fig. 3 (left plot), obtained from a entirely plane analysis. Similarly, the distribution of the normal stress in Fig. 7 matches well the distributions in Fig. 4 for both the TWKV and RBV formulations, and so is the shear stress distribution for the TWKV formulation in Fig. 5, with the top flange of the thin-walled part of the section being the most stressed by this stress component. This confirmations also include the fully unphysical, incorrect nature of the shear stresses obtained by the RBV formulation.
6 Concluding remarks
We have presented in this paper an analysis of two different treatments of restrained warping in elastic shafts. Specifically, we have considered the original TWKV formulation of Timoshenko–Wagner–Kappus–Vlasov, and the RBV formulation of Reissner–Benscoter–Vlasov, both of common use in the literature. These two formulations have been presented in the context of a prismatic shaft under torsion with fully restrained warping at its root.
We can draw the following concluding remarks, summarizing the main theoretical developments presented in this paper:
- 1.:
-
Perhaps the main reason for the detailed presentation here is to underline the constrained character of the original TWKV formulation, by which the rate of twist \(\phi ^\prime (z)\) directly defines the amplitude of the warping of the different cross sections. We refer to this condition as the warping-twist constraint. This constrained structure may (and will) result in an overall too stiff structural response predicted by this formulation depending of the cross-section’s topology.
- 2.:
-
The RBV formulation relaxes this constraint by considering an independent field \(\lambda (z)\) along the shaft to define the amplitude of the warping displacement, aside from the twist rotation \(\phi (z)\) itself. In this context, we have identified a parameter, denoted by \(\kappa _t^{(RBV)}\) and depending solely on the cross section geometry (including the distribution of the material parameters on it), whose limit \(\kappa _t^{(RBV)}\rightarrow \infty \) leads to an enforcement of the constraint in a penalty-type form.
- 3.:
-
Both formulations keep the basic distribution \({W}_{\scriptscriptstyle {SV}}(x,y)\) over all cross sections for the warping displacement and, consequently, still uniform in shape along the shaft. An unwanted consequence of this situation is that the resulting stresses for the RBV formulation are not in equilibrium and, thus, physically incorrect.
- 4.:
-
Remarkably, the TWKV formulation does not rely entirely on the assumed distribution of the warping displacement for its total stresses, but on the warping-twist constraint itself too. No warping shear strains are involved in this formulation, with the warping stresses appearing entirely from static equilibrium considerations. These warping stresses and their resultant torque (the bishear) appear then formally as Lagrange multipliers enforcing the constraint along the shaft. The analysis presented here clearly identified also the distribution of these warping stresses on the cross section.
- 5.:
-
Still, we have observed that this constrained structure of the TWKV formulation may result in difficulties, besides the aforementioned over-stiff character. First, the fourth-order differential equation on the twist rotation \(\phi (z)\) governing this formulation may be one of such difficulties, especially in a numerical setting, preferring instead the second-order system of differential equations in that twist rotation and the independent warping field \(\lambda (z)\) of the RBV formulation. But perhaps more concerning is the fact that no warping at a cross section leads necessarily to the vanishing of the Saint-Venant shear stresses associated with twisting and its resultant torque. We refer to this situation affecting the TWKV formulation as the torque anomaly. In particular, it forces the formulation to rely solely on the bishear to enforce balance of moments at, say, a fixed support, a situation that may (and will) distort the diagrams of different stress resultants along the shaft.
The example included in Sect. 5 illustrates the issues with the predicted stresses by each formulation. In particular, it shows the incorrectness of the RBV stresses noted in Item 3 above. So not only the analyses of Sect. 4.3 have shown this situation rigorously, but the values obtained in this example indicate that one may get a completely incorrect understanding on how the section takes the torsional loading and the resulting stresses. We can see the difficulties that this situation may cause if the stresses are needed to evaluate the section performance (say, involving plastic/fracture arguments at specific points or parts of it).
All the others theoretical results and conclusions obtained in this paper clearly ask for a more extensive and detailed numerical evaluation, involving in particular different type of cross sections, too extensive for this first paper on these issues. We have already compiled some results along these lines in [1], indicating, for instance, that the limit \(\kappa _t^{(RBV)}\rightarrow \infty \) is indeed achieved in the thin-wall limit \(t/h \rightarrow 0\) for open simply-connected section topologies but not for closed (hollow) multiply-connected sections. Actually, this situation also explains the well-known different nature of the torsional response of these two cross section topologies, illustrating the role play by the kinematic warping-twist constraint identified here. We plan to elaborate on these results further in a future publication with asymptotic thin-wall estimates of different torsional constants appearing in these arguments, in order to provide further understanding of the working of these different sections in torsion.
Similarly, the drawbacks and difficulties identified here for the existing formulations under study motivate the development of alternative treatments of restrained warping. In particular, the arguments in Item 3 above identify a possible route for improving on these existing formulations, namely the incorporation of additional components of the shape of the warping distribution along the shaft. With the proper choices, one may avoid the incorrect stresses appearing in the RBV formulation while still relaxing the warping-twist constraint and, thus, avoiding the high-order and torque anomalies behind the original TWKV formulation. We also plan to develop these ideas in forthcoming publications.
References
Armero, F.: On the modeling of restrained torsional warping in prismatic elastic shafts (a full report). UCB/SEMM Report 2021/03, University of California, Berkeley, CA (2021)
Benscoter, S.U.: A theory of torsion bending for multi-cell beams. J. Appl. Mech. 20, 25–34 (1954)
Bredt, R.: Kritische bemerkungen zur drehunfselasticität. Z. Ver. Dtsch. Ing. 40(785–790), 813–817 (1896). (in German)
Burgoyne, C.J., Brown, E.H.: Nonuniform elastic torsion. Int. J. Mech. Sci. 36, 23–38 (1994)
Coulomb, C.A.: Recherches théoriques et expérimentales sur la force de torsion et sur l’élasticité des fils de métal. Mém. Acad. Sci. pp. 229–269 (1784) (in French)
Epstein, M., Segev, R.: Vlasov’s beam paradigm and multivector grassmann statics. Math. Mech. Solids 24, 3167–3179 (2019)
Föppl, A.: Der drillungswiderstand von walzeisenträgern. Z. Ver. Dtsch. Ing. 60, 694–695 (1917). (in German)
Gjelsvik, A.: The Theory of Thin Walled Bars. Wiley, New York (1981)
Goodier, J.N.: Torsional and flexural buckling of bars of thin-walled open section under compressive and bending loads. J. Appl. Mech. Trans. ASME 9, A103–A107 (1942)
Gruttmann, F., Sauer, R., Wagner, W.: Theory and numerics of three-dimensional beams with elastoplastic material behavior. Int. J. Num. Methods Eng. 48, 1675–1702 (2000)
Kappus, R.: Twisting failure of centrally loaded open-section columns in the elastic range. Technical Memorandum no. 851, National Advisory Committee for Aeronautics, Washington, D.C. (1938)
Methods of analysis for torsion with variable twist: Kármán, Th.von., Christensen, N.B. J. Aero. Sci. 11, 110–124 (1944)
Oden, J.T., Ripperger, A.E.: Mechanics of Elastic Structures, 2nd edn. Hemisphere, Washington (1981)
Pilkey, W.D.: Analysis and Design of Elastic Beams. Wiley, New York (2002)
Popov, E.P.: Kelvin’s solution of torsion problem. ASCE J. Eng. Mech. 96, 1005–1012 (1970)
Prandtl, L.: Zur torsion von prismatischen stäben. Phys. Zeitschr. 4, 758–770 (1903). (in German)
Reissner, E.: On non-uniform torsion of cylindrical rods. J. Math. Phys. 31, 214–221 (1952)
Reissner, E.: On a simple variational analysis of small finite deformations of prismatical beams. J. Appl. Math. Phys. (ZAMP) 34, 642–648 (1983)
Saint-Venant, B.: Mémoire sur la Torsion des Prismes. Mém. Savants Étrangers, Paris (1855) (in French)
Salmon, C.G., Johnson, J.E., Malhas, F.A.: Steel Structures, Design and Behavior, 5th edn. Prentice Hall, Upper Saddle River (2009)
Seaburg, P.A., Carter, C.J.: Torsional Analysis of Structural Steel Members. Steel Design Guide Series 9, American Institute of Steel Construction (1997)
Simo, J.C., Armero, F., Taylor, R.L.: Improved tri-linear versions of assumed enhanced strain elements for 3d finite deformation problems. Comp. Meth. Appl. Mech. Eng. 110, 359–386 (1993)
Simo, J.C., Vu-Quoc, L.: A geometricall-exact rod model incorporating shear and torsion-warping deformation. Int. J. Solids Struct. 27, 371–393 (1991)
Sokolnikoff, I.S.: Mathematical Theory of Elasticity, 2nd edn. McGraw-Hill, New York (1956)
Timoshenko, S.P.: Torsional vibrations of shafts. Proc. St. Petersb. Polytechn. Inst. 3, 397–406 (1905). (in Russian)
Timoshenko, S.P.: Lateral buckling of i-beams under the influence of forces acting in the plane of largest rigidity. Proc. St. Petersburg Polytechnical Institute 4-5, 151–219, 3–34, 262–292 (1906). (in Russian)
Timoshenko, S.P.: Einige stabilitätsprobleme der elastizitätstheorie. Zeits. Ang. Math. Phys. (ZAMP) 58, 337–385 (1910). (in German)
Timoshenko, S.P., Gere, J.M.: Theory of Elastic Stability, 2nd edn. McGraw-Hill, New York (1961)
Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity. McGraw-Hill, New York (1951)
Trefftz, E.: über den schubmittelpunkt in einem durch eine einzellast gebogenen balken. Z. Angew. Math. Mech. 55, 220–225 (1935). (in German)
Vlasov, V.Z.: Thin-Walled Elastic Beams. Israel Program for Scientific Translations Ltd., Jerusalem (1961). (first Russian edition 1940)
Wagner, H.: Torsion and buckling of open sections. Technical Memorandum no. 807, National Advisory Committee for Aeronautics, Washington (1936)
Weinstein, A.: The center of shear and the center of twist. Q. Appl. Math. 5, 97–99 (1947)
Zbirohowski-Koscia, K.: Thin Walled Beams. Crosby Lockwood and Son Ltd., London (1967)
Acknowledgements
I would like to thank Sanjay Govindjee for enlightening discussions on the general topic of torsion and, specifically, for his help in digging out the original German literature on the subject.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Armero, F. On the modeling of restrained torsional warping: an analysis of two formulations. Z. Angew. Math. Phys. 73, 56 (2022). https://doi.org/10.1007/s00033-022-01684-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-022-01684-1