On a Conjecture on Pattern-Avoiding Machines

Abstract

Let s be West’s stack-sorting map, and let $s_{T}$ be the generalized stack-sorting map, where instead of being required to increase, the stack avoids subpermutations that are order-isomorphic to any permutation in the set T. In 2020, Cerbai, Claesson, and Ferrari introduced the $\sigma$-machine $s \circ s_{\sigma }$ as a generalization of West’s 2-stack-sorting-map $s \circ s$. As a further generalization, in 2021, Baril, Cerbai, Khalil, and Vajnovski introduced the $(\sigma , \tau )$-machine $s \circ s_{\sigma , \tau }$ and enumerated $\textrm{Sort}_{n}(\sigma ,\tau )$—the number of permutations in $S_n$ that are mapped to the identity by the $(\sigma , \tau )$-machine—for six pairs of length 3 permutations $(\sigma , \tau )$. In this work, we settle a conjecture by Baril, Cerbai, Khalil, and Vajnovski on the only remaining pair of length 3 patterns $(\sigma , \tau ) = (132, 321)$ for which $|\textrm{Sort}_{n}(\sigma , \tau )|$ appears in the OEIS. In addition, we enumerate $\textrm{Sort}_n(123, 321)$, which does not appear in the OEIS, but has a simple closed form.

1 Introduction

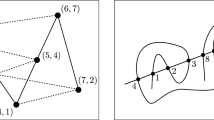
In 1990, Julian West [16] introduced the stack-sorting map s, a deterministic variation of Knuth’s [12] stack-sorting machine. In West’s stack-sorting map s, the input permutation is sent through a stack in a right-greedy manner such that the stack is increasing from top to bottom (see for example, Fig. 1).

Fig. 1

West’s stack-sorting map s on $\pi = 4213$

Since then, the stack-sorting map s has been generalized to $s_{\sigma }$ for permutations $\sigma$ [7]. Like s, the map $s_{\sigma }$ sends a permutation through a stack in a right-greedy manner. However, instead of insisting that the stack increases (i.e., avoids subsequences that are order-isomorphic to 21 when the stack is read from top to bottom), we insist that the stack avoids subsequences that are order-isomorphic to $\sigma$. Soon after, Berlow [2] extended $s_{\sigma }$ to stacks that must avoid all of the patterns in a given set. In the same year, Defant and Zheng [11] extended $s_{\sigma }$ to vincular patterns.

West’s stack-sorting map s derives its name from the easily verifiable result that for any $\pi \in S_n$, the permutation $s^{n-1}(\pi )$ is sorted (i.e., is the identity permutation). Naturally, one of the most classical questions on the stack-sorting map concerns the characterization of 1-stack-sortable permutations—the permutations $\pi \in S_n$ for which $s(\pi )$ is sorted. Knuth [12] was the first to answer this question; he showed that $s(\pi )$ is sorted if and only if $\pi$ avoids subsequences that are order-isomorphic to 231 and enumerated the number of such permutations in $S_n$ to be $n{\text {th}}$ Catalan number $\frac{1}{n+1} \left( {\begin{array}{c}2n\\ n\end{array}}\right)$.

With the question of which permutation get sorted after passing through one stack settled, it is then natural to ask about the permutations that are sorted after passing through multiple stacks in a series. A notable example is West’s 2-stack-sorting-map $s \circ s$. In 1990, West [16] characterized the 2-stack-sortable permutations—the permutations that are sorted after passing through West’s 2-stack-sorting-map—using barred patterns and conjectured that the number of 2-stack-sortable permutations in $S_n$ is $\frac{2}{(n+1)(2n+1)} \left( {\begin{array}{c}3n\\ n\end{array}}\right)$. Two years later in 1992, Zeilberger [17] affirmed West’s conjecture. Later, Cerbai [6] generalized some of the results on West’s 2-stack-sorting map to Cayley permutations. Only recently in 2020, Defant presented a polynomial time algorithm [10] that counts the number of permutations that are sorted after passing through a series of three stacks.

To better understand the permutations that are sortable under stacks in series, Cerbai, Claesson, and Ferrari [7] introduced the $\sigma$-machine $s \circ s_{\sigma }$ in 2020. It is then natural to ask about the permutations that get sorted after passing through the $\sigma -$machine once. Therefore, let $\textrm{Sort}_{n}(\sigma )$ denote the set of permutations in $S_n$ that are sorted after a single pass through the $\sigma$-machine. Equivalently, due to Knuth’s characterization of 1-stack sortable permutations, $\textrm{Sort}_n(\sigma )$ is the set of permutations $\pi$ where $s_{\sigma }(\pi )$ avoids 231. The most notable enumerations of the sequence $\textrm{Sort}_n(\sigma )$ are by Cerbai, Claesson, and Ferrari [7] and by Cerbai, Claesson, Ferrari, and Steingrímsson [8] in a subsequent work (see Table 1).

Table 1 Enumeration of $\textrm{Sort}_{n}(\sigma )$, for patterns $\sigma$ of length three

In 2021, Baril, Cerbai, Khalil, and Vajnovszki [1] introduced the $(\sigma , \tau )$-machine $s \circ s_{\sigma , \tau }$ as a further generalization of the $\sigma$-machine. For example, Fig. 2 illustrates that $\pi = 2314$ is sent to 3124 after passing through the (132, 321)-machine.

Fig. 2

The (132, 321)-machine on $\pi = 2314$

As an analog of $\textrm{Sort}_{n}(\sigma )$, let $\textrm{Sort}_{n}(\sigma , \tau )$ consist of the permutations in $S_n$ that are sorted after an iteration through the $(\sigma , \tau )$-machine. Permutations in $\textrm{Sort}_n(\sigma ,\tau )$ are said to be $(\sigma ,\tau )$-sortable. Baril, Cerbai, Khalil, and Vajnovszki [1] enumerated $\textrm{Sort}_{n}(\sigma , \tau )$ for several pairs of length 3 patterns $(\sigma , \tau )$ (see Table 2) and observed through numerical computation that the only remaining pair of length 3 permutations $(\sigma , \tau )$ for which $|\textrm{Sort}_{n}(\sigma , \tau )|$ may belong to the OEIS [14] is $(\sigma , \tau ) = (132, 321)$. As our first main result, in Sect. 3, we settle Baril, Cerbai, Khalil, and Vajnovszki’s conjecture that $\textrm{Sort}_{n}(132, 321)$ is enumerated by A102407 (see Conjecture 1 of [1]). First, the following theorem gives the generating function for $|\textrm{Sort}_{n}(132, 321)|$.

Table 2 Enumerations of $\textrm{Sort}_n(\sigma , \tau )$

Theorem 1.1

The generating function for $|\textrm{Sort}_{n}(132, 321)|$ is given by

$$\begin{aligned} \sum _{n\ge 0} |\textrm{Sort}_{n}(132, 321)| z^n =\frac{(1+z-z^2) - \sqrt{1-2z-5z^2-2z^3+z^4}}{2z}. \end{aligned}$$

Now, Baril, Cerbai, Khalil, and Vajnovszki’s conjecture [1] follows directly from Theorem 1.1.

Corollary 1.2

The sequence $|\textrm{Sort}_{n}(132,321)|$ is OEIS A102407 [14].

To prove Theorem 1.1, we first characterize $\textrm{Sort}_n(132,321)$ by avoidance of two (generalized) patterns of length three. We then use a bijection first discovered by West to map $\textrm{Sort}_n(132,321)$ to a set that we are able to enumerate directly. A more geometrical approach that involves a bijection with Dyck paths avoiding the subword dudu is also illustrated in Sect. 3.1.

Furthermore, in Sect. 4, we enumerate $\textrm{Sort}_n(123, 321)$. This sequence does not belong to the OEIS [14] but has a simple closed form for $n \ge 4$.

Theorem 1.3

For $n \ge 4$, it holds that $|\textrm{Sort}_{n}(123, 321)|=7 \cdot 2^{n-4}$.

We end the paper with some suggestions for future work.

2 Preliminaries

Let $[n]=\{1,2,\dots ,n\}$. A permutation of length n is a bijective map $\pi :[n]\rightarrow [n]$. Let $S_n$ be the set of permutations of length n. We denote a permutation $\pi \in S_n$ by the string $\pi =\pi _1 \pi _2 \cdots \pi _n$, where $\pi _i=\pi (i)$. Let $\textrm{ind}_\pi (i)=\pi ^{-1}(i)$ be the index such that $\pi _{\textrm{ind}_{\pi }(i)}=i$. For example, $\textrm{ind}_{12534}(5)=3$. If $i<j$ (respectively, $i>j$), we say that $\pi _i$ appears to the left of (resp. to the right of) $\pi _j$ in $\pi$. An entry $\pi _i$ is a left-to-right minimum (briefly, ltr minimum) of $\pi$ if $\pi _i$ is smaller than each entry that appears to its left. Furthermore, we let $\pi _{[i, j]}$ denote the subsequence $\pi _{i}\pi _{i+1}\cdots \pi _{j}$, and we let $\{\pi _{[i, j]}\}$ be the set $\{\pi _{i},\pi _{i+1},\dots , \pi _{j}\}$. For $k\ge 1$, we also let $\pi +k=(\pi _1+k)(\pi _2+k)\cdots (\pi _n+k)$ denote the string obtained by adding k to each entry of $\pi$. As an example to illustrate the above definitions, let $\pi =524613$. The ltr-minima of $\pi$ are 5, 2, and 1. For $i=2$ and $j=5$, we have $\pi _{[i,j]}=2461$ and $\{\pi _{[i,j]}\}=\{2,4,6,1\}$. Finally, we have $\pi +3=857946$.

A short introduction to permutation patterns can be found in Bevan’s note [3]. Let us recall some notions that will be used in this paper. Given two permutations $\pi \in S_n$ and $\rho \in S_m$, with $m\le n$, we say that $\pi$ contains the pattern $\rho$ if there exists some $c(1)< c(2)< \cdots < c(m)$ such that the subsequence $\mu = \pi _{c(1)}\pi _{c(2)} \cdots \pi _{c(m)}$ is order-isomorphic to $\rho$. If so, we say that $\mu$ is an occurrence of $\rho$ in $\pi$. If $\pi$ does not contain the pattern $\rho$, then $\pi$ avoids $\rho$. Let $\textrm{Av}_n(\rho )$ denote the set of permutations of length n that avoid $\rho$. Similarly, for a set of patterns T, we let $\textrm{Av}_{n}(T)$ be the set of permutations in $S_n$ avoiding all the patterns in T. Bivincular patterns [4] are obtained by allowing constraints of adjacency on positions and values. Mesh patterns generalize both classical and bivincular patterns in the following sense. A mesh pattern [5] is a pair $(\rho ,R)$, where $\rho \in S_m$ is a permutation and $R \subseteq \left[ 0,m \right] \times \left[ 0,m \right]$ is a set of pairs of integers. Each pair in R determines the lower left corners of unit squares which specify forbidden regions in the plot of permutations. An occurrence of the mesh pattern $(\rho ,R)$ in the permutation $\pi$ is an occurrence of the classical pattern $\rho$ such that no other points of $\pi$ occur in the forbidden regions specified by R. For the rest of this paper, we shall denote by $123^{\star }$ and $132^{\star }$ the bivincular patterns depicted–as mesh patterns–in Fig. 3. For example, an occurrence of $123^{\star }$ in a permutation $\pi$ is a classical occurrence $\pi _{c(1)}\pi _{c(2)}\pi _{c(3)}$ of 123 such that $c(3)=c(2)+1$ and $\pi _{c(3)}=\pi _{c(2)}+1$.

Fig. 3

Bivincular patterns $123^{\star }$ and $132^{\star }$

Lastly, we cite Knuth’s [12] lemma on the characterization of 1-stack-sortable permutations.

Lemma 2.1

(Knuth [12]) A permutation $\pi$ is 1-stack-sortable if and only if $\pi$ avoids 231.

2.1 West’s Bijection

In 1995, West [15] presented a new bijection between $\textrm{Av}_n(132)$ and $\textrm{Av}_n(123)$. Let $\pi = \pi _1 \pi _2 \cdots \pi _{n-1} \in S_{n-1}$. For $1 \le i \le n$, denote by $\pi ^{i}$ the permutation $\pi _{1} \pi _{2} \cdots \pi _{i-1} n \pi _{i} \cdots \pi _{n-1}$ obtained by inserting n in the ith site of $\pi$ (i.e. the position immediately before $\pi _i$, for $i=1,\dots ,n-1$, or at the end, if $i=n$). Given a pattern $\rho$, define the ith site of $\pi$ to be active with respect to $\rho$ if $\pi ^i$ avoids $\rho$. For example, if $\pi = 45231$, then $i \in \{1,3,5,6\}$ are active with respect to $\rho =132$, but $i \in \{2,4\}$ are not since both $\pi ^2=465231$ and $\pi ^4=452631$ contain 132. Now, let $\textrm{small}_k(\pi )$ denote the subsequence of the smallest k numbers in $\pi$. Given a pattern $\rho$, let $\textrm{Ac}_{j}(\pi ; \rho )$ denote the set of active sites in $\textrm{small}_{|\pi |+1-j}(\pi )$ with respect to the pattern $\rho$. Note that $\textrm{Ac}_1(\pi ; \rho )$ is equal to the number of active sites of $\pi$ with respect to $\rho$. For example, $|\textrm{Ac}_{1}(45231;132)| = |\textrm{Ac}_{2}(45231; 132)|= 4$, because the set of active sites with respect to 132 pattern for $\pi =45231$ is $\{1,3,5,6\}$ and for $\textrm{small}_{4}(\pi ) = 4231$ is $\{1,2,4,5\}$. The signature of $\pi$ with respect to $\rho$ is the word

$$\begin{aligned} {\mathfrak {S}}(\pi ; \rho )=|\textrm{Ac}_{1}(\pi ; \rho )| |\textrm{Ac}_{2}(\pi ; \rho )| \cdots |\textrm{Ac}_{n-1}(\pi ; \rho )|, \end{aligned}$$

where $\cdot$ denotes concatenation. For example, ${\mathfrak {S}}(45231; 132) = 44332$. In addition, for a set of permutations T, let ${\mathfrak {S}}(T; \rho ):= \{{\mathfrak {S}}(\pi ; \rho ) \mid \pi \in T\}$. West [15] showed that permutations in $\textrm{Av}(123)$, as well as permutations in $\textrm{Av}(132)$, are uniquely determined by their signature. Furthermore, he showed that ${\mathfrak {S}}(\textrm{Av}_{n}(132); 132) = {\mathfrak {S}}(\textrm{Av}_{n}(123); 123)$. This naturally induces a bijection between $\textrm{Av}_{n}(132)$ and $\textrm{Av}_{n}(123)$. For example, $\pi = 45231$ is the only $\pi \in \textrm{Av}_5(132)$ such that ${\mathfrak {S}}(\pi ; 132) = 44332,$ and $\rho = 42153$ is the only $\rho \in \textrm{Av}_5(123)$ such that ${\mathfrak {S}}(\rho ; 123) = 44332$.

3 The (132, 321)-Machine

This section is devoted to the (132, 321)-machine. First, we prove that $\textrm{Sort}_n(132, 321)=\textrm{Av}_n(123,132^{\star })$. Then, we show that West’s bijection maps $\textrm{Av}_n(123,132^{\star })$ to $\textrm{Av}_n(132,123^{\star })$. Finally, we enumerate $\textrm{Sort}_n(132,321)$ by providing a generating function for $\textrm{Av}_n(132,123^{\star })$. We end the section by sketching a bijection between $\textrm{Sort}_n(132,321)$ and the set of Dyck paths of semilength n that avoid dudu as a factor.

Let us begin by establishing a property that all ltr minima of the input permutation must satisfy.

Lemma 3.1

If $\pi _i$ is a ltr minimum of $\pi$ and $\textrm{ind}_{s_{132,321}(\pi )}(\pi _i)<\textrm{ind}_{s_{132,321}(\pi )}(\pi _j)$, then $j < i$.

Proof

Because $\pi _i$ is a ltr minimum and the stack must avoid the 132 pattern, the stack must be increasing from top to bottom right after $\pi _i$ enters the stack. Now, because $\mu _{2} > \mu _{3}$ in any 132 or 321 pattern $\mu$ and the numbers below $\pi _i$ in the stack are increasing, $\pi _i$ can only leave the stack after every number has entered or left the stack. Therefore, if $\pi _j$ appears to the right of $\pi _i$ in $s_{132,321}(\pi )$, then $\pi _j$ must have been in the stack when $\pi _i$ entered the stack. Thus, $j < i$. $\square$

Next, we show that any permutation in $\textrm{Sort}_{n}(132, 321)$ must avoid the 123 pattern.

Proposition 3.2

If $\pi \in \textrm{Sort}_{n}(132, 321)$, then $\pi \in \textrm{Av}_{n}(123)$.

Proof

Suppose otherwise. Let $\pi _{i}\pi _{j}\pi _{k}$ be the lexicographically smallest 123 pattern of $\pi$ so that $\pi _i$ is a ltr minimum. By Lemma 3.1, $\pi _i$ must be in the stack when $\pi _{k}$ enters the stack. Now, $\pi _{j}$ must leave the stack before $\pi _{k}$ enters the stack, because $\pi _{k}\pi _{j} \pi _{i}$ is a 321 pattern. As a result, $\pi _{j}$ must appear to left of $\pi _{k}$ in $s_{132,321}(\pi )$. Furthermore, by Lemma 3.1, $\pi _{i}$ must appear to the right of $\pi _{j}$ and $\pi _{k}$ in $s_{132,321}(\pi )$. Thus, $\pi _{j} \pi _{k} \pi _{i}$ is a 231 pattern in $s_{132,321}(\pi )$—a contradiction to $\pi \in \textrm{Sort}_{n}(132, 321)$ by Lemma 2.1. $\square$

Due to Proposition 3.2, the behavior of the (132, 321)-stack on any (132, 321)-sortable permutation is equivalent to the behavior of a 132-stack. Therefore,

$$\begin{aligned} \textrm{Sort}_n(132,321)=\textrm{Sort}_n(132)\cap \textrm{Av}(123). \end{aligned}$$

The next proposition shows that any permutation in $\textrm{Sort}_{n}(132, 321)$ must avoid the $132^{\star }$ pattern.

Proposition 3.3

If $\pi \in \textrm{Sort}_n(132, 321)$, then $\pi \in \textrm{Av}_{n}(132^{\star })$.

Proof

Suppose otherwise. Let $\pi _{i}\pi _{j}\pi _{j+1}$ be the lexicographically smallest $132^{\star }$ pattern of $\pi$ so that $\pi _i$ is a ltr minimum. Now, suppose that $\pi _j$ has just entered the stack. Because $\pi _{j} = \pi _{j+1} +1$, if $\pi _{j+1}$ entering the stack introduces a 132 or 321 pattern to the stack, then $\pi _{j+1}$ and $\pi _{j}$ must both be a part of the pattern. However, in a 132 pattern $\mu$, it must be that $\mu _{2} - \mu _{1} \ge 2$ and in a 321 pattern $\mu$, it must be that $\mu _{2} < \mu _{1}$. Yet, $\pi _{j} - \pi _{j+1} = 1$, and so the entrance of $\pi _{j+1}$ into the stack cannot introduce a 132 or 321 pattern. Therefore, $\pi _{j+1}$ must be to the left of $\pi _{j}$ in $s_{132,321}(\pi )$. In addition, by Lemma 3.1, $\pi _{i}$ must be to the right of $\pi _{j}$ and $\pi _{j+1}$ in $s_{132,321}(\pi )$. Thus, $\pi _{j+1} \pi _{j} \pi _{i}$ is a 231 pattern in $s_{132,321}(\pi )$—a contradiction to $\pi \in \textrm{Sort}_{n}(132, 321)$ by Lemma 2.1. $\square$

We shall prove that the conditions of Lemmas 3.2 and 3.3 are sufficient for a permutation to be in $\textrm{Sort}_{n}(132, 321)$. First, a simple lemma.

Lemma 3.4

If $\pi _i$ is not a ltr minimum of $\pi \in \textrm{Av}_{n}(123)$ and $i < j$, then $\pi _i > \pi _j$.

Proof

Suppose otherwise. Because $\pi _i$ is not a ltr minimum, there exists $\pi _k$ such that $\pi _k < \pi _i$ and $k < i$. Thus, $\pi _k \pi _{i} \pi _{j}$ is a 123 pattern in $\pi$—a contradiction. $\square$

Next, we prove two properties that all $\pi \in \textrm{Av}_{n}(123, 132^{\star })$ must satisfy.

Lemma 3.5

If $\pi _i$ is not a ltr minimum of $\pi \in \textrm{Av}_{n}(123, 132^{\star })$, then

$$\begin{aligned} \textrm{ind}_{s_{132,321}(\pi )}(\pi _i) < \textrm{ind}_{s_{132,321}(\pi )}(\pi _{i+1}). \end{aligned}$$

Proof

First, suppose that $\pi _{i+1}$ is a ltr minimum. Then because $\pi _i$ is not a ltr minimum, there must be some ltr minimum $\pi _j$ such that $\pi _j < \pi _i$ and $j < i$. Now, by Lemma 3.1, $\pi _j$ must be in the stack when $\pi _{i+1}$ enters the stack. Then, because $\pi _{i+1}$ is a ltr minimum, the subsequence $\pi _{i+1} \pi _{i} \pi _{j}$ must be a 132 pattern. Therefore, $\pi _{i}$ must leave the stack before $\pi _{i+1}$ enters the stack.

Next, suppose that $\pi _{i+1}$ is not a ltr minimum. First, because $\pi _i$ is not a ltr minimum, $\pi _i > \pi _{i+1}$ by Lemma 3.4. In addition, there is some ltr minimum $\pi _k$ such that $\pi _k < \pi _{i+1}$ and $k < i$. Furthermore, $\pi _{i} > \pi _{i+1} +1$, because otherwise, $\pi _{k}\pi _{i}\pi _{i+1}$ is a $132^{\star }$ pattern. Now, if $\pi _{i+1}+1$ appears to the right of $\pi _{i+1}$, then $\pi _k \pi _{i+1}(\pi _{i+1}+1)$ is a 123 pattern. Thus, by Lemma 3.4, $\pi _{i+1}+1$ must be a ltr minimum, and by Lemma 3.1, $\pi _{i+1}+1$ must be in the stack when $\pi _{i+1}$ enters the stack. Now, $\pi _{i}$ and $\pi _{i+1}+1$ cannot both be in the stack when $\pi _{i+1}$ enters the stack, because $\pi _{i+1} \pi _{i}(\pi _{i+1}+1)$ is a 132 pattern. Thus, $\pi _{i}$ must leave the stack before $\pi _{i+1}$ enters the stack. $\square$

Proposition 3.6

If $\pi \in \textrm{Av}_n(123,132^{\star })$, then $\pi \in \textrm{Sort}_n(132, 321).$

Proof

By Lemma 3.1, any ltr minimum $\pi _i$ must remain in the stack until every other number has entered the stack. By Lemma 3.5, any $\pi _i$ that is not a ltr minimum of $\pi$ must leave the stack before $\pi _{i+1}$ enters the stack. Therefore, any ltr minimum of $\pi$ must appear to the right of any number that is not a ltr minimum of $\pi$ in $s_{132,321}(\pi )$. Now, because the ltr minima of $\pi$ must decreasing from the left to right, by Lemma 3.1, the ltr minima of $\pi$ must appear in $s_{132,321}(\pi )$ in increasing order. Furthermore, by Lemmas 3.4 and 3.5, the numbers that are not ltr minima of $\pi$ must appear in $s_{132,321}(\pi )$ in decreasing order. Thus, $s_{132,321}(\pi )$ must avoid the 231 pattern and by Lemma 2.1, must be in $\textrm{Sort}_{n}(132,321)$. $\square$

Now, we collate Propositions 3.2, 3.3, and 3.6.

Theorem 3.7

For all n, it holds that $\textrm{Sort}_{n}(132, 321) = \textrm{Av}_{n}(123, 132^{\star })$.

Our next goal is to show that West’s bijection maps $\textrm{Av}_n(123,132^{\star })$ to $\textrm{Av}_{n}(132, 123^{\star })$. Recall from Sect. 2.1 that permutations in $\textrm{Av}_n(123)$, as well as in $\textrm{Av}(132)$, are uniquely determined by their signature. West’s bijection then follows from the equality between the corresponding sets of signatures

$$\begin{aligned} {\mathfrak {S}}(\textrm{Av}_n(123),123)={\mathfrak {S}}(\textrm{Av}_n(132),132). \end{aligned}$$

We wish to prove that any permutation $\pi \in \textrm{Av}_n(123)$ contains $132^{\star }$ if and only if there exists some $1\le i\le n-2$ such that

$$\begin{aligned} {\mathfrak {S}}(\pi ; 123)_{i} = {\mathfrak {S}}(\pi ; 123)_{i+1} \le {\mathfrak {S}}(\pi ; 123)_{i+2}. \end{aligned}$$

The desired result follows from the fact that the same property holds when we replace the pattern 123 with 132 and the pattern $132^{\star }$ with $123^{\star }$.

Let us take care of $\textrm{Av}_n(123,132^{\star })$ first. To start, we show that removing the maximum of a permutation preserves the property of avoiding both patterns.

Lemma 3.8

If $\pi \in \textrm{Av}_{n}(123, 132^{\star })$, then $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123, 132^{\star })$.

Proof

It is clear that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123)$. Suppose that $\textrm{small}_{n-1}(\pi ) \not \in \textrm{Av}_{n-1}(132^{\star })$. Then $\pi _j \pi _{\mathrm {ind_{\pi }(n)}-1} \pi _{\mathrm {ind_{\pi }(n)}+1}$ must be a $132^{\star }$ pattern in $\textrm{small}_{n-1}(\pi )$, because $\pi \in \textrm{Av}_{n}(132^{\star })$. However, then $\pi _{j} \pi _{\textrm{ind}_{\pi }(n)-1} n$ is a 123 pattern in $\pi$—a contradiction to $\pi \in \textrm{Av}_{n}(123, 132^{\star })$. $\square$

Now, let $\pi \in \textrm{Av}_n(123)$. It is easy to see that the set of active sites $\textrm{Ac}_1(\pi ;123)$ of $\pi$ with respect to 123 forms an interval. The entry $\pi _{|\textrm{Ac}_{1}(\pi ; 123)|}$ preceding the leftmost site that is not active can be characterized as follows.

Lemma 3.9

Let $\pi \in \textrm{Av}_{n}(123)$ and suppose that $\pi$ is not the decreasing permutation $n(n-1)\cdots 1$. Then $\pi _{|\textrm{Ac}_{1}(\pi ; 123)|} = \max \{ \pi _i \mid \pi _{i} + i \ne n+1 \}.$

Proof

We induct on n. The statement is vacuously true for $n = 1.$ First, suppose that $\pi _1 \ne n$. Clearly, $\pi ^j \in \textrm{Av}_n(123)$ for $1 \le j \le \textrm{ind}_\pi (n),$ since if $(\pi ^j)_a (\pi ^j)_b (n+1)$ is a 123 pattern in $\pi ^j,$ then $\pi _a \pi _b n$ is a 123 pattern in $\pi$. Conversely, if $j > \textrm{ind}_\pi (n)$, then $\pi ^j_1 n (n+1)$ is a 123 pattern in $\pi ^j,$ and so $j \not \in \textrm{Ac}_{1}(\pi ; 123)$. Hence, $\textrm{Ac}_{1}(\pi ; 123) = \{1, 2, \cdots , \textrm{ind}_\pi (n)\}$ and $\pi _{|\textrm{Ac}_1(\pi ; 123)|} = \max \{ \pi _i \mid \pi _{i} + i \ne n+1 \} = n$.

Now, suppose that $\pi _{1} = n$. Then $\textrm{Ac}_{1}(\pi ;123) = \{j\mid j-1 \in \textrm{Ac}_2(\pi ;123) \} \cup \{1\}$, because no 123 pattern in $\pi ^{j}$ for $1 \le j \le n+1$ begins with n or $n+1$. Thus, $|\textrm{Ac}_{1}(\pi ;123)| = |\textrm{Ac}_2(\pi ;123)| + 1$, and the statement of the lemma follows by the inductive hypothesis. $\square$

Proposition 3.10

If $\pi \in \textrm{Av}_n(123)$ and $|\textrm{Ac}_{i}(\pi ; 123)| = \mathfrak |\textrm{Ac}_{i+1}(\pi ; 123)| \le |\textrm{Ac}_{i+2}(\pi ; 123)|$ for some $1 \le i \le n-2$, then $\pi \not \in \textrm{Av}_n(132^{\star }).$

Proof

We induct on n; it is easy to see that the statement holds for $n \le 3$. Now, because ${\mathfrak {S}}_{n}(\pi ; 123) = |\textrm{Ac}_{1}(\pi ; 123)| {\mathfrak {S}}_{n}(\textrm{small}_{n-1}(\pi ; 123))$, if $n \ge 4$ and $2 \le i \le n-2$, then by Lemma 3.8 and the inductive hypothesis, $\pi \not \in \textrm{Av}_{n}(132^{\star })$. Thus, assume $i = 1$.

Next, if $\pi _1 =n$, then $|\textrm{Ac}_1(\pi ; 123)| = |\textrm{Ac}_2(\pi ;123)| + 1$ by Lemma 3.9. Similarly, if $\pi _1 = n-1$, then $|\textrm{Ac}_2(\pi ; 123)| = |\textrm{Ac}_3(\pi ;123)| + 1$ by Lemma 3.9 on $\textrm{small}_{n-1}(\pi )$. Thus, $\pi _1 \le n-2$.

Now, n appears to the left of $n-1$ in $\pi$, because $\pi \in \textrm{Av}_{n}(123)$ and $\pi _1 \le n-2$. But if $n (n-1)$ is not a substring of $\pi$, then by Lemma 3.9 and $\pi _1 \le n-2$,

$$\begin{aligned} |\textrm{Ac}_1(\pi ; 123)| = \textrm{ind}_\pi (n) < \textrm{ind}_{\textrm{small}_{n-1}(\pi )} (n-1) = |\textrm{Ac}_2(\pi ; 123)|. \end{aligned}$$

Thus, $\pi \not \in \textrm{Av}_{n}(132^{\star })$, because $\pi _1 n (n-1)$ form a $132^{\star }$ pattern in $\pi$. $\square$

The converse of Proposition 3.10 is also true, as we show below.

Proposition 3.11

If $\pi \in \textrm{Av}_n(123) {\setminus } \textrm{Av}_{n}(132^{\star })$, then for some $1 \le i \le n-2$, it holds that $|\textrm{Ac}_{i}(\pi ; 123)| = |\textrm{Ac}_{i+1}(\pi ; 123)| \le |\textrm{Ac}_{i+2}(\pi ; 123)|$.

Proof

We induct on n; the statement holds for $n \le 3,$ because ${\mathfrak {S}}_n(132; 123) = 222.$ Now, suppose for the sake of contradiction that $n \ge 4$ and that there is no $1\le i \le n-3$ such that $|\textrm{Ac}_{i}(\pi ; 123)| = \mathfrak |\textrm{Ac}_{i+1}(\pi ; 123)| \le |\textrm{Ac}_{i+2}(\pi ; 123)|.$ Then, since ${\mathfrak {S}}_{n}(\pi ; 123) = |\textrm{Ac}_{1}(\pi ; 123)| {\mathfrak {S}}_{n}(\textrm{small}_{n-1}(\pi ); 123),$ we have that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(132^{\star })$ from the inductive hypothesis. Now, $\pi \in \textrm{Av}_{n}(123) {\setminus } \textrm{Av}_{n}(132^{\star })$, but $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n}(132^{\star })$, and so $\textrm{ind}_{\pi }(n) = \textrm{ind}_{\pi }(n-1)-1 > 1$.

Now, $|\textrm{Ac}_{1}(\pi ; 123)| = \textrm{ind}_{\pi }(n)$ from Lemma 3.9. Similarly, $|\textrm{Ac}_{2}(\pi ; 123)| = \textrm{ind}_{\textrm{small}_{n-1}(\pi )}(n-1) = \textrm{ind}_{\pi }(n)$ from Lemma 3.9 on $\textrm{small}_{n-1}(\pi )$. Therefore, $|\textrm{Ac}_{1}(\pi ; 123)| = |\textrm{Ac}_{2}(\pi ; 123)|$. Now, because $\pi \in \textrm{Av}_{n}(123)$, the substring $\pi _{[1,\textrm{ind}_{\pi }(n)-1]}$ must be decreasing. Thus, for all $1 \le j \le \textrm{ind}_{\pi }(n)-1$, it must be that $\pi _j+j \le n-1$. Therefore, for each $1 \le j \le \textrm{ind}_{\pi }(n)-1$, if $\pi _j + j \ne n-1$, then $\pi _j \le n-2-j$. Thus, $n-2-j + \textrm{ind}_{\pi }(n-2-j) \ne n-1$ and by Lemma 3.9, $|\textrm{Ac}_{3}(\pi ; 123)| \ne j$. Thus, $|\textrm{Ac}_{3}(\pi ; 123)| \ge |\textrm{Ac}_{1}(\pi ; 123)| = |\textrm{Ac}_{2}(\pi ; 123)|$. $\square$

Now, propositions 3.10 and 3.11 characterize $\textrm{Av}_{n} (123, 132^{\star })$.

Theorem 3.12

For $\pi \in \textrm{Av}_{n}(123)$, there exists some $1 \le i \le n-2$ such that ${\mathfrak {S}}_{n}(\pi ; 123)_{i} = {\mathfrak {S}}_{n}(\pi ; 123)_{i+1} \le {\mathfrak {S}}_{n}(\pi ; 123)_{i+2}$ if and only if $\pi \not \in \textrm{Av}_{n}(132^{\star })$.

Let us now turn our attention to $\textrm{Av}_{n}(132, 123^{\star })$. We shall replicate the approach used for $\textrm{Av}_n(123,132^{\star })$ to obtain an analogous characterization of permutations in $\textrm{Av}_n(132)$ that contain $123^{\star }$.

Lemma 3.13

If $\pi \in \textrm{Av}_{n}(132, 123^{\star })$, then $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(132, 123^{\star })$.

Proof

It is clear that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(132)$. It thus suffices to show that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123^{\star })$. Suppose otherwise. Because $\pi \in \textrm{Av}_{n}(123^{\star })$, the $123^{\star }$ pattern in $\textrm{small}_{n-1}(\pi )$ must be $\textrm{small}_{n-1}(\pi )_{j} \textrm{small}_{n-1}(\pi )_{\textrm{ind}_{\pi }(n)-1} \textrm{small}_{n-1}(\pi )_{\textrm{ind}_{\pi }(n)}$ for some $j < \textrm{ind}_{\pi }(n)-1$. However, then $\pi _{j} n \textrm{small}_{n-1}(\pi )_{\textrm{ind}_{\pi }(n)}$ is a 132 pattern in $\pi$—a contradiction to $\pi \in \textrm{Av}_{n}(123, 132^{\star })$. $\square$

Given $\pi \in \textrm{Av}_{n}(132)$, we express $\textrm{Ac}_{1}(\pi ; 132)$ in terms of $\textrm{Ac}_{2}(\pi ; 132)$.

Lemma 3.14

If $\pi \in \textrm{Av}_{n}(132)$, then

$$\begin{aligned} \textrm{Ac}_{1}(\pi ; 132) =\{i \mid i-1 \in \textrm{Ac}_{2}(\pi ; 132) \cap [\textrm{ind}_{\pi }(n), n]\} \cup \{ 1\}. \end{aligned}$$

Proof

It is clear that $i \in \textrm{Ac}_{1}(\pi ; 132)$ if and only if $\{\pi _{[1, i-1]}\} = [n-i+2,n]$. Thus, if $i \le \textrm{ind}_{\pi }(n)$, then $i \in \textrm{Ac}_{1}(\pi ; 132)$ if and only if $i = 1$. But, if $\textrm{ind}_{\pi }(n) + 1 \le i$, then $\{\pi _{[1,i-1]}\} = [n-i+2, n]$ if and only if $\{\textrm{small}(\pi )_{[1, i-2]}\} = [n-i+2, n-1]$ if and only if $i-1 \in \textrm{Ac}_{2}(\pi ; 132)$. $\square$

The following results are the analogues of propositions 3.10 and 3.11 for the 132 pattern.

Proposition 3.15

If $\pi \in \textrm{Av}_n(132)$ and $|\textrm{Ac}_{i}(\pi ; 132)| = |\textrm{Ac}_{i+1}(\pi ; 132)| \le |\textrm{Ac}_{i+2}(\pi ; 132)|$ for some $1 \le i \le n-2$, then $\pi \not \in \textrm{Av}_n(123^{\star }).$

Proof

We induct on n; it is easy to see that the statement holds for $n \le 3$. Now, because ${\mathfrak {S}}_{n}(\pi ; 132) = |\textrm{Ac}_{1}(\pi ; 132)| {\mathfrak {S}}_{n}(\textrm{small}_{n-1}(\pi ; 132))$, if $n \ge 4$ and $2 \le i \le n-2$, then by Lemma 3.13 and the inductive hypothesis, $\pi \not \in \textrm{Av}_{n}(123^{\star })$. Thus, assume $i = 1$.

Now, if $\pi _1 = n,$ then by Lemma 3.14, $|\textrm{Ac}_{1}(\pi ; 132)| = |\textrm{Ac}_{2}(\pi ; 132)| +1$. Similarly, if $\pi _1 = n-1,$ then $|\textrm{Ac}_2(\pi ; 132)| = |\textrm{Ac}_3(\pi ; 132)| +1$ by Lemma 3.14 on $\textrm{small}_{n-1}(\pi )$. Thus, $\pi _1 \le n-2.$ Now, n appears to the right of $n-1$ in $\pi$, because $\pi \in \textrm{Av}_n(132)$ and $\pi _1 \le n-2$. Furthermore, $\pi \in \textrm{Av}_{n}(132)$ implies that $\{\pi _{[1, \textrm{ind}_{\pi }(n-1)]}\} = [n-\textrm{ind}_{\pi }(n-1),n-1]$ and $\{\pi _{[1, \textrm{ind}_{\pi }(n)]}\} = [n-\textrm{ind}_{\pi }(n),n]$. Thus, if $(n-1) n$ is not a substring of $\pi ,$ then $\{\textrm{ind}_{\pi }(n-1)+1, \textrm{ind}_{\pi }(n)\} \in \textrm{Ac}_2(\pi ; 132)$, from which it follows that $\textrm{Ac}_1(\pi ; 132) \le \textrm{Ac}_2(\pi ; 132) - 1$ by Lemma 3.14. Thus, $\pi \notin \textrm{Av}_n(123^{\star }),$ because $\pi _1 (n-1) n$ is a $123^{\star }$ pattern of $\pi .$ $\square$

Proposition 3.16

If $\pi \in \textrm{Av}_n(132) {\setminus } \textrm{Av}_{n}(123^{\star })$, then for some $1 \le i \le n-2$, it holds that $|\textrm{Ac}_{i}(\pi ; 132)| = \mathfrak |\textrm{Ac}_{i+1}(\pi ; 132)| \le |\textrm{Ac}_{i+2}(\pi ; 132)|$.

Proof

We induct on n; the statement holds for $n \le 3,$ because ${\mathfrak {S}}_n(123; 132) = 222.$ Now, suppose that $n \ge 4$ and suppose for the sake of contradiction that there is no i such that $|\textrm{Ac}_{i}(\pi ; 132)| = \mathfrak |\textrm{Ac}_{i+1}(\pi ; 132)| \le |\textrm{Ac}_{i+2}(\pi ; 132)|.$ Then, since ${\mathfrak {S}}_{n}(\pi ; 132) = |\textrm{Ac}_{1}(\pi ; 132)| {\mathfrak {S}}_{n}(\textrm{small}_{n-1}(\pi ); 132),$ we have that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123^{\star })$ from the inductive hypothesis. Now, $\pi \in \textrm{Av}_{n}(132) {\setminus } \textrm{Av}_{n}(123^{\star })$ but $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n}(123^{\star })$, and so $\textrm{ind}_{\pi }(n-1) = \textrm{ind}_{\pi }(n)-1 > 1$.

Now, because $\textrm{ind}_{\pi }(n-{\!}1) {\!}= {\!}\textrm{ind}_{\pi }(n){\!}-{\!}1$, it holds that $\textrm{Ac}_{2}(\pi ; 132) {\setminus } [\textrm{ind}_{\pi }(n), n] {\!}={\!} \{1\}$. Therefore, $|\textrm{Ac}_{1}(\pi ; 132)| =|\{i \mid i-1 \in \textrm{Ac}_{2}(\pi ; 132) \cap [\textrm{ind}_{\pi }(n), n]\}| +1 = |\textrm{Ac}_{2}(\pi ; 132)|$ by Lemma 3.14. Furthermore, because $\textrm{ind}_{\pi }(n-1) > 1$, it follows from Lemma 3.14 that $|\textrm{Ac}_{2}(\pi ; 132)|=|\{i \mid i-1 \in \textrm{Ac}_{3}(\pi ; 132) \cap [\textrm{ind}_{\pi }(n-1), n-1]\} \cup \{1\}| \le |\textrm{Ac}_{3}(\pi ; 132)|$. Now, $|\textrm{Ac}_{1}(\pi ; 123)| = |\textrm{Ac}_{2}(\pi ; 123)| \le |\textrm{Ac}_{3}(\pi ; 123)|$—a contradiction as sought. $\square$

Once again, we obtain a characterization of $\textrm{Av}_n(132, 123^{\star })$.

Theorem 3.17

For $\pi \in \textrm{Av}_{n}(132)$, there exists some $1 \le i \le n-2$ such that ${\mathfrak {S}}_{n}(\pi ; 132)_{i} = {\mathfrak {S}}_{n}(\pi ; 132)_{i+1} \le {\mathfrak {S}}_{n}(\pi ; 132)_{i+2}$ if and only if $\pi \not \in \textrm{Av}_{n}(123^{\star })$.

As an immediate corollary of Theorems 3.12 and 3.17, West’s bijection maps $\textrm{Av}_{n}(123, 132^{\star })$ to $\textrm{Av}_{n}(132, 123^{\star })$. We state this in the following theorem.

Theorem 3.18

West’s bijection [15] bijects $\textrm{Av}_{n}(123, 132^{\star })$ and $\textrm{Av}_{n}(132, 123^{\star })$. Therefore,

$$\begin{aligned} |\textrm{Av}_{n}(123, 132^{\star })|=|\textrm{Av}_{n}(132, 123^{\star })|. \end{aligned}$$

We are now able to give a generating function for the sequence $|\textrm{Av}_{n}(132, 123^{\star })|$. Let

$$\begin{aligned} f_{n} = |\{\pi \in \textrm{Av}_{n}(132) \mid \textrm{ind}_{\pi }(n)-1 = \textrm{ind}_{\pi }(n-1) > 1, \textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123^{\star })\}|, \end{aligned}$$

and let $g_{n} = |\textrm{Av}_{n}(132, 123^{\star })|$.

Lemma 3.19

For all $n\ge 2$, it holds that $f_n = g_{n-1}-g_{n-2}$.

Proof

It is straightforward from the definitions of $f_n$ and $g_n$ that

$$\begin{aligned} f_n&= |\{\pi \in \textrm{Av}_{n}(132) \mid \textrm{ind}_{\pi }(n)-1 = \textrm{ind}_{\pi }(n-1), \textrm{small}_{n-1} (\pi ) \in \textrm{Av}_{n-1}(123^{\star })\}| \\&\quad - |\{\pi \in \textrm{Av}_{n}(132) \mid \pi _1 = n-1, \pi _2 = n, \textrm{small}_{n-2}(\pi ) \in \textrm{Av}_{n-2}(123^{\star })\}| \\ {}&= |\{\pi \in \textrm{Av}_{n-1}(132) \mid \pi \in \textrm{Av}_{n-1}(123^{\star })\}| - |\{\pi \in \textrm{Av}_{n-2}(132) \mid \pi \in \textrm{Av}_{n-2}(123^{\star })\}| \\&= |\textrm{Av}_{n-1}(132, 123^{\star })| - |\textrm{Av}_{n-2}(132, 123^{\star })| =g_{n-1}-g_{n-2}. \quad \end{aligned}$$

$\square$

Next, we give another recursive relation between $f_n$ and $g_n$.

Lemma 3.20

For $n \ge 2$, it holds that $g_{n-1} g_{0} + g_{n-2} g_{1} + \cdots + g_{0}g_{n-1} = g_{n} + f_{n}$.

Proof

For each $\pi \in \textrm{Av}_{n}(132)$ such that $\textrm{small}_{n-1}(\pi ) \in \textrm{Av}_{n-1}(123^{\star })$, either $\pi \in \textrm{Av}_{n}(123^{\star })$ or $\textrm{ind}_{\pi }(n)-1 = \textrm{ind}_{\pi }(n-1) > 1$. Thus,

$$\begin{aligned} f_n + g_n = |\{\pi \in \textrm{Av}_n(132) \mid \textrm{small}_{n-1} (\pi ) \in \textrm{Av}_{n-1}(123^{\star })\}|. \end{aligned}$$

At the same time, for each $0 \le i \le n-1$,

$$\begin{aligned} g_{i} g_{n-1-i}&= |\{\pi _{[1, i]} + (i+1-n) \in \textrm{Av}_{i}(132) \mid \pi _{[1, i]} + (i+1-n) \in \textrm{Av}_{i}(123^{\star })\}| \\&\quad |\{\pi _{[i+2, n]} \in \textrm{Av}_{n-1-i}(132) \mid \pi _{[i+2, n]} \in \textrm{Av}_{n-1-i}(123^{\star })\}| \\ {}&= |\{\pi \in \textrm{Av}_n(132) \mid \textrm{small}_{n-1} (\pi ) \in \textrm{Av}_{n-1}(123^{\star }), \pi _{i+1} = n\}|. \end{aligned}$$

Therefore, $\sum _{i=0}^{n-1} g_{i} g_{n-1-i} = |\{\pi \in \textrm{Av}_n(132) \mid \textrm{small}_{n-1} (\pi ) \in \textrm{Av}_{n-1}(123^{\star })\}| = f_n + g_n$. $\square$

The main result of this section, Theorem 1.1, follows immediately.

Proof of Theorem 1.1

By Theorems 3.7 and 3.18, $|\textrm{Sort}_{n}(132, 321)| = |\textrm{Av}_{n}(123, 132^{\star })| = |\textrm{Av}_{n}(132, 123^{\star })|$. Now, let $G(z)=\sum _{n\ge 0}g_nz^n$. By Lemmas 3.19 and 3.20,

$$\begin{aligned} g_n+g_{n-1}-g_{n-2}=\sum _{i=0}^{n-1}g_ig_{n-1-i}, \end{aligned}$$

from which

$$\begin{aligned} G(z)-z-1+z(G(z)-1)-z^2G(z)&= zG(z)^2-z \\ \iff \ zG(z)^2+(z^2-z-1)G(z)+z+1&=0. \end{aligned}$$

Thus,

$$\begin{aligned} G(z) = \frac{(1+z-z^2) - \sqrt{1-2z-5z^2-2z^3+z^4}}{2z} \end{aligned}$$

is the generating function for $g_n = |\textrm{Av}_{n}(132, 123^{\star })| = |\textrm{Sort}_{n}(132, 321)|$. $\square$

3.1 A Bijection with Pattern-Avoiding Dyck Paths

The OEIS A102407 [14] counts the set of Dyck paths of semilength n that do not contain the word dudu as a factor. We give an alternative proof of Theorem 1.1 by showing that $\textrm{Av}_n(123,132^{\star })$ is in bijection with this set of Dyck paths. We sketch the construction below and leave the details to the reader.

A Dyck path is a path in the discrete plane ${\mathbb {Z}}\times {\mathbb {Z}}$ starting at the origin, ending on the $\pi$-axis, never falling below the $\pi$-axis and using two kinds of steps—up steps $u=(1,1)$ and down steps $d=(1,-1)$. The semilength of a Dyck path is the total number of its up steps, which is also the number of its down steps.

The ltr-min decomposition of a permutation $\pi$ with ltr minima $m_1,m_2,\dots ,m_k$ is

$$\begin{aligned} \pi =m_1B_1m_2B_2\cdots m_kB_k, \end{aligned}$$

where $B_j$ contains the entries between two ltr minima $m_j$ and $m_{j+1}$ for $1 \le j\le k-1$, and $B_k$ contains the entries to the right of $m_k$. The ltr-minima decomposition of $\pi$ induces a grid decomposition [8] of $\pi$, in which

$$\begin{aligned} H_i=\left\{ \rho \in \{ 1,2,\ldots ,n\}:m_i< \rho < m_{i-1} \right\} \end{aligned}$$

is the i-th horizontal strip of $\pi$ (note, $m_0=+ \infty$), and $B_j$ is the j-th vertical strip of $\pi$. For any two indices i, j, the cell of indices i, j of $\pi$ is $C_{i,j}=H_i\cap B_j$. It is clear that $C_{i,j} = \emptyset$ if $i>j$. The grid decomposition of $\pi =8 \,11 \,6 \,10 \,4 \,9 \,7 \,5 \,3 \,1 \,2$ is depicted in Fig. 4. We first prove that each cell of a 123-avoiding permutation $\pi$ contains at most one number if and only if $\pi$ is also $132^{\star }$-avoiding.

Proposition 3.21

If $\pi \in \textrm{Av}_n(123)$, then $\pi \in \textrm{Av}_{n}(132^{\star })$ if and only if $|C_{i,j}| \le 1$ for all i, j.

Proof

Suppose that $|C_{i,j}| \ge 2$. We prove that $\pi$ contains $132^{\star }$. First, the numbers in $B_j$ must all be greater than $m_j$ and appear in decreasing order in $\pi$, because $\pi \in \textrm{Av}_{n}(123)$. Therefore, the two leftmost entries of $\pi$ that are in $C_{i, j}$, say $\pi _{\ell }$ and $\pi _{\ell +1}$, must be adjacent in $\pi$. Similarly, once again since $\pi \in \textrm{Av}(123)$, the numbers in $H_i$ must appear in decreasing order, and thus, $\pi _{\ell }=\pi _{\ell +1}+1$. As a result, $m_i\pi _\ell \pi _{\ell +1}$ is an occurrence of $132^{\star }$ in $\pi$.

Conversely, if $\pi _k \pi _{\ell }\pi _{\ell +1}$ is an occurrence of $132^{\star }$, then neither $\pi _\ell$ nor $\pi _{\ell +1}$ can be an ltr minimum of $\pi$, and thus, $\pi _{\ell }$ and $\pi _{\ell +1}$ are in the same cell. $\square$

As a result, the grid decomposition of a $(123,132^{\star })$-avoiding permutation satisfies the following two properties:

• Each cell $C_{i,j}$ contains at most one point;

• If a cell $C_{i,j}$ is not empty, then all the cells located strictly northeast of $C_{i,j}$ (i.e. all the cells $C_{u,v}$, with $u<i$ and $v>j$) are empty.

Fig. 4

On the left, the grid decomposition of $\pi =8 \,11 \,6 \,10 \,4 \,9 \,7 \,5 \,3 \,1 \,2$. On the right, the corresponding Dyck path (rotated clockwise)

Rotem [9, 13] bijected 321-avoiding permutations with Dyck paths. The Rotem bijection can be reformulated for 123-avoiding permutations by composing the original map with the complement as follows. Let $\pi \in \textrm{Av}_n(123)$. Then, construct a sequence $b=b_1b_2\cdots b_n$ by letting $b_1=n$, and for $i\ge 2$,

$$\begin{aligned} b_i={\left\{ \begin{array}{ll} b_{i-1} &{}\quad \text {if }\pi _i\text { is a ltr minimum of }\pi ;\\ \pi _i-1 &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

For example, the sequence arising from the permutation of Fig. 4

$$\begin{aligned} \pi =8\cdot 11\cdot 6\cdot 10\cdot 4\cdot 9\cdot 7\cdot 5\cdot 3\cdot 1\cdot 2 \quad \text {is}\quad b=11\cdot 10\cdot 10\cdot 9\cdot 9\cdot 8\cdot 6\cdot 4\cdot 4\cdot 4\cdot 1. \end{aligned}$$

Then, represent the sequence b as a bar diagram by drawing a horizontal step of length one starting at $(i-1,b_i)$, for $i=1,\dots ,n$, and then connecting the ending point of each step with the starting point of the following one. The bar diagram of b is illustrated in Fig. 4. Finally, rotate the bar diagram counterclockwise to arrive at a Dyck path. For example, the Dyck path associated with b in Fig. 4 is $udu^2du^2dud^2ud^2u^3d^3ud$.

Now, let $\pi \in \textrm{Av}_n(123)$, and let P be the Dyck path associated with $\pi$ via the reformulated Rotem bijection. Note that P contains dudu as a factor if and only if, in the grid decomposition of $\pi$, the points corresponding to the up steps in the occurrence of dudu lie in the same cell; instead of giving a formal proof of this fact, we refer the reader to Fig. 5. By Proposition 3.21, this is in turn equivalent an occurrence of $132^{\star }$ in $\pi$. In other words, Rotem bijection maps $(123,132^{\star })$-avoiding permutations to Dyck paths that do not contain dudu as a factor; the desired bijection between $\textrm{Sort}_n(132,321)$ and Dyck paths avoiding dudu now follows immediately from Theorem 3.7.

Fig. 5

An occurrence of dudu in (the bar diagram of) a Dyck path corresponds to an occurrence of $132^{\star }$ in the associated permutation

4 The (123, 321)-Machine

In this section, we enumerate the set $\textrm{Sort}_n(123,321)$. A direct computation shows that the sequence $|\textrm{Sort}_n(123,321)|$ for $n\ge 1$ starts with 1, 2, 4, 7. Our goal is to prove that, for $n\ge 5$, this sequence obeys the simple recursion

$$\begin{aligned} |\textrm{Sort}_n(123,321)|=2|\textrm{Sort}_{n-1}(123,321)|. \end{aligned}$$

We start by proving that (123, 321)-sortable permutations avoid 123.

Proposition 4.1

If $\pi \in \textrm{Sort}_n (123,321),$ then $\pi \in \textrm{Av}_n (123)$.

Proof

Suppose otherwise. Let $\pi _i \pi _j \pi _k$ be the lexicographically smallest occurrence of 123 in $\pi$. Note that $\pi _i$ is a ltr minimum. Now, if $\pi _i$ is in the stack when $\pi _k$ enters the stack, $\pi _j \pi _k \pi _i$ is a 231 pattern in $\textrm{s}_{123, 321}(\pi )$, because $\pi _k \pi _j \pi _i$ is a 321 pattern. Thus, by Lemma 2.1, $\pi _i$ must leave the stack before $\pi _k$ enters the stack.

Now, because $\pi _i$ is a ltr minimum, the stack below $\pi _i$ must be decreasing, since the stack is 123-avoiding. But the stack must also be 321-avoiding, so there can be at most two numbers below $\pi _i$ in the stack. Therefore, for $\pi _i$ to leave the stack before $\pi _k$ enters the stack, either $\min \{\pi _{[i+1, k]}\} < \pi _{i}$, or the stack below $\pi _i$ reads $\pi _{b}\pi _{c}$ and $\max \{\pi _{[i+1, k]}\} > \pi _{b}$. In the first case, $\pi _i \pi _{k} \min \{\pi _{[i+1, k]}\}$ is a 231 pattern in $s_{123, 321}(\pi )$, and in the second case, $\pi _{b} \max \{\pi _{[i+1, k]}\} \pi _c$ is a 231 pattern in $s_{123, 321}(\pi )$. Hence, by Lemma 2.1, $\pi \in \textrm{Av}_n (123).$ $\square$

In analogy with what observed after Proposition 3.2, we have

$$\begin{aligned} \textrm{Sort}_n(132,321)=\textrm{Sort}_n(132)\cap \textrm{Av}(123). \end{aligned}$$

The following two results show that if $\pi \in \textrm{Sort}_n(123,321)$, then $\pi _1 \ge n-1$ and $\pi _n \le 2$.

Lemma 4.2

If $\pi \in \textrm{Sort}_n (123,321),$ then $\pi _1 \in \{n-1, n\}$.

Proof

Suppose otherwise. By Proposition 4.1, either $\pi _2 = n$ or $\pi _2 < \pi _1$. If $\pi _2=n$, then $s_{123,321}(\pi )_{[n-1,n]}=n \pi _1$. Therefore, $(n-1) n \pi _1$ is a 231 pattern in $s_{123,321}(\pi )$, and $\pi \not \in \textrm{Sort}_{n}(123, 321)$ by Lemma 2.1. Thus, $\pi _2 < \pi _1$, and as a result, the stack must only contain $\pi _1$ when 1 enters the stack. Then because $\pi _1$ and 1 do not exit the stack until the input permutation is empty, $s_{123,321}(\pi )_{[n-1, n]}= 1 \pi _1$. Furthermore, $s_{123,321}(\pi )_1 = n$, because otherwise, $s_{123,321}(\pi )_1 n 1$ is a 231 pattern in $s_{123,321}(\pi )$, and $\pi \not \in \textrm{Sort}_{n}(123, 321)$ by Lemma 2.1. Now, immediately after n leaves the stack, $\pi _{\textrm{ind}_{\pi }(n)-1}$ must leave the stack, because n cannot be part of a 321 or 123 pattern after the next number in the input permutation enters the stack. By Proposition 4.1, $\pi _{\textrm{ind}_{\pi }(n)-1} \ne n-1$. Thus, $\pi _{\textrm{ind}_\pi (n)-1} (n-1) 1$ is a 231 pattern in $s_{123,321}(\pi )$—a contradiction by Lemma 2.1. $\square$

Lemma 4.3

If $\pi \in \textrm{Sort}_n (123,321)$, then $\pi _n \in \{1, 2\}$.

Proof

Suppose otherwise. By Lemma 4.2, $\pi _1 \in \{n-1, n\}$, and so either $\pi _2 < \pi _1$, or $\pi _{[1,2]} = (n-1) n$. If $\pi _2 < \pi _1$, then the stack must only contain $\pi _1$ when 1 enters the stack. Otherwise, the stack reads $n (n-1)$ when 1 enters the stack. In either case, 1 cannot leave the stack until the input permutation is empty, and so 1 appears to the right of both 2 and $\pi _n$ in $s_{123,321}(\pi )$. Now, 2 must leave the stack before $\pi _n$ enters the stack, because $\pi _n 2 1$ is a 321 pattern. Thus, $2 \pi _n \cdot 1$ is a 231 pattern in $s_{123,321}(\pi )$—a contradiction by Lemma 2.1. $\square$

The positions of 1 and 2 play an important role in our characterization of (123, 321)-sortable permutations. From now on, assume $n\ge 5$. First we show that n appears to the left of 1 and 2 in any $\pi \in \textrm{Sort}_n(123,321)$. A consequence is that 21 must appear as a substring in the output $s_{123,321}(\pi )$ of the (123, 321)-stack.

Lemma 4.4

If $\pi \in \textrm{Sort}_n (123,321)$, then $\textrm{ind}_\pi (n) < \min (\textrm{ind}_\pi (1), \textrm{ind}_\pi (2))$.

Proof

By Lemma 4.2, $\pi _1 \ge n-1$. If $\pi _1=n$, then the claim is immediate. Thus, suppose that $\pi _1=n-1$. By Lemma 4.3, $\pi _n \in \{1,2\}$. Now, for the sake of contradiction, suppose that $\textrm{ind}_\pi (n) > \textrm{ind}_\pi (3-\pi _n)$. Then the stack must only contain $n-1$ when $3-\pi _n$ enters the stack and must read $(3-\pi _n) (n-1)$ when n enters the stack. Then $n (3-\pi _n) (n-1)$ cannot leave the stack until the input permutation is empty. Thus, $3 n (3-\pi _n)$ is a 231 pattern in $s_{123,321}(\pi )$—a contradiction by Lemma 2.1. $\square$

Lemma 4.5

If $\pi \in \textrm{Sort}_{n}(123, 321)$, then $\textrm{ind}_{s_{123,321}(\pi )}(2) = \textrm{ind}_{s_{123,321}(\pi )}(1)-1$.

Proof

By Lemmas 4.2 and 4.3, $\pi _{1} \in \{n-1, n\}$, and $\pi _{n} \in \{1, 2\}$. Therefore, just after $3-\pi _{n}$ enters the stack, the stack reads $(3-\pi _{n}) \pi _1$ or $(3-\pi _{n}) n (n-1)$, and $3-\pi _{n}$ must remain in the stack until $\pi _{[1, n-1]}$ has entered the stack. Furthermore, from Lemma 4.4, n cannot be above $3-\pi _n$ in the stack. Now, if $\pi _{n}= 1$, then $3-\pi _n=2$ must be the last number that leaves the stack before 1 enters the stack; after which, $\pi _n =1$ must leave the stack, because the input permutation is empty. If $\pi _{n} =2$, then $\pi _n=2$ must be right above $3-\pi _n = 1$ when $\pi _n =2$ enters the stack; after which, $\pi _n =2$ and $3-\pi _n =1$ must exit the stack in that order, because the input permutation is empty. $\square$

For the rest of this section, given a permutation $\pi \in S_n$ of length two or more, define $\textrm{swap}(\pi )$ as the permutations obtained from $\pi$ by interchanging 1 and 2. Furthermore, for $1\le i\le n+1$, let $\textrm{inc}_{i}(\pi )$ be the permutation obtained by inserting 1 in the i-th site of $\pi$, and suitably rescaling the other entries. More formally, let

$$\begin{aligned} \textrm{inc}_{i}(\pi )=\pi '_1\cdots \pi '_{i-1} 1 \pi '_{i}\cdots \pi '_n, \end{aligned}$$

where $\pi '_j=\pi _j+1$. For example, $\textrm{inc}_{2}(12543) = 213654$. It follows from the proof of Lemma 4.5 that if $n\ge 5$, then $\textrm{swap}$ preserves $s_{123, 321}(\pi )$ for $\pi \in \textrm{Sort}_{n}(123, 321)$.

Corollary 4.6

If $\pi \in \textrm{Sort}_n (123,321)$, then $s_{123,321}(\pi ) = s_{123,321} (\textrm{swap}(\pi ))$.

To complete our description of $\textrm{Sort}_n(123,321)$, we shall prove that a permutation $\pi$ is (123, 321)-sortable if and only if $\textrm{inc}_{n+1}(\pi )$ is.

Proposition 4.7

It holds that $\pi \in \textrm{Sort}_n (123,321)$ if and only if $\textrm{inc}_{n+1} (\pi ) \in \textrm{Sort}_{n+1} (123,321)$.

Proof

First, suppose that $\pi \in \textrm{Sort}_{n}(123, 321)$. Then by Lemma 2.1, $s_{123, 321}(\pi ) \in \textrm{Av}_{n}(231)$. Now, by Lemma 4.5, $s_{123, 321}(\textrm{inc}_{n+1}(\pi )) = \textrm{inc}_{\textrm{ind}_{\pi }(1)+1}(s_{123, 321}(\pi ))$. Thus, $s_{123, 321}(\textrm{inc}_{n+1}(\pi )) \in \textrm{Av}_{n+1}(231)$, and so $s_{123, 321}(\textrm{inc}_{n+1}(\pi )) \in \textrm{Sort}_{n+1}(123, 321)$ by Lemma 2.1.

Now, suppose that $\pi \not \in \textrm{Sort}_{n}(123, 321)$. Then by Lemma 2.1, $s_{123, 321}(\pi ) \not \in \textrm{Av}_{n}(231)$. Now, $s_{123, 321}(\textrm{inc}_{n+1}(\pi )) \not \in \textrm{Av}_{n}(231)$, for $s_{123, 321}(\pi )+1$ is a substring of $s_{123, 321}(\textrm{inc}_{n+1}(\pi ))$. Thus, $s_{123, 321}(\textrm{inc}_{n+1}(\pi )) \not \in \textrm{Sort}_{n+1}(123, 321)$ by Lemma 2.1. $\square$

Finally, we use Lemmas 4.3, 4.6, and 4.7 to prove Theorem 1.3.

Proof of Theorem 1.3

It is easy to check that the theorem statement holds for $n=4$. Now, by Corollary 4.6, $\pi \rightarrow \textrm{swap}(\pi )$ bijects $\textrm{Sort}_{n} (123, 321)$ to itself for $n \ge 5$. Thus, $|\textrm{Sort}_{n} (123,321)| = 2|\{\pi \in \textrm{Sort}_{n} (123,321) \mid \pi _n = 1\}|$ by Lemma 4.3 for $n \ge 5$. Also, by Proposition 4.7, $\pi \rightarrow \textrm{inc}_{n+1} (\pi )$ bijects $\textrm{Sort}_n (123,321)$ to $\{\pi \in \textrm{Sort}_{n+1} (123,321) \mid \pi _n=1\}$ for $n \ge 5$. Thus, $|\textrm{Sort}_{n}(123, 321)| = 2|\textrm{Sort}_{n-1}(123, 321)|$ for $n \ge 5$ as sought. $\square$

5 Future Directions

In addition to the statement of Theorem 1.1, Baril, Cerbai, Khalil, and Vajnovski [1] conjectured that $|\textrm{Sort}_{n}(132,213)| = |\textrm{Sort}_{n}(213,312)|$ for all $n \ge 1$; the conjecture remains open. Here, we refine their conjecture.

Conjecture 5.1

For any n and $1 \le i \le n$, we have the equidistributions

$$\begin{aligned} |\{\pi \in \textrm{Sort}_{n}(132, 213) \mid \pi _1 = i \}|&= |\{\pi \in \textrm{Sort}_n(213, 312) \mid \pi _1 = i\}| \end{aligned}$$

and

$$\begin{aligned} |\{\pi \in \textrm{Sort}_{n}(132, 213) \mid \pi _i = n \}|&= |\{\pi \in \textrm{Sort}_n(213, 312) \mid \pi _i = n\}|. \end{aligned}$$